Dynamically Consistent Parameterization of Mesoscale Eddies—Part II: Eddy Fluxes and Diffusivity from Transient Impulses

Abstract

This work continues development of the framework for dynamically consistent parameterization of mesoscale eddy effects in non-eddy-resolving ocean circulation models. Here, we refine and extend the previous results obtained for the double gyres and aim to account for the eddy backscatter mechanism that maintains eastward jet extension of the western boundary currents. We start by overcoming the local homogeneity assumption and by taking into account full large-scale circulation. We achieve this by considering linearized-dynamic responses to finite-time transient impulses. Feedback from these impulses on the large-scale circulation are referred to as footprints. We find that the local homogeneity assumption yields only quantitative errors in most of the gyres but breaks down in the eastward jet region, which is characterized by the most significant eddy effects. The approach taken provides new insights into the eddy/mean interactions and framework for parameterization of unresolved eddy effects. Footprints provide us with maps of potential vorticity anomalies expected to be induced by transient eddy forcing. This information is used to calculate the equivalent eddy potential vorticity fluxes and their divergences that partition the double-gyre circulation into distinct geographical regions with specific eddy effects. In particular, this allows approximation of the real eddy effects that maintain the eastward jet extension of the western boundary currents and its adjacent recirculation zones. Next, from footprints and their equivalent eddy fluxes and from underlying large-scale flow gradients, we calculate spatially inhomogeneous and anisotropic eddy diffusivity tensor. Its properties suggest that imposing parameterized source terms, that is, equivalent eddy flux divergences, is a better parameterization strategy than implementation of the eddy diffusion.

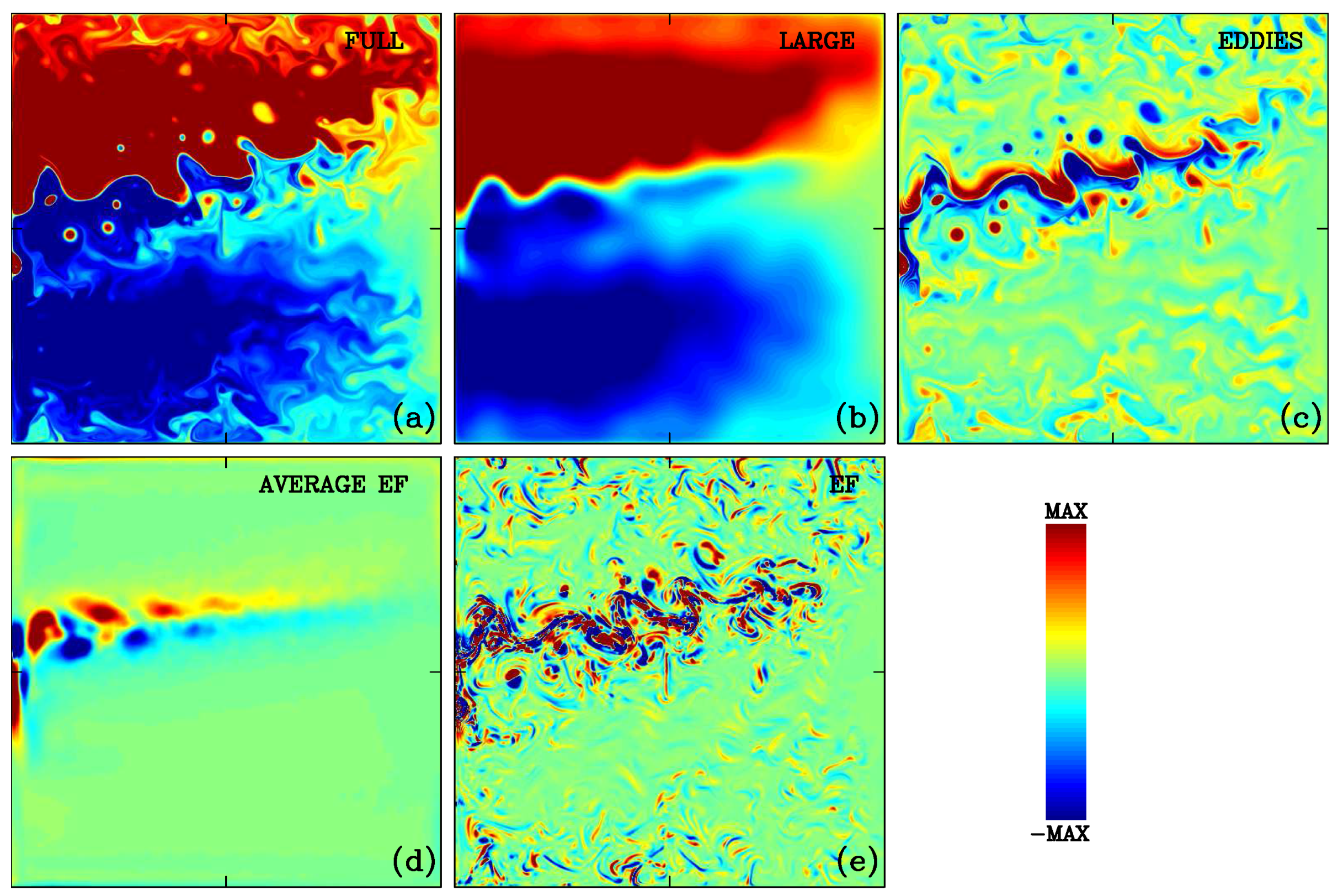
1. Introduction

Mesoscale oceanic eddies populate nearly all parts of the global ocean and play important roles in maintaining the oceanic general circulation (e.g., [1]). The most straightforward, but also the most computationally intensive and, thus, unfeasible, way of accounting for the eddy effects on the large-scale circulation is by resolving them dynamically with eddy-resolving ocean general circulation models (OGCMs). This brute-force approach requires computational grids with nominal resolution of about 1 km, which makes it feasible only for relatively short-time simulations, whereas the Earth system and climate modelling routinely require multiple and much longer simulations over centuries and millenia. The only way to afford these time scales is to parameterize the important eddy effects with simple and affordable but nevertheless accurate models embedded in non-eddy-resolving OGCMs. In this context, an eddy parameterization is a parametric mathematical model for use in some coarse-grained, reduced-dynamics ocean circulation models. Ideally, parameters involved are to be related to the explicitly resolved, large-scale circulation properties, thus resulting in a turbulence closure for the eddy scales. Over the last few decades, the search for suitable eddy parameterizations has remained a challenging theoretical topic with a clear practical dimension.

Development of mesoscale eddy parameterizations can be also viewed as a strategy for advancing our knowledge about the eddy dynamics and eddy/large-scale flow interactions. The prevailing approach strives to find some sort of diffusive closure for the eddy transport, assuming that eddies transport the corresponding flow property down its large-scale gradient and along isopycnals. In this sense, all ocean models implement eddy viscosity (e.g., Laplacian or biharmonic) for downgradient diffusion of momentum. Many models also implement eddy buoyancy diffusion [2], which simulates real effects of the baroclinic instability on large-scale currents and, thus, substantially improves model solutions in many parts of the global ocean. The baroclinic instability effects can be also parameterized in terms of large vertical viscosity in the momentum equations [3,4]. Eddy diffusion of potential vorticity is another parameterization approach [5,6], but its closure and ultimate implementations in OGCMs remain to be worked out. Along these lines, Eden [7] argued that, for some flows, eddy diffusivities of buoyancy and potential vorticity (PV) can be identical, but for general flows this is not true [8].

Most of the diffusive parameterization theories focus on either estimating various eddy diffusivities from data (e.g., [9,10]) or deriving eddy diffusivities from the large-scale flow properties. Several ideas were proposed for the latter. The classical idea is to relate linearly eddy diffusivity and local strain rate tensor of the large-scale flow [11], but this approach is phenomenological, and there is no theory for the linear coefficient involved. One idea is to find eddy diffusivity from the most unstable normal mode of the locally homogeneous linear-stability analysis (e.g., [12,13]). This can be interpreted as the single-wavenumber approach, and it was recently extended to incorporate a band of wavenumbers [14]. The other idea is that an eddy diffusivity coefficient can be found by assuming that the relevant time scale is given by the Eady growth rate, which in turn depends on the local stratification and magnitude of the large-scale vertical shear [15]. This can be viewed as an f-plane argument that does not take into account the planetary PV gradient and its orientation relative to the large-scale velocity and its shear. There are also eddy diffusivity theories for horizontally homogeneous flows [16], but their applicability to inhomogeneous flows is unclear. Another idea for deriving an eddy diffusivity closure is that a fully developed equilibrium state of the baroclinic turbulence is characterized by the comparable growth rates of primary and secondary instabilities of the large-scale flow patterns [17]. Finally, various spectral homogeneous-turbulence diffusivity approaches (e.g., [18]) base derivation of scale-dependent eddy diffusivity on the existence of a universal turbulent energy spectrum and on the mixing-length arguments; therefore, they do not apply to oceanic mesoscale eddies that are spatially inhomogeneous and exhibit no universal spectra.

Eventually, eddy diffusivities must be somehow derived from the flow dynamics, but until this happens, one can try at least to constrain the involved eddy diffusivities by the physical conservation laws assumed by the underlying dynamics. There were several studies introducing energy and momentum conservation constraints [19,20,21,22], but each approach takes into account conservation of a quadratic quantity at the expense of solving a dynamical prognostic equation for its evolution. This equation involves its own assumptions and approximations. It is argued that taking into account horizontal and vertical variations, as well as anisotropy of eddy diffusivities should be a high priority (e.g., [8,9]), but it remains unclear to what extent these factors can be captured along with assuming local flow homogeneity. Alternatively, one can assume specific spatial patterns of the eddy diffusivity (e.g., [23]), but this approach remains to be generalized. Finally, it remains unclear what to do with negative eddy diffusivities that arise from common situations with upgradient eddy fluxes [24] and make the whole eddy diffusion model ill-posed. Along this line, Jansen [25] proposed parameterizing upscale energy transfers by the negative Laplacian eddy viscosity stabilized by the additional hyperviscosity. Overall, relatively few studies propose abandoning the diffusion and look for other frameworks.

An emerging theoretical alternative to the diffusion is to account for the negative-diffusion eddy effects by imposing random forcing that induces upscale energy transfers and flow rectification. The forcing randomness is justified by highly transient and structurally complicated patterns of the actual eddy fluxes (e.g., [26,27,28]). First studies of this kind were made within the classical homogeneous-turbulence approach (e.g., [29,30,31]), and only more recent studies are spatially inhomogeneous (e.g., [32,33,34]). Determining random forcing, deriving its parameters and relating them to the large-scale flow remains to be done. So far, construction of random forcing is achieved by fitting patterns from the eddy-resolving simulations (e.g., [35,36]).

Another way to overcome problems of the diffusion approach is to solve explicitly some intermediate-complexity dynamical model for the momentum, buoyancy or PV ([37] (hereafter B15), [38] (hereafter G15)). In G15, the intermediate-complexity model relied on the local homogeneity assumption. It was driven by spatially correlated white-noise stochastic forcing, under assumption that the damping rates are consistent with $k^{-5/3}$ and $k^{-3}$ turbulent energy spectra for the long and short length scales, respectively. Here, parameters controlling the damping rates and stochastic-forcing structural properties remain to be justified and constrained. Choice of the applied time-averaging interval is another concern because intermediate-complexity model possesses modes that are linearly unstable and exponentially growing in time. Although the intermediate dynamics require extra computational costs, they can be alleviated by pre-computing the solutions for all possible configurations of the large-scale flow. The B15 study offers another direct dynamical approach, which is a precursor of this paper. This approach is based on analysis of the linear-dynamics responses to spatially localized, periodic forcing functions representing an elementary eddy flux divergence and referred to as transient impulses or plungers. Note that spatially localized forcing is very different from the classical spectral random forcing because it involves many phase-correlated Fourier harmonics with different wavenumbers. The plunger effectively rearranges PV and induces permanent changes of the background flow ([39,40,41,42]). In B15, the plunger effect is interpreted in terms of its footprint (i.e., large-scale feedback) that strongly depends on the underlying large-scale flow—this dependence provides the vital link for the eddy parameterization closure.

We start by introducing the model and its solution, and by explaining the relationship between transient impulses and the eddy backscatter mechanism that is responsible for maintaining the eastward jet and its adjacent recirculation zones. Then, we extend B15 results in two main directions. First, we overcome the local homogeneity assumption and demonstrate its consequences. This is achieved by considering full background flow and finite-time, rather than periodic, transient forcing impulses. Second, we use the upgraded plunger-footprint analyses to derive the dynamically consistent, anisotropic, and spatially inhomogeneous, equivalent eddy diffusivity tensor that incorporates information about the eddy backscatter. On the one hand, the eddy diffusivity map provides a new and powerful tool for understanding the eddy effects. On the other hand, the corresponding equivalent eddy fluxes can be used directly as the simple source term parameterizing the eddies. In Section 2, we describe the ocean model, the reference eddy-resolving solution and the eddy backscatter mechanism, as well as the linearized model and formulation of transient impulses. We present the main results in Section 3, followed by the discussion and conclusions in Section 4.

2. Statement of the Problem

2.1. Ocean Model

The dynamical model and its reference solution are adopted from B15; therefore, we discuss them briefly. The classical double-gyre quasigeostrophic PV model representing wind-driven midlatitude ocean gyres is configured in a flat-bottom square basin with three stacked isopycnal layers. The governing equations for the PV anomalies $q_i$ and velocity streamfunctions ${\psi }_i$ are

$$\begin{array}{ccc}\hfill \frac{\partial q_1}{\partial t}+J({\psi }_1,q_1)+\beta \frac{\partial {\psi }_1}{\partial x}& =& \frac{1}{{\rho }_1{H}_1}W+\nu {\nabla }^4{\psi }_1,\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill \frac{\partial q_2}{\partial t}+J({\psi }_2,q_2)+\beta \frac{\partial {\psi }_2}{\partial x}& =& \nu {\nabla }^4{\psi }_2,\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill \frac{\partial q_3}{\partial t}+J({\psi }_3,q_3)+\beta \frac{\partial {\psi }_3}{\partial x}& =& -\gamma {\nabla }^2{\psi }_3+\nu {\nabla }^4{\psi }_3,\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill q_1& =& {\nabla }^2{\psi }_1+S_1({\psi }_2-{\psi }_1),\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill q_2& =& {\nabla }^2{\psi }_2+S_{21}({\psi }_1-{\psi }_2)+S_{22}({\psi }_3-{\psi }_2),\hfill \end{array}$$

(5)

$$\begin{array}{ccc}\hfill q_3& =& {\nabla }^2{\psi }_3+S_3({\psi }_2-{\psi }_3),\hfill \end{array}$$

(6)

where the layer index starts from the top, and $J(,)$ is the Jacobian operator. The basin size is $2L=3840$ km, so that $-L\le x\le L,$ and $-L\le y\le L;$ the layer depths are $H_1=250$ m, $H_2=750$ m, and $H_3=3000$ m; ${\rho }_1={10}^3$ kg·m⁻³ is the upper layer density; $\beta =2\times {10}^{-11}$ m⁻¹·s⁻¹ is the planetary vorticity gradient; $\nu =20$ m²·s⁻¹ is the eddy viscosity; $\gamma =4\times {10}^{-8}$ s⁻¹ is the bottom friction; and the stratification parameters $S_1,S_{21},S_{22}$ and $S_3$ are chosen so that the first and second Rossby deformation radii are $R{d}_1=40$ km and $R{d}_2=20.6$ km, respectively. The prescribed steady Ekman pumping $W(x,y)$ is the only external forcing. The layer-wise model equations are augmented with the partial-slip lateral-boundary conditions and mass conservation constraints and solved by the high-resolution numerical algorithm [43] on the uniform ${513}^2$ grid with 7.5 km nominal resolution.

2.2. Reference Solution and Eddy Backscatter

The time-mean circulation and instantaneous snapshot shown in Figure 1 illustrate the double-gyre circulation and its well-developed eastward jet extension of the western boundary currents. The mean-flow kinetic energy is concentrated in the western boundary currents and the eastward jet, whereas the potential energy is stored in the gyres; it is shown further below that these fields are poorly correlated with the transient eddy forcing; therefore, they can not be used for scaling the linearized model solutions. We also show (Figure 1g–l) the time-mean PV anomaly gradient that will be used for estimating the eddy diffusivity. Away from the western boundary currents, the largest absolute values of the upper-ocean gradient are concentrated around the eastward jet and dominated by the meridional gradient component—this is the region where the local homogeneity assumption, assessed further below, is most likely problematic. In the deep ocean, the gradient has larger values near the basin boundaries rather than around the eastward jet. We also show absolute value of the upper-ocean PV flux (Figure 1m), which was used in B15 for scaling the linear solutions, and argue that it provides scaling which is relatively poor, though noticeably better than scaling by the mean-flow energy.

The reference solution is characterized by vigorous eddy fields that can be defined relative to either time-mean background flow (Figure 1a–c) or a low-pass, temporally evolving flow components. Although, in both cases, point-wise statistics of the eddies are qualitatively similar, only the latter flow decomposition illustrates the eddy backscatter mechanism (e.g., [26,32]) that maintains the eastward jet and its adjacent recirculation zones via positive correlations between the transient eddy forcing and the large-scale eastward jet. In order to illustrate fundamental properties of the backscatter, we spatially low-pass PV anomaly of the reference flow solution by a flat, $300\times 300$ km running-average filter centered on the reference point. In the vicinity of a lateral boundary, we limit the corresponding half-size of the filter by the shortest distance from the reference point to the boundary. Qualitative outcome of the flow decomposition is not sensitive to the filter width, as long as it spans at least several first Rossby deformation radii but remains much shorter than the basin size. We also calculate time average of the high-pass PV anomaly and move it to the low-pass component, so that by construction eddies represented by the high-pass field have zero time-mean. The resulting large-scale and eddy PV components (Figure 2a–c) are inverted to obtain the corresponding velocity streamfunction fields.

Given the flow decomposition, we define the eddy forcing as divergence of the eddy PV flux,

$$E_i(t,x,y)\equiv -\left[\nabla ·{\mathbf{u}}_i{q}_i-\nabla ·\langle {\mathbf{u}}_i\rangle \langle \overline{q_i}\rangle \right],i=1,2,3,$$

(7)

where angle brackets indicate large-scale fields. Eddy forcing is dominated by the upper-ocean part $E_1(t,x,y),$ which has the time-mean $\overline{E_1}$ and transient (i.e., fluctuation) $E_1^{\prime }$ components (Figure 2d,e). Only the time-mean eddy forcing enters the time-mean dynamical balance; therefore, one could erroneously conclude that only the time-mean eddy forcing is needed to maintain the eastward jet. This interpretation would be true only in the situation when the eastward jet stays in its time-mean state; however, as illustrated by Figure 2, this is never the case. In order to estimate actual importances of the eddy forcing components, we focus on the region of about 1/4 of the basin that includes the eastward jet and calculate correlations and covariances between the snapshots of the eddy forcing components and large-scale PV anomalies. We find that time-mean correlations are positive for both $\overline{E_1}$ and $E_1^{\prime };$ the former is about 30% and the latter is about 1%, suggesting that both components support the eastward jet. Although correlation between the jet and $E_1^{\prime }$ is small, the values of the latter are five orders of magnitude larger than those of $\overline{E_1};$ as a result, covariance of the jet with $E_1^{\prime }$ is ${10}^4$ times larger, suggesting that the eddy backscatter mechanism completely dominates over the more familiar effect of the time-mean diverging eddy fluxes. Thus, an adequate eddy parameterization must maintain the eastward jet and its adjacent recirculation zones far beyond the simple implementation of the time-mean eddy fluxes.

Now, let us characterize the eddies in terms of the eddy energy and PV fluxes. We find that the eddy energy is concentrated in a broader region encompassing the eastward jet (Figure 3a,d), and it is approximately equally and uniformly partitioned between the kinetic and potential energy components (not shown). Next, we find standard deviation ${\sigma }_i(x,y)$ of the eddy forcing (Figure 3b,e). Although σ is noticeably similar to the eddy energy (correlations of the corresponding fields around the eastward jet, in the upper, middle and deep layers are 0.92, 0.86 and 0.80, respectively), these fields have significant differences, which increase with depth (Figure 3c,f). Relative to the eddy forcing, the eddy energy is significantly more peaked around the eastward jet, at the expense of smaller values in the interior gyres. This indicates that correlations between the eddy energy and PV anomaly increases away from the eastward jet, thus resulting in more diverging eddy PV fluxes for the same eddy energy. To summarize, further below, we approximate transient eddy forcing by the plunger forcing imposed on the linearized model, but finding appropriate scaling for the plunger amplitudes is somewhat problematic. On the one hand, we have the perfect scaling in terms of ${\sigma }_i(x,y).$ On the other hand, it is not clear how to relate ${\sigma }_i(x,y)$ to the large-scale circulation because spatial correlations between ${\sigma }_i(x,y)$ and such time-mean flow fields, as the absolute value of the upper-ocean PV flux [28], or the mean flow kinetic and potential energies, or absolute value of the PV gradient, are all positive but relatively poor. Relating ${\sigma }_i(x,y)$ to the eddy energy is more justified, though neither perfect nor trivial, and this resonates with other parameterization ideas that are anchored on predicting the eddy energy (e.g., [13,25]). However, finding an accurate prognostic model for prediction of the eddy energy is another problem, well beyond the scope of this study. In what follows below, we circumnavigate this problem by resorting to the perfect scaling of transient impulses by ${\sigma }_1(x,y).$

2.3. Linearized Ocean Model and Transient Impulses

The governing equations are linearized around the time-mean circulation, given by the streamfunction $\Psi (x,y,z)$ and the corresponding PV anomaly $Q(x,y,z),$ and forced by the prescribed transient-impulse (plunger) forcing $P_1$ (restricted, for simplicity, to the upper layer):

$$\begin{array}{ccc}\hfill \frac{\partial q_1}{\partial t}+J({\Psi }_1,q_1)+J({\psi }_1,Q_1)+\beta \frac{\partial {\psi }_1}{\partial x}& =& \frac{1}{{\rho }_1{H}_1}W+\nu {\nabla }^4{\psi }_1+P_1,\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill \frac{\partial q_2}{\partial t}+J({\Psi }_2,q_2)+J({\psi }_2,Q_2)+\beta \frac{\partial {\psi }_2}{\partial x}& =& \nu {\nabla }^4{\psi }_2,\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill \frac{\partial q_3}{\partial t}+J({\Psi }_3,q_3)+J({\psi }_3,Q_3)+\beta \frac{\partial {\psi }_3}{\partial x}& =& -\gamma {\nabla }^2{\psi }_3+\nu {\nabla }^4{\psi }_3.\hfill \end{array}$$

(10)

Following B15, the spatial function of the simple transient impulse (plunger) located at $(x_0,y_0)$ is formulated as:

$$P_1(t,x,y;x_0,y_0)=2.16A\left(t\right)cos\left(\frac{\pi }{2}\frac{r}{r_0}\right),r<r_0,$$

(11)

$$P_1(t,x,y;x_0,y_0)=0,r\ge r_0,$$

(12)

where $r=\sqrt{{(x-x_0)}^2+{(y-y_0)}^2}$ is the distance from the plunger center, and the forcing is concentrated within radius $r_0.$ For brevity, our presentation focuses on the $r_0=60$ km case and on the transient impulses acting in the upper layer only. The time dependence of the transient-impulse forcing is chosen as the following piecewise-linear wavelet-like function,

$$A\left(t\right)=-\frac{t-T}{T}-1,0\le t<\frac{T}{2};A\left(t\right)=\frac{3(t-T)}{T}+1,\frac{T}{2}\le t<T,$$

$$A\left(t\right)=-\frac{3(t-T)}{T}+1,T\le t<\frac{3T}{2};A\left(t\right)=\frac{t-T}{T}-1,\frac{3T}{2}\le t<T,$$

(13)

which consists of the larger impulse surrounded by the pair of weaker opposite-sign impulses, so that the time mean of the function is zero, and, overall, the time interval of the forcing action is $2T.$ Thus, the forcing is no longer harmonic as in B15 and more consistent with the actual transient eddy forcing, but it also can be interpreted as a distributed in space and time version of Green’s function (e.g., [44]) for the linearized dynamics. For brevity, our presentation focuses on $T=50$ days, but we varied T over the range from 45 to 65 days and found that the results are qualitatively similar. The time scale T is fitted from the observed transient eddy forcing, which exhibits decaying and oscillating autocorrelations [32], and the transient impulse choice is the most simple wavelet function exhibiting similar autocorrelations. The main motivation for implementing finite-time impulses is that they are more physical than the periodic ones and do not assume temporal homogeneity. Each plunger-induced solution of the linearized model is obtained from zero initial conditions over the time interval $2T$ and saved for further analyses.

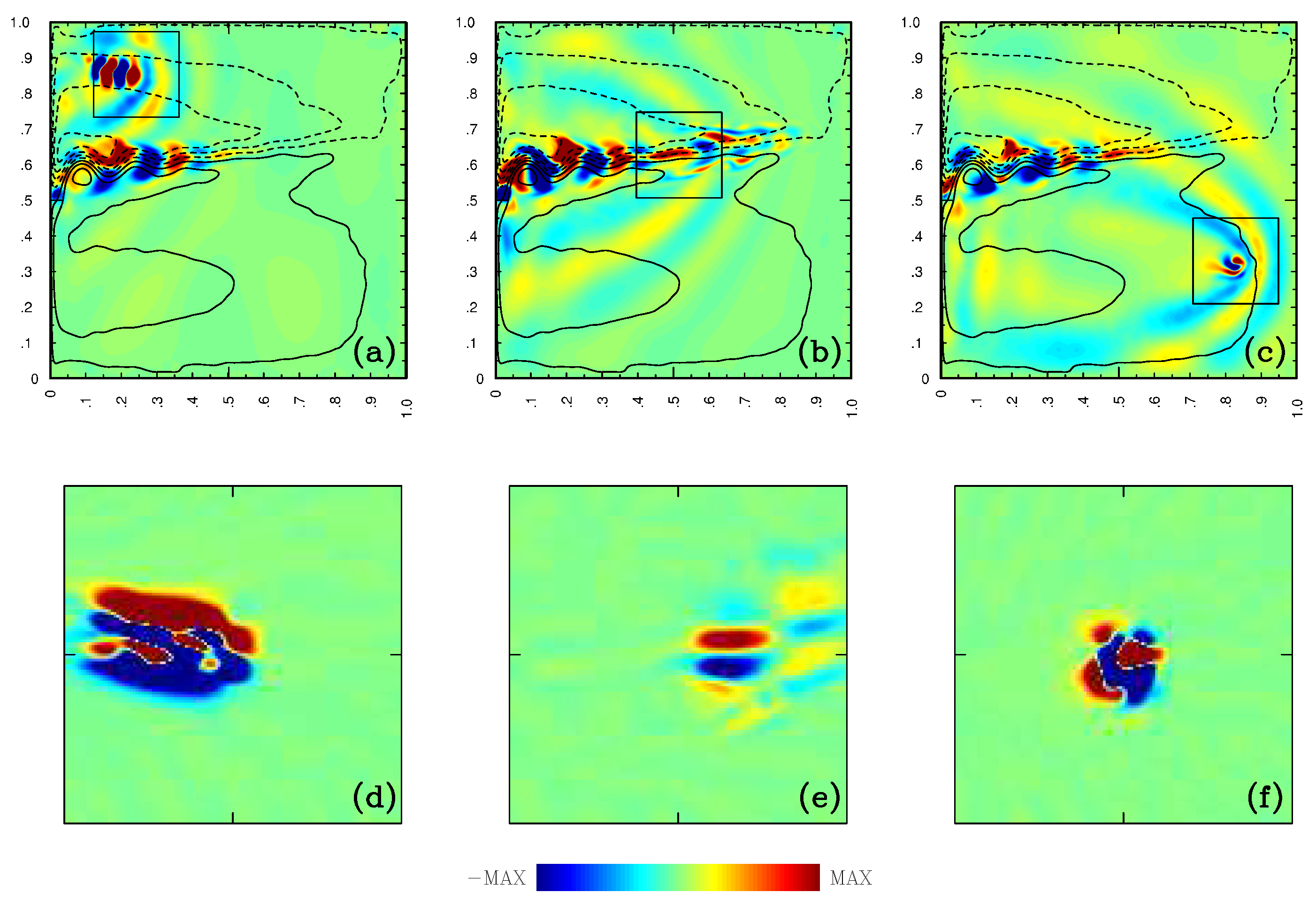
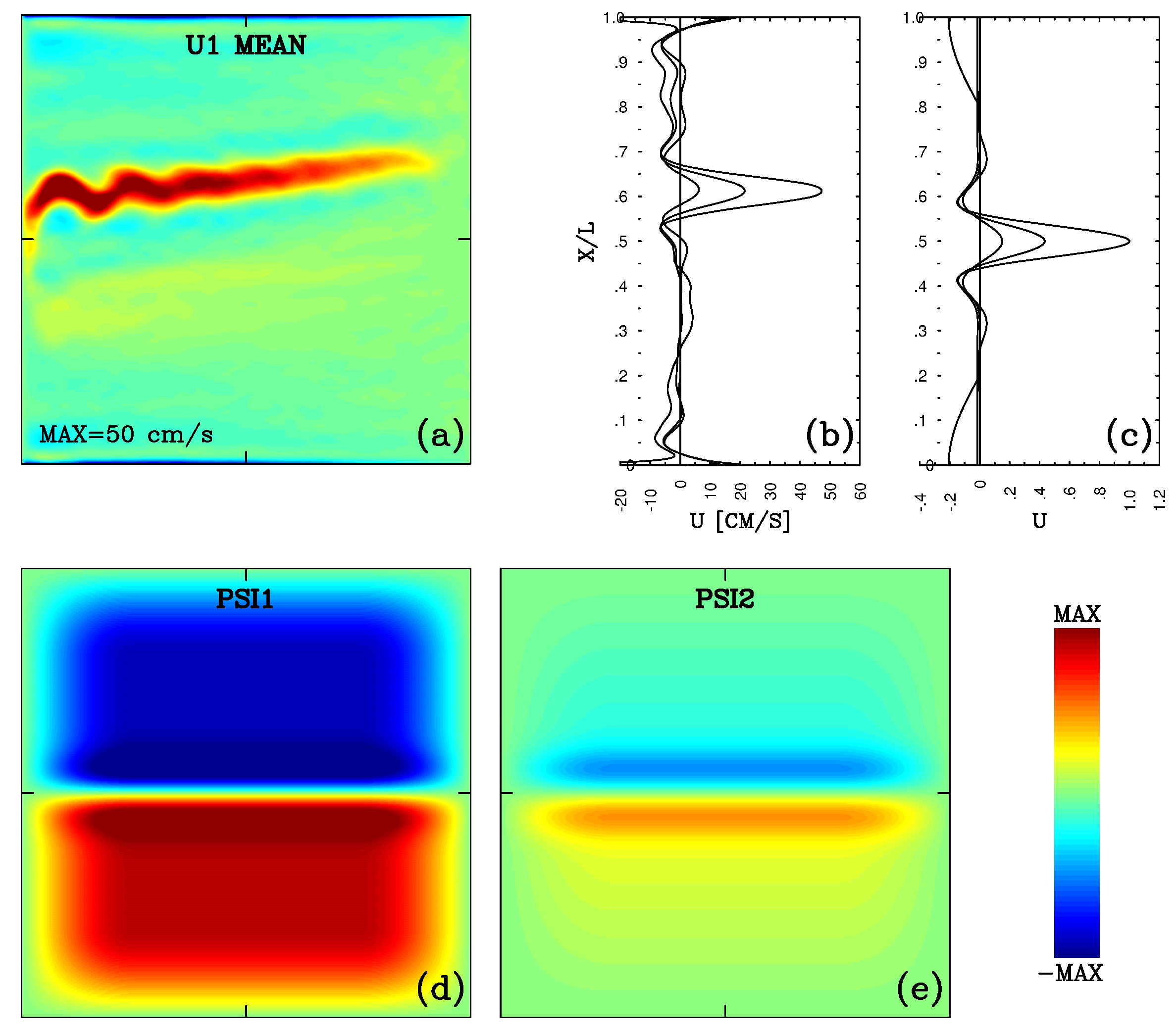
3. Transient-Impulse Solutions and Analyses

We consider a uniform ${125}^2$ horizontal grid, so that its nodes are at least $r_0$ away from the lateral boundaries, solve the linearized model (8)–(10) for ${125}^2$ transient impulses, one at a time, and analyze the outcome. First, we look at the transient-impulse flow patterns (Figure 4a–c) and find that, in the vicinity of the plunger and at the end of the forcing time interval, they resemble the periodic solutions studied in B15. Second, for each transient-impulse solution, we obtain the corresponding induced time-mean eddy PV flux (the layer index is omitted for simplicity, and the overbar denotes the time averaging over $2T$)

$$\mathbf{f}(x,y)\equiv \overline{\mathbf{u}q}\equiv \left(\overline{uq},\overline{vq}\right)$$

(14)

(not shown). The corresponding “footprint” (Figure 4d–f) is defined as the horizontal divergence of the eddy PV flux taken with the minus sign

$$F(x,y)=-\nabla ·\mathbf{f},$$

(15)

so that $F(x,y)$ can be interpreted as the cumulative PV forcing to be exerted on the background flow by the nonlinear interactions of the transient-impulse solution, if this solution were nonlinear. Transient-impulse solutions differ from the temporally periodic ones (not shown, but we checked this by comparing responses in a double-periodic domain with uniform background flows), especially in the far field, but this difference has a relatively weak effect on the footprints. The other noticeable difference from the periodic solutions is due to the inhomogeneous background-flow effect—we observe it by replacing the 2D background circulation with the uniform flow given by the velocity at the plunger location $(x_0,y_0)$ (the effect of the local homogeneity assumption is discussed further below). The third noticeable difference is due to the fact that the periodic solutions do not take into account natural instabilities of the background flow, whereas the transient-impulse solutions pick them up. The main instabilities grow in the eastward jet (Figure 4a–c), even if the plunger is located far away from it, but more vigorously if the plunger is close to the jet. However, these instabilities yield nearly negligible contributions to the footprints, especially for plungers located far away from the jet. To summarize, we find that the transient-impulse solutions not only produce meaningful and structurally rich maps of the footprints, but they also can be viewed as physically justified upgrades of the periodic solutions.

3.1. Equivalent Eddy PV Flux

The footprint pattern $F(x,y)$ can be also viewed as a nonlinearly driven redistribution of PV anomalies supplied by the imposed plunger forcing; hence, we can recast it in terms of the equivalent PV flux. Let us introduce this concept and show that it can be useful both for interpretation of the eddy effects and for upgrading the earlier simple treatment of footprints in B15. First, in each layer (layer indices are omitted), we calculate $F(x,y)$ anomalies accumulated to the north and south of the reference point $(x_0,y_0):$

$$F_{north}=\int {\int }_{y>y_0}F(x,y)dxdy,F_{south}=\int {\int }_{y<y_0}F(x,y)dxdy,$$

(16)

and similarly to the west and east of it, that is, $F_{west}$ and $F_{east}.$ Next, we calculate the “centers of mass” for these anomalies as illustrated by

$$y_{north}=\frac{1}{C}\int {\int }_{y>y_0}\left|y\right|\left|F(x,y)\right|dxdy,C=\int {\int }_{y>y_0}\left|F(x,y)\right|dxdy,$$

(17)

and $y_{south}, x_{west}$ and $x_{east}$ are found analogously. Although, the area of integration may cover the full basin, in practice, we integrate over the square with size $0.15L$ centered at $(x_0,y_0),$ in order to avoid remote and small contaminations of the footprint due to the above-discussed instabilities of the eastward jet. The equivalent eddy flux components are found as

$${\tilde{f}}_x=F_{north}{y}_{north}-F_{south}{y}_{south},{\tilde{f}}_y=F_{east}{x}_{east}-F_{west}{x}_{west},$$

(18)

so that the equivalent eddy flux is a simple measure of the amplitude of the PV anomaly generated by the transient impulse, and of its spatial orientation. The main difference between the equivalent and full eddy flux (14) is that the latter is a 2D vector field, whereas the former is a local single-vector quantity for each transient impulse. Of course, there is more information in the footprint pattern, but we treat it simplistically, motivated by the initial investigation purpose. Further below, we will refer to $\tilde{\mathbf{f}}$ simply as the eddy flux, while keeping in mind its definition (18). Note that the eddy flux can be straightforwardly decomposed into the relative-vorticity and isopycnal-stretching terms that can be interpreted as Reynolds and form stresses, but we leave the corresponding analyses beyond the scope of this paper.

We decompose the isopycnal eddy fluxes (e.g., as in [45]) into their gradient and agradient components found with respect to the time-mean large-scale PV field $\overline{Q}=\overline{q}+\beta y,$ so that

$$\tilde{\mathbf{f}}=-\kappa \nabla \overline{Q}-{\kappa }_{\perp }{\nabla }_{\perp }\overline{Q},{\nabla }_{\perp }\equiv \mathbf{k}\times \nabla =\left(\begin{array}{c}-\partial /\partial y\\ \partial /\partial x\end{array}\right),$$

(19)

or, equivalently,

$$\tilde{\mathbf{f}}=-\left(\kappa \frac{\partial \overline{Q}}{\partial x}-{\kappa }_{\perp }\frac{\partial \overline{Q}}{\partial y},{\kappa }_{\perp }\frac{\partial \overline{Q}}{\partial x}+\kappa \frac{\partial \overline{Q}}{\partial y}\right),$$

where the eddy diffusivity components are defined as

$$\kappa =-\frac{\tilde{\mathbf{f}}}{|\nabla \overline{Q}|}·\frac{\nabla \overline{Q}}{|\nabla \overline{Q}|},{\kappa }_{\perp }=-\frac{\tilde{\mathbf{f}}}{|\nabla \overline{Q}|}·\frac{{\nabla }_{\perp }\overline{Q}}{|\nabla \overline{Q}|}.$$

(20)

Thus, the eddy diffusivity tensor can be defined as the sum of its symmetric and antisymmetric parts (The importance of both symmetric (diffusive) and antisymmetric (advective) eddy-induced tracer transports has been addressed by Griffies [46]. More recently, Bachman and Fox-Kemper [47] estimated and compared passive-tracer κ and ${\kappa }_{\perp }$ in the Eady spin-down problem, and argued that their values are similar, but to what extent this can be applied to other geophysical flows remains unclear):

$$\mathbf{K}=\left(\begin{array}{cc}\kappa & -{\kappa }_{\perp }\\ {\kappa }_{\perp }& \kappa \end{array}\right)=\left(\begin{array}{cc}\kappa & 0\\ 0& \kappa \end{array}\right)+\left(\begin{array}{cc}0& -{\kappa }_{\perp }\\ {\kappa }_{\perp }& 0\end{array}\right),$$

(21)

and the flux-gradient relation can be compactly written as

$$\mathbf{f}=-\mathbf{K}\nabla \overline{Q}.$$

(22)

We calculate the eddy fluxes on the ${125}^2$ grid, as described above, scaled them by $\sigma (x,y)$ from the reference solution and found their divergence. By local rotation of the coordinate system, each flux field is also recast in terms of the gradient and agradient components. The fluxes themselves show how the transient forcing redistributes the PV, and their divergence shows the corresponding accumulation of the time-mean PV—hence, the large-scale effect induced by transient impulses. The negative/positive divergence of the flux describes the local accumulation of the positive/negative PV anomaly, and following B15, this anomaly can be added to the non-eddy-resolving model as the source term.

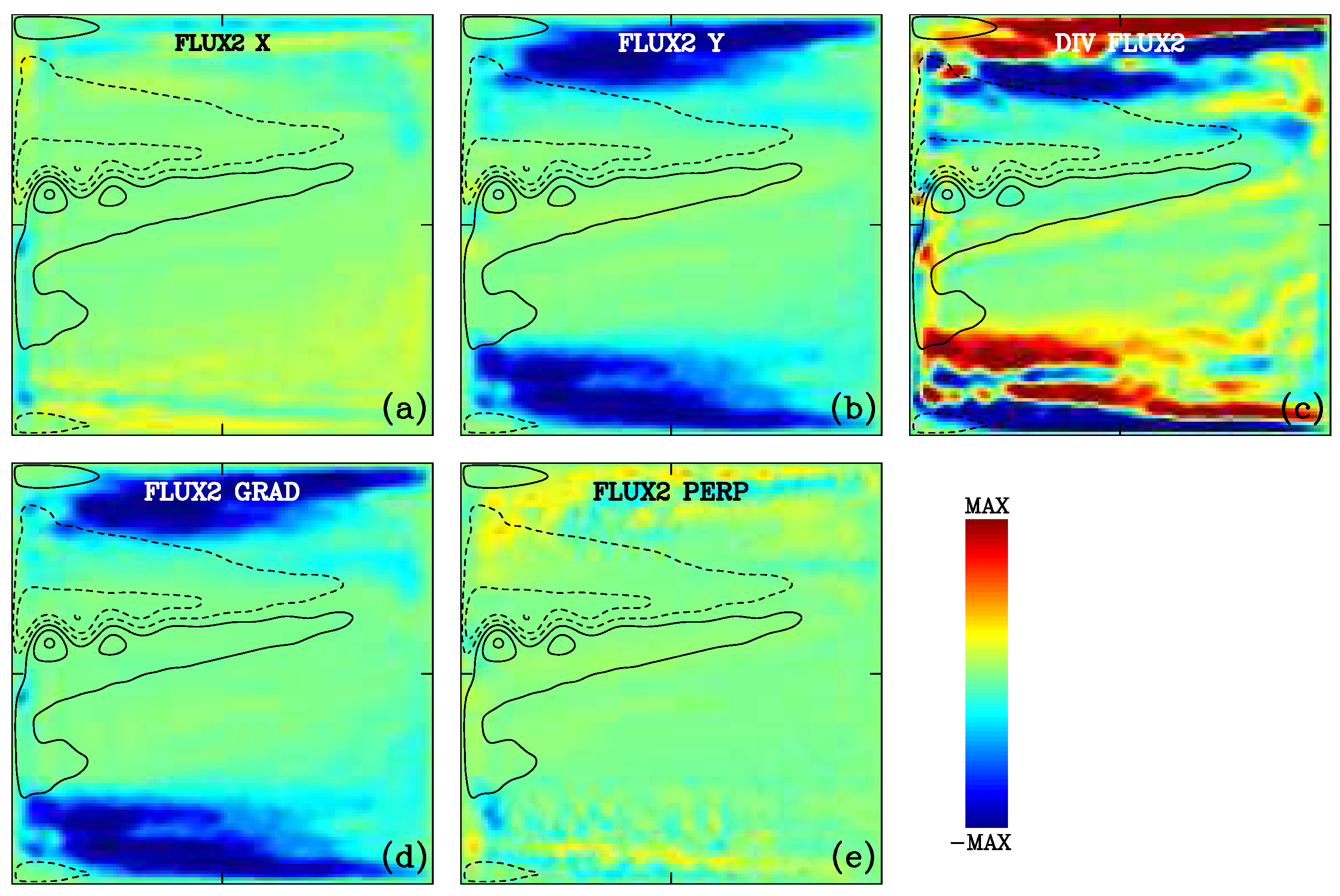
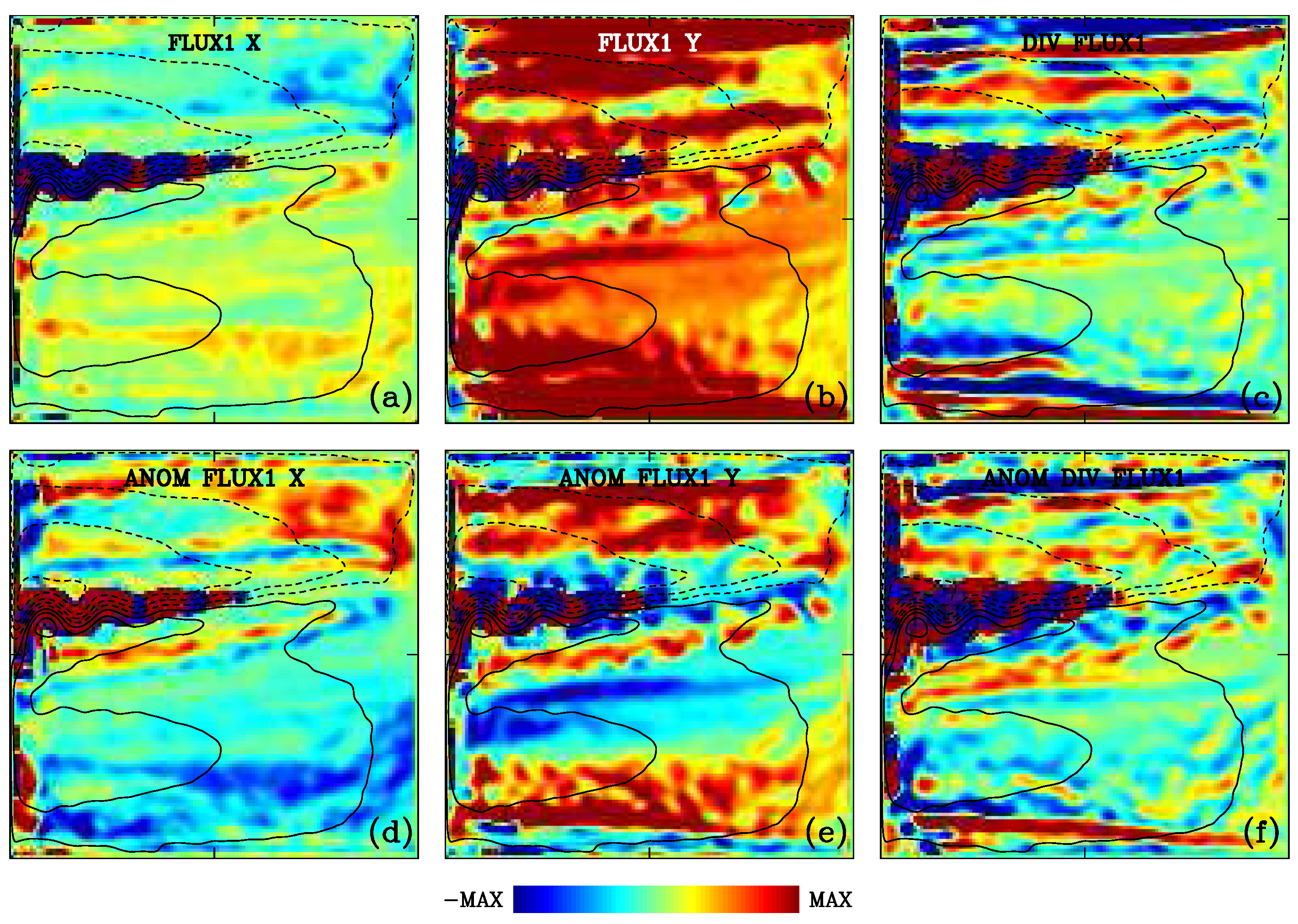
The upper- and deep-ocean eddy fluxes and their divergences, as well as the gradient and agradient components of the fluxes, are shown in Figure 5 and Figure 6. These patterns suggest several conclusions. First, almost everywhere, the meridional component of the eddy flux is larger than the zonal one. Second, orientation of the flux relative to the background PV gradient tells us that although the gradient component dominates, in the upper ocean, the agradient component is also significant. In the deep ocean, the gradient component is always negative (i.e., PV is fluxed down the gradient), whereas, in the upper ocean, it changes the sign to negative in the northern and southern parts of the double gyres and in the recirculation zones around the eastward jet. The latter sign changes are due to the sign changes in the PV gradient, rather than to the real flux reversals. The upper-ocean agradient flux component exhibits many sign reversals and characteristic recirculation cells to the north and south of the eastward jet. These recirculation cells are such that, in the immediate vicinity of the eastward jet, they advect downstream positive/negative PV anomalies. This is consistent with the downstream enstrophy advection mechanism ([26,42]). The upper-ocean flux divergence is characterized by two types of patterns: the anomalies around the eastward jet are such that they enhance the recirculation zones, and the anomalies in the northern and southern parts of the double gyres are such that they slow down the background westward return flows. The deep-ocean flux divergence is characterized only by the latter pattern. All these equivalent eddy flux effects are consistent with the actual eddy effects in the eddy-resolving double-gyre solutions (e.g., [26]).

Next, we find the eddy diffusivity tensor following (20) and (21) and analyze its properties (Figure 7). The eddy diffusivity components κ and ${\kappa }_{\perp }$ are similar to the corresponding eddy flux components, except around $(x,y)$ curves corresponding to zero background PV gradient; this is where κ and ${\kappa }_{\perp }$ become singular. Since we work with discrete solutions, these singularities cause no problems, because they are poorly resolved and manifested only by sharp differences between large, positive and negative values on the neighboring grid points. Positive values of $\kappa ,$ such as in the westward return flows of the gyres, correspond to the downgradient redistribution of PV, and the negative values describe the upgradient, antidiffusive eddy fluxes. The eddy diffusivity pattern in the recirculation zones is dominated by ${\kappa }_{\perp },$ and along the core of the eastward jet κ is mildly negative and decreasing in the downstream direction. In the deep ocean, ${\kappa }_{\perp }$ is relatively small, whereas κ is positive and significant only in the westward return flows of the gyres. Overall, we conclude that the eddy diffusivity is asymmetric, and its ${\kappa }_{\perp }$ part is significant and has to be taken into account. More importantly, the diffusivity components are negative and even singular in many parts of the basin, and this makes the whole idea of the diffusive eddy parameterization ill-posed. On the other hand, an eddy parameterization that directly imposes diverging eddy fluxes can be well-posed and more straightforward.

3.2. Local Homogeneity Assumption

We assess accuracy of the local homogeneity assumption by comparing the eddy fluxes calculated without it (all results in this paper) and with it. For this, we remove the flow inhomogeneity by assuming that transient impulses act on the horizontally homogeneous flow with the velocity components estimated at each reference location $(x_0,y_0)$ on the same ${125}^2$ grid. These solutions are similar to those from B15, but with several important differences: transient impulses are finite rather than periodic in time, solutions are found in the closed rather than double-periodic domain, and both zonal and meridional components of the background flow are taken into account. The resulting outcome is illustrated by Figure 8, which has to be compared with Figure 5a–c, and several conclusions can be drawn from it. First, the local homogeneity assumption completely fails in the eastward jet region, which is characterized by the largest values of the background PV gradient. Second, significant differences are found even in the interior gyres, where they are more quantitative rather than qualitative. Third, we simplify the local homogeneity even further, by setting to zero the meridional background-flow component, and find that the resulting differences are small. This suggests that taking into account only zonal background-flow component (as in B15) is justified simplification away from the eastward jet. Overall, we conclude that the transient-impulse approach indeed bypasses the local homogeneity assumption and is well justified.

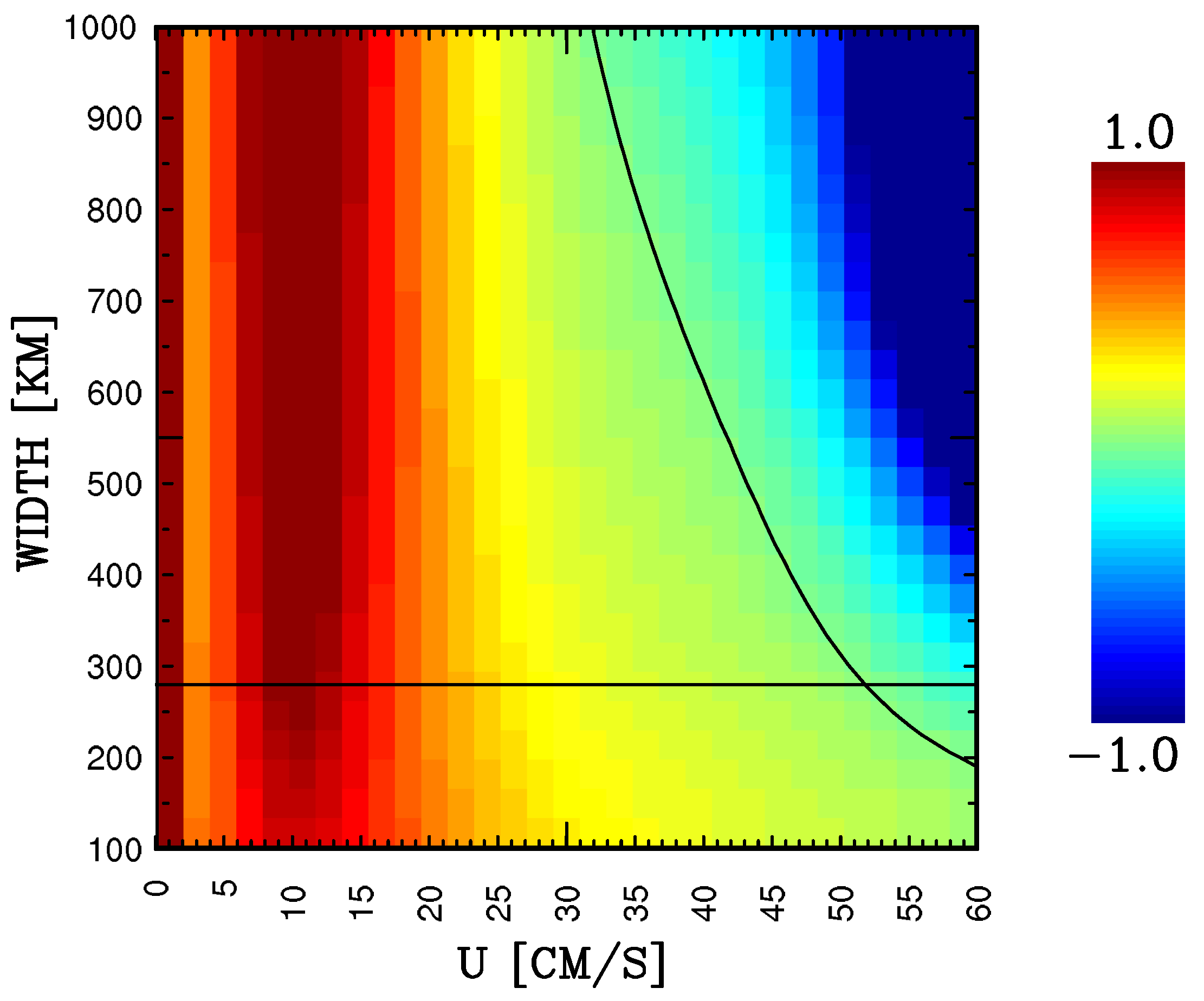
As we showed above, large inhomogeneities of the background flow have a significant effect on the transient-impulse responses and the resulting equivalent eddy fluxes. We explore this further by considering a highly idealized situation of the narrow eastward jet that was fitted to approximate the jet from the reference eddy-resolving solution (Figure 9a–c). The idealized jet profile (in all three isopycnal layers) is given by the following exponentially decaying oscillation:

$$u_1\left(\tilde{y}\right)=Uexp[-{(\tilde{y}/\tilde{w})}^2]cos\left[\frac{\tilde{y}}{p}\right],u_2\left(\tilde{y}\right)=0.45Uexp[-{\tilde{y}}^2/{\left(1.2\tilde{w}\right)}^2]cos\left[\frac{\tilde{y}}{0.92p}\right],$$

$$u_3\left(\tilde{y}\right)=0.15Uexp[-{\tilde{y}}^2/{\left(2.4\tilde{w}\right)}^2]cos\left[\frac{\tilde{y}}{0.80p}\right],$$

(23)

where the nondimensional meridional coordinate and the jet width are related to the dimensional variables as $\tilde{y}=512y/L$ and $\tilde{w}=512w/L,$ respectively, and parameter $p=1.67w/\pi$ is always kept fixed. The idealized jet is controlled by amplitude U and width $w,$ and it closely resembles the reference jet when $w=280$ km. We place the idealized jet in the center of the basin, find its velocity streamfunction by integration of the velocity profile, and taper the streamfunction to zero around the boundaries (Figure 9d,e), in order to satisfy the no-flow-through boundary condition for the synthetic flow.

Next, we position our standard transient-impulse forcing in the center of the basin and calculate its responses and footprints for a broad range of U and w values (Figure 10). The outcome clearly shows that the (across-jet) eddy flux strongly depends on the width of the jet, and for a strong enough jet it changes sign from the positive to negative. On the one hand, this result is a simple conceptual illustration of how the local homogeneity assumption fails. Applying this assumption to any point $(U,w)$ in Figure 10 is equivalent to taking w to infinity; as the Figure suggests, this results in large error in the equivalent eddy flux for fast and narrow eastward jets. On the other hand, this result implies that the tendency of transient eddy forcing to maintain the jet weakens with the jet strength and even reverses for strong enough jet. This is consistent with the eddy diffusivity across the eastward jet becoming more negative further downstream (Figure 7a).

4. Discussion and Conclusions

In this paper, we continue development of the new framework for parameterizing mesoscale eddy effects in non-eddy-resolving ocean circulation models. The central theme of the approach is its reliance on explicit dynamical solutions of an idealized model of the eddy effects; therefore, we refer to the approach as dynamically consistent. In Part I of this paper, we (a) focused on the eddy backscatter effect of the transient part of mesoscale eddy forcing; (b) proposed the “plunger-footprint” approach that translates simple and spatially localized, elementary transient forcing (i.e., plunger) into its nonlinearly rectified response (i.e., footprint); (c) related the footprint to the underlying large-scale flow; and (d) implemented the resulting cumulative effect of many footprints as the eddy parameterization in a non-eddy-resolving model of wind-driven ocean gyres ([28] hereafter, B15). Despite several significant shortcuts made, especially with how the large-scale flow information was treated, the parameterization demonstrated remarkable skills. In this paper, by making significant modifications of the approach, we not only fixed several problematic shortcuts but also gained new dynamical insights into the eddy/mean interactions.

We continued to focus on the classical, wind-driven double-gyre model and showed how the eddy backscatter mechanism maintains the eastward jet via positive correlations between the upper-ocean transient eddy forcing and the jet itself. In order to understand and model nonlinear flow rectification in response to the transient component of the eddy forcing, we constructed elementary, spatially localized and temporally transient forcing functions, referred to as the transient impulses (plungers), and imposed them on the governing quasigeostrophic potential vorticity dynamical equations linearized around the time-mean double-gyre reference solution. For each position of the transient impulse inside the double gyres, we found the corresponding flow solution and its nonlinear self-interaction, referred to as the footprint. The resulting footprints strongly depend on the underlying large-scale flow, and, therefore, vary across the gyres. At this point, we fixed the following shortcuts made in the previous theory and its implementation (B15). First, when solving the linearized dynamics, we took into account not only zonal but also meridional component of the mean large-scale flow. Second, we upgraded the time-periodic transient impulses to more general and realistic, finite-time impulses which take into account the decaying autocorrelations of the actual eddy forcing. We chose a simple wavelet-like piecewise-linear shape of the transient-impulse time dependence: one larger pulse is surrounded by two equal and smaller pulses with the opposite sign. In the presentation, we considered 50-day-long impulses, and the sensitivity study in the interval from 45 to 70 days showed that the results are qualitatively similar. Third, we overcame the local spatial homogeneity assumption that used only local flow information at each plunger position and allowed the Fourier transform, which greatly simplified the problem. Without the assumption, we had to solve the problem differently—by forward time stepping combined with the second-order finite differences. By comparing transient-impulse solutions with and without the local homogeneity assumption, we found that this assumption completely breaks down in the eastward jet, which is characterized by the most energetic eddies and significant eddy effects, and yields significant quantitative errors in other parts of the gyres. To summarize, we concluded that the proposed extensions of the theory and parameterization are important.

The transient-impulse approach provided us with several new insights into the double-gyre eddy/mean interactions. First, the footprints provided us with maps of the PV anomalies expected to be induced by a general transient eddy forcing acting on the top of the considered background circulation. This information was used to calculate the equivalent eddy PV fluxes and their divergences, and thus to partition the double-gyre circulation into distinct geographical regions with specific eddy effects. In particular, these results suggested that the eddies have to maintain the eastward jet extension of the western boundary currents and its adjacent recirculation zones and to slow down the western parts of the subtropical and subpolar gyres. In turn, these results are consistent with the actual eddy effects in the nonlinear double-gyre solutions (e.g., [26,48]). Second, from the equivalent eddy PV fluxes and the underlying large-scale PV gradients, we calculated a spatially inhomogeneous and anisotropic eddy diffusivity tensor. Both of its components along and across the large-scale PV gradient have multiple singularities where the gradient changes sign. Existence of these singularities is consistent with the fact that the eddy fluxes are driven mostly by nonlocal dynamical mechanisms; therefore, they can not be determined only by local gradients. Third, in many parts of the gyres, especially around the eastward jet and its adjacent recirculation zones, the resulting eddy diffusivity is found to be negative, that is, counter-gradient, which is consistent with some earlier studies (e.g., [26,45,49]). All these eddy diffusivity properties suggest that imposing estimated diverging eddy fluxes directly on non-eddy-resolving solutions is better parameterization strategy than relying on the eddy diffusion model. Finally, our results provided a new eddy diffusivity theory, which is complimentary to the existing ideas, such as invoking the linear-stability analysis under the local homogeneity assumption, constraining by the conservation laws, scaling by the Eady growth rate, and relying on the universal turbulent energy spectra (see Section 1).

There are several avenues for future upgrades of the proposed parameterization framework, and the most important one is extension beyond the quasigeostrophic to primitive-equation dynamics, which is the main tool of comprehensive OGCMs. Extension from linear to fully nonlinear transient impulses is another anticipated future development. Accounting for the large-scale low-frequency variability of the eastward jet and upgrading the transient-impulse forcing towards much more realistic multiscale patterns (e.g., by data-driven statistical models; see also [36]) will provide further advances to the whole approach. The transient-impulses approach can be also advanced as a powerful analytical tool for estimating eddy fluxes and diffusivities for both passive and active tracers. The fluxes and diffusivities can be used not only for eddy parameterizations but also for dynamical interpretations of the observations and model solutions, as well as for various practical predictions. To summarize, the framework being developed in this paper and its prequel (B15) is promising but requires further understanding and development. The main advantage, as well as the added complexity and extra capabilities of the new framework stems from its explicit use of the high-resolution dynamics—this constitutes the main difference from the mainstream approaches [2] that use dynamical arguments implicitly.