Abstract
In both developed and developing nations, with South Africa (SA) being one of the latter, the motor vehicle industry is one of the most important sectors. The SA automobile industry was not unaffected by the 2007/2008 global financial crisis (GFC). This study aims to assess the impact of the GFC on new car sales in SA through statistical modeling, an impact that has not previously been investigated or quantified. The data obtained indicate that the optimal model for assessing the aforementioned impact is the SARIMA (0,1,1)(0,0,2)12 model. This model’s suitability was confirmed using Akaike information criterion (AIC) and Bayesian information criterion (BIC), as well as the root mean square error (RMSE) and the mean absolute percentage error (MAPE). An upward trend is projected for new car sales in SA, which has positive implications for SA and its economy. The projections indicate that the new car sales rate has increased and has somewhat recovered, but it has not yet reached the levels expected had the GFC not occurred. This shows that SA’s new car industry has been negatively and severely impacted by the GFC and that the effects of the latter still linger today. The findings of this study will assist new car manufacturing companies in SA to better understand their industry, to prepare for future negative shocks, to formulate potential policies for stocking inventories, and to optimize marketing and production levels. Indeed, the information presented in this study provides talking points that should be considered in future government relief packages.
1. Introduction
The automotive sector is a critical industry in most developed and developing countries [1]. After 1994 and the end of apartheid, South Africa (SA), a developing country, has seen rapid economic growth [2]. The average yearly gross domestic product (GDP) growth rate for SA rose from 3.6% between 2000 and 2003 to 5.1% between 2004 and 2007 [3].
More labor-intensive economic sectors, including manufacturing (particularly automotive), mining, trade, and construction, faced high unemployment rates during the global financial crisis (GFC) of 2007/2008 [4]. Global consumer demand declined, and, to make matters worse, SA began to experience severe energy shortages, which had an adverse effect on the manufacturing sector, particularly the automotive industry. The value added by SA’s manufacturing decreased by 12.2% in 2009 [5]. Consequently, large decreases were experienced in the output of the automobile industry (34%), furniture industry (20%), and textile and apparel sector (14.6%). This had a negative impact on the country’s economy.
The SA automobile sector generated 6.8% of the nation’s GDP in 2018 (4.3% manufacturing and 2.5% retail) and directly employed about 110,000 people [6]. In 2019, the automobile industry contributed 300,000 jobs (100,000 directly in the manufacturing of vehicles and components and 200,000 indirectly). The sector contributed 6.4% to the national GDP and constituted 19% of the total manufacturing output [7].
According to [7], SA is the African continent’s top vehicle manufacturer (54.3%), with 9 major original equipment manufacturers (OEMs) producing 600,000 vehicles per annum as of 2019; these serve both the domestic (40%) and export markets (60%). As one of SA’s fastest-growing sectors, the automotive sector has long played a vital role in the country’s economy. In 2021, it was regarded as the cornerstone of the national industrial foundation and the main manufacturing sector of the nation’s economy. The automobile industry contributed 4.3% to GDP (2.4% manufacturing and 1.9% retail) in 2021 [8].
During the GFC, not only SA but other countries worldwide were affected by decreasing car sales. As per [9], the automotive industry, along with several other sectors, was significantly affected in 2008 and 2009. Tightening global financing conditions resulted in a nearly 25% drop in global vehicle sales from their peak in April 2008 to their trough in January 2009. Bai [10] reported that the financial and economic crisis had a strong negative effect on the automotive industry in Germany, with a 31% decline in passenger car sales and a 59% decrease in commercial vehicle sales by the end of 2009. The Chinese automotive industry experienced a 15% decline in its total automobile sales volume in 2009. In the first half of 2020, new car sales in European Union member states experienced an average decline of 36%, as reported by [11], due to yet another shock, namely, the COVID-19 pandemic.
Reliable automotive projections play a crucial role in strategic planning. SA reported a significant drop in new car sales between 2007 and 2008, reflecting the impact of the GFC on vehicle manufacturers worldwide [12]. The decline in new car sales and other sectors of the economy caused significant job losses, with damaging effects on workers’ living standards. Its state-of-the-art car assemblies make SA the economic powerhouse of southern Africa. Understanding how SA’s automotive industry was affected by the economic shock of the GFC provides valuable insights into similar economic shocks, including those experienced during the COVID-19 pandemic. These insights afford investors, customers, and other stakeholders an opportunity to understand the industry’s vulnerabilities, challenges, and opportunities during similar economic shocks. When South Africa sneezes, the rest of the southern African economic region catches a cold. In other words, the economy of all of southern Africa is affected when SA’s economy suffers.
The accurate forecasting of automotive sales helps dealers to dynamically change their marketing tactics and, in the case of a financial crisis, to make wise decisions for both the wider economy and the transportation sector. According to [13], accurate sales predictions strengthen the competitive edge of vehicle manufacturers in their efforts to optimize their production planning processes. Sales forecasting is crucial for the implementation of sustainable business strategies in the automotive sector. Any financial crisis or economic instability in a country influences purchase decisions related to cars and car products [14].
The aim of this study is to assess the effect of the GFC on new car sales in SA through the use of statistical modeling. The study hypothesizes that the GFC had negative long-term effects on new car sales in SA. Therefore, the researchers consider new car sale trends in SA before, during, and after the GFC. Scholarship regarding the effect of the GFC on new car sales on the African continent, and in SA in particular, is negligible. Understanding how much the SA automotive industry was impacted by the GFC, and how long the industry took (or will take) to recover from the repercussions, is crucial in preparing for future shocks.
The originality of this research should be viewed in the context of applying an already established statistical methodology to provide new insights into the complex relationship between global financial events and local market conditions, and by demonstrating the impact of a shock on new car sales in SA. The approach is used as a tool for understanding and predicting economic trends in Southern Africa based on the existing data. This study aims to fill an important gap in the existing scholarship, namely investigating the effect of an external shock, the GFC, on new car sales in SA. The study also serves as a frame of reference for similar research on the impact of the financial crisis either on other industries in SA, or in other neighboring countries.
Makatjane and Moroke [15] projected car sales in SA using both the seasonal autoregressive integrated moving average (SARIMA) and Holt–Winters models but did not specifically consider the effect of the GFC shock. Statistical models are capable of generating accurate short- and long-term motor vehicle sales forecasts. This allows firms to identify market demand patterns and improve market performance, minimize losses, determine product development strategies, and plan manufacturing and marketing policies more efficiently in anticipation of similar shocks in future.
Using ARIMA models for predicting car sales has been effective, even in the presence of anomalies, as demonstrated by several studies ([15,16,17,18,19]). However, [20] found that SARIMA models are superior in cases where seasonal unevenness is evident in the data; SARIMA models can also extract linear relationships within time series data, making it a suitable choice for this study. Studies by [21,22,23] further reinforced the usefulness of SARIMA models for prediction purposes. Machine learning algorithms have gained popularity [24], highlighting the need for a multi-phase, complex process to address data leakage problems. The SARIMA model is the preferred choice for this study since it is said to be more effective than most models, with the latter including exponential smoothing techniques [25].
2. Literature Review
Several authors have used the Box–Jenkins approach to forecast automotive sales ([17,26,27]). Common methods used for new car sales forecasting include time series, linear regression, machine learning, and grey forecasting methods. Autoregressive moving average (ARMA) and grey prediction are often the forecasting methods of choice [14]. In SA [15], monthly car sales are mostly forecast by using both the SARIMA and Holt–Winters models. In terms of short-term seasonal auto sales forecasting accuracy, the Holt–Winters model performed better than the SARIMA model.
In Indonesia [26], the ARIMA (2,1,2) and ARIMA (1,1,0) models were used to forecast new car and motorcycle sales, respectively. The results were important in assessing the effect of cars and motorcycles on traffic jams and accidents, as well as air pollution, in order to draft better policies.
The naïve method (NM), simple moving average (SMA), weighted moving average (WMA), simple linear regression (SLR), exponential smoothing (ES), Holt–Winter linear trend, autoregression (AR), ARMA, and ARIMA models were used in India [1] to compare the forecasted demand for vehicles. The Holt–Winter linear trend model was considered the most suitable. However, the modeling was conducted without considering shocks such as a GFC; therefore, the latter is considered in the current study. Shakti et al. [17] used an SARIMA(0,1,1)(0,1,1)12 model to predict 5-year tractor sales for the Mahindra Tractors Company in India. The forecasted average increase in future sales meant an improvement in the country’s GDP, and thus the economy. Such forecasts are at best true/correct if no shocks, such as the GFC experienced during 2007/2008, occur.
Pherwani and Kamath [18] concluded that sales forecasting is a crucial element in successful business management. The authors forecasted the total car sales in India using an ARIMA (1,1,0) model and concluded that their findings could guide motor vehicle companies to cover expenses and decide both employee wages and stocking inventory. The same Box–Jenkins methodology was used by [28] in India to model and predict automobile sales because of their significant impact on the economy through trade flows. However, the authors did not consider the impact of the GFC on car sales in their study. The current research aims to fill an important gap by investigating the effect of this external shock (the GFC) on new car sales, forecasting and providing information/data-based recommendations for inventory management, and other business operations in the automotive industry.
Chen [27] predicted Chinese automotive demand with the Box–Jenkins approach (an ARIMA model) using monthly data. The conclusion was that the ARIMA model generates better forecasts that could aid government in drafting automobile industry policies, as well as automobile enterprises in planning their output. Qu et al. [14] adopted the support vector regression (SVR) model to predict the monthly sales of automobiles in the Chinese car segment. The proposed grey wolf optimizer–support vector regression (GWO-SVR) model fitted the data well. Unlike the Box–Jenkins approach, the GWO-SVR approach is computationally expensive; it requires a significant number of computational resources and time to train and tune the model, especially when dealing with large amounts of data [29], such as with new car sales. The GWO-SVR also lacks interpretability as it uses machine learning techniques that do not provide clear insights into the underlying relationships between variables. Conversely, the ARIMA is a well-established time series model that provides interpretable coefficients that can help explain the relationship between variables.
Kaya and Yildirim [30] used an eight-layer deep neural network (DNN) model to forecast automobile sales. Several variables, such as the consumer confidence index (CCI), the exchange rate, the GDP, and the consumer price index (CPI), were considered. The authors recommend the use of their approach on various sales prediction problems. However, DNN models can be more challenging to use due to their high cost and the need for optimal architecture and hyper-parameter tuning, as noted by [31,32]. Furthermore, DNN models are more suitable to use with a large, homogeneous dataset with multiple observations, according to [33]. For a single variable such as new car sales, SARIMA models can lead to a higher forecasting accuracy and are therefore the preferred choice in this study.
Fantazzini and Toktamysova [34] used multivariate models, drawing on economic variables, and Google online search data to forecast Germany’s monthly car sales. The conclusion was that the models, which included Google search data, outperform other competing car models. Such models can, however, be very complicated and subjective. In multivariate models, variable selection is difficult and subjective, which may lead to overfitting and poor forecasting performance. Thus, the use of ARIMA models that do not require the selection of relevant predictors becomes important.
Kim et al. [25] forecasted offline retail sales during the COVID-19 pandemic period in South Korea by comparing ARIMA to several ETS methods. The conclusion was that the SARIMA (2,0,2)(1,0,0)12, ARIMA (1,0,1)(0,0,0)12, and ARIMA (2,0,3)(0,0,1)12 models were the best fit for retail sales in fashion, cosmetics, and sports categories, respectively, when compared to the naïve seasonal and Holt–Winter additive models. The forecasts showed that sales in the fashion retail category were increasing gradually, with sales in the cosmetics and sports retail categories increasing at a faster rate. The S/ARIMA models were better forecasting models than the ETS models, hence their adoption in the current study.
The simple and flexible Box–Jenkins approach is used in this paper to forecast new car sales in SA. Its suitability relies on its accuracy in forecasting, as well as its flexibility and adaptability to a wide range of time series data, such as new car sales. Brito et al. [35] concluded that the SARIMA models are more flexible in their application and more accurate in generating quality results.
3. Methodology
In this section, the forecasting methods used in the study are explained. The Box–Jenkins [36] methodology is employed in modeling and forecasting new car sales in SA. The ARIMA and SARIMA models are part of the Box–Jenkins approach.
3.1. ARIMA/SARIMA Models
The Box–Jenkins approach involves, firstly, the model identification stage, where the appropriate order of the model is identified through the use of both the autocorrelation function (ACF) and the partial autocorrelation function (PACF). An ARIMA model can be presented as an ARIMA (p,d,q) model, where p is the AR order, which allows the method to incorporate past values in forecasting future values, d is the number of nonseasonal differences needed to achieve stationarity, and q is the MA order which relies on the number of lagged forecast errors in obtaining the forecast values. When the data are not seasonal, the ARIMA (p,d,q) model is appropriate and is represented as:
where is the backward shift operator (), is a constant term, , and is the error variance term. is new car sales and and are polynomials of order p and q, respectively.
When the data exhibit seasonality, an SARIMA (p,d,q)(P,D,Q)s model is possible, and the extra terms are denoted as follows: P is the seasonal AR order, D is the seasonal differencing order, Q is the seasonal MA order, and s denotes the seasonality (s = 12 for monthly data). The following is a representation of an SARIMA (p,d,q) (P,D,Q)s model:
where and are polynomials of orders P and Q, respectively. The maximum likelihood estimator (MLE) method is used to generate optimal model parameters. When choosing the best model, the Akaike information criterion (AIC) and Bayesian information criterion (BIC) are used. The AIC can be written as:
where L is the likelihood function and m is the number of model parameters, as indicated by [37]. The BIC is given as:
where L is the likelihood function and m and n are the number of model parameters and observations, respectively.
3.2. Time Series Decomposition and Stationarity
Data decomposition is conducted to elucidate some of the time series’ characteristics. To model new car sales using the Box–Jenkins approach, the sales are transformed to make them stationary. A stationary series with statistical properties that do not change with time is needed to identify the model. The stationarity of the transformed new car sales is tested using the augmented Dicky–Fuller (ADF) test. All appropriate and possible data transformations will be suggested through the use of the Box–Cox transformation plot.
3.3. Model Adequacy
Good forecasts significantly minimize forecasting errors, and both the root mean square error (RMSE) and the mean absolute percentage error (MAPE) will be employed in making the assessment. The RMSE and the MAPE are given as:
where denotes original new car sales, is the projected/forecasted new car sales, and is the total number of years in the projected period.
4. Results
Data regarding new car sales in SA from January 1998 to November 2022 were obtained from Statistics South Africa’s Motor trade sales reports, available at https://www.statssa.gov.za/ (accessed on 2 February 2023). Data for the period from January 1998 to July 2006 are considered training data, and data for the period from August 2006 to July 2008 are the validation data. To assess the impact of the GFC on SA’s new car sales, forecasts ranging from August 2006 to December 2023 were created as expected future car sales and for comparison with the actual monthly sales in order. Data analysis was conducted using the R 4.2.2 software package.
4.1. Data and Descriptive Statistics
Table 1 presents the descriptive statistics of monthly new car sales in a monetary value.

Table 1.
Descriptive statistics of SA’s new car sales (January 1998–July 2008).
Monthly new car sales in SA average ZAR 17,281.41 million. The minimum and maximum monthly sales are ZAR 9065 million and ZAR 32,399 million, respectively. The time series plot of the original new car sales is shown in Figure 1.
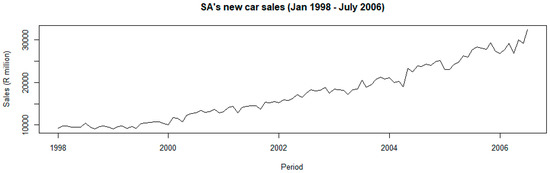
Figure 1.
Time series of original new car sales .
The plot shows a strong upward trend with non-constant variance, which suggests that the new car series is not stationary. Despite the growth in new car sales, the graph shows a sharp decrease in sales between 2004 and 2005. A decomposed time series is constructed to observe the major components of the data.
Figure 2 indicate a non-stationary series with a strong upward trend and some seasonal variation. This suggests the need for some data transformation, including differencing to achieve stationarity of the data. The Box–Cox technique is used in determining the best and appropriate data transformation to be applied.
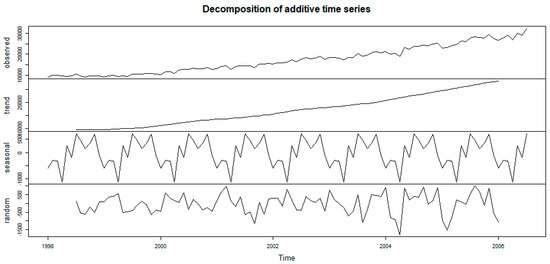
Figure 2.
Decomposed new car sales plot.
Figure 2 shows from top to bottom the whole time series, long-term trend component, seasonality component, and the random component.
Figure 3 below shows that the maximum loglikelihood of the transformation parameter lambda is 0. This suggests the need for a logarithm transformation to tame the variance and smooth the series. A logarithm transformation is applied to the new car sales data , and the log-transformed new car sales is denoted by A plot of is shown in Figure 4.
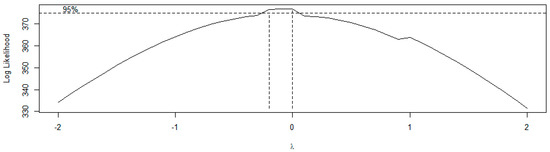
Figure 3.
Box–Cox plot of SA new car sales .
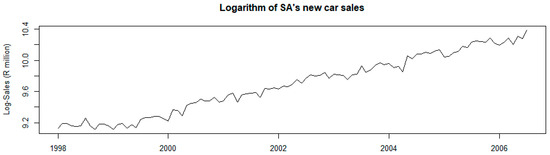
Figure 4.
Log-transformed new car sales .
A smoother but non-stationary series is exhibited in Figure 4. An ADF test is applied to the log-transformed data to examine the stationarity of the data. Table 2 presents the ADF test results of the log-transformed data.

Table 2.
ADF test results of log-transformed data .
The results presented in Table 2 confirm the non-stationarity of the log-transformed motor vehicle sales data as suggested by the p-value of 0.2444; therefore, we failed to reject the null hypothesis of the presence of unit root in the data. The series is non-stationary. An ordinary first difference is applied to the log-transformed data. Figure 5 is a graphic representation of the first difference in the log-transformed motor vehicle sales.
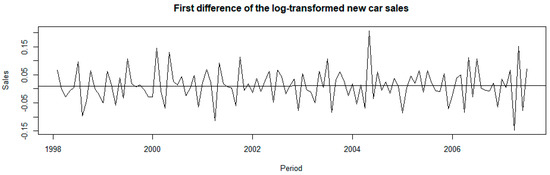
Figure 5.
First difference of the log-transformed new car sales.
Figure 5 depicts a stationary series; therefore, the first difference of the log-transformed new car sales shows the absence of a unit root. To further confirm this, an ADF test is employed on the first difference of the log-transformed new car sales. Table 3 is a summary of the results.

Table 3.
ADF test of first difference of the log-transformed new car sales.
At the 5% significance level, the log-transformed new car sales data are stationary after the first ordinary difference, as evidenced by the small p-value of 0.01. Both the ACF and PACF of the first difference of the log-transformed motor vehicle sales data are conducted to visualize the appropriate , and , as well for the identification of the tentative model. Figure 6 presents the ACF and PACF plots of the first ordinary differenced log-transformed data.
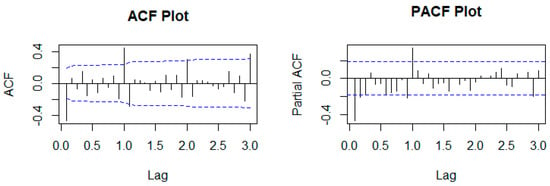
Figure 6.
ACF and PACF plots of the first ordinary differenced log-transformed data.
In the ACF and PACF plots, the blue lines are boundary lines used to identify statistically significant ACF or PACF coefficients or lags. The ACF and PACF plots of first ordinary differenced log-transformed new car sales suggest the use of models such as the SARIMA (0,1,1)(0,0,2)12 and SARIMA (0,1,1)(1,0,2)12. The EACF is plotted as well to further check the proposed models. The EACF is shown in Table 4.

Table 4.
The EACF.
The EACF results suggest employing a model such as SARIMA (0,1,1)(0,0,2)12. The suggested model is fitted with other models, and the best model is selected with the support of the AIC and BIC. Table 5 presents the fitted models together with AIC and BIC measures, as well as out-of-sample RMSE and MAPE values.

Table 5.
Fitted models’ AIC, BIC, and adequacy measures.
Table 5 shows that the SARIMA model with drift indicates the lowest values for most of the measures considered. It is thus deemed the best model for new car sales in SA. The SARIMA (0,1,1)(0,0,2)12 model is written as:
where is the mean of the log-transformed new car sales, is the non-seasonal MA model parameter, and and are the seasonal MA model parameters. The SARIMA model parameters are presented in Table 6.

Table 6.
SARIMA model parameters.
All the model parameters presented in Table 6 are statistically significant, as evidenced by large test statistics and small p-values. The ACF and PACF plots of the SARIMA model residuals are shown in Figure 7.
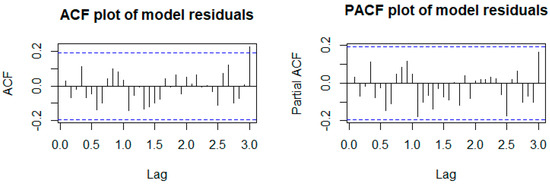
Figure 7.
ACF and PACF plots of the SARIMA (0,1,1)(0,0,2)12 model residuals.
The SARIMA (0,1,1)(0,0,2)12 model residuals seem to be uncorrelated. The model residuals’ Q-Q plot and histogram are constructed to check for normality. Figure 8 presents the normality plots.
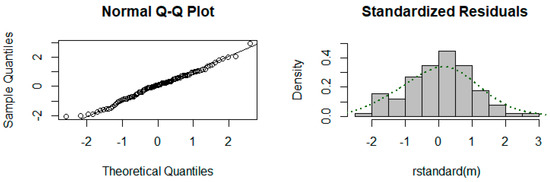
Figure 8.
Q-Q plot and histogram the SARIMA (0,1,1)(0,0,2)12 model residuals.
The Q-Q plot and histogram of the SARIMA (0,1,1)(0,0,2)12 model residuals suggest that the model residuals are indeed normally distributed. The SARIMA (0,1,1)(0,0,2)12 model is confirmed to be best suited to SA’s monthly new car sales; hence, the model is used to forecast future new car sales.
4.2. In-Sample and Out-of-Sample Forecasting
Forecasts of future new car sales for SA are important for the government’s tax purposes, as well as for all automotive industry stakeholders in terms of planning and marketing purposes and policy formulation. The SARIMA (0,1,1)(0,0,2)12 model is used to generate in-sample and out-of-sample forecasts for the next 209 months. Figure 9 shows the original series versus the in-sample fitted values.
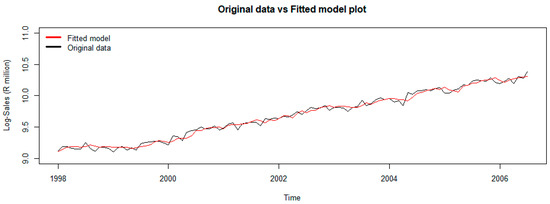
Figure 9.
Original versus fitted values (log-transformed data).
Figure 9 illustrates that the SARIMA (0,1,1)(0,0,2)12 model is valid. The fitted values and the original values do not differ significantly. This suggests that the model and the data are well-matched.
A 209-month out-of-sample forecast is made, with values compared to actual new automobile sales, covering the period from August 2006 to December 2023. The forecasts are presented in Figure 10.
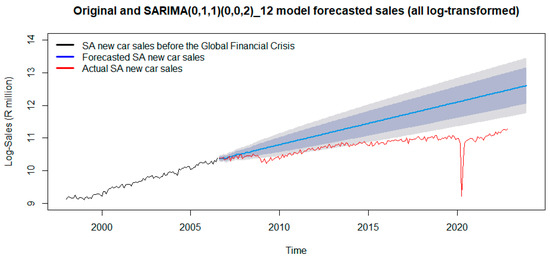
Figure 10.
Actual and forecasted new car sales (log-transformed data).
Table A1 in the annexure presents the actual and projected new car sales figures on the original scale after reversing the data transformations.
An increase in future new motor sales, after the GFC, is predicted. The disparity between the blue line (forecasted expected future new car sales had the GFC not occurred) and the red line (actual new car sales) reflects the impact of the GFC on the automotive industry’s new car sales. By July 2010, the sales had recovered to their pre-GFC levels, but not enough for the original sales trajectory to be maintained. Though the rate of increase in car sales somewhat recovered, the level remained stubbornly low. The rate of increase in car sales needs to increase further in order to attain the original trajectory. The COVID-19 pandemic (2020) further hampered the situation, as a sharp decrease was experienced. The noticeable steep decline at the beginning of 2020 suggests that the COVID-19 pandemic had an even greater impact on new car sales. Therefore, it will take some time for the sales to stabilize around the expected trajectory had the GFC and the pandemic not occurred. SA’s economy has been deprived of the maximum benefits that could have been provided by its automobile industry. To ensure that the automotive sector produces the necessary amount of goods and services, policies could be put in place to jumpstart the industry.
5. Discussion
This study evaluated and predicted the enduring effects of the GFC on new car sales in SA by using currently available empirical data. The results and conclusions have been derived through the application of standard statistical validation techniques to the fitted model. The analysis indicates new car sales in SA exhibit periodic fluctuations and seasonality, with higher sales being registered during certain months, such as December. The fitted model results show a positive outlook for future new car sales in SA; however, the SA automotive industry has been negatively affected by the GFC and is still to fully recover from its lingering effects. These findings align with previous research conducted by [38], who determined that the GFC had a detrimental effect on the automobile industry in the USA. Specifically, the authors identified a decline in car manufacturing company sales due to the prevailing market situation and the economic slump. Further, [10] similarly found that the GFC shock negatively affected the USA’s prominent automotive industry, as well as several other sectors of the American economy.
Rena and Msoni [4,39,40] arrived at similar conclusions regarding the negative impact of the GFC on the SA economy. The GFC resulted in the loss of almost a million jobs in 2009 alone, causing the real unemployment rate to rise to 32%. Moreover, the demand for SA products, including new cars, was marked by a significant decline due to reduced global demand ([39,40]). The private sector also suffered, as the GFC led to a substantial reduction in available credit, resulting in a sharp fall in the services sector, such as construction and automobiles, as highlighted by [40]. These findings indicate the severity of the GFC’s effect on SA’s economy, including the car manufacturing industry. This finding is echoed by [41], whose study suggests that the delay in the purchase of high-value items, such as new cars, by consumers, resulted in decreased income for large automotive firms.
The results of the aforementioned studies suggest that it will take time for the industry to fully recover from the GFC’s lingering negative effects to catch up to the expected trend line. Further, the findings indicate that the impact of external economic shocks, such as the GFC, can have long-lasting effects on the industry and undermine the ability to achieve sustainable growth. Policymakers and industry stakeholders could take this into account when developing strategies to promote the recovery and growth of the sector, including measures for mitigating the effects of external economic shocks and promoting innovation and competitiveness in the industry. The industry can become more resilient and better equipped to weather future economic challenges and disruptions, ensuring its continued contribution to SA’s economy, through information/data-led decisions. While the GFC devastated new car sales in SA, projected estimates suggest that new car sales will increase in the coming years as economic conditions keep improving.
6. Conclusions
This paper investigates how the GFC affected the sale of new cars in SA. A quantitative method (the Box–Jenkins technique) was chosen as the method of analysis because it can effectively capture important characteristics, such as long-term trends and seasonality in new car sales, while also providing more precise projections. A clear, increasing, uninterrupted trend in the new car sales series is evident. Actual post-GFC car sales show an increase, going forward, at about the same rate as before the GFC, but from a lower base. The lower rate of increase in future new car sales in SA addresses this paper’s research question regarding current and future new car sales. The study hypothesizes that the GFC has had a negative long-term impact on new car sales in SA.
The latter affects economic growth in SA since new car sales are often seen as an indicator of consumer confidence and economic growth. The increase, albeit at a lower rate, can help to stimulate SA’s economic growth and create jobs in the automotive industry and related sectors. The expected slower growth suggests an increasing demand for vehicles, which can lead to improved production and sales for automakers and dealerships. This will positively influence the supply chain for new car sales, as manufacturers and suppliers can increase production to meet the evidently increasing demand. Since increased demand for new cars can also drive innovation and improvements in technology, the latter could be evidenced in the automotive industry; automakers can work to differentiate their products and stay ahead of competitors. Consequently, new features and capabilities in vehicles, as well as improvements in vehicles’ fuel efficiency and environmental performance, may be expected.
It is interesting to note that, despite the concerted efforts of SA’s government and policymakers to restore stability, the 2007/2008 GFC resulted in a major reduction in new car sales, which contributed to the economy’s decline. Currently, new car sales have not reached the numbers expected in the absence of the GFC. This study’s findings confirm the hypothesis that the GFC had a significant and negative long-term impact on new car sales in SA. Given the potential for the automotive industry to generate employment and economic growth, it may be prudent for policymakers to focus on supporting the manufacturing and selling of new vehicles in the country as a way of growing the economy. By doing so, SA could benefit from increased economic activity, especially from neighboring countries, and improved earnings in this sector.
Saliently, while the study’s findings suggest a negative long-term impact of the GFC on new car sales in SA, the limitations of the SARIMA model used in the analysis may limit the generalizability of the results to other African countries. Factors such as the size and structure of the automotive industry, as well as the broader economic and social context, can vary significantly between countries. This may influence the GFC’s effect on new car sales in different ways. With its state-of-the-art car assemblies, SA is the dominant economic powerhouse in southern Africa. Many countries in the region import new cars from mainly South Africa and from second-hand markets in other countries, such as Japan.
Nonetheless, the research holds importance as the inferences derived from it could potentially be valuable within the South African setting and in neighboring countries.
7. Recommendations
Industrial policies expressly aimed at the automotive sector are needed to boost car sales to their expected levels. The government may help automakers by offering incentives to export more of their goods to other nations. SA may have lost some of its market to competitors, and such incentives are needed to regain those markets. New car sales generate more income, raising the GDP, tax, and living standards of a nation.
Author Contributions
T.M.—writing original draft of the manuscript, D.C.—review, editing, and supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The dataset is available at the following link: https://www.statssa.gov.za/, accessed on 2 February 2023.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
New car forecasts, actual and differences.
Table A1.
New car forecasts, actual and differences.
| Month | Predicted Sales | Actual Sales | Differences | Month | Predicted Sales | Actual Sales | Differences |
|---|---|---|---|---|---|---|---|
| Aug 2006 | 31,716 | 32,486 | −770 | May 2015 | 15-May | 97,484 | 48,708 |
| Sep 2006 | 31,832 | 32,326 | −494 | Jun 2015 | 15-Jun | 98,548 | 50,741 |
| Oct 2006 | 31,782 | 32,065 | −283 | Jul 2015 | 15-Jul | 99,624 | 53,733 |
| Nov 2006 | 32,572 | 32,695 | −123 | Aug 2015 | 15-Aug | 100,712 | 49,636 |
| Dec 2006 | 32,411 | 30,675 | 1736 | Sep 2015 | 15-Sep | 101,811 | 51,222 |
| Jan 2007 | 31,824 | 31,740 | 84 | Oct 2015 | 15-Oct | 102,923 | 51,867 |
| Feb 2007 | 32,623 | 31,924 | 699 | Nov 2015 | 15-Nov | 104,046 | 51,759 |
| Mar 2007 | 33,517 | 34,115 | −598 | Dec 2015 | 15-Dec | 105,182 | 49,180 |
| Apr 2007 | 33,482 | 29,423 | 4059 | Jan 2016 | 16-Jan | 106,331 | 49,867 |
| May 2007 | 34,295 | 34,232 | 63 | Feb 2016 | 16-Feb | 107,491 | 54,478 |
| Jun 2007 | 34,269 | 31,662 | 2607 | Mar 2016 | 16-Mar | 108,665 | 54,702 |
| Jul 2007 | 35,706 | 33,992 | 1714 | Apr 2016 | 16-Apr | 109,851 | 54,355 |
| Aug 2007 | 35,999 | 34,879 | 1120 | May 2016 | 16-May | 111,051 | 56,240 |
| Sep 2007 | 36,112 | 31,950 | 4162 | Jun 2016 | 16-Jun | 112,263 | 54,771 |
| Oct 2007 | 36,317 | 35,229 | 1088 | Jul 2016 | 113,489 | 57,272 | 56,217 |
| Nov 2007 | 37,050 | 35,739 | 1311 | Aug 2016 | 114,728 | 55,606 | 59,122 |
| Dec 2007 | 36,669 | 31,529 | 5140 | Sep 2016 | 115,980 | 55,303 | 60,677 |
| Jan 2008 | 37,023 | 33,381 | 3642 | Oct 2016 | 117,246 | 56,035 | 61,211 |
| Feb 2008 | 37,816 | 34,411 | 3405 | Nov 2016 | 118,526 | 58,352 | 60,174 |
| Mar 2008 | 38,484 | 34,590 | 3894 | Dec 2016 | 119,820 | 54,316 | 65,504 |
| Apr 2008 | 38,045 | 34,725 | 3320 | Jan 2017 | 121,128 | 53,674 | 67,454 |
| May 2008 | 39,002 | 34,634 | 4368 | Feb 2017 | 122,451 | 55,299 | 67,152 |
| Jun 2008 | 39,149 | 33,611 | 5538 | Mar 2017 | 123,788 | 60,342 | 63,446 |
| Jul 2008 | 40,449 | 36,996 | 3453 | Apr 2017 | 125,139 | 50,530 | 74,609 |
| Aug 2008 | 40,454 | 35,340 | 5114 | May 2017 | 126,505 | 57,943 | 68,562 |
| Sep 2008 | 40,896 | 33,979 | 6917 | Jun 2017 | 127,886 | 56,987 | 70,899 |
| Oct 2008 | 41,342 | 35,612 | 5730 | Jul 2017 | 129,283 | 56,489 | 72,794 |
| Nov 2008 | 41,794 | 33,232 | 8562 | Aug 2017 | 130,694 | 58,110 | 72,584 |
| Dec 2008 | 42,250 | 31,792 | 10,458 | Sep 2017 | 132,121 | 57,576 | 74,545 |
| Jan 2009 | 42,711 | 28,365 | 14,346 | Oct 2017 | 133,563 | 61,135 | 72,428 |
| Feb 2009 | 43,178 | 29,252 | 13,926 | Nov 2017 | 135,021 | 62,889 | 72,132 |
| Mar 2009 | 43,649 | 31,583 | 12,066 | Dec 2017 | 136,495 | 57,515 | 78,980 |
| Apr 2009 | 44,125 | 27,554 | 16,571 | Jan 2018 | 137,986 | 57,211 | 80,775 |
| May 2009 | 44,607 | 29,016 | 15,591 | Feb 2018 | 139,492 | 57,509 | 81,983 |
| Jun 2009 | 45,094 | 30,289 | 14,805 | Mar 2018 | 141,015 | 62,936 | 78,079 |
| Jul 2009 | 45,587 | 32,822 | 12,765 | Apr 2018 | 142,554 | 53,531 | 89,023 |
| Aug 2009 | 46,084 | 29,935 | 16,149 | May 2018 | 144,111 | 60,467 | 83,644 |
| Sep 2009 | 46,587 | 30,991 | 15,596 | Jun 2018 | 145,684 | 59,603 | 86,081 |
| Oct 2009 | 47,096 | 32,129 | 14,967 | Jul 2018 | 147,275 | 60,840 | 86,435 |
| Nov 2009 | 47,610 | 33,166 | 14,444 | Aug 2018 | 148,882 | 62,122 | 86,760 |
| Dec 2009 | 48,130 | 33,817 | 14,313 | Sep 2018 | 150,508 | 58,713 | 91,795 |
| Jan 2010 | 48,655 | 31,212 | 17,443 | Oct 2018 | 152,151 | 65,150 | 87,001 |
| Feb 2010 | 49,187 | 32,851 | 16,336 | Nov 2018 | 153,812 | 65,163 | 88,649 |
| Mar 2010 | 49,724 | 35,932 | 13,792 | Dec 2018 | 155,491 | 55,523 | 99,968 |
| Apr 2010 | 50,266 | 33,047 | 17,219 | Jan 2019 | 157,189 | 58,073 | 99,116 |
| May 2010 | 50,815 | 35,228 | 15,587 | Feb 2019 | 158,905 | 56,474 | 102,431 |
| Jun 2010 | 51,370 | 34,339 | 17,031 | Mar 2019 | 160,640 | 60,017 | 100,623 |
| Jul 2010 | 51,931 | 36,639 | 15,292 | Apr 2019 | 162,394 | 59,300 | 103,094 |
| Aug 2010 | 52,498 | 37,361 | 15,137 | May 2019 | 164,166 | 61,310 | 102,856 |
| Sep 2010 | 53,071 | 35,383 | 17,688 | Jun 2019 | 165,959 | 58,510 | 107,449 |
| Oct 2010 | 53,650 | 36,104 | 17,546 | Jul 2019 | 167,771 | 63,926 | 103,845 |
| Nov 2010 | 54,236 | 38,656 | 15,580 | Aug 2019 | 169,602 | 63,025 | 106,577 |
| Dec 2010 | 54,828 | 38,234 | 16,594 | Sep 2019 | 171,454 | 58,745 | 112,709 |
| Jan 2011 | 55,427 | 36,634 | 18,793 | Oct 2019 | 173,326 | 64,669 | 108,657 |
| Feb 2011 | 56,032 | 37,745 | 18,287 | Nov 2019 | 175,218 | 62,465 | 112,753 |
| Mar 2011 | 56,643 | 41,754 | 14,889 | Dec 2019 | 177,131 | 56,859 | 120,272 |
| Apr 2011 | 57,262 | 36,440 | 20,822 | Jan 2020 | 179,065 | 58,804 | 120,261 |
| May 2011 | 57,887 | 38,961 | 18,926 | Feb 2020 | 181,020 | 59,193 | 121,827 |
| Jun 2011 | 58,519 | 40,199 | 18,320 | Mar 2020 | 182,996 | 50,282 | 132,714 |
| Jul 2011 | 59,158 | 40,275 | 18,883 | Apr 2020 | 184,994 | 9984 | 175,010 |
| Aug 2011 | 59,804 | 42,306 | 17,498 | May 2020 | 187,013 | 30,529 | 156,484 |
| Sep 2011 | 60,457 | 42,951 | 17,506 | Jun 2020 | 189,055 | 50,658 | 138,397 |
| Oct 2011 | 61,117 | 41,373 | 19,744 | Jul 2020 | 191,119 | 54,854 | 136,265 |
| Nov 2011 | 61,784 | 44,273 | 17,511 | Aug 2020 | 193,205 | 55,427 | 137,778 |
| Dec 2011 | 62,458 | 41,470 | 20,988 | Sep 2020 | 195,315 | 58,247 | 137,068 |
| Jan 2012 | 63,140 | 40,655 | 22,485 | Oct 2020 | 197,447 | 59,408 | 138,039 |
| Feb 2012 | 63,830 | 42,712 | 21,118 | Nov 2020 | 199,603 | 58,928 | 140,675 |
| Mar 2012 | 64,526 | 45,275 | 19,251 | Dec 2020 | 201,782 | 55,940 | 145,842 |
| Apr 2012 | 65,231 | 41,466 | 23,765 | Jan 2021 | 203,985 | 52,684 | 151,301 |
| May 2012 | 65,943 | 45,722 | 20,221 | Feb 2021 | 206,212 | 56,411 | 149,801 |
| Jun 2012 | 66,663 | 44,620 | 22,043 | Mar 2021 | 208,463 | 62,668 | 145,795 |
| Jul 2012 | 67,391 | 45,567 | 21,824 | Apr 2021 | 210,739 | 59,186 | 151,553 |
| Aug 2012 | 68,126 | 46,476 | 21,650 | May 2021 | 213,040 | 61,068 | 151,972 |
| Sep 2012 | 68,870 | 44,368 | 24,502 | Jun 2021 | 215,365 | 59,124 | 156,241 |
| Oct 2012 | 69,622 | 48,716 | 20,906 | Jul 2021 | 217,717 | 55,584 | 162,133 |
| Nov 2012 | 70,382 | 49,240 | 21,142 | Aug 2021 | 220,094 | 61,961 | 158,133 |
| Dec 2012 | 71,151 | 43,992 | 27,159 | Sep 2021 | 222,496 | 63,794 | 158,702 |
| Jan 2013 | 71,927 | 46,613 | 25,314 | Oct 2021 | 224,925 | 64,650 | 160,275 |
| Feb 2013 | 72,713 | 45,936 | 26,777 | Nov 2021 | 227,381 | 68,640 | 158,741 |
| Mar 2013 | 73,506 | 47,922 | 25,584 | Dec 2021 | 229,863 | 63,570 | 166,293 |
| Apr 2013 | 74,309 | 47,992 | 26,317 | Jan 2022 | 232,373 | 64,307 | 168,066 |
| May 2013 | 75,120 | 49,884 | 25,236 | Feb 2022 | 234,910 | 66,109 | 168,801 |
| Jun 2013 | 75,940 | 46,508 | 29,432 | Mar 2022 | 237,474 | 71,747 | 165,727 |
| Jul 2013 | 76,769 | 51,491 | 25,278 | Apr 2022 | 240,067 | 66,563 | 173,504 |
| Aug 2013 | 77,608 | 50,521 | 27,087 | May 2022 | 242,688 | 71,587 | 171,101 |
| Sep 2013 | 78,455 | 47,449 | 31,006 | Jun 2022 | 245,337 | 69,060 | 176,277 |
| Oct 2013 | 79,311 | 51,721 | 27,590 | Jul 2022 | 248,016 | 73,233 | 174,783 |
| Nov 2013 | 80,177 | 50,689 | 29,488 | Aug 2022 | 250,724 | 77,045 | 173,679 |
| Dec 2013 | 81,053 | 46,061 | 34,992 | Sep 2022 | 253,461 | 77,864 | 175,597 |
| Jan 2014 | 81,937 | 48,487 | 33,450 | Oct 2022 | 256,228 | 76,149 | 180,079 |
| Feb 2014 | 82,832 | 47,779 | 35,053 | Nov 2022 | 259,025 | 78,537 | 180,488 |
| Mar 2014 | 83,736 | 49,783 | 33,953 | Dec 2022 | 261,853 | ||
| Apr 2014 | 84,650 | 47,428 | 37,222 | Jan 2023 | 264,712 | ||
| May-14 | 85,575 | 49,500 | 36,075 | Feb 2023 | 267,602 | ||
| Jun-14 | 86,509 | 49,823 | 36,686 | Mar 2023 | 270,523 | ||
| Jul-14 | 87,453 | 53,245 | 34,208 | Apr 2023 | 273,477 | ||
| Aug-14 | 88,408 | 51,309 | 37,099 | May 2023 | 276,462 | ||
| Sep-14 | 89,373 | 51,231 | 38,142 | Jun 2023 | 279,481 | ||
| Oct-14 | 90,349 | 54,108 | 36,241 | Jul 2023 | 282,532 | ||
| Nov-14 | 91,335 | 50,912 | 40,423 | Aug 2023 | 285,616 | ||
| Dec-14 | 92,332 | 48,832 | 43,500 | Sep 2023 | 288,735 | ||
| Jan-15 | 93,340 | 47,584 | 45,756 | Oct 2023 | 291,887 | ||
| Feb-15 | 94,360 | 47,442 | 46,918 | Nov 2023 | 295,073 | ||
| Mar-15 | 95,390 | 52,780 | 42,610 | Dec 2023 | 298,295 | ||
| Apr-15 | 96,431 | 46,863 | 49,568 |
References
- Jain, P.; Arora, P. Analysis of Time Series Forecasting Techniques for Indian Automotive Industry. J. Emerg. Technol. Innov. Res. 2021, 8, d831–d840. [Google Scholar]
- Committee of Central Bank Governors in SADC. SADC Bankers.Org: Recent Economic Developments. 2009. Available online: http//www.sadcbankers.org/SADC/SADC (accessed on 2 February 2023).
- Madubeko, V. The Global Financial Crisis and its Impact on the South African Economy. 2010. Available online: https://core.ac.uk/download/pdf/145049071.pdf (accessed on 5 February 2023).
- Rena, R.; Msoni, M. Global Financial Crises and Its Impact on the South African Economy: A Further Update. J. Econ. 2014, 5, 17–25. [Google Scholar] [CrossRef]
- National Treasury. Budget Review. 2010. Available online: https://www.treasury.gov.za/documents/national%20budget/2010/review/Budget%20Review.pdf (accessed on 5 February 2023).
- Automotive Export Manual. 2019. Available online: https://aidc.co.za/wp-content/uploads/2021/08/AutomotiveExportManual2019.pdf (accessed on 3 February 2022).
- Automotive Export Manual. 2021. Available online: https://naacam.org.za/wp-content/uploads/2021/04/AutomotiveExportManual2021.pdf (accessed on 5 February 2023).
- Automotive Export Manual. 2022. Available online: https://naamsa.net/wp-content/uploads/2022/05/Automotive-Export-Manual-2022.pdf (accessed on 3 February 2022).
- European Central Bank (ECB). Monthly Bulletin December 2010. Developments in the Euro Area and Global Car Industries. 2010, pp. 1–218. Available online: https://www.ecb.europa.eu/pub/pdf/mobu/mb201012en.pdf (accessed on 5 April 2023).
- Bai, X. The Effects of the 2007–2009 Economic Crisis on Global Automobile Industry. Applied Economics Theses. Paper 2. 2012. Available online: https://core.ac.uk/download/pdf/230661682.pdf (accessed on 5 April 2023).
- Török, L. The Link Between Car Sales and the Economic Crisis in the European Union at the Time of the COVID-19 Epidemic. Int. J. Econ. Bus. Adm. 2020, 8, 1033–1042. [Google Scholar]
- Kasekende, L.; Ndikumana, L.; Rajhi, T. Impact of the Global Financial and Economic Crisis on Africa; Working Papers Series No 96; African Development Bank: Tunis, Tunisia, 2009; pp. 1–29. [Google Scholar]
- Wachter, P.; Widmer, T.; Klein, A. Predicting Automotive Sales Using Pre-Purchase Online Search Data Proceedings of the 2019 Federated Conference on Computer Science and Information Systems; Ganzha, M., Maciaszek, L., Paprzycki, M., Eds.; ACSIS: Kobe, Japan, 2019; Volume 18, pp. 569–577. [Google Scholar] [CrossRef]
- Qu, F.; Wang, Y.-T.; Hou, W.-H.; Zhou, X.-Y.; Wang, X.-K.; Li, J.-B.; Wang, J.-Q. Forecasting of Automobile Sales Based on Support Vector Regression Optimized by the GreyWolf Optimizer Algorithm. Mathematics 2022, 10, 2234. [Google Scholar] [CrossRef]
- Makatjane, K.D.; Moroke, N.D. Comparative study of Holt-Winters Triple Exponential Smoothing and Seasonal ARIMA: Forecasting short term seasonal car sales in South Africa. Risk Gov. Control. Financ. Mark. Inst. 2016, 6, 71–82. [Google Scholar] [CrossRef]
- Almeida, A.; Brás, S.; Oliveira, I.; Sargento, S. Vehicular traffic flow prediction using deployed traffic counters in a city. Future Gener. Comput. Syst. 2022, 128, 429–442. [Google Scholar] [CrossRef]
- Shakti, S.P.; Hassan, M.K.; Zhenning, Y. Annual Automobile Sales Prediction Using ARIMA Model. Int. J. Hybrid Inf. Technol. 2017, 10, 13–22. [Google Scholar] [CrossRef]
- Pherwani, N.; Kamath, V. Using ARIMA Model to Forecast Sales of an Automobile Company. Int. J. Sci. Technol. Eng. 2017, 4, 77–82. [Google Scholar]
- Shetty, S.K.; Buktar, R. A comparative study of automobile sales forecasting with ARIMA, SARIMA and deep learning LSTM model. Int. J. Adv. Oper. Manag. 2022, 14, 366–387. [Google Scholar] [CrossRef]
- Dereti’c, N.; Stanimirovi´c, D.; Awadh, M.A.; Vujanovi´c, N.; Djuki´c, A. SARIMA Modelling Approach for Forecasting of Traffic Accidents. Sustainability 2022, 14, 4403. [Google Scholar] [CrossRef]
- Francis, H.; Kusiak, A. Prediction of engine demand with a data-driven approach. Procedia Comput. Sci. 2017, 103, 28–35. [Google Scholar] [CrossRef]
- Erjiang, E.; Yu, M.; Tian, X.; Tao, Y. Dynamic Model Selection Based on Demand Pattern Classification in Retail Sales Forecasting. Mathematics 2022, 10, 3179. [Google Scholar] [CrossRef]
- Petropoulos, F.; Apiletti, D.; Assimakopoulos, V.; Babai, M.Z.; Barrow, D.K.; Taieb, S.B.; Bergmeir, C.; Bessa, R.J.; Bijak, J.; Boylan, J.E.; et al. Forecasting: Theory and practice. Int. J. Forecast. 2022, 38, 705–871. [Google Scholar]
- Mora-Garcia, R.-T.; Cespedes-Lopez, M.-F.; Perez-Sanchez, V.R. Housing Price Prediction Using Machine Learning Algorithms in COVID-19 Times. Land 2022, 11, 2100. [Google Scholar] [CrossRef]
- Kim, H.-J.; Kim, J.-H.; Im, J.-B. Forecasting Offline Retail Sales in the COVID-19 Pandemic Period: A Case Study of a Complex Shopping Mall in South Korea. Buildings 2023, 13, 627. [Google Scholar] [CrossRef]
- Irhami, E.A.; Farizal, F. Forecasting the Number of Vehicles in Indonesia Using Auto Regressive Integrative Moving Average (ARIMA) Method. J. Phys. Conf. Ser. 2021, 1845, 012024. [Google Scholar] [CrossRef]
- Chen, D. Chinese automobile demand prediction based on ARIMA model. In Proceedings of the 2011 4th International Conference on Biomedical Engineering and Informatics (BMEI), Shanghai, China, 15–17 October 2011. [Google Scholar]
- Srigandan, S.; Venkatesh, A.; Srinivasan, S.; Vasudevan, N. Car sales forecasting using ARIMA model. Int. J. Sci. Innov. Eng. Technol. 2017, 1, 1–6. [Google Scholar]
- Rizzi, A.M. Support Vector Regression Model for BigData Systems. 2016. Available online: https://arxiv.org/pdf/1612.01458.pdf (accessed on 6 April 2023).
- Kaya, S.K.; Yildirim, Ö. A prediction model for automobile sales in Turkey using Deep Neural Networks. J. Ind. Eng. 2020, 31, 57–74. [Google Scholar]
- Chen, Z.; Cao, Y.; Liu, Y.; Wang, H.; Xie, T.; Liu, X. A comprehensive study on challenges in deploying deep learning-based software. In Proceedings of the 28th ACM Joint Meeting on European Software Engineering Conference and Symposium on the Foundations of Software Engineering, New York, NY, USA, 8–13 November 2020; pp. 750–762. [Google Scholar]
- Paleyes, A.; Urma, R.G.; Lawrence, N.D. Challenges in deploying machine learning: A survey of case studies. ACM Comput. Surv. 2020, 55, 1–29. [Google Scholar] [CrossRef]
- Makridakis, S.; Hyndman, R.J.; Petropoulos, F. Forecasting in social settings: The state of the art. Int. J. Forecast. 2020, 36, 15–28. [Google Scholar] [CrossRef]
- Fantazzini, D.; Toktamysova, Z. Forecasting German car sales using Google data and multivariate models. Int. J. Prod. Econ. 2015, 170, 97–135. [Google Scholar] [CrossRef]
- Brito, G.R.A.; Villaverde, A.R.; Quan, A.L.; Pérez, M.E.R. Comparison between SARIMA and Holt–Winters models for forecasting monthly stream flow in the western region of Cuba. SN Appl. Sci. 2021, 3, 671. [Google Scholar] [CrossRef]
- Box, G.; Jenkins, G. Time Series Analysis: Forecasting and Control; Holden-Day: San Francisco, CA, USA, 1970. [Google Scholar]
- Akaike, H. Information Theory and an Extension of the Maximum Likelihood Principle. In International Symposium on Information Theory; Petrov, B.N., Csaki, F., Eds.; Hungarian Academy of Sciences: Budapest, Hungary, 1973; pp. 267–281. [Google Scholar]
- Afzal, F.; Khan, S.M.; Sajid, M. Impact of Global Financial Crisis 2008 on Automobile Industry. Res. J. Financ. Account. 2013, 6, 136–145. [Google Scholar]
- Verick, S. The Global Financial Crisis and South Africa: What Has Been the Impact on the Labour Market? International Labour Office: Geneva, Switzerland, 2010; Available online: https://www.wiego.org/sites/default/files/migrated/publications/files/Verick_The_global_financial_crisis_and_south_africa_Sher_Verick.pdf (accessed on 10 April 2023).
- Mohamed, S. The Impact of the Global Economic Crisis on the South African Economy. A Paper for the Africa Task Force Workshop 9–10 July, Pretoria. 2009. Available online: https://policydialogue.org/files/events/Mohamed_impact_of_global_financial_crisis.pdf (accessed on 10 April 2023).
- Sitlu, V.M.; Panday, S.; Karodia, A.M. The Effects of the Global Economic and Financial Crisis on the South African Automotive Industry. Int. J. Adv. Manag. Econ. 2014, 3, 94–134. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).