A Catalogue of Tropical Cyclone Induced Instantaneous Peak Flows Recorded in Puerto Rico and a Comparison with the World’s Maxima
Abstract
1. Introduction
1.1. Background
1.2. Objectives
- (1)
- Develop a catalogue of instantaneous Qpa values and daily average rainfall rates for a selected group of TCs that affected PR from 1899 to 2020;
- (2)
- Compare the island’s TC-related Qpa values to the world’s flood envelope; and
- (3)
- Compare TC Qpa values and the associated 24 h rainfall rates for different regions of PR.
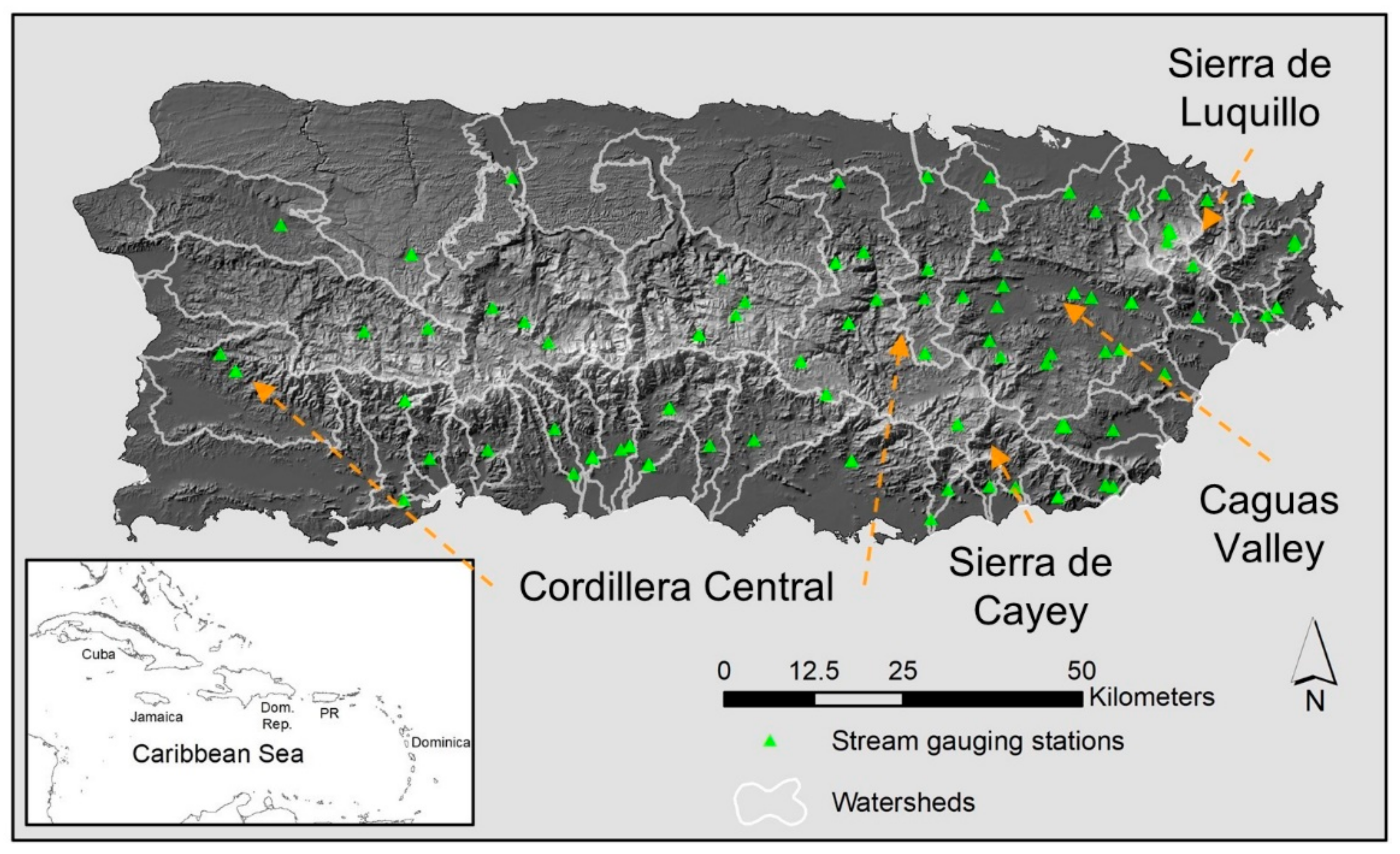
1.3. Study Area
2. Methods
2.1. Development of TC Qp and 24 h Rainfall Rate Database
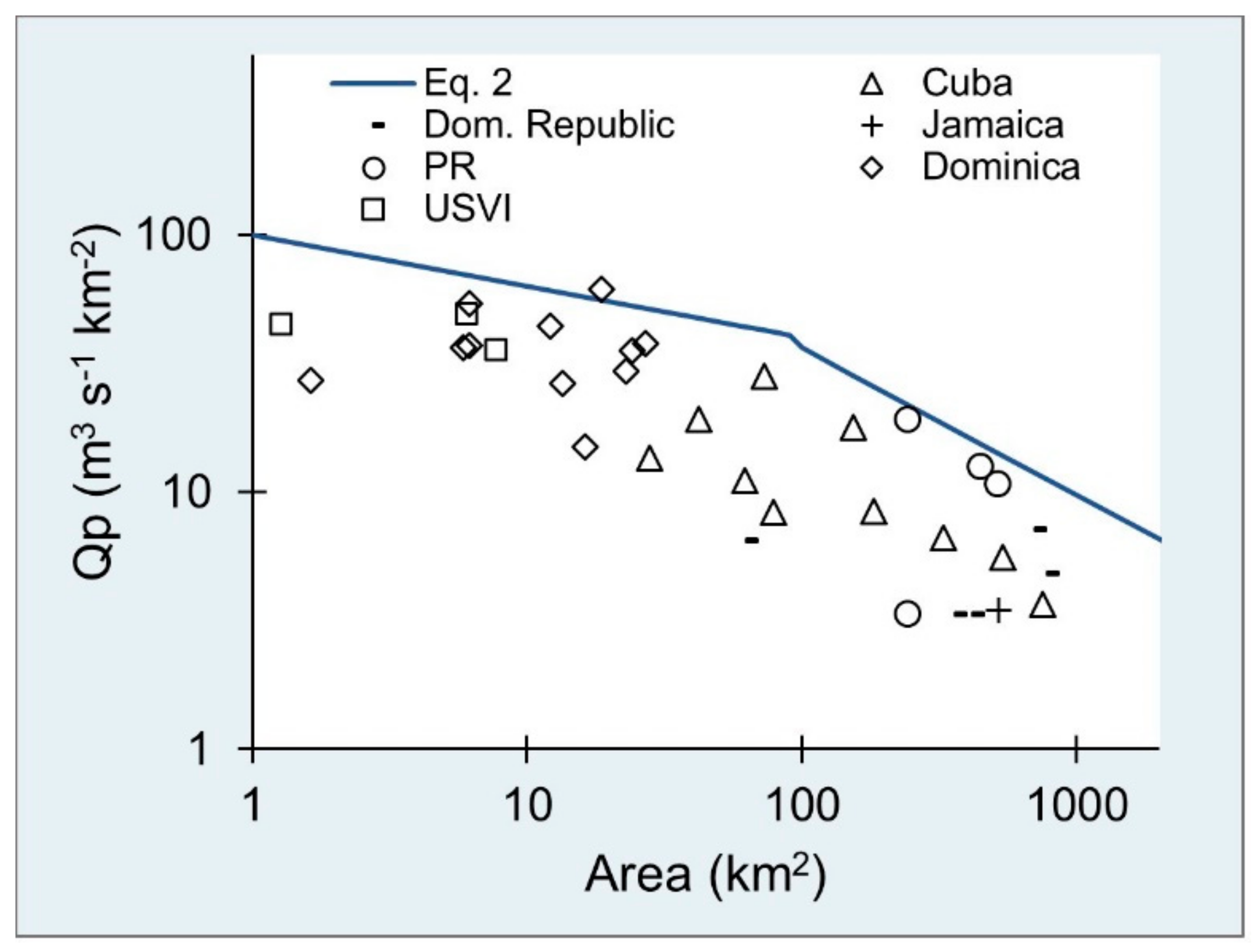
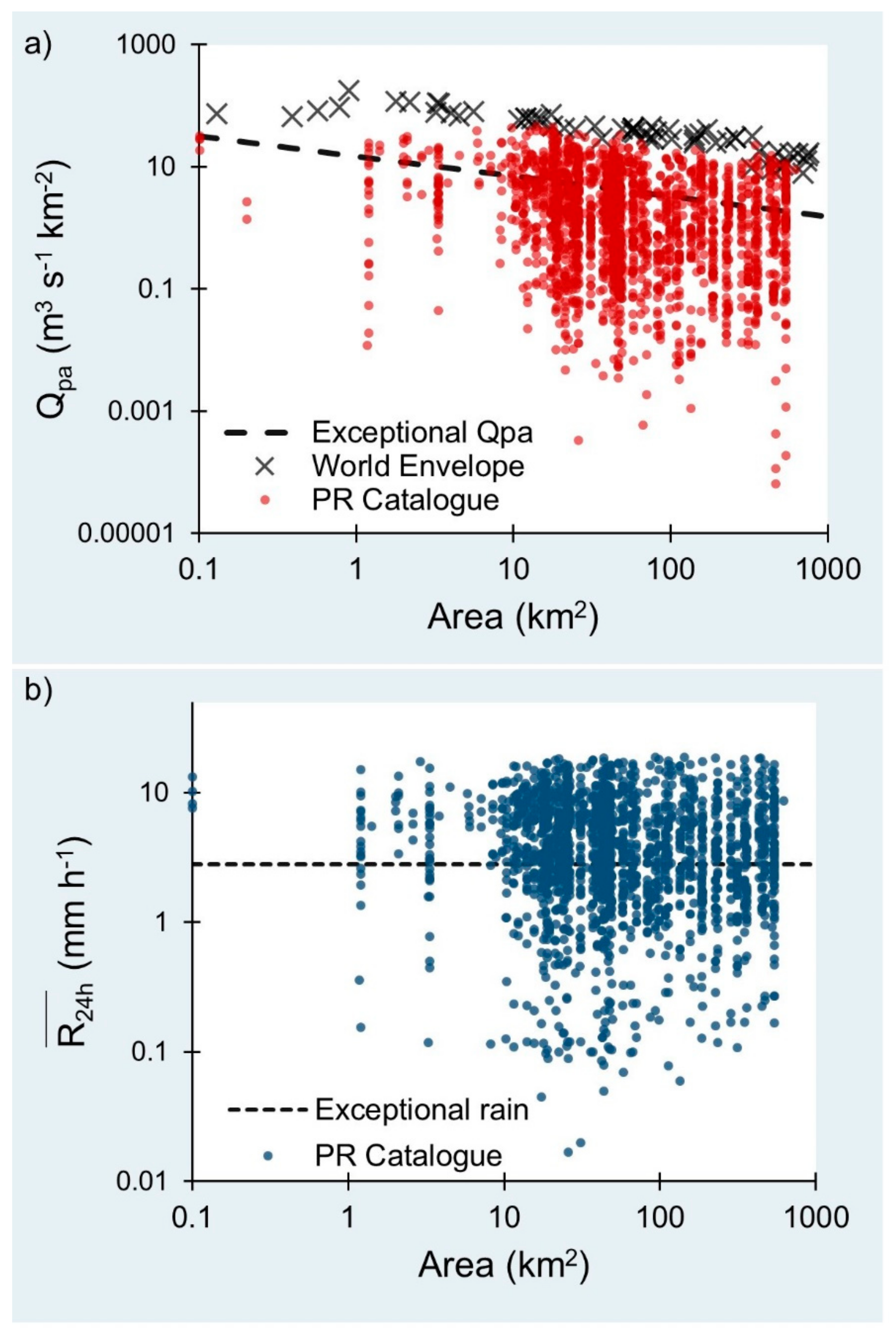
2.2. Comparison of PR’s TC Related Instantaneous Peak Flows with the World’s Envelope
2.3. Regional Qpa and Tendencies within PR
3. Results and Discussion
3.1. The PR Tropical Cyclone Instantaneous Peak Flow Catalogue
3.1.1. General Comments on the Catalogue
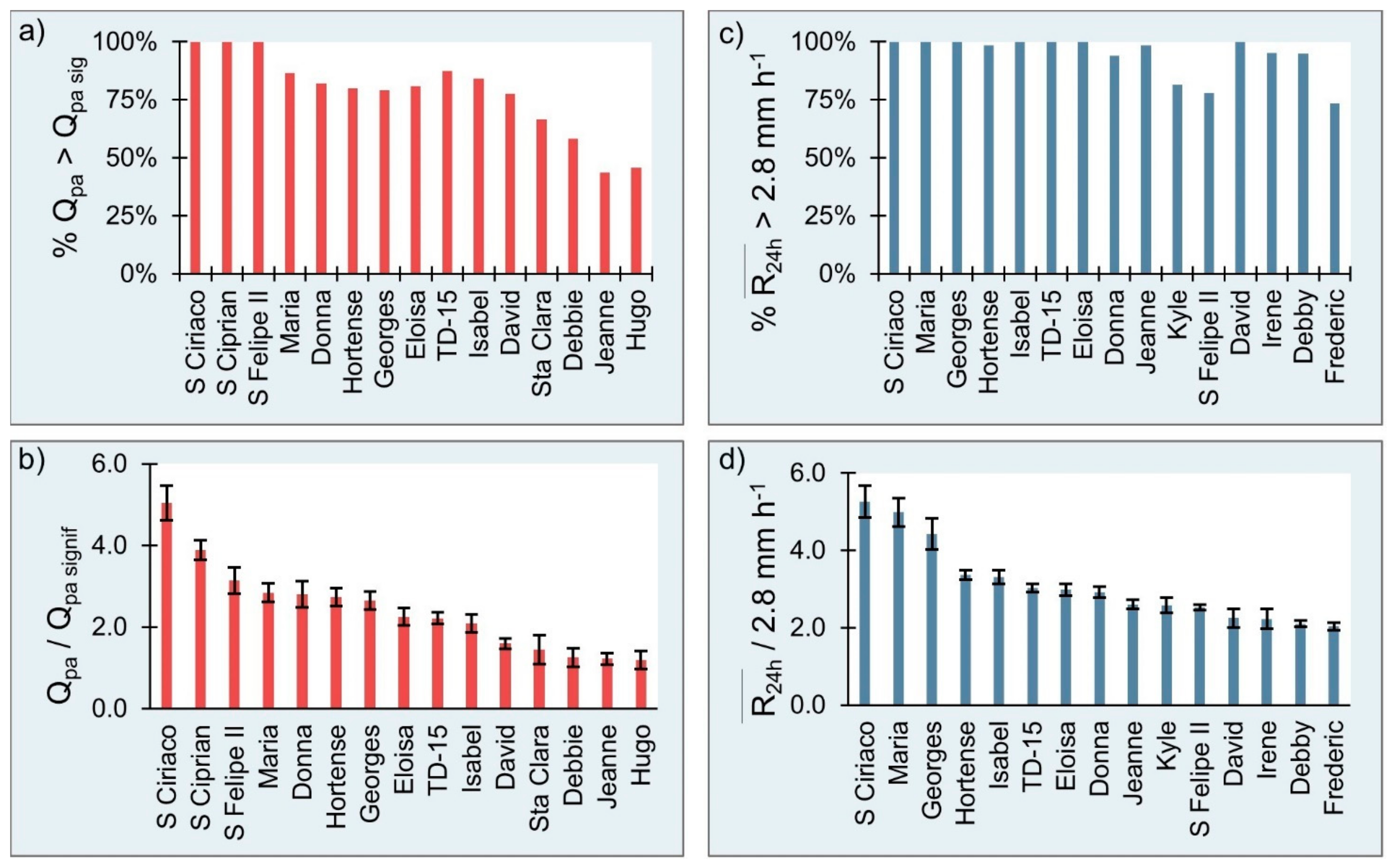
3.1.2. TCs with Exceptional Qpa and Values
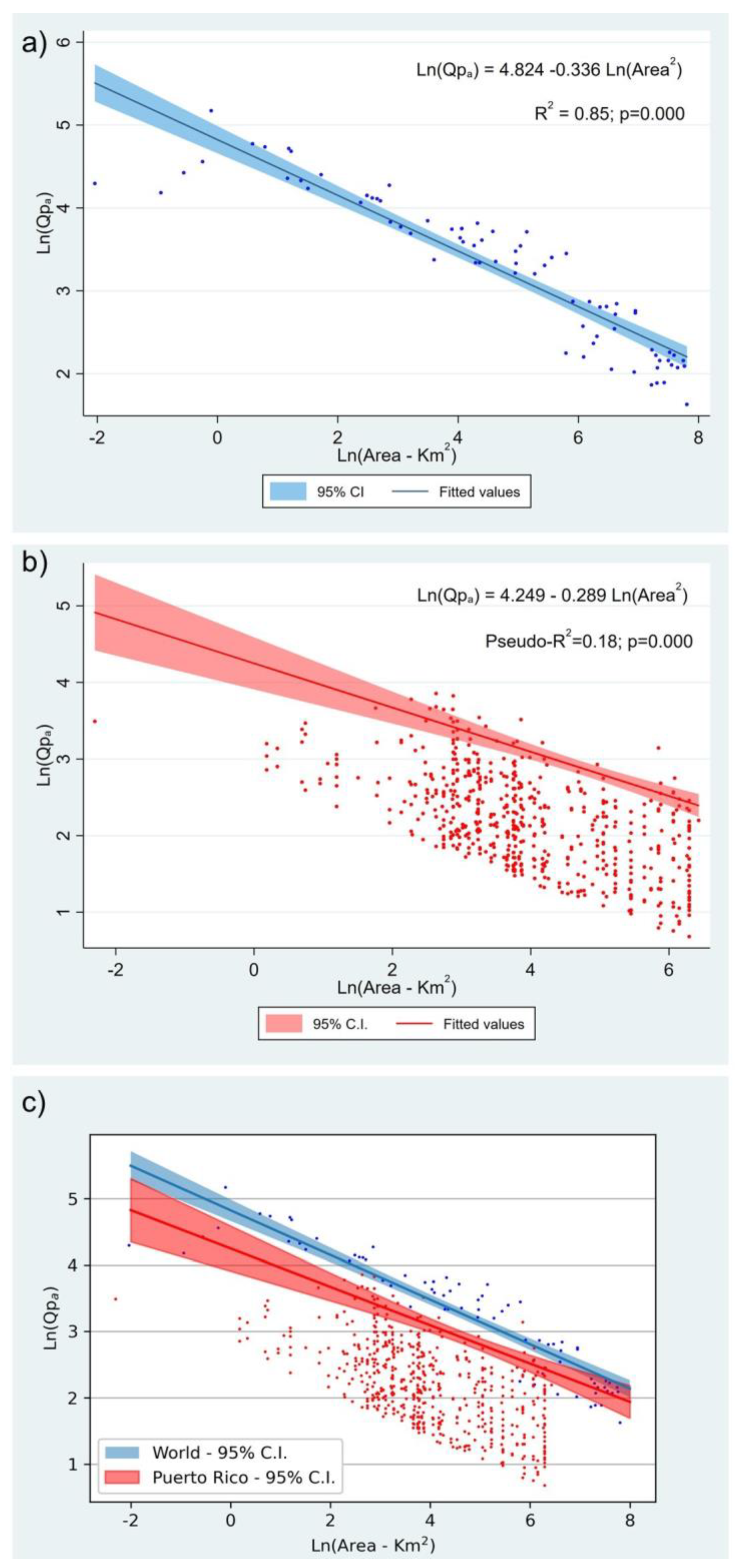
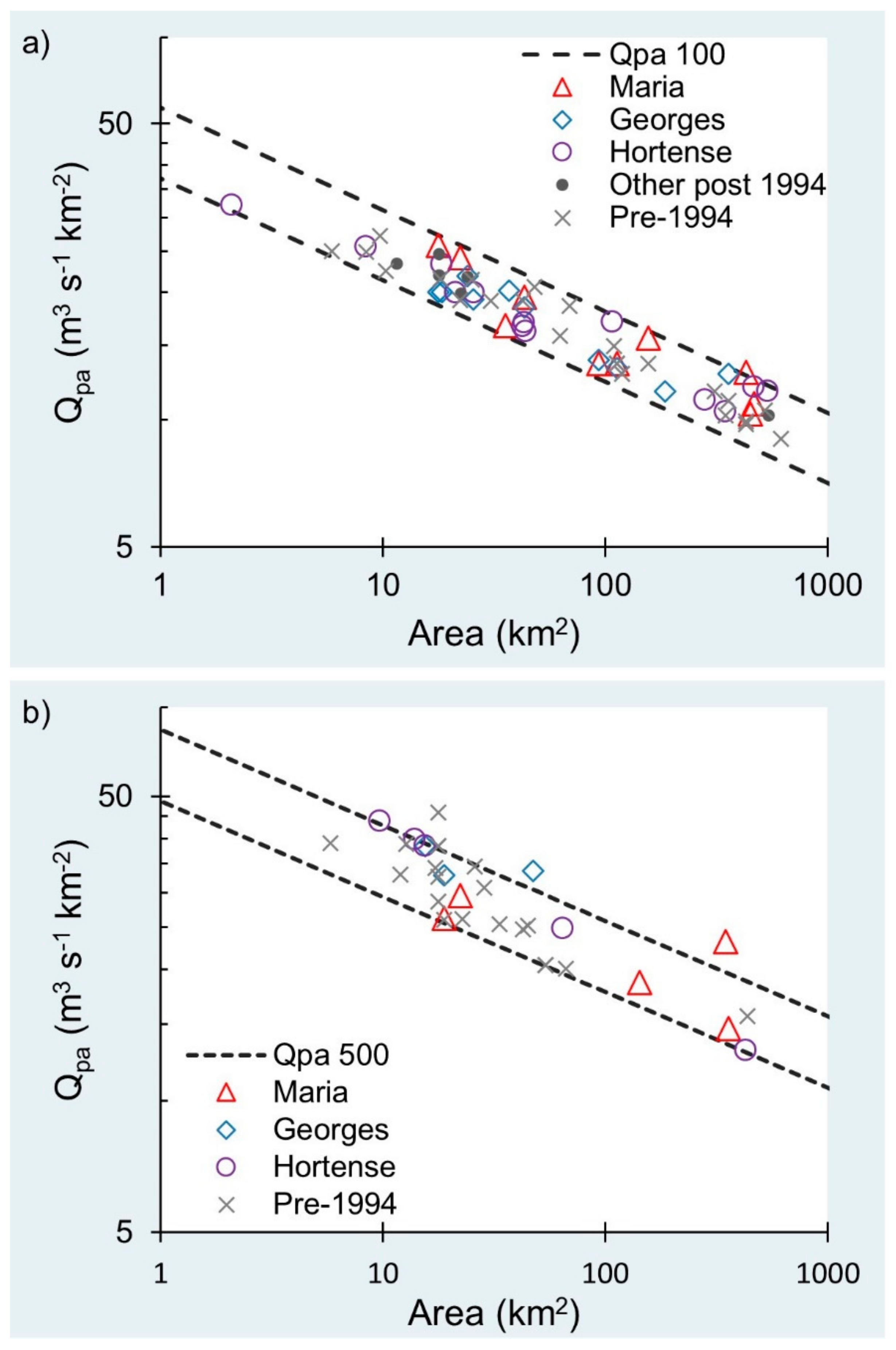
3.2. Worldwide and PR Qpa Envelopes
3.3. Qpa and Values by Region
3.4. Implications on Flood Management for Puerto Rico
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alexander, D. Natural Disasters; Routledge: London, UK, 2020. [Google Scholar]
- Smith, K.; Ward, R. Floods: Physical Processes and Human Impacts; John Wiley & Sons: New York, NY, USA, 1998. [Google Scholar]
- Adhikari, P.; Hong, Y.; Douglas, K.R.; Kirschbaum, D.B.; Gourley, J.; Adler, R.; Robert Brakenridge, G. A digitized global flood inventory (1998–2008): Compilation and preliminary results. Nat. Hazards 2010, 55, 405–422. [Google Scholar] [CrossRef]
- Kron, W.; Berz, G. Flood disasters and climate change, trends and options, a (Re-)Insurer’s view. In Global Change, Enough Water for All? Lozin, H.G.J.L., Hupfer, P., Menzel, L., Schonwiese, C.D., Eds.; University of Hamburg: Hamburg, Germany, 2007; pp. 268–273. [Google Scholar]
- Hu, P.; Zhang, Q.; Shi, P.; Chen, B.; Fang, J. Flood-induced mortality across the globe: Spatiotemporal pattern and influencing factors. Sci. Total Environ. 2018, 643, 171–182. [Google Scholar] [CrossRef] [PubMed]
- Baradaranshoraka, M.; Pinelli, J.-P.; Gurley, K.; Peng, X.; Zhao, M. Hurricane Wind versus Storm Surge Damage in the Context of a Risk Prediction Model. J. Struct. Eng. 2017, 143, 04017103. [Google Scholar] [CrossRef]
- Liao, Z.; Hong, Y.; Kirschbaum, D.; Liu, C. Assessment of shallow landslides from Hurricane Mitch in central America using a physically based model. Environ. Earth Sci. 2012, 66, 1697–1705. [Google Scholar] [CrossRef]
- Negri, A.J.; Burkardt, N.; Golden, J.H.; Halverson, J.B.; Huffman, G.J.; Larsen, M.C.; McGinley, J.A.; Updike, R.G.; Verdin, J.P.; Wieczorek, G.F. The hurricane-flood-landslide continuum. Bull. Am. Meteorol. Soc. 2005, 86, 1241–1247. [Google Scholar] [CrossRef]
- Rappaport, E.N. Fatalities in the United States from Atlantic Tropical Cyclones: New Data and Interpretation. Bull. Am. Meteorol. Soc. 2014, 95, 341–346. [Google Scholar] [CrossRef]
- Geerts, B.; Heymsfield, G.M.; Tian, L.; Halverson, J.B.; Guillory, A.; Mejia, M.I. Hurricane Georges’s Landfall in the Dominican Republic: Detailed Airborne Doppler Radar Imagery. Bull. Am. Meteorol. Soc. 2000, 81, 999–1018. [Google Scholar] [CrossRef]
- Lee, C.-S.; Huang, L.-R.; Shen, H.-S.; Wang, S.-T. A climatology model for forecasting typhoon rainfall in Taiwan. Nat. Hazards 2006, 37, 87–105. [Google Scholar] [CrossRef]
- Saito, H.; Korup, O.; Uchida, T.; Hayashi, S.; Oguchi, T. Rainfall conditions, typhoon frequency, and contemporary landslide erosion in Japan. Geology 2014, 42, 999–1002. [Google Scholar] [CrossRef]
- Whitfield, P.H. Floods in future climates: A review. J. Flood Risk Manag. 2012, 5, 336–365. [Google Scholar] [CrossRef]
- Arnell, N.W.; Gosling, S.N. The impacts of climate change on river flood risk at the global scale. Clim. Chang. 2016, 134, 387–401. [Google Scholar] [CrossRef]
- Kaenzig, R.; Piguet, E. Migration and climate change in Latin America and the Caribbean. In People on the Move in a Changing Climate; Piguet, E., Laczko, F., Eds.; Spinger: Dordrecht, The Netherlands, 2014; pp. 155–176. [Google Scholar]
- Lau, W.K.M.; Zhou, Y.P. Observed recent trends in tropical cyclone rainfall over the North Atlantic and the North Pacific. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Patricola, C.M.; Wehner, M.F. Anthropogenic influences on major tropical cyclone events. Nature 2018, 563, 339–346. [Google Scholar] [CrossRef]
- Kossin, J.P. A global slowdown of tropical-cyclone translation speed. Nature 2018, 558, 104–107. [Google Scholar] [CrossRef]
- Wilby, R.L.; Keenan, R. Adapting to flood risk under climate change. Prog. Phys. Geogr. 2012, 36, 348–378. [Google Scholar] [CrossRef]
- O’Connor, J.E.; Grant, G.E.; Costa, J.E. The geology and geography of floods. Anc. Floods Mod. Hazards Appl. Paleoflood Hydrol. Water Sci. Appl. Am. Geophys. Union 2002, 5, 359–395. [Google Scholar]
- O’Connor, J.E.; Costa, J.E. Spatial distribution of the largest rainfall-runoff floods from basins between 2.6 and 26,000 km2 in the United States and Puerto Rico. Water Resour. Res. 2004, 40, W01107. [Google Scholar] [CrossRef]
- Costa, J.E. A comparison of the largest rainfall-runoff floods in the United States with those of the People’s Republic of China and the world. J. Hydrol. 1987, 96, 101–115. [Google Scholar] [CrossRef]
- Rakhecha, P. Highest floods in India. Iahs Publ. 2002, 271, 167–172. [Google Scholar]
- Herschy, R. World Catalogue of Maximum Observed Floods; Issue 284; IAHS-AISH Publication: Oxfordshire, UK, 2003. [Google Scholar]
- Rodier, J.A.; Roche, M. World Catalogue of Maximum Observed Floods; IAHS-AISH Publication: Oxfordshire, UK, 1984; p. 354. [Google Scholar]
- Herschy, R. The world’s maximum observed floods. Flow Meas. Instrum. 2002, 13, 231–235. [Google Scholar] [CrossRef]
- Castellarin, A. Probabilistic envelope curves for design flood estimation at ungauged sites. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Gaume, E.; Bain, V.; Bernardara, P.; Newinger, O.; Barbuc, M.; Bateman, A.; Blaškovičová, L.; Blöschl, G.; Borga, M.; Dumitrescu, A. A compilation of data on European flash floods. J. Hydrol. 2009, 367, 70–78. [Google Scholar] [CrossRef]
- Pitlick, J. Relation between peak flows, precipitation, and physiography for five mountainous regions in the western USA. J. Hydrol. 1994, 158, 219–240. [Google Scholar] [CrossRef]
- Costa, J.E. Hydraulics and basin morphometry of the largest flash floods in the conterminous United States. J. Hydrol. 1987, 93, 313–338. [Google Scholar] [CrossRef]
- Ogden, F.L. Evidence of equilibrium peak runoff rates in steep tropical terrain on the island of Dominica during Tropical Storm Erika, August 27, 2015. J. Hydrol. 2016, 542, 35–46. [Google Scholar] [CrossRef]
- US-Geological-Survey. National Water Information System Data Available on the World Wide Web; US Geological Survey: Reston, VA, USA, 2021. [CrossRef]
- Smith, R.B.; Minder, J.R.; Nugent, A.D.; Storelvmo, T.; Kirshbaum, D.J.; Warren, R.; Lareau, N.; Palany, P.; James, A.; French, J. Orographic precipitation in the tropics: The Dominica Experiment. Bull. Am. Meteorol. Soc. 2012, 93, 1567–1579. [Google Scholar] [CrossRef]
- Vélez, A.; Martin-Vide, J.; Royé, D.; Santaella, O. Spatial analysis of daily precipitation concentration in Puerto Rico. Theor. Appl. Climatol. 2019, 136, 1347–1355. [Google Scholar] [CrossRef]
- Laing, A.G. Cases of Heavy Precipitation and Flash Floods in the Caribbean during El Niño Winters. J. Hydrometeorol. 2004, 5, 577–594. [Google Scholar] [CrossRef]
- Jury, M.R.; Sanchez, D.M. Composite Meteorological Forcing of Puerto Rican Springtime Flood Events. Weather Forecast. 2009, 24, 262–271. [Google Scholar] [CrossRef]
- Rasmussen, T. Natural disasters and their macroeconomic implications. In The Caribbean: From Vulnerability to Sustained Growth; International Monetary Fund: Washington, DC, USA, 2006; pp. 181–205. [Google Scholar]
- Kossin, J.P.; Camargo, S.J.; Sitkowski, M. Climate Modulation of North Atlantic Hurricane Tracks. J. Clim. 2010, 23, 3057–3076. [Google Scholar] [CrossRef]
- Pielke, R.A.; Rubiera, J.; Landsea, C.; Fernández, M.L.; Klein, R. Hurricane Vulnerability in Latin America and The Caribbean: Normalized Damage and Loss Potentials. Nat. Hazards Rev. 2003, 4, 101–114. [Google Scholar] [CrossRef]
- López-Marrero, T. An integrative approach to study and promote natural hazards adaptive capacity: A case study of two flood-prone communities in Puerto Rico. Geogr. J. 2010, 176, 150–163. [Google Scholar] [CrossRef]
- López-Marrero, T.; Hampton, J.; Vergara, E.; Quiroz, J.; Simovic, K.; Arevalo, H. Hazards and Disasters in the Insular Caribbean: A systematic literature review. Caribb. Geogr 2013, 18, 84–104. [Google Scholar]
- Chery, G.; Francis, L.; Hunte, S.-A.; Leon, P. Epidemiology of human leptospirosis in Saint Lucia, 2010–2017. Rev Panam Salud Publica 2020, 44, e160. [Google Scholar] [CrossRef]
- Hayhoe, K. Quantifying Key Drivers of Climate Variability and Change for Puerto Rico and the Caribbean: Final Report. 2013, p. 52. Available online: http://www.pr-ccc.org/wp-content/uploads/2014/08/PP_1-52_Hayhoe_Caribbean_Final_Report.pdf (accessed on 31 January 2021).
- Khalyani, A.H.; Gould, W.A.; Harmsen, E.; Terando, A.; Quinones, M.; Collazo, J.A. Climate change implications for tropical islands: Interpolating and interpreting statistically downscaled GCM projections for management and planning. J. Appl. Meteorol. Climatol. 2016, 55, 265–282. [Google Scholar] [CrossRef]
- Peterson, T.C.; Taylor, M.A.; Demeritte, R.; Duncombe, D.L.; Burton, S.; Thompson, F.; Porter, A.; Mercedes, M.; Villegas, E.; Semexant Fils, R.; et al. Recent changes in climate extremes in the Caribbean region. J. Geophys. Res. Atmos. 2002, 107, ACL 16-1–ACL 16-9. [Google Scholar] [CrossRef]
- Taylor, M.A.; Stephenson, T.S.; Chen, A.A.; Stephenson, K.A. Climate change and the Caribbean: Review and response. Caribb. Stud. 2012, 40, 169–200. [Google Scholar] [CrossRef]
- Dittmann, R.H. Annual Flood Death Statistics Per State Per Capita for the United States and Puerto Rico during the Period 1959–1991 (NOAA Technical Memorandum NWS SR-153, Issue; National Weather Service: Silver Spring, MD, USA, 1994. [Google Scholar]
- Hernández Ayala, J.J.; Matyas, C.J. Tropical cyclone rainfall over Puerto Rico and its relations to environmental and storm-specific factors. Int. J. Climatol. 2016, 36, 2223–2237. [Google Scholar] [CrossRef]
- Ramírez, A.; De Jesús-Crespo, R.; Martinó-Cardona, D.M.; Martínez-Rivera, N.; Burgos-Caraballo, S. Urban streams in Puerto Rico: What can we learn from the tropics? J. North Am. Benthol. Soc. 2009, 28, 1070–1079. [Google Scholar] [CrossRef]
- Scatena, F.; Larsen, M.C. Physical aspects of hurricane Hugo in Puerto Rico. Biotropica 1991, 317–323. [Google Scholar] [CrossRef]
- Schellekens, J.; Scatena, F.N.; Bruijnzeel, L.A.; van Dijk, A.I.J.M.; Groen, M.M.A.; van Hogezand, R.J.P. Stormflow generation in a small rainforest catchment in the Luquillo Experimental Forest, Puerto Rico. Hydrol. Process. 2004, 18, 505–530. [Google Scholar] [CrossRef]
- Ahmad, R.; Scatena, F.; Gupta, A. Morphology and sedimentation in Caribbean montane streams: Examples from Jamaica and Puerto Rico. Sediment. Geol. 1993, 85, 157–169. [Google Scholar] [CrossRef]
- Pike, A.S.; Scatena, F.N.; Wohl, E.E. Lithological and fluvial controls on the geomorphology of tropical montane stream channels in Puerto Rico. Earth Surf. Process. Landf. 2010, 35, 1402–1417. [Google Scholar] [CrossRef]
- Staes, C.; Orengo, J.C.; Malilay, J.; Rullán, J.; Noji, E. Deaths due to flash floods in Puerto Rico, January 1992: Implications for prevention. Int. J. Epidemiol. 1994, 23, 968–975. [Google Scholar] [CrossRef]
- Torres-Sierra, H. Flood of January 5–6, 1992, in Puerto Rico; US Department of the Interior: Washington, DC, USA; U.S. Geological Survey: Reston, VA, USA, 1996.
- Palm, R.; Hodgson, M.E. Natural Hazards in Puerto Rico. Geogr. Rev. 1993, 280–289. [Google Scholar] [CrossRef]
- Torres Molina, L.E. Floods Forecast in the Caribbean. In Flood Risk Management; InTech: London, UK, 2017; pp. 55–77. [Google Scholar]
- Smith, J.A.; Sturdevant-Rees, P.; Baeck, M.L.; Larsen, M.C. Tropical cyclones and the flood hydrology of Puerto Rico. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Hernández Ayala, J.J.; Keellings, D.; Waylen, P.R.; Matyas, C.J. Extreme floods and their relationship with tropical cyclones in Puerto Rico. Hydrol. Sci. J. 2017, 62, 2103–2119. [Google Scholar] [CrossRef]
- Terry, J.P.; Kostaschuk, R.A.; Wotling, G. Features of tropical cyclone-induced flood peaks on Grande Terre, New Caledonia. Water Environ. J. 2008, 22, 177–183. [Google Scholar] [CrossRef]
- Byrne Sr, M.J. Monitoring Storm Tide, Flooding, and Precipitation from Hurricane Maria in Puerto Rico and the US Virgin Islands, September 2017; Open-File Report 2331-1258; US Geological Survey: Reston, VA, USA, 2019.
- Li, Y.; Wright, D.B.; Byrne, P.K. The Influence of tropical cyclones on the evolution of river conveyance capacity in Puerto Rico. Water Resour. Res. 2020, 56, e2020WR027971. [Google Scholar] [CrossRef]
- Monroe, W.H. Some Tropical Landforms of Puerto Rico; Professional Paper 1159; US Geological Survey: Reston, VA, USA, 1980.
- Ewel, J.J.; Whitmore, J.L. The Ecological Life Zones of Puerto Rico and the U.S. Virgin Islands; Research Paper, Issue; United States Department of Agriculture: Washington, DC, USA, 1973.
- Bawiec, W.J. Geologic Terranes of Puerto Rico; U.S. Geological Survey: Reston, VA, USA, 1998; pp. 59–71.
- Soto, S.; Pintó, J. Delineation of natural landscape units for Puerto Rico. Appl. Geogr. 2010, 30, 720–730. [Google Scholar] [CrossRef]
- Parés-Ramos, I.K.; Gould, W.A.; Aide, T.M. Agricultural abandonment, suburban growth, and forest expansion in Puerto Rico between 1991 and 2000. Ecol. Soc. 2008, 13. [Google Scholar] [CrossRef]
- Helmer, E.; Ramos, O.; López, T.d.M.; Quinones, M.; Diaz, W. Mapping the forest type and land cover of Puerto Rico, a component of the Caribbean biodiversity hotspot. Caribb. J. Sci. 2002, 38, 165–183. [Google Scholar]
- Grau, H.R.; Aide, T.M.; Zimmerman, J.K.; Thomlinson, J.R.; Helmer, E.; Zou, X. The ecological consequences of socioeconomic and land-use changes in postagriculture Puerto Rico. BioScience 2003, 53, 1159–1168. [Google Scholar] [CrossRef]
- Rudel, T.K.; Perez-Lugo, M.; Zichal, H. When fields revert to forest: Development and spontaneous reforestation in post-war Puerto Rico. Prof. Geogr. 2000, 52, 386–397. [Google Scholar] [CrossRef]
- Gould, W.A.; Alarcón, C.; Fevold, B.; Jiménez, M.E.; Martinuzzi, S.; Potts, G.; Quiñones, M.; Solórzano, M.; Ventosa, E. The Puerto Rico Gap Analysis Project Volume 1: Land Cover, Vertebrate Species Distributions, and Land Stewardship; General Technical Report. IITF-39, 1; United States Department of Agriculture: Washington, DC, USA, 2008.
- Jury, M.; Malmgren, B.A.; Winter, A. Subregional precipitation climate of the Caribbean and relationships with ENSO and NAO. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Hosannah, N.; González, J.; Lunger, C.; Niyogi, D. Impacts of local convective processes on rain on the Caribbean Island of Puerto Rico. J. Geophys. Res. Atmos. 2019, 124, 6009–6026. [Google Scholar] [CrossRef]
- Méndez-Lázaro, P.A.; Nieves-Santiango, A.; Miranda-Bermúdez, J. Trends in total rainfall, heavy rain events, and number of dry days in San Juan, Puerto Rico, 1955-2009. Ecol. Soc. 2014, 19. [Google Scholar] [CrossRef][Green Version]
- Hernández Ayala, J.J.; Matyas, C.J. Spatial distribution of tropical cyclone rainfall and its contribution to the climatology of Puerto Rico. Phys. Geogr. 2018, 39, 1–20. [Google Scholar] [CrossRef]
- Thomas, M.A.; Mirus, B.B.; Smith, J.B. Hillslopes in humid-tropical climates aren’t always wet: Implications for hydrologic response and landslide initiation in Puerto Rico. Hydrol. Process. 2020, 34, 4307–4318. [Google Scholar] [CrossRef]
- Schellekens, J. The interception and runoff generating processes in the Bisley catchment, Luquillo Experimental Forest, Puerto Rico. Phys. Chem. Earthpart B Hydrol. Ocean. Atmos. 2000, 25, 659–664. [Google Scholar] [CrossRef]
- Ramos-Scharrón, C.E.; Thomaz, E.L. Runoff development and soil erosion in a wet tropical montane setting under coffee cultivation. Land Degrad. Dev. 2017, 28, 936–945. [Google Scholar] [CrossRef]
- Birkinshaw, S.J.; Bathurst, J.C.; Iroumé, A.; Palacios, H. The effect of forest cover on peak flow and sediment discharge—an integrated field and modelling study in central–southern Chile. Hydrol. Process. 2011, 25, 1284–1297. [Google Scholar] [CrossRef]
- Beschta, R.; Pyles, M.; Skaugset, A.; Surfleet, C. Peakflow responses to forest practices in the western cascades of Oregon, USA. J. Hydrol. 2000, 233, 102–120. [Google Scholar] [CrossRef]
- Harmsen, E.W.; Goyal, M.R.; Torres-Justiniano, S. Estimating evapotranspiration in Puerto Rico. J. Agric. Univ. Puerto Rico 2002, 86, 35–54. [Google Scholar] [CrossRef]
- Ramos-Scharrón, C.E.; Arima, E. Hurricane Maria’s Precipitation Signature in Puerto Rico: A Conceivable Presage of Rains to Come. Sci. Rep. 2019, 9, 15612. [Google Scholar] [CrossRef]
- López, M.A.; Fields, F.K. A Proposed Streamflow-Data Program for Puerto Rico; Caribbean District, Open File Report, Issue; US Geological Survey: Reston, VA, USA, 1970.
- López, M.A.; Colón-Dieppa, E.; Cobb, E.D. Floods in Puerto Rico, Magnitude and Frequency; Issue 78–141; US Geological Survey, Water Resources Investigations: Reston, VA, USA, 1979.
- Haire, W.J. Flood of October 5–10, 1970 in Puerto Rico; Water-Resources Bulletin, Issue; National Weather Service: Silver Spring, MD, USA, 1972. [Google Scholar]
- Barnes, H.H.; Bogart, D.B. Floods of September 6, 1960, in Eastern Puerto Rico; US Government Printing Office: Washington, DC, USA, 1961; Volume 451.
- Turnipseed, D.P.; Sauer, V.B. Discharge Measurements at Gaging Stations; US Geological Survey, Chapter 8 of Book 3, Section A, Techniques and Methods 3; US Geological Survey: Reston, VA, USA, 2010; p. 87.
- Dalrymple, T.; Benson, M. Measurement of Peak Discharge by the Slope-Area Method; US Geological Survey: Reston, VA, USA, 1968.
- Jarrett, R.D. Errors in slope-area computations of peak discharges in mountain streams. J. Hydrol. 1987, 96, 53–67. [Google Scholar] [CrossRef]
- Cook, J.L. Quantifying peak discharges for historical floods. J. Hydrol. 1987, 96, 29–40. [Google Scholar] [CrossRef]
- Li, C.; Wang, G.; Li, R. Maximum observed floods in China. Hydrol. Sci. J. 2013, 58, 728–735. [Google Scholar] [CrossRef]
- Cameron, A.C.; Trivedi, P.K. Microeconometrics: Methods and Applications; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Wooldridge, J.M. Econometric Analysis of Cross Section and Panel Data; MIT Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Waldmann, E. Quantile regression: A short story on how and why. Stat. Model. 2018, 18, 203–218. [Google Scholar] [CrossRef]
- Ramos-Ginés, O. Estimation of magnitude and frequency of floods for streams in Puerto Rico: New empirical models. Water Resour. Investig. Rep. 1999, 99, 4142. [Google Scholar]
- Daly, C.; Helmer, E.H.; Quiñones, M. Mapping the climate of Puerto Rico, Vieques, and Culebra. Int. J. Climatol. A J. R. Meteorol. Soc. 2003, 23, 1359–1381. [Google Scholar] [CrossRef]
- Carter, M.; Elsner, J. A statistical method for forecasting rainfall over Puerto Rico. Weather Forecast. 1997, 12, 515–525. [Google Scholar] [CrossRef]
- Carter, M.M.; Elsner, J. Convective rainfall regions of Puerto Rico. Int. J. Climatol. A J. R. Meteorol. Soc. 1996, 16, 1033–1043. [Google Scholar] [CrossRef]
- Malmgren, B.A.; Winter, A. Climate zonation in Puerto Rico based on principal components analysis and an artificial neural network. J. Clim. 1999, 12, 977–985. [Google Scholar] [CrossRef]
- National-Weather-Service. Public geographic areas of responsibility. In National Weather Service Manual 10-507; Department of Commerce, National Oceanic & Atmospheric Administration: Washington, DC, USA, 2018. [Google Scholar]
- López-Trujillo, D. Real Time Flood Alert System (RTFAS) for Puerto Rico; US Department of the Interior, US Geological Survey: Reston, VA, USA, 2010.
- Zar, J.H. Biostatistical Analysis; Pearson Education India: Delhi, India, 1999. [Google Scholar]
- Soler-López, L.R.; Gómez-Gómez, F. Sedimentation Survey of Lago Loíza, Puerto Rico, January 2004; Scientific Investigations Report, 2005-5239; US Department of the Interior: Washington, DC, USA; U.S. Geological Survey: Reston, VA, USA, 2005.
- Gellis, A.C.; Webb, R.M.; McIntyre, S.C.; Wolfe, W.J. Land-use effects on erosion, sediment yields, and reservoir sedimentation: A case study in the Lago Loiza basin, Puerto Rico. Phys. Geogr. 2006, 27, 39–69. [Google Scholar] [CrossRef]
- Pralle, S. Drawing lines: FEMA and the politics of mapping flood zones. Clim. Chang. 2019, 152, 227–237. [Google Scholar] [CrossRef]
- FEMA. Mitigation Assessment Team Report—Hurricanes Irma and Maria in Puerto Rico, Building Performance Observations, Recommendations, and Technical Guidance; FEMA P-2020: Washington, DC, USA, 2018. [Google Scholar]
- England, J.F., Jr.; Cohn, T.A.; Faber, B.A.; Stedinger, J.R.; Thomas, W.O., Jr.; Veilleux, A.G.; Kiang, J.E.; Mason, R.R., Jr. Guidelines for Determining Flood Flow Frequency—Bulletin 17C (1411342232); US Geological Survey: Reston, VA, USA, 2019.
- STARR-II. Puerto Rico Advisory Data and Products Post-Hurricanes Irma and Maria; FEMA Contract No. HSFE60-15-D-0005. 2018; p. 109. Available online: http://cedd.pr.gov/fema/wp-content/uploads/2018/06/Puerto_Rico_Advisory_Report_2018.05.23_Final_English.pdf (accessed on 31 March 2021).
- Maurer, E.P.; Kayser, G.; Doyle, L.; Wood, A.W. Adjusting flood peak frequency changes to account for climate change impacts in the western United States. J. Water Resour. Plan. Manag. 2018, 144, 05017025. [Google Scholar] [CrossRef]
- Lim, Y.-K.; Schubert, S.D.; Kovach, R.; Molod, A.M.; Pawson, S. The roles of climate change and climate variability in the 2017 Atlantic hurricane season. Sci. Rep. 2018, 8, 1–10. [Google Scholar] [CrossRef]
- Keellings, D.; Ayala, J.J.H. Extreme rainfall associated with Hurricane Maria over Puerto Rico and its connections to climate variability and change. Geophys. Res. Lett. 2019, 46, 2964–2973. [Google Scholar] [CrossRef]
| TC Name | Year | Area Range (km2) | # Qpa Values | Range of Qpa Values (m3 s−1 km−2) | ||
|---|---|---|---|---|---|---|
| San Ciriaco | 1899 | 48.2–540 | 9 | 8.2–20.6 | 9 | 8.7–18.6 |
| San Felipe II | 1928 | 53.9–540 | 9 | 4.3–15.8 | 9 | 2.0–10.9 |
| San Ciprián | 1932 | 53.9–429 | 3 | 8.8–14.7 | 3 | 4.0–7.1 |
| Santa Clara | 1956 | 39.9–347 | 3 | 1.8–6.5 | 3 | 4.3–6.6 |
| Donna | 1960 | 2.0–619 | 39 | 0.57–45.8 | 34 | 2.0–12.5 |
| TD-15 | 1970 | 1.4–540 | 80 | 0.56–39.1 | 73 | 3.1–17.6 |
| Eloisa | 1975 | 5.9–540 | 42 | 0.99–30.8 | 42 | 3.2–16.2 |
| David | 1979 | 7.1–540 | 40 | 1.0–16.0 | 40 | 3.7–9.1 |
| Fredric | 1979 | 12.2–540 | 15 | 0.28–11.0 | 15 | 0.9–9.3 |
| Debbie | 1982 | 13.9–358 | 12 | 1.0–16.7 | 12 | 1.8–9.9 |
| Isabel | 1985 | 0.2–540 | 44 | 1.4–38.8 | 42 | 4.6–16.3 |
| Emily | 1987 | 113–540 | 6 | 0.006–0.1 | 6 | 0.3–0.8 |
| Hugo | 1989 | 0.2–540 | 35 | 0.01–32.6 | 34 | 1.8–8.4 |
| Cindy | 1993 | 3.3–540 | 38 | 0.007–1.7 | 38 | 0.4–2.3 |
| Luis | 1995 | 3.3–540 | 40 | 0.0004–5.1 | 40 | 1.0–2.6 |
| Marilyn | 1995 | 3.3–540 | 45 | 0.013–4.0 | 44 | 1.8–4.6 |
| Hortense | 1996 | 0.1–540 | 66 | 0.15–80.4 | 65 | 2.5–13.3 |
| Grace | 1997 | 2.1–540 | 52 | 0.014–16.7 | 52 | 1.4–6.3 |
| Georges | 1998 | 0.1–540 | 58 | 0.57–82.2 | 57 | 7.2–18.9 |
| Lenny | 1999 | 2.1–540 | 57 | 0.006–7.5 | 57 | 1.0–5.8 |
| Jose | 1999 | 3.3–540 | 47 | 0.007–2.2 | 47 | 0.5–2.6 |
| Debby | 2000 | 2.1–540 | 57 | 0.06–17.3 | 57 | 1.6–9.6 |
| Dean | 2001 | 1.2–540 | 50 | 0.003–22.0 | 50 | 0.9–7.4 |
| Mindy | 2003 | 1.2–540 | 57 | 0.05–9.1 | 57 | 1.3–3.9 |
| Odette | 2003 | 1.2–540 | 55 | 0.04–12.6 | 55 | 1.0–3.5 |
| Frances | 2004 | 1.2–540 | 58 | 0.003–2.5 | 58 | 0.4–1.8 |
| Jeanne | 2004 | 0.1–540 | 62 | 0.13–32.8 | 62 | 2.5–10.3 |
| Chris | 2006 | 1.2–540 | 57 | 0.002–2.3 | 57 | 0.02–1.6 |
| Noel | 2007 | 1.2–540 | 60 | 0.019–24.5 | 60 | 1.0–7.0 |
| Olga | 2007 | 1.2–540 | 59 | 0.028–21.8 | 59 | 1.6–5.9 |
| Fay | 2008 | 1.2–540 | 56 | 0.0001–2.6 | 56 | 1.1–3.1 |
| Kyle | 2008 | 1.2–540 | 59 | 0.12–47.3 | 59 | 1.2–16.9 |
| Erika | 2009 | 3.3–540 | 57 | 0.01–5.2 | 57 | 0.30–2.5 |
| Earl | 2010 | 1.2–540 | 55 | 0.06–5.5 | 55 | 1.3–4.0 |
| Otto | 2010 | 1.2–540 | 57 | 0.06–8.0 | 57 | 2.0–10.5 |
| Irene | 2011 | 0.1–540 | 61 | 0.23–18.7 | 61 | 1.8–11.3 |
| Erika | 2015 | 1.2–540 | 61 | 0.0001–3.5 | 61 | 0.2–2.5 |
| Irma | 2017 | 1.2–540 | 62 | 0.31–10.8 | 62 | 1.7–7.0 |
| Maria | 2017 | 1.2–540 | 67 | 0.81–29.6 | 67 | 7.7–19.0 |
| Isaias | 2020 | 1.2–540 | 66 | 0.005–10.8 | 66 | 2.7–8.6 |
| Laura | 2020 | 1.2–540 | 66 | 0.005–5.9 | 66 | 0.02–0.6 |
| NWS Zone | # Qpa Values | Area Range (km2) | |
|---|---|---|---|
| 1 | 40 | 40 | 19.4–186 |
| 2 | 240 | 237 | 0.1–45.6 |
| 3 | 164 | 162 | 3.8–94.8 |
| 4 | 613 | 608 | 1.2–619 |
| 6 | 359 | 357 | 1.4–429 |
| 7 | 217 | 212 | 1.4–118 |
| 9 | 289 | 288 | 8.2–524 |
| TC | Year | Station Name | Station ID | Area (km2) | NWS Zone | Qpa (m3 s−1 km−2) | |
|---|---|---|---|---|---|---|---|
| San Ciriaco | 1899 | RG Arecibo at Dos Bocas Dam | 50027100 | 438 | 9 | 15.7 | 18.6 |
| San Ciriaco | 1899 | RG Arecibo at Cambalache | 50029000 | 524 | 9 | 10.5 | 14.8 |
| Donna | 1960 | R Turabo near La Plaza | 50053000 | 17.7 | 4 | 38.4 | 11.0 |
| Donna | 1960 | R Valenciano near las Piedras | 50056000 | 17.8 | 4 | 45.8 | 8.5 |
| Donna | 1960 | R Humacao at Humacao | None | 25.9 | 2 | 34.5 | -- |
| TD-15 | 1970 | R Turabo near La Plaza | 50053000 | 17.7 | 4 | 38.4 | 12.6 |
| Eloisa | 1975 | R Blanco at Florida | 50075500 | 28.5 | 2 | 30.8 | 8.6 |
| Hortense | 1996 | RG Manatí at Manatí | 50038100 | 429 | 6 | 13.1 | 9.7 |
| Hortense | 1996 | R de La Plata below La Plata Dam | 50045010 | 468 | 4 | 11.9 | 9.5 |
| Hortense | 1996 | RG Loíza at Quebrada Arenas | 50050900 | 15.5 | 4 | 38.4 | 10.6 |
| Hortense | 1996 | RG Loíza at 183 San Lorenzo | 50051800 | 64.7 | 4 | 24.9 | 11.5 |
| Hortense | 1996 | RG Loíza below dam | 50059050 | 540 | 4 | 11.7 | 12.5 |
| Georges | 1998 | RG Loíza at Quebrada Arenas | 50050900 | 15.5 | 4 | 38.4 | 10.1 |
| Georges | 1998 | RG de Patillas near Patillas | 50092000 | 47.4 | 3 | 33.6 | 7.8 |
| Georges | 1998 | RG Añasco near San Sebastián | 50144000 | 358 | 9 | 12.8 | 14.9 |
| Kyle | 2008 | R Maunabo at Lizas | 50090500 | 13.9 | 3 | 47.3 | 16.1 |
| Maria | 2017 | RG Manatí near Morovis | 50031200 | 143 | 6 | 18.7 | 19.0 |
| Maria | 2017 | RG Manatí at Ciales | 50035000 | 347 | 6 | 23.2 | 18.2 |
| Maria | 2017 | RG Manatí at Manatí | 50038100 | 429 | 6 | 12.9 | 18.3 |
| Maria | 2017 | RG Añasco near San Sebastián | 50144000 | 358 | 9 | 14.6 | 8.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramos-Scharrón, C.E.; Garnett, C.T.; Arima, E.Y. A Catalogue of Tropical Cyclone Induced Instantaneous Peak Flows Recorded in Puerto Rico and a Comparison with the World’s Maxima. Hydrology 2021, 8, 84. https://doi.org/10.3390/hydrology8020084
Ramos-Scharrón CE, Garnett CT, Arima EY. A Catalogue of Tropical Cyclone Induced Instantaneous Peak Flows Recorded in Puerto Rico and a Comparison with the World’s Maxima. Hydrology. 2021; 8(2):84. https://doi.org/10.3390/hydrology8020084
Chicago/Turabian StyleRamos-Scharrón, Carlos E., Caroline T. Garnett, and Eugenio Y. Arima. 2021. "A Catalogue of Tropical Cyclone Induced Instantaneous Peak Flows Recorded in Puerto Rico and a Comparison with the World’s Maxima" Hydrology 8, no. 2: 84. https://doi.org/10.3390/hydrology8020084
APA StyleRamos-Scharrón, C. E., Garnett, C. T., & Arima, E. Y. (2021). A Catalogue of Tropical Cyclone Induced Instantaneous Peak Flows Recorded in Puerto Rico and a Comparison with the World’s Maxima. Hydrology, 8(2), 84. https://doi.org/10.3390/hydrology8020084








