Generation of over 1000 Diffraction Spots from 2D Graded Photonic Super-Crystals
Abstract
1. Introduction
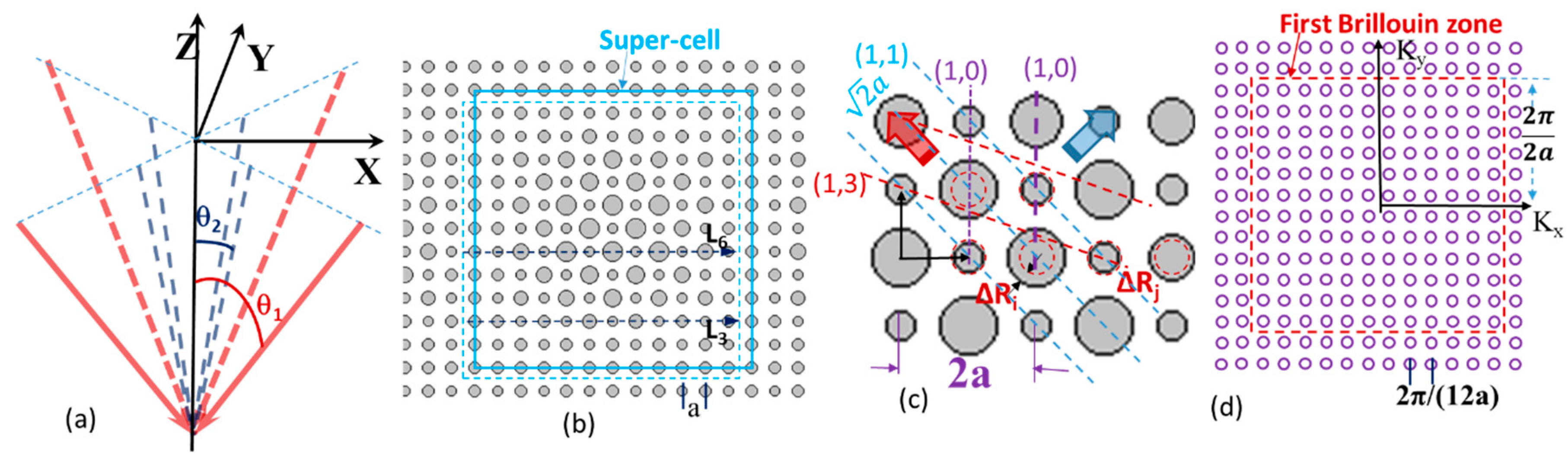
2. Fabrication and Simulation Methods
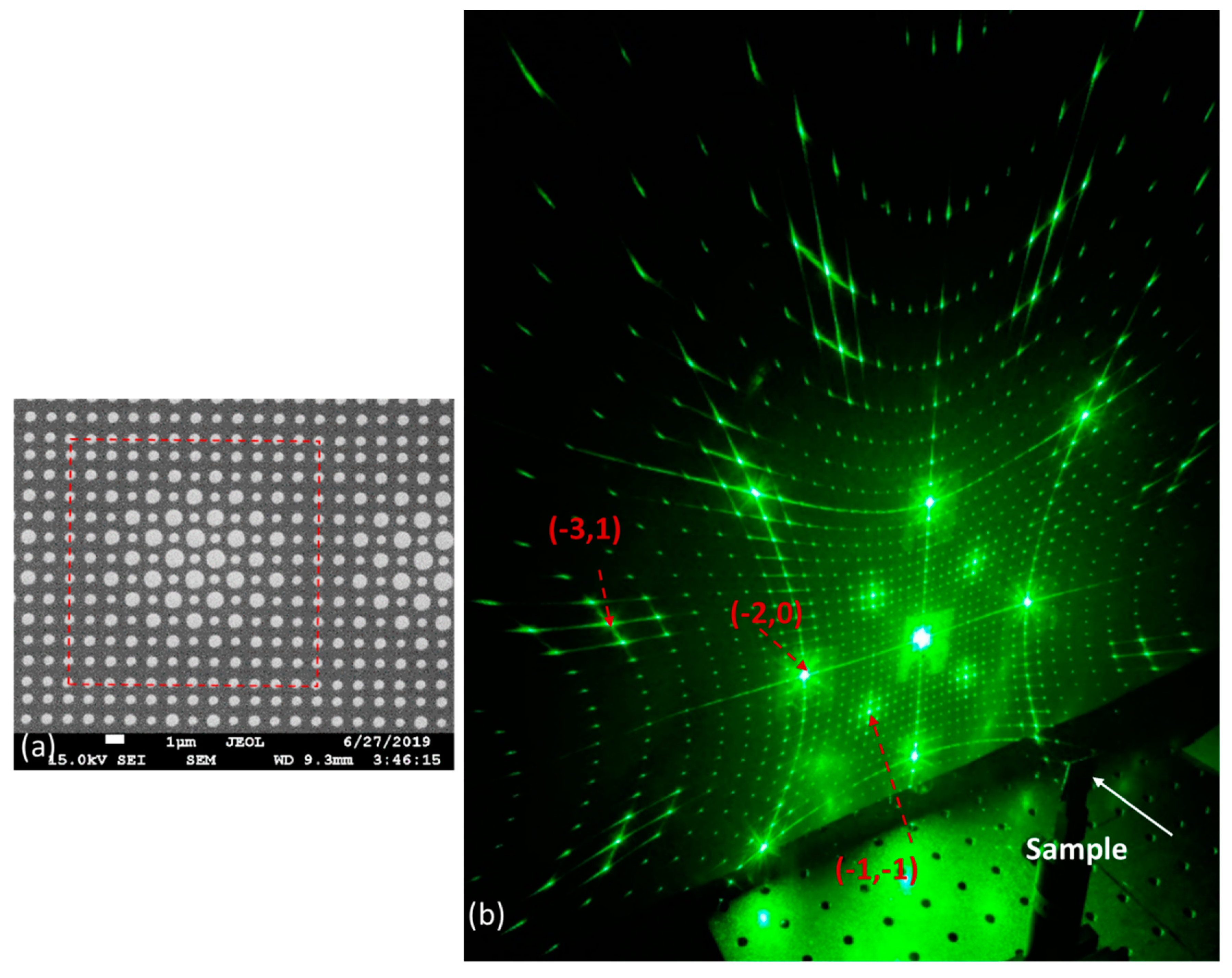
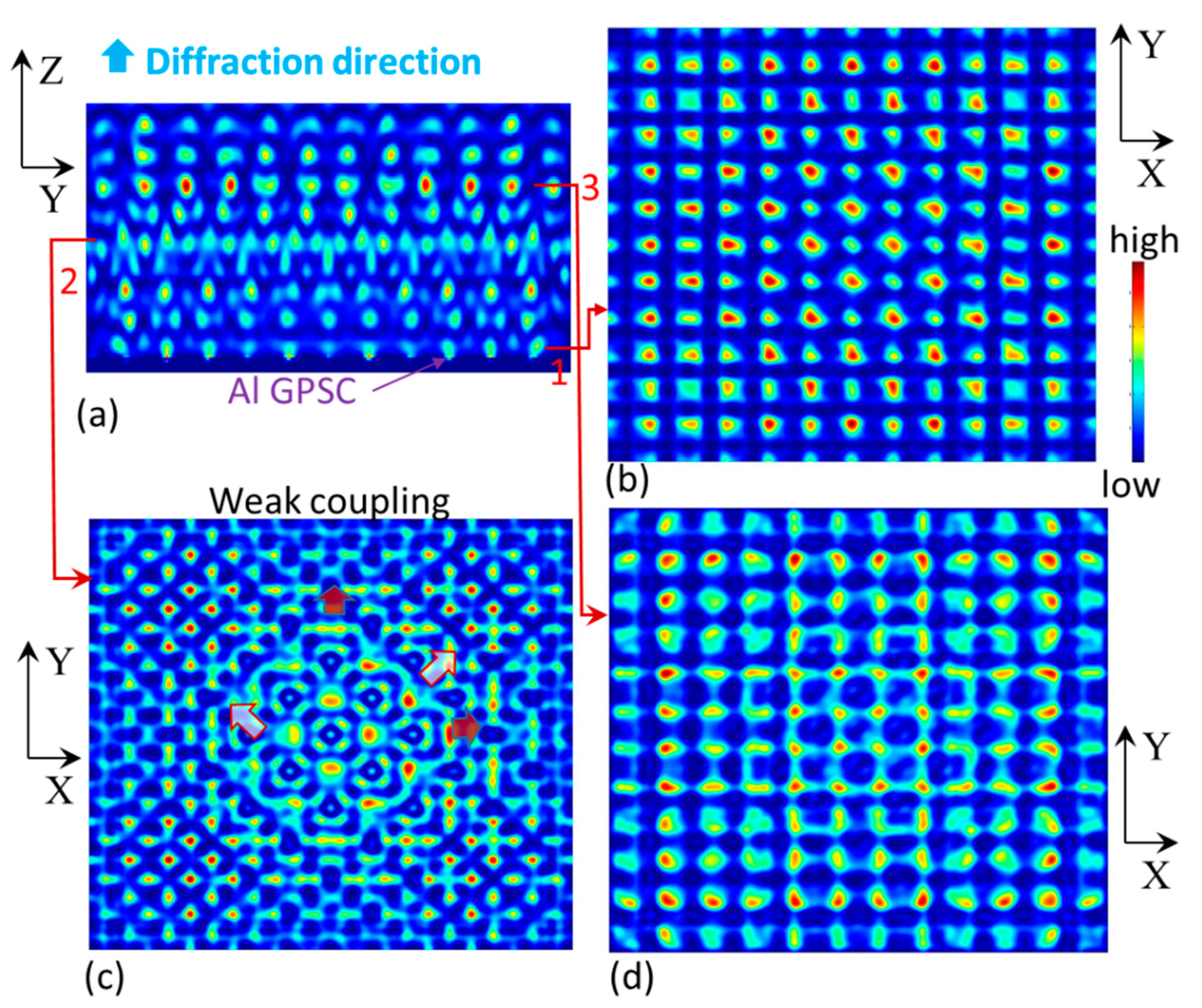
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shechtman, D.; Blech, I.; Gratias, D.; Cahn, J.W. Metallic phase with long range orientational order and no translational symmetry. Phys. Rev. Lett. 1984, 53, 1951–1953. [Google Scholar] [CrossRef]
- Harb, A.; Torres, F.; Ohlinger, K.; Lin, Y.; Lozano, K.; Xu, D.; Chen, K.P. Holographically formed three-dimensional Penrose-type photonic quasicrystal through a lab-made single diffractive optical element. Opt. Express 2010, 18, 20512–20517. [Google Scholar] [CrossRef] [PubMed]
- Yu, N.; Genevet, P.; Kats, M.; Aieta, F.; Tetienne, J.; Capasso, F.; Gaburro, Z. Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science 2011, 334, 333. [Google Scholar] [CrossRef] [PubMed]
- Rybin, M.; Samusev, K.; Lukashenko, S.; Kivshar, Y.; Limonov, M. Transition from two-dimensional photonic crystals to dielectric metasurfaces in the optical diffraction with a fine structure. Sci. Rep. 2016, 6, 30773. [Google Scholar] [CrossRef]
- Sell, D.; Yang, J.; Doshay, S.; Yang, R.; Fan, J.A. Large-Angle, Multifunctional Metagratings Based on Freeform Multimode Geometries. Nano Lett. 2017, 17, 3752–3757. [Google Scholar] [CrossRef]
- Lutkenhaus, J.; George, D.; Moazzezi, M.; Philipose, U.; Lin, Y. Digitally tunable holographic lithography using a spatial light modulator as a programmable phase mask. Opt. Express 2013, 21, 26227–26235. [Google Scholar] [CrossRef]
- Lin, Y.; Herman, P.R.; Darmawikarta, K. Design and holographic fabrication of tetragonal and cubic photonic crystals with phase mask: Toward the mass-production of three-dimensional photonic crystals. Appl. Phys. Lett. 2005, 86, 071117. [Google Scholar] [CrossRef]
- Centeno, E.; Cassagne, D. Graded photonic crystals. Opt. Lett. 2005, 30, 2278–2280. [Google Scholar] [CrossRef]
- Do, K.; Roux, X.; Marris-Morini, D.; Vivien, L.; Cassan, E. Experimental demonstration of light bending at optical frequencies using a non-homogenizable graded photonic crystal. Opt. Express 2012, 20, 4776–4783. [Google Scholar] [CrossRef]
- Zhu, Q.; Jin, L.; Fu, Y. Graded index photonic crystals: A review. Ann. Phys. 2015, 527, 205–218. [Google Scholar] [CrossRef]
- Li, Y.; Fu, Y.; Minin, O.; Minin, I. Ultra-sharp nanofocusing of graded index photonic crystal-based lenses perforated with optimized single defect. Opt. Mater. Express 2016, 6, 2628–2636. [Google Scholar] [CrossRef]
- Lowell, D.; Lutkenhaus, J.; George, D.; Philipose, U.; Chen, B.; Lin, Y. Simultaneous direct holographic fabrication of photonic cavity and graded photonic lattice with dual periodicity, dual basis, and dual symmetry. Opt. Express 2017, 25, 14444–14452. [Google Scholar] [CrossRef] [PubMed]
- Lowell, D.; Hassan, S.; Adewole, M.; Philipose, U.; Chen, B.; Lin, Y. Holographic fabrication of graded photonic super-crystals using an integrated spatial light modulator and reflective optical element laser projection system. Appl. Opt. 2017, 56, 9888. [Google Scholar] [CrossRef]
- Hassan, S.; Sale, O.; Lowell, D.; Hurley, N.; Lin, Y. Holographic fabrication and optical property of graded photonic super-crystals with a rectangular unit super-cell. Photonics 2018, 5, 34. [Google Scholar] [CrossRef]
- Hassan, S.; Lowell, D.; Lin, Y. High light extraction efficiency into glass substrate in organic light-emitting diodes by patterning the cathode in graded superlattice with dual periodicity and dual basis. J. Appl. Phys. 2017, 121, 233104. [Google Scholar] [CrossRef]
- Hassan, S.; Alnasser, K.; Lowell, D.; Lin, Y. Effects of Photonic Band Structure and Unit Super-Cell Size in Graded Photonic Super-Crystal on Broadband Light Absorption in Silicon. Photonics 2019, 6, 50. [Google Scholar] [CrossRef]
- Hassan, S.; Sale, O.; Alnasser, K.; Hurley, N.; Zhang, H.; Philipose, U.; Lin, Y. Broadband light-matter interaction due to resonance cavities in graded photonic super-crystals. OSA Contin. 2019, 2, 3272–3280. [Google Scholar] [CrossRef]
- Jin, J.; Yin, X.; Ni, L.; Soljačić, M.; Zhen, B.; Peng, C. Topologically enabled ultrahigh-Q guided resonances robust to out-of-plane scatterin. Nature 2019, 574, 501. [Google Scholar] [CrossRef]
- Li, S.; Zhou, C.; Liu, T.; Xia, S. Symmetry-protected bound states in the continuum supported by all-dielectric metasurface. Phys. Rev. A 2019, 100, 063803. [Google Scholar] [CrossRef]
- Crawford, M.H. LEDs for Solid-State Lighting: Performance Challenges and Recent Advances. IEEE J. Sel. Top. Quantum Electron. 2009, 15, 1028–1040. [Google Scholar] [CrossRef]
- Singh, D.; Basu, C.; Meinhardt-Wollweber, M.; Roth, B. LEDs for energy efficient greenhouse lighting. Renew. Sustain. Energy Rev. 2015, 49, 139–147. [Google Scholar] [CrossRef]
- Kuo, T.; Ding, T.; Lin, J.; Ma, S. Optical Design of an LED Lighting Source for Fluorescence Microscopes. Appl. Sci. 2019, 9, 4574. [Google Scholar] [CrossRef]
- Rakic, A.; Djurisic, A.; Elazar, J.; Majewski, M. Optical properties of metallic films for vertical-cavity optoelectronic devices. Appl. Opt. 1998, 37, 5271. [Google Scholar] [CrossRef] [PubMed]
- Oskooi, F.; Roundy, D.; Ibanescu, M.; Bermel, P.; Joannopoulos, J.D.; Johnson, S.G. MEEP: A flexible free-software package for electromagnetic simulations by the FDTD method. Comput. Phys. Commun. 2010, 181, 687. [Google Scholar] [CrossRef]
- Ni, L.; Jin, J.; Peng, C.; Li, Z. Analytical and statistical investigation on structural fluctuations induced radiation in photonic crystal slabs. Opt. Express 2017, 25, 5580–5593. [Google Scholar] [CrossRef]
- Ohlinger, K.; Lutkenhaus, J.; Arigong, B.; Zhang, H.; Lin, Y. Spatially addressable design of gradient index structures through spatial light modulator based holographic lithography. J. Appl. Phys. 2013, 114, 213102–213108. [Google Scholar] [CrossRef]
- Hassan, S.; Lowell, D.; Adewole, M.; George, D.; Zhang, H.; Lin, Y. Extraordinary light trapping enhancement in silicon solar cell patterned with graded photonic super-crystal. Photonics 2017, 4, 50. [Google Scholar] [CrossRef]
- Alnasser, K.; Hassan, S.; Kamau, S.; Zhang, H.; Lin, Y. Enhanced light extraction from organic light emitting diodes by reducing plasmonic loss through graded photonic super-crystals. J. Opt. Soc. Am. B 2020, 37, 1283. [Google Scholar] [CrossRef]
- Nadell, C.C.; Huang, B.; Malof, J.M.; Padilla, W.J. Deep learning for accelerated all-dielectric metasurface design. Opt. Express 2019, 27, 27523–27535. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hassan, S.; Jiang, Y.; Alnasser, K.; Hurley, N.; Zhang, H.; Philipose, U.; Lin, Y. Generation of over 1000 Diffraction Spots from 2D Graded Photonic Super-Crystals. Photonics 2020, 7, 27. https://doi.org/10.3390/photonics7020027
Hassan S, Jiang Y, Alnasser K, Hurley N, Zhang H, Philipose U, Lin Y. Generation of over 1000 Diffraction Spots from 2D Graded Photonic Super-Crystals. Photonics. 2020; 7(2):27. https://doi.org/10.3390/photonics7020027
Chicago/Turabian StyleHassan, Safaa, Yan Jiang, Khadijah Alnasser, Noah Hurley, Hualiang Zhang, Usha Philipose, and Yuankun Lin. 2020. "Generation of over 1000 Diffraction Spots from 2D Graded Photonic Super-Crystals" Photonics 7, no. 2: 27. https://doi.org/10.3390/photonics7020027
APA StyleHassan, S., Jiang, Y., Alnasser, K., Hurley, N., Zhang, H., Philipose, U., & Lin, Y. (2020). Generation of over 1000 Diffraction Spots from 2D Graded Photonic Super-Crystals. Photonics, 7(2), 27. https://doi.org/10.3390/photonics7020027





