Nonreciprocal Wavefront Manipulation in Synthetically Moving Metagratings

Abstract

We introduce a metasurface platform for nonreciprocal wave manipulation. We study metagratings composed of nonreciprocal bianisotropic particles supporting synthetic motion, which enable nonreciprocal energy transfer between tailored Floquet channels with unitary efficiency. Based on this framework, we derive the required electromagnetic polarizabilities to realize a metagrating supporting space wave circulation with unitary efficiency for free-space radiation and design a microwave metagrating supporting this functionality. The proposed concept opens new research venues to control free-space radiation with high efficiency beyond the limits dictated by Lorentz reciprocity.

Getting full control over light radiation requires materials with a vast range of characteristics. However, nature only provides us with a limited set of materials that can be utilized in order to manipulate electromagnetic waves. Artificial materials fill this gap by providing a rich platform to realize effective material properties not readily available in nature. Metasurfaces, as an important class of artificial materials, are two-dimensional arrays of artificially engineered subwavelength scatterers that provide a versatile platform to engineer the flow of electromagnetic waves, with promising applications from microwaves to optics [1,2,3,4,5,6]. Space-gradient metasurfaces are a special subclass of these electrically thin layers, tailored to exhibit spatially varying optical responses, thus providing a powerful tool to engineer the direction and wavefront of an incident wave in reflection and/or transmission. These surfaces have found many applications, including bending the flow of electromagnetic waves, cloaking, and sensing [7,8,9,10,11,12,13].

Although these devices have been driving significant excitement in the optics community, most of the relevant proposals to date provide responses that are strictly bound by Lorentz reciprocity. Breaking reciprocity opens a whole new set of functionalities that are impossible with reciprocal structures [14,15]. Different approaches can be employed to break reciprocity in these structures [16]. Magnetic gyrotropy (magnetized ferrite) or electric gyrotropy (magnetized plasma) have been among the first proposals to design nonreciprocal gradient metasurfaces (see, e.g., [17]). However, nonreciprocal metasurfaces based on these materials usually lead to bulky, expensive, and difficult-to-integrate devices. As an alternative approach, nonlinear gradient metasurfaces have been proposed for nonreciprocal anomalous refraction or reflection (see, e.g., [18]). However, these structures are intensity-dependent and may, as a result, distort the signal and not appeal several application areas.

Recently, the emerging field of time-varying metasurfaces has provided several interesting opportunities to expand the realm of exotic light-matter interactions with metasurfaces [19,20,21], including nonreciprocal responses [14,15]. In particular, it was shown that time-modulated gradient metasurfaces open new degrees of freedom for engineered nonreciprocal responses. This concept has recently been employed to design nonreciprocal surfaces for optical isolation and circulation [22,23,24]. Although surfaces with spatio-temporal modulation address many of the challenges related to the other approaches mentioned above, their functionalities are fundamentally limited by several issues: because of temporal modulation, we can generally expect frequency mixing with associated signal distortion [22,23,24]. Furthermore, dynamic modulation is an active approach that requires external energy applied to impart the required modulation signals, and correspondingly bulky feeding networks in the case of electro-optical modulations.

In this letter, we introduce nonreciprocal metagratings based on media in synthetic motion, which overcome the abovementioned challenges. We first derive the minimum physical requirements to realize such a platform, and then propose a design to implement unitary-efficiency free-space circulation. In 1908, three years after Einstein presented the special theory of relativity, Minkowski formulated the electrodynamics of moving media [25,26], which, at the time, was a mysterious problem within the framework of classical physics. The first part of Minkowski’s theory deals with the invariant nature of Maxwell’s equations, stating that Maxwell’s equations for a stationary medium are also valid for a medium that moves uniformly at velocity $v$ with respect to a stationary (fixed) reference frame. Then, constitutive relations for moving media are determined utilizing the special theory of relativity, assuming that the constitutive relations for the medium at rest are known [25,26].

$$\begin{array}{l}D=\epsilon E+(\epsilon \mu -{\epsilon }_0{\mu }_0)v\times H,\\ B=-(\epsilon \mu -{\epsilon }_0{\mu }_0)v\times E+\mu H.\end{array}$$

(1)

As expected, these constitutive relations are nonreciprocal in nature, showing opportunities to be employed as building blocks of nonreciprocal surfaces. However, in order to get considerable nonreciprocal response, the medium should be moving with a speed comparable to the speed of light which is not practical. However, analogous nonreciprocal constitutive relations in stationary artificial composite media, i.e., metamaterials at rest, may be obtained [27] by artificially engineering the inclusion bianisotropy to synthesize the electromagnetic behavior of a moving medium. The required coupling between electric and magnetic phenomena in this class of stationary engineered materials was termed bianisotropic “moving” coupling. Based on this concept, we can make stationary inclusions, which, as a function of the direction from which you look at them, respond electromagnetically as if the particles move towards you or against you (or in another direction) with a controllable speed. In the following, we present a platform based on bianisotropic moving particles for rerouting electromagnetic waves in a nonreciprocal fashion. Furthermore, we show how such nonreciprocal surfaces can be realized using stationary magnet-free inclusions.

Let us consider a two-dimensional array of bianisotropic moving particles located at a distance $h$ from a ground plane (Figure 1). We assume that the particles considered here can only provide electric moment in the $z$ direction and magnetic moment along $x$. The structure is illuminated with a transverse magnetic (TM) plane wave with electric field component $E_{\mathrm{inc}}=E_0\left(y\cos {\theta }_{\mathrm{inc}}+z\sin {\theta }_{\mathrm{inc}}\right)\exp \left(-j{k}_0\sin {\theta }_{\mathrm{inc}}y+j{k}_0\cos {\theta }_{\mathrm{inc}}z\right)$. Here, ${\eta }_0$ is the free-space wave impedance, $k_0$ is the free-space wavenumber, ${\theta }_{\mathrm{inc}}$ is the incidence angle, and $E_0$ is the amplitude of the incident electric field. Because of this illumination, surface electric and magnetic currents will be excited on the structure, which sustain the scattering from the array:

$$\begin{array}{l}{J}_{\mathrm{e}}\left(x,y,z\right)=z\hspace{0.17em}S{I}_{\mathrm{e}}^{\mathrm{z}}\delta \left(z-h\right){\displaystyle \sum _{m=-\infty }^{\infty }{\displaystyle \sum _{n=-\infty }^{\infty }\delta \left(x-ma\right)\delta \left(y-nb\right)\exp \left(-j{k}_{\mathrm{y}0}nb\right)}},\\ J_{\mathrm{m}}\left(x,y,z\right)=x\hspace{0.17em}S{I}_{\mathrm{m}}^{\mathrm{x}}\delta \left(z-h\right){\displaystyle \sum _{m=-\infty }^{\infty }{\displaystyle \sum _{n=-\infty }^{\infty }\delta \left(x-ma\right)\delta \left(y-nb\right)\exp \left(-j{k}_{\mathrm{y}0}nb\right)}},\end{array}$$

(2)

where $k_{\mathrm{y}0\mathrm{n}}=k_0\sin {\theta }_{\mathrm{inc}}+\frac{2n\pi }{b}$; $\delta (\cdot )$ is the Dirac’s delta function; and $a$, $b$ are the periodicities in the $x$ and $y$ directions, respectively, and $S=ab$ is the area of a unit cell. Here, $I_{\mathrm{e}}^{\mathrm{z}}$ and $I_{\mathrm{m}}^{\mathrm{x}}$ are the surface electric and magnetic current densities on each unit cell. The radiated fields can be written in terms of Floquet modal expansion with electric field component $E_{0\mathrm{n}}=\left(y-z\frac{k_{\mathrm{y}0\mathrm{n}}}{k_{\mathrm{z}0\mathrm{n}}}\right){\mathsf{\Theta }}_{0\mathrm{n}}\exp \left(-j{k}_{\mathrm{y}0\mathrm{n}}y-j{k}_{\mathrm{z}0\mathrm{n}}z\right)$, where ${\mathsf{\Theta }}_{0\mathrm{n}}=\left({\eta }_0\frac{k_{\mathrm{y}0\mathrm{n}}}{k_0}{I}_{\mathrm{e}}^{\mathrm{z}}+I_{\mathrm{m}}^{\mathrm{x}}\right)\cos \left(k_{\mathrm{z}0\mathrm{n}}h\right)$. Here, $k_{\mathrm{z}0\mathrm{n}}=\sqrt{k_0^2-k_{y0n}^2}$ is the wavenumber in the $z$ direction for the $0n$ mode (the first and second indices refer to the Floquet orders with respect to the $x$ and $y$ axes), $I_{\mathrm{e}}^{\mathrm{z}}$ and $I_{\mathrm{m}}^{\mathrm{x}}$ are the surface currents, which can be written in terms of effective electric ${\alpha }_{\mathrm{ee}}^{\mathrm{zz}}$, magnetic ${\alpha }_{\mathrm{mm}}^{\mathrm{xx}}$, and bianisotropic moving polarizabilities ${\alpha }_{\mathrm{me}}^{\mathrm{xz}}={\alpha }_{\mathrm{em}}^{\mathrm{zx}}$ as $I_{\mathrm{e}}^{\mathrm{z}}=\frac{j\omega }{S}\left({\alpha }_{\mathrm{ee}}^{\mathrm{zz}}{E}_{\mathrm{ext}}^{\mathrm{z}}+{\alpha }_{\mathrm{em}}^{\mathrm{zx}}{H}_{\mathrm{ext}}^{\mathrm{x}}\right)$ and $I_{\mathrm{m}}^{\mathrm{x}}=\frac{j\omega }{S}\left({\alpha }_{\mathrm{me}}^{xz}{E}_{\mathrm{ext}}^{\mathrm{z}}+{\alpha }_{\mathrm{mm}}^{\mathrm{xx}}{H}_{\mathrm{ext}}^{\mathrm{x}}\right)$, where $E_{\mathrm{ext}}^{\mathrm{z}}$ ($H_{\mathrm{ext}}^{\mathrm{x}}$) is the electric (magnetic) field in the absence of the array. Assuming no Ohmic loss, passivity requires that the total radiated power carried away from the metasurface through all Floquet channels equals the extinction power $P_{\mathrm{rad}}^{\mathrm{z}}=P_{\mathrm{ext}}$, where the radiated and extinction powers read $P_{\mathrm{rad}}^{\mathrm{z}}=\frac{1}{2}\mathrm{Re}\left\{{\displaystyle \sum _{\mathrm{k}=-\infty }^{\mathrm{k}=\infty }{E}_{0\mathrm{k}}}\times {{\displaystyle \sum _{\mathrm{k}=-\infty }^{\mathrm{k}=\infty }{H}_{0\mathrm{k}}}}^{*}\right\}\cdot z$ and $P_{\mathrm{ext}}=\frac{1}{2}\mathrm{Re}\left\{J_{\mathrm{e}}{}^{*}\cdot E_{\mathrm{ext}}+J_{\mathrm{m}}{}^{*}\cdot H_{\mathrm{ext}}\right\}$, respectively [28]. Applying these conditions will impose the following constraints on the effective polarizabilities of the inclusions:

$$\begin{array}{l}{\left|{\alpha }_{\mathrm{ee}}^{\mathrm{zz}}\right|}^2{\displaystyle \sum _{n=-\infty }^{n=\infty }{A}_{0\mathrm{n}}}+2\mathrm{Re}\left\{{\alpha }_{\mathrm{ee}}^{\mathrm{zz}}{\alpha }_{\mathrm{em}}^{\mathrm{zx}}{}^{*}{\displaystyle \sum _{n=-\infty }^{n=\infty }{B}_{0\mathrm{n}}}\right\}+{\left|{\alpha }_{\mathrm{em}}^{\mathrm{zx}}\right|}^2{\displaystyle \sum _{n=-\infty }^{n=\infty }{C}_{0\mathrm{n}}}=-\frac{S}{\omega {\eta }_0}\mathrm{Im}\left\{{\alpha }_{\mathrm{ee}}^{\mathrm{zz}}\right\},\\ {\left|{\alpha }_{\mathrm{em}}^{\mathrm{zx}}\right|}^2{\displaystyle \sum _{n=-\infty }^{n=\infty }{A}_{0\mathrm{n}}}+2\mathrm{Re}\left\{{\alpha }_{\mathrm{em}}^{\mathrm{zx}}{\alpha }_{\mathrm{mm}}^{\mathrm{xx}}{}^{*}{\displaystyle \sum _{n=-\infty }^{n=\infty }{B}_{0\mathrm{n}}}\right\}+{\left|{\alpha }_{\mathrm{mm}}^{\mathrm{xx}}\right|}^2{\displaystyle \sum _{n=-\infty }^{n=\infty }{C}_{0\mathrm{n}}}\hspace{0.17em}=-\frac{S}{\omega {\eta }_0}\mathrm{Im}\left\{{\alpha }_{\mathrm{mm}}^{\mathrm{xx}}\right\},\\ {\alpha }_{\mathrm{ee}}^{\mathrm{zz}}{\alpha }_{\mathrm{em}}^{\mathrm{zx}}{}^{*}{\displaystyle \sum _{n=-\infty }^{n=\infty }{A}_{0\mathrm{n}}}+{\alpha }_{\mathrm{ee}}^{\mathrm{zz}}{\alpha }_{\mathrm{mm}}^{\mathrm{xx}}{}^{*}{\displaystyle \sum _{n=-\infty }^{n=\infty }{B}_{0\mathrm{n}}}+{\left|{\alpha }_{\mathrm{em}}^{\mathrm{zx}}\right|}^2{\displaystyle \sum _{n=-\infty }^{n=\infty }{B}_{0\mathrm{n}}{}^{*}}+{\alpha }_{\mathrm{em}}^{\mathrm{zx}}{\alpha }_{\mathrm{mm}}^{\mathrm{xx}}{}^{*}{\displaystyle \sum _{n=-\infty }^{n=\infty }{C}_{0\mathrm{n}}}=-\frac{S}{\omega {\eta }_0}\mathrm{Im}\left\{{\alpha }_{\mathrm{em}}^{\mathrm{zx}}\right\},\end{array}$$

(3)

where ${\left|\frac{k_0}{k_{\mathrm{y}0\mathrm{n}}}\right|}^2{A}_{0\mathrm{n}}={\eta }_0\frac{k_0}{k_{\mathrm{y}0\mathrm{n}}}{B}_{0\mathrm{n}}={\eta }_{{}_0}^2{C}_{0\mathrm{n}}=\mathrm{Re}\left\{\frac{k_0}{k_{\mathrm{z}0\mathrm{n}}}\right\}{\left|\cos \left(k_{\mathrm{z}0\mathrm{n}}h\right)\right|}^2$.

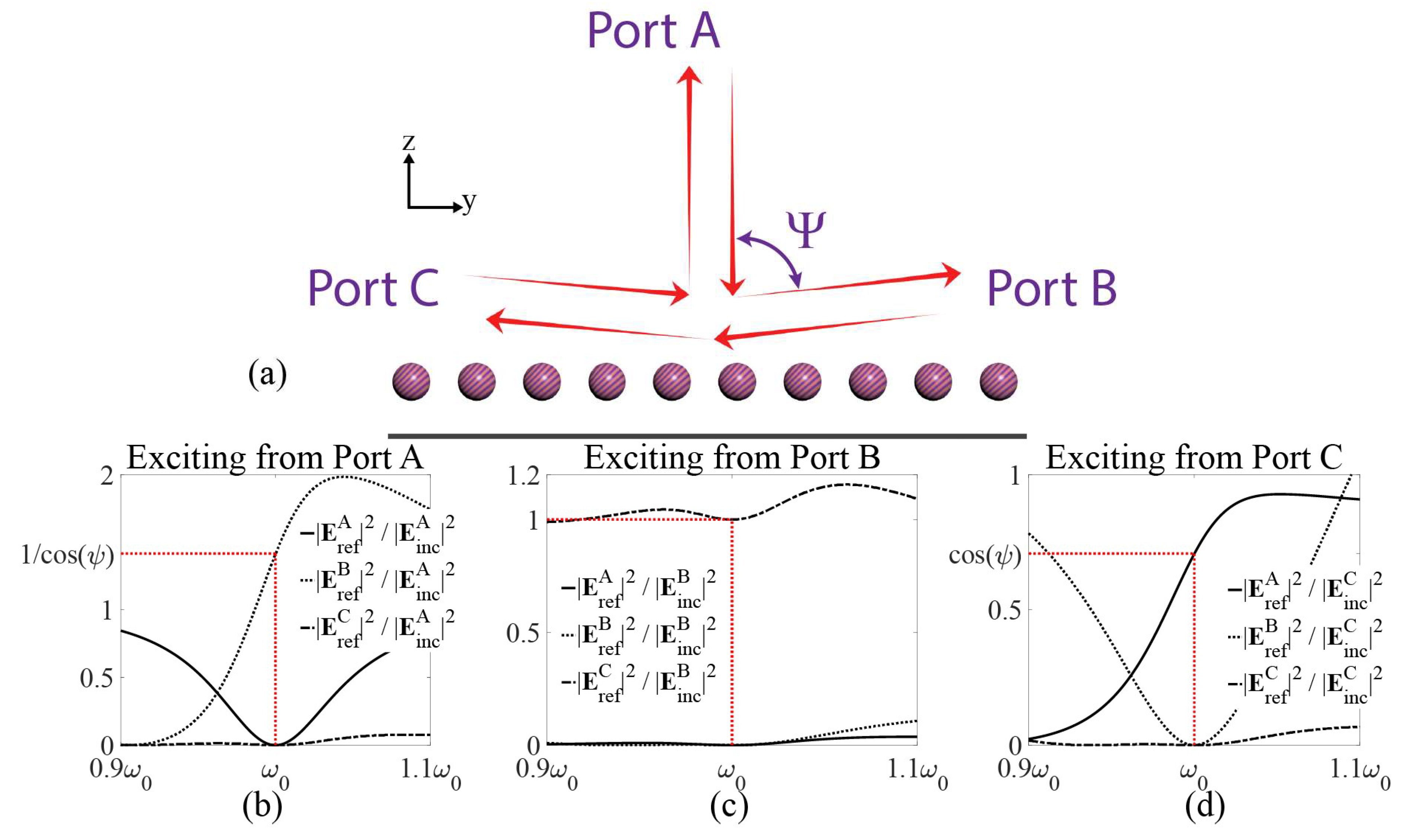
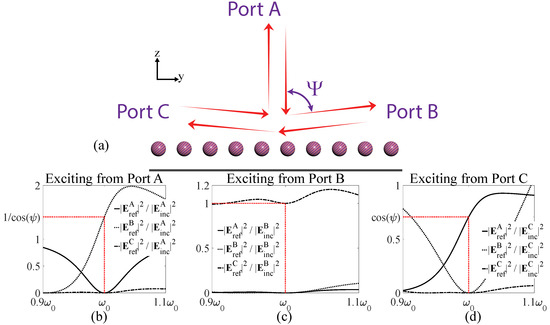
Now, we can tailor the polarizability response to define the desired nonreciprocal light-matter interactions. Depending on the defined functionality, bianisotropic particles with different polarizabilities, satisfying (3), will be required. As an example, here we design a metagrating that can operate as an ideal (i.e., with unitary efficiency) free-space circulator, realizing a surface that directs all the incident wave from direction A to B, all the incident wave from B to C, and all the incident wave from C back to A (Figure 1). First, we choose the periodicity so as to align three diffraction orders with the directions of interest (i.e., $b=\lambda /\sin (\psi )$, where $\lambda$ is the wavelength and $\psi$ is the angle of Floquet channels from the normal to the surface). In order to reroute all normally incident waves from A towards B, first we need to nullify the reflection into the specular direction, which can be achieved if ${\mathsf{\Theta }}_{00}=E_0$. Next, we need to make sure that no scattering trickles towards diffraction order C, which can be guaranteed if ${\mathsf{\Theta }}_{0(-1)}=0$. It can be shown that the required polarizabilities for such functionality read.

$${\eta }_0\sin \psi {\alpha }_{\mathrm{ee}}^{\mathrm{zz}}={\alpha }_{\mathrm{em}}^{\mathrm{zx}}=\frac{1}{{\eta }_0\sin \psi }{\alpha }_{\mathrm{mm}}^{\mathrm{xx}}=\frac{S}{j2\omega }\frac{1}{\sin \psi {\cos }^2\left(k_{0}h\right)}.$$

(4)

Substituting these polarizabilities into the third condition of (3), we can derive the design equation ${\cos }^2\left(k_{0}h\right)\cos \psi =4{\cos }^2\left(k_{0}h\cos \psi \right)$. As a second design step, we need to make sure that, if the layer is illuminated from direction B, all the energy is transferred into the Floquet channel C and no scattering happens towards A. It can be shown that in this case we need ${\mathsf{\Theta }}_{00}={\mathsf{\Theta }}_{0(-1)}={\mathsf{\Theta }}_{0(-2)}=0$ (when the excitation is from port B, 00, 0(-1), and 0(-2) Floquet channels are aligned with ports C, A, and B, respectively). This corresponds to requiring that, when the metagrating is excited from port B, the bianisotropic moving particles do not get excited at all. In this case, the incident wave only sees the ground plane and, as a result, all the illuminated wave gets reflected into the Floquet channel C as initially planned. It is quite interesting to note that, although the bianisotropic moving particles are stationary, from an electromagnetic standpoint, they seem to move with the speed of the incident wave away from B in the same direction, so that the incident wave never gets a chance to interact with them. Finally, we need to make sure that, if we excite the metagrating from port C, the illuminated wave will be fully directed into port A and no scattering will happen towards B or back to C. Using (4), it can be shown that for this case ${\mathsf{\Theta }}_{00}=0$ and ${\mathsf{\Theta }}_{00}={\mathsf{\Theta }}_{01}\sqrt{\cos \psi }=-E_0\cos \psi$ (when the excitation is from port C, 00, 01, and 02 Floquet channels are aligned with B, A, and C, respectively). Under these conditions, from an electromagnetic point of view, the layer seems to move in the direction antiparallel to the incident wave and, as it interacts with it, all the illuminated wave gets redirected into port A.

To understand how the metagrating behaves versus frequency, here we model the polarizabilities using the conventional Lorentz dispersion model which, near its resonance, can adequately describe the dipolar response of small inclusions, i.e., ${\alpha }_{\mathrm{ee}}^{\mathrm{zz}}=\frac{A_{\mathrm{ee}}}{{\omega }_{\mathrm{ee}}^2-{\omega }^2-j\omega {\delta }_{\mathrm{ee}}}$, ${\alpha }_{\mathrm{em}}^{\mathrm{zx}}=\frac{A_{\mathrm{em}}\omega }{{\omega }_{\mathrm{em}}^2-{\omega }^2-j\omega {\delta }_{\mathrm{em}}}$, and ${\alpha }_{\mathrm{mm}}^{\mathrm{xx}}=\frac{A_{\mathrm{mm}}{\omega }^2}{{\omega }_{\mathrm{mm}}^2-{\omega }^2-j\omega {\delta }_{\mathrm{mm}}}$, where $A_{\mathrm{ee}}$, $A_{\mathrm{em}}$, and $A_{\mathrm{mm}}$ are the amplitude coefficients and ${\delta }_{\mathrm{ee}}$, ${\delta }_{\mathrm{em}}$, and ${\delta }_{\mathrm{mm}}$ are the loss factors. Here, we assume that the resonance frequencies are the same for all polarizabilities (i.e., ${\omega }_{\mathrm{ee}}={\omega }_{\mathrm{em}}={\omega }_{\mathrm{mm}}={\omega }_0$). As an example, here we design the metagrating to circulate the free space wave between three Floquet channels located 45 degrees apart (see Figure 1). Amplitude coefficients $A_{\mathrm{ee}}$, $A_{\mathrm{em}}$, and $A_{\mathrm{mm}}$ can be calculated by substituting these polarizability expressions in (4) (note that, here, as an example, we assume ${\delta }_{\mathrm{ee}}=2{\delta }_{\mathrm{em}}=4{\delta }_{\mathrm{mm}}=0.4{\omega }_0$). Figure 1b–d show the amplitude of the reflected wave into different Floquet channels under excitation from different Floquet channels. It can be seen that at resonance (i.e., $\omega ={\omega }_0$), the surface is capable of circulating the space wave with unitary efficiency, which is impossible to achieve using gradient metasurfaces.

This concept is quite general, and different approaches can be taken to realize stationary particles with the required bianisotropic moving coupling. A simple approach can be based on ferrite inclusions, in order to get the required magnetic gyrotropy to break reciprocity, and combined with a proper set of electric dipoles in order to emulate the electromagnetic properties of a real moving inclusion [27,28,29,30]. However, as mentioned above, such inclusions require a magnetic bias, resulting in bulky and poorly integrable structures. Another recently proposed approach has been based on mimicking Faraday rotation using dc current bias [31]. 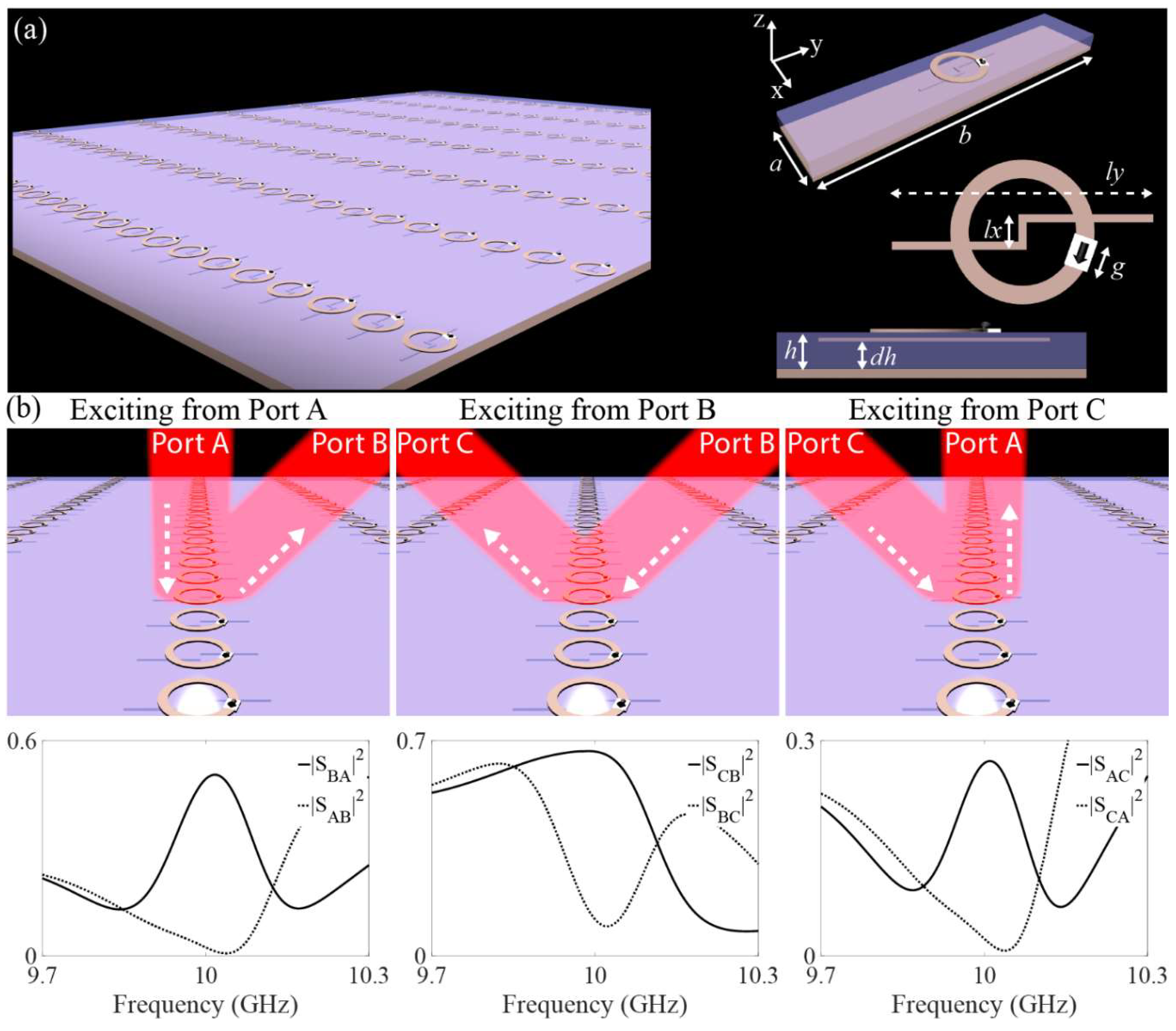Following this approach, recently magnet-free nonreciprocal bianisotropic inclusions were designed and utilized as the building blocks of nonreciprocal metasurfaces [32]. Here, inspired by these works, we design an artificial stationary inclusion with bianisotropic moving coupling. The inclusion is composed of a ring loaded with an ideal isolator, which allows rotational travelling wave only in one direction beneath the ring. An electric dipole in the form of a wire strip has been located underneath the ring that, in conjunction with the directional rotating magnetic dipole, provides the bianisotropic moving coupling. Based on this inclusion design, we simulate a nonreciprocal metagrating that is capable of ideally circulating space waves between three Floquet channels located 45 degrees apart. The designed metagrating is shown in Figure 2a. The results in Figure 2b show that the structure nicely circulates the space wave between three ports. As it can be seen from the simulated scattering parameters, despite the presence of realistic absorption loss due to the isolators used in the loops, the performance is close to ideal. As it was shown in the theoretical analysis, the nonreciprocal metagrating, in principle, can be designed to circulate space wave with unitary efficiency. Here, for the proof of concept, we considered the case in which the ports are located 45 degrees apart, however it should be noted that the involved ports can be located with almost 90-degree angular separation with respect to each other while providing unitary efficiency. More efficient inclusions can be utilized in order to provide the required nonreciprocal functionalities in a more efficient way.

To conclude, in this paper we have introduced a new conceptual platform for nonreciprocal wave manipulation with unitary efficiency. The proposed concept is based on nonreciprocal metagratings composed of stationary inclusions synthesizing bianisotropic moving coupling, while being stationary. As an example of nonreciprocal wave manipulation, we have shown that these metagratings can perform nonreciprocal circulation for space waves with unitary efficiency. There are a few important points that distinguish the proposed concept from other platforms presented for nonreciprocal wave manipulation. The proposed platform does not require a continuous profile of spatio-temporal modulation, but it simply consists of a periodic array of bianisotropic inclusions, where all the building blocks are identical. They are stationary, and simply biased by a dc current to break reciprocity. It was recently revealed how gradient metasurfaces suffer from fundamental bounds on conversion efficiency [12,33,34], yet, in the proposed design there is no fundamental limit on coupling to one diffraction order to the other [35], enabling a versatile platform for nonreciprocal wave manipulation with large efficiency. In contrast to structures based on spatio-temporal modulation, in the proposed design, no up- or down-conversion of frequency arises. The period in the array is comparable to the wavelength, avoiding severe challenges to translate these concepts to higher frequencies. We also envision similar concepts for nonreciprocal manipulation of acoustic waves based on similar principles.