Global–Local Cooperative Optimization in Photonic Inverse Design Algorithms
Abstract
1. Introduction
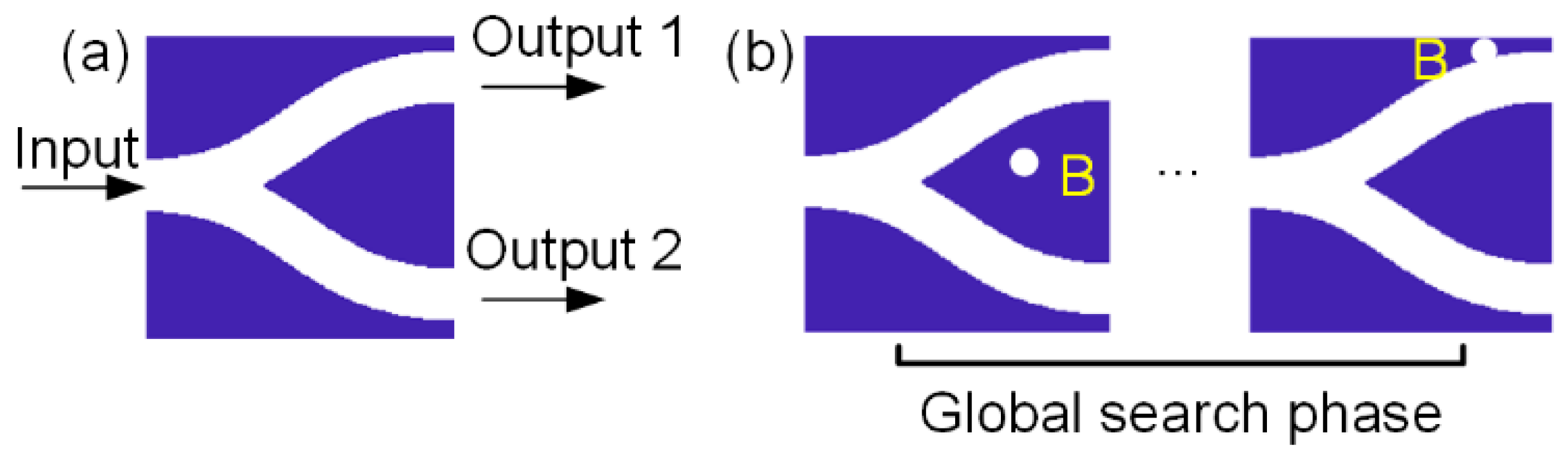
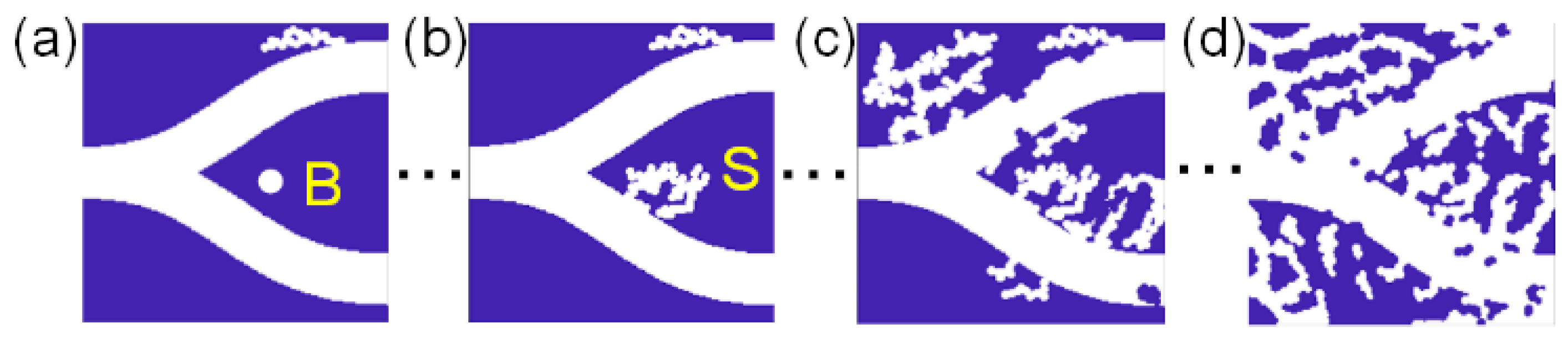
2. The Principle of the GLINT Inverse Design Algorithm
3. Simulation and Experimental Results
3.1. Dual-Port WDM Structure
3.2. The 90-Degree Bending Waveguides
3.3. Three-Port WDM Structure
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, X.; Zhou, Z.; Guo, Y.; Zhuang, M.; Jin, W.; Shen, B.; Chen, Y.; Huang, J.; Tao, Z.; Jin, M. High-coherence parallelization in integrated photonics. Nat. Commun. 2024, 15, 7892. [Google Scholar] [CrossRef] [PubMed]
- Weinstein, A.J.; Reed, M.D.; Jones, A.M.; Andrews, R.W.; Barnes, D.; Blumoff, J.Z.; Euliss, L.E.; Eng, K.; Fong, B.H.; Ha, S.D. Universal logic with encoded spin qubits in silicon. Nature 2023, 615, 817–822. [Google Scholar] [CrossRef] [PubMed]
- Altug, H.; Oh, S.-H.; Maier, S.A.; Homola, J. Advances and applications of nanophotonic biosensors. Nat. Nanotechnol. 2022, 17, 5–16. [Google Scholar] [CrossRef] [PubMed]
- Molesky, S.; Lin, Z.; Piggott, A.Y.; Jin, W.; Vucković, J.; Rodriguez, A.W. Inverse design in nanophotonics. Nat. Photonics 2018, 12, 659–670. [Google Scholar] [CrossRef]
- Su, L.; Piggott, A.Y.; Sapra, N.V.; Petykiewicz, J.; Vuckovic, J. Inverse design and demonstration of a compact on-chip narrowband three-channel wavelength demultiplexer. ACS Photonics 2018, 5, 301–305. [Google Scholar] [CrossRef]
- Lucas, E.; Yu, S.-P.; Briles, T.C.; Carlson, D.R.; Papp, S.B. Tailoring microcombs with inverse-designed, meta-dispersion microresonators. Nat. Photonics 2023, 17, 943–950. [Google Scholar] [CrossRef]
- Yang, K.Y.; Skarda, J.; Cotrufo, M.; Dutt, A.; Ahn, G.H.; Sawaby, M.; Vercruysse, D.; Arbabian, A.; Fan, S.; Alù, A. Inverse-designed non-reciprocal pulse router for chip-based LiDAR. Nat. Photonics 2020, 14, 369–374. [Google Scholar] [CrossRef]
- Liao, J.; Tian, Y.; Yang, Z.; Xu, H.; Tang, C.; Wang, Y.; Zhang, X.; Kang, Z. Inverse design of highly efficient and broadband mode splitter on SOI platform. Chin. Opt. Lett. 2024, 22, 011302. [Google Scholar] [CrossRef]
- Yu, Z.; Cui, H.; Sun, X. Genetically optimized on-chip wideband ultracompact reflectors and Fabry–Perot cavities. Photonics Res. 2017, 5, B15–B19. [Google Scholar] [CrossRef]
- Jin, X.; Xu, J.; Li, Y.; Xue, C.; Liao, R.; Fu, L.; Liu, M.; Shen, Y.; Quan, X.; Cheng, X. Fabrication-constrained inverse design and demonstration of high-performance grating couplers. Chin. Opt. Lett. 2024, 22, 112201. [Google Scholar] [CrossRef]
- Yang, K.Y.; Shirpurkar, C.; White, A.D.; Zang, J.; Chang, L.; Ashtiani, F.; Guidry, M.A.; Lukin, D.M.; Pericherla, S.V.; Yang, J. Multi-dimensional data transmission using inverse-designed silicon photonics and microcombs. Nat. Commun. 2022, 13, 7862. [Google Scholar] [CrossRef] [PubMed]
- Nikkhah, V.; Mencagli, M.J.; Engheta, N. Reconfigurable nonlinear optical element using tunable couplers and inverse-designed structure. Nanophotonics 2023, 12, 3019–3027. [Google Scholar] [CrossRef] [PubMed]
- Hughes, T.W.; Minkov, M.; Williamson, I.A.; Fan, S. Adjoint method and inverse design for nonlinear nanophotonic devices. ACS Photonics 2018, 5, 4781–4787. [Google Scholar] [CrossRef]
- Bendsøe, M.P. Optimal shape design as a material distribution problem. Struct. Optim. 1989, 1, 193–202. [Google Scholar] [CrossRef]
- Frellsen, L.F.; Ding, Y.; Sigmund, O.; Frandsen, L.H. Topology optimized mode multiplexing in silicon-on-insulator photonic wire waveguides. Opt. Express 2016, 24, 16866–16873. [Google Scholar] [CrossRef] [PubMed]
- Hammond, A.M.; Oskooi, A.; Johnson, S.G.; Ralph, S.E. Photonic topology optimization with semiconductor-foundry design-rule constraints. Opt. Express 2021, 29, 23916–23938. [Google Scholar] [CrossRef] [PubMed]
- Lalau-Keraly, C.M.; Bhargava, S.; Miller, O.D.; Yablonovitch, E. Adjoint shape optimization applied to electromagnetic design. Opt. Express 2013, 21, 21693–21701. [Google Scholar] [CrossRef] [PubMed]
- Piggott, A.Y.; Petykiewicz, J.; Su, L.; Vučković, J. Fabrication-constrained nanophotonic inverse design. Sci. Rep. 2017, 7, 1786. [Google Scholar] [CrossRef] [PubMed]
- Piggott, A.Y.; Lu, J.; Lagoudakis, K.G.; Petykiewicz, J.; Babinec, T.M.; Vučković, J. Inverse design and demonstration of a compact and broadband on-chip wavelength demultiplexer. Nat. Photonics 2015, 9, 374–377. [Google Scholar] [CrossRef]
- Shen, B.; Wang, P.; Polson, R.; Menon, R. An integrated-nanophotonics polarization beamsplitter with 2.4 × 2.4 μm2 footprint. Nat. Photonics 2015, 9, 378–382. [Google Scholar] [CrossRef]
- Shen, B.; Wang, P.; Polson, R.; Menon, R. Integrated metamaterials for efficient and compact free-space-to-waveguide coupling. Opt. Express 2014, 22, 27175–27182. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Li, G.; Huang, J.; Zhang, Z.; Yang, J.; Yang, C.; Qian, Y.; Xu, W.; Huang, H. Ultra-compact high efficiency and low crosstalk optical interconnection structures based on inverse designed nanophotonic elements. Sci. Rep. 2020, 10, 11993. [Google Scholar] [CrossRef] [PubMed]
- Sebbag, Y.; Talker, E.; Naiman, A.; Barash, Y.; Levy, U. Demonstration of an integrated nanophotonic chip-scale alkali vapor magnetometer using inverse design. Light Sci. Appl. 2021, 10, 54. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Li, H.; Chen, W.; Wang, P.; Dai, S.; Zhang, B.; Li, J.; Li, Y.; Fu, Q.; Dai, T. Direct-binary-search-optimized compact silicon-based polarization beam splitter using a pixelated directional coupler. Opt. Commun. 2021, 484, 126670. [Google Scholar] [CrossRef]
- Xu, K.; Liu, L.; Wen, X.; Sun, W.; Zhang, N.; Yi, N.; Sun, S.; Xiao, S.; Song, Q. Integrated photonic power divider with arbitrary power ratios. Opt. Lett. 2017, 42, 855–858. [Google Scholar] [CrossRef] [PubMed]
- Lu, L.; Liu, D.; Zhou, F.; Li, D.; Cheng, M.; Deng, L.; Fu, S.; Xia, J.; Zhang, M. Inverse-designed single-step-etched colorless 3 dB couplers based on RIE-lag-insensitive PhC-like subwavelength structures. Opt. Lett. 2016, 41, 5051–5054. [Google Scholar] [CrossRef] [PubMed]
- Ma, H.; Huang, J.; Zhang, K.; Yang, J. Ultra-compact and efficient 1 × 2 mode converters based on rotatable direct-binary-search algorithm. Opt. Express 2020, 28, 17010–17019. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Vučković, J. Nanophotonic computational design. Opt. Express 2013, 21, 13351–13367. [Google Scholar] [CrossRef] [PubMed]
- Li, N.; Xin, M.; Su, Z.; Magden, E.S.; Singh, N.; Notaros, J.; Timurdogan, E.; Purnawirman, P.; Bradley, J.D.; Watts, M.R. A silicon photonic data link with a monolithic erbium-doped laser. Sci. Rep. 2020, 10, 1114. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Tan, M.; Corcoran, B.; Wu, J.; Boes, A.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Hicks, D.G.; Morandotti, R. 11 TOPS photonic convolutional accelerator for optical neural networks. Nature 2021, 589, 44–51. [Google Scholar] [CrossRef] [PubMed]
- Singh, N.; Xin, M.; Li, N.; Vermeulen, D.; Ruocco, A.; Magden, E.S.; Shtyrkova, K.; Ippen, E.; Kärtner, F.X.; Watts, M.R. Silicon photonics optical frequency synthesizer. Laser Photonics Rev. 2020, 14, 1900449. [Google Scholar] [CrossRef]
- Xin, M.; Li, N.; Singh, N.; Ruocco, A.; Su, Z.; Magden, E.S.; Notaros, J.; Vermeulen, D.; Ippen, E.P.; Watts, M.R. Optical frequency synthesizer with an integrated erbium tunable laser. Light Sci. Appl. 2019, 8, 122. [Google Scholar] [CrossRef] [PubMed]




| Crosstalk (dB) | Input Wavelength (µm) | |||
|---|---|---|---|---|
| 1.45 | 1.55 | 1.65 | ||
| Output ports | up | −22.9 | −18.1 | — |
| middle | −36.5 | — | −18.0 | |
| down | — | −20.1 | −22.3 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Wang, T.; Zhang, Y.; Shen, Y.; Yang, J.; Zhang, K.; Pan, D.; Xin, M. Global–Local Cooperative Optimization in Photonic Inverse Design Algorithms. Photonics 2025, 12, 725. https://doi.org/10.3390/photonics12070725
Li M, Wang T, Zhang Y, Shen Y, Yang J, Zhang K, Pan D, Xin M. Global–Local Cooperative Optimization in Photonic Inverse Design Algorithms. Photonics. 2025; 12(7):725. https://doi.org/10.3390/photonics12070725
Chicago/Turabian StyleLi, Mingzhe, Tong Wang, Yi Zhang, Yulin Shen, Jie Yang, Ke Zhang, Dehui Pan, and Ming Xin. 2025. "Global–Local Cooperative Optimization in Photonic Inverse Design Algorithms" Photonics 12, no. 7: 725. https://doi.org/10.3390/photonics12070725
APA StyleLi, M., Wang, T., Zhang, Y., Shen, Y., Yang, J., Zhang, K., Pan, D., & Xin, M. (2025). Global–Local Cooperative Optimization in Photonic Inverse Design Algorithms. Photonics, 12(7), 725. https://doi.org/10.3390/photonics12070725






