Effects of Chromatic Dispersion on BOTDA Sensor

Abstract

This study investigates the influence of chromatic dispersion on the performance of Brillouin optical time-domain analysis (BOTDA) sensors, particularly under high-pump-power conditions, where nonlinear effects become significant. By incorporating dispersion terms into the coupled amplitude equations of stimulated Brillouin scattering (SBS), we theoretically analyzed the dispersion-induced pulse broadening effect and its impact on the Brillouin gain spectrum (BGS). Numerical simulations revealed that dispersion leads to a moderate broadening of pump pulses, resulting in slight changes to BGS characteristics, including increased peak power and reduced linewidth. To explore the interplay between dispersion and nonlinearity, we built a gain-based BOTDA experimental system and tested two types of fibers, namely standard single-mode fiber (SMF) with anomalous dispersion and dispersion-compensating fiber (DCF) with normal dispersion. Experimental results show that SMF is more prone to modulation instability (MI), which significantly degrades the signal-to-noise ratio (SNR) of the BGS. In contrast, DCF effectively suppresses MI and provides a more stable Brillouin signal. Despite SMF exhibiting narrower BGS linewidths, DCF achieves a higher SNR, aligning with theoretical predictions. These findings highlight the importance of fiber dispersion properties in BOTDA design and suggest that using normally dispersive fibers like DCF can improve sensing performance in long-range, high-power applications.

1. Introduction

The development of low-loss optical fibers by Corning in the 1970s not only revolutionized global communication networks but also opened new avenues for the exploration of distributed optical fiber sensing (DOFS) technologies [1]. Compared with traditional mechanical or electrical sensors, DOFS systems offer several advantages, including lightweight structure, compact size, strong immunity to electromagnetic interference, and high chemical stability. These systems enable non-intrusive detection and simultaneous multi-parameter sensing while exhibiting scalability and networking capabilities, making them well-suited for operation in complex environments [2,3]. As a result, DOFS provides effective solutions to the challenges faced by conventional sensing technologies in long-range and continuously distributed measurement scenarios. In recent years, the field has drawn increasing interest from research institutions and governments worldwide.

Among the various DOFS techniques, Brillouin optical time-domain analysis (BOTDA), which operates on the principle of stimulated Brillouin scattering (SBS), has emerged as one of the most prominent due to its strong signal intensity, wide dynamic range, and high measurement accuracy. Since its initial proposal in 1989 [4], BOTDA technology has undergone more than three decades of development, achieving a high level of maturity and commercialization. It now plays a critical role in ensuring the structural safety and operational monitoring of key infrastructures such as bridges, tunnels, power grids, and oil and gas pipelines [5,6].

Despite its proven performance in practical deployments, the sensing accuracy and spatial resolution of BOTDA systems remain constrained by several physical factors. Like all optical fiber link systems, chromatic dispersion is inherently present in BOTDA setups, especially in scenarios requiring long sensing distances or high spatial resolution. Dispersion broadens the optical pulses during propagation, increasing the interaction length between pump and probe waves. This may distort the time-domain Brillouin response, degrading the spatial resolution of the system.

In addition to dispersion alone, nonlinear optical effects further complicate the sensing process. To maintain a sufficient signal-to-noise ratio (SNR) over long distances, BOTDA systems often require high pump powers. Under such conditions, self-phase modulation (SPM) becomes significant. When coupled with dispersion, SPM not only broadens and distorts the pump spectrum but can also induce modulation instability (MI) and other complex nonlinear phenomena [7]. These effects compromise the accuracy and stability of Brillouin frequency shift (BFS) extraction.

In 2015, Li et al. demonstrated through theoretical analysis and experimental validation that fiber dispersion in coherent BOTDA systems can induce phase-to-intensity conversion during modulation, resulting in BGS distortion and measurement instability [8]. In 2016, the same team proposed a novel coherent BOTDA scheme based on an intensity modulator, which reduced BGS decoding errors caused by dispersion by approximately 6 MHz, achieving a spatial resolution of 3 m and a temperature resolution of <1 °C over a 40 km sensing fiber [9]. In the same year, Wang et al. investigated the impact of fiber dispersion on the performance of chaotic optical time-domain reflectometry (COTDR), revealing that dispersion severely limits the system’s dynamic range [10]. In 2022, the Gasser group proposed a distributed anti-Stokes Raman thermometry (DART) system employing standard single-mode fiber and superconducting nanowire single-photon detectors, showing that dispersion in the backscattered signal causes the minimum detectable temperature variation distance to increase by about 4 cm per kilometer of fiber length [11].

A detailed investigation into the role and mechanisms of chromatic dispersion in BOTDA systems is thus essential for enhancing both spatial resolution and measurement accuracy. This study focuses on the influence of dispersion on system performance, combining theoretical analysis and numerical simulations. It examines two key aspects, namely pulse broadening induced by dispersion and modulation instability resulting from the interaction between dispersion and nonlinear effects. The findings provide theoretical insights and technical references for optimizing the design and improving the performance of BOTDA sensors.

2. Basic Principle

2.1. Operating Principle of BOTDA System

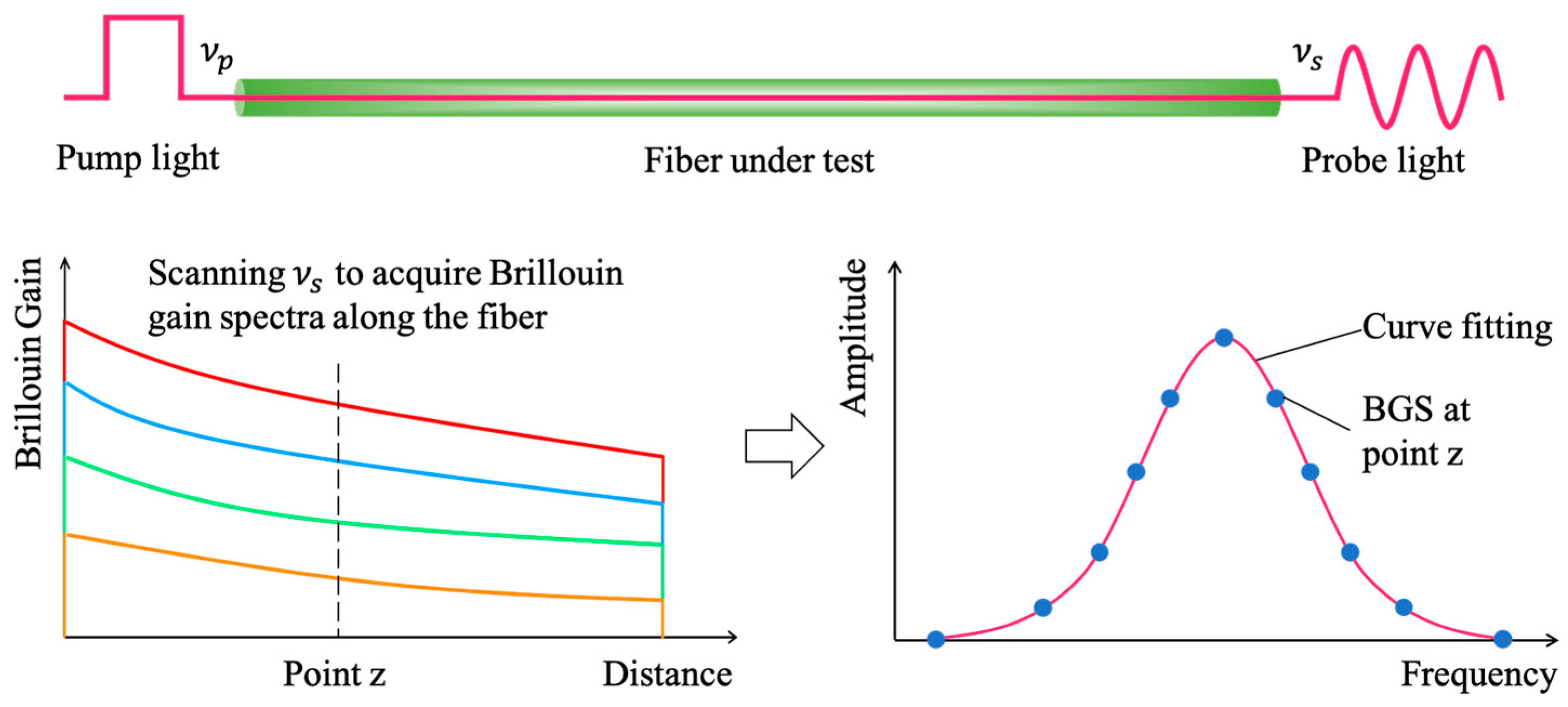
The fundamental operating principle of a BOTDA sensor is illustrated in Figure 1. A pulsed pump wave and a continuous probe wave are launched into opposite ends of the optical fiber. As they propagate, the interaction between these waves through the acoustic field gives rise to SBS. This interaction induces intensity modulation in the probe wave, which is subsequently converted into a time-domain electrical signal by a photodetector [12]. The resulting signal is acquired by an oscilloscope, enabling reconstruction of the Brillouin gain distribution along the fiber.

By sweeping the frequency offset between the pump and probe waves, a series of Brillouin gain traces can be obtained. Each trace corresponds to a specific frequency offset, and every point on the trace reflects the Brillouin gain at a particular fiber location under that offset. Collectively, these traces constitute the BGS along the sensing fiber.

The BGS measured at each fiber position is fitted to determine the peak gain frequency, which corresponds to the local BFS. Mapping the BFS along the entire length of the fiber enables a simultaneous extraction of distributed temperature and strain information.

2.2. Chromatic Dispersion

Although the pump and probe waves in a BOTDA system can achieve linewidths on the order of a few hertz, they are not strictly monochromatic [13]. According to information theory, an ideal single-frequency signal cannot carry meaningful information. As a result, both laser sources possess finite spectral bandwidths, rendering them susceptible to chromatic dispersion during propagation in the fiber. Among the various dispersion mechanisms, chromatic dispersion (CD) plays a particularly significant role in degrading pulse transmission quality.

In standard silica fibers, the refractive index varies with wavelength, and this wavelength-dependent behavior can be described by the Sellmeier equation. Due to the differing group velocities of various frequency components, phase mismatches accumulate during propagation, thereby altering the temporal envelope of the pulse. This frequency dependence is characterized by the propagation constant β(ω), which can be expanded in a Taylor series around the carrier angular frequency ${\omega }_0$ as follows:

$$\begin{array}{c}\beta \left(\omega \right)=\beta \left({\omega }_0\right)+{\displaystyle \frac{\mathrm{d}\beta }{\mathrm{d}\omega }}\left(\omega -{\omega }_0\right)+{\displaystyle \frac{1}{2}}{\displaystyle \frac{{\mathrm{d}}^2\beta }{\mathrm{d}{\omega }^2}}{\left(\omega -{\omega }_0\right)}^2+\cdots .\end{array}$$

(1)

This yields

$$\begin{array}{c}\beta \left(\omega \right)={\beta }_0+{\beta }_1\left(\omega -{\omega }_0\right)+{\displaystyle \frac{1}{2}}{\beta }_2{\left(\omega -{\omega }_0\right)}^2+\cdots ,\end{array}$$

(2)

Here, ${\beta }_1$ represents the inverse group velocity, while ${\beta }_2$ is the group velocity dispersion (GVD) coefficient.

Neglecting fiber loss and nonlinear effects, pulse propagation in the fiber can be described by a simplified nonlinear Schrödinger equation (NLSE) [14]:

$$\begin{array}{c}{\displaystyle \frac{\partial }{\partial z}}A\left(z,t\right)+j{\displaystyle \frac{{\beta }_2}{2}}{\displaystyle \frac{{\partial }^2}{\partial t^2}}A\left(z,t\right)=0,\end{array}$$

(3)

where $A\left(z,t\right)$ denotes the amplitude of the pump wave. Applying the Fourier transform method, the solution in the frequency domain is

$$\begin{array}{c}\tilde{A}\left(z,\omega \right)=\tilde{A}\left(0,\omega \right)\exp \left(j{\displaystyle \frac{{\beta }_{2}z{\omega }^2}{2}}\right)\mathrm{d}\omega .\end{array}$$

(4)

This expression reveals that dispersion imposes frequency-dependent phase shifts, leading to temporal pulse broadening in the time domain.

The dispersion coefficient $D$ is defined as the change in group delay per unit wavelength shift:

$$\begin{array}{c}D=-{\displaystyle \frac{{\lambda }^2}{2\pi c}}{\displaystyle \frac{{\mathrm{d}}^2\beta }{\mathrm{d}{\lambda }^2}},\end{array}$$

(5)

with units of ps/(nm·km). The accumulated temporal broadening $\mathsf{\Delta }T$ over a fiber length L is then

$$\mathsf{\Delta }T=D·\mathsf{\Delta }\lambda ·L.$$

(6)

Accordingly, the broadened pulse width $T_p$ after transmission becomes

$$T_p=T_0+\mathsf{\Delta }T,$$

(7)

where $T_0$ is the initial pulse width and $\mathsf{\Delta }\lambda$ is the laser linewidth. The dispersion coefficient $D$ is related to ${\beta }_2$ by

$$\begin{array}{c}D=-{\displaystyle \frac{2\pi C}{{\lambda }^2}}{\beta }_2.\end{array}$$

(8)

In the anomalous dispersion regime ($D>0$ or ${\beta }_2<0$), higher-frequency components travel more slowly than lower-frequency components; the opposite behavior is observed in the normal dispersion regime. In practice, the value of $D$ is typically specified by the fiber manufacturer or estimated using empirical formulas. One common approximation is

$$\begin{array}{c}D\left(\lambda \right)={\displaystyle \frac{S_0}{4}}\left(\lambda -{\displaystyle \frac{{\lambda }_0^4}{{\lambda }^3}}\right),\end{array}$$

(9)

where $S_0$ is the zero-dispersion slope and ${\lambda }_0$ is the zero-dispersion wavelength.

2.3. Stimulated Brillouin Scattering in Optical Fibers

SBS is a third-order nonlinear optical effect arising from the interaction between light and acoustic waves, and it is prevalent in single-mode optical fibers. When a pump wave of relatively low power is launched into the fiber, thermally induced acoustic fluctuations give rise to spontaneous Brillouin scattering (sp-BS), generating a weak backward-propagating wave with a slightly lower frequency than the pump. The intensity of the spontaneous Brillouin signal increases linearly with pump power.

As the pump power increases, the backward-propagating Stokes wave interferes with the forward-propagating pump wave, forming a periodic optical interference pattern. Driven by the electrostriction effect, this pattern excites longitudinal acoustic waves in the fiber. These acoustic waves, in turn, induce a periodic modulation of the refractive index through the photoelastic effect, forming a moving refractive index grating that enhances the Brillouin interaction, thereby generating a stronger Stokes wave [15].

This light–acoustic interaction establishes a positive feedback loop, where the coupling among the pump, Stokes, and acoustic fields leads to exponential growth of the Stokes wave, pushing the system into the SBS gain regime. Because energy preferentially transfers from high to low optical frequencies, anti-Stokes scattering lacks a similar feedback mechanism and therefore exhibits much lower gain than the Stokes component.

The coupling dynamics among the pump wave ($A_p$), the Stokes wave ($A_s$), and the acoustic field ($\mathsf{\Delta }\rho$) can be described by the following set of coupled differential equations [14]:

$$\begin{array}{c}{\displaystyle \frac{\partial A_p}{\partial z}}+{\displaystyle \frac{n}{c}}{\displaystyle \frac{\partial A_p}{\partial t}}+j{\displaystyle \frac{{\beta }_2}{2}}{\displaystyle \frac{{\partial }^2{A}_p}{\partial t^2}}=-{\displaystyle \frac{\alpha }{2}}{A}_p+j\gamma \left({\left|A_p\right|}^2+{\left|A_s\right|}^2\right)A_p+j{g}_1{A}_s\Delta \rho ,\end{array}$$

(10)

$$\begin{array}{c}-{\displaystyle \frac{\partial A_s}{\partial z}}+{\displaystyle \frac{n}{c}}{\displaystyle \frac{\partial A_s}{\partial t}}+j{\displaystyle \frac{{\beta }_2}{2}}{\displaystyle \frac{{\partial }^2{A}_s}{\partial t^2}}=-{\displaystyle \frac{\alpha }{2}}{A}_s+j\gamma \left({\left|A_s\right|}^2+{\left|A_p\right|}^2\right)A_s+j{g}_1{A}_p\Delta {\rho }^{*},\end{array}$$

(11)

$$\begin{array}{c}{v}_a{\displaystyle \frac{\partial \mathsf{\Delta }\rho }{\partial z}}+{\displaystyle \frac{\partial \mathsf{\Delta }\rho }{\partial t}}=-\left[j\left({\Omega }_B-\Omega \right)+{\displaystyle \frac{{\Gamma }_p}{2}}\right]\Delta \rho +j{\displaystyle \frac{{\mathit{e}}_{\mathit{p}}·{\mathit{e}}_{\mathit{s}}}{A_{\mathrm{eff}}}}{g}_2{A}_p{A}_s^{*},\end{array}$$

(12)

Here, $A_p$ and $A_s$ represent the complex amplitudes of the pump and Stokes waves, respectively, and $\mathsf{\Delta }\rho$ denotes the acoustic field amplitude. The parameters $\alpha$ and $\gamma$ are the fiber attenuation coefficient and nonlinear coefficient, respectively. $v_a$ is the speed of sound in the fiber, ${\Omega }_B$ is the Brillouin frequency shift, $\Omega$ is the acoustic angular frequency, and ${\Gamma }_p$ is the pump pulse linewidth. ${\mathit{e}}_{\mathit{p}}$ and ${\mathit{e}}_{\mathit{s}}$ are the normalized polarization vectors of the pump and Stokes waves, respectively, and $A_{\mathrm{eff}}$ is the effective fiber core area. The coupling coefficients $g_1$ and $g_2$ are defined as

$$\begin{array}{c}{g}_1={\displaystyle \frac{\omega {\gamma }_e⟨F^2{F}_{\rho }⟩}{2nc{\rho }_0⟨F^2⟩}},\end{array}$$

(13)

$$\begin{array}{c}{g}_2={\displaystyle \frac{\omega {\gamma }_e⟨F^2{F}_{\rho }⟩}{2c^2{v}_a⟨F_{\rho }^2⟩}},\end{array}$$

(14)

where the integrals are evaluated over the transverse x–y cross-sectional area of the fiber.

According to Eggleton et al. [16], the SBS interaction time in nanophotonic waveguides is typically short, ranging from a few nanoseconds to several hundred nanoseconds. This corresponds to acoustic propagation distances of only tens to hundreds of microns. Therefore, for BOTDA systems operating over sensing distances of several kilometers to tens of kilometers, the spatial evolution of the acoustic field can be neglected. Under this quasi-static approximation, the coupled equations simplify to

$$\begin{array}{c}{\displaystyle \frac{\partial A_p}{\partial z}}+{\displaystyle \frac{n}{c}}{\displaystyle \frac{\partial A_p}{\partial t}}+j{\displaystyle \frac{{\beta }_2}{2}}{\displaystyle \frac{{\partial }^2{A}_p}{\partial t^2}}=-{\displaystyle \frac{\alpha }{2}}{A}_p+j{g}_1{A}_s\mathsf{\Delta }\rho ,\end{array}$$

(15)

$$\begin{array}{c}-{\displaystyle \frac{\partial A_s}{\partial z}}+{\displaystyle \frac{n}{c}}{\displaystyle \frac{\partial A_s}{\partial t}}+j{\displaystyle \frac{{\beta }_2}{2}}{\displaystyle \frac{{\partial }^2{A}_s}{\partial t^2}}=-{\displaystyle \frac{\alpha }{2}}{A}_s+j{g}_1{A}_p\mathsf{\Delta }{\rho }^{*},\end{array}$$

(16)

$$\begin{array}{c}{\displaystyle \frac{\partial \Delta \rho }{\partial t}}=-\left[{\Gamma }_p/2+j\left({\Omega }_B-\Omega \right)\right]\Delta \rho +j{\displaystyle \frac{\left({\mathit{e}}_{\mathit{p}}·{\mathit{e}}_{\mathit{s}}\right)g_2}{A_{\mathrm{eff}}}}{A}_p{A}_s^{*}.\end{array}$$

(17)

2.4. Dispersion-Related Nonlinear Effects

Under high-power conditions, the dielectric response of optical fibers exhibits nonlinear behavior. To improve the SNR in long-distance BOTDA systems, high-power pump waves are typically employed [17]. However, the associated nonlinear effects can significantly impair signal transmission performance in fibers.

By applying a change in variables to Equation (1) and neglecting the Brillouin gain term, the evolution of the pump field can be expressed as

$$\begin{array}{c}{\displaystyle \frac{\partial A_p}{\partial z}}+j{\displaystyle \frac{{\beta }_2}{2}}{\displaystyle \frac{{\partial }^2{A}_p}{\partial {\tau }^2}}+{\displaystyle \frac{\alpha }{2}}{A}_p-j\gamma {\left|A_p\right|}^2{A}_p=0,\end{array}$$

(18)

where $\tau =\mathrm{t}-\mathrm{z}\mathrm{n}/\mathrm{c}$. The last three terms on the left-hand side represent GVD, fiber attenuation, and nonlinear Kerr effects, respectively.

In the case of multimode fibers, suppose three optical modes E₁, E₂, and E₃ are present, with corresponding amplitudes $A_1$, $A_2$, and $A_3$. The evolution equation for the mode $A_1$ is given by

$$\begin{array}{c}{\displaystyle \frac{\partial A_1}{\partial z}}+j{\displaystyle \frac{{\beta }_0^{″}}{2}}{\displaystyle \frac{{\partial }^2{A}_1}{\partial {\tau }^2}}+{\displaystyle \frac{\alpha }{2}}{A}_1-j\gamma {\left|A_1\right|}^2{A}_1-2j\gamma \left({\left|A_2\right|}^2+{\left|A_3\right|}^2\right)A_1-2j\gamma A_2{A}_3{A}_1^{*}=0,\end{array}$$

(19)

Here, the last three nonlinear terms on the left-hand side correspond to SPM, cross-phase modulation (XPM), and four-wave mixing (FWM), respectively. Since this study focuses on single-mode fibers (SMF), the contributions from XPM and FWM are negligible, and the equation simplifies to

$$\begin{array}{c}{\displaystyle \frac{\partial A_1}{\partial z}}+j{\displaystyle \frac{{\beta }_0^{″}}{2}}{\displaystyle \frac{{\partial }^2{A}_1}{\partial {\tau }^2}}+{\displaystyle \frac{\alpha }{2}}{A}_1-j\gamma {\left|A_1\right|}^2{A}_1=0.\end{array}$$

(20)

SPM refers to the spectral broadening of high-power optical pulses due to nonlinear phase shifts induced by the pulse itself during propagation. The induced phase shift is given by

$$\begin{array}{c}\varphi \left(L,t\right)=\gamma {\left|A\left(0,t\right)\right|}^2{\displaystyle \frac{1-e^{-\alpha L}}{\alpha }}=\gamma {\left|A\left(0,t\right)\right|}^2{L}_{eff},\end{array}$$

(21)

where $L_{eff}$ is the effective interaction length and ${\left|A\left(0,t\right)\right|}^2$ denotes the input power profile. Clearly, the SPM-induced phase shift is proportional to the input optical power, indicating that higher powers lead to more pronounced spectral broadening.

3. Dispersion-Induced Pulse Broadening in BOTDA

3.1. Numerical Simulation and Analysisl

To effectively stimulate SBS, the pump pulse width is typically set to exceed 10 ns. Under such conditions, the pump pulse duration is much longer than the phonon lifetime, allowing it to be approximated as a quasi-continuous wave (quasi-CW). Under the quasi-CW approximation, the interaction among the pump wave, probe wave, and acoustic wave reaches a steady-state balance, and their temporal evolution can be neglected. Accordingly, the following steady-state coupled amplitude equations can be established:

$$\begin{array}{c}{\displaystyle \frac{\mathrm{d}{A}_p}{\mathrm{d}z}}=-{\displaystyle \frac{\alpha }{2}}{A}_p+j{g}_1{A}_s\mathsf{\Delta }\rho ,\end{array}$$

(22)

$$\begin{array}{c}-{\displaystyle \frac{\mathrm{d}{A}_s}{\mathrm{d}z}}=-{\displaystyle \frac{\alpha }{2}}{A}_s+j{g}_1{A}_p\mathsf{\Delta }{\rho }^{*},\end{array}$$

(23)

$$\begin{array}{c}\mathsf{\Delta }\rho ={\displaystyle \frac{\left(e_p·e_s\right)g_2}{\left({\Omega }_B-\Omega \right)-j{\Gamma }_p/2}}{\displaystyle \frac{A_p{A}_s^{*}}{A_{\mathrm{eff}}}}.\end{array}$$

(24)

By substituting Equation (24) into Equations (22) and (23), the spatial evolution of the pump and probe wave amplitudes can be expressed in terms of optical power as

$$\begin{array}{c}{\displaystyle \frac{\mathrm{d}{P}_p}{\mathrm{d}z}}=-\alpha P_p-{\displaystyle \frac{g_B{\left(\mathsf{\Delta }\nu \right) }_{{\nu }_B,\mathsf{\Delta }{\nu }_B}}{A_{eff}}}{P}_s{P}_p,\end{array}$$

(25)

$$\begin{array}{c}-{\displaystyle \frac{\mathrm{d}{P}_s}{\mathrm{d}z}}=-\alpha P_s+{\displaystyle \frac{g_B{\left(\mathsf{\Delta }\nu \right) }_{{\nu }_B,\mathsf{\Delta }{\nu }_B}}{A_{eff}}}{P}_p{P}_s,\end{array}$$

(26)

where the Brillouin gain coefficient is defined as

$$\begin{array}{c}{g}_B{\left(\mathsf{\Delta }\nu \right) }_{{\nu }_B,\mathsf{\Delta }{\nu }_B} = g_{B0}{\displaystyle \frac{e_p·e_s}{1+{\left[\left(\mathsf{\Delta }\nu -{\nu }_B\right)/\left(\mathsf{\Delta }{\nu }_B/2\right)\right]}^{ 2}}}.\end{array}$$

(27)

Under the assumption of negligible pump depletion, the pump power remains approximately constant along the fiber. Assuming that the probe light is launched from the fiber end at $z=L$ and the pump light is injected from the input end at $z=0$, the pump power distribution is

$$\begin{array}{c}{P}_p\left(z\right)=P_p\left(0\right)e^{-\alpha z}.\end{array}$$

(28)

By substituting Equation (28) into Equation (26) and solving, the probe power at $z=0$ after propagating a length $L$ becomes

$$\begin{array}{c}{P}_s\left(0\right)=P_s\left(L\right)\exp \left[{\displaystyle \frac{g_B{P}_p\left(0\right)L_{eff}}{A_{eff}}}-\alpha L\right].\end{array}$$

(29)

The Brillouin signal can be regarded as the energy gain experienced by the probe wave through the SBS process, defined as the difference in power between the output and input probe waves:

$$\begin{array}{c}{P}_b\left(\nu \right)=P_s\left(L\right)e^{-\alpha L}\left[\exp \left({\displaystyle \frac{g_B{P}_p\left(0\right)L_{eff}}{A_{eff}}}\right)-1\right].\end{array}$$

(30)

Considering that the pump pulse has a finite temporal width, the effective interaction length is corrected as [18]

$$\begin{array}{c}{L}_{eff}={\displaystyle \frac{T_p}{2}}{\displaystyle \frac{c}{n}}.\end{array}$$

(31)

By substituting Equation (31) into Equation (30), the Brillouin gain signal of a gain-based BOTDA system as a function of pump pulse width is expressed as

$$\begin{array}{c}{P}_b\left(\nu \right)=P_s\left(0\right)e^{-\alpha L}\left[\exp \left({\displaystyle \frac{g_B{P}_p\left(L\right)c{T}_p}{2n{A}_{eff}}}\right)-1\right],\end{array}$$

(32)

where $T_p$ is the dispersion-broadened pump pulse width defined in Equation (7).

3.2. Numerical Verification

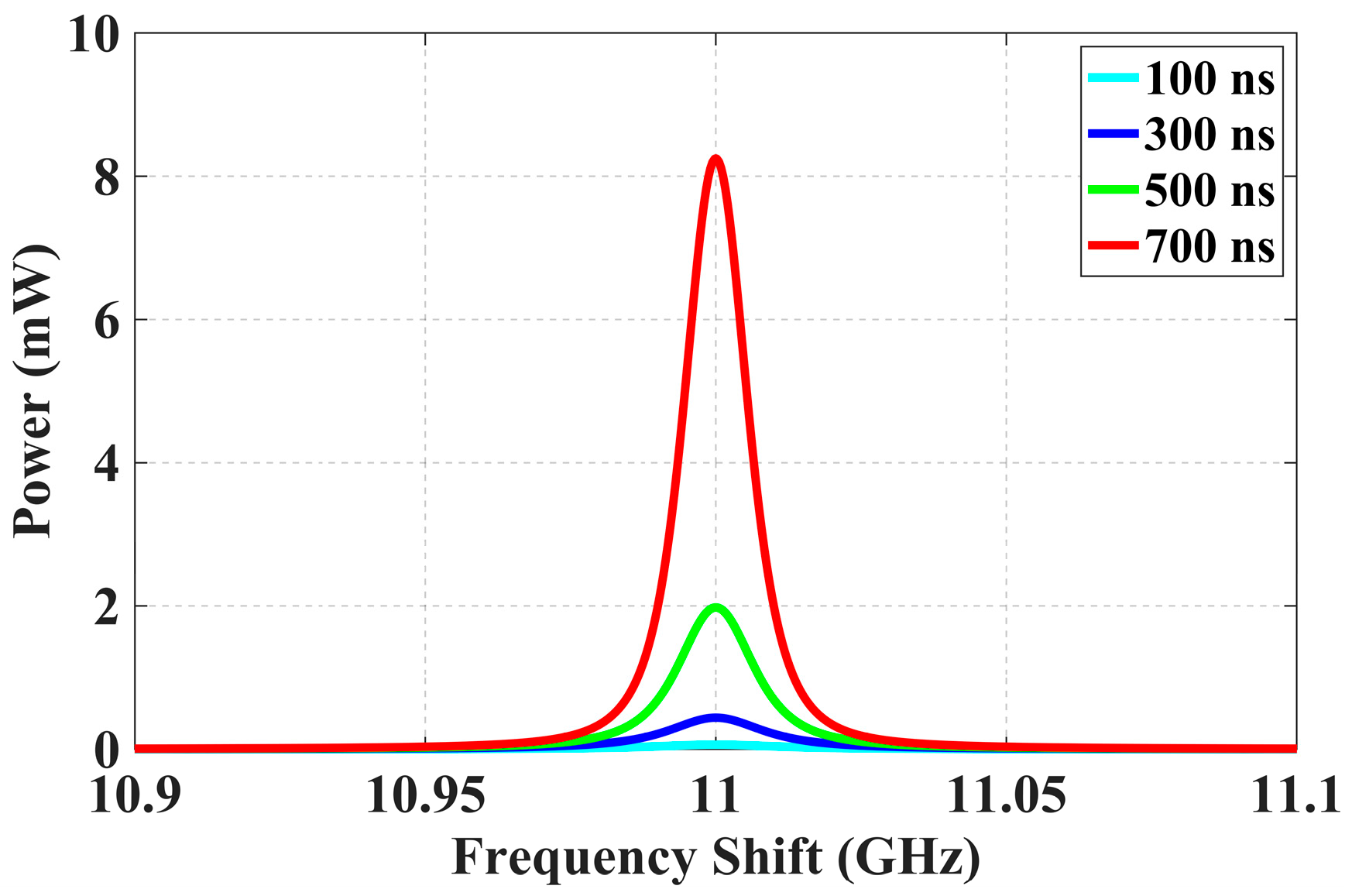
Based on Equation (32), we first analyze the characteristics of the BGS under ideal conditions (i.e., zero dispersion). The initial pump power is set to 60 mW, the probe power to 0.1 mW, and the fiber length to 10 km. Simulations were conducted in MATLAB R2021b for three pump pulse widths, namely 300 ns, 500 ns, and 700 ns. The results are shown in Figure 2.

As shown in Figure 2, the shape of the BGS undergoes significant changes as the pump pulse width increases. To further quantify this effect, we calculated the trends of BGS peak gain and linewidth with respect to pulse width in MATLAB, as shown in Figure 3.

From Figure 3, it is observed that the BGS linewidth gradually decreases as the pump pulse width increases, while the peak gain increases accordingly. Notably, the growth rate of the peak gain accelerates when the pulse width exceeds approximately 700 ns. These results indicate that the pump pulse width significantly affects the characteristics of the BGS.

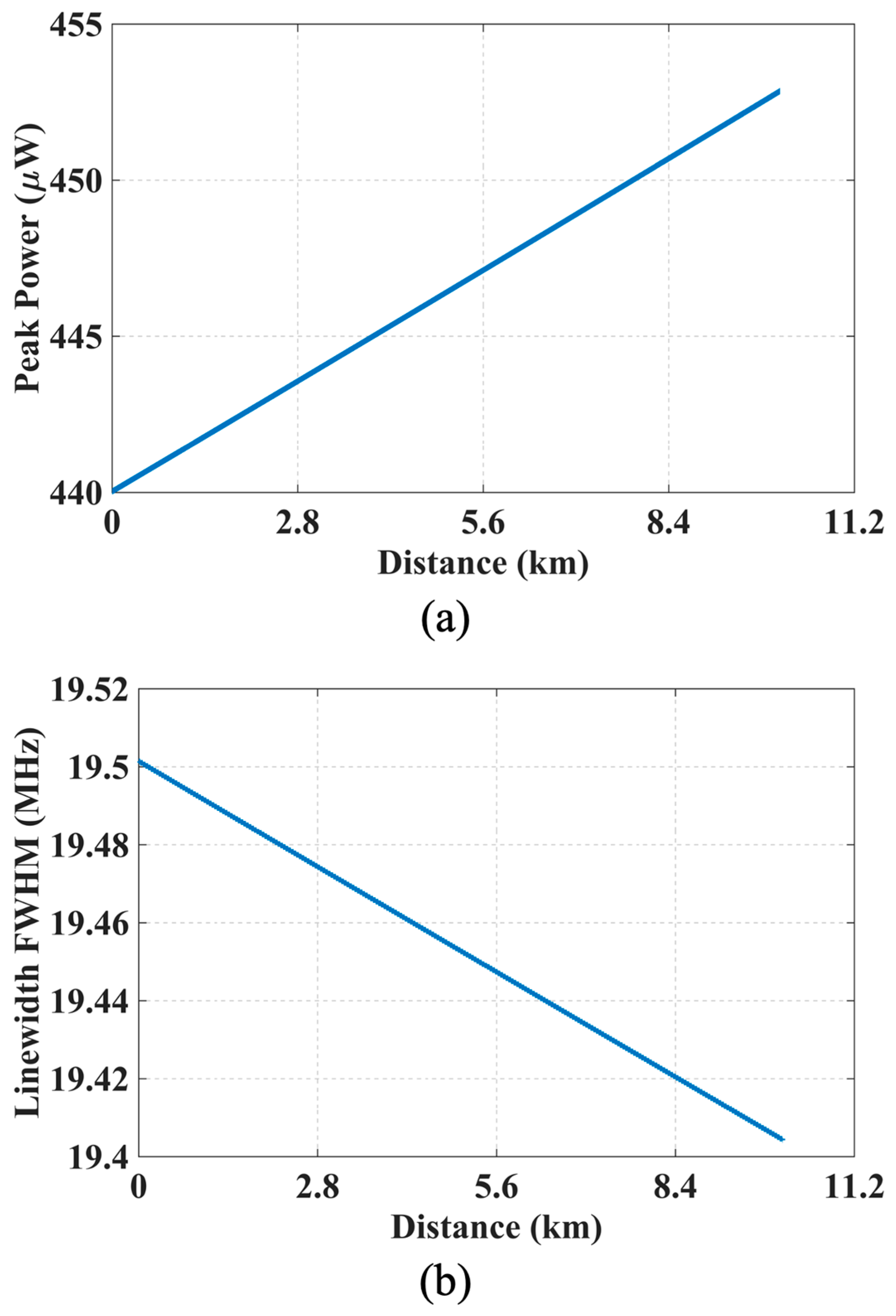
Based on the previous theoretical analysis, it is known that chromatic dispersion in optical fibers leads to temporal broadening of the pump pulse. Therefore, we next investigate the dispersion-induced broadening effect. A simulation was carried out in MATLAB for an initial pump pulse width of 300 ns. The results are presented in Figure 4.

Figure 4 shows that under the influence of dispersion-induced pulse broadening, both the peak power and linewidth of the BGS experience slight variations along the fiber. Specifically, the peak power increases by approximately 0.125 dB, while the linewidth decreases by only 0.1 MHz. Given that the typical BGS linewidth is around 30 MHz, the reduction accounts for merely 0.33%. Similarly, the gain variation corresponding to a 0.125 dB increase in power is less than 3%.

Therefore, under the simulation conditions considered in this study, the impact of dispersion-induced pulse broadening on the BGS is relatively minor. Its overall effect on system performance can be considered negligible, and it will not be addressed separately in the following sections.

4. Dispersion and Self-Phase Modulation in BOTDA

4.1. Theoretical Analysis

Under the steady-state assumption adopted in the previous section and neglecting both dispersion and attenuation, Equation (20) can be solved to yield

$$\begin{array}{c}{A}_1=\sqrt{P_0}{e}^{i\varphi },\end{array}$$

(33)

indicating that the pump wave undergoes only phase modulation during propagation, while its amplitude remains unchanged. However, when dispersion is taken into account, a perturbation term can be introduced to modify Equation (33), leading to the following expression:

$$\begin{array}{c}{A}_1=\left(\sqrt{P_0}+\widehat{W}\right)e^{i\varphi },\end{array}$$

(34)

where $\widehat{W}$ denotes the perturbation induced by chromatic dispersion. By substituting Equation (34) into Equation (20) and solving it, the perturbation term is obtained as [14,19]

$$\begin{array}{c}\widehat{W}\left(z,t\right)=\widehat{W_1}\mathit{exp}\left[j\left(Kz-\Omega t\right)\right]+\widehat{W_2}\mathit{exp}\left[-j\left(Kz-\Omega t\right)\right],\end{array}$$

(35)

where $K$ and $\Omega$ are the wave number and angular frequency of the perturbation, respectively. For Equation (35) to hold, the following dispersion relation must be satisfied:

$$\begin{array}{c}K=\pm {\displaystyle \frac{1}{2}}\left|{\beta }_0^{″}\Omega \right| {\left[{\Omega }^2+{\displaystyle \frac{4\gamma P_{0}sgn\left({\beta }_2\right)}{{\beta }_0^{″}}}\right]}^{1/2},\end{array}$$

(36)

where $\mathrm{s}\mathrm{g}\mathrm{n}\left({\beta }_2\right)$ is the sign function, taking the value +1 for ${\beta }_2\hspace{0.17em}>\hspace{0.17em}0$ and −1 for ${\beta }_2\hspace{0.17em}<\hspace{0.17em}0$. In the normal dispersion regime (${\beta }_2\hspace{0.17em}>\hspace{0.17em}0$), the value of $K$ remains purely real for all $\Omega$, implying that the perturbation remains bounded and the steady-state solution of the pump field remains stable. However, in the anomalous dispersion regime (${\beta }_2\hspace{0.17em}<\hspace{0.17em}0$), K may acquire an imaginary component, leading to exponential growth of the perturbation term $\widehat{W}$ along the propagation direction. This instability eventually causes the quasi-continuous pump wave to break up into a train of ultrashort pulses—a phenomenon known as MI [20].

In summary, chromatic dispersion not only leads to temporal broadening of the pump pulse, but when the fiber dispersion coefficient is positive, it can also interact with the SPM effect to induce MI, significantly impacting the performance of BOTDA systems.

4.2. Experimental Setup

To investigate the combined effects of chromatic dispersion and nonlinearities on the BOTDA system, two types of optical fibers were selected for testing, namely standard SMF and dispersion-compensating fiber (DCF). Their key parameters are listed in

Table 1. Parameters of test fibers.

Fiber Type	BFS (MHz)	${\mathit{\beta }}_2$$(\mathbf{p}{\mathbf{s}}^2/\mathbf{k}\mathbf{m})$	${\mathit{A}}_{\mathit{e}\mathit{f}\mathit{f}}$$\left(\mathsf{\mu }{\mathbf{m}}^2\right)$
SMF	10,739	−22.9	80
DCF	10,153	21	20

.

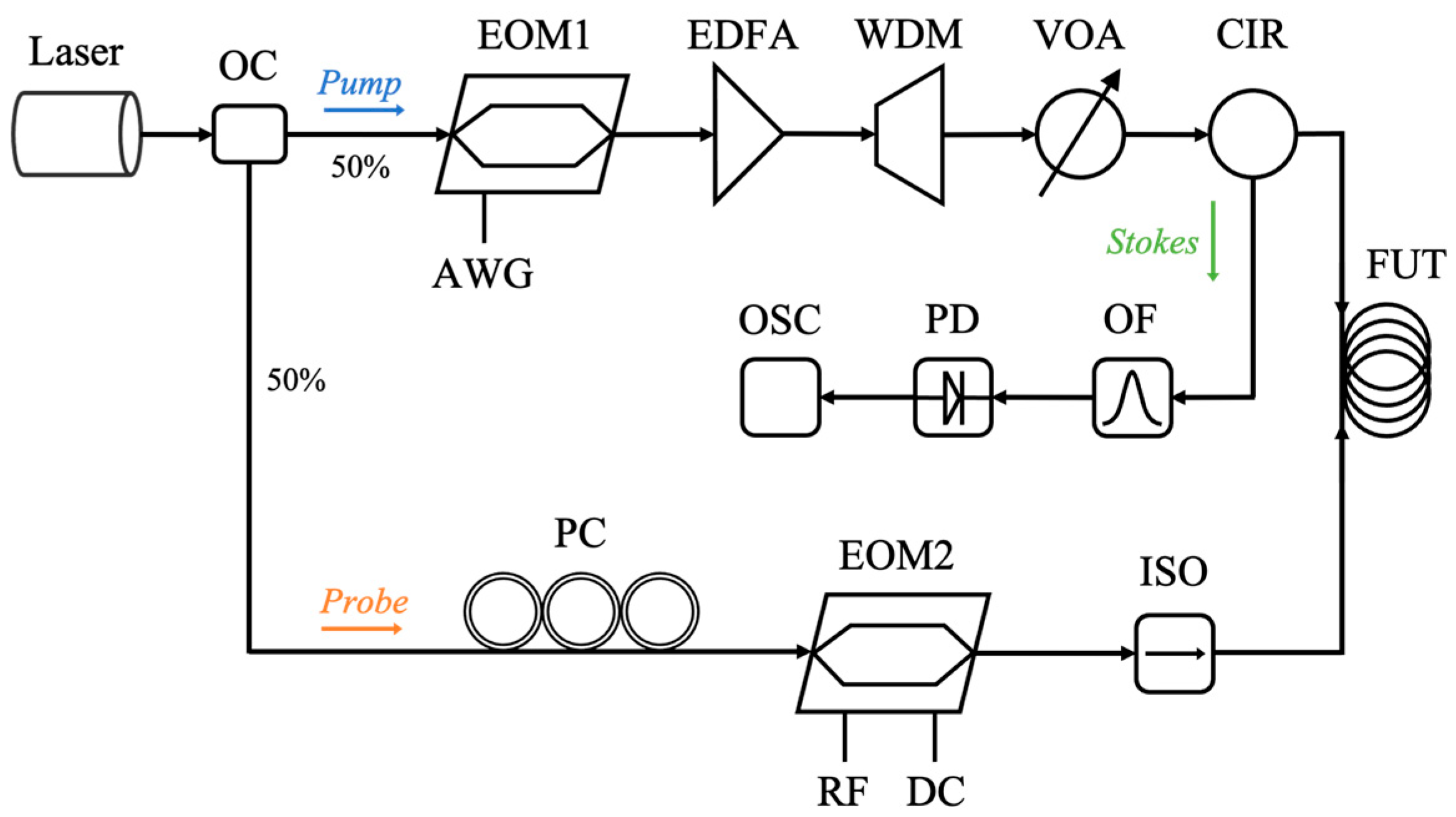
Based on these fibers, a gain-based BOTDA system with direct detection was constructed, as illustrated in Figure 5.

A continuous-wave laser operating at a center wavelength of 1550 nm is divided into two branches by an optical coupler. In the upper branch, an arbitrary waveform generator drives the electro-optic modulator (EOM1) to generate high-extinction-ratio pump pulses with a width of 100 ns and a repetition period of 200 μs. These pulses are amplified by an erbium-doped fiber amplifier (EDFA), spectrally filtered by a wavelength division multiplexer (WDM), and subsequently power-tuned by a variable optical attenuator before being injected into the test fiber via a circulator.

In the lower branch, a radio-frequency signal generator performs frequency sweeping around the BFS of the fiber under test in 2 MHz steps. This signal modulates a second electro-optic modulator (EOM2) to generate frequency-shifted probe light. After passing through an optical isolator, the probe wave is also launched into the test fiber. Notably, in order to mitigate the impact of optical attenuation, both the Stokes and anti-Stokes components are retained in the fiber during the experiment [21].

At the receiving end, the output signal is filtered to isolate the Stokes component, which is then detected by a photodetector and recorded using an oscilloscope for subsequent processing. The key components of the system are listed in

Table 2. Key components used in the experimental setup and their specifications.

Component	Model	Manufacturer	Key Specifications
Laser	KG-ELD-C35-10-M-FC/APC	CONQUER (Beijing, China)	Wavelength: 1548.934 nm, Linewidth < 1 MHz, Peak Power: 10.2 dBm
EDFA	WE-1550-HD	PREVAIL (Hangzhou, China)	Bandwidth: 1545–1565 nm Input: −3–+10 dBm Output: up to 23 dBm
OF	BVF-300CL-SM-FA	Alnair Labs (Tokyo, Japan)	Wavelength range: 1525–1610 nm Bandwidth Tunability: 0.03–3 nm Input: <27 dBm
PD	P6703B	Tektronix (Beaverton, OR, USA)	Wavelength range: 1100–1650 nm Bandwidth: 1.2 GHz Conversion gain: 1.02 V/mW
OSC	WAVERUNNER 8404M	Teledyne LeCroy (New York, NY, USA)	Bandwidth: 4 GHz Sampling Rate: up to 40 GS/s Max Memory: 128 Mpts

.

4.3. Experimental Results and Analysis

By arranging the acquired Brillouin gain signals in the order of scanning frequency, the BGS can be reconstructed, as shown in Figure 6. The left panel depicts the BGS obtained from the standard SMF, while the right panel shows that of the DCF. As observed in both cases, the gain increases significantly as the probe frequency approaches the BFS. Additionally, a pronounced gain is present near the fiber’s input end (0 km), which is primarily attributed to Fresnel reflection at the fiber connection interface.

In BOTDA systems, multiple sources of noise are inevitable, including laser source noise, intrinsic noise from the photodetector, and broadband intensity noise stemming from the Brillouin scattering process [22]. Among these, the SNR plays a critical role in determining the sensing performance and measurement accuracy of the BOTDA system.

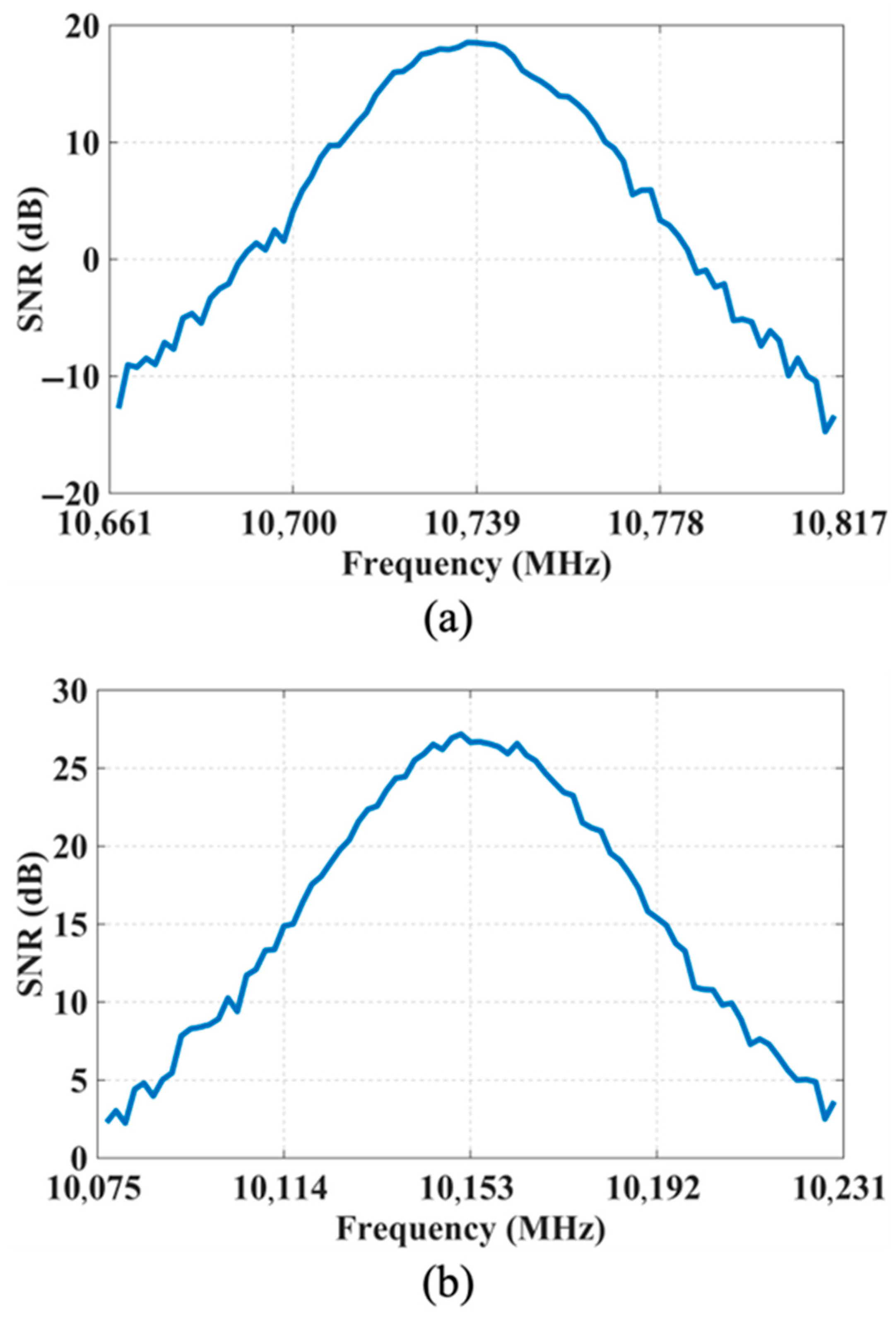
In recent years, wavelet denoising (WD) techniques have attracted significant attention for their ability to suppress noise effectively without requiring additional hardware complexity [23]. In this work, a WD algorithm was implemented in MATLAB and applied to the experimental data from both SMF and DCF. The resulting SNR distributions are illustrated in Figure 7.

In theory, SMF exhibits a larger effective mode area, which reduces the light intensity and thereby weakens SPM. As the strength of SPM is proportional to optical intensity, SMF is expected to exhibit weaker nonlinear distortion and thus a higher BGS SNR. However, the experimental results reveal average SNR values of 4.41 dB for SMF and 15.38 dB for DCF, contradicting the theoretical prediction.

This discrepancy can be attributed to the presence of MI in the SMF. As previously analyzed, MI tends to occur in fibers exhibiting anomalous dispersion characteristics, such as SMF. At high pump powers, MI can amplify weak system noise—such as amplified spontaneous emission (ASE) and quantum noise—into significant perturbations, which mask the original Brillouin signal and reduce the SNR. Conversely, the normal dispersion characteristic of DCF suppresses MI, enabling more stable Brillouin signal acquisition under the same pump power conditions.

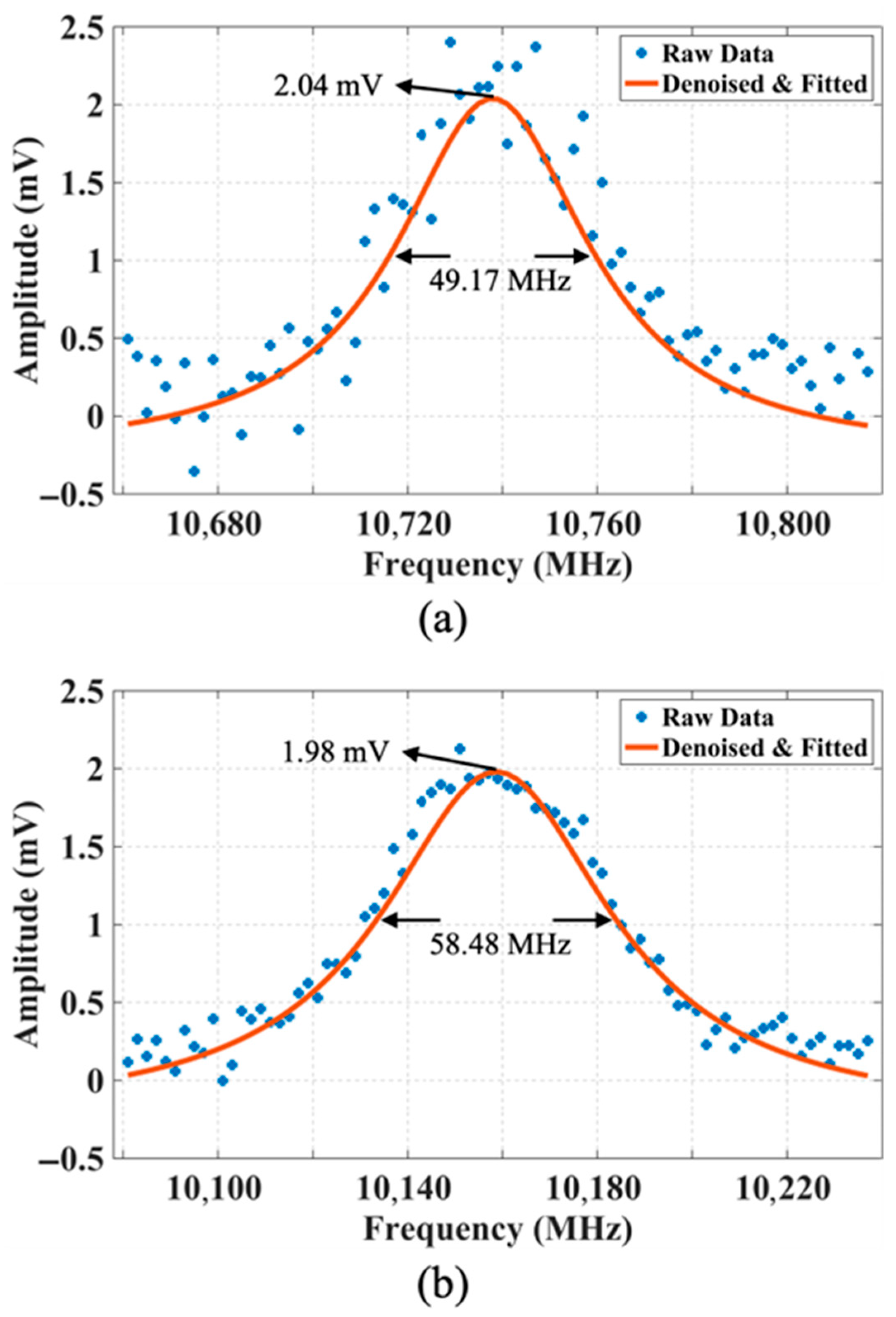
To eliminate the interference caused by Fresnel reflection at the fiber connection, we focus our analysis on the central region of both fibers. After applying wavelet denoising and fitting the data with a Lorentzian curve, the BGSs at the 10 km position are plotted in Figure 8. The linewidth and peak gain of the SMF BGS are approximately 49.17 MHz and 2.04 mV, respectively, while those of the DCF are about 58.48 MHz and 1.98 mV.

Compared to the typical Brillouin linewidth of 30 MHz, both fibers exhibit significant spectral broadening due to SPM. The broadening is more pronounced in DCF, primarily because of its smaller effective mode area, which enhances nonlinear effects. Nevertheless, the similar peak intensities observed in both fibers indicate that the Brillouin scattering process in DCF remains stable, even under stronger nonlinear influence.

5. Discussion

The results presented in this study reveal that chromatic dispersion plays a multi-faceted role in the performance of BOTDA systems. While the dispersion-induced temporal broadening of pump pulses has a relatively minor impact on the BGS under moderate pulse widths and power levels, its influence becomes more pronounced when combined with nonlinear effects such as SPM. This interplay can give rise to MI, which significantly degrades the SNR and the overall reliability of Brillouin sensing.

In comparison to previous studies, our findings are consistent with those of Li et al. [8,9], who reported that fiber dispersion contributes to phase-to-intensity conversion and decoding errors in coherent BOTDA systems. However, unlike their studies—which focused on coherent detection architectures and emphasized modulation–demodulation schemes—our study investigates BOTDA systems based on direct detection, which are more commonly employed in practical long-range sensing scenarios due to their lower complexity and cost. To the best of our knowledge, few prior studies have systematically examined the impact of dispersion on direct-detection BOTDA systems under high-pump-power-conditions.

Moreover, Gasser et al. [11] observed that dispersion in backscattered signals introduces spatial resolution degradation in DART systems, whereas our experimental results demonstrate that normally dispersive fibers (e.g., DCF) can actually enhance system stability by mitigating MI despite their higher nonlinear susceptibility.

Notably, the comparative analysis between standard SMF and DCF highlights the critical trade-offs in BOTDA design. While SMF exhibits narrower BGS linewidths due to its larger mode field diameter and lower nonlinearity, its anomalous dispersion profile makes it more susceptible to MI under high pump power, resulting in significant SNR degradation. On the other hand, DCF exhibits stronger nonlinear broadening but maintains a more stable BGS with a superior SNR, which aligns with theoretical predictions based on dispersion–SPM interaction.

These observations suggest that BOTDA system designers must carefully consider the dispersion properties of the sensing fiber, especially in high-power or long-range applications. The use of normally dispersive fibers offers a practical strategy to suppress unwanted nonlinearities and improve sensing quality. Furthermore, the combined modeling and experimental approach in this study provides a useful framework for analyzing dispersion–nonlinearity interactions in other types of distributed optical fiber sensors. These findings not only validate the theoretical framework but also offer practical guidance for engineers developing BOTDA-based distributed sensing networks, particularly for long-distance structural health monitoring and environmental sensing applications.

In addition, the broadening and distortion of the BGS due to chromatic dispersion and nonlinear effects may affect the accuracy of frequency shift extraction algorithms. Traditional approaches such as Lorentzian curve fitting (LCF), widely used in commercial BOTDA systems, are particularly sensitive to reduced peak sharpness and SNRs. While more advanced techniques—such as the backward correlation method (BWC), generalized linear model (GLM) machine learning algorithms, and image processing-based methods—have shown increased robustness in low-SNR environments, they may still be influenced by dispersion-induced spectral deformation. Therefore, the observed effects introduce an additional challenge for accurate BFS extraction, which should be considered in future signal processing algorithm development for BOTDA systems.

To provide further practical guidance for system designers, we also estimate the degree of performance degradation caused by chromatic dispersion based on our simulated and experimental findings. For instance, the dispersion-induced BGS distortion may result in a BFS uncertainty of approximately ±1.5 MHz. According to commonly used sensitivity coefficients in silica fibers (~1 MHz/°C and ~0.05 MHz/με), this translates to a temperature error of ±1.5 °C or a strain error of ±30 με. Although such errors are relatively modest, they may be critical in high-precision sensing applications. Furthermore, in the presence of modulation instability—especially under high pump power in SMF—the SNR deterioration also leads to spatial resolution degradation. We estimate a resolution reduction of up to 20%, increasing the effective spatial resolution from approximately 25 m to around 30 m. These values are consistent with our observed data and reflect realistic trade-offs when chromatic dispersion and nonlinear effects are not properly mitigated. This analysis highlights the importance of jointly considering dispersion and nonlinearity in both system architecture and signal processing design.

6. Conclusions

This study systematically investigated the impact of chromatic dispersion on the performance of BOTDA sensing systems based on direct detection. A set of coupled amplitude equations incorporating dispersion terms was derived within the framework of stimulated Brillouin scattering, and numerical simulations were conducted to investigate how dispersion-induced pulse broadening influences the BGS.

The simulation results indicate that dispersion induces a moderate temporal broadening of pump pulses, which leads to minor variations in the BGS—primarily a slight increase in peak gain and a marginal narrowing of linewidth. Under the conditions studied, these effects are sufficiently small such that the impact of dispersion-induced broadening on overall system performance can be considered negligible, consistent with the interpretation in Section 3.2. However, in high-power BOTDA scenarios, chromatic dispersion interacts with nonlinear effects—particularly SPM—to trigger MI, which causes severe signal degradation.

Experimental validation using standard SMF and DCF confirmed that SMF’s anomalous dispersion profile makes it more prone to MI, resulting in a lower SNR despite exhibiting narrower BGS linewidths. In contrast, DCF, with its normal dispersion characteristics, effectively suppresses MI and enables more stable signal acquisition under the same pump conditions.

In summary, chromatic dispersion affects BOTDA systems in both direct and indirect ways. While the direct effect of dispersion-induced pulse broadening is limited, its indirect contribution to MI through nonlinear interactions is significant. For long-range and high-power applications, using normally dispersive fibers—such as DCF—can suppress nonlinear distortions and enhance overall system robustness. These findings offer valuable insights for the design and optimization of BOTDA systems employing direct detection architectures.