Optical Characteristics of GaAs Spherical Quantum Dots Based on Single and Double Quartic Anharmonic Potentials: The Role of Structural Parameters
Abstract
1. Introduction
2. Theory
2.1. Single and Double Quartic Potential Profiles
2.2. Radial Schrödinger’s Equations
3. Results and Discussion
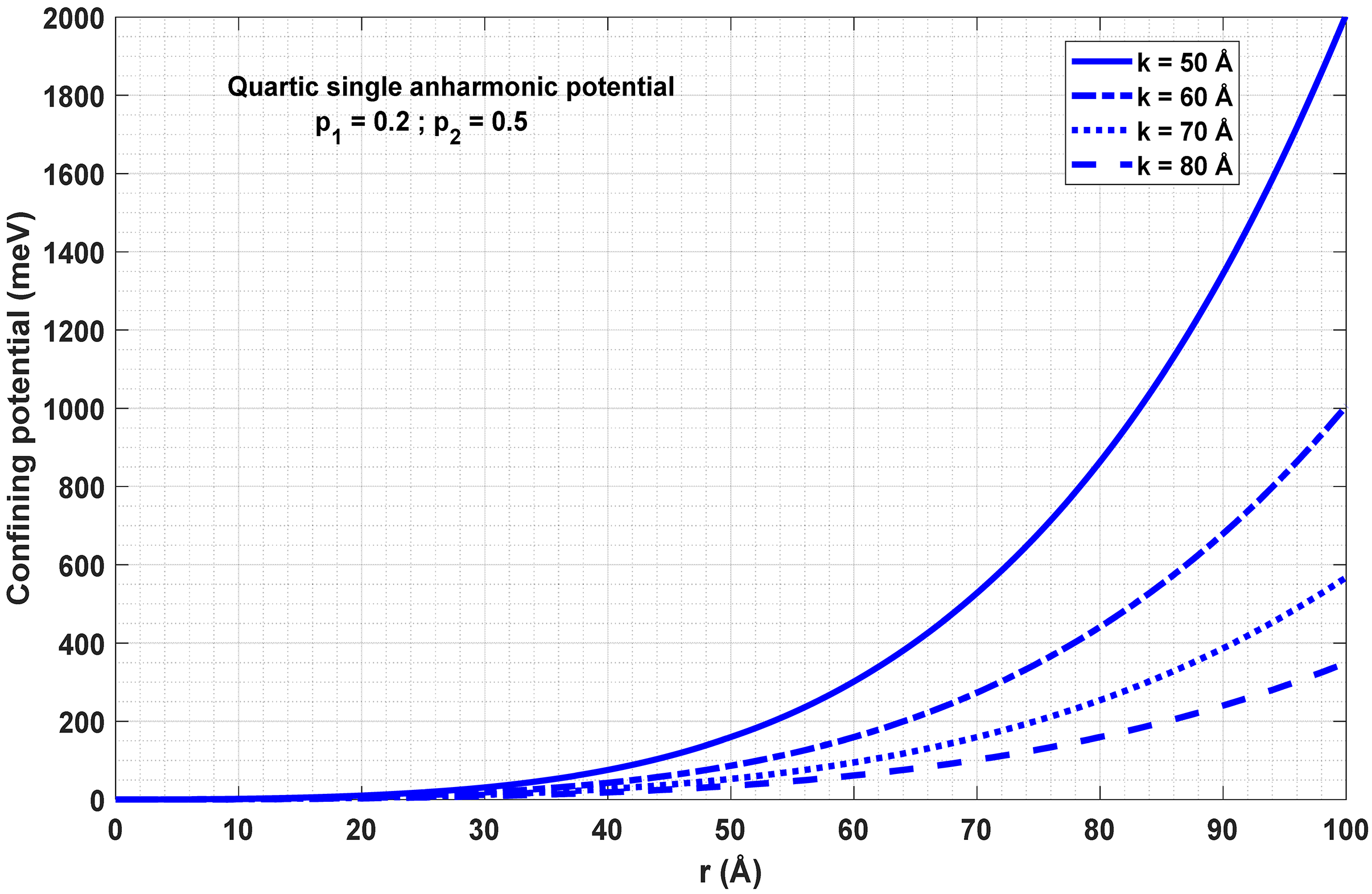
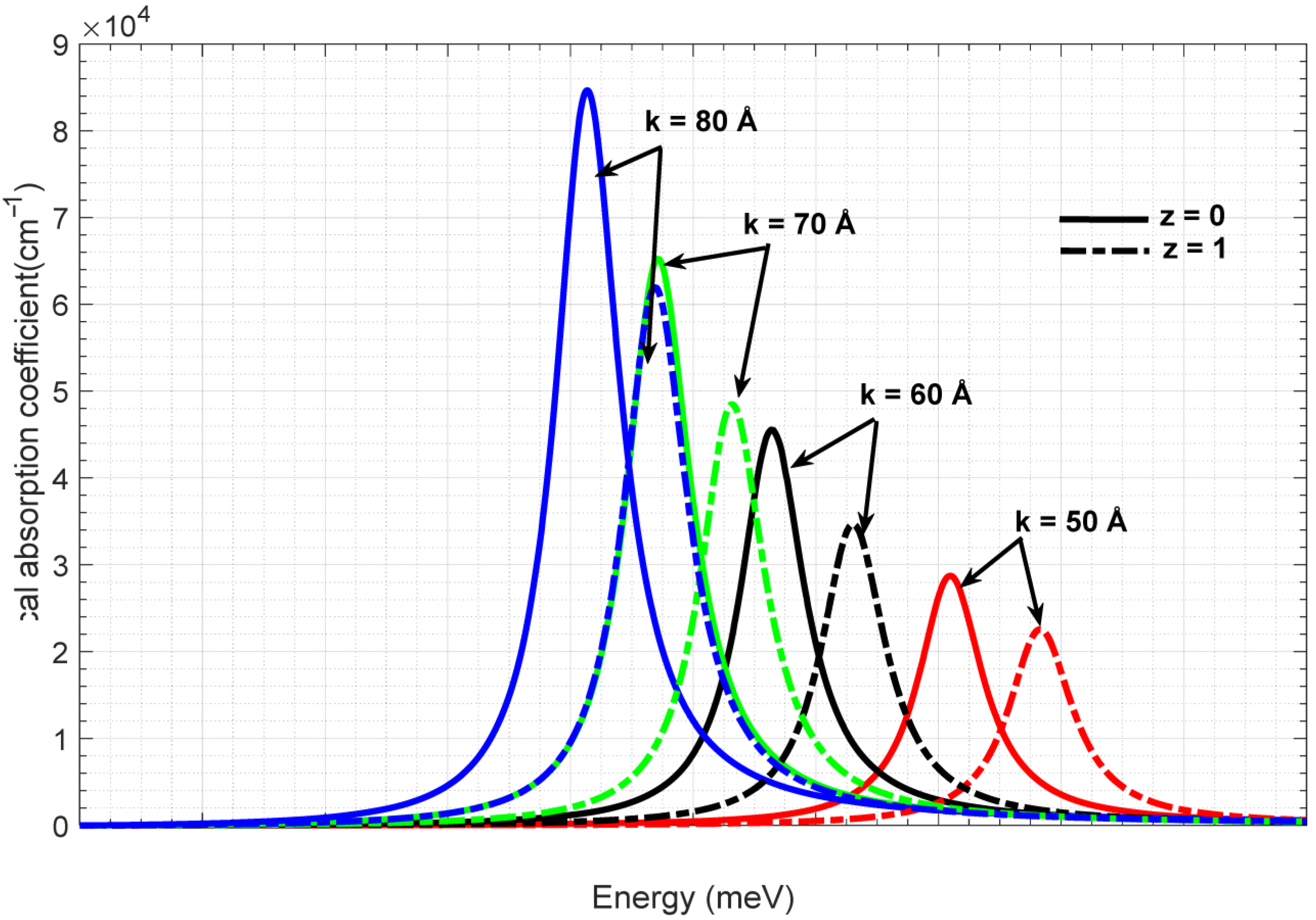
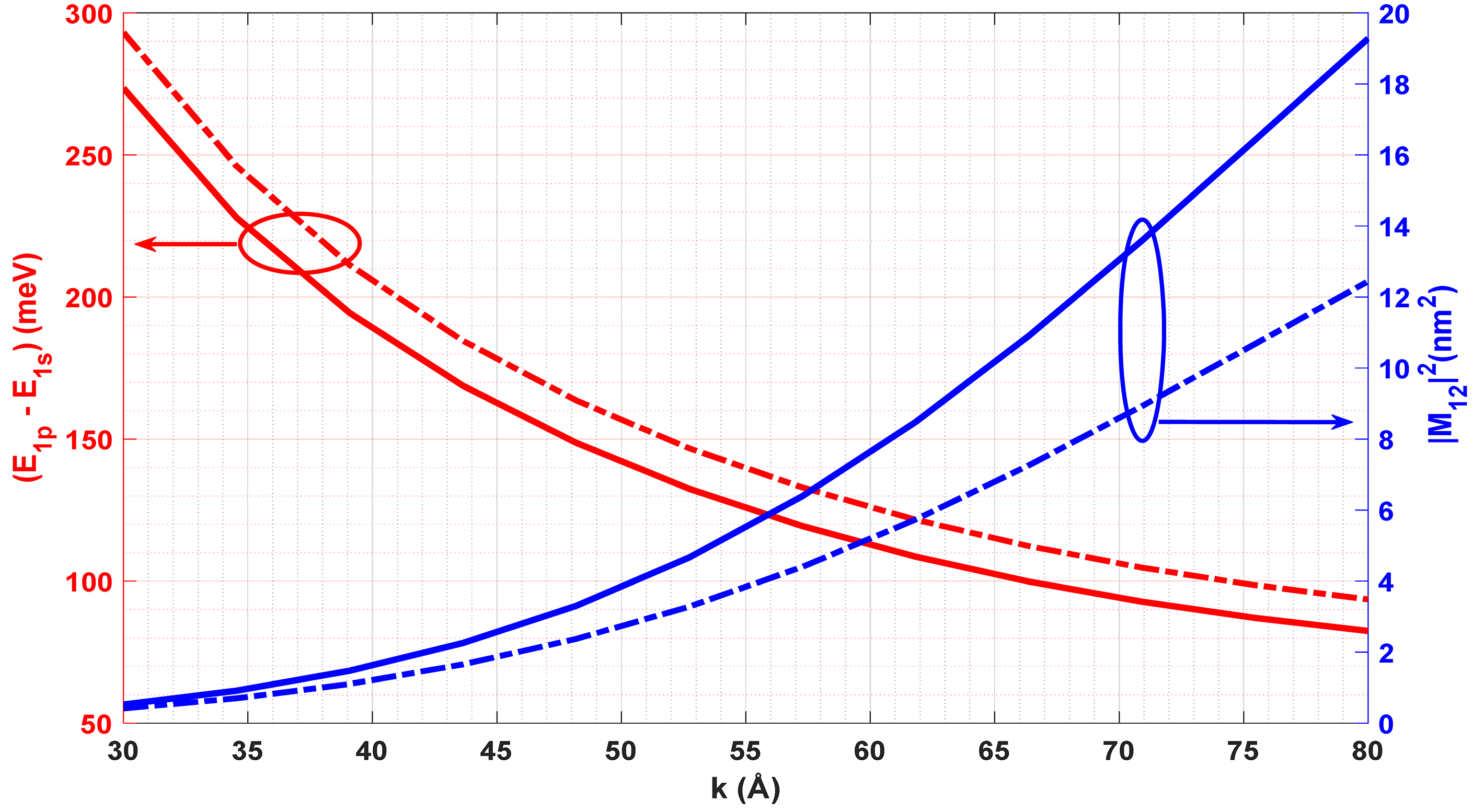
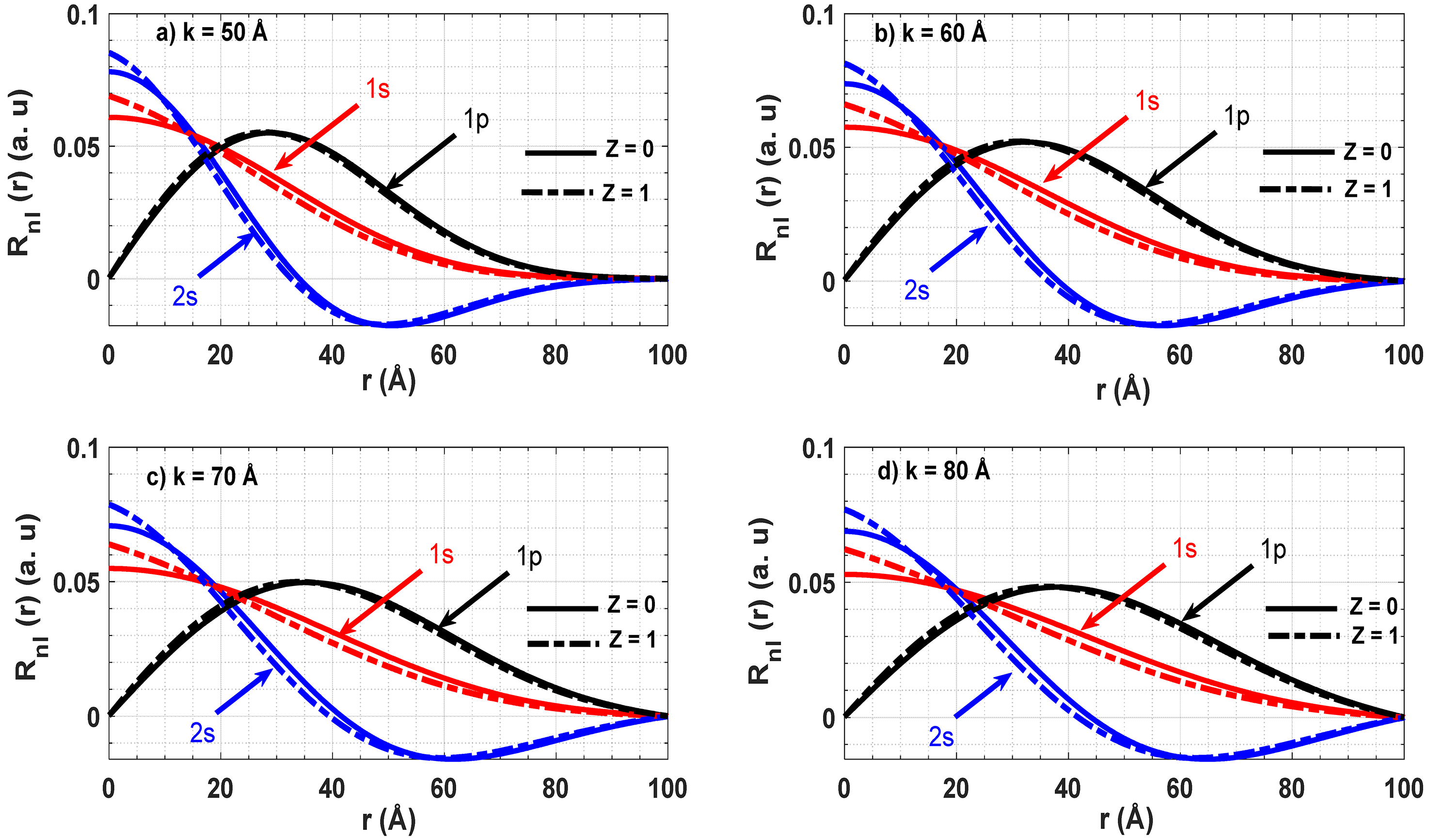
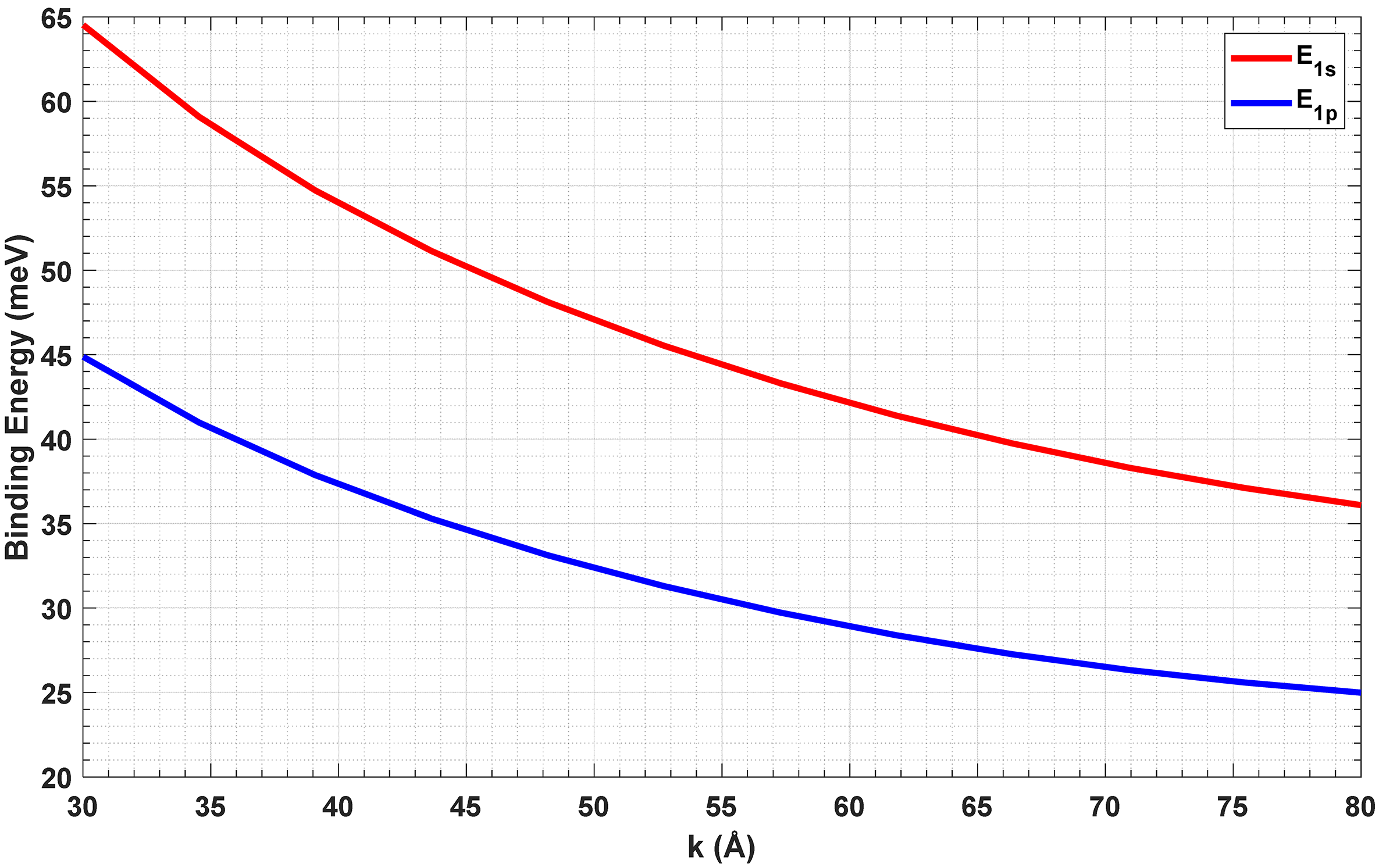
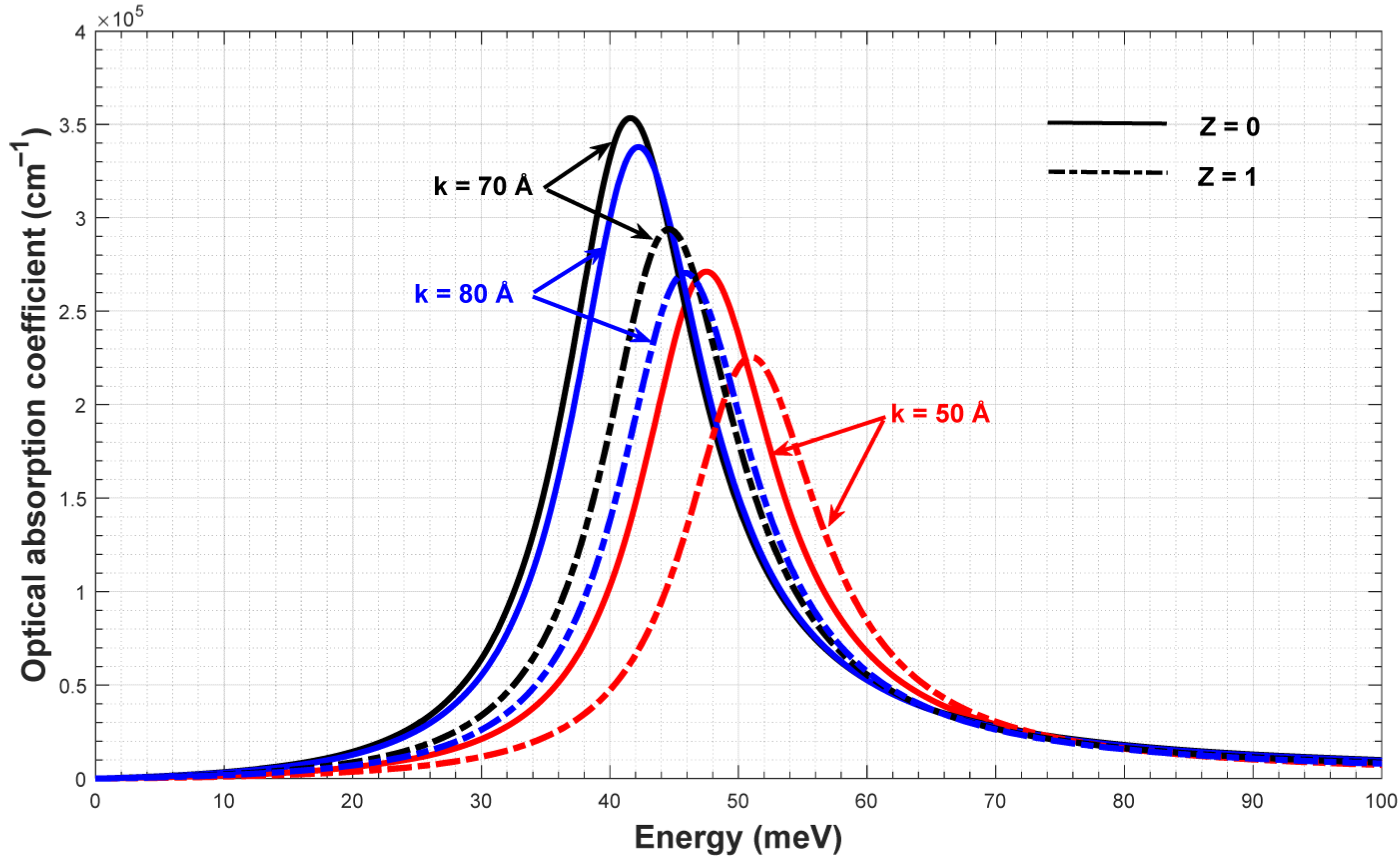
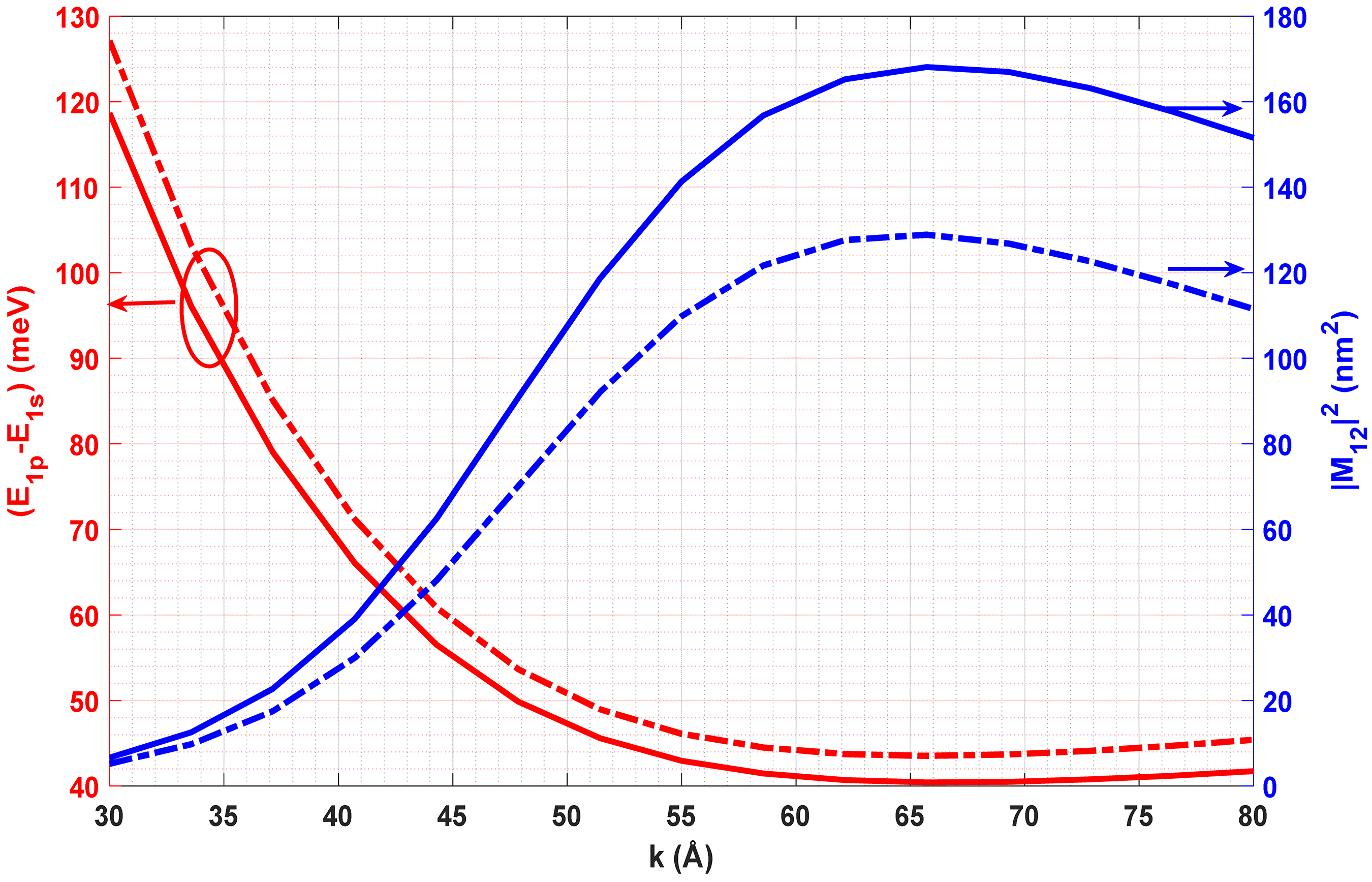
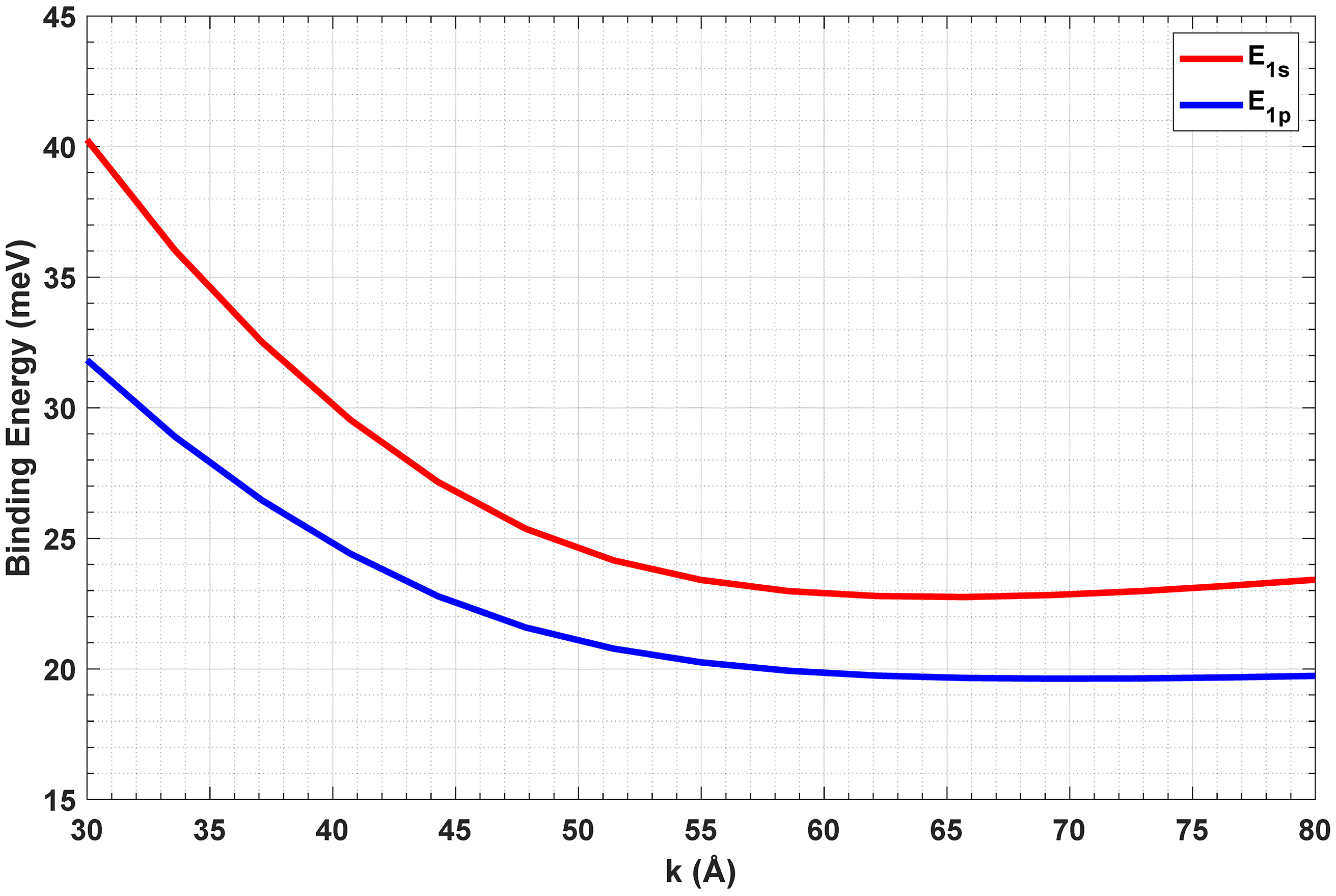
3.1. Single Quartic Anharmonic Oscillator
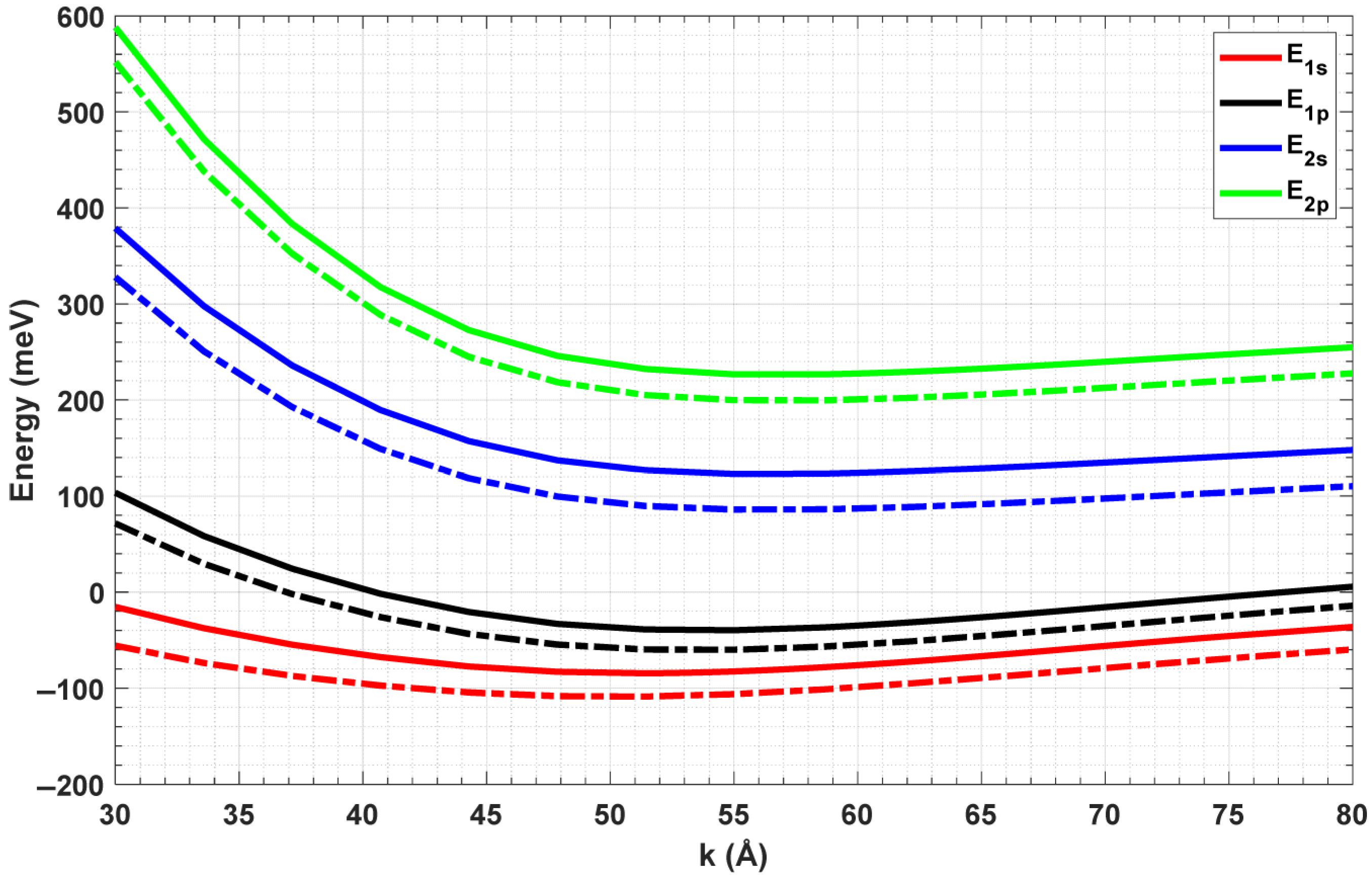
3.2. Double Quartic Anharmonic Oscillator
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Villegas-Martínez, B.M.; Moya-Cessa, H.M.; Soto-Eguibar, F. Exact and approximated solutions for the harmonic and anharmonic repulsive oscillators: Matrix method. Eur. Phys. J. D 2020, 74, 137. [Google Scholar] [CrossRef]
- Panek, T.; Hoeske, A.A.; Jacob, C.R. On the choice of coordinates in anharmonic theoretical vibrational spectroscopy: Harmonic vs. anharmonic coupling in vibrational configuration interaction. J. Chem. Phys. 2019, 150, 054107. [Google Scholar] [CrossRef] [PubMed]
- Sharma, A.; Sastri, O.S.K.S. Numerical simulation of quantum anharmonic oscillator, embedded within an infinite square well potential, by matrix methods using Gnumeric spreadsheet. Eur. J. Phys. 2020, 41, 055402. [Google Scholar] [CrossRef]
- Landi, G.T.; de Oliveira, M.J. Fourier’s law from a chain of coupled anharmonic oscillators under energy-conserving noise. Phys. Rev. E 2013, 87, 052126. [Google Scholar] [CrossRef]
- Fletcher, N.H. Harmonic? Anharmonic? Inharmonic? Am. J. Phys. 2002, 70, 1205. [Google Scholar] [CrossRef]
- Adelakun, A.O.; Dele, A.D. Solution of quantum anharmonic oscillator with quartic perturbation. Adv. Phys. Theor. Appl. 2014, 27, 38–43. [Google Scholar]
- Sous, A.J. Solution for the eigenenergies of sextic anharmonic oscillator potential . Mod. Phys. Lett. A 2006, 21, 1675–1682. [Google Scholar] [CrossRef]
- Pathak, A. Generalized quantum anharmonic oscillator using an operator ordering approach. J. Phys. A Math. Gen. 2000, 33, 5607–5613. [Google Scholar] [CrossRef]
- Yücel, M.B.; Kasapoglu, E.; Duque, C.A. Effects of Intense Laser Field on Electronic and Optical Properties of Harmonic and Variable Degree Anharmonic Oscillators. Nanomaterials 2022, 12, 1620. [Google Scholar] [CrossRef]
- Sakiroglu, S.; Yücel, M.B.; Kasapoglu, E. The effects of the variable mass on the electronic and nonlinear optical properties of octic anharmonic oscillators. Eur. Phys. J. Plus 2023, 138, 946. [Google Scholar] [CrossRef]
- Al Sdran, N.; Maiz, F. Airy function approach and Numerov method to study the anharmonic oscillator potentials . AIP Adv. 2016, 6, 065323. [Google Scholar] [CrossRef]
- Maiz, F.; Alqahtani, M.M.; Al Sdran, N.; Ghnaim, I. Sextic and decatic anharmonic oscillator potentials: Polynomial solutions. Phys. B Condens. Matter 2018, 530, 101–105. [Google Scholar] [CrossRef]
- Gaudreau, P.; Slevinsky, R.M.; Safouhi, H. An asymptotic expansion for energy eigenvalues of anharmonic oscillators. Ann. Phys. 2013, 337, 261–277. [Google Scholar] [CrossRef]
- Shah, B.P. Bound state eigenfunctions of an anharmonic oscillator in one dimension: A Numerov method approach. Int. J. Adv. Appl. Math. Mech. 2014, 2, 102–109. [Google Scholar]
- Budaca, R.; Buganu, P.; Chabab, M.; Lahbas, A.; Oulne, M. Extended study on a quasi-exact solution of the Bohr Hamiltonian. Ann. Phys 2016, 375, 65–90. [Google Scholar] [CrossRef]
- Ciftci, H.; Hall, R.L.; Saad, N. Construction of exact solutions to eigenvalue problems by the asymptotic iteration method. J. Phys. A. Math. Gen. 2005, 38, 1147–1155. [Google Scholar] [CrossRef]
- Maiz, F.; Alqahtani, M.M.; Ghnaim, I. Sextic and decatic anharmonic oscillator potentials including odd power terms: Polynomial solutions. AIP Con. Proc. 2018, 1976, 020034. [Google Scholar]
- Gaudreau, P.J.; Slevinsky, R.M.; Safouhi, H. Computing energy eigenvalues of anharmonic oscillators using the double exponential Sinc collocation method. Ann. Phys. 2015, 360, 520–538. [Google Scholar] [CrossRef]
- Maiz, F.; AlFaify, S. Quantum anharmonic oscillator: The airy function approach. Phys. B Cond. Matt. 2014, 441, 17–20. [Google Scholar] [CrossRef]
- Sous, A.J. The Asymptotic Iteration Method for the Eigenenergies of the a Novel Hyperbolic Single Wave Potential. J. Appl. Math. Phys. 2015, 3, 1406–1411. [Google Scholar] [CrossRef]
- de Souza Dutra, A.; de Castro, A.S.; Boschi-Filho, H. Approximate analytic expression for the eigenenergies of the anharmonic oscillator . Phys. Rev. A 1995, 51, 3480–3484. [Google Scholar] [CrossRef] [PubMed]
- Fernandez, F.M.; Guardiola, R. Accurate eigenvalues and eigenfunctions for quantum-mechanical anharmonic oscillators. J. Phys. A Math. Gen. 1993, 26, 7169. [Google Scholar] [CrossRef]
- Ivanov, I.A. Sextic and octic anharmonic oscillators: Connection between strong-coupling and weak-coupling expansions. J. Phys. A Math. Gen. 1998, 31, 5697. [Google Scholar] [CrossRef]
- Jafarpour, M.; Afshar, D. Calculation of energy eigenvalues for the quantum anharmonic oscillator with a polynomial potential. J. Phys. A Math. Gen. 2002, 35, 87. [Google Scholar] [CrossRef]
- Sharma, L.K.; Fiase, J.O. Non-perturbative energy expressions for the generalized anharmonic oscillator. Eur. J. Phys. 2000, 21, 167. [Google Scholar] [CrossRef]
- Speliotopoulos, A.D. The general structure of eigenvalues in nonlinear oscillators. J. Phys. A Math. Gen. 2000, 33, 3809. [Google Scholar] [CrossRef]
- Ikhdair, S.M.; Sever, R. Am alternative simple solution of the sextic anharmonic oscillator and perturbed coulomb problems. Int. J. Mod. Phys. C 2007, 18, 1571–1581. [Google Scholar] [CrossRef]
- Barakat, T. The asymptotic iteration method for the eigenenergies of the anharmonic oscillator potential . Phys. Lett. A 2005, 344, 411–417. [Google Scholar] [CrossRef]
- Hammada, M.M.; Yahiaa, M.M.; Motawehb, H.A.; Domac, S.B. Critical potentials and fluctuations phenomena with quartic, sextic, and octic anharmonic oscillator potentials. Nucl. Phys. A 2020, 1004, 122036. [Google Scholar] [CrossRef]
- Alauwaji, R.M.; Dakhlaoui, H.; Algraphy, E.; Ungan, F.; Wong, B.M. Binding Energies and Optical Properties of Power-Exponential and Modified Gaussian Quantum Dots. Molecules 2024, 29, 3052. [Google Scholar] [CrossRef]
- Dakhlaoui, H.; Belhadj, W.; Elabidi, H.; Ungan, F.; Wong, B.M. GaAs Quantum Dot Confined with a Woods–Saxon Potential: Role of Structural Parameters on Binding Energy and Optical Absorption. Inorganics 2023, 11, 401. [Google Scholar] [CrossRef]
- Tas, H.; Sahin, M. The inter-sublevel optical properties of a spherical quantum dot-quantum well with and without a donor impurity. J. Appl. Phys. 2012, 112, 053717. [Google Scholar] [CrossRef]
- Altuntas, I.; Dakhlaoui, H.; Mora-Ramos, M.E.; Ungan, F. Combined effects of electric, magnetic, and intense terahertz laser fields on the nonlinear optical properties in GaAs/GaAlAs quantum well with exponentially confinement potential. Eur. Phys. J. Plus 2023, 136, 1174. [Google Scholar] [CrossRef]
- Dakhlaoui, H.; Altuntas, I.; Mora-Ramos, M.E.; Ungan, F. Numerical simulation of linear and nonlinear optical properties in heterostructure based on triple Gaussian quantum wells: Effects of applied external fields and structural parameters. Eur. Phys. J. Plus 2021, 136, 894. [Google Scholar] [CrossRef]
- Dakhlaoui, H. Influence of doping layer concentration on the electronic transitions in symmetric AlxGa(1-x)N/GaN double quantum wells. Opt.—Int. J. Light Electron Opt. 2013, 124, 3726–3729. [Google Scholar] [CrossRef]
- Ed-Dahmouny, A.; Arraoui, R.; Jaouane, M.; Fakkahi, A.; Sali, A.; Es-Sbai, N.; El-Bakkari, K.; Zeiri, N.; Duque, C.A. The influence of the electric and magnetic fields on donor impurity electronic states and optical absorption coefficients in a core/shell GaAs/Al0.33Ga0.67As ellipsoidal quantum dot. Eur. Phys. J. Plus 2023, 138, 774. [Google Scholar] [CrossRef]
- Ed-Dahmouny, A.; Sali, A.; Es-Sbai, N.; Arraoui, R.; Duque, C.A. The impact of hydrostatic pressure and temperature on the binding energy, linear, third-order nonlinear, and total optical absorption coefficients and refractive index changes of a hydrogenic donor impurity confined in GaAs/AlxGa1−xAs double quantum dots. Eur. Phys. J. Plus 2022, 137, 784. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alashqar, N.A.; Belhadj, W.; Al-Shameri, N.S.; Dakhlaoui, H.; Ungan, F.; Wang, S. Optical Characteristics of GaAs Spherical Quantum Dots Based on Single and Double Quartic Anharmonic Potentials: The Role of Structural Parameters. Photonics 2025, 12, 675. https://doi.org/10.3390/photonics12070675
Alashqar NA, Belhadj W, Al-Shameri NS, Dakhlaoui H, Ungan F, Wang S. Optical Characteristics of GaAs Spherical Quantum Dots Based on Single and Double Quartic Anharmonic Potentials: The Role of Structural Parameters. Photonics. 2025; 12(7):675. https://doi.org/10.3390/photonics12070675
Chicago/Turabian StyleAlashqar, Najah Abdullah, Walid Belhadj, Najla S. Al-Shameri, Hassen Dakhlaoui, Fatih Ungan, and Sake Wang. 2025. "Optical Characteristics of GaAs Spherical Quantum Dots Based on Single and Double Quartic Anharmonic Potentials: The Role of Structural Parameters" Photonics 12, no. 7: 675. https://doi.org/10.3390/photonics12070675
APA StyleAlashqar, N. A., Belhadj, W., Al-Shameri, N. S., Dakhlaoui, H., Ungan, F., & Wang, S. (2025). Optical Characteristics of GaAs Spherical Quantum Dots Based on Single and Double Quartic Anharmonic Potentials: The Role of Structural Parameters. Photonics, 12(7), 675. https://doi.org/10.3390/photonics12070675





