Abstract
We present a numerical investigation of the bound-state pulse formation mechanism and evolutionary dynamics based on the pump strength and spectral filtering bandwidth in the all-fiber Mamyshev oscillator. Through the numerical simulation and analysis, the different mode-locked pulses’ (such as single pulses, bound-state pulses, and chaotic multi-pulses) regime transformation conditions are quantified. The results suggest that with an increase in the pump strength, the sub-pulse energy and output coupler of the Mamyshev oscillator show an inverse proportion trend, which plays an important role in increasing the number of sub-pulses in the bound-state pulses’ state. Furthermore, optimization schemes, such as adjusting the filter bandwidth and slowing down the accumulation of nonlinear effects, are proposed to achieve a high-energy pulse output in the Mamyshev oscillator.
1. Introduction
High-energy ultrafast fiber laser, a topic of crucial importance in nonlinear optics, has been extensively utilized in the material processing [1,2], biomedical, and optical imaging fields [3,4]. However, ultrafast fiber lasers are prone to nonlinear effects that can negatively influence the pulse quality, and the accumulation of excessive nonlinear phase shift can lead to the pulse splitting, which hinders the generation of high-energy pulses. In recent years, a new type of oscillator consisting of two cascaded Mamyshev regenerators using self-phase modulation and offset spectral filtering [5,6,7] has been shown to exhibit a significantly higher nonlinear tolerance and environmental stability [8,9,10].
In 2016, A. M. Perego and N. Tarasov et al. verified the dissipative Faraday instability theory through experiments [11,12]; two chirped Bragg gratings with frequency detuning were used to complete mode locking. The operating principle of this new mode-locked structure was very similar to that of the Mamyshev oscillator. In 2017, Wise et al. demonstrated a 1 μm Yb-doped Mamyshev oscillator in a ring cavity configuration, where the pulse could accumulate a nonlinear phase shift of 60 π and still remain stable [13]. It was also theoretically predicted that the Mamyshev oscillator could generate pulses with a peak power exceeding 10 MW. In 2019, Hu et al. demonstrated a high-peak-power Mamyshev oscillator based on single polarization, where the single-pulse energy exceeded 1 μJ and the peak power was as high as 13 MW [14], which validated the theoretical prediction made in Ref. [13]. In another instance, Liu et al. demonstrated an all solid-state Mamyshev oscillator for the first time [15]. In 2021, Zhou et al. realized Mamyshev mode-locked oscillation output based on an all-fiber seed injection structure with a peak power of 1.15 MW [16]. In 2022, Wise et al. demonstrated a simplistic design for a high-performance all-fiber Mamyshev oscillator, which is the first experimental demonstration of a ring Mamyshev oscillator with a passive arm [17]. Thus far, Mamyshev oscillators have achieved significant development in various aspects, such as mode-locking start methods, wavelength extension, pulse evolution, pulse energy improvement, and transverse mode control [18,19]. In addition, in order to meet the engineering requirements of high-energy mode-locked pulses, self-starting, pulse-free splitting Mamyshev oscillators are still a pressing need [20].
Mamyshev oscillators can not only generate high-quality pulses, but also can provide a promising platform for investigating pulse evolution dynamics due to their environmental stability [21,22]. Similar to most natural or artificial saturable absorbers (SAs), Mamyshev oscillators can exhibit different multi-pulse patterns when the parameters are appropriately set. In addition, exploring strategies for the formation of a multi-pulse state through the suppression of pulse splitting is also useful for obtaining a high-energy single pulse.
In 2017, A. M. Perego et al. numerically simulated the dynamics of high-repetition multiple pulses in the Mamyshev oscillator structure. By changing the detuning state of the offset filter, the dynamic processes of multi pulses, random pulses, and their transition state were observed [23]. In 2019, Wang et al. numerically studied the dissipative Faraday instability pattern formation in 2 μm Tm-doped Mamyshev oscillators [24]. In 2020, Luo et al. reported an Er-doped Mamyshev oscillator in the 1.5 μm band, wherein multi-pulse patterns such as a random distribution state and bound state were observed by adjusting the pump power levers of the two arms [25]. In 2021, Zhang et al. experimentally demonstrated a self-starting Yb-doped Mamyshev oscillator. In addition, the evolution of the bound states were also simulated by the influence of offset spectral filtering [26]. However, thus far, the internal multi-pulse formation mechanism and evolutionary dynamics in the all-fiber Mamyshev oscillator, based on the influence of spectral filtering bandwidth and laser gain, still remain uncertain, which are essential for carrying out theoretical simulations and mechanism analyses.
In this paper, the evolution dynamics of multi-pulse bound state solitons in an all fiber Mamyshev oscillator are studied using numerical simulations. By adjusting the filter bandwidth and pump power, the different dynamic patterns of mode-locked pulses, such as single pulses, bound-state pulses, and chaotic multi-pulses, could be observed. The results suggest that, with an increase in the pump strength, the sub-pulse energy and output coupler of the Mamyshev oscillator show an inverse proportion trend, which plays an important role in increasing the number of sub-pulses in the bound-state pulse state. Furthermore, optimization schemes, such as adjusting the filter bandwidth and slowing down the accumulation of nonlinear effects, are proposed to achieve a high-energy pulse output in the Mamyshev oscillator. Findings from the numerical simulations impart new insights on the soliton dynamics of multi-pulse formation and provide guidelines for optimizing the output pulse energy in the Mamyshev oscillator.
2. Theoretical Model
The simplified laser cavity scheme of the Mamyshev oscillator based on a 1 μm Yb-doped fiber (YDF) is shown in Figure 1. The unidirectional ring cavity is made up of 16 m long single-mode fibers (SMFs), two segments of 3.5 m long YDFs, and two Gaussian spectral filters with variable center wavelengths and filter bandwidths. To simulate pulse propagation in the Mamyshev oscillator, the numerical simulation is performed in a lumped propagation model. The pulse propagation within the different fiber sections is modeled using the extended nonlinear Schrödinger (NLS) equation [22,27,28,29]:
where is the slowly varying envelope electric field, is the transmission distance, and is the normalized time from the center of the pulse. and are second-order dispersion and third-order dispersion, respectively. is the nonlinear Kerr coefficient and is the gain bandwidth. The gain effect of YDF and the pump is described by the gain coefficient , which is defined as [22,27,28,29]:
where is the small signal gain coefficient, is the gain saturation energy, is defined as the pulse energy, and is the time required for a cavity round-trip. The small signal gain coefficient for the passive fiber is 0.
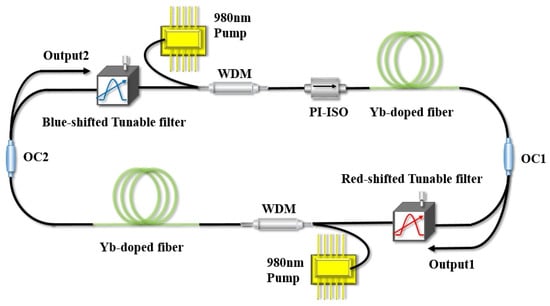
Figure 1.
Schematic diagram of Mamyshev oscillator with ring laser cavity based on 1 μm Yb-doped fiber. OC: optical coupler; SMF: single mode fiber; WDM: wavelength division multiplexing; and PI-ISO: polarization independent isolator.
It should be noted that the Mamyshev oscillator studied in this research work is in the condition of total net positive dispersion, and the duration of the generated pulse from the laser cavity is not compressed. From the simulation, the mode-locked pulse duration obtained is far more than 1 ps. Therefore, the influence of high-order nonlinear effects on the pulse transmission in the optical fiber, such as the self-steepening effect and stimulated Raman scattering, is very weak, which can be ignored [29].
The functions of the offset spectral filters are reflected by the Gaussian transmission curves, which are in the frequency domain [24]. The frequency detuning between the center wavelengths of the two offset spectral filters is defined as , the bandwidth of the 3 dB spectral filter is represented as , and the output coupling ratios of the optical couplers are denoted by and . The physical parameters of commercially available fibers are used for the propagation model, and the corresponding parameters of the fibers are listed in Table 1.

Table 1.
Parameters used in the simulation.
Additional parameters for the simulation model are: = 40 nm, = = 0.3 and = 16 nm. The center wavelengths of the two bandpass filters are about 1056 nm and 1072 nm.
3. Influence of the Key Parameters on Multi-Pulse Dynamics
To numerically simulate the evolution of pulses in the Mamyshev oscillator, the split-step Fourier method is used, and the initial signal is injected, which consists of a Gaussian pulse and weak random noise at the bottom [22,30]. Due to its excellent noise suppression ability, it is very difficult for the Mamyshev oscillator to achieve self-start mode locking through the noise pulses generated by spontaneous emission. In fact, it is often necessary to use the starting arm, inject the seed source, or adjust the filter parameters to help the oscillator start mode locking. In this simulation, seed injection is used to start the oscillator. If the initial signal contains only Gaussian white noise, the stability of the mode-locking starting state cannot be guaranteed due to the randomness of the white noise. Therefore, the combination of Gaussian pulse and random noise at the bottom as the initial signal can be used in the simulation. The Gaussian pulse in the initial signal helps the oscillator realize stable self-start and accelerate the convergence of calculation to a stable working state [26]. After that, the intensity of the initial Gaussian-shaped pulse is found to increase sharply in the YDF section. The pulse width rapidly expands due to the normal dispersion of the gain and passive fibers. Then, the pulse is filtered by a red-shifted wavelength filter, and due to the huge energy loss caused by offset filtering, the width and intensity of the pulse will be drastically decreased [13,22,26]. The temporal evolution of the pulse as a result of the pulse propagation in the gain fibers and passive fibers continues to occur until the pulse is filtered by a blue-shifted wavelength filter.
Owing to the self-phase modulation effect of the gain and passive fibers, the spectrum of the mode-locked pulse exhibits a drastic expansion [16,22,29]. When the pulse goes through the red-shifted wavelength filter, only the low-frequency region of the spectrum is preserved, which reduces the spectrum width. Similarly, the blue-shifted filter only permits the high-frequency region of the spectrum to be transmitted. Through offset spectral filtering, the spectrum of noise pulses will be completely filtered, which confers a strong ability for noise suppression to Mamyshev oscillators that enhances their environmental stability.
3.1. Influence of Filtering Bandwidth
Herein, the values of and are immutably set to 5 and 16 nm, respectively. When is set to 2 nm, a stable single-pulse with high energy can be obtained. The temporal and spectral evolutions of such a pulse are described in Figure 2a,b, respectively. It can be seen that the remarkable ability to reshape the pulse and suppress noise are caused by the narrow bandwidth of the bandpass filter. When is slightly increased to 4 nm, a two-pulse bound state can be obtained, as shown in Figure 2c,d. As is increased, more noise can pass through the offset spectral filters and be amplified, and the pulses that pass through the filters share the same laser gain. Eventually, under the gain competition in the cavity, only two solitons can be stably transmitted and they would have identical peak powers. Since the parameters of the two solitons are identical, spectral interference fringes can be seen in the spectral pattern of a two-pulse bound state [31,32]. When the value of is increased to 6.5 nm, a three-pulse bound state is obtained, as shown in Figure 2e,f. In addition, when is further increased to 7 nm, the three-pulse bound state can still be formed, but the noise suppression ability decreases significantly due to the high value of . Thus, a continuous noise wave can be observed in the temporal and spectral evolution of the pulse, as shown in Figure 2g,h. For this stage, the Mamyshev oscillator operates at a critical mode-locked state, and the mode-locked state can be established, but is not stable. The saturable absorption effect of cascaded spectral filtering cannot completely filter out the existing noise, and this will lead to some of the noise being able to achieve gain amplification in the fiber laser cavity. However, due to the limitation of saturation gain in the laser system and the gain competition between pulses, the noise pulse cannot reach a mode-locking state, and finally exists in the form of continuous noise at the bottom. After this, further increasing the filtering bandwidth will cause the oscillator to enter a chaotic multi-pulse state. Due to the large overlap in the passband range of the two filters, numerous noise pulses with overlapping frequencies can pass through the filters and be amplified, resulting in a decrease in the oscillator’s saturation absorption and the emergence of chaotic pulses.
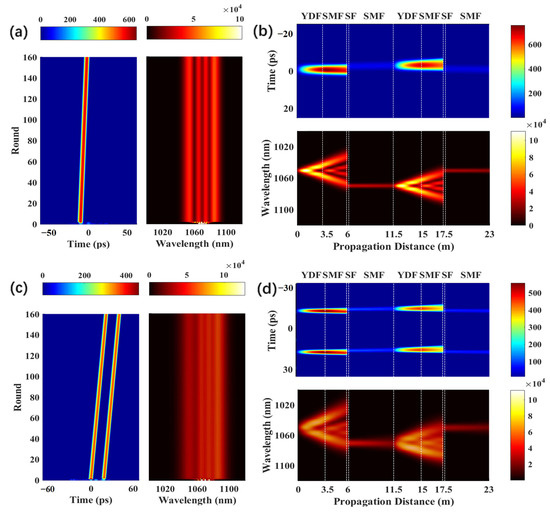
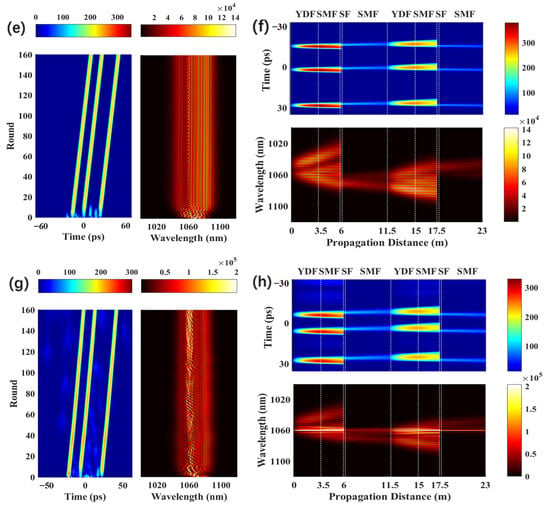
Figure 2.
The pulse shape and spectral evolution of the soliton operation over 160 roundtrips at the output of OC1, when the σ is (a,b) 2 nm, (c,d) 4 nm (e,f) 6.5 nm, and (g,h) 7 nm.
In the previous section, how different output pulse states can be obtained by changing the filtering bandwidth under the conditions of the same system gain was studied. In addition, the relationship between the formation of a multi-pulse state and the filter bandwidth was explained from the perspective of noise suppression ability and mode-locking stability. In fact, a change in the filter bandwidth is also closely related to the energy of the mode-locked pulse. This can be seen from the corresponding relationship between the maximum monopulse energy and the filter bandwidth in Figure 3, where the maximum monopulse energy of the oscillator increases with a decrease in the filter bandwidth. Especially when the filter bandwidth is less than 4 nm, the maximum single-pulse energy is significantly enhanced. When the Mamyshev oscillator works in a net positive dispersion environment, a higher single-pulse energy often means greater nonlinear accumulation, and the nonlinear effect in the spectrum is mainly manifested in the spectral broadening caused by SPM. One condition for the stable existence of a single pulse in the oscillator is that the spectral broadening brought about by SPM is balanced with the spectral loss of the filter. In the case of abundant system gain, if the filtering bandwidth is too large, the pulse spectrum cannot be effectively shaped after being broadened, and finally it will lead to pulse splitting.
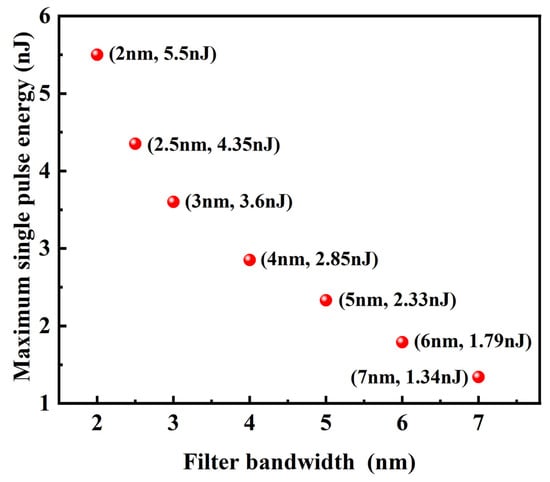
Figure 3.
The relationship between the maximum monopulse energy and the filter bandwidth.
Considering Figure 3, this does not mean that the narrower the filter bandwidth, the greater the increase in mode-locking monopulse energy. In fact, when the filter bandwidth is less than 2 nm, the conversion rate between the pulse energy and the system gain is very low due to the huge energy loss caused by spectral filtering. When the filtering bandwidth is less than 1.5 nm, the oscillator cannot be started, even with the injection of seed light. Finally, it can be concluded that only within the scope of the available conditions is the smaller filter bandwidth beneficial for improving the maximum single-pulse energy output of the Mamyshev oscillator.
3.2. Influence of Small-Signal Gain
In the simulations, the pump power also plays a significant role in the formation of a multi-pulse state based on the Mamyshev oscillator. When = 6 nm, = 16 nm, and = 1.0 , a stable single-pulse operation is obtained, as shown in Figure 4a,b. In addition, starting the Mamyshev oscillator is challenging when < 1.0 . Although the initial seed signal can pass through the offset filter, the final pulse amount will be depleted due to the limited gain obtained from the cavity. The spectrum of the pulse widens when is increased from 1.0 to 2.5 due to the higher gain. Under these conditions, additional noise pulses are amplified to pass through the filter, which eventually results in a two-pulse bound state, as shown in Figure 4c,d. When is further increased to 8 and 10 , three-pulse and four-pulse bound states are formed in the Mamyshev oscillator, as depicted in Figure 4e–h.
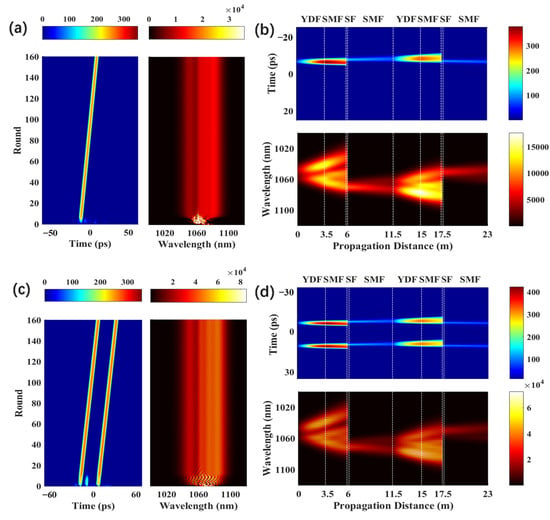
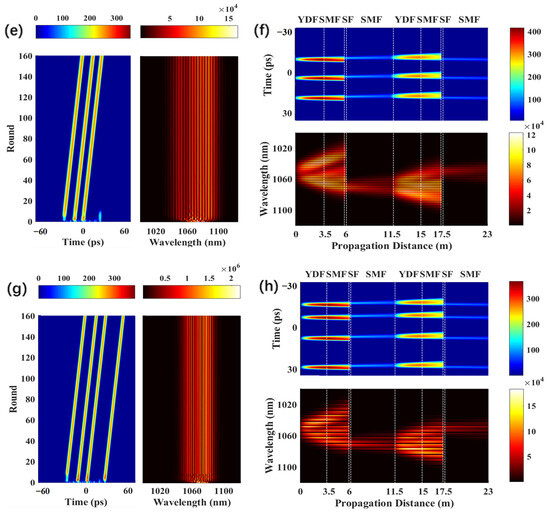
Figure 4.
Pulse shape and spectral evolution of the soliton operation over 160 roundtrips at the output of OC1, when the is (a,b) 1.0 , (c,d) 2.5 , (e,f) 8.0 , and (g,h) 10.0 .
The results from the simulations on bound states indicate that the pulse energy is limited by the nonlinear effect, and, on the contrary, further increasing the pump strength will not amplify the pulse. Instead, the background noise will be amplified, which promotes the formation of a multi-pulse state. To further reflect the impact of the accumulation of nonlinear effects in the oscillator on the pulse energy, is set to 6 nm and is set to 16 nm. When the value of is increased from 0.85 to 5 , the corresponding spectral patterns of pulses are obtained, as shown in Figure 5 and Figure 6.
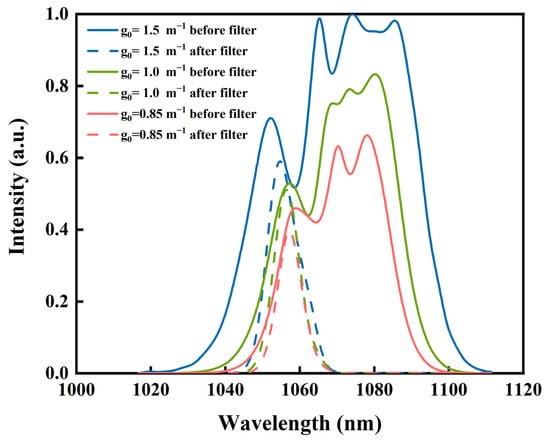
Figure 5.
The spectral profiles of single pulse before and after the interaction with the blue-shift filter.
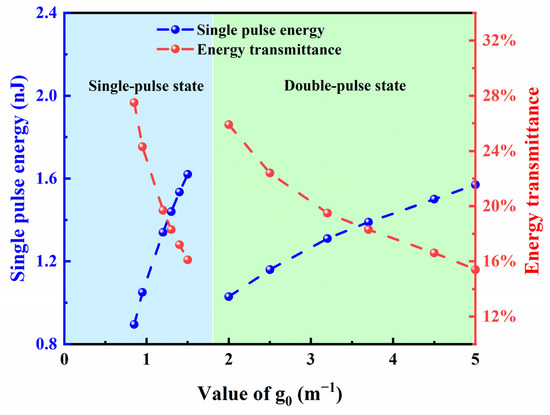
Figure 6.
The relationship between single-pulse energy and energy transmittance with (0.85 to 5 .
As shown in Figure 5, when is increased from 0.85 to 1.5 , the single-pulse energy before the filter is amplified. Additionally, the spectral density is also significantly enhanced. However, due to the fixed range of the bandpass filter, the spectral width and spectral density of the pulses gradually increase after the filter. Eventually, the unequal spectral growth rate between the pulses before and after the filter leads to negative feedback absorption of the pulse energy. As the spectral bandwidth increases, the loss ratio increases due to the spectral filtering effect. Thus, the high-energy pulse will experience a lower energy transmittance than the low-energy pulse, which limits the increase in single-pulse energy and promotes the emergence of a multi-pulse state.
From Figure 6, it also can be intuitively observed that, in the single-pulse region with < 1.8 , the pulse energy continuously increases with laser gain, while the energy transmittance decreases accordingly. When > 1.8 , the oscillator enters a double-pulse state, where the energy and transmittance of each sub-pulse have the same trend compared with the single-pulse state.
In fact, the downside of the energy transmittance in the Mamyshev oscillator is the accumulation of nonlinear effects, which leads to the over-broadening of the spectrum and a reduction in the spectral transmittance. In this phenomenon, although the spectral broadening caused by self-phase modulation is helpful for the start-up and operation of the Mamyshev oscillator, excessive nonlinear accumulation is not conducive to a higher single-pulse energy output. Therefore, in order to achieve a higher single-pulse energy output, a free-space structure or large mode field photonic crystal fibers can be adopted in the design of the Mamyshev oscillator to avoid the pulse splitting and instability caused by excessive nonlinear accumulation [13,25,33,34,35].
4. Conclusions
In summary, we present a numerical investigation of the bound-state formation mechanism and evolutionary dynamics based on the pump strength and spectral filtering bandwidth in the all-fiber Mamyshev oscillator. The simulation results show that a variety of pulse states, such as the single-pulse state, bound-state pulses, and chaotic multi-pulse state, can be observed by tuning the filter bandwidth and pump strength. The results reveal that the energy limitation of the single pulse in the Mamyshev oscillator is caused by the accumulation of nonlinear effects. Furthermore, an optimized Mamyshev oscillator is simulated, which can obtain a high-energy pulse by suppressing the formation of the multi-pulse state. These simulations aid with a better understanding of the dynamics involved in the formation of multi-pulses and can lead to optimized designs of the Mamyshev oscillator that achieve a high-energy pulse output.
Author Contributions
Conceptualization, T.Z. and Y.Q.; formal analysis, Z.B.; software, B.Y.; data curation, J.D.; writing—original draft preparation, T.Z.; writing—review and editing, Y.Q. and Z.L.; supervision, D.Y. and Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by National Natural Science Foundation of China (62375075), Hebei Natural Science Foundation (F2022202036), and the China Postdoctoral Science Foundation under Grant (2022M712485).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhou, Y.; Lin, W.; Cheng, H.; Wang, W.; Yang, Z. Composite filtering effect in a SESAM mode-locked fiber laser with a 3.2-GHz fundamental repetition rate: Switchable states from single soliton to pulse bunch: Erratum. Opt. Express 2018, 26, 10842–10857. [Google Scholar] [CrossRef]
- Li, H.; Wang, Z.; Li, C.; Zhang, J.; Xu, S. Mode-locked Tm fiber laser using SMF-SIMF-GIMF-SMF fiber structure as a saturable absorber. Opt. Express 2017, 25, 26546–26553. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Yang, S.; He, C.; Lin, X. Vector pure-quartic soliton molecule fiber laser. Chaos Solitons Fractals 2023, 175, 113978. [Google Scholar] [CrossRef]
- Zhang, Y.; Qi, Y.; Sheng, Q.; Bai, Z.; Wang, Y.; Shi, W.; Lu, Z. Tunable vortex beams generation in visible band via Pr3+: YLF laser with a spot defect. Appl. Phys. Lett. 2023, 123, 251117. [Google Scholar] [CrossRef]
- Lin, D.; Feng, Y.; Ren, Z.; Richardson, D.J. The generation of femtosecond optical vortex beams with megawatt powers directly from a fiber based Mamyshev oscillator. Nanophotonics 2021, 11, 847–854. [Google Scholar] [CrossRef]
- Zheng, J.; Yang, S.; Zhu, Z.; Lau, K.; Li, L. 72-fs Er-doped Mamyshev oscillator. J. Light. Technol. 2021, 40, 2123–2127. [Google Scholar] [CrossRef]
- Olivier, M.; Boulanger, V.; Savary, F.G.; Sidorenko, P.; Wise, F.W. Femtosecond fiber Mamyshev oscillator at 1550 nm. Opt. Lett. 2019, 44, 851–854. [Google Scholar] [CrossRef] [PubMed]
- Piechal, B.; Szczepanek, J.; Kardas, T.M.; Stepanenko, Y. Mamyshev Oscillator with a Widely Tunable Repetition Rate. J. Light. Technol. 2020, 39, 574–581. [Google Scholar] [CrossRef]
- Rochette, M.; Chen, L.R.; Sun, K.; Hernandez-Cordero, J. Multiwavelength and Tunable Self-Pulsating Fiber Cavity Based on Regenerative SPM Spectral Broadening and Filtering. IEEE Photonics Technol. Lett. 2008, 20, 1497–1499. [Google Scholar] [CrossRef]
- Regelskis, K.; Želudevičius, J.; Viskontas, K.; Račiukaitis, G. Ytterbium-doped fiber ultrashort pulse generator based on self-phase modulation and alternating spectral filtering. Opt. Lett. 2015, 40, 5255–5258. [Google Scholar] [CrossRef]
- Perego, M.; Tarasov, N.; Churkin, V.; Turitsyn, K.; Staliunas, K. Pattern Generation by Dissipative Parametric Instability. Phys. Rev. Lett. 2016, 116, 028701. [Google Scholar] [CrossRef] [PubMed]
- Tarasov, N.; Perego, A.M.; Churkin, D.V.; Staliunas, K.; Turitsyn, S.K. Mode-locking via dissipative Faraday instability. Nat. Commun. 2016, 7, 12441. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Ziegler, Z.M.; Wright, L.G.; Wise, F.W. Megawatt peak power from a Mamyshev oscillator. Optica 2017, 4, 649–654. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Liao, R.; Zhao, J.; Cui, J.; Hu, M. Femtosecond Mamyshev oscillator with 10-MW-level peak power. Optica 2019, 6, 194–197. [Google Scholar]
- Nie, M.; Wang, J.; Huang, S. Solid-state Mamyshev oscillator. Photonics Res. 2019, 7, 1175–1181. [Google Scholar] [CrossRef]
- Wang, T.; Ren, B.; Li, C.; Wu, J. Over 80 nJ Sub-100 fs All-Fiber Mamyshev Oscillator. IEEE J. Sel. Top. Quantum Electron. 2021, 27, 6. [Google Scholar] [CrossRef]
- Haig, H.; Sidorenko, P.; Thorne, R.; Wise, F.W. Megawatt pulses from an all-fiber and self-starting femtosecond oscillator. Opt. Lett. 2022, 47, 762–765. [Google Scholar] [CrossRef]
- Repgen, P.; Schuhbauer, B.; Hinkelmann, M.; Wandt, D. Mode-locked pulses from a thulium-doped fiber Mamyshev oscillator. Opt. Express 2020, 28, 13837–13844. [Google Scholar] [CrossRef]
- Repgen, P.; Wandt, D.; Morgner, U.; Neumann, J.; Kracht, D. Sub-50 fs, J-level pulses from a Mamyshev oscillator–amplifier system. Opt. Lett. 2019, 44, 5973–5976. [Google Scholar] [CrossRef]
- Zheng, J.; Yang, S.; Zhu, Z.; Lau, K.; Li, L. Low mode-locking threshold and sub-90 fs Er-doped Mamyshev oscillator. Opt. Commun. 2022, 508, 127711.1–127711.4. [Google Scholar] [CrossRef]
- Cao, B.; Zhao, K.; Gao, C.; Xiao, X.; Bao, C.; Yang, C. Observation of pulsating dissipative solitons in a Mamyshev oscillator. Phys. Rev. A 2021, 106, 023519. [Google Scholar] [CrossRef]
- Zhang, Y.; Dai, K.; Zhang, B.; Chen, D.; Guan, Z. Investigations on pulse dynamics and offset spectral filtering in Er-doped Mamyshev fiber oscillator. Opt. Commun. 2023, 529, 129103. [Google Scholar] [CrossRef]
- Perego, A.M. High-repetition-rate, multi-pulse all-normal-dispersion fiber laser. Opt. Lett. 2017, 42, 3574–3577. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Yao, S.; Grelu, P.; Xiao, X.; Yang, C. Pattern formation in 2-μm Tm Mamyshev oscillators associated with the dissipative Faraday instability. Photonics Res. 2019, 7, 1287–1295. [Google Scholar] [CrossRef]
- Luo, Z.; Liu, M.; Wei, Z.; Luo, A.; Xu, S. Multipulse dynamics in a Mamyshev oscillator. Opt. Lett. 2020, 45, 2620–2623. [Google Scholar]
- Yan, D.; Li, X.; Zhang, S.; Liu, J. Pulse dynamic patterns in a self-starting Mamyshev oscillator. Opt. Express 2021, 29, 9805–9815. [Google Scholar] [CrossRef] [PubMed]
- Mao, D.; Wang, H.; Zhang, H.; Zeng, C.; Du, Y.; He, Z.; Sun, Z.; Zhao, J. Synchronized multi-wavelength soliton fiber laser via intracavity group delay modulation. Nat. Commun. 2021, 12, 6712. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Zhu, Z.; Qi, Y.; Jin, L.; Li, L.; Lin, X. Internal motion within pulsating pure-quartic soliton molecules in a fiber laser. Chaos Solitons Fractals 2023, 172, 113544. [Google Scholar] [CrossRef]
- Agrawal, G.P. Applications of Nonlinear Fiber Optics; Academic Press: New York, NY, USA, 2007. [Google Scholar]
- Zhang, Z.; Luo, M.; Chen, J.; Chen, L.; Liu, M.; Luo, A.; Xu, W.; Luo, Z. Pulsating dynamics in a pure-quartic soliton fiber laser. Opt. Lett. 2022, 47, 1750–1753. [Google Scholar] [CrossRef]
- Pitois, S.; Finot, C.; Provost, L.; Richardson, D.J. Generation of localized pulses from incoherent wave in optical fiber lines made of concatenated Mamyshev regenerators. J. Opt. Soc. Am. B 2010, 25, 1537–1547. [Google Scholar] [CrossRef]
- Du, Y.; Shu, X. Pulse dynamics in all-normal dispersion ultrafast fiber lasers. J. Opt. Soc. Am. B 2017, 34, 553–558. [Google Scholar] [CrossRef]
- Lin, D.; Xu, D.; He, J.; Feng, Y. The Generation of 1.2 μJ Pulses from a Mamyshev Oscillator Based on a High Concentration, Large-Mode-Area Yb-Doped Fiber. J. Light. Technol. 2022, 40, 7175–7179. [Google Scholar] [CrossRef]
- Wang, J.; Qi, Y.; Bai, Z.; Ding, J.; Yan, B.; Wang, Y.; Lu, Z. Recent advance of high-energy ultrafast mode-locked oscillators based on Mamyshev mechanism with different starting modes. Opt. Eng. 2022, 61, 120901. [Google Scholar] [CrossRef]
- Zheng, J.; Yang, S.; Zhu, Z. Recent research progress of Mamyshev oscillator for high energy and ultrashort pulse generation. Opt. Fiber Technol. 2021, 67, 102691.1–102691.11. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).