Geometrically Shaped Odd-Bit QAM Constellations Suitable for Principal Component-Based Phase Estimation
Abstract
1. Introduction
2. Principles
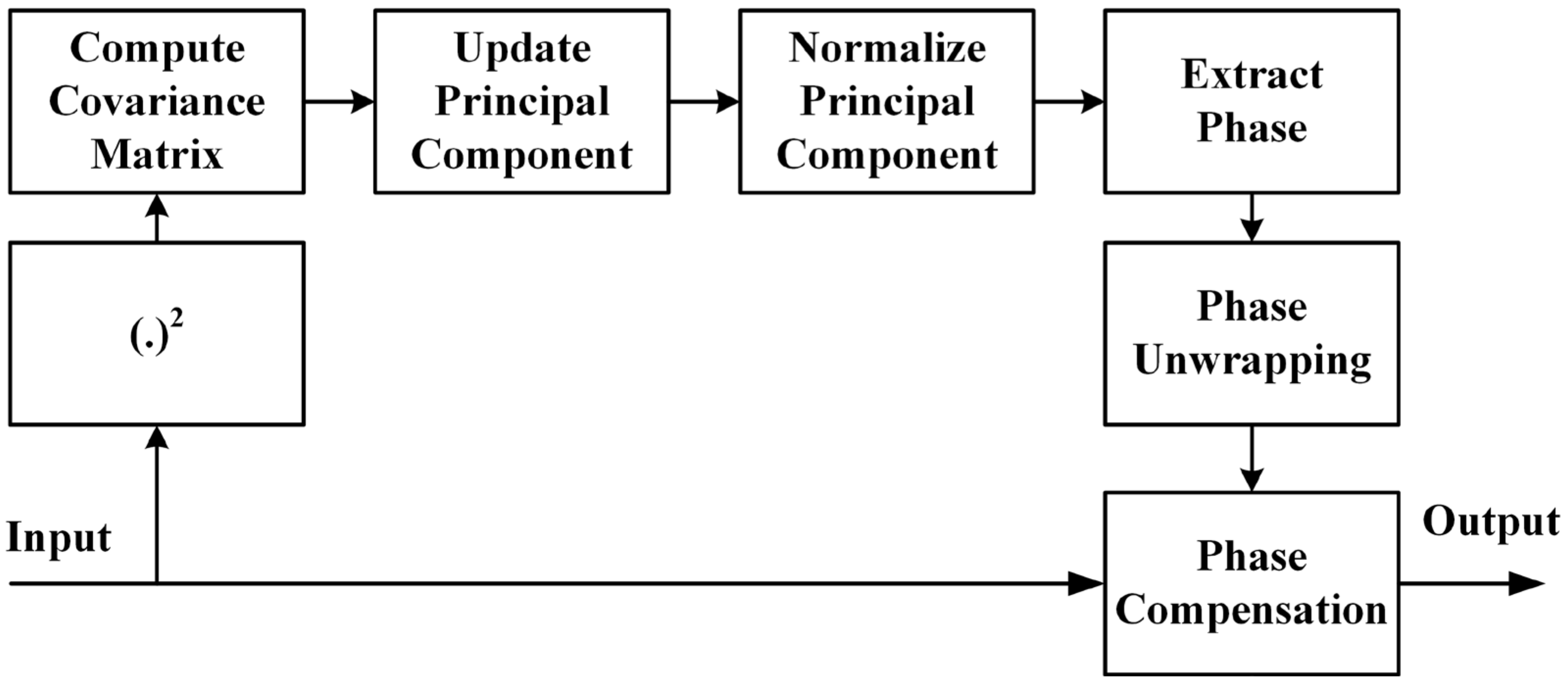
2.1. Principal Component-Based Phase Estimation Algorithm
2.2. Interplay of PCPE and Odd-Bit QAM Signals
2.3. Geometric Shaping Scheme Based on Pair-Wise Optimization Algorithm
2.4. Geometrically Shaping of Odd-Bit QAM Constellations for Compatibility with the PCPE Algorithm
3. Results
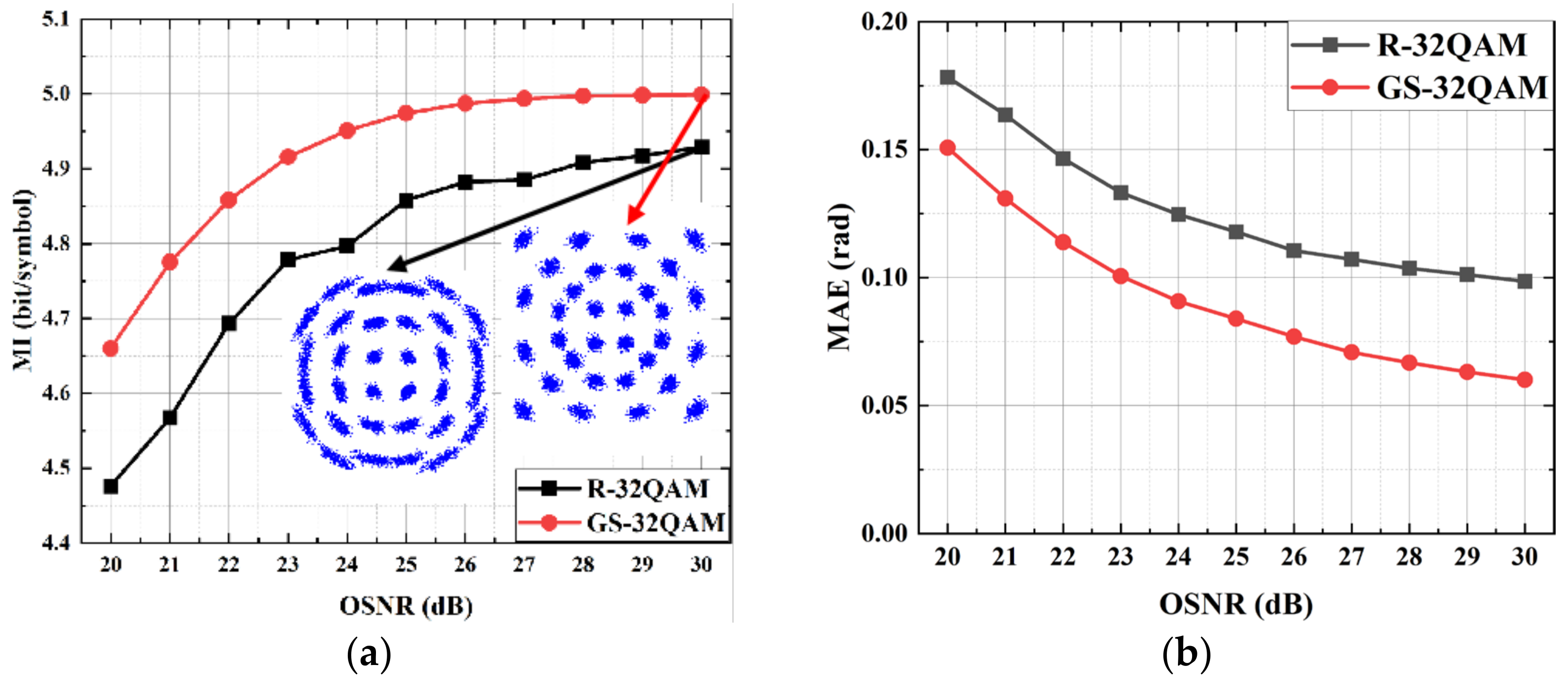
3.1. Monte Carlo Simulation Results
3.2. VPItransmissionMaker Simulation Results
4. Discussion
4.1. The Design Rationale of the GS Constellation Structure
4.2. Sensitivity Analysis
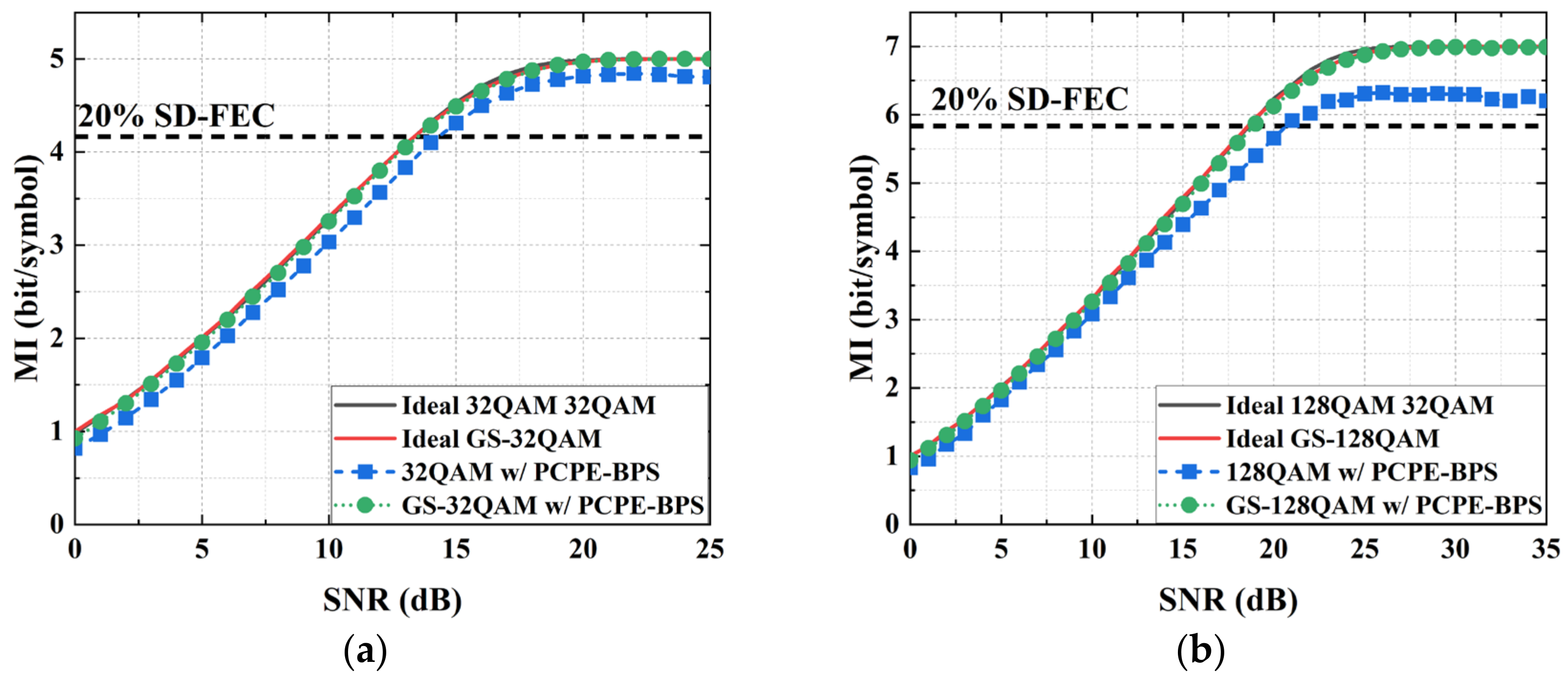
4.3. Compatibility Analysis with the Cascading PCPE-BPS Algorithm
5. Conclusions and Future Research Details
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Deng, N.; Zong, L.; Jiang, H.; Duan, Y.; Zhang, K. Challenges and Enabling Technologies for Multi-Band WDM Optical Networks. J. Light. Technol. 2022, 40, 3385–3394. [Google Scholar] [CrossRef]
- Yang, Y.; Sung, K.W.; Wosinska, L.; Chen, J. Hybrid Fiber and Microwave Protection for Mobile Backhauling. J. Opt. Commun. Netw. 2014, 6, 869–878. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, D.; Zhang, C.; Ye, B.; Jia, Y.; Li, J.; Zhang, M. Reliable and Low-complexity Multiple Performance Parameters Prediction for Optical Network Equipment. In Proceedings of the Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 5–9 March 2023. [Google Scholar]
- Montalvo, J.; Torrijos, J.A.; Cortés, D. New approaches in optical access networks to increase network flexibility and achieve 5G targets: An operator’s view. In Proceedings of the European Conference on Optical Communications (ECOC), Brussels, Belgium, 6–10 December 2020. [Google Scholar]
- Higashimori, K.; Inuzuka, F.; Ohara, T. Physical topology optimization for highly reliable and efficient wavelength-assignable optical networks. J. Opt. Commun. Netw. 2022, 14, 16–24. [Google Scholar] [CrossRef]
- Arabul, E.; Oliveira, R.D.; Wang, R.; Nejabati, R.; Simeonidou, D. Experimental Demonstration of Integrated Low-Cost High-Precision Timing Solution for Optical Transport Networks Supporting 5G. In Proceedings of the Optical Fiber Communication Conference (OFC), San Diego, CA, USA, 5–9 March 2023. [Google Scholar]
- Kong, M.; Shi, J.; Sang, B.; Ding, J.; Wang, K.; Li, W.; Wang, F.; Liu, C.; Wang, Y.; Wei, Y.; et al. 800-Gb/s/carrier WDM Coherent Transmission Over 2000 km Based on Truncated PS-64QAM Utilizing MIMO Volterra Equalizer. J. Light. Technol. 2022, 40, 2830–2839. [Google Scholar] [CrossRef]
- Zhu, L.; Yao, H.; Chang, H.; Tian, Q.; Zhang, Q.; Xin, X.; Yu, F.R. Adaptive Optics for Orbital Angular Momentum-Based Internet of Underwater Things Applications. IEEE Internet Things J. 2022, 9, 24281–24299. [Google Scholar] [CrossRef]
- Pan, X.; Wu, D.; Li, X.; Guo, D.; Li, Z.; Yan, H.; Wang, C.; Bi, J.; Yu, C.; Liu, X.; et al. Photonic-aided W-band dual-vector RF signal generation and detection enabled by bandpass delta-sigma modulation and heterodyne detection. Opt. Lett. 2023, 48, 2146–2149. [Google Scholar] [CrossRef] [PubMed]
- Reza, A.G.; Troncoso Costas, M.; Browning, C.; Barry, L. 124.8-Gbit/s Net Data Rate Capacity for IM/DD Optical Intra-Data Center Interconnections by Utilizing Probabilistically Shaped PAM-8 and Digital Linear Feed-Forward Equalizers. In Proceedings of the Asia Communications and Photonics Conference (ACP), Shenzhen, China, 5–8 November 2022. [Google Scholar]
- Tauber, D.; Smith, B.; Lewis, D.; Muhigana, E.; Nissov, M.; Govan, D.; Hu, J.; Zhou, Y.; Wang, J.; Jiang, W.; et al. Role of Coherent Systems in the Next DCI Generation. J. Light. Technol. 2022, 41, 1139–1151. [Google Scholar] [CrossRef]
- Matsushita, A.; Nakamura, M.; Yamamoto, S.; Hamaoka, F.; Kisaka, Y. 41-Tbps C-Band WDM Transmission with 10-bps/Hz Spectral Efficiency Using 1-Tbps/λ Signals. J. Light. Technol. 2020, 38, 2905–2911. [Google Scholar] [CrossRef]
- Yu, J.; Kong, M.; Wang, K.; Ding, J.; Wei, Y. Large Capacity, High Spectral Efficiency and Long Distance Optical Transmission Based on High-Order QAM. In Proceedings of the Asia Communications and Photonics Conference (ACP), Shanghai, China, 24–27 October 2021. [Google Scholar]
- Faruk, M.S.; Savory, S.J. Digital Signal Processing for Coherent Transceivers Employing Multilevel Formats. J. Light. Technol. 2017, 35, 1125–1141. [Google Scholar] [CrossRef]
- Fatadin, I.; Ives, D.; Savory, S.J. Laser linewidth tolerance for 16-QAM coherent optical systems using QPSK partitioning. IEEE Photon. Technol. Lett. 2010, 22, 631–633. [Google Scholar] [CrossRef]
- Fang, Q.; Zhou, X.; Li, R.; Gao, Y.; Wang, S.; Li, F.; Long, K. Polarization Controller Based on Variable-Step Greedy Linear Descent for Self-Homodyne Coherent Transmission Systems. Photonics 2023, 10, 770. [Google Scholar] [CrossRef]
- Diniz, J.C.M.; Fan, Q.; Ranzini, S.M.; Khan, F.N.; Ros, F.D.; Zibar, D.; Lau, A.P.T. Low-complexity carrier phase recovery based on principal component analysis for square-QAM modulation formats. Opt. Express 2019, 27, 15617–15626. [Google Scholar] [CrossRef] [PubMed]
- Börjeson, E.; Larsson-Edefors, P. Benchmarking of Carrier Phase Recovery Circuits for M-QAM Coherent Systems. In Proceedings of the Optical Fiber Communication Conference (OFC), Washington, DC, USA, 6–11 June 2021. [Google Scholar]
- Zhao, J. Phase Recovery in Probabilistically-Shaped Optical Communication Systems. In Proceedings of the Asia Communications and Photonics Conference (ACP) and International Conference on Information Photonics and Optical Communications (IPOC), Beijing, China, 24–27 October 2020. [Google Scholar]
- Ning, P.; Fan, Z.; Chen, L.-K.; Zhao, J. Comparison of CPR Methods in Probabilistically-shaped Coherent Systems with MB/QMB Distributions. In Proceedings of the Opto-Electronics and Communications Conference (OECC), Hong Kong, China, 3–7 July 2021. [Google Scholar]
- Han, Y.; Ren, J.; Liu, B.; Li, Y.; Ullah, R.; Mao, Y.; Wu, X.; Chen, S.; Wang, B.; Wu, Y.; et al. Highly secure non-orthogonal multiple access based on key accompanying transmission in training sequence. Opt. Express 2024, 32, 1979–1997. [Google Scholar] [CrossRef]
- Jovanovic, O.; Yankov, M.P.; Da Ros, F.; Zibar, D. End-to-end Learning of a Constellation Shape Robust to Variations in SNR and Laser Linewidth. In Proceedings of the European Conference on Optical Communication (ECOC), Bordeaux, France, 13–16 September 2021. [Google Scholar]
- Rode, A.; Geiger, B.; Schmalen, L. Geometric Constellation Shaping for Phase-noise Channels Using a Differentiable Blind Phase Search. In Proceedings of the 2022 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 6–10 March 2022. [Google Scholar]
- Dzieciol, H.; Liga, G.; Sillekens, E.; Bayvel, P.; Lavery, D. Geometric Shaping of 2-D Constellations in the Presence of Laser Phase Noise. J. Light. Technol. 2020, 39, 481–490. [Google Scholar] [CrossRef]
- Zhang, S.; Yaman, F. Design and Comparison of Advanced Modulation Formats Based on Generalized Mutual Information. J. Light. Technol. 2018, 36, 416–423. [Google Scholar] [CrossRef]
- Zhang, S.; Yaman, F.; Mateo, E.; Inoue, T.; Nakamura, K.; Inada, Y. A Generalized Pairwise Optimization for Designing Multi-Dimensional Modulation Formats. In Proceedings of the Optical Fiber Communication Conference, Los Angeles, CA, USA, 19–23 March 2017. [Google Scholar]
- Zhang, S.; Qu, Z.; Yaman, F.; Mateo, E.; Inoue, T.; Nakamura, K.; Inada, Y.; Djordjevic, I.B. Flex-Rate Transmission using Hybrid Probabilistic and Geometric Shaped 32QAM. In Proceedings of the Optical Fiber Communication Conference, San Diego, CA, USA, 11–15 March 2018. [Google Scholar]
- Ding, J.; Zhang, J.; Wei, Y.; Zhao, F.; Li, C.; Yu, J. Comparison of Geometrically Shaped 32-QAM and Probabilistically Shaped 32-QAM in a Bandwidth-Limited IM-DD System. J. Light. Technol. 2020, 38, 4352–4358. [Google Scholar] [CrossRef]
- Ding, J.; Sang, B.; Wang, Y.; Kong, M.; Wang, F.; Zhu, B.; Zhao, L.; Zhou, W.; Yu, J. High Spectral Efficiency WDM Transmission Based on Hybrid Probabilistically and Geometrically Shaped 256QAM. J. Light. Technol. 2021, 39, 5494–5501. [Google Scholar] [CrossRef]
- Liang, Z.; Chen, B.; Lei, Y.; Liga, G.; Alvarado, A. Analytical Model of Nonlinear Fiber Propagation for General Dual-Polarization Four-Dimensional Modulation Formats. J. Light. Technol. 2024, 42, 606–620. [Google Scholar] [CrossRef]












Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Lv, K.; Zhang, Q.; Zhu, L.; Xin, X. Geometrically Shaped Odd-Bit QAM Constellations Suitable for Principal Component-Based Phase Estimation. Photonics 2024, 11, 140. https://doi.org/10.3390/photonics11020140
Wang X, Lv K, Zhang Q, Zhu L, Xin X. Geometrically Shaped Odd-Bit QAM Constellations Suitable for Principal Component-Based Phase Estimation. Photonics. 2024; 11(2):140. https://doi.org/10.3390/photonics11020140
Chicago/Turabian StyleWang, Xishuo, Kai Lv, Qi Zhang, Lei Zhu, and Xiangjun Xin. 2024. "Geometrically Shaped Odd-Bit QAM Constellations Suitable for Principal Component-Based Phase Estimation" Photonics 11, no. 2: 140. https://doi.org/10.3390/photonics11020140
APA StyleWang, X., Lv, K., Zhang, Q., Zhu, L., & Xin, X. (2024). Geometrically Shaped Odd-Bit QAM Constellations Suitable for Principal Component-Based Phase Estimation. Photonics, 11(2), 140. https://doi.org/10.3390/photonics11020140





