Abstract
Silicon Carbide (SiC) is the predominant substrate material for optoelectronic-integrated devices. However, it challenges the wafer-slicing process because of its high hardness, brittleness, and other material characteristics. Laser processing has gained prominence as the primary method, leveraging its merits of high efficiency, precision, and micro-destructiveness. In this study, a finite element method is applied to calculate the temperature field distribution resulting from the electric field of a Gaussian beam. The simulation considers laser propagation inside 4H-SiC, non-linear absorption, and spherical aberration induced by the refractive index of the material. The influence of laser pulse energy and focusing depth are considered. The results indicate that the modification depths decrease with the increasing focusing depth. With the increase of laser pulse energy, the depth of the modification layer increases continuously. Moreover, an experimental setup has been devised to furnish valuable references in validating the proposed model.
1. Introduction
Transparent hard materials such as Silicon Carbide (SiC), classified as third-generation semiconductor materials, are distinguished by their wide band gap, superior thermal conductivity, and rapid carrier packet mobility. Among the diverse isomers of SiC single crystals, 4H-SiC emerges as a preferred variant owing to its heightened electron mobility, high current density, and improved conduction characteristics. This crystal is well-suited for developing optoelectronic integrated devices capable of withstanding extreme conditions of elevated temperature, frequency, power, and resistance to radio waves [1,2,3,4,5]. Moreover, in recent years, the potential of photoelectric integration technology in quantum communication with high security has been paid close attention and recognized. Therefore, it is imperative to study and explore the processing means of SiC [6,7,8].
The inherent hardness and limited plasticity of SiC present challenges in achieving precision during wafer slicing through the wire saw process of diamond wire slicing [9]. Recently, many new methods offered a viable alternative, such as the synergistic processing of wet-oxidation-assisted chemical mechanical polishing and thermal annealing [10], laser modification, and so on [11]. At sufficiently high laser energy density, the tunneling ionization is initiated inside the SiC [12]. In this process, the electrons within the material undergo excitation induced by the laser, transitioning from the valence band to the conduction band through the tunneling effect [13]. The intensified local energy concentration can manifest in various outcomes, including alterations in color [14,15], modifications to the local refractive index [16], and micro-explosions accompanied by thermal cracking [17]. Notably, 4H-SiC’s transparency in the most common laser-excited wavelengths enables the theoretical focus of laser energy within the material, facilitating laser modification. This aspect has spurred considerable research interest and explorations in the field.
In 2016, the Siltectra company introduced a novel SiC wafer-slicing technology named COLD SPLIT during the European Conference on Silicon Carbide and Related Materials [18]. Lin et al. used the focus of picosecond pulsed laser beams inside the material to achieve a laser-modified layer characterized by a high fault density in 2022 [19]. The study also delved into the influence of etching speed and etching interval, presenting optimized laser parameters in the paper. In the same year, Zhang et al. investigated the impact of pulse duration on the internal modification process [20]. Their findings demonstrated a proportional relationship with both the height and width of the modified layers. The subsequent year witnessed further advancements, as Wang et al. demonstrated that maintaining a good surface quality could mitigate damage to the wafer surface during femtosecond laser slicing [21].
Understanding the intricate factors influencing the quality and morphology of materials due to laser-induced modification is a pivotal endeavor across numerous applications. A wealth of research has been dedicated to unraveling these complexities, yielding noteworthy findings with numerical simulation. In 2018, A.F. Mohammed et al. conducted research by using finite element simulation, uncovering that the 193 nm ArF laser induced temperature rise of 4H-SiC as a function of laser fluence. They observed two different surface modification morphologies with a low or high laser fluence [22]. In 2023, Huang et al. utilized femtosecond lasers to enhance the surface modification of 4H-SiC [23]. Employing multi-physics finite element and molecular dynamics models, they established that a high electronic temperature gradient is responsible for subsurface void generation. Furthermore, Wang et al. explored the correlation between laser intensity and the internal nonlinear refractive index of 4H-SiC in 2023 [24]. Utilizing finite element and two-temperature models, they elucidated the energy deposition dynamics during internal processing, emphasizing the dynamic equilibrium of nonlinear self-focusing and plasma defocusing in transparent materials.
Nevertheless, prevailing research models often overlook the intricate transmission of laser energy inside the material. Instead, they simplify the laser as a heat input with a specific energy density. It is typically represented as either a surface heat source applied on the boundary, or a body heat source embedded within the material. The stretch focus zone, induced by distinct refractive indices of the material and the external environment, is also critical in laser wafer slicing. In this study, a picosecond pulsed laser with a wavelength of 1064 nm is employed to process 4H-SiC. Utilizing the finite element method, the model effectively simulates the internal electric field, with the resultant electric field distribution used to calculate the internal temperature field distribution. This comprehensive approach considers the transfer mechanisms inside the 4H-SiC material, the non-linear absorption process, and the phenomenon of spot stretching induced by refractive index differences. The study systematically examines the laser pulse energy and focusing depth to analyze the change in the electrical-induced temperature field. Furthermore, experiments involving laser modification inside the 4H-SiC materials are conducted. These experimental observations enhance the analysis of the relationship between the established model and the outcomes derived from practical experimentation.
2. Numerical Model Simulation
Laser pulse modification exhibits its efficacy on the surface and within the interior of 4H-SiC. Focusing a high-energy pulse inside the 4H-SiC generates a modified layer with an uneven temperature field and micro-explosion. Rapid local heat propagation extends beyond the laser focus zone. The finite element method explains the formation of the modified layers by calculating electric and temperature fields inside the 4H-SiC. The simulations adhere to the following assumptions:
- (1)
- The incident laser’s light field distribution follows a Gaussian distribution.
- (2)
- The property parameters of 4H-SiC in the model remain constant with temperature variations.
- (3)
- Considering a pulse width of 10 ps for the excitation laser and an electron-to-ion transformation time scale of 10−12 to 10−10 s [25], the photoelectron interaction is negligible. In contrast, lattice relaxation is considered so that the heat conduction model is exclusively utilized.
- (4)
- The laser acts as an electromagnetic wave; its electric field is entirely absorbed in the focal zone, ignoring the absorption and ablation on the surface of 4H-SiC.
- (5)
- SiC material modification is usually accompanied by Si vapor generation [19]. Therefore, the modified threshold is set as 1687.15 K, which is the boiling point of silicon.
As illustrated in Figure 1a, the simulated region employs 4H-SiC with dimensions a = 50 μm and b = 200 μm, situated in an air environment maintained at 293.15 K. The simulation involves the application of a picosecond laser featuring an excitation wavelength of 1064 nm and a pulse width of 10 ps. The excited beam, characterized by a spot radius of ω0 = 1 μm, interacts within the interior of 4H-SiC. The mesh is set to a maximum value of 0.08 μm and a minimum value of 0.002 μm evenly distributed over the simulated area. Since this process is a transient picosecond pulsed laser modification, the results are observed after 10 ps of the thermal diffusion.
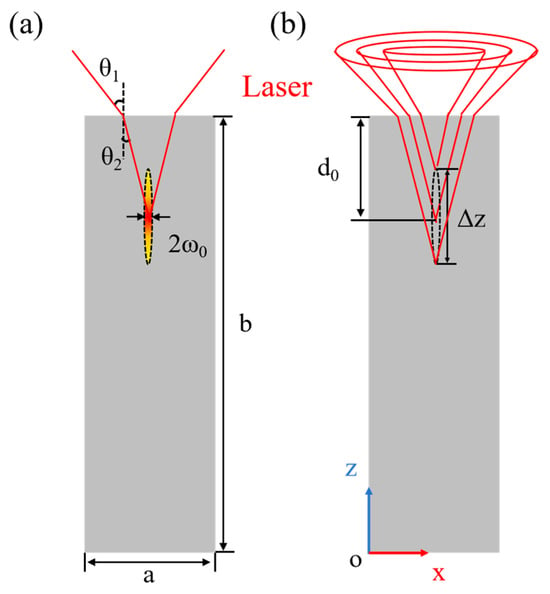
Figure 1.
(a) A two-dimensional model diagram of the x–z plane of numerical simulation. (b) Diagram of the laser propagation inside the 4H-SiC to form a stretch focus zone.
As depicted in Figure 1b, when an objective lens is used to focus a picosecond pulsed laser, the inherent disparity in refractive indices between the material and environment induces spherical aberration. This phenomenon leads to a distinct pupillary radius of the laser reaching disparate positions along the optical axis, consequently leading to the elongation of the focus zone. Under the condition of solely considering geometric optics and employing paraxial approximations during the focusing period, this stretch length can be expressed as [26]:
where d0 represents the focusing depth, n denotes the refractive index of the 4H-SiC, and NA signifies the numerical aperture of the objective.
It is noteworthy that Gaussian beams primarily serve as approximations of the Helmholtz equation derived from Maxwell’s equations [27]:
where ω, R, and η are the radius of the beam, Wavefront curvature, and Gouy phase shift, respectively. The total electric field needs to be solved according to the Helmholtz equation: . Because the relationship between laser intensity and electric field is [28]:
where ε0 is the vacuum dielectric constant, c is the speed of light.
Hence, converting laser intensity into a thermal energy source inside the material is achievable. Namely,
In the two-dimensional model, the volume is simplified as the incident laser intensity depth within the material, denoted as d0, which also signifies the focusing depth. β is the absorption coefficient equal to 1 at the focus zone in this model. The initial conditions are Ex = Ey = Ez = 0, with the source import exclusively present in the z = b plane.
Within this model, the thermal conduction differential equation in the Cartesian coordinate system is expressed as follows [29]:
where k represents the heat conduction coefficient, T denotes temperature, ρ stands for density, and c0 is the specific heat capacity of 4H-SiC.
Convection heat transfer inside the material is defined. The convection heat transfer coefficient along the laser propagation direction is set at 10 W/(m2·K), while the convection heat transfer coefficient perpendicular to the laser propagation direction is considered infinite. Notably, whether it is a laser or a heat source, the incident direction is specified as the -z-direction.
For the transient heat transfer problem, the initial conditions are outlined as follows:
Subsequently, the boundary conditions are established as T = f1(t) across all boundaries except the incident plane, where f1(t) designates the environmental temperature. The electric and temperature fields are then computed upon these considerations.
3. Materials and Methods
The experimental apparatus employed is illustrated in Figure 2. The test sample is positioned on an electrically controlled translation platform, with the computer controlling the platform’s movement along the x and y-directions to facilitate laser scanning. The adjustment of the focusing depth is accomplished by displacing the objective lens.
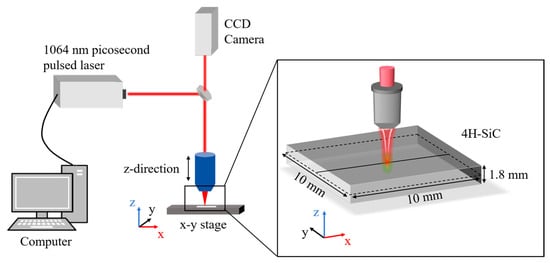
Figure 2.
Schematic diagram of the experimental device and the process of laser working inside the 4H-SiC 3D model.
The 1064 nm laser, sourced from Coherent’s HYPER RAPID laser system (with M2 < 1.2), transits the reflector and enters the objective lens, which characterized by a numerical aperture (NA) 0.4, is used to focus on the incident laser. After calculating, the spot radius = 2.7 μm, F = 8 mm is the focal length, and D = 1 mm represents the diameter of the laser. The calculated spot radius aligns closely with the radius of the measured spot of approximately 3 μm in the experiment. Figure 2 also displays the enlarged laser processing inside the material. The test specimen employed is a 4H-SiC with dimensions of 10 mm × 10 mm × 1.8 mm. Subsequently, the modification layer morphology and cross-sectional damages of the samples were evaluated using an optical microscope (OM, German ZEISS Axio Scope A1).
This experimental investigation focuses primarily on altering the laser pulse energy, focusing depth, as delineated in Table 1. According to the definition of NA in geometric optics [30],

Table 1.
Factor and level distribution of the orthogonal experiments for laser modification.
The calculated focusing depth is also displayed in Table 1. Employing orthogonal experiments, it systematically examines the impact of variations in the process parameters of laser modification.
4. Results and Discussion
4.1. Electrical-Induced Temperature Field
The finite element method was employed to construct a model, and an investigation into the influences of focusing depth and laser pulse energy on depths of modification layer was conducted.
As the laser beam irradiates the material surface, some incident energy penetrates a confined depth, transforming into heat energy. In Figure 3a, the computation of the electric field is conducted by utilizing Maxwell’s and Helmholtz’s equations, treating it as the heat source. Subsequently, in Figure 3b, the temperature field is calculated using a thermal conduction model. The resulting distribution of the electrical-induced temperature field at 10 ps is visually depicted. Notably, the temperature field aligns relatively with the electric field at the energy E = 60 μJ, focusing at d0 = 100 μm. Furthermore, the phenomenon of focal zone elongation, attributed to the refractive index disparity, is easily observed.
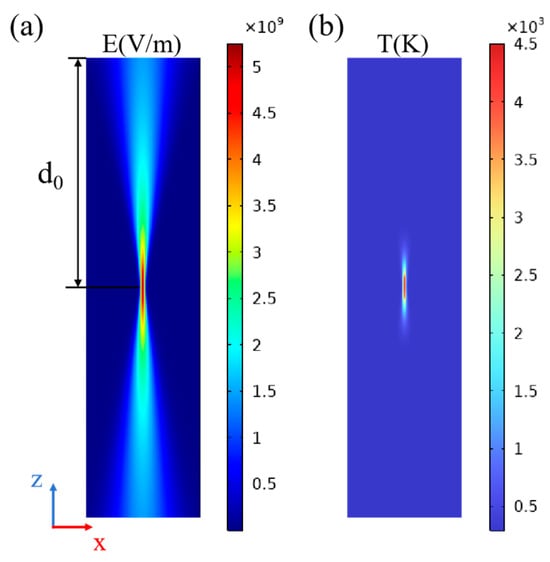
Figure 3.
Simulation diagram of (a) electric field and (b) electrical-induced temperature field distribution with laser pulse energy of E = 60 μJ and focusing depth d0 = 100 μm inside the 4H-SiC at 10 ps.
As depicted in Figure 4, at an energy of E = 10 μJ and 20 μJ, it is noteworthy that the internal temperature of the material fails to attain the boiling temperature characteristic of silicon after 10 ps of the thermal diffusion. As the laser pulse energy increases, a rise in energy absorption occurs, resulting in an amplified heat transformation, leading to its diffusion throughout the surrounding region. It can be explained that the increase of energy corresponds to an increase in the electric field E(x, z), as dictated by Equation (3), delineating the relationship between the electric field and laser intensity. It is discernible that the variation in modification depth aligns consistently with the energy.
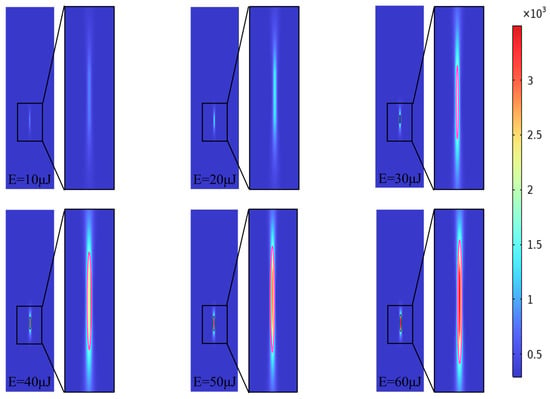
Figure 4.
The simulated distribution of the electrical-induced temperature field as the laser pulse energy increases from 10 μJ to 60 μJ at 10 ps. The pink lines in each enlarged temperature field of different energies are 1687.15 K isotherm.
In Figure 5, it is evident that the modification depth decreases with the increasing focusing depth at 10 ps. While the stretch length of the laser spot is directly proportional to the focusing depth, it is crucial to note that the significant losses. The energy of focus zone in the 4H-SiC can be influenced by numerous factors, such as the absorption of the material and the uneven distribution of laser pulse energy. The numerical simulation results detailing the change of modification depth at 1687.15 K are presented in Figure 6a. As the laser pulse energy increase and the temperature reaches the damage threshold, the modification depth exhibits an increase. The laser pulse energy density experiences a gradual decrease, eventually losing its ability with a deeper focusing depth to modified 4H-SiC, which is consistent with the results in Figure 6b.
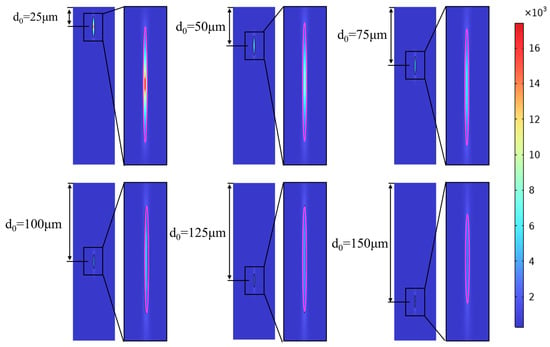
Figure 5.
The simulated electrical-induced temperature field distribution as the focusing depth increases from 25 μm to 150 μm at 10 ps. The pink lines in each enlarged temperature field of different focusing depths are 1687.15 K isotherm.
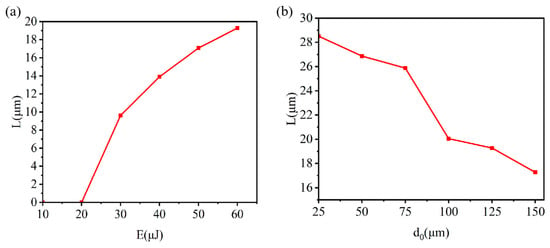
Figure 6.
(a) The change curves of modification depth L under the increasing of laser pulse energy E at 10 ps. (b) The change curves of modification depth L under the increasing of focusing depth d0 in the simulated model at 10 ps.
4.2. Experimental Analysis
In the experiment, it is investigated that the impact of laser pulse energy and focusing depth on modification layer morphology and size, specifically, the radius and depth of modification layer, utilizing orthogonal experiment. The morphological characteristics were observed using an optical microscope.
The linear fitting of the objective lens displacement and the focusing depth within 4H-SiC along the z-direction is displayed in Figure 7. The laser pulse energy is E = 10 μJ, and the repetition frequency is f = 100 kHz. In this part, z0 represents the distance of the objective lens movements. The experimental results reveal that the moving distance of the focus zone inside the 4H-SiC is 2.71 times that of the objective lens.
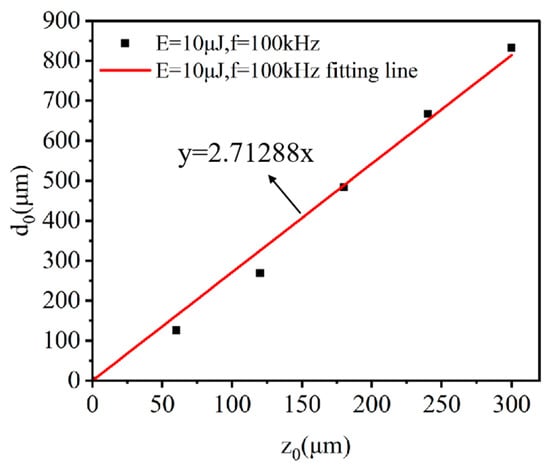
Figure 7.
The linear fitting relationship between the displacement of objective lens z0 and the focusing depth d0.
This process involves a laser beam with a scanning speed of 200 mm/s and a repetition frequency of 12.5 kHz. Illustrated in Figure 8a, the focusing depth is 126.5 μm with a gradual increase in laser pulse energy ranging from 10 μJ to 60 μJ inside the 4H-SiC. With the infusion of additional energy into the material, the temperature within the adjacent 4H-SiC environment experiences an increase through heat diffusion, ultimately culminating in attaining the boiling temperature, characterized by an expanding modification radius. In Figure 8b, the modification induced by laser energy at 40 μJ is depicted with a progressively increasing focusing depth ranging from 0 μm to 667.8 μm. There is a noticeable decrease in energy density, wherein, as the focus zone deepens, the modification radius diminishes, resulting in a lighter color.

Figure 8.
(a) Microscope modification layer morphology with laser pulse energy increasing from 10 μJ to 60 μJ at a focusing depth of d0 = 126.5 μm. (b) The microscope modification morphology was changed with focusing depth increasing from 0 μm to 667.8 μm at a laser pulse energy of E = 40 μJ.
Compared with the results of numerical simulation, the surface will be ablated inevitably, which is easily observed with the optical microscope. Despite the relatively low laser pulse energies of 10 μJ and 20 μJ, it is noteworthy that the energy is still sufficient to induce the formation of a modified radius on the surface.
In Figure 9a, at low energy, such as 10 μJ, 20 μJ and 30 μJ, the ablation radius begins to decrease when the focusing depth reaches 483.9 μm, whereas at high energy, its radius increases. Throughout the propagation of the laser beam, the continuous absorption of energy by 4H-SiC follows Lambert-Beer’s law, and part of the laser pulse energy is distributed transversely, leading to a reduction in energy density. When the laser pulse energy falls below the material’s damage threshold, no damage occurs. This reduction tendency aligns with the results obtained through numerical simulation. Once the energy is sufficiently increased, the modification radius enlarges as the laser penetrates deeper into 4H-SiC. This can also be verified by Figure 9a at E = 50 μJ and 60 μJ.
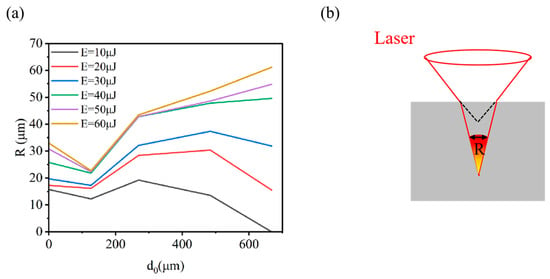
Figure 9.
(a) The modification radius changes curve with the variation of laser pulse energy E and focusing depth d0. (b) Schematic model diagram of modification radius inside the material.
Another observation in the experiment is the widening of the radius of modification layer as the focus zone deepens. This phenomenon is elucidated with the assistance of Figure 9b. The laser pulse energy accumulates at the top of the spot, forming a cometary shape inside the 4H-SiC. Because the incident laser is a Gaussian beam, which satisfies the formula for the equation , and ω0 is the waist radius, λ is the laser wavelength, z1 is the distance on the optical axis from the waist. The energy density absorbed by 4H-SiC surpasses the modification threshold before reaching the designated focusing depth, the premature modification of 4H-SiC will occur. In such cases, the deeper the focus zone, the further away from the waist, and the bigger the R.
Moreover, when the laser is precisely focused on the shallow inner layer, the modification radius is observed to be smaller than that on the surface. This discrepancy can be attributed to the fact that, during surface modification, the reaction of 4H-SiC with O2 at elevated temperatures generates SiO2 and CO2 [31], with the diffusion of Si vapor. In contrast, the absence of O2 inside hinders the oxidation reaction, resulting in the boiling of only Si at elevated temperatures. The expansion of the Si vapor within the interior relies solely on the solid’s limited region, which, due to its shorter diffusion distance compared to air, leads to a smaller modification radius than that on the surface.
Figure 10 illustrates the depth of modification layer changes at a repetition frequency of f = 12.5 kHz and an energy of E = 60 μJ. In Figure 10b, an enlarged figure of E = 60 μJ is presented. At focusing depths of 126.5 μm and 263.9 μm, where the spherical aberration is not substantial, and the energy loss is limited, the resulting modification zone is more conspicuous and exhibits an elliptical shape. Contrastingly, at focusing depths of 483.9 μm and 667.8 μm, the modification depth expands vertically, forming a conical shape with an extended stretch length.
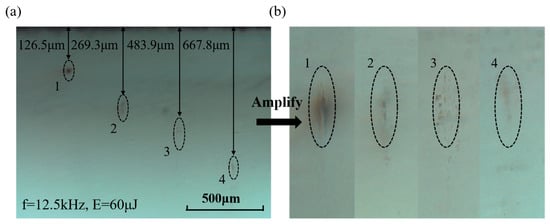
Figure 10.
4H-SiC cross-section microscope topography and magnification at f = 12.5 kHz with E = 60 μJ. And (b) is the enlarged morphology of (a).
The modification depth, described as L, increases with a rising focusing depth, as depicted in Figure 11a. The modification depth spans from 0 μm to 87.5 μm, while the focusing depth increases from 0 μm to 667.8 μm. As the focus zone deepens inside the material, the modification depth’s growth rate diminishes, even decreasing. The increase of modification depth is because the self-focusing and plasma defocusing inside the material, which is inherent inside the 4H-SiC [24]. The incident laser spot, being focused on multiple depths, results in uneven energy distribution. The reduction can be attributed to the decline in energy density, which was just mentioned. With an increase in repetition frequency, the overlap rate of the modification radius rises, which means the increase of laser pulse energy, as shown in Figure 11b. Multi-pulse modification at the same location continuously accumulates thermal influence within the material. Consequently, the modification depth expands rapidly under a high repetition frequency. However, at a frequency of f = 12.5 kHz and a focusing depth of 667.8 μm, the result suggests a commencement of decline, indicating an inadequacy of laser pulse energy to facilitate the deeper completion of the modification process.
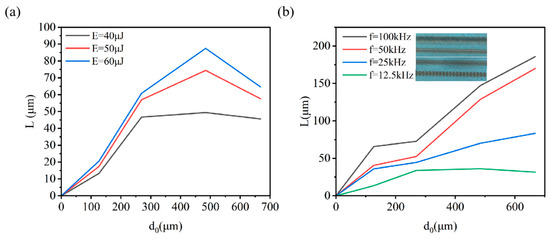
Figure 11.
The curve graph of modification depth L varies with the (a) focusing depth d0, laser pulse energy E, and (b) focusing depth d0, repetition frequency f.
5. Conclusions
In summary, we used the finite element method employed in simulating the electrical-induced temperature field inside the 4H-SiC and it has yielded reasonable results. The model considers the spherical aberration caused by the refractive index of the material, along with the non-linear absorption process occurring inside the 4H-SiC. The conclusions are summarized as follows:
- (1)
- The simulation method employed here provides a reasonable calculation process for the electrical-induced temperature field at 10 ps inside the 4H-SiC. It simulated the change of electrical-induced temperature field with the increasing of laser pulse energy and focusing depth. The simulation results indicate that the modification depth increases with the rise in laser pulse energy. However, a counter trend is observed as the increase of focusing depth. This means that to form a modified layer deep in the material, more energy is needed.
- (2)
- In experiment, the increase of the modification radius is observed to correlate with an increase of laser pulse energy. Deeper layers of 4H-SiC exhibit a larger modification radius compared to shallow layers. This phenomenon is attributed to the laser beam being absorbed and fully heated by the material before reaching the designed focusing depth, contributing to the spot radius expansion, further enhancing the modification radius.
- (3)
- In experiment, the depth of modification increases with the increase of laser pulse energy. Besides, as the focusing depth increases, this leads to a concurrent increase in the modification depth because of self-focusing within certain limits. However, it is crucial to note that beyond a certain point, the decreased energy density becomes a decisive factor. As the focusing depth further increases, the diminishing energy density contributes to a subsequent reduction in the extent of the modification depth.
Author Contributions
Conceptualization, S.Z.; methodology, S.Z.; software, Y.S.; validation, Y.S., H.H., H.L. and Z.D.; formal analysis, Y.S.; investigation, Z.D. and Y.S.; resources, S.Z. and X.L.; data curation, Y.S; writing original draft preparation, Y.S.; writing review and editing, S.Z. and G.Z.; visualization, Y.S.; supervision, S.Z., X.L. and G.Z.; project administration, X.L. and S.Z.; funding acquisition X.L. and S.Z.; All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially supported by National Key R&D Program of China (No. 2022YFB3605800), the CAS Project for Young Scientists in Basic Research, Grant No. YSBR-065, National Natural Science Foundation of China (No. 62225507, No. U2033211, No. 62175230, No. 62175232, No. 62275244), Scientific Instrument Developing Project of the Chinese Academy of Sciences, Grant No. YJKYYQ20200001, Key Program of the Chinese Academy of Sciences (ZDBS-ZRKJZ-TLC018).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Acknowledgments
Useful suggestions and revisions of the English version of this manuscript given by Jingyuan Zhang are also acknowledged.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Mandal, K.C.; Kleppinger, J.W.; Chaudhuri, S.K. Advances in High-Resolution Radiation Detection Using 4H-SiC Epitaxial Layer Devices. Micromachines 2020, 11, 254. [Google Scholar] [CrossRef]
- Shi, X.; Zhang, J.; Fan, W.; Lu, Y.; Peng, N.; Rottwitt, K.; Ou, H. Compact low-birefringence polarization beam splitter using vertical-dual-slot waveguides in silicon carbide integrated platforms. Photonics Res. 2022, 10, A8–A13. [Google Scholar] [CrossRef]
- Zhou, X.; Lü, Y.; Guo, H.; Song, X.; Wang, Y.; Liang, S.; Bu, A.; Feng, Z. High-stability 4H-SiC avalanche photodiodes for UV detection at high temperatures. Chin. Opt. Lett. 2023, 21, 032502. [Google Scholar] [CrossRef]
- Cheng, J.; Peng, Z.; Zhang, W.; Shao, L. Metal-Free High-Overtone Bulk Acoustic Resonators with Outstanding Acoustic Match and Thermal Stability. IEEE Electron Device Lett. 2023, 44, 1877–1880. [Google Scholar] [CrossRef]
- Tang, Z.; Tang, X.; Zhang, Y.; Zhao, P.; Sun, Y.; Zhang, Y. 4H-SiC integrated circuits for high-temperature applications. J. Cryst. Growth 2023, 605, 127060. [Google Scholar] [CrossRef]
- Cao, X.; Li, B.; Wang, Y.; Fu, Y.; Yin, H.; Chen, Z. Experimental quantum e-commerce. Sci. Adv. 2024, 10, eadk3258. [Google Scholar] [CrossRef] [PubMed]
- Yin, H.; Fu, Y.; Li, C.; Weng, C.; Li, B.; Gu, J.; Lu, Y.; Huang, S.; Chen, Z. Experimental quantum secure network with digital signatures and encryption. Natl. Sci. Rev. 2022, 10, nwac228. [Google Scholar] [CrossRef] [PubMed]
- Wei, K.; Li, W.; Tan, H.; Li, Y.; Min, H.; Zhang, W.; Li, H.; You, L.; Wang, Z.; Jiang, X.; et al. High-Speed Measurement-Device-Independent Quantum Key Distribution with Integrated Silicon Photonics. Phys. Rev. X 2020, 10, 031030. [Google Scholar] [CrossRef]
- Hardin, C.W.; Qu, J.; Shih, A.J. Fixed Abrasive Diamond Wire Saw Slicing of Single-Crystal Silicon Carbide Wafers. Mater. Manuf. Process. 2004, 19, 355–367. [Google Scholar] [CrossRef]
- Shi, X.; Lu, Y.; Chaussende, D.; Rottwitt, K.; Ou, H. Wet-Oxidation-Assisted Chemical Mechanical Polishing and High-Temperature Thermal Annealing for Low-Loss 4H-SiC Integrated Photonic Devices. Materials 2023, 16, 2324. [Google Scholar] [CrossRef] [PubMed]
- Liao, Y.; Shin, S.; Kim, M. Ultraviolet antireflective porous nanoscale periodic hole array of 4H-SiC by Photon-Enhanced Metal-assisted chemical etching. Appl. Surf. Sci. 2022, 581, 152387. [Google Scholar] [CrossRef]
- Wu, S.; Wu, D.; Xu, J.; Hanada, Y.; Suganuma, R.; Wang, H.; Makimura, T.; Sugioka, K.; Midorikawa, K. Characterization and mechanism of glass microwelding by double-pulse ultrafast laser irradiation. Opt. Express 2012, 20, 28893–28905. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; He, H.; Han, S.; Jiang, L.; Du, J.; Yu, H.; Lin, X.; Zhang, G. Research on key issues of laser splitting of transparent hard and brittle materials. Infrared Laser Eng. 2024, 53, 20230487. [Google Scholar]
- Qiu, J.; Kojima, K.; Miura, K.; Mitsuyu, T.; Hirao, K. Infrared femtosecond laser pulse–induced permanent reduction of Eu3+ to Eu2+ in a fluorozirconate glass. Opt. Lett. 1999, 24, 786–788. [Google Scholar] [CrossRef]
- Qiu, J.; Jiang, X.; Zhu, C.; Inouye, H.; Si, J.; Hirao, K. Optical properties of structurally modified glasses doped with gold ions. Opt. Lett. 2004, 29, 370–372. [Google Scholar] [CrossRef]
- Davis, K.M.; Miura, K.; Sugimoto, N.; Hirao, K. Writing waveguides in glass with a femtosecond laser. Opt. Lett. 1996, 21, 1729–1731. [Google Scholar] [CrossRef]
- Cai, Y.; Yang, L.; Zhang, H.; Wang, Y. Laser cutting silicon-glass double layer wafer with laser induced thermal-crack propagation. Opt. Lasers Eng. 2016, 82, 173–185. [Google Scholar] [CrossRef]
- Erwei, S. The Growth and Defects of Silicon Carbide Crystal; Science Press: Beijing, China, 2012. [Google Scholar]
- Han, S.; Yu, H.; He, C.; Zhao, S.; Ning, C.; Jiang, L.; Lin, X. Laser slicing of 4H-SiC wafers based on picosecond laser-induced micro-explosion via multiphoton processes. Opt. Laser Technol. 2022, 154, 108323. [Google Scholar] [CrossRef]
- Zhang, Y.; Xie, X.; Huang, Y.; Hu, W.; Long, J. Internal modified structure of silicon carbide prepared by ultrafast laser for wafer slicing. Ceram. Int. 2023, 49, 5249–5260. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Q.; Yao, Y.; Che, L.; Zhang, B.; Nie, H.; Wang, R. Influence of Surface Preprocessing on 4H-SiC Wafer Slicing by Using Ultrafast Laser. Crystals 2023, 13, 15. [Google Scholar] [CrossRef]
- Mohammed, A.F.; Al-Jarwany, Q.A.; Clarke, A.J.; Amaral, T.M.; Lawrence, J.; Kemp, N.T.; Walton, C.D. Ablation threshold measurements and surface modifications of 193 nm laser irradiated 4H-SiC. Chem. Phys. Lett. 2018, 713, 194–202. [Google Scholar] [CrossRef]
- Huang, Y.; Zhou, Y.; Li, J.; Zhu, F. Femtosecond laser surface modification of 4H-SiC improves machinability. Appl. Surf. Sci. 2023, 615, 156436. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, C.; Liu, F.; Zheng, H.; Cheng, G.J. Ultrafast pulsed laser stealth dicing of 4H-SiC wafer: Structure evolution and defect generation. J. Manuf. Process. 2022, 81, 562–570. [Google Scholar] [CrossRef]
- Jiang, L.; Wang, A.-D.; Li, B.; Cui, T.-H.; Lu, Y.-F. Electrons dynamics control by shaping femtosecond laser pulses in micro/nanofabrication: Modeling, method, measurement and application. Light Sci. Appl. 2018, 7, 17134. [Google Scholar] [CrossRef]
- Sun, Q.; Jiang, H.; Liu, Y.; Zhou, Y.; Yang, H.; Gong, Q. Effect of spherical aberration on the propagation of a tightly focused femtosecond laser pulse inside fused silica. J. Opt. A Pure Appl. Opt. 2005, 7, 655. [Google Scholar] [CrossRef]
- Nirmala, K.S.; Ramana, M.S.; Tewari, S.P. Tuning of ring laser by varying the Gouy phase. Opt. Commun. 2011, 284, 2560–2564. [Google Scholar] [CrossRef]
- Halliday, D.; Resnick, R.; Walker, J. Fundamentals of Physics; Wiley: Hoboken, NJ, USA, 2002. [Google Scholar]
- Harish, D.V.N.; Bharatish, A.; Murthy, H.N.N.; Anand, B.; Subramanya, K.N. Investigation of thermal residual stresses during laser ablation of tantalum carbide coated graphite substrates using micro-Raman spectroscopy and COMSOL multiphysics. Ceram. Int. 2021, 47, 3498–3513. [Google Scholar] [CrossRef]
- Youngworth, K.; Brown, T. Focusing of high numerical aperture cylindrical-vector beams. Opt. Express 2000, 7, 77–87. [Google Scholar] [CrossRef]
- Gao, R.; Gao, S.; Fan, G.; Liu, J.; Wang, Q.; Zhao, H.; Qu, S. Enhancement of surface photoconductivityin 6H-SiC crystal modified by femtosecond laser pulse irradiation. Acta Phys. Sin. 2014, 63, 6. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).