The Effect of Quantum Noise on Multipartite Entanglement from a Cascaded Parametric Amplifier
Abstract
1. Introduction
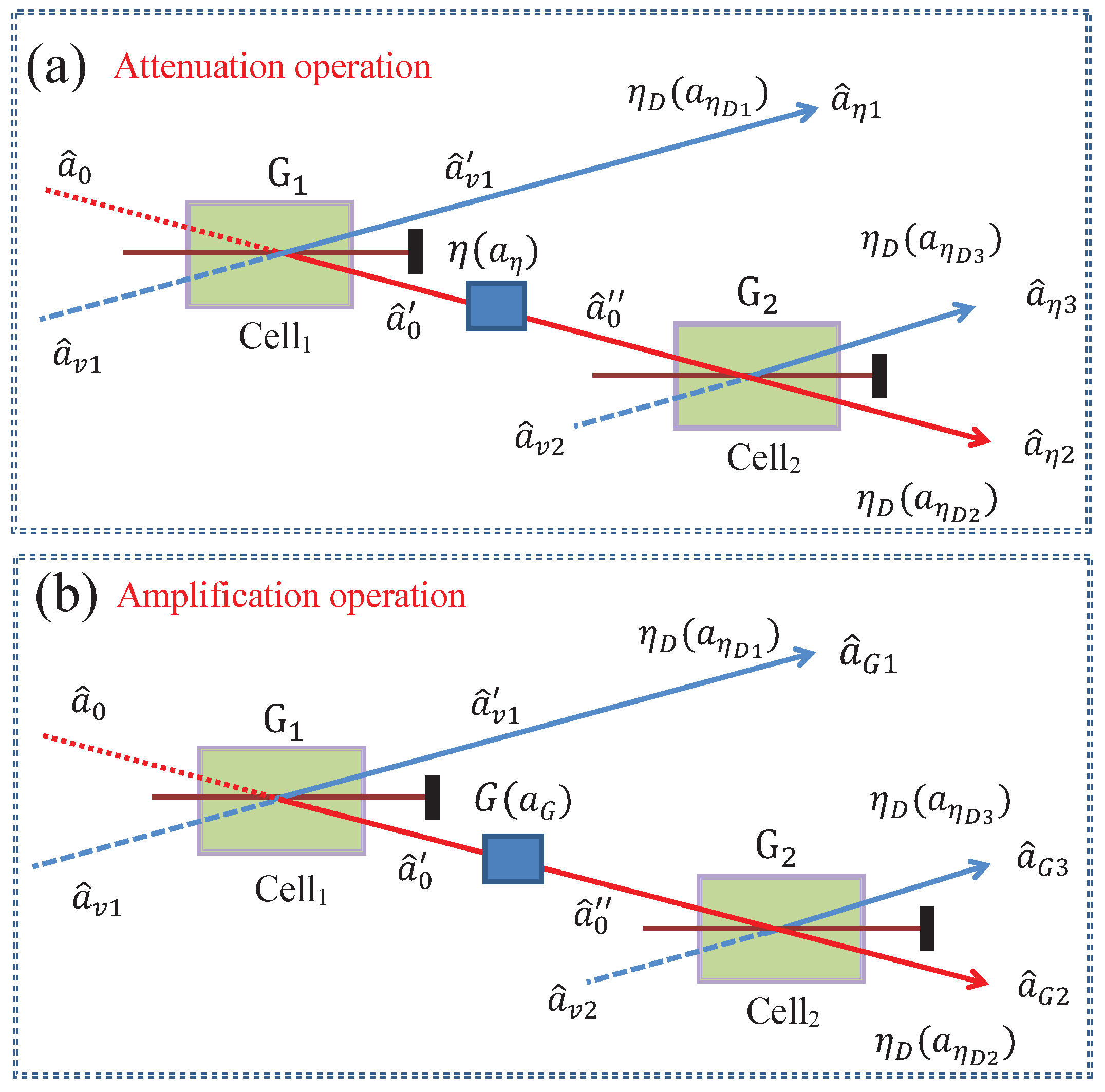
2. Cascaded FWM Processes under the Cases of the Attenuation and Amplification Operations
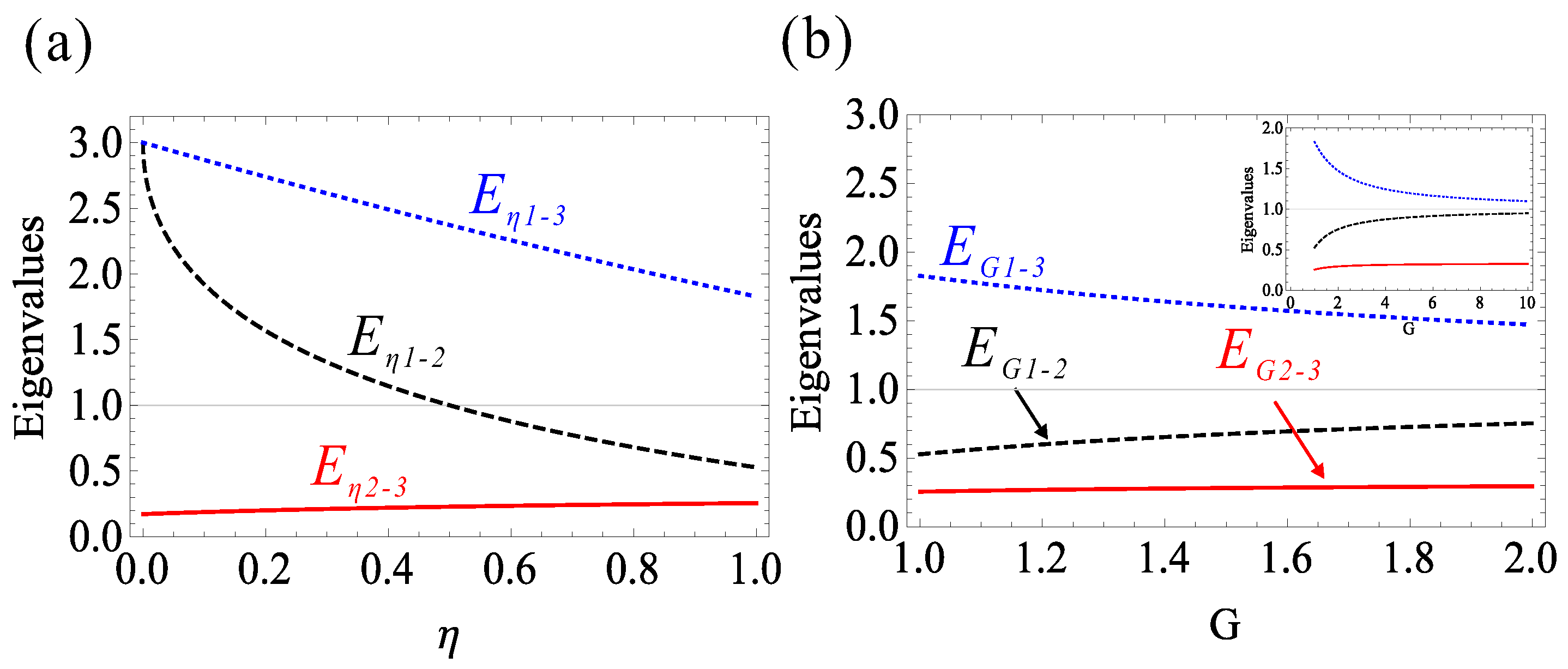
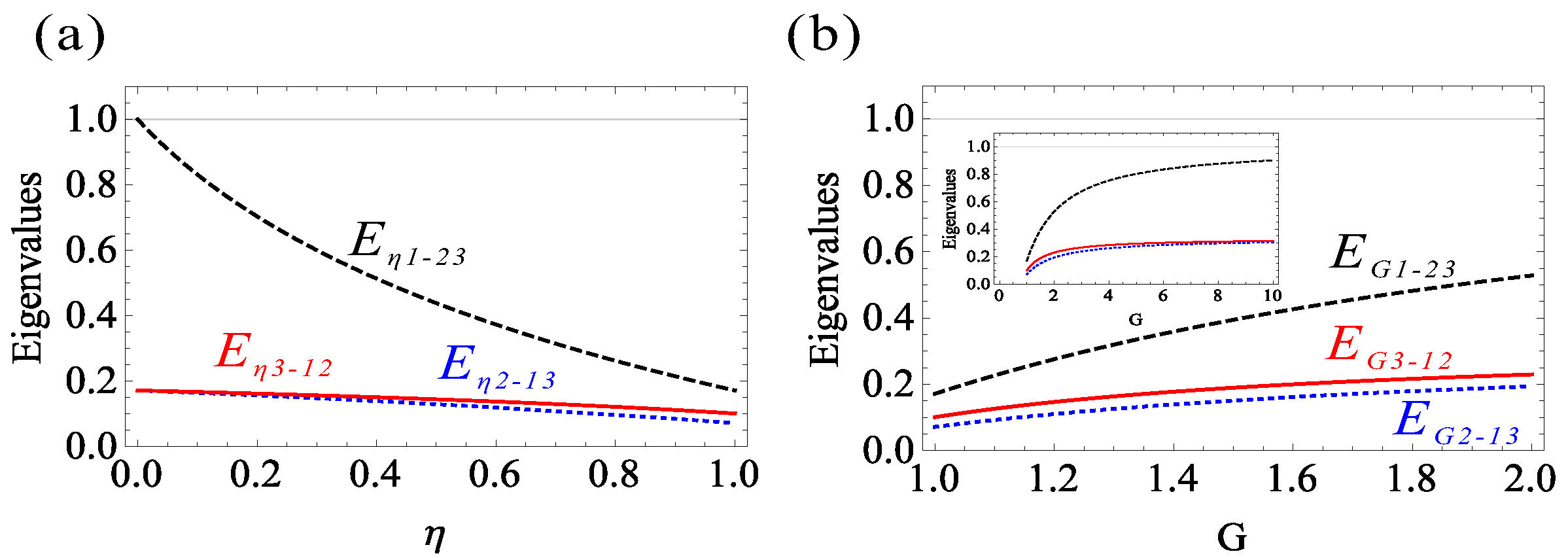
3. The Effect of the Detector Imperfections on Bipartite and Tripartite Entanglement
4. The Effect of Attenuation Operation and Amplification Operation G on Bipartite and Tripartite Entanglement
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shi, Z.; Dolgaleva, K.; Boyd, R.W. Quantum noise properties of non-ideal optical amplifiers and attenuator. J. Opt. 2011, 13, 125201. [Google Scholar] [CrossRef]
- Daniel, D.J.; Milburn, G.J. Destruction of quantum coherence in a nonlinear oscillator via attenuation and amplification. Phys. Rev. A 1989, 39, 4628–4640. [Google Scholar]
- Gagatsos, C.N.; Fiurášek, J.; Zavatta, A.; Bellini, M.; Cerf, N.J. Heralded noiseless amplification and attenuation of non-Gaussian states of light. Phys. Rev. A 2014, 89, 062311. [Google Scholar]
- Filippov, S.N.; Ziman, M. Entanglement sensitivity to signal attenuation and amplification. Phys. Rev. A 2014, 90, 010301. [Google Scholar] [CrossRef]
- Boyer, V.; Marino, A.M.; Pooser, R.C.; Lett, P.D. Entangled Images from Four-Wave Mixing. Science 2008, 321, 544–547. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Ru, N.; Lin, P. Generation of Three-Mode Entanglement Based on Parametric Amplifiers Using Quantum Entanglement Swapping. Photonics 2022, 9, 687. [Google Scholar]
- Yu, S.; Liu, H.; Jing, J. Generation of octapartite entanglement by connecting two symmetric cascaded four-wave mixing processes with one linear beam splitter. J. Opt. Soc. Am. B 2022, 39, 619–625. [Google Scholar]
- Mohamed, A.-B.A.; Khalil, E.M.; Abd-Rabbou, M.Y. Nonclassical atomic system dynamics time-dependently interacts with finite entangled pair coherent parametric converter cavity fields. Opt. Quan. Electron. 2021, 53, 344. [Google Scholar]
- Khalil, E.M.; Mohamed, A.-B.A.; Obada, A.-S.F.; Eleuch, H. Quasi-Probability Husimi-Distribution Information and Squeezing in a Qubit System Interacting with a Two-Mode Parametric Amplifier Cavity. Mathematics 2020, 8, 1830. [Google Scholar] [CrossRef]
- Marino, A.M.; Pooser, R.C.; Boyer, V.; Lett, P.D. Tunable delay of Einstein-Podolsky-Rosen entanglement. Nature 2009, 457, 859–862. [Google Scholar] [CrossRef]
- Pooser, R.C.; Marino, A.M.; Boyer, V.; Jones, K.M.; Lett, P.D. Low-Noise Amplification of a Continuous-Variable Quantum State. Phys. Rev. Lett. 2009, 103, 010501. [Google Scholar] [CrossRef] [PubMed]
- Jing, J.; Liu, C.; Zhou, Z.; Ou, Z.Y.; Zhang, W. Realization of a nonlinear interferometer with parametric amplifiers. Appl. Phys. Lett. 2011, 99, 011110. [Google Scholar] [CrossRef]
- Hudelist, F.; Kong, J.; Liu, C.; Jing, J.; Ou, Z.Y.; Zhang, W. Quantum metrology with parametric amplifier-based photon correlation interferometers. Nat. Commun. 2014, 5, 3049. [Google Scholar] [CrossRef]
- Clark, J.B.; Glasser, R.T.; Glorieux, Q.; Vogl, U.; Li, T.; Jones, K.M.; Lett, P.D. Quantum mutual information of an entangled state propagating through a fast-light medium. Nat. Photon. 2014, 8, 515–519. [Google Scholar] [CrossRef]
- Qin, Z.; Cao, L.; Wang, H.; Marino, A.M.; Zhang, W.; Jing, J. Experimental Generation of Multiple Quantum Correlated Beams from Hot Rubidium Vapor. Phys. Rev. Lett. 2014, 113, 023602. [Google Scholar] [CrossRef]
- Wang, H.; Zheng, Z.; Wang, Y.; Jing, J. Generation of tripartite entanglement from cascaded four-wave mixing processes. Opt. Express 2016, 24, 23459–23470. [Google Scholar] [CrossRef]
- Shen, L.; Shi, Z.; Yang, Z. Coherent State Control to Recover Quantum Entanglement and Coherence. Entropy 2019, 21, 917. [Google Scholar] [CrossRef]
- Wei, T.; Lv, S.; Jing, J. Effect of losses on multipartite entanglement from cascaded four-wave mixing processes. J. Opt. Soc. Am. B 2018, 35, 2806–2814. [Google Scholar] [CrossRef]
- Simon, R. Peres-Horodecki Separability Criterion for Continuous Variable Systems. Phys. Rev. Lett. 2000, 84, 2726–2729. [Google Scholar] [CrossRef]
- Werner, R.F.; Wolf, M.M. Bound Entangled Gaussian States. Phys. Rev. Lett. 2001, 86, 3658–3661. [Google Scholar] [CrossRef]
- Barbosa, F.A.S.; de Faria, A.J.; Coelho, A.S.; Cassemiro, K.N.; Villar, A.S.; Nussenzveig, P.; Martinelli, M. Disentanglement in bipartite continuous-variable systems. Phys. Rev. A 2011, 84, 052330. [Google Scholar] [CrossRef]
- Barbosa, F.A.S.; Coelho, A.S.; de Faria, A.J.; Cassemiro, K.N.; Villar, A.S.; Nussenzveig, P.; Martinelli, M. Robustness of bipartite Gaussian entangled beams propagating in lossy channels. Nat. Photon. 2010, 4, 858–861. [Google Scholar] [CrossRef]
- Mazeas, F.; Traetta, M.; Bentivegna, M.; Kaiser, F.; Aktas, D.; Zhang, W.; Ramos, C.A.; Ngah, L.A.; Lunghi, T.; Picholle, É.; et al. High-quality photonic entanglement for wavelength-multiplexed quantum communication based on a silicon chip. Opt. Express 2016, 24, 28731–28738. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhang, M.; Li, K.; Hu, J. Study on the surface properties and biocompatibility of nanosecond laser patterned titanium alloy. Opt. Laser Technol. 2021, 139, 106987. [Google Scholar] [CrossRef]
- Akca, B.I.; Považay, B.; Alex, A.; Wörhoff, K.; de Ridder, R.M.; Drexler, W.; Pollnau, M. Miniature spectrometer and beam splitter for an optical coherence tomography on a silicon chip. Opt. Express 2013, 21, 16648–16656. [Google Scholar] [CrossRef] [PubMed]
- Sibson, P.; Erven, C.; Godfrey, M.; Miki, S.; Yamashita, T.; Fujiwara, M.; Sasaki, M.; Terai, H.; Tanner, M.G.; Natarajan, C.M.; et al. Chip-based quantum key distribution. Nat. Commun. 2017, 8, 13984. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Zhang, Y.; Zhang, X.; Chen, J.; Gong, H.; Zhao, C. The Effect of Quantum Noise on Multipartite Entanglement from a Cascaded Parametric Amplifier. Photonics 2023, 10, 307. https://doi.org/10.3390/photonics10030307
Wang H, Zhang Y, Zhang X, Chen J, Gong H, Zhao C. The Effect of Quantum Noise on Multipartite Entanglement from a Cascaded Parametric Amplifier. Photonics. 2023; 10(3):307. https://doi.org/10.3390/photonics10030307
Chicago/Turabian StyleWang, Hailong, Yajuan Zhang, Xiong Zhang, Jun Chen, Huaping Gong, and Chunliu Zhao. 2023. "The Effect of Quantum Noise on Multipartite Entanglement from a Cascaded Parametric Amplifier" Photonics 10, no. 3: 307. https://doi.org/10.3390/photonics10030307
APA StyleWang, H., Zhang, Y., Zhang, X., Chen, J., Gong, H., & Zhao, C. (2023). The Effect of Quantum Noise on Multipartite Entanglement from a Cascaded Parametric Amplifier. Photonics, 10(3), 307. https://doi.org/10.3390/photonics10030307



