Experimental Synthesis and Demonstration of the Twisted Laguerre–Gaussian Schell-Mode Beam
Abstract
1. Introduction
2. Theory
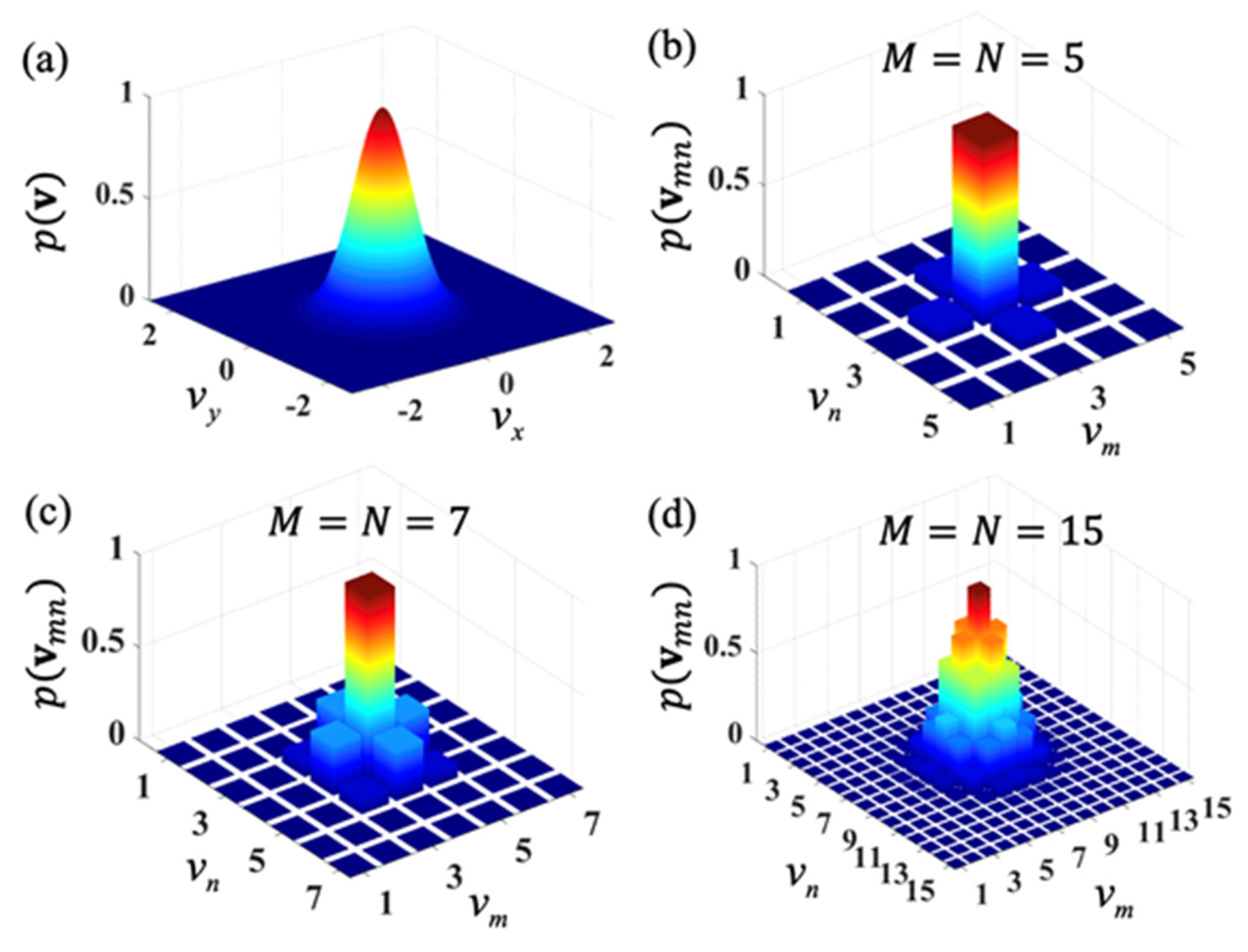
2.1. Pseudo-Mode Representation for a TLGSM Beam
2.2. Examining the Propagation Properties with Pseudo-Mode Representation
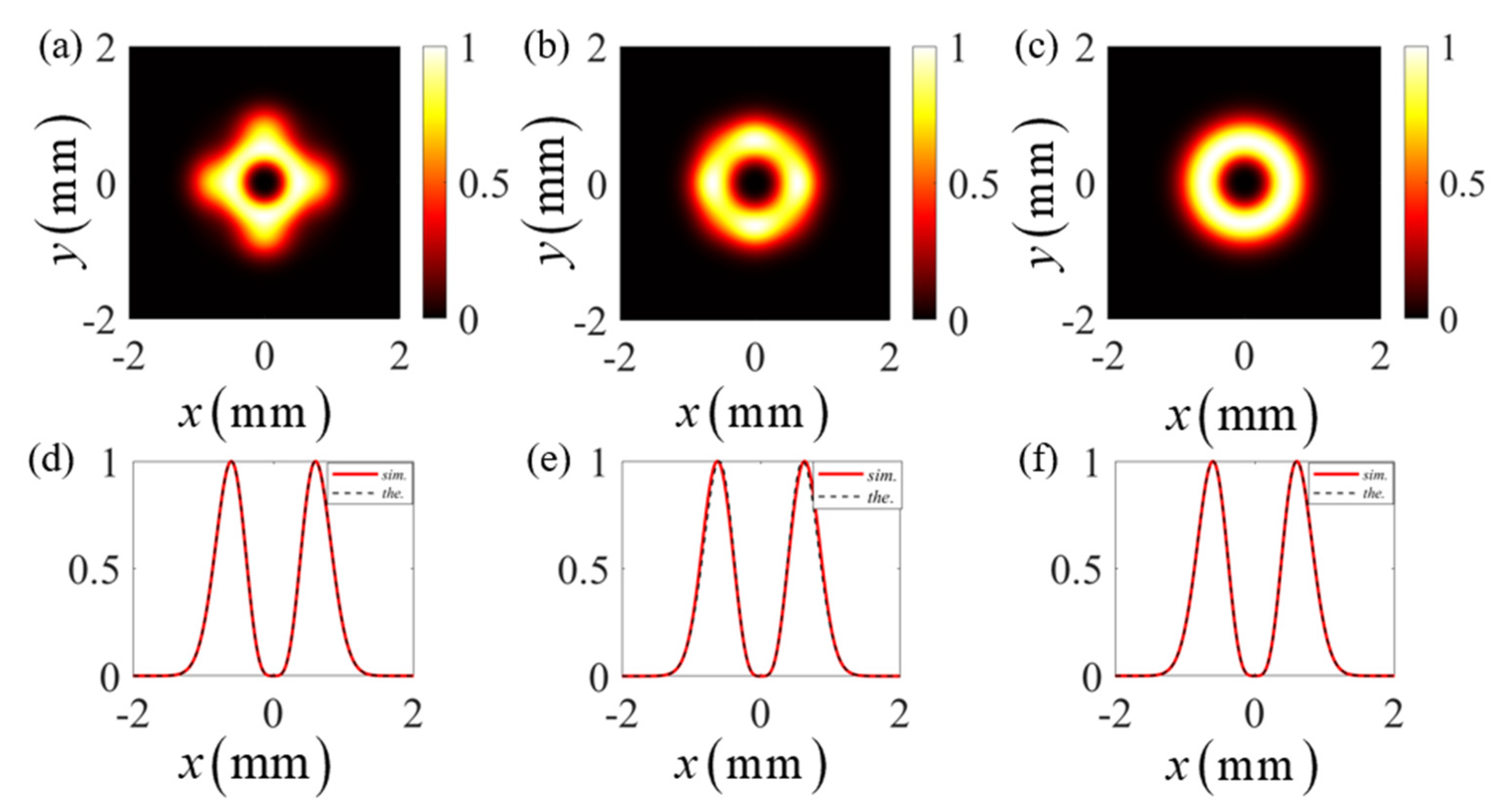
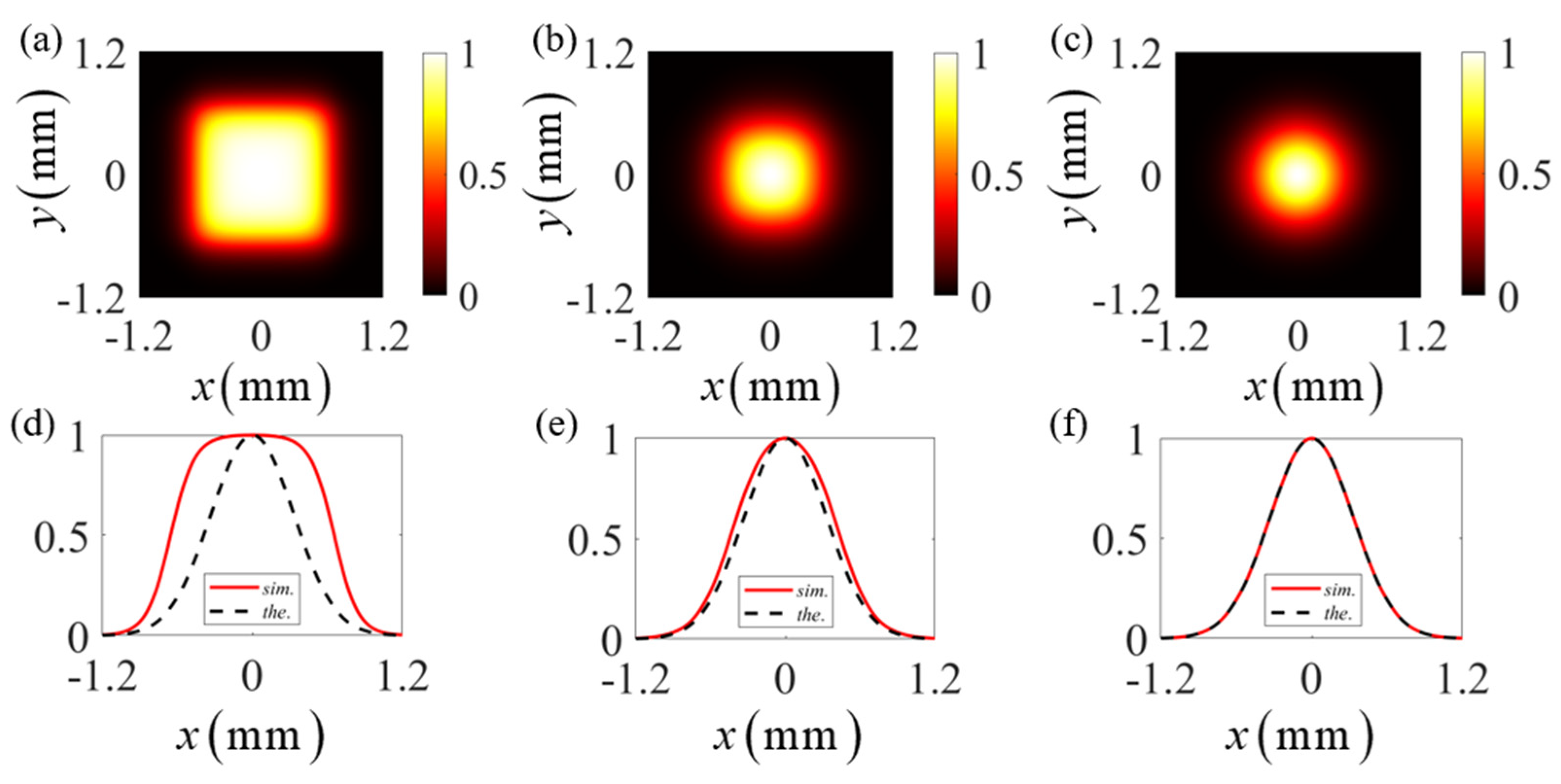
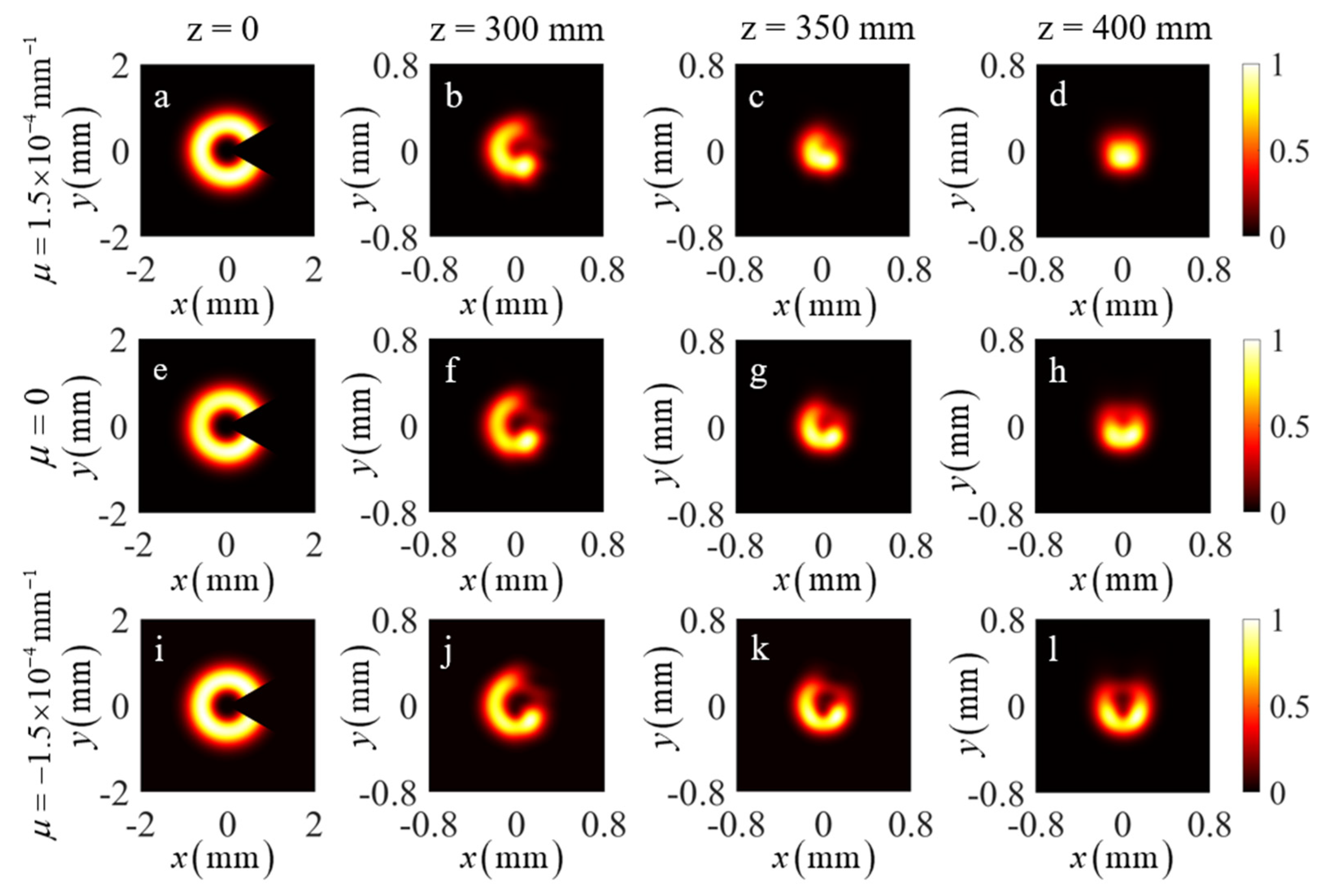
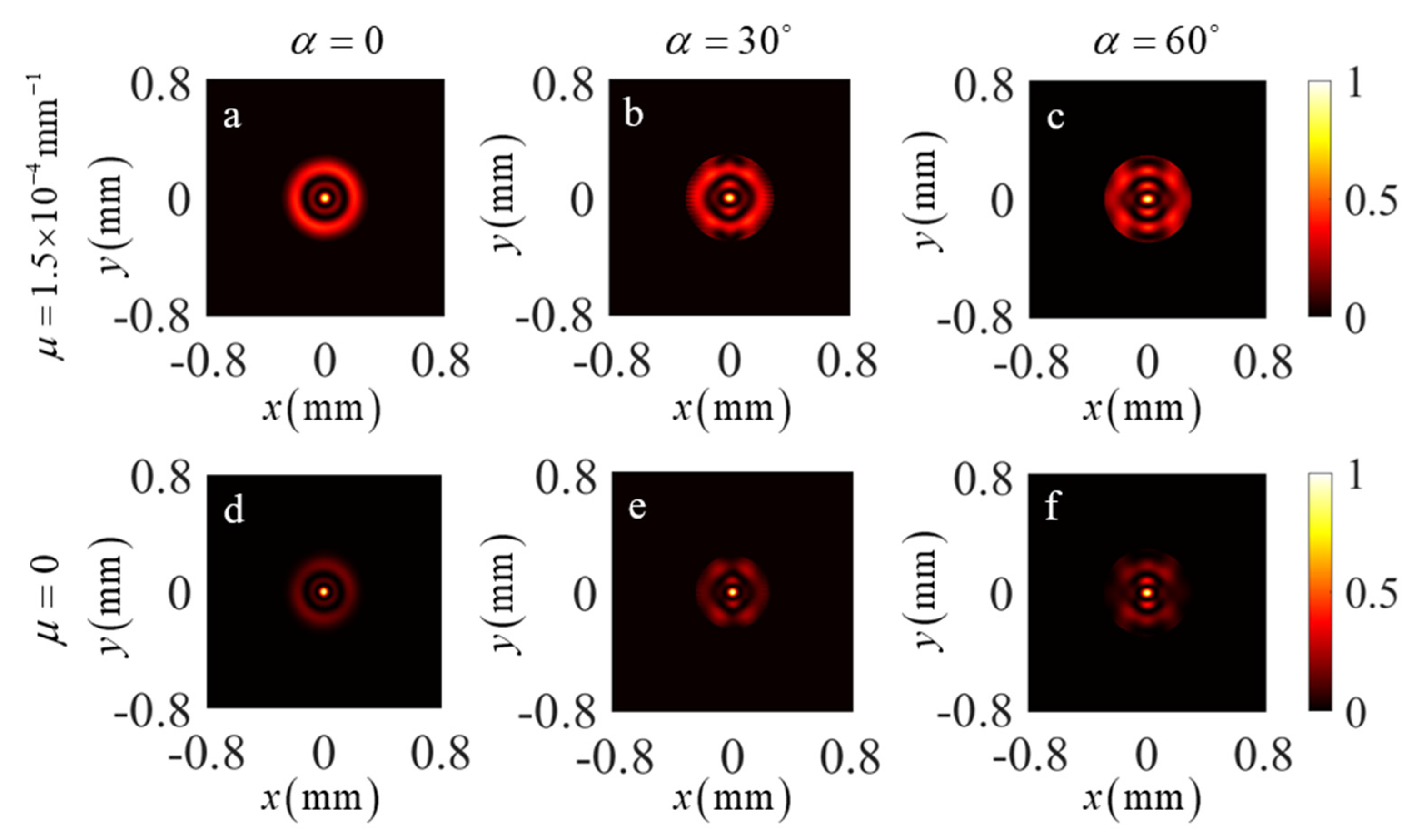
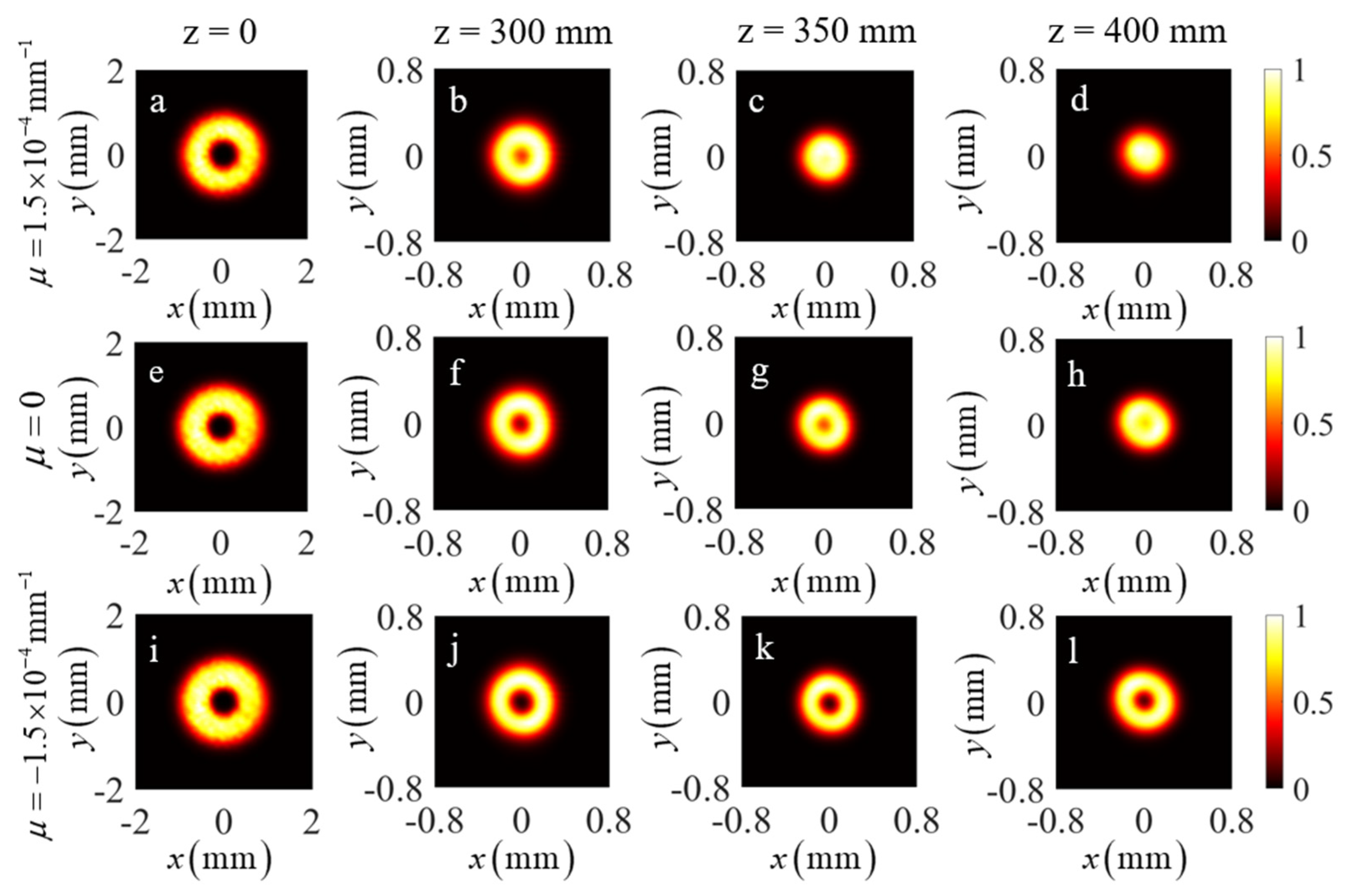
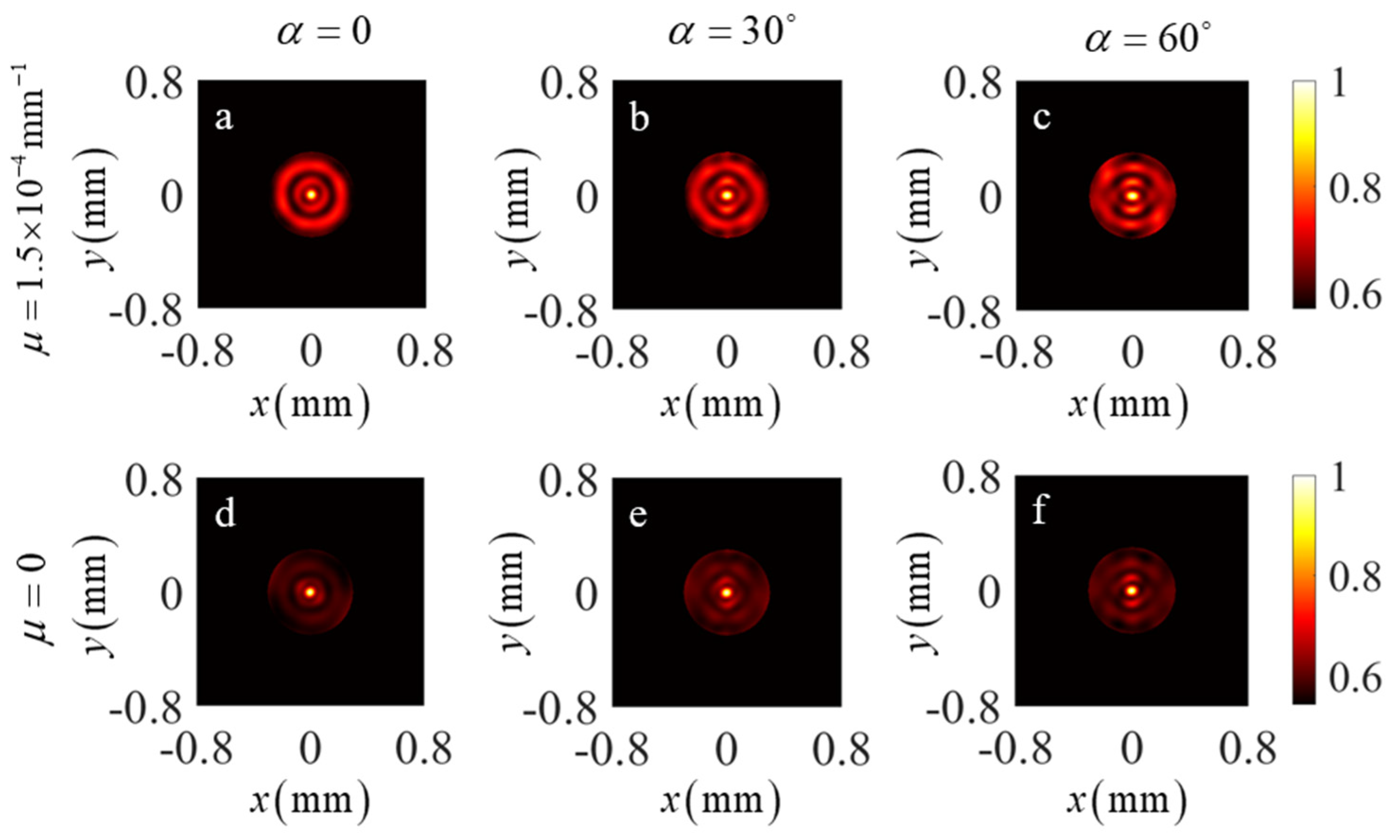
3. Experiment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Friberg, A.T.; Setälä, T. Electromagnetic theory of optical coherence. J. Opt. Soc. Am. A 2016, 33, 2431–2442. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Cai, Y. Optical coherence structure: A novel tool for light manipulation. Sci. China Technol. Sci. 2022, 65, 740–742. [Google Scholar] [CrossRef]
- Korotkova, O.; Chen, X. Phase structuring of the complex degree of coherence. Opt. Lett. 2018, 43, 4727–4730. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Korotkova, O. Complex degree of coherence modeling with famous planar curves. Opt. Lett. 2018, 43, 6049–6052. [Google Scholar] [CrossRef]
- Chen, X.; Korotkova, O. Phase structuring of 2D complex coherence states. Opt. Lett. 2019, 44, 2470–2473. [Google Scholar] [CrossRef]
- Korotkova, O. Multi-Gaussian Schell-model source with a complex coherence. J. Opt. 2019, 21, 045607. [Google Scholar] [CrossRef]
- Chen, Y.; Ponomarenko, S.A.; Cai, Y. Experimental generation of optical coherence lattices. Appl. Phys. Lett. 2016, 109, 061107. [Google Scholar] [CrossRef]
- Wan, L.; Zhao, D. Controllable rotating Gaussian Schell-model beams. Opt. Lett. 2019, 44, 735–738. [Google Scholar] [CrossRef]
- Wan, L.; Zhao, D. Generalized partially coherent beams with nonseparable phases. Opt. Lett. 2019, 44, 4714–4717. [Google Scholar] [CrossRef]
- Pan, R.; Liu, X.; Tang, J.; Ye, H.; Liu, Z.; Ma, P.; Wen, W.; Hoenders, B.J.; Cai, Y.; Liang, C. Enhancing the self-reconstruction ability of the degree of coherence of a light beam via manipulating the cross-phase structure. Appl. Phys. Lett. 2021, 119, 111105. [Google Scholar] [CrossRef]
- Jin, Y.; Wang, H.; Liu, L.; Chen, Y.; Wang, F.; Cai, Y. Orientation-selective sub-Rayleigh imaging with spatial coherence lattices. Opt. Express 2022, 30, 9548–9561. [Google Scholar] [CrossRef]
- Chen, Y.; Ponomarenko, S.; Cai, A.Y. Self-steering partially coherent beams. Sci. Rep. 2017, 7, 39957. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Chen, Y.; Wang, F.; Ponomarenko, S.A.; Cai, Y. Measuring complex degree of coherence of random light fields with generalized Hanbury Brown–Twiss experiment. Phys. Rev. Appl. 2020, 13, 044042. [Google Scholar] [CrossRef]
- Dong, Z.; Huang, Z.; Chen, Y.; Wang, F.; Cai, Y. Measuring complex correlation matrix of partially coherent vector light via a generalized Hanbury Brown–Twiss experiment. Opt. Express 2020, 28, 20634–20644. [Google Scholar] [CrossRef] [PubMed]
- Peng, D.; Huang, Z.; Liu, Y.; Chen, Y.; Wang, F.; Ponomarenko, S.A.; Cai, Y. Optical coherence encryption with structured random light. PhotoniX 2021, 2, 6. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Y.; Wang, F.; Cai, Y.; Liang, C.; Korotkova, O. Robust far-field imaging by spatial coherence engineering. Opto-Electron. Adv. 2021, 4, 210027. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, X.; Dong, Z.; Peng, D.; Chen, Y.; Wang, F.; Cai, Y. Robust Far-Field Optical Image Transmission with Structured Random Light Beams. Phys. Rev. Appl. 2022, 17, 024043. [Google Scholar] [CrossRef]
- Dong, M.; Zhao, C.; Cai, Y.; Yang, Y. Partially coherent vortex beams: Fundamentals and applications. Sci. China Phys. Mech. Astron. 2021, 64, 224201. [Google Scholar] [CrossRef]
- Simon, R.; Mukunda, N. Twisted Gaussian Schell-model beams. J. Opt. Soc. Am. A 1993, 10, 95–109. [Google Scholar] [CrossRef]
- Cai, Y.; Lin, Q.; Korotkova, O. Ghost imaging with twisted Gaussian Schell-model beam. Opt. Express 2009, 17, 2453–2464. [Google Scholar] [CrossRef]
- Zhao, C.; Cai, Y.; Korotkova, O. Radiation force of scalar and electromagnetic twisted Gaussian Schell-model beams. Opt. Express 2009, 17, 21472–21487. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Cai, Y.; Eyyuboğlu, H.T.; Baykal, Y. Twist phase-induced reduction in scintillation of a partially coherent beam in turbulent atmosphere. Opt. Lett. 2012, 37, 184–186. [Google Scholar] [CrossRef] [PubMed]
- Tong, Z.; Korotkova, O. Beyond the classical Rayleigh limit with twisted light. Opt. Lett. 2012, 37, 2595–2597. [Google Scholar] [CrossRef] [PubMed]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef]
- Padgett, M.J. Orbital angular momentum 25 years on. Opt. Express 2017, 25, 11265–11274. [Google Scholar] [CrossRef]
- Trichili, A.; Salem, A.B.; Dudley, A.; Zghal, M.; Forbes, A. Encoding information using Laguerre Gaussian modes over free space turbulence media. Opt. Lett. 2016, 41, 3086–3089. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Yang, J.; Fazal, I.M.; Ahmed, N.; Yan, Y.; Huang, H.; Ren, Y.; Dolinar, S.; Tur, M.; Willner, A.E. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 2012, 6, 488–496. [Google Scholar] [CrossRef]
- Willig, K.I.; Rizzoli, S.O.; Westphal, V.; Jahn, R.; Hell, S.W. STED microscopy reveals that synaptotagmin remains clustered after synaptic vesicle exocytosis. Nature 2006, 440, 935–939. [Google Scholar] [CrossRef]
- Wang, B.; Brooks, N.J.; Johnsen, P.C.; Jenkins, N.W.; Esashi, Y.; Binnie, I.; Tanksalvala, M.; Kapteyn, H.C.; Murnane, M.M. High-fidelity ptychographic imaging of highly periodic structures enabled by vortex high harmonic beams. arXiv 2023, arXiv:2301.05563. [Google Scholar]
- Roxworthy, B.J.; Toussaint, K.C. Optical trapping with π-phase cylindrical vector beams. New J. Phys. 2010, 12, 073012. [Google Scholar] [CrossRef]
- Li, Z.; Liu, T.; Ren, Y.; Qiu, S.; Wang, C.; Wang, H. Direction-sensitive detection of a spinning object using dual-frequency vortex light. Opt. Express 2021, 29, 7453–7463. [Google Scholar] [CrossRef]
- Wang, B.; Tanksalvala, M.; Zhang, Z.; Murnane, M.; Kapteyn, H.; Liao, C. Coherent Fourier scatterometry using orbital angular momentum beams for defect detection. Opt. Express 2021, 29, 3342–3358. [Google Scholar] [CrossRef]
- Mccarter, M.R.; Saleheen, A.; Singh, A.; Tumbleson, R.; Woods, J.S.; Tremsin, A.S.; Scholl, A.; De Long, L.E.; Hastings, J.T.; Morley, S.A.; et al. Antiferromagnetic real-space configuration probed by x-ray orbital angular momentum phase dichroism. arXiv 2022, arXiv:2205.03475. [Google Scholar]
- Ponomarenko, S.A. Twist phase and classical entanglement of partially coherent light. Opt. Lett. 2021, 46, 5958–5961. [Google Scholar] [CrossRef] [PubMed]
- Ponomarenko, S.A. Classical entanglement of twisted random light propagating through atmospheric turbulence. J. Opt. Soc. Am. 2022, 39, C1–C5. [Google Scholar] [CrossRef] [PubMed]
- Serna, J.; Movilla, J.M. Orbital angular momentum of partially coherent beams. Opt. Lett. 2001, 26, 405–407. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Huang, Y.; Chen, Y.; Guo, L.; Cai, Y. Orbital angular moment of an electromagnetic Gaussian Schell-model beam with a twist phase. Opt. Express 2015, 23, 30283–30296. [Google Scholar] [CrossRef]
- Peng, X.; Liu, L.; Wang, F.; Popov, S.; Cai, Y. Twisted Laguerre-Gaussian Schell-model beam and its orbital angular moment. Opt. Express 2018, 26, 33956–33969. [Google Scholar] [CrossRef]
- Peng, X.; Wang, H.; Liu, L.; Wang, F.; Popov, S.; Cai, Y. Self-reconstruction of twisted Laguerre-Gaussian Schell-model beams partially blocked by an opaque obstacle. Opt. Express 2020, 28, 31510–31523. [Google Scholar] [CrossRef]
- Friberg, A.T.; Tervonen, E.; Turunen, J. Interpretation and experimental demonstration of twisted Gaussian Schell-model beams. J. Opt. Soc. Am. A 1994, 11, 1818–1826. [Google Scholar] [CrossRef]
- Wang, H.; Peng, X.; Liu, L.; Wang, F.; Cai, Y.; Ponomarenko, S.A. Generating bona fide twisted Gaussian Schell-model beams. Opt. Lett. 2019, 44, 3709–3712. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhang, X.; Wang, H.; Ye, Y.; Liu, L.; Chen, Y.; Wang, F.; Cai, Y. Generating a twisted Gaussian Schell-model beam with a coherent-mode superposition. Opt. Express 2021, 29, 41964–41974. [Google Scholar] [CrossRef]
- Tian, C.; Zhu, S.; Huang, H.; Cai, Y.; Li, Z. Customizing twisted Schell-model beams. Opt. Lett. 2020, 45, 5880–5883. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Peng, X.; Zhang, H.; Liu, L.; Chen, Y.; Wang, F.; Cai, Y. Experimental synthesis of partially coherent beam with controllable twist phase and measuring its orbital angular momentum. Nanophotonics 2022, 11, 689–696. [Google Scholar] [CrossRef]
- Wang, F.; Lv, H.; Chen, Y.; Cai, Y.; Korotkova, O. Three modal decompositions of Gaussian Schell-model sources: Comparative analysis. Opt. Express 2021, 29, 29676–29689. [Google Scholar] [CrossRef]
- Gori, F.; Santarsiero, M. Devising genuine spatial correlation functions. Opt. Lett. 2007, 32, 3531–3533. [Google Scholar] [CrossRef]
- Collins, S.A. Lens-System Diffraction Integral Written in Terms of Matrix Optics. J. Opt. Soc. Am. 1970, 60, 1168–1177. [Google Scholar] [CrossRef]
- Wang, R.; Zhu, S.; Chen, Y.; Huang, H.; Li, Z.; Cai, Y. Experimental synthesis of partially coherent sources. Opt. Lett. 2020, 45, 1874–1877. [Google Scholar] [CrossRef]
- Zhu, X.; Yu, J.; Chen, Y.; Wang, F.; Korotkova, O.; Cai, Y. Experimental synthesis of random light sources with circular coherence by digital micro-mirror device. Appl. Phys. Lett. 2020, 117, 121102. [Google Scholar] [CrossRef]
- Zhu, X.; Yu, J.; Wang, F.; Chen, Y.; Cai, Y.; Korotkova, O. Synthesis of vector nonuniformly correlated light beams by a single digital mirror device. Opt. Lett. 2021, 46, 2996–2999. [Google Scholar] [CrossRef] [PubMed]
- Vaity, P.; Banerji, J.; Singh, R. Measuring the topological charge of an optical vortex by using a tilted convex lens. Phys. Lett. A 2013, 377, 1154–1156. [Google Scholar] [CrossRef]
- da Silva, B.P.; Tasca, D.S.; Galvão, E.F.; Khoury, A.Z. Astigmatic tomography of orbital-angular-momentum superpositions. Phys. Rev. A 2019, 99, 043820. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, Y.; Wang, H.; Liu, L.; Chen, Y.; Wang, F.; Cai, Y. Experimental Synthesis and Demonstration of the Twisted Laguerre–Gaussian Schell-Mode Beam. Photonics 2023, 10, 314. https://doi.org/10.3390/photonics10030314
Xia Y, Wang H, Liu L, Chen Y, Wang F, Cai Y. Experimental Synthesis and Demonstration of the Twisted Laguerre–Gaussian Schell-Mode Beam. Photonics. 2023; 10(3):314. https://doi.org/10.3390/photonics10030314
Chicago/Turabian StyleXia, Yuning, Haiyun Wang, Lin Liu, Yahong Chen, Fei Wang, and Yangjian Cai. 2023. "Experimental Synthesis and Demonstration of the Twisted Laguerre–Gaussian Schell-Mode Beam" Photonics 10, no. 3: 314. https://doi.org/10.3390/photonics10030314
APA StyleXia, Y., Wang, H., Liu, L., Chen, Y., Wang, F., & Cai, Y. (2023). Experimental Synthesis and Demonstration of the Twisted Laguerre–Gaussian Schell-Mode Beam. Photonics, 10(3), 314. https://doi.org/10.3390/photonics10030314






