Artificial Immune System in Doing 2-Satisfiability Based Reverse Analysis Method via a Radial Basis Function Neural Network
Abstract
1. Introduction
2. 2 Satisfiability Logic Representation
- A set of m logical variables, . Each variable stores a binary value of that exemplify TRUE and FALSE, respectively.
- Each variable in can be set of literals, where positive literal and negative literal is defined as and , respectively.
- Consisting of a set of n distinct clauses, . Each is connected by logical AND (). Every k literals will form a single and connected by logical OR ().
3. Radial Basis Function Neural Network (RBFNN)
4. 2-Satisfiability Based Reverse Analysis Method (2SATRA) in RBFNN
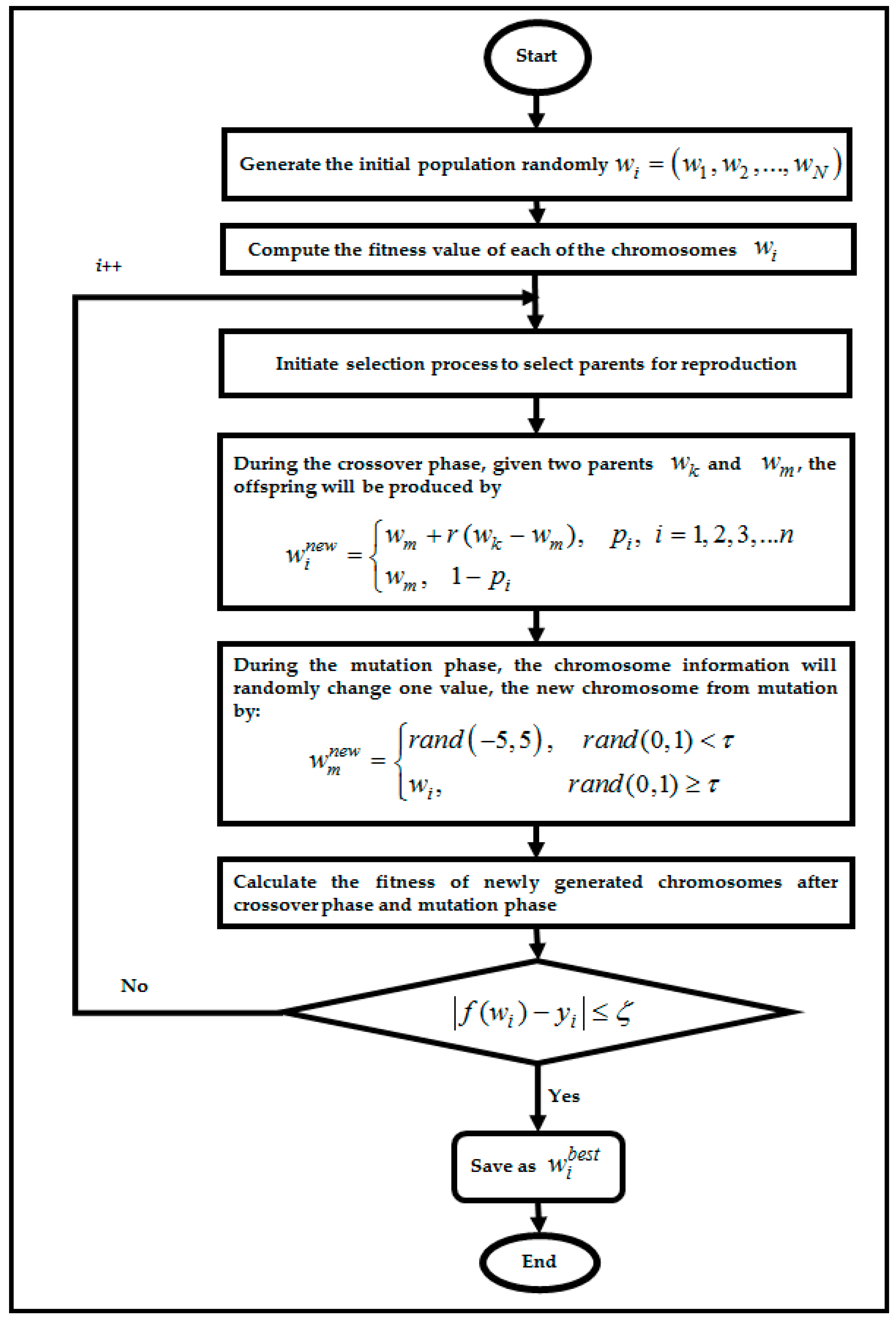
4.1. Genetic Algorithm in RBFNN-2SATRA
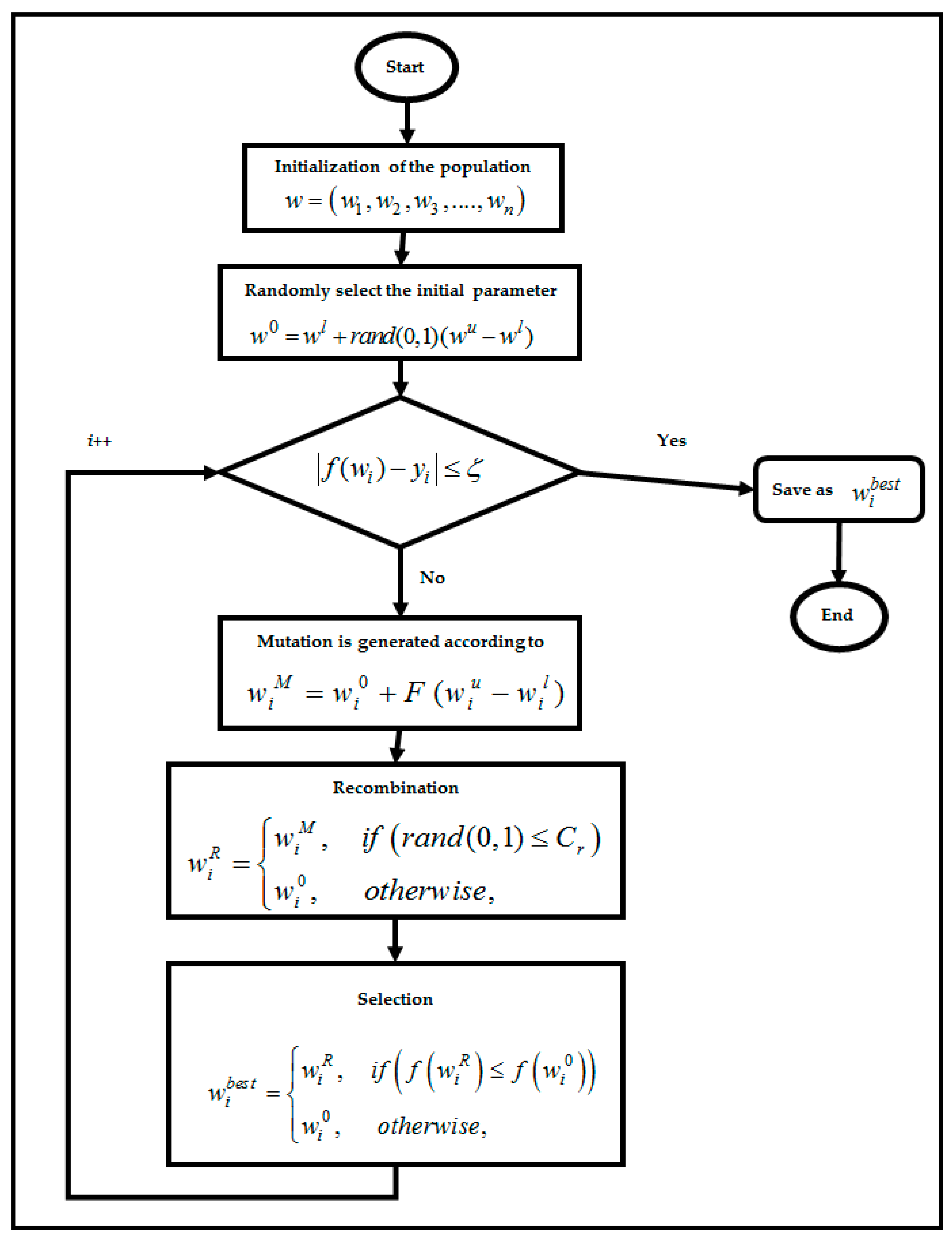
4.2. Differential Evolution Algorithm in RBFNN-2SATRA
4.3. Particle Swarm Optimization Algorithm in RBFNN-2SATRA
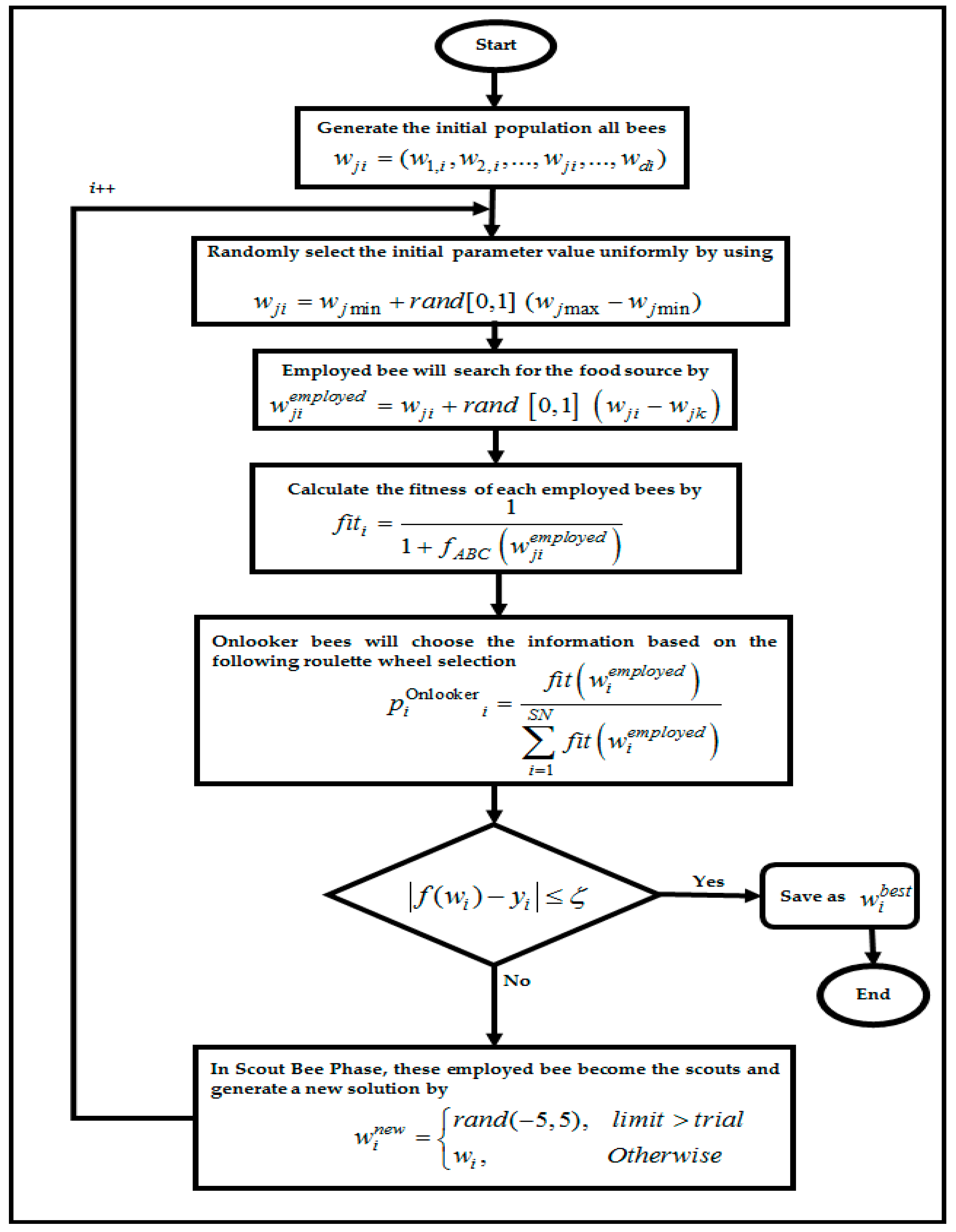
4.4. Artificial Bee Colony Algorithm in RBFNN-2SATRA
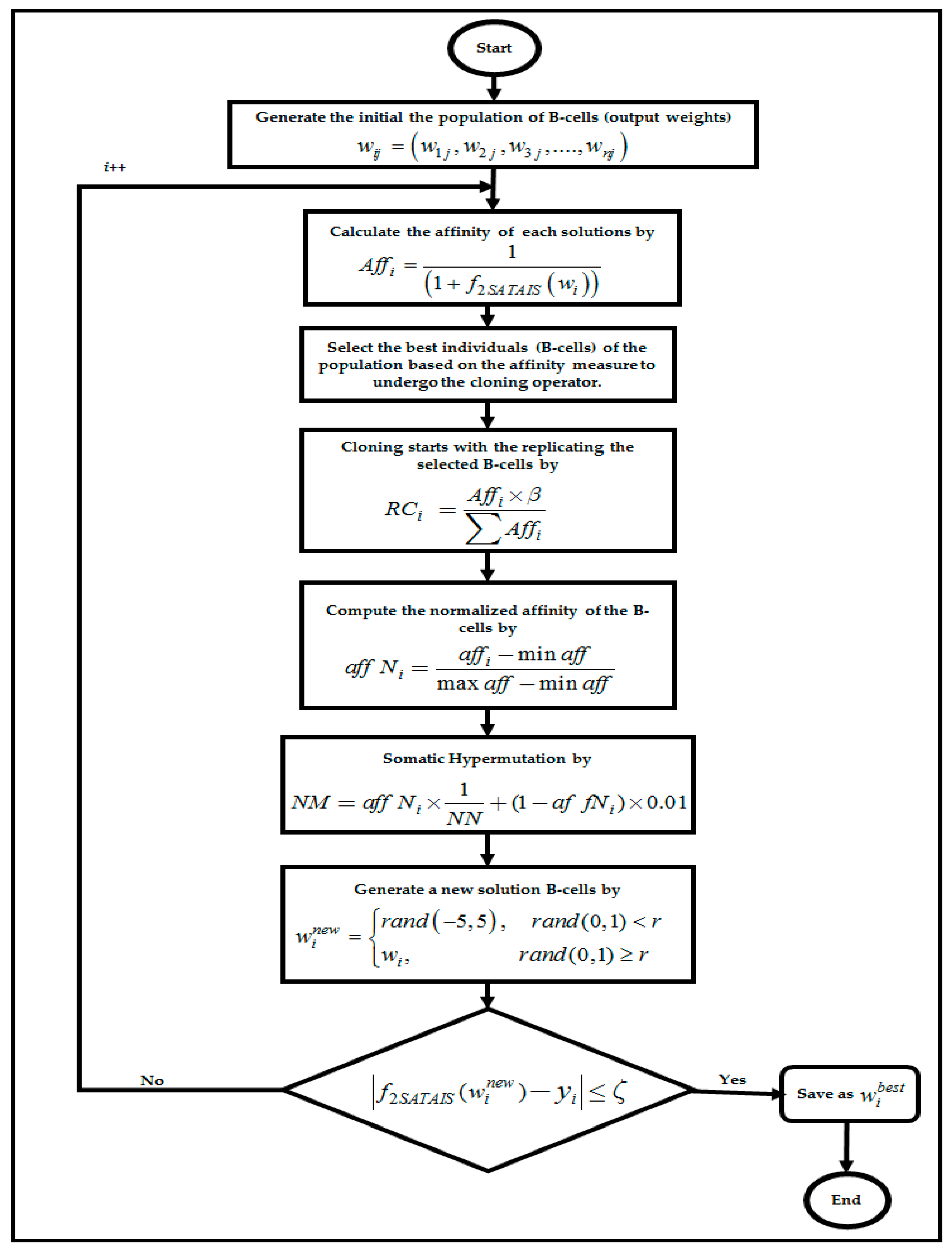
4.5. Artificial Immune System Algorithm in RBFNN-2SATRA
5. Experimental Setup
6. Datasets Description
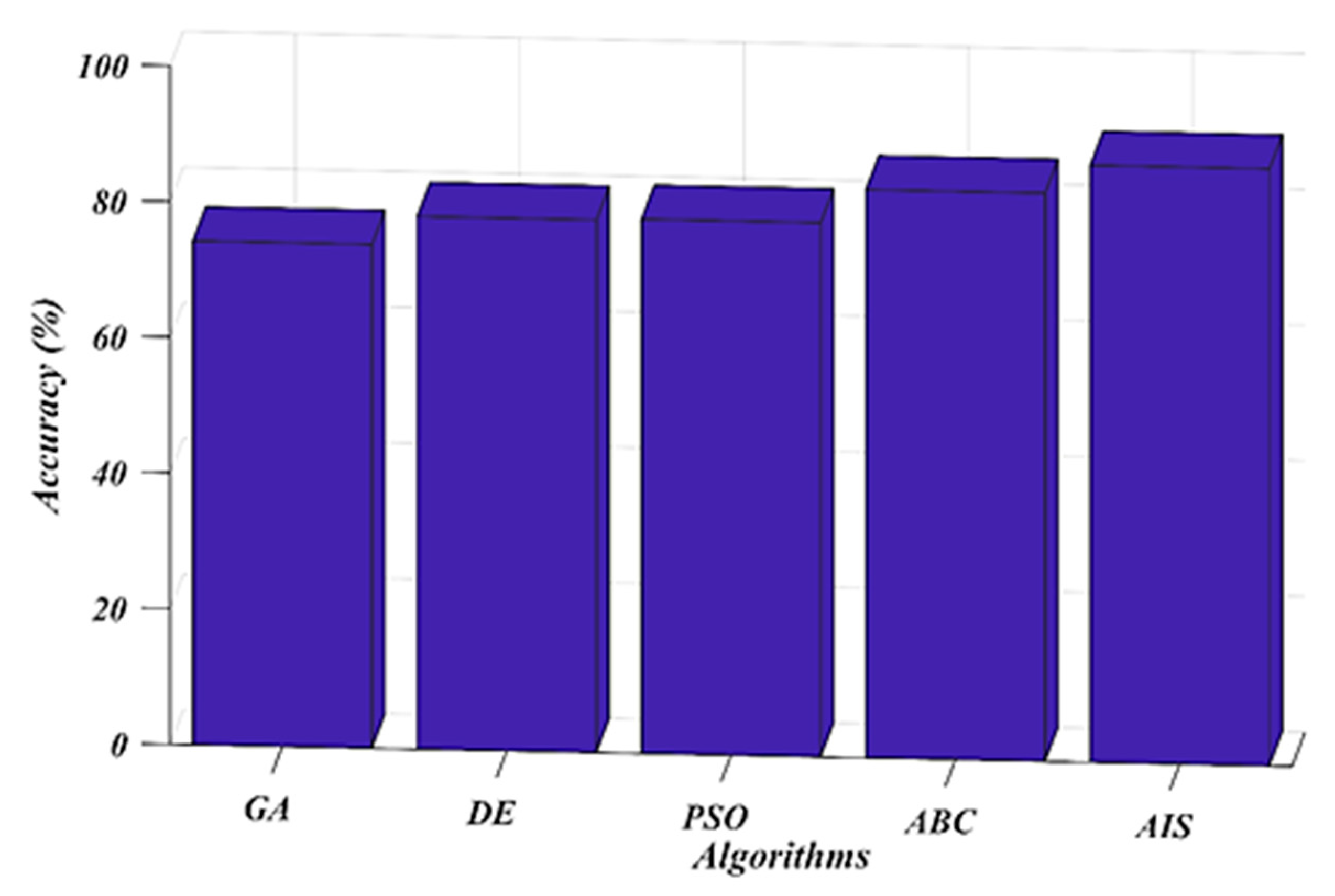
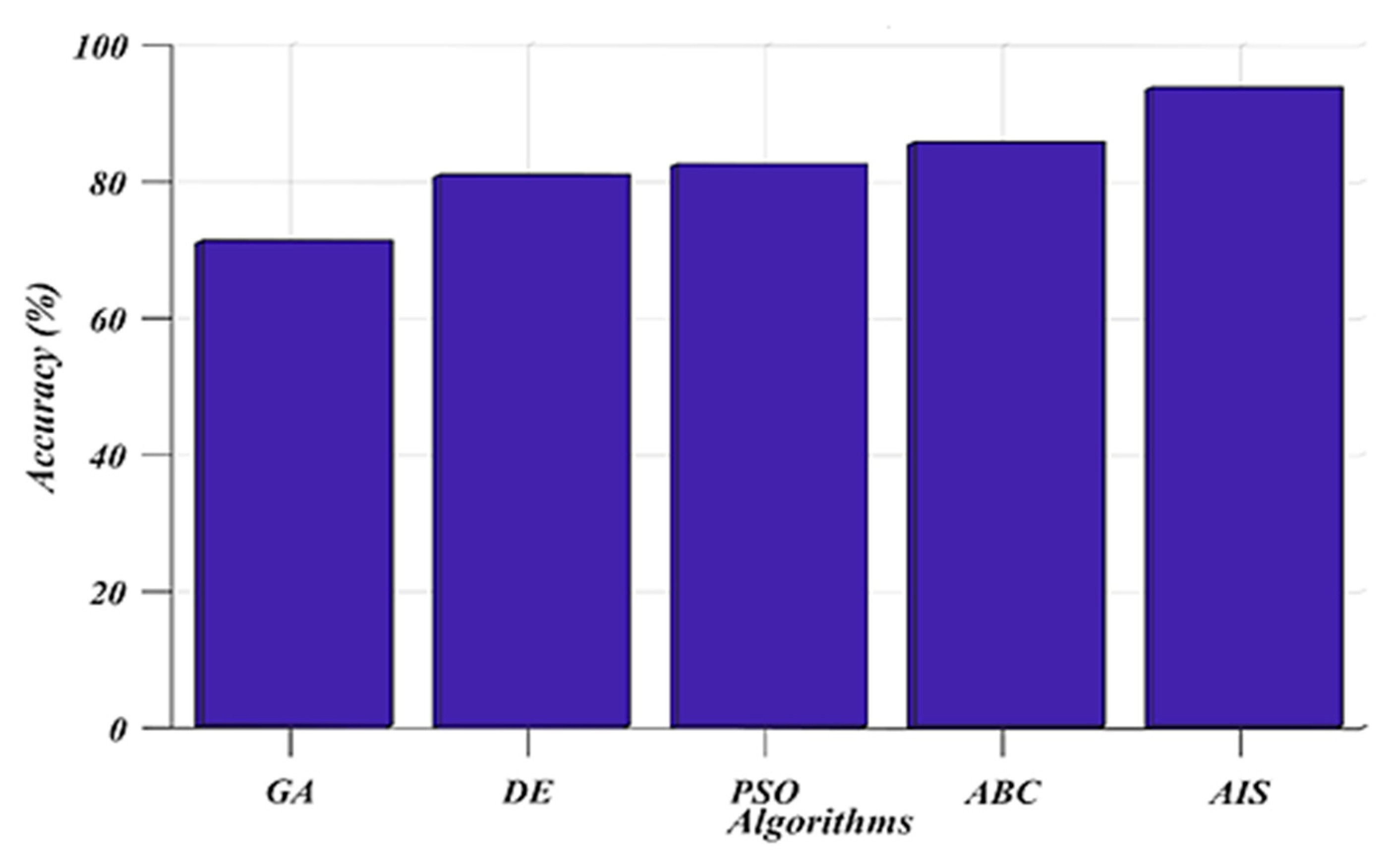
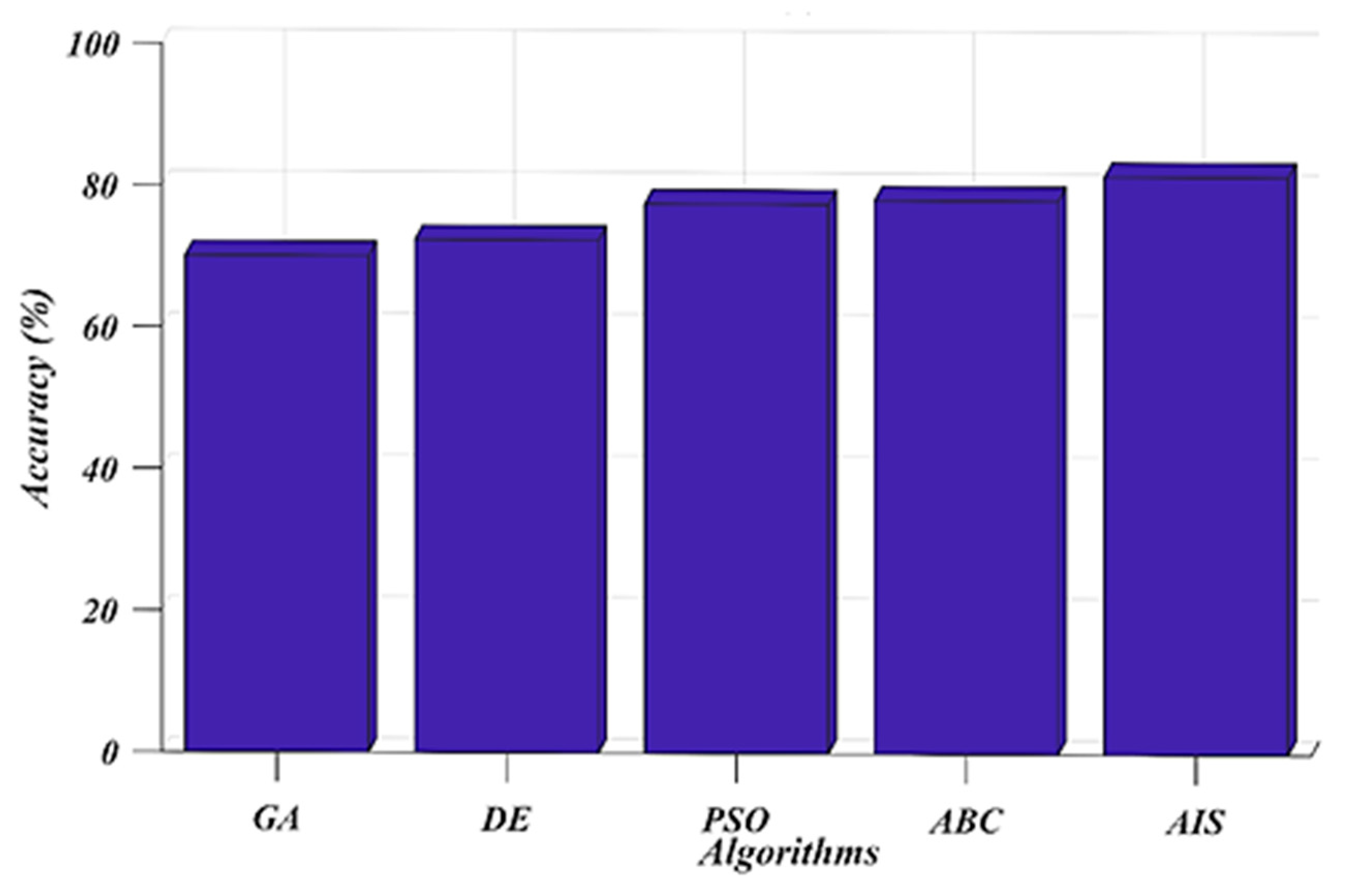
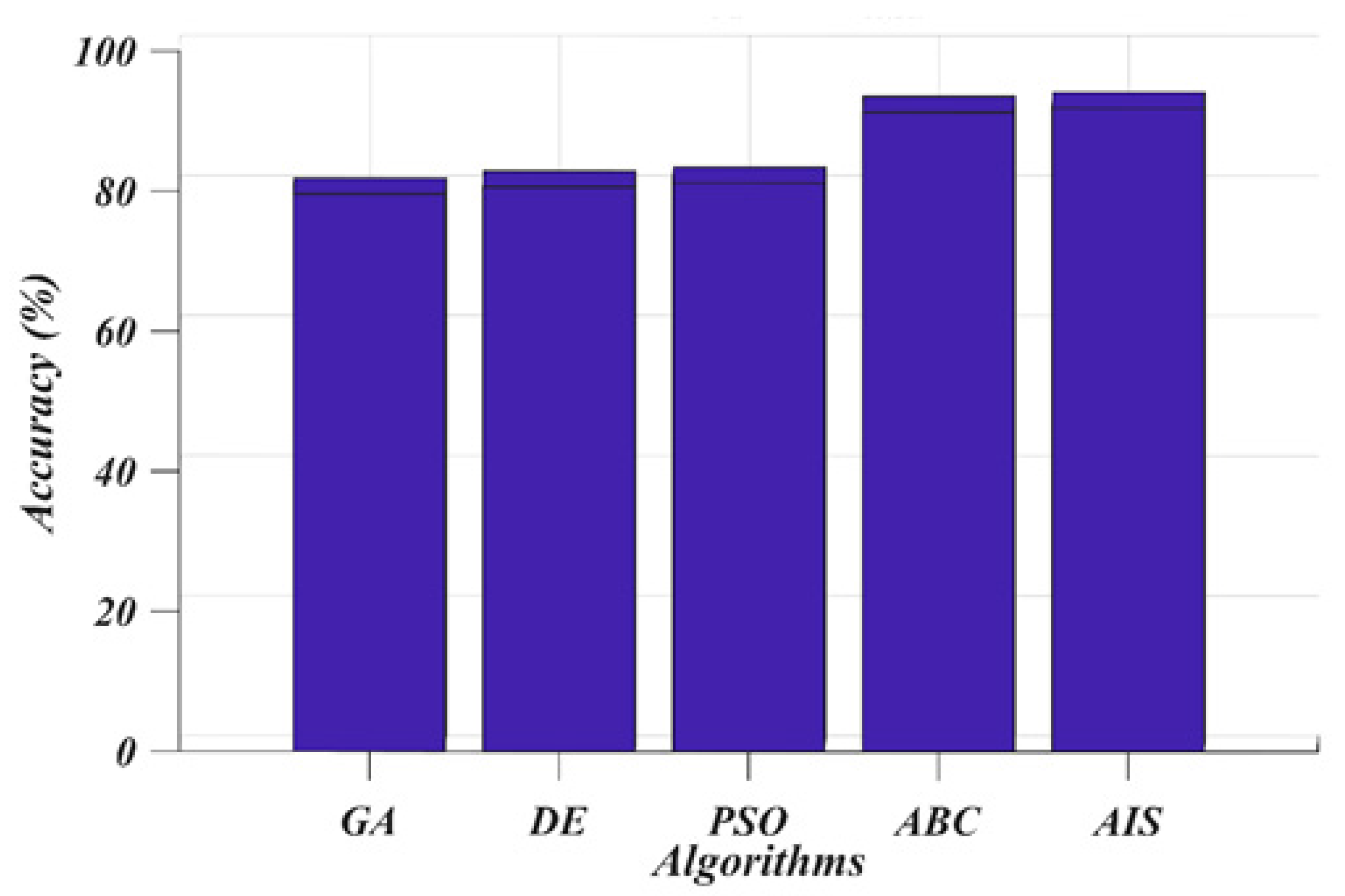
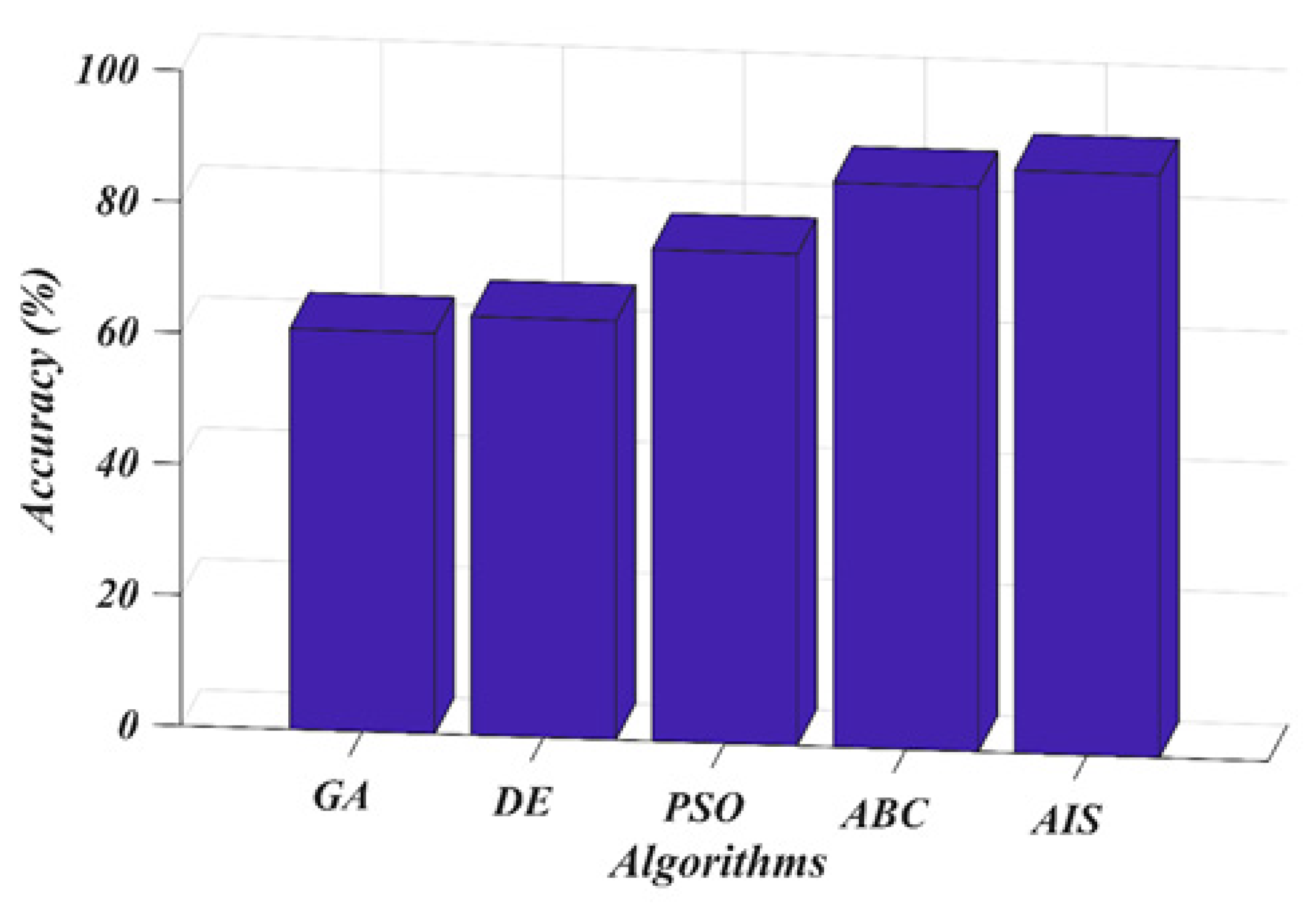
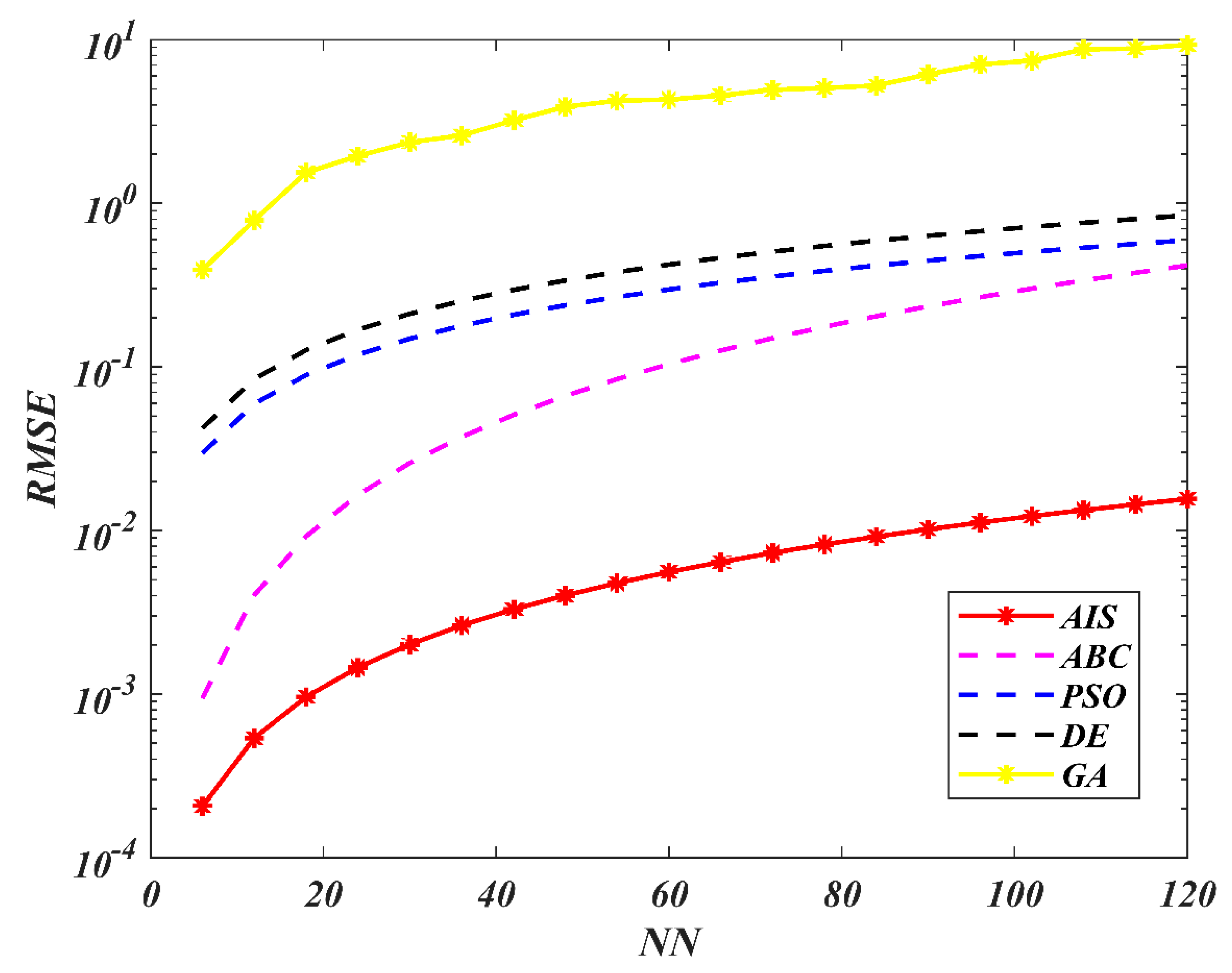
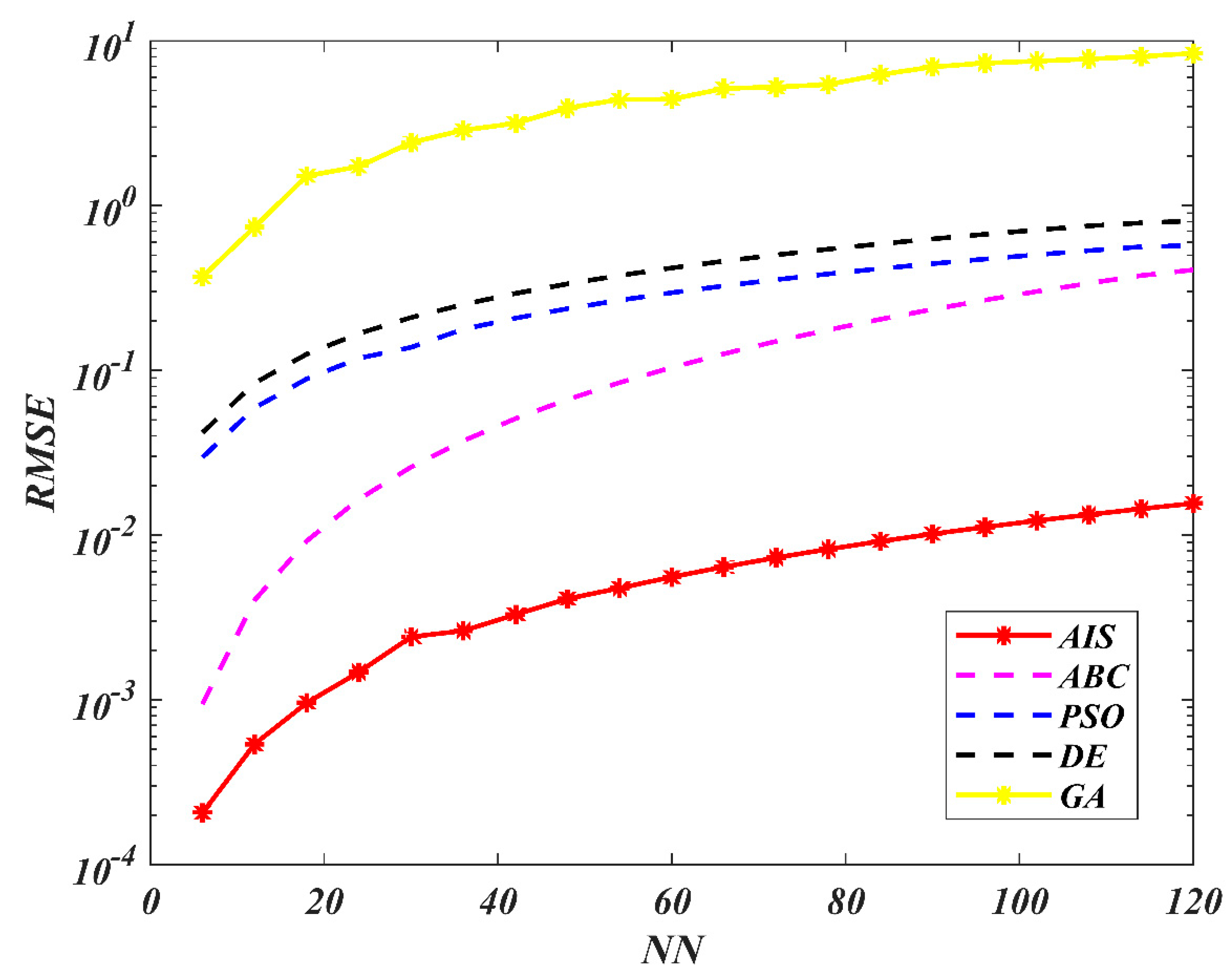
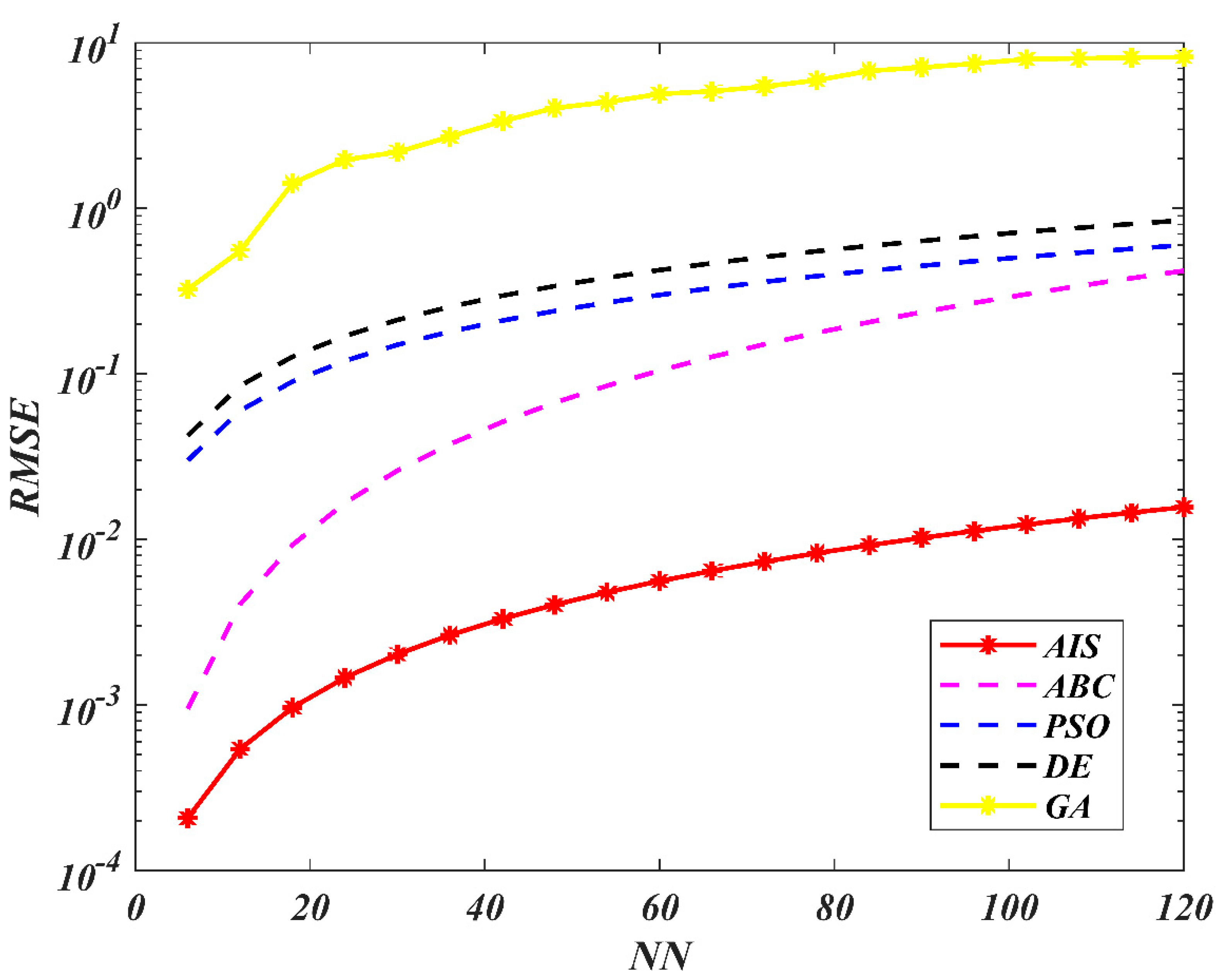
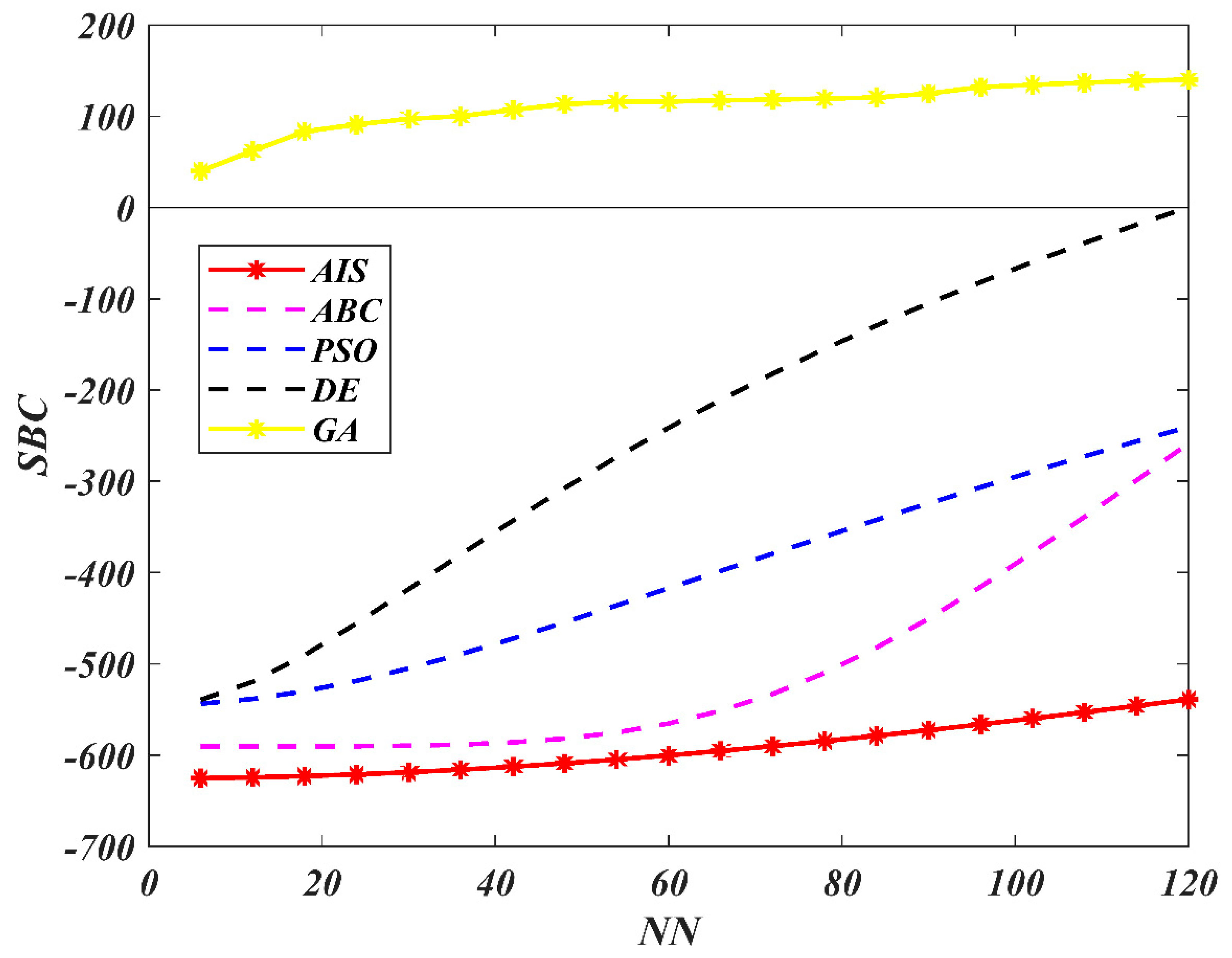
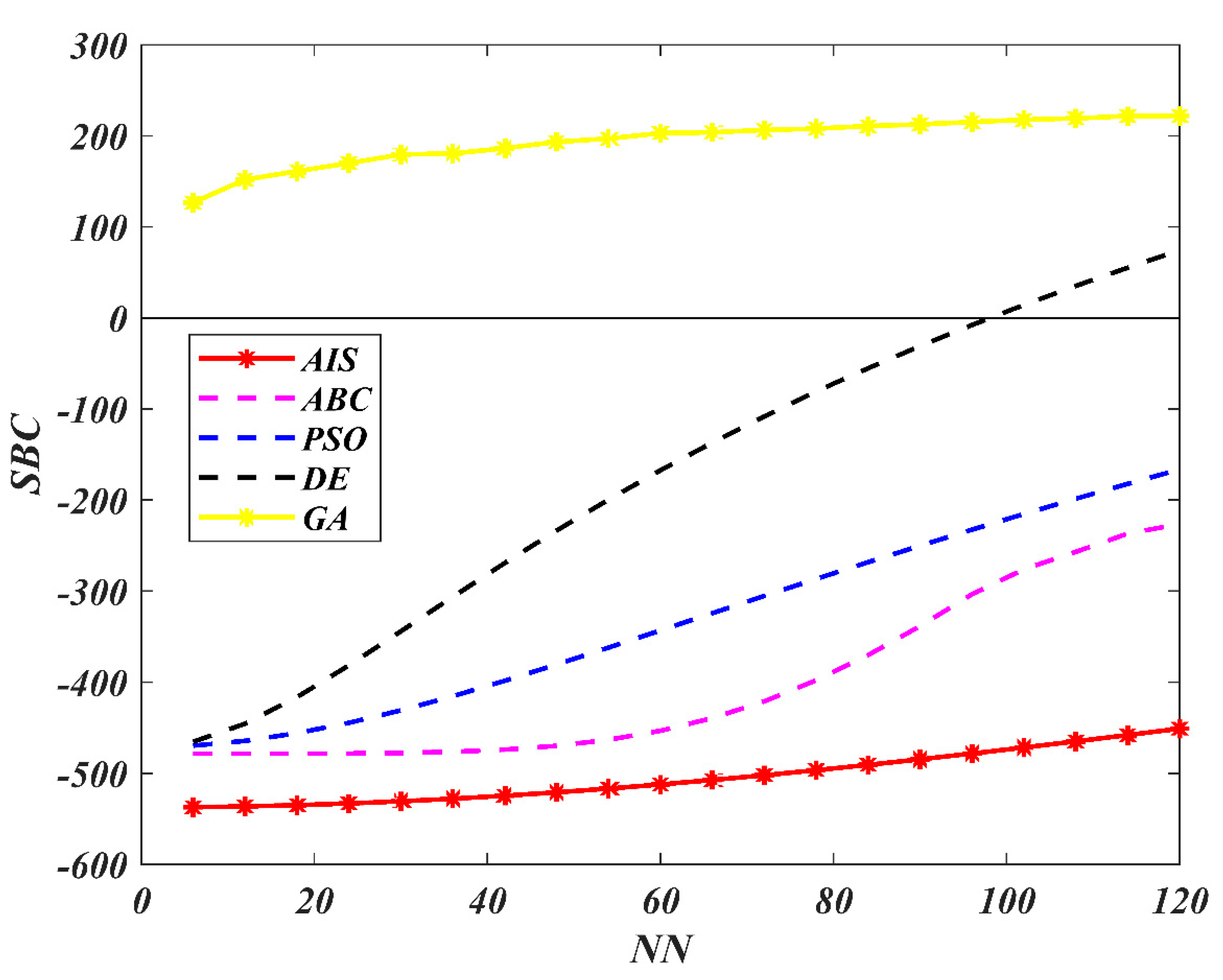
7. Results and Discussion
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, Z.; He, G.; Li, M.; Ma, L.; Chen, Q.; Huang, J.; Cao, J.; Feng, S.; Gao, H.; Wang, S. RBF neural network based RFID indoor localization method using artificial immune system. In Proceedings of the 2018 Chinese Control And Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 2837–2842. [Google Scholar]
- Yu, B.; He, X. Training radial basis function networks with differential evolution. In Proceedings of the Institute of Electrical and Electronics Engineers (IEEE) International Conference on Granular Computing, Atlanta, GA, USA, 10–12 May 2006; pp. 157–160. [Google Scholar]
- Moody, J.; Darken, C.J. Fast Learning in Networks of Locally-Tuned Processing Units. Neural Comput. 1989, 1, 281–294. [Google Scholar] [CrossRef]
- Yu, H.; Xie, T.; Paszczynski, S.; Wilamowski, B.M. Advantages of Radial Basis Function Networks for Dynamic System Design. IEEE Trans. Ind. Electron. 2011, 58, 5438–5450. [Google Scholar] [CrossRef]
- Qadir, A.; Gazder, U.; Choudhary, K.U.N. Artificial Neural Network Models for Performance Design of Asphalt Pavements Reinforced with Geosynthetics. Transp. Res. Rec. J. Transp. Res. Board 2020, 0361198120924387. [Google Scholar] [CrossRef]
- Gan, M.; Peng, H.; Dong, X.-P. A hybrid algorithm to optimize RBF network architecture and parameters for nonlinear time series prediction. Appl. Math. Model. 2012, 36, 2911–2919. [Google Scholar] [CrossRef]
- Yu, H.; Reiner, P.D.; Xie, T.; Bartczak, T.; Wilamowski, B.M. An Incremental Design of Radial Basis Function Networks. IEEE Trans. Neural Networks Learn. Syst. 2014, 25, 1793–1803. [Google Scholar] [CrossRef] [PubMed]
- Dash, C.S.K.; Saran, A.; Sahoo, P.; Dehuri, S.; Cho, S.-B. Design of self-adaptive and equilibrium differential evolution optimized radial basis function neural network classifier for imputed database. Pattern Recognit. Lett. 2016, 80, 76–83. [Google Scholar] [CrossRef]
- Yang, J.; Ma, J. Feed-forward neural network training using sparse representation. Expert Syst. Appl. 2019, 116, 255–264. [Google Scholar] [CrossRef]
- Mansor, M.A.; Jamaludin, S.Z.M.; Kasihmuddin, M.S.M.; Alzaeemi, S.A.; Basir, F.M.; Sathasivam, S. Systematic Boolean Satisfiability Programming in Radial Basis Function Neural Network. Processes 2020, 8, 214. [Google Scholar] [CrossRef]
- Alzaeemi, S.A.; Mansor, M.A.; Kasihmuddin, M.S.M.; Sathasivam, S.; Mamat, M. Radial basis function neural network for 2 satisfiability programming. Indones. J. Electr. Eng. Comput. Sci. 2020, 18, 459–469. [Google Scholar] [CrossRef]
- Kasihmuddin, M.S.B.M.; Bin Mansor, M.A.; Alzaeemi, S.A.; Sathasivam, S. Satisfiability Logic Analysis Via Radial Basis Function Neural Network with Artificial Bee Colony Algorithm. Int. J. Interact. Multimedia Artif. Intell. 2020. [Google Scholar] [CrossRef]
- Hamadneh, N.; Sathasivam, S.; Choon, O.H. Higher order logic programming in radial basis function neural network. Appl. Math. Sci. 2012, 6, 115–127. [Google Scholar]
- Hamadneh, N.; Sathasivam, S.; Tilahun, S.L.; Choon, O.H. Satisfiability of logic programming based on radial basis function neural networks. In Proceedings of the 21ST NATIONAL SYMPOSIUM ON MATHEMATICAL SCIENCES (SKSM21): Germination of Mathematical Sciences Education and Research towards Global Sustainability, Penang, Malaysia, 6–8 November 2013; pp. 547–550. [Google Scholar] [CrossRef]
- Sathasivam, S.; Abdullah, W.A.T.W. Logic mining in neural network: Reverse analysis method. Computing 2010, 91, 119–133. [Google Scholar] [CrossRef]
- Kho, L.C.; Kasihmuddin, M.S.M.; Mansor, M.; Sathasivam, S. Logic Mining in League of Legends. Pertanika J. Sci. Technol. 2020, 28, 211–225. [Google Scholar]
- Alway, A.; Zamri, N.E.; Kasihmuddin, M.S.M.; Mansor, M.A.; Sathasivam, S. Palm Oil Trend Analysis via Logic Mining with Discrete Hopfield Neural Network. Pertanika J. Sci. Technol. 2020, 28, 967–981. [Google Scholar]
- Zamri, N.E.; Mansor, M.A.; Kasihmuddin, M.S.M.; Alway, A.; Jamaludin, S.Z.M.; Alzaeemi, S.A. Amazon Employees Resources Access Data Extraction via Clonal Selection Algorithm and Logic Mining Approach. Entropy 2020, 22, 596. [Google Scholar] [CrossRef]
- Kasihmuddin, M.S.M.; Mansor, M.A.; Jamaludin, S.Z.M.; Sathasivam, S. Systematic Satisfiability Programming in Hopfield Neural Network-A Hybrid Expert System for Medical Screening. Comput. Appl. Math. 2020, 2, 1–6. [Google Scholar]
- Mansor, M.A.; Sathasivam, S.; Kasihmuddin, M.S.M. Artificial immune system algorithm with neural network approach for social media performance metrics. In Proceedings of the 25TH NATIONAL SYMPOSIUM ON MATHEMATICAL SCIENCES (SKSM25): Mathematical Sciences as the Core of Intellectual Excellence, Pahang, Malaysia, 27–29 August 2017. [Google Scholar] [CrossRef]
- Hamadneh, N.; Sathasivam, S.; Tilahun, S.L.; Choon, O.H. Learning Logic Programming in Radial Basis Function Network via Genetic Algorithm. J. Appl. Sci. 2012, 12, 840–847. [Google Scholar] [CrossRef]
- Ayala, H.V.H.; Coelho, L.D.S. Cascaded evolutionary algorithm for nonlinear system identification based on correlation functions and radial basis functions neural networks. Mech. Syst. Signal Process. 2016, 68, 378–393. [Google Scholar] [CrossRef]
- Karaboga, D.; Kaya, E. Training ANFIS by Using an Adaptive and Hybrid Artificial Bee Colony Algorithm (aABC) for the Identification of Nonlinear Static Systems. Arab. J. Sci. Eng. 2018, 44, 3531–3547. [Google Scholar] [CrossRef]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic Algorithms and the Optimal Allocation of Trials. SIAM J. Comput. 1973, 2, 88–105. [Google Scholar] [CrossRef]
- Dandagwhal, R.D.; Kalyankar, V.D. Design Optimization of Rolling Element Bearings Using Advanced Optimization Technique. Arab. J. Sci. Eng. 2019, 44, 7407–7422. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Holland, J.H. Genetic Algorithms and Machine Learning. Mach. Learn. 1988, 3, 95–99. [Google Scholar] [CrossRef]
- Pandey, M.; Zakwan, M.; Sharma, P.K.; Ahmad, Z. Multiple linear regression and genetic algorithm approaches to predict temporal scour depth near circular pier in non-cohesive sediment. ISH J. Hydraul. Eng. 2018, 26, 1–8. [Google Scholar] [CrossRef]
- Jing, Z.; Chen, J.; Li, X. RBF-GA: An adaptive radial basis function metamodeling with genetic algorithm for structural reliability analysis. Reliab. Eng. Syst. Saf. 2019, 189, 42–57. [Google Scholar] [CrossRef]
- Ilonen, J.; Kamarainen, J.-K.; Lampinen, J. Differential Evolution Training Algorithm for Feed-Forward Neural Networks. Neural Process. Lett. 2003, 17, 93–105. [Google Scholar] [CrossRef]
- Saha, A.; Konar, A.; Rakshit, P.; Ralescu, A.L.; Nagar, A. Olfaction recognition by EEG analysis using differential evolution induced Hopfield neural net. In Proceedings of the 2013 International Joint Conference on Neural Networks (IJCNN), Dallas, TX, USA, 4–9 August 2013; pp. 1–8. [Google Scholar] [CrossRef]
- Chauhan, N.; Ravi, V.; Chandra, D.K. Differential evolution trained wavelet neural networks: Application to bankruptcy prediction in banks. Expert Syst. Appl. 2009, 36, 7659–7665. [Google Scholar] [CrossRef]
- Tao, W.; Chen, J.; Gui, Y.; Kong, P. Coking energy consumption radial basis function prediction model improved by differential evolution algorithm. Meas. Control. 2019, 52, 1122–1130. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the MHS’95. Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Qasem, S.N.; Shamsuddin, S.M.H. Improving performance of radial basis function network based with particle swarm optimization. In Proceedings of the 2009 IEEE Congress on Evolutionary Computation, Trondheim, Norway, 18–21 May 2009; pp. 3149–3156. [Google Scholar] [CrossRef]
- Alexandridis, A.; Chondrodima, E.; Sarimveis, H. Cooperative learning for radial basis function networks using particle swarm optimization. Appl. Soft Comput. 2016, 49, 485–497. [Google Scholar] [CrossRef]
- Tsekouras, G.E.; Trygonis, V.; Maniatopoulos, A.; Rigos, A.; Chatzipavlis, A.; Tsimikas, J.; Mitianoudis, N.; Velegrakis, A. A Hermite neural network incorporating artificial bee colony optimization to model shoreline realignment at a reef-fronted beach. Neurocomputing 2018, 280, 32–45. [Google Scholar] [CrossRef]
- Kasihmuddin, M.S.M.; Mansor, M.; Sathasivam, S. Robust Artificial Bee Colony in the Hopfield Network for 2-Satisfiability Problem. Pertanika J. Sci. Technol. 2017, 25, 453–468. [Google Scholar]
- Kurban, T.; Besdok, E. A Comparison of RBF Neural Network Training Algorithms for Inertial Sensor Based Terrain Classification. Sensors 2009, 9, 6312–6329. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Duan, H. Artificial Bee Colony approach to information granulation-based fuzzy radial basis function neural networks for image fusion. Optik 2013, 124, 3103–3111. [Google Scholar] [CrossRef]
- Jafrasteh, B.; Fathianpour, N. A hybrid simultaneous perturbation artificial bee colony and back-propagation algorithm for training a local linear radial basis neural network on ore grade estimation. Neurocomputing 2017, 235, 217–227. [Google Scholar] [CrossRef]
- Satapathy, S.K.; Dehuri, S.; Jagadev, A.K. ABC optimized RBF network for classification of EEG signal for epileptic seizure identification. Egypt. Informatics J. 2017, 18, 55–66. [Google Scholar] [CrossRef]
- Aljarah, I.; Faris, H.; Mirjalili, S.; Al-Madi, N. Training radial basis function networks using biogeography-based optimizer. Neural Comput. Appl. 2016, 29, 529–553. [Google Scholar] [CrossRef]
- Jiang, S.; Lu, C.; Zhang, S.; Lu, X.; Tsai, S.-B.; Wang, C.-K.; Gao, Y.; Shi, Y.; Lee, C.-H. Prediction of Ecological Pressure on Resource-Based Cities Based on an RBF Neural Network Optimized by an Improved ABC Algorithm. IEEE Access 2019, 7, 47423–47436. [Google Scholar] [CrossRef]
- Menad, N.A.; Hemmati-Sarapardeh, A.; Varamesh, A.; Shamshirband, S. Predicting solubility of CO2 in brine by advanced machine learning systems: Application to carbon capture and sequestration. J. CO2 Util. 2019, 33, 83–95. [Google Scholar] [CrossRef]
- Dasgupta, D. (Ed.) Chapter Title. In Artificial Immune Systems and Their Applications; Springer Science and Business Media LLC: Berlin, Germany, 1999. [Google Scholar]
- De Castro, L.; Von Zuben, C.J.; De Castro, L.N. Learning and optimization using the clonal selection principle. IEEE Trans. Evol. Comput. 2002, 6, 239–251. [Google Scholar] [CrossRef]
- Hunt, J.E.; Cooke, D.E. Learning using an artificial immune system. J. Netw. Comput. Appl. 1996, 19, 189–212. [Google Scholar] [CrossRef]
- Layeb, A. A Clonal Selection Algorithm Based Tabu Search for Satisfiability Problems. J. Adv. Inf. Technol. 2012, 3, 138–146. [Google Scholar] [CrossRef]
- Valarmathy, S.; Ramani, R. Evaluating the Efficiency of Radial Basis Function Classifier with Different Feature Selection for Identifying Dementia. J. Comput. Theor. Nanosci. 2019, 16, 627–632. [Google Scholar] [CrossRef]
- Hamadneh, N. Grey Optimization Problems Using Prey-Predator Algorithm. In Advances in Data Mining and Database Management; IGI Global: Hershey, PA, USA, 2018; pp. 31–46. [Google Scholar]
- Mansor, M.; Kasihmuddin, M.S.M.; Sathasivam, S. Artificial Immune System Paradigm in the Hopfield Network for 3-Satisfiability Problem. Pertanika J. Sci. Technol. 2017, 25, 1173–1188. [Google Scholar]
- Dua, D.; Graff, C. UCI Machine Learning Repository. 2017. Available online: http://archive.ics.uci.edu/ml (accessed on 24 September 2018).
- Kasihmuddin, M.S.M.; Mansor, M.; Sathasivam, S. Artificial Bee Colony in the Hopfield Network for Maximum k-Satisfiability Problem. J. Inform. Math. Sci. 2016, 8, 317–334. [Google Scholar]
- Miyashiro, R.; Matsui, T. A polynomial-time algorithm to find an equitable home–away assignment. Oper. Res. Lett. 2005, 33, 235–241. [Google Scholar] [CrossRef]
- Even, S.; Itai, A.; Shamir, A. On the complexity of time table and multi-commodity flow problems. In Proceedings of the 16th Annual Symposium on Foundations of Computer Science (sfcs 1975), Berkeley, CA, USA, 13–15 October 1975; pp. 184–193. [Google Scholar] [CrossRef]
- Mukherjee, S.; Roy, S.; Shyamapada, M. Multi terminal net routing for island style FPGAs using nearly-2-SAT computation. In Proceedings of the 2015 19th International Symposium on VLSI Design and Test, Ahmedabad, India, 26–29 June 2015; pp. 1–6. [Google Scholar] [CrossRef]
- De Leon-Delgado, H.; Praga-Alejo, R.J.; González-González, D.S.; Cantú-Sifuentes, M. Multivariate statistical inference in a radial basis function neural network. Expert Syst. Appl. 2018, 93, 313–321. [Google Scholar] [CrossRef]
- Idri, A.; Zakrani, A.; Zahi, A. Design of radial basis function neural networks for software effort estimation. In Proceedings of the 11th International Design Conference—DESIGN 2010, Zagreb, Croatia, 17–20 May 2010; pp. 513–519. [Google Scholar]
- Kopal, I.; Harničárová, M.; Valíček, J.; Krmela, J.; Lukáč, O. Radial Basis Function Neural Network-Based Modeling of the Dynamic Thermo-Mechanical Response and Damping Behavior of Thermoplastic Elastomer Systems. Polymers 2019, 11, 1074. [Google Scholar] [CrossRef]
- Hamadneh, N.; Sathasivam, S. Solving Satisfiability Logic Programming Using Radial Basis Function Neural Networks. J. Eng. Appl. Sci. 2017, 4, 1–7. [Google Scholar] [CrossRef]
- Friedrichs, F.; Schmitt, M. On the power of Boolean computations in generalized RBF neural networks. Neurocomputing 2005, 63, 483–498. [Google Scholar] [CrossRef]
- Awad, M. Optimization RBFNNs parameters using genetic algorithms: Applied on function approximation. IJCSS 2010, 4, 295–307. [Google Scholar]
- Eshelman, L.J.; Schaffer, J.D. Real-Coded Genetic Algorithms and Interval-Schemata. In Foundations of Genetic Algorithms; Whitley, L.D., Ed.; Elsevier B.V.: Amsterdam, The Netherlands, 1993; Volume 2, pp. 187–202. [Google Scholar]
- Wang, S.L.; Morsidi, F.; Ng, T.F.; Budiman, H.; Neoh, S.C. Insights into the effects of control parameters and mutation strategy on self-adaptive ensemble-based differential evolution. Inf. Sci. 2020, 514, 203–233. [Google Scholar] [CrossRef]
- Opara, K.R.; Arabas, J. Differential Evolution: A survey of theoretical analyses. Swarm Evol. Comput. 2019, 44, 546–558. [Google Scholar] [CrossRef]
- Fukuyama, Y.; Yoshida, H. A particle swarm optimization for reactive power and voltage control in electric power systems. In Proceedings of the 2001 Congress on Evolutionary Computation (IEEE Cat No 01TH8546), Seoul, Korea, 27–30 May 2001; Volume 1, pp. 87–93. [Google Scholar] [CrossRef]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization; Technical Report-TR06; Computer Engineering Department, Engineering Faculty, Erciyes University: Kayseri, Turkey, 2005. [Google Scholar]
- De Castro, L.; Jos, F.; Von Zuben, A.A. Artificial Immune Systems: Part II–A Survey of Applications; Technical Report for University of Campinas School of Electrical and Computer Engineering: Campinas, Brazil, February 2000. [Google Scholar]
- Kasihmuddin, M.S.M.; Sathasivam, S.; Mansor, M.A. Hybrid genetic algorithm in the Hopfield network for maximum 2-satisfiability problem. In Proceedings of the 24th National Symposium on Mathematical Sciences (SKSM24), Terengganu, Malaysia, 27–29 September 2016; p. 050001. [Google Scholar] [CrossRef]
- Mansor, M.A.; Sathasivam, S. Accelerating Activation Function for 3- Satisfiability Logic Programming. Int. J. Intell. Syst. Appl. 2016, 8, 44–50. [Google Scholar] [CrossRef]
- Mansor, M.A.; Sathasivam, S. Performance analysis of activation function in higher order logic programming. ADVANCES IN INDUSTRIAL AND APPLIED MATHEMATICS. Proceedings of 23rd Malaysian National Symposium of Mathematical Sciences (SKSM23), Johor Bahru, Malaysia, 24–26 November 2015. [Google Scholar] [CrossRef]
- Sathasivam, S. Upgrading logic programming in Hopfield network. Sains Malays 2010, 39, 115–118. [Google Scholar]
- Kasihmuddin, M.S.M.; Mansor, M.A.; Sathasivam, S. Discrete Hopfield Neural Network in Restricted Maximum k-Satisfiability Logic Programming. Sains Malays 2018, 47, 1327–1335. [Google Scholar] [CrossRef]
- Lichman, M. UCI Machine Learning Repository. 2013. Available online: http://archive.ics.uci.edu/ml (accessed on 4 April 2013).
- Hamadneh, N. An improvement of radial basis function neural network architecture based on metaheuristic algorithms. Appl. Math. Sci. 2020, 14, 489–497. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |



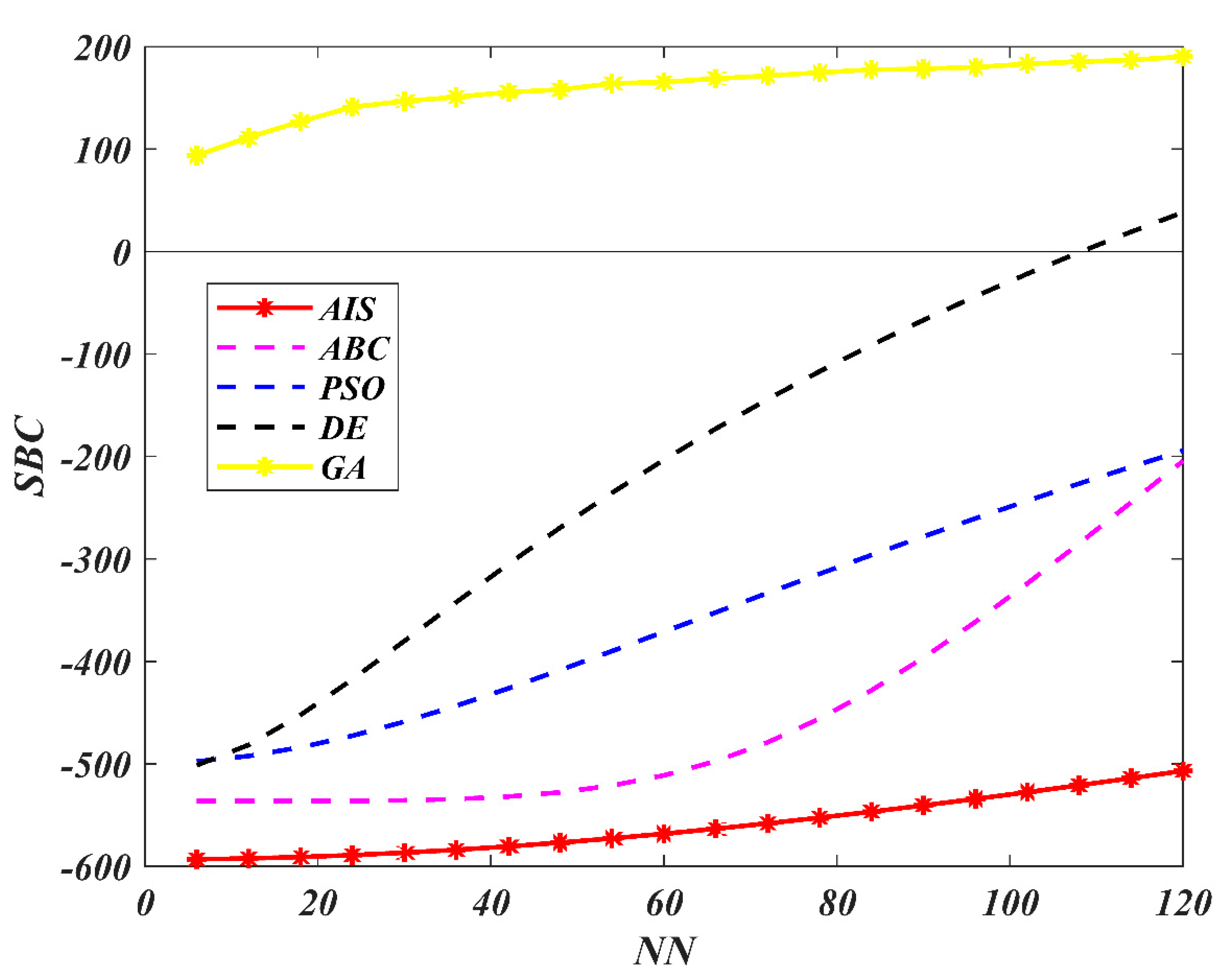
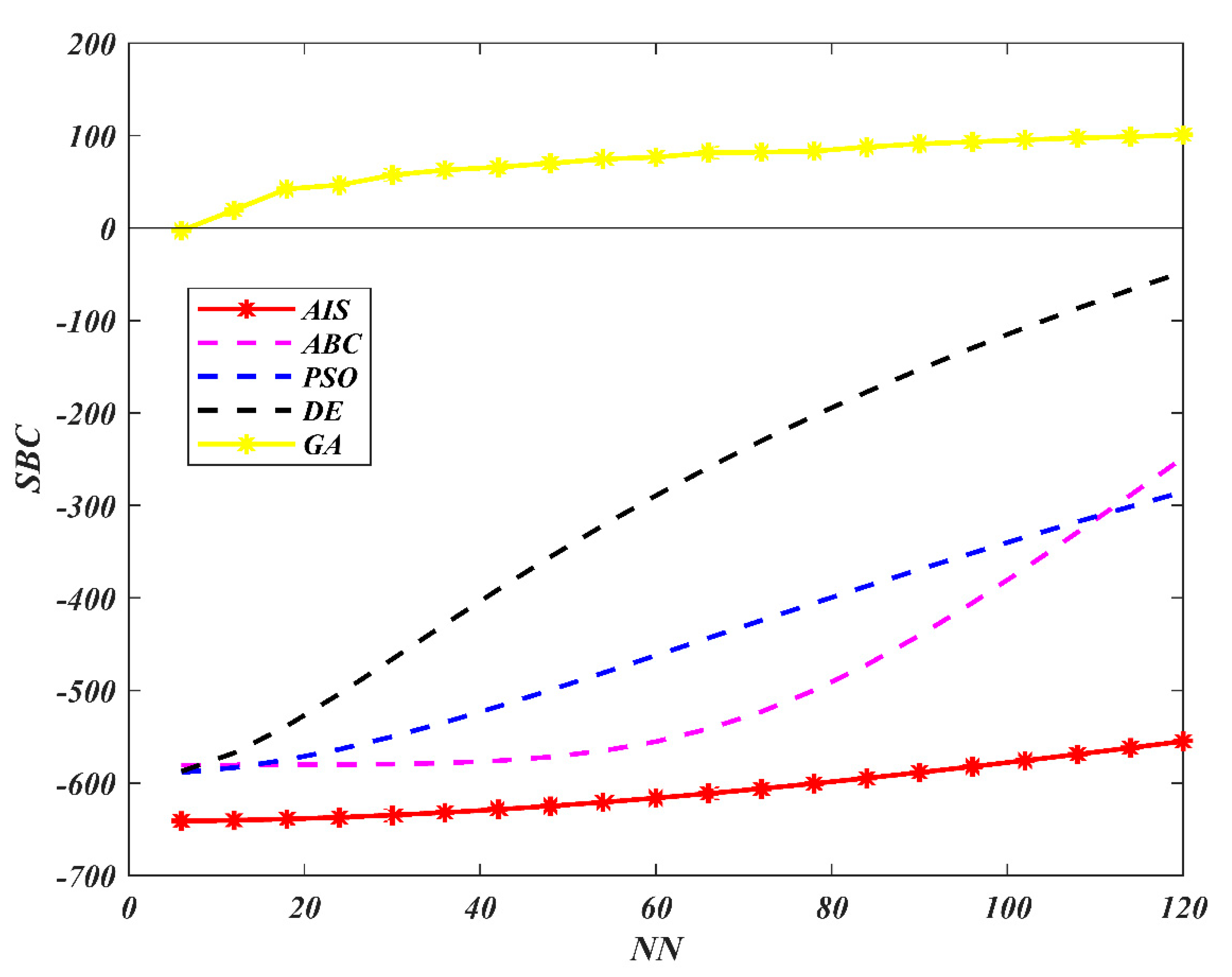
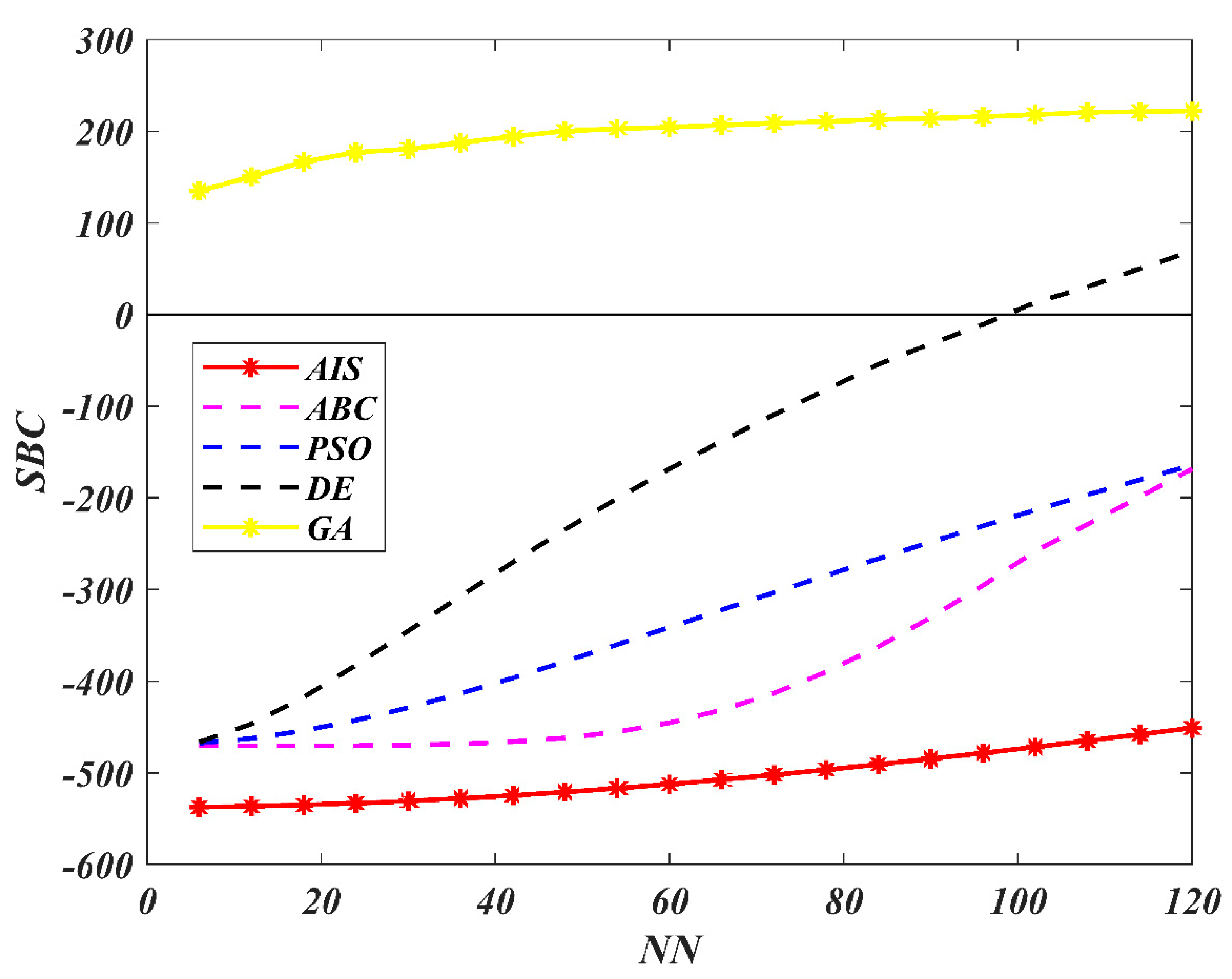
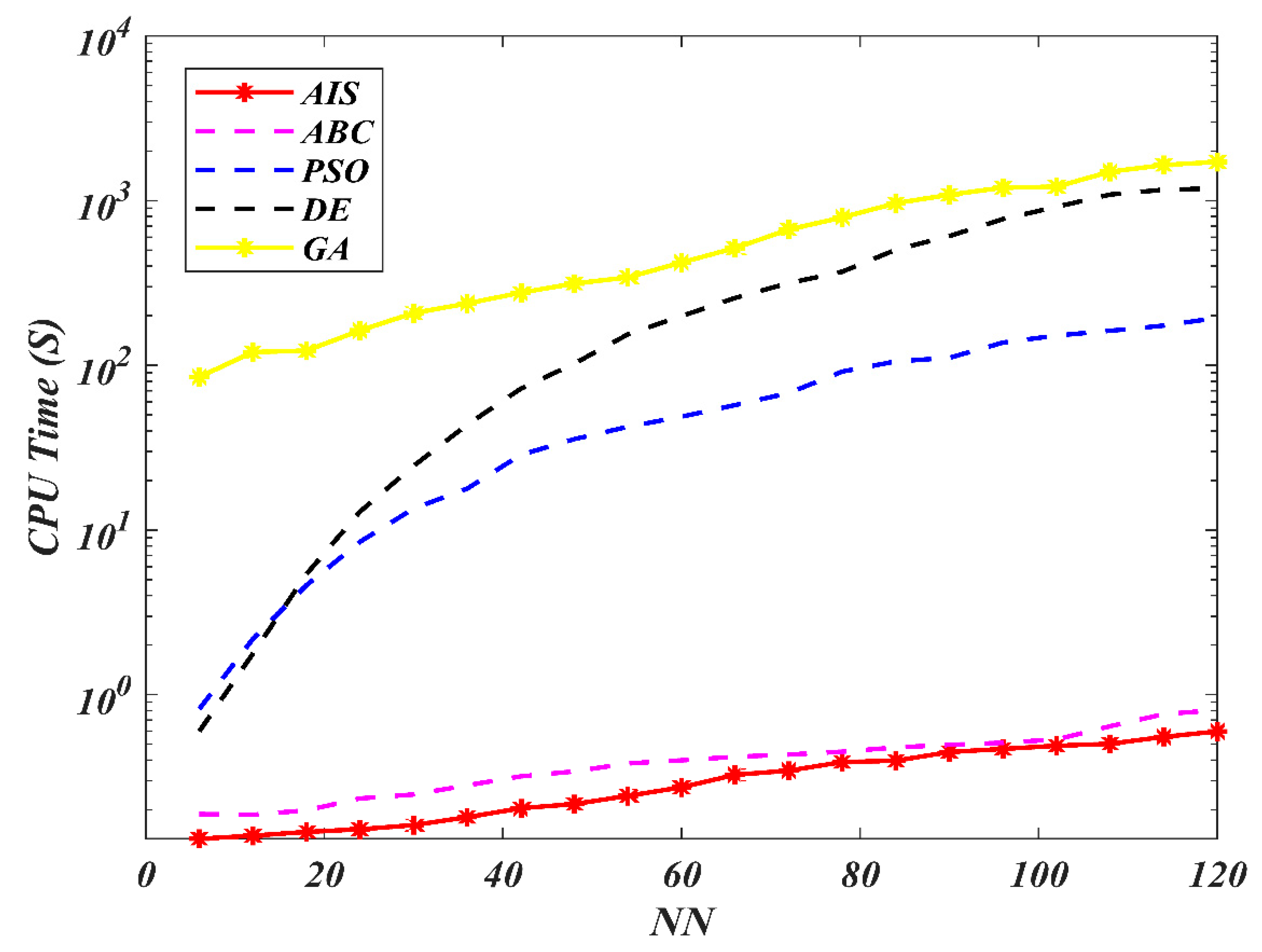
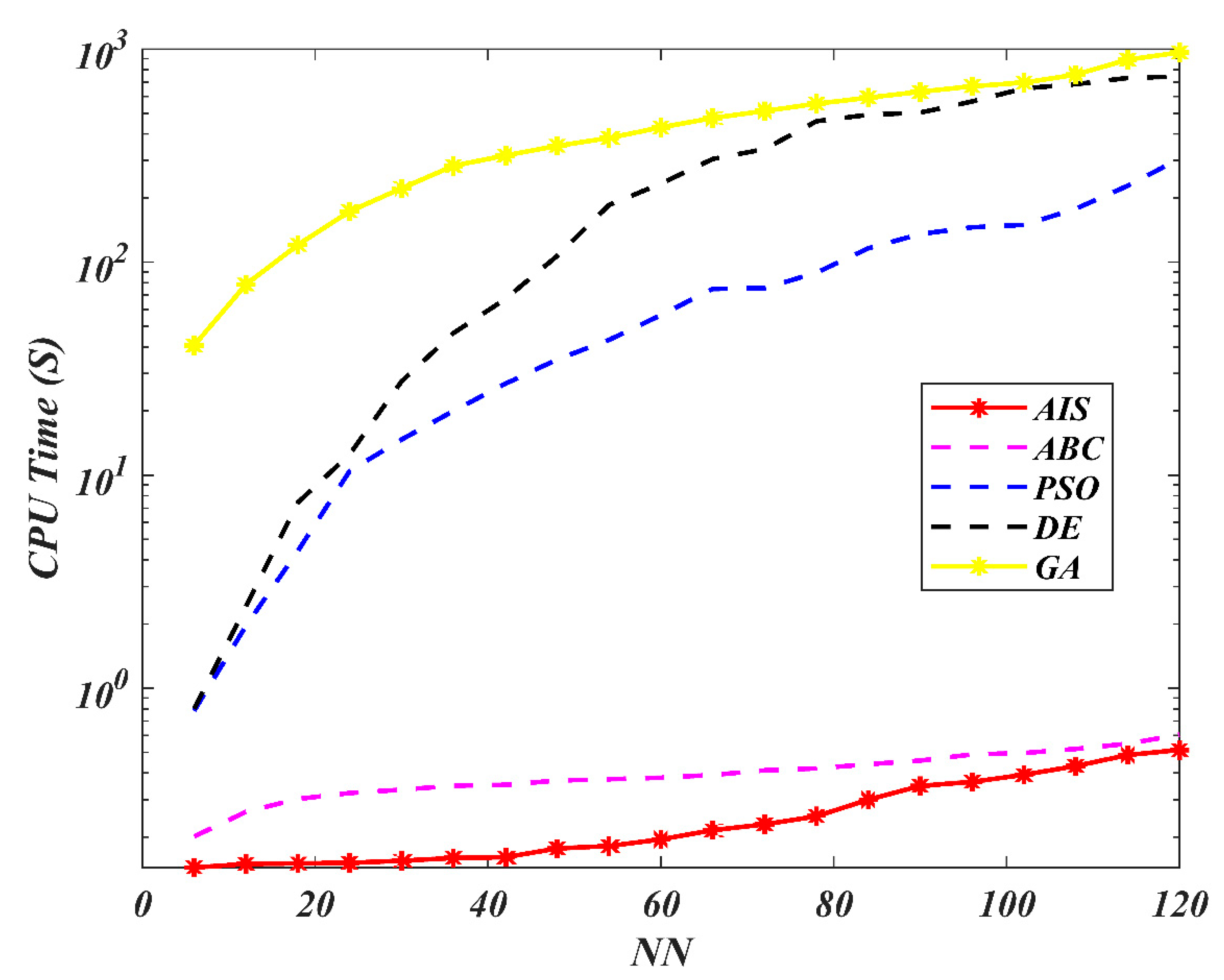
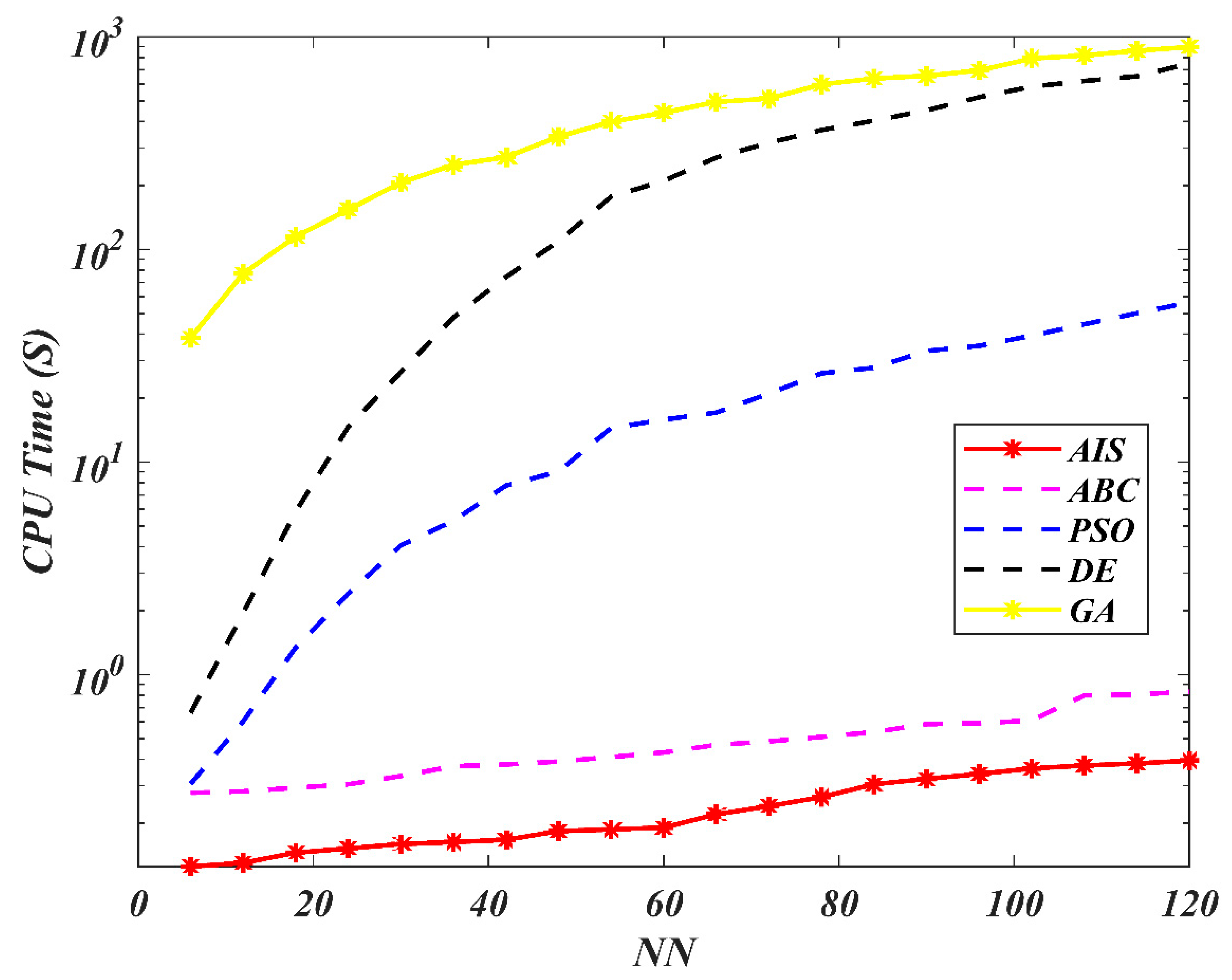
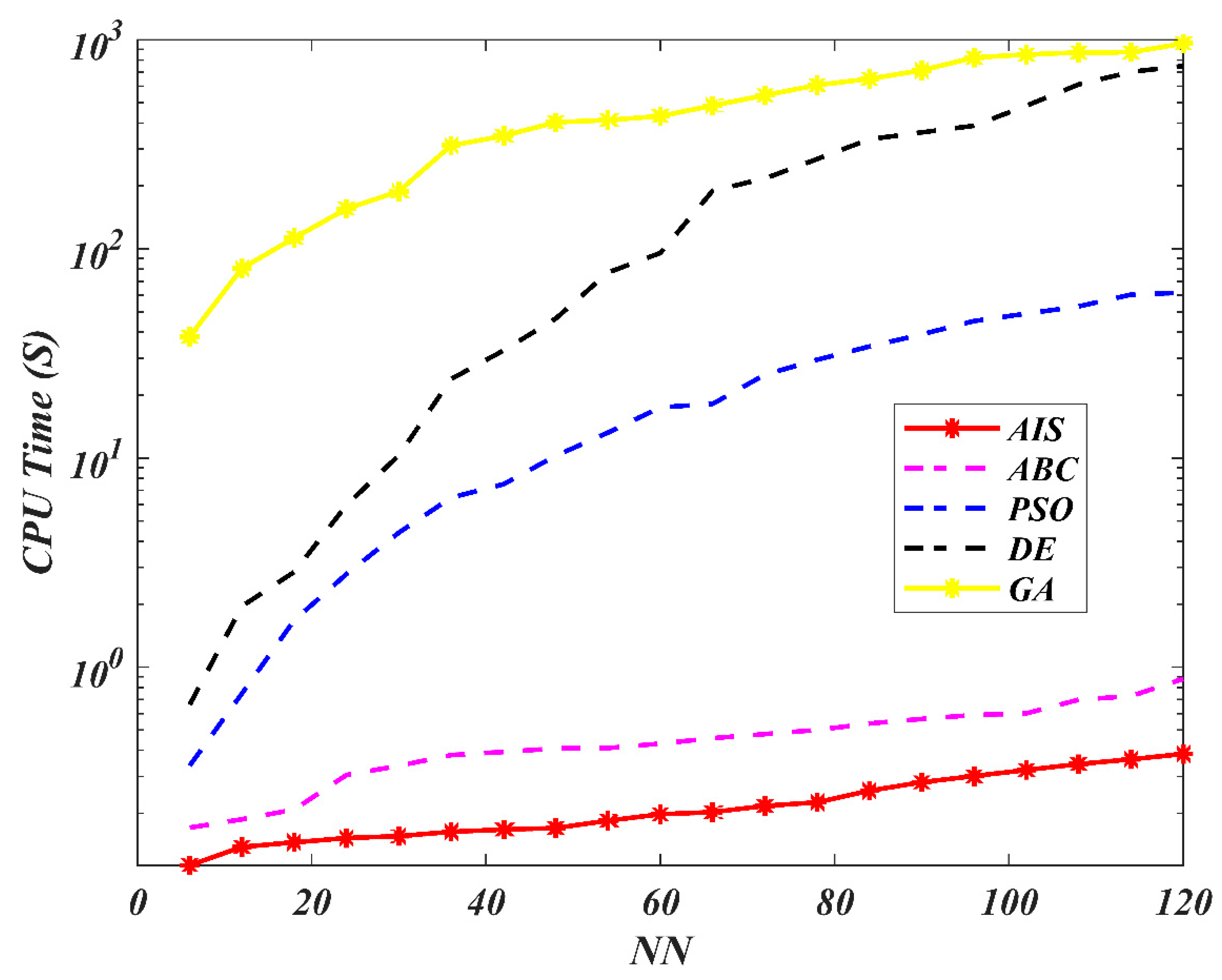
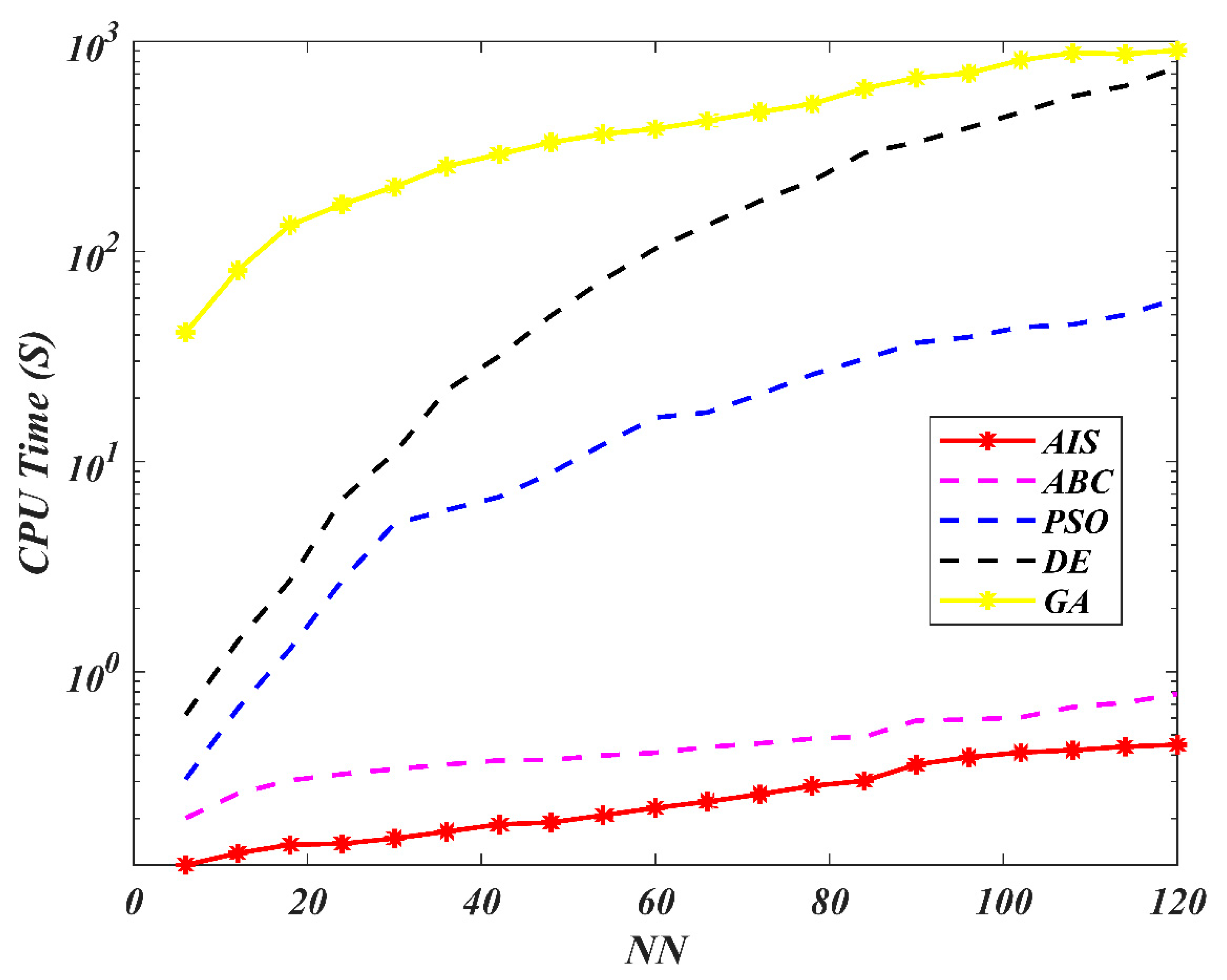
| AIS | ABC | PSO | |||
| Parameter | Value | Parameter | Value | Parameter | Value |
| Number of iteration | 10,000 | No_Employed_bees | 50 | 0.6 | |
| 200 | No_Onlooker_bees | 50 | 2 | ||
| Population size | 100 | No_Scout_bees | 1 | 2 | |
| Limit | 1000 | = | [0,1] | ||
| Trial | 10,000 | Number of iteration | 10,000 | ||
| DE | GA | ||||
| Parameter | Value | Parameter | Value | ||
| Number of iteration | 10,000 | Number of iteration | 10,000 | ||
| [0,1] | Selection type | Wheel selection | |||
| [0,2] | Number of individuals | 50 | |||
| Population | 50 | Mutation ratio | 1 | ||
| Number of iteration | 10,000 | Mutation type | Uniform | ||
| Crossover ratio | 1 | ||||
| Benchmark Datasets | Field | Attributes | Instances | Training Samples | Testing Samples |
|---|---|---|---|---|---|
| German Credit Dataset (GCR) | Finance | Duration of Credit (month) Payment Status of Previous Credit Amount Value Savings/Stocks Length of current employment Installment percent Creditability | 1000 | 600 | 400 |
| Hepatitis Dataset (HR) | Medical | Sex Steroid Antiviral Fatigue Malaise Anorexia Die or live | 155 | 93 | 62 |
| Congressional Voting Records Dataset (CVR) | Social Science | Handicapped infant Water-project-cost-sharing El-Salvador-aid Religious-groups-in-schools Aid-to-Nicaraguan-contras Immigration Rep/demo (P) | 435 | 261 | 174 |
| Car Evaluation Dataset (CE) | Business | Buying Price Maintenance Doors Number Person Number Size Boot Safety Values | 1728 | 1037 | 691 |
| Postoperative Patient Dataset (PP) | Medical | L-CORE (patient’s internal temperature in C) L-SURF (patient’s surface temperature in C) L-O2(oxygen saturation in %) L-BP (last measurement of blood pressure) CORE-STBL (stability of patient’s core temperature) BP-STBL (stability of patient’s blood pressure) Decision ADM-DECS(discharge decision) | 90 | 54 | 36 |
| Data Set | Metric | Algorithms | ||||
|---|---|---|---|---|---|---|
| GA | DE | PSO | ABC | AIS | ||
| German Credit Dataset | MAE | 0.2575 | 0.215 | 0.2125 | 0.1625 | 0.12 |
| MAPE% | 0.064375 | 0.05375 | 0.053125 | 0.040625 | 0.03 | |
| Hepatitis Dataset | MAE | 0.290323 | 0.193548 | 0.177419 | 0.145161 | 0.064516 |
| MAPE% | 0.468262 | 0.312175 | 0.28616 | 0.234131 | 0.104058 | |
| Congressional Voting Records Dataset | MAE | 0.298851 | 0.275862 | 0.224138 | 0.218391 | 0.183908 |
| MAPE% | 0.171753 | 0.158541 | 0.128815 | 0.125512 | 0.104694 | |
| Car Evaluation Dataset | MAE | 0.204052 | 0.193922 | 0.188133 | 0.086831 | 0.081042 |
| MAPE% | 0.02953 | 0.028064 | 0.027226 | 0.012566 | 0.011728 | |
| Postoperative Patient Dataset | MAE | 0.388889 | 0.361111 | 0.25 | 0.138889 | 0.111111 |
| MAPE% | 1.080246 | 1.003086 | 0.694444 | 0.385802 | 0.308642 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alzaeemi, S.A.; Sathasivam, S. Artificial Immune System in Doing 2-Satisfiability Based Reverse Analysis Method via a Radial Basis Function Neural Network. Processes 2020, 8, 1295. https://doi.org/10.3390/pr8101295
Alzaeemi SA, Sathasivam S. Artificial Immune System in Doing 2-Satisfiability Based Reverse Analysis Method via a Radial Basis Function Neural Network. Processes. 2020; 8(10):1295. https://doi.org/10.3390/pr8101295
Chicago/Turabian StyleAlzaeemi, Shehab Abdulhabib, and Saratha Sathasivam. 2020. "Artificial Immune System in Doing 2-Satisfiability Based Reverse Analysis Method via a Radial Basis Function Neural Network" Processes 8, no. 10: 1295. https://doi.org/10.3390/pr8101295
APA StyleAlzaeemi, S. A., & Sathasivam, S. (2020). Artificial Immune System in Doing 2-Satisfiability Based Reverse Analysis Method via a Radial Basis Function Neural Network. Processes, 8(10), 1295. https://doi.org/10.3390/pr8101295





