Election Algorithm for Random k Satisfiability in the Hopfield Neural Network

Abstract

Election Algorithm (EA) is a novel variant of the socio-political metaheuristic algorithm, inspired by the presidential election model conducted globally. In this research, we will investigate the effect of Bipolar EA in enhancing the learning processes of a Hopfield Neural Network (HNN) to generate global solutions for Random k Satisfiability (RANkSAT) logical representation. Specifically, this paper utilizes a bipolar EA incorporated with the HNN in optimizing RANkSAT representation. The main goal of the learning processes in our study is to ensure the cost function of RANkSAT converges to zero, indicating the logic function is satisfied. The effective learning phase will affect the final states of RANkSAT and determine whether the final energy is a global minimum or local minimum. The comparison will be made by adopting the same network and logical rule with the conventional learning algorithm, namely, exhaustive search (ES) and genetic algorithm (GA), respectively. Performance evaluation analysis is conducted on our proposed hybrid model and the existing models based on the Root Mean Square Error (RMSE), Mean Absolute Error (MAE), Sum of Squared Error (SSE), and Mean Absolute Error (MAPE). The result demonstrates the capability of EA in terms of accuracy and effectiveness as the learning algorithm in HNN for RANkSAT with a different number of neurons compared to ES and GA.

1. Introduction

Artificial Neural Networks (ANNs) have emerged as a powerful computational model, developed by modelling the biological brain processing information into systematic procedures of mathematical formulation. ANNs are extensively applied in various computational and prediction tasks such as in pandemic diseases analysis [1], pattern recognition [2], logic extraction [3], function approximation [4], and complex analysis [5]. Over the years, researchers have utilized ANN to solve complex optimization problems suitable to an ANN’s capability to provide alternative ways to perform computation and understand information compared to conventional statistical methods.

Hopfield and Tank formulated Hopfield Neural Network (HNN) in 1985 to provide a network for solving combinatorial problems [6]. HNN is a variant of ANN, which demonstrates the structure of feedback and recurrent interconnected neurons with no existence of hidden layers. HNNs exhibit great performance in pattern recognition [7], fault detection [8], and clustering tasks [9]. Several distinctive features of HNNs include Content Addressable Memory (CAM), Minimization of Energy as the neuron state changed, and fault tolerance [10]. Conjointly, HNN complies with the discrete structure of the problem and solves it by minimizing the energy function that corresponds to the solution of the problem. One of the most relevant challenges faced by the HNN is the output representation produced in solving and learning the intended problem. This argument leads to the introduction of a symbolic rule that governs the information embedded in the HNN. One of the earliest pursuits in representing ANN in terms of logical rules was coined by Abdullah [11]. This work implemented a logical rule into the standard HNN by utilizing the relationship of the cost function and the energy function. In pursuing the argument of this paradigm, one may ask: what type of logical rule can be represented in an ANN? Sathasivam [12] proposed Horn Satisfiability (HornSAT) in HNN by implementing nonoscillatory synaptic weight. From this perspective, Kasihmuddin et al. [10] proposed 2 Satisfiability (2SAT) representation in HNN. The proposed network achieved more than 90% of global minimum solutions during the retrieval phase of HNN. Similar observations were made in [13] as 3 Satisfiability (3-SAT) was implemented as the logical rule in HNN. As an extension of k Satisfiability representation, Maximum Satisfiability [14] became the first unsatisfiable logical rule that has been implemented in HNN. Although the cost function obtained is not zero, the performance metric showed that most of the retrieved states achieved global minimum energy. Since the introduction of these logical rules, [15] initiated a hybrid HNN model by implementing 2SAT to verify the properties of the Bezier Curve model. In addition, a work by [16] used an HNN with 3-SAT to optimize pattern satisfiability (Pattern-SAT). The proposed work showed that information embedded in 3SAT yielded a better result for Pattern-SAT. The work by [17] utilized 3SAT integrated with an HNN to configure a Very Large-Scale Integrated (VLSI) circuit. The proposed hybrid network achieved more that 90% accuracy in terms of circuit verification. In another development, Hamadneh et al. [18] proposed logic programming in a Radial Basis Function Neural Network (RBFNN). Logic programming is embedded in RBFNN by calculating the width and the centre of the hidden layer. These studies were extended by Alzaeemi et al. [19] and Mansor et al. [20] where they proposed 2 Satisfiability in RBFNN. The proposed logical rule reduced the complexity of the network by fixing the value of the parameters involved in the RBFNN. Note that, the common denominator in these studies is the implementation of the systematic logical rule in the ANN. There is no recent effort to implement a nonsystematic logical rule in an ANN.

From a computational intelligence point of view, metaheuristics algorithms are interesting for several reasons. First, the computation via metaheuristics can be implemented with a minimum level of bias. The algorithm can search for the optimal solution without complex mathematical derivation. For instance, Genetic Algorithm (GA) can screen the whole search space without compromising any possible optimal search space. This is due to the capability of the metaheuristics algorithm to utilize both local search and global search mechanisms to find the optimal solution. Second, metaheuristics algorithms are commonly used to reduce the computational complexity of another intelligence system. As the number of constraints grow, standard standalone ANN will be computationally burdening and tend to be trapped in a suboptimal solution. In several studies [21,22,23], metaheuristics algorithms were reported to compliment ANN in solving optimization problems. Extensive empirical studies have been conducted to investigate the effect of metaheuristics in optimizing HNN. Kasihmuddin et al. [10,24] proposed GA and Artificial Bee Colony (ABC) for optimizing 2SAT in HNN. The proposed hybrid HNN minimizes the cost function of the 2SAT in the HNN. In another development, Mansor et al. [13] proposed the use of the Artificial Immune System (AIS) in optimizing 3SAT integrated in HNN. The proposed AIS is later implemented in Maximum Satisfiability [25]. The main challenge in finding a suitable metaheuristic for Satisfiability representation is the structure of the logical rule. In this case, the first order logical rule coupled with different logical order is difficult to satisfy compared to higher systematic order logical rules.

In practice, an optimal metaheuristics algorithm must be able to cover a wide range of solutions and create several independent computations. Election Algorithm (EA) is a class of socio-political metaheuristics [26], which combines the mechanisms of evolutionary algorithm and swarm optimization. It was coined by [27], in which the algorithm was developed by modelling the presidential election process. The algorithm involves multiple layers of optimization, namely, positive advertisement, negative advertisement, and coalition, which are suitable for use by the learning algorithm. Similar to other metaheuristics algorithms such as GA and ABC, EA can be used in both continuous and discrete optimizations. The whole process is governed by the campaign process by improving the eligibility of the candidates (solutions of the constrained optimization problem) [28]. This algorithm combines the capability of the local search in a partitioned search space. Due to its unique way of improving the current solution, clinical iterative improvement for EA is reported to reduce the probability of the solution to achieve a nonimproving solution (suboptimal solution). The capacity of the EA in searching the optimal solution for constrained optimization has led to a more robust EA, such as Chaotic EA. In current development, [29] proposed a novel Chaotic Election Algorithm for function optimization by using the standard boundary-constrained benchmark function. Although chaotic EA has been reported as a tremendous success in finding the optimal solution, the capacity of the basic EA is worth investigating. In this study, we will adopt EA as the learning algorithm in an HNN to generate global minimum solutions for Random k Satisfiability (RANkSAT).

The contributions of the present paper are: (1) New logical rule;RAN2SAT is proposed by considering first and second order logic $\left(k\le 2\right)$. (2) We implemented RAN2SAT in the HNN by minimizing the cost function and Lyapunov Energy Function. (3) A new EA is proposed to optimize the learning phase of HNN by incorporating RAN2SAT. The effectiveness of the EA using RAN2SAT will be compared to the state-of-the-art GA. By constructing an effective HNN work model, the proposed learning method will be beneficial for logic mining [3] and other variants of HNN [30]. The rest of this paper is organized in the following way. The new Random k Satisfiability representation is formally described in Section 2. In Section 3, the proposed RAN2SAT is embedded into HNN. The structure of the cost function and the energy function for RAN2SAT will be explained in detail. Section 4 presents the proposed EA and the existing work of GA using RAN2SAT. Section 5 reports the experimental setup, the performance metrics involved, and the general implementation of the network. The results and discussion are reported in Section 6. Finally, Section 7 concludes the paper with future directions.

2. The Proposed Random k Satisfiability (RANkSAT)

Random k Satisfiability (RANkSAT) is a class of nonsystematic Boolean logic representation. It consists of random number of literals (can be the negated literals) per clause. RANkSAT is represented in Conjunctive Normal Form (CNF), where each clause contains random number of variables connected by an OR operator. The fundamental structure of RANkSAT is not restricted compared to conventional kSAT [17] logical representation. Hence, the general formulation for RANkSAT is given as

$$P_{RANkSAT}=\underset{i=0}{\overset{n}{\wedge }}{C}_i^{\left(2\right)}\underset{i=0}{\overset{m}{\wedge }}{C}_i^{\left(1\right)}$$

(1)

where $n\in ◜$, $n>0$ and $m\in ◜$, $m>0$. Therefore, the clause in $P_{RANkSAT}$ is defined as

$$C_i^{\left(k\right)}=\{\begin{array}{l}\left(A_i\vee B_i\right) , k=2\\ D_i , k=1 \end{array}$$

(2)

where $A_i\in \left\{A_i,\neg A_i\right\}$, $B_i\in \left\{B_i,\neg B_i\right\}$, and $D_i\in \left\{D_i,\neg D_i\right\}$. In particular, the first and second order clause are denoted as $C_i^{\left(1\right)}$ and $C_i^{\left(2\right)}$, respectively. In this study, $F_r$ is a Conjunctive Normal Form (CNF) formula where the clauses are chosen uniformly, independently without replacement among all $2^r\left(\begin{array}{l}m+n\\ v\end{array}\right)$ nontrivial clause of length $r$. Note that, $A_i$ exists in the $C_i^{\left(k\right)}$, if the $C_i^{\left(k\right)}$ contains either $A_i$ or $\neg A_i$ and the mapping of $V\left(F_r\right)\to \left\{-1, 1\right\}$ is called logical interpretation. According to [3], the Boolean value for the mapping is expressed as 1 (TRUE) and −1 (FALSE). In theory, the example of RANkSAT formula for $k\le 2$ is given as

$$P_{RAN2SAT}=\left(A_1\vee \neg B_1\right)\wedge \left(\neg A_2\vee B_2\right)\wedge \neg D_1$$

(3)

According to Equation (3), $P_{RANkSAT}$ comprises of $C_1^{\left(2\right)}=\left(A_1\vee \neg B_1\right)$, $C_2^{\left(2\right)}=\left(\neg A_2\vee B_2\right)$, and $C_1^{\left(1\right)}=\neg D_1$. Therefore, the outcome of Equation (3) is $P_{RANkSAT}=-1$ if $\left(A_1,A_2,B_1,B_2,D_1\right)=\left(1,1,1,1,1\right)$ with two clauses satisfied $\left(C_1^{\left(2\right)},C_2^{\left(1\right)}\right)$. In this study, we investigated the RAN2SAT for the case of $k\le 2$.

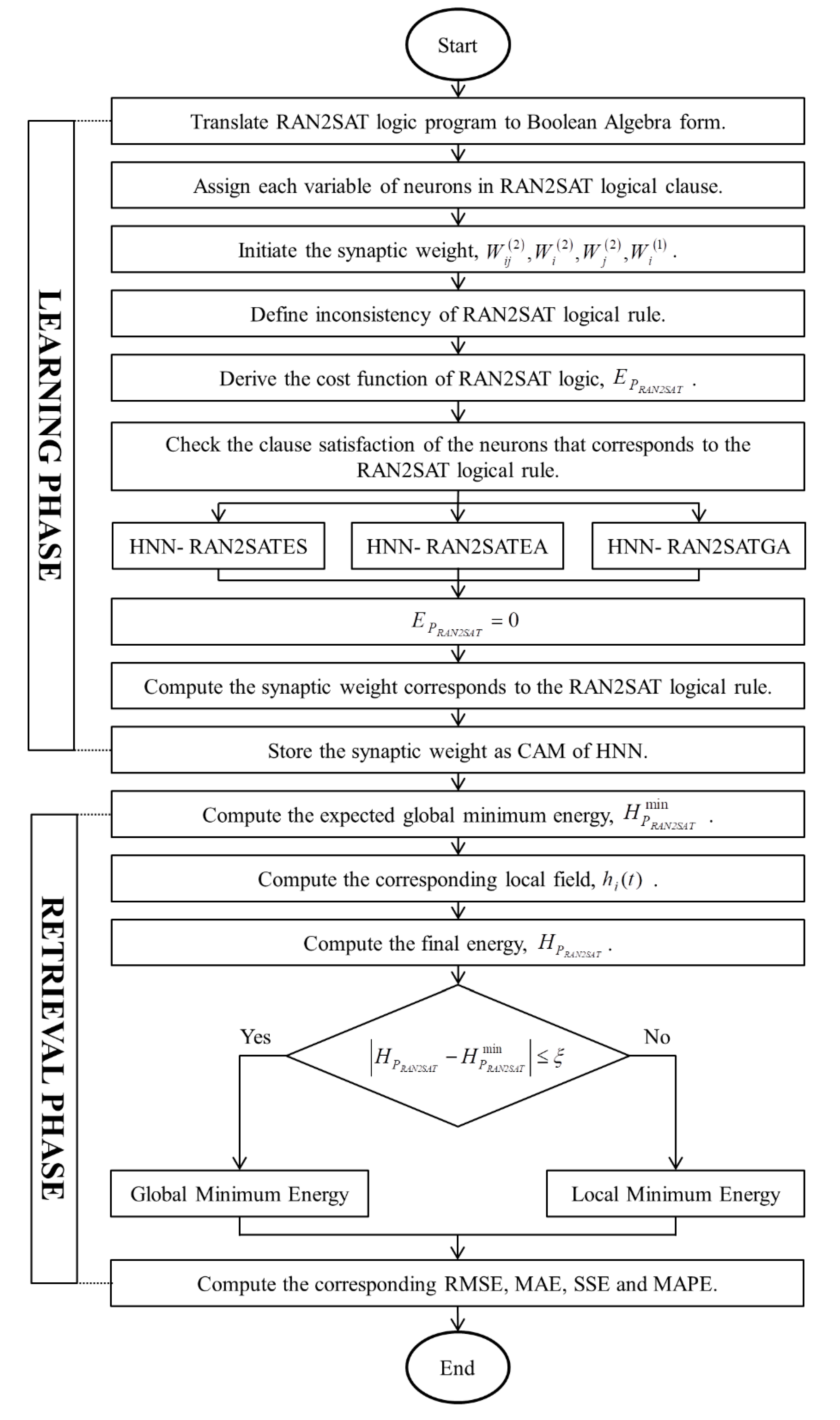
3. RAN2SAT in a Hopfield Neural Network

The fundamental architecture and structure of a Hopfield Neural Network (HNN) consists of discrete interconnected bipolar neurons without any hidden neurons [31]. The synaptic weights are strictly symmetrical in manner, without self-mapping among the interconnected neurons. Hence, the Content Addressable Memory (CAM) is studied as a dynamic storage system for the synaptic weights [12]. Given an initial vector that is mapped to the neuron state $S_i=\left(S_1,S_2,S_3,\dots ,S_n\right)$ and without any noise intervention, the HNN will converge to the equilibrium that corresponds to the minimum value of $H_p$ [32]. Henceforth, the final state of the HNN corresponds to the solution of the combinatorial problem. The neurons in HNN are represented in bipolar form, $S_i\in \left(-1,1\right)$ conform to the dynamics $S_i\to \mathrm{sgn}\left(h_i\right)$. The general asynchronous updating rule of the HNN is given by:

$$S_i\left(t+1\right)=\{\begin{array}{l} 1 , if {\displaystyle \sum _j^N{W}_{ij}{S}_j\left(t\right)+\beta }\\ -1 , otherwise\end{array}$$

(4)

where $W_{ij}$ describes the synaptic weight matrix of HNN, which establishes the strength of the connections from neuron j to i with predetermined bias $\beta$. In this study, the HNN is implemented as the central network in training the $P_{RAN2SAT}$. The formalism of logic programming in HNN does not impose any restriction on the accepted type of clauses as long as the proposed propositional logic is satisfiable [33]. $P_{RAN2SAT}$ can be embedded into the HNN by assigning each variable with neurons $D_i$ to the defined cost function. Furthermore, the generalized cost function $E_{P_{RAN2SAT}}$ that governs the combinations of HNN and $P_{RAN2SAT}$ is given as

$$E_{P_{RAN2SAT}}={\displaystyle \sum _{i=1}^{NC}{\displaystyle \prod _{j=1}^{m+n}{T}_{ij}}}$$

(5)

where $NC$ and $m+n$ are the number of clauses and the number variables in $P_{RAN2SAT}$, respectively. Note that the inconsistency of $P_{RAN2SAT}$ is given as:

$$T_{ij}=\{\begin{array}{l}\frac{1}{2}\left(1-S_A\right) , if \neg A\\ \frac{1}{2}\left(1+S_A\right) , otherwise\end{array}$$

(6)

The value of $E_{P_{RAN2SAT}}$ is proportional to the number of “inconsistencies” of the clause $\left(C_i^k=-1\right)$. The more $C_i^k$ that is unsatisfied, the higher the value of $E_{P_{RAN2SAT}}$. Minimum $E_{P_{RAN2SAT}}$ corresponds to the “most consistent” selection of $S_i$. Hence, the updating rule for $P_{RAN2SAT}$ in HNN is defined as:

$$h\left(t\right)={\displaystyle \sum _{j=1,i\ne j}^{m+n}{W}_{ij}^{\left(2\right)}{S}_j\left(t\right)+W_i^{\left(1\right)}}$$

(7)

$$S_i\left(t+1\right)=\{\begin{array}{l} 1 , {\displaystyle \sum _{j=1,i\ne j}^{m+n}{W}_{ij}^{\left(2\right)}{S}_j\left(t\right)+W_i^{\left(1\right)}}\ge 0\\ -1 , {\displaystyle \sum _{j=1,i\ne j}^{m+n}{W}_{ij}^{\left(2\right)}{S}_j\left(t\right)+W_i^{\left(1\right)}}<0\end{array}$$

(8)

where $W_{ij}^{\left(2\right)}$ and $W_i^{\left(1\right)}$ are second and first order synaptic weights of the embedded $P_{RAN2SAT}$. Equations (7) and (8) are important to ensure the neurons $S_i$ will always converge to $E_{RAN2SAT}\to 0$. The quality of the retrieved $S_i$ can be evaluated by employing the Lyapunov energy function, $H_{P_{RAN2SAT}}$, defined as:

$$H_{P_{{}_{RAN2SAT}}}=-\frac{1}{2}{\displaystyle \sum _{i=1,i\ne j}^{m+n}{\displaystyle \sum _{j=1,i\ne j}^{m+n}{W}_{ij}^{\left(2\right)}{S}_i{S}_j}-{\displaystyle \sum _{i=1,i\ne j}^{m+n}{W}_i^{\left(1\right)}{S}_j}}$$

(9)

The structure of Equation (9) is valid for RAN2SAT logical representation for the case of $k\le 2$. Equation (7) describes that the energy portrayed from the $P_{RAN2SAT}$ always decreases monotonically. The value of $H_{P_{RAN2SAT}}$ indicates the value of the energy with respect to the absolute final energy $H_{P_{RAN2SAT}}^{\min }$ attained from $P_{RAN2SAT}$ [11]. Hence, the value of $H_{P_{RAN2SAT}}^{\min }$ can be further computed by using the following formula:

$$H_{P_{RAN2SAT}}^{\min }=-\left(\frac{\theta +2\eta }{4}\right)$$

(10)

where $\theta =n\left(C_i^{\left(2\right)}\right)$ and $\eta =n\left(C_i^{\left(1\right)}\right)$ that corresponds to $P_{RAN2SAT}$. Hence, the quality of the final neuron state can be properly examined by checking the following condition:

$$\left|H_{P_{RAN2SAT}}-H_{P_{RAN2SAT}}^{\min }\right|\le \xi$$

(11)

where $\xi$ is the predetermined tolerance value. Note that, if the embedded $P_{RAN2SAT}$ does not satisfy Equation (11), the final state attained will be trapped in a local minimum solution. It should be mentioned that, $W_{ij}^{\left(2\right)}$ and $W_i^{\left(1\right)}$ can be effectively obtained by using the Wan Abdullah method [11]. Hebbian learning was reported to produce an oscillating neuron state that will result in a suboptimal value of $H_{P_{RAN2SAT}}$. In this paper, the implementation of $P_{RAN2SAT}$ in HNN is denoted as the HNN-RAN2SAT model.

4. Learning Model for HNN-RAN2SAT

4.1. Election Algorithm (EA)

Election Algorithm (EA) is a metaheuristics algorithm inspired by the socio-political phenomenon of presidential elections conducted by a majority of the countries in the world. This algorithm was introduced by [27] for finding solutions for function approximation. Inspired by other evolutionary algorithm such as GA, EA relies on an intelligent search by implementing three iterative operators, i.e., positive advertisement, negative advertisement, and coalition. Each of the operators comprises an individual that can be effectively divided into candidates and voters, similar to the actual electoral system where a candidate must be initially selected from the party and the best candidate will end up with the most votes. In this situation, the candidate will assert dominance and influence their supporters (voter) and increase the chances of the candidate winning the election. Interestingly, this algorithm provides partitions in a solution space where each partition is represented by a party and is coordinated by one candidate. Each party will optimize both voters and candidates until the election day. In this paper, we utilize EA to find the optimal assignment for RAN2SAT that minimizes the cost function during the learning phase of the HNN. The basic motivation for choosing EA was due to the structure of RAN2SAT, consisting of first and second order logic. In [12], the complexity of the logic programming in the HNN increased sharply because the probability of getting $E_{P_{RAN2SAT}}=0$ for the first order clause is small. This limitation requires an algorithm that can effectively flip the neuron state based on the previous improved solution with a wide solution space. In general, the fitness function or eligibility value for the candidate $L_j$ in EA is given by

$$f_{L_j}={\displaystyle \sum _{i=0}^m{C}_i^{\left(2\right)}}+{\displaystyle \sum _{i=0}^n{C}_i^{\left(1\right)}}$$

(12)

where $C_i^{\left(2\right)}$ and $C_i^{\left(1\right)}$ are second and first order RAN2SAT clauses, respectively, and are given as

$$C_i^{\left(2\right)}=\{\begin{array}{l}1 , Satisfied\\ 0 , otherwise\end{array}$$

(13)

$$C_i^{\left(1\right)}=\{\begin{array}{l}1 , Satisfied\\ 0 , otherwise\end{array}$$

(14)

Each neuron string in the HNN represents the assignment that corresponds RAN2SAT instances. Similar to the other fitness functions of the general metaheuristics in [10,34], the objective function of our proposed EA is to maximize the eligibility of the candidate (neuron string):

$$\max \left[f_{L_j}\right]$$

(15)

In the basic EA proposed by [27], each individual in the search space will be optimized so that it can satisfy the continuous function. The implementation of EA in HNN is abbreviated as HNN-RAN2SATEA. The stages involved in HNN-RAN2SATEA are as follows:

4.1.1. Initialization

A random population $N_{POP}$ of individuals consisting of voters and candidates (RAN2SAT assignment) $S_i\in \left[S_1,S_2,S_3,\dots ,S_N\right]$, $S_i=\left\{-1,1\right\}$ is initialized. The state of each individual is given as 1 (TRUE) and −1 (FALSE), which corresponds to the possible assignment for RAN2SAT.

4.1.2. Forming Initial Parties

In this stage, the solution space is divided into $N_{party}$ parties. The fraction of voters in each party is given as follows:

$$N_j=\frac{N_{POP}}{N_{party}}, j=1,2,3,4$$

(16)

where $N_{party}$ is the number of party $j$ that is predefined earlier. The eligibility of each individual (voters or potential candidate) is evaluated based on Equation (12). The individual that has the highest eligibility value for party $j$ will be elected as a candidate $L_j$. The rest of the individuals are regarded as voters $v_i^j$ for that candidate. The similarity of belief between the candidate $L_j$ and the voter $v_i^j$ is represented in the form of distance:

$$dist\left(f_{L_j},f_{v_i^j}\right)=f_{L_j}-f_{v_i^j}$$

(17)

where $f_{L_j}^{}$ and $f_{v_i^j}^{}$ are the eligibility of the candidate and voters, respectively.

4.1.3. Positive Advertisement

In this stage, the candidate will expose their plans and try to influence the voting decisions made by the voters. Hence the number of voters that will be influenced by the candidate is given as follows

$$N_{S_j}={\sigma }^p{N}_j, j=1,2,3,4$$

(18)

where ${\sigma }^p$ is a positive advertisement rate, ${\sigma }^p\in \left[0,0.5\right]$. The reasonable effect from the candidate to the voter is defined as the eligibility distance coefficient ${\omega }_{v_i^{ j}}$ given by:

$${\omega }_{v_i^{ j}}=\frac{1}{dist\left(f_{L_j},f_{v_i^j}\right)+1}$$

(19)

Hence, the updating (state flipping) of each voter is based on the following equation:

$$S_{v_i^{ j}}=N_{j }{\omega }_{v_i^{ j}}$$

(20)

where $N_j=m+n$, a sum of first and second order of RAN2SAT. The eligibility for each voter and candidate will be evaluated based on Equation (12). In this stage, there is a possibility that the voter will replace the current candidate if the eligibility of the voter is higher than the present candidate.

4.1.4. Negative Advertisement

In this stage, the candidate will try to attract voters from other parties that are not in party $j$. Negative advertisements will lead to an increase in popularity of the candidate from different parties. The number of voters that are influenced from the negative advertisement is as follows:

$$N_{v_i^{\ast }}={\sigma }^n\left(1-\frac{N_j}{N_{party}}\right)$$

(21)

where $v_i^{\ast }$ is voters from other parties and ${\sigma }^n$ is a negative advertisement rate, ${\sigma }^n\in \left[0,0.5\right]$. The similarity of beliefs between the candidate $L_j$ and voter $v_i^{\ast }$ is defined as follows

$$dist\left(f_{L_j},f_{v_i^{\ast }}\right)=f_{L_j}-f_{v_i^{\ast }}$$

(22)

The reasonable effect from the candidate to the voter from another party is defined based on the eligibility distance coefficient ${\omega }_{v_i^{\ast }}$.

$${\omega }_{v_i^{\ast }}=\frac{1}{dist\left(f_{L_j},f_{v_i^{\ast }}\right)+1}$$

(23)

$$S_{v_i^{ \ast }}=N_{v_i^{\ast }}{\omega }_{v_i^{ \ast }}$$

(24)

where $N_j=m+n$. The eligibility of each voter and candidate is evaluated based on Equation (12). In this stage, there is a possibility that the voter will replace the current candidate.

4.1.5. Coalition

Similar to the process of candidate coalition, the candidate will form a partnership with an individual (voter and candidate) from another party. In this case, the parties will exist codependently with each other. The effect of both candidates from both parties within the same coalition is computed based on Equation (23).

4.1.6. Election Day

If the termination criteria for Stages 3–5 are satisfied, the election will be conducted to evaluate the final eligibility of all the candidate. If $f_{L_j}^{}=m+n$, the candidate will be elected, otherwise stages 3–5 are repeated until the specified number of iterations is reached. In this paper, the maximum iteration $Ir$ is considered as the stopping criteria of the proposed algorithm. Algorithm 1 shows the detailed procedure of the proposed HNN-RAN2SATEA.

Algorithm 1 Detailed Procedure of the Proposed HNN-RAN2SATEA
1	Initialize the population $N_{POP}$ consisting $S_i\in \left[S_1,S_2,S_3,\dots ,S_{N_{POP}}\right]$;
2	while$\left(g\le Ir\right)$ or $f_{L_j}=f_{m+n}$
3	Forming Initial Parties by using Equation (16);
4	for	$j\in \left\{1,2,3,\dots ,N_{party}\right\}$do
5		Calculate the similarity between the voter and the candidate by using Equation (17);
6	end
7		{Positive Advertisement}
8		for	$S_i\in \left\{1,2,3,\dots ,N_{S_j}\right\}$do
9			Evaluate the number of voters $N_{S_j}$ Equation (18);
10			Evaluate the reasonable effect from the candidate ${\omega }_{v_i^{ j}}$ by using Equation (19);
11			Update the neuron state according to Equation (20);
12			if	$f_{v_i^j}>f_{L_j}$
13				Assign $v_i^j$ as new $L_j$;
14			else
15				Remain $L_j$
16		end
17		{Negative Advertisement}
18		for	$S_i\in \left\{1,2,3,\dots ,N_{v_i^{\ast }}\right\}$do
19			Evaluate the similarity between the voter from other party and the candidate by using Equation (22);
20			Evaluate the reasonable effect from the candidate ${\omega }_{v_i^{\ast }}$ by using Equation (23);
21			Update the neuron state according to Equation (24);
22			if	$f_{v_i^{\ast }}>f_{L_j}$
23				Assign $v_i^{\ast }$ as new $L_j$;
24			else
25				Remain $L_j$
26		end
27		{Coalition}
28		for	$S_i\in \left\{1,2,3,\dots ,N_{v_i^{\ast }}\right\}$do
29			Evaluate the similarity between the voter from other party and the candidate by using (22);
30			Evaluate the reasonable effect from the candidate ${\omega }_{v_i^{\ast }}$ by using Equation (23);
31			Update the neuron state according to Equation (24);
32			if	$f_{v_i^{\ast }}>f_{L_j}$
33				Assign $v_i^{\ast }$ as new $L_j$
34			else
35				Remain $L_j$
36		end
37	end while
38	return Output the final neuron state

4.2. Genetic Algorithm (GA)

Genetic Algorithm (GA) is a variant of a random-based evolutionary algorithm, utilized as an effective searching technique or as a learning algorithm. The pioneering work of [35] developed the idea of the nonfit solutions being improved with each iteration by employing genetic operators. It was formally described as Messy GA in [36], which functions as a learning algorithm. Kasihmuddin et al. [10] proposed GA for performing kSAT logical representation during the learning phase of HNN. In their work, neurons in the HNN were represented as information that made up the chromosomes. We adapted the same structure for GA for performing RANkSAT. The possible assignment of RAN2SAT in GA is represented as chromosomes $S_i$. The fitness function $f_{S_i}$ of each $S_i$ is given by:

$$f_{S_i}={\displaystyle \sum _{i=0}^m{C}_i^{\left(2\right)}}+{\displaystyle \sum _{i=0}^n{C}_i^{\left(1\right)}}$$

(25)

where $C_i^{\left(2\right)}$ and $C_i^{\left(1\right)}$ are second and first order RAN2SAT clause, respectively, and were given as

$$C_i^{\left(2\right)}=\{\begin{array}{l}1 , Satisfied\\ 0 , otherwise\end{array}$$

(26)

$$C_i^{\left(1\right)}=\{\begin{array}{l}1 , Satisfied\\ 0 , otherwise\end{array}$$

(27)

Each neuron string in the HNN represents an assignment that corresponds to RAN2SAT instances. The objective function of proposed GA is to maximize the fitness of the $S_i$ (neuron string):

$$\max \left[f_{S_i}\right]$$

(28)

Note that the proposed GA is the state-of-the-art, and the fitness function is tailored to RAN2SAT representation. The implementation of GA in HNN is abbreviated as HNN-RAN2SATGA. The stages involved in HNN-RAN2SATGA are as follows:

4.2.1. Initialization

Initialize $N_{POP}$ chromosome $S_i$ where $S_i\in \left\{S_1,S_2,\dots ,S_{N_{POP}}\right\}$. The state of neuron in each $S_i$ is represented by 1 (TRUE) and −1 (FALSE).

4.2.2. Fitness Evaluation

The fitness $f_{S_i}$ of each $S_i$ is evaluated based on Equation (25). In this case, the proposed model only accommodates $f_{S_i}\in ◜$. Note that the maximum fitness of $S_i$ is $f_{S_i}=f_{m+n}$ and if $f_{S_i}$ reaches maximum fitness, the algorithm will be terminated.

4.2.3. Selection

$N_D$ chromosomes that acquire a high value of $f_{S_i}$ will be selected. The selection of the chromosomes is based on the following equation:

$$N_D=\lambda N_{POP}$$

(29)

where $\lambda$ is the selection rate of the chromosomes, ranging to $\lambda \in \left[0,1\right]$. This stage is vital because lower values of $f_{S_i}$ will not be included in the next stage.

4.2.4. Crossover

The genetic diversification of the $S_i$ occurs during this stage. Crossover involves exchange of two substructures from both $S_i$. Note that the location of the crossover is determined randomly. The following process illustrates crossover between $S_1$ and $S_2$:

Before Crossover

$S_1$	−1	1	1	−1	1	1
$S_2$	1	−1	1	1	1	−1

After Crossover

$S_1$	1	1	−1	−1	1	1
$S_2$	1	−1	1	−1	1	1

4.2.5. Mutation

The mutation operator performs state flipping from 1 to −1 or vice versa. The mutation will theoretically enhance the average fitness of the $S_i$. Note that there is a chance that the $f_{S_i}$ will reduce if the wrong state is flipped during this stage. Stages 1 to 5 are repeated a predetermined number of times if generation $gen$ is reached. Algorithm 2 shows the detailed procedure of HNN-RAN2SATGA.

Algorithm2 Detailed Procedure of the Proposed HNN-RAN2SATGA
1	Initialize the $N_{POP}$ chromosomes population consisting $S_i\in \left[S_1,S_2,\dots ,S_{N_{POP}}\right]$;
2	while$g\le Gen$ or $f_{S_i}=f_{m+n}$
3		Initialize $N_{POP}-N_D$ random $S_i$;
4		{Selection}
5		for	$i\in \left\{1,2,3,\dots ,N_{POP}\right\}$do
6			Calculate the fitness of each $S_i$ by using Equation (25);
7			Evaluate $N_D$ by using Equation (29);
8		end
9		{Crossover}
10		for	$S_i\in \left\{1,2,3,\dots ,N_D\right\}$do
11			Exchange the states of the selected two $S_i$ at a random point.
12		end
13		{Mutation}
14		for	$S_i\in \left\{1,2,3,\dots ,N_D\right\}$do
15			Flipping states from of $S_i$ the random location;
16			Evaluate the fitness of the $S_i$ according to Equation (25);
17		end
18	end while
19	return Output the final $S_i$ state.

5. HNN Model Experimental Setup

In this study, EA has been incorporated into an HNN in the search for an optimal solution for RAN2SAT logic representation. The proposed hybrid computational model will be compared with the existing HNN-RAN2SATES [37] and HNN-RAN2SATGA [10] models. Both HNN models employ simulated datasets to establish RAN2SAT logical clauses. To achieve a meaningful comparison between the existing HNN models, all source code was formulated based on the simulation program developed in Dev C++ release version 5.11 running on a device with an Intel ^® Celeron^® CPU B800@2GHz processor with 4 GB RAM utilizing Windows 8.1.

Table 1. List of parameters used in Hopfield Neural Network-Random 2 Satisfiability Exhaustive Search (HNN-RAN2SATES) [37].

Parameter	Value
Neuron Combination	100
Number of Trials	100
Tolerance Value $\left(\xi \right)$	0.001
Number of Strings	100
Selection Rate $\left(\lambda \right)$	0.1

,

Table 2. List of parameters used in Hopfield Neural Network-Random 2 Satisfiability Genetic Algorithm (HNN-RAN2SATGA) [10].

Parameter	Value
Neuron Combination	100
Number of Trials	100
Tolerance Value $\left(\xi \right)$	0.001
Number of Generations $\left(Gen\right)$	1000
Number of Chromosomes $\left(N_{POP}\right)$	120
Selection Rate $\left(\lambda \right)$	0.1
Crossover Rate	0.9
Mutation Rate	0.01

and

Table 3. List of parameters used in Hopfield Neural Network-Random 2 Satisfiability Election Algorithm (HNN-RAN2SATEA).

Parameter	Value
Neuron Combination	100
Number of Trials	100
Tolerance Value $\left(\xi \right)$	0.001
Number of Learning	100
Number of Candidates $\left(N_{POP}\right)$	120
Number of Parties $\left(N_{party}\right)$	4
Positive Advertisement Rate $\left({\sigma }^p\right)$	0.5
Negative Advertisement Rate $\left({\sigma }^n\right)$	0.5
Maximum Iterations $\left(Ir\right)$	100

indicate the appropriate parameters during each HNN model execution.

5.1. Performance Metric for HNN-RAN2SAT Models

In this study, the training phase of the HNN-RAN2SATEA model is compared against the other existing HNN models. To prove the efficacy of the HNN-RAN2SATEA model, we compared the proposed algorithm with HNN-RAN2SATES and HNN-RAN2SATGA to find the root mean square error (RMSE), mean absolute error (MAE), sum of squared error (SSE), and mean absolute percentage error (MAPE).

5.1.1. Root Mean Square Error (RMSE)

RMSE is used to provide information on a model’s short-term results by reporting the real discrepancy between the expected value and the calculated value [38]. When introducing RMSE, the fundamental presumption is that the mistakes are rational and meet a normal distribution [39]. Therefore, RMSE gives a clear description of the distribution of errors. The RMSE formula takes the following equation:

$$RMSE={\displaystyle \sum _{i=1}^n\sqrt{\frac{1}{n}{\left(f_{ NC}-f_{ i}\right)}^2}}$$

(30)

where $f_{ NC}$ is highest fitness achieved in the network based on the HNN-RAN2SAT model, $f_{ i}$ fitness computed by the network and $n$ is the number of iteration before $f_{ NC}=f_{ i}$.

5.1.2. Mean Absolute Error (MAE)

MAE is described as the average difference between the expected value and the calculated value in the solution space of the given data. The work by [40] stated that MAE is comparatively easy to compute, and it is the most appropriate indicator of average magnitude of error. MAE is ideal for a model with uniform distribution [41]. The MAE equation can be expressed as:

$$MAE={\displaystyle \sum _{i=1}^n\frac{1}{n}\left|f_{ NC}-f_{ i}\right|}$$

(31)

5.1.3. Sum of Squared Error (SSE)

In learning neural networks, the sum of squared errors between the expected value and the actual value is commonly minimized. This criterion’s success is attributed in part to the presence of solvable algorithms for their minimization [42]. The SSE formula is as follows:

$$SSE={\displaystyle \sum _{i=1}^n{\left(f_{ NC}-f_{ i}\right)}^2}$$

(32)

5.1.4. Mean Absolute Percentage Error (MAPE)

MAPE calculates the size of error by percentage. It has been argued that the MAPE is strongly suited for forecasting applications, especially in situations where adequate data is accessible [43,44]. One of the key factors for its popularity is its simplicity of interpretation and understanding [45]. The MAPE formula can be computed as:

$$MAPE={\displaystyle \sum _{i=1}^n\frac{100}{n}\frac{\left|f_{ NC}-f_{ i}\right|}{\left|f_{ i}\right|}}$$

(33)

5.2. Implementation of HNN-RAN2SAT Models

The HNN-RAN2SAT models were implemented in a systematic procedure, as shown in Figure 1, where the difference is the learning algorithm deployed during the learning phase. Both variables and clauses were initially randomized. The executions of these models were carried out based on Figure 1.

6. Results and Discussion

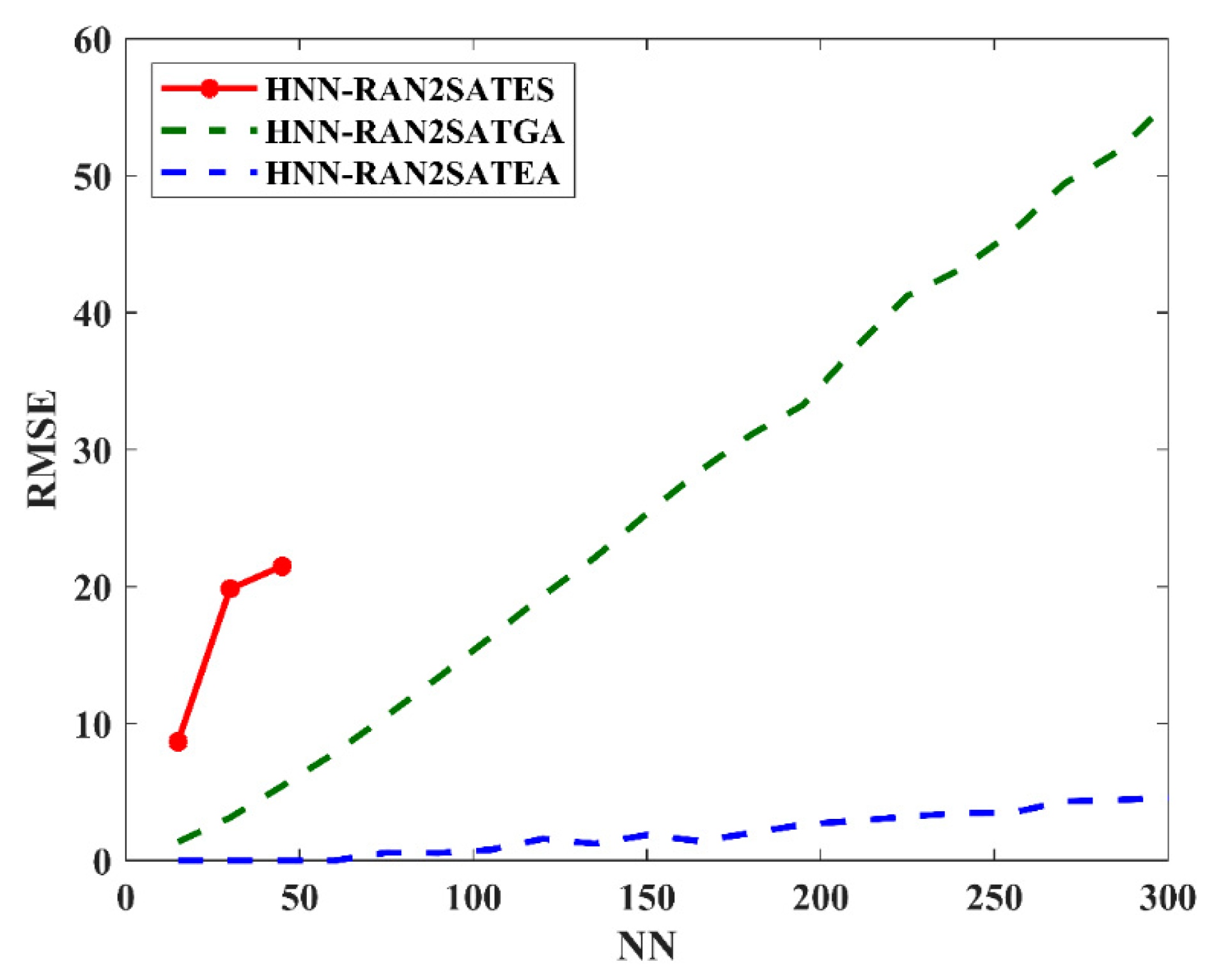
Figure 2, Figure 3, Figure 4 and Figure 5 demonstrate the performance of HNN-RAN2SAT in terms of RMSE, MAE, SSE, and MAPE, respectively. Based on Figure 2 and Figure 5, the general trend of the RMSE, MAE, SSE, and MAPE values for HNN-RAN2SAT increased with the increase of the number of neurons. The increment in the error evaluations portrays the complexities of the neuron states of RAN2SAT. 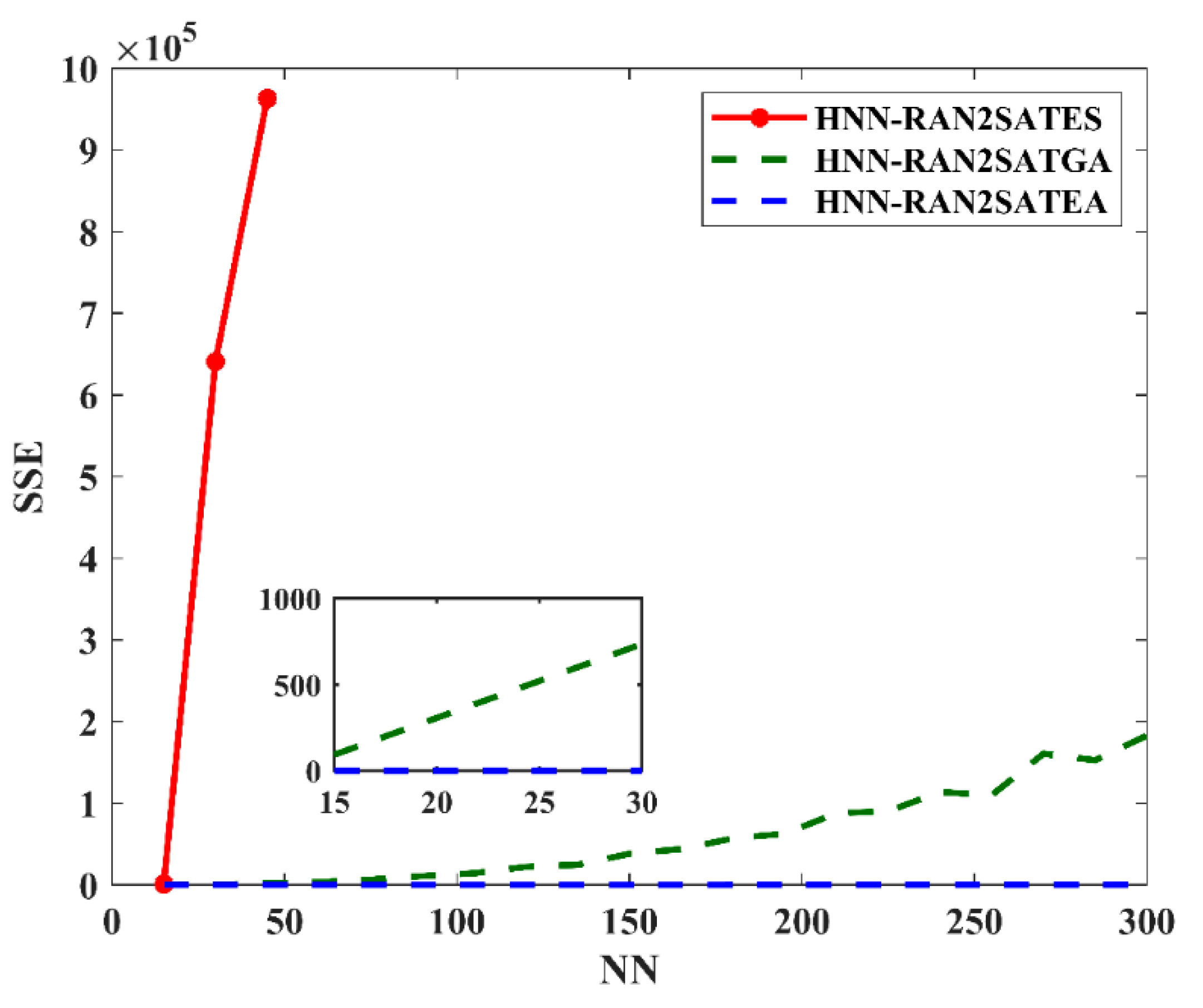Based on the RMSE and MAE evaluation during the learning phase, the proposed method, HNN-RAN2SATEA, manages to achieve $E_{p_{RAN2SAT}}=0$, 1200% lower than HNN-RAN2SATGA. The main reason is that the optimization layers in EA have a better partition in solution spaces, meaning $E_{p_{RAN2SAT}}=0$ can be achieved in fewer iterations. According to SSE analysis, it was reported that HNN-RAN2SATEA recorded a lower SSE, about 2150% lower than HNN-RAN2SATGA. This demonstrates the capability of ES in reducing the sensitivity of the model towards error by minimizing the iterations.

In addition, the MAPE for HNN-RAN2SATEA is 26% lower than that of HNN-RAN2SATGA. Based on MAPE, we can observe the percentage of error of the models. To sum up, based on Figure 2, Figure 3, Figure 4 and Figure 5, HNN-RAN2SATEA can retrieve a more accurate final state that than HNN-RAN2SATGA and HNN-RAN2SATES. Meanwhile, the ES employed the ‘exhaustive’ trial and error searching technique, and only functions until $NN=45$. This is due to the nature of ES, which suffers from neuron oscillation and computational burden, especially in the case of inconsistent interpretation $\neg P_{RAN2SAT}$ as the number of neuron increases. Thus, RMSE, MAE, SSE, and MAPE analysis are stopped at $NN=45$ for HNN-RAN2SATES due to the ineffectiveness of the learning algorithm. The solutions were trapped at the local minima due to neuron oscillations. From Figure 2, Figure 3, Figure 4 and Figure 5, it is clear that HNN-RAN2SATEA outperformed the other two models, HNN-RAN2SATGA and HNN-RAN2SATES, in optimizing the global minimum solutions based on RAN2SAT logical representation.

The effectiveness of HNN-RAN2SATEA can be seen from the perspective of the logical representation, RAN2SAT, and EA. The randomized structure of RAN2SAT diversifies the logical structure during the learning phase. Thus, the structure indicates the diversification of the final states produced by the model. Hence, dynamic exchanges of solutions occur in EA, where the chance of attaining diversified $P_{RAN2SAT}$ solutions is much higher. Hence, HNN-RAN2SATEA will generate more variation of $P_{RAN2SAT}$ clauses that can attain $E_{p_{RAN2SAT}}=0$. On the contrary, the nature of ES in HNN-RAN2SATES will cause problems for the case of inconsistent interpretation $\neg P_{RAN2SAT}$. Additionally, the mechanism of GA will create lower diversification of $P_{RAN2SAT}$ as the early solutions are typically nonfit and require optimization operators such as cloning, crossover, and mutation before achieving $E_{p_{RAN2SAT}}=0$. The utilization of EA deals effectively with the higher learning complexity of $P_{RAN2SAT}$ as the number of neurons increases during the simulation. This indicates the robustness of the global and local search procedures in HNN-RAN2SATEA.

The capability of HNN-RAN2SATEA to generate the global solution is related to the effectiveness of the global search and local search EA, which act as the learning algorithm. The local search in EA is promising during the early stage compared to GA and ES. This implies that the better optimization operators in EA facilitate the learning process for $P_{RAN2SAT}$ logical representation. Leader selection (candidate eligibility) requires an optimization operator that accelerates the process of obtaining the best leader (solution).

HNN-RAN2SATEA employs a more diversified optimization layer consisting of three layers in order to improve the solution in a particular partition of the solution space [27]. The first optimization layer, known as positive advertisement, will create the optimization among the party. Secondly, the negative advertisement allows the other party to take the voters from a specific part. Thirdly, coalitions provide a tremendous optimization impact in obtaining the most voters (more solutions), as our case is in attaining global solutions. The coalition process will form a unified party with greater eligibility within a shorter timeframe [28]. These features in EA lead HNN-RAN2SAT to reduce the iterations needed during the learning phase, ensuring minimum error evaluation at the end of the simulations.

The systematic solution space partition in HNN-RAN2SATEA improves the global and local search process for obtaining global solutions. The partition of the solution space allows the model to effectively find the solution in all defined spaces. Specifically, the solution spaces for HNN-RAN2SATEA are given as four spaces. On the contrary, HNN-RAN2SATGA adopted one partition of the overall solution space, which results in nonfit solutions during early stages of the model. On the same note, HNN-RAN2SATGA assimilated only one solution space, and the searching process utilized the trial and error mechanism, which requires more iterations to obtain the global solution.

EA was only implemented as the learning algorithm, without direct intervention in the retrieval phase. A different approach can be employed for optimizing the retrieval phase of HNN-RAN2SATEA. Different types of Hopfield Neural Networks, such as Mutation Hopfield Neural Network [30], Mean Field Theory Hopfield Network [46], Boltzman Hopfield [47], and Kernel Hopfield Network [48], drive the local minimum solution to the global minimum solution in different ways. More performance metrics can be investigated to authenticate our results. Similarity indices, such as Jaccard’s Index [49], Sokhal-Sneath2 Index [50], and Variation Index [50], can be employed to assess the similarity between the final states obtained by the model. In addition, we adopt Symmetric Mean Absolute Percentage Error (SMAPE) [51], Median Absolute Percentage Error [48], Fitness energy landscape [52], computation time [53], and specificity analysis [54].

7. Conclusions

Firstly, EA has been proposed as a learning algorithm during the learning phase of the first order and second order clauses of RAN2SAT. Thus, the capability of EA is determined by the systematic optimization layers, positive advertisement, negative advertisement, and the coalition operator, which successfully minimize the error evaluations towards the global solution. Secondly, we compared the effectiveness of EA in the learning phase with the existing algorithm, GA, and ES while manipulating the number of neurons. The findings showed that HNN-RAN2SATEA outperformed the other two models, HNN-RAN2SATES and HNN-RAN2SATGA, due to its effective learning mechanism, especially in partitioning the solution spaces to reduce complexity. The effective partitioning of the search space in EA allowed the searching process to be more accurate without undergoing intensive processes. It was found that HNN-RAN2SATES experienced neuron oscillations when $NN\ge 45$, indicating the weakness of ES as the learning mechanism. This work has successfully highlighted the capability of EA and RAN2SAT during the learning phase for generating more diversified interpretations that lead to global minimum solutions. Extending from our study, different classes of Hopfield Neural Networks can be adopted, such as Mutation Hopfield Neural Network [30], Mean Field Theory Hopfield network [46], Boltzmann Hopfield [47], and Kernel Hopfield Network [48], in order to investigate the impact of the retrieval phase. These works are currently in progress and will be reported in the future.