Extremal p-Adic L-Functions

Abstract

In this note, we propose a new construction of cyclotomic p-adic L-functions that are attached to classical modular cuspidal eigenforms. This allows for us to cover most known cases to date and provides a method which is amenable to generalizations to automorphic forms on arbitrary groups. In the classical setting of ${\mathrm{GL}}_2$ over $\mathbb{Q}$, this allows for us to construct the p-adic L-function in the so far uncovered extremal case, which arises under the unlikely hypothesis that p-th Hecke polynomial has a double root. Although Tate’s conjecture implies that this case should never take place for ${\mathrm{GL}}_2/\mathbb{Q}$, the obvious generalization does exist in nature for Hilbert cusp forms over totally real number fields of even degree, and this article proposes a method that should adapt to this setting. We further study the admissibility and the interpolation properties of these extremal p-adic L-functions $L_p^{\mathrm{ext}}(f,s)$, and relate $L_p^{\mathrm{ext}}(f,s)$ to the two-variable p-adic L-function interpolating cyclotomic p-adic L-functions along a Coleman family.

1. Introduction

Let $f\in S_{k+2}({\mathsf{\Gamma }}_1\left(N\right),ϵ)$ be a modular cuspidal eigeform for ${\mathsf{\Gamma }}_1\left(N\right)$ with nebentypus $ϵ$ and weight $k+2$. The study of the complex L-function $L(s,\pi )$ attached to the automorphic representation $\pi$ of ${\mathrm{GL}}_2\left(\mathbb{A}\right)$ generated by f is a very important topic in modern Number Theory. Understanding this complex valued analytic function is the key point for some of the most important problems in mathematics, such as the Birch and Swinnerton–Dyer conjecture.

Back in the middle of the seventies, Vishik [1] and Amice-Vélu [2] defined a p-adic measure ${\mu }_{f,p}$ of ${\mathbb{Z}}_p^{\times }$ that is associated with f, under the hypothesis that p does not divide N. The construction of this measure was the starting point for the theory of p-adic L-functions attached to modular cuspforms. The p-adic L-function $L_p(f,s)$ is a ${\mathbb{C}}_p$-valued analytic function that interpolates the critical values of the L-function $L(s,\pi )$. The function $L_p(f,s)$ is defined by means of ${\mu }_{f,p}$ as

$$L_p(f,s):={\int }_{{\mathbb{Z}}_p^{\times }}\exp (s·\log \left(\mathrm{x}\right))d{\mu }_{f,p}\left(x\right),$$

where $\exp$ and $\log$ are, respectively, the p-adic exponential and p-adic logarithm functions.

Mazur, Tate, and Teitelbaum extended, in [3], the definition of ${\mu }_{f,p}$ to more general situations and proposed a p-adic analogue of the Birch and Swinnerton–Dyer conjecture, replacing the complex L-function $L(s,\pi )$ with its p-adic counterpart $L_p(f,s)$. It has been shown that $L_p(f,s)$ is directly related with the (p-adic, or eventually l-adic) cohomology of modular curves, and this makes the p-adic Birch and Swinnerton–Dyer conjectures become more tractable. In fact, the theory of p-adic L-functions has grown tremendously during the last years. Many results, whose complex counterparts are inaccessible with current techniques, have been proven in the analogous p-adic scenarios.

1.1. Main Results

In this note, we provide a reinterpretation of the construction of the p-adic measures ${\mu }_{f,p}$. Our approach exploits the theory of automorphic representations and, in that sense, it is similar to the construction that was provided by Spiess in [4] for weights strictly greater than 2. This opens the door to possible generalizations of p-adic measures attached to automorphic representations of ${\mathrm{GL}}_2\left({\mathbb{A}}_F\right)$ of any weight, for any number field F.

We are able to construct ${\mu }_{f,p}$ in every possible situation, except when the local automorphic representation ${\pi }_p$ attached to f is supercuspidal, and we hope that our work clarifies why it is not expected to find good p-adic measures in the latter case.

We obtain a genuinely new construction in the unlikely setting where the p-th Hecke polynomial has a double root. In this case, our main result (Theorem 5) reads, as follows:

Theorem 1.

Let $f={\sum }_{n\ge 1}{a}_n{q}^n\in S_{k+2}({\mathsf{\Gamma }}_1\left(N\right),ϵ)$ be a cuspform, and assume that $P\left(X\right):=X^2-a_{p}X+ϵ\left(p\right)p^{k+1}$ has a double root α. Subsequently, there exists a locally analytic p-adic measure ${\mu }_{f,p}^{\mathrm{ext}}$ of ${\mathbb{Z}}_p^{\times }$, such that, for any locally polynomial character $\chi ={\chi }_0\left(x\right)x^m$ with $m\le k$:

$${\int }_{{\mathbb{Z}}_p^{\times }}\chi d{\mu }_{f,p}^{\mathrm{ext}}=\frac{4\pi }{{\mathsf{\Omega }}_f^{\pm }{i}^m}·e_p^{\mathrm{ext}}({\pi }_p,{\chi }_0)·L\left(m-k+\frac{1}{2},\pi ,{\chi }_0\right).$$

(1)

Here, $L\left(s,\pi ,{\chi }_0\right)$ denotes the complex the L-function of π that is twisted by ${\chi }_0$, and we have set

$$e_p^{\mathrm{ext}}({\pi }_p,{\chi }_0)=\left\{\begin{array}{cc}{(1-p^{-1})}^{-1}\left(p^{k-m}{\alpha }^{-1}+p^{m-k-1}\alpha -2p^{-1}\right);\hfill & {\chi }_0{\mid }_{{\mathbb{Z}}_p^{\times }}=1;\hfill \\ -{(1-p^{-1})}^{-1}r{p}^{r(m-k-1)}{\alpha }^r\tau \left({\chi }_0\right);\hfill & \mathrm{cond}\left({\chi }_0\right)=r>0,\hfill \end{array}\right.$$

where $\tau \left({\chi }_0\right)$ is the Gauss sum attached to ${\chi }_0$.

We call ${\mu }_{f,p}^{\mathrm{ext}}$the extremal p-adic measure. Coleman and Edixhoven showed in [5] that $P\left(X\right)$ never has double roots if the weight is 2, namely, $k=0$. Moreover, they showed that assuming Tate’s conjecture the polynomial $P\left(X\right)$ can never be a square for general weights $k+2$. Because we believe in Tate’s conjecture, we expect that this situation never occurs; hence, surely the hypothesis of the theorem is never fulfilled and ${\mu }_{f,p}^{\mathrm{ext}}$ can never be constructed. Because these extremal scenarios do appear in nature for other reductive groups, for instance, for ${\mathrm{GL}}_2/F$ where F is a totally real number field of even degree over $\mathbb{Q}$ (see [6], Section 3.3.1), we believe that our result above is potentially powerful. We plan to employ the approach of this note to cover these cases in the near future.

Notice that, in the unlikely situation of the above theorem, the two p-adic measures ${\mu }_{f,p}$ and ${\mu }_{f,p}^{\mathrm{ext}}$ coexist. Thus, one can define the p-adic L-function

$$L_p^{\mathrm{ext}}(f,s):={\int }_{{\mathbb{Z}}_p^{\times }}\exp (s·\log \left(\mathrm{x}\right))d{\mu }_{f,p}^{\mathrm{ext}}\left(x\right),$$

called the extremal p-adic L-function, which coexists with $L_p(f,s)$, and satisfies the interpolation property (1) with completely different Euler factors $e_p^{\mathrm{ext}}({\pi }_p,{\chi }_0)$ from the classical scenario.

In the non-critical setting, namely when the roots of the Hecke polynomial are distinct, there is a classical result that relates ${\mu }_{f,p}$ to a two-variable p-adic L-function ${\mathcal{L}}_p$ that interpolates ${\mu }_{g,p}$, as g ranges over a Coleman family passing through f. In [7], Betina and Williams have recently extended this result to this critical setting. They construct an element

$${\mathcal{L}}_p\in T{\widehat{\otimes }}_{{\mathbb{Q}}_p}\mathcal{R},$$

where $\mathcal{R}$ is the ${\mathbb{Q}}_p$-algebra of locally analytic distributions of ${\mathbb{Z}}_p^{\times }$ and T is certain Hecke algebra defining a connected component of the eigencurve. Because an element of the Coleman family corresponds to a morphism $g:T\to {\overline{\mathbb{Q}}}_p$, the function ${\mathcal{L}}_p$ is characterized by the property

$${\mathcal{L}}_p=C\left(g\right)·{\mu }_{g,p},$$

where $C\left(g\right)\in {\overline{\mathbb{Q}}}_p^{\times }$ is a constant normalized so that $C\left(f\right)=1$. The following result that was proved in Section 7.4 relates ${\mathcal{L}}_p$ to our extremal p-adic measure ${\mu }_{f,p}^{\mathrm{ext}}$:

Theorem 2.

Let $t\in T$ the element corresponding to $U_p-\alpha$. We have that

$$\frac{\partial {\mathcal{L}}_p}{\partial t}\left(f\right)\in {\alpha }^{-1}{\mu }_{f,p}^{\mathrm{ext}}+{\overline{\mathbb{Q}}}_p{\mu }_{f,p}.$$

This last result implies that these extremal p-adic L-functions are analogous to the so-called secondary p-adic L-functions that are defined by Bellaïche in [8].

1.2. Summary and Structure of the Paper

This paper consists of two principal achievements: on the one hand, we provide a reinterpretation of the p-adic cyclotomic distributions ${\mu }_{f,p}$ giving rise to the p-adic L-functions $L_p(f,p)$. After recalling the classical theory in Section 3, we introduce, in Section 4, our construction. Thanks to its local nature, this construction is available in every possible situation, except when the associated local automorphic representation is supercuspidal. We also provide sufficient conditions for our locally constant distributions ${\mu }_{f,p}$ to be extended to admissible locally analytic measures. Moreover, we exploit the automorphic nature of our construction in order to compute the interpolation properties of ${\mu }_{f,p}$, namely, the relation between such p-adic distributions and the classical L-functions $L(s,\pi )$.

On the other hand, exploiting the same techniques used in this new reinterpretation of the classical p-adic cyclotomic distributions ${\mu }_{f,p}$, we introduce, in Section 5, a genuinely new type of p-adic distribution ${\mu }_{f,p}^{\mathrm{ext}}$. Because such distribution is included in the formalism of the construction described above, we can prove its admissibility and, as shown in Theorem 1, we can describe its interpolation properties. Thus, ${\mu }_{f,p}^{\mathrm{ext}}$ extends to a locally analytic p-adic measure, giving rise to the extremal p-adic L-function $L_p^{\mathrm{ext}}(f,s)$.

There are several classical results that help in understanding better the classical p-adic measures ${\mu }_{f,p}$. The first one is the relation between ${\mu }_{f,p}$ and the so-called overconvergent modular symbols. Such overconvergent modular symbols are locally analytic extensions of the modular symbols attached to f. Pollack and Stevens showed, in [9], that we can obtain the p-adic measures ${\mu }_{f,p}$ alternatively by evaluating the corresponding overconvergent modular symbols at the degree zero divisor $0-\infty$. It is rather natural to ask ourselves whether there is an analogous description for ${\mu }_{f,p}^{\mathrm{ext}}$. In Section 6, we prove that this is indeed the case, and ${\mu }_{f,p}^{\mathrm{ext}}$ can be realized as the evaluation of the corresponding overconvergent modular symbol at $0-\infty$.

The second classical result relies on the relation ${\mu }_{f,p}$ with the eigencurve. The eigencurve is a rigid analytic space, whose points classify eigenvalues of the Hecke operators acting on the spaces of modular forms of any weight. For many interesting arithmetic applications, such as the Iwasawa Main Conjecture, it is convenient to construct a function ${\mathcal{L}}_p$ on the eigencurve, with values in certain ${\mathbb{Q}}_p$-algebra $\mathcal{R}$ of locally analytic distributions of ${\mathbb{Z}}_p^{\times }$, whose evaluation at the set of eigenvalues that are associated with f is given by ${\mu }_{f,p}$. In the non-critical setting, the construction of this two-variable p-adic L-function ${\mathcal{L}}_p$ is rather classical, but, in our critical setting, it is a very recent result due to Betina and Williams in [7]. In Section 7, we are able to relate our new p-adic measure ${\mu }_{f,p}^{\mathrm{ext}}$ with ${\mathcal{L}}_p$. Indeed, we prove, in Theorem 2, that the derivative of ${\mathcal{L}}_p$ with respect to $(U_p-\alpha )$ is given by the measure ${\mu }_{f,p}^{\mathrm{ext}}$.

1.3. Conclusions and Future Research

This new reinterpretation of the construction of ${\mu }_{f,p}$ has some interesting advantages. On the one side, it is purely automorphic and local. It relies on the construction of a well-behaved local morphism $\delta$ from the space of locally constant functions of ${\mathbb{Z}}_p^{\times }$ to the underlying space of the local automorphic representation that is associated with f (see Section 4.4). This formalism is totally transferable to the case of any automorphic representation of ${\mathrm{GL}}_2$ over any number field, because it only depends on the behaviour of the local automorphic representation. Hence, we expect to be able to construct p-adic measures and p-adic L-functions that are associated with any automorphic representation of ${\mathrm{GL}}_2$ for any weight over any number field. Some of the cases in this research line correspond to the work of Spiess in [4]. Moreover, if we exchange ${\mathbb{Z}}_p^{\times }$ by any torus in ${\mathrm{GL}}_2\left(F\right)$, for any p-adic field F, we expect to generalize the morphisms $\delta$ in order to obtain anti-cyclotomicp-adic L-functions that are associated with automorphic forms over quaternion algebras and certain quadratic extensions of the base field, extending our results in [10]. Hence, this formalism opens the door to many possible generalizations in many new and interesting scenarios.

On the other side, because the existence of ${\mu }_{f,p}$ is subject to the existence of a morphism $\delta$ with good properties, we expect that our work can shed some light on the problem of determining the existence of admissible p-adic L-functions when the local automorphic representation is supercuspidal. After a preliminary study of the possible morphisms $\delta$ in this situation, we believe that such an admissible measure may not exist, and it would be an interesting line of research to study whether that is indeed the case.

The main feature of the article is this new extremal p-adic measure ${\mu }_{f,p}^{\mathrm{ext}}$ that arises under the unlikely hypothesis that the p-th Hecke polynomial has a double root. This hypothesis is equivalent to the non semi-simplicity of the Hecke operator $U_p$, and it is excluded for ${\mathrm{GL}}_2$ over $\mathbb{Q}$ while assuming Tate’s conjecture. Although we have already noted that this construction can be generalized to the Hilbert setting where there are concrete examples where this hypothesis actually occur, such an irregular situation over $\mathbb{Q}$ is still interesting, as it is considered in this article. Indeed, the existence of ${\mu }_{f,p}^{\mathrm{ext}}$ with the mentioned interpolation properties and its relation with the two variable p-adic L-function ${\mathcal{L}}_p$ could lead to a better understanding of the semi-simplicity of $U_p$. The idea is to derive a contradiction starting from this irregular setting by exploring the properties of ${\mu }_{f,p}^{\mathrm{ext}}$.

1.4. Notation

For any ring R, we denote by $\mathcal{P}{\left(k\right)}_R:={\mathrm{Sym}}^k\left(R^2\right)$ the R-module of homogeneous polynomials in two variables with coefficients in R, endowed with an action of ${\mathrm{GL}}_2\left(R\right)$:

$$\left(\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)\ast P\right)(x,y):=P\left((x,y)\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)\right).$$

(2)

We denote by $V{\left(k\right)}_R:={\mathrm{Hom}}_R(\mathcal{P}{\left(k\right)}_R,R)$ and $V\left(k\right):=V{\left(k\right)}_{\mathbb{C}}$. Similarly, we define the (right-) action of $A\in {\mathrm{GL}}_2{\left(\mathbb{R}\right)}^{+}$ on the set of modular forms of weight $k+2$

$$(f\mid A)\left(z\right):=\rho {(A,z)}^{k+2}·f\left(Az\right);\rho \left(\left(\begin{array}{cc}a& b\\ c& d\end{array}\right),z\right):=\frac{(ad-bc)}{cz+d}.$$

We will denote by $dx$ the Haar measure of ${\mathbb{Q}}_p$ so that $\mathrm{vol}\left({\mathbb{Z}}_p\right)=1$. Similarly, we write $d^{\times }x$ for the Haar measure of ${\mathbb{Q}}_p^{\times }$ so that $\mathrm{vol}\left({\mathbb{Z}}_p^{\times }\right)=1$. By abuse of notation, will will also denote by $d^{\times }x$ the corresponding Haar measure of the group of ideles ${\mathbb{A}}^{\times }$.

For any local character $\chi :{\mathbb{Q}}_p^{\times }\to {\mathbb{C}}^{\times }$, write

$$L(s,\chi )=\left\{\begin{array}{cc}{(1-\chi \left(p\right)p^{-s})}^{-1},\hfill & \chi \mathrm{unramified}\\ 1,\hfill & \mathrm{otherwise}.\end{array}\right.$$

2. Local Integrals

In this section $\psi :{\mathbb{Q}}_p\to {\mathbb{C}}^{\times }$ will be a non-trivial additive character, such that $ker\left(\psi \right)={\mathbb{Z}}_p$.

Lemma 1.

For all $s\in {\mathbb{Q}}_p^{\times }$ and $n>0$, we have

$${\int }_{s+p^n{\mathbb{Z}}_p}\psi \left(ax\right)dx=p^{-n}\psi \left(sa\right)·1_{{\mathbb{Z}}_p}\left(p^{n}a\right).$$

In particular,

$${\int }_{{\mathbb{Z}}_p^{\times }}\psi \left(ax\right)dx=\left\{\begin{array}{cc}(1-p^{-1}),\hfill & a\in {\mathbb{Z}}_p\hfill \\ -p^{-1},\hfill & a\in p^{-1}{\mathbb{Z}}_p^{\times }\hfill \\ 0,\hfill & otherwise\hfill \end{array}\right.$$

Proof. 

We compute

$$\begin{array}{ccc}\hfill {\int }_{s+p^n{\mathbb{Z}}_p}\psi \left(xa\right)dx& =& {\int }_{p^n{\mathbb{Z}}_p}\psi \left((s+x)a\right)dx=\psi \left(sa\right){\int }_{{\mathbb{Z}}_p}\left|x{p}^n\right|\psi \left(x{p}^{n}a\right)d^{\times }x\hfill \\ & =& p^{-n}\psi \left(sa\right){\int }_{{\mathbb{Z}}_p}\psi \left(x{p}^{n}a\right)dx=p^{-n}\psi \left(sa\right)·1_{{\mathbb{Z}}_p}\left(p^{n}a\right).\hfill \end{array}$$

To deduce the second part, notice that

$${\int }_{{\mathbb{Z}}_p^{\times }}\psi \left(ax\right)dx=\sum _{s\in {(\mathbb{Z}/p\mathbb{Z})}^{\times }}{\int }_{s+p{\mathbb{Z}}_p}\psi \left(ax\right)dx=p^{-1}\sum _{s\in {(\mathbb{Z}/p\mathbb{Z})}^{\times }}\psi \left(sa\right)1_{{\mathbb{Z}}_p}\left(pa\right).$$

Hence the result follows. □

Lemma 2.

Let $\chi :{\mathbb{Z}}_p^{\times }\to {\mathbb{C}}^{\times }$ be a character of conductor $n\ge 1$. Let $1+p^n{\mathbb{Z}}_p\subset U\subseteq {\mathbb{Z}}_p^{\times }$ be an open subgroup. We have

$${\int }_U\chi \left(x\right)\psi \left(ax\right)d^{\times }x=0,unless\left|a\right|=p^n.$$

Proof. 

We compute

$$\begin{array}{ccc}\hfill {\int }_U\chi \left(x\right)\psi \left(ax\right)d^{\times }x& =& \sum _{s\in U/(1+p^n{\mathbb{Z}}_p)}\chi \left(s\right){\int }_{s+p^n{\mathbb{Z}}_p}\psi \left(ax\right)dx\hfill \\ & =& p^{-n}{1}_{{\mathbb{Z}}_p}\left(p^{n}a\right)\sum _{s\in U/(1+p^n{\mathbb{Z}}_p)}\chi \left(s\right)\psi \left(sa\right).\hfill \end{array}$$

Hence the integral $I:={\int }_U\chi \left(x\right)\psi \left(ax\right)d^{\times }x$ must be zero if $a\notin p^{-n}{\mathbb{Z}}_p$. Moreover, if $a\in p^{-n+1}{\mathbb{Z}}_p$,

$$I={\int }_U\chi \left(x(1+p^{n-1})\right)\psi \left(ax(1+p^{n-1})\right)d^{\times }x=\chi (1+p^{n-1})I=0,$$

and the result follows. □

3. Classical Cyclotomic p-Adic L-Function

3.1. Classical Modular Symbols

Let $f\in S_{k+2}(N,ϵ)$ be a modular cuspidal newform of weight $(k+2)$ level ${\mathsf{\Gamma }}_1\left(N\right)$ and nebentypus $ϵ$.

By definition, we have

$$(f\mid A)\left(z\right)·\left(A^{-1}P\right)(1,-z)·dz=det\left(A\right)·f\left(Az\right)·P(1,-Az)·d\left(Az\right),A\in {\mathrm{GL}}_2{\left(\mathbb{R}\right)}^{+},$$

for any $P\in V\left(k\right)$. Hence, if we denote by ${\Delta }_0$ the group of degree zero divisors of ${\mathbb{P}}^1\left(\mathbb{Q}\right)$ with the natural action of ${\mathrm{GL}}_2\left(\mathbb{Q}\right)$, we obtain the Modular Symbol:

$$\begin{array}{ccc}& & {\varphi }_f^{\pm }\in {\mathrm{Hom}}_{{\mathsf{\Gamma }}_1\left(N\right)}({\Delta }_0,V\left(k\right));\hfill \\ & & {\varphi }_f^{\pm }(s-t)\left(P\right):=2\pi i\left({\int }_t^{s}f\left(z\right)P(1,-z)dz\pm {\int }_{-t}^{-s}f\left(z\right)P(1,z)dz\right).\hfill \end{array}$$

Notice that ${\mathsf{\Gamma }}_1\left(N\right)$-equivariance follows from relation

$${\varphi }_{f\mid A}^{\pm }\left(D\right)=det\left(A\right)·A^{-1}\left({\varphi }_f^{\pm }\left(AD\right)\right),A\in {\mathrm{GL}}_2{\left(\mathbb{R}\right)}^{+},$$

(3)

deduced from the above equality and the fact that $\left(\begin{array}{cc}1& \\ & -1\end{array}\right)$ normalizes ${\mathsf{\Gamma }}_1\left(N\right)$. The following result is well known and classical:

Proposition 1.

There exists periods ${\mathsf{\Omega }}_{\pm }$, such that

$${\varphi }_f^{\pm }={\mathsf{\Omega }}_{\pm }·{\phi }_f^{\pm },$$

for some ${\phi }_f^{\pm }\in {\mathrm{Hom}}_{{\mathsf{\Gamma }}_1\left(N\right)}({\Delta }_0,V{\left(k\right)}_{R_f})$, where $R_f$ is the ring of coefficients of f.

3.2. Classical p-Adic Distributions

Given $f\in S_{k+2}(N,ϵ)$, we will assume that f is an eigenvector for the Hecke operator $T_p$ with eigenvalue $a_p$. Let $\alpha$ be a non-zero root of the Hecke polynomial $X^2-a_{p}X+ϵ\left(p\right)p^{k+1}$.

We will construct distributions ${\mu }_{f,\alpha }^{\pm }$ of locally polynomial functions of ${\mathbb{Z}}_p^{\times }$ of degree less that k attached to f (and $\alpha$ in case $p\nmid N$). Because the open sets $U(a,n)=a+p^n{\mathbb{Z}}_p$ ($a\in {\mathbb{Z}}_p^{\times }$ and $n\in \mathbb{N}$) form a basis of ${\mathbb{Z}}_p^{\times }$, it is enough to define the image of $P\left(1,\frac{x-a}{p^n}\right)1_{U(a,n)}\left(x\right)$, for any $P\in \mathcal{P}{\left(k\right)}_{\mathbb{Z}}$

$${\int }_{U(a,n)}P\left(1,\frac{x-a}{p^n}\right)d{\mu }_{f,\alpha }^{\pm }\left(x\right):=\frac{1}{{\alpha }^n}{\phi }_{f_{\alpha }}^{\pm }\left(\frac{a}{p^n}-\infty \right)\left(P\right),$$

(4)

where $f_{\alpha }\left(z\right):=f\left(z\right)-\beta ·f\left(pz\right)$ and $\beta =\frac{ϵ\left(p\right)p^{k+1}}{\alpha }$. It defines a distribution because ${\mu }_{f,\alpha }^{\pm }$ satisfies additivity, namely, since

$$P\left(1,\frac{x-a}{p^n}\right)1_{U(a,n)}\left(x\right)=\sum _{b\equiv a\mathrm{mod}{p}^n}\left({\gamma }_{a,b}P\right)\left(1,\frac{x-b}{p^{n+1}}\right)1_{U(b,n+1)}\left(x\right),{\gamma }_{a,b}:=\left(\begin{array}{cc}1& \frac{b-a}{p^n}\\ 0& p\end{array}\right),$$

it can be shown that

$${\int }_{U(a,n)}P\left(1,\frac{x-a}{p^n}\right)d{\mu }_{f,\alpha }^{\pm }\left(x\right)=\sum _{b\equiv a\mathrm{mod}{p}^n}{\int }_{U(b,n+1)}\left({\gamma }_{a,b}P\right)\left(1,\frac{x-b}{p^{n+1}}\right)d{\mu }_{f,\alpha }^{\pm }\left(x\right),$$

because, by (3), we have that $U_p{\phi }_{f_{\alpha }}^{\pm }=\alpha ·{\phi }_{f_{\alpha }}^{\pm }$, where

$$\left(U_p{\phi }_{f_{\alpha }}^{\pm }\right)\left(D\right):=\sum _{c\in \mathbb{Z}/p\mathbb{Z}}{\left(\begin{array}{cc}1& c\\ & p\end{array}\right)}^{-1}{\phi }_{f_{\alpha }}^{\pm }\left(\left(\begin{array}{cc}1& c\\ & p\end{array}\right)D\right).$$

(5)

The following result shows that, under certain hypothesis, we can extend ${\mu }_{f,\alpha }^{\pm }$ to a locally analytic measure.

Theorem 3

(Visnik, Amice-Vélu). Fix an integer h, such that $1\le h\le k+1$. Suppose that α satisfies ${\mathrm{ord}}_p\alpha <h$. Therefore, there exists a locally analytic measure ${\mu }_{f,\alpha }^{\pm }$ satifying:

• ${\int }_{U(a,n)}P\left(1,\frac{x-a}{p^n}\right)d{\mu }_{f,\alpha }^{\pm }\left(x\right):=\frac{1}{{\alpha }^n}{\phi }_{f_{\alpha }}^{\pm }\left(\frac{a}{p^n}-\infty \right)\left(P\right)$, for any locally polynomial function $P\left(1,\frac{x-a}{p^n}\right)1_{U(a,n)}\left(x\right)$ of degree strictly less than h.
• For any $m\ge 0$,

  $${\int }_{U(a,n)}{(x-a)}^{m}d{\mu }_{f,\alpha }^{\pm }\left(x\right)\in {\left(\frac{p^m}{\alpha }\right)}^n{\alpha }^{-1}.$$
• If $F\left(x\right)={\sum }_{m\ge 0}{c}_m{(x-a)}^m$ is convergent on $U(a,n)$, then

  $${\int }_{U(a,n)}F\left(x\right)d{\mu }_{f,\alpha }^{\pm }\left(x\right)=\sum _{m\ge 0}{c}_m{\int }_{U(a,n)}{(x-a)}^{m}d{\mu }_{f,\alpha }^{\pm }\left(x\right).$$

If we assume that there exists such a root $\alpha$ with ${\mathrm{ord}}_p\alpha <k+1$, then we define ${\mu }_{f,\alpha }:={\mu }_{f,\alpha }^{+}+{\mu }_{f,\alpha }^{-}$ and the (cyclotomic) p-adic L-function:

$$L_p(f,\alpha ,s):={\int }_{{\mathbb{Z}}_p^{\times }}\exp (s·\log \left(\mathrm{x}\right))d{\mu }_{f,\alpha }\left(x\right).$$

Remark 1.

Write $V_f$ the $\overline{\mathbb{Q}}\left[{\mathrm{GL}}_2\left(\mathbb{Q}\right)\right]$-representation generated by f. For any $g\in V_f$, write

$${\phi }_g^{\pm }(s-t)\left(P\right):=\frac{2\pi i}{{\mathsf{\Omega }}_{\pm }}\left({\int }_t^{s}g\left(z\right)P(1,-z)dz\pm {\int }_{-t}^{-s}g\left(z\right)P(1,z)dz\right).$$

(6)

Relation (3) implies that the morphism

$${\phi }^{\pm }:V_f⟶\mathrm{Hom}\left({\Delta }_0,V{\left(k\right)}_{\overline{\mathbb{Q}}}\right)[det],g\mapsto {\phi }_g^{\pm },$$

(7)

is ${\mathrm{GL}}_2\left(\mathbb{Q}\right)$-equivariant.

4. p-Adic L-Functions

In this section, we provide a reinterpretation of the distributions ${\mu }_{f,{\alpha }_p}^{\pm }$. Let $f\in S_{k+2}({\mathsf{\Gamma }}_1\left(N\right),ϵ)$ be a cuspidal newform as above and let p be any prime. Fix the embedding

$${\mathbb{Z}}_p^{\times }\hookrightarrow {\mathbb{Q}}_p^{\times }\hookrightarrow {\mathrm{GL}}_2\left({\mathbb{Q}}_p\right);x⟼\left(\begin{array}{cc}x& \\ & 1\end{array}\right).$$

(8)

Assumption 1.

Assume that there exists a ${\mathbb{Z}}_p^{\times }$-equivariant morphisms

$$\delta :C({\mathbb{Z}}_p^{\times },L)⟶V,$$

where L is certain finite extension of the coefficient field $\mathbb{Q}\left({\left\{a_n\right\}}_n\right)$, and V is certain model over L of the local automorphic representation ${\pi }_p$ generated by f. Additionally, assume that, for big enough n,

$$\left(\begin{array}{cc}1& s\\ & p^n\end{array}\right)\delta \left(1_{U(s,n)}\right)=\frac{1}{{\gamma }^n}\sum _{i=0}^m{c}_i(s,n)V_i,$$

(9)

where m is fixed, $V_i\in V$ do not depend neither s nor n, and $c_i(s,n)\in {\mathcal{O}}_L$.

4.1. p-Adic Distributions

Let us consider the subgroup

$${\widehat{K}}_1\left(N\right)=\left\{g\in {\mathrm{GL}}_2\left(\widehat{\mathbb{Z}}\right):g\equiv \left(\begin{array}{cc}\ast & \ast \\ 0& 1\end{array}\right)\mathrm{mod}N\right\}.$$

By strong approximation we have that ${\mathrm{GL}}_2\left({\mathbb{A}}_f\right)={\mathrm{GL}}_2{\left(\mathbb{Q}\right)}^{+}{\widehat{K}}_1\left(N\right)$. Thus, for any ${\mathrm{GL}}_2\left({\mathbb{A}}_f\right)\ni g=h_g{k}_g$, where $h_g\in {\mathrm{GL}}_2{\left(\mathbb{Q}\right)}^{+}$, $k_g\in {\widehat{K}}_1\left(N\right)$ are well defined up to multiplication by ${\mathsf{\Gamma }}_1\left(N\right)={\mathrm{GL}}_2{\left(\mathbb{Q}\right)}^{+}\cap {\widehat{K}}_1\left(N\right)$. Write $K:={\widehat{K}}_1\left(N\right)\cap {\mathrm{GL}}_2\left({\mathbb{Z}}_p\right)$. By strong multiplicity one, ${\pi }_p^K$ is one dimensional. Therefore, $V^K=L{w}_0$ and $V=L\left[{\mathrm{GL}}_2\left({\mathbb{Q}}_p\right)\right]w_0$. Notice that we have a natural morphism

$${\phi }_{f,p}^{\pm }:V⟶\mathrm{Hom}({\Delta }_0,V{\left(k\right)}_L);{\phi }_{f,p}^{\pm }\left(g{w}_0\right)=det\left(h_g\right)·{\phi }_{f\mid h_g^{-1}}^{\pm }.$$

Remark 2.

If $g\in {\mathrm{GL}}_2\left({\mathbb{Q}}_p\right)$ then $h_g\in {\widehat{K}}_1{\left(N\right)}^p:={\widehat{K}}_1\left(N\right)\cap {\prod }_{\ell \ne p}{\mathrm{GL}}_2\left({\mathbb{Q}}_{\ell }\right)$. This implies that, for any $h\in {\mathrm{GL}}_2{\left(\mathbb{Q}\right)}^{+}\cap {\widehat{K}}_1{\left(N\right)}^p$, we have $h_{hg}=h·h_g$ for all $g\in {\mathrm{GL}}_2\left({\mathbb{Q}}_p\right)$. By (3), this implies that ${\phi }_{f,p}^{\pm }\left(hv\right)=h\ast {\phi }_{f,p}^{\pm }\left(v\right)$, for all $v\in V\subset {\pi }_p$, where the action of $h\in {\mathrm{GL}}_2{\left(\mathbb{Q}\right)}^{+}\cap {\widehat{K}}_1{\left(N\right)}^p$ is given by

$$(h\ast \phi )\left(D\right):=h\left(\phi \left(h^{-1}D\right)\right),\phi \in \mathrm{Hom}({\Delta }_0,V{\left(k\right)}_L).$$

Remark 3.

By definition, for any $\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)\in {\mathsf{\Gamma }}_0\left(N\right)$, we have

$$f\left(\frac{az+b}{cz+d}\right)=ϵ\left(d\right)·{(cz+d)}^{k+2}f\left(z\right),f\mid \left(\begin{array}{cc}a& b\\ c& d\end{array}\right)=ϵ\left(d\right)·f.$$

For any $z\in {\mathbb{Q}}_p^{\times }$, such that $z=p^{n}u$ where $u\in {\mathbb{Z}}_p^{\times }$, we can choose $d\in \mathbb{Z}$ such that $d\equiv u^{-1}\mathrm{mod}N{\mathbb{Z}}_p$ and $d\equiv p^n\mathrm{mod}N{\mathbb{Z}}_{\ell }$, for $\ell \ne p$. Let us choose $A=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)\in {\mathsf{\Gamma }}_0\left(N\right)$, and we have

$$(z,1)=p^n{A}^{-1}(uA, p^{-n}A)\in {\mathrm{GL}}_2\left({\mathbb{A}}_f\right),(uA, p^{-n}A)\in {\widehat{K}}_1\left(N\right).$$

This implies that, if ${\epsilon }_p$ is the central character of ${\pi }_p$,

$${\epsilon }_p\left(z\right){\phi }_{f,p}^{\pm }\left(w_0\right)={\phi }_{f,p}^{\pm }\left(z{w}_0\right)=det\left(p^n{A}^{-1}\right)·{\phi }_{f\mid p^{-n}A}^{\pm }=p^{-nk}ϵ\left(d\right)·{\phi }_f^{\pm }$$

Hence, ${\epsilon }_p={ϵ}_p^{-1}{|·|}^k$, where ${ϵ}_p=ϵ{\mid }_{{\mathbb{Z}}_p^{\times }}$.

Let $C_k({\mathbb{Z}}_p^{\times },{\mathbb{C}}_p)$ be the space of locally polynomial functions of ${\mathbb{Z}}_p^{\times }$ of degree less that k. Notice that we have a ${\mathbb{Z}}_p^{\times }$-equivariant isomorphism

$$ı:C({\mathbb{Z}}_p^{\times },\mathbb{Z}){\otimes }_{\mathbb{Z}}\mathcal{P}{\left(k\right)}_{{\mathbb{C}}_p}(-k)⟶C_k({\mathbb{Z}}_p^{\times },{\mathbb{C}}_p);h\otimes P⟼P(1,x)·h\left(x\right),$$

(10)

where $(-k)$ stands for the twist by the character $x\mapsto x^{-k}$.

Fixing $L\hookrightarrow {\mathbb{C}}_p$, we define the distributions ${\mu }_{f,\delta }^{\pm }$ that are attached to f and $\delta$:

$${\int }_{{\mathbb{Z}}_p^{\times }}ı(h\otimes P)\left(x\right)d{\mu }_{f,\delta }^{\pm }\left(x\right):={\phi }_{f,p}^{\pm }\left(\delta \left(h\right)\right)(0-\infty )\left(P\right).$$

(11)

4.2. Admissible Distributions

We have just constructed a distribution

$${\mu }_{f,\delta }^{\pm }:C_k({\mathbb{Z}}_p^{\times },{\mathbb{C}}_p)⟶{\mathbb{C}}_p.$$

This section is devoted to extend this distribution to a locally analytic measure ${\mu }_{f,\delta }^{\pm }\in \mathrm{Hom}\left(C_{\mathrm{loc}-\mathrm{an}}({\mathbb{Z}}_p^{\times },{\mathbb{C}}_p),{\mathbb{C}}_p\right)$.

Definition 1.

Write $v_p:{\mathbb{C}}_p\to \mathbb{Q}\cup \{-\infty \}$ the usual normalized p-adic valuation. For any $h\in {\mathbb{R}}^{+}$, a distribution $\mu \in \mathrm{Hom}(C_k({\mathbb{Z}}_p^{\times },{\mathbb{C}}_p),{\mathbb{C}}_p)$ ish-admissible if

$$v_p\left({\int }_{U(a,n)}gd\mu \right)\ge v_p\left(A\right)-n·h,$$

for some fixed $A\in {\mathbb{C}}_p$, and any $g\in C_k({\mathbb{Z}}_p^{\times },{\mathcal{O}}_{{\mathbb{C}}_p})$ which is polynomical in a small enough $U(a,n)\subseteq {\mathbb{Z}}_p^{\times }$. We will denote a previous relation by

$${\int }_{U(a,n)}gd\mu \in A·p^{-nh}{\mathcal{O}}_{{\mathbb{C}}_p}.$$

Proposition 2.

If $h<k+1$, a h-admissible the distribution μ can be extended to a locally analytic measure, such that

$${\int }_{U(a,n)}gd\mu \in A·p^{-nh}{\mathcal{O}}_{{\mathbb{C}}_p},$$

for any $g\in C({\mathbb{Z}}_p^{\times },{\mathcal{O}}_{{\mathbb{C}}_p})$ which is analytic in $U(a,n)$.

Proof. 

Notice that any locally analytic function is topologically generated by functions of the form $P_m^{a,N}\left(x\right):={\left(\frac{x-a}{p^N}\right)}^m{1}_{U(a,N)}\left(x\right)$, where $m\in \mathbb{N}$. By definition, we have defined the values $\mu \left(P_m^{a,N}\right)$ when $m\le k$. If $m>h$, we define $\mu \left(P_m^{a,N}\right)={lim}_{n\to \infty }{a}_n$, where

$$a_n=\sum _{b\mathrm{mod}{p}^n;b\equiv a\mathrm{mod}{p}^N}\sum _{j\le h}{\left(\frac{b-a}{p^N}\right)}^{m-j}\left(\genfrac{}{}{0pt}{}{m}{j}\right)p^{j(n-N)}\mu \left(P_j^{b,n}\right).$$

This definition agrees with $\mu$ when $h<m\le k$ because $p^{j(n-N)}\mu \left(P_j^{b,n}\right)\stackrel{n}{\to }0$ when $j>h$, hence

$$\underset{n\to \infty }{lim}{a}_n=\sum _{b\mathrm{mod}{p}^n;b\equiv a\mathrm{mod}{p}^N}\sum _{j=0}^m{\left(\frac{b-a}{p^N}\right)}^{m-j}\left(\genfrac{}{}{0pt}{}{m}{j}\right)p^{j(n-N)}\mu \left(P_j^{b,n}\right)=\mu \left(P_m^{a,N}\right).$$

The limit converges because ${\left\{a_n\right\}}_n$ is Cauchy. Indeed by additivity

$$a_{n_2}-a_{n_1}=\sum _{j\le h}\sum _{b\equiv a\left(p^{n_2}\right)}\sum _{b^{\prime }\equiv b\left(p^{n_1}\right)}\sum _{s=h+1}^{m}r\left(s\right)\left(\genfrac{}{}{0pt}{}{s}{j}\right){\left(\frac{b^{\prime }-b}{p^N}\right)}^{s-j}{p}^{(n_2-N)j}\mu \left(P_j^{b^{\prime },n_2}\right),$$

where $r\left(s\right)=\left(\genfrac{}{}{0pt}{}{m}{s}\right){\left(\frac{b^{\prime }-a}{p^N}\right)}^{m-s}$. Because

$${\left(\frac{b^{\prime }-b}{p^N}\right)}^{s-j}{p}^{(n_2-N)j}\mu \left(P_j^{b^{\prime },n_2}\right)\in A·p^{-Ns}{p}^{(n_1-n_2)(s-j)}{p}^{(s-h)n_2}{\mathcal{O}}_{{\mathbb{C}}_p},$$

we have that $a_{n+1}-a_n\stackrel{n}{\to }0$.

It is clear by the definition that $\mu \left(P_m^{a,N}\right)\in A·p^{-Nh}{\mathcal{O}}_{{\mathbb{C}}_p}$ for all $m,a$ and N. Moreover, it extends to a locally analytic measure by continuity, which is determined by the image of locally polynomial functions of degree at most h. □

Notice that, for all $m\le k$,

$$P_m^{a,n}\left(x\right)={\left(\frac{x-a}{p^n}\right)}^m{1}_{U(a,n)}\left(x\right)=ı\left(1_{U(a,n)}\otimes {\left(\frac{Y-aX}{p^n}\right)}^m{X}^{k-m}\right).$$

Using property (9) and Remarks 2 and 3, we compute that

$$\begin{array}{ccc}\hfill {\int }_{{\mathbb{Z}}_p^{\times }}{P}_m^{a,n}d{\mu }_{f,p}^{\pm }& =& {\phi }_{f,p}^{\pm }\left(\delta \left(1_{U(a,n)}\right)\right)(0-\infty )\left({\left(\frac{Y-aX}{p^n}\right)}^m{X}^{k-m}\right)\hfill \\ & =& \sum _{i=0}^m\frac{c_i(a,n)}{{\gamma }^n}·{\phi }_{f,p}^{\pm }\left(p^{-n}\left(\begin{array}{cc}{p}^n& -a\\ & 1\end{array}\right)V_i\right)(0-\infty )\left({\left(\frac{Y-aX}{p^n}\right)}^m{X}^{k-m}\right)\hfill \\ & =& \sum _{i=0}^m\frac{c_i(a,n)}{{\epsilon }_p{\left(p\right)}^n{\gamma }^n}·{\phi }_{f,p}^{\pm }\left(V_i\right)\left(\frac{a}{p^n}-\infty \right)\left({\left(p^{-n}Y\right)}^m{\left(p^{-n}X\right)}^{k-m})\right)\hfill \\ & =& \sum _{i=0}^m\frac{c_i(a,n)}{{\gamma }^n}·{\phi }_{f,p}^{\pm }\left(V_i\right)\left(\frac{a}{p^n}-\infty \right)\left(Y^m{X}^{k-m}\right).\hfill \end{array}$$

Notice that ${\phi }_{f,p}^{\pm }\left(V_i\right)\in \mathrm{Hom}{({\Delta }_0,V{\left(k\right)}_L)}_{ϵ}^{{\mathsf{\Gamma }}_1\left(N{p}^r\right)}:={\mathrm{Hom}}_{{\mathsf{\Gamma }}_1\left(N{p}^r\right)}{({\Delta }_0,V{\left(k\right)}_L)}_{ϵ}$ for some big enough $r\in \mathbb{N}$, where the subindex $ϵ$ indicates that the action of ${\mathsf{\Gamma }}_1\left(N{p}^r\right)/{\mathsf{\Gamma }}_0\left(N{p}^r\right)$ is given by the character $ϵ$. By Manin’s trick, we have that

$${\mathrm{Hom}}_{{\mathsf{\Gamma }}_1\left(N{p}^r\right)}{({\Delta }_0,V{\left(k\right)}_L)}_{ϵ}\simeq {\mathrm{Hom}}_{{\mathsf{\Gamma }}_1\left(N{p}^r\right)}{({\Delta }_0,V{\left(k\right)}_{{\mathcal{O}}_L})}_{ϵ}{\otimes }_{{\mathcal{O}}_L}L.$$

Because $Y^m{X}^{k-m}\in \mathcal{P}{\left(k\right)}_{{\mathcal{O}}_L}$, $c(a,n)\in {\mathcal{O}}_L$ and the functions $P_m^{a,n}$ generate $C_k({\mathbb{Z}}_p^{\times },{\mathcal{O}}_{{\mathbb{C}}_p})$, we obtain that

$${\int }_{U(a,n)}gd{\mu }_{f,\delta }^{\pm }\in \frac{A}{{\gamma }^n}{\mathcal{O}}_{{\mathbb{C}}_p},\mathrm{for} \mathrm{all} g\in C_k({\mathbb{Z}}_p^{\times },{\mathcal{O}}_{{\mathbb{C}}_p}),$$

(12)

for some fixed $A\in L$. We deduce the following result.

Theorem 4.

Fix an embedding $L\hookrightarrow {\mathbb{C}}_p$. We have that ${\mu }_{f,\delta }^{\pm }$ is $v_p\left(\gamma \right)$-admissible.

Definition 2.

If we assume that $v_p\left(\gamma \right)<k+1$, we define the cyclotomic p-adic measure attached to f and δ

$${\mu }_{f,\delta }:={\mu }_{f,\delta }^{+}+{\mu }_{f,\delta }^{-}.$$

4.3. Interpolation Properties

Given the modular form $f\in S_{k+2}\left({\mathsf{\Gamma }}_1\left(N\right)\right)$, we can define an automorphic form $\varphi :{\mathrm{GL}}_2\left(\mathbb{Q}\right)\backslash {\mathrm{GL}}_2\left(\mathbb{A}\right)\to \mathbb{C}$ associated with f. Indeed, one has that ${\mathrm{GL}}_2\left(\mathbb{A}\right)={\mathrm{GL}}_2\left(\mathbb{Q}\right)({\mathrm{GL}}_2{\left(\mathbb{R}\right)}^{+}\times {\mathrm{GL}}_2\left({\mathbb{A}}_f\right))$, hence $\varphi$ can be seen as the ${\mathrm{GL}}_2\left(\mathbb{Q}\right)$-invariant function of ${\mathrm{GL}}_2\left(\mathbb{A}\right)$, whose restriction to ${\mathrm{GL}}_2{\left(\mathbb{R}\right)}^{+}\times {\mathrm{GL}}_2\left({\mathbb{A}}_f\right)$ is

$$\varphi (g_{\infty },g_f)=\frac{det\left(\gamma \right)}{det\left(g_{\infty }\right)}·f\mid {\gamma }^{-1}{g}_{\infty }\left(i\right),g_f=\gamma k\in {\mathrm{GL}}_2{\left(\mathbb{Q}\right)}^{+}{\widehat{K}}_1\left(N\right),g_{\infty }=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right).$$

Given $g\in {\mathrm{GL}}_2\left({\mathbb{Q}}_p\right)$, we compute ${\phi }_{f,p}^{\pm }\left(g{w}_0\right)(0-\infty )\left(Y^m{X}^{k-m}\right)=$

$$\begin{array}{ccc}& =& det\left(h_g\right)·{\phi }_{f\mid h_g^{-1}}^{\pm }(0-\infty )\left(Y^m{X}^{k-m}\right)\hfill \\ & =& \frac{-2\pi det\left(h_g\right)}{{\mathsf{\Omega }}_f^{\pm }}·\left({\int }_{\infty }^{0}f\mid h_g^{-1}\left(ix\right){(-ix)}^{m}dx\pm {\int }_{\infty }^{0}f\mid h_g^{-1}\left(ix\right){\left(ix\right)}^{m}dx\right)\hfill \\ & =& \frac{2\pi }{{\mathsf{\Omega }}_f^{\pm }}·{\int }_{{\mathbb{R}}^{+}}{x}^{m-k}·\varphi \left(\left(\begin{array}{cc}x& \\ & 1\end{array}\right),g\right)d^{\times }x·({(-i)}^m\pm i^m).\hfill \end{array}$$

This implies that, if we consider the automorphic representation $\pi$ generated by $\varphi$, and the ${\mathrm{GL}}_2\left({\mathbb{Q}}_p\right)$-equivariant morphism

$${\varphi }_f:{\pi }_p⟶\pi :g{w}_0⟼g\varphi ,$$

we have that

$${\phi }_{f,p}^{\pm }\left(\delta \left(h\right)\right)(0-\infty )\left(Y^m{X}^{k-m}\right)=\frac{4\pi {(-i)}^m}{{\mathsf{\Omega }}_f^{\pm }}·{\int }_{{\mathbb{R}}^{+}}{x}^{m-k}·{\varphi }_f\left(\delta \left(h\right)\right)\left(\left(\begin{array}{cc}x& \\ & 1\end{array}\right),1\right)d^{\times }x·\left(\frac{1\pm {(-1)}^m}{2}\right).$$

Let H be the maximum subgroup of ${\mathbb{Z}}_p^{\times }$ such that $h{\mid }_{sH}$ is constant, for all $sH\in {\mathbb{Z}}_p^{\times }/H$. Notice that $h={\sum }_{s\in {\mathbb{Z}}_p^{\times }/H}h\left(s\right)1_{sH}$. Moreover, for all $v\in {\pi }_p$, the automorphic form ${\varphi }_f\left(v\right)$ is $U^p:={\prod }_{\ell \ne p}{\mathbb{Z}}_{\ell }^{\times }$-invariant when embedded in ${\mathrm{GL}}_2\left({\mathbb{A}}_f\right)$ by means of (8). Hence, if we consider ${\phi }_{f,p}:={\phi }_{f,p}^{+}+{\phi }_{f,p}^{-}$, then we have ${\phi }_{f,p}\left(\delta \left(h\right)\right)(0-\infty )\left(Y^m{X}^{k-m}\right)=$

$$\begin{array}{ccc}& =& \sum _{sH\in {\mathbb{Z}}_p^{\times }/H}\frac{4\pi h\left(s\right)}{i^m{\mathsf{\Omega }}_f^{\pm }}·{\int }_{{\mathbb{R}}^{+}}{\int }_{U^p}{x}^{m-k}{\varphi }_f\left(\delta \left(1_{sH}\right)\right)\left(\left(\begin{array}{cc}x& \\ & 1\end{array}\right),1,\left(\begin{array}{cc}t& \\ & 1\end{array}\right)\right)d^{\times }x{d}^{\times }t\hfill \\ & =& \sum _{sH\in {\mathbb{Z}}_p^{\times }/H}\frac{4\pi h\left(s\right)}{i^m{\mathsf{\Omega }}_f^{\pm }}·{\int }_{{\mathbb{R}}^{+}}{\int }_{U^p}{x}^{m-k}{\varphi }_f\left(\delta \left(1_H\right)\right)\left(\left(\begin{array}{cc}x& \\ & 1\end{array}\right),\left(\begin{array}{cc}s& \\ & 1\end{array}\right),\left(\begin{array}{cc}t& \\ & 1\end{array}\right)\right)d^{\times }x{d}^{\times }t\hfill \\ & =& \frac{4\pi }{{\mathsf{\Omega }}_f^{\pm }\mathrm{vol}\left(H\right)}·{\int }_{{\mathbb{A}}^{\times }/{\mathbb{Q}}^{\times }}\tilde{h}\left(y\right)·{\varphi }_f\left(\delta \left(1_H\right)\right)\left(\begin{array}{cc}y& \\ & 1\end{array}\right)d^{\times }y,\hfill \end{array}$$

where $\tilde{h}\left(y\right)={(-i)}^m·h(y_p\left|y\right|y_{\infty }^{-1}{)·|y|}^{m-k}$, for all $y={\left(y_v\right)}_v\in {\mathbb{A}}^{\times }$, and ${\mathsf{\Omega }}_f^{\pm }$ is ${\mathsf{\Omega }}_f^{+}$ or ${\mathsf{\Omega }}_f^{-}$, depending on whether m is even or odd.

Let $\chi \in C_k({\mathbb{Z}}_p^{\times },{\mathbb{C}}_p)$ be a locally polynomial character. This implies that $\chi \left(x\right)={\chi }_0\left(x\right)x^m$, for some natural $m\le k$ and some locally constant character ${\chi }_0$. In particular $\chi =ı({\chi }_0\otimes Y^m{X}^{k-m})$. We deduce that

$${\int }_{{\mathbb{Z}}_p^{\times }}\chi \left(x\right)d{\mu }_{f,\delta }\left(x\right):=\frac{4\pi }{{\mathsf{\Omega }}_f^{\pm }{i}^m\mathrm{vol}\left(H\right)}·{\int }_{{\mathbb{A}}^{\times }/{\mathbb{Q}}^{\times }}{\tilde{\chi }}_0\left(y\right){\left|y\right|}^{m-k}{\varphi }_f\left(\delta \left(1_H\right)\right)\left(\begin{array}{cc}y& \\ & 1\end{array}\right)d^{\times }y,$$

where ${\tilde{\chi }}_0\left(y\right):={\chi }_0(y_p\left|y\right|y_{\infty }^{-1})$.

Let $\psi :\mathbb{A}/\mathbb{Q}\to {\mathbb{C}}^{\times }$ be a global additive character and we define the Whittaker model element

$$W_{\delta }^H:{\mathrm{GL}}_2\left(\mathbb{A}\right)⟶\mathbb{C};W_{\delta }^H\left(g\right):={\int }_{\mathbb{A}/\mathbb{Q}}{\varphi }_f\left(\delta \left(1_H\right)\right)\left(\left(\begin{array}{cc}1& x\\ & 1\end{array}\right)g\right)\psi (-x)dx.$$

This element admits a expression $W_{\delta }^H\left(g\right)={\prod }_v{W}_{\delta ,v}^H\left(g_v\right)$, if $g=\left(g_v\right)\in {\mathrm{GL}}_2\left(\mathbb{A}\right)$. Moreover, by Theorem 3.5.5 in [11], it provides the Fourier expansion

$${\varphi }_f\left(\delta \left(1_H\right)\right)\left(g\right)=\sum _{a\in {\mathbb{Q}}^{\times }}{W}_{\delta }^H\left(\left(\begin{array}{cc}a& \\ & 1\end{array}\right)g\right).$$

We compute

$$\begin{array}{ccc}\hfill {\int }_{{\mathbb{A}}^{\times }/{\mathbb{Q}}^{\times }}{\tilde{\chi }}_0\left(y\right){\left|y\right|}^{m-k}{\varphi }_f\left(\delta \left(1_H\right)\right)\left(\begin{array}{cc}y& \\ & 1\end{array}\right)d^{\times }y& =& {\int }_{{\mathbb{A}}^{\times }}{\tilde{\chi }}_0\left(y\right){\left|y\right|}^{m-k}{W}_{\delta }^H\left(\begin{array}{cc}y& \\ & 1\end{array}\right)d^{\times }y\hfill \\ & =& \prod _v{\int }_{{\mathbb{Q}}_v^{\times }}{\tilde{\chi }}_0\left(y_v\right){\left|y_v\right|}^{m-k}{W}_{\delta ,v}^H\left(\begin{array}{cc}{y}_v& \\ & 1\end{array}\right)d^{\times }{y}_v.\hfill \end{array}$$

By definition of $\delta$, when $v\ne p$ the element $W_{\delta ,v}^H$ correspond to the new-vector, thus by Proposition 3.5.3 in [11]

$${\int }_{{\mathbb{Q}}_v^{\times }}{\tilde{\chi }}_0\left(y_v\right){\left|y_v\right|}^{m-k}{W}_{\delta ,v}^H\left(\begin{array}{cc}{y}_v& \\ & 1\end{array}\right)d^{\times }{y}_v=L_v\left(m-k+\frac{1}{2},{\pi }_v,{\tilde{\chi }}_0\right),v\ne p.$$

By Section 3.5 of [11], We conclude

$${\int }_{{\mathbb{Z}}_p^{\times }}\chi \left(x\right)d{\mu }_{f,\delta }\left(x\right)=\frac{4\pi }{{\mathsf{\Omega }}_f^{\pm }{i}^m}·e_{\delta }({\pi }_p,{\chi }_0)·L\left(m-k+\frac{1}{2},\pi ,{\tilde{\chi }}_0\right),$$

where the Euler factor

$$e_{\delta }({\pi }_p,{\chi }_0)=\frac{L_p{\left(m-k+\frac{1}{2},{\pi }_p,{\tilde{\chi }}_0\right)}^{-1}}{\mathrm{vol}\left(H\right)}{\int }_{{\mathbb{Q}}_p^{\times }}{\tilde{\chi }}_0\left(y_p\right){\left|y_p\right|}^{m-k}{W}_{\delta ,p}^H\left(\begin{array}{cc}{y}_p& \\ & 1\end{array}\right)d^{\times }{y}_p.$$

4.4. The Morphisms $\delta$

In this section, we will construct morphisms $\delta$ satisfying Assumption 1. The only case that will be left is the case when ${\pi }_p$ is supercuspidal. In this situation, we will not be able to construct admissible p-adic distributions.

Let ${\pi }_p$ be the local representation. Let $W:{\pi }_p\to \mathbb{C}$ be the Whittaker functional, and let us consider the Kirillov model $\mathcal{K}$ that is given by the embedding

$$\lambda :{\pi }_p\hookrightarrow \mathcal{K};\lambda \left(v\right)\left(y\right)=W\left(\left(\begin{array}{cc}y& \\ & 1\end{array}\right)v\right).$$

Recall that the Kirillov model lies in the space of locally constant functions $\varphi :{\mathbb{Q}}_p^{\times }\to \mathbb{C}$ endowed with the action

$$\left(\begin{array}{cc}1& x\\ & 1\end{array}\right)\varphi \left(y\right)=\psi \left(xy\right)\varphi \left(y\right),\left(\begin{array}{cc}a& \\ & 1\end{array}\right)\varphi \left(y\right)=\varphi \left(ay\right).$$

(13)

We construct the ${\mathbb{Z}}_p^{\times }$-equivariant morphism

$$\delta :C({\mathbb{Z}}_p^{\times },\mathbb{C})⟶\mathcal{K};\delta \left(h\right)\left(y\right)={\int }_{{\mathbb{Z}}_p^{\times }}\mathsf{\Psi }\left(zy\right)h\left(z\right)\psi (-zy)d^{\times }z,$$

(14)

for a well chosen locally constant function $\mathsf{\Psi }$. Notice that, if $h=1_H$ for H small enough

$$\delta \left(h\right)\left(y\right)=\mathsf{\Psi }\left(y\right){\int }_H\psi (-zy)d^{\times }z=\mathrm{vol}\left(H\right)\mathsf{\Psi }\left(y\right),\mathrm{if} \left|y\right|<<0.$$

This implies that, in order to choose $\mathsf{\Psi }$, we need to control how $\mathcal{K}$ looks like:

• By Theorem 4.7.2 in [11], if ${\pi }_p=\pi ({\chi }_1,{\chi }_2)$ principal series then $\mathcal{K}$ consists on functions $\varphi$, such that $\varphi \left(y\right)=0$ for $\left|y\right|>>0$, and

  $$\varphi \left(y\right)=\left\{\begin{array}{cc}{C}_1{\left|y\right|}^{1/2}{\chi }_1\left(y\right)+C_2{\left|y\right|}^{1/2}{\chi }_2\left(y\right),\hfill & {\chi }_1\ne {\chi }_2,\hfill \\ C_1{\left|y\right|}^{1/2}{\chi }_1\left(y\right)+C_2{v}_p\left(y\right){\left|y\right|}^{1/2}{\chi }_1\left(y\right),\hfill & {\chi }_1={\chi }_2,\hfill \end{array}\right.\left|y\right|<<0,$$

  for some constants $C_1$ and $C_2$.
• By Theorem 4.7.3 in [11], if ${\pi }_p=\sigma ({\chi }_1,{\chi }_2)$ a special representation such that ${\chi }_1{\chi }_2^{-1}={|·|}^{-1}$ then $\mathcal{K}$ consists on functions $\varphi$, such that $\varphi \left(y\right)=0$ for $\left|y\right|>>0$, and

  $$\varphi \left(y\right)={C\left|y\right|}^{1/2}{\chi }_2\left(y\right),\left|y\right|<<0,$$

  for some constant C.
• By Theorem 4.7.1 in [11], if ${\pi }_p$ is supercuspidal then $\mathcal{K}=C_c({\mathbb{Q}}_p^{\times },\mathbb{C})$.

By Lemmas 1 and 2 we have that $\delta \left(h\right)\left(y\right)=0$ for y with big absolute value. This implies that

• In case ${\pi }_p=\pi ({\chi }_1,{\chi }_2)$ with ${\chi }_1\ne {\chi }_2$, we can choose

  $$\mathsf{\Psi }={|·|}^{1/2}{\chi }_1\mathrm{or}\mathsf{\Psi }={|·|}^{1/2}{\chi }_2.$$
• In case ${\pi }_p=\pi ({\chi }_1,{\chi }_2)$ with ${\chi }_1={\chi }_2$, we can choose

  $$\mathsf{\Psi }={|·|}^{1/2}{\chi }_1\mathrm{or}\mathsf{\Psi }=v·{|·|}^{1/2}{\chi }_1.$$
• In case ${\pi }_p=\sigma ({\chi }_1,{\chi }_2)$, we have

  $$\mathsf{\Psi }={|·|}^{1/2}{\chi }_2.$$
• In case ${\pi }_p$ supercuspidal, it is not possible to choose any $\mathsf{\Psi }$.

We have to prove whether $\delta$ satisfies the property (9): if $\mathsf{\Psi }$ is invariant under the action of $1+p^n{\mathbb{Z}}_p$,

$$\begin{array}{ccc}\hfill \left(\begin{array}{cc}1& a\\ & p^n\end{array}\right)\delta \left(1_{U(a,n)}\right)\left(y\right)=& =& \left(\begin{array}{cc}{p}^n& \\ & p^n\end{array}\right)\left(\begin{array}{cc}{p}^{-n}& \\ & 1\end{array}\right)\left(\begin{array}{cc}1& a\\ & 1\end{array}\right)\delta \left(1_{U(a,n)}\right)\left(y\right)\hfill \\ & =& {\epsilon }_p\left(p^n\right)·\psi \left(a{p}^{-n}y\right)·\delta \left(1_{U(a,n)}\right)\left(p^{-n}y\right)\hfill \\ & =& {\epsilon }_p{\left(p\right)}^n·{\int }_{U(a,n)}\mathsf{\Psi }\left(p^{-n}yz\right)\psi \left(p^{-n}y(a-z)\right)d^{\times }z\hfill \\ & =& \frac{{\epsilon }_p{\left(p\right)}^n·\mathsf{\Psi }\left(p^{-n}ya\right)·{\left|p\right|}^n}{1-p^{-1}}·{\int }_{{\mathbb{Z}}_p}\psi \left(yz\right)dz\hfill \\ & =& \frac{{\epsilon }_p{\left(p\right)}^n·{\left|p\right|}^n}{1-p^{-1}}·\mathsf{\Psi }\left(p^{-n}ya\right)·1_{{\mathbb{Z}}_p}\left(y\right),\hfill \end{array}$$

because $d^{\times }x={(1-p^{-1})}^{-1}{\left|x\right|}^{-1}dx$.

• If $\mathsf{\Psi }$ is a character, then we deduce the property (9) with $m=0$, $\gamma =\mathsf{\Psi }\left(p\right)p{\epsilon }_p{\left(p\right)}^{-1}$, $c_0(a,n)=\mathsf{\Psi }\left(a\right)$ and $V_0={(1-p^{-1})}^{-1}\mathsf{\Psi }\left(y\right)1_{{\mathbb{Z}}_p}\left(y\right)$.
• If $\mathsf{\Psi }=v_p·\chi$, with $\chi$ a character, it also satisfies property (9) with $m=1$, $\gamma =\chi \left(p\right)p{\epsilon }_p{\left(p\right)}^{-1}$, $c_0(a,n)=-n\chi \left(a\right)$, $c_1(a,n)=\chi \left(a\right)$, $V_0={(1-p^{-1})}^{-1}\chi \left(y\right)1_{{\mathbb{Z}}_p}\left(y\right)$ and $V_1={(1-p^{-1})}^{-1}{v}_p\left(y\right)\chi \left(y\right)1_{{\mathbb{Z}}_p}\left(y\right)$.

4.5. Computation Euler Factors

We first define the Gauss sum attached to a character:

Definition 3.

For any character $\chi :{\mathbb{Z}}_p^{\times }\to {\mathbb{C}}^{\times }$ of conductor $n\ge 0$,

$$\tau \left(\chi \right)=\tau (\chi ,\psi )=p^n{\int }_{{\mathbb{Z}}_p^{\times }}\chi \left(x\right)\psi (-p^{-n}x)dx.$$

The following result describes the Euler factors in each of the situations:

Proposition 3.

We have the following cases:

$\left(i\right)$

If $\mathsf{\Psi }={|·|}^{1/2}{\chi }_i$,

$$e_{\delta }({\pi }_p,{\chi }_0)=\left\{\begin{array}{cc}\frac{{(1-p^{-1})}^{-1}{p}^{r(m-k-\frac{1}{2})}{\chi }_i{\left(p\right)}^{-r}\tau ({\chi }_0{\chi }_i,\psi )}{L(m-k+1/2,{\tilde{\chi }}_0{\chi }_j)L(k-m+1/2,{\tilde{\chi }}_0{\chi }_i^{-1})},\hfill & {\pi }_p=\pi ({\chi }_i,{\chi }_j);\\ \frac{{(1-p^{-1})}^{-1}{p}^{r(m-k-\frac{1}{2})}{\chi }_i{\left(p\right)}^{-r}\tau ({\chi }_0{\chi }_i,\psi )}{L(k-m+1/2,{\tilde{\chi }}_0{\chi }_i^{-1})},\hfill & {\pi }_p=\sigma ({\chi }_i,{\chi }_j),\end{array}\right.$$

where r is the conductor of ${\chi }_i{\chi }_0$.

$\left(ii\right)$

If $\mathsf{\Psi }=v_p·{|·|}^{1/2}{\chi }_i$,

$$e_{\delta }({\pi }_p,{\chi }_0)=\left\{\begin{array}{cc}\frac{p^{k-m-\frac{1}{2}}{\chi }_i\left(p\right)+p^{m-k-\frac{1}{2}}{\chi }_i{\left(p\right)}^{-1}-2p^{-1}}{1-p^{-1}};\hfill & {\chi }_0{\chi }_i{\mid }_{{\mathbb{Z}}_p^{\times }}=1;\hfill \\ \frac{-r{p}^{r(m-k-\frac{1}{2})}{\chi }_i{\left(p\right)}^{-r}\tau ({\chi }_0{\chi }_i,\psi )}{1-p^{-1}};\hfill & \mathrm{cond}\left({\chi }_0{\chi }_i\right)=r>0.\hfill \end{array}\right.$$

Proof. 

In order to compute the Euler factors $e_{\delta }({\pi }_p,{\chi }_0)$, we have to compute the local periods

$$I_{\delta }:=\frac{1}{\mathrm{vol}\left(H\right)}{\int }_{{\mathbb{Q}}_p^{\times }}{\tilde{\chi }}_0{\left(y\right)\left|y\right|}^{m-k}{W}_{\delta ,p}^H\left(\begin{array}{cc}y& \\ & 1\end{array}\right)d^{\times }y=\frac{1}{\mathrm{vol}\left(H\right)}{\int }_{{\mathbb{Q}}_p^{\times }}{\tilde{\chi }}_0\left(y\right){\left|y\right|}^{m-k}\delta \left(1_H\right)\left(y\right)d^{\times }y.$$

Recalling that ${\tilde{\chi }}_0$ is H-invariant, we obtain

$$I_{\delta }=\frac{1}{\mathrm{vol}\left(H\right)}{\int }_{{\mathbb{Q}}_p^{\times }}{\tilde{\chi }}_0{\left(y\right)\left|y\right|}^{m-k}{\int }_H\mathsf{\Psi }\left(zy\right)\psi (-zy)d^{\times }z{d}^{\times }y={\int }_{{\mathbb{Q}}_p^{\times }}{\tilde{\chi }}_0\left(x\right){\left|x\right|}^{m-k}\mathsf{\Psi }\left(x\right)\psi (-x)d^{\times }x.$$

In case $\left(i\right)$, we have that $\mathsf{\Psi }={|·|}^{1/2}{\chi }_i$; hence, by Lemmas 1 and 2

$$\begin{array}{ccc}\hfill I_{\delta }& =& \sum _n{p}^{n(k-m-\frac{1}{2})}{\chi }_i{\left(p\right)}^n{\int }_{{\mathbb{Z}}_p^{\times }}{\chi }_0\left(x\right){\chi }_i\left(x\right)\psi (-p^{n}x)d^{\times }x\hfill \\ & =& \left\{\begin{array}{cc}\sum _{n\ge 0}{p}^{n(k-m-\frac{1}{2})}{\chi }_i{\left(p\right)}^n-{(1-p^{-1})}^{-1}{p}^{m-k-\frac{1}{2}}{\chi }_i{\left(p\right)}^{-1};\hfill & {\chi }_0{\chi }_i{\mid }_{{\mathbb{Z}}_p^{\times }}=1;\hfill \\ {(1-p^{-1})}^{-1}{p}^{r(m-k-\frac{1}{2})}{\chi }_i{\left(p\right)}^{-r}\tau ({\chi }_0{\chi }_i,\psi );\hfill & \mathrm{cond}\left({\chi }_0{\chi }_i\right)=r>0\hfill \end{array}\right.\hfill \\ & =& \left\{\begin{array}{cc}{(1-p^{-1})}^{-1}(1-p^{m-k-\frac{1}{2}}{\chi }_i{\left(p\right)}^{-1}){(1-p^{k-m-\frac{1}{2}}{\chi }_i\left(p\right))}^{-1};\hfill & {\chi }_0{\chi }_i{\mid }_{{\mathbb{Z}}_p^{\times }}=1;\hfill \\ {(1-p^{-1})}^{-1}{p}^{r(m-k-\frac{1}{2})}{\chi }_i{\left(p\right)}^{-r}\tau ({\chi }_0{\chi }_i,\psi );\hfill & \mathrm{cond}\left({\chi }_0{\chi }_i\right)=r>0,\hfill \end{array}\right.\hfill \end{array}$$

because $e_{\delta }({\pi }_p,{\chi }_0)=L_p{(m-k+1/2,{\pi }_p,{\tilde{\chi }}_0)}^{-1}·I_{\delta }$ and

$$\begin{array}{ccc}\hfill L_p(s,{\pi }_p,{\tilde{\chi }}_0)& =& \left\{\begin{array}{cc}L(s,{\tilde{\chi }}_0{\chi }_i)·L(s,{\tilde{\chi }}_0{\chi }_j),\hfill & {\pi }_p=\pi ({\chi }_i,{\chi }_j),\\ L(s,{\tilde{\chi }}_0{\chi }_i),\hfill & {\pi }_p=\sigma ({\chi }_i,{\chi }_j),\end{array}\right.\hfill \end{array}$$

part $\left(i\right)$ follows.

In case $\left(ii\right)$, we have that $\mathsf{\Psi }=v_p·{|·|}^{1/2}{\chi }_i$; hence, we compute

$$\begin{array}{ccc}\hfill I_{\delta }& =& \sum _{n}n{p}^{n(k-m-\frac{1}{2})}{\chi }_i{\left(p\right)}^n{\int }_{{\mathbb{Z}}_p^{\times }}{\chi }_0\left(x\right){\chi }_i\left(x\right)\psi (-p^{n}x)d^{\times }x\hfill \\ & =& \left\{\begin{array}{cc}\sum _{n\ge 0}n{p}^{n(k-m-\frac{1}{2})}{\chi }_i{\left(p\right)}^n+{(1-p^{-1})}^{-1}{p}^{m-k-\frac{1}{2}}{\chi }_i{\left(p\right)}^{-1};\hfill & {\chi }_0{\chi }_i{\mid }_{{\mathbb{Z}}_p^{\times }}=1;\hfill \\ -r{(1-p^{-1})}^{-1}{p}^{r(m-k-\frac{1}{2})}{\chi }_i{\left(p\right)}^{-r}\tau ({\chi }_0{\chi }_i,\psi );\hfill & \mathrm{cond}\left({\chi }_0{\chi }_i\right)=r>0\hfill \end{array}\right.\hfill \\ & =& \left\{\begin{array}{cc}\frac{p^{k-m-\frac{1}{2}}{\chi }_i\left(p\right)+p^{m-k-\frac{1}{2}}{\chi }_i{\left(p\right)}^{-1}-2p^{-1}}{(1-p^{-1}){(1-p^{k-m-\frac{1}{2}}{\chi }_i\left(p\right))}^2};\hfill & {\chi }_0{\chi }_i{\mid }_{{\mathbb{Z}}_p^{\times }}=1;\hfill \\ -r{(1-p^{-1})}^{-1}{p}^{r(m-k-\frac{1}{2})}{\chi }_i{\left(p\right)}^{-r}\tau ({\chi }_0{\chi }_i,\psi );\hfill & \mathrm{cond}\left({\chi }_0{\chi }_i\right)=r>0,\hfill \end{array}\right.\hfill \end{array}$$

where the second equality follows from the identity ${\sum }_{n>0}n{x}^n=x{(1-x)}^{-2}$. The result then follows. □

5. Extremal p-Adic L-Functions

If ${\pi }_p=\pi ({\chi }_1,{\chi }_2)$ or $\sigma ({\chi }_1,{\chi }_2)$ with ${\chi }_1$ unramified, then the Hecke polynomial $X^2-a_{p}X+ϵ\left(p\right)p^{k+1}=(x-\alpha )(x-\beta )$, where $\alpha =p^{1/2}{\chi }_1{\left(p\right)}^{-1}$. This implies that, if $\gamma =\alpha$ has small enough valuation, then we can always construct $v\left(\alpha \right)$-admissible distributions ${\mu }_{\alpha }^{\pm }$ and ${\mu }_{\alpha }={\mu }_{\alpha }^{+}+{\mu }_{\alpha }^{-}$. In fact, if ${\pi }_p=\pi ({\chi }_1,{\chi }_2)$ and ${\chi }_2$ is also unramified, we can sometimes construct a second $v_p\left(\beta \right)$-admissible distribution ${\mu }_{\beta }$.

By previous computations, the interpolation property implies that, for any locally polynomial character $\chi ={\chi }_0\left(x\right)x^m\in C_k({\mathbb{Z}}_p^{\times },{\mathbb{C}}_p)$,

$${\int }_{{\mathbb{Z}}_p^{\times }}\chi d{\mu }_{\alpha }=\frac{4\pi }{{\mathsf{\Omega }}_f^{\pm }{i}^m}·e_p({\pi }_p,{\chi }_0)·L\left(m-k+\frac{1}{2},\pi ,{\chi }_0\right),$$

with

$$e_p({\pi }_p,{\chi }_0)=\left\{\begin{array}{cc}{(1-p^{-1})}^{-1}(1-ϵ\left(p\right){\alpha }^{-1}{p}^m)(1-{\alpha }^{-1}{p}^{k-m});\hfill & {\chi }_0{\chi }_2{\mid }_{{\mathbb{Z}}_p^{\times }}=1;\hfill \\ {(1-p^{-1})}^{-1}{p}^{rm}{\alpha }^{-r}\tau ({\chi }_0{\chi }_2,\psi );\hfill & \mathrm{cond}\left({\chi }_0{\chi }_2\right)=r>0.\hfill \end{array}\right.$$

This interpolation formula coincides (up to constant) with the classical interpolation formula of the distribution ${\mu }_{f,\alpha }$ that is defined in Section 3.2. Indeed, it is easy to prove that ${\phi }_{f_{\alpha }}^{\pm }$ is proportional to ${\phi }_{f,p}^{\pm }\left(V_0\right)$ (see Equation (15)); hence, the fact that ${\mu }_{f,\alpha }^{\pm }$ is proportional to ${\mu }_{\alpha }^{\pm }$ follows from (4), (11) and property (9). In fact, if $\mathsf{\Psi }$ is a character, then all of the the admissible p-adic distributions that are constructed in this paper are twists of the p-adic distributions described in Section 3.2 (also in [3]); hence, for those situations, we only provide a new interpretation of classical constructions.

The only genuine new construction is for the case $\mathsf{\Psi }=v_p·{|·|}^{1/2}\chi$ and ${\pi }_p=\pi (\chi ,\chi )$.

Theorem 5.

Let $f\in S_{k+2}({\mathsf{\Gamma }}_1\left(N\right),ϵ)$ be a newform, and assume that ${\pi }_p=\pi (\chi ,\chi )$. There exists a $(k+1)/2$-admissible distribution ${\mu }_{f,p}^{\mathrm{ext}}$ of ${\mathbb{Z}}_p^{\times }$, such that, for any locally polynomial character $\chi ={\chi }_0\left(x\right)x^m\in C_k({\mathbb{Z}}_p^{\times },{\mathbb{C}}_p)$,

$${\int }_{{\mathbb{Z}}_p^{\times }}\chi d{\mu }_{f,p}^{\mathrm{ext}}=\frac{4\pi }{{\mathsf{\Omega }}_f^{\pm }{i}^m}·e_p^{\mathrm{ext}}({\pi }_p,{\chi }_0)·L\left(m-k+\frac{1}{2},\pi ,{\chi }_0\right),$$

with

$$e_p^{\mathrm{ext}}({\pi }_p,{\chi }_0)=\left\{\begin{array}{cc}\frac{p^{k-m-\frac{1}{2}}\chi \left(p\right)+p^{m-k-\frac{1}{2}}\chi {\left(p\right)}^{-1}-2p^{-1}}{1-p^{-1}};\hfill & {\chi }_0\chi {\mid }_{{\mathbb{Z}}_p^{\times }}=1;\hfill \\ \frac{-r{p}^{r(m-k-\frac{1}{2})}\chi {\left(p\right)}^{-r}\tau ({\chi }_0\chi ,\psi )}{1-p^{-1}};\hfill & \mathrm{cond}\left({\chi }_0\chi \right)=r>0.\hfill \end{array}\right.$$

Proof. 

The only thing that is left to prove is that ${\mu }_{f,p}^{\mathrm{ext}}$ is $(k+1)/2$-admissible, but this directly follows from Theorem 4 and the fact that

$${\epsilon }_p={ϵ}_p^{-1}{|·|}^k={\chi }^2,\gamma =\chi \left(p\right)p{\left|p\right|}^{\frac{1}{2}}{\epsilon }_p{\left(p\right)}^{-1}=\chi \left(p\right)p^{\frac{1}{2}+k}{ϵ}_p\left(p\right).$$

Hence, $v_p\left(\gamma \right)=\frac{1}{2}+k+v_p\left(\chi \left(p\right)\right)=\frac{k+1}{2}$. □

Remark 4.

Notice that ${\mu }_{f,p}^{\mathrm{ext}}$ has been constructed as the sum

$${\mu }_{f,p}^{\mathrm{ext}}={\mu }_{f,p}^{\mathrm{ext},+}+{\mu }_{f,p}^{\mathrm{ext},-}.$$

Definition 4.

We call ${\mu }_{f,p}^{\mathrm{ext}}$ extremal p-adic measure. Because $(k+1)/2<k+1$, by Proposition 2, we can extend ${\mu }_{f,p}^{\mathrm{ext}}$ to a locally analytic measure. Hence, we define the extremal p-adic L-function

$$L_p^{\mathrm{ext}}(f,s):={\int }_{{\mathbb{Z}}_p^{\times }}\exp (s·\log \left(\mathrm{x}\right))d{\mu }_{f,p}^{\mathrm{ext}}\left(x\right).$$

Hence, we conclude that, in the conjecturally impossible situation that ${\pi }_p=\pi (\chi ,\chi )$, two p-adic L-functions coexist

$$L_p(f,s),L_p^{\mathrm{ext}}(f,s).$$

Their corresponding interpolation properties look similar, but they have completely different Euler factors.

Alternative Description

In the classical setting that us described in Section 3 ($\chi$ unramified), p-adic distributions ${\mu }_{f,p}^{\pm }$ are given by Equation (4), while extremal p-adic distributions satisfy

$$\begin{array}{ccc}\hfill {\int }_{U(a,n)}P\left(1,\frac{x-a}{p^n}\right)d{\mu }_{f,p}^{\mathrm{ext},\pm }\left(x\right)& =& {\phi }_{f,p}^{\pm }\left(\delta \left(1_{U(a,n)}\right)\right)(0-\infty )\left(P\left(X,\frac{Y-aX}{p^n}\right)\right)\hfill \\ & =& \frac{1}{{\alpha }^n}·{\phi }_{f,p}^{\pm }(V_1-n{V}_0)\left(\frac{a}{p^n}-\infty \right)\left(P\right),\hfill \end{array}$$

where $V_0={(1-p^{-1})}^{-1}{\left|y\right|}^{1/2}\chi \left(y\right)1_{{\mathbb{Z}}_p}\left(y\right)$ and $V_1={(1-p^{-1})}^{-1}{v}_p\left(y\right){\left|y\right|}^{1/2}\chi \left(y\right)1_{p{\mathbb{Z}}_p}\left(y\right)$. Using the relations (13), we compute the action of the Hecke operator $T_p$ on $V_0+V_1$:

$$\begin{array}{ccc}\hfill T_p(V_0+V_1)& =& \left(\begin{array}{cc}{p}^{-1}& \\ & 1\end{array}\right)(V_0+V_1)+\sum _{c\in \mathbb{Z}/p\mathbb{Z}}\left(\begin{array}{cc}1& p^{-1}c\\ & p^{-1}\end{array}\right)(V_0+V_1)\hfill \\ & =& (V_0+V_1)\left(p^{-1}y\right)+\frac{1}{{\epsilon }_p\left(p\right)}(V_0+V_1)\left(py\right)\sum _{c\in \mathbb{Z}/p\mathbb{Z}}\psi \left(cy\right)\hfill \\ & =& \frac{{\alpha \left|y\right|}^{1/2}\chi \left(y\right)}{(1-p^{-1})}\left(v_p\left(y\right)1_{{\mathbb{Z}}_p}\left(p^{-1}y\right)+\frac{1+v_p\left(py\right)}{p}\sum _{c\in \mathbb{Z}/p\mathbb{Z}}\psi \left(cy\right)1_{{\mathbb{Z}}_p}\left(py\right)\right)\hfill \\ & =& \frac{{\left|y\right|}^{1/2}\chi \left(y\right)}{(1-p^{-1})}2\alpha \left(1+v_p\left(y\right)\right)1_{{\mathbb{Z}}_p}\left(y\right)=2\alpha (V_0+V_1),\hfill \end{array}$$

because $\alpha =\gamma =p^{1/2}\chi {\left(p\right)}^{-1}={\epsilon }_p{\left(p\right)}^{-1}{p}^{1/2}\chi \left(p\right)$. Similarly,

$$U_p{V}_0=\sum _{c\in \mathbb{Z}/p\mathbb{Z}}\left(\begin{array}{cc}1& p^{-1}c\\ & p^{-1}\end{array}\right)V_0=\frac{1}{{\epsilon }_p\left(p\right)}{V}_0\left(py\right)\sum _{c\in \mathbb{Z}/p\mathbb{Z}}\psi \left(cy\right)=\alpha V_0.$$

(15)

Hence, $V_0$ and $V_1$ are basis of the generalized eigenspace of $U_p$, in which $V_0$ is the eigenvector and $V_0+V_1$ is the newform. This implies that (up to constant) ${\phi }_{f,p}^{\pm }\left(V_0\right)\stackrel{·}{=}{\phi }_{f_{\alpha }}^{\pm }$, where $f_{\alpha }$ is the p-specialization defined in Section 3.2, while we have that ${\phi }_{f,p}^{\pm }(V_0+V_1)\stackrel{·}{=}{\phi }_f^{\pm }$. We conclude that, in terms of the classical definitions given in Section 3.2, the extremal distribution can be described as

$${\int }_{U(a,n)}P\left(1,\frac{x-a}{p^n}\right)d{\mu }_{f,p}^{\mathrm{ext},\pm }\left(x\right)=\frac{1}{{\alpha }^n}·{\phi }_{f-(n+1)f_{\alpha }}^{\pm }\left(\frac{a}{p^n}-\infty \right)\left(P\right).$$

6. Overconvergent Modular Symbols

For any $r\in p^{\mathbb{Q}}$, let $B[{\mathbb{Z}}_p,r]=\{z\in {\mathbb{C}}_p,\exists a\in {\mathbb{Z}}_p,|z-a|\le r\}$. We denote, by $A\left[r\right]$, the ring of affinoid function on $B[{\mathbb{Z}}_p,r]$. The ring $A\left[r\right]$ has structure of ${\mathbb{Q}}_p$-Banach algebra with the norm ${\Vert f\Vert }_r={\sup }_{z\in B[{\mathbb{Z}}_p,r]}\left|f\left(z\right)\right|$. Denote, by $D\left[r\right]={\mathrm{Hom}}_{{\mathbb{Q}}_p}(A\left[r\right],{\mathbb{Q}}_p)$, the continuous dual. It is also a Banach space with the norm

$${\Vert \mu \Vert }_r={\sup }_{f\in A\left[r\right]}\frac{\left|\mu \right(f\left)\right|}{{\Vert f\Vert }_r}.$$

We define

$$D^{†}\left[r\right]:=\underset{r^{\prime }\in p^{\mathbb{Q}},r^{\prime }>r}{\underleftarrow{lim}}D\left[r^{\prime }\right],$$

where the projective limit is taken with respect the usual maps $D\left[r_2\right]\to D\left[r_1\right]$, $r_1>r_2$. Because these maps are injective and compact, the space $D^{†}\left[r\right]$ is endowed with structure of Frechet space.

Given an affinoid ${\mathbb{Q}}_p$-algebra R and a character $w:{\mathbb{Z}}_p\to R^{\times }$, such that $w\in A\left[r\right]{\widehat{\otimes }}_{{\mathbb{Q}}_p}R$, we can define an action of the monoid

$${\sum }_0\left(p\right)=\left\{\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)\in {\mathrm{M}}_2\left({\mathbb{Z}}_p\right),p\nmid a,p\mid c,ad-bc\ne 0\right\}$$

on $A\left[r\right]{\widehat{\otimes }}_{{\mathbb{Q}}_p}R$ and $D\left[r\right]{\widehat{\otimes }}_{{\mathbb{Q}}_p}R$ given by

$$\begin{array}{ccc}\hfill \left(\gamma {\ast }_{w}f\right)\left(z\right)& =& w(a+cz)·f\left(\frac{b+dz}{a+cz}\right),f\in A\left[r\right]{\widehat{\otimes }}_{{\mathbb{Q}}_p}R,\hfill \\ \hfill \left(\gamma {\ast }_w\mu \right)\left(f\right)& =& \mu \left({\gamma }^{-1}{\ast }_{w}f\right),{\gamma }^{-1}\in {\sum }_0\left(p\right),\mu \in D\left[r\right]{\widehat{\otimes }}_{{\mathbb{Q}}_p}R.\hfill \end{array}$$

Write $D_w\left[r\right]$ for the space $D\left[r\right]{\widehat{\otimes }}_{{\mathbb{Q}}_p}R$ with the corresponding action. Similarly, we define

$$D_w^{†}:=\underset{r^{\prime }\in p^{\mathbb{Q}},r^{\prime }>r}{\underleftarrow{lim}}{D}_w\left[r\right]=D^{†}\left[r\right]{\widehat{\otimes }}_{{\mathbb{Q}}_p}R,$$

where the second equality follows from Lemma 3.2 in [8]. Compatibility with base change and Lemma 3.5 in [8] imply that, given a morphism of affinoid ${\mathbb{Q}}_p$-algebras $\phi :R\to R^{\prime }$, we have isomorphisms

$$D_w\left[r\right]{\otimes }_R{R}^{\prime }\stackrel{\simeq }{⟶}{D}_{\phi \circ w}\left[r\right],D_w^{†}\left[r\right]{\otimes }_R{R}^{\prime }\stackrel{\simeq }{⟶}{D}_{\phi \circ w}^{†}\left[r\right].$$

(16)

Definition 5.

We call the space ${\mathrm{Hom}}_{\mathsf{\Gamma }}({\Delta }_0,D_w^{†}\left[r\right])$ the space of modular symbols of weight w. We denote, by ${\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }({\Delta }_0,D_w^{†}\left[r\right])$, the subgroup of ${\mathrm{Hom}}_{\mathsf{\Gamma }}({\Delta }_0,D_w^{†}\left[r\right])$ of elements that are fixed or multiplied by $-1$ by the involution given by $\left(\begin{array}{cc}-1& \\ & 1\end{array}\right)$.

The action of ${\sum }_0\left(p\right)$ on $D_w^{†}\left[r\right]$ induces an action of $U_p$ on ${\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }({\Delta }_0,D_w^{†}\left[r\right])$ given by the Formula (5).

Assume that R is reduced and its norm $|·|$ extends the norm of ${\mathbb{Q}}_p$. Write as usual $v_p\left(x\right)=-log\left|x\right|/logp$, so that $v_p\left(p\right)=1$. Let us consider

$$R\left\{\left\{T\right\}\right\}:=\left\{\sum _{n\ge 0}{a}_n{T}^n,a_n\in R,\underset{n}{lim}(v_p\left(a_n\right)-n\nu )=\infty \mathrm{for} \mathrm{all}\nu \in \mathbb{R}\right\}.$$

Given $F\left(T\right)\in R\left\{\right\{T\left\}\right\}$ and $\nu \in \mathbb{R}$,

$$N(F,\nu ):=max\{n\in \mathbb{N},v_p\left(a_n\right)-n\nu ={\inf }_m(v_p\left(a_m\right)-m\nu )\}.$$

A polynomial $Q\left(T\right)\in R\left[T\right]\subseteq R\left\{\right\{T\left\}\right\}$ is $\nu$-dominant if it has degree $N(Q,\nu )$ and, for all $x\in \mathrm{Sp}\left(R\right)$, we have $N(Q,\nu )=N(Q_x,\nu )$. We say that $F\left(T\right)\in R\left\{\right\{T\left\}\right\}$ is ν-adapted if there exists a (unique) decomposition $F\left(T\right)=Q\left(T\right)·G\left(T\right)$, where $Q\left(T\right)\in R\left[T\right]$ is a $\nu$-dominant polynomial of degree $N(F,\nu )$ and $Q\left(0\right)=G\left(0\right)=1$.

Because ${\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }({\Delta }_0,D_w\left[r\right])$ satisfies property (Pr) of Section 2 of [12] and $U_p$ acts compactly, then one can define the characteristic power series $F\left(T\right)\in R\left\{\right\{T\left\}\right\}$ of $U_p$ acting on ${\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }({\Delta }_0,D_w\left[r\right])$. We say that R is ν-adapted for some $\nu \in \mathbb{R}$, if F is $\nu$-adapted. If this is the case, then we can define the submodule ${\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }{({\Delta }_0,D_w\left[r\right])}^{\le \nu }$ of slope bounded by ν modular symbols as the kernel of $Q\left(U_p\right)$ in ${\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }({\Delta }_0,D_w\left[r\right])$.

We write ${\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }{({\Delta }_0,D_w^{†}\left[r\right])}^{\le \nu }$ for the intersection

$${\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }{({\Delta }_0,D_w^{†}\left[r\right])}^{\le \nu }:={\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }({\Delta }_0,D_w^{†}\left[r\right])\cap {\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }{({\Delta }_0,D_w\left[r^{\prime }\right])}^{\le \nu }$$

in ${\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }({\Delta }_0,D_w\left[r^{\prime }\right])$, for any $r^{\prime }>r$.

6.1. Control Theorem

Let us consider the character

$$k:{\mathbb{Z}}_p^{\times }\to {\mathbb{Q}}_p^{\times },x⟼x^k.$$

We have a morphism of ${\sum }_0\left(p\right)$-modules

$${\rho }_k^{\ast }:D_k^{†}\left[1\right]⟶V\left(k\right):=V{\left(k\right)}_{{\mathbb{Q}}_p};{\rho }_k^{\ast }\left(\mu \right)\left(P\right):=\mu \left(P(1,z)\right).$$

This provides a morphism

$${\rho }_k^{\ast }:{\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }({\Delta }_0,D_k^{†}\left[1\right])⟶{\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }({\Delta }_0,V\left(k\right))$$

(17)

Theorem 6

(Steven’s control Theorem). The above morphism induces an isomorphism of ${\mathbb{Q}}_p$-vector spaces

$${\rho }_k^{\ast }:{\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }{({\Delta }_0,D_k^{†}\left[1\right])}^{<k+1}⟶{\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }{({\Delta }_0,V\left(k\right))}^{<k+1}.$$

Proof. 

See Theorem 7.1 in [13] and Theorem 5.4 in [9]. □

6.2. Extremal Modular Symbols

Let $f\in S_{k+2}(N,ϵ)$, as before, and assume that the Hecke polynomial $x^2-a_{p}x+ϵ\left(p\right)p^{k+1}$ has a double root $\alpha$. We have defined admissible locally analytic measures ${\mu }_{f,p}^{\mathrm{ext},\pm }$ that are characterized by

$${\int }_{a+p^n{\mathbb{Z}}_p}P\left(1,\frac{x-a}{p^n}\right)d{\mu }_{f,p}^{\mathrm{ext},\pm }\left(x\right)=\frac{1}{{\alpha }^n}·{\phi }_{f-(n+1)f_{\alpha }}^{\pm }\left(\frac{a}{p^n}-\infty \right)\left(P\right),$$

for any $P\in \mathcal{P}{\left(k\right)}_{\mathbb{Q}}$. Our aim is to describe ${\mu }_{f,p}^{\mathrm{ext},\pm }$ as the evaluation at $0-\infty$ of certain overconvergent modular symbol ${\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }({\Delta }_0,D_k^{†}\left[0\right])$.

Notice that, if we write $g_n:=f-(n+1)f_{\alpha }$ and ${\gamma }_{a,n}:=\left(\begin{array}{cc}1& a\\ & p^n\end{array}\right)$,

$$\begin{array}{ccc}\hfill {\int }_{{\mathbb{Z}}_p}{\gamma }_{a,n}^{-1}\left({\rho }_k\left(P\right)1_{{\mathbb{Z}}_p}\right)\left(x\right)d{\mu }_{f,p}^{\mathrm{ext},\pm }\left(x\right)& =& {\int }_{a+p^n{\mathbb{Z}}_p}P\left(1,\frac{x-a}{p^n}\right)d{\mu }_{f,p}^{\mathrm{ext},\pm }\left(x\right)\hfill \\ & =& \frac{1}{{\alpha }^n}·{\phi }_{g_n}^{\pm }\left(\frac{a}{p^n}-\infty \right)\left(P\right)\hfill \\ & =& \frac{1}{{\alpha }^n}·{\phi }_{g_n}^{\pm }\left({\gamma }_{a,n}(0-\infty )\right)\left(P\right)\hfill \\ & =& {\left(\frac{1}{p\alpha }\right)}^n·{\phi }_{g_n{\mid }_{{\gamma }_{a,n}}}^{\pm }\left(0-\infty \right)\left({\gamma }_{a,n}^{-1}P\right).\hfill \end{array}$$

Moreover, the elements ${\gamma }_{a,n}^{-1}\left({\rho }_k\left(P\right)1_{{\mathbb{Z}}_p}\right)\in A\left[p^{-n}\right]$ for all $n\in \mathbb{N}$, $a\in {\mathbb{Z}}_p$, and these functions form a dense set in ${\bigcup }_{n\ge 0}A\left[p^{-n}\right]$.

Lemma 3.

For any divisor $D\in {\Delta }_0$, the expression

$${\gamma }_{a,n}^{-1}\left({\rho }_k\left(P\right)1_{{\mathbb{Z}}_p}\right)⟼{\left(\frac{1}{p\alpha }\right)}^n·{\phi }_{g_n{\mid }_{{\gamma }_{a,n}}}^{\pm }\left(D\right)\left({\gamma }_{a,n}^{-1}P\right)$$

extends to a measure in ${\widehat{\phi }}_{\mathrm{ext}}^{\pm }\left(D\right)\in D_k^{†}\left[1\right]$.

Proof. 

We have to show additivity, namely, since

$${\gamma }_{a,n}^{-1}\left({\rho }_k\left(P\right)1_{{\mathbb{Z}}_p}\right)=\sum _{b\equiv a\mathrm{mod}{p}^n}{\gamma }_{b,n+1}^{-1}\left({\rho }_k\left({\gamma }_{b}P\right)1_{{\mathbb{Z}}_p}\right),{\gamma }_b:=\left(\begin{array}{cc}1& \frac{b-a}{p^n}\\ 0& p\end{array}\right),$$

we have to show that

$${\left(\frac{1}{p\alpha }\right)}^n·{\phi }_{g_n{\mid }_{{\gamma }_{a,n}}}^{\pm }\left(D\right)\left({\gamma }_{a,n}^{-1}P\right)=\sum _{b\equiv a\mathrm{mod}{p}^n}{\left(\frac{1}{p\alpha }\right)}^{n+1}·{\phi }_{g_{n+1}{\mid }_{{\gamma }_{b,n+1}}}^{\pm }\left(D\right)\left({\gamma }_{b,n+1}^{-1}{\gamma }_{b}P\right).$$

Indeed, we have that ${\gamma }_{b,n+1}^{-1}{\gamma }_b={\gamma }_{a,n}^{-1}$, thus the above equation follows from the fact that $g_n\in S_{k+2}(\mathsf{\Gamma },ϵ)$ satisfies $U_p{g}_{n+1}=\frac{1}{p}{\sum }_{b\equiv a}{g}_{n+1}{\mid }_{{\gamma }_b}=\alpha ·g_n$.

First, we notice that, by (3), for any $P\in \mathcal{P}{\left(k\right)}_{{\mathbb{Z}}_p}$,

$${\widehat{\phi }}_{\mathrm{ext}}^{+}\left(D\right)\left({\gamma }_{a,N}^{-1}\left({\rho }_k\left(P\right)1_{{\mathbb{Z}}_p}\right)\right)={\left(\frac{1}{\alpha }\right)}^N·{\phi }_{g_N}^{+}\left({\gamma }_{a,N}D\right)\left(P\right)\in A·p^{-N\frac{k+1}{2}}{\mathcal{O}}_{{\mathbb{C}}_p},$$

for big enough N, since $v_p\left(\alpha \right)=(k+1)/2$.

On the other hand, any locally analytic function is topologically generated by functions of the form $P_m^{a,N}\left(x\right):={\left(\frac{x-a}{p^N}\right)}^m{1}_{a+p^N}\left(x\right)$, where $m\in \mathbb{N}$. The functions ${\gamma }_{a,N}^{-1}\left({\rho }_k\left(P\right)1_{{\mathbb{Z}}_p}\right)$ are generated by $P_m^{a,N}$, when $m\le k$; hence, our distribution must be determined by

$${\widehat{\phi }}_{\mathrm{ext}}^{\pm }\left(D\right)\left(P_m^{a,N}\right)={\left(\frac{1}{p\alpha }\right)}^N·{\phi }_{g_N{\mid }_{{\gamma }_{a,N}}}^{\pm }\left(D\right)\left({\gamma }_{a,N}^{-1}\left(x^{k-m}{y}^m\right)\right),m\le k.$$

If $m>k$, we define ${\widehat{\phi }}_{\mathrm{ext}}^{\pm }\left(D\right)\left(P_m^{a,N}\right)={lim}_{n\to \infty }{a}_n$, where

$$a_n=\sum _{b\mathrm{mod}{p}^n;b\equiv a\mathrm{mod}{p}^N}\sum _{j\le k}{\left(\frac{b-a}{p^N}\right)}^{m-j}\left(\genfrac{}{}{0pt}{}{m}{j}\right)p^{j(n-N)}{\widehat{\phi }}_{\mathrm{ext}}^{\pm }\left(D\right)\left(P_j^{b,n}\right).$$

The limit converge because ${\left\{a_n\right\}}_n$ is Cauchy, indeed by additivity

$$a_{n_2}-a_{n_1}=\sum _{j\le h}\sum _{b\equiv a\left(p^{n_2}\right)}\sum _{b^{\prime }\equiv b\left(p^{n_1}\right)}\sum _{s=k+1}^{m}r\left(s\right)\left(\genfrac{}{}{0pt}{}{s}{j}\right){\left(\frac{b^{\prime }-b}{p^N}\right)}^{s-j}{p}^{(n_2-N)j}{\widehat{\phi }}_{\mathrm{ext}}^{\pm }\left(D\right)\left(P_j^{b^{\prime },n_2}\right),$$

where $r\left(s\right)=\left(\genfrac{}{}{0pt}{}{m}{s}\right){\left(\frac{b^{\prime }-a}{p^N}\right)}^{m-s}$. Because

$${\left(\frac{b^{\prime }-b}{p^N}\right)}^{s-j}{p}^{(n_2-N)j}{\widehat{\phi }}_{\mathrm{ext}}^{\pm }\left(D\right)\left(P_j^{b^{\prime },n_2}\right)\in A·p^{-Ns}·p^{(n_1-n_2)(s-j)}{p}^{n_2\left(s-\frac{k+1}{2}\right)}{\mathcal{O}}_{{\mathbb{C}}_p},$$

we have that $a_{n+1}-a_n\stackrel{n}{\to }0$. Hence, we have extended ${\widehat{\phi }}_{\mathrm{ext}}^{\pm }\left(D\right)$ to a locally analytic measure by continuity, which is determined by the image of locally polynomial functions of degree at most k. □

The above lemma implies that ${\widehat{\phi }}_{\mathrm{ext}}^{\pm }\in \mathrm{Hom}({\Delta }_0,D_k^{†}\left[1\right])$. Let us check that it is $\mathsf{\Gamma }$-equivariant: For any $g\in \mathsf{\Gamma }$, it is easy to show that $g{\gamma }_{a,n}^{-1}{1}_{{\mathbb{Z}}_p}={\gamma }_{g^{-1}a,n}^{-1}{1}_{{\mathbb{Z}}_p}$, where $\left(\begin{array}{cc}\alpha & \beta \\ \gamma & \delta \end{array}\right)a=\frac{\beta +\delta a}{\alpha +\gamma a}$. Thus by (7)

$$\begin{array}{ccc}\hfill {\widehat{\phi }}_{\mathrm{ext}}^{\pm }\left(gD\right)\left(g{\gamma }_{a,n}^{-1}\left({\rho }_k\left(P\right)1_{{\mathbb{Z}}_p}\right)\right)& =& {\widehat{\phi }}_{\mathrm{ext}}^{\pm }\left(gD\right)\left({\gamma }_{g^{-1}a,n}^{-1}\left({\rho }_k\left({\gamma }_{g^{-1}a,n}g{\gamma }_{a,n}^{-1}P\right)1_{{\mathbb{Z}}_p}\right)\right)\hfill \\ & =& {\left(\frac{1}{p\alpha }\right)}^n·{\phi }_{g_n{\mid }_{{\gamma }_{g^{-1}a,n}}}^{\pm }\left(gD\right)\left(g{\gamma }_{a,n}^{-1}P\right)\hfill \\ & =& {\left(\frac{1}{p\alpha }\right)}^n·{\phi }_{g_n{\mid }_{{\gamma }_{g^{-1}a,n}g}}^{\pm }\left(D\right)\left({\gamma }_{a,n}^{-1}P\right)\hfill \\ & =& {\widehat{\phi }}_{\mathrm{ext}}^{\pm }\left(D\right)\left({\gamma }_{a,n}^{-1}\left({\rho }_k\left(P\right)1_{{\mathbb{Z}}_p}\right)\right)\hfill \end{array}$$

where the last equality has been obtained from the fact that ${\gamma }_{g^{-1}a,n}g{\gamma }_{a,n}^{-1}\in \mathsf{\Gamma }$ and $g_n$ is $\mathsf{\Gamma }$-invariant for all n. One easily checks that ${\widehat{\phi }}^{\pm }$ is in the corresponding $\left(\begin{array}{cc}-1& \\ & 1\end{array}\right)$-subspace

$${\widehat{\phi }}_{\mathrm{ext}}^{\pm }\in {\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }({\Delta }_0,D_k^{†}\left[1\right]).$$

From the definition, it is easy to check the following result

Proposition 4.

The measures ${\mu }_{f,p}^{\mathrm{ext},\pm }$ and ${\mu }_{f,p}^{\mathrm{ext}}$ can be obtained as

$${\mu }_{f,p}^{\mathrm{ext},\pm }={\widehat{\phi }}_{\mathrm{ext}}^{\pm }(0-\infty ){\mid }_{{\mathbb{Z}}_p^{\times }},{\mu }_{f,p}^{\mathrm{ext}}={\widehat{\phi }}_{\mathrm{ext}}(0-\infty ){\mid }_{{\mathbb{Z}}_p^{\times }},$$

where ${\widehat{\phi }}_{\mathrm{ext}}:={\widehat{\phi }}_{\mathrm{ext}}^{+}+{\widehat{\phi }}_{\mathrm{ext}}^{-}$.

6.3. Action of $U_p$

Recall that the action of ${\sum }_0\left(p\right)$ on ${\mathrm{Hom}}_{\mathsf{\Gamma }}({\Delta }_0,D_k^{†}\left[1\right])$ provides an action of the Hecke operator $U_p$; the aim of this section is to compute $U_p{\widehat{\phi }}_{\mathrm{ext}}^{\pm }$. Notice that it is enough to compute the image of the functions $f_{a,n,P}:={\gamma }_{a,n}^{-1}\left({\rho }_k\left(P\right)1_{{\mathbb{Z}}_p}\right)$:

$$\begin{array}{ccc}\hfill \left(U_p{\widehat{\phi }}_{\mathrm{ext}}^{\pm }\right)\left(D\right)\left(f_{a,n,P}\right)& =& \sum _{c\mathrm{mod}p}{\widehat{\phi }}_{\mathrm{ext}}^{\pm }\left({\gamma }_{c,1}D\right)\left({\gamma }_{c,1}{\gamma }_{a,n}^{-1}\left({\rho }_k\left(P\right)1_{{\mathbb{Z}}_p}\right)\right)\hfill \\ & =& {\widehat{\phi }}_{\mathrm{ext}}^{\pm }\left({\gamma }_{a,1}D\right)\left({\gamma }_{0,n-1}^{-1}\left({\rho }_k\left(P\right)1_{{\mathbb{Z}}_p}\right)\right)\hfill \\ & =& {\left(\frac{1}{p\alpha }\right)}^{n-1}·{\phi }_{g_{n-1}{\mid }_{{\gamma }_{0,n-1}}}^{\pm }\left({\gamma }_{a,1}D\right)\left({\gamma }_{0,n-1}^{-1}P\right)\hfill \\ & =& \frac{1}{p}{\left(\frac{1}{p\alpha }\right)}^{n-1}·{\phi }_{g_{n-1}{\mid }_{{\gamma }_{0,n-1}{\gamma }_{a,1}}}^{\pm }\left(D\right)\left({\gamma }_{a,1}^{-1}{\gamma }_{0,n-1}^{-1}P\right)\hfill \\ & =& \alpha {\left(\frac{1}{p\alpha }\right)}^n·{\phi }_{g_{n-1}{\mid }_{{\gamma }_{a,n}}}^{\pm }\left(D\right)\left({\gamma }_{a,n}^{-1}P\right).\hfill \end{array}$$

Because $g_n=g_{n-1}-f_{\alpha }$, we deduce that

$$U_p{\widehat{\phi }}_{\mathrm{ext}}^{\pm }=\alpha ·\left({\widehat{\phi }}_{\mathrm{ext}}^{\pm }+{\widehat{\phi }}^{\pm }\right),$$

(18)

where ${\widehat{\phi }}^{\pm }\in {\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }({\Delta }_0,D_k^{†}\left[1\right])$ is the classical overconvergent modular symbol corresponding through Theorem 6 to the eigenvector with the eigenvalue $\alpha$ given by $f_{\alpha }$.

6.4. Specialization of ${\widehat{\phi }}_{\mathrm{ext}}^{\pm }$

Theorem 6 asserts that the morphism ${\rho }_k^{\ast }$ of (17) becomes an isomorphism when we restrict ourselves to generalized eigenspaces for $U_p$ with valuation of the eigenvector strictly less than $k+1$. We have seen that ${\widehat{\phi }}_{\mathrm{ext}}^{\pm }$ lives in the eigenspace of eigenvalue $\alpha$, and we know that $v_p\left(\alpha \right)=(k+1)/2$. Thus, it bijectively corresponds to an element of ${\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }({\Delta }_0,V\left(k\right))$. We can easily compute the image ${\rho }_k^{\ast }{\widehat{\phi }}_{\mathrm{ext}}^{\pm }$ just calculating the image of the polynomical functions ${\rho }_k\left(P\right)1_{{\mathbb{Z}}_p}$:

$${\widehat{\phi }}_{\mathrm{ext}}^{\pm }\left(D\right)\left({\rho }_k\left(P\right)1_{{\mathbb{Z}}_p}\right)={\left(\frac{1}{p\alpha }\right)}^0·{\phi }_{g_0}^{\pm }\left(D\right)\left(P\right)={\phi }_{f-f_{\alpha }}^{\pm }\left(D\right)\left(P\right).$$

Thus, ${\rho }_k^{\ast }{\widehat{\phi }}_{\mathrm{ext}}^{\pm }={\phi }_{f-f_{\alpha }}^{\pm }$, that corresponds via Eichler–Shimura to the modular form $f-f_{\alpha }$. This fact fits with Theorem 6 since $f-f_{\alpha }$ belongs to the generalized eigenspace, indeed, ${(U_p-\alpha )}^2(f-f_{\alpha })=0$.

7. Extremal p-Adic L-Functions in Families

7.1. Weight Space

Let $\mathcal{W}/{\mathbb{Q}}_p$ be the standard one-dimensional weight space. It is a rigid analytic space that can classify characters of ${\mathbb{Z}}_p^{\times }$, namely,

$$\mathcal{W}={\mathrm{Hom}}_{\mathrm{cnt}}({\mathbb{Z}}_p^{\times },{\mathbb{G}}_m).$$

If L is any normed extension of ${\mathbb{Q}}_p$, we write $\tilde{w}:{\mathbb{Z}}_p^{\times }\to L^{\times }$ for the continuous morphism of groups corresponding to a point $w\in \mathcal{W}\left(L\right)$.

If $k\in \mathbb{Z}$, then the morphism $\tilde{k}\left(t\right)=t^k$ for all $t\in {\mathbb{Z}}_p^{\times }$ defines a point in $\mathcal{W}\left({\mathbb{Q}}_p\right)$ that we will also denote by k. Thus $\mathbb{Z}\subset \mathcal{W}\left({\mathbb{Q}}_p\right)$, and we call points in $\mathbb{Z}$ inside $\mathcal{W}\left({\mathbb{Q}}_p\right)$ integral weights.

If $W=\mathrm{Sp}R$ is an admissible affinoid of $\mathcal{W}$, the immersion $\mathrm{Sp}\left(R\right)=W\hookrightarrow \mathcal{W}$ defines an element $K\in \mathcal{W}\left(R\right)$, such that, for every $w\in W\left({\mathbb{Q}}_p\right)\hookrightarrow \mathcal{W}\left({\mathbb{Q}}_p\right)$, we have $\tilde{w}=w\circ \tilde{K}$. By Lemma 3.3 in [8], there exists $r\left(W\right)>1$, such that the morphism

$${\mathbb{Z}}_p⟶R^{\times },z⟼\tilde{K}(1+pz)$$

belongs to $A\left[r\right(W\left)\right]\left(R\right)$. We say that W is nice if the points $\mathbb{Z}\cap W$ are dense in W and both R and $R_0/p{R}_0$ are PID, where $R_0$ is the unit ball for the supremum norm in R.

7.2. The Eigencurve

For a fixed nice affinoid subdomain $W=\mathrm{Sp}R$ of $\mathcal{W}$, we can consider the R-modules ${\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }({\Delta }_0,D_{\tilde{K}}\left[r\right])$, for $1<r\le r\left(W\right)$. By Proposition 3.6 in [8], we have that the space ${\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }({\Delta }_0,D_{\tilde{K}}\left[r\right])$ is potentially orthonormalizable Banach R-module. The elements of the Hecke algebra $\mathcal{H}=\mathbb{Z}[T_q,⟨n⟩,U_p]$ act continuously and $U_p$ acts compactly.

If we consider ${\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }({\Delta }_0,D_{\tilde{K}}^{†}\left[r\right])$, Theorem 3.10 in [8] asserts that, for any $w\in W\left({\mathbb{Q}}_p\right)$ and any real number $1<r\le r\left(W\right)$, there natural $\mathcal{H}$-equivariant morphism

$${\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }({\Delta }_0,D_{\tilde{K}}^{†}\left[r\right]){\otimes }_{R,w}{\mathbb{Q}}_p⟶{\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }({\Delta }_0,D_{\tilde{w}}\left[r\right])$$

(19)

is always injective and surjective except when $w=0$ and the sign ± is −1.

The R-modules ${\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }({\Delta }_0,D_w\left[r\right])$ for all $1<r\le r\left(W\right)$ are all $\nu$-adapted if one is, in which case we say that $W=\mathrm{Sp}R$ is $\nu$-adapted. If W is $\nu$-adapted, the restriction maps define isomorphisms between the R-modules ${\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }{({\Delta }_0,D_{\tilde{w}}\left[r\right])}^{\le \nu }$ for all $1<r\le r\left(W\right)$. Thus, we obtain an isomorphism

$${\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }{({\Delta }_0,D_{\tilde{w}}^{†}\left[r\right])}^{\le \nu }\simeq {\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }{({\Delta }_0,D_{\tilde{w}}\left[r\right])}^{\le \nu },1<r\le r\left(W\right),$$

(20)

as seen in Proposition 3.11 in [8].

The eigencurves ${\mathcal{C}}^{\pm }\stackrel{\kappa }{\to }\mathcal{W}$ can be constructed as the union of local pieces

$${\mathcal{C}}_{W,\nu }^{\pm }⟶W=\mathrm{Sp}R,$$

where $\nu \in \mathbb{R}$ is a real and W is a nice affinoid subspace adapted to $\nu$. By definition,

$${\mathcal{C}}_{W,\nu }^{\pm }=\mathrm{Sp}{\mathbb{T}}_{W,\nu }^{\pm },$$

where ${\mathbb{T}}_{W,\nu }^{\pm }$ is the R-subalgebra of ${\mathrm{End}}_R\left({\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }{({\Delta }_0,D_{\tilde{K}}^{†}\left[1\right])}^{\le \nu }\right)$ generated by the image of the Hecke algebra $\mathcal{H}$.

Remark 5.

The cuspidal parts of ${\mathcal{C}}_{W,\nu }^{+}$ and ${\mathcal{C}}_{W,\nu }^{-}$ coincide by Theorem 3.27 in [8]; hence, we will sometimes identify certain neighbourhoods of cuspidal points.

7.3. Specialization

Let $w\in W\left({\mathbb{Q}}_p\right)$ and write ${\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }{({\Delta }_0,D_{\tilde{w}}^{†}\left[1\right])}_g^{\le \nu }$ for the image of the composition.

$${\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }{({\Delta }_0,D_{\tilde{K}}^{†}\left[1\right])}^{\le \nu }{\otimes }_{R,w}{\mathbb{Q}}_p\stackrel{\left(19\right)}{⟶}{\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }{({\Delta }_0,D_{\tilde{w}}\left[1\right])}^{\le \nu }\stackrel{\left(20\right)}{⟶}{\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }{({\Delta }_0,D_{\tilde{w}}^{†}\left[1\right])}^{\le \nu }$$

(21)

In analogy with previous definition, we write ${\mathbb{T}}_{w,\nu }^{\pm }$ for the ${\mathbb{Q}}_p$-subalgebra of the endomorphism ring ${\mathrm{End}}_{{\mathbb{Q}}_p}\left({\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }{({\Delta }_0,D_{\tilde{w}}^{†}\left[1\right])}_g^{\le \nu }\right)$ generated by the image of the Hecke algebra $\mathcal{H}$. By definition, there is a correspondence between points $x\in \mathrm{Spec}{\mathbb{T}}_{w,\nu }^{\pm }\left({\overline{\mathbb{Q}}}_p\right)$ and systems of $\mathcal{H}$-eigenvalues appearing in ${\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }{({\Delta }_0,D_{\tilde{w}}^{†}\left[1\right])}_g^{\le \nu }$. For any such x, we denote, by

$${\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }{({\Delta }_0,D_{\tilde{w}}^{†}\left[1\right])}_{\left(x\right)}$$

the generalized eigenspace of the corresponding eigenvalues. Similarly, we denote, by ${\left({\mathbb{T}}_{w,\nu }^{\pm }\right)}_{\left(x\right)}$, the localization of ${\mathbb{T}}_{w,\nu }^{\pm }{\otimes }_{{\mathbb{Q}}_p}{\overline{\mathbb{Q}}}_p$ at the maximal ideal corresponding to x. We have that

$${\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }{({\Delta }_0,D_{\tilde{w}}^{†}\left[1\right])}_{\left(x\right)}={\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }{({\Delta }_0,D_{\tilde{w}}^{†}\left[1\right])}^{\le \nu }{\otimes }_{{\mathbb{T}}_{w,\nu }^{\pm }}{\left({\mathbb{T}}_{w,\nu }^{\pm }\right)}_{\left(x\right)}.$$

(22)

Because, by definition ${\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }{({\Delta }_0,D_{\tilde{K}}^{†}\left[1\right])}^{\le \nu }{\otimes }_{R,w}{\mathbb{Q}}_p\simeq {\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }{({\Delta }_0,D_{\tilde{w}}^{†}\left[1\right])}_g^{\le \nu }$, we have a natural specialization map

$$s_w:{\mathbb{T}}_{W,\nu }^{\pm }{\otimes }_{R,w}{\mathbb{Q}}_p⟶{\mathbb{T}}_{w,\nu }^{\pm }.$$

By Lemme 6.6 in [14] the morphism $s_w$ is surjective for all $w\in \mathcal{W}\left({\mathbb{Q}}_p\right)$ and its kernel is nilpotent. In particular,

$$\mathrm{Spec}{\mathbb{T}}_{w,\nu }^{\pm }\left({\overline{\mathbb{Q}}}_p\right)={\kappa }^{-1}\left(w\right)\left({\overline{\mathbb{Q}}}_p\right),\kappa :{\mathcal{C}}^{\pm }⟶\mathcal{W}.$$

Given $x\in \mathrm{Spec}{\mathbb{T}}_{w,\nu }^{\pm }\left({\overline{\mathbb{Q}}}_p\right)\subset {\mathcal{C}}_{W,\nu }^{\pm }\left({\overline{\mathbb{Q}}}_p\right)$, we can consider the rigid analytic localization ${\left({\mathbb{T}}_{W,\nu }^{\pm }\right)}_{\left(x\right)}$ of ${\mathbb{T}}_{W,\nu }^{\pm }{\otimes }_{{\mathbb{Q}}_p}{\overline{\mathbb{Q}}}_p$ at the maximal ideal corresponding to x. Notice that, if we denote by $R_{\left(w\right)}$ the rigid analytic localization of $R{\otimes }_{{\mathbb{Q}}_p}{\overline{\mathbb{Q}}}_p$ at the maximal ideal corresponding to w, then ${\left({\mathbb{T}}_{W,\nu }^{\pm }\right)}_{\left(x\right)}$ is naturally a $R_{\left(w\right)}$-algebra. Localizing at x, we obtain a surjective local morphism of finite local ${\overline{\mathbb{Q}}}_p$-algebras with nilpotent kernel

$$s_w:{\left({\mathbb{T}}_{W,\nu }^{\pm }\right)}_{\left(x\right)}{\otimes }_{R_{\left(w\right)},w}{\overline{\mathbb{Q}}}_p⟶{\left({\mathbb{T}}_{w,\nu }^{+}\right)}_{\left(x\right)}.$$

(23)

Lemma 4.

We have that

$${\left({\mathbb{T}}_{w,\nu }^{\pm }\right)}_{\left(x\right)}\simeq {\overline{\mathbb{Q}}}_p\left[X\right]/X^2,$$

where X corresponds to the element of the Hecke algebra $U_p-\alpha$.

Proof. 

Equation (22) shows that ${\left({\mathbb{T}}_{w,\nu }^{\pm }\right)}_{\left(x\right)}$ is the ${\mathbb{Q}}_p$-subalgebra of the endomorphism ring ${\mathrm{End}}_{{\mathbb{Q}}_p}\left({\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }{({\Delta }_0,D_{\tilde{w}}^{†}\left[1\right])}_{\left(x\right)}^{\le \nu }\right)$ that is generated by the image of the Hecke algebra $\mathcal{H}$. By Theorem 6, we have

$${\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }{({\Delta }_0,D_{\tilde{w}}^{†}\left[1\right])}_{\left(x\right)}^{\le \nu }={\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }{({\Delta }_0,V\left(k\right))}_{\left(x\right)}^{\le \nu }={\overline{\mathbb{Q}}}_p{\widehat{\phi }}^{\pm }+{\overline{\mathbb{Q}}}_p{\widehat{\phi }}_{\mathrm{ext}}^{\pm }.$$

Hence, we can embed

$${\left({\mathbb{T}}_{w,\nu }^{\pm }\right)}_{\left(x\right)}\hookrightarrow \mathrm{End}({\overline{\mathbb{Q}}}_p{\widehat{\phi }}^{\pm }+{\overline{\mathbb{Q}}}_p{\widehat{\phi }}_{\mathrm{ext}}^{\pm })\simeq {\mathrm{M}}_2\left({\overline{\mathbb{Q}}}_p\right).$$

Hecke operators $T_q$ and $⟨n⟩$ act by scalar matrices, and the action of the operator $U_p$ is described in Section 6.3. More precisely, $X=U_p-\alpha$ is given by the matrix $\left(\begin{array}{cc}0& \alpha \\ 0& 0\end{array}\right)$ with respect to the basis ${\widehat{\phi }}^{\pm },{\widehat{\phi }}_{\mathrm{ext}}^{\pm }$. Thus, $X^2=0$ and the result follows. □

Definition 6.

Any classical cuspidal non-critical $y\in {\mathcal{C}}^{\pm }\left({\overline{\mathbb{Q}}}_p\right)$ corresponds to a p-stabilized normalized cuspidal modular symbol ${\phi }_{f_{{\alpha }^{\prime }}^{\prime }}^{\pm }$ of weight $\kappa \left(y\right)+2$. In this situation, we write

$${\mu }_y^{\pm }:={\mu }_{f^{\prime },{\alpha }^{\prime }}^{\pm }.$$

Analogously, in our irregular situation that is given by $x\in {\mathcal{C}}^{\pm }\left({\overline{\mathbb{Q}}}_p\right)$, we write

$${\mu }_x^{\mathrm{ext},\pm }:={\mu }_{f,p}^{\mathrm{ext},\pm }.$$

7.4. Two Variable p-Adic L-Functions

In this irregular situation, Betina and Williams define, in [7], two variable p-adic L-functions ${\mathcal{L}}_p^{\pm }$ that interpolate the p-adic L-functions ${\mu }_y^{\pm }$ as $y\in {\mathcal{C}}^{\pm }\left({\overline{\mathbb{Q}}}_p\right)$ runs over classical points in a neighbourhood of $x\in {\mathcal{C}}^{\pm }\left({\overline{\mathbb{Q}}}_p\right)$. In this section, we recall their construction and we give a relation between ${\mathcal{L}}_p^{\pm }$ and ${\mu }_x^{\mathrm{ext},\pm }$.

Proposition 5.

The space ${\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }{({\Delta }_0,D_{\tilde{K}}^{†}\left[1\right])}_{\left(x\right)}$ is a free ${\left({\mathbb{T}}_{W,\nu }^{\pm }\right)}_{\left(x\right)}$-module of rank one.

Proof. 

Proposition 4.10 in [7]. □

Corollary 1.

After possibly shrinking W, there exists a connected component $V=\mathrm{Sp}\left(T\right)\subset {\mathcal{C}}_{W,\nu }^{\pm }$ through x, such that T is Gorestein and

$${\mathcal{M}}_{\pm }:={\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }{({\Delta }_0,D_{\tilde{K}}^{†}\left[1\right])}^{\le \nu }{\otimes }_{{\mathbb{T}}_{W,\nu }^{\pm }}T$$

is a free T-module of rank one.

Proof. 

Corollary 4.11 in [7]. □

From the formalism of Gorestein rings, it follows that the R-linear dual ${\mathcal{M}}_{\pm }^{\vee }:={\mathrm{Hom}}_R({\mathcal{M}}_{\pm },R)$ is free of rank one over T. Let $\mathcal{R}$ be the ${\mathbb{Q}}_p$-algebra of locally analytic distributions of ${\mathbb{Z}}_p^{\times }$. We have a natural morphism $D^{†}\left[1\right]\to \mathcal{R}$ that is provided by the extension-by-zero map. This induces a morphism $\iota :D_{\tilde{K}}^{†}\left[1\right]\to \mathcal{R}{\widehat{\otimes }}_{{\mathbb{Q}}_p}R$ and a R-linear morphism

$$\begin{array}{ccc}\hfill \mathrm{Mel}:{\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }({\Delta }_0,D_{\tilde{K}}^{†}\left[1\right])& ⟶& \mathcal{R}{\widehat{\otimes }}_{{\mathbb{Q}}_p}R\hfill \\ \hfill \phi & ⟼& \iota \left(\phi (0-\infty )\right)\hfill \end{array}$$

Because V is a connected component of the eigencurve, ${\mathcal{M}}_{\pm }$ is a direct summand of ${\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }{({\Delta }_0,D_{\tilde{K}}^{†}\left[1\right])}^{\le \nu }$. Thus, the restriction of $\mathrm{Mel}$ defines an element of $\mathcal{R}{\widehat{\otimes }}_{{\mathbb{Q}}_p}{\mathcal{M}}_{\pm }^{\vee }$.

Definition 7.

By choosing a basis of ${\mathcal{M}}_{\pm }^{\vee }$ over T, the above construction provides

$${\mathcal{L}}_p^{\pm }\in \mathcal{R}{\widehat{\otimes }}_{{\mathbb{Q}}_p}T$$

called the the two variables p-adic L-function.

Write ${\overline{\mathbb{Q}}}_p\left[\epsilon \right]:={\overline{\mathbb{Q}}}_p\left[X\right]/\left(X^2\right)$, and let us consider the morphism

$$x{\left[\epsilon \right]}^{\ast }:T⟶T_{\left(x\right)}={\left(T_{W,\nu }^{\pm }\right)}_{\left(x\right)}⟶{\left(T_{W,\nu }^{\pm }\right)}_{\left(x\right)}{\otimes }_{R_{\left(w\right)},w}{\overline{\mathbb{Q}}}_p\stackrel{s_w}{⟶}{\left(T_{w,\nu }^{\pm }\right)}_{\left(x\right)}\simeq {\overline{\mathbb{Q}}}_p\left[\epsilon \right],$$

given by (23) and Lemma 4. This provides a point $x\left[ϵ\right]\in V\left({\overline{\mathbb{Q}}}_p\left[\epsilon \right]\right)$ lying above $x\in V\left({\overline{\mathbb{Q}}}_p\right)$.

Theorem 7.

For any $y\in V\left({\overline{\mathbb{Q}}}_p\right)$ corresponding to a small slope p-stabilized cuspidal eigenform,

$${\mathcal{L}}_p^{\pm }=C^{\pm }\left(y\right)·{\mu }_y^{\pm }\in \mathcal{R},$$

for some $C^{\pm }\left(y\right)\in {\overline{\mathbb{Q}}}_p^{\times }$. We can normalize ${\mathcal{L}}_p^{\pm }$ by choosing the right T-basis ${\varphi }^{\pm }$ of ${\mathcal{M}}_{\pm }^{\vee }$, so that $C^{\pm }\left(x\right)=1$. Moreover, for a good choice of ${\varphi }^{\pm }$,

$${\mathcal{L}}_p^{\pm }\left(x\left[ϵ\right]\right)={\mu }_x^{\pm }+{\alpha }^{-1}{\mu }_x^{\mathrm{ext},\pm }\epsilon \in \mathcal{R}{\otimes }_{{\mathbb{Q}}_p}{\overline{\mathbb{Q}}}_p\left[\epsilon \right].$$

Proof. 

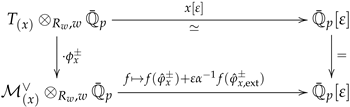
The first part of this theorem corresponds to Theorem 5.2 in [7]. Here, we can extend their arguments to also deduce the second part of the theorem.

By definition

$$\mathrm{Mel}={\mathcal{L}}_p^{\pm }{\varphi }^{\pm }\in \mathcal{R}{\widehat{\otimes }}_{{\mathbb{Q}}_p}{\mathcal{M}}_{\pm }^{\vee }.$$

For any point $y\in V\left({\overline{\mathbb{Q}}}_p\right)$, write $w=\kappa \left(y\right)\in W\left({\overline{\mathbb{Q}}}_p\right)$. If we denote ${\mathcal{M}}_{\left(y\right)}:={\mathcal{M}}_{\pm }{\otimes }_T{T}_{\left(y\right)}$, we have

$${\mathcal{M}}_{\left(y\right)}^{\vee }{\otimes }_{R_w,w}{\overline{\mathbb{Q}}}_p={\mathrm{Hom}}_{R_w}({\mathcal{M}}_{\left(y\right)},R_w){\otimes }_{R_w,w}{\overline{\mathbb{Q}}}_p={\mathrm{Hom}}_{{\overline{\mathbb{Q}}}_p}({\mathcal{M}}_{\left(y\right)}{\otimes }_{R_w,w}{\overline{\mathbb{Q}}}_p,{\overline{\mathbb{Q}}}_p),$$

because ${\mathcal{M}}_{\left(y\right)}$ is a finite free $R_w$-module. By Proposition 4.3 in [7] and the control Theorem 6, the composition (21) provides an isomorphism

$$\begin{array}{ccc}\hfill {\mathcal{M}}_{\left(y\right)}{\otimes }_{R_w,w}{\overline{\mathbb{Q}}}_p& =& {\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }{({\Delta }_0,D_{\tilde{w}}^{†}\left[1\right])}_{\left(y\right)}\simeq {\mathrm{Hom}}_{\mathsf{\Gamma }}^{\pm }{({\Delta }_0,V\left(w\right))}_{\left(y\right)}\hfill \\ & =& \left\{\begin{array}{cc}{\overline{\mathbb{Q}}}_p{\widehat{\phi }}_y^{\pm },\hfill & \mathrm{regular} \mathrm{case},\hfill \\ {\overline{\mathbb{Q}}}_p{\widehat{\phi }}_y^{\pm }+{\overline{\mathbb{Q}}}_p{\widehat{\phi }}_{y,\mathrm{ext}}^{\pm },\hfill & \mathrm{irregular} \mathrm{case}.\hfill \end{array}\right.\hfill \end{array}$$

We observe that, since

$$T_{\left(y\right)}{\otimes }_{R_w,w}{\overline{\mathbb{Q}}}_p=\left\{\begin{array}{cc}{\overline{\mathbb{Q}}}_p,\hfill & \mathrm{regular} \mathrm{case},\hfill \\ {\overline{\mathbb{Q}}}_p\left[ϵ\right],\hfill & \mathrm{irregular} \mathrm{case},\hfill \end{array}\right.$$

a $T_{\left(y\right)}{\otimes }_{R_w,w}{\overline{\mathbb{Q}}}_p$-basis for ${\mathcal{M}}_{\left(y\right)}^{\vee }{\otimes }_{R_w,w}{\overline{\mathbb{Q}}}_p$ is given by ${\varphi }_y^{\pm }$ with ${\varphi }_y^{\pm }\left({\widehat{\phi }}_y^{\pm }\right)=1$ and ${\varphi }_y^{\pm }\left({\widehat{\phi }}_{y,\mathrm{ext}}^{\pm }\right)=0$. Notice first that the point $y:T\to {\overline{\mathbb{Q}}}_p$ factors through $T_{\left(y\right)}{\otimes }_{R_w,w}{\overline{\mathbb{Q}}}_p\to {\overline{\mathbb{Q}}}_p$, and it fits into the commutative diagram

Because ${\varphi }_y^{\pm }$ corresponds to the specialization of ${\varphi }^{\pm }$ up to constant, we compute

$$C^{\pm }\left(y\right)·{\mu }_y^{\pm }=C^{\pm }\left(y\right)·{\widehat{\phi }}_y^{\pm }(0-\infty )=C^{\pm }\left(y\right)·\mathrm{Mel}\left({\widehat{\phi }}_y^{\pm }\right)={\mathcal{L}}_p^{\pm }\left(y\right)·{\varphi }_y^{\pm }\left({\widehat{\phi }}_y^{\pm }\right)={\mathcal{L}}_p^{\pm }\left(y\right),$$

for some $C^{\pm }\left(y\right)\in {\overline{\mathbb{Q}}}_p$, so that $C^{\pm }\left(y\right)·{\varphi }^{\pm }={\varphi }_y^{\pm }$. This proves the first assertion. For the second, notice that $C^{\pm }\left(x\right)=1$ and we have the commutative diagram

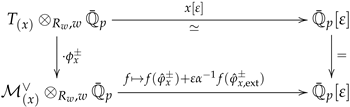
Because by (18) we have $(U_p-\alpha ){\widehat{\phi }}_{x,\mathrm{ext}}^{\pm }=\alpha {\widehat{\phi }}_x^{\pm }$. Again, we compute

$$\begin{array}{ccc}\hfill {\mu }_x^{\pm }+{\alpha }^{-1}{\mu }_x^{\mathrm{ext},\pm }\epsilon & =& {\widehat{\phi }}_x^{\pm }(0-\infty )+{\alpha }^{-1}{\widehat{\phi }}_{x,\mathrm{ext}}^{\pm }(0-\infty )\epsilon =\mathrm{Mel}\left({\widehat{\phi }}_x^{\pm }\right)+\epsilon {\alpha }^{-1}\mathrm{Mel}\left({\widehat{\phi }}_{x,\mathrm{ext}}^{\pm }\right)\hfill \\ & =& {\mathcal{L}}_p^{\pm }\left(x\left[\epsilon \right]\right)·\left({\varphi }_x^{\pm }\left({\widehat{\phi }}_x^{\pm }\right)+\epsilon {\alpha }^{-1}{\varphi }_x^{\pm }\left({\widehat{\phi }}_{x,\mathrm{ext}}^{\pm }\right)\right)={\mathcal{L}}_p^{\pm }\left(x\left[\epsilon \right]\right),\hfill \end{array}$$

and the result follows. □

Notice that there is no canonical choice of ${\varphi }_x^{\pm }$, even though we impose $C^{\pm }\left(x\right)=1$. In fact, $(1+\epsilon c)·{\varphi }_x^{\pm }$ with $c\in {\overline{\mathbb{Q}}}_p$ is also a basis, so that $C^{\pm }\left(x\right)=1$. For any such a change of basis, we obtain

$${\mathcal{L}}_p^{\pm }\left(x\left[ϵ\right]\right)={(1+\epsilon c)}^{-1}({\mu }_x^{\pm }+{\alpha }^{-1}{\mu }_x^{\mathrm{ext},\pm }\epsilon )={\mu }_x^{\pm }+({\alpha }^{-1}{\mu }_x^{\mathrm{ext},\pm }-c{\mu }_x^{\pm })\epsilon .$$

The following result does not depend on the choice of the generator ${\varphi }^{\pm }$:

Corollary 2.

Let $t\in T$ the element corresponding to $U_p-\alpha$. Subsequently,

$$\frac{\partial {\mathcal{L}}_p^{\pm }}{\partial t}\left(x\right)\in {\alpha }^{-1}{\mu }_x^{\mathrm{ext},\pm }+{\overline{\mathbb{Q}}}_p{\mu }_x^{\pm }.$$