A Hybrid Multiple Criteria Decision-Making Technique to Evaluate Regional Intellectual Capital: Evidence from China

Abstract

With the dawn of economic globalization and the knowledge economy, intellectual capital has become the most important factor to determine economic growth. However, due to resource endowment, location conditions, policy differences, and other factors, provinces in China show sizeable differences in regional intellectual capital (RIC), which affects the coordinated development of the regional economy. Evaluating RIC is a typical multiple-criteria decision-making (MCDM) problem. Therefore, this study employs a set of MCDM techniques to solve this problem. First, the Delphi method is used to determine the formal decision structure based on a systematic literature review. A novel hybrid method, namely, the Grey-based Decision-Making Trial and Evaluation Laboratory (DEMATEL) and Analytic Network Process (ANP), i.e., GDANP, is employed to obtain the relative weight of each criterion. Finally, based on the data of 31 provinces in China, the Technique for Order Preference by Similarity to an Ideal Solution (TOPSIS) is used to evaluate the RIC. According to the questionnaires filled out by an expert panel, we establish an evaluation index of RIC with 21 criteria. Based on the results of empirical study, the level of RIC in different regions in China is quite different. Furthermore, the RIC ranking is largely consistent with the provincial gross domestic product (GDP) ranking, in line with the current status of development in the regions. Indeed, this paper shows that the proposed hybrid method can effectively measure the level of RIC.

1. Introduction

Since the 1980s, as the economic development model began to transition away from an investment-driven phase towards an innovation-driven phase, the world economy entered a period of industrial restructuring, and economic development aligned itself with the knowledge economy era. In the modern world, intellectual capital (IC) has become one of the most valuable assets of an organization, region, or country [1]. In this process, IC separated from other factors of production, and became the engine of economic growth and technological progress [2]. IC reveals the important role of knowledge in regional development, and it helps to explore the key knowledge that affects regional innovation capabilities, while identifying new growth points. For example, advanced countries create national value through service innovation, research, and development, or an increase in gross domestic product (GDP) per working hour [3]. The development potential of any organization is embedded in its IC, which is considered to be the basic resource for creating value at regional and national levels [4].

Due to the complex and diverse attributes of IC, proposing a universal definition of IC is a great challenge for contemporary researchers. IC was first proposed by Galbraith [5], and he suggested that IC should be more accurately transformed into an intellectual act, rather than knowledge or pure intelligence. Since then, many scholars have actively engaged in the study of IC. Khalique [6] proposed that IC can be considered as a collection of intangible assets or resources. IC can create organizational value and provide a competitive boundary for organizations. According to the popular view, Stewart [7] defined IC as the most valuable form of capital, and it can be regarded as the sum of personal knowledge and ability, which can bring competitive advantages. These competitive advantages are not only owned by enterprises or organizations but are also owned by the countries. The concept of regional intellectual capital (RIC) was put forward. Stam and Andriessen [8] pointed out that RIC was “the sum of all intangible resources that can be used by countries or regions that can produce comparative advantages and create future benefits through integration”. Furthermore, Schiuma and Lerro [9] interpreted RIC as a group of knowledge assets that are attributed to a region, and it significantly promotes innovation momentum and the mechanism underlying the creation of regional value. Measuring RIC is a complex process. IC is a multi-dimensional category that cannot be measured directly, but which can be identified by its attributes [10]. However, there is no widely accepted index at present. In particular, establishing a scientific and systematic index is the first priority. Thus, this paper used the Delphi method to establish a universal index with high consensus. This is the first aim of this paper.

Because many factors will affect RIC together, and the factors have conflicting or competing relations among them, the evaluation of RIC is a typical multiple-criteria decision-making (MCDM) problem. Traditionally, obtaining the relative weights is the first step to evaluation. Calabrese et al. [11] used the Analytic Hierarchy Process (AHP) method to obtain the weight of each factor to effectively analyze how the factors influenced IC of the company. Wang and He [12] calculated the determinants’ rankings of the company’s IC using the Analytic Network Process (ANP) method. Moreover, some scholars proposed some methods to evaluate RIC. Chen and Chen [13] used the Vlse Kriterijumska Optimizacija I Kompromisno Resenje (VIKOR) to rank five types of universities for innovation development from the IC perspective. Michalczuk et al. [10] constructed a ranking and classification of EU countries based on IC resources using the Technique for Order Preference by Similarity to an Ideal Solution (TOPSIS). However, the AHP method needs to satisfy the assumption that the criteria are independent of each other [14]. The ANP method can solve this problem, but it requires a large number of pairwise comparisons, and it is not easy to achieve consistency [15]. What is more, how to effectively measure the RIC ranking of 31 provinces is also a topic worthy of discussion. Therefore, the key problem is to select a scientific and appropriate evaluation method. This is another aim of this study.

In this paper, we will answer the question of how to effectively measure RIC in China. In order to solve this problem, we use the Delphi method to determine the formal evaluation index by obtaining the consensus by an expert panel. Then, to calculate the relative weights of each criterion, this paper employed a hybrid decision model known as the Grey-Decision Making Trial and Evaluation Laboratory (grey-DEMATEL)-based Analytic Network Process (i.e., GDANP), developed by Jiang [16], to recover the limitations of the aforementioned methods, avoiding the tedious questionnaire of DEMATEL. Furthermore, the RIC ranking of provinces was obtained by TOPSIS.

The remainder of this paper is organized as follows. Section 2 analyzes the influencing dimensions and criteria of IC and establishes the prototype decision structure. Section 3 describes the methodology used in this paper. Section 4 develops the formal evaluating index using the Delphi method based on the experts’ opinions, and finds the RIC ranking of each region in China by the proposed hybrid model. Based on the empirical study, Section 5 presents the management implications. Section 6 discusses the various outcomes, and Section 7 provides the conclusions of this study.

2. Literature Review

2.1. Components of Intellectual Capital

Currently, there are many studies on the factors affecting RIC. For example, Rossi et al. [17] proposed that the RIC should be considered from the perspective of human capital, structural capital, and relational capital based on previous theories. Lin [18] divided IC into human, market, process, and innovation capital. Incze and Vasilache [19] assessed the level of IC in Romanian IT MNCs and SMEs from three perspectives: human capital, structural capital, and relational capital. It is not difficult to see that the evaluation index is composed of different dimensions and criteria. However, no consensus has yet emerged. Michalczuk and Fiedorczuk [20] put forward that RIC should include “thinking” and “non-thinking”. As the part of “thinking”, human capital appears in almost every conceptual model of analysis. The differences in scholars’ views are mainly reflected in the “non-thinking” component. In their study, they divided RIC into human capital, social capital, structural capital, developmental capital, and relational capital. This paper refers to the most popular three-level component model: human capital, structural capital, and relational capital [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42].

The most important component of RIC is human capital, which is generally accepted by scholars [4,9,10,18,43,44,45,46,47,48,49,50,51]. Measuring and evaluating knowledge in human capital is a very important and interesting area [52]. Human capital represents the knowledge, education, and competencies of individuals in realizing national tasks and goals [53]. It consists of a set of knowledge, skills, and capabilities developed and deployed at the individual level in order to be productive, efficient, and innovative [54]. Human capital reflects a population’s total capabilities as reflected in education, knowledge, health, experience, motivation, intuition, entrepreneurship, and expertise [18]. According to the human capital theory developed by American economists Schultz and Becker in the 1960s, improving the quality of the population has become the core of human capital. Human capital provides resources for the development and cultivation of other areas of intellectual assets, such as R&D and training, because the human factor is the most important link in the process of value creation [18]. This paper used the level of regional education development, health care, and employment to measure regional human capital.

Structural capital is another important dimension of RIC [10,47]. The information and digital revolution have established new ways of learning and communication in the world [42], creating enormous opportunities for regional development. In this context, technology and infrastructure have gained considerable attention. Structural capital refers to the “infrastructure” or “knowledge platform” that contributes to the safe, orderly, and efficient functioning of the regional economic and social capital structure, and it can therefore be regarded as a mechanism that transforms human capital into wealth [46]. This type of capital encompasses several types of structures: organizational, communicative, technological, informative, and process-related, as well as other intangible resources, such as intellectual property (e.g., patents, trademarks, scientific achievements), innovations, or R&D activity [55]. This paper divided structural capital into process capital and innovation capital. Process capital is defined as the knowledge stock embedded in the infrastructure of a region [48], which plays a role in cooperation and the flow of knowledge [56]. Innovation capital is defined as a nation’s future intellectual wealth, and it refers to the capability for innovation that sustains a nation’s competitive advantage [50]. It also reflects a region’s investment in future market competitiveness [56].

Similarly, relational capital is one of the key factors to measure RIC [10,46,47]. Relational capital is the value that is inherent in the country’s external relations. It represents connections that facilitate cooperation, the attractiveness and competitiveness of the economy, and the country’s image in the eyes of its partners, investors, and individuals. In order to survive in a highly competitive environment, it is necessary to maintain good relations with investors, consumers, and suppliers [41]. Relational capital can be assessed in terms of the country’s international integration as well as its internal and external activities [20]. Relational capital embodies the knowledge that is generated by the relationship between the region and the environment. It involves the ability to implant and self-generate value, product demand, investment potential, and joint projects [57]. It is not only important to create relationship capital, but a successful organization should also be able to maintain its relationship capital [58]. A region needs to continuously provide attractive and competitive solutions that can satisfy the needs of internal and external users, and it should strive to achieve success in its internal and external relations by focusing on customer loyalty, economic openness, and trade partner satisfaction. This paper measured regional relationship capital from the perspective of internal and external relations.

2.2. Prototype Decision Structure

Based on the literature above, this study selected and integrated the criteria influencing RIC. Next, according to the definitions of selected criteria, the criteria were divided into three dimensions, namely human capital, structural capital, and relational capital, respectively. Then, the prototype decision structure was established, as shown in Table 1.

Table 1. Prototype decision structure.

Regional Human Capital
Aspects	Criteria	Reference
Educational development	The amount of local fiscal expenditure on education per capita	[46]
	The number of higher education schools	[4,53]
	The number of years of education per capita	[18]
Medical health level	The number of doctors per 10,000 people	[46]
	The number of medical beds per 10,000 people	[46]
	Total health expenditure	[44]
Employment status	The number of employed persons	[59]
	Unemployment rate	[57,59]
Regional Structural Capital
Aspects	Criteria	Reference
Process capital	The number of Internet subscribers	[3]
Innovation capital	The number of persons engaged in science and technology per 10,000 people	[46]
	The number of invention and patent applications	[46]
Regional Relational Capital
Aspects	Criteria	Reference
Internal relations	Consumer price index	[18]
External relations	Foreign direct investment intensity	[60]
	The total import and export volume accounted for the proportion of GDP	[46]

In this prototype decision structure, regional human capital consists of the level of educational development, the level of medical health, and the employment status. People, as the core of IC, are directly influenced by the above factors. When analyzing the human capital of a region, it is important to first fully examine the education situation [53]. The level of educational development reflects the base and potential of a region’s talent and is the basic building block of human capital [61]. Three criteria were selected from the literature. Among them, the amount of local fiscal expenditure on education per capita reflects the importance that regional governments attach to local talent cultivation, the number of higher education schools reflects the regional capacity and resources to cultivate high-end talent, and the number of years of education per capita represents the basic education level of the region. The health level also reflects the situation of human capital to a certain extent [18], showing the protection of local labor. Similarly, three medical health criteria were selected. The number of doctors per 10,000 people and the number of medical beds per 10,000 people reflect the basic situation of hospitals, and total health expenditure reflects the importance of health care by the regional government. Human capital captures the knowledge and skills of individuals and organizations to achieve their goals, which includes employability [59]. Measuring the employment status helps to reflect the supply and demand of the labor force, so as to effectively reflect the human capital of labor market. We have selected the classical measures—the number of employed persons and unemployment rate.

Regional structural capital is divided into process capital and innovation capital. This paper argues that regional structural capital provides the infrastructure and platform for talent to function. Process capital can maintain and increase the output of human capital [18]. In the context of the information age, this paper selects the number of Internet subscribers as a measure from the literature. Innovation capital reflects the importance a region places on future competitiveness, which in turn encourages future growth [18]. Based on the literature review, this paper selected two innovation criteria, including the number of persons engaged in science and technology per 10,000 people from the human side and the number of invention and patent applications from the output outcome side.

Relational capital represents the sum of available and potential resources in the system network [62]. Regional relationship capital is analyzed in terms of internal and external relationships, reflecting the business environment in which IC plays a role. For internal relationships, the consumer price index indicator selected from the literature in this paper captures the consumer spending power within the region. For external relationships, foreign direct investment intensity reflects external recognition of whether the region is worth investing in, and the total import and export volume accounting for the proportion of GDP is used to measure the ability to transact with outside the region.

3. Methodology

Evaluating RIC is a typical MCDM problem. Thus, it was first necessary to determine the competing criteria to be included in the structure of the RIC evaluation. The Delphi method, which considers the consensus of an expert panel, was used to form the formal decision structure; its procedure is described in Section 3.1. In Section 3.2, we introduced the GDANP technique that was used to identify the critical factors. In Section 3.3, we described the TOPSIS method, which was used to rank the RIC level of 31 provinces in China.

3.1. Delphi Method

The Delphi method involves participants reaching consensus on a question through their anonymity to each other, using their written responses to a questionnaire, for prediction and information gathering [63]. Ouyang et al. [64] claimed that the Delphi method relies on the experience and intuition of experts to provide different views on the same topic, and they understand each other in order to achieve agreement in another round of adjustment. This helps to avoid conflicts among experts. As a tool for decision-making by expert groups, the Delphi method has been successfully applied in various fields, such as regional development [65,66], tourism [67,68], and medical health [69,70]. In this paper, the quartile deviation (QD) is defined as one-half the interquartile range (IQR), which is the difference between the 25th and the 75th percentiles in the frequency distribution, applied to determine consistency [71]. The QD consensus level is shown in Table 2. If the QD value is ≤0.6, it is considered a high consensus level.

Table 2. QD consensus level [71].

Consensus	High	Moderate	Low
QD	QD ≤ 0.6	0.6 ≤ QD ≤ 1	1 ≤ QD

Before calculating the QD value, a questionnaire on RIC was distributed to each expert, who provided their opinion on the appropriateness of the criteria. Next, experts were asked to rate the necessity of the criteria for inclusion in the decision structure. A five-point Likert scale was used, and the relationship between rank and necessity is shown in Table 3. We called this process Round one. Round one must be repeated until an acceptable QD value is obtained.

Table 3. Relationship between rating and necessity.

Rating	1	2	3	4	5
Necessity	Strongly unnecessary	Unnecessary	Average	Necessary	Strongly necessary

3.2. Grey DEMATEL-Based ANP

Since evaluating RIC is a typical MCDM problem, many MCDM techniques can be considered (e.g., AHP, ANP, and DEMATEL). However, these methods have more or fewer limitations, such as the independence assumption of AHP, and the consistency test of AHP and ANP [72]. A hybrid model named DEMATEL-based ANP (DANP) proposed by Ouyang [64] can solve these problems effectively. In practice, DANP uses a direct influence matrix, which involves numbers of items in the process of pairwise comparisons. A troublesome problem is that the greater the number of criteria is, the more time a respondent requires to fill out the direct influence matrix. Often, the quality of questionnaires can be influenced to a certain degree as respondents become bored and tired. Therefore, Jiang [16] developed a decision model, GDANP, which can avoid pairwise comparisons by automatically generating the direct influence matrix. Moreover, GDANP also allows the negative value that cannot be handled by AHP and ANP [16]. Nowadays, the GDANP method has been successfully used in supplier selection [73,74] and two sector interaction [16].

The procedure of the GDANP is as follows:

Step 1: Generating the direct influence matrix by Grey relational analysis (GRA)

Based on the results of Delphi, the direct influence matrix is constructed by the grey relational matrix and grey self-relational matrix, which are calculated using GRA. To perform GRA, we must first compute the grey relational coefficients (GRCs) for each factor. Let the reference sequence be X₀ = {x₀(1), x₀(2), …, x₀(n)}, and the comparison sequence is X_i = {x_i(1), x_i(2), …, x_i(n)}. Then,

$$\mathsf{\xi }\left(x_0{\left(k\right),x}_i\left(k\right)\right)=\frac{\underset{i}{\mathit{min}}\underset{k}{\mathit{min}}\left|x_0{\left(k\right)-x}_i\left(k\right)\right|+\rho \underset{i}{\mathit{max}}\underset{k}{\mathit{max}}\left|x_0{\left(k\right)-x}_i\left(k\right)\right|}{\left|x_0{\left(k\right)-x}_i\left(k\right)\right|+\rho \underset{i}{\mathit{max}}\underset{k}{\mathit{max}}\left|x_0{\left(k\right)-x}_i\left(k\right)\right|},\mathit{for}1\le i\le n,1\le k\le m,$$

(1)

where ρ is the discriminative coefficient (0 ≤ ρ ≤ 1), and usually ρ = 0.5.

The grey relational grade (GRG) can be represented in this instance as

$$\mathrm{z}\left(x_0{\left(k\right),x}_i\left(k\right)\right)={\sum }_{i=1}^n{w}_i{\xi (x}_0{\left(k\right),x}_i\left(k\right)),$$

(2)

where w_i is the relative importance of attribute i. z(x₀(k), x_i(k)) ranges from 0 to 1, and the sum of w₁, w₂, …, w_n is one. As a result, the direct influence matrix Z is

$$\mathbf{Z}=\left[\begin{array}{ccc}\begin{array}{cc}{z(x}_1{,x}_1)& {z(x}_1{,x}_2)\end{array}& \cdots & {z(x}_1{,x}_n)\\ \begin{array}{cc}{z(x}_2{,x}_1)& {z(x}_2{,x}_2)\end{array}& \cdots & {z(x}_2{,x}_n)\\ ⋮& \ddots & ⋮\\ z\begin{array}{cc}{(x}_n{,x}_1)& {z(x}_n{,x}_2)\end{array}& \cdots & {z(x}_n{,x}_n)\end{array}\right].$$

(3)

Step 2: Obtaining the relative weights by DANP

In the direct influence matrix of DANP, all of the diagonal elements are zero. Z is then normalized to produce the normalized direct influence matrix:

X = λZ,

(4)

where

$$\lambda =\frac{1}{\underset{i,j}{\mathit{max}}\left\{max{\sum }_{i=1}^n{z}_{ij},max{\sum }_{j=1}^n{z}_{ij}\right\}}.$$

(5)

Then, the total influence matrix T is generated by

T = X(I − X)⁻¹

(6)

Next, the total influence matrix is regarded as the unweighted supermatrix of ANP. After normalization, we can obtain the limited supermatrix and the relative weights of each criterion.

3.3. TOPSIS Method

The TOPSIS method was firstly developed by Hwang and Yoon in 1981. In recent years, the TOPSIS method and another ranking tool called VIKOR have both become popular in decision making. However, they are essentially different in principle. Ranking obtained by VIKOR only focuses on positive ideal solutions. While pursuing good fortune and avoiding evil is people’s eternal pursuit, TOPSIS is concerned with both positive and negative ideal solutions, so as to consider the problem comprehensively. Therefore, the TOPSIS method is widely used in various fields, such as logistics and transportation [75,76,77], manufacturing [78,79], and commerce [80,81].

The basic principle of TOPSIS is that the chosen alternative should have the shortest distance from the ideal solution and the farthest distance from the negative ideal solution. The TOPSIS procedure consists of the following steps:

(1)

Calculate the normalized decision matrix. The normalized value x_i(k) is calculated by

$$x_i\left(k\right)=\frac{x_i\left(k\right)}{{\mathit{max}(x}_i)},\mathit{for}1\le i\le n,1\le k\le m,$$

(7)

where $x_i\left(k\right)$ is a “larger-the-better” criterion. Furthermore,

$$x_i\left(k\right)=\frac{{\mathit{min}(x}_i)}{x_i\left(k\right)},for1\le i\le n,1\le k\le m,$$

(8)

where $x_i\left(k\right)$ is a “smaller-the-better “criterion, and where max(x_i) and min(x_i) represent the maximum and minimum values.

(2)

Calculate the weighted normalized decision matrix. The weighted normalized value v_i(k) is calculated as follows:

V_i(k) = w_ix_i(k), i = 1, …, n; k = 1, …, m,

(9)

where w_i is the weight of the ith attribute or criterion, and ${\sum }_{i=1}^n{w}_i=1$.

(3)

Determine the positive ideal and negative ideal solution.

$$V^{*}=\left\{v_1^{*}{,\dots \dots ,v}_n^{*}\right\}=\{\underset{i}{\mathit{max}}{v}_i\left(k\right)|i=1,\dots ,n\},$$

(10)

$$V^{-}=\left\{v_1^{-}{,\dots \dots ,v}_n^{-}\right\}=\{\underset{i}{\mathit{min}}{v}_i\left(k\right)|i=1,\dots ,n\}.$$

(11)

(4)

Calculate the separation measures, using the n-dimensional Euclidean distance. The separation of each alternative from the ideal solution is given as

$$D_k^{*}=\sqrt{{\sum }_{k=1}^m{{(v}_i{\left(k\right)-v}_i^{*}\left(k\right))}^2},i=1,\dots ,n.$$

(12)

Similarly, the separation from the negative ideal solution is given as

$$D_k^{-}=\sqrt{{\sum }_{k=1}^m{{(v}_i{\left(k\right)-v}_i^{-}\left(k\right))}^2},i=1,\dots ,n.$$

(13)

(5)

Calculate the relative distance from the positive ideal solution alternative [75]:

$$C_k^{*}{=D}_k^{-}{/(D}_k^{*}{+D}_k^{-}),k=1,\dots ,m.$$

(14)

(6)

Rank the preference order.

The framework of the proposed hybrid model in this paper is shown as Figure 1.

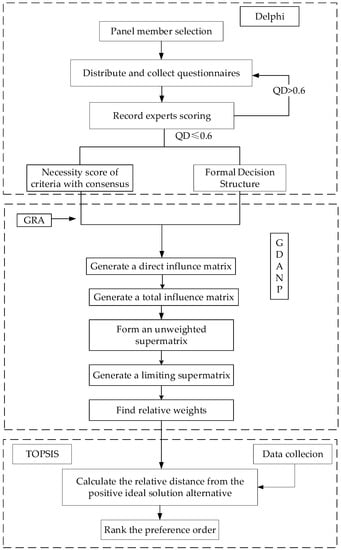
Figure 1. Empirical framework.

4. RIC Evaluation of China

4.1. Determining the Formal Decision Structure

Academics and government researchers often focus on RIC research. By examining the three key factors of RIC, namely human capital, structural capital, and relationship capital, we approached experts from related fields and members of government staff and created a group of eight experts whose professional backgrounds are shown in Table 4. The panel was invited to rate the necessity of including criteria for the prototype (Table 1) in the formal research structure.

Table 4. Professional backgrounds of the selected eight experts for the Delphi survey.

Expert	Organization	Position	Duties	Seniority
A	Dalian University of Technology	Head of Economics Department	Economic system analysis and management	15
B	Harbin Institute of Technology	Vice president	Industrial economics	22
C	Shandong University	Associate professor	New institutional economics	16
D	Shandong University	Professor	Economic theory and macroeconomic policy	28
E	Dalian University of Technology	Vice president	Industrial economics	10
F	Huancui District Development and Reform Commission	Deputy director	National economy and social development strategy and planning	10
G	China Society for the study of foreign economic theories	Standing director	Public economics	25
H	Tianjin Development and Reform Commission	Deputy director	Development Economics	30

After three rounds of the Delph survey, the panel members reached consensus on all criteria. All QD consensus levels were below 0.6, achieving an acceptable level of consensus. Table 5 shows the results of the third round of the Delphi, and the formal decision structure is presented in Table 6.

Table 5. The results of the third round of the Delphi survey.

Criteria	Ascending Order								Mean	QD	Classification
The amount of local fiscal expenditure on education per capita	4.10	4.05	4.50	3.90	4.70	4.70	4.95	4.70	4.45	0.31	High Consensus
The number of higher education institutions	4.30	4.50	4.50	4.00	4.60	4.50	5.00	4.50	4.49	0.08	High Consensus
The number of years of education per capita	4.50	4.50	4.50	5.00	4.80	4.05	5.00	4.50	4.61	0.20	High Consensus
The number of licensed (assistant) doctors per 10,000 people	3.75	4.00	4.50	4.10	4.85	4.40	5.00	4.50	4.39	0.31	High Consensus
The number of medical beds per 10,000 people	4.00	4.00	4.50	4.10	4.75	4.80	5.00	4.30	4.43	0.29	High Consensus
The amount of local fiscal expenditure on health per capita	4.50	4.50	5.00	3.00	4.15	4.00	4.50	4.00	4.21	0.25	High Consensus
The number of health education trainers in health education professional institutions	3.95	3.55	4.50	2.90	4.00	4.45	4.00	4.55	3.99	0.36	High Consensus
Unemployment rate	3.70	4.50	4.50	2.20	4.50	4.30	4.20	4.50	4.05	0.28	High Consensus
The number of employed persons	4.10	4.50	4.55	2.55	3.60	4.80	5.00	4.75	4.23	0.46	High Consensus
The number of public employment service instructors	3.95	3.50	4.25	3.25	3.95	4.50	5.00	4.55	4.12	0.40	High Consensus
Passenger volume of transportation industry	4.10	4.50	4.50	4.00	4.40	4.30	5.00	4.60	4.43	0.18	High Consensus
The number of Internet users	4.35	4.00	4.50	3.15	3.65	4.05	4.10	4.55	4.04	0.30	High Consensus
Express volume	4.20	4.35	4.50	5.00	3.55	4.25	5.00	4.50	4.42	0.26	High Consensus
Railway operating mileage	4.50	4.50	5.00	4.00	3.75	3.00	4.50	4.10	4.17	0.31	High Consensus
Highway operating mileage	4.25	4.00	4.50	3.00	3.50	4.55	5.00	4.00	4.10	0.39	High Consensus
The number of R&D personnel	4.20	4.00	4.50	4.90	4.65	4.75	4.40	4.15	4.44	0.26	High Consensus
The number of invention patents authorized	4.10	4.55	4.50	3.20	4.65	4.50	5.00	3.90	4.30	0.30	High Consensus
Commodity market activity	3.65	4.00	4.50	4.00	4.10	4.50	2.95	4.50	4.03	0.34	High Consensus
Consumer price index	4.05	3.00	5.00	4.20	4.10	4.05	4.15	4.00	4.07	0.08	High Consensus
Total investment of foreign invested enterprises	4.55	4.55	4.50	4.05	4.60	4.50	5.00	4.55	4.54	0.04	High Consensus
Total import and export	5.00	4.50	5.00	4.60	4.00	4.00	4.20	4.05	4.42	0.39	High Consensus

Table 6. The formal decision structure.

Dimensions	Aspects	Criteria
Regional human capital	Education development	The amount of local fiscal expenditure on education per capita (x1)
		The number of higher education institutions (x2)
		The number of years of education per capita (x3)
	Medical health level	The number of licensed (assistant) doctors per 10,000 people (x4)
		The number of medical beds per 10,000 people (x5)
		The amount of local fiscal expenditure on health per capita (x6)
		The number of health education trainers in health education professional institutions (x7)
	Employment situation	Unemployment rate (x8)
		The number of employed persons (x9)
		The number of public employment service instructors (x10)
Regional structural capital	Process capital	The passenger volume of the transportation industry (x11)
		The number of Internet users (x12)
		Express volume (x13)
		Railway operating mileage (x14)
		Highway operating mileage (x15)
	Innovation capital	The number of R&D personnel (x16)
		The number of invention patents authorized (x17)
Regional relationship capital	Internal relations	Commodity market activity (proportion of total retail sales of social consumer goods in GDP) (x18)
		Consumer price index (x19)
	External relations	The total investment of foreign-invested enterprises (x20)
		Total import and export (x21)

4.2. Obtaining the Weight of Factors Influencing RIC

In this subsection, the GDANP method was employed to identify critical factors influencing RIC (the results of each step are shown in Appendix A).

GRGs were calculated using Equations (1) and (2), as shown in Table A1. To compute the GRGs, the importance of all of the attributes (i.e., experts) was assumed to be equal. From Equation (2), GRGs is shown in the last column of Table A1. Table A2 shows the grey self-relational matrix. According to Equation (3), it is also the initial direct influence matrix.

By using Equation (4), the normalized direct influence matrix was obtained, as shown in Table A3. According to Equation (6), the total influence matrix is shown in Table A4.

Table A5 shows the weighted supermatrix, which was obtained by normalizing the total influence matrix. Table A6 presents the limited supermatrix derived from the weighted supermatrix.

After the above process, the weights of criteria were finally obtained. Table 7 illustrates the weight of the formal decision structure.

Table 7. The weight of criteria influencing RIC.

Dimensions	Aspects	Criteria	Weight
Regional human capital	Education development	x1	0.0485736
		x2	0.0504187
		x3	0.0502033
	Medical health level	x4	0.0488057
		x5	0.0486574
		x6	0.0449674
		x7	0.0464527
	Employment situation	x8	0.0490993
		x9	0.0481779
		x10	0.0466581
Regional structural capital	Process capital	x11	0.0501493
		x12	0.0458645
		x13	0.0504681
		x14	0.0421389
		x15	0.0475357
	Innovation capital	x16	0.0493820
		x17	0.0485582
Regional relationship capital	Internal relations	x18	0.0459618
		x19	0.0432266
	External relations	x20	0.0495749
		x21	0.0451260

4.3. Ranking of the Intellectual Capital of Provinces in China

Governments regularly publish relevant statistics, and these may be used to analyze the current state of development. Because the historical data in this study were objective rather than subjective, the data were used to evaluate the development of RIC in China (the results of each step are shown in Appendix A). Table A7 describes the relevant data of 31 provinces in China throughout 2018, which were sourced from the China Statistics Bureau [82] and the China Statistical Yearbook [83].

Because the measurement scales were different for the criteria used in this study, it was necessary to normalize the raw data. The criteria that were selected to describe the development of RIC included both larger-the-better criteria and smaller-the-better criteria. Therefore, Equation (7) and Equation (8) were suitable for normalization, as shown in Table A8.

According to Equation (9), the weighted normalized decision matrix is shown in Table A9. As can be seen in Table A9, we obtained the positive ideal solution (V*) and negative ideal solution (V⁻) by using Equation (10) and Equation (11). As shown in Table A10, Equation (12) and Equation (13) were used to separate each alternative from the positive ideal solution and the negative ideal solution. On this basis, we used Equation (14) to calculate the relative distance from the positive ideal solution alternative [75] in Table A10.

As can be seen in Table 8 and Figure 2, according to the relative distance from the positive ideal solution alternative [75], we obtained the RIC ranking of 31 provinces in China, together with the provincial GDP ranking.

Table 8. Ranking of RIC and GDP of provinces in China.

Province	Results of the TOPSIS Method	Ranking of the Intellectual Capital of Provinces	GDP Ranking of China’s Provinces in 2018
Guangdong Province	0.673	1	1
Jiangsu Province	0.530	2	2
Zhejiang Province	0.468	3	4
Shandong Province	0.439	4	3
Henan Province	0.413	5	5
Beijing City	0.395	6	12
Hunan Province	0.390	7	8
Hebei Province	0.390	8	9
Sichuan Province	0.386	9	6
Hubei Province	0.355	10	7
Shanghai City	0.320	11	11
Liaoning Province	0.307	12	14
Anhui Province	0.306	13	13
Inner Mongolia Autonomous Region	0.283	14	21
Shaanxi Province	0.283	15	15
Jiangxi Province	0.282	16	16
Guizhou Province	0.268	17	25
Heilongjiang Province	0.268	18	23
Fujian Province	0.263	19	10
Guangxi Zhuang Autonomous Region	0.255	20	18
Shanxi Province	0.248	21	22
Gansu Province	0.242	22	27
Yunnan Province	0.239	23	20
Xinjiang Uygur Autonomous Region	0.236	24	26
Tibet Autonomous Region	0.235	25	31
Jilin Province	0.228	26	24
Chongqing City	0.221	27	17
Qinghai Province	0.219	28	30
Tianjin City	0.204	29	19
Ningxia Hui Autonomous Region	0.155	30	29
Hainan Province	0.133	31	28

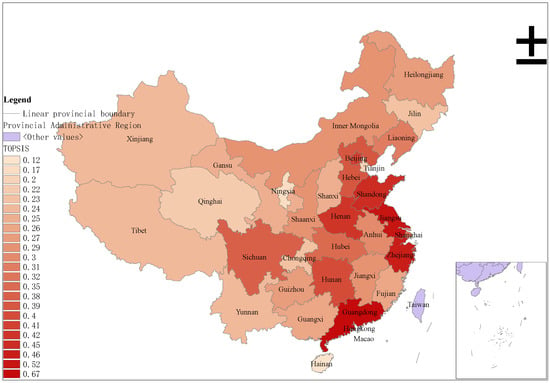
Figure 2. TOPSIS results by province in China.

In order to better understand this paper, we used Guangdong Province as an example to introduce the calculation process in detail. First, after the standardized calculation of the data of 31 provinces, we used the weight obtained by the GDANP method for weighted standardization to obtain V_i, using Equation (9). The positive ideal solution (V*) and negative ideal solution (V⁻) were selected under each indicator. Next, D_K* and D_K⁻ were then evaluated using Equations (12) and (13). For Guangdong Province,

$$D_K^{*}=\sqrt{\begin{array}{c}{(0.01912-0.04857)}^2+{(0.04589-0.05042)}^2+{(0.03788-0.05020)}^2+{(0.02546-0.04881)}^2+{(0.03073-0.04866)}^2\\ +{(0.01867-0.04497)}^2+{(0.02446-0.04645)}^2+{(0.02864-0.04910)}^2+{(0.04818-0.04818)}^2+\\ {(0.01607-0.04666)}^2+{(0.05015-0.05015)}^2+{(0.04586-0.04586)}^2+{(0.05047-0.05047)}^2+\\ {(0.01481-0.04214)}^2+{(0.04754-0.04754)}^2+{(0.04938-0.04938)}^2+{(0.04856-0.04856)}^2+{(0.02505-0.04596)}^2+\\ {(0.04310-0.04323)}^2+{(0.04957-0.04957)}^2+{(0.04513-0.04513)}^2\end{array}}=0.07496$$

$$D_K^{-}=\sqrt{\begin{array}{c}{(0.01912-0.00946)}^2+{(0.04589-0.00211)}^2+{(0.03788-0.02266)}^2+{(0.02546-0.02016)}^2+{(0.03073-0.02951)}^2\\ +{(0.01867-0.01023)}^2+{(0.02446-0.00052)}^2+{(0.02864-0.01718)}^2+{(0.04818-0.00176)}^2+\\ {(0.01607-0.00046)}^2+{(0.05015-0.00049)}^2+{(0.04586-0.00085)}^2+{(0.05047-0.00003)}^2+\\ {(0.01481-0.00165)}^2+{(0.04754-0.00423)}^2+{(0.04938-0.0001)}^2+{(0.04856-0.00008)}^2+{(0.02505-0.01577)}^2+\\ {(0.04310-0.04280)}^2+{(0.04957-0.00007)}^2+{(0.04513-0.00003)}^2\end{array}}=0.15453$$

Finally, the relative distance from the positive ideal solution alternative [75] was calculated by Equation (14). For Guangdong Province, $C_k^{*}=\frac{0.15453}{\left(0.15453+0.07496\right)}=0.67336$.

The TOPSIS data of Guangdong Province are listed in Table 9.

Table 9. The TOPSIS data of Guangdong Province.

	x1	x2	x3	x4	x5	x6	x7	x8	x9	x10	x11	x12	x13	x14	x15	x16	x17	x18	x19	x20	x21
ω	4.86%	5.04%	5.02%	4.88%	4.87%	4.50%	4.65%	4.91%	4.82%	4.67%	5.01%	4.59%	5.05%	4.21%	4.75%	4.94%	4.86%	4.60%	4.32%	4.96%	4.51%
Vi	0.019	0.046	0.038	0.025	0.031	0.019	0.024	0.029	0.048	0.016	0.050	0.046	0.050	0.015	0.048	0.049	0.049	0.025	0.043	0.050	0.045
V*	0.049	0.050	0.050	0.049	0.049	0.045	0.046	0.049	0.048	0.047	0.050	0.046	0.050	0.042	0.048	0.049	0.049	0.046	0.043	0.050	0.045
V−	0.009	0.002	0.023	0.020	0.030	0.010	0.001	0.017	0.002	0.000	0.000	0.001	0.000	0.002	0.004	0.000	0.000	0.016	0.043	0.000	0.000
DK*	0.075
DK−	0.155
CK*	0.673

4.4. Results of Analysis

The weighted ranking of criteria determined by the GDANP method was reasonable. According to the proportion, three dimensions were ranked, namely human capital (48.2%), structural capital (33.4%), and relationship capital (18.4%). The number of higher education institutions (5.04%), express volume (5.05%), and the total investment of foreign-invested enterprises (4.96%) were the criteria with the highest proportion in the above three dimensions, respectively.

As shown in Table 8, the empirical results revealed a positive correlation between the GDP ranking and the level of RIC. It can be seen from Figure 2 that the RIC rankings of China’s provinces were generally dominated by eastern provinces, which is in line with Chinese regional development.

As shown in Figure 3, we found significant differences between the RIC ranking and the GDP ranking of nine provinces, among which the RIC rankings of six provinces were better than the GDP ranking, and these provinces included Beijing, Inner Mongolia Autonomous Region, Heilongjiang Province, Guizhou Province, Gansu Province, and Tibet Autonomous Region. The RIC rankings of three provinces, namely Fujian Province, Chongqing, and Tianjin were inferior to the GDP ranking. The following is a detailed analysis that explained the reasons for the ranking of the above nine provinces.

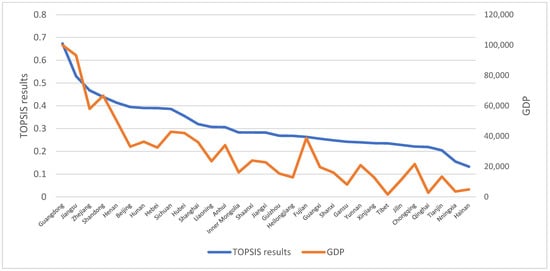
Figure 3. Comparisons on RIC and GDP of provinces in China.

According to the statistical data, the amount of local fiscal expenditure on education and health per capita, express volume, the number of R&D personnel, the number of invention patents authorized, and the investment volume of foreign-invested enterprises in Tianjin and Chongqing in 2018 was far lower than that of the other two municipalities under the direct control of the central government, which explained why the RIC rankings of these municipalities were inferior to the GDP rankings. Furthermore, the number of medical beds per 10,000 people in Fujian Province was lower than that of Beijing, Shanghai, Liaoning, Heilongjiang, Shaanxi, Jiangxi, Anhui, and Guizhou. Moreover, the number of health education trainers in professional health education institutions in Fujian Province was also low. These explained why the RIC ranking of Fujian lagged behind the provinces outlined above, whose GDP rankings were inferior to that of Fujian.

For Beijing, the amount of local fiscal expenditure on education per capita, the number of years of education per capita, the number of licensed (assistant) doctors per 10,000 people, the amount of local fiscal expenditure on health per capita, unemployment rate, and consumer price index ranked first among 31 provinces, making its RIC ranking better than GDP ranking. With respect to the Inner Mongolia Autonomous Region, process capital is the most prominent advantage, especially railroad operating mileage and highway operating mileage. Moreover, the number of licensed (assistant) doctors per 10,000 people and commodity market activity also surpasses Jiangxi, Shaanxi, Fujian, Guangxi, Yunnan, Chongqing, and Tianjin. As a result, although the GDP ranking of these regions was better than that of Inner Mongolia, their RIC ranking was inferior to that of Inner Mongolia. Guizhou Province is also well-developed in terms of process capital, particularly with regard to passenger volume in the transportation industry and highway operating mileage. In this respect, Guizhou Province outperformed Fujian, Heilongjiang, Guangxi, Shanxi, Yunnan, Jilin, Chongqing, and Tianjin, and therefore its RIC ranking was higher than them. Heilongjiang Province outperformed Fujian, Guangxi, Shanxi, Yunnan, Chongqing, and Tianjin with respect to its commodity market activity and railway operating mileage. As such, it had a higher RIC ranking. Gansu Province attaches great importance to health education and training. The number of health education trainers in professional health education institutions in Gansu Province is several times greater than that of Yunnan, Xinjiang, Jilin, Chongqing, and Tianjin, and its RIC ranking was therefore higher than that of these regions. Although the economic development level of Tibet Autonomous Region is low, the amount of local financial expenditure on education and health per capita is far higher than that of Qinghai, Jilin, Chongqing, Tianjin, Ningxia, and Hainan. Therefore, the GDP ranking of Tibet Autonomous Region lagged behind, but its RIC ranking was better than the aforementioned provinces.

It can be concluded that the level of RIC was closely related to regional comprehensive development. Thus, it is critical to identify ways of ensuring a steady increase in the level of RIC.

5. Managerial Implications

It is imperative to focus on RIC, and governments and enterprises must pay greater attention to this issue. The research results obtained from the intellectual capital indicator system and ranking provided guidance for regional governments that can help them to make more informed decisions in this era of the knowledge economy. Governments should take targeted measures to correct the problems and deficiencies identified in the empirical analysis and improve the level of development of regional integration. In the areas of regional education, healthcare, employment, talent mobility infrastructure, innovation and investment, and the operation of internal and external relations, provinces should pay greater attention to improving the relevant conditions in their own provinces. The following content proposes some suggestions with regard to three components of regional integration.

First, human capital represents the core of RIC and is the eternal driving force of the economic development. Considering that the constructed intellectual capital indicator system is based on human capital as the main evaluation factor, provinces should increase their investment in education, health care, employment, and other public utilities to improve the overall quality of human capital. Financial investment in human capital is an indispensable factor for regional development. Among the municipalities that are under the direct control of the central government, Tianjin and Chongqing should focus on allocating finances to local education, so that the financial educational support received by each individual is maintained at a reasonable level. The demographic dividend is disappearing, and labor shortages and rising costs are becoming increasingly prominent. As such, it is necessary to further promote universal education and higher education, so as to encourage a transition away from a reliance on quantitative and cost advantages, and to instead focus on quality advantages. Therefore, provinces should continue to focus on the accumulation and enhancement of human capital to achieve a steady improvement in this area. Furthermore, the number of healthcare talents in Tianjin, Chongqing, and Fujian Province needs to be improved; otherwise, this situation will prove detrimental to healthcare services as a result of inadequate talent management and a lack of understanding about medical risks. These provinces should improve the incentive mechanism, implement a performance assessment system, strengthen safety and security efforts, and ensure full-coverage liability insurance.

Secondly, regional structural capital provides a platform for human capital to play a role, and it is a key link in efforts to enhance regional scientific and technological innovation, so as to ensure quality human capital. This paper proposes that the relationship between structural capital and human capital is benign and complementary. Investment in human capital is critical for the development of innovation capital in structural capital. The continuous supply of R&D personnel depends upon the local education level, while a steady improvement in the regional innovation level will also stimulate and promote the development and convergence of local talent. Municipalities such as Tianjin and Chongqing should focus on cultivating and attracting R&D personnel and encourage the development of invention patents. At the same time, process capital provides fundamental facilities to ensure the flow of talent. Inner Mongolia, Guizhou, and Heilongjiang have achieved a high level of process capital by virtue of their relatively superior geographical conditions. Provinces should focus on improving the construction of infrastructure and boosting social circulation and information communication mechanisms.

In addition, regional relational capital reflects the network of relationships within and outside the region, which can generate resource and information advantages. Relational capital reflects the business environment and investment potential of a region. It represents the coordination and sustainability of joint development within and outside the region, and it is thus relevant for stakeholders who share concerns about the region’s future. As the world economy becomes increasingly more inclusive, and as trade between countries becomes more frequent, foreign investment offers a fundamental means of promoting economic development. Foreign investment activities take into account the influence of regional location factors. An increase in the level of IC is conducive to attracting foreign investment and will likewise improve the level of IC in the region. Compared with Beijing and Shanghai, Tianjin and Chongqing need to actively attract foreign investment, enhance the scale of high-tech enterprise industries in the region, balance the quantity and quality of foreign investment to help optimize the industrial structure, and accelerate the urbanization process.

Finally, regional development should be coordinated, and regions with developed IC should strive to drive backward regions, in order to narrow the regional gap. As can be seen from Figure 2, IC shows a decreasing trend from the eastern coast to western inland areas. In order to achieve overall progress of the country, the government should encourage cross-regional cooperation between advantaged regions and disadvantaged regions and realize the advantaged regions to drive the disadvantaged regions through project experience exchange and resource complementation. The optimization of spatial flow and the allocation of production factors, as well as investment, talents, goods, and services should be strengthened among regions to achieve a rational division of labor and specialization, so as to enhance the level of IC.

In brief, RIC is the result of many factors, including the regional economy, politics, education, science, technology, and culture. It is an unstoppable trend that seeks to enhance RIC and promote regional development.

6. Discussion

The main research contributions of this paper are as follows: to begin with, this paper innovatively combines the Delphi method and the GDANP method further to improve the comprehensive RIC index evaluation system. We constructed a prototype decision structure on the basis of studying the literature, and the members of the expert group formed based on the Delphi method provided suggestions and scoring. This process effectively avoids the confrontation between experts. After constructing a formal decision structure according to the Delphi method, this paper uses the GDANP method to calculate the weight of each indicator in the system. The GDANP method can avoid the need for respondents to fill in the cumbersome DEMATEL questionnaire and can effectively solve the negative value, which cannot be solved in other methods, such as ANP, AHP, etc. [16].

Next, this paper specifically analyzes the RIC level of each province in China using the TOPSIS method, which provides a reference for the study of IC and regional development status based on Chinese national conditions. The TOPSIS method obtains the ranking by calculating the relative distance from the positive ideal solution alternative [75].

This study has some limitations. There is a lack of support among experts from the 31 provinces, and only eight experts in the field are selected. Moreover, due to insufficient domestic statistical data, many plausible criteria are not applied in this study. In addition, this paper did not conduct an in-depth analysis of the relationship between IC and regional economic efficiency by applying the index. In the future, this will be a direction for further research in this area. For example, the relationship between the role of IC and prefecture-level cities’ economic development could be carried out.

7. Conclusions

Given the immateriality, inherent complexity, and dynamics of capital, the concept of RIC is inconsistent. Based on previous literature and empirical research, this article defined RIC as a variety of intangible assets in a region, and indicators were examined at three levels, namely human capital, structural capital, and relationship capital. In order to comprehensively evaluate the level of RIC, 21 four-level indicators were selected around the three-level evaluation index, and a formal decision structure was constructed (Table 6). Among them, 14 indicators were sourced from the previous literature, and seven indicators were compiled from experience. By combining the Delphi method with the GDANP technique, this paper obtained weight to the formal decision structure (Table 7). According to the weight, the secondary evaluation indicators were ranked as regional human capital (48.2%), regional structural capital (33.4%), and regional relationship capital (18.4%). The empirical results (Table 8) revealed a positive correlation between the GDP ranking and the level of RIC. In Figure 2, it can be seen that the RIC rankings of China’s provinces were generally dominated by eastern provinces, which is in line with Chinese regional development. It is concluded that RIC played an important role in regional development.