Filters in Strong BI-Algebras and Residuated Pseudo-SBI-Algebras

Abstract

The concept of basic implication algebra (BI-algebra) has been proposed to describe general non-classical implicative logics (such as associative or non-associative fuzzy logic, commutative or non-commutative fuzzy logic, quantum logic). However, this algebra structure does not have enough characteristics to describe residual implications in depth, so we propose a new concept of strong BI-algebra, which is exactly the algebraic abstraction of fuzzy implication with pseudo-exchange principle (PEP). Furthermore, in order to describe the characteristics of the algebraic structure corresponding to the non-commutative fuzzy logics, we extend strong BI-algebra to the non-commutative case, and propose the concept of pseudo-strong BI (SBI)-algebra, which is the common extension of quantum B-algebras, pseudo-BCK/BCI-algebras and other algebraic structures. We establish the filter theory and quotient structure of pseudo-SBI- algebras. Moreover, based on prequantales, semi-uninorms, t-norms and their residual implications, we introduce the concept of residual pseudo-SBI-algebra, which is a common extension of (non-commutative) residual lattices, non-associative residual lattices, and also a special kind of residual partially-ordered groupoids. Finally, we investigate the filters and quotient algebraic structures of residuated pseudo-SBI-algebras, and obtain a unity frame of filter theory for various algebraic systems.

1. Introduction

The fuzzy implication is an important operator in fuzzy logic. It plays a very important role in the theoretical establishment and application of fuzzy set theory. It is widely used in various fields, such as approximate reasoning, image processing, fuzzy control and word calculation. In different literature, we can see different definitions of fuzzy implications [1,2,3,4]. In this paper, we use a widely accepted definition, which is defined in literature [1] (see Definition 1). In order to further study the fuzzy implication, lots of scholars have given many properties of fuzzy implication, such as exchange principle (EP), ordering principle (OP), etc. (see Definition 2). However, the above properties have strong constraints, therefore, some scholars put forward the pseudo-exchange principle (PEP) with weaker restriction condition [2]. (PEP) condition is as follows:

$$x\le y\to z\iff y\le x\to z.$$

It is necessary to construct a new implication operator based on the above properties. For example, Min et al. [5] constructed a new fuzzy implication from the perspective of additive generator and semigroup. Another construction idea is to construct new fuzzy implication with the help of semigroup order and theory implication. For example, in non-classical mathematical logic, logical propositions are represented by symbols, and the relations between propositions are described by an axiomatic system, the conjunction $A\otimes B$ and the implication $A\to B$ are related by an adjunction

$$A\otimes B\le C\iff A\le B\to C,$$

(1)

where ≤ stands for the logical entailment. To explore a more general fuzzy aggregation operator and corresponding implication operator, more general fuzzy logic formal system has become one of the research hotspots in recent years.

For example, algebraic structures with one implication operator, BCK/BCI algebras, BI-algebras, etc.; algebraic structures with double implication operators, quantum B-algebras, pseudo-BCK/BCI algebras [6,7,8,9], etc.; algebraic structures with binary operators and implication operators, residuated lattices, non-associative residuated lattices, etc. [10,11,12]. The most important structure is a basic implication algebra (BI-algebra for short) proposed in literature [13]. BI-algebra is the algebraic abstraction of associative/non-associative fuzzy logic, commutative/non-commutative fuzzy logic. This algebra can be used to describe many other algebraic structures, such as BCK/BCI-algebras, quantum B-algebras, pseudo-BCK/BCI-algebras, etc.

In propositional logic system, t-norm is used as the explanation of fuzzy aggregation operator ⊗, meanwhile, many scholars expand their research on t-norm from the aspects of commutativity, associativity, unit element and so on. The researches obtained the concepts of pseudo-t-norm, uninorm, semi-uninorm and so forth [14]. At the same time, the algebraic structures corresponding to the above binary operators have been proposed successively, such as commutative residuated lattice, non-commutative residuated lattice, non-associative residuated lattice, residuated ordered groupoid, pseudo-BCK/BCI-algebra, etc [8,9,11,15,16]. In the same way, in reference [14], Professor Liu Huawen proposed the concept of a semi-uninorm, which is an extension of a uninorm to remove commutativity and associativity; the conditions of two kinds of implications induced by a semi-uninorm are studied in detail.

Filter theory plays an important role in computer science and non-classical logic. From a logical point of view, various filters correspond to various sets of provable formulas. The properties of several kinds of fuzzy filters on the residual lattice are studied [10,11,12], which makes the structure of filters on residual lattice more clear. Therefore, on the basis of many theoretical researches on filters, the interrelation and hierarchical structure of various filter concepts are systematically analyzed, and construction is particularly important.

According to the above introduction, the research on implication operator, aggregation operator and their relationship have been very deep. In this paper, in order to describe the characteristics of residual implication in depth, we add some new characteristics to BI-algebra. First, we add the (PEP) condition to BI-algebra, so we get strong BI-algebra (SBI-algebra for short). However, basic implication algebra and strong BI-algebra describe algebraic structures with an implication operator. In order to describe the corresponding algebraic structure of noncommutative logic, we extend strong BI-algebra to pseudo-SBI-algebra, which has two kinds of implications. We establish the filter theory and quotient structure of pseudo-SBI-algebra. From the above introduction, it can be seen that binary operation ⊗ is also an important part of fuzzy logic. So, combined pseudo-SBI-algebra with ⊗, we get a new algebra structure, residuated pseudo-SBI-algebra. For the sake of uniform the filter structures of residuated lattices, non-associative residuated lattices and other algebras, we establish the filter and quotient structures of residuated pseudo-SBI-algebras.

2. Preliminaries

Definition 1

([1]). A function $I:{[0,1]}^2\to [0,1]$ is called a fuzzy implication if it satisfies, for all $x,x_1,x_2,y,y_1,y_2\in [0,1]$, the following conditions:

$$if{x}_1\le x_2,thenI(x_1,y)\ge I(x_2,y),i.e.,I(·,y)isdecreasing,$$

(2)

$$if{y}_1\le y_2,thenI(x,y_1)\le I(x,y_2),i.e.,I(x,·)isincreasing,$$

(3)

$$I(0,0)=1,$$

(4)

$$I(1,1)=1,$$

(5)

$$I(1,0)=0.$$

(6)

Definition 2

([1,2]). A fuzzy implication I is said to satisfy

$(1)$ the left neutrality property, if

$$I(1,y)=y,y\in [0,1];$$

(7)

$(2)$ the exchange principle, if

$$I(x,I(y,z))=I(y,I(x,z)),x,y,z\in [0,1];$$

(8)

$(3)$ the identity principle, if

$$I(x,x)=1,x\in [0,1];$$

(9)

$(4)$ the ordering property, if

$$I(x,y)=1ifandonlyifx\le y,x,y\in [0,1];$$

(10)

$(5)$ the pseudo-exchange principle, if

$$I(x,z)\ge y\iff I(y,z)\ge x,x,y,z\in [0,1].$$

(11)

Definition 3

([13]). Let $(X,\le )$ be a partially ordered set, which has a binary operation →. Then X is a basic implication algebra(BI-algebra for short) if and only if: for all $x,y,z\in X,$

$(1)$if $x\le y,$ then $z\to x\le z\to y;$

$(2)$if $x\le y,$ then $y\to z\le x\to z;$

A BI-algebra X is called normal if and only if:

$(3)\forall x,y\in X,x\to x=y⇝y;$

$(4)\forall x,y,z\in X,$ let $e=x\to x=y\to y,$ $x\le y$ if and only if $x\to y=e.$

Definition 4

([13]). Let $(X,\to ,\le )$ be a BI-algebra, F is a nonempty set of X. Then F is called a filter of X if it satisfies:

$(1)\forall x\in F,$ if $x\le y\in X,$ then $y\in F;$

$(2)\forall x\in F,$$x\to x\in F;$

$(3)\forall x\in F,y\in X,$ if $x\to y\in F,$ then $y\in F;$

$(4)\forall x\in X,$ if $y\to z\in F,$ then $(x\to y)\to (x\to z)\in F;$

$(5)\forall x\in X,$ if $y\to z\in F,$ then $(z\to x)\to (y\to x)\in F.$

Let $(X,\to ,\le ,e)$ be a normal BI-algebra, the filter F of X is called regular, when it satisfies:

$(6)\forall x\in X,$ when $(x\to y)\to e\in F$ and $(y\to z)\to e\in F,$ then there exists $(x\to z)\to e\in F.$

Definition 5

([17,18]). Let X be a non-empty set endows with operation $\to .$ Then

$(1)$ If X satisfies:

$(BCC-1)y\to z\le (x\to y)\to (x\to z);$

$(BCC-2)1\to x=x;$

$(BCC-3)x\le x;$

$(BCC-4)x\le y,y\le x\Rightarrow x=y;$

$(BCC-5)x\le 1;$

$(BCC-6)x\le y\iff x\to y=1.$

Then $(X,\to ,1)$ is a BCC-algebra.

$(2)$If X satisfies $(BCC-3)-(BCC-6)$ and

$(BCK-1)x\to y\le (y\to z)\to (x\to z);$

$(BCK-2)x\le (x\to y)\to y.$

Then $(X,\le ,\to ,1)$ is a BCK-algebra.

Any BCK-algebra is a BCC-algebra.

Definition 6

([19]). Let P be a complete lattice, “&” be a binary operation on P. Then $(P,\&)$ is called a prequantale if it satisfies: $\forall a\in P,b_{\alpha }\subseteq P,$

$$a\&(\bigvee b_{\alpha })=\bigvee (a\&b_{\alpha });(\bigvee b_{\alpha })\&a=\bigvee (b_{\alpha }\&a).$$

Definition 7

([14]). Let L be a complete lattice, U be a binary operation on L. Then L is called a semi-uninorm if and only if:

$(U1)$there exists a neutral element $e\in L,$ i.e., $U(e,x)=U(x,e)=x$ for all $x\in L$;

$(U2)U$ is non-decreasing in each variable.

Definition 8

([16]). A residuated partially-ordered groupoid is a partially ordered set $(L,\le )$ endows with operation ⊗, which satisfies: $\forall x,y,z\in X,$

$$y\le x\to z\iff x\otimes y\le z\iff x\le y⇝z$$

Definition 9

([10,15,20,21]). Let $(L,\wedge ,\vee )$ be a lattice, which has the bottom element 0 and the top element 1. Then for all $x,y,z\in L,$

$(1)$If L satisfies:

$(i)(L,\otimes ,1)$ is a monoid, which has the unit 1.

$(ii)x\le y\to z\iff x\otimes y\le z\iff y\le x⇝z.$

Then $(L;\wedge ,\vee ,\otimes ,\to ,⇝,0,1)$ is a residuated lattice.

$(2)$If L satisfies:

$(iii)(L,\otimes ,1)$ is a groupoid which is commutative and has the unit 1.

$(iv)x\otimes y\le z\iff x\le y\to z.$

Then $(L;\wedge ,\vee ,\otimes ,\to ,0,1)$ is a non-associative residuated lattice.

$(3)$If L satisfies $(i),(iii),(iv)$, then L is a commutative residuated lattice.

$(4)$If L satisfies $(ii)$ and:

$(v)(L,\otimes ,1)$ is a groupoid which is non-commutative and has the unit 1.

Then $(L;\wedge ,\vee ,\otimes ,\to ,⇝,0,1)$ is a residuated lattice-ordered groupoid.

Proposition 1

([22]). Let $(L;\wedge ,\vee ,\otimes ,\to ,⇝,0,1)$ be a residuated lattice, then,

$(1)\forall x,y\in L,x\le y$ if and only if $x\to y=1$ if and only if $x⇝y=1;$

$(2)\forall x,y\in L,x\otimes (x⇝y)\le y,(x\to y)\otimes x\le y;$

$(3)\forall x,y,z\in L,x\to (y⇝z)=y⇝(x\to z);$

$(4)\forall x,y,z\in L,$if $x\le y,$ then $x\otimes z\le y\otimes z,z\otimes x\le z\otimes y;$

$(5)\forall x,y,z\in L,$if $x\le y,$ then $z\to x\le z\to y,y\to z\le x\to z;$

$(6)\forall x,y,z\in L,$if $x\le y,$ then $z⇝x\le z⇝y,y⇝z\le x⇝z.$

Definition 10

([5,22,23,24]). Let L be a residuated lattice. F is a nonempty subset of X, then F is called a filter if it satisfies:

$(RLF1)1\in F;$

$(RLF2)\forall x\in F,$$x\to y\in F\Rightarrow y\in F;$

$(RLF3)\forall x\in F,$$x⇝y\in F\Rightarrow y\in F.$

Definition 11

([11]). Let L be a non-associative residuated lattice, F be a nonempty subset of X. Then F is called a filter if and only if:

$(NA1)1\in F;$

$(NA2)$for any $x,y\in L,$ if $x,x\to y\in F,$ then $y\in F;$

$(NA3)$for any $x,y\in L,$ let $a\otimes F=\{a\otimes f|f\in F\}$ for any $a\in L,$ then $(x\otimes y)\otimes F=x\otimes (y\otimes F).$

Definition 12

([7,25]). A quantum B-algebra is a partially ordered set $(X,\le )$ which satisfies: $\forall x,y,z\in X,$

$(1)y\to z\le (x\to y)\to (x\to z);$

$(2)y⇝z\le (x⇝y)⇝(x⇝z);$

$(3)$if $y\le z,$ then $x\to y\le x\to z;$

$(4)x\le y\to z$ if and only if $y\le x⇝z.$

A quantum B-algebra is called commutative if it satisfies: $\forall x,y\in X,$

$(5)x\to y=x⇝y.$

A quantumB-algebra is called unital if $\forall x\in X,$

$(6)$ there exists $u\in X,$ s.t. $u\to x=u⇝x=x.$

Proposition 2

([21]). An algebra structure $(X,\to ,⇝,\le )$ is a quantum B-algebra if and only if: for all $x,y,z\in X,$

$(1)x\to (y⇝z)=y⇝(z\to z);$

$(2)$if $y\le z,$ then $x\to y\le x\to z;$

$(3)x\le y\to z$ if and only if $y\le x⇝z.$

Definition 13

([8,9]). An algebra structure $(A;\le ,\to ,⇝,0)$ with a binary operation ≤ is a pseudo-BCK-algebra if and only if $\forall x,y,z\in A,$ verifying the axioms:

$(1)(y\to z)⇝(x\to z)\ge x\to y,(y⇝z)\to (x⇝z)\ge x⇝y;$;

$(2)(x\to y)⇝y\ge x,(x⇝y)\to y\ge x;$

$(3)x\le x;$

$(4)x\le 1;$

$(5)x\le y,y\le x\Rightarrow x=y;$

$(6)x\le y\iff x\to y=1\iff x⇝y=1.$

Proposition 3

([9,26]). Let $(A;\le ,\to ,⇝,0)$ be a pseudo-BCK-algebra, then,

$(1)\forall x,y,z\in A,x\to (y⇝z)=y⇝(x\to z);$

$(2)x\le y\to z$ if and only if $y\le x⇝z;$

$(3)$if $x\le y,$ then $z\to x\le z\to y;$

$(4)$if $x\le y,$ then $y\to z\le x\to z;$

$(5)$if $x\le y,$ then $z⇝x\le z⇝y;$

$(6)$if $x\le y,$ then $z⇝x\le z⇝y.$

Proposition 4

([7]). Let A be a pseudo-BCK-algebra, then A is a quantum B-algebra.

3. Strong BI-Algebras and Left/Right Residuated BI-Algebras

Condition PEP was proposed in literature [2], which is defined on interval $[0,1].$ In this paper, we get rid of the limit of interval, and extend this condition to a partial order set.

BI-algebra is an algebraic framework of general implication operators, which has a wide range of adaptability. However, there are not many characteristics it can extract. If we want to describe the characteristics of residual implication in depth, it is not enough to use BI-algebra alone. We need to add new characteristics to BI-algebra to describe the properties of residual implication. In this section, we use the PEP property of fuzzy implication [2] for reference, and add PEP condition on the basis of BI-algebra to form strong BI-algebra.

At the same time, in BI-algebra, only implicative operation is involved, not multiplication operation ⊗. In the study of fuzzy logic and related algebra structures, multiplication operation embodies the properties of t-norm, non-associative t-norm, semi-uninorm, quantale and other structures. Therefore, we should not only study the implication operation, but also study the algebraic structure with binary operations like t-norm, non-associative t-norm, semi uninorm and so on. Therefore, in this section, on the basis of BI-algebra, we add multiplication operation ⊗, and get left/right residuated BI-algebras.

Definition 14.

A strong BI-algebra(SBI-algebra for short) is a basic implication algebra which satisfies:

$$\forall x,y,z\in X,x\le y\to z\mathit{if}\mathit{and}\mathit{only}\mathit{if}y\le x\to z.$$

Next, we will give equivalent conditions of the above definition.

Proposition 5.

Let $(X,\le )$ be a partially ordered set which has a binary operation →. Then $(X,\to ,\le )$ is a strong BI-algebra if and only if:

$(1)\forall x,y,z\in X,$ if $x\le y$ then $z\to x\le z\to y;$

$(2)\forall x,y,z\in X,$$x\le y\to z$ if and only if $y\le x\to z.$

Proof. 

For any $x,y,z\in X,$ assume that $x\le y$. Since $y\to z\le y\to z$, by (2) we have $y\le (y\to z)\to z$. Thus, $x\le y\le (y\to z)\to z.$ Using (2) again, we can get that $y\to z\le x\to z.$ Thus, the proposition holds. □

Example 1.

Define

$$x{\to }_{GD}y=\left\{\begin{array}{cc}\hfill 1,& \hfill ifx\le y,\\ \hfill y,& \hfill ifx\ge y.\end{array}\right.$$

$$x{\to }_{TD}y=\left\{\begin{array}{cc}\hfill 1,& \hfill ifx<1,\\ \hfill y,& \hfill ifx=1.\end{array}\right.$$

Then $([0,1],{\to }_{GD},\le )$ is a strong BI-algebra (SBI-algebra), and $([0,1],{\to }_{TD},\le )$ is a BI-algebra but it is not strong, since $1\le 0.9{\to }_{TD}0.6,0.9>0.6=1{\to }_{TD}0.6.$

In paper [3], Mesiar and Mesiarová give a condition ([3], Theorem 5) for t-norm to get corresponding residual implication. Through research, if the given t-norm is left continuous, then its corresponding implication satisfies (EP) and (OP) conditions, and the corresponding one also satisfies (PEP) conditions, i.e., the implication is strong BI-algebra. Specific examples are as follows.

Example 2

([3]). Let $T:{[0,1]}^2\to [0,1]$ be given by

$$T(x,y)=\left\{\begin{array}{cc}\hfill 0,& \hfill if(x,y)\in {[0,\frac{1}{2}]}^2,\\ \hfill 2xy-x-y+1,& \hfill if(x,y)\in {[\frac{1}{2},1]}^2,\\ \hfill min(x,y),& \hfill otherwise.\end{array}\right.$$

Using Theorem 5 in [3], the implication $I_T:{[0,1]}^2\to [0,1]$ is given by

$$I_T(x,y)=\left\{\begin{array}{cc}\hfill 1,& \hfill ifx\le y,\\ \hfill \frac{1}{2},& \hfill if0<y<x\le \frac{1}{2},\\ \hfill \frac{y+x-1}{2x-1},& \hfill if\frac{1}{2}<y<x\le 1,\\ \hfill y,& \hfill otherwise.\end{array}\right.$$

Then $I_T$ is a resiudal implication, because of the left continuity of T, $([0,1],\to ,\le )$ is a strong BI-algebra, and the implication satisfies the (EP), (OP) and (PEP) condition.

Example 3.

Let $X=[0,1],\forall x,y\in X,$ define the operation on X as following:

$$x\to y=\left\{\begin{array}{cc}\hfill 0,& \hfill ifx>0andy=0\\ \hfill 1,& \hfill otherwise\end{array}\right.$$

Then $([0,1],\to ,\le )$ is a SBI-algebra, and the implication operator → satisfies the exchange principle, and it does not satisfy the (OP) condition, since $1=0.8\to 0.4,0.8>0.4.$

Example 4.

Let $X=[0,1],\forall x,y\in X,$ define the operation on X as following:

$$x\to y=max(0.5-x,y).$$

Then $([0,1],\to ,\le )$ is a BI-algebra, but it is not a strong BI-algebra (SBI-algebra), since $0.7\le 0.9\to 0.8,0.9>0.7\to 0.8.$ Moreover, the implication operator → does not satisfy the ordering property, since $0.7<0.8,0.7\to 0.8\ne 1.$

Example 5.

Let $X=[0,1],\forall x,y\in X,$ define the operation on X as following:

$$x\to y=\left\{\begin{array}{cc}0,\hfill & \hfill if\frac{2}{3}<x\le 1and0\le y\le \frac{1}{3}\\ max\{1-x,y\},\hfill & \hfill if0\le x\le \frac{2}{3}and\frac{1}{3}\le y\le 1\\ min\{1-x,y\},\hfill & \hfill if(\frac{2}{3}\le x\le 1andy=\frac{1}{3})or(x=\frac{2}{3}and0\le y\le \frac{1}{3})\\ \frac{1}{4}-\frac{1}{4}x+\frac{3}{4}y,\hfill & \hfill otherwise.\end{array}\right.$$

Then $([0,1],\to ,\le )$ is a strong BI-algebra (SBI-algebra), and the implication operator → satisfies the (OP) condition and the pseudo-exchange principle (PEP).

Proposition 6.

Let X be a SBI-algebra. Then,

$(1)\forall x,y\in X,x\le (x\to y)\to y$;

$(2)\forall x,y\in X,x\to y=((x\to y)\to y)\to y.$

Proof. 

$(1)$For any $x,y\in X,$ from $x\to y\le x\to y,$ using Definition 14, we can get $x\le (x\to y)\to y.$

$(2)$For any $x,y\in X,$ by (1), we can get that $x\to y\le ((x\to y)\to y)\to y$ and $x\le (x\to y)\to y.$ Using Definition 3(2), $x\to y\ge ((x\to y)\to y)\to y.$ Thus, $x\to y=((x\to y)\to y)\to y.$ □

Professor Liu Hua-Wen has proposed fuzzy boundary weak implications in [4], in this paper, we get the fuzzy weak implication by removing its boundary property.

Definition 15.

Fuzzy weak implication (fuzzy w-implication for short) is a function $I:{[0,1]}^2\to [0,1]$ which satisfies:

$(I1)I$ is non-increasing in its first variable;

$(I2)I$ is non-decreasing in its second variable.

Clearly, the fuzzy weak implication is the background of strong BI-algebra, now we give the condition that makes this implication to a strong BI-algebra.

Proposition 7.

Let → be a fuzzy weak implication with ordering exchange principle (PEP). Then $([0,1],\to ,\le )$ is a strong BI-algebra.

Proof. 

From the non-increasing and non-decreasing properties of implication operator → in Definition 15, we know that $([0,1],\to ,\le )$ is a BI-algebra, and with (PEP) condition, i.e., $x\le y\to z$ if and only if $y\le x\to z$. Thus, $([0,1],\to ,\le )$ is a strong BI-algebra. □

Above all, we have discussed the background of strong BI-algebra, below, we give the relationships between strong BI-algebra and some algebraic structures.

Proposition 8.

$(1)$ Every commutative quantum B-algebra is a strong BI-algebra. Conversly, a strong BI-algebra X is a commutative quantum B-algebra, if X satisfies $x\to (y\to z)=y\to (x\to z);$

$(2)$ Let X be a strong BI-algebra, if X satisfies the conditions of BCC-algebra, then X is a BCK-algebra.

Proof. 

$(1)$ Using Definition 12 and Proposition 5, we know that every commutative quantum B-algebra is a strong BI-algebra.

Let $(X,\to ,\le )$ be a strong BI-algebra, $x\to y=x⇝y$, if X satisfies $x\to (y\to z)=y\to (x\to z)$, then from Proposition 2, X is a commutative quantum B-algebra.

$(2)$ According to Definition 5, $(BCK2)-(BCK-6)$ holds. At the same time, using Proposition 5 and $(BCC-1)$, $(BCK-1)$ holds. □

The following Figure 1 summarizes the relationships between strong BI-algebra and some algebraic structures.

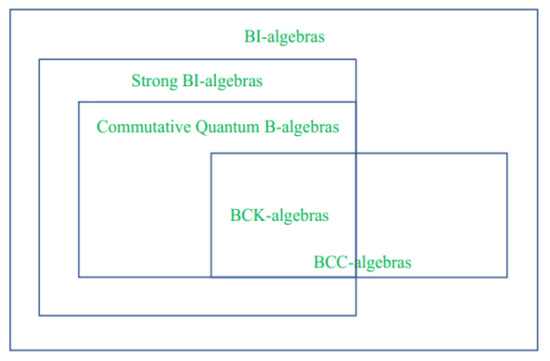
Figure 1. The relationships among strong BI-algebra and some algebraic structures.

In the above, we have defined strong BI-algebra, an algebraic structure with only an implication operator and ordered relation. In the existing research, it is also very important to express the operators with structure properties such as t-norm, semi-uninorm and quantale. In this paper, ⊗ is used to represent this kind of operators. Next, according to the relationship between implication and multiplication ⊗, we propose some abstract algebraic structures with two kinds of operations.

Definition 16.

Let $(X,\le )$ be a partially ordered set, where “$\le$” is a binary relation on X.

$(1)$ If X satisfies:

$(i)(X,\to ,\le )$ is a BI-algebra;

$(ii)\forall x,y,z\in X,x\le y$⇒$x\otimes z\le y\otimes z$ and $z\otimes x\le z\otimes y.$

Then $(X,\to ,\otimes ,\le )$ is called a BI-groupoid.

$(2)$ If X satisfies $(i)$ and

$(iii)\forall x,y,z\in X,x\otimes y\le z$ if and only if $x\le y\to z.$

Then $(X,\to ,\otimes ,\le )$ is called a left residuated BI-algebra.

$(3)$ If X satisfies $(i)$ and

$(iv)\forall x,y,z\in X,x\otimes y\le z$ if and only if $y\le x\to z$.

Then $(X,\to ,\otimes ,\le )$ is called a right residuated BI-algebra.

$(4)$ If $(X,\to ,\otimes ,\le )$ is both left and right residuated BI-algebra, then $(X,\to ,\otimes ,\le )$ is called residuated SBI-algebra.

We can use Figure 2 to describe the relationships among these definitions.

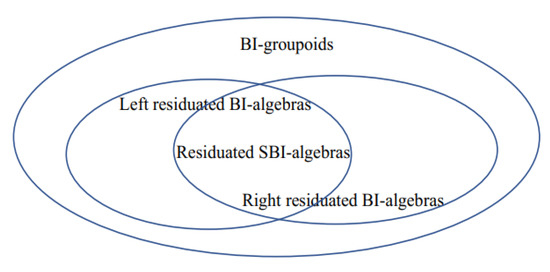
Figure 2. The relationships among some algebraic structures.

Example 6.

Let $L=[0,1],$ define semi-uninorm ⊗ and its correspondent residual implication → as follows:

$$x\otimes y=\left\{\begin{array}{cc}\frac{1}{4}xy,\hfill & \hfill ify=0orx<\frac{1}{2}\\ y,\hfill & \hfill ifx=\frac{1}{2}\\ 1,\hfill & \hfill otherwise.\end{array}\right.$$

$$x\to y=sup\{z\in [0,1]|x\otimes z\le y\}=\left\{\begin{array}{cc}1,\hfill & \hfill ifx=0ory=1\\ min\{1,\frac{4y}{x}\},\hfill & \hfill if0<x<\frac{1}{2}\\ y,\hfill & \hfill ifx=\frac{1}{2}\\ 0,\hfill & \hfill otherwise.\end{array}\right.$$

In this example, ⊗ is non-commutative, → is non-increasing in first variable and non-decreasing in second variabe. However, → does not satisfy the adjoint property, since $\frac{1}{2}\le \frac{1}{4}\to \frac{1}{5}=1\to \frac{1}{2}\otimes \frac{1}{4}=\frac{1}{4}\nleqq \frac{1}{5}$.

Example 7.

Let $X=[0,1].$ $\forall x,y,z\in X,$ define t-norm ⊗ and → on X as following:

$$x\otimes y=T_{LK}=max(x+y-1,0),$$

$$x\to y=I_{LK}=min(1,1-x+y).$$

Then the operation → is a residual implication. Because binary operation ⊗ is continuous, ⊗ and → satisfy adjoint property. It is verified that $(X,\to ,\otimes ,\le )$ is a residuated SBI-algebra.

Next, we will introduce the example of finite order.

Example 8.

Let $X=\{0,a,b,c,1\}$ where $0<a<b,c<1.$ Define the operations $\otimes ,\to ,⇝$ as Table 1, Table 2 and Table 3:

Table 1. The operation ⊗ on X.

⊗	0	a	b	c	1
0	0	0	0	0	0
a	0	0	0	a	a
b	0	a	b	a	b
c	0	0	0	c	c
1	0	a	b	c	1

Table 2. The operation → on X.

→	0	a	b	c	1
0	1	1	1	1	1
a	c	1	1	1	1
b	c	c	1	c	1
c	0	b	b	1	1
1	0	a	b	c	1

Table 3. The operation ⇝ on X.

⇝	0	a	b	c	1
0	1	1	1	1	1
a	b	1	1	1	1
b	0	c	1	c	1
c	b	b	b	1	1
1	0	a	b	c	1

Then, $(X,\to ,\otimes ,\le )$ is a left residuated BI-algebra, $(X,⇝,\otimes ,\le )$ is a right residuated BI-algebra. In this example, the binary operation ⊗ is non-commutative, → and ⇝ do not satisfy (PEP) condition, since $c\le b\to 0$ but $b\nleqq c\to 0=0,b\le c⇝0$ but $c\nleqq b⇝0=0.$

The definitions and properties of residuated lattice, non-associative residuated lattice and pseudo-BL-algebra are introduced in the literatures [10,15,21,27]. Here we give the relationships between these algebras and left/right residuated BI-algebra.

Proposition 9.

$(1)$Let $(L,\wedge ,\vee ,\otimes ,\to ,⇝,0,1)$ be a pseudo-BL-algebra, then $(L,\to ,\otimes )$ is a left residuated BI-algebra, $(L,⇝,\otimes )$ is a right residuated BI-algebra;

$(2)$Let $(L,\wedge ,\vee ,\otimes ,\to ,⇝,0,1)$ be a residuated lattice, then $(L,\to ,\otimes )$ is a left residuated BI-algebra, $(L,⇝,\otimes )$ is a right residuated BI-algebra;

$(3)$Let $(L,\wedge ,\vee ,\otimes ,\to ,0,1)$ be a non-associative residuated lattice, then $(L,\to ,\otimes )$ is residuated SBI-algebra.

Proof. 

$(1)$ We can get some properties of pseudo-BL-algebra $(X,\wedge ,\vee ,\otimes ,\to ,⇝,0,1)$ from literature [28] as follows:

$(i)$if $x\le y,$ then $z\to x\le z\to y$ and $z⇝x\le z⇝y;$

$(ii)$if $x\le y,$ then $y\to z\le x\to z$ and $y⇝z\le x⇝z;$

$(iii)x\otimes y\le z$ if and only if $x\le y\to z$ if and only if $y\le x⇝z.$

Using $(i)$ and $(ii)$, we know that $(X,\to ,\le )$ and $(X,⇝,\le )$ are BI-algebras.

Then use condition $(iii)$, we know that $(L,\to ,\otimes )$ is a left residuated BI-algebra, and $(L,⇝,\otimes )$ is a right residuated BI-algebra;

$(2)$ Similar to the proof of (1), the conclusion in Proposition 9(2) is tenable by using the related properties in Proposition 1.

$(3)$ By the propositions of non-associative residuated lattice in literature [29], the conclusion is established. □

Next, we give some propositions of left/right residuated BI-algebras and residuated SBI-algebras.

Proposition 10.

Let $(X,\to ,\otimes ,\le )$ be a left residuated BI-algebra, then,

$(1)\forall x,y\in X,x\le y\to (x\otimes y);$

$(2)\forall x,y\in X,(x\to y)\otimes x\le y;$

$(3)\forall x,y,z\in X,$ if $x\le y,$ then $x\otimes z\le y\otimes z$ and $z\otimes x\le z\otimes y.$

Proof. 

$(1)\forall x,y\in X,$ using the reflexivity of ≤, we have $x\otimes y\le x\otimes y.$ Applying Definition 16(2), there exists $x\le y\to (x\otimes y).$

$(2)\forall x,y\in X,$$x\to y\le x\to y$ can be obtained form the reflexivity of ≤. Applying Definition 16(2), it is clear that $(x\to y)\otimes x\le y.$

$(3)\forall x,y,z\in X,$ assume $x\le y$, from (1), we have $y\le z\to (y\otimes z),$ using $x\le y$, $x\le z\to (y\otimes z).$ Applying to Definition 16(2), there exists $x\otimes z\le y\otimes z.$

$\forall x,y,z\in X,$ assume $x\le y$, by Definition 16(2), we have that $y\to (z\otimes y)\le x\to (z\otimes y).$ From (1), there exists $z\le y\to (z\otimes y).$ Thus, $z\le x\to (z\otimes y).$ Then using Definition 16(2), $z\otimes x\le z\otimes y.$ □

Proposition 11.

Let $(X,\to ,\otimes ,\le )$ be a right residuated BI-algebra, then,

$(1)\forall x,y\in X,y\le x\to (x\otimes y);$

$(2)\forall x,y\in X,x\otimes (x\to y)\le y;$

$(3)\forall x,y,z\in X,$ if $x\le y,$ then $x\otimes z\le y\otimes z$ and $z\otimes x\le z\otimes y.$

Proposition 12.

Let $(X,\to ,\otimes ,\le )$ be a residuated SBI-algebra, then for any $x,y,z\in X,$

$(1)\forall x,y\in X,$ there exists $x\le y\to (x\otimes y)$ and $y\le x\to (x\otimes y);$

$(2)\forall x,y\in X,$ there exists $(x\to y)\otimes x\le y$ and $x\otimes (x\to y)\le y;$

$(3)\forall x,y,z\in X,$ if $x\le y,$ then there exists $x\otimes z\le y\otimes z$ and $z\otimes x\le z\otimes y.$

The proofs of Propositions 11 and 12 are similar to the proof of Proposition 10, so the proofs are omitted here.

Proposition 13.

Let $(X,\to ,\otimes ,\le )$ be a residuated SBI-algebra, then the binary operation ⊗ is commutative, i.e., $x\otimes y=y\otimes x.$

Proof. 

Let $(X,\to ,\otimes ,\le )$ be a residuated SBI-algebra, then the following equations hold

$$x\otimes y\le z\iff x\le y\to z;$$

(12)

$$x\otimes y\le z\iff y\le x\to z.$$

(13)

Using the reflexivity, $x\otimes y\le x\otimes y,$ according to Equation (12), we have $x\le y\to (x\otimes y),$ then from Equation (13), $y\otimes x\le x\otimes y.$ Conversly, we can get $x\otimes y\le y\otimes x.$ Above all, using antisymmetry, we have $x\otimes y=y\otimes x.$ □

4. Pseudo-SBI-Algebras and Filters

4.1. Pseudo-SBI-Algebras

In the above chapters, we have discussed strong BI-algebra, which added the (PEP) condition on the basis of BI-algebra. However, strong BI-algebra only includes one implication. As we all know, in fuzzy logic, there are many logic algebra structures with double implications, like quantum B-algebra, pseudo-BCK-algebra and so on. In order to characterize the properties of these algebraic structures, SBI-algebra is used as the basis, we define a new concept—pseudo-SBI-algebra.

Definition 17.

Let $(X,\le )$ be a partially ordered set, → and ⇝ binary operations on X:

$(1)$ If X satisfies:

$(i)(X,\to ,\le )$ and $(X,⇝,\le )$ are BI-algebras;

$(ii)\forall x,y\in X,x\le (x\to y)⇝y\iff x\le (x⇝y)\to y.$

Then $(X,\to ,⇝,\le )$ is a pseudo-BI-algebra.

$(2)$ If X satisfies $(i)$ and:

$(iii)x\le y\to z$ if and only if $y\le x⇝z.$

Then $(X,\to ,⇝,\le )$ is called a pseudo-SBI-algebra.

Normal pseudo-SBI-algebra is a pseudo-SBI-algebra which satisfies:

$(iv)\forall x,y\in X,x\to x=$$y⇝y,$ denote $e=x\to x=$$y⇝y;$

Remark 1.

$(1)$ If pseudo-SBI-algebra $(X,\to ,⇝,\le )$ satisfies $x\to y=x⇝y$, $(X,\to ,\le )$ or $(X,⇝,\le )$ is a strong BI-algebra.

$(2)$ We call the condition $(iii)$ in Definition 17 generalized (PEP)(the abbreviation is (GPEP)).

Example 9.

Let $X=\{0,a,b,1\}$. Define operations → and ⇝ on X as Table 4 and Table 5; the order relation defined on X is as follows: $0\le a\le 1,0\le b\le 1$. The operations → and ⇝ are both basic implication algebra. Especially, both operations satisfy $(\forall x\in X),$ $x\to x=1,x⇝x=1.$ Then X is a normal pseudo-SBI-algebra without an unit element, the algebra structure X is not a quantum B-algebra, since

$$a=a\to 0\nleqq 0=(1\to a)\to (1\to 0)$$

Table 4. The operation → on X.

→	0	a	b	1
0	1	1	1	1
a	a	1	1	1
b	b	1	1	1
1	0	1	1	1

Table 5. The operation ⇝ on X.

⇝	0	a	b	1
0	1	1	1	1
a	a	1	1	1
b	b	1	1	1
1	a	1	1	1

Next, we will give an example in which the element 1 is not maximal.

Example 10

([12]). Let $X=\{a,b,c,d,e,1\}$, the operations → and ⇝ on X are defined as Table 6 and Table 7; Define the order relation on X as follows: $a,b,c,d,e,1$ (that is, $\forall x,y\in X,x\le y\iff x=y$). Then X is a normal pseudo-SBI-algebra, and element 1 is not maximal but a left unit element, since $1\to x=1⇝x=x.$ In fact, X is a pseudo-BCI-algebra.

Table 6. The operation → on X.

→	a	b	c	d	e	1
a	1	a	d	e	c	b
b	b	1	e	c	d	a
c	d	e	1	a	b	c
d	e	c	b	1	a	d
e	c	d	a	b	1	e
1	a	b	c	d	e	1

Table 7. The operation ⇝ on X.

⇝	a	b	c	d	e	1
a	1	a	e	c	d	b
b	b	1	d	e	c	a
c	e	d	1	b	a	c
d	c	e	a	1	b	d
e	d	c	b	a	1	e
1	a	b	c	d	e	1

In this example, X satisfies condition (EP), (OP) and (GPEP) when they have two different implication operators.

Proposition 14.

Let X be a pseudo-SBI-algebra. Then,

$(1)\forall x,y\in X,x\le (x\to y)⇝y;x\le (x⇝y)\to y;$

$(2)\forall x,y\in X,x\to y=((x\to y)⇝y)\to y;x⇝z=((x⇝y)\to y)⇝y;$

$(3)\forall x,y\in X,$ if $x\le y,$ then $y\to x\le x\to x\le x\to y;$

$(4)\forall x,y\in X,$ if $x\le y,$ then $y⇝x\le x⇝x\le x⇝y;$

$(5)\forall x,y\in X,$ if $x\le y,u\le v,$ then $y\to u\le x\to v,v\to x\le u\to y;$

$(6)\forall x,y\in X,$ if $x\le y,u\le v,$ then $y⇝u\le x⇝v,v⇝x\le u⇝y.$

Proof. 

$(1)$ For any $x,y\in X$, from $x\to y\le x\to y$, by Definition 17(2),we can get $x\le (x\to y)⇝y$; from $x⇝y\le x⇝y$, we can get $x\le (x⇝y)\to y.$

$(2)$ For any $x,y\in X$, through $(x\to y)⇝y\le (x\to y)⇝y$, by Definition 17(2), we can get $(x\to y)\le ((x\to y)⇝y)\to y$. From $(1)$, $x\le (x\to y)⇝y$, thus, $((x\to y)⇝y)\to y\le x\to y$.

Sum up, $x\to y=((x\to y)⇝y)\to y.$

The proofs of (3)–(6) are apparent. □

After derivation, we give a simplified definition of pseudo-SBI-algebra.

Proposition 15.

A partially ordered set $(X,\le )$ is considered to be a pseudo-SBI-algebra if and only if:

$(1)\forall x,y,z\in X,$ if $x\le y,$ then $z\to x\le z\to y;$

$(2)\forall x,y,z\in X,x\le y\to z$ if and only if $y\le x⇝z.$

Proof. 

We only proof the part of sufficiency.

$(1)$ Proof that if $x\le y$ then $y\to z\le x\to z.$

For any $x,y,z\in X$, assume that $x\le y$, from $(1)$, we have $y\le (y\to z)⇝z,$ thus, $x\le y\to x\le y\le (y\to z)⇝z$, which means that $x\le (y\to z)⇝z$. By Definition 17(2), $y\to z\le x\to z.$

$(2)$ Proof that if $x\le y$ then $z⇝x\le z⇝y.$

For any $x,y,z\in X$, assume that $x\le y$, from $(1)$, we have $z\le (z⇝x)\to x$, use Definition 17(1), $(z⇝x)\to x\le (z⇝x)\to y$, thus by Definition 17(2), conclusion $z⇝x\le z⇝y$ holds.

$(3)$ Proof that if $x\le y$ then $y⇝z\le x⇝z.$

For any $x,y,z\in X$, assume that $x\le y$, from $(1)$, we have $y\le (y\to z)⇝z$, thus, $x\le y\to x\le y\le (y\to z)⇝z$, which means that $x\le (y\to z)⇝z$. Then through Definition 17(2), we can conclude that $y⇝z\le x⇝z$ holds.

Above all, we know that $(X,\to ,\le )$ and $(X,⇝,\le )$ are BI-algebras.

After that, by condition (2) in this proposition, the conclusion was established. □

Theorem 1.

Let $(X,\le ,\to ,⇝)$ be a pseudo-SBI-algebra. If X satisfies $x\to (y⇝z)=y⇝(x\to z)$, then X is a quantum B-algebra.

Proof. 

$(1)$Certificate $y\to z\le (x\to y)\to (x\to z).$

For any $x,y,z\in X$, assume that X satisfies $x\to (y⇝z)=y⇝(x\to z)$. From Proposition 14(1), we have $y\le (y\to z)⇝z$, then by Definition 17(2), there exists $x\to y\le x\to ((y\to z)⇝z)=(y\to z)⇝(x\to z)$. Hence, $y\to z\le (x\to y)\to (x\to z).$

$(2)$Using $(1),$ we can get that $x\to y\le (y\to z)⇝(x\to z).$

$(3)$ Certificate $y⇝z\le (x⇝y)⇝(x⇝z).$ For any $x,y,z\in X$, assume that X satisfies $x\to (y⇝z)=y⇝(x\to z)$. From Proposition 14(1), we have $y\le (y⇝z)\to z$, then by Definition 17(2), we can get $x⇝y\le x⇝((y⇝z)\to z)=(y⇝z)\to (x⇝z)$. Hence, $y⇝z\le (x⇝y)⇝(x⇝z).$

$(4)$ Using $(3)$, there exists $x⇝y\le (y⇝z)\to (x⇝z).$

Above all, we can get this theorem. □

Example 11

([7]). Let G be a partially ordered group with residuals

$$x\to y=y{x}^{-1},x⇝y=x^{-1}y,$$

G has a unit element $u=1$, then G is a pseudo-SBI-algebra, also, the residuals → and ⇝ satisfy $x\to (y⇝z)=y⇝(x\to z).$ Thus, G is also a quantum B-algebra.

The algebraic structures of pseudo-BCK-algebra and quantum B-algebra have been widly discussed in literatures [6,7,8,9,12,13,26]. Using these conclusions, we can get a proposition as follows.

Proposition 16.

$(1)$ Let $(X,\to ,⇝,\le )$ be a quantum B-algebra, then $(X,\to ,⇝,\le )$ is a pseudo-SBI-algebra;

$(2)$ Let $(X,\to ,⇝,\le )$ be a pseudo-BCK-algebra, then $(X,\to ,⇝,\le )$ is a normal pseudo-SBI-algebra with the element $e=1$;

$(3)$ If $(X,\to ,⇝,\le )$ is a pseudo-SBI-algebra, then $(X,\to ,\le )$ and $(X,⇝,\le )$ are basic implication algebras.

Proof. 

$(1)$ It is clear.

$(2)$ From Proposition 4, we have that every pseudo-BCK-algebra is a quantum B-algebra. Then using (1), every pseudo-BCK-algebra is a pseudo-SBI-algebra. □

We can use Figure 3 to describe Proposition 16.

Figure 3. The relationships among some algebraic structures.

4.2. Filters of Pseudo-SBI-Algebras

Filter theory plays an important role in computer science and non-classical logics. Many scholars use filters to make their corresponding algebraic structures clearer. So in this section, we give filters and quotient structures of pseudo-SBI-algebras.

Definition 18.

Let X be a pseudo-SBI-algebra, F be a nonempty subset of X. Then F is called a filter of X if:

$(1)F$ is a filter of basic implication algebra $(X,\to ,\le );$

$(2)F$ is a filter of basic implication algebra $(X,⇝,\le ).$

Filter F is called normal, if:

$(3)x,y\in X,x\to y\in F$ if and only if $x⇝y\in F.$

Proposition 17.

If F is a filter of pseudo-SBI-algebra X. Then,

$(1)\forall x\in F,$ if $y\in X,$ there extsts $(x⇝y)\to y\in F;$

$(2)\forall x\in F,$ if $y\in X,$ there exists $(x\to y)⇝y\in F.$

Proof. 

$(1)$Suppose there exists $x\in F,y\in X.$ From Proposition 14(1), there exists $x\le (x⇝y)\to y.$ Then using Definition 18, conclusion $(x⇝y)\to y\in F$ holds.

$(2)$Assume that $x\in F,y\in X.$ From Proposition 14(1), there exists $x\le (x\to y)⇝y.$ Then using Definition 18, the conclusion $(x\to y)⇝y\in F$ is proved. □

Definition 19.

Let X be a normal pseudo-SBI-algebra, F is a filter of X. Then F is called regular if and only if:

$(1)\forall x\in X,$ if $(x\to y)\to e\in F$ and $(y\to z)\to e\in F,$ then $(x\to z)\to e\in F.$

$(2)\forall x\in X,$ if $(x⇝y)⇝e\in F$ and $(y⇝z)⇝e\in F,$ then $(x⇝z)⇝e\in F.$

Example 12.

$(1)$In Example 9, X is a pseuso SBI-algebra. Then F is a filter of X if $F=\left\{1\right\}$.

$(2)$In Example 10, X is a pseuso SBI-algebra. Let $F=\{1,r,s\}$, then F is a filter of X.

Proposition 18.

Let F be a regular filter of normal pseudo-SBI-algebra X. Then,

$(1)\forall x,y,z\in F,$ if $e\to (x\to y)\in F$ and $e\to (y\to z)\in F$, then $e\to (x\to z)\in F,(z\to x)\to e\in F.$

$(2)\forall x,y,z\in F,$ if $e⇝(x⇝y)\in F$ and $e⇝(y⇝z)\in F$, then $e⇝(x⇝z)\in F,(z⇝x)⇝e\in F.$

Proof. 

$(1)$ By Definition 17(iv),

$$e\to (x\to y)\in F\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}(x\to x)\to (x\to y)\in F,$$

$$e\to (y\to z)\in F\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}(y\to y)\to (y\to z)\in F.$$

Using Definition 18 and Definition 4(3), there exists $x\to y\in F,y\to z\in F$. Applying Definition 4(4), from $y\to z\in F$, we get

$$(x\to y)\to (x\to z)\in F$$

From this and $x\to y\in F$, by Definition 4(3), we have $x\to z\in F.$ Using Definition 18 and Definition 4(4) and (5),

$$(x\to x)\to (x\to z)\in F,$$

$$(z\to x)\to (x\to x)\in F.$$

Thus,

$$e\to (x\to z)\in F,(z\to x)\to e\in F.$$

$(2)$ The proof is similar to $(1)$. □

Theorem 2.

Let X be a pseudo-SBI-algebra, F be a normal filter of X. The binary relation ${\approx }_F$ on X is defined as follows: $\forall x,y\in X,$

$$x{\approx }_{F}y\mathit{if}\mathit{and}\mathit{only}\mathit{if}x\to y\in F\mathit{and}y\to x\in F.$$

Then binary relation ${\approx }_F$ is a congruence relation.

Proof. 

$(1)$Reflexivity: for any $x\in X$, we can get $x\to x\in F$ from Definition 4(2), which means $x{\approx }_{F}x.$

Symmetry: for any $x,y\in X$, suppose that $x{\approx }_{F}y$, then the conclusion $y{\approx }_{F}x$ can be drawn.

Transitivity: in case $x{\approx }_{F}y$ and $y{\approx }_{F}z.$ It can be obtained by the definition of ${\approx }_F$ that $x\to y\in F,y\to x\in F,y\to z\in F$ and $z\to y\in F.$

Afterwards, using $y\to x\in F,y\to z\in F$ and Definition 4(4) and (5), we have $(x\to y)\to (x\to z)\in F$ and $(z\to y)\to (z\to x)\in F.$ From the above formula and Definition $4(3)$, we can get that $x\to z\in F$ and $z\to x\in F.$ As a result, $x{\approx }_{F}z.$

Above all, we know that ${\approx }_F$ is an equivalence relation on X.

$(2)$ Assume $x{\approx }_{F}y.$ Thereupon, $x\to y\in F$ and $y\to x\in F.$ Then from $x\to y\in F$ we can get $(z\to x)\to (z\to y)\in F$ and $(z\to y)\to (z\to x)\in F$ by using Definition $4(4)$. Therefore, conclusion $(z\to x){\approx }_F(z\to y)$ holds.

According to Definition 4(5), by $y\to x\in F$, we get that $(y\to z)\to (x\to z)\in F$ and $(x\to z)\to (y\to z)\in F,$ i.e., $(x\to z){\approx }_F(y\to z).$

Use the same proof, if $x{\approx }_{F}y,$ consequently, $(z⇝x){\approx }_F(z⇝y)$ and $(x⇝z){\approx }_F(y⇝z)$ hold.

Above all, binary relation ${\approx }_F$ is a congruence relation on X. □

Theorem 3.

In case $(X,\to ,⇝,\le ,e)$ be a normal pseudo-SBI-algebra and the filter F be regular. The quotient operations → and ⇝, and binary relation ≤ on $X{/}_{{\approx }_F}$ is defined as follows:

$${\left[x\right]}_F\to {\left[y\right]}_F={[x\to y]}_F,{\left[x\right]}_F⇝{\left[y\right]}_F={[x⇝y]}_F.$$

$${\left[x\right]}_F\le {\left[y\right]}_F\mathit{if}\mathit{and}\mathit{only}\mathit{if}({\left[x\right]}_F\to {\left[y\right]}_F={\left[e\right]}_F)\mathit{if}\mathit{and}\mathit{only}\mathit{if}({\left[x\right]}_F⇝{\left[y\right]}_F={\left[e\right]}_F),\forall x,y\in X.$$

Then,$(X{/}_{{\approx }_F},\to ,⇝,\le ,{\left[e\right]}_F)$ is a normal pseudo-SBI-algebra.

Proof. 

Firstly, we prove that binary relation ≤ is a partial order.

$(1)$Reflexivity: $\forall x\in X,$ from ${\left[x\right]}_F\to {\left[x\right]}_F={[x\to x]}_F={\left[e\right]}_F$, we can get ${\left[x\right]}_F\le {\left[x\right]}_F.$

$(2)$ Symmetry: in the event of ${\left[x\right]}_F\le {\left[y\right]}_F$ and ${\left[y\right]}_F\le {\left[x\right]}_F,$ which means ${\left[x\right]}_F\to {\left[y\right]}_F={[x\to y]}_F={\left[e\right]}_F$ and ${\left[y\right]}_F\to {\left[x\right]}_F={[y\to x]}_F={\left[e\right]}_F.$

As a result, e$\to (x\to y)\in F$ and $e\to (y\to x)\in F$ hold. Using Definition 4(2) and (3), we have $x\to y\in F,y\to x\in F.$

$(3)$ Transitivity: in case ${\left[x\right]}_F\le {\left[y\right]}_F,{\left[y\right]}_F\le {\left[z\right]}_F,$ which means that $e\to (x\to y)\in F,(x\to y)\to e\in F$ and $e\to (y\to x)\in F,(y\to x)\to e\in F.$

Conclusion $(x\to y)\in F$ and $(y\to z)\in F$ can be obtained by Definition 4(2) and (3). It is clear that $(x\to y)\to (x\to z)\in F$ by Definition $4(4)$, thus, $(x\to z)\in F.$

Apparently,$(x\to x)\to (x\to z)\in F,$ i.e., $e\to (x\to z)=(x\to x)\to (x\to z)\in F.$

From $(x\to y)\to e\in F$ and $(y\to z)\to e\in F,$ applying regularity of F, we have $(x\to z)\to e\in F.$

Above all, we have $(x\to z){\approx }_{F}e,$ i.e., conclusion ${\left[x\right]}_F\le {\left[z\right]}_F$ holds.

Therefore, the binary operation ≤ on $X{/}_{{\approx }_f}$ is a partial order.

Secondly, using Theorem 2, binary operation ${\approx }_F$ is a congruence relation on X.

Use the first proof and the second proof, $(X{/}_{{\approx }_F},\to ,⇝,\le ,{\left[e\right]}_F)$ is a pseudo-SBI-algebra. Because of ${\left[x\right]}_F\to {\left[x\right]}_F={\left[y\right]}_F⇝{\left[y\right]}_F={\left[e\right]}_F,\forall x,y\in X,$ $X{/}_{{\approx }_F}$ is a normal SBI-algebra. □

5. Residuated Pseudo-SBI-algebras and Filters

5.1. Residuated Pseudo-SBI-algebras

In Section 3, we have discussed left/right residuated SBI-algebra and residuated SBI-algebra, but these algebra structures only have one implication operator. In this section, On the basis of residuated SBI-algebra, we expand one implication operation into two, and then we get residuated pseudo-SBI-algebra.

Definition 20.

A residuated pseudo- SBI-algebra is an algebraic structure $(X,\to ,⇝,\otimes ,\le )$ which satisfies:

$(1)(X,\otimes ,\to )$ is a left residuated BI-algebra;

$(2)(X,\otimes ,⇝)$ is a right residuated BI-algebra.

A normal residuated pseudo-SBI-algebra is a residuated pseudo-SBI-algebra which satisfies:

$(4)\forall x,y\in X,x\to x=$$y⇝y,$ denote $e=x\to x=$$y⇝y.$

Proposition 19.

A partially ordered set $(X,\le )$ is considered to be a residuated pseudo-SBI-algebra if it satisfies:

$(1)x\le y\to z\to x\le z\to y;$

$(2)x\le y\to z\iff x\otimes y\le z\iff y\le x⇝z.$

Proof. 

By the proof of Proposition 15, we know that $(X,\to ,\le )$ and $(X,⇝,\le )$ are BI-algebras. After that, using condition (2) in this proposition, $(X,\to ,\otimes ,\le )$ is a left residuated BI-algebra, $(X,⇝,\otimes ,\le )$ is a right residuated BI-algebra. Above all, $(X,\to ,⇝,\otimes ,\le )$ is a residuated pseudo-BI-algebra. □

Example 13.

Let us consider pseudo-t-norm ⊗ on $[0,1]$ by:

$$x\otimes y=\left\{\begin{array}{cc}0,\hfill & \hfill if0\le x\le \frac{1}{2},0\le y\le \frac{1}{2}\\ min(x,y),\hfill & \hfill otherwise.\end{array}\right.$$

The operation ⊗ is not commutative, two implication operators can be induced:

$$x\to y=\left\{\begin{array}{cc}max(\frac{1}{4},y),\hfill & \hfill ifx\le \frac{1}{2}andx>y\\ y,\hfill & \hfill ifx>\frac{1}{2}andx>y\\ 1,\hfill & \hfill ifx\le y\end{array}\right.$$

and

$$x⇝y=\left\{\begin{array}{cc}\frac{1}{2},\hfill & \hfill ifx\le \frac{1}{4}andx>y\\ y,\hfill & \hfill ifx>\frac{1}{4}andx>y\\ 1,\hfill & \hfill ifx\le y.\end{array}\right.$$

Then $([0,1],\to ,⇝,\otimes ,\le )$ is a residuated pseudo-SBI-algebra, and ⊗ has the unit element 1.

Example 14.

Let $X=\{0,a,b,c,d,1\}$. Define the order as follows: $0<a<c<d<1,0<b<c<d<1$. Define operations ⊗, → and ⇝ as Table 8, Table 9 and Table 10. Then X is a residuated pseudo-SBI-algebra, and ⊗ has the unit element 1, X is normal, because $x\to x=x⇝x=1,$ $\forall x\in X.$ The implication operator → and ⇝ have the left unit element 1, $1\to x=1⇝x=x,$ $\forall x\in X.$

Table 8. The operation ⊗ on X.

⊗	0	a	b	c	d	1
0	0	0	0	0	0	0
a	0	0	0	0	a	a
b	0	0	0	0	b	b
c	0	0	0	0	c	c
d	0	0	0	0	d	d
1	0	a	b	c	d	1

Table 9. The operation → on X.

→	0	a	b	c	d	1
0	1	1	1	1	1	1
a	d	1	d	1	1	1
b	d	d	1	1	1	1
c	d	d	d	1	1	1
d	0	a	b	c	1	1
1	0	a	b	c	d	1

Table 10. The operation ⇝ on X.

⇝	0	a	b	c	d	1
0	1	1	1	1	1	1
a	c	1	c	1	1	1
b	c	c	1	1	1	1
c	c	c	c	1	1	1
d	c	c	c	c	1	1
1	0	a	b	c	d	1

Next, we will give an example, whose binary operation ⊗ is associative, and does not have the unit element.

Example 15.

Let $X=\{0,a,b,1\}$. Define operations ⊗, → and ⇝ on X as Table 11, Table 12 and Table 13; the order on X is: $0\le a\le 1,0\le b\le 1$. Then X is a residuated pseudo-SBI-algebra.

Table 11. The operation ⊗ on X.

⊗	0	a	b	1
0	0	0	0	b
a	0	a	b	1
b	0	b	b	1
1	0	1	1	1

Table 12. The operation → on X.

→	0	a	b	1
0	1	1	1	1
a	0	b	b	1
b	0	a	a	1
1	0	0	0	1

Table 13. The operation ⇝ on X.

⇝	0	a	b	1
0	1	1	1	1
a	0	b	b	1
b	0	a	a	1
1	0	b	b	1

Left residuated lattice-ordered groupoid and it’s properties have been studied in literature [20]. Referring to these and the existing definitions of residuated lattice-ordered groupoid, we will give some properties of residuated lattice-ordered groupoid. Then, we investigate the relations between the residuated pseudo-SBI-algebras and the residuated lattices, residuated lattice-ordered groupoid and residuated partially-ordered groupoid.

Proposition 20.

If L is a residuated lattice-ordered groupoid. Then,

$(1)\forall x,y\in L,(x\to y)\otimes x\le y\le x\to (y\otimes x);$

$(2)\forall x,y\in L,x\otimes (x⇝y)\le y\le x⇝(x\otimes y);$

$(3)\forall x,y,z\in L,$ if $x\le y,$ then $x\otimes z\le y\otimes z,z\otimes x\le z\otimes y;$

$(4)\forall x,y,z\in L,$ if $x\le y,$ then $z\to x\le z\to y;$

$(5)\forall x,y,z\in L,$ if $x\le y,$ then $y\to z\le x\to z;$

$(6)\forall x,y,z\in L,$ if $x\le y,$ then $z⇝x\le z⇝y;$

$(7)\forall x,y,z\in L,$ if $x\le y,$ then $y⇝z\le x⇝z.$

Proof. 

$(1)\forall x,y,z\in X.$ Through $x\to y\le x\to y,$ as a result, $(x\to y)\otimes x\le y$ holds. Through $y\otimes x\le y\otimes x,$ we can get that $y\le x\to (y\otimes x).$

$(2)\forall x,y,z\in X.$ Through $x⇝y\le x⇝y,$ we know that $x\otimes (x⇝y)\le y.$ Then from $x\otimes y\le x\otimes y,$ there exists $y\le x⇝(x\otimes y).$

$(3)\forall x,y,z\in X,$ assume that $x\le y.$

From (1), we can get $y\le z\to (y\otimes z),$ and because $x\le y$, we have $x\le z\to (y\otimes z).$ Applying Definition 9(4), $x\otimes z\le y\otimes z.$

Using the property of residuated lattice-ordered groupoid (see [20,30]), $y\to (z\otimes y)\le x\to (z\otimes y).$ From (2), there exists $z\le y\to (z\otimes y)$. Thus, $z\le x\to (z\otimes y).$ Applying Definition 9(4), conclusion $z\otimes x\le z\otimes y$ is established.

$(4)\forall x,y,z\in X,$ in case $x\le y.$ Using $(1),$ we have that $(z\to x)\otimes z\le x.$ From $x\le y,$ $(z\to x)\otimes z\le y$ exists. The conclusion $z\to x\le z\to y$ is holding by Definition 9(4).

$(5)\forall x,y,z\in X,$ assume that $x\le y.$ Using $(1)$, there exists $(y\to z)\otimes y\le z,$ due to the isotonicity of ⊗, there exists $(y\to z)\otimes x\le (y\to z)\otimes y,$ thus, $(y\to z)\otimes x\le z.$ Applying Definition 9(4), conclusion $y\to z\le x\to z$ holds.

The proof of (6) and (7) is similar to (4) and (5). □

Proposition 21.

$(1)$If $(X,\to ,⇝,\otimes ,\le )$ is a residuated pseudo-SBI-algebra, then $(X,\to ,⇝,\otimes ,\le )$ is a residuated partially-ordered groupoid;

$(2)$ Let $(L;\wedge ,\vee ,\otimes ,\to ,⇝,0,1)$ be a residuated lattice-ordered groupoid, then $(L,\to ,⇝,\le )$ is a residuated pseudo-SBI-algebra;

$(3)$ Let $(L;\wedge ,\vee ,\otimes ,\to ,⇝,0,1)$ be a residuated lattice, then $(L,\to ,⇝,\le )$ is a residuated pseudo-SBI-algebra.

Proof. 

$(1)$ Denote left residuated BI-algebra as $(X,\otimes ,\to ,\le )$, and right residuated BI-algebra as $(X,\otimes ,⇝,\le )$. Then from Definition 20, we know $x\le y\to z$ if and only if $x\otimes y\le z$ if and only if $y\le x⇝z.$ Applying Definition 8, it is clear that every residuated pseudo-SBI-algebra is a residuated partially-ordered groupoid.

$(2)$ Assume that L is a residuated lattice-ordered groupoid. Applying Proposition 20, $(L,\to ,\le )$ and $(L,⇝,\le )$ are BI-algebras. Then from Definition 9(4), $(L,\otimes ,\to )$ and $(L,\otimes ,⇝)$ satisfy $x\otimes y\le z\iff x\le y\to z$ and $x\otimes y\le z\iff y\le x⇝z.$ Thus, every residuated lattice-ordered groupoid is a residuated pseudo-SBI-algebra.

$(3)$ Assume that L is a residuated lattice. Using Proposition 3, we can know that L about → and ⇝ constitutes a quantum B-algebra. From Proposition 14, clearly, L can constitute a pseudo-SBI-algebra about → and ⇝. Because Definition 9(1), every residuated lattice is a residuated pseudo-SBI-algebra. □

Proposition 22.

Let $(X,\to ,⇝,\otimes ,\le )$ be a residuated pseudo-SBI-algebra, then,

$(1)\forall x,y\in X,(x\to y)\otimes x\le y\le x\to (y\otimes x);$

$(2)\forall x,y\in X,x\otimes (x⇝y)\le y\le x⇝(x\otimes y);$

$(3)\forall x,y,z\in X,$ if $x\le y,$ then $x\otimes z\le y\otimes z,z\otimes x\le z\otimes y;$

$(4)\forall x,y\in X,x\otimes (x⇝(x\otimes y))=x\otimes y;$

$(5)\forall x,y\in X,(x\to (y\otimes x))\otimes x=y\otimes x;$

$(6)\forall x,y\in X,x\to ((x\to y)\otimes x)=x\to y;$

$(7)\forall x,y\in X,x⇝(x\otimes (x⇝y))=x⇝y;$

$(8)\forall x,y\in X,(x\to ((x\to y)\otimes x))\otimes x=(x\to y)\otimes x;$

$(9)\forall x,y\in X,x\otimes (x⇝(x\otimes (x⇝y)))=x\otimes (x⇝y);$

$(10)\forall x,y\in X,x\to ((x\to (y\otimes x))\otimes x)=x\to (y\otimes x);$

$(11)\forall x,y\in X,x⇝(x\otimes (x⇝(x\otimes y)))=x⇝(x\otimes y).$

Proof. 

$(1)$$\forall x,y\in X.$ Through $x\to y\le x\to y,$ there is a conclusion $(x\to y)\otimes x\le y.$ Through $y\otimes x\le y\otimes x,$ we can get that $y\le x\to (y\otimes x).$

$(2)$$\forall x,y\in X.$ Through $x⇝y\le x⇝y,$ we know that $x\otimes (x⇝y)\le y.$ Through $x\otimes y\le x\otimes y,$ conclusion $y\le x⇝(x\otimes y)$ is holding.

$(3)\forall x,y,z\in X,$ assume that $x\le y.$

From (1), we can get $y\le z\to (y\otimes z),$ and because $x\le y$, we have $x\le z\to (y\otimes z).$ Applying Definition 20, $x\otimes z\le y\otimes z.$

Using Definition 3(2), $y\to (z\otimes y)\le x\to (z\otimes y).$ From Proposition 22(1), there exists $z\le y\to (z\otimes y)$. Thus, $z\le x\to (z\otimes y).$ Applying Definition 20, we have $z\otimes x\le z\otimes y.$

$(4)\forall x,y\in X.$ By Proposition 22(2), $y\le x⇝(x\otimes y),$ and because of Proposition 22(3), there exists $x\otimes y\le x\otimes (x⇝(x\otimes y)).$ Using Proposition 22(2) again, $x\otimes (x⇝(x\otimes y))\le x\otimes y.$ Thus, $x\otimes (x⇝(x\otimes y))=x\otimes y.$

$(5)\forall x,y\in X.$ From Proposition 22(1), there is a conclusion $y\le x\to (y\otimes x),$ by Proposition 22(3), $y\otimes x\le (x\to (y\otimes x))\otimes x$ holds. Using Proposition 22(1) again, there exists $(x\to (y\otimes x))\otimes x\le y\otimes x.$ Sum up, $(x\to (y\otimes x))\otimes x=y\otimes x.$

$(6)\forall x,y\in X.$ From Proposition 22(1), we have $(x\to y)\otimes x\le y,$ using Definition 20(1), $x\to ((x\to y)\otimes x)\le x\to y.$ Applying Proposition 22(1) again, we can get $x\to y\le x\to ((x\to y)\otimes x).$ Above, $x\to ((x\to y)\otimes x)=x\to y.$

$(7)\forall x,y\in X.$ Using Proposition 22(2), $x\otimes (x⇝y)\le y,$ and because Definition 20, we have $x⇝(x\otimes (x⇝y))\le x⇝y.$ Applying Proposition 22(2), there is a conclusion $x⇝y\le x⇝(x\otimes (x⇝y)).$ Thus, there exists $x⇝(x\otimes (x⇝y))=x⇝y.$

We can get (8)–(11) from above. □

Next, we will use Figure 4 to describe Proposition 21.

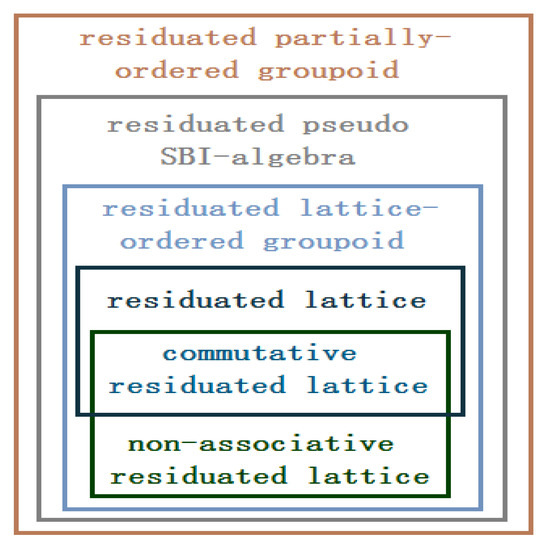
Figure 4. The relationships among some residuated algebraic structures.

The literature [30] has listed many properties of residuated partially-ordered groupoid. Using Proposition 21, residuated pseudo-SBI-algebra is a special residuated partially-ordered groupoid. Combined with [30], we can get the following properties of residuated pseudo-SBI-algebra.

Proposition 23.

Let $(X,\to ,⇝,\otimes ,\le )$ be a residuated pseudo-SBI-algebra. Then

$(1)$ If $\bigvee A$ and $\bigvee B$ exist for $A,B\subseteq X,$ then so does ${\bigvee }_{x\in A,y\in B}(x\otimes y),$ and

$$(\bigvee A)\otimes (\bigvee B)=\underset{x\in A,y\in B}{\bigvee }(x\otimes y).$$

$(2)$ If $\bigvee A$ and $\bigwedge B$ exist for $A,B\subseteq X,$ then ${\bigwedge }_{x\in A}(x\to z),{\bigwedge }_{x\in A}(x⇝z),$ ${\bigwedge }_{y\in B}(z\to y),{\bigwedge }_{y\in B}(z⇝y)$ exist for any $z\in X,$ and

$$z\to (\wedge B)=\underset{y\in B}{\bigwedge }(z\to y),z⇝(\wedge B)=\underset{y\in B}{\bigwedge }(z⇝y),$$

$$(\vee A)\to z=\underset{x\in A}{\bigwedge }(x\to z),(\vee A)⇝z=\underset{x\in A}{\bigwedge }(x⇝z).$$

$(3)x\to z=max\{y\in X|y\otimes x\le z\},x⇝z=max\{y\in X|x\otimes y\le z\}.$

According to the proposition above, we can see that in every residuated pseudo-SBI-algebra, $x\to y$ and $x⇝y$ always have the maximum.

According to the Proposition 1.2 in ref. [5], the above conclusion holds.

Theorem 4.

Let $X=(X,\otimes ,\to ,⇝,\le )$ be a residuated pseudo-SBI-algebra. Then condition $T1$ is equivalent to condition $T{1}^{{}^{\prime }}$, and condition $T2$ is equivalent to condition $T{2}^{{}^{\prime }}$:

$(T1)\forall x,y,z\in X,y⇝z\le (x⇝y)⇝(x⇝z).$

$(T{1}^{{}^{\prime }})$$\forall x,y,z\in X,x\otimes (y\otimes z)\le (x\otimes y)\otimes z.$

$(T2)$$\forall x,y,z\in X,y\to z\le (x\to y)\to (x\to z).$

$(T{2}^{{}^{\prime }})\forall x,y,z\in X,(x\otimes y)\otimes z\le x\otimes (y\otimes z).$

The proof can refer to Theorems 2.1 and 2.2 in ref. [30].

5.2. Filters of Residuated Pseudo-SBI-Algebras

In this section, the concept of filter and quotient structure of a residuated pseudo-SBI-algebra are proposed. We use the filter and quotient structure to character the structure of residuated pseudo-SBI-algebra. The theory of filters for residuated pseudo-SBI-algebras is more extensive than the filters of a non-associative residuated lattice.

Definition 21.

Let X be a pseudo-SBI-algebra, and $A,B$ be the subsets of X, define an order relation ${⪯}_{order}$ as follows:

$$\forall A,B\subseteq X,A{⪯}_{order}B⟺\forall a\in A,\exists b\in B,s.t.a\le b.$$

It is easy to verify that ${⪯}_{order}$ is a partial order relation on the power set of X. Corresponding to order relation ${⪯}_{order}$, a weak equal relation ${\approx }_{order}$ is defined as follows:

$\forall A,B\subseteq X,$$A{\approx }_{order}B⟺A{⪯}_{order}B,B{⪯}_{order}A.$

Definition 22.

Let X be a residuated pseudo-SBI-algebra, F be a nonempty subset of X, then F is called a filter of X if and only if:

$(1)\forall x\in F,$ if $x\le y,$ then $y\in F.$

$(2)\forall x,y\in X,$ if $x,x\to y\in F,$ then $y\in F.$

$(3)\forall x,y\in X,(x\otimes y)\otimes F{\approx }_{order}x\otimes (y\otimes F),(x\otimes F)\otimes y{\approx }_{order}x\otimes (F\otimes y),(F\otimes x)\otimes y{\approx }_{order}F\otimes (x\otimes y),$ where $a\otimes F=\{a\otimes f|f\in F\},F\otimes a=\{f\otimes a|f\in F\},$ $\forall a\in X.$

$(4)\forall x,y\in X,F\otimes (x\otimes F){\approx }_{order}F\otimes x.$

Filter F is called normal if:

$(5)\forall x,y\in X,x\to y\in F\iff x⇝y\in F.$

Proposition 24.

In case F is a filter of residuated pseudo-SBI-algebra. Then,

$(1)\forall x,y\in X,$ if $x,x⇝y\in F,$ then $y\in F;$

$(2)\forall x,y\in F,x\otimes y\in F;$

$(3)\forall x,y,z\in X,x⇝(y⇝z)\in F$⇒$(y\otimes x)⇝z\in F;$

$(4)\forall x,y,z\in X,(y\otimes x)⇝z\in F$⇒$x⇝(y⇝z)\in F;$

$(5)(y⇝z)⇝(x⇝z)\in F\iff (x\otimes (y⇝z))⇝z\in F.$

Proof. 

$(1)\forall x,y\in X,$ in the event of $x,x⇝y\in F.$ Using Proposition 14(1), we can get $x\le (x⇝y)\to y.$ Then by Definition 22(1), $(x⇝y)\to y\in F.$ Applying Definition 22(2), $y\in F.$

$(2)$Assume that $x\in F$ and $y\in F$. Known that $x\otimes y\le x\otimes y,$ then $x\le y\to (x\otimes y)\in F,$ using Definition 22(1) and (2), we can get that $x\otimes y\in F.$

$(3)$Denote $x⇝(y⇝z)=f_1\in F$, there is a conclusion $f_1\le x⇝(y⇝z).$ Through Definition 20(2), there is a conclusion

$$x\otimes f_1\le y⇝z,y\otimes (x\otimes f_1)\le z.$$

The next conclusion can be obtained by Definition 22(3), i.e., there exists $f_2\in F$ such that

$$(y\otimes x)\otimes f_2\le y\otimes (x\otimes f_1)\le z.$$

The conclusion $f_2\le (y\otimes x)⇝z.$ is given by Definition 20. By Definition $22(1)$ we have $(y\otimes x)⇝z\in F.$

$(4)$ Denote $(y\otimes x)⇝z=f_3\in F,$ then $f_3\le (y\otimes x)⇝z.$ By Definition 20,$(y\otimes x)\otimes f_3\le z.$ Similarly, there exists $f_4\in F$ such that the verdict

$$y\otimes (x\otimes f_4)\le (y\otimes x)\otimes f_3\le z$$

holds.

Conclusion $x\otimes f_4\le y⇝z,f_4\le x⇝(y⇝z)$ can be obtained from Definition 20. Then from Definition $22(1)$ we have $x⇝(y⇝z)\in F.$

$(5)$Denote $(x\otimes (y⇝z))⇝z=f_5,$ then $f_5\le (x\otimes (y⇝z))⇝z.$ By Definition 20,$(x\otimes$$(y⇝z))\otimes f_5\le z.$ Applying Definition $22(3),$ here’s $f_6\in F$ such that

$$x\otimes ((y⇝z)\otimes f_6)\le (x\otimes (y⇝z))\otimes f_5\le z.$$

We can get the next conclusion from Definition 20, i.e.,

$$(y⇝z)\otimes f_6\le x⇝z.$$

Thus

$$f_6\le (y⇝z)⇝(x⇝z).$$

By Definition $22(1)$ there is $(y⇝z)⇝(x⇝z)\in F.$ □

Proposition 25.

If L is a residuated pseudo-SBI-algebra, F is a filter of L. After that, F must be a filter of $(L,\wedge ,\vee ,\otimes ,\to ,0,1)$ and $(L,\wedge ,\vee ,\otimes ,⇝,0,1)$ when they are non-associative residuated lattices.

Proof. 

$(1)$Proof Definition 11 $(NA1).$ Using Definition 22, it is clear that $1\in F.$

$(2)$Proof Definition 11 $(NA2).$ This can be verified by Definition 22(2).

$(3)$Proof Definition 11 $(NA3).$ We can get this condition from Definition 22(3).

Sum up, F is the filter of non-associative residuated lattice $(L,\wedge ,\vee ,\otimes ,\to ,0,1)$. Dual, the other holds. □

Proposition 26.

If L is a residuated pseudo-SBI-algebra, F is a filter of L. After that, F must be a filter of L when $(L,\wedge ,\vee ,\otimes ,\to ,⇝,0,1)$ is a residuated lattice.

Proof. 

$(1)$Proof of Definition 10 $(RLF1).$ Using Definition 22, it is clear that $1\in F.$

$(2)$Proof of Definition 10 $(RLF2).$ This can be verified by Definition 22(2).

$(3)$Proof of Definition 10 $(RLF3).$ We can prove this by Proposition 24(1).

Thus, F is the filter of residuated lattice $(L,\wedge ,\vee ,\otimes ,\to ,⇝,0,1)$. □

Example 16.

In Example 15, X is a residuated pseudo-SBI-algebra. Let $F=\{a,b,1\}$, then F is a filter of X.

Example 17.

Let $X=\{0,a,b,c,d,e,1\}$. Operation ⊗ is a commutative, and defined as Table 14; → and ⇝ are defined as Table 15; define the order on X as follows: $0\le e\le d\le c\le a\le 1,0\le e\le d\le c\le b\le 1$. Verified, X is a residuated pseudo-SBI-algebra.

Table 14. The operation ⊗ on X.

⊗	0	a	b	c	d	e	1
0	0	0	0	0	0	0	0
a	0	a	c	c	d	e	a
b	0	c	b	c	d	e	b
c	0	c	c	d	d	e	c
d	0	d	d	d	d	e	d
e	0	e	e	e	e	0	e
1	0	a	b	c	d	e	1

Table 15. The operation $\to /⇝$ on X.

$\to /⇝$	0	a	b	c	d	e	1
0	1	1	1	1	1	1	1
a	0	1	b	b	d	e	1
b	0	a	1	a	d	e	1
c	0	1	1	1	c	e	1
d	0	1	1	1	1	e	1
e	e	1	1	1	1	1	1
1	0	a	b	c	d	e	1

Let $F=\{a,b,c,d,1\}$, then F is a filter of X as a non-associative residuated lattice.

Proposition 27.

Let F be a normal filter of residuated pseudo-SBI-algebra X. Then,

$(1)\forall x,y\in X,$ if $x⇝y\in F,$ then $(y⇝z)⇝(x⇝z)\in F;$

$(2)\forall x,y\in X,$ if $x\to y\in F,$ then $(y\to z)\to (x\to z)\in F;$

$(3)\forall x,y\in X,$ if $x⇝y\in F,$ then $(z⇝x)⇝(z⇝y)\in F;$

$(4)\forall x,y\in X,$ if $x\to y\in F,$ then $(z\to x)\to (z\to y)\in F.$

Proof. 

$(1)$Remember that $x⇝y=f_1\in F,$ then $f_1\le x⇝y,$ applying Definition 20,$x\otimes f_1\le y.$ Using Proposition 22(2) and (3), we know that

$$(x\otimes f_1)\otimes (y⇝z)\le y\otimes (y⇝z)\le z.$$

Here’s $f_2\in F$ which make the next conclusion holds by Definition 22(3).

$$x\otimes (f_2\otimes (y⇝z))\le (x\otimes f_1)\otimes (y⇝z)\le z.$$

According to Definition 20, there exists

$$f_2\otimes (y⇝z)\le x⇝z,f_2\le (y⇝z)\to (x⇝z).$$

By Definition 22(1), there exists $(y⇝z)\to (x⇝z)\in F.$ Then from Definition 22(5),$(y⇝z)⇝$$(x⇝z)\in F.$

$(2)$Remember that $x\to y=f_3\in F,$ then $f_3\le x\to y,$ according to Definition 20,$f_3\otimes x\le y.$ Using Proposition 22(1) and (3), we know that

$$(y\to z)\otimes (f_3\otimes x)\le (y\to z)\otimes y\le z.$$

Applying Definition 22(3), $f_4\in F$ can be used to prove

$$((y\to z)\otimes f_4)\otimes x\le (y\to z)\otimes (f_3\otimes x)\le z.$$

Then by Definition 20(2)

$$(y\to z)\otimes f_4\le x\to z,f_4\le (y\to z)⇝(x\to z).$$

By Definition 22(1) there is a conclusion $(y\to z)⇝(x\to z)\in F.$ Through Definition 22(5),$(y\to z)\to (x\to z)\in F.$

The proof of $(3)$ and $(4)$ is similar to $(1)$ and $(2).$ □

Theorem 5.

Let X be a residuated pseudo-SBI-algebra, F be a normal filter. Definition of binary relation ${\approx }_F$ on X is given by: $\forall x,y\in X,$

$$x{\approx }_{F}y\iff x\to y\in Fandy\to x\in F.$$

Then, the binary relation ${\approx }_f$ is a congruence relation.

Proof. 

$(1)$Clearly, binary relation ${\approx }_F$ is an equivalent relation on X.

$(2)$Proof that ${\approx }_F$ is a congruence relation on X.

For operation ⊗: If $x{\approx }_{F}y,a{\approx }_{F}b,$ then we have $x\to y\in F$ and $a⇝b\in F.$ Applying Proposition 22(1) and (2), we have $(x\to y)\otimes x\le y,a\otimes (a⇝b)\le b.$

Then according to Definition 20, we have $y\otimes b\ge ((x\to y)\otimes x)\otimes (a\otimes (a⇝b)).$

Because of $x\to y\in F,a⇝b\in F,$ there exists $f_1,f_2\in F$, such that $y\otimes b\ge (f_1\otimes x)\otimes (a\otimes f_2).$

Using Definition 22(3), there exists $f_3,f_4\in F$ such that $y\otimes b\ge f_3\otimes ((x\otimes a)\otimes f_4),$ by Definition 22(4),

$$f_3\otimes ((x\otimes a)\otimes f_4)\le f_5\otimes (x\otimes a)\le y\otimes b.$$

By Definition 20, $f_5\le (x\otimes a)\to (y\otimes b).$ Applying Definition 22(1), $(x\otimes a)\to (y\otimes b)\in F$ holds. The proof of $(y\otimes b)\to (x\otimes a)\in F$ is similar. Thus,$(x\otimes a){\approx }_F(y\otimes b).$

For operation →: Supposing that $x{\approx }_{F}y,a{\approx }_{F}b.$ By Proposition 25(2), there exists conclusions $(x\to a)\to (y\to a)\in F,(y\to a)\to (x\to a)\in F$ by the means of $x\to y\in F$ and $y\to x\in F,$

Thereupon, $(x\to a){\approx }_F(y\to a)$ holds. By Proposition 27(4), through $a\to b\in F$ and $b\to a\in F,$ there is a conclusion

$$(y\to a)\to (y\to b)\in F,(y\to b)\to (y\to a)\in F.$$

Therefore, $(y\to a){\approx }_F(y\to b).$ As a result, $(x\to a){\approx }_F(y\to b)$ is holding.

For operation ⇝: Assume $x{\approx }_{F}y,a{\approx }_{F}b,$ it follows that $x⇝y\in F$, $y⇝x\in F;a⇝b\in F$, $b⇝a\in F.$

Applying Proposition 27(1), there is a conclusion $(x⇝a)⇝(y⇝a)\in F,(y⇝a)⇝(x⇝a)\in F.$

It follows that $(x⇝a){\approx }_F(y⇝a).$ By Proposition 27(3), through $(a⇝b)\in F$ and $(b⇝a)\in F,$ there exists

$$(y⇝a)⇝(y⇝b)\in F,(y⇝b)⇝(y⇝a)\in F.$$

Which means $(y⇝a){\approx }_F(y⇝b).$ Hence $(x⇝a){\approx }_F(y⇝b).$

Above all, ${\approx }_F$ is a congruence relation on X. □

Theorem 6.

Let X be a residuated pseudo-SBI-algebra, and F be a normal filter. The Definition of quotient operations → and ⇝, binary operation ⊗ and binary relation ≤ on $X{/}_{{\approx }_F}$ are given by:

$${\left[x\right]}_F\to {\left[y\right]}_F={[x\to y]}_F;{\left[x\right]}_F⇝{\left[y\right]}_F={[x⇝y]}_F;$$

$${\left[x\right]}_F\otimes {\left[y\right]}_F={[x\otimes y]}_F;{\left[x\right]}_F\le {\left[y\right]}_F\mathit{if}\mathit{and}\mathit{only}\mathit{if}x\to y\in Fandy\to x\in F,\forall x,y,\in X.$$

Then, $(X{/}_{\approx F},\to ,⇝,\otimes ,\le )$ is a residuated pseudo-SBI-algebra, and there exists $(X,\to ,⇝,\otimes ,\le )\sim (X{/}_{\approx F},\to ,⇝,\otimes ,\le ).$

Proof. 

It is clear that the binary relation ≤ on $X{/}_{{\approx }_F}$ is a partially order on X.

Thereupon, the results are holding by Theorem 5. □

6. Conclusions

In this paper, based on basic implication algebra, we get some new concepts and their properties.

Based on fuzzy weak implication, we add (PEP) condition to basic implication algebra and get strong BI-algebra (SBI-algebra for short). It is important that the SBI-algebra is a fuzzy weak implication which satisfies condition (PEP) (see Proposition 7). A SBI-algebra X is a BCK-algebra if X is also a BCC-algebra. Strong BI-algerba mentioned above is generally applicable to the structure of single implication algebras. We extend this algebra to two implications. Thus, we get pseudo-SBI-algebra, which is the algebraic abstraction of commutative/non-commutative fuzzy implication. Pseudo-SBI-algebras can include quantum B-algebras, pseudo-BCI/BCK-algebras, etc. (see Proposition 14). In the next, we studied the filter theory and quotient structure of pseudo-SBI-algebras.

As we all know, a kind of cycle multiplication represented by t-norm is a very important branch of fuzzy logic. Therefore, on the basis of BI-algebra and SBI-algebra, we propose left/right residuated BI-algebra and residuated SBI-algebra, which contain two kinds of operators: fuzzy implication and fuzzy aggregation operator. It is important that residuated lattices and non-associative residuated-lattices can be included (see Proposition 9). Moreover, the binary operation ⊗ in the residuated strong BI-algebra must be commutative (see Proposition 13), but in a left/right residuated BI-algebra, ⊗ cannot be commutative. On the basis of left/right residuated BI-algebra, we propose an important concept of residuated pseudo-SBI algebra, which has two implication operators. Residuated pseudo-SBI-algebra unifies the residuated lattice, non-associative residuated lattice, and residuated lattice-ordered groupoid (see Proposition 21). Moreover, it has been verified that implication $x\to y$ and $x⇝y$ in residuated pseudo-SBI-algebra always have the maximum (see Proposition 23). Next, we give the filter of residuated pseudo-SBI-algebra, which unifies the filter of residuated lattice and non-associative residuated lattice.

In the existing research, the theory of ideal is also a research focus, and the notion of ideal has a dual relationship with filter. In this paper, we studied the filters of pseudo-SBI-algebras and residual pseudo-SBI-algebras, and we will study the correlation of their ideals. Moreover, we will explore deeply their category properties in the future.