Blown-Up Hirzebruch Surfaces and Special Divisor Classes

Abstract

We work on special divisor classes on blow-ups ${\mathbf{F}}_{p,r}$ of Hirzebruch surfaces over the field of complex numbers, and extend fundamental properties of special divisor classes on del Pezzo surfaces parallel to analogous ones on surfaces ${\mathbf{F}}_{p,r}$. We also consider special divisor classes on surfaces ${\mathbf{F}}_{p,r}$ with respect to monoidal transformations and explain the tie-ups among them contrast to the special divisor classes on del Pezzo surfaces. In particular, the fundamental properties of quartic rational divisor classes on surfaces ${\mathbf{F}}_{p,r}$ are studied, and we obtain interwinded relationships among rulings, exceptional systems and quartic rational divisor classes along with monoidal transformations. We also obtain the effectiveness for the rational divisor classes on ${\mathbf{F}}_{p,r}$ with positivity condition.

1. Introduction

In this article, we work over the field of complex numbers. Algebraic surfaces birational to the projective plane are rational surfaces. When a rational surface has no ($-1$)-curve, the rational surface is either a projective plane or a Hirzebruch surface. According to the blow-up/down of ($-1$)-curves, it is natural to expect analogies between the studies of blown-up projective planes and the blown-up Hirzebruch surfaces [1,2,3]. For del Pezzo surfaces, ($-1$)-curves are rational and the configuration of ($-1$)-curves are closely related to the vertices of Gosset polytopes [4,5]. Moreover, the rational divisor classes D on del Pezzo surfaces with $D^2=0$, $-1$are fundamental objects and it turns out that these are also understood by the symmetry of Gosset polytopes. Therefore, we introduce rational divisor classes on Hirzebruch surfaces and study the fundamental properties along the symmetry of Gosset polytopes.

A del Pezzo surface is a smooth irreducible surface $S_r$ such that the anticanonical divisor class $-K_{S_r}$ is ample. Each del Pezzo surface can be constructed by blowing up ${\mathbb{P}}^2$ at r points ($0\le r\le 8$) in a general position unless it is ${\mathbb{P}}^1\times {\mathbb{P}}^1$(for this case $1\le r\le 7$ we get $S_{r+1}$). For each $k\in \mathbb{Z}$, we consider rational divisor classes D with $D^2=k$.

$${\mathcal{S}}_r\left(k\right):=\left\{D\in \mathrm{Pic}\left(S_r\right)\left|D^2=k,-K_{S_r}·D=k+2\right.\right\}.$$

For $k=-2,-1,0,1$, we call the rational divisor classes as special divisor classes denoted by another notations.

$$\begin{array}{cc}\hfill {\mathbf{R}}_r& :={\mathcal{S}}_r(-2)=\left\{d\in \mathrm{Pic}\left(S_r\right)\left|d^2=-2,d·K_{S_r}=0\right.\right\}\left(\mathrm{roots}\right),\hfill \\ \hfill {\mathbf{L}}_r& :={\mathcal{S}}_r(-1)=\{l\in \mathrm{Pic}\left(S_r\right)\left|l^2=-1,l·K_{S_r}=-1\right.\}\left(\mathrm{lines}\right),\hfill \\ \hfill {\mathbf{M}}_r& :={\mathcal{S}}_r\left(0\right)=\{m\in \mathrm{Pic}\left(S_r\right)\left|m^2=0,m·K_{S_r}=-2\right.\}\left(\mathrm{rulings}\right),\hfill \\ \hfill {\mathcal{E}}_r& :={\mathcal{S}}_r\left(1\right)=\{e\in \mathrm{Pic}\left(S_r\right)\left|e^2=1,e·K_{S_r}=-3\right.\}(\mathrm{exceptional}\mathrm{systems}).\hfill \end{array}$$

We call a special divisor class in ${\mathcal{S}}_r(-2)={\mathbf{R}}_r$ as a root d. We define a reflection ${\sigma }_d$ on $K_{S_r}^{\perp }$ in $\mathrm{Pic}\left(S_r\right)$ by

$${\sigma }_d\left(D\right):=D+(D·d)d\mathrm{for}D\in K_{S_r}^{\perp },$$

and the reflections given by roots generate the Weyl group $W\left(S_r\right)=E_r$ for each $3\le r\le 8$ where the extended list of $E_r$ contains $E_3=A_1\times A_2$, $E_4=A_4$ and $E_5=D_5$. This reflection ${\sigma }_d$ on $K_{S_r}^{\perp }\subset$Pic$\left(S_r\right)$ can be extended to a map of $\mathrm{Pic}\left(S_r\right)$. Moreover, since the reflection ${\sigma }_d$preserves the intersection $·$and $K_{S_r}$, the Weyl group $W\left(S_r\right)$acts on each subset of $\mathrm{Pic}\left(S_r\right)$consisting of divisor classes $D$satisfying $D·K_{S_r}=\alpha$, $D^2=\beta$for fixed integers $\alpha$and $\beta$. Thus, there is a natural representation of $W\left(S_r\right)$ on ${\mathcal{S}}_r\left(k\right)$.

A line l is a special divisor class in ${\mathcal{S}}_r(-1)={\mathbf{L}}_r$ including a smooth rational curve embedded by a linear system $|-K_{S_r}|$ as a projective line. For $3\le r\le 8$, the set ${\mathbf{L}}_r$ of lines in $\mathrm{Pic}\left(S_r\right)$is finite, and the Weyl group $E_r$ is its symmetry group. Moreover, ${\mathbf{L}}_r$is bijective to the set of vertices in a Gosset polytope ${(r-4)}_{21}$, a r-dimensional semiregular polytope of the Coxeter group $E_r$, discovered by Gosset. In particular, the set of 27-lines on $S_6$ is bijective to the set of vertices of a Gosset polytope $2_{21}$, and Coxeter [6] used the bijection to study the geometry of $2_{21}$. The bijection between the set of vertices in ${(r-4)}_{21}$and the set ${\mathbf{L}}_r$of lines is applied in many different research fields [7]. In particular, the classical approach to the configurations of lines on del Pezzo surfaces can be found in the study of Du Val [8], and recently applications of the configurations of lines via representation theory are studied by Manivel [9].

A ruling $m$with $m^2=0,$ $K_{S_r}·m=-2$in ${\mathcal{S}}_r\left(0\right)={\mathbf{M}}_r$ is a divisor class in $\mathrm{Pic}\left(S_r\right)$ which gives a fibration of $S_r$ over ${\mathbb{P}}^1$. Since a ruling in $S_r$ consists of a sum of two lines, the quadratic relations are related to rulings. Batyrev and Popov [10] conjectured that generators of Cox ring of $S_r$ for $4\le r\le 8$ have quadratic relations. There are several partial results [11,12,13,14,15] to work for the conjecture of Batyrev and Popov which is finally proved in [16,17]. Moreover, the first author [4] showed that rulings in ${\mathbf{M}}_r$ correspond to $(r-1)$-crosspolytopes of the polytope ${(r-4)}_{21}$, and studied more in [5].

An exceptional system $e$with $e^2=1,$ $K_{S_r}·e=-3$in ${\mathcal{S}}_r\left(1\right)={\mathcal{E}}_r$is a divisor class in $\mathrm{Pic}\left(S_r\right)$ whose linear system gives a regular map from $S_r$ to ${\mathbb{P}}^2$. For $S_6$, each linear system with the above conditions contains a twisted cubic curve. In fact, there is a correspondence between exceptional systems in ${\mathcal{S}}_r\left(1\right)$ and $(r-1)$-simplexes of the polytope ${(r-4)}_{21}$ [4]. These divisor classes play an important role in the first author’s works [4,5].

By using the special divisor classes defined above, we can derive more relations on top of the bijection between vertices in ${(r-4)}_{21}$and lines in $\mathrm{Pic}\left(S_r\right)$. In [4], the first author showed that the convex hull of ${\mathbf{L}}_r$in $\mathrm{Pic}\left(S_r\right)$ is the Gosset polytope ${(r-4)}_{21}$ and extends the bijection to correspondences between special divisor classes ($resp$. skew m-lines $1\le m\le r$, rulings, and exceptional systems) in $\mathrm{Pic}\left(S_r\right)$ and faces ($resp$. $(m-1)$-simplexes $1\le m\le r$, crosspolytope facets, and $(r-1)$-simplex facets) in ${(r-4)}_{21}$. Moreover, in [5] the configurations of lines are studied according to the combinatorial data of the polytope ${(r-4)}_{21}$ along the above correspondences between basic divisor classes and faces in the Gosset polytopes.

As an extension of the studies of special divisor classes on a del Pezzo surface, we consider the blow-ups of Hirzebruch surfaces. Let ${\mathbf{F}}_p$ be a Hirzebruch surface ${\mathbb{P}}_{{\mathbb{P}}^1}({\mathcal{O}}_{{\mathbb{P}}^1}\oplus {\mathcal{O}}_{{\mathbb{P}}^1}\left(p\right)),p\ge 0$ which is a rational ruled surface considered as a ${\mathbb{P}}^1$-fibration over ${\mathbb{P}}^1$ containing a special section, which is a $(-p)$-curve. The Hirzebruch surfaces have only one ruling except for ${\mathbf{F}}_0=$ ${\mathbb{P}}^1\times {\mathbb{P}}^1$. For $p\ne 1$, a Hirzebruch surface ${\mathbf{F}}_p$is a relatively minimal rational surface which is not the projective plane ${\mathbb{P}}^2$. In particular, ${\mathbf{F}}_1$is a blow-up of the projective plane ${\mathbb{P}}^2$ at one point. As a del Pezzo surface is a blown-up surface of ${\mathbb{P}}^2$, we consider rational surfaces ${\mathbf{F}}_{p,r}$ given by blowing up of Hirzebruch surfaces ${\mathbf{F}}_p$ at r points in general position according to the study on del Pezzo surfaces.

Definition 1

([18], Definition 2.1). Distinct points $p_1,p_2,\dots ,p_r$ on ${\mathbf{F}}_p$ are in general position if a point $p_j$ for each $j=1,2,\dots ,r$ is not in the special section on ${\mathbf{F}}_p$ for $p\ne 0$ and there are no two points $p_{j_1},p_{j_2}$ for $j_1\ne j_2\in \{1,2,\dots ,r\}$ in a same fiber of a ${\mathbb{P}}^1$-fibration over ${\mathbb{P}}^1$.

For $p=0$, ${\mathbf{F}}_{0,r}$ with $r\ge 1$ is considered as a blown-up $S_{r+1}$of a projective plane ${\mathbb{P}}^2$ at $r+1$ points in general position. We define ${\mathbf{F}}_{0,0}={\mathbf{F}}_0$ as ${\mathbb{P}}^1\times {\mathbb{P}}^1$. For $p=1$, ${\mathbf{F}}_{1,r}$ with $r\ge 0$ is also a blown-up $S_{r+1}$. When $p\ne 1$, a blown-up Hirzebruch surface ${\mathbf{F}}_{p,r}$ has a relative minimal rational surface ${\mathbf{F}}_p$.

As a positivity condition of a del Pezzo surface came from an ampleness of the anticanonical divisor class, we need a positive self intersection number of the canonical divisor class on a surface ${\mathbf{F}}_{p,r}$ (i.e., $K_{{\mathbf{F}}_{p,r}}^2>0$). The positivity of $K_{{\mathbf{F}}_{p,r}}^2$ implies that the intersection matrix of the orthogonal complement of $K_{{\mathbf{F}}_{p,r}}$ is negative definite by Hodge index theorem.

As our approach to a blow-up of a Hirzebruch surface is relatively new, in Section 2.1 we discuss about non-negative dimensions of linear systems of some divisor classes D in the Picard group of a blown-up Hirzebruch surface ${\mathbf{F}}_{p,r}$ such that $D^2=k$, $K_{{\mathbf{F}}_{p,r}}·D=-\left(k+2\right)$ for an integer $k\ge -1$. We obtain a criterion of the effectiveness for the divisor class D as follows.

Theorem 1

(Theorem 2). For integers $0\le r\le 8$, $p\ge 0$ and $k\ge -1$, each divisor class D in $\mathrm{Pic}\left({\mathbf{F}}_{p,r}\right)$ such that $D^2=k$, $K_{{\mathbf{F}}_{p,r}}·D=-k-2$ is effective, and the dimension of the linear system $\left|D\right|$ is greater than or equal to $k+1$.

Then, we extend the results [4] for del Pezzo surfaces to roots, lines, rulings and exceptional systems for blown-up Hirzebruch surfaces. We provide correspondences in [19] that are compatible with the Weyl group $W\left({\mathbf{F}}_{p,r}\right)=E_{r+1}$ between special divisor classes in the Picard group $\mathrm{Pic}\left({\mathbf{F}}_{p,r}\right)$ and subpolytopes of a Gosset polytope ${(r-3)}_{21}$.

In this article, we focus on explaining relations among roots, lines, rulings and exceptional systems on each surface ${\mathbf{F}}_{p,r}$ with respect to monoidal transformations. These relations for roots and lines via monoidal transformations are obtained as straightforward comparisons, but rulings on ${\mathbf{F}}_{p,7}$and exceptional systems on ${\mathbf{F}}_{p,r}$involve nontrivial issues. To resolve these issues, we consider quartic rational divisor classes, skew a-lines and sextic divisor classes. In particular, we show that sextics $D^2=10,D·K_{{\mathbf{F}}_{p,6}}=-6$ on ${\mathbf{F}}_{p,6}$consist of two $E_7$Weyl orbits and use them to understand exceptional systems on ${\mathbf{F}}_{p,6}$ via monoidal transformations.

2. Rational Divisor Classes on Blown-Up Hirzebruch Surfaces

The Picard group of a Hirzebruch surface ${\mathbf{F}}_p$$(p\ge 0)$ is generated by a class f representing a fiber and the class s of the special section of a ${\mathbb{P}}^1$-fibration over ${\mathbb{P}}^1$, namely, $\mathrm{Pic}\left({\mathbf{F}}_p\right)=\mathbb{Z}f⨁\mathbb{Z}s$, where $f^2=0,$ $f·s=1$ and $s^2=-p$. As Hirzebruch surfaces are ruled, all the fibers are isomorphic and numerically equivalent. The canonical divisor class $K_{{\mathbf{F}}_p}$is given as $K_{{\mathbf{F}}_p}\equiv (-p-2)f-2s$. For further detail, see ([3] Chapter III).

In this section, we consider rational surfaces ${\mathbf{F}}_{p,r}$ obtained by the blow-up of ${\mathbf{F}}_p$ at r points in general position. Then ${\mathbf{F}}_{p,r}$ has a natural fibration ${\varphi }_p:{\mathbf{F}}_{p,r}⟶{\mathbb{P}}^1$ and its general fiber is $f\in \mathrm{Pic}\left({\mathbf{F}}_{p,r}\right)$. We consider a rational divisor class $D\in {\mathcal{S}}_{p,r}\left(k\right)$ as an element of

$$\mathrm{Pic}\left({\mathbf{F}}_{p,r}\right)=\mathbb{Z}f\oplus \mathbb{Z}s\oplus \mathbb{Z}{e}_1\oplus \cdots \oplus \mathbb{Z}{e}_r,$$

namely, $D\equiv af+bs+{\sum }_{i=1}^r{x}_i{e}_i$ for some $a,b$ and $x_i\in \mathbb{Z}$, where $e_i$ is the i-th exceptional divisor class on ${\mathbf{F}}_{p,r}$.

We define rational divisor classes on ${\mathbf{F}}_{p,r}$.

Definition 2.

For $k\in \mathbb{Z}$, the ${\mathcal{S}}_{p,r}\left(k\right)$ is a set of rational divisor classes on ${\mathbf{F}}_{p,r}$ with self intersection number $k$defined as

$${\mathcal{S}}_{p,r}\left(k\right):=\left\{D\in \mathrm{Pic}\left({\mathbf{F}}_{p,r}\right)\left|D^2=k,K_{{\mathbf{F}}_{p,r}}·D=-\left(k+2\right)\right.\right\}.$$

In [19], the authors introduced the following special divisor classes (roots, lines, rulings, and exceptional systems) on ${\mathbf{F}}_{p,r}$as an extension of study on special divisor classes on del Pezzo surfaces. It was naturally obtained that the parallel study on ${\mathbf{F}}_{p,r}$to the one on correspondences between special divisor classes on del Pezzo surfaces and subpolytopes of Gosset polytopes.

$$\begin{array}{cc}\hfill {\mathbf{R}}_{p,r}& :={\mathcal{S}}_{p,r}(-2)=\left\{d\in \mathrm{Pic}\left({\mathbf{F}}_{p,r}\right)\left|d^2=-2,d·K_{{\mathbf{F}}_{p,r}}=0\right.\right\}\left(\mathrm{roots}\right),\hfill \\ \hfill {\mathbf{L}}_{p,r}& :={\mathcal{S}}_{p,r}(-1)=\left\{l\in \mathrm{Pic}\left({\mathbf{F}}_{p,r}\right)\left|l^2=l·K_{{\mathbf{F}}_{p,r}}=-1\right.\right\}\left(\mathrm{lines}\right),\hfill \\ \hfill {\mathbf{M}}_{p,r}& :={\mathcal{S}}_{p,r}\left(0\right)=\left\{m\in \mathrm{Pic}\left({\mathbf{F}}_{p,r}\right)\left|m^2=0,m·K_{{\mathbf{F}}_{p,r}}=-2\right.\right\}\left(\mathrm{rulings}\right),\hfill \\ \hfill {\mathcal{E}}_{p,r}& :={\mathcal{S}}_{p,r}\left(1\right)=\left\{e\in \mathrm{Pic}\left({\mathbf{F}}_{p,r}\right)\left|e^2=1,e·K_{{\mathbf{F}}_{p,r}}=-3\right.\right\}(\mathrm{exceptional}\mathrm{systems}).\hfill \end{array}$$

We also add one more rational divisor classes to our attention.

$${\mathcal{Q}}_{p,r}:={\mathcal{S}}_{p,r}\left(2\right)=\left\{q\in \mathrm{Pic}\left({\mathbf{F}}_{p,r}\right)\left|q^2=2,q·K_{{\mathbf{F}}_{p,r}}=-4\right.\right\}(\mathrm{quartic}\mathrm{rational}).$$

When we fix a fibration ${\varphi }_p:{\mathbf{F}}_{p,r}⟶{\mathbb{P}}^1$ and its general fiber $f\in \mathrm{Pic}\left({\mathbf{F}}_{p,r}\right)$, for each subset $\mathbf{B}$ of $\mathrm{Pic}\left({\mathbf{F}}_{p,r}\right)$, we define ${\mathbf{B}}^0$and ${\mathbf{B}}^{+}$ by

$$\begin{array}{c}{\mathbf{B}}^0:=\mathbf{B}\cap \left\{D\in \mathrm{Pic}\left({\mathbf{F}}_{p,r}\right)\left|D·f=0\right.\right\}\mathrm{and}\hfill \\ {\mathbf{B}}^{+}:=\mathbf{B}\cap \left\{D\in \mathrm{Pic}\left({\mathbf{F}}_{p,r}\right)\left|D·f\ne 0\right.\right\}.\hfill \end{array}$$

Note that we often omit the subscript $p,r$ (e.g., denote ${\mathbf{F}}_{p,r}$ as $\mathbf{F}$) if there is no confusion.

2.1. Linear Systems of Special Divisor Classes

For $0\le r\le 8$ and $p\ge 0$, if $k\ge -1$ then we verify that there is a linearly equivalent effective divisor class for each rational divisor class $D\equiv af+bs+{\sum }_{i=1}^r{x}_i{e}_i\in {\mathcal{S}}_{p,r}\left(k\right)$.

Lemma 1.

When $1\le r\le 8$ and $p\ge 0$, each rational divisor class $af+bs+{\sum }_{i=1}^r{x}_i{e}_i$ in ${\mathcal{S}}_{p,r}\left(k\right),$ $k\ge -1,$satisfies a, $b\in {\mathbb{Z}}^{+}(=\mathbb{N}\cup \left\{0\right\})$. Moreover, a is positive if $1\le r\le 7$, $k\ge 0$, $p\ge 1$, and b is positive if $k>0$.

Proof. 

From $D^2=k$ and $D·K_{\mathbf{F}}=(af+bs+{\sum }_{i=1}^r{x}_i{e}_i)((-2-p)f-2s+{\sum }_{i=1}^r{e}_i)=-k-2$, we induce

$$p{b}^2+\sum _{i=1}^r{x}_i^2=2ab-k\mathrm{and}(-2+p)b-\sum _{i=1}^r{x}_i+k+2=2a.$$

(1)

By combining these equations, we have

$$\frac{1}{4}(r-8)b^2+(k+2)b-k=\sum _{i=1}^r{\left(x_i+\frac{b}{2}\right)}^2\ge 0.$$

(2)

When $1\le r\le 7$ and $k\ge -1$, we get $b>-1$. Moreover, if $k>0$, then $b>0$. When $r=8$and $k\ge -1$, we also obtain $b\ge 0$because $(k+2)b\ge k$ and there is no $D$with $b=-1$and $k=-1$.

We consider the following cases to conclude $a\ge 0$. (i) If $k\ge 0$, $p\ge 0$ and $b>0$, then $a\ge 0$by Equation (1). (ii) If $k\ge 0$, $p\ge 0$and $b=0$, then there is the only divisor class $D=f$in ${\mathcal{S}}_{p,r}\left(0\right)$so that $a=0$. (iii) If $k=-1$, $p\ge 0$and $b>0$, then $a\ge 0$since Equation (1) implies $2ab\ge -1$. (iv) If $k=-1$, $p\ge 0$and $b=0$, then there are the divisor classes $e_i$, $f-e_i$ for some $i\in \{1,\dots ,r\}$so that $a\ge 0$.

One can easily obtain a is positive if $k\ge 0$ and $p\ge 1$in (i). □

Remark 1.

When $r=0$ and $p\ge 0$, we also obtain $a\ge 0$ and $b\ge 0$ for $k\ge -1$.

Remark 2.

For $1\le r\le 7$, $k\ge -1$ and $p\ge 0,$ the number of elements of ${\mathcal{S}}_{p,r}\left(k\right)$ is finite by (2) in Lemma 1.

Now, we consider the effectiveness of rational divisor classes in ${\mathcal{S}}_{p,r}\left(k\right)$ when $0\le r\le 8$, $p\ge 0$ and $k\ge -1$ as follows.

Theorem 2.

For integers $0\le r\le 8$, $p\ge 0$ and $k\ge -1$, each rational divisor class $D\in {\mathcal{S}}_{p,r}\left(k\right)$ is effective and the dimension of the corresponding linear system $\left|D\right|$ is greater than or equal to $k+1$.

Proof. 

When $1\le r\le 8$ we have

$$\begin{array}{cc}\hfill H^2\left(\mathbf{F},{\mathcal{O}}_{\mathbf{F}}\left(D\right)\right)& =H^0\left(\mathbf{F},{\mathcal{O}}_{\mathbf{F}}\left(K_{\mathbf{F}}-D\right)\right)\hfill \\ \hfill & \subset H^0\left(\mathbf{F},{\mathcal{O}}_{\mathbf{F}}\left(K_{\mathbf{F}}-\sum _{i\in I_{-}}{x}_i{e}_i\right)\right)\hfill \end{array}$$

for $D\equiv af+bs+{\sum }_{i=1}^r{x}_i{e}_i$ by Lemma 1, where $I_{-}$ is the set of i such that $x_i<0$ for $1\le i\le r$.

We assume that $x_i<0$ for some i and consider

$$0⟶{\mathcal{O}}_{\mathbf{F}}\left(K_{\mathbf{F}}\right)⟶{\mathcal{O}}_{\mathbf{F}}\left(K_{\mathbf{F}}-\sum _{i\in I_{-}}{x}_i{e}_i\right)⟶{\left.{\mathcal{O}}_{\mathbf{F}}\left(K_{\mathbf{F}}-\sum _{i\in I_{-}}{x}_i{e}_i\right)\right|}_{-{\sum }_{i\in I_{-}}{x}_i{e}_i}⟶0$$

to get

$$\begin{array}{cc}\hfill & H^0\left(\mathbf{F},{\mathcal{O}}_{\mathbf{F}}\left(K_{\mathbf{F}}-\sum _{i\in I_{-}}{x}_i{e}_i\right)\right)\hfill \\ \hfill & =H^0\left(-\sum _{i\in I_{-}}{x}_i{e}_i,{\left.{\mathcal{O}}_{\mathbf{F}}\left(K_{\mathbf{F}}-\sum _{i\in I_{-}}{x}_i{e}_i\right)\right|}_{-{\sum }_{i\in I_{-}}{x}_i{e}_i}\right)=0.\hfill \end{array}$$

Here the first equality is obtained from

$$h^0\left(\mathbf{F},{\mathcal{O}}_{\mathbf{F}}\left(K_{\mathbf{F}}\right)\right)=h^1\left(\mathbf{F},{\mathcal{O}}_{\mathbf{F}}\left(K_{\mathbf{F}}\right)\right)=0$$

which is given by the fact $\mathbf{F}$ is birational to a Hirzebruch surface, and the second equality is deduced from

$$\begin{array}{cc}\hfill & H^0\left(-\sum _{i\in I_{-}}{x}_i{e}_i,{\left.{\mathcal{O}}_{\mathbf{F}}\left(K_{\mathbf{F}}-\sum _{i\in I_{-}}{x}_i{e}_i\right)\right|}_{-{\sum }_{i\in I_{-}}{x}_i{e}_i}\right)\hfill \\ \hfill & =\underset{i\in I_{-}}{⨁}{H}^0\left(-x_i{e}_i,{\left.{\mathcal{O}}_{\mathbf{F}}\left(K_{\mathbf{F}}-\sum _{i\in I_{-}}{x}_i{e}_i\right)\right|}_{-x_i{e}_i}\right)=0\hfill \end{array}$$

since $x_i(1-x_i)<0$ for all $i\in I_{-}$. Therefore, we obtain

$$H^2\left(\mathbf{F},{\mathcal{O}}_{\mathbf{F}}\left(D\right)\right)=0,$$

and moreover,

$$h^0\left(\mathbf{F},{\mathcal{O}}_{\mathbf{F}}\left(D\right)\right)-h^1\left(\mathbf{F},{\mathcal{O}}_{\mathbf{F}}\left(D\right)\right)=\chi \left({\mathcal{O}}_{\mathbf{F}}\left(D\right)\right)=\chi \left({\mathcal{O}}_{\mathbf{F}}\right)+\frac{1}{2}\left(D^2-K_{\mathbf{F}}·D\right)=k+2.$$

It implies $h^0\left(\mathbf{F},{\mathcal{O}}_{\mathbf{F}}\left(D\right)\right)\ge k+2.$ When $r=0$, we obtain $u\equiv af+bs$ with $a\ge 0$ and $b\ge 0$ by Remark 1 if it exists. Hence each special divisor class $u\in {\mathcal{S}}_{p,r}\left(k\right)$ for $0\le r\le 8$, $p\ge 0$ and $k\ge -1$ is effective. □

Remark 3.

Lahyane showed in ([20] Lemma 2.2) that every line is effective on a smooth rational surface such that the anticanonical divisor class $-K$ is nef. It implies an effectiveness of a line in ${\mathbf{L}}_{p,r}$ for $p=0,1,2$ with $r=0,1,\dots ,7$ under Jiang’s stronger definition, ([21] Remark 7.1), than Definition 1. Because Jiang [21] provided under the definition, ([21] Remark 7.1), that $-K_{{\mathbf{F}}_{p,r}}$ is nef for $0\le r\le 7$ in Example 7.1 when $p=0,1$, and in Theorem 7.2 when $p=2$.

Lahyane and Harbourne gave an effectiveness criterion for a line on a smooth rational surface with $K^2\ge 0$ in ([22] Lemma 3.2). Their result contains the effectiveness of lines in ${\mathbf{L}}_{p,r}$ for $0\le r\le 8$ which is a part of Theorem 2.

3. Positivity Condition of the Canonical Divisor Classes

In this section we extend the study on special divisor classes on del Pezzo surfaces in [4,5] to analogous ones of blown-up Hirzebruch surfaces. Corresponding issues on special divisor classes on Hirzebruch surfaces via Weyl action to related divisors on del Pezzo surfaces are explained in [19].

From now on, we focus on the blow-up ${\mathbf{F}}_{p,r}$ of a Hirzebruch surface ${\mathbf{F}}_p$ at r points in general position only for $r=1,2,\dots ,7$, so that we have the positivity condition,

$$K_{{\mathbf{F}}_{p,r}}^2=8-r>0.$$

Due to this condition, the intersection matrix of the orthogonal complement of $K_{{\mathbf{F}}_{p,r}}$ in $\mathrm{Pic}\left({\mathbf{F}}_{p,r}\right)$ is negative definite by Hodge index theorem.

The Picard group $\mathrm{Pic}\left({\mathbf{F}}_{p,r}\right)$ is generated by a general fiber f and the special p-section s (i.e., $(-p)$-curve) of a fibration over ${\mathbb{P}}^1$, and r exceptional curves $e_i$, $i=1,2,\dots ,r$ on ${\mathbf{F}}_{p,r}$ over ${\mathbf{F}}_p$. As we know from Remark 2, each of ${\mathbf{R}}_{p,r}$, ${\mathbf{L}}_{p,r}$, ${\mathbf{M}}_{p,r}$, ${\mathcal{E}}_{p,r}$and ${\mathcal{Q}}_{p,r}$ has a finite number of elements. As Lemma 1, by solving the corresponding systems of integer equations

$$k=D^2=2ab-b^{2}p-\sum _{i=1}^r{x}_i^2,k+2=-K_{{\mathbf{F}}_{p,r}}·D=\left(2-p\right)b+2a+\sum _{i=1}^r{x}_i$$

for $k=-2,-1,0,1,2$, we obtain the following tables. We also apply the similar procedure to ${\mathbf{R}}_{p,r}^0$, ${\mathbf{L}}_{p,r}^0$, ${\mathbf{M}}_{p,r}^0$,${\mathcal{E}}_{p,r}^0$and ${\mathcal{Q}}_{p,r}^0$.

Remark 4.

The numerical data in the Table 1 and Table 2 are independent of p because each of them presents the cardinal of the orbit(s) given by Weyl group whose nature is determined by $r$in Section 3.2.

Table 1. Numbers of elements of ${\mathbf{R}}_{p,r},{\mathbf{L}}_{p,r},{\mathbf{M}}_{p,r},{\mathcal{E}}_{p,r},{\mathcal{Q}}_{p,r}$.

r	1	2	3	4	5	6	7
${\mathbf{R}}_{p,r}$	2	8	20	40	72	126	240
${\mathbf{L}}_{p,r}$	3	6	10	16	27	56	240
${\mathbf{M}}_{p,r}$	2	3	5	10	27	126	2160
${\mathcal{E}}_{p,r}$	1	2	5	16	72	576	$17,520$
${\mathcal{Q}}_{p,r}$	1	3	10	40	216	2072	$82,560$

Table 2. Numbers of elements of ${\mathbf{R}}_{p,r}^0,{\mathbf{L}}_{p,r}^0,{\mathbf{M}}_{p,r}^0,{\mathcal{E}}_{p,r}^0,{\mathcal{Q}}_{p,r}^0$.

r	1	2	3	4	5	6	7
${\mathbf{R}}_{p,r}^0$	0	4	12	24	40	60	84
${\mathbf{L}}_{p,r}^0$	2	4	6	8	10	12	14
${\mathbf{M}}_{p,r}^0$	1	1	1	1	1	1	1
${\mathcal{E}}_{p,r}^0$	0	0	0	0	0	0	0
${\mathcal{Q}}_{p,r}^0$	0	0	0	0	0	0	0

3.1. Monoidal Transformations

From Table 1 and Table 2, we derive interesting relationships among ${\mathbf{R}}_{p,r}^{+}$, ${\mathbf{L}}_{p,r}^{+}$, ${\mathbf{M}}_{p,r}^{+}$ and ${\mathcal{E}}_{p,r}^{+}$along with monoidal transformations described in below.

We consider the birational morphism ${\varphi }_h:{\mathbf{F}}_{p+1,r+1}\to {\mathbf{F}}_{p+1,r}$given by the blow-up of a point $x$in ${\mathbf{F}}_{p+1,r}$, which is not in the $(p+1)$-section (i.e., $-(p+1)$-curve), to an exceptional divisor class $e_{r+1}$ on ${\mathbf{F}}_{p+1,r+1}$. Here, we observe that $f-e_{r+1}$is also a line on ${\mathbf{F}}_{p+1,r+1}$satisfying $\left(f-e_{r+1}\right)·e_{r+1}=1$. In fact, for any line l and ruling $f^{\prime }$with $f^{\prime }·l=0$ on a blown-up Hirzebruch surface ${\mathbf{F}}_{p,r}$, $f^{\prime }-l$is also a line satisfying $\left(f^{\prime }-l\right)·l=1$. From this choice of $(-1)$-curve $f-e_{r+1}$, we get another birational morphism ${\varphi }_v:{\mathbf{F}}_{p+1,r+1}\to {\mathbf{F}}_{p,r}$given by blowing down $f-e_{r+1}$. Here, since $\left(f-e_{r+1}\right)·s=f·s=1$, the exceptional curve $f-e_{r+1}$is blown down to a point y in the p-section in ${\mathbf{F}}_{p,r}$. We denote ${\varphi }_h^{*}$and ${\varphi }_v^{*}$ as total transforms induced from ${\varphi }_h$and ${\varphi }_v$respectively.

The above is depicted as the following diagram (Figure 1). This diagram is extended not only infinitely up but also infinitely to the right.

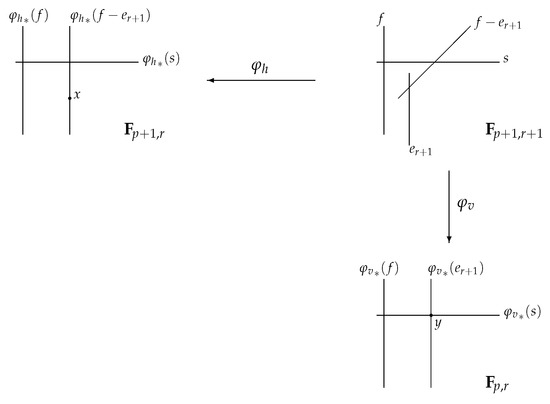
Figure 1. Monoidal transformations.

Moreover, we can make the following diagram (Figure 2) for $p=1,2,3,\dots$ from the above elementary transformation.

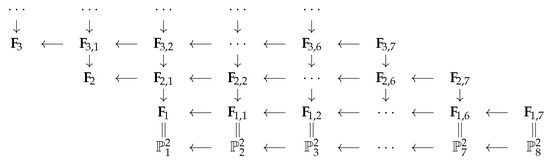
Figure 2. Chain of monoidal transformations.

Here, ${\mathbb{P}}_r^2$ is r-th blow-up of the projective plane ${\mathbb{P}}^2$ at r points in general position.

3.2. Root Systems and Weyl Groups

When $p=1$, since the blown-up Hirzebruch surfaces ${\mathbf{F}}_{1,r}$can be considered as del Pezzo surfaces $S_{r+1}$, the numerical data in Table 1 and Table 2 match with those of del Pezzo surfaces in [4]. Furthermore, as those special divisor classes on the del Pezzo surfaces $S_{r+1}={\mathbf{F}}_{1,r}$ are identified as orbits of Weyl groups given by the root spaces in [4], we can also obtain the parallel results for the special divisor classes on ${\mathbf{F}}_{p,r}$by considering the root system on ${\mathbf{F}}_{p,r}$and the corresponding E-type Weyl group action.

Here, we introduce the simple roots of root systems on ${\mathbf{F}}_{p,r}$so that we can see the corresponding Weyl group is E-type. Further study on ${\mathbf{F}}_{p,r}$ along the Weyl action and corresponding Gosset polytopes was dealt in [19].

Once we have the positivity condition $K_{{\mathbf{F}}_{p,r}}^2>0$, the inner product given by the intersection on $\mathrm{Pic}\left({\mathbf{F}}_{p,r}\right)$induces a negative definite metric on ${\left(\mathbb{Z}{K}_{{\mathbf{F}}_{p,r}}\right)}^{\perp }$ in $\mathrm{Pic}\left({\mathbf{F}}_{p,r}\right)$where each root defines a natural reflection. To define reflections on ${\left(\mathbb{Z}{K}_{{\mathbf{F}}_{p,r}}\right)}^{\perp }$ in $\mathrm{Pic}\left({\mathbf{F}}_{p,r}\right)$, we consider a root system

$${\mathbf{R}}_{p,r}=\{d\in \mathrm{Pic}\left({\mathbf{F}}_{p,r}\right)\mid d^2=-2,d·K_{{\mathbf{F}}_{p,r}}=0\},$$

with simple roots

$$\begin{array}{cc}\hfill & \left\{\begin{array}{c}{d}_0=e_1-e_2\hfill \\ d_1=\frac{p-2}{2}f+s\hfill \\ d_2=f-e_1-e_2\hfill \\ d_i=e_{i-1}-e_i,3\le i\le r\hfill \\ (\mathrm{Note}\mathrm{that}\mathrm{we}\mathrm{have}\mathrm{only}{d}_0,d_1,d_2\mathrm{when}r=2)\hfill \end{array}\right.\mathrm{if}p\mathrm{is}\mathrm{even},\hfill \\ \hfill & \left\{\begin{array}{c}{d}_0=f-e_1-e_2\hfill \\ d_1=\frac{p-1}{2}f+s-e_1\hfill \\ d_i=e_{i-1}-e_i,2\le i\le r\hfill \end{array}\right.\mathrm{if}p\mathrm{is}\mathrm{odd}\hfill \end{array}$$

corresponding to Coxeter–Dynkin diagram of type $E_{r+1},r\ge 2$ (Figure 3).

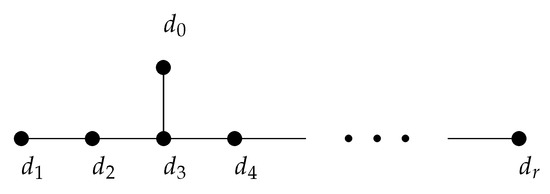
Figure 3. Coxeter–Dynkin diagram of type $E_{r+1},r\ge 2$.

Since each element d in ${\mathbf{R}}_{p,r}$ defines a reflection ${\sigma }_d$ on ${\left(\mathbb{Z}{K}_{{\mathbf{F}}_{p,r}}\right)}^{\perp }$ in $\mathrm{Pic}\left({\mathbf{F}}_{p,r}\right)$,

$${\sigma }_d\left(D\right):=D+\left(D·d\right)d\mathrm{for}D\in {\left(\mathbb{Z}{K}_{{\mathbf{F}}_{p,r}}\right)}^{\perp },$$

the corresponding Weyl group $W\left({\mathbf{F}}_{p,r}\right)$ is $E_{r+1}$ where $2\le r\le 7$. If we add the orthogonality condition to f, then the corresponding Weyl group will be $D_{r-1}$-type, where each root system is determined by $d_1·f=1$and $d_i·f=0$. The similar consideration for del Pezzo surfaces can be found in [18,23,24] with an orthogonality condition to the fixed fiber class.

4. Special Divisor Classes and Monoidal Transformations

In this section we deal with a relation among rulings, exceptional systems and quartic rational divisor classes on ${\mathbf{F}}_{p,r}$ via monoidal transformations. We require the positivity condition of

$$K_{{\mathbf{F}}_{p,r}}^2=8-r,$$

and so r is to be an integer $1,2,\dots ,6$ or 7.

To characterize special divisor classes $D$via monoidal transformations, we consider the intersection between a line and $D$since the birational maps ${\varphi }_h$and ${\varphi }_v$are defined by the choices of $(-1)$-curves contained in special divisor classes lines. Then, we identify the subset of special divisor classes with a fixed intersection by other special divisor classes or certain rational divisor classes. For roots and lines, the tie-ups of special divisors with others are obtained by straightforward comparisons via monoidal transformations. We need to resolve nontrivial issues involved for rulings and the exceptional systems on ${\mathbf{F}}_{p,7}$. For rulings on ${\mathbf{F}}_{p,7}$, we use skew a-lines which are given by $l_1+\dots +l_a$where $l_1,\dots ,l_a$are disjoint lines. For the exceptional systems, we consider sextic divisor classes on ${\mathbf{F}}_{p,6}$and their orbit structures induced by $E_7$Weyl group. Then the rational quartic divisor classes appear to characterize the exceptional systems via monoidal transformations.

We note that ${\mathbf{M}}_{p,r}={\mathbf{M}}_{p,r}^{+}\dot{\cup }\left\{f\right\}$, and we remark that ${\mathcal{E}}_{p,r}={\mathcal{E}}_{p,r}^{+}$ (resp. ${\mathcal{Q}}_{p,r}={\mathcal{Q}}_{p,r}^{+}$) because each exceptional system e (resp. quartic rational divisor class q) satisfies $f·e>0$ (resp. $f·q>0$) by Lemma 1. Thus, it is rather natural for us to consider ${\mathbf{M}}_{p,r}$, ${\mathcal{E}}_{p,r}$ and ${\mathcal{Q}}_{p,r}$ instead of ${\mathbf{M}}_{p,r}^{+}$, ${\mathcal{E}}_{p,r}^{+}$ and ${\mathcal{Q}}_{p,r}^{+}$.

4.1. Lines and Monoidal Transformations

4.1.1. Intersection between Lines

For any two lines $l$and $l^{\prime }$on ${\mathbf{F}}_{p,r}$, by Hodge index theorem and $K_{{\mathbf{F}}_{p,r}}^2>0$, we have

$$K_{{\mathbf{F}}_{p,r}}^2{\left(l\pm l^{\prime }\right)}^2\le {\left(K_{{\mathbf{F}}_{p,r}}·l\pm K_{{\mathbf{F}}_{p,r}}·l^{\prime }\right)}^2$$

and we obtain

$$-1\le l·l^{\prime }\le \frac{2}{8-r}+1.$$

Therefore, the possible intersection numbers between lines are given as

$$l·l^{\prime }=\left\{\begin{array}{c}-1,0,1\mathrm{for}r\le 5\\ -1,0,1,2\mathrm{for}r=6\\ -1,0,1,2,3\mathrm{for}r=7\end{array}\right..$$

4.1.2. Lines via Monoidal Transformations

According to the list of intersections of lines, we describe ${\mathbf{L}}_{p+1,r+1}^{+}$.

Theorem 3.

For $0\le r\le 6$,

$$\begin{array}{cc}\hfill {\mathbf{L}}_{p+1,r+1}^{+}& ={\varphi }_h^{*}\left({\mathbf{L}}_{p+1,r}^{+}\right)\dot{\cup }\left({\varphi }_h^{*}\left({\mathbf{M}}_{p+1,r}^{+}\right)-e_{r+1}\right)\dot{\cup }{H}_{p+1,r+1}\hfill \\ \hfill & ={\varphi }_v^{*}\left({\mathbf{L}}_{p,r}^{+}\right)\dot{\cup }\left({\varphi }_v^{*}\left({\mathbf{M}}_{p,r}^{+}\right)-(f-e_{r+1})\right)\dot{\cup }{V}_{p+1,r+1},\hfill \end{array}$$

where

$$\left\{\begin{array}{c}{H}_{p+1,r+1}=V_{p+1,r+1}=\varnothing \mathrm{for}r\le 4,\hfill \\ H_{p+1,6}=\left\{-K_{{\mathbf{F}}_{p+1,6}}-e_6\right\},V_{p+1,6}=\left\{-K_{{\mathbf{F}}_{p+1,6}}-f+e_6\right\},\hfill \\ H_{p+1,7}=\left\{{\varphi }_h^{*}(\tilde{l}-K_{{\mathbf{F}}_{p+1,6}})-2e_7\left|\tilde{l}\in {\mathbf{L}}_{p+1,6}\right.\right\}\dot{\cup }\left\{-2K_{{\mathbf{F}}_{p+1,7}}-e_7\right\},\hfill \\ V_{p+1,7}=\left\{{\varphi }_v^{*}\left(\tilde{l}-K_{{\mathbf{F}}_{p,6}}\right)-2(f-e_7)\left|\tilde{l}\in {\mathbf{L}}_{p,6}\right.\right\}\dot{\cup }\left\{-2K_{{\mathbf{F}}_{p+1,7}}-f+e_7\right\}.\hfill \end{array}\right.$$

Proof. 

We consider the map ${\varphi }_v$ induced by a line $f-e_{r+1}$.

For each line $l$in the set ${\mathbf{L}}_{p+1,r+1}^{+}$on ${\mathbf{F}}_{p+1,r+1}$, we consider the following cases according to the intersection $l·(f-e_{r+1})$.

(Case 1) $l·(f-e_{r+1})=0$ for $r\le 6$

Such $l$corresponds to a line ${{\varphi }_v}_{*}\left(l\right)$on ${\mathbf{F}}_{p,r}$with ${{\varphi }_v}_{*}\left(l\right)·{{\varphi }_v}_{*}\left(f\right)=l·f\ne 0$. Thus we have

$$\left\{l\in {\mathbf{L}}_{p+1,r+1}^{+}\left|l·(f-e_{r+1})=0\right.\right\}={\varphi }_v^{*}\left({\mathbf{L}}_{p,r}^{+}\right).$$

(Case 2) $l·(f-e_{r+1})=1$ for $r\le 6$

Such $l$can be written as ${\varphi }_v^{*}\left(D\right)-(f-e_{r+1})$with a divisor class $D$on ${\mathbf{F}}_{p,r}$ satisfying

$$\begin{array}{cc}\hfill D^2& ={\varphi }_v^{*}{\left(D\right)}^2={(l+f-e_{r+1})}^2=0,\hfill \\ \hfill D·K_{{\mathbf{F}}_{p,r}}& ={\varphi }_v^{*}\left(D\right)·{\varphi }_v^{*}\left(K_{{\mathbf{F}}_{p,r}}\right)\hfill \\ \hfill & =(l+f-e_{r+1})·\left(K_{{\mathbf{F}}_{p+1,r+1}}-f+e_{r+1}\right)=-2.\hfill \end{array}$$

Thus $D$is a ruling on ${\mathbf{F}}_{p,r}$with $D·{{\varphi }_v}_{*}\left(f\right)={\varphi }_v^{*}\left(D\right)·f=(l+f-e_{r+1})·f=l·f\ne 0$ and

$$\left\{l\in {\mathbf{L}}_{p+1,r+1}^{+}\left|l·(f-e_{r+1})=1\right.\right\}={\varphi }_v^{*}\left({\mathbf{M}}_{p,r}^{+}\right)-(f-e_{r+1}).$$

(Case 3) $l·(f-e_{r+1})=2$ for $r=5,6$

Such $l$can be written as ${\varphi }_v^{*}\left(D\right)-2(f-e_{r+1})$with $D$satisfying

$$\begin{array}{cc}\hfill D^2& ={\varphi }_v^{*}{\left(D\right)}^2={(l+2f-2e_{r+1})}^2=3,\hfill \\ \hfill D·K_{{\mathbf{F}}_{p,r}}& ={\varphi }_v^{*}\left(D\right)·{\varphi }_v^{*}\left(K_{{\mathbf{F}}_{p,r}}\right)\hfill \\ \hfill & =(l+2f-2e_{r+1})·\left(K_{{\mathbf{F}}_{p+1,r+1}}-f+e_{r+1}\right)=-3.\hfill \end{array}$$

Moreover, $D·{{\varphi }_v}_{*}\left(f\right)={\varphi }_v^{*}\left(D\right)·f=(l+2f-2e_{r+1})·f=l·f\ne 0$.

When $r=5$, $-K_{{\mathbf{F}}_{p,5}}$is the only divisor class on ${\mathbf{F}}_{p,5}$satisfying the above conditions. Thus

$$\begin{array}{cc}\hfill \left\{l\in {\mathbf{L}}_{p+1,6}^{+}\left|l·(f-e_6)=2\right.\right\}& =\left\{{\varphi }_v^{*}(-K_{{\mathbf{F}}_{p,5}})-2(f-e_6)\right\}\hfill \\ \hfill & =\left\{-K_{{\mathbf{F}}_{p+1,6}}-f+e_6\right\}=V_{p+1,6}.\hfill \end{array}$$

When $r=6$, such $D$corresponds to a line $\tilde{l}$ on ${\mathbf{F}}_{p,6}$ via $D\equiv$$\tilde{l}-K_{{\mathbf{F}}_{p,6}}$. Therefore

$$\left\{l\in {\mathbf{L}}_{p+1,7}^{+}\left|l·(f-e_7)=2\right.\right\}=\left\{{\varphi }_v^{*}\left(\tilde{l}-K_{{\mathbf{F}}_{p,6}}\right)-2(f-e_7)\left|\tilde{l}\in {\mathbf{L}}_{p,6}\right.\right\}.$$

(Case 4) $l·(f-e_{r+1})=3$ for $r=6$

Such $l$can be written as ${\varphi }_v^{*}\left(D\right)-3(f-e_7)$with $D$satisfying

$$\begin{array}{cc}\hfill D^2& ={\varphi }_v^{*}{\left(D\right)}^2={(l+3f-3e_7)}^2=8,\hfill \\ \hfill D·K_{{\mathbf{F}}_{p,6}}& ={\varphi }_v^{*}\left(D\right)·{\varphi }_v^{*}\left(K_{{\mathbf{F}}_{p,6}}\right)\hfill \\ \hfill & =(l+3f-3e_7)·\left(K_{{\mathbf{F}}_{p+1,7}}-f+e_7\right)=-4.\hfill \end{array}$$

Moreover, $D·{{\varphi }_v}_{*}\left(f\right)={\varphi }_v^{*}\left(D\right)·f=(l+3f-3e_7)·f=l·f\ne 0$.

In fact, $-2K_{{\mathbf{F}}_{p,6}}$is the only divisor class on ${\mathbf{F}}_{p,6}$with the above conditions. Thus, we have

$$\left\{l\in {\mathbf{L}}_{p+1,7}^{+}\left|l·(f-e_7)=3\right.\right\}=\left\{{\varphi }_v^{*}\left(-2K_{{\mathbf{F}}_{p,6}}\right)-3(f-e_7)\right\}=\left\{-2K_{{\mathbf{F}}_{p+1,7}}-f+e_7\right\},$$

and we conclude

$$V_{p+1,7}=\left\{{\varphi }_v^{*}(\tilde{l}-K_{{\mathbf{F}}_{p,6}})-2(f-e_7)\left|\tilde{l}\in {\mathbf{L}}_{p,6}\right.\right\}\dot{\cup }\left\{-2K_{{\mathbf{F}}_{p+1,7}}-f+e_7\right\}.$$

By applying a similar process for $l·e_{r+1}$, we derive the equality for ${\varphi }_h$and obtain

$$\begin{array}{cc}\hfill H_{p+1,6}& =\left\{-K_{{\mathbf{F}}_{p+1,6}}-e_6\right\},\hfill \\ \hfill H_{p+1,7}& =\left\{{\varphi }_h^{*}(\tilde{l}-K_{{\mathbf{F}}_{p+1,6}})-2e_7\left|\tilde{l}\in {\mathbf{L}}_{p+1,6}\right.\right\}\dot{\cup }\left\{-2K_{{\mathbf{F}}_{p+1,7}}-e_7\right\}.\hfill \end{array}$$

 □

Remark 5.

Comparing Table 1 and Table 2, we get

$$\begin{array}{cc}\hfill 44& =\left|{\mathbf{L}}_{p+1,6}^{+}\right|=\left|{\mathbf{L}}_{p,5}^{+}\right|+\left|{\mathbf{M}}_{p,5}^{+}\right|+\left|V_{p+1,6}\right|=17+26+1,\hfill \\ \hfill 44& =\left|{\mathbf{L}}_{p+1,6}^{+}\right|=\left|{\mathbf{L}}_{p+1,5}^{+}\right|+\left|{\mathbf{M}}_{p+1,5}^{+}\right|+\left|H_{p+1,6}\right|=17+26+1,\hfill \\ \hfill 226& =\left|{\mathbf{L}}_{p+1,7}^{+}\right|=\left|{\mathbf{L}}_{p,6}^{+}\right|+\left|{\mathbf{M}}_{p,6}^{+}\right|+\left|V_{p+1,7}\right|=44+125+57,\hfill \\ \hfill 226& =\left|{\mathbf{L}}_{p+1,7}^{+}\right|=\left|{\mathbf{L}}_{p+1,6}^{+}\right|+\left|{\mathbf{M}}_{p+1,6}^{+}\right|+\left|H_{p+1,7}\right|=44+125+57.\hfill \end{array}$$

4.2. Roots and Monoidal Transformations

4.2.1. Intersection between a Line and a Root

For any two roots $d$and $d^{\prime }$on ${\mathbf{F}}_{p,r}$, by Hodge index theorem and $K_{{\mathbf{F}}_{p,r}}^2>0$, we have

$$K_{{\mathbf{F}}_{p,r}}^2{\left(d\pm d^{\prime }\right)}^2\le {\left(K_{{\mathbf{F}}_{p,r}}·d\pm K_{{\mathbf{F}}_{p,r}}·d^{\prime }\right)}^2=0.$$

Thus we obtain

$$-2\le d·d^{\prime }\le 2.$$

For a line $l$and a root $d$on ${\mathbf{F}}_{p,r}$, we have

$$K_{{\mathbf{F}}_{p,r}}^2{\left(l\pm d\right)}^2\le {(K_{{\mathbf{F}}_{p,r}}·l\pm K_{{\mathbf{F}}_{p,r}}·d)}^2=1$$

and it implies

$$-\frac{1}{2(8-r)}-\frac{3}{2}\le l·d\le \frac{1}{2(8-r)}+\frac{3}{2}.$$

Thus, the possible intersection numbers between lines and roots are given as

$$l·d=\left\{\begin{array}{c}-1,0,1\mathrm{for}r\le 6\\ -2,-1,0,1,2\mathrm{for}r=7\end{array}\right..$$

4.2.2. Roots via Monoidal Transformations I

According to the list of intersections of lines and roots, we describe ${\mathbf{R}}_{p+1,r+1}^{+}$.

Theorem 4.

For $0\le r\le 6$,

$$\begin{array}{cc}\hfill {\mathbf{R}}_{p+1,r+1}^{+}& ={\varphi }_h^{*}\left({\mathbf{R}}_{p+1,r}^{+}\right)\dot{\cup }\left({\varphi }_h^{*}\left({\mathbf{L}}_{p+1,r}^{+}\right)-e_{r+1}\right)\dot{\cup }\left(-{\varphi }_h^{*}\left({\mathbf{L}}_{p+1,r}^{+}\right)+e_{r+1}\right)\dot{\cup }{H}_{p+1,r+1}\hfill \\ \hfill & ={\varphi }_v^{*}\left({\mathbf{R}}_{p,r}^{+}\right)\dot{\cup }\left({\varphi }_v^{*}\left({\mathbf{L}}_{p,r}^{+}\right)-\left(f-e_{r+1}\right)\right)\dot{\cup }\left(-{\varphi }_v^{*}\left({\mathbf{L}}_{p,r}^{+}\right)+\left(f-e_{r+1}\right)\right)\dot{\cup }{V}_{p+1,r+1},\hfill \end{array}$$

where

$$\left\{\begin{array}{c}{H}_{p+1,r+1}=V_{p+1,r+1}=\varnothing forr\le 5,\hfill \\ H_{p+1,7}=\left\{\pm \left(K_{{\mathbf{F}}_{p+1,7}}+e_7\right)\right\},\hfill \\ V_{p+1,7}=\left\{\pm \left(K_{{\mathbf{F}}_{p+1,7}}+f-e_7\right)\right\}.\hfill \end{array}\right.$$

Proof. 

We consider the map ${\varphi }_h$ given by a line $e_{r+1}$.

For each root $d$in the set ${\mathbf{R}}_{p+1,r+1}^{+}$ on ${\mathbf{F}}_{p+1,r+1}$, we consider the following cases according to the intersection $d·e_{r+1}$.

(Case 1) $d·e_{r+1}=0$ for $r\le 6$

Such $d$corresponds to a root ${{\varphi }_h}_{*}\left(d\right)$on ${\mathbf{F}}_{p,r}$with ${{\varphi }_h}_{*}\left(d\right)·{{\varphi }_h}_{*}\left(f\right)=d·f\ne 0$. Thus

$$\left\{d\in {\mathbf{R}}_{p+1,r+1}^{+}\left|d·e_{r+1}=0\right.\right\}={\varphi }_h^{*}\left({\mathbf{R}}_{p+1,r}^{+}\right).$$

(Case 2) $\pm d·e_{r+1}=1$ for $r\le 6$

Such $\pm d$can be written as ${\varphi }_h^{*}\left(D\right)-e_{r+1}$with $D$satisfying

$$\begin{array}{cc}\hfill D^2& ={\varphi }_h^{*}{\left(D\right)}^2={(\pm d+e_{r+1})}^2=-1,\hfill \\ \hfill D·K_{{\mathbf{F}}_{p+1,r}}& ={\varphi }_h^{*}\left(D\right)·{\varphi }_h^{*}\left(K_{{\mathbf{F}}_{p+1,r}}\right)\hfill \\ \hfill & =(\pm d+e_{r+1})·\left(K_{{\mathbf{F}}_{p+1,r+1}}-e_{r+1}\right)=-1.\hfill \end{array}$$

Thus $D$is a line on ${\mathbf{F}}_{p+1,r}$with $D·{{\varphi }_h}_{*}\left(f\right)={\varphi }_h^{*}\left(D\right)·f=(\pm d+e_{r+1})·f=\pm d·f\ne 0$, and so

$$\left\{d\in {\mathbf{R}}_{p+1,r+1}^{+}\left|\pm d·e_{r+1}=1\right.\right\}=\pm \left({\varphi }_h^{*}\left({\mathbf{L}}_{p+1,r}^{+}\right)-e_{r+1}\right).$$

(Case 3) $\pm d·e_{r+1}=2$ for $r=6$

Such $\pm d$can be written as ${\varphi }_h^{*}\left(D\right)-2e_7$with $D$satisfying

$$\begin{array}{cc}\hfill D^2& ={\varphi }_h^{*}{\left(D\right)}^2={(\pm d+2e_7)}^2=2,\hfill \\ \hfill D·K_{{\mathbf{F}}_{p+1,6}}& ={\varphi }_h^{*}\left(D\right)·{\varphi }_h^{*}\left(K_{{\mathbf{F}}_{p+1,6}}\right)\hfill \\ \hfill & =(\pm d+2e_7)·\left(K_{{\mathbf{F}}_{p+1,7}}-e_7\right)=-2.\hfill \end{array}$$

Moreover, $D·{{\varphi }_h}_{*}\left(f\right)={\varphi }_h^{*}\left(D\right)·f=(\pm d+2e_7)·f=\pm d·f\ne 0$. In fact, $-K_{{\mathbf{F}}_{p+1,6}}$is the only possible $D$on ${\mathbf{F}}_{p+1,6}$with the above conditions. Thus $\pm d\equiv {\varphi }_h^{*}\left(-K_{{\mathbf{F}}_{p+1,6}}\right)-2e_7\equiv -K_{{\mathbf{F}}_{p+1,7}}-e_7,$and

$$H_{p+1,7}=\left\{\pm \left(K_{{\mathbf{F}}_{p+1,7}}+e_7\right)\right\}.$$

By applying a similar process for $d·(f-e_{r+1})$, we derive the equality for ${\varphi }_v$and obtain

$$V_{p+1,7}=\left\{\pm \left(K_{{\mathbf{F}}_{p+1,7}}+f-e_7\right)\right\}.$$

 □

Remark 6.

Comparing Table 1 and Table 2, we obtain

$$\begin{array}{cc}\hfill 156& =\left|{\mathbf{R}}_{p+1,7}^{+}\right|=\left|{\mathbf{R}}_{p+1,6}^{+}\right|+2\left|{\mathbf{L}}_{p+1,6}^{+}\right|+\left|H_{p+1,7}\right|=66+88+2,\hfill \\ \hfill 156& =\left|{\mathbf{R}}_{p+1,7}^{+}\right|=\left|{\mathbf{R}}_{p,6}^{+}\right|+2\left|{\mathbf{L}}_{p,6}^{+}\right|+\left|V_{p+1,7}\right|=66+88+2.\hfill \end{array}$$

4.2.3. Roots via Monoidal Transformations II

For a root $d$and a ruling $f^{\prime }$on ${\mathbf{F}}_{p,r}$, we have

$$K_{{\mathbf{F}}_{p,r}}^2{\left(d\pm f^{\prime }\right)}^2\le {(K_{{\mathbf{F}}_{p,r}}·d\pm K_{{\mathbf{F}}_{p,r}}·f^{\prime })}^2=4$$

and it implies

$$-\frac{2}{8-r}-1\le f^{\prime }·d\le \frac{2}{8-r}+1$$

Thus, the possible intersection numbers between rulings and roots are given as

$$f^{\prime }·d=\left\{\begin{array}{c}0,\pm 1\mathrm{for}r\le 5\\ 0,\pm 1,\pm 2\mathrm{for}r=6\\ 0,\pm 1,\pm 2,\pm 3\mathrm{for}r=7\end{array}\right..$$

We observe that a root $d$on ${\mathbf{F}}_{p+1,r+1}$with $d·f\ne 0$cannot satisfy both $d·e_{r+1}=0$and $d·(f-e_{r+1})=0$. Moreover, we obtain another version of Theorem 4 as follows.

Theorem 5.

For $0\le r\le 6$,

$${\mathbf{R}}_{p+1,r+1}^{+}={\varphi }_h^{*}\left({\mathbf{R}}_{p+1,r}^{+}\right)\dot{\cup }{\varphi }_v^{*}\left({\mathbf{R}}_{p,r}^{+}\right)\dot{\cup }{A}_{p+1,r+1},$$

where

$$\left\{\begin{array}{c}{A}_{p+1,r+1}=\varnothing forr\le 4,\hfill \\ A_{p+1,6}=\left\{\pm \left(-K_{{\mathbf{F}}_{p+1,6}}-f\right)\right\},\hfill \\ A_{p+1,7}=\left\{\pm \left({\varphi }_h^{*}\left(l\right)-K_{{\mathbf{F}}_{p+1,7}}-f\right)\left|l\in {\mathbf{L}}_{p+1,6}^0\right.\right\}\hfill \\ =\left\{\pm \left({\varphi }_v^{*}\left(l\right)-K_{{\mathbf{F}}_{p+1,7}}-f\right)\left|l\in {\mathbf{L}}_{p,6}^0\right.\right\}.\hfill \end{array}\right.$$

Proof. 

We consider the following cases according to the intersection numbers $d·e_{r+1}$ for roots $d$in the set ${\mathbf{R}}_{p+1,r+1}^{+}$on ${\mathbf{F}}_{p+1,r+1}$. Note that $d·f\ne 0$.

(Case 1) $d·e_{r+1}=0$(and $d·\left(f-e_{r+1}\right)\ne 0$) for $r\le 6$

Such $d$corresponds to a root ${{\varphi }_h}_{*}\left(d\right)$on ${\mathbf{F}}_{p+1,r}$with ${{\varphi }_h}_{*}\left(d\right)·{{\varphi }_h}_{*}\left(f\right)=d·f\ne 0$. Thus we have

$$\left\{d\in {\mathbf{R}}_{p+1,r+1}^{+}\left|d·e_{r+1}=0,d·\left(f-e_{r+1}\right)\ne 0\right.\right\}={\varphi }_h^{*}\left({\mathbf{R}}_{p+1,r}^{+}\right).$$

(Case 2) $\pm d·e_{r+1}=1$and $d·\left(f-e_{r+1}\right)=0$for $r\le 6$

By applying Theorem 4, as in (Case 1) we get

$$\left\{d\in {\mathbf{R}}_{p+1,r+1}^{+}\left|d·e_{r+1}\ne 0,d·\left(f-e_{r+1}\right)=0\right.\right\}={\varphi }_v^{*}\left({\mathbf{R}}_{p,r}^{+}\right).$$

Moreover, when $r=6$, if $d·e_7=\pm 2$, then $d·\left(f-e_7\right)=\pm \left(K_{{\mathbf{F}}_{p+1,7}}+e_7\right)·\left(f-e_7\right)=0$ by the (Case 3) in the proof of Theorem 4. Therefore, for $r=6$ we also get

$$\left\{d\in {\mathbf{R}}_{p+1,r+1}^{+}\left|d·e_{r+1}\ne 0,d·\left(f-e_{r+1}\right)=0\right.\right\}={\varphi }_v^{*}\left({\mathbf{R}}_{p,r}^{+}\right).$$

(Case 3) $\pm d·e_{r+1}=1$and $\pm d·\left(f-e_{r+1}\right)=1$for $r\le 6$(By Theorem 4, there are no other cases.)

Here,

$$d·f=d·\left(f-e_{r+1}\right)+d·e_{r+1}=\pm 2\mathrm{since}d·f\ne 0.$$

When $r\le 4$, since $\left|d·f\right|\le 1$, $A_{p+1,r+1}=\varnothing$.

When $r=5$or$6$, there are possible cases $(d·e_{r+1},d·\left(f-e_{r+1}\right))=(1,1)$or $(-1,-1)$. For the case $(d·e_{r+1},d·\left(f-e_{r+1}\right))=(1,1)$, the root $d$can be written as ${\varphi }_h^{*}\left(D\right)-f-e_{r+1}$for a divisor class D on ${\mathbf{F}}_{p+1,r}$with ${\varphi }_h^{*}\left(D\right)·\left(f-e_{r+1}\right)=2$. Moreover, $D$satisfies

$$\begin{array}{cc}\hfill D^2& ={\varphi }_h^{*}{\left(D\right)}^2={\left(d+f+e_{r+1}\right)}^2=3,\hfill \\ \hfill D·K_{{\mathbf{F}}_{p+1,r}}& ={\varphi }_h^{*}\left(D\right)·{\varphi }_h^{*}\left(K_{{\mathbf{F}}_{p+1,r}}\right)\hfill \\ \hfill & =\left(d+f+e_{r+1}\right)·\left(K_{{\mathbf{F}}_{p+1,r+1}}-e_{r+1}\right)=-3.\hfill \end{array}$$

If $r=5$, such a divisor class D on ${\mathbf{F}}_{p+1,5}$ must be $-K_{{\mathbf{F}}_{p+1,5}}$. Therefore,

$$d\equiv {\varphi }_h^{*}\left(-K_{{\mathbf{F}}_{p+1,5}}\right)-f-e_6\equiv -K_{{\mathbf{F}}_{p+1,6}}-f.$$

If $r=6$, such a divisor class D on ${\mathbf{F}}_{p+1,6}$ corresponds to a line l on ${\mathbf{F}}_{p+1,6}$via $D\equiv -K_{{\mathbf{F}}_{p+1,6}}+l$satisfying ${\varphi }_h^{*}\left(l\right)·f={\varphi }_h^{*}\left(D+K_{{\mathbf{F}}_{p+1,6}}\right)·f=0$. Thus, we have

$$d\equiv {\varphi }_h^{*}\left(-K_{{\mathbf{F}}_{p+1,6}}+l\right)-f-e_7\equiv {\varphi }_h^{*}\left(l\right)-K_{{\mathbf{F}}_{p+1,7}}-f,$$

where ${\varphi }_h^{*}\left(l\right)$ with $l\in {\mathbf{L}}_{p+1,6}^0$ is a line on ${\mathbf{F}}_{p+1,7}$. By applying a similar procedure to the case $(d·e_{r+1},d·\left(f-e_{r+1}\right))=(-1,-1)$, we conclude

$$A_{p+1,6}=\left\{\pm \left(-K_{{\mathbf{F}}_{p+1,6}}-f\right)\right\}\mathrm{and}{A}_{p+1,7}=\left\{\pm \left({\varphi }_h^{*}\left(l\right)-K_{{\mathbf{F}}_{p+1,7}}-f\right)\left|l\in {\mathbf{L}}_{p+1,6}^0\right.\right\}.$$

Similarly, by applying ${\varphi }_v$ for $A_{p+1,7}$we obtain

$$A_{p+1,7}=\left\{\pm \left({\varphi }_v^{*}\left(l\right)-K_{{\mathbf{F}}_{p+1,7}}-f\right)\left|l\in {\mathbf{L}}_{p,6}^0\right.\right\}.$$

 □

Remark 7.

Comparing Table 1 and Table 2, we have

$$\begin{array}{cc}\hfill 66& =\left|{\mathbf{R}}_{p+1,6}^{+}\right|=\left|{\mathbf{R}}_{p+1,5}^{+}\right|+\left|{\mathbf{R}}_{p,5}^{+}\right|+\left|A_{p+1,6}\right|=32+32+2,\hfill \\ \hfill 156& =\left|{\mathbf{R}}_{p+1,7}^{+}\right|=\left|{\mathbf{R}}_{p+1,6}^{+}\right|+\left|{\mathbf{R}}_{p,6}^{+}\right|+\left|A_{p+1,7}\right|=66+66+24.\hfill \end{array}$$

4.3. Rulings and Monoidal Transformations

4.3.1. Intersection between a Line and a Ruling

For a line $l$and a ruling $m$on ${\mathbf{F}}_{p,r}$, the possible intersection numbers between lines and rulings are given by the following lemma.

Lemma 2.

The possible intersection numbers between lines and rulings are given as

$$l·m=\left\{\begin{array}{c}0,1forr\le 4\\ 0,1,2forr=5,6\\ 0,1,2,3,4forr=7\end{array}\right..$$

(3)

Proof. 

For a line $l$and a ruling $m$on ${\mathbf{F}}_{p,r}$, we have

$$K_{{\mathbf{F}}_{p,r}}^2{\left(l\pm m\right)}^2\le {(K_{{\mathbf{F}}_{p,r}}·l\pm K_{{\mathbf{F}}_{p,r}}·m)}^2$$

and it impiles

$$-\frac{1}{2(8-r)}-\frac{1}{2}\le l·m\le \frac{9}{2(8-r)}+\frac{1}{2}.$$

Thus, the possible intersection numbers between lines and rulings are given as

$$l·m=\left\{\begin{array}{c}0,1\mathrm{for}r\le 4\\ 0,1,2\mathrm{for}r=5,6\\ -1\le l·m\le 5\mathrm{for}r=7\end{array}\right..$$

For $r=7,$ by applying the Hodge inequality to get $m·l=5$(resp. $-1$), there is a constant $n$with $m+l\equiv n{K}_{{\mathbf{F}}_{p,7}}$(resp. $m-l\equiv n{K}_{{\mathbf{F}}_{p,7}}$). Since $K_{{\mathbf{F}}_{p,7}}·\left(m+l\right)=-3$(resp. $K_{{\mathbf{F}}_{p,7}}·\left(m-l\right)=-1$), the constant $n$is equal to $-3$(resp. $-1$). But $m^2={(-3K_{{\mathbf{F}}_{p,7}}-l)}^2=2$(resp. $m^2={(-K_{{\mathbf{F}}_{p,7}}+l)}^2=2$) which is impossible since $m^2=0$. □

4.3.2. Rulings via Monoidal Transformations

Now, we consider monoidal transformations for ${\mathbf{M}}_{p+1,r+1}$ given by lines $f-e_{r+1}$ and $e_{r+1}$ on ${\mathbf{F}}_{p+1,r+1}$. According to Lemma 2, the case $r=6$ (i.e., the case ${\mathbf{M}}_{p+1,7}$) involves more nontrivial issues than the others so that we deal with them after the next theorem for the cases $0\le r\le 5$.

Theorem 6.

For a fixed line $e_{r+1}$ on ${\mathbf{F}}_{p+1,r+1},0\le r\le 5$,

$$\begin{array}{cc}\hfill {\mathbf{M}}_{p+1,r+1}& ={\varphi }_h^{*}\left({\mathbf{M}}_{p+1,r}\right)\dot{\cup }\left({\varphi }_h^{*}\left({\mathcal{E}}_{p+1,r}\right)-e_{r+1}\right)\dot{\cup }{H}_{p+1,r+1}\hfill \\ \hfill & ={\varphi }_v^{*}\left({\mathbf{M}}_{p,r}\right)\dot{\cup }\left({\varphi }_v^{*}\left({\mathcal{E}}_{p,r}\right)-\left(f-e_{r+1}\right)\right)\dot{\cup }{V}_{p+1,r+1},\hfill \end{array}$$

where

$$\left\{\begin{array}{c}{H}_{p+1,r+1}=V_{p+1,r+1}=\varnothing forr\le 3,\hfill \\ H_{p+1,5}=\left\{-K_{{\mathbf{F}}_{p+1,5}}-e_5\right\},V_{p+1,5}=\left\{-K_{{\mathbf{F}}_{p+1,5}}-\left(f-e_5\right)\right\},\hfill \\ H_{p+1,6}={\varphi }_h^{*}\left({\mathbf{L}}_{p+1,5}\right)-K_{{\mathbf{F}}_{p+1,6}}-e_6,\hfill \\ V_{p+1,6}={\varphi }_v^{*}\left({\mathbf{L}}_{p,5}\right)-K_{{\mathbf{F}}_{p+1,6}}-(f-e_6).\hfill \end{array}\right.$$

Proof. 

We consider the map ${\varphi }_h$ induced by a line $e_{r+1}$ on ${\mathbf{F}}_{p+1,r+1}$.

For each ruling $m$in the set ${\mathbf{M}}_{p+1,r+1}$on ${\mathbf{F}}_{p+1,r+1}$, the intersection number $m·e_{r+1}$may vary as in Lemma 2, and we check the following cases.

(Case 1) $m·e_{r+1}=0$ for $r\le 5$

Such ruling $m$corresponds to a ruling ${{\varphi }_h}_{*}\left(m\right)$on ${\mathbf{F}}_{p+1,r}$. Thus we have

$$\left\{m\in {\mathbf{M}}_{p+1,r+1}\left|m·e_{r+1}=0\right.\right\}={\varphi }_h^{*}\left({\mathbf{M}}_{p+1,r}\right).$$

(Case 2) $m·e_{r+1}=1$ for $r\le 5$

Such ruling $m$can be written as ${\varphi }_h^{*}\left(D\right)-e_{r+1}$with a divisor class D on ${\mathbf{F}}_{p+1,r}$ satisfying

$$\begin{array}{cc}\hfill D^2& ={\varphi }_h^{*}{\left(D\right)}^2={(m+e_{r+1})}^2=1,\hfill \\ \hfill D·K_{{\mathbf{F}}_{p+1,r}}& ={\varphi }_h^{*}\left(D\right)·{\varphi }_h^{*}\left(K_{{\mathbf{F}}_{p+1,r}}\right)\hfill \\ \hfill & =\left(m+e_{r+1}\right)·\left(K_{{\mathbf{F}}_{p+1,r+1}}-e_{r+1}\right)=-3.\hfill \end{array}$$

Thus the divisor class D on ${\mathbf{F}}_{p+1,r}$ is an exceptional system on ${\mathbf{F}}_{p+1,r}$, and we get

$$\left\{m\in {\mathbf{M}}_{p+1,r+1}\left|m·e_{r+1}=1\right.\right\}={\varphi }_h^{*}\left({\mathcal{E}}_{p+1,r}\right)-e_{r+1}.$$

(Case 3) $m·e_{r+1}=2$ for $r=4,5$

Such ruling $m$can be written as ${\varphi }_h^{*}\left(D\right)-2e_{r+1}$with a divisor class D on ${\mathbf{F}}_{p+1,r}$ satisfying

$$\begin{array}{cc}\hfill D^2& ={\varphi }_h^{*}{\left(D\right)}^2={(m+2e_{r+1})}^2=4,\hfill \\ \hfill D·K_{{\mathbf{F}}_{p+1,r}}& ={\varphi }_h^{*}\left(D\right)·{\varphi }_h^{*}\left(K_{{\mathbf{F}}_{p+1,r}}\right)\hfill \\ \hfill & =(m+2e_{r+1})·(K_{{\mathbf{F}}_{p+1,r+1}}-e_{r+1})=-4.\hfill \end{array}$$

When $r=4$, $-K_{{\mathbf{F}}_{p+1,4}}$is the only divisor class on ${\mathbf{F}}_{p+1,4}$ satisfying the above conditions for D. Thus we have

$$\begin{array}{cc}\hfill \left\{m\in {\mathbf{M}}_{p+1,5}\left|m·e_5=2\right.\right\}& =\left\{{\varphi }_h^{*}\left(-K_{{\mathbf{F}}_{p+1,4}}\right)-2e_5\right\}\hfill \\ \hfill & =\left\{-K_{{\mathbf{F}}_{p+1,5}}-e_5\right\}=H_{p+1,5}.\hfill \end{array}$$

When $r=5$, such $D$corresponds to a line $\tilde{l}$ on ${\mathbf{F}}_{p+1,5}$ via $D=$$\tilde{l}-K_{{\mathbf{F}}_{p+1,5}}$. Therefore

$$\begin{array}{cc}\hfill \left\{m\in {\mathbf{M}}_{p+1,6}\left|m·e_6=2\right.\right\}& =\left\{{\varphi }_h^{*}\left(\tilde{l}-K_{{\mathbf{F}}_{p+1,5}}\right)-2e_6\left|\tilde{l}\in {\mathbf{L}}_{p+1,5}\right.\right\}\hfill \\ \hfill & ={\varphi }_h^{*}\left({\mathbf{L}}_{p+1,5}\right)-K_{{\mathbf{F}}_{p+1,6}}-e_6=H_{p+1,6}.\hfill \end{array}$$

Similarly, by considering a line $f-e_{r+1}$ on ${\mathbf{F}}_{p+1,r+1}$ and ${\varphi }_v$we also derive the equality for ${\varphi }_v$including

$$\begin{array}{cc}\hfill V_{p+1,5}& =\left\{-K_{{\mathbf{F}}_{p+1,5}}-f+e_5\right\},\hfill \\ \hfill V_{p+1,6}& ={\varphi }_v^{*}\left({\mathbf{L}}_{p,5}\right)-K_{{\mathbf{F}}_{p+1,6}}-(f-e_6).\hfill \end{array}$$

 □

Remark 8.

Comparing Table 1 and Table 2, we get

$$\begin{array}{cc}\hfill 27& =\left|{\mathbf{M}}_{p+1,5}\right|=\left|{\mathbf{M}}_{p+1,4}\right|+\left|{\mathcal{E}}_{p+1,4}\right|+\left|H_{p+1,5}\right|=10+16+1,\hfill \\ \hfill 27& =\left|{\mathbf{M}}_{p+1,5}\right|=\left|{\mathbf{M}}_{p,4}\right|+\left|{\mathcal{E}}_{p,4}\right|+\left|V_{p+1,5}\right|=10+16+1,\hfill \\ \hfill 126& =\left|{\mathbf{M}}_{p+1,6}\right|=\left|{\mathbf{M}}_{p+1,5}\right|+\left|{\mathcal{E}}_{p+1,5}\right|+\left|H_{p+1,6}\right|=27+72+27,\hfill \\ \hfill 126& =\left|{\mathbf{M}}_{p+1,6}\right|=\left|{\mathbf{M}}_{p,5}\right|+\left|{\mathcal{E}}_{p,5}\right|+\left|V_{p+1,6}\right|=27+72+27.\hfill \end{array}$$

4.3.3. Skew A-Lines on ${\mathbf{F}}_{p,r}$

In the following, we need to define skew 2-lines, skew 3-lines, and skew r-lines on ${\mathbf{F}}_{p,r}$. A divisor class $D$in $\mathrm{Pic}\left({\mathbf{F}}_{p,r}\right)$ is called a skew a-line if it can be written as a sum of disjoint lines on ${\mathbf{F}}_{p,r}$, namely,

$$D\equiv l_1+\dots +l_a\mathrm{where}{l}_i,i=1,\dots ,a,\mathrm{are}\mathrm{lines}\mathrm{on}{\mathbf{F}}_{p,r}\mathrm{with}{l}_i·l_j=0\mathrm{for}i\ne j.$$

Remark 9.

We use a term of a skew a-line on ${\mathbf{F}}_{p,r}$ even if the disjoint a-lines are not really skew because we follow the ([4] Section 5) and ([19] Section 2.3).

Note that for each skew a-line, the choice of disjoint lines representing the skew a-line is unique up to permutation (see [4,19]). We denote the set of skew a-lines on ${\mathbf{F}}_{p,r}$ as

$${\mathbf{L}}_{p,r}^a:=\left\{D\in \mathrm{Pic}\left({\mathbf{F}}_{p,r}\right)\left|D\mathrm{is}\mathrm{a}\mathrm{skew}a-\mathrm{line}\mathrm{on}{\mathbf{F}}_{p,r}\right.\right\}.$$

In [4,19], we know that ${\mathbf{L}}_{p,r}^a$ is bijectively related to $a-1$simplexes in corresponding a Gosset polytope ${(r-3)}_{21}$. In particular, skew 2-lines ${\mathbf{L}}_{p,6}^2$ (resp. skew 3-lines ${\mathbf{L}}_{p,6}^3$) is bijectively related to edges (resp. 2-simplexes) of a Gosset polytope $3_{21}$, and so $\left|{\mathbf{L}}_{p,6}^2\right|=756$ (resp. $\left|{\mathbf{L}}_{p,6}^3\right|=4032$). We can also get $\left|{\mathbf{L}}_{p,5}^2\right|=216$. Moreover, each skew a-line $D$satisfies $D^2=-a$and $D·K_{{\mathbf{F}}_{p,r}}=-a$, and the converse is also true for $a=2,3$by checking the numbers of divisor classes $D$satisfying equations in the below (Table 3).

Table 3. Number of $D\mathrm{with}{D}^2=-a\mathrm{and}D·K_{{\mathbf{F}}_{p,r}}=-a$.

a	${\mathbf{F}}_{\mathit{p},2}$	${\mathbf{F}}_{\mathit{p},3}$	${\mathbf{F}}_{\mathit{p},4}$	${\mathbf{F}}_{\mathit{p},5}$	${\mathbf{F}}_{\mathit{p},6}$	${\mathbf{F}}_{\mathit{p},7}$
2	6	30	80	216	756	6720
3	2	30	160	720	4032	$60,480$

Thus we obtain the following lemma which is also known to hold true for del Pezzo surfaces ([4] Theorem 5.2).

Lemma 3.

For $a=2,3$, a divisor class $D$on ${\mathbf{F}}_{p,r}$ with $D^2=-a$and $D·K_{{\mathbf{F}}_{p,r}}=-a$is a skew a-line on ${\mathbf{F}}_{p,r}$.

4.3.4. Rulings on ${\mathbf{F}}_{p+1,7}$ via Monoidal Transformations

Now we consider $r=6$, i.e., ${\mathbf{F}}_{p+1,7}$.

Theorem 7.

For a fixed line $e_7$ on ${\mathbf{F}}_{p+1,7}$, we have

$$\begin{array}{cc}\hfill {\mathbf{M}}_{p+1,7}& ={\varphi }_h^{*}\left({\mathbf{M}}_{p+1,6}\right)\dot{\cup }\left({\varphi }_h^{*}\left({\mathcal{E}}_{p+1,6}\right)-e_7\right)\dot{\cup }\left({\varphi }_h^{*}\left({\mathbf{L}}_{p+1,6}^2\right)-K_{{\mathbf{F}}_{p+1,7}}-e_7\right)\hfill \\ \hfill & \dot{\cup }\left({\varphi }_h^{*}\left({\mathcal{E}}_{p+1,6}\right)-K_{{\mathbf{F}}_{p+1,7}}-2e_7\right)\dot{\cup }\left({\varphi }_h^{*}\left({\mathbf{M}}_{p+1,6}\right)-2K_{{\mathbf{F}}_{p+1,7}}-2e_7\right)\hfill \\ \hfill & ={\varphi }_v^{*}\left({\mathbf{M}}_{p,6}\right)\dot{\cup }\left({\varphi }_v^{*}\left({\mathcal{E}}_{p,6}\right)-\left(f-e_7\right)\right)\dot{\cup }\left({\varphi }_v^{*}\left({\mathbf{L}}_{p,6}^2\right)-K_{{\mathbf{F}}_{p+1,7}}-\left(f-e_7\right)\right)\hfill \\ \hfill & \dot{\cup }\left({\varphi }_v^{*}\left({\mathcal{E}}_{p,6}\right)-K_{{\mathbf{F}}_{p+1,7}}-2\left(f-e_7\right)\right)\dot{\cup }\left({\varphi }_v^{*}\left({\mathbf{M}}_{p,6}\right)-2K_{{\mathbf{F}}_{p+1,7}}-2\left(f-e_7\right)\right).\hfill \end{array}$$

Proof. 

We consider the map ${\varphi }_h$ induced by a line $e_7$on ${\mathbf{F}}_{p+1,7}$.

For each ruling $m$in the set ${\mathbf{M}}_{p+1,7}$on ${\mathbf{F}}_{p+1,7}$, $m·e_{r+1}$may vary as in Lemma 2, and we check the following cases.

As in Theorem 6, the cases $m·e_7=0$and $m·e_7=1$ are given as

$$\left\{m\in {\mathbf{M}}_{p+1,7}\left|m·e_7=0\right.\right\}={\varphi }_h^{*}\left({\mathbf{M}}_{p+1,6}\right)$$

and

$$\left\{m\in {\mathbf{M}}_{p+1,7}\left|m·e_7=1\right.\right\}={\varphi }_h^{*}\left({\mathcal{E}}_{p+1,6}\right)-e_7$$

respectively.

(Case $m·e_7=2$)

Again as in Theorem 6, such ruling $m$can be written as ${\varphi }_h^{*}\left(D\right)-2e_7$with $D$satisfying

$$\begin{array}{cc}\hfill D^2& ={\varphi }_h^{*}{\left(D\right)}^2={(m+2e_7)}^2=4,\hfill \\ \hfill D·K_{{\mathbf{F}}_{p+1,6}}& ={\varphi }_h^{*}\left(D\right)·{\varphi }_h^{*}\left(K_{{\mathbf{F}}_{p+1,6}}\right)\hfill \\ \hfill & =(m+2e_7)·(K_{{\mathbf{F}}_{p+1,7}}-e_7)=-4.\hfill \end{array}$$

Since $(D+K_{{\mathbf{F}}_{p+1,6}})·K_{{\mathbf{F}}_{p+1,6}}=-2$and ${(D+K_{{\mathbf{F}}_{p+1,6}})}^2=-2$, by Lemma 3 the divisor class $D+K_{{\mathbf{F}}_{p+1,6}}$is bijectively related to a skew 2-line on ${\mathbf{F}}_{p+1,6}$, namely in ${\mathbf{L}}_{p+1,6}^2$. Thus we have

$$\begin{array}{cc}\hfill & \left\{m\in {\mathbf{M}}_{p+1,7}\left|m·e_7=2\right.\right\}\hfill \\ \hfill & =\left\{{\varphi }_h^{*}\left(l_1+l_2-K_{{\mathbf{F}}_{p+1,6}}\right)-2e_7\left|l_1,l_2\in {\mathbf{L}}_{p+1,6}\mathrm{with}{l}_1·l_2=0\right.\right\}\hfill \\ \hfill & ={\varphi }_h^{*}\left({\mathbf{L}}_{p+1,6}^2\right)-K_{{\mathbf{F}}_{p+1,7}}-e_7.\hfill \end{array}$$

(Case $m·e_7=3$)

As the above, a ruling $m$with $m·e_7=3$ can be written as ${\varphi }_h^{*}\left(D\right)-3e_7$with a divisor class $D$on ${\mathbf{F}}_{p+1,6}$satisfying $D^2=9$and $D·K_{{\mathbf{F}}_{p+1,6}}=-5$. Since $(D+K_{{\mathbf{F}}_{p+1,6}})·K_{{\mathbf{F}}_{p+1,6}}=-3$and ${(D+K_{{\mathbf{F}}_{p+1,6}})}^2=1$, the divisor class $D+K_{{\mathbf{F}}_{p+1,6}}$is bijectively related to an exceptional system on ${\mathbf{F}}_{p+1,6}$. Therefore, we obtain

$$\begin{array}{cc}\hfill & \left\{m\in {\mathbf{M}}_{p+1,7}\left|m·e_7=3\right.\right\}\hfill \\ \hfill & =\left\{{\varphi }_h^{*}\left(e-K_{{\mathbf{F}}_{p+1,6}}\right)-3e_7\left|e\in {\mathcal{E}}_{p+1,6}\right.\right\}\hfill \\ \hfill & ={\varphi }_h^{*}\left({\mathcal{E}}_{p+1,6}\right)-K_{{\mathbf{F}}_{p+1,7}}-2e_7.\hfill \end{array}$$

(Case $m·e_7=4$)

A ruling $m$with $m·e_7=4$ can be written as ${\varphi }_h^{*}\left(D\right)-4e_7$with a divisor class $D$on ${\mathbf{F}}_{p+1,6}$satisfying $D^2=16$and $D·K_{{\mathbf{F}}_{p+1,6}}=-6$. Since $(D+2K_{{\mathbf{F}}_{p+1,6}})·K_{{\mathbf{F}}_{p+1,6}}=-2$and ${(D+2K_{{\mathbf{F}}_{p+1,6}})}^2=0$, the divisor class $D+2K_{{\mathbf{F}}_{p+1,6}}$is bijectively related to a ruling on ${\mathbf{F}}_{p+1,6}$ so that we have

$$\begin{array}{cc}\hfill & \left\{m\in {\mathbf{M}}_{p+1,7}\left|m·e_7=4\right.\right\}\hfill \\ \hfill & =\left\{{\varphi }_h^{*}\left(m-2K_{{\mathbf{F}}_{p+1,6}}\right)-4e_7\left|m\in {\mathbf{M}}_{p+1,6}\right.\right\}\hfill \\ \hfill & ={\varphi }_h^{*}\left({\mathbf{M}}_{p+1,6}\right)-2K_{{\mathbf{F}}_{p+1,7}}-2e_7.\hfill \end{array}$$

Similarly, we derive the equality for ${\varphi }_v.$ □

Remark 10.

Comparing Table 1 and Table 2, we obtain

$$\begin{array}{cc}\hfill 2160& =\left|{\mathbf{M}}_{p+1,7}\right|\hfill \\ \hfill & =\left|{\mathbf{M}}_{p+1,6}\right|+\left|{\mathcal{E}}_{p+1,6}\right|+\left|{\mathbf{L}}_{p+1,6}^2\right|+\left|{\mathcal{E}}_{p+1,6}\right|+\left|{\mathbf{M}}_{p+1,6}\right|\hfill \\ \hfill & =\left|{\mathbf{M}}_{p,6}\right|+\left|{\mathcal{E}}_{p,6}\right|+\left|{\mathbf{L}}_{p,6}^2\right|+\left|{\mathcal{E}}_{p,6}\right|+\left|{\mathbf{M}}_{p,6}\right|\hfill \\ \hfill & =126+576+756+576+126.\hfill \end{array}$$

4.4. Exceptional Systems and Monoidal Transformations

We introduce sextic divisor classes to appear on the way to monoidal transformations for exceptional systems on ${\mathbf{F}}_{p,r}$. We also study basic properties of these divisor classes. The properties are not crucial to understand the monoidal transformations for exceptional systems, but since these divisor classes were not considered beforehand, we study their properties for the sake of completeness.

4.4.1. Sextic Divisor Classes on ${\mathbf{F}}_{p,6}$

To study monoidal transformations for exceptional systems on ${\mathbf{F}}_{p,7}$, we need to introduce a sextic divisor class D via the anti-canonical degree with respect to the canonical divisor class $K_{{\mathbf{F}}_{p,6}}$ on ${\mathbf{F}}_{p,6}$ which is given by $D^2=10,D·K_{{\mathbf{F}}_{p,6}}=-6$and its set is denoted as

$${\mathcal{S}}_{p,6}:=\left\{D\in \mathrm{Pic}\left({\mathbf{F}}_{p,6}\right)\left|D^2=10,D·K_{{\mathbf{F}}_{p,6}}=-6\right.\right\}.$$

Either direct computation or by applying Lattice theory to $(D+3K_{{\mathbf{F}}_{p,6}})·K_{{\mathbf{F}}_{p,6}}=0$and ${(D+3K_{{\mathbf{F}}_{p,6}})}^2=-8$, we obtain $\left|{\mathcal{S}}_{p,6}\right|=4158$. By considering Weyl action of $E_7$, we know that there are more than one orbit in ${\mathcal{S}}_{p,6}$. To characterize elements of each orbit we introduce

$$\mathsf{\Phi }\left(D\right):=\frac{1}{2}\left(D+K_{{\mathbf{F}}_{p,6}}\right)$$

for each $D$in ${\mathcal{S}}_{p,6}$. In the following, by checking that $\mathsf{\Phi }\left(D\right)$ is in $\mathrm{Pic}\left({\mathbf{F}}_{p,6}\right)$ or not, we identify each orbit in ${\mathcal{S}}_{p,6}$.

Now we prove that ${\mathcal{S}}_{p,6}$ consists of two orbits of $E_7$ action.

(1) (Orbit I) We consider a subset of ${\mathcal{S}}_{p,6}$ given as

$${\mathcal{S}}_{p,6}\left(I\right):=\left\{2m-K_{{\mathbf{F}}_{p,6}}\in \mathrm{Pic}\left({\mathbf{F}}_{p,6}\right)\left|m\mathrm{is}\mathrm{a}\mathrm{ruling}\mathrm{on}{\mathbf{F}}_{p,6}\right.\right\}\subset {\mathcal{S}}_{p,6}$$

which consists of $126$elements. The $E_7$-Weyl group preserves $K_{{\mathbf{F}}_{p,6}}$and transitively acts on the set ${\mathbf{M}}_{p,6}$ of rulings on ${\mathbf{F}}_{p,6}$. Thus it forms a single orbit. Note that $\mathsf{\Phi }(2m-K_{{\mathbf{F}}_{p,6}})=\frac{1}{2}\left(\left(2m-K_{{\mathbf{F}}_{p,6}}\right)+K_{{\mathbf{F}}_{p,6}}\right)=m\in \mathrm{Pic}\left({\mathbf{F}}_{p,6}\right)$. Moreover, we conclude that the set of such divisor classes is bijectively related to the set of rulings on ${\mathbf{F}}_{p,6}$ which contains $126$elements, and we obtain the following lemma.

Lemma 4.

For a sextic divisor class $D$in ${\mathcal{S}}_{p,6}$, $\mathsf{\Phi }\left(D\right)$is in $\mathrm{Pic}\left({\mathbf{F}}_{p,6}\right)$ if and only if $\mathsf{\Phi }\left(D\right)$is a ruling.

(2) (Orbit II)

As in [4,19], each exceptional system $e$on ${\mathbf{F}}_{p,6}$ corresponds to a 6-simplex consisting of a skew 7-line $l_1+l_2+\dots +l_7$ via $3e+K_{{\mathbf{F}}_{p,6}}\equiv l_1+l_2+\dots +l_7$. For each line $l_i$in the skew 7-line, we consider a divisor class

$$e+l_i-K_{{\mathbf{F}}_{p,6}}$$

which satisfies $\left(e+l_i-K_{{\mathbf{F}}_{p,6}}\right)·K_{{\mathbf{F}}_{p,6}}=-6$and ${\left(e+l_i-K_{{\mathbf{F}}_{p,6}}\right)}^2=10$. We define a subset of $\mathrm{Pic}\left({\mathbf{F}}_{p,6}\right)$

$${\mathcal{S}}_{p,6}\left(II\right):=\left\{e+l_i-K_{{\mathbf{F}}_{p,6}}\in \mathrm{Pic}\left({\mathbf{F}}_{p,6}\right)\left|\begin{array}{c}e\mathrm{is}\mathrm{an}\mathrm{exceptional}\mathrm{system}\mathrm{on}{\mathbf{F}}_{p,6},\\ 3e+K_{{\mathbf{F}}_{p,6}}\equiv l_1+l_2+\dots +l_7\end{array}\right.\right\}.$$

Indeed, this is an orbit, since $E_7$-Weyl group acts trivially on $K_{{\mathbf{F}}_{p,6}}$ and transitively on the set of exceptional systems, and the isotropy group acts transitively on the skew 7-lines.

Lemma 5.

For each $e+l_i-K_{{\mathbf{F}}_{p,6}}$in ${\mathcal{S}}_{p,6}\left(II\right)$,$\mathsf{\Phi }(e+l_i-K_{{\mathbf{F}}_{p,6}})$is not in $\mathrm{Pic}\left({\mathbf{F}}_{p,6}\right)$ and $e+l_i-K_{{\mathbf{F}}_{p,6}}$ is uniquely determined.

Proof. 

Since $\mathsf{\Phi }(e+l_i-K_{{\mathbf{F}}_{p,6}})·l_i=\left(\frac{e+l_i}{2}\right)·l_i=-\frac{1}{2}$, $\mathsf{\Phi }(e+l_i-K_{{\mathbf{F}}_{p,6}})$is not in $\mathrm{Pic}\left({\mathbf{F}}_{p,6}\right)$.

To show $e+l_i-K_{{\mathbf{F}}_{p,6}}$is uniquely determined, we consider two pairs, $\left(e,l_i\right)$and $\left(\tilde{e},{\tilde{l}}_i\right)$, of an exceptional system and a line which satisfy $e+l_i\equiv \tilde{e}+{\tilde{l}}_i$. Without losing the generality, we may assume $e\not\equiv \tilde{e}$and $l_i\not\equiv {\tilde{l}}_i$.

First of all, we observe $l_i$is not related to the exceptional system $\tilde{e}$via a skew 7-line ${\tilde{l}}_1+{\tilde{l}}_2+\cdots +{\tilde{l}}_7$ (i.e. $l_i\not\equiv {\tilde{l}}_j$ for all $j\in \{1,2,\dots ,7\}$). Indeed, suppose that $l_i\equiv {\tilde{l}}_j$ for some j. We have $l_i·{\tilde{l}}_i=0$ and $l_i·\tilde{e}=0$ since $l_i\not\equiv {\tilde{l}}_i$ and $3\tilde{e}+K_{{\mathbf{F}}_{p,6}}\equiv {\tilde{l}}_1+{\tilde{l}}_2+\cdots +{\tilde{l}}_7$. It gives a contradiction by $-1=l_i·\left(e+l_i\right)=l_i·\left(\tilde{e}+{\tilde{l}}_i\right)=0$. Thus $l_i$is not one of ${\tilde{l}}_j$in ${\tilde{l}}_1+{\tilde{l}}_2+\cdots +{\tilde{l}}_7$.

Since $l_i$ is not related to the exceptional system $\tilde{e}$via a skew 7-line ${\tilde{l}}_1+{\tilde{l}}_2+\cdots +{\tilde{l}}_7$, we have

$$l_i·\left(3\tilde{e}+K_{{\mathbf{F}}_{p,6}}\right)=l_i·\left({\tilde{l}}_1+{\tilde{l}}_2+\cdots +{\tilde{l}}_7\right)>0.$$

Indeed, the possible intersection number among two lines $l^{\prime },l^{″}$ is $\ge -1$, and $l^{\prime }\equiv l^{″}$ when $l^{\prime }·l^{″}=-1$ (See Section 4.1.1). Observe that a skew 7-line consists of 7-lines whose 7 is the maximum t for which there exists a t-skew line (See ([4] Table 2 and Theorem 5.1) and [19]). So any line which is not in the skew 7-line ${\tilde{l}}_1+{\tilde{l}}_2+\cdots +{\tilde{l}}_7$ must have a positive intersection number with the skew 7-line.

Thus $l_i·\tilde{e}>0$. It implies $0\le l_i·{\tilde{l}}_i=l_i·\left(l_i+e-\tilde{e}\right)=-1-l_i·\tilde{e}\le -2$which is impossible.

Hence $e+l_i-K_{{\mathbf{F}}_{p,6}}$is uniquely determined. □

By applying Lemma 5, we conclude the subset ${\mathcal{S}}_{p,6}\left(II\right)$ consists of $7\times 576$elements. Since $126+7\times 576=\left|{\mathcal{S}}_{p,6}\right|$, these two forms, ${\mathcal{S}}_{p,6}\left(I\right)$ and ${\mathcal{S}}_{p,6}\left(II\right)$, are disjoint orbits of the set ${\mathcal{S}}_{p,6}$ of sextic divisors.

In summary we have

Proposition 1.

$$\begin{array}{cc}\hfill {\mathcal{S}}_{p,6}& =\left\{2m-K_{{\mathbf{F}}_{p,6}}\in \mathrm{Pic}\left({\mathbf{F}}_{p,6}\right)\left|m\mathit{is}a\mathit{ruling}\right.\right\}\hfill \\ \hfill & \dot{\bigcup }\left\{e+l_i-K_{{\mathbf{F}}_{p,6}}\in \mathrm{Pic}\left({\mathbf{F}}_{p,6}\right)\left|\begin{array}{c}e\mathit{is}\mathit{an}\mathit{exceptional}\mathit{system}\mathit{on}{\mathbf{F}}_{p,6},\\ 3e+K_{{\mathbf{F}}_{p,6}}\equiv l_1+l_2+\dots +l_7\end{array}\right.\right\}\hfill \\ \hfill & \left(\mathrm{i}.\mathrm{e}.{\mathcal{S}}_{p,6}={\mathcal{S}}_{p,6}\left(I\right)\dot{\cup }{\mathcal{S}}_{p,6}\left(II\right)\right).\hfill \end{array}$$

Moreover, for each $D$in ${\mathcal{S}}_{p,6}$, D is in ${\mathcal{S}}_{p,6}\left(I\right)$ iff $\mathsf{\Phi }\left(D\right)$ is in $\mathrm{Pic}\left({\mathbf{F}}_{p,6}\right)$, and $D$is in ${\mathcal{S}}_{p,6}\left(II\right)$ iff $\mathsf{\Phi }\left(D\right)$ is not in $\mathrm{Pic}\left({\mathbf{F}}_{p,6}\right)$.

4.4.2. Intersection between a Line and an Exceptional System

For a line $l$and an exceptional system $e$on ${\mathbf{F}}_{p,r}$, the possible intersection numbers between lines and exceptional systems are given by the following lemma.

Lemma 6.

The possible intersection numbers between lines and exceptional systems are given as

$$l·e=\left\{\begin{array}{c}0,1\mathit{for}r=1,2,3\\ 0,1,2\mathit{for}r=4,5\\ 0,1,2,3\mathit{for}r=6\\ -1,0,1,2,3,4,5,6,7\mathit{for}r=7\end{array}\right..$$

(4)

Proof. 

For a line $l$and an exceptional system $e$on ${\mathbf{F}}_{p,r}$, we have

$$K_{{\mathbf{F}}_{p,r}}^2{\left(l\pm e\right)}^2\le {(K_{{\mathbf{F}}_{p,r}}·l\pm K_{{\mathbf{F}}_{p,r}}·e)}^2$$

and it implies

$$-\frac{2}{8-r}\le l·e\le \frac{8}{8-r}.$$

Thus, the possible intersection numbers between lines and exceptional systems are given as

$$l·e=\left\{\begin{array}{c}0,1\mathrm{for}r=1,2,3\\ 0,1,2\mathrm{for}r=4,5\\ -1\le l·e\le 4\mathrm{for}r=6\\ -2\le l·e\le 8\mathrm{for}r=7\end{array}\right..$$

For $r=6,$ by applying Hodge inequality to get $l·e=4$(resp. $-1$), there is a constant $n$with $e+l\equiv n{K}_{{\mathbf{F}}_{p,6}}$(resp. $e-l\equiv n{K}_{{\mathbf{F}}_{p,6}}$). Since $K_{{\mathbf{F}}_{p,6}}·\left(e+l\right)=-4$(resp. $K_{{\mathbf{F}}_{p,6}}·\left(e-l\right)=-2$), the constant $n$is equal to $-2$(resp. $-1$). But $e^2={(-2K_{{\mathbf{F}}_{p,6}}-l)}^2=3$(resp. $e^2={(-K_{{\mathbf{F}}_{p,6}}+l)}^2=3$ ) which is impossible since $e^2=1$.

For $r=7$, as the above, to get $l·e=8$(resp. $l·e=-2$), $e+l\equiv n{K}_{{\mathbf{F}}_{p,7}}$(resp. $e-l\equiv n{K}_{{\mathbf{F}}_{p,7}}$) for some constant n. Since $K_{{\mathbf{F}}_{p,7}}·\left(e+l\right)=-4$(resp. $K_{{\mathbf{F}}_{p,7}}·\left(e-l\right)=-2$), the constant $n$is equal to $-4$(resp. $-2$). But $e^2={(-4K_{{\mathbf{F}}_{p,7}}-l)}^2=7$(resp. $e^2={(-2K_{{\mathbf{F}}_{p,7}}+l)}^2=7$ ) which is impossible since $e^2=1$. □

4.4.3. Exceptional Systems via Monoidal Transformations

Now, we consider monoidal transformations for ${\mathcal{E}}_{p+1,r+1}$ given by lines $f-e_{r+1}$ and $e_{r+1}$ on ${\mathbf{F}}_{p,r+1}$. According to Lemma 6, the case $r=6$ (i.e., the case ${\mathcal{E}}_{p+1,7}$) involves more nontrivial issues than the others so that we deal with them after the following theorem for the cases $0\le r\le 5$.

Theorem 8.

For a fixed line $e_{r+1}$ on ${\mathbf{F}}_{p+1,r+1},0\le r\le 5$,

$$\begin{array}{cc}\hfill {\mathcal{E}}_{p+1,r+1}& ={\varphi }_h^{*}\left({\mathcal{E}}_{p+1,r}\right)\dot{\cup }\left({\varphi }_h^{*}\left({\mathcal{Q}}_{p+1,r}\right)-e_{r+1}\right)\dot{\cup }{H}_{p+1,r+1}\hfill \\ \hfill & ={\varphi }_v^{*}\left({\mathcal{E}}_{p,r}\right)\dot{\cup }\left({\varphi }_v^{*}\left({\mathcal{Q}}_{p,r}\right)-\left(f-e_{r+1}\right)\right)\dot{\cup }{V}_{p+1,r+1},\hfill \end{array}$$

where

$$\left\{\begin{array}{c}{H}_{p+1,r+1}=V_{p+1,r+1}=\varnothing \mathit{for}r\le 2,\hfill \\ H_{p+1,4}=\left\{-K_{{\mathbf{F}}_{p+1,4}}-e_4\right\},V_{p+1,4}=\left\{-K_{{\mathbf{F}}_{p+1,4}}-\left(f-e_4\right)\right\},\hfill \\ H_{p+1,5}={\varphi }_h^{*}\left({\mathbf{L}}_{p+1,4}\right)-K_{{\mathbf{F}}_{p+1,5}}-e_5,\hfill \\ V_{p+1,5}={\varphi }_v^{*}\left({\mathbf{L}}_{p,4}\right)-K_{{\mathbf{F}}_{p+1,5}}-(f-e_5),\hfill \\ H_{p+1,6}=\left({\varphi }_h^{*}\left({\mathbf{L}}_{p+1,5}^2\right)-K_{{\mathbf{F}}_{p+1,6}}-e_6\right)\dot{\cup }\left({\varphi }_h^{*}\left({\mathcal{E}}_{p+1,5}\right)-K_{{\mathbf{F}}_{p+1,6}}-2e_6\right),\hfill \\ V_{p+1,6}=\left({\varphi }_v^{*}\left({\mathbf{L}}_{p,5}^2\right)-K_{{\mathbf{F}}_{p+1,6}}-(f-e_6)\right)\dot{\cup }\left({\varphi }_v^{*}\left({\mathcal{E}}_{p,5}\right)-K_{{\mathbf{F}}_{p+1,6}}-2(f-e_6)\right).\hfill \end{array}\right.$$

Proof. 

We consider the map ${\varphi }_h$ induced from a line $e_{r+1}$ on ${\mathbf{F}}_{p+1,r+1}$.

For each exceptional system $e$in the set ${\mathcal{E}}_{p+1,r+1}$on ${\mathbf{F}}_{p+1,r+1}$, the intersection number $e·e_{r+1}$may vary as in Lemma 6, and we check the following cases according to them.

(Case 1) $e·e_{r+1}=0$ for $r\le 5$

An exceptional system $e$on ${\mathbf{F}}_{p+1,r+1}$ with $e·e_{r+1}=0$corresponds to an exceptional system ${{\varphi }_h}_{*}\left(e\right)$on ${\mathbf{F}}_{p+1,r}$. Thus we have

$$\left\{e\in {\mathcal{E}}_{p+1,r+1}\left|e·e_{r+1}=0\right.\right\}={\varphi }_h^{*}\left({\mathcal{E}}_{p+1,r}\right).$$

(Case 2) $e·e_{r+1}=1$ for $r\le 5$

Such exceptional system $e$can be written as ${\varphi }_h^{*}\left(D\right)-e_{r+1}$with a divisor class $D$on ${\mathbf{F}}_{p+1,r}$ satisfying

$$\begin{array}{cc}\hfill D^2& ={\varphi }_h^{*}{\left(D\right)}^2={(e+e_{r+1})}^2=2,\hfill \\ \hfill D·K_{{\mathbf{F}}_{p+1,r}}& ={\varphi }_h^{*}\left(D\right)·{\varphi }_h^{*}\left(K_{{\mathbf{F}}_{p+1,r}}\right)\hfill \\ \hfill & =(e+e_{r+1})·\left(K_{{\mathbf{F}}_{p+1,r+1}}-e_{r+1}\right)=-4.\hfill \end{array}$$

Therefore, the divisor class $D$is a quartic rational divisor class on ${\mathbf{F}}_{p+1,r}$, and so

$$\left\{e\in {\mathcal{E}}_{p+1,r+1}\left|e·e_{r+1}=1\right.\right\}={\varphi }_h^{*}\left({\mathcal{Q}}_{p+1,r}\right)-e_{r+1}.$$

(Case 3) $e·e_{r+1}=2$ for $r=3,4$

Such $e$can be written as ${\varphi }_h^{*}\left(D\right)-2e_{r+1}$with $D$satisfying

$$\begin{array}{cc}\hfill D^2& ={\varphi }_h^{*}{\left(D\right)}^2={(e+2e_{r+1})}^2=5,\hfill \\ \hfill D·K_{{\mathbf{F}}_{p+1,r}}& ={\varphi }_h^{*}\left(D\right)·{\varphi }_h^{*}\left(K_{{\mathbf{F}}_{p+1,r}}\right)\hfill \\ \hfill & =(e+2e_{r+1})·\left(K_{{\mathbf{F}}_{p+1,r+1}}-e_{r+1}\right)=-5.\hfill \end{array}$$

When $r=3$, $-K_{{\mathbf{F}}_{p+1,3}}$is the only divisor class on ${\mathbf{F}}_{p+1,3}$ satisfying the above conditions for D. Thus

$$\begin{array}{cc}\hfill \left\{e\in {\mathcal{E}}_{p+1,4}\left|e·e_4=2\right.\right\}& =\left\{{\varphi }_h^{*}\left(-K_{{\mathbf{F}}_{p+1,3}}\right)-2e_4\right\}\hfill \\ \hfill & =\left\{-K_{{\mathbf{F}}_{p+1,4}}-e_4\right\}=H_{p+1,4}.\hfill \end{array}$$

When $r=4$, such $D$corresponds to a line $\tilde{l}$ on ${\mathbf{F}}_{p+1,4}$ via $D=$$\tilde{l}-K_{{\mathbf{F}}_{p+1,4}}$. Therefore

$$\begin{array}{cc}\hfill \left\{e\in {\mathcal{E}}_{p+1,5}\left|e·e_5=2\right.\right\}& =\left\{{\varphi }_h^{*}\left(\tilde{l}-K_{{\mathbf{F}}_{p+1,4}}\right)-2e_5\left|\tilde{l}\in {\mathbf{L}}_{p+1,4}\right.\right\}\hfill \\ \hfill & ={\varphi }_h^{*}\left({\mathbf{L}}_{p+1,4}\right)-K_{{\mathbf{F}}_{p+1,5}}-e_5=H_{p+1,5}.\hfill \end{array}$$

(Case 4) $e·e_6=2$ or 3

(i) An exceptional system $e$on ${\mathbf{F}}_{p+1,6}$ with $e·e_6=2$ can be written as ${\varphi }_h^{*}\left(D\right)-2e_6$with a divisor class $D$on ${\mathbf{F}}_{p+1,5}$satisfying $D^2=5$and $D·K_{{\mathbf{F}}_{p+1,5}}=-5$. Since $(D+K_{{\mathbf{F}}_{p+1,5}})·K_{{\mathbf{F}}_{p+1,5}}=-2$and ${(D+K_{{\mathbf{F}}_{p+1,5}})}^2=-2$, the divisor class $D+K_{{\mathbf{F}}_{p+1,5}}$is bijectively related to a skew 2-line ${\mathbf{L}}_{p,5}^2$ by Lemma 3. Thus we have

$$\begin{array}{cc}\hfill & \left\{e\in {\mathcal{E}}_{p+1,6}\left|e·e_6=2\right.\right\}\hfill \\ \hfill & =\left\{{\varphi }_h^{*}\left(l_1+l_2-K_{{\mathbf{F}}_{p+1,5}}\right)-2e_6\left|l_1,l_2\in {\mathbf{L}}_{p+1,5}\mathrm{with}{l}_1·l_2=0\right.\right\}\hfill \\ \hfill & ={\varphi }_h^{*}\left({\mathbf{L}}_{p+1,5}^2\right)-K_{{\mathbf{F}}_{p+1,6}}-e_6.\hfill \end{array}$$

(ii) An exceptional system $e$on ${\mathbf{F}}_{p+1,6}$ with $e·e_6=3$ can be written as ${\varphi }_h^{*}\left(D\right)-3e_6$with a divisor class $D$on ${\mathbf{F}}_{p+1,5}$satisfying $D^2=10$and $D·K_{{\mathbf{F}}_{p+1,5}}=-6$. Since $(D+K_{{\mathbf{F}}_{p+1,5}})·K_{{\mathbf{F}}_{p+1,5}}=-3$and ${(D+K_{{\mathbf{F}}_{p+1,5}})}^2=1$, the divisor class $D+K_{{\mathbf{F}}_{p+1,5}}$is bijectively related to an exceptional system on ${\mathbf{F}}_{p+1,5}$. Therefore, we obtain

$$\begin{array}{cc}\hfill & \left\{e\in {\mathcal{E}}_{p+1,6}\left|e·e_6=3\right.\right\}\hfill \\ \hfill & =\left\{{\varphi }_h^{*}\left(e-K_{{\mathbf{F}}_{p+1,5}}\right)-3e_6\left|e\in {\mathcal{E}}_{p+1,5}\right.\right\}\hfill \\ \hfill & ={\varphi }_h^{*}\left({\mathcal{E}}_{p+1,5}\right)-K_{{\mathbf{F}}_{p+1,6}}-2e_6.\hfill \end{array}$$

Similarly, we derive the equality for ${\varphi }_v$and obtain

$$\begin{array}{cc}\hfill V_{p+1,4}& =\{-K_{{\mathbf{F}}_{p+1,4}}-f+e_4\},\hfill \\ \hfill V_{p+1,5}& ={\varphi }_v^{*}\left({\mathbf{L}}_{p,4}\right)-K_{{\mathbf{F}}_{p+1,5}}-(f-e_5),\hfill \\ \hfill V_{p+1,6}& =\left({\varphi }_v^{*}\left({\mathbf{L}}_{p,5}^2\right)-K_{{\mathbf{F}}_{p+1,6}}-(f-e_6)\right)\dot{\cup }\left({\varphi }_v^{*}\left({\mathcal{E}}_{p,5}\right)-K_{{\mathbf{F}}_{p+1,6}}-2(f-e_6)\right).\hfill \end{array}$$

 □

Remark 11.

When we consider skew 2-lines on ${\mathbf{F}}_{p+1,5}$ and ${\mathbf{F}}_{p,5}$, we have the following data in Table 1 and Table 2.

$$\begin{array}{cc}\hfill 16=\left|{\mathcal{E}}_{p+1,4}\right|& =\left|{\mathcal{E}}_{p+1,3}\right|+\left|{\mathcal{Q}}_{p+1,3}\right|+\left|H_{p+1,4}\right|\hfill \\ \hfill & =\left|{\mathcal{E}}_{p,3}\right|+\left|{\mathcal{Q}}_{p,3}\right|+\left|V_{p+1,4}\right|=5+10+1,\hfill \\ \hfill 72=\left|{\mathcal{E}}_{p+1,5}\right|& =\left|{\mathcal{E}}_{p+1,4}\right|+\left|{\mathcal{Q}}_{p+1,4}\right|+\left|H_{p+1,5}\right|\hfill \\ \hfill & =\left|{\mathcal{E}}_{p,4}\right|+\left|{\mathcal{Q}}_{p,4}\right|+\left|V_{p+1,5}\right|=16+40+16,\hfill \\ \hfill 576=\left|{\mathcal{E}}_{p+1,6}\right|& =\left|{\mathcal{E}}_{p+1,5}\right|+\left|{\mathcal{Q}}_{p+1,5}\right|+\left|H_{p+1,6}\right|\hfill \\ \hfill & =\left|{\mathcal{E}}_{p+1,5}\right|+\left|{\mathcal{Q}}_{p+1,5}\right|+\left|{\mathbf{L}}_{p+1,5}^2\right|+\left|{\mathcal{E}}_{p+1,5}\right|\hfill \\ \hfill & =72+216+216+72,\hfill \\ \hfill 576=\left|{\mathcal{E}}_{p+1,6}\right|& =\left|{\mathcal{E}}_{p,5}\right|+\left|{\mathcal{Q}}_{p,5}\right|+\left|V_{p+1,6}\right|\hfill \\ \hfill & =\left|{\mathcal{E}}_{p,5}\right|+\left|{\mathcal{Q}}_{p,5}\right|+\left|{\mathbf{L}}_{p,5}^2\right|+\left|{\mathcal{E}}_{p,5}\right|\hfill \\ \hfill & =72+216+216+72.\hfill \end{array}$$

4.4.4. Exceptional Systems of ${\mathcal{E}}_{p+1,7}$ via Monoidal Transformations

We deal with the case $r=6$ (i.e., the case ${\mathcal{E}}_{p+1,7}$) as follows. In this case we use sextic divisor classes to describe exceptional systems via monoidal transformations.

Theorem 9.

For a fixed line $e_7$ on ${\mathbf{F}}_{p+1,7}$,

$$\begin{array}{cc}\hfill {\mathcal{E}}_{p+1,7}& ={\varphi }_h^{*}\left({\mathcal{E}}_{p+1,6}\right)\dot{\cup }\left({\varphi }_h^{*}\left({\mathcal{Q}}_{p+1,6}\right)-e_7\right)\dot{\cup }{H}_{p+1,7}\hfill \\ \hfill & ={\varphi }_v^{*}\left({\mathcal{E}}_{p,6}\right)\dot{\cup }\left({\varphi }_v^{*}\left({\mathcal{Q}}_{p,6}\right)-\left(f-e_7\right)\right)\dot{\cup }{V}_{p+1,7},\hfill \end{array}$$

where

$$\left\{\begin{array}{c}{H}_{p+1,7}=\left\{-K_{{\mathbf{F}}_{p+1,7}}+2e_7\right\}\dot{\cup }\left({\varphi }_h^{*}\left({\mathbf{L}}_{p+1,6}^3\right)-K_{{\mathbf{F}}_{p+1,7}}-e_7\right)\hfill \\ \dot{\cup }\left({\varphi }_h^{*}\left({\mathcal{S}}_{p+1,6}\right)-3e_7\right)\dot{\cup }\left({\varphi }_h^{*}\left({\mathbf{L}}_{p+1,6}^3\right)-2K_{{\mathbf{F}}_{p+1,7}}-2e_7\right)\hfill \\ \dot{\cup }\left({\varphi }_h^{*}\left({\mathcal{Q}}_{p+1,6}\right)-5K_{{\mathbf{F}}_{p+1,7}}\right)\dot{\cup }\left({\varphi }_h^{*}\left({\mathcal{E}}_{p+1,6}\right)-5K_{{\mathbf{F}}_{p+1,7}}-e_7\right)\hfill \\ \dot{\cup }\left\{-5K_{{\mathbf{F}}_{p+1,7}}-2e_7\right\},\hfill \\ V_{p+1,7}=\left\{-K_{{\mathbf{F}}_{p+1,7}}+2\left(f-e_7\right)\right\}\dot{\cup }\left({\varphi }_v^{*}\left({\mathbf{L}}_{p,6}^3\right)-K_{{\mathbf{F}}_{p+1,7}}-\left(f-e_7\right)\right)\hfill \\ \dot{\cup }\left({\varphi }_v^{*}\left({\mathcal{S}}_{p,6}\right)-3\left(f-e_7\right)\right)\dot{\cup }\left({\varphi }_v^{*}\left({\mathbf{L}}_{p,6}^3\right)-2K_{{\mathbf{F}}_{p+1,7}}-2\left(f-e_7\right)\right)\hfill \\ \dot{\cup }\left({\varphi }_v^{*}\left({\mathcal{Q}}_{p,6}\right)-5K_{{\mathbf{F}}_{p+1,7}}\right)\dot{\cup }\left({\varphi }_v^{*}\left({\mathcal{E}}_{p,6}\right)-5K_{{\mathbf{F}}_{p+1,7}}-\left(f-e_7\right)\right)\hfill \\ \dot{\cup }\left\{-5K_{{\mathbf{F}}_{p+1,7}}-2\left(f-e_7\right)\right\}.\hfill \end{array}\right.$$

Proof. 

We consider the map ${\varphi }_h$ induced by a line $e_7$on ${\mathbf{F}}_{p+1,7}$.

For each exceptional system $e$in the set${\mathcal{E}}_{p+1,7}$on ${\mathbf{F}}_{p+1,7}$, $e·e_{r+1}$may vary as in Lemma 6, and we check each case of $e·e_7=-1,0,\cdots ,7$.

As in Theorem 8, the cases $e·e_7=0$and $e·e_7=1$ are given as

$$\left\{e\in {\mathcal{E}}_{p+1,7}\left|e·e_7=0\right.\right\}={\varphi }_h^{*}\left({\mathcal{E}}_{p+1,6}\right)$$

and

$$\left\{e\in {\mathcal{E}}_{p+1,7}\left|e·e_7=1\right.\right\}={\varphi }_h^{*}\left({\mathcal{Q}}_{p+1,6}\right)-e_7$$

respectively.

(Case $e·e_7=-1$)

An exceptional system $e$on ${\mathbf{F}}_{p+1,7}$ with $e·e_7=-1$ can be written as ${\varphi }_h^{*}\left(D\right)+e_7$with a divisor class $D$on ${\mathbf{F}}_{p+1,6}$satisfying $D^2=2$ and $D·K_{{\mathbf{F}}_{p+1,6}}=-2$. The divisor class $-K_{{\mathbf{F}}_{p+1,6}}$is the only class with the given condition for D. Thus, we have

$$\begin{array}{cc}\hfill & \left\{e\in {\mathcal{E}}_{p+1,7}\left|e·e_7=-1\right.\right\}\hfill \\ \hfill & =\left\{{\varphi }_h^{*}\left(-K_{{\mathbf{F}}_{p+1,6}}\right)+e_7\right\}=\left\{-K_{{\mathbf{F}}_{p+1,7}}+2e_7\right\}.\hfill \end{array}$$

(Case $e·e_7=2$)

An exceptional system $e$on ${\mathbf{F}}_{p+1,7}$ satisfying $e·e_7=2$ can be written as ${\varphi }_h^{*}\left(D\right)-2e_7$with a divisor class $D$on ${\mathbf{F}}_{p+1,6}$satisfying $D^2=5$and $D·K_{{\mathbf{F}}_{p+1,6}}=-5$. By applying Lemma 3 to $(D+K_{{\mathbf{F}}_{p+1,6}})·K_{{\mathbf{F}}_{p+1,6}}=-3$and ${(D+K_{{\mathbf{F}}_{p+1,6}})}^2=-3$, the divisor class $D+K_{{\mathbf{F}}_{p+1,6}}$is bijectively related to a skew 3-line of ${\mathbf{L}}_{p,6}^3$ on ${\mathbf{F}}_{p+1,6}$. Thus, we obtain

$$\begin{array}{cc}\hfill & \left\{e\in {\mathcal{E}}_{p+1,7}\left|e·e_7=2\right.\right\}\hfill \\ \hfill & =\left\{{\varphi }_h^{*}\left(l_1+l_2+l_3-K_{{\mathbf{F}}_{p+1,6}}\right)-2e_7\left|\begin{array}{c}{l}_1,l_2,l_3\in {\mathbf{L}}_{p+1,6}\\ \mathrm{with}{l}_i·l_j=0,i\ne j\end{array}\right.\right\}\hfill \\ \hfill & ={\varphi }_h^{*}\left({\mathbf{L}}_{p+1,6}^3\right)-K_{{\mathbf{F}}_{p+1,7}}-e_7.\hfill \end{array}$$

(Case $e·e_7=3$)

An exceptional system $e$on ${\mathbf{F}}_{p+1,7}$ satisfying $e·e_7=3$ can be written as ${\varphi }_h^{*}\left(D\right)-3e_7$with a divisor class D on ${\mathbf{F}}_{p+1,6}$satisfying $D^2=10$and $D·K_{{\mathbf{F}}_{p+1,6}}=-6$ which is a sextic divisor in ${\mathcal{S}}_{p+1,6}$ on ${\mathbf{F}}_{p+1,6}$ (See Section 4.4.1). Thus, we obtain

$$\left\{e\in {\mathcal{E}}_{p+1,7}\left|e·e_7=3\right.\right\}={\varphi }_h^{*}\left({\mathcal{S}}_{p+1,6}\right)-3e_7.$$

(Case $e·e_7=4$)

An exceptional system $e$on ${\mathbf{F}}_{p+1,7}$ with $e·e_7=4$ can be written as ${\varphi }_h^{*}\left(D\right)-4e_7$with a divisor class D on ${\mathbf{F}}_{p+1,6}$satisfying $D^2=17$and $D·K_{{\mathbf{F}}_{p+1,6}}=-7$. By applying Lemma 3 to $(D+2K_{{\mathbf{F}}_{p+1,6}})·K_{{\mathbf{F}}_{p+1,6}}=-3$and ${(D+2K_{{\mathbf{F}}_{p+1,6}})}^2=-3$, the divisor class $D+2K_{{\mathbf{F}}_{p+1,6}}$is bijectively related to a skew 3-line of ${\mathbf{L}}_{p,6}^3$ on ${\mathbf{F}}_{p+1,6}$. Thus, we obtain

$$\begin{array}{cc}\hfill & \left\{e\in {\mathcal{E}}_{p+1,7}\left|e·e_7=4\right.\right\}\hfill \\ \hfill & =\left\{{\varphi }_h^{*}\left(l_1+l_2+l_3-2K_{{\mathbf{F}}_{p+1,6}}\right)-4e_7\left|\begin{array}{c}{l}_1,l_2,l_3\in {\mathbf{L}}_{p+1,6}\\ \mathrm{with}{l}_i·l_j=0,i\ne j\end{array}\right.\right\}\hfill \\ \hfill & ={\varphi }_h^{*}\left({\mathbf{L}}_{p+1,6}^3\right)-2K_{{\mathbf{F}}_{p+1,7}}-2e_7.\hfill \end{array}$$

(Case $e·e_7=5$)

Such exceptional system $e$can be written as ${\varphi }_h^{*}\left(D\right)-5e_7$with a divisor class $D$on ${\mathbf{F}}_{p+1,6}$ satisfying $D^2=26$and $D·K_{{\mathbf{F}}_{p+1,6}}=-8$. Since $(D+5K_{{\mathbf{F}}_{p+1,6}})·K_{{\mathbf{F}}_{p+1,6}}=2$and ${(D+5K_{{\mathbf{F}}_{p+1,6}})}^2=-4$, the divisor class $D+5K_{{\mathbf{F}}_{p+1,5}}$is bijectively related to a quartic rational divisor class on ${\mathbf{F}}_{p+1,6}$. Therefore, we have

$$\begin{array}{cc}\hfill & \left\{e\in {\mathcal{E}}_{p+1,7}\left|e·e_7=5\right.\right\}\hfill \\ \hfill & =\left\{{\varphi }_h^{*}\left(q-5K_{{\mathbf{F}}_{p+1,6}}\right)-5e_7\left|q\in {\mathcal{Q}}_{p+1,6}\right.\right\}\hfill \\ \hfill & ={\varphi }_h^{*}\left({\mathcal{Q}}_{p+1,6}\right)-5K_{{\mathbf{F}}_{p+1,7}}.\hfill \end{array}$$

(Case $e·e_7=6$)

Such exceptional system $e$can be written as ${\varphi }_h^{*}\left(D\right)-6e_7$with a divisor class $D$on ${\mathbf{F}}_{p+1,6}$ satisfying $D^2=37$and $D·K_{{\mathbf{F}}_{p+1,6}}=-9$. Since $(D+5K_{{\mathbf{F}}_{p+1,6}})·K_{{\mathbf{F}}_{p+1,6}}=1$and ${(D+5K_{{\mathbf{F}}_{p+1,6}})}^2=-3$, the divisor class $D+5K_{{\mathbf{F}}_{p+1,5}}$corresponds an exceptional system on ${\mathbf{F}}_{p+1,6}$. Therefore, we have

$$\begin{array}{cc}\hfill & \left\{e\in {\mathcal{E}}_{p+1,7}\left|e·e_7=6\right.\right\}\hfill \\ \hfill & =\left\{{\varphi }_h^{*}\left(e-5K_{{\mathbf{F}}_{p+1,6}}\right)-6e_7\left|e\in {\mathcal{E}}_{p+1,6}\right.\right\}\hfill \\ \hfill & ={\varphi }_h^{*}\left({\mathcal{E}}_{p+1,6}\right)-5K_{{\mathbf{F}}_{p+1,7}}-e_7.\hfill \end{array}$$

(Case $e·e_7=7$)

An exceptional system $e$on ${\mathbf{F}}_{p+1,7}$ with $e·e_7=7$ can be written as ${\varphi }_h^{*}\left(D\right)-7e_7$with a divisor class D on ${\mathbf{F}}_{p+1,6}$satisfying $D^2=50$ and $D·K_{{\mathbf{F}}_{p+1,6}}=-10$. Since $(D+5K_{{\mathbf{F}}_{p+1,6}})·K_{{\mathbf{F}}_{p+1,6}}=0$and ${(D+5K_{{\mathbf{F}}_{p+1,6}})}^2=0$, the divisor class $-5K_{{\mathbf{F}}_{p+1,6}}$is the only class with the given condition. Thus, we have

$$\left\{e\in {\mathcal{E}}_{p+1,7}\left|e·e_7=7\right.\right\}=\left\{{\varphi }_h^{*}\left(-5K_{{\mathbf{F}}_{p+1,6}}\right)-7e_7\right\}=\left\{-5K_{{\mathbf{F}}_{p+1,7}}-2e_7\right\}.$$

Similarly, we obtain the equality for $V_{p+1,7}$. □

Remark 12.

We use Table 2 with skew 3-lines on ${\mathbf{F}}_{p+1,6}$ (resp. ${\mathbf{F}}_{p,6}$) and sextic divisor classes on ${\mathbf{F}}_{p+1,6}$ (resp. ${\mathbf{F}}_{p,6}$) to obtain the following.

$$\begin{array}{cc}\hfill & \left|{\mathcal{E}}_{p+1,7}\right|=17520,\left|{\mathcal{E}}_{p+1,6}\right|(\mathrm{resp}.\left|{\mathcal{E}}_{p,6}\right|)=576,\left|{\mathcal{Q}}_{p+1,6}\right|(\mathrm{resp}.\left|{\mathcal{Q}}_{p,6}\right|)=2072,\hfill \\ \hfill & \left|{\mathbf{L}}_{p+1,6}^3\right|(\mathrm{resp}.\left|{\mathbf{L}}_{p,6}^3\right|)=4032,\left|{\mathcal{S}}_{p+1,6}\right|(\mathrm{resp}.\left|{\mathcal{S}}_{p,6}\right|)=4158.\hfill \end{array}$$

$$\begin{array}{cc}\hfill 17,520=\left|{\mathcal{E}}_{p+1,7}\right|& =\left|\left\{-K_{{\mathbf{F}}_{p+1,7}}+2e_7\right\}\right|+\left|{\mathcal{E}}_{p+1,6}\right|+\left|{\mathcal{Q}}_{p+1,6}\right|+\left|{\mathbf{L}}_{p+1,6}^3\right|+\left|{\mathcal{S}}_{p+1,6}\right|\hfill \\ \hfill & +\left|{\mathbf{L}}_{p+1,6}^3\right|+\left|{\mathcal{Q}}_{p+1,6}\right|+\left|{\mathcal{E}}_{p+1,6}\right|+\left|\left\{-5K_{{\mathbf{F}}_{p+1,7}}-2e_7\right\}\right|\hfill \\ \hfill & =\left|\left\{-K_{{\mathbf{F}}_{p+1,7}}+2(f-e_7)\right\}\right|+\left|{\mathcal{E}}_{p,6}\right|+\left|{\mathcal{Q}}_{p,6}\right|+\left|{\mathbf{L}}_{p,6}^3\right|+\left|{\mathcal{S}}_{p,6}\right|\hfill \\ \hfill & +\left|{\mathbf{L}}_{p,6}^3\right|+\left|{\mathcal{Q}}_{p,6}\right|+\left|{\mathcal{E}}_{p,6}\right|+\left|\left\{-5K_{{\mathbf{F}}_{p+1,7}}-2(f-e_7)\right\}\right|\hfill \\ \hfill & =1+576+2072+4032+4158+4032+2072+576+1.\hfill \end{array}$$