Filtering-Based Parameter Identification Methods for Multivariable Stochastic Systems

Abstract

This paper presents an adaptive filtering-based maximum likelihood multi-innovation extended stochastic gradient algorithm to identify multivariable equation-error systems with colored noises. The data filtering and model decomposition techniques are used to simplify the structure of the considered system, in which a predefined filter is utilized to filter the observed data, and the multivariable system is turned into several subsystems whose parameters appear in the vectors. By introducing the multi-innovation identification theory to the stochastic gradient method, this study produces improved performances. The simulation numerical results indicate that the proposed algorithm can generate more accurate parameter estimates than the filtering-based maximum likelihood recursive extended stochastic gradient algorithm.

1. Introduction

System identification is the theory and methods of establishing the mathematical models of dynamical systems [1,2,3,4,5] and some identification approaches have been proposed for scalar systems and multivariable systems [6,7,8,9,10,11]. Multivariable systems exist more widely in modern large-scale industrial processes, multivariable systems can more accurately describe the characteristics of dynamic processes, and have extensive application prospects to study the identification methods of multivariable systems [12,13,14]. The identification methods of multivariable systems can be regarded as an extension of those of scalar systems [15,16]. Therefore, how to identify the multivariable systems by extending the identification methods of scalar systems has attracted much attention. This paper focuses on the identification issues of multivariable systems with complex structures and many parameters. For decades, many parameter estimation methods have been developed for multivariable systems, such as the stochastic gradient methods [17], the iterative methods [18], the recursive least-squares methods [19,20] and the blind identification methods [21]. The maximum likelihood algorithm has good statistical properties and can deal with colored noises directly [22,23,24]. The present study aims to investigate a more efficient algorithm based on the maximum likelihood principle, the negative gradient search, the data filtering, and the multi-innovation identification theory.

The complex structures and high dimensions in the parameter matrices of the multivariable systems lead to the increase in computational complexity [25,26,27]. Inspired by the hierarchical control based on the decomposition-coordination principle for large-scale systems, the hierarchical identification can be served as the solution to reduce the computational intensity by decomposing the identification model into several subsystems with smaller dimension and fewer variables [28]. Differing from the hierarchical identification [29], the model decomposition technique, which is based on the matrix row and column multiplication expansion, is an effective method to reduce the computational burden. Recently, the model decomposition technique are used in [30,31] to reduce the computational complexity by transforming the multivariable system into several small-scale subsystems with only the parameter vectors to be determined. By changing the noise model structure of the subsystem to whiten the colored noise, an adaptive filter is designed to filter the observed data, then the subsystem identification model is further simplified and the parameter estimation accuracy is improved [32,33,34]. For ARX models with unmeasurable outputs, a modified Kalman filter was designed and a new multi-step-length formulation was derived to improve the performance of the gradient iterative algorithm [35].

The advantage of the stochastic gradient methods is that they need less computational effort compared to existing identification methods [36,37]. Due to their zigzagging behavior, the stochastic gradient methods have slow convergence rates [38,39]. The focus of this paper is to investigate a new method with computational efficiency by introducing the multi-innovation identification theory into the stochastic gradient method. The innovation is the useful information that can improve the accuracy of parameter estimation or state estimation. From the viewpoint of innovation modification, the multi-innovation identification theory improves the convergence rate and parameter estimation accuracy from the following two aspects [40,41]. Firstly, the multi-innovation method uses not only the current data but also the past data in each recursive calculation step, which is the reason to improve the convergence rate. Secondly, the multi-innovation method repeatedly utilizes the available data in the neighboring two recursions, which is the reason to improve the parameter estimation accuracy. In this aspect, multi-innovation methods have been developed in [42,43]. It is well known that an increasing innovation length leads to better parameter estimation accuracy, but the price paid is a large computational effort [44,45]. The difficulty arises as to how to choose the innovation length.

In summary, although a filtering and maximum likelihood-based recursive least-squares algorithm is available for multivariable systems with complex structures and colored noises [32], there remains a need for enhancing the parameter estimation accuracy with computational efficiency. Motivated by these considerations, this paper has the following contributions:

• The data filtering and model decomposition techniques are used to reduce the computational complexity of the multivariable systems contaminated by uncertain disturbances.
• A filtering-based multivariable maximum likelihood multi-innovation extended stochastic gradient (F-M-ML-MIESG) algorithm is proposed for improved parameter estimation accuracy while retaining desired computational performance.
• The noise model parameters are dealt with directly using the maximum likelihood principle.

Briefly, this paper is recognized as follows. Section 2 describes the multivariable system with unmeasurable disturbances, derives the subsystem identification model, and forms the identification problems. Section 3 develops a filtering-based multivariable maximum likelihood recursive extended stochastic gradient (F-M-ML-RESG) algorithm. Section 4 introduces the multi-innovation identification theory to the F-M-ML-RESG algorithm to derive an F-M-ML-MIESG algorithm. Section 5 gives a numerical example to verify the proposed algorithms. Finally, Section 6 summarizes the study.

2. The System Description and Identification Model

Symbols Meaning

$\mathbf{0}$:	The zero matrix of appropriate sizes.
${\mathbf{1}}_n$:	An n-dimensional column vector whose entries are all 1.
$\mathit{I}$ or ${\mathit{I}}_n$:	The identity matrix of appropriate sizes or $n\times n$.
${\mathit{X}}^{\mathrm{T}}$:	The transpose of the vector or matrix $\mathit{X}$.
$\parallel \mathit{X}\parallel$:	The norm of the vector or matrix $\mathit{X}$.
$A=:X$:	X is defined by A.
$X:=A$:	X is defined by A.
k:	The time variable.
${\widehat{\mathit{\theta }}}_k$:	The estimate of $\mathit{\theta }$ at time k.
$p_0$:	A large positive constant, e.g., $p_0={10}^6$.

Consider the following multivariable controlled autoregressive autoregressive moving average (M-CARARMA) model:

$$\mathit{A}\left(q\right){\mathit{y}}_k=\mathit{Q}\left(q\right){\mathit{u}}_k+\frac{D\left(q\right)}{C\left(q\right)}{\mathit{v}}_k,$$

(1)

where ${\mathit{y}}_k\in {ℝ}^m$ and ${\mathit{u}}_k\in {ℝ}^r$ are the output and input vectors, respectively, ${\mathit{v}}_k{\in }^m$ denotes random white noise vector with zero mean and variance ${\sigma }^2$. The polynomials $\mathit{A}\left(q\right)$, $\mathit{Q}\left(q\right)$, $C\left(q\right)$, and $D\left(q\right)$ are expressed as

$$\begin{array}{ccc}\hfill \mathit{A}\left(q\right)& :=& {\mathit{I}}_m+{\mathit{A}}_1{q}^{-1}+{\mathit{A}}_2{q}^{-2}+\cdots +{\mathit{A}}_{n_a}{q}^{-n_a},{\mathit{A}}_l=\left[a_{ij}^l\right]\in {ℝ}^{m\times m},\mathrm{ł}=1,2,\cdots ,n_a,\hfill \\ \hfill \mathit{Q}\left(q\right)& :=& {\mathit{Q}}_1{q}^{-1}+{\mathit{Q}}_2{q}^{-2}+\cdots +{\mathit{Q}}_{n_b}{q}^{-n_b},{\mathit{B}}_l=\left[b_{ij}^l\right]\in {ℝ}^{m\times r},\mathrm{ł}=1,2,\cdots ,n_b,\hfill \\ \hfill C\left(q\right)& :=& 1+c_1{q}^{-1}+c_2{q}^{-2}+\cdots +c_{n_c}{q}^{-n_c},c_l\in ℝ,\mathrm{ł}=1,2,\cdots ,n_c,\hfill \\ \hfill D\left(q\right)& :=& 1+d_1{q}^{-1}+d_2{q}^{-2}+\cdots +d_{n_d}{q}^{-n_d}.d_l\in ℝ,\mathrm{ł}=1,2,\cdots ,n_d,\hfill \end{array}$$

Assume that $\mathit{y}\left(k\right)=\mathbf{0}$, $\mathit{u}\left(k\right)=\mathbf{0}$, and $\mathit{v}\left(k\right)=\mathbf{0}$ for $k⩽0$, the orders $n_a$, $n_b$, $n_c$, and $n_d$ are known. Differing from the work in [32], the focus of this paper is to derive a new method to identify the polynomial coefficients ${\mathit{A}}_l$, ${\mathit{Q}}_l$, $c_l$, and $d_l$. Referring to the work in [32], in order to reduce the computational complexity, Equation (1) is decomposed into several subsystems. Then, the ith subsystem can be represented as

$$\begin{array}{ccc}\hfill v_{i,k}& =& \frac{C\left(q\right)}{D\left(q\right)}\left[\sum _{l=0}^{n_a}{\mathit{A}}_{li}{\mathit{y}}_{k-l}-\sum _{l=1}^{n_b}{\mathit{Q}}_{li}{\mathit{u}}_{k-l}\right]\hfill \\ & =& \frac{C\left(q\right)}{D\left(q\right)}[{\mathit{A}}_i\left(q\right){\mathit{y}}_k-{\mathit{Q}}_i\left(q\right){\mathit{u}}_k],i=1,2,\cdots ,m.\hfill \end{array}$$

(2)

Define

$$\begin{array}{ccc}\hfill {\mathit{a}}_i& :=& {[{\mathit{A}}_{1i},{\mathit{A}}_{2i},\cdots ,{\mathit{A}}_{n_{a}i}]}^{\mathrm{T}}\in {ℝ}^{m{n}_a},{\mathit{b}}_i:={[{\mathit{Q}}_{1i},{\mathit{Q}}_{2i},\cdots ,{\mathit{Q}}_{n_{b}i}]}^{\mathrm{T}}\in {ℝ}^{r{n}_b},\hfill \\ \hfill \mathit{c}& :=& {[c_1,c_2,\cdots ,c_{n_c}]}^{\mathrm{T}}\in {ℝ}^{n_c},\mathit{d}:={[d_1,d_2,\cdots ,d_{n_d}]}^{\mathrm{T}}\in {ℝ}^{n_d},\hfill \\ \hfill {\mathit{y}}_{1,k}& :=& C\left(q\right){\mathit{y}}_k,{\mathit{u}}_{1,k}:=C\left(q\right){\mathit{u}}_k,\hfill \\ \hfill {\mathit{\phi }}_{i1,k}& :=& \left[\begin{array}{c}{\mathit{\phi }}_{a,k}\\ {\mathit{\phi }}_{b,k}\\ {\mathit{\phi }}_{id,k}\end{array}\right],{\mathit{\theta }}_{i1}:=\left[\begin{array}{c}{\mathit{a}}_i\\ {\mathit{b}}_i\\ \mathit{d}\end{array}\right]\in {ℝ}^{n_0},n_0:=m{n}_a+r{n}_b+n_d,\hfill \\ \hfill {\mathit{\phi }}_{a,k}& :=& {[-{\mathit{y}}_{1,k-1}^{\mathrm{T}},-{\mathit{y}}_{1,k-2}^{\mathrm{T}},\cdots ,-{\mathit{y}}_{1,k-n_a}^{\mathrm{T}}]}^{\mathrm{T}}\in {ℝ}^{m{n}_a},\hfill \\ \hfill {\mathit{\phi }}_{b,k}& :=& {[{\mathit{u}}_{1,k-1}^{\mathrm{T}},{\mathit{u}}_{1,k-2}^{\mathrm{T}},\cdots ,{\mathit{u}}_{1,k-n_b}^{\mathrm{T}}]}^{\mathrm{T}}\in {ℝ}^{r{n}_b},\hfill \\ \hfill {\mathit{\phi }}_{ic,k}& :=& {[-w_{i,k-1},-w_{i,k-2},\cdots ,-w_{i,k-n_c}]}^{\mathrm{T}}\in {ℝ}^{n_c},\hfill \\ \hfill {\mathit{\phi }}_{id,k}& :=& {[v_{i,k-1},v_{i,k-2},\cdots ,v_{i,k-n_d}]}^{\mathrm{T}}\in {ℝ}^{n_d},\hfill \\ \hfill {\mathit{\phi }}_{i0,k}& :=& {[-{\mathit{y}}_{k-1}^{\mathrm{T}},-{\mathit{y}}_{k-2}^{\mathrm{T}},\cdots ,-{\mathit{y}}_{k-n_a}^{\mathrm{T}},{\mathit{u}}_{k-1}^{\mathrm{T}},{\mathit{u}}_{k-2}^{\mathrm{T}},\cdots ,{\mathit{u}}_{k-n_b}^{\mathrm{T}}]}^{\mathrm{T}}\in {ℝ}^{m{n}_a+r{n}_b},\hfill \\ \hfill {\mathit{\theta }}_{i0}& :=& \left[\begin{array}{c}{\mathit{a}}_i\\ {\mathit{b}}_i\end{array}\right]\in {ℝ}^{m{n}_a+r{n}_b}.\hfill \end{array}$$

From (2), it follows that

$${\mathit{A}}_i\left(q\right){\mathit{y}}_k={\mathit{Q}}_i\left(q\right){\mathit{u}}_k+\frac{D\left(q\right)}{C\left(q\right)}{v}_{i,k}.$$

Multiplying both sides of the above equation by $C\left(q\right)$ gives

$${\mathit{A}}_i\left(q\right)C\left(q\right){\mathit{y}}_k={\mathit{Q}}_i\left(q\right)C\left(q\right){\mathit{u}}_k+D\left(q\right)v_{i,k}.$$

That is,

$${\mathit{A}}_i\left(q\right){\mathit{y}}_{1,k}={\mathit{Q}}_i\left(q\right){\mathit{u}}_{1,k}+D\left(q\right)v_{i,k}.$$

Then, the subsystem identification model can be expressed as

$$\begin{array}{ccc}\hfill y_{i1,k}& =& [e_i-{\mathit{A}}_i\left(q\right)]{\mathit{y}}_{1,k}+{\mathit{Q}}_i\left(q\right){\mathit{u}}_{1,k}+D\left(q\right)v_{i,k}\hfill \\ & =& {\mathit{a}}_i^{\mathrm{T}}{\mathit{\phi }}_{a,k}+{\mathit{b}}_i^{\mathrm{T}}{\mathit{\phi }}_{b,k}+{\mathit{\phi }}_{id,k}^{\mathrm{T}}\mathit{d}+v_{i,k}\hfill \\ & =& {\mathit{\theta }}_{i1}^{\mathrm{T}}{\mathit{\phi }}_{i1,k}+v_{i,k}.\hfill \end{array}$$

(3)

Define an intermediate variable

$$w_{i,k}:=\frac{D\left(q\right)}{C\left(q\right)}{v}_{i,k},$$

(4)

or

$$w_{i,k}=[1-C\left(q\right)]w_{i,k}+D\left(q\right)v_{i,k}.$$

From (4), it follows that

$$\begin{array}{ccc}\hfill w_{i,k}& =& [1-C\left(q\right)]w_{i,k}+[D\left(q\right)-1]v_{i,k}+v_{i,k}\hfill \\ & =& {\mathit{\phi }}_{ic,k}^{\mathrm{T}}\mathit{c}+{\mathit{\phi }}_{id,k}^{\mathrm{T}}\mathit{d}+v_{i,k}\hfill \\ & =& y_{i,k}-[e_i-{\mathit{A}}_i\left(q\right)]{\mathit{y}}_k-{\mathit{Q}}_i\left(q\right){\mathit{u}}_k\hfill \\ & =& y_{i,k}-{\mathit{\theta }}_{i0}^{\mathrm{T}}{\mathit{\phi }}_{i0,k}.\hfill \end{array}$$

Define

$$w_{1,k}:=w_{i,k}-{\mathit{\phi }}_{id,k}^{\mathrm{T}}\mathit{d},$$

or

$$w_{1,k}={\mathit{\phi }}_{ic,k}^{\mathrm{T}}\mathit{c}+v_{i,k}.$$

(5)

3. The F-M-ML-RESG Algorithm

This section derives an F-M-ML-RESG algorithm to identify ${\mathit{\theta }}_{i1}$ in (3) and $\mathit{c}$ in (5) by applying the negative gradient search and maximum likelihood principle based on the observed data {${\mathit{u}}_k$, ${\mathit{y}}_k$:$k=1,2,3,\cdots$}.

Define the criterion function as

$$J({\mathit{\theta }}_{i1},k)=\frac{1}{2}\sum _{k=1}^L{v}_{i,k}^2,$$

where

$$v_{i,k}=\frac{1}{D\left(q\right)}[{\mathit{A}}_i\left(q\right){\mathit{y}}_{1,k}-{\mathit{Q}}_i\left(q\right){\mathit{u}}_{1,k}].$$

(6)

By minimizing $J({\mathit{\theta }}_{i1},k)$, the maximum likelihood estimate ${\widehat{\mathit{\theta }}}_{i1}\left(k\right)$ can be obtained [30,31]. Define the polynomial estimates of ${\mathit{A}}_i\left(q\right)$, ${\mathit{Q}}_i\left(q\right)$, and $D\left(q\right)$ at time k as

$$\begin{array}{ccc}\hfill {\widehat{\mathit{A}}}_i(k,q)& =& {\mathit{e}}_i+{\widehat{\mathit{A}}}_{1i,k}{q}^{-1}+{\widehat{\mathit{A}}}_{2i,k}{q}^{-2}+\cdots +{\widehat{\mathit{A}}}_{n_{a}i,k}{q}^{-n_a},\hfill \\ \hfill {\widehat{\mathit{Q}}}_i(k,q)& =& {\widehat{\mathit{Q}}}_{1i,k}{q}^{-1}+{\widehat{\mathit{Q}}}_{2i,k}{q}^{-2}+\cdots +{\widehat{\mathit{Q}}}_{n_{b}i,k}{q}^{-n_b},\hfill \\ \hfill \widehat{D}(k,q)& =& 1+{\widehat{d}}_{1,k}{q}^{-1}+{\widehat{d}}_{2,k}{q}^{-2}+\cdots +{\widehat{d}}_{n_d,k}{q}^{-n_d}.\hfill \end{array}$$

Let ${\widehat{v}}_{i,k}$ represent the estimate of $v_{i,k}$ at time k. Computing the gradient of $v_{i,k}$ in (6) with respect to ${\mathit{A}}_{li}$, ${\mathit{Q}}_{li}$, and $d_l$ at point ${\mathit{\theta }}_{i1}={\widehat{\mathit{\theta }}}_{i1,k-1}$ yields

$$\begin{array}{ccc}\hfill \frac{\partial v_{i,k}}{\partial {\mathit{A}}_{li}^{\mathrm{T}}}{|}_{{\widehat{\mathit{\theta }}}_{i1,k-1}}& =& {\left[\widehat{D}(k-1,q)\right]}^{-1}{q}^{-l}{\widehat{\mathit{y}}}_{1,k}=:q^{-l}{\widehat{\mathit{y}}}_{1\mathrm{f},k},\hfill \\ \hfill \frac{\partial v_{i,k}}{\partial {\mathit{Q}}_{li}^{\mathrm{T}}}{|}_{{\widehat{\mathit{\theta }}}_{i1,k-1}}& =& -{\left[\widehat{D}(k-1,q)\right]}^{-1}{q}^{-l}{\widehat{\mathit{u}}}_{1,k}=:-q^{-l}{\widehat{\mathit{u}}}_{1\mathrm{f},k},\hfill \\ \hfill \frac{\partial v_{i,k}}{\partial d_l}{|}_{{\widehat{\mathit{\theta }}}_{i1,k-1}}& =& -{\left[\widehat{D}(k-1,q)\right]}^{-1}{q}^{-l}{\widehat{v}}_{i,k}=:-q^{-l}{\widehat{v}}_{i\mathrm{f},k},\hfill \end{array}$$

where ${\widehat{\mathit{y}}}_{1\mathrm{f},k}$, ${\widehat{\mathit{u}}}_{1\mathrm{f},k}$, and ${\widehat{v}}_{i\mathrm{f},k}$ are defined by

$$\begin{array}{ccc}\hfill {\widehat{\mathit{y}}}_{1\mathrm{f},k}& :=& {\left[\widehat{D}(k-1,q)\right]}^{-1}{\widehat{\mathit{y}}}_{1,k},\hfill \\ \hfill {\widehat{\mathit{u}}}_{1\mathrm{f},k}& :=& {\left[\widehat{D}(k-1,q)\right]}^{-1}{\widehat{\mathit{u}}}_{1,k},\hfill \\ \hfill {\widehat{v}}_{i\mathrm{f},k}& :=& {\left[\widehat{D}(k-1,q)\right]}^{-1}{\widehat{v}}_{i,k}.\hfill \end{array}$$

Referring to the work in [32], it follows that

$$\begin{array}{ccc}\hfill {\widehat{\mathit{y}}}_{1\mathrm{f},k}& =& {\mathit{y}}_k+\sum _{l=1}^{n_c}{\widehat{c}}_{l,k-1}{\mathit{y}}_{k-l}-{\widehat{d}}_{1,k-1}{\widehat{\mathit{y}}}_{1\mathrm{f},k-1}-{\widehat{d}}_{2,k-1}{\widehat{\mathit{y}}}_{1\mathrm{f},k-2}-\cdots -{\widehat{d}}_{n_d,k-1}{\widehat{\mathit{y}}}_{1\mathrm{f},k-n_d},\hfill \\ \hfill {\widehat{\mathit{u}}}_{1\mathrm{f},k}& =& {\mathit{u}}_k+\sum _{l=1}^{n_c}{\widehat{c}}_{l,k-1}{\mathit{u}}_{k-l}-{\widehat{d}}_{1,k-1}{\widehat{\mathit{u}}}_{1\mathrm{f},k-1}-{\widehat{d}}_{2,k-1}{\widehat{\mathit{u}}}_{1\mathrm{f},k-2}-\cdots -{\widehat{d}}_{n_d,k-1}{\widehat{\mathit{u}}}_{1\mathrm{f},k-n_d},\hfill \\ \hfill {\widehat{v}}_{i\mathrm{f},k}& =& {\widehat{v}}_{i,k}-\sum _{l=1}^{n_d}{\widehat{d}}_{l,k-1}{\widehat{v}}_{i\mathrm{f},k-l}.\hfill \end{array}$$

(7)

Define

$$\begin{array}{ccc}\hfill {\widehat{\mathit{\phi }}}_{a,k}& :=& {[-{\widehat{\mathit{y}}}_{1,k-1}^{\mathrm{T}},-{\widehat{\mathit{y}}}_{1,k-2}^{\mathrm{T}},\cdots ,-{\widehat{\mathit{y}}}_{1,k-n_a}^{\mathrm{T}}]}^{\mathrm{T}}\in {ℝ}^{m{n}_a},\hfill \\ \hfill {\widehat{\mathit{\phi }}}_{b,k}& :=& {[{\widehat{\mathit{u}}}_{1,k-1}^{\mathrm{T}},{\widehat{\mathit{u}}}_{1,k-2}^{\mathrm{T}},\cdots ,{\widehat{\mathit{u}}}_{1,k-n_b}^{\mathrm{T}}]}^{\mathrm{T}}\in {ℝ}^{r{n}_b},\hfill \\ \hfill {\widehat{\mathit{\phi }}}_{id,k}& :=& {[{\widehat{v}}_{i,k-1},{\widehat{v}}_{i,k-2},\cdots ,{\widehat{v}}_{i,k-n_d}]}^{\mathrm{T}}\in {ℝ}^{n_d},\hfill \\ \hfill {\widehat{\mathit{\phi }}}_{i1,k}& :=& \left[\begin{array}{c}{\widehat{\mathit{\phi }}}_{a,k}\\ {\widehat{\mathit{\phi }}}_{b,k}\\ {\widehat{\mathit{\phi }}}_{id,k}\end{array}\right]\in {ℝ}^{n_0}.\hfill \end{array}$$

From (3), it follows that $v_{i,k}=y_{i1,k}-{\mathit{\theta }}_{i1}^{\mathrm{T}}{\mathit{\phi }}_{i1,k}$. Replacing $y_{i1,k}$, ${\mathit{\phi }}_{i1,k}$, and ${\mathit{\theta }}_{i1}$ with ${\widehat{y}}_{i1,k}$, ${\widehat{\mathit{\phi }}}_{i1,k}$, and ${\widehat{\mathit{\theta }}}_{i1,k}$ yields the estimate of $v_{i,k}$ as

$${\widehat{v}}_{i,k}={\widehat{y}}_{i1,k}-{\widehat{\mathit{\theta }}}_{i1,k}^{\mathrm{T}}{\widehat{\mathit{\phi }}}_{i1,k}.$$

(8)

Substituting (8) into (7) results in

$${\widehat{v}}_{i\mathrm{f},k}={\widehat{v}}_{i,k}-{\widehat{d}}_{1,k-1}{\widehat{v}}_{i\mathrm{f},k-1}-{\widehat{d}}_{2,k-1}{\widehat{v}}_{i\mathrm{f},k-2}-\cdots -{\widehat{d}}_{n_d,k-1}{\widehat{v}}_{i\mathrm{f},k-n_d}.$$

Hence, the filtered information vector ${\widehat{\mathit{\phi }}}_{i1\mathrm{f},k}$ can be written as

$$\begin{array}{ccc}\hfill {\widehat{\mathit{\phi }}}_{i1\mathrm{f},k}& =& [-{\widehat{\mathit{y}}}_{1\mathrm{f},k-1}^{\mathrm{T}},-{\widehat{\mathit{y}}}_{1\mathrm{f},k-2}^{\mathrm{T}},\cdots ,-{\widehat{\mathit{y}}}_{1\mathrm{f},k-n_a}^{\mathrm{T}},{\widehat{\mathit{u}}}_{1\mathrm{f},k-1}^{\mathrm{T}},{\widehat{\mathit{u}}}_{1\mathrm{f},k-2}^{\mathrm{T}},\cdots ,\hfill \\ & & {\widehat{\mathit{u}}}_{1\mathrm{f},k-n_b}^{\mathrm{T}},{\widehat{v}}_{i\mathrm{f},k-1},{\widehat{v}}_{i\mathrm{f},k-2},\cdots ,{\widehat{v}}_{i\mathrm{f},k-n_d}{]}^{\mathrm{T}}\in {ℝ}^{n_0}.\hfill \end{array}$$

Rewrite the cost function in a recursive form:

$$J({\mathit{\theta }}_{i1},k)=J({\mathit{\theta }}_{i1},k-1)+\frac{1}{2}{v}_{i,k}^2.$$

Applying the negative gradient search and minimizing $J({\mathit{\theta }}_{i1},k)$ result in [15]

$$\begin{array}{ccc}\hfill {\widehat{\mathit{\theta }}}_{i1,k}& =& {\widehat{\mathit{\theta }}}_{i1,k-1}-\frac{1}{r_{i,k}}\mathrm{grad}\left[J({\mathit{\theta }}_{i1,k-1},k)\right],\hfill \\ \hfill r_{i,k}& =& r_{i,k-1}+{\parallel {\mathit{\phi }}_{i1,k}\parallel }^2,r_{i,0}=1.\hfill \end{array}$$

Define

$${\mathit{\phi }}_{i1\mathrm{f},k}:=-\mathrm{grad}\left[v_{i,k}\right]{|}_{{\widehat{\mathit{\theta }}}_{i1,k-1}}=-\frac{\partial v_{i,k}}{\partial {\mathit{\theta }}_{i1}}{|}_{{\widehat{\mathit{\theta }}}_{i1,k-1}}.$$

Referring to the work in [18,42,43], $\mathrm{grad}\left[J({\mathit{\theta }}_{i1,k-1},k)\right]$ can be represented as

$$\mathrm{grad}\left[J({\mathit{\theta }}_{i1,k-1},k)\right]=-{\mathit{\phi }}_{i1\mathrm{f},k}{v}_{i,k}.$$

Therefore, an F-M-ML-RESG method can be obtained:

$$\begin{array}{ccc}\hfill {\widehat{\mathit{\theta }}}_{i1,k}& =& {\widehat{\mathit{\theta }}}_{i1,k-1}+\frac{{\mathit{\phi }}_{i1\mathrm{f},k}}{r_{i,k}}{v}_{i,k},\hfill \\ \hfill r_{i,k}& =& r_{i,k-1}+{\parallel {\mathit{\phi }}_{i1\mathrm{f},k}\parallel }^2,r_{i,0}=1.\hfill \end{array}$$

From (5), the estimate of $\mathit{c}$ at time k can be obtained by minimizing the following cost function

$$J\left(\mathit{c}\right):=\sum _{k=1}^L{[w_{1,k}-{\mathit{\phi }}_{ic,k}^{\mathrm{T}}\mathit{c}]}^2.$$

Since the unmeasured terms $v_{i\mathrm{f},k-1}$ in ${\mathit{\phi }}_{i1\mathrm{f},k}$ exist, to address this identification difficulty, the unmeasured terms can be replaced with their corresponding estimates of $v_{i\mathrm{f},k-1}$. Define the innovation $e_{i1,k}:={\widehat{y}}_{i1,k}-{\widehat{\mathit{\theta }}}_{i1,k-1}^{\mathrm{T}}{\widehat{\mathit{\phi }}}_{i1,k}$. Therefore, the F-M-ML-RESG method can be summarized as follows:

$$\begin{array}{ccc}\hfill {\widehat{\mathit{\theta }}}_{i1,k}& =& {\widehat{\mathit{\theta }}}_{i1,k-1}+\frac{{\widehat{\mathit{\phi }}}_{i1\mathrm{f},k}}{r_{i1,k}}{e}_{i1,k},\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill e_{i1,k}& =& {\widehat{y}}_{i1,k}-{\widehat{\mathit{\theta }}}_{i1,k-1}^{\mathrm{T}}{\widehat{\mathit{\phi }}}_{i1,k},\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill r_{i1,k}& =& r_{i1,k-1}+{\parallel {\widehat{\mathit{\phi }}}_{i1\mathrm{f},k}\parallel }^2,\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill {\widehat{v}}_{i,k}& =& {\widehat{y}}_{i1,k}-{\widehat{\mathit{\theta }}}_{i1,k}^{\mathrm{T}}{\widehat{\mathit{\phi }}}_{i1,k},\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill {\widehat{\mathit{d}}}_k& =& \frac{1}{m}\sum _{i=1}^m{\widehat{\mathit{d}}}_{i,k},\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill {\widehat{\mathit{\phi }}}_{i1,k}& =& [-{\widehat{\mathit{y}}}_{1,k-1}^{\mathrm{T}},-{\widehat{\mathit{y}}}_{1,k-2}^{\mathrm{T}},\cdots ,-{\widehat{\mathit{y}}}_{1,k-n_a}^{\mathrm{T}},{\widehat{\mathit{u}}}_{1,k-1}^{\mathrm{T}},{\widehat{\mathit{u}}}_{1,k-2}^{\mathrm{T}},\cdots ,\hfill \\ & & {\widehat{\mathit{u}}}_{1,k-n_b}^{\mathrm{T}},{\widehat{v}}_{i,k-1},{\widehat{v}}_{i,k-2},\cdots ,{\widehat{v}}_{i,k-n_d}{]}^{\mathrm{T}},\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill {\widehat{\mathit{\phi }}}_{i1\mathrm{f},k}& =& [-{\widehat{\mathit{y}}}_{1\mathrm{f},k-1}^{\mathrm{T}},-{\widehat{\mathit{y}}}_{1\mathrm{f},k-2}^{\mathrm{T}},\cdots ,-{\widehat{\mathit{y}}}_{1\mathrm{f},k-n_a}^{\mathrm{T}},{\widehat{\mathit{u}}}_{1\mathrm{f},k-1}^{\mathrm{T}},{\widehat{\mathit{u}}}_{1\mathrm{f},k-2}^{\mathrm{T}},\cdots ,\hfill \\ & & {\widehat{\mathit{u}}}_{1\mathrm{f},k-n_b}^{\mathrm{T}},{\widehat{v}}_{i\mathrm{f},k-1},{\widehat{v}}_{i\mathrm{f},k-2},\cdots ,{\widehat{v}}_{i\mathrm{f},k-n_d}{]}^{\mathrm{T}},\hfill \end{array}$$

(15)

$$\begin{array}{ccc}\hfill {\widehat{\mathit{y}}}_{1\mathrm{f},k}& =& {\widehat{\mathit{y}}}_{1,k}-{\widehat{d}}_{1,k-1}{\widehat{\mathit{y}}}_{1\mathrm{f},k-1}-{\widehat{d}}_{2,k-1}{\widehat{\mathit{y}}}_{1\mathrm{f},k-2}-\cdots -{\widehat{d}}_{n_d,k-1}{\widehat{\mathit{y}}}_{1\mathrm{f},k-n_d},\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill {\widehat{\mathit{u}}}_{1\mathrm{f},k}& =& {\widehat{\mathit{u}}}_{1,k}-{\widehat{d}}_{1,k-1}{\widehat{\mathit{u}}}_{1\mathrm{f},k-1}-{\widehat{d}}_{2,k-1}{\widehat{\mathit{u}}}_{1\mathrm{f},k-2}-\cdots -{\widehat{d}}_{n_d,k-1}{\widehat{\mathit{u}}}_{1\mathrm{f},k-n_d},\hfill \end{array}$$

(17)

$$\begin{array}{ccc}\hfill {\widehat{v}}_{i\mathrm{f},k}& =& {\widehat{v}}_{i,k}-{\widehat{d}}_{1,k-1}{\widehat{v}}_{i\mathrm{f},k-1}-{\widehat{d}}_{2,k-1}{\widehat{v}}_{i\mathrm{f},k-2}-\cdots -{\widehat{d}}_{n_d,k-1}{\widehat{v}}_{i\mathrm{f},k-n_d},\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\hfill {\widehat{\mathit{y}}}_{1,k}& =& {\mathit{y}}_k+\sum _{l=1}^{n_c}{\widehat{c}}_{l,k-1}{\widehat{\mathit{y}}}_{k-l},\hfill \end{array}$$

(19)

$$\begin{array}{ccc}\hfill {\widehat{\mathit{u}}}_{1,k}& =& {\mathit{u}}_k+\sum _{l=1}^{n_c}{\widehat{c}}_{l,k-1}{\widehat{\mathit{u}}}_{k-l},\hfill \end{array}$$

(20)

$$\begin{array}{ccc}\hfill {\widehat{\mathit{c}}}_{i,k}& =& {\widehat{\mathit{c}}}_{i,k-1}+\frac{{\widehat{\mathit{\phi }}}_{ic,k}}{r_{i2,k}}{e}_{i2,k},\hfill \end{array}$$

(21)

$$\begin{array}{ccc}\hfill e_{i2,k}& =& {\widehat{w}}_{i,k}-{\widehat{\mathit{\phi }}}_{id,k}^{\mathrm{T}}{\widehat{\mathit{d}}}_k-{\widehat{\mathit{\phi }}}_{ic,k}^{\mathrm{T}}{\widehat{\mathit{c}}}_{i,k-1},\hfill \end{array}$$

(22)

$$\begin{array}{ccc}\hfill r_{i2,k}& =& r_{i2,k-1}+{\parallel {\widehat{\mathit{\phi }}}_{ic,k}\parallel }^2,\hfill \end{array}$$

(23)

$$\begin{array}{ccc}\hfill {\widehat{\mathit{\phi }}}_{ic,k}& =& {[-{\widehat{w}}_{i,k-1},-{\widehat{w}}_{i,k-2},\cdots ,-{\widehat{w}}_{i,k-n_c}]}^{\mathrm{T}},\hfill \end{array}$$

(24)

$$\begin{array}{ccc}\hfill {\widehat{\mathit{\phi }}}_{id,k}& =& {[{\widehat{v}}_{i,k-1},{\widehat{v}}_{i,k-2},\cdots ,{\widehat{v}}_{i,k-n_d}]}^{\mathrm{T}},\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill {\widehat{w}}_{i,k}& =& y_{i,k}-{\widehat{\mathit{\theta }}}_{i0,k}^{\mathrm{T}}{\mathit{\phi }}_{i0,k},\hfill \end{array}$$

(26)

$$\begin{array}{ccc}\hfill {\mathit{\phi }}_{i0,k}& =& {[-{\mathit{y}}_{k-1}^{\mathrm{T}},-{\mathit{y}}_{k-2}^{\mathrm{T}},\cdots ,-{\mathit{y}}_{k-n_a}^{\mathrm{T}},{\mathit{u}}_{k-1}^{\mathrm{T}},{\mathit{u}}_{k-2}^{\mathrm{T}},\cdots ,{\mathit{u}}_{k-n_b}^{\mathrm{T}}]}^{\mathrm{T}},\hfill \end{array}$$

(27)

$$\begin{array}{ccc}\hfill {\widehat{\mathit{\theta }}}_{i0,k}\left(k\right)& =& {[{\widehat{\mathit{a}}}_{i,k}^{\mathrm{T}},{\widehat{\mathit{b}}}_{i,k}^{\mathrm{T}}]}^{\mathrm{T}},\hfill \end{array}$$

(28)

$$\begin{array}{ccc}\hfill {\widehat{\mathit{\theta }}}_{i1,k}& =& {[{\widehat{\mathit{a}}}_{i,k}^{\mathrm{T}},{\widehat{\mathit{b}}}_{i,k}^{\mathrm{T}},{\widehat{\mathit{d}}}_k^{\mathrm{T}}]}^{\mathrm{T}},\hfill \end{array}$$

(29)

$$\begin{array}{ccc}\hfill {\widehat{\mathrm{\Theta }}}_k& =& {[{\widehat{\mathit{\theta }}}_{1,k}^{\mathrm{T}},{\widehat{\mathit{\theta }}}_{2,k}^{\mathrm{T}},\cdots ,{\widehat{\mathit{\theta }}}_{m,k}^{\mathrm{T}}]}^{\mathrm{T}}.\hfill \end{array}$$

(30)

The steps of the F-M-ML-RESG method for computing ${\widehat{\mathit{\theta }}}_{i1,k}$, ${\widehat{\mathit{c}}}_{i,k}$ and ${\widehat{\mathrm{\Theta }}}_k$ are listed below:

• Initialization: Let $k=1$, and set the initial values ${\widehat{\mathit{\theta }}}_{i1,0}={\mathbf{1}}_{n_0}/p_0$, ${\widehat{\mathit{c}}}_{i,0}={\mathbf{1}}_{n_c}/p_0$, $r_{i1,0}=1$, $r_{i2,0}=1$, ${\widehat{\mathit{y}}}_{1,j}=\mathbf{0}$, ${\widehat{\mathit{u}}}_{1,j}=\mathbf{0}$, ${\widehat{\mathit{y}}}_{1\mathrm{f},j}=\mathbf{0}$, ${\widehat{\mathit{u}}}_{1\mathrm{f},j}=\mathbf{0}$, ${\widehat{\mathit{v}}}_{i\mathrm{f},j}=\mathbf{0}$, ${\widehat{w}}_{i,j}=1/p_0$, and ${\widehat{v}}_{i,j}=1/p_0$ for $j⩽0$, $p_0={10}^6$.
• Collect ${\mathit{u}}_k$ and ${\mathit{y}}_k$, compute ${\widehat{\mathit{y}}}_{1,k}$ and ${\widehat{\mathit{u}}}_{1,k}$ by (19) and (20), respectively.
• Construct ${\widehat{\mathit{\phi }}}_{i1,k}$ and ${\mathit{\phi }}_{i0,k}$ by (14) and (27), respectively, compute ${\widehat{v}}_{i,k}$ by (12).
• Compute ${\widehat{\mathit{y}}}_{1\mathrm{f},\mathrm{k}}$, ${\widehat{\mathit{u}}}_{1\mathrm{f},\mathrm{k}}$, and ${\widehat{v}}_{i\mathrm{f},\mathrm{k}}$ by (16)–(18), respectively, construct ${\widehat{\mathit{\phi }}}_{i1\mathrm{f},k}$ by (15).
• Compute $e_{i1,k}$ and $r_{i1,k}$ by (10) and (11), respectively.
• Compute ${\widehat{\mathit{\theta }}}_{i1,k}$ by (9), update ${\widehat{\mathit{\theta }}}_{i0,k}$ by (28), compute ${\widehat{\mathit{d}}}_k$ by (13), update ${\widehat{\mathit{\theta }}}_{i1,k}$ by (29).
• Construct ${\widehat{\mathit{\phi }}}_{ic,k}$ and ${\widehat{\mathit{\phi }}}_{id,k}$ by (24) and (25), respectively.
• Compute $e_{i2,k}$, $r_{i2,k}$, and ${\widehat{w}}_{i,k}$ by (22), (23), and (26), respectively.
• Update ${\widehat{\mathit{c}}}_{i,k}$ by (21).
• If $k<L$, let $k:=k+1$ and go to Step 2; otherwise, terminate this computational procedure and obtain $\widehat{\mathrm{\Theta }}$${}_k$ by (30).

The flowchart of computing the estimates ${\widehat{\mathit{\theta }}}_{i1,k}$, ${\widehat{\mathit{c}}}_{i,k}$ and ${\widehat{\mathrm{\Theta }}}_k$ by the F-M-ML-RESG algorithm in (9)–(30) is shown in Figure 1.

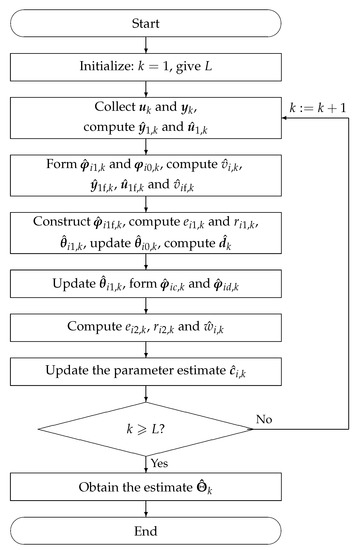
Figure 1. The flowchart of computing the F-M-ML-RESG estimates ${\widehat{\mathit{\theta }}}_{i1,k}$, ${\widehat{\mathit{c}}}_{i,k}$ and ${\widehat{\mathrm{\Theta }}}_k$.

4. The F-M-ML-MIESG Algorithm

In order to further enhance the parameter estimation accuracy of the F-M-ML-RESG method, by introducing the multi-innovation identification theory, an F-M-ML-MIESG method is investigated. Define the information matrix ${\widehat{\mathit{\Gamma }}}_{i1}(p,k)$, the filtered information matrix ${\widehat{\mathit{\Gamma }}}_{i1\mathrm{f}}(p,k)$, and the stacked output vector ${\widehat{\mathit{Y}}}_{i1}(p,k)$ as

$$\begin{array}{ccc}\hfill {\widehat{\mathit{\Gamma }}}_{i1}(p,k)& :=& [{\widehat{\mathit{\phi }}}_{i1,k},{\widehat{\mathit{\phi }}}_{i1,k-1},\cdots ,{\widehat{\mathit{\phi }}}_{i1,k-p+1}]\in {ℝ}^{n_0\times p},\hfill \\ \hfill {\widehat{\mathit{\Gamma }}}_{i1\mathrm{f}}(p,k)& :=& [{\widehat{\mathit{\phi }}}_{i1\mathrm{f},k},{\widehat{\mathit{\phi }}}_{i1\mathrm{f},k-1},\cdots ,{\widehat{\mathit{\phi }}}_{i1\mathrm{f},k-p+1}]\in {ℝ}^{n_0\times p},\hfill \\ \hfill {\widehat{\mathit{Y}}}_{i1}(p,k)& :=& {[{\widehat{y}}_{i1,k},{\widehat{y}}_{i1,k-1},\cdots ,{\widehat{y}}_{i1,k-p+1}]}^{\mathrm{T}}\in {ℝ}^p,\hfill \end{array}$$

where p is the innovation length. Define the stacked output vector ${\widehat{\mathit{W}}}_i(p,k)$, the information matrix ${\widehat{\mathit{\Gamma }}}_{ic}(p,k)$, and the information matrix ${\widehat{\mathit{\Gamma }}}_{id}(p,k)$ as

$$\begin{array}{ccc}\hfill {\widehat{\mathit{\Gamma }}}_{ic}(p,k)& :=& [{\widehat{\mathit{\phi }}}_{ic,k},{\widehat{\mathit{\phi }}}_{ic,k-1},\cdots ,{\widehat{\mathit{\phi }}}_{ic,k-p+1}]\in {ℝ}^{n_c\times p},\hfill \\ \hfill {\widehat{\mathit{\Gamma }}}_{id}(p,k)& :=& [{\widehat{\mathit{\phi }}}_{id,k},{\widehat{\mathit{\phi }}}_{id,k-1},\cdots ,{\widehat{\mathit{\phi }}}_{id,k-p+1}]\in {ℝ}^{n_d\times p},\hfill \\ \hfill {\widehat{\mathit{W}}}_i(p,k)& :=& {[{\widehat{w}}_{i,k},{\widehat{w}}_{i,k-1},\cdots ,{\widehat{w}}_{i,k-p+1}]}^{\mathrm{T}}\in {ℝ}^p.\hfill \end{array}$$

Referring to the work in [18,42,43], Equation (10) becomes the following equation:

$${\mathit{E}}_{i1}(p,k)={\widehat{\mathit{Y}}}_{i1}(p,k)-{\widehat{\mathit{\Gamma }}}_{i1}^{\mathrm{T}}(p,k){\widehat{\mathit{\theta }}}_{i1,k-1}.$$

Equation (22) can be reformulated into the following equation:

$${\mathit{E}}_{i2}(p,k)={\widehat{\mathit{W}}}_i(p,k)-{\widehat{\mathit{\Gamma }}}_{id}^{\mathrm{T}}(p,k){\widehat{\mathit{d}}}_i\left(k\right)-{\widehat{\mathit{\Gamma }}}_{ic}^{\mathrm{T}}(p,k){\widehat{\mathit{c}}}_{i,k-1}.$$

Based on the F-M-ML-RESG method in (9)–(30), the F-M-ML-MIESG method can be obtained as follows:

$$\begin{array}{ccc}\hfill {\widehat{\mathit{\theta }}}_{i1,k}& =& {\widehat{\mathit{\theta }}}_{i1,k-1}+\frac{{\widehat{\mathit{\Gamma }}}_{i1\mathrm{f}}(p,k)}{r_{i1,k}}{\mathit{E}}_{i1}(p,k),\hfill \end{array}$$

(31)

$$\begin{array}{ccc}\hfill {\mathit{E}}_{i1}(p,k)& =& {\widehat{\mathit{Y}}}_{i1}(p,k)-{\widehat{\mathit{\Gamma }}}_{i1}^{\mathrm{T}}(p,k){\widehat{\mathit{\theta }}}_{i1,k-1},\hfill \end{array}$$

(32)

$$\begin{array}{ccc}\hfill r_{i1,k}& =& r_{i1,k-1}+{\parallel {\widehat{\mathit{\phi }}}_{i1\mathrm{f},k}\parallel }^2,\hfill \end{array}$$

(33)

$$\begin{array}{ccc}\hfill {\widehat{v}}_{i,k}& =& {\widehat{y}}_{i1,k}-{\widehat{\mathit{\theta }}}_{i1,k}^{\mathrm{T}}{\widehat{\mathit{\phi }}}_{i1,k},\hfill \end{array}$$

(34)

$$\begin{array}{ccc}\hfill {\widehat{\mathit{d}}}_k& =& \frac{1}{m}\sum _{i=1}^m{\widehat{\mathit{d}}}_{i,k},\hfill \end{array}$$

(35)

$$\begin{array}{ccc}\hfill {\widehat{\mathit{\Gamma }}}_{i1}(p,k)& =& [{\widehat{\mathit{\phi }}}_{i1,k},{\widehat{\mathit{\phi }}}_{i1,k-1},\cdots ,{\widehat{\mathit{\phi }}}_{i1,k-p+1}],\hfill \end{array}$$

(36)

$$\begin{array}{ccc}\hfill {\widehat{\mathit{\Gamma }}}_{i1\mathrm{f}}(p,k)& =& [{\widehat{\mathit{\phi }}}_{i1\mathrm{f},k},{\widehat{\mathit{\phi }}}_{i1\mathrm{f},k-1},\cdots ,{\widehat{\mathit{\phi }}}_{i1\mathrm{f},k-p+1}],\hfill \end{array}$$

(37)

$$\begin{array}{ccc}\hfill {\widehat{\mathit{Y}}}_{i1}(p,k)& =& {[{\widehat{y}}_{i1,k},{\widehat{y}}_{i1,k-1},\cdots ,{\widehat{y}}_{i1,k-p+1}]}^{\mathrm{T}},\hfill \end{array}$$

(38)

$$\begin{array}{ccc}\hfill {\widehat{\mathit{\phi }}}_{i1,k}& =& [-{\widehat{\mathit{y}}}_{1,k-1}^{\mathrm{T}},-{\widehat{\mathit{y}}}_{1,k-2}^{\mathrm{T}},\cdots ,-{\widehat{\mathit{y}}}_{1,k-n_a}^{\mathrm{T}},{\widehat{\mathit{u}}}_{1,k-1}^{\mathrm{T}},{\widehat{\mathit{u}}}_{1,k-2}^{\mathrm{T}},\cdots ,\hfill \\ & & {\widehat{\mathit{u}}}_{1,k-n_b}^{\mathrm{T}},{\widehat{v}}_{i,k-1},{\widehat{v}}_{i,k-2},\cdots ,{\widehat{v}}_{i,k-n_d}{]}^{\mathrm{T}},\hfill \end{array}$$

(39)

$$\begin{array}{ccc}\hfill {\widehat{\mathit{\phi }}}_{i1\mathrm{f},k}& =& [-{\widehat{\mathit{y}}}_{1\mathrm{f},k-1}^{\mathrm{T}},-{\widehat{\mathit{y}}}_{1\mathrm{f},k-2}^{\mathrm{T}},\cdots ,-{\widehat{\mathit{y}}}_{1\mathrm{f},k-n_a}^{\mathrm{T}},{\widehat{\mathit{u}}}_{1\mathrm{f},k-1}^{\mathrm{T}},{\widehat{\mathit{u}}}_{1\mathrm{f},k-2}^{\mathrm{T}},\cdots ,\hfill \\ & & {\widehat{\mathit{u}}}_{1\mathrm{f},k-n_b}^{\mathrm{T}},{\widehat{v}}_{i\mathrm{f},k-1},{\widehat{v}}_{i\mathrm{f},k-2},\cdots ,{\widehat{v}}_{i\mathrm{f},k-n_d}{]}^{\mathrm{T}},\hfill \end{array}$$

(40)

$$\begin{array}{ccc}\hfill {\widehat{\mathit{y}}}_{1\mathrm{f},k}& =& {\widehat{\mathit{y}}}_{1,k}-{\widehat{d}}_{1,k-1}{\widehat{\mathit{y}}}_{1\mathrm{f},k-1}-{\widehat{d}}_{2,k-1}{\widehat{\mathit{y}}}_{1\mathrm{f},k-2}-\cdots -{\widehat{d}}_{n_d,k-1}{\widehat{\mathit{y}}}_{1\mathrm{f},k-n_d},\hfill \end{array}$$

(41)

$$\begin{array}{ccc}\hfill {\widehat{\mathit{u}}}_{1\mathrm{f},k}& =& {\widehat{\mathit{u}}}_{1,k}-{\widehat{d}}_{1,k-1}{\widehat{\mathit{u}}}_{1\mathrm{f},k-1}-{\widehat{d}}_{2,k-1}{\widehat{\mathit{u}}}_{1\mathrm{f},k-2}-\cdots -{\widehat{d}}_{n_d,k-1}{\widehat{\mathit{u}}}_{1\mathrm{f},k-n_d},\hfill \end{array}$$

(42)

$$\begin{array}{ccc}\hfill {\widehat{v}}_{i\mathrm{f},k}& =& {\widehat{v}}_{i,k}-{\widehat{d}}_{1,k-1}{\widehat{v}}_{i\mathrm{f},k-1}-{\widehat{d}}_{2,k-1}{\widehat{v}}_{i\mathrm{f},k-2}-\cdots -{\widehat{d}}_{n_d,k-1}{\widehat{v}}_{i\mathrm{f},k-n_d},\hfill \end{array}$$

(43)

$$\begin{array}{ccc}\hfill {\widehat{\mathit{y}}}_{1,k}& =& {\mathit{y}}_k+\sum _{l=1}^{n_c}{\widehat{c}}_{l,k-1}{\widehat{\mathit{y}}}_{k-l},\hfill \end{array}$$

(44)

$$\begin{array}{ccc}\hfill {\widehat{\mathit{u}}}_{1,k}& =& {\mathit{u}}_k+\sum _{l=1}^{n_c}{\widehat{c}}_{l,k-1}{\widehat{\mathit{u}}}_{k-l},\hfill \end{array}$$

(45)

$$\begin{array}{ccc}\hfill {\widehat{\mathit{c}}}_{i,k}& =& {\widehat{\mathit{c}}}_{i,k-1}+\frac{{\widehat{\mathit{\Gamma }}}_{ic}(p,k)}{r_{i2,k}}{\mathit{E}}_{i2}(p,k),\hfill \end{array}$$

(46)

$$\begin{array}{ccc}\hfill {\mathit{E}}_{i2}(p,k)& =& {\widehat{\mathit{W}}}_i(p,k)-{\widehat{\mathit{\Gamma }}}_{id}^{\mathrm{T}}(p,k){\widehat{\mathit{d}}}_{i,k}-{\widehat{\mathit{\Gamma }}}_{ic}^{\mathrm{T}}(p,k){\widehat{\mathit{c}}}_{i,k-1},\hfill \end{array}$$

(47)

$$\begin{array}{ccc}\hfill r_{i2,k}& =& r_{i2,k-1}+{\parallel {\widehat{\mathit{\phi }}}_{ic,k}\parallel }^2,\hfill \end{array}$$

(48)

$$\begin{array}{ccc}\hfill {\widehat{\mathit{\Gamma }}}_{ic}(p,k)& =& [{\widehat{\mathit{\phi }}}_{ic,k},{\widehat{\mathit{\phi }}}_{ic,k-1},\cdots ,{\widehat{\mathit{\phi }}}_{ic,k-p+1}],\hfill \end{array}$$

(49)

$$\begin{array}{ccc}\hfill {\widehat{\mathit{\Gamma }}}_{id}(p,k)& =& [{\widehat{\mathit{\phi }}}_{id,k},{\widehat{\mathit{\phi }}}_{id,k-1},\cdots ,{\widehat{\mathit{\phi }}}_{id,k-p+1}],\hfill \end{array}$$

(50)

$$\begin{array}{ccc}\hfill {\widehat{\mathit{W}}}_i(p,k)& =& {[{\widehat{w}}_{i,k},{\widehat{w}}_{i,k-1},\cdots ,{\widehat{w}}_{i,k-p+1}]}^{\mathrm{T}},\hfill \end{array}$$

(51)

$$\begin{array}{ccc}\hfill {\widehat{\mathit{\phi }}}_{ic,k}& =& {[-{\widehat{w}}_{i,k-1},-{\widehat{w}}_{i,k-2},\cdots ,-{\widehat{w}}_{i,k-n_c}]}^{\mathrm{T}},\hfill \end{array}$$

(52)

$$\begin{array}{ccc}\hfill {\widehat{\mathit{\phi }}}_{id,k}& =& {[{\widehat{v}}_{i,k-1},{\widehat{v}}_{i,k-2},\cdots ,{\widehat{v}}_{i,k-n_d}]}^{\mathrm{T}},\hfill \end{array}$$

(53)

$$\begin{array}{ccc}\hfill {\widehat{w}}_{i,k}& =& y_{i,k}-{\widehat{\mathit{\theta }}}_{i0,k}^{\mathrm{T}}{\widehat{\mathit{\phi }}}_{i0,k},\hfill \end{array}$$

(54)

$$\begin{array}{ccc}\hfill {\mathit{\phi }}_{i0,k}& =& {[-{\mathit{y}}_{k-1}^{\mathrm{T}},-{\mathit{y}}_{k-2}^{\mathrm{T}},\cdots ,-{\mathit{y}}_{k-n_a}^{\mathrm{T}},{\mathit{u}}_{k-1}^{\mathrm{T}},{\mathit{u}}_{k-2}^{\mathrm{T}},\cdots ,{\mathit{u}}_{k-n_b}^{\mathrm{T}}]}^{\mathrm{T}},\hfill \end{array}$$

(55)

$$\begin{array}{ccc}\hfill {\widehat{\mathit{\theta }}}_{i0,k}& =& {[{\widehat{\mathit{a}}}_{i,k}^{\mathrm{T}},{\widehat{\mathit{b}}}_{i,k}^{\mathrm{T}}]}^{\mathrm{T}},\hfill \end{array}$$

(56)

$$\begin{array}{ccc}\hfill {\widehat{\mathit{\theta }}}_{i1,k}& =& {[{\widehat{\mathit{a}}}_{i,k}^{\mathrm{T}},{\widehat{\mathit{b}}}_{i,k}^{\mathrm{T}},{\widehat{\mathit{d}}}_k^{\mathrm{T}}]}^{\mathrm{T}},\hfill \end{array}$$

(57)

$$\begin{array}{ccc}\hfill {\widehat{\mathrm{\Theta }}}_k& =& {[{\widehat{\mathit{\theta }}}_{1,k}^{\mathrm{T}},{\widehat{\mathit{\theta }}}_{2,k}^{\mathrm{T}},\cdots ,{\widehat{\mathit{\theta }}}_{m,k}^{\mathrm{T}}]}^{\mathrm{T}}.\hfill \end{array}$$

(58)

The F-M-ML-RESG method is a special case of the F-M-ML-MIESG method because, when $p=1$, the F-M-ML-MIESG method degenerates into the F-M-ML-RESG method. The proposed approaches in the paper can combine other estimation algorithms [46,47,48,49,50] to study the parameter identification problems of linear and nonlinear systems with different disturbances [51,52,53,54,55], and can be applied to other fields [56,57,58,59,60] such as signal processing and process control systems. The F-M-ML-MIESG method consists of the following steps for computing ${\widehat{\mathit{\theta }}}_{i1,k}$, ${\widehat{\mathit{c}}}_{i,k}$ and $\widehat{\mathrm{\Theta }}$${}_k$:

• Initialization: Let $k=1$, and set the initial values ${\widehat{\mathit{\theta }}}_{i1,0}={\mathbf{1}}_{n_0}/p_0$, ${\widehat{\mathit{c}}}_{i,0}={\mathbf{1}}_{n_c}/p_0$, $r_{i1,0}=1$, $r_{i2,0}=1$, ${\widehat{\mathit{y}}}_{1,j}=\mathbf{0}$, ${\widehat{\mathit{u}}}_{1,j}=\mathbf{0}$, ${\widehat{\mathit{y}}}_{1\mathrm{f},j}=\mathbf{0}$, ${\widehat{\mathit{u}}}_{1\mathrm{f},j}=\mathbf{0}$, ${\widehat{\mathit{v}}}_{i\mathrm{f},j}\left(j\right)=\mathbf{0}$, ${\widehat{w}}_{i,j}=1/p_0$, and ${\widehat{v}}_{i,j}=1/p_0$ for $j⩽0$, $p_0={10}^6$.
• Collect ${\mathit{u}}_k$ and ${\mathit{y}}_k$, compute ${\widehat{\mathit{y}}}_{1,k}$ and ${\widehat{\mathit{u}}}_{1,k}$ by (44) and (45), respectively.
• Form ${\widehat{\mathit{\phi }}}_{i1,k}$, ${\mathit{\phi }}_{i0,k}$, and ${\widehat{\mathit{Y}}}_{i1}(p,k)$ by (39), (55), and (38), respectively.
• Compute ${\widehat{\mathit{y}}}_{1\mathrm{f},k}$, ${\widehat{\mathit{u}}}_{1\mathrm{f},k}$, and ${\widehat{v}}_{i\mathrm{f},k}$ by (41)–(43), respectively.
• Form ${\widehat{\mathit{\phi }}}_{i1\mathrm{f},k}$, ${\widehat{\mathit{\Gamma }}}_{i1}(p,k)$, and ${\widehat{\mathit{\Gamma }}}_{i1\mathrm{f}}(p,k)$ by (40), (36), and (37), respectively.
• Compute ${\mathit{E}}_{i1}(p,k)$, $r_{i1,k}$, and ${\widehat{\mathit{\theta }}}_{i1,k}$ by (32), (33), and (31), respectively.
• Update ${\widehat{\mathit{\theta }}}_{i0,k}$, ${\widehat{\mathit{d}}}_k$, and ${\widehat{\mathit{\theta }}}_{i1,k}$ by (56), (35), and (57), respectively.
• Compute ${\widehat{v}}_{i,k}$ and ${\widehat{w}}_{i,k}$ by (34) and (54), respectively.
• Form ${\widehat{\mathit{\phi }}}_{ic,k}$ and ${\widehat{\mathit{\phi }}}_{id,k}$ by (52) and (53), respectively.
• Form ${\widehat{\mathit{\Gamma }}}_{ic}(p,k)$, ${\widehat{\mathit{\Gamma }}}_{id}(p,k)$, and ${\widehat{\mathit{W}}}_i(p,k)$ by (49), (50), and (51), respectively.
• Compute ${\mathit{E}}_{i2}(p,k)$ and $r_{i2,k}$ by (47) and (48), respectively.
• Update ${\widehat{\mathit{c}}}_{i,k}$ by (46).
• If $k<L$, let $k:=k+1$ and go to Step 2; otherwise, terminate this computational procedure and obtain ${\widehat{\mathrm{\Theta }}}_k$ by (58).

The flowchart of computing the estimates ${\widehat{\mathit{\theta }}}_{i1,k}$, ${\widehat{\mathit{c}}}_{i,k}$ and ${\widehat{\mathrm{\Theta }}}_k$ by the F-M-ML-MIESG algorithm in (31)–(58) is shown in Figure 2.

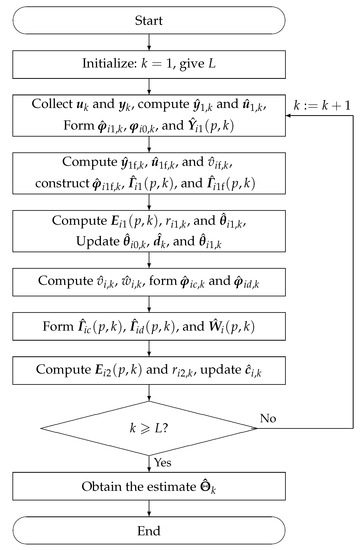
Figure 2. The flowchart of computing the F-M-ML-MIESG estimates ${\widehat{\mathit{\theta }}}_{i1,k}$, ${\widehat{\mathit{c}}}_{i,k}$ and ${\widehat{\mathrm{\Theta }}}_k$.

The model decomposition technique is applied to solve the coupling relationship between the input and output variables of the multivariable system. Thus, the complexity of system identification algorithms is reduced. The data filtering technique is used to filter the observed data. Hence, the subsystem identification model is simplified. The proposed method is based on the data filtering technique, the coupling identification concept, the multi-innovation identification theory, and the negative gradient search for improved parameter estimation and computational performance. The maximum likelihood principle is utilized to estimate the parameters of the noise model directly.

5. Examples

Example 1. 

Consider the following M-CARARMA model

$$\begin{array}{ccc}\hfill \mathit{A}\left(q\right){\mathit{y}}_k& =& \mathit{Q}\left(q\right){\mathit{u}}_k+\frac{D\left(q\right)}{C\left(q\right)}{\mathit{v}}_k,\hfill \\ \hfill \left[\begin{array}{c}{y}_{1,k}\\ y_{2,k}\end{array}\right]& +& \left[\begin{array}{cc}\hfill 0.34& \hfill 0.21\\ \hfill -0.47& \hfill 0.19\end{array}\right]\left[\begin{array}{c}{y}_{1,k-1}\\ y_{2,k-1}\end{array}\right]=\left[\begin{array}{cc}\hfill 2.43& \hfill -0.59\\ \hfill -2.52& \hfill 0.27\end{array}\right]\left[\begin{array}{c}{u}_{1,k-1}\\ u_{2,k-1}\end{array}\right]+\frac{D\left(q\right)}{C\left(q\right)}\left[\begin{array}{c}{v}_{1,k}\\ v_{2,k}\end{array}\right],\hfill \\ \hfill \mathit{A}\left(q\right)& =& \mathit{I}+{\mathit{A}}_1{q}^{-1}=\mathit{I}+\left[\begin{array}{cc}\hfill a_{11}& \hfill a_{12}\\ \hfill a_{21}& \hfill a_{22}\end{array}\right]q^{-1}\hfill \\ & =& \left[\begin{array}{cc}\hfill 1+0.34q^{-1}& \hfill 0.21q^{-1}\\ \hfill -0.47q^{-1}& \hfill 1+0.19q^{-1}\end{array}\right],\hfill \\ \hfill \mathit{Q}\left(q\right)& =& {\mathit{Q}}_1{q}^{-1}=\left[\begin{array}{cc}\hfill b_{11}& \hfill b_{12}\\ \hfill b_{21}& \hfill b_{22}\end{array}\right]q^{-1}=\left[\begin{array}{cc}\hfill 2.43q^{-1}& \hfill -0.59q^{-1}\\ \hfill -2.52q^{-1}& \hfill 0.27q^{-1}\end{array}\right],\hfill \\ \hfill C\left(q\right)& =& 1+c_1{q}^{-1}+c_2{q}^{-2}=1+0.18q^{-1}+0.10q^{-2},\hfill \\ \hfill D\left(q\right)& =& 1+d_1{q}^{-1}+d_2{q}^{-2}=1+0.07q^{-1}+0.12q^{-2},\hfill \\ \hfill {\mathit{\theta }}_1& =& [a_{11},a_{12},b_{11},b_{12},c_1,c_2,d_1,d_2]\hfill \\ & =& [0.34,0.21,2.43,-0.59,0.18,0.10,0.07,0.12],\hfill \\ \hfill {\mathit{\theta }}_2& =& [a_{21},a_{22},b_{21},b_{22},c_1,c_2,d_1,d_2]\hfill \\ & =& [-0.47,0.19,-2.52,0.27,0.18,0.10,0.07,0.12],\hfill \\ \hfill {\mathbf{\Theta }}^{\mathrm{T}}& =& [a_{11},a_{12},a_{21},a_{22},b_{11},b_{12},b_{21},b_{22},c_1,c_2,d_1,d_2]\hfill \\ & =& [0.34,0.21,-0.47,0.19,2.43,-0.59,-2.52,0.27,0.18,0.10,0.07,0.12],\hfill \end{array}$$

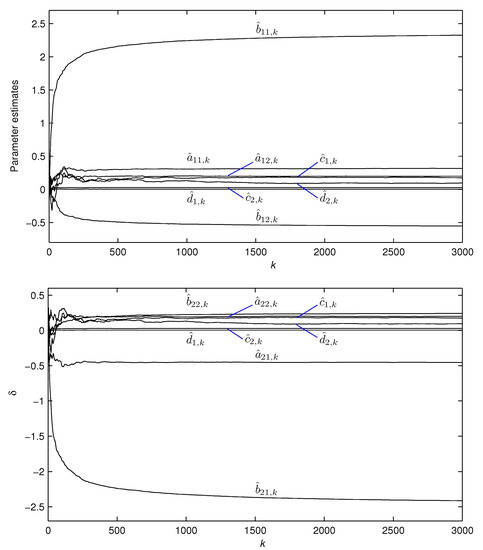
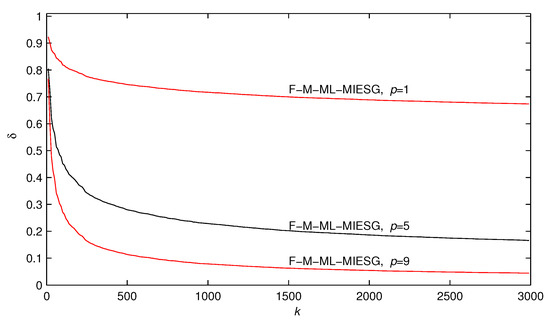
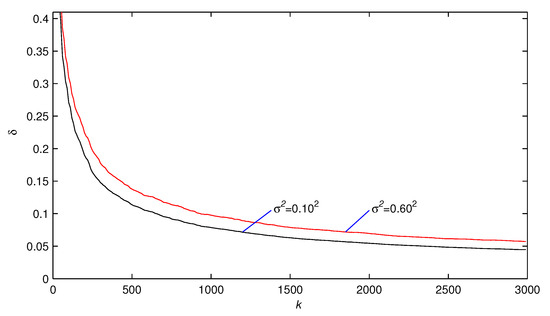
where $\left\{u_{1,k}\right\}$ and $\left\{u_{2,k}\right\}$ are persistent excitation signal sequences with zero mean and unit variance, $\left\{v_{1,k}\right\}$ and $\left\{v_{2,k}\right\}$ are white noise sequences with zero mean and different variances. Taking the data length $L=3000$ and the noise variances ${\sigma }_1^2={\sigma }_2^2=0.{10}^2$ with $p=9$, applying the F-M-ML-MIESG method in (31)–(58) to the example model, the parameter estimates and their errors $\delta :=\parallel {\widehat{\mathit{\theta }}}_k-\mathit{\theta }\parallel /\parallel \mathit{\theta }\parallel$ are shown in Table 1, the parameter estimates ${\widehat{\mathit{\theta }}}_{1,k}$ and ${\widehat{\mathit{\theta }}}_{2,k}$ versus k are shown in Figure 3. When ${\sigma }_1^2={\sigma }_2^2=0.{10}^2$, the F-M-ML-MIESG parameter estimation errors versus k with different innovation lengths p are shown in Figure 4. When $p=9$, the F-M-ML-MIESG parameter estimation errors versus k with different noise variances are shown in Figure 5.

Table 1. The F-M-ML-MIESG estimates and errors (${\sigma }^2=0.{10}^2$, $p=9$).

k	100	200	500	1000	2000	3000	True Values
$a_{11}$	0.31820	0.29087	0.30058	0.30718	0.31435	0.31705	0.34000
$a_{12}$	0.19071	0.19015	0.19849	0.20414	0.19826	0.19930	0.21000
$a_{21}$	−0.49919	−0.46008	−0.45017	−0.45085	−0.45203	−0.45256	−0.47000
$a_{22}$	0.19094	0.20269	0.19320	0.19148	0.19971	0.19937	0.19000
$b_{11}$	1.78343	1.97435	2.15929	2.24258	2.30107	2.32585	2.43000
$b_{12}$	−0.36392	−0.43090	−0.49287	−0.52493	−0.54330	−0.55194	−0.59000
$b_{21}$	−1.84309	−2.04914	−2.23926	−2.32552	−2.38841	−2.41420	−2.52000
$b_{22}$	0.10917	0.16315	0.20417	0.22542	0.23612	0.24193	0.27000
$c_1$	0.19719	0.16972	0.15718	0.16812	0.18093	0.17411	0.18000
$c_2$	0.30485	0.14739	0.13923	0.13329	0.09666	0.09603	0.10000
$d_1$	0.00360	0.00345	0.00422	0.00412	0.00426	0.00443	0.07000
$d_2$	0.02543	0.02647	0.02684	0.02739	0.02792	0.02811	0.12000
$\delta (\%)$	27.09774	18.98626	11.36214	7.87495	5.44330	4.46325

Figure 3. The F-M-ML-MIESG parameter estimates versus k (${\sigma }^2=0.{10}^2$, $p=9$).

Figure 4. The F-M-ML-MIESG estimation errors versus k with different innovation lengths (${\sigma }^2=0.{10}^2$).

Figure 5. The F-M-ML-MIESG estimation errors versus k with different ${\sigma }^2$ ($p=9$).

Example 2. 

Consider the following another 3-input and 3-output system:

$$\begin{array}{ccc}\hfill \mathit{A}\left(q\right){\mathit{y}}_k& =& \mathit{Q}\left(q\right){\mathit{u}}_k+\frac{D\left(q\right)}{C\left(q\right)}{\mathit{v}}_k,\hfill \\ \hfill \left[\begin{array}{c}{y}_{1,k}\\ y_{2,k}\\ y_{3,k}\end{array}\right]& +& \left[\begin{array}{ccc}\hfill -0.30& \hfill 0.45& \hfill 0.28\\ \hfill -0.40& \hfill 0.20& \hfill 0.50\\ \hfill 0.25& \hfill 0.30& \hfill 0.50\end{array}\right]\left[\begin{array}{c}{y}_{1,k-1}\\ y_{2,k-1}\\ y_{3,k-1}\end{array}\right]\hfill \\ & =& \left[\begin{array}{ccc}\hfill 1.35& \hfill -0.70& \hfill 0.90\\ \hfill -2.25& \hfill 1.10& \hfill 0.10\\ \hfill 0.30& \hfill 0.10& \hfill 0.30\end{array}\right]\left[\begin{array}{c}{u}_{1,k-1}\\ u_{2,k-1}\\ u_{3,k-1}\end{array}\right]+\frac{D\left(q\right)}{C\left(q\right)}\left[\begin{array}{c}{v}_{1,k}\\ v_{2,k}\\ v_{3,k}\end{array}\right],\hfill \\ \hfill C\left(q\right)& =& 1+c_1{q}^{-1}=1+0.25q^{-1},\hfill \\ \hfill D\left(q\right)& =& 1+d_1{q}^{-1}=1-0.10q^{-1},\hfill \\ \hfill {\mathit{\theta }}_1& =& [a_{11},a_{12},a_{13},b_{11},b_{12},b_{13},c_1,d_1]\hfill \\ & =& [-0.30,0.45,0.28,1.35,-0.70,0.90,0.25,-0.10],\hfill \\ \hfill {\mathit{\theta }}_2& =& [a_{21},a_{22},a_{23},b_{21},b_{22},b_{23},c_1,d_1]\hfill \\ & =& [-0.40,0.20,0.50,-2.25,1.10,0.10,0.25,-0.10],\hfill \\ \hfill {\mathit{\theta }}_3& =& [a_{31},a_{32},a_{33},b_{31},b_{32},b_{33},c_1,d_1]\hfill \\ & =& [0.25,0.30,0.50,0.30,0.10,0.30,0.25,-0.10].\hfill \end{array}$$

The simulation conditions of this example are similar to those in Example 1. Applying the F-M-ML-MIESG algorithm to estimate the parameters of this example system, the simulation results are shown in Table 2, Figure 6 and Figure 7.

Table 2. The F-M-ML-MIESG estimates and errors (${\sigma }^2=0.{10}^2$, $p=9$).

k	100	200	500	1000	2000	3000	True Values
$a_{11}$	−0.27269	−0.32691	−0.29484	−0.29755	−0.29976	−0.29662	−0.30000
$a_{12}$	0.48292	0.47925	0.46018	0.45462	0.45439	0.45430	0.45000
$a_{13}$	0.14916	0.16587	0.20604	0.22856	0.24342	0.24838	0.28000
$a_{21}$	−0.37780	−0.36285	−0.38617	−0.38781	−0.39033	−0.39405	−0.40000
$a_{22}$	0.12212	0.12412	0.16615	0.18400	0.18349	0.18549	0.20000
$a_{23}$	0.38669	0.42406	0.44468	0.45743	0.46705	0.47374	0.50000
$a_{31}$	0.26876	0.24843	0.25928	0.25579	0.25030	0.25315	0.25000
$a_{32}$	0.31417	0.29867	0.29703	0.29889	0.29861	0.30047	0.30000
$a_{33}$	0.38377	0.41180	0.43509	0.45396	0.46774	0.47453	0.50000
$b_{11}$	0.94218	1.05946	1.15933	1.21302	1.25295	1.27135	1.35000
$b_{12}$	−0.62282	−0.63298	−0.65448	−0.66639	−0.67653	−0.67960	−0.70000
$b_{13}$	0.76671	0.79860	0.82568	0.84453	0.86025	0.86675	0.90000
$b_{21}$	−1.72820	−1.88151	−2.00584	−2.08070	−2.13062	−2.15230	−2.25000
$b_{22}$	0.96728	0.98775	1.02537	1.04164	1.05887	1.06517	1.10000
$b_{23}$	0.21155	0.17143	0.14957	0.13677	0.12570	0.12159	0.10000
$b_{31}$	0.17930	0.21668	0.24420	0.25904	0.27193	0.27810	0.30000
$b_{32}$	0.01120	0.03576	0.06050	0.07209	0.07881	0.08311	0.10000
$b_{33}$	0.26013	0.26116	0.27545	0.28067	0.28621	0.28834	0.30000
$c_1$	0.15333	0.21247	0.22209	0.24500	0.20059	0.23616	0.25000
$d_1$	−0.02364	−0.02344	−0.02373	−0.02411	−0.02439	−0.02471	−0.10000
$\delta (\%)$	23.89260	17.23794	11.32504	8.03089	5.70767	4.79640

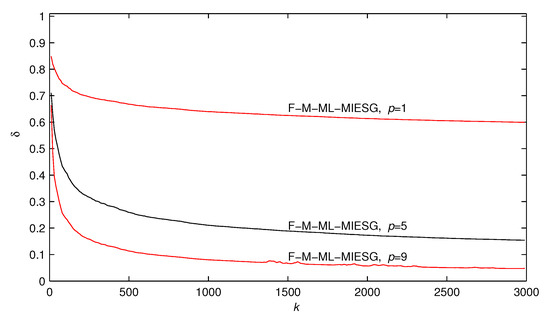
Figure 6. The F-M-ML-MIESG estimation errors versus k with different innovation lengths (${\sigma }^2=0.{10}^2$).

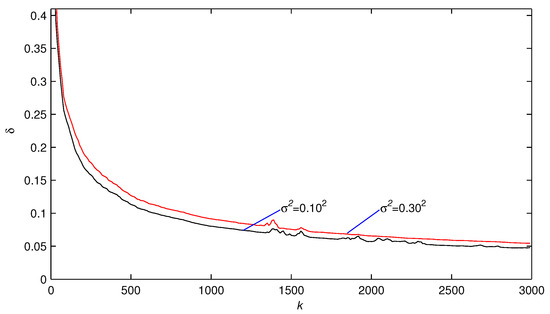
Figure 7. The F-M-ML-MIESG estimation errors versus k with different ${\sigma }^2$ ($p=9$).

From these simulations, it can be observed that

• The parameter estimation errors of the F-M-ML-MIESG method decease as k increases, as shown in Table 1 and Table 2 and Figure 3.
• The parameter estimation errors of the F-M-ML-MIESG algorithm become smaller as p increases, as shown in Figure 4 and Figure 6.
• Under the same noise variances, when $p\ge 2$, the F-M-ML-MIESG method generates more accurate parameter estimates than the F-M-ML-RESG method, as shown in Figure 4 and Figure 6.
• For the same data length and the same innovation length, the F-M-ML-MIESG method converges quickly to the true values as the noise variance decreases, as shown in Figure 5 and Figure 7.

6. Conclusions

This paper considers the parameter estimation of the linear M-CARARMA system with an ARMA noise. By means of an adaptive linear filter, the subsystem identification model is simplified, then an F-M-ML-MIESG method is discussed by introducing the multi-innovation identification theory to the stochastic gradient method. The purpose of an adaptive filter is to improve the parameter estimation accuracy by filtering the observed data without changing the relationship between input and output data. Both the model decomposition technique and the data filtering technique are used to reduce the system complexity, and the identification model is simplified. The simulation validation demonstrates that the F-M-ML-MIESG method provides a higher parameter estimation accuracy than the F-M-ML-RESG method when $p\ge 2$. The proposed filtering-based parameter identification methods for multivariable stochastic systems in this paper can be extended to study the identification issues of other scalar and multivariable stochastic systems with colored noises [61,62,63,64,65,66] and can be applied to some engineering application systems [67,68,69,70,71,72,73] such as filtering, estimation, prediction [74,75,76,77,78,79,80,81], and so on.