Admissible Semimorphisms of icl-Groupoids

Abstract

If M is an algebra in a semidegenerate congruence-modular variety $\mathcal{V}$, then the set $Con(M)$ of congruences of M is an integral complete l-groupoid (= $icl$-groupoid). For any morphism $f:M\to N$ of $\mathcal{V}$, consider the map $f^{•}:Con(M)\to Con(N)$, where, for each congruence $\epsilon$ of M, $f^{•}(\epsilon )$ is the congruence of N generated by $f(\epsilon )$. Then, $f^{•}$ is a semimorphism of $icl$-groupoids, i.e., it preserves the arbitrary joins and the top congruences. The neo-commutative $icl$-groupoids were introduced recently by the author as an abstraction of the lattices of congruences of Kaplansky neo-commutative rings. In this paper, we define the admissible semimorphisms of $icl$-groupoids. The basic construction of the paper is a covariant functor defined by the following: $(1)$ to each semiprime and neo-commutative $icl$-groupoid A, we assign a coherent frame $R(A)$ of radical elements of A; and $(2)$ to an admissible semimorphism of $icl$-groupoids $u:A\to B$, we assign a coherent frame morphism $u^{\rho }:R(A)\to R(B)$. By means of this functor, we transfer a significant amount of results from coherent frames and coherent frame morphisms to the neo-commutative $icl$-groupoids and their admissible semimorphisms. We study the m-prime spectra of neo-commutative $icl$-groupoids and the going-down property of admissible semimorphisms. Using some transfer properties, we characterize some classes of admissible semimorphisms of $icl$-groupoids: Baer and weak-Baer semimorphisms, quasi r-semimorphisms, quasi $r^{*}$-semimorphisms, quasi rigid semimorphisms, etc.

1. Introduction

The integral complete l-groupoids (= $icl$-groupoids) are multiplicative lattices in which several properties of ideals of the unital rings can be abstractized (see [1]).

Let A be an algebra in a congruence-modular variety $\mathcal{V}$. Then, the complete lattice $Con(A)$ of the congruences of A is endowed with a binary operation $[·,·]$, named commutator operation (see [2]). The semidegenerate varieties were introduced by Kollar in [3] by the property that their nontrivial algebras have one-element subalgebras. An important remark is that for any algebra A in a semidegenerate congruence-modular variety $\mathcal{V}$, the lattice $Con(A)$ becomes an $icl$-groupoid. In this way, the $icl$-groupoids offer a setting for an abstract theory for lattices of congruences of algebras in a semidegenerate congruence-modular variety.

The variety $\mathcal{V}$ can be organized as a category (denoted also by $\mathcal{V}$) in an usual way: the objects are the algebras of $\mathcal{V}$ and the morphisms are the homomorphisms between these algebras. In the case of studying the functorial properties of important constructions, it is preferable not to work with the entire class of homomorphisms but with some of its subclasses. For example, the admissible morphisms of $\mathcal{V}$ (defined in [4]) are necessary in the study of the functoriality of reticulation.

Naturally, the challenge lies in finding an abstract version of the morphisms of $\mathcal{V}$ and their properties. With each morphism $f:A\to B$ of $\mathcal{V}$, we canonically associate the function $f^{•}:Con(B)\to Con(A)$, which maps any congruence $\chi$ of A to its inverse image $f^{-1}(\chi )$. The assignment $f\mapsto f^{•}$ is the vehicle by which we determine the entities that abstract morphisms. In general, $f^{•}$ is not a morphism of $icl$-groupoids; it preserves the arbitrary joins and the top congruences, but not the commutator operation. This observation leads to the notion of semimorphism of $icl$-groupoids; they will preserve the arbitrary joins and the top elements but not the multiplication.

In this paper, we will study some important classes of semimorphisms of $icl$-groupoids. First of all, we will define and characterize the admissible semimorphisms as an abstraction of admissible morphisms in a semidegenerate congruence- modular variety $\mathcal{V}$. Remarkable properties of some classes of morphisms in $\mathcal{V}$ will be highlighted, which can be extended to properties of the admissible semimorphisms of $icl$-groupoids. The most important results of this paper will be obtained for the admissible semimorphisms of neo-commutative $icl$-groupoids. The reason for this choice is that in the proofs of most of the results, Lemma 4 is used, which describes the radical of an element of a neo-commutative element $icl$-groupoid.

We will now briefly present the structure of this paper. Section 2 contains a collection of notions and elementary facts on integral complete l-groupoids (the material is contained in [1,5,6,7]). Section 3 recalls some definitions and results from universal algebra: the commutator operation on congruences of algebras in congruence-modular varieties [2], semidegenerate varieties [3,8], and neo-commutative algebras. For the notions of universal algebra that are not mentioned in this paper, we refer the reader to the monograph [9].

In Section 4, we find the definition of the admissible morphisms of $icl$-groupoids and more of their characterizations. The category $NCom-iclG{R}^{*}$ of neo-commutative $icl$-groupoids and their admissible coherent semimorphisms is introduced as the framework for most of the results of this paper. Theorem 2 allows for the construction of the covariant functor ${(·)}^{\rho }$ from $NCom-iclG{R}^{*}$ to the category $CohFrm$ of coherent frames. The functor ${(·)}^{\rho }$ will be used to transfer some properties of the morphisms of $NCom-iclG{R}^{*}$ to the morphisms of $CohFrm$ and vice versa. The transfer properties associated with this functor will be the main tool for most of the proofs presented in this paper.

Section 5 deals with the minimal m-prime elements of a semiprime neo-commutative $icl$-groupoid A. We first characterize the minimal m-prime elements of A, and then, we study two topologies on the set $Min(A)$ of these elements. Consequently, we obtain two topological spaces: $Mi{n}_Z(A)$, endowed with a Zariski-style topology, and $Mi{n}_F(A)$, endowed with a flat topology.

Following some ideas of [10], in Section 6, we study the going-down property for the category $NCom-iclG{R}^{*}$. We prove that the functor ${(·)}^{\rho }:NCom-iclG{R}^{*}\to CohFrm$ preserves the going-down property, and then we obtain a characterization theorem for the admissible semimorphisms of $NCom-iclG{R}^{*}$ fulfilling the going-down property. We use the going-down property to characterize the neo-commutative $icl$-groupoids of Krull dimension 0 and Krull dimension at most 1. In Section 7, we define the Baer and weak-Baer morphisms of the category $NCom-iclG{R}^{*}$ and we prove two theorems for their characterization.

Section 8 deals with three classes of morphisms of $NCom-iclG{R}^{*}$: quasi r-morphisms, quasi $r^{*}$-morphisms, and quasi morphisms. They generalize three classes of ring extensions studied in [11]: quasi r-extensions, quasi $r^{*}$-extensions, and quasi rigid extensions. We prove that the functor ${(·)}^{\rho }$ preserves these three types of morphisms, and we obtain the generalizations of some results of [11]. Among them, we mention the algebro-topological characterization characterizations of the quasi r-morphisms and the quasi $r^{*}$-morphisms of $NCom-iclG{R}^{*}$.

2. Preliminaries on Integral Complete l-Groupoids

This section contains some notions and basic properties of the integral complete l-groupoids (see ref. [1]).

According to ref. [1] (p.172), an algebraic structure $(A,\bigvee ,\wedge ,·,0,1)$ is a complete l-groupoid (=$cl$-groupoid) if $(A,\bigvee ,\wedge ,0,1)$ is a complete lattice and · is a multiplication satisfying the following infinite distributive law: for all $S\subseteq A$ and $a\in A$, $a·(\bigvee S)=\bigvee \{a·x|s\in S\}$ and $(\bigvee S)·a=\bigvee \{x·a|x\in S\}$. The $cl$-groupoid $(A,\bigvee ,\wedge ,·,0,1)$ will be shortly denoted by A and we shall write $ab$ instead of $a·b$. A is said to be an integral $cl$ - groupoid (=$icl$-groupoid) if $a1=1a=a$ for any $a\in A$. We shall denote by $K(A)$ the set of compact elements of A. A is said to be algebraic if any $a\in A$ has the form $a=\bigvee X$ for some subset X of $K(A)$.

Let $A,B$ be two $icl$-groupoids. A map $u:A\to B$ is said to be a morphism of $icl$-groupoids if it preserves the arbitrary joins, the multiplication, and the top elements.

Lemma 1 

([1]). Let A be an integral $cl$-groupoid and $a,b,c\in A$. Then, the following holds:

(1) 

$a\le b$ implies $ac\le bc$ and $ca\le cb$;

(2) 

$ab\le a\wedge b$.

By Lemma 1 (2), the $icl$-groupoids are complete multiplicative lattices in the sense of Definition 2.1 of [5]. They include some important classes of complete multiplicative lattices: quantales [12,13], frames [14,15], etc. A quantale is an $icl$-groupoid in which the multiplication is associative, and a frame is a quantale in which the multiplication coincides with the meet operation.

As usual, we define the left and the right residuation operations on each $icl$-groupoid A: $a{\to }_{l}b=\bigvee \left\{x\right|xa\le b\}$ and $a{\to }_{r}b=\bigvee \left\{x\right|ax\le b\}$. Thus, A becomes a residuated lattice (cf. [1], p. 327). The basic arithmetical properties of a residuated lattice can be found in [16]. The two annihilator operations on A are defined by

$a^{{\perp }_l}=a{\to }_{l}0=\bigvee \{x\in A|xa=0\}$ and $a^{{\perp }_l}=a{\to }_{r}0=\bigvee \{x\in A|ax=0\}$.

Let us fix an algebraic $icl$-groupoid A such that $1\in K(A)$.

Following Definition 6.1 of [5], for any element $a\in A$, the following sequence $a^{(0)},a^{(1)},\cdots ,a^{(n)},\dots$ is defined by an induction on n:

$$a^{(0)}=a,a^{(n+1)}={(a^{(n)})}^2={(a^2)}^{(n)}$$

(1)

By using Lemma 1 (1), it follows that the sequence $a^{(0)},a^{(1)},\cdots ,a^{(n)},\dots$ is monotone decreasing.

Lemma 2 

([5]). If $a,b\in A$ and n is a natural number, then the following inequality holds:

$${(a\vee b)}^{(2n)}\le a^{(n)}\vee b^{(n)}$$

(2)

An element $p<1$ of an $icl$-groupoid A is m-prime if for all $a,b\in A$, $ab\le p$ implies $a\le p$ or $b\le p$. If A is an algebraic $icl$-groupoid, then $p<1$ is m-prime if and only if for all $c,d\in K(A)$, $cd\le p$ implies $c\le p$ or $d\le p$. The set $Spec(A)$ of m-prime elements of A is called the m-prime spectrum of A. We denote by $Min(A)$ the set of minimal m-prime elements of A. For each $p\in Spec(A)$, there exists $q\in Min(A)$ such that $q\le p$.

Following [1,5], the radical $\rho (a)={\rho }_A(a)$ of an element $a\in A$ is defined by $\rho (a)=\bigwedge \{p\in Spec(A)|a\le p\}$; if $a=\rho (a)$, then a is a radical element. We shall denote by $R(A)$ the set of radical elements of A. A is said to be semiprime if $\rho (0)=0$.

According to Section 3 of [5], the function ${\rho }_A:A\to A$ is a closure operator on A. Then, ${\displaystyle \rho (\underset{i\in I}{\bigvee }{a}_i)=\rho (\underset{i\in I}{\bigvee }\rho (a_i))}$, for any family ${\left\{a_i\right\}}_{i\in I}$ of elements of A. If ${\left\{a_i\right\}}_{i\in I}$ is a family of radical elements, then we denote ${\displaystyle \underset{i\in I}{\overset{·}{\bigvee }}{a}_i=\rho (\underset{i\in I}{\bigvee }{a}_i)}$. Then, ${\displaystyle (R(A),\stackrel{·}{\bigvee },\wedge ,\rho (0),1)}$ is a frame (see Example 3.5(a) of [5]).

Using (1), we obtain $\rho (a^{(n)})=\rho (a)$, for any $a\in A$ and for all natural numbers n.

For any element a of A, we denote $D_A(a)=D(a)=\{p\in Spec(A)|a\nleqq p\}$ and $V_A(A)=V(a)=\{p\in Spec(A)|a\le p\}$.

Remark 1 

([5]). For all $a,b$ of A and $S\subseteq A$, the following hold:

• $V(1)=\varnothing$; $V(0)=Spec(A)$; $V(ab)=V(a)\cup V(b)$; $V(\bigvee S)={\bigcap }_{s\in S}V(s)$;
• $D(0)=\varnothing$; $D(1)=Spec(A)$; $D(ab)=D(a)\cap D(b)$; $D(\bigvee S)={\bigcup }_{s\in S}D(s)$.

Proposition 1 

([5]). Let $a,b$ be two elements of A. Then, the following hold:

(1) 

$V(\rho (a))=V(a)$; $D(\rho (a))=D(a)$;

(2) 

$\rho (a)\le \rho (b)$ iff $V(b)\subseteq V(a)$ iff $D(a)\subseteq D(b)$;

(3) 

$\rho (a)=\rho (b)$ iff $V(a)=V(b)$ iff $D(a)=D(b)$.

According to Remark 1 and Proposition 1, $Spec(A)$ is endowed with a topology whose open sets are ${(D(a))}_{a\in A}$. This topological space will be denoted by $Spe{c}_Z(A)$. If A is an algebraic $icl$-groupoid, then the family ${\left\{D(c)\right\}}_{c\in K(A)}$ is a basis of open sets for this topology. The topology introduced here generalizes the Zariski topology (defined on the prime spectrum $Spec(R)$ of a commutative ring R [17]).

Definition 1. 

An algebraic $icl$-groupoid A is said to be a quasi-commutative groupoid if $1\in K(A)$, and for all compact elements $c,d$ of A, there exists $e\in K(A)$ such that $e\le cd$ and $\rho (e)=\rho (cd)$.

Definition 2. 

A neo-commutative $icl$-groupoid is an algebraic $icl$-groupoid A such that $1\in K(A)$ and $K(A)$ is closed under multiplication.

Remark 2. 

If R is a unital ring, then the following hold:

• R is a quasi-commutative ring in the sense of [18] iff $Id(R)$ is a quasi-commutative $icl$-groupoid;
• R is a neo-commutative ring in the sense of [19] iff $Id(R)$ is a neo-commutative $icl$-groupoid.

Lemma 3. 

If A is quasi-commutative groupoid, then $R(A)$ is a coherent frame.

Proof. 

By Theorem 4.18 of [6], the quasi-commutative groupoid A is a spectral groupoid (in the sense of Definition 4.16 of [6]); so, the m-prime spectrum $Spec(A)$ of A is a spectral space. Therefore, by Theorem 3.6 of [5], it follows that $R(A)$ is a compact algebraic frame, closed under finite intersections. Thus, $R(A)$ is a coherent frame.

□

Remark 3. 

Any neo-commutative $icl$-groupoid is a quasi-commutative groupoid. Therefore, according to Lemma 3, if A is a neo-commutative groupoid, then $R(A)$ is a coherent frame.

Lemma 4. 

If A is a neo-commutative $icl$-groupoid, then for any $a\in A$, we have

$\rho (a)=\bigvee \{c\in K(A)|c^{(n)}\le a$ for some integer $n\ge 0\}$.

Proof. 

The equality $\rho (a)=\bigvee \{c\in K(A)|c^{(n)}\le a$ for some integer $n\ge 0\}$ follows by applying Theorem 7.4(b) of [5].

□

Let A be a neo-commutative $icl$-groupoid. For all $c,d\in K(A)$, we have $D(c)\cap D(d)=D(cd)$ and $cd\in K(A)$. Then, the family ${\left\{D(c)\right\}}_{c\in K(A)}$ is closed under finite intersections; so, it is a base of the topological space $Spe{c}_Z(A)$.

We also remark that for all $c,d\in K(A)$, $V(c)\cap V(d)=V(c\vee d)$ and $c\vee d\in K(A)$; so, the family ${\left\{D(c)\right\}}_{c\in K(A)}$ is a base for a topology on $Spec(A)$ (named the flat topology or the inverse topology). We shall denote by $Spe{c}_F(A)$ the m-prime spectrum $Spec(A)$ endowed with the flat topology.

3. Congruences of Algebras in a Semidegenerate Congruence-Modular Variety

Let A be an algebra of a fixed congruence $\tau$. We denote by $Con(A)$ the complete lattice of the congruences of A; ${\Delta }_A$ and ${\nabla }_A$ are the bottom congruence and the top congruence of $Con(A)$. If X is a subset of $A^2$, then $C{g}_A(X)$ is the congruence of A generated by X; if $a,b\in A$, then $C{g}_A(a,b)$ denotes the (principal) congruence generated by $\{(a,b)\}$. The finitely generated congruences of A are the compact elements of the $Con(A)$; $K(A)$ denotes the set of compact congruences of A.

Let $A/\theta$ be the quotient algebra of A associated with $\theta \in Con(A)$; we denote by $a/\theta$ the congruence class of $a\in A$ (modulo $\theta$). If $p_{\theta }:A\to A/\theta$ is the canonical surjective morphism (defined by $p_{\theta }(a)=a/\theta$), then $(C{g}_A(X)\vee \theta )/\theta =C{g}_{A/\theta }(X/\theta )$ for each subset X of $A^2$. Therefore, we obtain the following description of the set of compact congruences of $A/\theta$: $K(A/\theta )=\{(\alpha \vee \theta )/\theta |\alpha \in K(A)\}=p_{\theta }(K(A))$.

Let us fix a congruence-modular variety $\mathcal{V}$ of algebras of signature $\tau$. Recall from [2] (p.31), that the commutator is the greatest operation ${[·,·]}_A$ on the congruence lattices $Con(A)$ of members A of $\mathcal{V}$ such that for any surjective morphism $f:A\to B$ of $\mathcal{V}$ and for any $\alpha ,\beta \in Con(A)$, the following axioms are fulfilled:

$${[\alpha ,\beta ]}_A\subseteq \alpha \cap \beta$$

(3)

$${[\alpha ,\beta ]}_A\vee Ker(f)=f^{-1}({[f(\alpha \vee Ker(f)),f(\beta \vee Ker(f))]}_B).$$

(4)

By (4), we obtain that for all congruences $\alpha ,\beta ,\theta$ of A, the following equality holds:

$$({[\alpha ,\beta ]}_A\vee \theta )/\theta ={[(\alpha \vee \theta )/\theta ,(\beta \vee \theta )/\theta ]}_{A/\theta }.$$

(5)

Recall from [2] that the commutator operation is commutative, increasing in each argument and distributive with respect to arbitrary joins. If there is no danger of confusion, then we write $[\alpha ,\beta ]$ instead of ${[\alpha ,\beta ]}_A$.

Proposition 2. 

(see [2], Theorem 8.5) For any congruence-modular variety $\mathcal{V}$, the following properties are equivalent:

(1) 

$[{\nabla }_A,{\nabla }_A]={\nabla }_A$, for all $A\in \mathcal{V}$;

(2) 

$[\theta ,{\nabla }_A]=\theta$, for all $A\in \mathcal{V}$ and $\theta \in Con(A)$.

According to Kollar’s paper [3], a variety $\mathcal{V}$ is said to be semidegenerate if no nontrivial algebra in $\mathcal{V}$ has one-element subalgebras. By Kollar’s Theorem ([3], p. 266), a variety $\mathcal{V}$ is semidegenerate if and only if for any algebra A in $\mathcal{V}$, the congruence ${\nabla }_A$ is compact.

Proposition 3. 

(see [8], Lemma 5.2(2)) If $\mathcal{V}$ is a semidegenerate congruence-modular variety, then $[{\nabla }_A,{\nabla }_A]={\nabla }_A$, for each algebra A in $\mathcal{V}$.

Remark 4. 

Let $\mathcal{V}$ be a semidegenerate congruence-modular variety and A an algebra of $\mathcal{V}$. By applying Propositions 2 and 3, it follows that $[\theta ,{\nabla }_A]=\theta$, for any $\theta \in Con(A)$. Then, the structure $(Con(A),\vee ,\wedge ,[·,·],\to ,{\Delta }_A,{\nabla }_A)$ is an algebraic $icl$-groupoid.

Following [19], a ring R is neo-commutative if the product of two finitely generated ideals of R is a finitely generated ideal. We note that this notion can be generalized to a universal algebra framework: an algebra A of the semidegenerate congruence-modular variety $\mathcal{V}$ is said to be neo-commutative if $K(A)$ is closed under commutator operation.

4. Admissible Semimorphisms of $icl$-Groupoids

4.1. Admissible Semimorphisms

Let $\mathcal{V}$ be a semidegenerate congruence-modular variety and $f:M\to N$ a morphism of $\mathcal{V}$. Let us consider the functions $f^{•}:Con(M)\to Con(N)$ and $f^{*}:Con(N)\to Con(M)$ defined by $f^{•}(\theta )=C{g}_N(f(\theta ))$ and $f^{*}(\chi )=f^{-1}(\chi )$, for all $\theta \in Con(M)$ and $\chi \in Con(N)$.

Lemma 5. 

The following hold:

(1) 

$f^{•}$ is the left adjoint of $f^{*}$;

(2) 

$f^{•}$ preserves the arbitrary joins and $f^{*}$ preserves the arbitrary meets.

Definition 3. 

Let $A,B$ be two $icl$-groupoids. A map $u:A\to B$ is said to be a semimorphism of $icl$-groupoids if it preserves the arbitrary joins. A semimorphism of $icl$-groupoids $u:A\to B$ is a morphism of $icl$-groupoids if it preserves the multiplication.

Remark 5. 

According to Lemma 5, if $f:M\to N$ is a morphism of a semidegenerate congruence-modular variety $\mathcal{V}$, then $f^{•}:Con(M)\to Con(N)$ is a semimorphism of $icl$-groupoids.

Let $u:A\to B$ be a semimorphism of $icl$-groupoids. Then, u has a right adjoint $u_{*}:B\to A$ defined by $u_{*}(b)=\bigvee \{a\in A|u(a)\le b\}$, for any $b\in B$. Then, for all $a\in A,b\in B$, $u(a)\le b$ if and only if $a\le u_{*}(b)$.

Recall that an algebraic $icl$-groupoid is coherent if 1 is compact and $K(A)$ is closed to multiplication. The semimorphism of $icl$-groupoids $u:A\to B$ is said to be coherent if $u(K(A))\subseteq K(B)$.

Lemma 6. 

If $u:A\to B$ is a semimorphism of $icl$-groupoids, then the following hold:

(1) 

$a\le u_{*}(u(a))$, for any $a\in A$;

(2) 

$u(u_{*}(b))\le b$, for any $b\in B$.

The following lemma is well known. For the sake of completeness, we will present its proof.

Lemma 7. 

Assume that $A,B$ are two algebraic $icl$-groupoids and $u:A\to B$ is a surjective semimorphism of $icl$-groupoids. If u preserves the compact elements, then $u(K(A))=K(B)$.

Proof. 

By hypothesis, $u(K(A))\subseteq K(B)$. In order to prove the converse inclusion, let d be a compact element of B. However, u is a surjective map, so one can find an element x of A such that $d=u(x)$. Since A is an algebraic $icl$-groupoid, $x={\bigvee }_{i\in I}{c}_i$ for a family ${(c_i)}_{i\in I}$ of compact elements of A. Then, $d=u(x)={\bigvee }_{i\in I}u(c_i)$ and $\left\{u(c_i)\right|i\in I\}\subseteq K(B)$. Then, there exists a finite subset J of I such that $d\le {\bigvee }_{i\in J}u(c_i)=u({\bigvee }_{i\in J}{c}_i)\le d$. If $c={\bigvee }_{i\in J}{c}_i$, then $c\in K(A)$ and $d=u(c)$. It follows that $K(B)\subseteq u(K(A))$, so $u(K(A))=K(B)$.

□

Theorem 1. 

If $u:A\to B$ is a semimorphism of $icl$-groupoids, then the following are equivalent:

(1) 

For any $p\in B$, $p\in Spec(B)$ implies $u_{*}(p)\in Spec(A)$;

(2) 

${\rho }_B(u(ab))={\rho }_B(u(a)u(b))$, for all $a,b\in A$;

(3) 

${\rho }_B(u(ab))={\rho }_B(u(a))\wedge {\rho }_B(u(b))$, for all $a,b\in A$;

(4) 

${\rho }_B(u(ab))\ge {\rho }_B(u(a)u(b))$, for all $a,b\in A$.

Proof. 

$(1)\Rightarrow (2)$ Let p be an m-prime element of B and $a,b\in A$. By hypothesis (1), $u_{*}(p)$ is an m-prime element of A. Therefore, by using the adjointness of u and $u_{*}$, we obtain the following equivalences:

$u(ab)\le p$ iff $ab\le u_{*}(p)$ iff $a\le u_{*}(p)$ or $b\le u_{*}(p)$ iff $u(a)\le p$ or $u(b)\le p$ iff $u(a)u(b)\le p$.

Then, $V_B(u(ab))=V_B(u(a)u(b))$, and hence, by using Proposition 1 (3), we obtain ${\rho }_B(u(ab))={\rho }_B(u(a)u(b))$.

$(2)\Rightarrow (1)$ Assume that $p\in Spec(B)$. We have to prove that $u_{*}(p)\in Spec(A)$. Let $a,b$ be two elements of A. By using the adjointness property and hypothesis (2), we obtain the following equivalences:

$ab\le u_{*}(p)$ iff $u(ab)\le p$ iff ${\rho }_B(u(ab))\le p$ iff ${\rho }_B(u(a)u(b))\le p$ iff $u(a)u(b)\le p$ iff $u(a)\le p$ or $u(b)\le p$ iff $a\le u_{*}(p)$ or $b\le u_{*}(p)$.

It follows that $u_{*}(p)$ is an m-prime element of A.

$(2)\iff (3)$ According to Lemma 3.4 of [5], we have ${\rho }_B(xy)={\rho }_B(x)\wedge {\rho }_B(y)$ for all $x,y\in B$. Then, ${\rho }_B(u(a)u(b))={\rho }_B(u(a))\wedge {\rho }_B(u(b))$, so the equivalence of (2) and (3) follows.

$(3)\iff (4)$ Obviously.

□

Definition 4. 

A semimorphism of $icl$-groupoids $u:A\to B$ is said to be admissible if it fulfills the equivalent properties of 1.

Recall from [20] that a morphism $f:M\to N$ of a semidegenerate congruence-modular variety $\mathcal{V}$ is admissible if $f^{*}(\varphi )\in Spec(M)$ for each $\varphi \in Spec(N)$. Then, $f^{•}:Con(M)\to Con(N)$ is an admissible semimorphism of $icl$-groupoids if and only if f is an admissible morphism of $\mathcal{V}$.

Corollary 1. 

If $u:A\to B$ is an admissible semimorphism of $icl$-groupoids, then ${\rho }_B(u(a^{(n)}))={\rho }_B(u(a))$, for any $a\in A$ and for any integer $n\ge 0$.

Proof. 

We shall prove the desired equality by induction on n. For $n=1$, the equality is obvious. Suppose that the equality holds for the natural number n and for any $a\in A$. We need to show that ${\rho }_B(u(a^{(n+1)}))={\rho }_B(u(a))$ for any $a\in A$. Recall from (1) that $a^{(n+1)}={(a^2)}^{(n)}$. Therefore, using the induction hypothesis and Theorem 1(3), we obtain

$${\rho }_B(u(a^{(n+1)}))={\rho }_B(u({(a^2)}^{(n)}))={\rho }_B(u(a^2))={\rho }_B((u(a))\wedge {\rho }_B((u(a))={\rho }_B(u(a)).$$

□

Corollary 2. 

Assume that $A,B$ are two algebraic $icl$-groupoids and $u:A\to B$ is a semimorphism of $icl$-groupoids. Then, the following are equivalent:

(1) 

For any $p\in B$, $p\in Spec(B)$ implies $u_{*}(p)\in Spec(A)$;

(2) 

${\rho }_B(u(cd))={\rho }_B(u(c)u(d))$, for all $c,d\in K(A)$;

(3) 

${\rho }_B(u(cd))={\rho }_B(u(c))\wedge {\rho }_B(u(d))$, for all $c,d\in K(A)$;

(4) 

${\rho }_B(u(cd))\ge {\rho }_B(u(c)u(d))$, for all $,d\in K(A)$.

Proof. 

$(1)\Rightarrow (2)\Rightarrow (3)\Rightarrow (4)$ By Theorem 1.

$(4)\Rightarrow (1)$ Let $a,b\in K(A)$, so there exist two collections ${\left\{c_i\right\}}_{i\in I},{\left\{d_j\right\}}_{j\in J}$ of compact elements of A such that $a={\bigvee }_{i\in I}{c}_i$ and $b={\bigvee }_{j\in J}{d}_j$ (because A is an algebraic $icl$-groupoid).

Since u is a semimorphism of $icl$-groupoids and ${\rho }_B:B\to R(B)$ preserves the arbitrary joins, the following identities hold:

$${\displaystyle {\rho }_B(u(ab))={\rho }_B(u(\underset{i\in I,j\in J}{\bigvee }{c}_i{d}_j))={\rho }_B(\underset{i\in I,j\in J}{\bigvee }u(c_i{d}_j))=\underset{i\in I,j\in J}{\overset{·}{\bigvee }}{\rho }_B(u(c_i{d}_j))}$$

$${\displaystyle {\rho }_B(u(a)u(b))={\rho }_B(\underset{i\in I,j\in J}{\bigvee }u(c_i)u(d_j))=\underset{i\in I,j\in J}{\overset{·}{\bigvee }}{\rho }_B(u(c_i)u(d_j)).}$$

By hypothesis $(4)$, ${\rho }_B(u(c_i{d}_j))\ge {\rho }_B(u(c_i)u(d_j))$, for all $i\in I$ and $j\in J$, and hence, ${\rho }_B(u(ab))\ge {\rho }_B(u(a)u(b))$. Therefore, by once again using Theorem 1, it follows that for any $p\in B$, $p\in Spec(B)$ implies $u_{*}(p)\in Spec(A)$.

□

In general, a semimorphism of $icl$-groupoids does not preserve the top elements (see ref. [21]).

Lemma 8. 

If $u:A\to B$ is an admissible morphism of $icl$-groupoids and the top elements of $A,B$ are compact, then $u(1)=1$.

Proof. 

Assume by absurdum that $u(1)<1$, so $u(1)\le m$ for some $m\in Max(A)$. Therefore, using Lemma 6 (1) and the hypothesis, we obtain the contradiction $1\le u_{*}(u(1))\le u_{*}(m)\in Spec(A)$. It follows that $u(1)=1$.

□

Proposition 4. 

If A is a neo-commutative groupoid, then $K(R(A))={\rho }_A(K(A))$.

Proof. 

Firstly, we shall prove that ${\rho }_A(K(A))\subseteq K(R(A))$. Assume that $x\in {\rho }_A(K(A))$; hence, $x={\rho }_A(c)$ for some $c\in K(A)$. In order to show that x is a compact element of the frame $R(A)$, consider a set ${\left\{a_i\right\}}_{i\in I}\subseteq R(A)$ such that ${\displaystyle x\le \underset{i\in I}{\overset{·}{\bigvee }}{a}_i}$, and hence, $c\le {\rho }_A(c)\le {\rho }_A({\bigvee }_{i\in I}{a}_i)$. By Lemma 4, there exists an integer $n\ge 0$ such that $c^{(n)}\le {\bigvee }_{i\in I}{a}_i$. But $c^{(n)}\in K(A)$ (because A is neo-commutative), so $c^{(n)}\le {\bigvee }_{i\in J}{a}_i$ for some finite subset J of I. Then, ${\displaystyle x={\rho }_A(c)={\rho }_A(c^{(n)})\le {\rho }_A({\bigvee }_{i\in J}{a}_i)=\underset{i\in J}{\overset{·}{\bigvee }}{a}_i}$, hence $x\in K(R(A))$. The map ${\rho }_A:A\to R(A)$ is a surjective morphism of $icl$-groupoids (it preserves the arbitrary joins, the finite meets, and the top elements). We have proven that ${\rho }_A$ preserves the compacts elements; therefore, using Lemma 7, we obtain $K(R(A))={\rho }_A(K(A))$.

□

4.2. The Main Functorial Construction

Let us consider the following categories:

-

$Alg-iclGR$: The category of algebraic $icl$-groupoids and the usual morphisms of $icl$-groupoids;

-

$Alg-iclG{R}^{*}$: The category of algebraic $icl$-groupoids and the admissible semimorphisms of $icl$-groupoids;

-

$NCom-iclGR$: The category of neo-commutative $icl$-groupoids and their coherent morphisms;

-

$NCom-iclG{R}^{*}$: The category of neo-commutative $icl$-groupoids and their admissible coherent semimorphisms.

Let $u:A\to B$ be a morphism of $Alg-iclG{R}^{*}$. For any $a\in R(A)$, we set $u^{\rho }(a)={\rho }_B(u(a))$. Then, we obtain a map $u^{\rho }:R(A)\to R(B)$.

Theorem 2. 

If $u:A\to B$ is a morphism of the category $Alg-iclG{R}^{*}$, then the following hold:

(1) 

The following diagram is commutative:

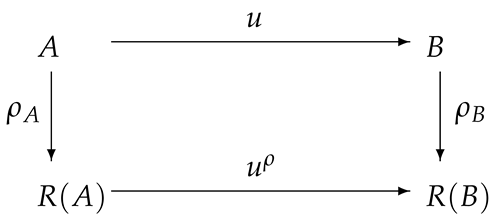
(2) 

$u^{\rho }:R(A)\to R(B)$ is the unique frame morphism for which the previous diagram is commutative;

• If u is a morphism of $NCom-iclG{R}^{*}$, then $u^{\rho }$ is a coherent frame morphism.

Proof. 

$(1)$ Let a be an element of A. We have to prove that ${\rho }_B(u(a))=u^{\rho }({\rho }_A(a))$. By the definition of the map $u^{\rho }$, we have $u^{\rho }({\rho }_A(a))={\rho }_B(u({\rho }_A(a)))$, so we need to show that ${\rho }_B(u(a))={\rho }_B(u({\rho }_A(a)))$.

From $a\le {\rho }_A(a)$, we obtain the inequality ${\rho }_B(u(a))\le {\rho }_B(u({\rho }_A(a)))$ (because ${\rho }_A$ and u are isotone maps). For proving the converse inequality ${\rho }_B(u({\rho }_A(a)))\le {\rho }_B(u(a))$, it suffices to check that $u({\rho }_A(a))\le {\rho }_B(u(a))$. Let q be an m-prime element of B such that $u(a)\le q$; hence, $a\le u_{*}(q)$ (by the adjointness property). The semimorphism u is supposed to be admissible, so $u_{*}(q)\in Spec(A)$; therefore, ${\rho }_A(a)\le q$. A new application of the adjointness property gives $u({\rho }_A(a))\le u_{*}(q)$. It follows that $u({\rho }_A(a))\le {\rho }_B(u(a))$, and so, the equality ${\rho }_B(u(a))=u^{\rho }({\rho }_A(a))$ is verified. Thus, the diagram is commutative.

$(2)$ Now, we shall prove that $u^{\rho }:R(A)\to R(B)$ is a frame morphism. Let ${\left\{a_i\right\}}_{i\in I}$ be a family of radical elements of the frame $R(A)$. By using the commutativity of the diagram and the fact that u preserves the arbitrary joins, we obtain

$${\displaystyle u^{\rho }(\underset{i\in I}{\overset{·}{\bigvee }}{a}_i)=u^{\rho }({\rho }_A(\underset{i\in I}{\bigvee }{a}_i))={\rho }_B(u((\underset{i\in I}{\bigvee }{a}_i))={\rho }_B(\underset{i\in I}{\bigvee }u(a_i))=\underset{i\in I}{\overset{·}{\bigvee }}{u}^{\rho }(a_i).}$$

Then, $u^{\rho }$ preserves the arbitrary joins. Let $a,b$ be two elements of $R(A)$, so $a={\rho }_A(x),b={\rho }_A(y)$ for some elements $x,y$ of A. By hypothesis, the semimorphism u is admissible. Therefore, by using the commutativity of the diagram and Theorem 1, the following equalities hold:

$$u^{\rho }(a\wedge b)=u^{\rho }({\rho }_A(x)\wedge {\rho }_A(y))=u^{\rho }({\rho }_A(xy))={\rho }_B(u(xy))=$$

$${\rho }_B(u(x))\wedge {\rho }_B(u(y))=u^{\rho }({\rho }_A(x))\wedge u^{\rho }({\rho }_A(y))=u^{\rho }(a)\wedge u^{\rho }(b).$$

Then, $u^{\rho }$ preserves the finite meets. By hypothesis, u is an admissible semimorphism of $icl$-groupoids. By Lemma 8, we obtain $u(1)=1$; hence, $u^{\rho }(1)={\rho }_B(u(1))={\rho }_B(1)=1$. Thus, $u^{\rho }$ is a frame morphism. The unicity of $u^{\rho }$ follows from the commutativity of the diagram.

$(3)$ Let a be a compact element of the frame $R(A)$. By hypothesis, A is neo-commutative; hence, by applying Proposition 4, there exists a compact element c of A such that $a={\rho }_A(c)$. In accordance with the commutativity of the diagram, we have $u^{\rho }(a)=u^{\rho }({\rho }_A(c))={\rho }_B(u(c))$. We observe that u and ${\rho }_B$ preserve the compact elements (by the hypothesis of $(3)$ and Proposition 1); therefore, $u^{\rho }(a)$ is a compact element of $R(B)$. Therefore, we conclude that $u^{\rho }$ is a coherent frame morphism.

□

If $u:A\to B,v:B\to C$ are two morphisms of the category $Alg-iclG{R}^{*}$, then using Theorem 2, we obtain ${(v\circ u)}^{\rho }=v^{\rho }\circ u^{\rho }$. Thus, the assignments $A\mapsto R(A)$ and $u:A\to B\mapsto u^{\rho }:R(A)\to R(B)$ define a covariant functor ${(·)}^{\rho }:NCom-iclG{R}^{*}\to CohFrm$.

Proposition 5. 

Let $u:A\to B$ be a morphism of $NCom-iclG{R}^{*}$. If $b\in R(B)$, then $u_{*}(b)\in R(A)$.

Proof. 

For proving $u_{*}(b)\in R(A)$, it suffices to check that ${\rho }_A(u_{*}(b))\le u_{*}(b)$. Assume that c is a compact element of A such that $c\le {\rho }_A(u_{*}(b))$.

According to the hypothesis, A is a neo-commutative $icl$-groupoid; hence, by using Lemma 4, one can find an integer $n\ge 0$ such that $c^{(n)}\le u_{*}(b)$, and hence, $u(c^{(n)})\le b$ (by the adjointness property). Then, we obtain ${\rho }_B(u(c^{(n)}))\le {\rho }_B(b)\le b$. According to Corollary 1, we have ${\rho }_B(u(c^{(n)}))={\rho }_B(u(c))$, so $u(c)\le {\rho }_B(u(c))\le b$. A new application of the adjointness property gives $c\le u_{*}(b)$. It follows that ${\rho }_A(u_{*}(b))\le u_{*}(b)$.

□

By Proposition 5, for any morphism $u:A\to B$ of $NCom-iclG{R}^{*}$, we obtain a map $u_{*}{|}_{R(B)}:R(B)\to R(A)$.

Corollary 3. 

For any morphism $u:A\to B$ of $NCom-iclG{R}^{*}$, we have ${(u^{\rho })}_{*}=u_{*}{|}_{R(B)}$.

Proof. 

We need to show that $u_{*}{|}_{R(B)}:R(B)\to R(A)$ is the right adjoint of the frame morphism $u^{\rho }:R(A)\to R(B)$. By virtue of the adjointness property, for all $a\in R(A)$ and $b\in R(B)$, the following equivalences hold:

$u^{\rho }(a)\le b$ iff ${\rho }_B(u(a))\le b$ iff $u(a)\le b$ iff $a\le u_{*}(b)$.

Therefore, $u_{\rho }{|}_{R(B)}$ is the right adjoint of $u^{*}:R(A)\to R(B)$.

□

Assume that $u:A\to B$ is a morphism of $NCom-iclG{R}^{*}$. According to the definition of an admissible semimorphism, one can consider the map $Spec(u):Spec(B)\to Spec(A)$ defined by $Spec(u)(q)=u_{*}(q)$, for any $q\in Spec(B)$.

Lemma 9. 

If $u:A\to B$ is a morphism of $NCom-iclG{R}^{*}$, then for any $a\in A$, the following hold:

(1) 

${(Spec(u))}^{-1}(V_A(a))=V_B(u(a))$;

(2) 

${(Spec(u))}^{-1}(D_A(a))=D_B(u(a))$.

Proof. 

$(1)$ If $q\in Spec(B)$, then $q\in {(Spec(u))}^{-1}(V_A(a))$ iff $u_{*}(q)\in V_A(a)$ iff $a\le u_{*}(q)$ iff $q\in V_B(u(a))$.

$(2)$ Similarly. □

Corollary 4. 

If $u:A\to B$ is a morphism of $NCom-iclG{R}^{*}$, then the map $Spec(u):Spec(B)\to Spec(A)$ is continuous with respect to each of the Stone–Zariski and the flat topologies.

Proof. 

Recall that ${\left\{V_A(c)\right\}}_{c\in K(A)}$ (respectively, ${\left\{V_B(d)\right\}}_{d\in K(B)}$) is a basis for the topological space $Spe{c}_F(A)$ (respectively, $Spe{c}_F(B)$). Let c be a compact element of A. Then, $u(c)$ is a compact element of B (by Proposition 4); so, $V_B(u(c))$ belongs to the basis of $Spe{c}_F(B)$. By virtue of Lemma 9 (1), ${(Spec(u))}^{-1}(V_A(a))$ belongs to the basis of $Spe{c}_F(B)$, and hence, $Spec(u):Spe{c}_F(B)\to Spe{c}_F(A)$ is continuous. The fact that $Spec(u):Spe{c}_Z(B)\to Spe{c}_Z(A)$ is continuous follows in a similar way.

□

5. Minimal m-Prime Spectrum

Let us consider an $icl$- groupoid A such that $1\in K(A)$. We denote by $Min(A)$ the set of minimal m-prime elements of A. For each $p\in Spec(A)$, there exists $q\in Min(A)$ such that $q\le p$. $Min(A)$ is called the minimal m-prime spectrum of A. In Section 2, we observed that the m-prime spectrum $Spec(A)$ of A coincides with the prime spectrum $Spec(R(A))$ of the frame $R(A)$; therefore, $Min(A)=Min(R(A))$.

If M is an algebra of a semidegenerate congruence-modular variety $\mathcal{V}$, then we denote by $Min(M)$ the minimal m-prime spectrum $Min(Con(M))$ of the $icl$-groupoid $Con(M)$. $Min(M)$ will be called the minimal m-prime spectrum of the algebra M.

Recall from [1] that the residuation operations ${\to }_l$ and ${\to }_r$ fulfill the following “residuation properties”: for all $a,b,x\in A$, $x\le a{\to }_{l}b$ iff $xa\le b$ and $a{\to }_{r}b$ iff $ax\le b$. Particularly, $x\le a^{{\perp }_l}$ iff $xa=0$ and $x\le a^{{\perp }_r}$ iff $ax=0$.

Lemma 10 

([6]). If A is semiprime, then for all $a,b\in A$, the following equivalence holds: $ab=0$ if and only if $a\wedge b=0$.

Corollary 5 

([6]). If A is semiprime, then $a^{{\perp }_l}=a^{{\perp }_r}$ for any $a\in A$.

By virtue of Corollary 5, for any element a of a semiprime $icl$-groupoid A, we denote $a^{{\perp }_A}=a^{{\perp }_l}=a^{{\perp }_r}$.

Lemma 11. 

If A is semiprime, then ${({\rho }_A(a))}^{{\perp }_A}=a^{{\perp }_A}$.

Proof. 

Let x be an arbitrary element of A. Since A is semiprime, the following equivalences hold: $x\le {({\rho }_A(a))}^{{\perp }_A}$ iff $x{\rho }_A(a)=0$ iff ${\rho }_A(x{\rho }_A(a))=0$ iff ${\rho }_A(x)\wedge {\rho }_A(a)=0$ iff ${\rho }_A(xa)=0$ iff $xa=0$ iff $x\le a^{{\perp }_A}$. Therefore, we conclude that ${({\rho }_A(a))}^{{\perp }_A}=a^{{\perp }_A}$.

□

Let us denote by → the residuation operation of the frame $R(A)$. Then, for all $a,b,x\in R(A)$, we have $x\le a\to b$ if and only if $x\wedge b\le b$.

Lemma 12. 

Assume that $a,b\in R(A)$. Then, the following hold:

(1) 

$a{\to }_{l}b=a{\to }_{r}b=a\to b$;

(2) 

$a^{{\perp }_{R(A)}}=a{\to }_l{\rho }_A(0)=a{\to }_r{\rho }_A(0)$;

(3) 

If A is semiprime, then $a^{{\perp }_{R(A)}}=a^{{\perp }_A}$;

(4) 

For any $x\in A$, $x{\to }_{l}a={\rho }_A(x)\to a=x{\to }_{r}a$.

Proof. 

$(1)$ We shall prove only the equality $a{\to }_{l}b=a\to b$. In order to show that $a{\to }_{l}b\le a\to b$, assume that x is an element of A such that $x\le a{\to }_{l}b$; hence, $xa\le b$. Then, ${\rho }_A(x)\in R(A)$ and ${\rho }_A(x)\wedge a={\rho }_A(x)\wedge {\rho }_A(a)={\rho }_A(xa)\le {\rho }_A(b)=b$, so ${\rho }_A(x)\le a\to b$. Thus, $x\le a\to b$; therefore, $a{\to }_{l}b\le a\to b$.

In order to establish the converse inequality $a\to b\le a{\to }_{l}b$, assume that $x\in A$ and $x\le a\to b$. Then, ${\rho }_A(x)\le a\to b$, and hence, we obtain ${\rho }_A(xa)={\rho }_A(x)\wedge {\rho }_A(a)={\rho }_A(x)\wedge a\le b$. It follows that $xa\le b$; hence, $x\le a\to b$. We conclude that $a\to b\le a{\to }_{l}b$, so $a{\to }_{l}b=a\to b$.

$(2)$ We apply $(1)$ for $b=0$.

$(3)$ By $(2)$, we take into account that ${\rho }_A(0)=0$.

$(4)$ We prove only the equality $x{\to }_{l}a={\rho }_A(x)\to a$. It suffices to prove that for any $c\in A$, $cx\le a$ if and only if $c{\rho }_A(x)\le a$. Assume that $cx\le a$, so $c{\rho }_A(x)\le {\rho }_A(c){\rho }_A(x)\le {\rho }_A(cx)\le {\rho }_A(a)=a$. The converse implication follows immediately.

□

Lemma 13. 

Let L be a coherent frame and $p\in Spec(L)$. Then, the following are equivalent:

(1) 

$p\in Min(L)$;

(2) 

For any $c\in K(L)$, $c\le p$ implies $c^{{\perp }_A}\nleqq p$.

Now, we will use the previous lemma and the covariant functor ${(·)}^{\rho }$ to obtain a characterization of the minimal m-prime elements in a semiprime neo-commutative groupoid.

Theorem 3. 

Let A be a semiprime neo-commutative groupoid and $p\in Spec(A)$. Then, the following are equivalent:

(1) 

$p\in Min(A)$;

(2) 

$p\in Min(R(A))$;

(3) 

For any $x\in K(R(A))$, $x\le p$ implies $x^{{\perp }_{R(A)}}\nleqq p$;

(4) 

For any $c\in K(A)$, $c\le p$ implies $c^{{\perp }_A}\nleqq p$.

Proof. 

$(1)\iff (2)$ By $Min(A)=Min(R(A))$.

$(2)\iff (3)$ By Lemma 13 applied to the coherent frame $R(A)$.

$(3)\Rightarrow (4)$ Let c be a compact element of A such that $c\le p$. Thus, ${\rho }_A(c)\in K(R(A))$ (by Proposition 4) and ${\rho }_A(c)\le p$. According to hypothesis $(3)$, we obtain ${({\rho }_A(c))}^{{\perp }_{R(A)}}\nleqq p$. By Lemma 12 (3), we obtain ${({\rho }_A(c))}^{{\perp }_A}\nleqq p$. But $c\le {\rho }_A(c)$ implies ${({\rho }_A(c))}^{{\perp }_A}\le c^{{\perp }_A}$; hence, $c^{{\perp }_A}\nleqq p$.

$(4)\Rightarrow (3)$ Let x be a compact element such that $x\le p$. By Proposition 4, there exists $c\in K(A)$ such that $x={\rho }_A(c)$, so $c\le p$. In accordance with hypothesis $(4)$, we have $c^{{\perp }_A}\nleqq p$. According to Lemmas 11 and 12, we have $c^{{\perp }_A}={({\rho }_A(c))}^{{\perp }_A}={({\rho }_A(c))}^{{\perp }_{R(A)}}=x^{{\perp }_{R(A)}}$, and so, $x^{{\perp }_{R(A)}}\nleqq p$.

□

For the rest of this section, we will assume that A is a semiprime neo-commutative $icl$-groupoid.

By restricting the topologies of $Spe{c}_Z(A)$ and $Spe{c}_F(A)$ to $Min(A)$, we obtain two topological spaces:

• $Mi{n}_Z(A)$, having ${\{D(c)\cap Min(A))\}}_{c\in K(A)}$ as a basis;
• $Mi{n}_F(A)$, having ${\{V(c)\cap Min(A))\}}_{c\in K(A)}$ as a basis.

Lemma 14. 

(1)$Spe{c}_Z(A)=Spe{c}_Z(R(A))$;

(2) 

$Spe{c}_F(A)=Spe{c}_F(R(A))$.

Proof. 

$(1)$ Firstly, we observe that $Spec(A)=Spec(R(A))$. We know that ${\left\{D_A(c)\right\}}_{c\in K(A)}$ is a basis of $Spe{c}_Z(A)$ and ${\left\{D_{R(A)}(c)\right\}}_{c\in K(R(A))}$ is a basis of $Spe{c}_Z(R(A))$. Since $D_A(c)=D_{R(A)}({\rho }_A(c))$, for each $c\in K(A)$ (cf. Proposition 1(1)) and $K(R(A))=\left\{{\rho }_A(c)\right|c\in K(A)\}$ (cf. Proposition 4), it follows that the two bases ${\left\{D_A(c)\right\}}_{c\in K(A)}$ and ${\left\{D_{R(A)}(c)\right\}}_{c\in K(R(A))}$ coincide.

$(2)$ Similarly. □

Corollary 6.

(1)$Mi{n}_Z(A)=Mi{n}_Z(R(A))$;

(2) 

$Mi{n}_F(A)=Mi{n}_F(R(A))$.

Corollary 7. 

(1)$Mi{n}_Z(A)$ is a zero-dimensional Hausdorff space;

(2) 

$Mi{n}_F(A)$ is a compact $T_1$-space.

Proof. 

$(1)$ By hypothesis, A is a neo-commutative $icl$-groupoid; hence, using Lemma 3, it follows that $R(A)$ is a coherent frame. Therefore, one can apply Lemma 3.11 and Proposition 3.12 of [22] to the coherent frame $R(A)$, and find that $Mi{n}_Z(R(A))$ is a zero-dimensional Hausdorff space. By virtue of the equality $Mi{n}_Z(A)=Mi{n}_Z(R(A))$ of Corollary 6 (1), we obtain that $Mi{n}_Z(A)$ is a zero-dimensional Hausdorff space.

$(2)$ By Lemma 4.1 of [22], $Mi{n}_F(R(A))$ is a compact $T_1$-space. Due to the equality of Corollary 6(2), it follows that $Mi{n}_F(A)$ is a compact $T_1$-space.

□

Lemma 15. 

For all compact elements $c,d$ of A, ${\rho }_A(c)\le {({\rho }_A(d))}^{{\perp }_A}$ if and only if $c\le d^{{\perp }_A}$.

Proof. 

Since A is semiprime, the following equivalences hold:

${\rho }_A(c)\le {({\rho }_A(d))}^{{\perp }_A}$ iff ${\rho }_A(c)\wedge {\rho }_A(d)=0$ iff ${\rho }_A(cd)=0$ iff $cd=0$ iff $c\le d^{{\perp }_A}$.

□

Lemma 16. 

Let L be a coherent frame. Then, the following are equivalent:

(1) 

$Mi{n}_Z(L)$ is a compact space;

(2) 

$Mi{n}_Z(L)=Mi{n}_F(L)$;

(3) 

For any $c\in K(L)$, there exists $d\in K(L)$ such that $d\le c^{{\perp }_L}$ and $c^{{\perp }_L}\wedge d^{{\perp }_L}=0$.

Proof. 

See Theorem 4.5 of [22]. □

Lemma 17. 

The following properties are equivalent:

(1) 

For any $c\in K(A)$, there exists $d\in K(A$) such that $d\le c^{{\perp }_A}$ and $c^{{\perp }_A}\wedge d^{{\perp }_A}=0$;

(2) 

For any $x\in K(R(A))$, there exists $y\in K(R(A))$ such that $y\le x^{{\perp }_{R(A)}}$ and $x^{{\perp }_{R(A)}}\wedge y^{{\perp }_{R(A)}}=0$.

Proof. 

$(1)\Rightarrow (2)$ Assume that x is a compact element of the frame $R(A)$, so $x={\rho }_A(c)$ for some compact element c of A (cf. Proposition 4). Then, there exists a compact element d of A such that $d\le c^{{\perp }_A}$ and $c^{{\perp }_A}\wedge d^{{\perp }_A}=0$. By a new application of Proposition 4, $y={\rho }_A(d)$ is a compact element of the frame $R(A)$. Using Lemmas 11 and 12, we obtain $c^{{\perp }_A}={({\rho }_A(c))}^{{\rho }_A}=x^{{\perp }_A}=x^{{\perp }_{R(A)}}$ and $d^{{\perp }_A}=d^{{\perp }_{R(A)}}$. According to Lemma 15, $d\le c^{{\perp }_A}$ implies $y={\rho }_A(d)\le {({\rho }_A(c))}^{{\perp }_A}=x^{{\perp }_{R(A)}}$. Also, $c^{{\perp }_A}\wedge d^{{\perp }_A}=0$ implies $x^{{\perp }_{R(A)}}\wedge y^{{\perp }_{R(A)}}=0$.

$(2)\Rightarrow (1)$ Let c be a compact element of A; hence, $x={\rho }_A(c)$ is a compact element of the frame $R(A)$. By hypothesis $(2)$, there exists $y\in K(R(A))$ such that $y\le x^{{\perp }_{R(A)}}$ and $x^{{\perp }_{R(A)}}\wedge y^{{\perp }_{R(A)}}=0$. Using Proposition 4, $y={\rho }_A(d)$ for some compact element d of A. Then, $d\le c^{{\perp }_A}$ (by Lemma 15) and $c^{{\perp }_A}\wedge d^{{\perp }_A}=x^{{\perp }_{R(A)}}\wedge y^{{\perp }_{R(A)}}=0$.

□

Theorem 4. 

The following properties are equivalent:

(1) 

$Mi{n}_Z(A)$ is a compact space;

(2) 

$Mi{n}_Z(A)=Mi{n}_F(A)$;

(3) 

For any $c\in K(A)$, there exists $d\in K(A)$ such that $d\le c^{{\perp }_A}$ and $c^{{\perp }_A}\wedge d^{{\perp }_A}=0$.

Proof. 

$(1)\iff (2)$ In accordance with Lemma 16 (the equivalence of $(1)$ and $(2)$ applied to the coherent frame $R(A)$) and Corollary 6, the following properties are equivalent:

• $Mi{n}_Z(A)$ is a compact space;
• $Mi{n}_Z(R(A))$ is a compact space;
• $Mi{n}_Z(R(A))=Mi{n}_F(R(A))$;
• $Mi{n}_Z(A)=Mi{n}_F(A)$.

$(2)\iff (3)$ By virtue of Lemma 16 (the equivalence of $(2)$ and $(3)$ applied to the coherent frame $R(A)$) and Lemma 17, the following properties are equivalent:

• $Mi{n}_Z(A)=Mi{n}_F(A)$;
• $Mi{n}_Z(R(A))=Mi{n}_F(R(A))$;
• For any $x\in K(R(A))$ there exists $y\in K(R(A))$ such that $y\le x^{{\perp }_{R(A)}}$ and $x^{{\perp }_{R(A)}}\wedge y^{{\perp }_{R(A)}}=0$;
• For any $c\in K(A)$, there exists $d\in K(A$) such that $d\le c^{{\perp }_A}$ and $c^{{\perp }_A}\wedge d^{{\perp }_A}=0$.

□

Definition 5. 

A morphism $u:A\to B$ of $NCom-iclG{R}^{*}$ is minimalisant if $u_{*}(q)\in Min(A)$ for any $q\in Min(B)$.

Proposition 6. 

Let $u:A\to B$ be a morphism of $NCom-iclG{R}^{*}$. Then, the following are equivalent:

(1) 

$u:A\to B$ is minimalisant;

(2) 

The frame morphism $u^{\rho }:R(A)\to R(B)$ is minimalisant.

Proof. 

Recall that $Min(A)=Min(R(A))$ and $Min(B)=Min(R(B))$. According to Corollary 3, ${(u^{\rho })}_{*}(q)=u_{*}(q)$ for any $q\in R(B)$. Then, the following properties are equivalent:

• for each $q\in Min(A)$, $u_{*}(q)\in Min(A)$;
• for each $q\in Min(R(A))$, ${(u^{\rho })}_{*}(q)\in Min(A)$.

□

6. Going-Down Property

6.1. Characterization of Going-Down Property

The going-down property is commonly used in commutative algebra for the study of remarkable classes of rings. For example, it can be used in the characterization of commutative rings of Krull dimension 0 (see Proposition 2.1 of [23]).

The going-down property on algebraic frames was studied by Dube in [10]. Among the numerous results of the mentioned work, we find theorems for the characterization of the algebraic frames of Krull dimension 0 and of Krull dimension at most 1 (see Section 4 of [10]).

In this section, we shall study the going-down property in the category $NCom-iclG{R}^{*}$. We obtain a characterization theorem for the objects of Krull dimension 0.

We shall define the going-down property for the morphisms of the category $NCom-iclG{R}^{*}$ by using the formulation given in [10].

Definition 6. 

Let $u:A\to B$ be a semimorphism of $icl$-groupoids and p an m-prime element of A. We say the following:

(1) 

u goes down to p if $q\in Spec(B)$ and $p\le u_{*}(q)$ imply that there exists $r\in Spec(B)$ such that $r\le q$ and $p=u_{*}(r)$;

(2) 

u satisfies the going-down property (=$GD$-property) if u goes down to each $p\in Spec(A)$.

Proposition 7. 

Let $u:A\to B$ be a morphism of $NCom-iclG{R}^{*}$ and $p\in Spec(A)$. Then, the following are equivalent:

(1) 

u goes down to p;

(2) 

The frame morphism $u^{\rho }$ goes down to p.

Proof. 

Recall that $Spec(A)=Spec(R(A))$ and $Spec(B)=Spec(R(B))$. The equivalence of $(1)$ and $(2)$ follows by using Corollary 3. □

Corollary 8. 

If $u:A\to B$ is a morphism of $NCom-iclG{R}^{*}$, then the following are equivalent:

(1) 

u verifies the $GD$-property;

(2) 

$u^{\rho }$ verifies the $GD$-property.

Theorem 5. 

Let $u:A\to B$ be a morphism of $NCom-iclG{R}^{*}$ and $p\in Spec(A)$. Then, the following are equivalent:

(1) 

u goes down to p;

(2) 

For any $q\in Spec(B)$ that is minimal over $u(p)$, $u_{★}(q)=p$;

(3) 

For any $q\in Spec(B)$ that is minimal over $u(p)$, $c\in K(A),d\in K(B)$ and ${\rho }_B(u(c)d)\le {\rho }_B(u(p))$ imply $c\le p$ or $d\le q$;

(4) 

$u^{\rho }$ goes down to p;

(5) 

For any $q\in Spec(R(B))$ that is minimal over $u^{\rho }(p)$, ${(u^{\rho })}_{*}(q)=p$;

(6) 

For any $q\in Spec(R(B))$ that is minimal over $u^{\rho }(p)$, $x\in K(R(A))$, $y\in K(R(B))$, and $u^{\rho }(x)\wedge y\le u^{\rho }(p)$ imply $x\le p$ or $y\le q$.

Proof. 

$(4)\iff (5)\iff (6)$ These equivalences follow by applying Theorem 3.6 of [10] to the frame morphism $u^{\rho }:R(A)\to R(B)$ and $p\in Spec(R(A))$.

$(1)\iff (4)$ By Proposition 7.

$(2)\iff (5)$ Firstly, we observe that $q\in Spec(B)$ is minimal over $u(p)$ if and only if $q\in Spec(R(B))$ is minimal over $u^{\rho }(p)={\rho }_B(u(p))$ (recall that $Spec(B)=Spec(R(B))$). By Corollary 3, we have ${(u^{\rho })}_{★}(q)=u_{★}(q)$, so the equivalence of $(2)$ of $(5)$ follows immediately.

$(3)\Rightarrow (6)$ Assume that $x\in K(R(A))$, $y\in K(R(B))$, and $u^{\rho }(x)\wedge y\le u^{\rho }(p)$. By Proposition 4, one can find $c\in K(A)$ and $d\in K(B)$ such that $x={\rho }_A(c)$ and $y={\rho }_B(d)$. We remark that $u^{\rho }(x)\wedge y=u^{\rho }({\rho }_A(c))\wedge {\rho }_B(d)={\rho }_B(u(c))\wedge {\rho }_B(d)={\rho }_B(u(c)d)$ and $u^{\rho }(p)={\rho }_B(u(p))$; hence, ${\rho }_B(u(c)d)\le {\rho }_B(u(c)d)$. Using hypothesis $(3)$, we obtain $c\le p$ or $d\le q$. Therefore, $x={\rho }_A(c)\le {\rho }_A(p)=p$ and $y={\rho }_B(d)\le {\rho }_B(q)=q$.

$(6)\Rightarrow (3)$ Assume that $c\in K(A),d\in K(B)$ and ${\rho }_B(u(c)d)\le {\rho }_B(u(p))$; hence, using the commutativity of the diagram from Theorem 2, we obtain $u^{\rho }({\rho }_A(c))\wedge {\rho }_B(d)={\rho }_B(u(c))\wedge {\rho }_B(d)={\rho }_B(u(c)d)\le {\rho }_B(u(p))=u^{\rho }(p)$. By Proposition 4, we have ${\rho }_A(c)\in K(R(A)),{\rho }_B(d)\in K(R(B))$; therefore, by virtue of hypothesis $(6)$, we obtain ${\rho }_A(c)\le p$ or ${\rho }_B(d)\le q$. Thus, we obtain $c\le p$ or $d\le q$. □

Let us fix an element $a\in A$ and denote ${[a)}_A=\{x\in A|a\le x\}$. Consider the following multiplication ${·}_a$ on ${[a)}_A:x{·}_{a}y=xy\vee a$, for all $x,y\in {[a)}_A$.

It is easy to see that ${[a)}_A$ is closed under arbitrary joins of A. By a straightforward computation, we obtain that $({[a)}_A,\bigvee ,{·}_a,a,1)$ is an $icl$-groupoid.

Remark 6. 

For all $x,y\in {[a)}_A$, we have $ax\le a\le y$ and $xa\le a\le y$, so $a\le x{\to }_{l}y$ and $a\le x{\to }_{r}y$. Then, $x{\to }_{l}y$ and $x{\to }_{r}y$ belong to ${[a)}_A$, so the restrictions of ${\to }_l$ and ${\to }_r$ to ${[a)}_A\times {[a)}_A$ are exactly the residuation operations of the $icl$-groupoid ${[a)}_A$.

Consider the map $u_a^A:A\to {[a)}_A$ defined by $u_a^A(x)=x\vee a$, for any $x\in A$.

Lemma 18. 

$u_a^A$ is a coherent morphism of $icl$-groupoids.

Proof. 

It is easy to prove that $u_a^A$ preserves the arbitrary joins and $u_a^A(1)=1$. For all $x,y\in {[a)}_A$, we have

$$u_a^A(xy)=xy\vee a=(x\vee a)(y\vee a)\vee a=u_a^A(x){·}_a{u}_a^A(y).$$

Then, $u_a^A$ preserves the multiplication, so it is a morphism of $icl$-groupoids. Let $c\in K(A)$ and ${\left\{x_i\right\}}_{i\in I}$ be a family of elements of ${[a)}_A$ such that $u_a^A(c)\le {\bigvee }_{i\in I}{x}_i$, so $c\le {\bigvee }_{i\in I}{x}_i$. Thus, $c\le {\bigvee }_{i\in J}{x}_i$, for some finite subset J of I, and so, $u_a^A(c)=c\vee a\le {\bigvee }_{i\in J}{x}_i$. Then, $u_a^A(c)$ is a compact element of ${[a)}_A$, so $u_a^A$ is coherent.

□

Corollary 9. 

If A is a neo-commutative $icl$-groupoid, then $K({[a)}_A)=\{c\vee a|c\in K(A)\}$.

Proof. 

By Lemma 18, $u_a^A$ is a surjective coherent morphism of $icl$-groupoids. Therefore, using Lemma 7, it follows that

$$K({[a)}_A)=u_a^A(K(A))=\{c\vee a|c\in K(A)\}.$$

□

Corollary 10. 

If A is a neo-commutative $icl$-groupoid, then ${[a)}_A$ is a neo-commutative $icl$-groupoid.

Proof. 

Assume that $x,y\in K({[a)}_A)$; hence, $x=c\vee a$ and $y=d\vee a$ for some $c,d\in K(A)$ (cf. Corollary 9). Then, $x{·}_{a}y=(c\vee a)(d\vee a)=cd\vee a$ and $cd\in K(A)$ (because A is neo-commutative). Thus, $x{·}_{a}y\in K({[a)}_A)$, and so, the $icl$-groupoid ${[a)}_A$ is neo-commutative. □

Lemma 19. 

If A is a neo-commutative $icl$-groupoid, then the following hold:

(1) 

$Spec({[a)}_A)=\{p\in Spec(A)|a\le p\}$;

(2) 

${\rho }_{{[a)}_A}={\rho }_A{|}_{{[a)}_A}$;

(3) 

$R({[a)}_A)=R(A)\cap {[a)}_A$.

Proof. 

$(1)$ Assume that $p\in Spec(A)$ and $a\le p$. Let $x,y$ be two elements of ${[a)}_A$ such that $x{·}_{a}y\le p$, so $xy\le p$. Then, $x\le p$ or $y\le p$, so $p\in Spec({[a)}_A$. It follows that $\{p\in Spec(A)|a\le p\}\subseteq Spec({[a)}_A)$.

Conversely, suppose that $p\in Spec({[a)}_A)$. Let $x,y$ be two compact elements of ${[a)}_A$ such that $xy\le p$, so there exists $c,d\in K(A)$ such that $x=a\vee c$ and $y=a\vee d$ (cf. Corollary 9). Hence, we obtain $(c\vee a){·}_a(d\vee a)=cd\vee a\le p$. Thus, $c\le c\vee a\le p$ or $d\le d\vee a\le p$, and hence, $p\in Spec(A)$. Therefore, we have proven that $Spec({[a)}_A)\subseteq \{p\in Spec(A)|a\le p\}$.

$(2)$ By virtue of $(1)$, for each $x\in {[a)}_A$, the following hold:

$${\rho }_{{[a)}_A}(x)=\bigwedge \{p\in Spec({[a)}_A)|x\le p\}=\bigwedge \{p\in Spec(A)|a\le p,x\le p\}=$$

$$=\bigwedge \{p\in Spec(A)|x\le p\}={\rho }_A(x).$$

$(3)$ By $(2)$, for any $x\in A$, the following equivalences hold: $x\in R({[a)}_A)$ iff ${\rho }_{{[a)}_A}(x)=x$ and $a\le x$ iff ${\rho }_A(x)=x$ and $a\le x$ iff $x\in R(A)\cap {[a)}_A)$.

□

6.2. Going-Down and Krull Dimension

For the rest of this section, A will be a neo-commutative $icl$-groupoid.

Lemma 20. 

For any $x\in R(A)$, ${\displaystyle {(u_a^A)}^{\rho }(x)={\rho }_A(a)\dot{\vee }x}$.

Proof. 

Let x be an element of $R(A)$. Using the definition of ${(u_a^A)}^{\rho }$ and Lemma 19 (2), we obtain

$${\displaystyle {(u_a^A)}^{\rho }(x)={\rho }_{{[a)}_A}(u_a^A(x))={\rho }_A(u_a^A(x))={\rho }_A(a\vee x)={\rho }_A(a)\dot{\vee }{\rho }_A(x)={\rho }_A(a)\dot{\vee }x}$$

□

Lemma 21. 

The following properties are equivalent:

(1) 

Any morphism $u:A\to B$ of the category $NCom-iclG{R}^{*}$ satisfies the $GD$-property;

(2) 

Any coherent frame morphism $v:R(A)\to L$ satisfies the $GD$-property.

Proof. 

$(1)\Rightarrow (2)$ Let $v:R(A)\to L$ be a morphism of $CohFrm$. Consider the map $u:A\to L$ defined by $u=v\circ {\rho }_A$. It is easy to see that u is a morphism of $NCom-iclG{R}^{*}$. We observe that $L=R(L)$, ${\rho }_L=1_L$ and $u^{\rho }=v$. By hypothesis $(1)$, u satisfies the $GD$-property. Therefore, applying Corollary 8, it follows that $v=u^{\rho }$ satisfies the $GD$-property.

$(2)\Rightarrow (1)$ Let $u:A\to B$ be a morphism of the category $NCom-iclG{R}^{*}$. We know that $u^{\rho }:R(A)\to R(B)$ is a morphism of $CohFrm$ (cf. Theorem 2(3)). By hypothesis $(2)$, $u^{\rho }$ satisfies the $GD$-property. By virtue of Corollary 8, u satisfies the $GD$-property. □

Lemma 22. 

The following properties are equivalent:

(1) 

For any $p\in Spec(A)$, the morphism $u_p^A:A\to {[p)}_A$ of $NCom-iclG{R}^{*}$ satisfies the $GD$-property;

(2) 

For any $p\in Spec(A)$, the morphism $u_p^{R(A)}:R(A)\to {[p)}_{R(A)}$ of $CohFrm$ satisfies the $GD$-property.

Proof. 

Recall that $Spec(A)=Spec(R(A))$. For any $p\in Spec(A)$, we have ${[p)}_{R(A)}={[p)}_A\cap R(A)=R({[p)}_A)$ (cf. Lemma 19 (3)). According to Lemma 20, for each $x\in R(A)$, the following equalities hold:

$${\displaystyle {(u_p^A)}^{\rho }(x)={\rho }_A(p)\dot{\vee }x=p\dot{\vee }x=u_p^{R(A)}(x)}$$

It follows that ${(u_p^A)}^{\rho }=u_p^{R(A)}$. Therefore, by virtue of Corollary 8, it follows that $u_p^A:A\to {[p)}_A$ satisfies the $GD$-property if and only if the frame morphism $u_p^{R(A)}:R(A)\to {[p)}_{R(A)}$ satisfies the $GD$-property. □

Lemma 23. 

The following properties are equivalent:

(1) 

For any $p\in Spec(A)-Min(A)$, the morphism $u_p^A:A\to {[p)}_A$ of $NCom-iclG{R}^{*}$ satisfies the $GD$-property;

(2) 

For any $p\in Spec(A)-Min(A)$, the morphism $u_p^{R(A)}:R(A)\to {[p)}_{R(A)}$ of $CohFrm$ satisfies the $GD$-property.

Proof. 

Similar to the proof of Lemma 22. □

Following [10], a frame morphism $u:L\to M$ is called nearly open (respectively, slightly open) if $u(a^{{\perp }_L})={(u(a))}^{{\perp }_M}$, for all $a\in A$ (respectively, $a\in K(A)$). We extend this notion to the category $NCom-iclG{R}^{*}$: a morphism $u:A\to B$ of $NCom-iclG{R}^{*}$ is said to be nearly open (respectively, slightly open) if the equalities $u(a{\to }_l{\rho }_A(0))=u(a){\to }_l{\rho }_B(0)$ and $u(a{\to }_r{\rho }_A(0))=u(a){\to }_r{\rho }_B(0)$ are satisfied for any $a\in A$ (respectively, $a\in K(A)$).

Lemma 24. 

For any morphism $u:A\to B$ of $NCom-iclG{R}^{*}$, the following are equivalent:

(1) 

u is nearly open;

(2) 

$u(a{\to }_l{\rho }_A(0))=u(a){\to }_l{\rho }_B(0)$ for any $a\in A$;

(3) 

$u(a{\to }_r{\rho }_A(0))=u(a){\to }_r{\rho }_B(0)$ for any $a\in A$.

Proof. 

Using Lemma 12 (4), the following equalities hold:

$$a{\to }_l{\rho }_A(0))={\rho }_A(a)\to {\rho }_A(0)=a{\to }_r{\rho }_A(0)$$

$$u(a){\to }_l{\rho }_B(0)={\rho }_B(u(a))\to {\rho }_B(0)=u(a){\to }_r{\rho }_B(0)$$

By means of these equalities, the equivalence of the three properties (1)–(3) follows immediately. □

Lemma 25. 

Assume that A is an object of the category $NCom-iclG{R}^{*}$. Then, for any $p\in Spec(A)$, the following are equivalent:

(1) 

$u_p^A$ is nearly open;

(2) 

$p\vee (a{\to }_l{\rho }_A(0))=a{\to }_{l}p$, for any $a\in A$;

(3) 

$p\vee (a{\to }_r{\rho }_A(0))=a{\to }_{r}p$, for any $a\in A$.

Proof. 

$(1)\iff (2)$ Let a be an element of A. Using the definition of the morphism $u_p^A:A\to {[p)}_A$ and Lemma 19 (2), the following equalities hold:

$$u_p^A(a{\to }_l{\rho }_A(0))=p\vee (a{\to }_l{\rho }_A(0))$$

$$u_p^A(a){\to }_l{\rho }_{{[p)}_A}(p)=(a\vee p){\to }_{l}p=a{\to }_{l}p$$

Therefore, using Lemma 24, it follows that the following sentences are equivalent:

• $u_p^A$ is nearly open;
• $u_p^A(a{\to }_l{\rho }_A(0))=u_p^A(a){\to }_l{\rho }_{{[p)}_A}(p)$, for any $a\in A$;
• $p\vee (a{\to }_r{\rho }_A(0))=a{\to }_{r}p$, for any $a\in A$.

$(1)\iff (3)$ This equivalence follows in a similar way. □

Lemma 26. 

Assume that A is an object of the category $NCom-iclG{R}^{*}$. Then, for any $p\in Spec(A)$, the following are equivalent:

(1) 

$u_p^{R(A)}$ is nearly open;

(2) 

$p\vee (x\to {\rho }_A(0))=x\to p$, for any $x\in R(A)$.

Proof. 

Let x be an element of the frame $R(A)$. Using the definition of the morphism $u_p^{R(A)}:R(A)\to {[p)}_{R(A)}$ and Lemma 19 (2), the following equalities hold:

$$u_p^{R(A)}(x^{{\perp }_{R(A)}})=p\vee (x\to {\rho }_A(0))$$

$${(u_p^{R(A)}(x))}^{{\perp }_{R({[p)}_{R(A)})}}=(p\vee x)\to {\rho }_{{[p)}_A}(p)=(x\vee p)\to p=x\to p$$

By definition, $u_p^{R(A)}$ is nearly open if and only if for any $x\in R(A)$, the following equality holds:

$$u_p^{R(A)}(x^{{\perp }_{R(A)}})={(u_p^{R(A)}(x))}^{{\perp }_{R({[p)}_{R(A)})}}.$$

Therefore, using the previous equalities, the equivalence of $(1)$ and $(2)$ follows immediately.

□

Lemma 27. 

Assume that A is an object of the category $NCom-iclG{R}^{*}$. Then, for any $p\in Spec(A)$, the following are equivalent:

(1) 

The morphism $u_p^A$ of $NCom-iclG{R}^{*}$ is nearly open;

(2) 

The morphism $u_p^{R(A)}$ of $CohFrm$ is nearly open.

Proof. 

$(1)\Rightarrow (2)$ Assume that $u_p^A$ is nearly open. Let x be an element of the frame $R(A)$. By Lemma 25, we have $p\vee (x{\to }_l{\rho }_A(0))=x{\to }_{l}p$. We remark that $x,p,{\rho }_A(0)$ and ${\rho }_B(0)$ are elements of $R(A)$. By virtue of Lemma 12, we obtain $x{\to }_l{\rho }_A(0)=x\to {\rho }_A(0)$ and $x{\to }_{l}p=x\to p$; therefore, $p\vee (x\to {\rho }_A(0))=x\to p$. According to Lemma 26, $u_p^{R(A)}$ is nearly open.

$(2)\Rightarrow (1)$ Assume that $u_p^{R(A)}$ is nearly open. Let x be an element of A; hence, $x={\rho }_A(a)$ is an element of $R(A)$. By Lemma 26, $p\vee (x\to {\rho }_A(0))=x\to p$. Using Lemma 12 (4), we obtain

$$a{\to }_l{\rho }_A(0)={\rho }_A(a)\to {\rho }_A(0)=x\to {\rho }_A(0)$$

$$a{\to }_{l}p={\rho }_A(a)\to p=x\to p$$

Thus, $p\vee (a{\to }_l{\rho }_A(0))=a{\to }_{l}p$, for any $a\in A$. In accordance with Lemma 25, $u_p^A$ is nearly open.

□

Corollary 11. 

If A is an object of the category $NCom-iclG{R}^{*}$, then the following are equivalent:

(1) 

For any $p\in Spec(A)-Min(A)$, $u_p^A$ is nearly open;

(2) 

For any $p\in Spec(A)-Min(A)$, $u_p^{R(A)}$ is nearly open.

Corollary 12. 

If A is an object of the category $NCom-iclG{R}^{*}$, then the following are equivalent:

(1) 

For any $p\in Spec(A)-Min(A)$, $u_p^A$ is slightly open;

(2) 

For any $p\in Spec(A)-Min(A)$, $u_p^{R(A)}$ is slightly open.

Proof. 

Similar to the proof of Corollary 11. □

If $p_0<p_1<\dots <p_n$ is a chain of m-prime elements of the $icl$-groupoid A, then the integer n is called the length of chain. As usual, the (Krull) dimension of A (=$dim(A)$) is the supremum of the lengths of chains of m-prime elements of A. We remark that $dim(A)=0$ iff $Max(A)=Spec(A)$ iff $Min(A)=Spec(A)$.

The following result is a generalization of Propositions 4.2 and 4.6 of [10]. The theorem can also be viewed as an abstraction of a part of Proposition 2.1 of [23].

Theorem 6. 

Let A be a neo-commutative $icl$-groupoid. Then, the following are equivalent:

(1) 

$dim(A)=0$;

(2) 

$din(R(A))=0$;

(3) 

Any morphism $u:A\to B$ of the category $NCom-iclG{R}^{*}$ satisfies the $GD$-property;

(4) 

Any coherent frame morphism $v:R(A)\to L$ satisfies the $GD$-property;

(5) 

For any $p\in Spec(A)$, $u_p^A$ satisfies the $GD$-property;

(6) 

For any $p\in Spec(A)$, the frame morphism $u_p^{R(A)}:R(A)\to {[p)}_{R(A)}$ satisfies the $GD$-property;

(7) 

For any $p\in Spec(A)-Min(A)$, $u_p^A$ satisfies the $GD$-property;

(8) 

For any $p\in Spec(A)-Min(A)$, $u_p^{R(A)}:R(A)\to {[p)}_{R(A)}$ satisfies the $GD$-property;

(9) 

For any $p\in Spec(A)-Min(A)$, $u_p^A$ is nearly open;

(10) 

For any $p\in Spec(A)-Min(A)$, $u_p^{R(A)}$ is nearly open;

(11) 

For any $p\in Spec(A)-Min(A)$, $u_p^A$ is slightly open;

(12) 

For any $p\in Spec(A)-Min(A)$, $u_p^{R(A)}$ is slightly open.

(13) 

$Spe{c}_Z(A)$ is a $T_1$-space;

(14) 

$Spe{c}_Z(R(A))$ is a $T_1$-space.

Proof. 

$(2)\iff (4)\iff (6)\iff (8)\iff (10)\iff (12)\iff (14)$ We apply Propositions 4.2 and 4.6 of [10] to the coherent frame $R(A)$.

$(1)\iff (2)$ Recall that $Spec(A)=Spec(R(A)$ and $Min(A)=Min(R(A))$. Then, $dim(A)=0$ if and only if $dim(R(A))=0$.

$(3)\iff (4)$ By Lemma 21.

$(5)\iff (6)$ By Lemma 22.

$(7)\iff (8)$ By Lemma 23.

$(9)\iff (10)$ By Corollary 11.

$(11)\iff (12)$ By Corollary 12.

$(13)\iff (14)$ By Lemma 14.

□

Following [10] (p. 1805), we say that a topological space X is a $T_{YS}$-space if for all distinct elements $x,y$ of X, $\overline{\left\{x\right\}}\cap \overline{\left\{y\right\}}=\varnothing$ or $\left\{x\right\}$ or $\left\{y\right\}$.

Theorem 7. 

Let A be a neo-commutative $icl$-groupoid. Then, the following are equivalent:

(1) 

For any $p\in Spec(A)-Max(A)$, $u_p^A$ satisfies the $GD$-property;

(2) 

For any $p\in Spec(A)-Max(A)$, $u_p^{R(A)}:R(A)\to {[p)}_{R(A)}$ satisfies the $GD$-property;

(3) 

$dim(A)\le 1$ and each $p\in Spec(A)$ is above exactly one minimal m-prime element of A;

(4) 

$dim(R(A))\le 1$ and each $p\in Spec(R(A))$ is above exactly one minimal prime element of $R(A)$;

(5) 

$Spe{c}_Z(A)$ is a $T_{YS}$-space;

(6) 

$Spe{c}_Z(R(A))$ is a $T_{YS}$-space.

Proof. 

$(2)\iff (4)\iff (6)$ We apply Proposition 4.8 of [10] to the coherent frame $R(A)$.

$(1)\iff (2)$ Similar to the proof of Lemma 22.

$(3)\iff (4)$ By $Spec(A)=Spec(R(A)$, $Max(A)=Max(R(A))$, $Min(A)=Min(R(A))$ and $dim(A)=dim(R(A))$.

$(5)\iff (6)$ By $Spe{c}_Z(A)=Spe{c}_Z(R(A))$ (cf. Lemma 14 (1)). □

7. Baer and Weak-Baer Morphisms

Let $f:M\to N$ be a morphism of a congruence modular variety $\mathcal{V}$. We say that f is a Baer morphism (respectively, a weak-Baer morphism) of $\mathcal{V}$ if for all $\theta ,\chi \in Con(A)$ (respectively, $\theta ,\chi \in K(A)$), ${\theta }^{{\perp }_M}={\chi }^{{\perp }_N}$ implies ${(f^{•}(\theta ))}^{{\perp }_N}={(f^{•}(\chi ))}^{{\perp }_N}$. We note that the previous two notions are universal algebra generalizations of the Baer ring morphisms and the weak-Baer ring morphisms.

The previous discussion leads to the following definition.

Definition 7. 

Assume that $u:A\to B$ is a semimorphism of $icl$-groupoids:

(1) 

We say that u is a Baer semimorphism (of $icl$-groupoids) if for all $a,b\in A$, $a^{{\perp }_A}=b^{{\perp }_A}$ implies ${(u(a))}^{{\perp }_B}={(u(b))}^{{\perp }_B}$.

(2) 

We say that u is a weak-Baer semimorphism (of $icl$-groupoids) if for all $c,d\in K(A)$, $c^{{\perp }_A}=d^{{\perp }_A}$ implies ${(u(c))}^{{\perp }_B}={(u(d))}^{{\perp }_B}$.

We observe that for any morphism $f:M\to N$ of $\mathcal{V}$, the following equivalences hold:

•f is a Baer morphism of $\mathcal{V}$ if and only if $f^{•}$ is a Baer semimorphism of $icl$-groupoids;

•f is a weak-Baer morphism of $\mathcal{V}$ if and only if $f^{•}$ is a weak-Baer semimorphism of $icl$-groupoids.

The Baer quantale morphisms and the weak-Baer quantale morphisms (defined in [24]) are particular cases of the notions introduced in Definition 7.

Lemma 28. 

Let $L,Q$ be two coherent frames and $u:L\to Q$ be a coherent frame morphism. Then, the following are equivalent:

(1) 

u is a Baer frame morphism;

(2) 

For any $a\in L$, $a^{{\perp }_L}=0$ implies ${(u(a))}^{{\perp }_Q}=0$;

(3) 

For all $a,b\in L$, $a^{{\perp }_L}\le b^{{\perp }_L}$ implies ${(u(a))}^{{\perp }_Q}\le {(u(b))}^{{\perp }_Q}$;

(4) 

For any $a\in L$, ${(u(a^{{\perp }_L}))}^{{\perp }_Q{\perp }_Q}={(u(a))}^{{\perp }_Q}$.

Proof. 

We apply Proposition 5.1 of [24] to the coherent frame morphism u. □

Throughout the rest of this section, we will work with semiprime $icl$-groupoids.

The following theorem emphasizes the behaviour of the covariant functor ${(·)}^{\rho }:NCom-iclG{R}^{*}\to CohFrm$ with respect to the Baer and weak-Baer morphisms.

Theorem 8. 

Let $u:A\to B$ be a morphism of $NCom-iclG{R}^{*}$. Then, the following hold:

(1) 

u is a weak-Baer morphism of $NCom-iclG{R}^{*}$ if and only if $u^{\rho }$ is weak-Baer frame morphism;

(2) 

u is a Baer morphism of $NCom-iclG{R}^{*}$ if and only if $u^{\rho }$ is Baer frame morphism.

Proof. 

$(1)$ Assume that u is a weak-Baer morphism of $NCom-iclG{R}^{*}$. We have to prove that $u^{\rho }:R(A)\to R(B)$ is a weak-Baer frame morphism. Let $x,y$ be two compact elements of the coherent frame $R(A)$ such that $x^{{\perp }_{R(A)}}=y^{{\perp }_{R(A)}}$. Applying Proposition 4, one can find two compact elements $c,d$ of A such that $x={\rho }_A(c)$ and $y={\rho }_A(d)$. By Lemmas 11 and 12, we obtain

$$c^{{\perp }_A}={({\rho }_A(c))}^{{\perp }_A}=x^{{\perp }_{R(A)}}=y^{{\perp }_{R(A)}}={({\rho }_A(d))}^{{\perp }_A}=d^{{\perp }_A}.$$

Using the hypothesis that u is a weak-Baer morphism of $NCom-iclG{R}^{*}$, we obtain ${(u(c))}^{{\perp }_B}={(u(d))}^{{\perp }_B}$. According to Theorem 2 and Lemmas 11 and 12, the following equalities hold:

$${(u^{\rho }(x))}^{{\perp }_{R(B)}}={(u^{\rho }({\rho }_A(c)))}^{{\perp }_{R(B)}}={({\rho }_B(u(c)))}^{{\perp }_{R(B)}}={({\rho }_B(u(c)))}^{{\perp }_B}={(u(c))}^{{\perp }_B}.$$

In a similar way, we obtain ${(u^{\rho }(y))}^{{\perp }_{R(A)}}={(u(d))}^{{\perp }_B}$, and hence, ${(u^{\rho }(x))}^{{\perp }_{R(B)}}={(u^{\rho }(y))}^{{\perp }_{R(A)}}$, so $u^{\rho }$ is a weak-Baer frame morphism.

Conversely, suppose that $c,d\in K(A)$ and $c^{{\perp }_A}=d^{{\perp }_A}$. Therefore, by applying Lemmas 11 and 12, we obtain ${({\rho }_A(c))}^{{\perp }_{R(A)}}={({\rho }_A(c))}^{{\perp }_A}={({\rho }_A(d))}^{{\perp }_A}={({\rho }_A(d))}^{{\perp }_{R(A)}}$. But ${\rho }_A(c),{\rho }_A(d)\in K(R(A))$, so we obtain ${(u^{\rho }({\rho }_A(c)))}^{{\perp }_{R(B)}}={(u^{\rho }({\rho }_A(d)))}^{{\perp }_{R(B)}}$ (because $u^{\rho }$ is assumed to be a weak-Baer frame morphism).

Using Theorem 2 and Lemmas 11 and 12, the following equalities hold:

$${(u(c))}^{{\perp }_B}={({\rho }_B(u(c)))}^{{\perp }_B}={(u^{\rho }({\rho }_A(c)))}^{{\perp }_{R(B)}}={(u^{\rho }({\rho }_A(d)))}^{{\perp }_{R(B)}}=\dots ={(u(c))}^{{\perp }_B}.$$

Then, u is a weak-Baer morphism of $NCom-iclG{R}^{*}$.

$(2)$ Similar to the proof of $(1)$. □

The following two propositions will characterize the Baer and weak-Baer admissible semimorphisms of $icl$-groupoids. The first one will be proven using the transferring properties of the functor ${(·)}^{\rho }$, while the proof of the second one will use Theorem 1 and the elementary arithmetic in $icl$-groupoids.

Proposition 8. 

Let $u:A\to B$ be a morphism of the category $NCom-iclG{R}^{*}$. Then, the following are equivalent:

(1) 

u is a Baer morphism of $NCom-iclG{R}^{*}$;

(2) 

For any $a\in A$, $a^{{\perp }_A}=0$ implies ${(u(a))}^{{\perp }_B}=0$;

(3) 

For all $a,b\in A$, $a^{{\perp }_A}\le b^{{\perp }_A}$ implies ${(u(a))}^{{\perp }_B}\le {(u(b))}^{{\perp }_B}$;

(4) 

For any $a\in A$, ${(u(a^{{\perp }_A}))}^{{\perp }_B{\perp }_B}={(u(a))}^{{\perp }_B}$.

Proof. 

This proof will use Theorem 8 (2) for transferring the equivalences (1)–(4) of Lemma 28 into the equivalences of properties that characterize the notion of Baer morphism of $NCom-iclG{R}^{*}$. We shall illustrate this method for proving the implication $(1)\Rightarrow (4)$. Assume that u is a Baer morphism of $NCom-iclG{R}^{*}$. Recall that $A,B$ are semiprime. Using Theorem 8, it follows that $u^{\rho }:R(A)\to R(B)$ is a Baer frame morphism. Applying Lemma 28 to the Baer frame morphism $u^{\rho }$ and $\rho (a)\in R(A)$, we obtain

$${(u^{\rho }({({\rho }_A(a))}^{{\perp }_{R(A)}}))}^{{\perp }_{R(B)}{\perp }_{R(B)}}={(u^{\rho }({\rho }_A(a)))}^{{\perp }_{R(B)}}.$$

By Lemmas 11 and 12, we have ${({\rho }_A(a))}^{{\perp }_{R(A))}}=a^{{\perp }_A}$. Therefore, we obtain

$u^{\rho }({({\rho }_A(a))}^{{\perp }_{R(A)}})=u^{\rho }(a^{{\perp }_A})={\rho }_B(u(a^{{\perp }_A}))$. Then, we obtain

$${(u^{\rho }({({\rho }_A(a))}^{{\perp }_{R(A)}}))}^{{\perp }_{R(B)}{\perp }_{R(B)}}={({\rho }_B(u(a^{{\perp }_A})))}^{{\perp }_{R(B)}{\perp }_{R(B)}}={(u(a^{{\perp }_A}))}^{{\perp }_{R(B)}{\perp }_{R(B)}}$$

(the last equality follows by using Lemma 11). By virtue of Theorem 2 and Lemma 11, we have ${(u^{\rho }({\rho }_A(a)))}^{{\perp }_{R(B)}}={({\rho }_B(u(a)))}^{{\perp }_B}={(u(a))}^{{\perp }_B}$. Therefore, we conclude that ${(u(a^{{\perp }_A}))}^{{\perp }_B{\perp }_B}={(u(a))}^{{\perp }_B}$.

□

Proposition 9. 

Let $u:A\to B$ be a morphism of the category $NCom-iclG{R}^{*}$. Then, the following are equivalent:

(1) 

u is a weak-Baer morphism of $NCom-iclG{R}^{*}$;

(2) 

For any $c\in K(A)$, $c^{{\perp }_A}=0$ implies ${(u(c))}^{{\perp }_B}=0$;

(3) 

For all $c,d\in K(A)$, $c^{{\perp }_A}\le d^{{\perp }_A}$ implies ${(u(c))}^{{\perp }_B}\le {(u(d))}^{{\perp }_B}$;

• For any $c\in K(A)$, ${(u(c^{{\perp }_A}))}^{{\perp }_B{\perp }_B}={(u(c))}^{{\perp }_B}$.

Proof. 

We shall give a direct proof of this proposition.

$(1)\Rightarrow (3)$ Assume that $c,d\in K(A)$ and $c^{{\perp }_A}\le d^{{\perp }_A}$, so ${(c\vee d)}^{{\perp }_A}=c^{{\perp }_A}\wedge d^{{\perp }_A}=c^{{\perp }_A}$. Therefore, using hypothesis $(1)$, we obtain the following equalities:

$${(u(c))}^{{\perp }_B}={(u(c\vee d))}^{{\perp }_B}={(u(c)\vee u(d))}^{{\perp }_B}={(u(c))}^{{\perp }_B}\wedge {(u(d))}^{{\perp }_B}$$

Then, we obtain the inequality ${(u(c))}^{{\perp }_B}\le {(u(d))}^{{\perp }_B}$.

$(3)\Rightarrow (1)$ Obviously.

$(3)\Rightarrow (2)$ We set $d=1$ in $(3)$.

$(2)\Rightarrow (4)$ Recall that the $icl$-groupoids are supposed to be semiprime. According to Lemma 10, from $c^{{\perp }_A}{c}^{{\perp }_A{\perp }_A}=0$, we obtain ${(c\vee c^{{\perp }_A})}^{{\perp }_A}=c^{{\perp }_A}\wedge c^{{\perp }_A{\perp }_A}=0$. By hypothesis $(2)$, we obtain ${(u(c\vee c^{{\perp }_A}))}^{{\perp }_B}=0$, hence ${(u(c))}^{{\perp }_B}\wedge {(u(c^{{\perp }_A}))}^{{\perp }_B}={(u(c)\vee u(c^{{\perp }_A}))}^{{\perp }_B}={(u(c\vee c^{{\perp }_A}))}^{{\perp }_B}=0$. Then, by Lemma 10, we have ${(u(c))}^{{\perp }_B}{(u(c^{{\perp }_A}))}^{{\perp }_B}=0$, so we obtain ${(u(c))}^{{\perp }_B}\le {(u(c^{{\perp }_A}))}^{{\perp }_B{\perp }_B}$.

By Theorem 1, we have $u(c)u(c^{{\perp }_A})\le {\rho }_B(u(c)u(c^{{\perp }_A})={\rho }_B(u(c{c}^{{\perp }_A}))={\rho }_B(u(0))$. But $u(0)=0$ and ${\rho }_B(0)=0$; hence, $u(c)u(c^{{\perp }_A})=0$. Thus, $u(c)\le {(u(c^{{\perp }_A}))}^{{\perp }_B}$, so we obtain the converse inequality ${(u(c^{{\perp }_A}))}^{{\perp }_B{\perp }_B}\le {(u(c))}^{{\perp }_B}$.

$(4)\Rightarrow (2)$ Assume $c\in K(A)$ and $c^{{\perp }_A}=0$; hence, ${(u(c))}^{{\perp }_B}={(u(0))}^{{\perp }_B{\perp }_B}=0^{{\perp }_B{\perp }_B}=0$.

$(4)\Rightarrow (1)$ Assume that $c^{{\perp }_A}=d^{{\perp }_A}$. Using hypothesis $(4)$, we obtain

$${(u(c))}^{{\perp }_B}=(u{(c^{{\perp }_A})}^{{\perp }_B{\perp }_B}=(u{(d^{{\perp }_A})}^{{\perp }_B{\perp }_B}={(u(d))}^{{\perp }_B}$$

Therefore, u is a weak-Baer morphism of $NCom-iclG{R}^{*}$.

□

Proposition 10. 

Any minimalisant morphism $u:A\to B$ of the category $NCom-iclG{R}^{*}$ is a weak-Baer morphism of $NCom-iclG{R}^{*}$.

Proof. 

Assume that the morphism $u:A\to B$ of the category $NCom-iclG{R}^{*}$ is minimalisant. According to Proposition 6, the frame morphism $u^{\rho }:R(A)\to R(B)$ is minimalisant. By virtue of Proposition 6.5 of [24] applied to $u^{\rho }$, it follows that this frame morphism is minimalisant. Therefore, by using Proposition 8 (1), we obtain that u is a weak-Baer morphism of $NCom-iclG{R}^{*}$. □

8. Three Classes of Admissible Semimorphisms of $icl$-Groupoids

8.1. Starting from a Universal Algebra Setting

Generalizing some results from [11] on ring extensions, the paper [20] studies the corresponding classes of extensions in a congruence-modular variety $\mathcal{V}$. Starting from these types of extensions, we will now define three classes of morphisms in $\mathcal{V}$.

Let $f:M\to N$ be a morphism of the congruence-modular variety $\mathcal{V}$. Then, we say the following:

• f is a quasi r-morphism if for all $\psi \in Min(N)$ and $\beta \in K(N)$ such that $\beta \not\subset \psi$, there exists $\alpha \in K(M)$ such that $f^{•}(\alpha )\not\subset \psi$ and ${\beta }^{{\perp }_N}\subseteq {(f^{•}(\alpha ))}^{{\perp }_N}$;
• f is a quasi $r^{*}$-morphism if for all $\psi \in Min(N)$ and $\beta \in K(N)$ such that $\beta \subseteq \psi$, there exists $\alpha \in K(M)$ such that $f^{•}(\alpha )\subseteq \psi$ and ${(f^{•}(\alpha ))}^{{\perp }_N}\subseteq {\beta }^{{\perp }_N}$;
• f is a quasi rigid morphism if for any $\beta \in K(N)$, there exists $\alpha \in K(M)$ such that ${\beta }^{{\perp }_N}={(f^{•}(\alpha ))}^{{\perp }_N}$.

In this section, we will generalize these three notions to the abstract framework offered by the category $NCom-iclG{R}^{*}$. We will prove that the functor ${(·)}^{\rho }:NCom-iclG{R}^{*}\to CohFrm$ preserves these types of morphisms, which will lead to obtaining some theorems for their characterization.

8.2. Quasi r-Morphisms

Let us fix the following entities:

• A and B are two semiprime objects of the category $NCom-iclG{R}^{*}$ (=semiprime neo-commutative $icl$-groupoids);
• $u:A\to B$ is a morphism of $NCom-iclG{R}^{*}$ (=an admissible semimorphism of $icl$-groupoids).

Definition 8. 

The morphism $u:A\to B$ is said to be a quasi r-morphism of $NCom-iclG{R}^{*}$ if for all $q\in Min(B)$ and $d\in K(B)$ such that $d\nleqq q$, there exists $c\in K(A)$ such that $u(c)\nleqq q$ and $d^{{\perp }_B}\le {(u(c))}^{{\perp }_B}$.

We remark that a morphism $f:M\to N$ of the congruence-modular variety $\mathcal{V}$ is a quasi r-morphism of $\mathcal{V}$ if and only if $f^{•}:Con(M)\to Con(N)$ is a quasi r-morphism of $NCom-iclG{R}^{*}$. We note that the notion introduced by the previous definition also generalizes the notions of quasi r-quantale morphism and quasi r-frame morphism (defined in [24]).

Theorem 9. 

The following properties are equivalent:

(1) 

u is a quasi r-morphism of $NCom-iclG{R}^{*}$;

(2) 

$u^{\rho }$ is a quasi r-frame morphism.

Proof. 

$(1)\Rightarrow (2)$ Assume that $q\in Min(R(B))$ and $y\in K(R(B))$ satisfy the property $y\nleqq q$. Thus, $q\in Min(B)$ and $y={\rho }_B(d)$ for some compact element d of B (cf. Proposition 4). Then, ${\rho }_B(d)\nleqq q$, so we obtain $d\nleqq q$ (because $q\in Spec(B)$ implies that $d\le q$ iff ${\rho }_B(d)\le q$). In accordance with hypothesis $(1)$, there exists $c\in K(A)$ such that $u(c)\nleqq q$ and $d^{{\perp }_B}\le {(u(c))}^{{\perp }_B}$. We set $x={\rho }_A(c)$. By virtue of Theorem 2 (1), we have ${\rho }_B(u(c))=u^{\rho }(({\rho }_A(c))$, so the following implications hold:

$u(c)\nleqq q\Rightarrow {\rho }_B(u(c))\nleqq q\Rightarrow u^{\rho }(({\rho }_A(c))\le q\Rightarrow u^{\rho }(x)\le q$.

By applying Theorem 2 (1) and Lemmas 11 and 12, the following hold:

$$y^{{\perp }_{R(B)}}={({\rho }_B(d))}^{{\perp }_{R(B)}}={({\rho }_B(d))}^{{\perp }_B}=d^{{\perp }_B}$$

$${(u^{\rho }(x))}^{{\perp }_{R(B)}}={(u^{\rho }(x))}^{{\perp }_B}={(u^{\rho }({\rho }_B(c)))}^{{\perp }_B}={({\rho }_B(u(c)))}^{{\perp }_B}={(u(c))}^{{\perp }_B}$$

Therefore, from $d^{{\perp }_B}\le {(u(c))}^{{\perp }_B}$, we obtain $y^{{\perp }_{R(B)}}\le {(u^{\rho }(x))}^{{\perp }_{R(B)}}$. We conclude that $u^{\rho }$ is a quasi r-frame morphism.

$(2)\Rightarrow (1)$ Suppose that $q\in Min(B)$, $d\in K(B)$ and $d\nleqq q$; hence, $q\in Min(K(B))$, ${\rho }_B(d)\in K(R(B))$ and ${\rho }_B(d)\nleqq q$. Let us denote $y={\rho }_B(d)$. Using the hypothesis that $u^{\rho }$ is a quasi r-frame morphism, one can find a compact element x of the frame $R(A)$ such that $u^{\rho }(x)\nleqq q$ and $y^{{\perp }_{R(B)}}\le {(u^{\rho }(x))}^{{\perp }_{R(B)}}$. By Proposition 4, there exists $c\in K(A)$ such that ${\rho }_B(c)=x$. Using an argument similar to the one in the proof of the implication $(1)\Rightarrow (2)$, we obtain $u(c)\nleqq q$ and $d^{{\perp }_B}\le {(u(c))}^{{\perp }_B}$. Then, u is a quasi r-morphism of $NCom-iclG{R}^{*}$.

□

Let $u:A\to B$ be a minimalisant morphism of the category $NCom-iclG{R}^{*}$. Then, one can take the map $\Gamma (u):Min(B)\to Min(A)$ defined by $\Gamma (u)(q)=u_{*}(q)$, for any $q\in Min(B)$. By Proposition 6, the coherent frame morphism $u^{\rho }:R(A)\to R(B)$ is minimalisant, so one can consider the map $\Gamma (u^{\rho }):Min(R(B))\to Min(R(A))$. Therefore, for any $q\in Min(R(B))$, we obtain $\Gamma (u^{\rho })(q)={(u^{\rho })}_{*}(q)=u_{*}(q)$ (cf. Corollary 3).

Proposition 11. 

Let $u:A\to B$ be a minimalisant morphism of the category $NCom-iclG{R}^{*}$ and $a\in A,b\in B,c\in K(A),d\in K(B)$. Then, the following equalities hold:

(1) 

${(\Gamma (u))}^{-1}(D_A(a)\cap Min(A))={(\Gamma (u^{\rho }))}^{-1}(D_{R(A)}({\rho }_A(a))\cap Min(R(A)))$;

(2) 

$\Gamma (u)(D_B(b)\cap Min(B))=\Gamma (u^{\rho })(D_{R(B)}({\rho }_B(b))\cap Min(R(B)))$;

(3) 

${(\Gamma (u))}^{-1}(V_A(c)\cap Min(A))={(\Gamma (u^{\rho }))}^{-1}(V_{R(A)}({\rho }_A(c))\cap Min(R(A)))$;

(4) 

$\Gamma (u)(V_B(d)\cap Min(B))=\Gamma (u^{\rho })(V_{R(B)}({\rho }_B(d))\cap Min(R(B)))$.

Proof. 

We shall prove only the equality of $(3)$. Recall that $Min(A)=Min(R(A))$ and $Min(B)=Min(R(B))$. For each $q\in Spec(B)$, we have ${(u^{\rho })}_{*}(q)=u_{*}(q)$ (cf. Corollary 3), and hence, the following properties are equivalent:

• $q\in {(\Gamma (u))}^{-1}(V_A(c)\cap Min(A))$;
• $\Gamma (u)(q)\in V_A(c)\cap Min(A)$;
• $c\le u_{*}(q)$ and $u_{*}(q)\in Min(A)$;
• ${\rho }_A(c)\le u_{*}(q)$ and $u_{*}(q)\in Min(R(A))$;
• ${\rho }_A(c)\le {(u^{\rho })}_{*}(q)$ and ${(u^{\rho })}_{*}(q)\in Min(R(A))$;
• $q\in {(\Gamma (u^{\rho }))}^{-1}(V_{R(A)}({\rho }_A(c))\cap Min(R(A)))$.

Then, the equality from $(3)$ is proven. The other equalities follow in a similar way.

□

Lemma 29. 

If $u:A\to B$ is a minimalisant morphism of $NCom-iclG{R}^{*}$, then the following are equivalent:

(1) 

$\Gamma (u):Mi{n}_Z(B)\to Mi{n}_Z(A)$ is a continuous map;

(2) 

$\Gamma (u^{\rho }):Mi{n}_Z(R(B))\to Mi{n}_Z(R(A))$ is a continuous map.

Proof. 

In accordance with Proposition 11 (1), the following are equivalent:

• $\Gamma (u)$ is a continuous map;
• For any $a\in A$, ${(\Gamma (u))}^{-1}(D_A(a)\cap Min(A))$ is an open subset of $Mi{n}_Z(B)$;
• For any $a\in A$, ${(\Gamma (u^{\rho }))}^{-1}(D_{R(A)}({\rho }_A(a))\cap Min(R(A)))$ is an open subset of $Mi{n}_Z(R(B))$;
• $\Gamma (u^{\rho })$ is a continuous map.

□

Lemma 30. 

If $u:A\to B$ is a minimalisant morphism of $NCom-iclG{R}^{*}$, then the following are equivalent:

(1) 

$\Gamma (u):Mi{n}_Z(B)\to Mi{n}_Z(A)$ is an open map;

(2) 

$\Gamma (u^{\rho }):Mi{n}_Z(R(B))\to Mi{n}_Z(R(A))$ is an open map.

Proof. 

Similar to the proof of Lemma 29, using Proposition 11 (2). □

Lemma 31. 

If $u:A\to B$ is a minimalisant morphism of $NCom-iclG{R}^{*}$, then the following are equivalent:

(1) 

$\Gamma (u):Mi{n}_Z(B)\to Mi{n}_Z(A)$ is a homeomorphism;

(2) 

$\Gamma (u^{\rho }):Mi{n}_Z(R(B))\to Mi{n}_Z(R(A))$ is a homeomorphism.

Proof. 

Recall that $Mi{n}_Z(A)=Mi{n}_Z(R(A))$ and $Mi{n}_Z(A)=Mi{n}_Z(R(A))$. By Corollary 3, for each $q\in Min(B)$, we have $\Gamma (u^{\rho })(q)=\Gamma (u)(q)$, so $\Gamma (u)$ is a bijective map if and only if $\Gamma (u^{\rho })$ is a bijective map.

Therefore, applying Lemmas 29 and 30, it follows that the properties $(1)$ and $(2)$ are equivalent. □

Lemma 32. 

If $f:L\to Q$ is a coherent frame morphism, then the following are equivalent:

(1) 

$f:Mi{n}_Z(L)\to Mi{n}_Z(Q)$ is a quasi r-frame morphism;

(2) 

f is minimalisant and $\Gamma (f):Mi{n}_Z(Q)\to Mi{n}_Z(L)$ is a homeomorphism.

Proof. 

We apply Theorem 7.2 of [24] to the particular case of the coherent frame morphism $f:L\to Q$. □

Theorem 10. 

If $u:A\to B$ is a morphism of $NCom-iclG{R}^{*}$, then the following are equivalent:

(1) 

u is a quasi r-morphism of $NCom-iclG{R}^{*}$;

(2) 

u is minimalisant and $\Gamma (u):Mi{n}_Z(B)\to Mi{n}_Z(A)$ is a homeomorphism.

Proof. 

By applying Theorem 9, the following equivalence follows:

(a) u is a quasi r-morphism if and only if $u^{\rho }$ is a quasi r-frame morphism.

According to Lemma 32, we obtain

(b) $u^{\rho }$ is a quasi r-frame morphism if and only if $u^{\rho }:R(A)\to R(B)$ is minimalisant and $\Gamma (u^{\rho }):Mi{n}_Z(R(B))\to Mi{n}_Z(R(A))$ is a homeomorphism.

Taking into account Proposition 6 and Lemma 31, we obtain

(c) $u^{\rho }$ is minimalisant and $\Gamma (u^{\rho }):Mi{n}_Z(R(B))\to Mi{n}_Z(R(A))$ is a homeomorphism if and only if u is minimalisant and $\Gamma (u):Mi{n}_Z(B)\to Mi{n}_Z(A)$ is a homeomorphism.

By virtue of the equivalences (a)–(c), it follows that the properties $(1)$ and $(2)$ are equivalent. □

We note that Theorem 7.2 of ref. [24] and the equivalence $(ii)\iff (iii)$ of Theorem 6.17 of ref. [20] are particular cases of the previous result.

8.3. Quasi $r^{*}$-Morphisms

The following definition introduces a concept that generalizes both the quasi $r^{*}$-quantale morphisms and quasi $r^{*}$-frame morphisms (defined in [24]).

Definition 9. 

The morphism $u:A\to B$ is said to be a quasi $r^{*}$-morphism of $NCom-iclG{R}^{*}$ if for all $q\in Min(B)$ and $d\in K(B)$ such that $d\le q$, there exists $c\in K(A)$ such that $u(c)\le q$ and ${(u(c))}^{{\perp }_B}\le d^{{\perp }_B}$.

A morphism $f:M\to N$ of a congruence-modular variety $\mathcal{V}$ is a quasi $r^{*}$-morphism of $\mathcal{V}$ if and only if $f^{•}:Con(M)\to Con(N)$ is a quasi $r^{*}$-morphism of $NCom-iclG{R}^{*}$.

Theorem 11. 

The following properties are equivalent:

(1) 

u is a quasi $r^{*}$-morphism of $NCom-iclG{R}^{*}$;

(2) 

$u^{\rho }$ is a quasi $r^{*}$-frame morphism.

Proof. 

$(1)\Rightarrow (2)$ Assume that u is a quasi $r^{*}$-morphism of $NCom-iclG{R}^{*}$. In order to show that $u^{\rho }$ is a quasi $r^{*}$-frame morphism, suppose that q is a minimal prime element of the frame $R(B)$ and y is a compact element of $R(B)$ such that $y\le q$. By Proposition 4, $y={\rho }_B(d)$ for some $d\in K(B)$; hence, $d\le {\rho }_B(d)\le q$. We know that $Min(B)=Min(R(A))$, so $y\in Min(B)$. Thus, there exists $c\in K(A)$ such that $u(c)\le q$ and ${(u(c))}^{{\perp }_B}\le d^{{\perp }_B}$.

Let us denote $x={\rho }_A(c)$, so $x\in K(R(A))$ (cf. Proposition 4). Using Theorem 2 (1), we obtain $u^{\rho }(x)=u^{\rho }({\rho }_A(c)))={\rho }_B(u(c))\le q$. Recall from the proof of Theorem 9 that ${(u(c))}^{{\perp }_B}={(u^{\rho }(x))}^{{\perp }_{R(B)}}$ and $d^{{\perp }_B}=y^{{\perp }_{R(B)}}$, so ${(u^{\rho }(x))}^{{\perp }_{R(B)}}\le y^{{\perp }_{R(B)}}$. Therefore, we conclude that $u^{\rho }$ is a quasi $r^{*}$-frame morphism.

$(2)\Rightarrow (1)$ Assume that $q\in Min(B)$, $d\in K(B)$ and $d\le q$. Then, $q\in Min(R(B))$, ${\rho }_B(d)\in K(R(B))$ and ${\rho }_B(d)\le {\rho }_B(q)=q$. Applying the hypothesis $(2)$, we can find an element $x\in K(R(A))$ such that $u^{\rho }(x)\le q$ and ${(u^{\rho }(x))}^{{\perp }_{R(B)}}\le {({\rho }_B(d))}^{{\perp }_{R(B)}}$.

Thus, there exists an element $c\in K(A)$ such that $x={\rho }_A(c)$. Therefore, using Theorem 2 (1) and the proof of Theorem 9 we obtain

$$u(c)\le {\rho }_B(u(c))=u^{\rho }({\rho }_A(c))=u^{\rho }(x)\le q$$

$${(u(c))}^{{\perp }_B}={(u^{\rho }(x))}^{{\perp }_{R(B)}}\le {({\rho }_B(d))}^{{\perp }_{R(B)}}=d^{{\perp }_B}$$

It follows that u is a quasi $r^{*}$-morphism of $NCom-iclG{R}^{*}$.

□

Lemma 33. 

If $f:L\to Q$ is a coherent frame morphism, then the following are equivalent:

(1) 

$f:Mi{n}_F(L)\to Mi{n}_F(Q)$ is a quasi $r^{*}$-frame morphism;

(2) 

f is minimalisant and $\Gamma (f):Mi{n}_F(Q)\to Mi{n}_F(L)$ is a homeomorphism.

Proof. 

We apply Theorem 8.2 of [24] to the frame morphism $f:L\to Q$. □

Lemma 34. 

If $u:A\to B$ is a minimalisant morphism of $NCom-iclG{R}^{*}$, then the following are equivalent:

(1) 

$\Gamma (u):Mi{n}_F(B)\to Mi{n}_F(A)$ is a continuous map;

(2) 

$\Gamma (u^{\rho }):Mi{n}_F(R(B))\to Mi{n}_F(R(A))$ is a continuous map.

Proof. 

In accordance with Propositions 11 (1) and 4, the following are equivalent:

• $\Gamma (u)$ is a continuous map;
• For any $a\in K(A)$, ${(\Gamma (u))}^{-1}(D_A(a)\cap Min(A))$ is an open subset of $Mi{n}_Z(B)$;
• For any $a\in K(A)$, ${(\Gamma (u^{\rho }))}^{-1}(D_{R(A)}({\rho }_A(a))\cap Min(R(A)))$ is an open subset of $Mi{n}_Z(R(B))$;
• $\Gamma (u^{\rho })$ is a continuous map.

□

Lemma 35. 

If $u:A\to B$ is a minimalisant morphism of $NCom-iclG{R}^{*}$, then the following are equivalent:

(1) 

$\Gamma (u):Mi{n}_F(B)\to Mi{n}_F(A)$ is an open map;

(2) 

$\Gamma (u^{\rho }):Mi{n}_F(R(B))\to Mi{n}_F(R(A))$ is an open map.

Proof. 

By using Propositions 11 (4) and 4, the following statements are equivalent:

• $\Gamma (u)$ is an open map;
• For any $d\in K(B)$, $\Gamma (u)(V_B(d)\cap Min(B))$ is an open subset of $Mi{n}_F(A)$;
• For any $d\in K(B)$, $\Gamma (u^{\rho })(V_{R(B)}({\rho }_B(d))\cap Min(R(B)))$ is an open subset of $Mi{n}_F(A)$;
• $\Gamma (u^{\rho })$ is an open map.

□

Lemma 36. 

If $u:A\to B$ is a minimalisant morphism of $NCom-iclG{R}^{*}$, then the following are equivalent:

(1) 

$\Gamma (u):Mi{n}_F(B)\to Mi{n}_F(A)$ is a homeomorphism;

(2) 

$\Gamma (u^{\rho }):Mi{n}_F(R(B))\to Mi{n}_F(R(A))$ is a homeomorphism.

Proof. 

We know from Lemma 31 that $\Gamma (u)$ is a bijective map if and only if $\Gamma (u^{\rho })$ is a bijective map. Then, we apply Lemmas 34 and 35. □

Theorem 12. 

If $u:A\to B$ is a morphism of $NCom-iclG{R}^{*}$, then the following are equivalent:

(1) 

u is a quasi $r^{*}$-morphism;

(2) 

u is minimalisant and $\Gamma (u):Mi{n}_F(B)\to Mi{n}_F(A)$ is a homeomorphism.

Proof. 

Using Theorem 11, Proposition 6, and Lemmas 33 and 36, we obtain the equivalence of the following statements:

• u is a quasi $r^{*}$-morphism;
• $u^{\rho }$ is a quasi $r^{*}$-frame morphism;
• $u^{\rho }$ is minimalisant and $\Gamma (u^{\rho }):Mi{n}_F(R(B))\to Mi{n}_F(R(A))$ is a homeomorphism.
• u is minimalisant and $\Gamma (u):Mi{n}_F(B)\to Mi{n}_F(A)$ is a homeomorphism.

□

8.4. Quasi Rigid Morphisms

Now, we shall define the quasi rigid morphisms of the category $NCom-iclG{R}^{*}$ as an abstraction of the quasi $r^{*}$-quantale morphisms and the quasi $r^{*}$-frame morphisms (defined in [24]).

Definition 10. 

The morphism $u:A\to B$ of $NCom-iclG{R}^{*}$ is said to be quasi rigid if for any $d\in K(B)$, there exists $c\in K(A)$ such that $d^{{\perp }_B}={(u(c))}^{{\perp }_B}$.

Theorem 13. 

The following properties are equivalent:

(1) 

u is a quasi rigid morphism of $NCom-iclG{R}^{*}$;

(2) 

$u^{\rho }$ is a quasi rigid frame morphism.

Proof. 

$(1)\Rightarrow (2)$ Assume that u is a quasi rigid morphism of $NCom-iclG{R}^{*}$. Let y be a compact element of the frame $R(B)$, so there exists $d\in K(B)$ such that $y={\rho }_B(d)$ (cf. Proposition 4). By hypothesis $(1)$, there exists $c\in K(A)$ such that $d^{{\perp }_B}={(u(c))}^{{\perp }_B}$. Denote $x={\rho }_A(c)$. Thus, x is a compact element of the frame $R(A)$ (cf. Proposition 4). From the proof of Theorem 9, we know that ${(u(c))}^{{\perp }_B}={(u^{\rho }(x))}^{{\perp }_{R(B)}}$ and $d^{{\perp }_B}=y^{{\perp }_{R(B)}}$, so ${(u^{\rho }(x))}^{{\perp }_{R(B)}}=y^{{\perp }_{R(B)}}$. Then, $u^{\rho }$ is a quasi rigid frame morphism.

$(2)\Rightarrow (1)$ Similarly. □

Proposition 12. 

Any quasi rigid morphism $u:A\to B$ of $NCom-iclG{R}^{*}$ is a quasi r-morphism and a quasi $r^{*}$- morphism of $NCom-iclG{R}^{*}$.

Proof. 

Recall from Theorem 2 (3) that $u^{\rho }:R(A)\to R(B)$ is a coherent frame morphism. In accordance with Theorem 13, $u^{\rho }$ is a quasi rigid frame morphism. By Proposition 9.1 of [24], it follows that $u^{\rho }$ is a quasi r-frame morphism and a quasi $r^{*}$-frame morphism. Therefore, using Theorems 9 and 12, we find that u is a quasi r-morphism and a quasi $r^{*}$ morphism of $NCom-iclG{R}^{*}$. □

Lemma 37. 

Let A be a semiprime object of $NCom-iclG{R}^{*}$. For each $c\in K(A)$, $c^{{\perp }_A}=\bigwedge D_A(c)$.

Proof. 

Let c be a compact element of A; hence, ${\rho }_A(c)\in R(A)$. We know that $R(A)$ is a coherent frame (cf. Lemma 3), and hence, using Lemma 4 of [25], we obtain

$${({\rho }_A(c))}^{{\perp }_{Rad(A)}}=\bigwedge \{p\in Min(R(A))|{\rho }_A(c)\nleqq p\}$$

Recall that $Min(A)=Min(R(A))$. According to Lemmas 11 and 12 (3), we have ${({\rho }_A(c))}^{{\perp }_{Rad(A)}}={({\rho }_A(c))}^{{\perp }_A}=c^{{\perp }_A}$; therefore,

$$c^{{\perp }_A}=\bigwedge \{p\in Min(R(A))|{\rho }_A(c)\nleqq p\}=\bigwedge \{p\in Min(A)|c\nleqq p\}=\bigwedge D_A(c).$$

□

Corollary 13. 

Let A be a semiprime object of $NCom-iclG{R}^{*}$. For all $c,d\in K(A)$, $V_A(c)=V_A(d)$ implies $c^{{\perp }_A}=d^{{\perp }_A}$.

Proof. 

If $V_A(c)=V_A(d)$, then $D_A(c)=D_A(d)$; so, using Lemma 37, we obtain $c^{{\perp }_A}=\bigwedge D_A(c)=\bigwedge D_A(d)=d^{{\perp }_A}$ □

Theorem 14. 

Let $u:A\to B$ be a morphism of $NCom-iclG{R}^{*}$. If $Mi{n}_Z(B)$ is a compact space, then the following properties are equivalent:

(1) 

u is a quasi $r^{*}$-morphism of $NCom-iclG{R}^{*}$;

(2) 

u is a quasi rigid morphism of $NCom-iclG{R}^{*}$.

Proof. 

$(1)\Rightarrow (2)$ Assume that u is a quasi $r^{*}$-morphism of $NCom-iclG{R}^{*}$. Let d be a compact element of B. By virtue of the hypothesis, for each $q\in Min(B)$ such that $d\le q$, there exists $c_q\in K(A)$ such that $u(c_q)\le q$ and ${(u(c_q))}^{{\perp }_B}\le d^{{\perp }_B}$. The last two inequalities imply that

$$V_B(d)=\bigcup \left\{V_B(u(c_q))\right|q\in V_B(d)\}$$

Since $Mi{n}_Z(B)$ is a compact, there exist an integer $n\ge 1$ and $q_1,\dots ,q_n\in V_B(d)$ such that $V_B(d)={\bigcup }_{i=1}^n{V}_B(u(c_{q_i}))$. Using Proposition 1 (1), we have $V_B(u(c_{q_i}))=V_B({\rho }_B(u(c_{q_i})))$, for any $i=1,\dots ,n$. Therefore, in accordance with Theorem 1, the following equalities hold:

$$V_B(d)=\bigcup _{i=1}^n{V}_B({\rho }_B(u(c_{q_i})))=V_B({\rho }_B(u(c_{q_1}))\cdots {\rho }_B(u(c_{q_n})))=$$

$$=V_B({\rho }_B(u(c_{q_1})\cdots {\rho }_B(u(c_{q_n})))=V_B({\rho }_B(c_{q_1}\cdots c_{q_n})))=V_B(u(c_{q_1}\cdots c_{q_n}))$$

Let us denote $c=c_{q_1}\cdots c_{q_n}$, so $c\in K(A)$ and $V_B(d)=V_B(u(c))$. By Proposition 4, we have $u(c)\in K(B)$; therefore, using Corollary 13, we obtain $d^{{\perp }_B}={(u(c))}^{{\perp }_B}$. Then, u is a quasi rigid morphism of $NCom-iclG{R}^{*}$.

$(2)\Rightarrow (1)$ By Proposition 12.

□