Inference for Parameters of Exponential Distribution under Combined Type II Progressive Hybrid Censoring Scheme

Abstract

In recent years, various forms of progressive hybrid censoring schemes (PHCS) have gained significant traction in survival and reliability analysis studies due to their versatility. However, these PHCS variants are often characterized by complexity stemming from the multitude of parameters involved in their specification. Consequently, the primary objective of this paper is to propose a unified approach termed combined type II progressive hybrid censoring scheme (${\mathrm{ComT}}_2$PHCS) capable of encompassing several existing PHCS variations. Our analysis focuses specifically on the exponential distribution (ExDist). Bayesian inference techniques are employed to estimate the parameters of the ExDist under the ${\mathrm{ComT}}_2$PHCS. Additionally, we conduct fundamental distributional analyses and likelihood inference procedures. We derive the conditional moment-generating function (CondMGF) of maximum likelihood estimator (MLE) for parameters of the ExDist under ${\mathrm{ComT}}_2$PHCS. Further, we use CondMGF for the distribution of MLE for parameters of ExDist under ${\mathrm{ComT}}_2$PHCS. Finally, we provide an illustrative example to elucidate the inference methods derived in this paper.

1. Introduction

Due to constraints in cost and time, life-testing and reliability studies often necessitate termination before all failures are observed. Censoring techniques are extensively utilized to reduce test duration and costs. For this reason, the progressive censoring scheme (PCS) has gained popularity in reliability research (Ref. [1]).

The PCS arises in reliability studies as follows. Consider a test in which n units are subjected to reliability tests. ${\mathcal{R}}_i$ remaining test units are randomly eliminated from the test when the ith failure($X_{i:m:n}$) occurs. This continues until the mth failure is observed, where the test is terminated and the remaining units(${\mathcal{R}}_m=n-m-{\sum }_{i=1}^{m-1}{\mathcal{R}}_i$) are eliminated. The ordered failure time $\mathit{x}=(x_{1:m:n},x_{2:m:n},\cdots ,x_{m:m:n})$ is called progressive censored data (PCD). Here, the integer m and the PCS $\mathcal{R}=\left({\mathcal{R}}_1,{\mathcal{R}}_2,\cdots ,{\mathcal{R}}_m\right)$ are pre-assigned, and the joint PDF (Ref. [1]) of PCD can be expressed by

$$\begin{array}{cc}\hfill f\left(\mathit{x}\right)=& {\kappa }^{\prime }\left(m\right)\prod _{i=1}^{m}f\left(x_{i:m:n}\right){\left[1-\mathcal{F}\left(x_{i:m:n}\right)\right]}^{{\mathcal{R}}_i},\hfill \end{array}$$

(1)

where ${\kappa }^{\prime }\left(a\right)={\prod }_{i_1=1}^a{\sum }_{i_2=i_1}^m\left({\mathcal{R}}_{i_2}+1\right)$, and X denotes the absolutely continuous random variable with PDF $f\left(x\right)$ and CDF $\mathcal{F}\left(x\right)$.

One of the drawbacks of the PCS is that the time of the reliability test can be very long if units are highly reliable. To address this concern, Refs. [2,3,4,5] introduced a variety of schemes, including type I progressive hybrid censroing scheme (${\mathrm{T}}_1$PHCS), type II progressive hybrid censroing scheme (${\mathrm{T}}_2$PHCS), generalized type I progressive hybrid censoring scheme (${\mathrm{GenT}}_1$PHCS), and generalized type II progressive hybrid censoring scheme (${\mathrm{GenT}}_2$PHCS).

In ${\mathrm{T}}_1$PHCS (Figure 1a), the integer m and the time $\mathcal{T}$ are pre-fixed. If $\mathcal{T}<X_{m:m:n}$, the test concludes at $\mathcal{T}$ (Case I). If $X_{m:m:n}<\mathcal{T}$, the test concludes at $X_{m:m:n}$ (Case II). In ${\mathrm{T}}_2$PHCS (Figure 1b), integers m and $\mathcal{T}$ are also pre-fixed. If $\mathcal{T}<X_{m:m:n}$, the test concludes at $X_{m:m:n}$ (Case I). If $X_{m:m:n}<\mathcal{T}$, the test concludes at $\mathcal{T}$ (Case II). ${\mathrm{T}}_1$PHCS guarantees the completion of the test at time $\mathcal{T}$. However, the drawback of the ${\mathrm{T}}_1$PHCS is that the number of observed failures is random. There might be instances where the number of observed failures is minimal, possibly even zero. Consequently, this randomness can render the statistical inference process inapplicable. Under the ${\mathrm{T}}_2$PHCS, a specific number, m, of failures is assured. However, the drawback of the ${\mathrm{T}}_2$PHCS is the random duration of the reliability test. Consequently, if units exhibit high reliability, the test duration can be prolonged.

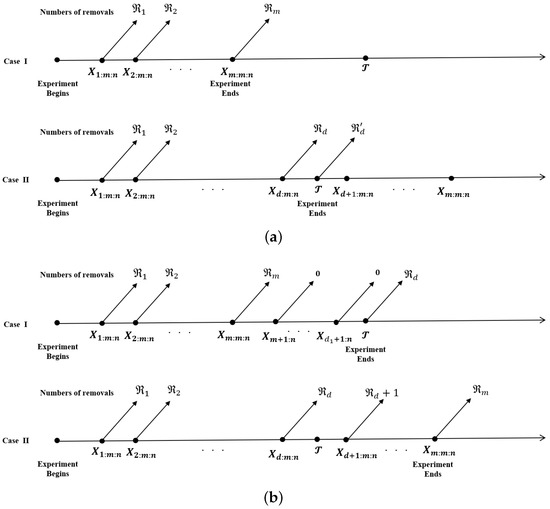
Figure 1. (a) ${\mathrm{T}}_1$PHCS; (b) ${\mathrm{T}}_2$PHCS.

In ${\mathrm{GenT}}_1$PHCS (Figure 2a), integers k and m and the time $\mathcal{T}$ are pre-fixed such that $k<m$. If $\mathcal{T}<X_{k:m:n}$, the test concludes at $X_{k:m:n}$ (Case I). If $X_{k:m:n}<\mathcal{T}<X_{m:m:n}$, the test concludes at $\mathcal{T}$ (Case II). If $X_{m:m:n}<\mathcal{T}$, the test concludes at $X_{m:m:n}$ (Case III). In ${\mathrm{GenT}}_2$PHCS (Figure 2b), the integer m and the times ${\mathcal{T}}_1$ and ${\mathcal{T}}_2$ are pre-fixed such that $0<{\mathcal{T}}_1<{\mathcal{T}}_2$. If $X_{m:m:n}<{\mathcal{T}}_1$, the test concludes at ${\mathcal{T}}_1$ (Case I). If $\mathcal{T}<X_{m:m:n}<{\mathcal{T}}_2$, the test concludes at $X_{m:m:n}$ (Case II). If ${\mathcal{T}}_2<X_{m:m:n}$, the test concludes at ${\mathcal{T}}_2$ (Case III). Under ${\mathrm{GenT}}_1$PrHyCS, a minimum number k of failures is guaranteed. However, one of the limitations of ${\mathrm{GenT}}_1$PHCS is the randomness of the reliability test duration. Consequently, if units exhibit high reliability, the duration of the reliability test may significantly extend. ${\mathrm{GenT}}_2$PrHyCS guarantees the completion of the test at time ${\mathcal{T}}_2$. However, ${\mathrm{GenT}}_2$PHCS exhibits a drawback in that the number of observed failures is random, potentially resulting in a minimal number of observed failures, possibly even zero. Consequently, this randomness may render the statistical inference process inapplicable.

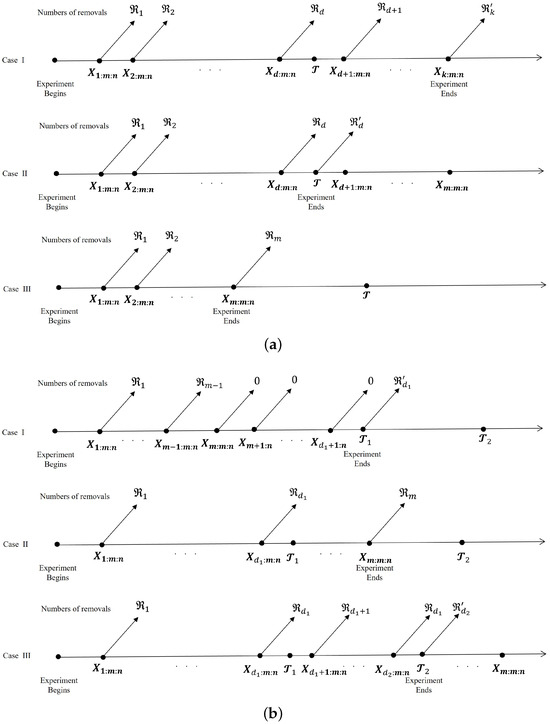
Figure 2. (a) ${\mathrm{GenT}}_1$PHCS; (b) ${\mathrm{GenT}}_2$PHCS.

Recently, some studies on PHCS have been carried out by many authors (Refs. [6,7,8,9,10,11,12,13,14,15,16,17,18,19]). Ref. [6] investigated exact likelihood inference for an exponential parameter under adaptive ${\mathrm{GenT}}_1$PHCS. Ref. [7] analyzed the reliability characteristics of bathtub-shaped distributions under adaptive ${\mathrm{T}}_1$PHCS. Ref. [8] delved into inference for a general family of inverted exponentiated distributions with partially observed competing risks under ${\mathrm{GenT}}_1$PHCS. Ref. [9] discussed Bayesian survival analysis for Hjorth data under adaptive ${\mathrm{T}}_2$PHCS. Ref. [10] examined statistical inference of adaptive ${\mathrm{T}}_2$PHCS with dependent competing risks under bivariate exponential distribution. Ref. [11] discussed improved maximum likelihood estimation of the shape-scale family based on ${\mathrm{GenT}}_1$PHCS. Ref. [12] investigated estimation and prediction for Burr type III distribution based on unified PHCS. Ref. [13] addressed Bayesian and maximum likelihood estimation of uncertainty measures of the inverse Weibull distribution under generalized adaptive PHCS. Ref. [14] focused on estimation for Kies distribution with ${\mathrm{Gen}}_1$PHCS under partially observed competing risks model. Ref. [15] explored the survival analysis of the several extended exponential model from adaptive PHCS and its enginnering applications. Ref. [16] conducted computational analysis for Frechet parameters of life from ${\mathrm{GenT}}_2$PHCS, with applications in physics and engineering. Ref. [17] discussed inference on adaptive PHCS under partially accelerated life test for odd Lindley Half-Logistic distribution. Ref. [18] examined statistical analysis and applications of Poisson-Exponential distribution under adaptive PHCS. Ref. [19] addressed statistical analysis of inverse Lindley data using adaptive ${\mathrm{T}}_2$PHCS with applications.

These four types of PHCS are highly complex due to the large number of parameters involved in specifying the censoring procedure. Additionally, if data reliability is excessively high, issues such as unobserved data or excessively long experiment durations may arise if the PHCS is improperly set in advance. Therefore, the objective of this paper is to propose a ${\mathrm{ComT}}_2$PHCS that encompasses these four types of PHCS. We specifically consider the ExDist under ${\mathrm{ComT}}_2$PHCS. Bayesian inference for the parameters of ExDist under ${\mathrm{ComT}}_2$PHCS is established, and we conduct basic distributional analyses as well as likelihood inference.

A detailed description of ${\mathrm{ComT}}_2$PHCS will be provided in Section 2. In Section 3, we derive the Bayesian estimator and credible interval for the parameters of ExDist under ${\mathrm{ComT}}_2$PHCS. Additionally, we derive the CondMGF of the MLE for the parameters of ExDist under ${\mathrm{ComT}}_2$PHCS. Using CondMGF, we explore the distribution of MLE for the parameters of ExDist under ${\mathrm{ComT}}_2$PHCS. Subsequently, in Section 4, we present the results of a simulation study under ${\mathrm{ComT}}_2$PHCS, including the mean squared error (MSE), bias, confidence length (CL), and coverage percentage (CP) of the MLE. Furthermore, we provide an example to elucidate the inference methods derived in this paper. Finally, concluding remarks are presented in Section 5.

2. Combined Type II Progressive Hybrid Censoring

Using the PCS, ${\mathrm{ComT}}_2$PHCS can be described as follows. The ${\mathcal{T}}_1$ and ${\mathcal{T}}_2$($0<{\mathcal{T}}_1<{\mathcal{T}}_2<\infty$), and integers m and k are pre-assigned ($k\le m\le n$). Additionally, PCS $\mathcal{R}=({\mathcal{R}}_1,{\mathcal{R}}_2,\cdots ,{\mathcal{R}}_m)$ is pre-assigned. Let ${\mathcal{D}}_1$ and ${\mathcal{D}}_2$ denote the number of failures up to pre-assigned times ${\mathcal{T}}_1$ and ${\mathcal{T}}_2$, respectively. Furthermore, $d_1$ and $d_2$ represent the observed values of ${\mathcal{D}}_1$ and ${\mathcal{D}}_2$, respectively. If $X_{m:m:n}<{\mathcal{T}}_1$, the reliability test concludes at $X_{m:m:n}$ (Case I). If $X_{k:m:n}<{\mathcal{T}}_1$, the reliability test concludes by eliminating all remaining units (${\mathcal{R}}_{d_1}^{\prime }=n-d_1-{\sum }_{i=1}^{d_1}{\mathcal{R}}_i$) at ${\mathcal{T}}_1$ (Case II). If ${\mathcal{T}}_1<X_{k:m:n}<X_{m:m:n}<{\mathcal{T}}_2$, the reliability test concludes by eliminating all remaining units (${\mathcal{R}}_m=n-m-{\sum }_{i=1}^{m-1}{\mathcal{R}}_i$) at $X_{m:m:n}$ (Case III). If ${\mathcal{T}}_1<X_{k:m:n}<{\mathcal{T}}_2<X_{m:m:n}$, the reliability test concludes by eliminating all remaining units (${\mathcal{R}}_{d_2}^{\prime }=n-d_2-{\sum }_{i=1}^{d_2}{\mathcal{R}}_i$) at ${\mathcal{T}}_2$ (Case IV). If ${\mathcal{T}}_2<X_{k:m:n}$, the reliability test concludes by eliminating all remaining units (${\mathcal{R}}_{d_2}^{\prime }=n-d_2-{\sum }_{i=1}^{d_2}{\mathcal{R}}_i$) at ${\mathcal{T}}_2$ (Case V). In summary, ${\mathrm{ComT}}_2$PHCS entails five distinct cases, as illustrated in Figure 3.

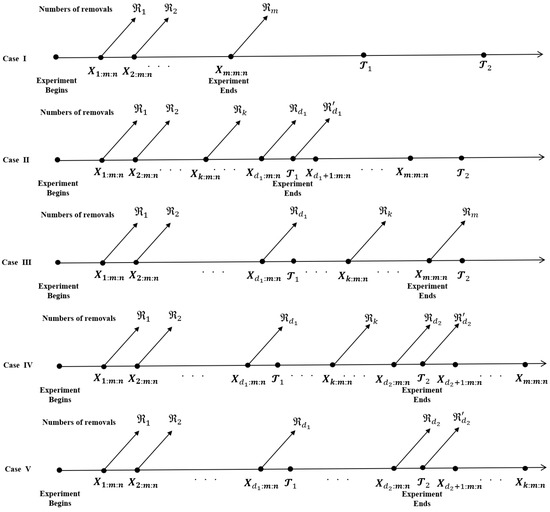
Figure 3. Schematic representation of ${\mathrm{ComT}}_2$PHCS.

• Case I: $\{X_{1:m:n},\cdots ,X_{k:m:n},\cdots ,X_{m:m:n}\}$, if $X_{k:m:n}<X_{m:m:n}<{\mathcal{T}}_1$.
• Case II: $\{X_{1:m:n},\cdots ,X_{k:m:n},\cdots ,X_{d_1:m:n}\}$, if $X_{k:m:n}<{\mathcal{T}}_1<X_{m:m:n}$.
• Case III: $\{X_{1:m:n},\cdots ,X_{d_1:m:n},\cdots ,X_{k:m:n},\cdots ,X_{m:m:n}\}$, if ${\mathcal{T}}_1<X_{k:m:n}<X_{m:m:n}<{\mathcal{T}}_2$.
• Case IV: $\{X_{1:m:n},\cdots ,X_{k:m:n},\cdots ,X_{d_2:m:n}\}$, if ${\mathcal{T}}_1<X_{k:m:n}<{\mathcal{T}}_2<X_{m:m:n}$.
• Case V: $\{X_{1:m:n},\cdots ,X_{d_2:m:n}\}$, if ${\mathcal{T}}_2<X_{k:m:n}$. Here, $X_{k:m:n}<X_{d_1:m:n}<{\mathcal{T}}_1<X_{d_1+1:m:n}$, and $X_{d_1+1:m:n},\cdots ,X_{m:m:n}$ are not observed for Case II. ${\mathcal{T}}_1<X_{k:m:n}<X_{d_2:m:n}<{\mathcal{T}}_2<X_{d_2+1:m:n}$, and $X_{d_2+1:m:n},\cdots ,X_{m:m:n}$ are not observed for Case IV. $X_{d_2:m:n}<{\mathcal{T}}_2<X_{d_2+1:m:n}<X_{k:m:n}$, and $X_{d_2+1:m:n},\cdots ,X_{m:m:n}$ are not observed for Case V.

This ${\mathrm{ComT}}_2$PHCS combined ${\mathrm{T}}_1$PHCS, ${\mathrm{T}}_2$PHCS, ${\mathrm{GenT}}_1$PHCS, and ${\mathrm{GenT}}_2$PHCS. It is evident that the proposed ${\mathrm{ComT}}_2$PHCS introduces a second termination time, ${\mathcal{T}}_2$, alongside ${\mathcal{T}}_1$, and the second integer, k, in addition to m, to offer greater flexibility compared to ${\mathrm{T}}_1$PHCS, ${\mathrm{T}}_2$PHCS, ${\mathrm{GenT}}_1$PHCS, and ${\mathrm{GenT}}_2$PHCS. Additionally, this scheme enables the collection of more observations, enhancing the inference process. Under ${\mathrm{ComT}}_2$PHCS, we ensure that the test concludes within the specified time, ${\mathcal{T}}_2$. Here, ${\mathcal{T}}_2$ denotes the maximum test duration allowed by the tester. Consequently, ${\mathrm{ComT}}_2$PHCS provides testers with a wider array of options to mitigate challenges such as prolonged test durations and the potential absence of observed failures.

3. Inference

3.1. Conditional Maximum Likelihood Estimator

Based on the four scenarios as explained in Section 2, the likelihood function ($\mathcal{L}$) of ${\mathrm{ComT}}_2$PHCS can be derived as

$$\begin{array}{c}\hfill \mathcal{L}\left(\lambda \right|\mathit{x})=\left\{\begin{array}{c}{\kappa }^{\prime }\left(m\right)\prod _{i=1}^{m}f\left(x_{i:m:n}\right){\left[1-\mathcal{F}\left(x_{i:m:n}\right)\right]}^{{\mathcal{R}}_i},\hfill \\ {\mathcal{D}}_1=m,\hfill \\ {\kappa }^{\prime }\left({\mathcal{D}}_1\right)\prod _{i_1=1}^{{\mathcal{D}}_1}f\left(x_{i:m:n}\right){\left[1-\mathcal{F}\left(x_{i:m:n}\right)\right]}^{{\mathcal{R}}_i}{\left[1-\mathcal{F}\left({\mathcal{T}}_1\right)\right]}^{{\mathcal{R}}_{d_1}^{\prime }},\hfill \\ {\mathcal{D}}_1=k,k+1,\cdots ,m-1,\hfill \\ {\kappa }^{\prime }\left(m\right)\prod _{i=1}^{m}f\left(x_{i:m:n}\right){\left[1-\mathcal{F}\left(x_{i:m:n}\right)\right]}^{{\mathcal{R}}_i},\hfill \\ {\mathcal{D}}_1=0,1,\cdots ,k-1,{\mathcal{D}}_2=m,\hfill \\ {\kappa }^{\prime }\left({\mathcal{D}}_2\right)\prod _{i=1}^{{\mathcal{D}}_2}f\left(x_{i:m:n}\right){\left[1-\mathcal{F}\left(x_{i:m:n}\right)\right]}^{{\mathcal{R}}_i}{\left[1-\mathcal{F}\left({\mathcal{T}}_2\right)\right]}^{{\mathcal{R}}_{d_2}^{\prime }},\hfill \\ {\mathcal{D}}_2=1,\cdots ,k-1,{\mathcal{D}}_2=k,k+1,\cdots ,m-1,\hfill \\ {\kappa }^{\prime }\left({\mathcal{D}}_2\right)\prod _{i=1}^{{\mathcal{D}}_2}f\left(x_{i:m:n}\right){\left[1-\mathcal{F}\left(x_{i:m:n}\right)\right]}^{{\mathcal{R}}_i}{\left[1-\mathcal{F}\left({\mathcal{T}}_2\right)\right]}^{{\mathcal{R}}_{d_2}^{\prime }},\hfill \\ {\mathcal{D}}_2=1,\cdots ,m-1,\hfill \end{array}\right.\end{array}$$

(2)

where ${\kappa }^{\prime }\left(a\right)={\prod }_{i_1=1}^a{\sum }_{i_2=i_1}^m\left({\mathcal{R}}_{i_2}+1\right)$, ${\mathcal{R}}_{d_1}^{\prime }=n-d_1-{\sum }_{i_1=1}^{d_1}{\mathcal{R}}_{i_1}$ for Case II and ${\mathcal{R}}_{d_2}^{\prime }=n-d_2-{\sum }_{i_1=1}^{d_2}{\mathcal{R}}_{i_1}$ for Cases IV and V. Here, the MLE does not exist when ${\mathcal{D}}_2=0$ for Case V. Therefore, in order to estimate MLE, the inference results that follow are conditional on ${\mathcal{D}}_2\ge 1$.

A random variable X is said to have ExDist with parameter $\lambda$ if its PDF is provided by

$$\begin{array}{c}\hfill f(x;\lambda )=\frac{1}{\lambda }{e}^{-x/\lambda },x>0,\lambda >0.\end{array}$$

(3)

From Equations (2) and (3), we obtain the conditional MLE (CondMLE) of the parameters of ExDist under ${\mathrm{ComT}}_2$PHCS as

$$\begin{array}{c}\hfill \widehat{\lambda }=\left\{\begin{array}{cc}\frac{1}{m}\left[\sum _{i=1}^m\left({\mathcal{R}}_i+1\right)x_{i:m:n}\right],\hfill & {\mathcal{D}}_1=m,\hfill \\ \hfill & \\ \frac{1}{d_1}\left[\sum _{i=1}^{d_1}\left({\mathcal{R}}_i+1\right)x_{i:m:n}+{\mathcal{R}}_{d_1}^{\prime }{\mathcal{T}}_1\right],\hfill & {\mathcal{D}}_1=k,k+1,\cdots ,m-1,\hfill \\ \hfill & \\ \frac{1}{m}\left[\sum _{i=1}^m\left({\mathcal{R}}_i+1\right)x_{i:m:n}\right],\hfill & {\mathcal{D}}_1=0,1,\cdots ,k-1,{\mathcal{D}}_2=m,\hfill \\ \hfill & \\ \frac{1}{d_2}\left[\sum _{i=1}^{d_2}\left({\mathcal{R}}_i+\right)x_{i:m:n}+{\mathcal{R}}_{d_2}^{\prime }{\mathcal{T}}_2\right],\hfill & {\mathcal{D}}_1=0,1,\cdots ,k-1,{\mathcal{D}}_2=k,\cdots ,m-1,\hfill \\ \hfill & \\ \frac{1}{d_2}\left[\sum _{i=1}^{d_2}\left({\mathcal{R}}_i+\right)x_{i:m:n}+{\mathcal{R}}_{d_2}^{\prime }{\mathcal{T}}_2\right],\hfill & {\mathcal{D}}_2=1,\cdots ,k-1.\hfill \end{array}\right.\end{array}$$

(4)

3.2. Bayesian Inference

In this subsection, we approach the problem from a Bayesian perspective. In the context of exponential distribution, $\lambda$ may be reasonably modeled using inverse gamma prior with parameters a and b. Here, parameters a and b are both assumed to be positive. When $a=b=0.0001$, we obtain non-informative priors of $\lambda$. The posterior density of $\lambda$ based on the inverse gamma priors is provided by

$$\begin{array}{c}\hfill \pi \left(\lambda \right|\mathit{x})=\left\{\begin{array}{c}{c}_1{\lambda }^{-(m+a)-1}exp\{-\frac{1}{\lambda }\left[b+\sum _{i=1}^m({\mathcal{R}}_i+1)x_{i:m:n}\right]\},\hfill \\ {\mathcal{D}}_1=m,\hfill \\ \hfill & \\ c_2{\lambda }^{-(d_1+a)-1}exp\{-\frac{1}{\lambda }\left[b+\sum _{i=1}^{d_1}({\mathcal{R}}_i+1)x_{i:m:n}+{\mathcal{R}}_{d_1}^{\prime }{\mathcal{T}}_1\right]\},\hfill \\ {\mathcal{D}}_1=k,k+1,\cdots ,m-1,\hfill \\ \hfill & \\ c_3{\lambda }^{-(m+a)-1}exp\{-\frac{1}{\lambda }\left[b+\sum _{i=1}^m({\mathcal{R}}_i+1)x_{i:m:n}\right]\},\hfill \\ {\mathcal{D}}_1=0,1,\cdots ,k-1,{\mathcal{D}}_2=m,\hfill \\ \hfill & \\ c_4{\lambda }^{-(d_2+a)-1}exp\{-\frac{1}{\lambda }\left[b+\sum _{i=1}^{d_2}({\mathcal{R}}_i+1)x_{i:m:n}+{\mathcal{R}}_{d_2}^{\prime }{\mathcal{T}}_2\right]\},\hfill \\ {\mathcal{D}}_2=1,\cdots ,k-1,{\mathcal{D}}_2=k,k+1,\cdots ,m-1,\hfill \\ \hfill & \\ c_5{\lambda }^{-(d_2+a)-1}exp\{-\frac{1}{\lambda }\left[b+\sum _{i=1}^{d_2}({\mathcal{R}}_i+1)x_{i:m:n}+{\mathcal{R}}_{d_2}^{\prime }{\mathcal{T}}_2\right]\},\hfill \\ {\mathcal{D}}_2=1,\cdots ,m-1,\hfill \end{array}\right.\end{array}$$

(5)

where $c_i$ represents the normalizing constants that ensure $\pi \left(\lambda \right|\mathit{x})$ is proper density function.

From Equation (5), it is clear that the posterior density function is the density function of an inverse gamma random variable with parameters $\mathcal{U}+a$ and $b+{\sum }_{i=1}^{\mathcal{U}}({\mathcal{R}}_i+1)x_{i:m:n}+\mathcal{W}$. Here, $\mathcal{U}=m$ for Cases I and III, $\mathcal{U}=d_1$ for Case II, and $\mathcal{U}=d_2$ for Cases IV and V. Also, $\mathcal{W}=0$ for Cases I and III, $\mathcal{W}={\mathcal{R}}_{d_1}^{\prime }{\mathcal{T}}_1$ for Case II, and $\mathcal{U}={\mathcal{R}}_{d_2}^{\prime }{\mathcal{T}}_2$ for Cases IV and V. Therefore, the Bayesian estimate of $\lambda$ under squared error loss is

$$\begin{array}{c}\hfill {\widehat{\lambda }}_{B_1}=\left\{\begin{array}{cc}\frac{b+{\sum }_{i=1}^m({\mathcal{R}}_i+1)x_{i:m:n}}{m+a-1},\hfill & {\mathcal{D}}_1=m,\hfill \\ \hfill & \\ \frac{b+{\sum }_{i=1}^{d_1}\left({\mathcal{R}}_i+1\right)x_{i:m:n}+{\mathcal{R}}_{d_1}^{\prime }{\mathcal{T}}_1}{d_1+a-1},\hfill & {\mathcal{D}}_1=k,k+1,\cdots ,m-1,\hfill \\ \hfill & \\ \frac{b+{\sum }_{i=1}^m({\mathcal{R}}_i+1)x_{i:m:n}}{m+a-1},\hfill & {\mathcal{D}}_1=0,1,\cdots ,k-1,{\mathcal{D}}_2=m,\hfill \\ \hfill & \\ \frac{b+{\sum }_{i=1}^{d_2}\left({\mathcal{R}}_i+\right)x_{i:m:n}+{\mathcal{R}}_{d_2}^{\prime }{\mathcal{T}}_2}{d_2+a-1},\hfill & {\mathcal{D}}_1=0,1,\cdots ,k-1,{\mathcal{D}}_2=k,\cdots ,m-1,\hfill \\ \hfill & \\ \frac{b+{\sum }_{i=1}^{d_2}\left({\mathcal{R}}_i+\right)x_{i:m:n}+{\mathcal{R}}_{d_2}^{\prime }{\mathcal{T}}_2}{d_2+a-1},\hfill & {\mathcal{D}}_2=1,\cdots ,k-1.\hfill \end{array}\right.\end{array}$$

(6)

For the non-informative prior ($a=b=0.0001$), the Bayesian estimate (${\widehat{\lambda }}_{B_2}$) under squared error loss can be obtained easily.

The credible interval for $\lambda$ is obtained easily from the posterior distribution. We observe that, a posteriori, $Z=\frac{\lambda }{2\left[b+{\sum }_{i=1}^{\mathcal{U}}({\mathcal{R}}_i+1)x_{i:m:n}+\mathcal{W}\right]}$ follows $Inv-{\chi }_{2(\mathcal{U}+a)}^2$ distribution. Consequently, the $100(1-\alpha )\%$ credible interval for $\lambda$ is

$$\begin{array}{c}\hfill \left[\frac{2\left[b+{\sum }_{i=1}^{\mathcal{U}}({\mathcal{R}}_i+1)x_{i:m:n}+\mathcal{W}\right]}{{\chi }_{2(\mathcal{U}+a),1-\frac{\alpha }{2}}^2},\frac{2\left[b+{\sum }_{i=1}^{\mathcal{U}}({\mathcal{R}}_i+1)x_{i:m:n}+\mathcal{W}\right]}{{\chi }_{2(\mathcal{U}+a),\frac{\alpha }{2}}^2}\right],\end{array}$$

where ${\chi }_{df,\alpha }^2$ is the lower $\alpha$-th percentile point of the ${\chi }^2$ distribution with $df$ degrees of freedom.

3.3. Exact Inference for Conditional MLE

Lemma 1. 

The conditional joint density of ${\mathit{ComT}}_2$PHCD is provided by

Case I (${\mathcal{D}}_1=m$):

$$\begin{array}{cc}\hfill f\left(x_{1:m:n},\cdots ,x_{m:m:n}|{\mathcal{D}}_1=m\right)=\frac{{\kappa }^{\prime }\left(m\right)}{P\left({\mathcal{D}}_1=m\right)}\prod _{i=1}^{m}f\left(x_{i:m:n}\right)& {\left\{1-\mathcal{F}\left(x_{i:m:n}\right)\right\}}^{{\mathcal{R}}_i},\hfill \\ \hfill & -\infty <x_{1:m:n}<\cdots <x_{m:m:n}<{\mathcal{T}}_1.\hfill \end{array}$$

Case II (${\mathcal{D}}_1=k,k+1,\cdots ,m-1$):

$$\begin{array}{cc}\hfill f\left(x_{1:m:n},\cdots ,x_{d_1:m:n}|{\mathcal{D}}_1=d_1\right)=\frac{{\kappa }^{\prime }\left(d_2\right){\left\{1-\mathcal{F}\left({\mathcal{T}}_1\right)\right\}}^{{\mathcal{R}}_{d_1}^{\prime }}}{P\left({\mathcal{D}}_1=d_1\right)}& \prod _{i=1}^{d_1}f\left(x_{i:m:n}\right){\left\{1-\mathcal{F}\left(x_{i:m:n}\right)\right\}}^{{\mathcal{R}}_j},\hfill \\ \hfill & -\infty <x_{1:m:n}<\cdots <x_{d_1:m:n}<{\mathcal{T}}_1.\hfill \end{array}$$

Case III (${\mathcal{D}}_1=0,1,\cdots ,k-1$ and ${\mathcal{D}}_2=m$):

$$\begin{array}{c}\hfill f\left(x_{1:m:n},\cdots ,x_{m:m:n}|{\mathcal{D}}_1=d_1,{\mathcal{D}}_2=m\right)=\frac{{\kappa }^{\prime }\left(m\right)}{P\left({\mathcal{D}}_1=d_1,{\mathcal{D}}_2=m\right)}\prod _{i=1}^{m}f\left(x_{i:m:n}\right){\left\{1-\mathcal{F}\left(x_{i:m:n}\right)\right\}}^{{\mathcal{R}}_i},\\ \hfill -\infty <x_{1:m:n}<\cdots <x_{d_1:m:n}<{\mathcal{T}}_1<\cdots <x_{k:m:n}<\cdots <x_{m:m:n}<{\mathcal{T}}_2.\end{array}$$

Case IV (${\mathcal{D}}_1=1,\cdots ,k-1$ and ${\mathcal{D}}_2=k,\cdots ,m-1$):

$$\begin{array}{cc}\hfill f\left(x_{1:m:n},\cdots ,x_{d_2:m:n}|{\mathcal{D}}_1=d_1,{\mathcal{D}}_2=d_2\right)=& \frac{{\kappa }^{\prime }\left(d_2\right){\left\{1-\mathcal{F}\left({\mathcal{T}}_2\right)\right\}}^{{\mathcal{R}}_{d_2}^{\prime }}}{P\left({\mathcal{D}}_1=d_1,{\mathcal{D}}_2=d_2\right)}\hfill \\ \hfill & \times \prod _{i=1}^{d_2}f\left(x_{i:m:n}\right){\left\{1-\mathcal{F}\left(x_{i:m:n}\right)\right\}}^{{\mathcal{R}}_i},\hfill \\ \hfill & -\infty <x_{1:m:n}<\cdots <x_{d_1:m:n}<{\mathcal{T}}_1<\cdots <x_{k:m:n}<\cdots <x_{d_2:m:n}<{\mathcal{T}}_2.\hfill \end{array}$$

Case V (${\mathcal{D}}_2=1,\cdots ,k-1$):

$$\begin{array}{cc}\hfill f\left(x_{1:m:n},\cdots ,x_{d_2:m:n}|{\mathcal{D}}_2=d_2\right)=\frac{{\kappa }^{\prime }\left(d_2\right){\left\{1-\mathcal{F}\left({\mathcal{T}}_2\right)\right\}}^{{\mathcal{R}}_{d_2}^{\prime }}}{P\left({\mathcal{D}}_2=d_2\right)}& \prod _{i=1}^{d_2}f\left(x_{i:m:n}\right){\left\{1-\mathcal{F}\left(x_{i:m:n}\right)\right\}}^{{\mathcal{R}}_i},\hfill \\ \hfill & -\infty <x_{1:m:n}<\cdots <x_{d_2:m:n}<{\mathcal{T}}_2.\hfill \end{array}$$

Proof. 

From Equation (1), Cases I and III are straightforward. Case II is derived by writing the event $\{{\mathcal{D}}_1=d_1\}$ as $\{X_{d_1:m:n}\le {\mathcal{T}}_1<X_{d_1+1:m:n}\}$ and integrating with respect to $X_{d_1+1:m:n}$ (from ${\mathcal{T}}_1$ to ∞) in the joint density function $X_{1:m:n},X_{2:m:n},\cdots ,X_{d_1:m:n}$ obtained from Equation (1). Cases IV and V are derived by writing the event $\{{\mathcal{D}}_2=d_2\}$ as $\{X_{d_2:m:n}\le {\mathcal{T}}_2<X_{d_2+1:m:n}\}$ and integrating with respect to $X_{d_2+1:m:n}$ (from ${\mathcal{T}}_2$ to ∞) in the joint density function $X_{1:m:n},X_{2:m:n},\cdots ,X_{d_2:m:n}$ obtained from Equation (1). □

Theorem 1. 

Conditional on ${\mathcal{D}}_2\ge 1$, the CondMGF of CondMLE of ExDist under ${\mathit{ComT}}_2$PHCS is provided by

$$\begin{array}{cc}\hfill {\mathcal{M}}_{\widehat{\lambda }}\left(t\right)=& E\left(e^{t\widehat{\lambda }}\right)\hfill \\ \hfill =& \frac{1}{1-{\tau }_2^n}\left[\frac{{\kappa }^{\prime }\left(m\right)}{{\left(1-\lambda t/m\right)}^m}\sum _{i=0}^m{\kappa }_{i,m}\left({\mathcal{R}}^{\mathbf{1},\mathit{m}}\right){\tau }_1^{\left(1-\lambda t/m\right){\mathcal{R}}_{m-i+1}^{*}}\right.\hfill \\ \hfill & +\sum _{d_1=k}^{m-1}\frac{{\kappa }^{\prime }\left(d_1\right)}{{\left(1-\lambda t/d_1\right)}^{d_1}}\sum _{i=0}^{d_1}{\kappa }_{i,d_1}\left({\mathcal{R}}^{\mathbf{1},{\mathit{d}}_{\mathbf{1}}}\right){\tau }_1^{\left(1-\lambda t/d_1\right){\mathcal{R}}_{d_1-i+1}^{*}}\hfill \\ \hfill & +\sum _{d_1=0}^{k-1}\frac{{\kappa }^{\prime }\left(m\right)}{{\left(1-\lambda t/m\right)}^m}\sum _{i_1=0}^{d_1}\sum _{i_2=0}^{m-d_1}{\kappa }_{i_1,d_1}\left({\mathcal{R}}^{\mathbf{1},{\mathit{d}}_{\mathbf{1}}}\right){\kappa }_{i_2,m-d_1}\left({\mathcal{R}}^{{\mathit{d}}_{\mathbf{1}}+\mathbf{1},\mathit{m}}\right)\hfill \\ \hfill & \times {\tau }_1^{\left(1-\lambda t/m\right){\sum }_{j=d_1-i_1+1}^{m-i_2}\left({\mathcal{R}}_j+1\right)}{\tau }_2^{\left(1-\lambda t/m\right){\sum }_{j=m-i_2+1}^m\left({\mathcal{R}}_j+1\right)}\hfill \\ \hfill & +\sum _{d_1=0}^{k-1}\sum _{d_2=k}^{m-1}\frac{{\kappa }^{\prime }\left(d_2\right)}{{\left(1-\lambda t/d_2\right)}^{d_2}}\sum _{i_1=0}^{d_1}\sum _{i_2=0}^{d_2-d_1}{\kappa }_{i_1,d_1}\left({\mathcal{R}}^{\mathbf{1},{\mathit{d}}_{\mathbf{1}}}\right){\kappa }_{i_2,d_2-d_1}\left({\mathcal{R}}^{{\mathit{d}}_{\mathbf{1}}+\mathbf{1},{\mathit{d}}_{\mathbf{2}}}\right)\hfill \\ \hfill & \times {\tau }_1^{\left(1-\lambda t/d_2\right){\sum }_{j=d_1-i_1+1}^{d_2-i_2}\left({\mathcal{R}}_j+1\right)}{\tau }_2^{\left(1-\lambda t/d_2\right){\sum }_{j=d_2-i_2+1}^{d_2}\left({\mathcal{R}}_j+1\right)}\hfill \\ \hfill & +\left.\sum _{d_2=1}^{k-1}\frac{{\kappa }^{\prime }\left(d_2\right)}{{\left(1-\lambda t/d_2\right)}^{d_2}}\sum _{i=0}^{d_2}{\kappa }_{i,d_2}\left({\mathcal{R}}^{\mathbf{1},{\mathit{d}}_{\mathbf{2}}}\right){\tau }_2^{\left(1-\lambda t/d_2\right){\mathcal{R}}_{d_2-i+1}^{*}}\right],\hfill \end{array}$$

where ${\mathcal{R}}^{\mathit{a},\mathit{b}}=\left({\mathcal{R}}_a+1,{\mathcal{R}}_{a+1}+1,\cdots ,{\mathcal{R}}_b+1\right)$, ${\mathcal{R}}_j^{*}={\sum }_{i=j}^m\left({\mathcal{R}}_i+1\right)$, ${\tau }_i=e^{-{\mathcal{T}}_i/\lambda }$ for $i=1$ and 2.

Proof. 

Conditional on ${\mathcal{D}}_2\ge 1$, the CondMGF of CondMLE of ExDist under ${\mathrm{ComT}}_2$PHCS is provided by

$$\begin{array}{cc}\hfill {\mathcal{M}}_{\widehat{\lambda }}\left(t\right)=& E\left(e^{t\widehat{\lambda }}\right)\hfill \\ \hfill =& \frac{1}{1-{\tau }_2^n}\left[E\left(e^{t\widehat{\lambda }}|{\mathcal{D}}_1=m\right)P\left({\mathcal{D}}_1=m\right)\right.\hfill \\ \hfill & +\sum _{d_1=k}^{m-1}E\left(e^{t\widehat{\lambda }}|{\mathcal{D}}_1=d_1\right)P\left({\mathcal{D}}_1=d_1\right)\hfill \\ \hfill & +\sum _{d_1=0}^{k-1}E\left(e^{t\widehat{\lambda }}|{\mathcal{D}}_1=d_1,{\mathcal{D}}_2=m\right)P\left({\mathcal{D}}_1=d_1,{\mathcal{D}}_2=m\right)\hfill \\ \hfill & +\sum _{d_1=0}^{k-1}\sum _{d_2=k}^{m-1}E\left(e^{t\widehat{\lambda }}|{\mathcal{D}}_1=d_1,{\mathcal{D}}_2=d_2\right)P\left({\mathcal{D}}_1=d_1,{\mathcal{D}}_2=d_2\right)\hfill \\ \hfill & \left.+\sum _{d_2=1}^{k-1}E\left(e^{t\widehat{\lambda }}|{\mathcal{D}}_2=d_2\right)P\left({\mathcal{D}}_2=d_2\right)\right].\hfill \end{array}$$

(7)

For Case I (${\mathcal{D}}_1=m$),

$$\begin{array}{cc}\hfill E\left(e^{t\widehat{\lambda }}\right.& |\left.{\mathcal{D}}_1=m\right)P\left({\mathcal{D}}_1=m\right)\hfill \\ \hfill =& {\kappa }^{\prime }\left(m\right){\int }_0^{{\mathcal{T}}_1}\cdots {\int }_0^{x_{2:m:n}}\prod _{j=1}^{m}f\left(x_{j:m:n}\right){\left\{1-\mathcal{F}\left(x_{j:m:n}\right)\right\}}^{{\mathcal{R}}_j}{e}^{t\widehat{\lambda }}d{x}_1\cdots d{x}_m\hfill \\ \hfill =& {\kappa }^{\prime }\left(m\right){\int }_0^{{\mathcal{T}}_1}\cdots {\int }_0^{x_{2:m:n}}\prod _{j=1}^{m}f\left(x_{j:m:n}\right){\left\{1-\mathcal{F}\left(x_{j:m:n}\right)\right\}}^{\left(1+{\mathcal{R}}_j\right)\left(1-t\lambda /m\right)-1}d{x}_1\cdots d{x}_m\hfill \\ \hfill =& \frac{{\kappa }^{\prime }\left(m\right)}{{\left(1-t\lambda /m\right)}^m}\sum _{i=0}^m{\kappa }_{i,m}\left({\mathcal{R}}^{\mathbf{1},\mathit{m}}\right){\tau }_1^{\left(1-t\lambda /m\right){\mathcal{R}}_{m-i+1}^{*}}.\hfill \end{array}$$

(8)

For Case II (${\mathcal{D}}_1=k,k+1,\cdots ,m-1$),

$$\begin{array}{cc}\hfill E\left(e^{t\widehat{\lambda }}\right.& |\left.{\mathcal{D}}_1=d_1\right)P\left({\mathcal{D}}_1=d_1\right)\hfill \\ \hfill =& {\kappa }^{\prime }\left(d_1\right){\tau }_1^{{\mathcal{R}}_{d_1}^{*}}{\int }_0^{{\mathcal{T}}_1}\cdots {\int }_0^{x_{2:m:n}}\prod _{j=1}^{d_1}f\left(x_{j:m:n}\right){\left\{1-\mathcal{F}\left(x_{j:m:n}\right)\right\}}^{{\mathcal{R}}_j}{e}^{t\widehat{\lambda }}d{x}_1\cdots d{x}_{d_1}\hfill \\ \hfill =& {\kappa }^{\prime }\left(d_1\right){\tau }_1^{{\mathcal{R}}_{d_1}^{*}(1-t\lambda /d_1)}{\int }_0^{{\mathcal{T}}_1}\cdots {\int }_0^{x_{2:m:n}}\prod _{j=1}^{d_1}f\left(x_{j:m:n}\right)\hfill \\ \hfill & \times {\left\{1-\mathcal{F}\left(x_{j:m:n}\right)\right\}}^{\left(1+{\mathcal{R}}_j\right)\left(1-t\lambda /d_1\right)-1}d{x}_1\cdots d{x}_{d_1}\hfill \\ \hfill =& \frac{{\kappa }^{\prime }\left(d_1\right)}{{\left(1-t\lambda /d_1\right)}^{d_1}}\sum _{i=0}^{d_1}{\kappa }_{i,d_1}\left({\mathcal{R}}^{\mathbf{1},{\mathit{d}}_{\mathbf{1}}}\right){\tau }_1^{\left(1-t\lambda /d_1\right){\mathcal{R}}_{d_1-i+1}^{*}}.\hfill \end{array}$$

(9)

For Case III (${\mathcal{D}}_1=0,1,\cdots ,k-1$ and ${\mathcal{D}}_2=m$),

$$\begin{array}{cc}\hfill E\left(e^{t\widehat{\lambda }}\right.& |\left.{\mathcal{D}}_1=d_1,{\mathcal{D}}_2=m\right)P\left({\mathcal{D}}_1=d_1,{\mathcal{D}}_2=m\right)\hfill \\ \hfill =& {\kappa }^{\prime }\left(m\right){\int }_{{\mathcal{T}}_1}^{{\mathcal{T}}_2}\cdots {\int }_{x_{m-1:m:n}}^{{\mathcal{T}}_2}{\int }_0^{{\mathcal{T}}_1}\cdots {\int }_0^{x_{2:m:n}}\prod _{j=1}^{m}f\left(x_{j:m:n}\right)\hfill \\ \hfill & \times {\left\{1-\mathcal{F}\left(x_{j:m:n}\right)\right\}}^{{\mathcal{R}}_j}{e}^{t\widehat{\lambda }}d{x}_1\cdots d{x}_{d_1}d{x}_m\cdots d{x}_{d_1+1}\hfill \\ \hfill =& {\kappa }^{\prime }\left(m\right){\int }_{{\mathcal{T}}_1}^{{\mathcal{T}}_2}\cdots {\int }_{x_{m-1:m:n}}^{{\mathcal{T}}_2}{\int }_0^{{\mathcal{T}}_1}\cdots {\int }_0^{x_{2:m:n}}\prod _{j=1}^{m}f\left(x_{j:m:n}\right)\hfill \\ \hfill & \times {\left\{1-\mathcal{F}\left(x_{j:m:n}\right)\right\}}^{\left(1+{\mathcal{R}}_j\right)\left(1-t\lambda /m\right)-1}d{x}_1\cdots d{x}_{d_1}d{x}_m\cdots d{x}_{d_1+1}\hfill \\ \hfill =& \frac{{\kappa }^{\prime }\left(m\right)}{{\left(1-t\lambda /m\right)}^{d_1}}\sum _{i_1=0}^{d_1}{\kappa }_{i_1,d_1}\left({\mathcal{R}}^{\mathbf{1},{\mathit{d}}_{\mathbf{1}}}\right){\tau }_1^{\left(1-t\lambda /m\right){\sum }_{j=d_1-i_1+1}^{d_1}\left({\mathcal{R}}_j+1\right)}\hfill \\ \hfill & \times {\int }_{{\mathcal{T}}_1}^{{\mathcal{T}}_2}\cdots {\int }_{x_{m-1:m:n}}^{{\mathcal{T}}_2}\prod _{j=d_1+1}^{m}f\left(x_{j:m:n}\right)\hfill \\ \hfill & \times {\left\{1-\mathcal{F}\left(x_{j:m:n}\right)\right\}}^{\left(1+{\mathcal{R}}_j\right)\left(1-t\lambda /m\right)-1}d{x}_m\cdots d{x}_{d_1+1}\hfill \\ \hfill =& \frac{{\kappa }^{\prime }\left(m\right)}{{\left(1-t\lambda /m\right)}^m}\sum _{i_1=0}^{d_1}\sum _{i_2=0}^{m-d_1}{\kappa }_{i_1,d_1}\left({\mathcal{R}}^{\mathbf{1},{\mathit{d}}_{\mathbf{1}}}\right){\kappa }_{i_2,m-d_1}\left({\mathcal{R}}^{{\mathit{d}}_{\mathbf{1}}+\mathbf{1},\mathit{m}}\right)\hfill \\ \hfill & \times {\tau }_1^{\left(1-t\lambda /m\right){\sum }_{j=d_1-i_1+1}^{m-i_2}\left({\mathcal{R}}_j+1\right)}{\tau }_2^{\left(1-t\lambda /m\right){\sum }_{j=m-i_2+1}^m\left({\mathcal{R}}_j+1\right)}.\hfill \end{array}$$

(10)

For Case IV (${\mathcal{D}}_1=0,1,\cdots ,k-1$ and ${\mathcal{D}}_2=k,k+1,\cdots ,m-1$),

$$\begin{array}{cc}\hfill E\left(e^{t\widehat{\lambda }}\right.& |\left.{\mathcal{D}}_1=d_1,{\mathcal{D}}_2=d_2\right)P\left({\mathcal{D}}_1=d_1,{\mathcal{D}}_2=d_2\right)\hfill \\ \hfill =& {\kappa }^{\prime }\left(d_2\right){\tau }_2^{{\mathcal{R}}_{d_2}^{*}}{\int }_{{\mathcal{T}}_1}^{{\mathcal{T}}_2}\cdots {\int }_{x_{d_2-1:m:n}}^{{\mathcal{T}}_2}{\int }_0^{{\mathcal{T}}_1}\cdots {\int }_0^{x_{2:m:n}}\prod _{j=1}^{d_2}f\left(x_{j:m:n}\right)\hfill \\ \hfill & \times {\left\{1-\mathcal{F}\left(x_{j:m:n}\right)\right\}}^{{\mathcal{R}}_j}{e}^{t\widehat{\lambda }}d{x}_1\cdots d{x}_{d_1}d{x}_{d_2}\cdots d{x}_{d_1+1}\hfill \\ \hfill =& {\kappa }^{\prime }\left(d_2\right){\tau }_2^{{\mathcal{R}}_{d_2}^{*(1-t\lambda /d_2)}}{\int }_{{\mathcal{T}}_1}^{{\mathcal{T}}_2}\cdots {\int }_{x_{d_2-1:m:n}}^{{\mathcal{T}}_2}{\int }_0^{{\mathcal{T}}_1}\cdots {\int }_0^{x_{2:m:n}}\prod _{j=1}^{d_2}f\left(x_{j:m:n}\right)\hfill \\ \hfill & \times {\left\{1-\mathcal{F}\left(x_{j:m:n}\right)\right\}}^{\left(1+{\mathcal{R}}_j\right)\left(1-t\lambda /d_2\right)-1}d{x}_1\cdots d{x}_{d_1}d{x}_{d_2}\cdots d{x}_{d_1+1}\hfill \\ \hfill =& \frac{{\kappa }^{\prime }\left(d_2\right)}{{\left(1-t\lambda /d_2\right)}^{d_1}}\sum _{i_1=0}^{d_1}{\kappa }_{i_1,d_1}\left({\mathcal{R}}^{\mathbf{1},{\mathit{d}}_{\mathbf{1}}}\right){\tau }_1^{\left(1-t\lambda /d_2\right){\sum }_{j=d_1-i_1+1}^{d_1}\left({\mathcal{R}}_j+1\right)}\hfill \\ \hfill & \times {\tau }_2^{{\mathcal{R}}_{d_2}^{*(1-t\lambda /d_2)}}{\int }_{{\mathcal{T}}_1}^{{\mathcal{T}}_2}\cdots {\int }_{x_{d_2-1:m:n}}^{{\mathcal{T}}_2}\prod _{j=d_1+1}^{d_2}f\left(x_{j:m:n}\right)\hfill \\ \hfill & \times {\left\{1-\mathcal{F}\left(x_{j:m:n}\right)\right\}}^{\left(1+{\mathcal{R}}_j\right)\left(1-t\lambda /d_2\right)-1}d{x}_{d_2}\cdots d{x}_{d_1+1}\hfill \\ \hfill =& \frac{{\kappa }^{\prime }\left(d_2\right)}{{\left(1-t\lambda /d_2\right)}^{d_2}}\sum _{i_1=0}^{d_1}\sum _{i_2=0}^{d_2-d_1}{\kappa }_{i_1,d_1}\left({\mathcal{R}}^{\mathbf{1},{\mathit{d}}_{\mathbf{1}}}\right){\kappa }_{i_2,d_2-d_1}\left({\mathcal{R}}^{{\mathit{d}}_{\mathbf{1}}+\mathbf{1},{\mathit{d}}_{\mathbf{2}}}\right)\hfill \\ \hfill & \times {\tau }_1^{\left(1-t\lambda /d_2\right){\sum }_{j=d_1-i_1+1}^{d_2-i_2}\left({\mathcal{R}}_j+1\right)}{\tau }_2^{\left(1-t\lambda /d_2\right)\left\{{\mathcal{R}}_{d_2}^{*}+{\sum }_{j=d_2-i_2+1}^{d_2}\left({\mathcal{R}}_j+1\right)\right\}}.\hfill \end{array}$$

(11)

For Case V (${\mathcal{D}}_2=1,2,\cdots ,k-1$),

$$\begin{array}{cc}\hfill E\left(e^{t\widehat{\lambda }}\right.& |\left.{\mathcal{D}}_2=d_2\right)P\left({\mathcal{D}}_2=d_2\right)\hfill \\ \hfill =& {\kappa }^{\prime }\left(d_2\right){\tau }_2^{{\mathcal{R}}_{d_2}^{*}}{\int }_0^{{\mathcal{T}}_2}\cdots {\int }_0^{x_{2:m:n}}\prod _{j=1}^{d_2}f\left(x_{j:m:n}\right){\left\{1-\mathcal{F}\left(x_{j:m:n}\right)\right\}}^{{\mathcal{R}}_j}{e}^{t\widehat{\lambda }}d{x}_1\cdots d{x}_{d_2}\hfill \\ \hfill =& {\kappa }^{\prime }\left(d_2\right){\tau }_2^{{\mathcal{R}}_{d_2}^{*}(1-t\lambda /d_2)}{\int }_0^{{\mathcal{T}}_2}\cdots {\int }_0^{x_{2:m:n}}\prod _{j=1}^{d_2}f\left(x_{j:m:n}\right)\hfill \\ \hfill & \times {\left\{1-\mathcal{F}\left(x_{j:m:n}\right)\right\}}^{\left(1+{\mathcal{R}}_j\right)\left(1-t\lambda /d_2\right)-1}d{x}_1\cdots d{x}_{d_2}\hfill \\ \hfill =& \frac{{\kappa }^{\prime }\left(d_2\right)}{{\left(1-t\lambda /d_2\right)}^{d_2}}\sum _{i=0}^{d_2}{\kappa }_{i,d_2}\left({\mathcal{R}}^{\mathbf{1},{\mathit{d}}_{\mathbf{2}}}\right){\tau }_2^{\left(1-t\lambda /d_2\right){\mathcal{R}}_{d_2-i+1}^{*}}.\hfill \end{array}$$

(12)

Then, the theorem follows readily upon substituting Equations (8)–(12) into Equation (7). □

Corollary 1. 

Conditional on ${\mathcal{D}}_2\ge 1$, the first and second moments and MSE of CondMLE of ExDist under ${\mathit{ComT}}_2$PHCS are provided by

$$\begin{array}{cc}\hfill E_{\lambda }& \left(\widehat{\lambda }\right)\hfill \\ \hfill =& \lambda +\frac{1}{1-{\tau }_2^n}\left[{\mathcal{T}}_1\frac{{\kappa }^{\prime }\left(m\right)}{m}\sum _{i=0}^m{\mathcal{R}}_{m-i+1}^{*}{\kappa }_{i,m}\left({\mathcal{R}}^{\mathbf{1},\mathit{m}}\right){\tau }_1^{{\mathcal{R}}_{m-i+1}^{*}}\right.\hfill \\ \hfill & +{\mathcal{T}}_1\sum _{d_1=k}^{m-1}\frac{{\kappa }^{\prime }\left(d_1\right)}{d_1}\sum _{i=0}^{d_1}{\mathcal{R}}_{d_1-i+1}^{*}{\kappa }_{i,d_1}\left({\mathcal{R}}^{\mathbf{1},{\mathit{d}}_{\mathbf{1}}}\right){\tau }_1^{{\mathcal{R}}_{d_1-i+1}^{*}}\hfill \\ \hfill & +\sum _{d_1=0}^{k-1}\frac{{\kappa }^{\prime }\left(m\right)}{m}\sum _{i_1=0}^{d_1}\sum _{i_2=0}^{m-d_1}{\kappa }_{i_1,d_1}\left({\mathcal{R}}^{\mathbf{1},{\mathit{d}}_{\mathbf{1}}}\right){\kappa }_{i_2,m-d_1}\left({\mathcal{R}}^{{\mathit{d}}_{\mathbf{1}}+\mathbf{1},\mathit{m}}\right){\tau }_1^{{\sum }_{j=d_1-i_1+1}^{m-i_2}\left({\mathcal{R}}_j+1\right)}\hfill \\ \hfill & \times {\tau }_2^{{\sum }_{j=m-i_2+1}^m\left({\mathcal{R}}_j+1\right)}\left\{{\mathcal{T}}_1\sum _{j=d_1-i_1+1}^{m-i_2}\left({\mathcal{R}}_j+1\right)+{\mathcal{T}}_2\sum _{j=m-i_2+1}^m\left({\mathcal{R}}_j+1\right)\right\}\hfill \\ \hfill & +\sum _{d_1=0}^{k-1}\sum _{d_2=k}^{m-1}\frac{{\kappa }^{\prime }\left(d_2\right)}{d_2}\sum _{i_1=0}^{d_1}\sum _{i_2=0}^{d_2-d_1}{\kappa }_{i_1,d_1}\left({\mathcal{R}}^{\mathbf{1},{\mathit{d}}_{\mathbf{1}}}\right){\kappa }_{i_2,d_2-d_1}\left({\mathcal{R}}^{{\mathit{d}}_{\mathbf{1}}+\mathbf{1},{\mathit{d}}_{\mathbf{2}}}\right){\tau }_1^{{\sum }_{j=d_1-i_1+1}^{d_2-i_2}\left({\mathcal{R}}_j+1\right)}\hfill \\ \hfill & \times {\tau }_2^{{\sum }_{j=d_2-i_2+1}^{d_2}\left({\mathcal{R}}_j+1\right)}\left\{{\mathcal{T}}_1\sum _{j=d_1-i_1+1}^{d_2-i_2}\left({\mathcal{R}}_j+1\right)+{\mathcal{T}}_2\left(R_{d_2}^{*}+\sum _{j=d_2-i_2+1}^{d_2}\left({\mathcal{R}}_j+1\right)\right)\right\}\hfill \\ \hfill & \left.+{\mathcal{T}}_2\sum _{d_2=1}^{k-1}\frac{{\kappa }^{\prime }\left(d_2\right)}{d_2}\sum _{i=0}^{d_2}{\mathcal{R}}_{d_2-i+1}^{*}{\kappa }_{i,d_2}\left({\mathcal{R}}^{\mathbf{1},{\mathit{d}}_{\mathbf{2}}}\right){\tau }_2^{{\mathcal{R}}_{d_2-i+1}^{*}}\right],\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill E_{\lambda }& \left({\widehat{\lambda }}^2\right)\hfill \\ \hfill =& {\lambda }^2+\frac{1}{1-{\tau }_2^n}\left[\frac{{\kappa }^{\prime }\left(m\right)}{m}\sum _{i=0}^m{\kappa }_{i,m}\left({\mathcal{R}}^{\mathbf{1},\mathit{m}}\right){\tau }_1^{{\mathcal{R}}_{m-i+1}^{*}}\left\{{\lambda }^2+\frac{{\mathcal{T}}_1^2{R}_{m-i+1}^{{*}^2}}{m}\right\}\right.\hfill \\ \hfill & +\sum _{d_1=k}^{m-1}\frac{{\kappa }^{\prime }\left(d_1\right)}{d_1}\sum _{i=0}^{d_1}{\kappa }_{i,d_1}\left({\mathcal{R}}^{\mathbf{1},{\mathit{d}}_{\mathbf{1}}}\right){\tau }_1^{{\mathcal{R}}_{d_1-i+1}^{*}}\left\{{\lambda }^2+\frac{{\mathcal{T}}_1^2{R}_{d_1-i+1}^{{*}^2}}{d_1}\right\}\hfill \\ \hfill & +\sum _{d_1=0}^{k-1}\frac{{\kappa }^{\prime }\left(m\right)}{m}\sum _{i_1=0}^{d_1}\sum _{i_2=0}^{m-d_1}{\kappa }_{i_1,d_1}\left({\mathcal{R}}^{\mathbf{1},{\mathit{d}}_{\mathbf{1}}}\right){\kappa }_{i_2,m-d_1}\left({\mathcal{R}}^{{\mathit{d}}_{\mathbf{1}}+\mathbf{1},\mathit{m}}\right){\tau }_1^{{\sum }_{j=d_1-i_1+1}^{m-i_2}\left({\mathcal{R}}_j+1\right)}\hfill \\ \hfill & \times {\tau }_2^{{\sum }_{j=m-i_2+1}^m\left({\mathcal{R}}_j+1\right)}\left\{{\lambda }^2+\frac{{\left({\mathcal{T}}_1{\sum }_{j=d_1-i_1+1}^{m-i_2}\left({\mathcal{R}}_j+1\right)+{\mathcal{T}}_2{\sum }_{j=m-i_2+1}^m\left({\mathcal{R}}_j+1\right)\right)}^2}{m}\right\}\hfill \\ \hfill & +\sum _{d_1=0}^{k-1}\sum _{d_2=k}^{m-1}\frac{{\kappa }^{\prime }\left(d_2\right)}{d_2}\sum _{i_1=0}^{d_1}\sum _{i_2=0}^{d_2-d_1}{\kappa }_{i_1,d_1}\left({\mathcal{R}}^{\mathbf{1},{\mathit{d}}_{\mathbf{1}}}\right){\kappa }_{i_2,d_2-d_1}\left({\mathcal{R}}^{{\mathit{d}}_{\mathbf{1}}+\mathbf{1},{\mathit{d}}_{\mathbf{2}}}\right){\tau }_1^{{\sum }_{j=d_1-i_1+1}^{d_2-i_2}\left({\mathcal{R}}_j+1\right)}\hfill \\ \hfill & \times {\tau }_2^{{\sum }_{j=d_2-i_2+1}^{d_2}\left({\mathcal{R}}_j+1\right)}\left\{\frac{{\left({\mathcal{T}}_1{\sum }_{j=d_1-i_1+1}^{d_2-i_2}\left({\mathcal{R}}_j+1\right)+{\mathcal{T}}_2\left({\sum }_{j=d_2-i_2+1}^{d_2}\left({\mathcal{R}}_j+1\right)+R_{d_2}^{*}\right)\right)}^2}{d_2}\right.\hfill \\ \hfill & +{\lambda }^2\}+\sum _{d_2=1}^{k-1}\frac{{\kappa }^{\prime }\left(d_2\right)}{d_2}\sum _{i=0}^{d_2}{\kappa }_{i,d_2}\left({\mathcal{R}}^{\mathbf{1},{\mathit{d}}_{\mathbf{2}}}\right){\tau }_2^{{\mathcal{R}}_{d_2-i+1}^{*}}\left\{{\lambda }^2+\frac{{\mathcal{T}}_2^2{R}_{d_2-i+1}^{{*}^2}}{d_2}\right\}\hfill \\ \hfill & +2\lambda \left\{E\left(\widehat{\lambda }\right)-\lambda \right\}],\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill M& S{E}_{\lambda }\left(\widehat{\lambda }\right)\hfill \\ \hfill =& \frac{1}{1-{\tau }_2^n}\left[\frac{{\kappa }^{\prime }\left(m\right)}{m}\sum _{i=0}^m{\kappa }_{i,m}\left({\mathcal{R}}^{\mathbf{1},\mathit{m}}\right){\tau }_1^{{\mathcal{R}}_{m-i+1}^{*}}\left\{{\lambda }^2+\frac{{\mathcal{T}}_1^2{R}_{m-i+1}^{{*}^2}}{m}\right\}\right.\hfill \\ \hfill & +\sum _{d_1=k}^{m-1}\frac{{\kappa }^{\prime }\left(d_1\right)}{d_1}\sum _{i=0}^{d_1}{\kappa }_{i,d_1}\left({\mathcal{R}}^{\mathbf{1},{\mathit{d}}_{\mathbf{1}}}\right){\tau }_1^{{\mathcal{R}}_{d_1-i+1}^{*}}\left\{{\lambda }^2+\frac{{\mathcal{T}}_1^2{R}_{d_1-i+1}^{{*}^2}}{d_1}\right\}\hfill \\ \hfill & +\sum _{d_1=0}^{k-1}\frac{{\kappa }^{\prime }\left(m\right)}{m}\sum _{i_1=0}^{d_1}\sum _{i_2=0}^{m-d_1}{\kappa }_{i_1,d_1}\left({\mathcal{R}}^{\mathbf{1},{\mathit{d}}_{\mathbf{1}}}\right){\kappa }_{i_2,m-d_1}\left({\mathcal{R}}^{{\mathit{d}}_{\mathbf{1}}+\mathbf{1},\mathit{m}}\right){\tau }_1^{{\sum }_{j=d_1-i_1+1}^{m-i_2}\left({\mathcal{R}}_j+1\right)}\hfill \\ \hfill & \times {\tau }_2^{{\sum }_{j=m-i_2+1}^m\left({\mathcal{R}}_j+1\right)}\left\{{\lambda }^2+\frac{{\left({\mathcal{T}}_1{\sum }_{j=d_1-i_1+1}^{m-i_2}\left({\mathcal{R}}_j+1\right)+{\mathcal{T}}_2{\sum }_{j=m-i_2+1}^m\left({\mathcal{R}}_j+1\right)\right)}^2}{m}\right\}\hfill \\ \hfill & +\sum _{d_1=0}^{k-1}\sum _{d_2=k}^{m-1}\frac{{\kappa }^{\prime }\left(d_2\right)}{d_2}\sum _{i_1=0}^{d_1}\sum _{i_2=0}^{d_2-d_1}{\kappa }_{i_1,d_1}\left({\mathcal{R}}^{\mathbf{1},{\mathit{d}}_{\mathbf{1}}}\right){\kappa }_{i_2,d_2-d_1}\left({\mathcal{R}}^{{\mathit{d}}_{\mathbf{1}}+\mathbf{1},{\mathit{d}}_{\mathbf{2}}}\right){\tau }_1^{{\sum }_{j=d_1-i_1+1}^{d_2-i_2}\left({\mathcal{R}}_j+1\right)}\hfill \\ \hfill & \times {\tau }_2^{{\sum }_{j=d_2-i_2+1}^{d_2}\left({\mathcal{R}}_j+1\right)}\left\{\frac{{\left({\mathcal{T}}_1{\sum }_{j=d_1-i_1+1}^{d_2-i_2}\left({\mathcal{R}}_j+1\right)+{\mathcal{T}}_2\left({\sum }_{j=d_2-i_2+1}^{d_2}\left({\mathcal{R}}_j+1\right)+R_{d_2}^{*}\right)\right)}^2}{d_2}\right.\hfill \\ \hfill & +{\lambda }^2\}+\left.\sum _{d_2=1}^{k-1}\frac{{\kappa }^{\prime }\left(d_2\right)}{d_2}\sum _{i=0}^{d_2}{\kappa }_{i,d_2}\left({\mathcal{R}}^{\mathbf{1},{\mathit{d}}_{\mathbf{2}}}\right){\tau }_2^{{\mathcal{R}}_{d_2-i+1}^{*}}\left\{{\lambda }^2+\frac{{\mathcal{T}}_2^2{R}_{d_2-i+1}^{{*}^2}}{d_2}\right\}\right].\hfill \end{array}$$

(15)

Theorem 2. 

With conditional ${\mathcal{D}}_2\ge 1$, the CondPDF of CondMLE of ExDist under ${\mathrm{ComT}}_2$PHCS is provided by

$$\begin{array}{cc}\hfill g_{\widehat{\lambda }}\left(x\right)=& \frac{1}{1-{\tau }_2^n}\left[{\kappa }^{\prime }\left(m\right)\sum _{i=0}^m{\kappa }_{i,m}\left({\mathcal{R}}^{\mathbf{1},\mathit{m}}\right){\tau }_1^{{\mathcal{R}}_{m-i+1}^{*}}{\gamma }_m\left(x,\frac{{\mathcal{T}}_1{\mathcal{R}}_{m-i+1}^{*}}{m}\right)\right.\hfill \\ \hfill & +\sum _{d_1=k}^{m-1}{\kappa }^{\prime }\left(d_1\right)\sum _{i=0}^{d_1}{\kappa }_{i,d_1}\left({\mathcal{R}}^{\mathbf{1},{\mathit{d}}_{\mathbf{1}}}\right){\tau }_1^{{\mathcal{R}}_{d_1-i+1}^{*}}{\gamma }_{d_1}\left(x,\frac{{\mathcal{T}}_1{\mathcal{R}}_{d_1-i+1}^{*}}{d_1}\right)\hfill \\ \hfill & +\sum _{d_1=0}^{k-1}{\kappa }^{\prime }\left(m\right)\sum _{i_1=0}^{d_1}\sum _{i_2=0}^{m-d_1}{\kappa }_{i_1,d_1}\left({\mathcal{R}}^{\mathbf{1},{\mathit{d}}_{\mathbf{1}}}\right){\kappa }_{i_2,m-d_1}\left({\mathcal{R}}^{{\mathit{d}}_{\mathbf{1}}+\mathbf{1},\mathit{m}}\right)\hfill \\ \hfill & \times {\tau }_1^{{\sum }_{j=d_1-i_1+1}^{m-i_2}\left({\mathcal{R}}_j+1\right)}{\tau }_2^{{\sum }_{j=m-i_2+1}^m\left({\mathcal{R}}_j+1\right)}\hfill \\ \hfill & \times {\gamma }_m\left(x,\frac{{\mathcal{T}}_1{\sum }_{j=d_1-i_1+1}^{m-i_2}\left({\mathcal{R}}_j+1\right)+{\mathcal{T}}_2{\sum }_{j=m-i_2+1}^m\left({\mathcal{R}}_j+1\right)}{m}\right)\hfill \\ \hfill & +\sum _{d_1=0}^{k-1}\sum _{d_2=k}^{m-1}{\kappa }^{\prime }\left(d_2\right)\sum _{i_1=0}^{d_1}\sum _{i_2=0}^{d_2-d_1}{\kappa }_{i_1,d_1}\left({\mathcal{R}}^{\mathbf{1},{\mathit{d}}_{\mathbf{1}}}\right){\kappa }_{i_2,d_2-d_1}\left({\mathcal{R}}^{{\mathit{d}}_{\mathbf{1}}+\mathbf{1},{\mathit{d}}_{\mathbf{2}}}\right)\hfill \\ \hfill & \times {\tau }_1^{{\sum }_{j=d_1-i_1+1}^{d_2-i_2}\left({\mathcal{R}}_j+1\right)}{\tau }_2^{{\sum }_{j=d_2-i_2+1}^{d_2}\left({\mathcal{R}}_j+1\right)}\hfill \\ \hfill & \times {\gamma }_{d_2}\left(x,\frac{{\mathcal{T}}_1{\sum }_{j=d_1-i_1+1}^{d_2-i_2}\left({\mathcal{R}}_j+1\right)+{\mathcal{T}}_2\left\{R_{d_2}^{*}+{\sum }_{j=d_2-i_2+1}^{d_2}\left({\mathcal{R}}_j+1\right)\right\}}{d_2}\right)\hfill \\ \hfill & \left.+\sum _{d_2=1}^{k-1}{\kappa }^{\prime }\left(d_2\right)\sum _{i=0}^{d_2}{\kappa }_{i,d_2}\left({\mathcal{R}}^{\mathbf{1},{\mathit{d}}_{\mathbf{2}}}\right){\tau }_2^{{\mathcal{R}}_{d_2-i+1}^{*}}{\gamma }_{d_2}\left(x,\frac{{\mathcal{T}}_2{\mathcal{R}}_{d_2-i+1}^{*}}{d_2}\right)\right],\hfill \end{array}$$

where ${\gamma }_a\left(x,b\right)=\frac{{\left(a/\lambda \right)}^b}{\left(a-1\right)!}<x-b{>}^{a-1}{e}^{-\frac{a}{\lambda }\left(x-b\right)}$, and $<b>=max\left(b,0\right)$.

Proof. 

From Theorem 1, the CondMGF of CondMLE of ExDist under ${\mathrm{ComT}}_2$PHCS is provided by

$$\begin{array}{cc}\hfill {\mathcal{M}}_{\widehat{\lambda }}\left(t\right)=& E\left(e^{t\widehat{\lambda }}\right)\hfill \\ \hfill =& \frac{1}{1-{\tau }_2^n}\left[\frac{{\kappa }^{\prime }\left(m\right)}{{\left(1-\lambda t/m\right)}^m}\sum _{i=0}^m{\kappa }_{i,m}\left({\mathcal{R}}^{\mathbf{1},\mathit{m}}\right){\tau }_1^{\left(1-\lambda t/m\right){\mathcal{R}}_{m-i+1}^{*}}\right.\hfill \\ \hfill & +\sum _{d_1=k}^{m-1}\frac{{\kappa }^{\prime }\left(d_1\right)}{{\left(1-\lambda t/d_1\right)}^{d_1}}\sum _{i=0}^{d_1}{\kappa }_{i,d_1}\left({\mathcal{R}}^{\mathbf{1},{\mathit{d}}_{\mathbf{1}}}\right){\tau }_1^{\left(1-\lambda t/d_1\right){\mathcal{R}}_{d_1-i+1}^{*}}\hfill \\ \hfill & +\sum _{d_1=0}^{k-1}\frac{{\kappa }^{\prime }\left(m\right)}{{\left(1-\lambda t/m\right)}^m}\sum _{i_1=0}^{d_1}\sum _{i_2=0}^{m-d_1}{\kappa }_{i_1,d_1}\left({\mathcal{R}}^{\mathbf{1},{\mathit{d}}_{\mathbf{1}}}\right){\kappa }_{i_2,m-d_1}\left({\mathcal{R}}^{{\mathit{d}}_{\mathbf{1}}+\mathbf{1},\mathit{m}}\right)\hfill \\ \hfill & \times {\tau }_1^{\left(1-\lambda t/m\right){\sum }_{j=d_1-i_1+1}^{m-i_2}\left({\mathcal{R}}_j+1\right)}{\tau }_2^{\left(1-\lambda t/m\right){\sum }_{j=m-i_2+1}^m\left({\mathcal{R}}_j+1\right)}\hfill \\ \hfill & +\sum _{d_1=0}^{k-1}\sum _{d_2=k}^{m-1}\frac{{\kappa }^{\prime }\left(d_2\right)}{{\left(1-\lambda t/d_2\right)}^{d_2}}\sum _{i_1=0}^{d_1}\sum _{i_2=0}^{d_2-d_1}{\kappa }_{i_1,d_1}\left({\mathcal{R}}^{\mathbf{1},{\mathit{d}}_{\mathbf{1}}}\right){\kappa }_{i_2,d_2-d_1}\left({\mathcal{R}}^{{\mathit{d}}_{\mathbf{1}}+\mathbf{1},{\mathit{d}}_{\mathbf{2}}}\right)\hfill \\ \hfill & \times {\tau }_1^{\left(1-\lambda t/d_2\right){\sum }_{j=d_1-i_1+1}^{d_2-i_2}\left({\mathcal{R}}_j+1\right)}{\tau }_2^{\left(1-\lambda t/d_2\right){\sum }_{j=d_2-i_2+1}^{d_2}\left({\mathcal{R}}_j+1\right)}\hfill \\ \hfill & +\left.\sum _{d_2=1}^{k-1}\frac{{\kappa }^{\prime }\left(d_2\right)}{{\left(1-\lambda t/d_2\right)}^{d_2}}\sum _{i=0}^{d_2}{\kappa }_{i,d_2}\left({\mathcal{R}}^{\mathbf{1},{\mathit{d}}_{\mathbf{2}}}\right){\tau }_2^{\left(1-\lambda t/d_2\right){\mathcal{R}}_{d_2-i+1}^{*}}\right].\hfill \end{array}$$

Because $exp\left[tb/a\right]{\left(1-t\lambda /a\right)}^{-a}$ is the moment-generating function of $Y+b/a$ at t, where Y is a gamma random variable with PDF ${\gamma }_a\left(x,0\right)$, the theorem readily follows. □

Theorem 3. 

Conditional on ${\mathcal{D}}_2\ge 1$, it can be explained as

$$\begin{array}{cc}\hfill P_{\lambda }& \left(\widehat{\lambda }>t\right)\hfill \\ \hfill =& \frac{1}{1-{\tau }_2^n}\left[\frac{{\kappa }^{\prime }\left(m\right)}{(m-1)!}\sum _{i=0}^m{\kappa }_{i,m}\left({\mathcal{R}}^{\mathbf{1},\mathit{m}}\right){\tau }_1^{{\mathcal{R}}_{m-i+1}^{*}}\Gamma \left(m,{\mathcal{A}}_m\left(\frac{{\mathcal{T}}_1{\mathcal{R}}_{m-i+1}^{*}}{m}\right)\right)\right.\hfill \\ \hfill & +\sum _{d_1=k}^{m-1}\frac{{\kappa }^{\prime }\left(d_1\right)}{(d_1-1)!}\sum _{i=0}^{d_1}{\kappa }_{i,d_1}\left({\mathcal{R}}^{\mathbf{1},{\mathit{d}}_{\mathbf{1}}}\right){\tau }_1^{{\mathcal{R}}_{d_1-i+1}^{*}}\Gamma \left(d_1,{\mathcal{A}}_{d_1}\left(\frac{{\mathcal{T}}_1{\mathcal{R}}_{d_1-i+1}^{*}}{d_1}\right)\right)\hfill \\ \hfill & +\sum _{d_1=0}^{k-1}\frac{{\kappa }^{\prime }\left(m\right)}{m}\sum _{i_1=0}^{d_1}\sum _{i_2=0}^{m-d_1}{\kappa }_{i_1,d_1}\left({\mathcal{R}}^{\mathbf{1},{\mathit{d}}_{\mathbf{1}}}\right){\kappa }_{i_2,m-d_1}\left({\mathcal{R}}^{{\mathit{d}}_{\mathbf{1}}+\mathbf{1},\mathit{m}}\right)\hfill \\ \hfill & \times {\tau }_1^{{\sum }_{j=d_1-i_1+1}^{m-i_2}\left({\mathcal{R}}_j+1\right)}{\tau }_2^{{\sum }_{j=m-i_2+1}^m\left({\mathcal{R}}_j+1\right)}\hfill \\ \hfill & \times \Gamma \left(m,{\mathcal{A}}_m\left(\frac{{\mathcal{T}}_1{\sum }_{j=d_1-i_1+1}^{m-i_2}\left({\mathcal{R}}_j+1\right)+{\mathcal{T}}_2{\sum }_{j=m-i_2+1}^m\left({\mathcal{R}}_j+1\right)}{m}\right)\right)\hfill \\ \hfill & +\sum _{d_1=0}^{k-1}\sum _{d_2=k}^{m-1}\frac{{\kappa }^{\prime }\left(d_2\right)}{(d_2-1)!}\sum _{i_1=0}^{d_1}\sum _{i_2=0}^{d_2-d_1}{\kappa }_{i_1,d_1}\left({\mathcal{R}}^{\mathbf{1},{\mathit{d}}_{\mathbf{1}}}\right){\kappa }_{i_2,d_2-d_1}\left({\mathcal{R}}^{{\mathit{d}}_{\mathbf{1}}+\mathbf{1},{\mathit{d}}_{\mathbf{2}}}\right)\hfill \\ \hfill & \times {\tau }_1^{{\sum }_{j=d_1-i_1+1}^{d_2-i_2}\left({\mathcal{R}}_j+1\right)}{\tau }_2^{{\sum }_{j=d_2-i_2+1}^{d_2}\left({\mathcal{R}}_j+1\right)}\hfill \\ \hfill & \times \Gamma \left(d_2,{\mathcal{A}}_{d_2}\left(\frac{{\mathcal{T}}_1{\sum }_{j=d_1-i_1+1}^{d_2-i_2}\left({\mathcal{R}}_j+1\right)+{\mathcal{T}}_2\left\{R_{d_2}^{*}+{\sum }_{j=d_2-i_2+1}^{d_2}\left({\mathcal{R}}_j+1\right)\right\}}{d_2}\right)\right)\hfill \\ \hfill & \left.+\sum _{d_2=1}^{k-1}\frac{{\kappa }^{\prime }\left(d_2\right)}{(d_2-1)!}\sum _{i=0}^{d_2}{\kappa }_{i,d_2}\left({\mathcal{R}}^{\mathbf{1},{\mathit{d}}_{\mathbf{2}}}\right){\tau }_2^{{\mathcal{R}}_{d_2-i+1}^{*}}\Gamma \left(d_2,{\mathcal{A}}_{d_2}\left(\frac{{\mathcal{T}}_2{\mathcal{R}}_{d_2-i+1}^{*}}{d_2}\right)\right)\right],\hfill \end{array}$$

where $\Gamma \left(a,b\right)={\int }_b^{\infty }{t}^{a-1}{e}^{-t}dt$, and ${\mathcal{A}}_a\left(b\right)=\left(a/\lambda \right)<t-b>$.

Proof. 

Let

$$\begin{array}{c}\hfill g_a\left(x,b\right)=\frac{{\left(a/\lambda \right)}^a}{\left(a-1\right)!}{\left(x-b\right)}^{a-1}{e}^{-\frac{a}{\lambda }\left(x-b\right)}.\end{array}$$

Then,

$$\begin{array}{c}\hfill {\int }_t^{\infty }{\gamma }_a\left(x,b\right)dx={\int }_{max\left(t,b\right)}^{\infty }{g}_a\left(x,b\right)dx,\end{array}$$

where ${\gamma }_a\left(x,b\right)=\frac{{\left(a/\lambda \right)}^b}{\left(a-1\right)!}<x-b{>}^{a-1}{e}^{-\frac{a}{\lambda }\left(x-b\right)}$, and $<b>=max\left(b,0\right)$. Therefore,

$$\begin{array}{cc}\hfill {\int }_t^{\infty }{\gamma }_a\left(x,b\right)dx=& {\int }_{\frac{a}{\lambda }<t-b>}^{\infty }\frac{y^{a-1}}{\left(a-1\right)!}{e}^{-y}dy\hfill \\ \hfill =& \frac{\Gamma \left(a,{\mathcal{A}}_a\left(b\right)\right)}{\left(a-1\right)!}.\hfill \end{array}$$

□

In order to derive a confidence interval (CI) for $\lambda$, suppose that $P_{\lambda }\left(\widehat{\lambda }>t\right)$ is an increasing function of $\lambda$. Then, a $100(1-\alpha )\%$ lower confidence bound for $\lambda$ is ${\lambda }_L$. Similarly, a $100(1-\alpha )\%$ CI for $\lambda$ is $\left({\lambda }_L,{\lambda }_U\right)$. Here, ${\lambda }_L$ and ${\lambda }_U$ satisfy the equations $\alpha /2=P_{{\lambda }_L}\left(\widehat{\lambda }>{\widehat{\lambda }}_{obs}\right)$ and $1-\alpha /2=P_{{\lambda }_U}\left(\widehat{\lambda }>{\widehat{\lambda }}_{obs}\right)$, respectively. Here, ${\widehat{\lambda }}_{obs}$ is the observed value of $\widehat{\lambda }$.

4. Example and Simulation Results

4.1. Example

A PCD (Ref. [20]) generated from the failure times of 18 ball bearings is used to explain the inference for parameters under ${\mathrm{ComT}}_2$PHCS. Table 1 represents the PCD ($m=8$) generated from the failure times of 18 ball bearings ($n=18$). We use the Kolmogorov–Smirnov test to test if this dataset fits ExDist or not. The p-value for this test is 0.9715, and it means that these example data fit ExDist.

Table 1. Example data.

i	1	2	3	4	5	6	7	8
${\mathcal{R}}_i$	0	3	0	0	3	0	0	5
$x_{i:m:n}$	0.1788	0.3300	0.4212	0.4848	0.6864	0.8412	0.9864	1.0584

In this example, we take $\mathcal{T}={\mathcal{T}}_1=1.5$, ${\mathcal{T}}_2=2.0$, $k=4$ (Case I), $\mathcal{T}={\mathcal{T}}_1=0.7$, ${\mathcal{T}}_2=2.0$, $k=4$ (Case II), ${\mathcal{T}}_1=0.7$, ${\mathcal{T}}_2=2.0$, $k=6$ (Case III), ${\mathcal{T}}_1=0.7$, ${\mathcal{T}}_2=1.0$, $k=6$ (Case IV), and ${\mathcal{T}}_1=0.4$, ${\mathcal{T}}_2=0.6$, $k=6$ (Case V). Table 2 presents the MLE, Bayesian estimate, MSE, and SE caculated frome Equations (4), (6), (13), (14), and (15). Also, we have contained the $95\%$ CI and credible interval for parameters under ${\mathrm{ComT}}_2$PHCS. Further, the PDF of CondMLE for parameters under ${\mathrm{ComT}}_2$PHCS is presented in Figure 4.

Table 2. Inference of parameters for example.

Case		$\widehat{\mathit{\lambda }}$	MSE	SE.	95% CI for $\mathit{\lambda }$
Case I	$\widehat{\lambda }$	1.6661	0.3470	0.5891	(0.5115, 2.8206)
	${\widehat{\lambda }}_{B_1}$	1.6328			(0.8879, 2.9736)
	${\widehat{\lambda }}_{B_2}$	1.9041			(0.9241, 3.8590)
Case II	$\widehat{\lambda }$	2.1501	0.5779	0.7602	(0.2655, 4.0347)
	${\widehat{\lambda }}_{B_1}$	1.9643			(0.9534, 3.9812)
	${\widehat{\lambda }}_{B_2}$	2.6876			(1.0497, 6.6218)
Case III	$\widehat{\lambda }$	1.6661	0.3940	0.6283	(0.4811, 2.8511)
	${\widehat{\lambda }}_{B_1}$	1.6328			(0.8879, 2.9736)
	${\widehat{\lambda }}_{B_2}$	1.9041			(0.9241, 3.8590)
Case IV	$\widehat{\lambda }$	1.8540	0.4297	0.6555	(0.4805, 3.2275)
	${\widehat{\lambda }}_{B_1}$	1.7753			(0.9352, 3.3320)
	${\widehat{\lambda }}_{B_2}$	2.1630			(0.9938, 4.6113)
Case V	$\widehat{\lambda }$	2.4012	0.7207	0.8490	(0.0480, 4.7544)
	${\widehat{\lambda }}_{B_1}$	2.1008			(0.9652, 4.4787)
	${\widehat{\lambda }}_{B_2}$	3.2016			(1.0955, 8.8128)

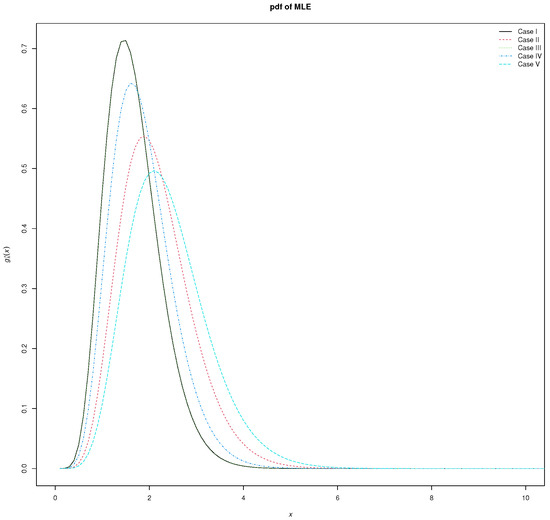
Figure 4. The PDF of CondMLE for example.

4.2. Simulation Results

To evaluate the effectiveness of the point and interval estimators of parameters, we consider various ${\mathrm{ComT}}_2$PHCS (n, m, k, $\mathcal{R}$, ${\mathcal{T}}_1$, and ${\mathcal{T}}_2$). For PCS, we consider four PCS schemes: Scheme (a): ${\mathcal{R}}_m=n-m$ and ${\mathcal{R}}_i=0$ for $i=1,\cdots ,m-1$. Scheme (b): ${\mathcal{R}}_1=n-m$ and ${\mathcal{R}}_i=0$ for $i=2,\cdots ,m$. Scheme (c): ${\mathcal{R}}_{m/2}=n-m$ and ${\mathcal{R}}_i=0$ for $i=1,\cdots ,m/2-1,m/2+1,\cdots ,m$. Scheme (d): ${\mathcal{R}}_1={\mathcal{R}}_m=(n-m)/2$ and ${\mathcal{R}}_i=0$ for $i=2,\cdots ,m-1$. Using the four different PCSs, we generate PCD. In each different PCS, we take $\lambda =1$. If $X_{m:m:n}<{\mathcal{T}}_1$ (Case I), the ${\mathrm{ComT}}_2$PHCD is $\{X_{1:m:n},\cdots ,X_{m:m:n}\}$. If $X_{k:m:n}<{\mathcal{T}}_1<X_{m:m:n}$(Case II), we find $d_1$ such that $X_{d_1:m:n}<{\mathcal{T}}_1<X_{d_1+1:m:n}$, and the ${\mathrm{ComT}}_2$PHCD is $\{X_{1:m:n},\cdots ,X_{d_1:m:n}\}$. If ${\mathcal{T}}_1<X_{k:m:n}<{\mathcal{T}}_2$(Case III), the ${\mathrm{ComT}}_2$PHCD is $\{X_{1:m:n},\cdots ,X_{k:m:n}\}$. If ${\mathcal{T}}_2<X_{k:m:n}$(Case IV), we find $d_2$ such that $X_{d_2:m:n}<{\mathcal{T}}_2<X_{d_2+1:m:n}$, and the ${\mathrm{ComT}}_2$PHCD is $\{X_{1:m:n},\cdots ,X_{d_2:m:n}\}$.

For ${\mathrm{ComT}}_2$PHCS, the procedure is reiterated 1000 times. We compute the average MSE and bias for $\widehat{\lambda }$, ${\widehat{\lambda }}_{B_1}$, and ${\widehat{\lambda }}_{B_2}$, respectively. Additionally, we determine the average CL and CP for $\widehat{\lambda }$, ${\widehat{\lambda }}_{B_1}$, and ${\widehat{\lambda }}_{B_2}$, respectively. Point estimators are assessed using MSE and bias, while interval estimators are evaluated using CL and CP. If the interval estimator performs adequately, the nominal level equals the CP. The results are presented in Table 3 and Table 4.

Table 3. The MSE and bias of $\widehat{\lambda }$ under ${\mathrm{ComT}}_2$PHCS.

					${\mathcal{T}}_2=1.5$			${\mathcal{T}}_2=2.0$
n	m	${\mathcal{T}}_{\mathbf{1}}$	k	Sch.	$\widehat{\mathit{\lambda }}$	${\widehat{\mathit{\lambda }}}_{{\mathit{B}}_{\mathbf{1}}}$	${\widehat{\mathit{\lambda }}}_{{\mathit{B}}_{\mathbf{2}}}$	$\widehat{\mathit{\lambda }}$	${\widehat{\mathit{\lambda }}}_{{\mathit{B}}_{\mathbf{1}}}$	${\widehat{\mathit{\lambda }}}_{{\mathit{B}}_{\mathbf{2}}}$
60	54	0.8	25	(a)	0.0302 (0.0117) †	0.0290 (0.0387)	0.0352 (0.0440)	0.0300 (0.0115)	0.0288 (0.0385)	0.0349 (0.0438)
				(b)	0.0362 (−0.0065)	0.0321 (0.0256)	0.0395 (0.0281)	0.0333 (−0.0153)	0.0288 (0.0158)	0.0348 (0.0162)
				(c)	0.0326 (−0.0001)	0.0300 (0.0324)	0.0368 (0.0365)	0.0303 (−0.0042)	0.0277 (0.0283)	0.0337 (0.0318)
				(d)	0.0281 (−0.0002)	0.0262 (0.0309)	0.0316 (0.0348)	0.0263 (−0.0035)	0.0244 (0.0276)	0.0293 (0.0308)
			27	(a)	0.0273 (0.0071)	0.0261 (0.0342)	0.0313 (0.0386)	0.0268 (0.0066)	0.0257 (0.0337)	0.0307 (0.0381)
				(b)	0.0360 (0.0002)	0.0326 (0.0300)	0.0400 (0.0333)	0.0331 (−0.0074)	0.0295 (0.0207)	0.0355 (0.0222)
				(c)	0.0322 (−0.0073)	0.0289 (0.0241)	0.0350 (0.0265)	0.0299 (−0.0120)	0.0264 (0.0191)	0.0317 (0.0204)
				(d)	0.0284 (−0.0072)	0.0256 (0.0227)	0.0305 (0.0247)	0.0257 (−0.0134)	0.0228 (0.0163)	0.0268 (0.0172)
			30	(a)	0.0240 (−0.0030)	0.0224 (0.0239)	0.0262 (0.0263)	0.0231 (−0.0041)	0.0215 (0.0228)	0.0252 (0.0251)
				(b)	0.0333 (0.0077)	0.0311 (0.0357)	0.0379 (0.0403)	0.0300 (0.0018)	0.0279 (0.0278)	0.0332 (0.0307)
				(c)	0.0328 (−0.0023)	0.0299 (0.0259)	0.0359 (0.0286)	0.0307 (−0.0064)	0.0276 (0.0207)	0.0328 (0.0223)
				(d)	0.0305 (−0.0054)	0.0275 (0.0215)	0.0326 (0.0231)	0.0277 (−0.0136)	0.0244 (0.0129)	0.0285 (0.0131)
60	48	0.8	25	(a)	0.0310 (0.0131)	0.0298 (0.0400)	0.0362 (0.0455)	0.0309 (0.0129)	0.0297 (0.0398)	0.0360 (0.0452)
				(b)	0.0309 (−0.0067)	0.0279 (0.0253)	0.0337 (0.0280)	0.0271 (−0.0148)	0.0239 (0.0171)	0.0286 (0.0185)
				(c)	0.0327 (0.0097)	0.0309 (0.0396)	0.0379 (0.0450)	0.0321 (0.0088)	0.0303 (0.0386)	0.0372 (0.0439)
				(d)	0.0292 (0.0070)	0.0277 (0.0367)	0.0336 (0.0415)	0.0281 (0.0050)	0.0266 (0.0346)	0.0322 (0.0391)
			27	(a)	0.0277 (0.0078)	0.0265 (0.0348)	0.0317 (0.0392)	0.0269 (0.0067)	0.0258 (0.0338)	0.0308 (0.0380)
				(b)	0.0327 (−0.0069)	0.0292 (0.0230)	0.0351 (0.0248)	0.0284 (−0.0166)	0.0247 (0.0127)	0.0292 (0.0128)
				(c)	0.0293 (0.0021)	0.0273 (0.0319)	0.0329 (0.0356)	0.0275 (−0.0017)	0.0254 (0.0282)	0.0304 (0.0313)
				(d)	0.0263 (−0.0035)	0.0243 (0.0258)	0.0289 (0.0286)	0.0249 (−0.0074)	0.0228 (0.0218)	0.0269 (0.0239)
			30	(a)	0.0240 (−0.0045)	0.0222 (0.0223)	0.0260 (0.0245)	0.0224 (−0.0074)	0.0206 (0.0194)	0.0239 (0.0210)
				(b)	0.0337 (−0.0033)	0.0306 (0.0235)	0.0366 (0.0257)	0.0294 (−0.0124)	0.0261 (0.0131)	0.0308 (0.0136)
				(c)	0.0288 (−0.0091)	0.0258 (0.0191)	0.0306 (0.0206)	0.0262 (−0.0164)	0.0230 (0.0114)	0.0270 (0.0117)
				(d)	0.0268 (−0.0125)	0.0239 (0.0149)	0.0281 (0.0157)	0.0250 (−0.0198)	0.0218 (0.0070)	0.0253 (0.0067)
	42	0.8	25	(a)	0.0324 (0.0133)	0.0311 (0.0402)	0.0379 (0.0459)	0.0322 (0.0131)	0.0309 (0.0399)	0.0376 (0.0456)
				(b)	0.0298 (0.0036)	0.0281 (0.0334)	0.0341 (0.0380)	0.0277 (0.0002)	0.0260 (0.0300)	0.0314 (0.0341)
				(c)	0.0329 (0.0098)	0.0312 (0.0379)	0.0381 (0.0432)	0.0327 (0.0096)	0.0310 (0.0377)	0.0379 (0.0430)
				(d)	0.0297 (0.0067)	0.0283 (0.0351)	0.0343 (0.0400)	0.0286 (0.0050)	0.0272 (0.0334)	0.0330 (0.0381)
			27	(a)	0.0284 (0.0071)	0.0271 (0.0342)	0.0325 (0.0387)	0.0274 (0.0054)	0.0261 (0.0325)	0.0313 (0.0367)
				(b)	0.0271 (−0.0059)	0.0249 (0.0235)	0.0296 (0.0260)	0.0243 (−0.0124)	0.0219 (0.0170)	0.0259 (0.0186)
				(c)	0.0293 (0.0045)	0.0277 (0.0327)	0.0333 (0.0370)	0.0282 (0.0027)	0.0266 (0.0310)	0.0320 (0.0350)
				(d)	0.0263 (−0.0009)	0.0247 (0.0275)	0.0295 (0.0309)	0.0246 (−0.0043)	0.0229 (0.0241)	0.0273 (0.0271)
			30	(a)	0.0238 (−0.0067)	0.0220 (0.0201)	0.0257 (0.0221)	0.0219 (−0.0114)	0.0200 (0.0153)	0.0232 (0.0165)
				(b)	0.0275 (−0.0135)	0.0244 (0.0141)	0.0288 (0.0149)	0.0244 (−0.0225)	0.0211 (0.0046)	0.0245 (0.0041)
				(c)	0.0249 (−0.0101)	0.0226 (0.0177)	0.0266 (0.0193)	0.0231 (−0.0151)	0.0206 (0.0125)	0.0241 (0.0134)
				(d)	0.0249 (−0.0120)	0.0224 (0.0155)	0.0262 (0.0166)	0.0226 (−0.0186)	0.0199 (0.0086)	0.0231 (0.0088)
40	36	0.8	15	(a)	0.0475 (0.0218)	0.0444 (0.0597)	0.0602 (0.0722)	0.0474 (0.0216)	0.0444 (0.0596)	0.0601 (0.0720)
				(b)	0.0471 (0.0106)	0.0429 (0.0570)	0.0588 (0.0691)	0.0427 (0.0055)	0.0389 (0.0521)	0.0526 (0.0626)
				(c)	0.0509 (0.0177)	0.0466 (0.0599)	0.0641 (0.0727)	0.0500 (0.0169)	0.0458 (0.0592)	0.0629 (0.0717)
				(d)	0.0479 (0.0214)	0.0448 (0.0631)	0.0614 (0.0768)	0.0457 (0.0190)	0.0428 (0.0608)	0.0585 (0.0739)
			17	(a)	0.0423 (0.0162)	0.0398 (0.0547)	0.0525 (0.0653)	0.0409 (0.0145)	0.0384 (0.0530)	0.0506 (0.0632)
				(b)	0.0451 (−0.0028)	0.0393 (0.0421)	0.0521 (0.0487)	0.0406 (−0.0103)	0.0348 (0.0344)	0.0448 (0.0384)
				(c)	0.0454 (0.0111)	0.0416 (0.0539)	0.0558 (0.0644)	0.0442 (0.0100)	0.0405 (0.0528)	0.0540 (0.0628)
				(d)	0.0410 (0.0092)	0.0379 (0.0514)	0.0500 (0.0610)	0.0379 (0.0044)	0.0348 (0.0467)	0.0455 (0.0550)
			20	(a)	0.0365 (0.0011)	0.0332 (0.0394)	0.0420 (0.0452)	0.0339 (−0.0033)	0.0306 (0.0351)	0.0382 (0.0396)
				(b)	0.0480 (0.0008)	0.0421 (0.0400)	0.0554 (0.0460)	0.0439 (−0.0060)	0.0379 (0.0316)	0.0483 (0.0348)
				(c)	0.0424 (−0.0041)	0.0372 (0.0367)	0.0480 (0.0417)	0.0407 (−0.0087)	0.0352 (0.0316)	0.0447 (0.0349)
				(d)	0.0406 (−0.0053)	0.0355 (0.0342)	0.0454 (0.0384)	0.0365 (−0.0153)	0.0311 (0.0239)	0.0389 (0.0256)
	32	0.8	15	(a)	0.0486 (0.0247)	0.0456 (0.0626)	0.0622 (0.0758)	0.0484 (0.0245)	0.0455 (0.0624)	0.0619 (0.0756)
				(b)	0.0531 (−0.0072)	0.0451 (0.0435)	0.0626 (0.0518)	0.0463 (−0.0166)	0.0387 (0.0341)	0.0518 (0.0391)
				(c)	0.0517 (0.0146)	0.0469 (0.0609)	0.0656 (0.0745)	0.0510 (0.0139)	0.0463 (0.0603)	0.0645 (0.0736)
				(d)	0.0480 (0.0174)	0.0446 (0.0613)	0.0612 (0.0748)	0.0444 (0.0130)	0.0412 (0.0573)	0.0562 (0.0696)
			17	(a)	0.0424 (0.0174)	0.0400 (0.0559)	0.0529 (0.0668)	0.0416 (0.0167)	0.0392 (0.0553)	0.0518 (0.0659)
				(b)	0.0559 (−0.0013)	0.0476 (0.0443)	0.0657 (0.0520)	0.0493 (−0.0121)	0.0412 (0.0324)	0.0545 (0.0359)
				(c)	0.0470 (0.0020)	0.0416 (0.0483)	0.0562 (0.0573)	0.0441 (−0.0019)	0.0388 (0.0444)	0.0517 (0.0520)
				(d)	0.0433 (0.0015)	0.0388 (0.0453)	0.0513 (0.0534)	0.0387 (−0.0059)	0.0342 (0.0381)	0.0445 (0.0443)
			20	(a)	0.0373 (0.0034)	0.0341 (0.0419)	0.0433 (0.0481)	0.0352 (0.0011)	0.0322 (0.0397)	0.0405 (0.0455)
				(b)	0.0532 (0.0131)	0.0476 (0.0533)	0.0651 (0.0637)	0.0462 (0.0053)	0.0412 (0.0431)	0.0539 (0.0498)
				(c)	0.0478 (0.0012)	0.0420 (0.0423)	0.0556 (0.0490)	0.0453 (−0.0032)	0.0393 (0.0365)	0.0511 (0.0411)
				(d)	0.0463 (−0.0028)	0.0404 (0.0366)	0.0525 (0.0414)	0.0416 (−0.0120)	0.0355 (0.0271)	0.0449 (0.0292)
40	28	0.8	15	(a)	0.0492 (0.0255)	0.0462 (0.0632)	0.0629 (0.0766)	0.0489 (0.0250)	0.0459 (0.0628)	0.0625 (0.0760)
				(b)	0.0458 (0.0180)	0.0428 (0.0600)	0.0586 (0.0731)	0.0445 (0.0165)	0.0416 (0.0586)	0.0567 (0.0712)
				(c)	0.0500 (0.0234)	0.0465 (0.0627)	0.0636 (0.0759)	0.0498 (0.0230)	0.0463 (0.0624)	0.0632 (0.0754)
				(d)	0.0481 (0.0224)	0.0450 (0.0621)	0.0617 (0.0755)	0.0478 (0.0218)	0.0447 (0.0615)	0.0612 (0.0748)
			17	(a)	0.0423 (0.0182)	0.0399 (0.0566)	0.0530 (0.0677)	0.0413 (0.0167)	0.0390 (0.0551)	0.0516 (0.0659)
				(b)	0.0387 (0.0046)	0.0355 (0.0471)	0.0469 (0.0559)	0.0365 (0.0002)	0.0333 (0.0428)	0.0436 (0.0505)
				(c)	0.0435 (0.0165)	0.0407 (0.0565)	0.0543 (0.0676)	0.0425 (0.0153)	0.0397 (0.0554)	0.0529 (0.0661)
				(d)	0.0397 (0.0100)	0.0370 (0.0504)	0.0490 (0.0603)	0.0383 (0.0075)	0.0356 (0.0481)	0.0468 (0.0573)
			20	(a)	0.0353 (−0.0016)	0.0319 (0.0366)	0.0403 (0.0419)	0.0322 (−0.0078)	0.0287 (0.0303)	0.0357 (0.0341)
				(b)	0.0394 (−0.0049)	0.0345 (0.0347)	0.0441 (0.0389)	0.0367 (−0.0133)	0.0313 (0.0256)	0.0392 (0.0275)
				(c)	0.0365 (−0.0055)	0.0323 (0.0341)	0.0411 (0.0387)	0.0344 (−0.0109)	0.0300 (0.0285)	0.0376 (0.0317)
				(d)	0.0367 (−0.0066)	0.0323 (0.0325)	0.0409 (0.0366)	0.0340 (−0.0136)	0.0293 (0.0251)	0.0365 (0.0274)
20	18	0.8	5	(a)	0.1309 (0.0696)	0.1061 (0.1278)	0.2253 (0.1922)	0.1298 (0.0689)	0.1053 (0.1272)	0.2237 (0.1913)
				(b)	0.1369 (0.0666)	0.1089 (0.1300)	0.2460 (0.2029)	0.1350 (0.0655)	0.1075 (0.1292)	0.2428 (0.2015)
				(c)	0.1321 (0.0610)	0.1056 (0.1230)	0.2248 (0.1855)	0.1312 (0.0605)	0.1049 (0.1226)	0.2235 (0.1848)
				(d)	0.1356 (0.0679)	0.1089 (0.1284)	0.2375 (0.1970)	0.1330 (0.0666)	0.1069 (0.1274)	0.2334 (0.1953)
			7	(a)	0.1090 (0.0574)	0.0928 (0.1190)	0.1789 (0.1736)	0.1054 (0.0549)	0.0901 (0.1169)	0.1728 (0.1702)
				(b)	0.1036 (0.0461)	0.0880 (0.1153)	0.1710 (0.1702)	0.0970 (0.0410)	0.0831 (0.1111)	0.1591 (0.1631)
				(c)	0.1109 (0.0497)	0.0928 (0.1149)	0.1797 (0.1680)	0.1081 (0.0470)	0.0906 (0.1127)	0.1746 (0.1645)
				(d)	0.1113 (0.0529)	0.0938 (0.1176)	0.1834 (0.1736)	0.1046 (0.0485)	0.0889 (0.1140)	0.1720 (0.1677)
			9	(a)	0.0799 (0.0250)	0.0690 (0.0917)	0.1169 (0.1251)	0.0732 (0.0173)	0.0633 (0.0849)	0.1043 (0.1144)
				(b)	0.0900 (0.0196)	0.0743 (0.0912)	0.1282 (0.1236)	0.0758 (0.0035)	0.0624 (0.0769)	0.1017 (0.1009)
				(c)	0.0863 (0.0219)	0.0728 (0.0917)	0.1250 (0.1256)	0.0781 (0.0117)	0.0657 (0.0828)	0.1102 (0.1119)
				(d)	0.0879 (0.0212)	0.0735 (0.0903)	0.1262 (0.1230)	0.0735 (0.0057)	0.0616 (0.0767)	0.1009 (0.1023)
	16	0.8	5	(a)	0.1483 (0.0752)	0.1173 (0.1321)	0.2544 (0.2000)	0.1476 (0.0750)	0.1168 (0.1319)	0.2533 (0.1997)
				(b)	0.1738 (0.0854)	0.1332 (0.1578)	0.3417 (0.2652)	0.1627 (0.0791)	0.1264 (0.1532)	0.3190 (0.2559)
				(c)	0.1531 (0.0631)	0.1181 (0.1341)	0.2646 (0.2070)	0.1537 (0.0633)	0.1186 (0.1343)	0.2653 (0.2072)
				(d)	0.1693 (0.0844)	0.1298 (0.1462)	0.3123 (0.2343)	0.1608 (0.0813)	0.1246 (0.1440)	0.2979 (0.2301)
			7	(a)	0.1110 (0.0544)	0.0934 (0.1166)	0.1805 (0.1698)	0.1078 (0.0527)	0.0910 (0.1153)	0.1754 (0.1676)
				(b)	0.1286 (0.0384)	0.1005 (0.1209)	0.2070 (0.1787)	0.1081 (0.0223)	0.0861 (0.1077)	0.1625 (0.1529)
				(c)	0.1220 (0.0471)	0.0990 (0.1227)	0.2010 (0.1831)	0.1173 (0.0436)	0.0954 (0.1198)	0.1929 (0.1785)
				(d)	0.1125 (0.0476)	0.0934 (0.1193)	0.1843 (0.1757)	0.0958 (0.0375)	0.0817 (0.1112)	0.1551 (0.1619)
			9	(a)	0.0823 (0.0257)	0.0707 (0.0930)	0.1191 (0.1260)	0.0748 (0.0201)	0.0648 (0.0885)	0.1068 (0.1188)
				(b)	0.1358 (0.0332)	0.1030 (0.1073)	0.2059 (0.1525)	0.1158 (0.0140)	0.0883 (0.0894)	0.1584 (0.1180)
				(c)	0.1072 (0.0186)	0.0847 (0.0962)	0.1533 (0.1319)	0.0982 (0.0088)	0.0773 (0.0873)	0.1333 (0.1156)
				(d)	0.1069 (0.0231)	0.0849 (0.0956)	0.1531 (0.1301)	0.0818 (0.0028)	0.0659 (0.0784)	0.1074 (0.1014)
	14	0.8	5	(a)	0.1506 (0.0729)	0.1176 (0.1293)	0.2617 (0.1983)	0.1501 (0.0726)	0.1172 (0.1290)	0.2609 (0.1978)
				(b)	0.1527 (0.0677)	0.1187 (0.1365)	0.2859 (0.2232)	0.1495 (0.0659)	0.1167 (0.1353)	0.2796 (0.2206)
				(c)	0.1548 (0.0621)	0.1185 (0.1271)	0.2662 (0.1961)	0.1545 (0.0620)	0.1183 (0.1270)	0.2657 (0.1959)
				(d)	0.1438 (0.0684)	0.1133 (0.1315)	0.2574 (0.2058)	0.1414 (0.0672)	0.1118 (0.1306)	0.2529 (0.2041)
			7	(a)	0.1183 (0.0564)	0.0987 (0.1179)	0.1910 (0.1721)	0.1091 (0.0520)	0.0922 (0.1143)	0.1761 (0.1661)
				(b)	0.1181 (0.0355)	0.0949 (0.1123)	0.1919 (0.1680)	0.1022 (0.0239)	0.0840 (0.1029)	0.1603 (0.1512)
				(c)	0.1282 (0.0485)	0.1035 (0.1179)	0.2051 (0.1739)	0.1176 (0.0441)	0.0965 (0.1145)	0.1874 (0.1678)
				(d)	0.1104 (0.0464)	0.0922 (0.1155)	0.1804 (0.1707)	0.0998 (0.0400)	0.0849 (0.1104)	0.1620 (0.1618)
			9	(a)	0.0865 (0.0229)	0.0731 (0.0899)	0.1246 (0.1226)	0.0746 (0.0152)	0.0644 (0.0835)	0.1044 (0.1117)
				(b)	0.1170 (0.0129)	0.0891 (0.0875)	0.1675 (0.1207)	0.1004 (−0.0017)	0.0771 (0.0744)	0.1307 (0.0960)
				(c)	0.1016 (0.0170)	0.0815 (0.0910)	0.1444 (0.1246)	0.0854 (0.0052)	0.0694 (0.0810)	0.1155 (0.1075)
				(d)	0.0973 (0.0183)	0.0788 (0.0898)	0.1378 (0.1219)	0.0809 (0.0037)	0.0661 (0.0771)	0.1073 (0.1007)

^† MSE (Bias).

Table 4. The CP and CL of $\widehat{\lambda }$ under ${\mathrm{ComT}}_2$PHCS.

					${\mathcal{T}}_2=1.5$			${\mathcal{T}}_2=2.0$
n	m	${\mathcal{T}}_{\mathbf{1}}$	k	Sch.	$\widehat{\mathit{\lambda }}$	${\widehat{\mathit{\lambda }}}_{{\mathit{B}}_{\mathbf{1}}}$	${\widehat{\mathit{\lambda }}}_{{\mathit{B}}_{\mathbf{2}}}$	$\widehat{\mathit{\lambda }}$	${\widehat{\mathit{\lambda }}}_{{\mathit{B}}_{\mathbf{1}}}$	${\widehat{\mathit{\lambda }}}_{{\mathit{B}}_{\mathbf{2}}}$
60	54	0.8	25	(a)	93.4 (0.6993) ‡	96.0 (0.7029)	94.9 (0.7415)	93.5 (0.6987)	95.9 (0.7024)	94.8 (0.7410)
				(b)	93.4 (0.7143)	96.0 (0.7195)	95.3 (0.7604)	93.8 (0.7079)	96.2 (0.7133)	95.9 (0.7532)
				(c)	93.5 (0.7071)	96.0 (0.7113)	95.0 (0.7511)	93.6 (0.7067)	95.8 (0.7109)	94.8 (0.7506)
				(d)	94.3 (0.7048)	96.7 (0.7094)	96.0 (0.7487)	94.4 (0.7017)	97.0 (0.7063)	95.9 (0.7453)
			27	(a)	93.3 (0.6864)	96.5 (0.6907)	95.8 (0.7268)	93.5 (0.6830)	96.7 (0.6875)	96.0 (0.7231)
				(b)	93.4 (0.6857)	95.7 (0.6919)	94.7 (0.7273)	93.8 (0.6720)	95.6 (0.6785)	95.3 (0.7119)
				(c)	93.5 (0.6958)	96.2 (0.7006)	95.7 (0.7381)	93.5 (0.6925)	96.1 (0.6975)	95.6 (0.7345)
				(d)	94.3 (0.6871)	96.0 (0.6924)	95.2 (0.7284)	94.4 (0.6802)	96.5 (0.6857)	95.4 (0.7207)
			30	(a)	93.3 (0.6515)	95.9 (0.6569)	95.2 (0.6870)	93.5 (0.6403)	95.7 (0.6460)	95.1 (0.6746)
				(b)	93.4 (0.6455)	95.7 (0.6518)	94.6 (0.6805)	93.8 (0.6207)	95.6 (0.6274)	95.1 (0.6528)
				(c)	93.5 (0.6577)	95.7 (0.6637)	95.0 (0.6945)	93.4 (0.6453)	95.2 (0.6516)	94.6 (0.6807)
				(d)	94.3 (0.6481)	95.5 (0.6542)	94.7 (0.6835)	94.4 (0.6312)	95.8 (0.6375)	94.4 (0.6647)
	48	0.8	25	(a)	93.6 (0.6973)	95.7 (0.7011)	94.8 (0.7392)	93.6 (0.6966)	95.6 (0.7004)	94.7 (0.7385)
				(b)	93.1 (0.7139)	95.7 (0.7209)	94.6 (0.7610)	92.8 (0.6945)	96.1 (0.7022)	94.7 (0.7391)
				(c)	94.2 (0.7262)	96.1 (0.7311)	95.3 (0.7739)	94.2 (0.7246)	96.2 (0.7295)	95.6 (0.7721)
				(d)	93.7 (0.7170)	96.1 (0.7221)	95.3 (0.7633)	93.5 (0.7118)	96.1 (0.7171)	95.4 (0.7575)
			27	(a)	93.2 (0.6859)	96.4 (0.6903)	95.8 (0.7261)	93.3 (0.6834)	96.4 (0.6878)	95.6 (0.7234)
				(b)	93.1 (0.6833)	95.6 (0.6901)	94.5 (0.7244)	92.8 (0.6539)	96.1 (0.6613)	94.7 (0.6911)
				(c)	93.9 (0.7057)	95.9 (0.7114)	95.0 (0.7501)	93.7 (0.6981)	96.2 (0.7041)	95.5 (0.7416)
				(d)	93.7 (0.6879)	95.8 (0.6939)	94.7 (0.7297)	93.4 (0.6766)	95.5 (0.6829)	94.6 (0.7170)
			30	(a)	93.2 (0.6542)	95.5 (0.6595)	94.7 (0.6900)	93.3 (0.6470)	95.9 (0.6525)	95.0 (0.6820)
				(b)	92.4 (0.6570)	95.4 (0.6624)	94.3 (0.6930)	92.1 (0.6196)	96.0 (0.6254)	94.5 (0.6504)
				(c)	93.9 (0.6611)	95.6 (0.6674)	94.6 (0.6983)	93.7 (0.6408)	95.9 (0.6474)	95.0 (0.6753)
				(d)	93.7 (0.6433)	95.6 (0.6495)	94.5 (0.6779)	93.4 (0.6201)	95.5 (0.6266)	94.6 (0.6519)
	42	0.8	25	(a)	94.1 (0.6962)	96.1 (0.7001)	95.6 (0.7380)	94.1 (0.6960)	96.1 (0.6998)	95.6 (0.7378)
				(b)	91.9 (0.7132)	96.2 (0.7204)	95.2 (0.7599)	91.5 (0.6777)	96.2 (0.6856)	95.3 (0.7187)
				(c)	93.2 (0.7362)	96.3 (0.7427)	95.0 (0.7869)	92.9 (0.7279)	96.4 (0.7347)	95.2 (0.7774)
				(d)	93.3 (0.7189)	96.5 (0.7250)	95.7 (0.7664)	93.4 (0.7107)	96.2 (0.7171)	95.6 (0.7572)
			27	(a)	93.9 (0.6865)	96.7 (0.6909)	96.5 (0.7269)	93.8 (0.6858)	96.7 (0.6903)	96.5 (0.7262)
				(b)	90.9 (0.7015)	96.1 (0.7074)	95.1 (0.7452)	9.4 (0.6614)	96.0 (0.6676)	95.1 (0.6985)
				(c)	93.2 (0.7048)	96.0 (0.7118)	94.6 (0.7498)	92.8 (0.6887)	96.0 (0.6960)	94.7 (0.7313)
				(d)	93.2 (0.6848)	96.2 (0.6914)	95.4 (0.7263)	93.4 (0.6687)	95.9 (0.6758)	95.1 (0.7082)
			30	(a)	93.9 (0.6596)	95.9 (0.6649)	95.7 (0.6961)	93.8 (0.6580)	96.4 (0.6634)	96.1 (0.6944)
				(b)	92.4 (0.6983)	95.7 (0.7029)	94.4 (0.7406)	91.6 (0.6565)	95.6 (0.6612)	94.5 (0.6919)
				(c)	92.3 (0.6770)	95.8 (0.6827)	94.4 (0.7163)	91.9 (0.6511)	95.9 (0.6569)	94.5 (0.6862)
				(d)	93.1 (0.6495)	96.2 (0.6553)	95.2 (0.6844)	93.3 (0.6255)	95.7 (0.6318)	94.8 (0.6573)
40	36	0.8	15	(a)	94.1 (0.8729)	96.7 (0.8761)	95.7 (0.9554)	94.1 (0.8717)	96.9 (0.8750)	95.9 (0.9540)
				(b)	94.4 (0.9014)	97.5 (0.9064)	96.6 (0.9938)	94.3 (0.8970)	97.6 (0.9024)	96.8 (0.9887)
				(c)	94.1 (0.8843)	96.5 (0.8883)	95.6 (0.9702)	94.0 (0.8833)	96.6 (0.8873)	95.9 (0.9690)
				(d)	94.1 (0.8883)	97.0 (0.8921)	96.0 (0.9759)	94.0 (0.8863)	97.2 (0.8903)	96.2 (0.9736)
			17	(a)	94.1 (0.8571)	97.6 (0.8620)	96.5 (0.9360)	94.1 (0.8534)	97.6 (0.8584)	96.7 (0.9316)
				(b)	94.4 (0.8660)	97.2 (0.8739)	96.1 (0.9498)	94.3 (0.8544)	97.0 (0.8630)	96.2 (0.9362)
				(c)	94.1 (0.8696)	97.4 (0.8752)	96.5 (0.9521)	94.0 (0.8664)	97.5 (0.8722)	96.6 (0.9483)
				(d)	94.1 (0.8600)	96.9 (0.8665)	96.3 (0.9412)	94.0 (0.8532)	97.2 (0.8600)	96.6 (0.9331)
			20	(a)	94.0 (0.7968)	96.9 (0.8050)	95.5 (0.8623)	94.1 (0.7789)	96.8 (0.7880)	95.7 (0.8415)
				(b)	94.4 (0.7985)	96.8 (0.8080)	95.6 (0.8647)	94.2 (0.7671)	96.5 (0.7777)	95.4 (0.8275)
				(c)	94.1 (0.8027)	96.6 (0.8118)	95.8 (0.8701)	93.9 (0.7843)	96.7 (0.7942)	95.6 (0.8483)
				(d)	94.1 (0.7925)	96.5 (0.8018)	95.8 (0.8576)	93.8 (0.7684)	96.8 (0.7786)	95.9 (0.8292)
40	32	0.8	15	(a)	92.8 (0.8664)	96.6 (0.8701)	95.5 (0.9475)	92.7 (0.8654)	96.5 (0.8692)	95.4 (0.9463)
				(b)	93.3 (0.9240)	96.6 (0.9318)	95.5(1.0255)	93.2 (0.9101)	96.9 (0.9189)	95.6(1.0087)
				(c)	92.7 (0.9018)	96.2 (0.9072)	95.0 (0.9938)	92.6 (0.9001)	96.6 (0.9057)	95.3 (0.9919)
				(d)	93.5 (0.9052)	96.8 (0.9099)	96.0 (0.9983)	93.5 (0.9000)	96.7 (0.9051)	96.2 (0.9922)
			17	(a)	92.6 (0.8524)	97.2 (0.8576)	96.4 (0.9302)	92.6 (0.8483)	97.2 (0.8538)	96.3 (0.9254)
				(b)	93.3 (0.8641)	96.6 (0.8746)	95.3 (0.9486)	93.2 (0.8361)	96.5 (0.8481)	94.9 (0.9146)
				(c)	92.6 (0.8854)	96.4 (0.8925)	95.5 (0.9735)	92.5 (0.8813)	96.9 (0.8887)	95.9 (0.9685)
				(d)	93.5 (0.8716)	96.2 (0.8790)	95.4 (0.9562)	93.4 (0.8593)	96.1 (0.8674)	95.4 (0.9417)
			20	(a)	92.6 (0.8036)	96.5 (0.8116)	95.3 (0.8704)	92.5 (0.7913)	96.5 (0.7999)	95.0 (0.8559)
				(b)	92.7 (0.8142)	96.5 (0.8224)	95.1 (0.8834)	92.4 (0.7713)	96.3 (0.7806)	94.7 (0.8309)
				(c)	92.6 (0.8177)	96.0 (0.8273)	94.7 (0.8886)	92.4 (0.7953)	96.1 (0.8056)	94.8 (0.8615)
				(d)	93.5 (0.7984)	96.0 (0.8079)	94.9 (0.8647)	93.4 (0.7667)	95.6 (0.7774)	94.7 (0.8272)
	28	0.8	15	(a)	93.4 (0.8727)	95.9 (0.8760)	94.0 (0.9552)	93.4 (0.8723)	95.9 (0.8757)	94.1 (0.9547)
				(b)	92.8 (0.9195)	96.3 (0.9316)	94.5(1.0232)	92.7 (0.8878)	96.5 (0.9020)	95.1 (0.9838)
				(c)	92.9 (0.9374)	96.6 (0.9442)	95.6(1.0419)	93.0 (0.9352)	96.7 (0.9422)	95.6(1.0392)
				(d)	93.3 (0.9191)	96.6 (0.9249)	95.6(1.0174)	93.3 (0.9103)	97.0 (0.9168)	95.7(1.0070)
			17	(a)	93.3 (0.8559)	96.6 (0.8609)	95.2 (0.9344)	93.1 (0.8543)	96.7 (0.8595)	95.4 (0.9325)
				(b)	92.8 (0.8788)	96.3 (0.8890)	94.5 (0.9673)	92.6 (0.8311)	96.5 (0.8434)	95.1 (0.9076)
				(c)	92.9 (0.8967)	96.4 (0.9063)	95.3 (0.9900)	93.0 (0.8836)	96.5 (0.8941)	95.4 (0.9740)
				(d)	93.3 (0.8688)	96.1 (0.8778)	94.8 (0.9540)	93.3 (0.8506)	96.3 (0.8609)	95.0 (0.9324)
			20	(a)	93.3 (0.8112)	95.8 (0.8190)	93.9 (0.8795)	93.1 (0.8068)	96.0 (0.8149)	94.5 (0.8743)
				(b)	91.9 (0.8653)	96.1 (0.8712)	93.8 (0.9469)	91.6 (0.8111)	96.2 (0.8184)	94.3 (0.8787)
				(c)	92.6 (0.8365)	96.3 (0.8452)	95.0 (0.9115)	92.5 (0.8044)	95.8 (0.8138)	94.6 (0.8716)
				(d)	93.3 (0.8043)	95.8 (0.8133)	94.4 (0.8716)	93.3 (0.7731)	96.0 (0.7836)	94.5 (0.8341)
20	18	0.8	5	(a)	93.7(1.3307)	97.1(1.3029)	94.4(1.6288)	93.7(1.3294)	97.2(1.3018)	94.5(1.6271)
				(b)	93.6(1.3925)	97.3(1.3599)	94.7(1.7410)	93.6(1.3899)	97.3(1.3579)	94.8(1.7375)
				(c)	93.5(1.3357)	97.2(1.3113)	94.0(1.6406)	93.5(1.3346)	97.2(1.3105)	94.0(1.6391)
				(d)	93.4(1.3605)	97.2(1.3301)	94.3(1.6825)	93.4(1.3578)	97.2(1.3280)	94.3(1.6788)
			7	(a)	93.7(1.2949)	97.6(1.2780)	95.5(1.5702)	93.6(1.2883)	97.9(1.2726)	95.7(1.5611)
				(b)	93.6(1.3268)	97.6(1.3141)	95.9(1.6305)	93.5(1.3124)	98.0(1.3025)	96.0(1.6102)
				(c)	93.5(1.3018)	97.7(1.2880)	95.0(1.5846)	93.4(1.2951)	98.0(1.2826)	95.1(1.5755)
				(d)	93.4(1.3141)	97.5(1.2977)	95.4(1.6054)	93.3(1.3028)	97.5(1.2887)	95.6(1.5897)
			9	(a)	93.7(1.1930)	96.8(1.1963)	95.7(1.4165)	93.6(1.1694)	96.9(1.1761)	95.3(1.3844)
				(b)	93.6(1.2109)	97.1(1.2182)	95.0(1.4470)	93.5(1.1624)	97.6(1.1769)	95.4(1.3796)
				(c)	93.5(1.2115)	96.7(1.2163)	94.5(1.4466)	93.4(1.1844)	97.2(1.1932)	95.2(1.4096)
				(d)	93.4(1.2003)	96.7(1.2055)	94.2(1.4295)	93.3(1.1592)	96.9(1.1707)	94.9(1.3737)
	16	0.8	5	(a)	93.8(1.3434)	96.0(1.3097)	92.8(1.6525)	93.8(1.3425)	96.0(1.3091)	92.8(1.6515)
				(b)	92.4(1.4759)	97.9(1.4344)	94.6(1.8977)	92.4(1.4707)	97.9(1.4306)	94.7(1.8897)
				(c)	92.2(1.3811)	96.5(1.3527)	92.7(1.7205)	92.2(1.3806)	96.5(1.3523)	92.7(1.7198)
				(d)	93.5(1.3982)	96.8(1.3641)	94.2(1.7507)	93.4(1.3949)	96.8(1.3616)	94.2(1.7457)
			7	(a)	93.8(1.2913)	96.9(1.2743)	94.1(1.5652)	93.7(1.2799)	96.9(1.2653)	94.0(1.5494)
				(b)	92.4(1.3589)	97.1(1.3503)	94.3(1.6945)	92.4(1.3247)	96.7(1.3235)	94.9(1.6437)
				(c)	92.2(1.3367)	97.2(1.3231)	93.8(1.6442)	92.1(1.3250)	97.3(1.3144)	93.9(1.6273)
				(d)	93.5(1.3279)	96.9(1.3149)	95.4(1.6323)	93.4(1.3104)	96.7(1.3012)	95.4(1.6074)
			9	(a)	93.8(1.1896)	96.1(1.1935)	94.5(1.4116)	93.7(1.1660)	96.2(1.1741)	94.6(1.3790)
				(b)	92.3(1.2262)	97.0(1.2341)	94.0(1.4763)	92.3(1.1621)	96.5(1.1803)	93.9(1.3801)
				(c)	92.2(1.2291)	96.8(1.2368)	94.4(1.4770)	92.1(1.1927)	96.6(1.2068)	94.3(1.4250)
				(d)	93.5(1.2081)	96.6(1.2153)	94.2(1.4433)	93.4(1.1610)	96.0(1.1759)	94.0(1.3767)
20	14	0.8	5	(a)	92.9(1.3443)	96.3(1.3124)	93.0(1.6502)	92.8(1.3437)	96.3(1.3119)	93.0(1.6493)
				(b)	92.4(1.5870)	97.7(1.5311)	94.0(2.1026)	92.4(1.5691)	98.0(1.5182)	94.5(2.0743)
				(c)	92.7(1.4300)	96.5(1.4032)	93.9(1.8042)	92.7(1.4303)	96.5(1.4033)	93.9(1.8045)
				(d)	92.4(1.4634)	96.7(1.4168)	94.0(1.8614)	92.4(1.4561)	96.7(1.4115)	94.0(1.8505)
			7	(a)	92.9(1.2890)	98.0(1.2734)	95.0(1.5620)	92.8(1.2850)	98.2(1.2702)	95.0(1.5565)
				(b)	92.4(1.3972)	97.4(1.3918)	93.4(1.7605)	92.4(1.3394)	97.7(1.3465)	94.3(1.6703)
				(c)	92.7(1.3860)	98.0(1.3731)	95.3(1.7316)	92.7(1.3777)	98.1(1.3666)	95.7(1.7200)
				(d)	92.4(1.3473)	97.6(1.3353)	95.7(1.6653)	92.4(1.3209)	97.5(1.3146)	96.1(1.6275)
			9	(a)	92.9(1.1956)	97.0(1.1998)	95.0(1.4192)	92.8(1.1822)	97.5(1.1888)	95.5(1.4009)
				(b)	92.2(1.2977)	97.4(1.2962)	93.4(1.5850)	92.1(1.2084)	97.6(1.2214)	94.0(1.4451)
				(c)	92.6(1.2600)	97.4(1.2686)	94.9(1.5267)	92.6(1.2195)	97.2(1.2347)	94.8(1.4659)
				(d)	92.4(1.2290)	96.7(1.2354)	94.4(1.4747)	92.4(1.1705)	96.9(1.1875)	95.1(1.3910)

^‡ CP (CL).

From Table 3, in terms of the lowest MSE and bias values, the following observations are drawn:

• As sample size (n) increases, all examined estimates demonstrate improved performance.
• For fixed n, k, and ${\mathcal{T}}_2$, the MSEs and biases decrease as m (PCD size) increases.
• For fixed n, m, and ${\mathcal{T}}_2$, the MSEs and biases decrease as k increases.
• For fixed n, m, and k, the MSEs and biases decrease as ${\mathcal{T}}_2$ increases.
• Bayesian estimates of parameters, utilizing the inverse gamma prior distribution, exhibit satisfactory behavior compared to likelihood estimates.
• Bayesian estimates with respect to inverse gamma prior distribution yield more accurate results than others (MLE and non-informative prior distribution).
• Comparing among the proposed PCSs reveals that the proposed parameter estimates perform better using Scheme (a) than others.

From Table 4, in terms of the lowest average CL and CP values, the following observations occur:

• As sample size (n) increases, all examined estimates demonstrate improved performance.
• For fixed n, k, and ${\mathcal{T}}_2$, the CL decrease as m increases.
• For fixed n, m, and k, the CL decreases as the ${\mathcal{T}}_2$ increases.
• For fixed n, m, and ${\mathcal{T}}_2$, the CL decreases as the k increases.
• The CP closely aligns with its corresponding nominal level as n, m, k, and ${\mathcal{T}}_2$ increase.
• Credible intervals of parameters, utilizing the inverse gamma prior distribution, exhibit satisfactory behavior compared to likelihood estimates.
• Credible intervals with respect to the inverse gamma prior distribution yield more accurate results than others (MLE and non-informative prior distribution).
• Comparing among the proposed PCS reveals that the proposed parameter estimates perform better using Scheme (a) than others.

5. Concluding Remarks

${\mathrm{T}}_1$PHCS, ${\mathrm{T}}_2$PHCS, ${\mathrm{GenT}}_1$PHCS, and ${\mathrm{GenT}}_2$PHCS exhibit considerable complexity due to the numerous parameters required to specify the PHCS procedure. Additionally, in cases of excessively high data reliability, issues such as unobserved data or excessively long experiment durations may arise if the PHCS is improperly configured in advance. From this perspective, we propose a more comprehensive censoring scheme—${\mathrm{ComT}}_2$PHCS. ${\mathrm{ComT}}_2$PHCS integrates ${\mathrm{T}}_1$PHCS, ${\mathrm{T}}_2$PHCS, ${\mathrm{GenT}}_1$PHCS, and ${\mathrm{GenT}}_2$PHCS. It is evident that ${\mathrm{ComT}}_2$PHCS incorporates a second termination time, ${\mathcal{T}}_2$, in addition to ${\mathcal{T}}_1$, and the second number, k, in addition to m, providing greater flexibility compared to ${\mathrm{T}}_1$PHCS, ${\mathrm{T}}_2$PHCS, ${\mathrm{GenT}}_1$PHCS, and ${\mathrm{GenT}}_2$PHCS. Moreover, ${\mathrm{ComT}}_2$PHCS facilitates increased observations, which enhances the inference process. Under ${\mathrm{ComT}}_2$PHCS, we can ensure that the test would be finished in time ${\mathcal{T}}_2$. Therefore, ${\mathrm{ComT}}_2$PHCS provides the tester with more options to overcome limitations such as long test duration and the possibility of not observing any failures.

We considered the ExDist under ${\mathrm{ComT}}_2$PHCS and established Bayesian inference for the parameters of ExDist under ${\mathrm{ComT}}_2$PHCS. Additionally, we derived the CondMGF of MLE for the parameters of ExDist under ${\mathrm{ComT}}_2$PHCS. Further, using CondMGF, we obtained the distribution of the MLE for the parameters of ExDist under ${\mathrm{ComT}}_2$PHCS.

Consequently, the MSEs, biases, and CL decrease as n, m, k, and ${\mathcal{T}}_2$ increase. Bayesian estimates, with credible intervals of the parameter, due to the inverse gamma prior distribution, exhibit satisfactory performance compared to likelihood estimates. Moreover, Bayesian estimates with respect to inverse gamma prior distribution yield more accurate results than others (MLE and non-informative prior distribution). Furthermore, upon comparing the proposed PCS, it is evident that the proposed parameter estimates perform better using Scheme (a) than others. The CP closely aligns with the corresponding nominal levels as n, m, k, and ${\mathcal{T}}_2$ increase.