On m-Negative Sets and Out Mondirected Topologies in the Human Nervous System

Abstract

Using the monophonic paths in the theory of directed graphs, this paper constructs a new topology called the out mondirected topology, which characterizes the graphs that induce indiscrete or discrete topology. We give and study some of the relations and properties, such as the relationship between the isomorphic relation, in directed graphs and the homeomorphic property in out mondirected topological spaces, compactness, ${\mathbb{D}}_{\pm }$-connectedness, connectedness and ${\mathbb{D}}_{\pm }$-discrete properties. Finally, we apply our results of out mondirected topological spaces in the nervous system of the human body, such as in the messenger signal network, in diagrams of sensory neuron cells and in models of two distinct nicotinic receptor types based on the second messenger signal.

1. Introduction

The graph theory and general topology are important topics in the field of mathematics. Several researchers have studied the relation between general topology and graph theory by constructing some topologies on a vertex set of graphs and on the edge set for undirected simple graphs or directed graphs. Most of these constructions were on the set of vertices in the theory of undirected simple graphs. In the theory of undirected graphs, Jafarian et al. [1] introduced and investigated the graphic topological space of a graph ℵ as a pair $(\wp (\aleph ),T_{\mathcal{A}\wp })$, where $T_{\mathcal{A}\wp }$ is an Alexandroff topology on $\wp (\aleph )$, which is induced by a sub-basis $\mathcal{A}\wp$ and is in the family of the open neighborhoods of the vertices in ℵ. In 2018, Nada et al. [2] presented a relation on graphs to induce new types of topological structures. Abdu and Kilicman [3], in 2018, introduced new constructions of topologies, i.e., incidence topology, on the set of vertices for undirected simple graphs $\aleph =(\wp (\aleph ),\eta (\aleph \left)\right)$ without isolated vertices. These topologies have a sub-basis $S_{IG}$ given by $S_{IG}=\{ends\left(\epsilon \right):\epsilon \in \eta (\aleph )\}$. Kilicman and Abdu [4] used the directed graphs $\aleph =(\wp (\aleph ),\eta (\aleph \left)\right)$ to introduce two constructions of topologies on the set $\eta (\aleph )$, which is called compatible edge topology and incompatible edge topology. In 2019, Gamorez et al. [5] constructed the topology ${\tau }_{\aleph }$ of undirected simple graphs $\aleph =(\wp (\aleph ),\eta (\aleph \left)\right)$ and described the topological spaces that are induced by the tensor product of two graphs and an edge corona. Through using the hop neighborhoods of a graph under the notions of unary and binary operations, Nianga and Canoy [6], in 2019, constructed a topology of undirected simple graphs, and, in [7], they introduced some topologies on the vertex set in the theory of undirected simple graphs using the class of open hop neighborhoods. Sari and Kopuzlu [8], in 2020, generated a topology on the vertex set $\wp (\aleph )$ in the theory of undirected simple graphs without the isolated vertices $\aleph =(\wp (\aleph ),\eta (\aleph \left)\right)$, and they also presented the openness and the continuity of functions via the topologies generated by the graphs. In 2021, Zomam et al. [9] introduced and investigated some conditions for the local and finite properties of graphs to obtain an Alexandroff property for graphic topological spaces. In [10], Anabel and Sergio used monophonic eccentric neighborhoods to define a new neighborhood system and to construct a topology on the vertex set in the theory of undirected graphs. In this type of construction, they characterized the graphs that induce a particular point topology, a discrete topology and an indiscrete topology. In [11], Chiaselotti et al. applied rough set theory to information tables induced from finite directed graphs without loops and multiples arcs, that is, they used the adjacency matrix of a digraph as a particular type of information table and explored, on digraphs, the notions of indiscernibility partitions, lower and upper approximations, generalized core, reducts and the discernibility matrix. In the theory of directed graphs, the pathless directed topological spaces on the vertex set $\wp (\aleph )$ were introduced by Othman et al. [12] in 2022. They presented the relation between the pathless directed topological spaces and the relative topologies and E-generated subdirected graphs, and they also studied some of the properties of pathless topologies with some applications on the blood circulation in the human body. Othman et al. [13], in 2023, introduced the concept of a C-set as a subset of the vertex set $\wp (\aleph )$ in a directed graph $\aleph =(\wp (\aleph ),\eta (\aleph \left)\right)$ to construct a topology on $\wp (\aleph )$, which is called $L_2$-directed topological spaces. In 2023, Abu-Gdairi et al. [14] introduced the novel 1-neighborhood system (1-NS) tools, and they used this system with rough set generalizations to construct a new topology, which they called the heart topological graph model. They introduced algorithms for decision making and for generating graph topologies, that is, they explained the role of the topological visualization in the medical field by conducting graph analysis and constructing rough sets using neighborhood systems. In [15], Atik et al. applied rough set theory to information tables induced from finite directed graphs without loops and multiples arcs, that is, they used the adjacency matrix of a digraph as a particular type of information table, and they explored, on digraphs, the notions of indiscernibility partitions, lower and upper approximations, generalized core, reducts and the discernibility matrix. In [16], Shokry and Aly introduced some neighborhood systems to construct a new topology in the theory of graphs, and they also applied some topological properties on a graph in a medical application of the human heart.

This paper consists of six sections with an introduction section. Section 2 introduces a new class of monophonic paths called the m-negative path class. We have constructed a new topology in the theory of directed graphs using m-negative paths, which are called out mondirected topologies, and also we characterized those directed graphs that induce the indiscrete out mondirected topologies or discrete topologies. Section 3 shows the homeomorphic property in out mondirected topologies and its relations with graphic isomorphic relations in directed simple graphs. In Section 4, we present some of the fundamental topological properties on out mondirected topologies such as connectedness, compactness, etc. We define a new class of connected graphs and discrete topologies, say ${\mathbb{D}}_{\pm }$-connectedness and ${\mathbb{D}}_{\pm }$-discrete, respectively. Section 5 includes some examples to illustrate how our results are applicable, that is, it presents the connectedness, ${\mathbb{D}}_{\pm }$-connectedness and the ${\mathbb{D}}_{\pm }$-discrete properties of diagrams of the networks in the nervous system of the human body, such as diagrams of sensory neuron cells [17] and models of two distinct nicotinic receptor types based on the second messenger signal, the classification of cholinergic receptors and the classification of adrenergic receptors, which are introduced by [18]. The discussion and conclusions are presented in Section 6.

By a directed graph ℵ, we mean the pair $(\wp (\aleph ),\eta (\aleph \left)\right)$ of a non-empty vertex set $\wp (\aleph )$ and directed edge set $\eta (\aleph )$. If $\epsilon \in \eta (\aleph )$ is an edge in $\eta (\aleph )$ with the initial point $x\in \wp (\aleph )$ and end point $y\in \wp (\aleph )$, then ${\epsilon }_{xy}$ denotes $\epsilon$ and $\wp \left({\epsilon }_{xy}\right)=\{x,y\}$. The two directed edges ${\epsilon }_{xy}$ and ${\epsilon }_{x^{\prime }{y}^{\prime }}^{\prime }$ are said to have the same direction (or adjacent directed edges) if $y=x^{\prime }$ or $y^{\prime }=x$. For any $x\in \wp (\aleph )$, ${\mathbb{D}}_x$ is the number of elements of the set $\eta (\aleph )$ that join with x; ${\mathbb{D}}_x^{+}$ is the number of elements of the set $\eta (\aleph )$ that arrived in x; and ${\mathbb{D}}_x^{-}$ is the number of elements of the set $\eta (\aleph )$ that started from x. For $x\in \wp (\aleph )$, the edge ${\epsilon }_{xx}$ is called a loop. If two directed edges have the same initial vertex and the same end vertex, then they are called parallel edges. A directed graph ℵ is called a simple graph if it is without loops and parallel edges. In any simple directed $\aleph =(\wp (\aleph ),\eta (\aleph \left)\right)$, if there is directed edge from x into y, it will be denoted by ${\aleph }_{xy}$, where $x,y\in \wp (\aleph )$. In this paper, a directed path P will be defined as an alternating sequence of distinct directed edges and distinct vertices of the form $\{{\epsilon }_{1^{\prime }{2}^{\prime }}^1,{\epsilon }_{2^{\prime }{3}^{\prime }}^2,{\epsilon }_{3^{\prime }{4}^{\prime }}^3,\dots \}$. The directed path that starts and ends at the same vertex is called a closed directed path. A directed graph ℵ is called weakly connected if an undirected graph $Un(\aleph )$ is connected, where $Un(\aleph )$ denotes the graph that is obtained by replacing all of the directed edges of ℵ with undirected edges. A directed graph ℵ is called connected if, for any $x\ne y\in \wp (\aleph )$, there is a directed path from x into y or from y into x. A directed graph ℵ is called strongly connected if we can move along the directed edges from any vertex into any other vertex in $\wp (\aleph )$. A directed graph ℵ is called a finite if $\wp (\aleph )$ and $\eta (\aleph )$ are both finite sets, and it is called locally finite if ${\mathbb{D}}_x$ is a finite number for all $x\in \wp (\aleph )$. The cycle directed graph $C_n$ with $n>2$ is a simple directed graph with n vertices and n edges such that ${\mathbb{D}}_x^{+}={\mathbb{D}}_x^{-}=1$ for all $x\in \wp \left(C_n\right)$. By $K_{n\to m}$, we mean a complete bipartite directed graph with $n,m>0$, which is defined as a simple directed graph, where its vertices can be partitioned into two subsets $V_n$ with n vertices and $V_m$ with m vertices; there is no edge with endpoints in the same subset; no directed edge with initial points in $V_m$; and every vertex in $V_n$ directs by directed edges to all the vertices in $V_m$. A complete bipartite directed graph $K_{n,m}$ with $n,m>0$ is a simple directed graph whose vertices can be partitioned into two subsets, i.e., $V_n$ with n vertices and $V_m$ with m vertices, such that no directed edge has both endpoints in the same subset and every possible directed edge that could connect vertices in different subsets is part of the graph. A complete directed graph $K_n$ with $n>0$ is a simple directed graph with n vertices such that ${\mathbb{D}}_x^{+}={\mathbb{D}}_x^{-}=n$ for all $x\in \wp (\aleph )$. For any simple graph $\aleph =(\wp (\aleph ),\eta (\aleph \left)\right)$ and for $a\in \wp (\aleph )$, the open in-neighborhood ${\mathbb{N}}^{+}\left(a\right)$ of a is the family of all the elements $b\in \wp (\aleph )$ such that there is ${\epsilon }_{ba}\in \eta (\aleph )$ and the open out-neighborhood ${\mathbb{N}}^{-}\left(a\right)$ of a is the family of all the elements $b\in \wp (\aleph )$ such that there is ${\epsilon }_{ab}\in \eta (\aleph )$. For the vertex $a\in \wp (\aleph )$, the closed in-neighborhood ${\mathbb{N}}^{+}\left[a\right]$ of a is given by ${\mathbb{N}}^{+}\left[a\right]={\mathbb{N}}^{+}\left(a\right)\cup \left\{a\right\}$ and the closed out-neighborhood ${\mathbb{N}}^{-}\left[a\right]$ of a is given by ${\mathbb{N}}^{-}\left[a\right]={\mathbb{N}}^{-}\left(a\right)\cup \left\{a\right\}$. For the vertex $a\in \wp (\aleph )$, the open neighborhood $\mathbb{N}\left(a\right)$ of a is given by $\mathbb{N}\left(a\right)={\mathbb{N}}^{+}\left(a\right)\cup {\mathbb{N}}^{-}\left(a\right)$ and the closed neighborhood $\mathbb{N}\left[a\right]$ of a is given by $\mathbb{N}\left[a\right]=\mathbb{N}\left(a\right)\cup \left\{a\right\}.$ A directed edge joining two non-adjacent vertices in a directed path P in a graph ℵ is called a chord of a path P, and a chordless directed path P is called a monophonic directed path with ${\partial }_{\aleph }P$, which denotes the length of P.

2. The Out Mondirected Topological Spaces

Let $\aleph =(\wp (\aleph ),\eta (\aleph \left)\right)$ be any simple directed graph. A monophonic directed path P is called an m-negative path if ${\mathbb{D}}_x^{-}>{\mathbb{D}}_x^{+}$ for some $x\in \wp \left(P\right)$, where $\wp \left(P\right)$ denotes the set of all vertices of P. A vertex $x\in \wp (\aleph )$ is called an m-negative vertex of a vertex $y\in \wp (\aleph )$ if there is an m-negative path P between them where the length is greater than one (i.e., ${\partial }_{\aleph }P>1$). For the vertex $x\in \wp (\aleph )$, the m-negative open neighborhood ${\mathbb{N}}^e\left(x\right)$ of x is the set of all the m-negative vertices of x, and the m-negative closed neighborhood ${\mathbb{N}}_x^e$ of x is ${\mathbb{N}}_x^e={\mathbb{N}}^e\left(x\right)\cup \left\{x\right\}$. The set of all the m-negative closed neighborhoods of the vertices in ℵ will be denoted by $\mathcal{NP}(\aleph )$. For any simple directed graph $\aleph =(\wp (\aleph ),\eta (\aleph \left)\right)$, the out mondirected topology on $\wp (\aleph )$ is denoted by $T_{\mathcal{NP}(\aleph )}$ and is defined by a topology generated by a sub-basis $\mathcal{NP}(\aleph )$.

Example 1.

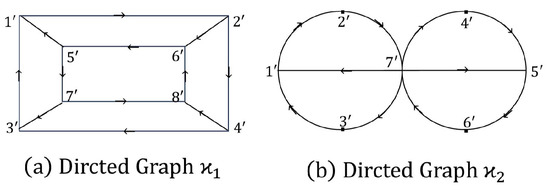
The directed graph ${\aleph }_1=(\wp \left({\aleph }_1\right),\eta \left({\aleph }_1\right))$ has the vertices $2^{\prime }$, $4^{\prime }$, $6^{\prime }$ and $7^{\prime }$, which satisfy the property ${\mathbb{D}}_x^{-}>{\mathbb{D}}_x^{+}$ in Figure 1a. As such, the sub-basis $\mathcal{NP}\left({\aleph }_1\right)$ is given by $\mathcal{NP}\left({\aleph }_1\right)=\{{\mathbb{N}}_i^e:i=1^{\prime },2^{\prime },3^{\prime },4^{\prime },5^{\prime },6^{\prime },7^{\prime },8^{\prime }\},$ where

$${\mathbb{N}}_{1^{\prime }}^e=\{1^{\prime },4^{\prime },6^{\prime },7^{\prime },8^{\prime }\},{\mathbb{N}}_{2^{\prime }}^e=\{2^{\prime },3^{\prime },5^{\prime },7^{\prime },8^{\prime }\},{\mathbb{N}}_{3^{\prime }}^e=\{2^{\prime },3^{\prime },5^{\prime },6^{\prime }\},$$

$${\mathbb{N}}_{4^{\prime }}^e=\{1^{\prime },4^{\prime },5^{\prime },6^{\prime }\},{\mathbb{N}}_{5^{\prime }}^e=\{2^{\prime },3^{\prime },4^{\prime },5^{\prime },8^{\prime }\},{\mathbb{N}}_{6^{\prime }}^e=\{1^{\prime },3^{\prime },4^{\prime },6^{\prime },7^{\prime }\},$$

$${\mathbb{N}}_{7^{\prime }}^e=\{1^{\prime },2^{\prime },6^{\prime },7^{\prime }\},{\mathbb{N}}_{8^{\prime }}^e=\{1^{\prime },2^{\prime },5^{\prime },8^{\prime }\}.$$

Note that $T_{\mathcal{NP}\left({\aleph }_1\right)}$ is a discrete topology on $\wp \left({\aleph }_1\right)$. Also note that, in Figure 1b, only ${\mathbb{D}}_{7^{\prime }}^{-}>{\mathbb{D}}_{7^{\prime }}^{+}$. The sub-basis $\mathcal{NP}\left({\aleph }_2\right)$ is given by

$$\mathcal{NP}\left({\aleph }_2\right)=\{{\mathbb{N}}_i^e:i=1^{\prime },2^{\prime },3^{\prime },4^{\prime },5^{\prime },6^{\prime },7^{\prime }\},$$

where

$${\mathbb{N}}_{1^{\prime }}^e=\{1^{\prime },6^{\prime }\},{\mathbb{N}}_{2^{\prime }}^e=\{2^{\prime },3^{\prime },4^{\prime },5^{\prime }\},{\mathbb{N}}_{3^{\prime }}^e=\{2^{\prime },3^{\prime },6^{\prime }\},$$

$${\mathbb{N}}_{4^{\prime }}^e=\{2^{\prime },4^{\prime },6^{\prime }\},{\mathbb{N}}_{5^{\prime }}^e=\{2^{\prime },5^{\prime }\},{\mathbb{N}}_{6^{\prime }}^e=\{1^{\prime },3^{\prime },4^{\prime },6^{\prime }\},{\mathbb{N}}_{7^{\prime }}^e=\left\{7^{\prime }\right\}.$$

Figure 1. The out mondirected topology on ${\aleph }_1$ and ${\aleph }_2$.

Let $\aleph =(\wp (\aleph ),\eta (\aleph \left)\right)$ be any directed graph. It is clear that if $x\in \wp (\aleph )$ is an isolated vertex then the set $\left\{x\right\}$ is an open set in the out mondirected topological space $(\wp (\aleph ),T_{\mathcal{NP}(\aleph )})$. Also, if ${\aleph }_{xy}\in \eta (\aleph )$ is an isolated directed edge, then the sets $\left\{x\right\}$ and $\left\{y\right\}$ are open sets. Furthermore, if we isolate the path P in ℵ of length two of the form $P=\{{\aleph }_{xy},{\aleph }_{yz}\}$ or $P=\{{\aleph }_{xy},{\aleph }_{zy}\}$, then the sets $\left\{x\right\}$, $\left\{y\right\}$, and $\left\{z\right\}$ are also open sets.

In a complete bipartite directed graph $K_{n\to m}$ with $n,m>0$, all of the directed paths are of length one. As such, the out mondirected topological space $(\wp \left(K_{n\to m}\right),T_{\mathcal{NP}\left(K_{n\to m}\right)})$ will be a discrete space.

Proposition 1.

The out mondirected topological space of a complete bipartite directed graph $K_{n,m}$ is a discrete space.

Proof. 

Let $\wp \left(K_{n,m}\right)={\wp }_n\cup {\wp }_m$ and $x\in \wp \left(K_{n,m}\right)$. Since ${\wp }_n\cap {\wp }_m=\varnothing$, then $x\in {\wp }_n$ or $x\in {\wp }_m$. Suppose that $x\in {\wp }_n$. Let $y\in {\wp }_m$ be any vertex. By the definition of $K_{n,m}$, there are two directed edges: ${\left(K_{n,m}\right)}_{xy}$ and ${\left(K_{n,m}\right)}_{yx}$. Hence, any monophonic directed path between x and y will be of length one. As such, $y\notin {\mathbb{N}}_x^e$. Let $y\in {\wp }_n$ be any vertex. Then, any monophonic directed path of x and y has the length two. Since for all $z\in {\wp }_n$, ${\mathbb{D}}_z^{-}={\mathbb{D}}_z^{+}=m$ and for all $z\in {\wp }_m$, ${\mathbb{D}}_z^{-}={\mathbb{D}}_z^{+}=n$, then $y\notin {\mathbb{N}}_x^e$, that is, ${\mathbb{N}}_x^e=\left\{x\right\}$ for all $x\in {\wp }_n$. Similarly, ${\mathbb{N}}_x^e=\left\{x\right\}$ for all $x\in {\wp }_m$, that is, the out mondirected topological space of the complete bipartite directed graph $K_{n,m}$ is a discrete space. □

Note that, in a directed graph $K_n$ with $n>0$, for any $x,y\in \wp \left(K_n\right)$, there are two directed edges ${\left(K_n\right)}_{xy}$ and ${\left(K_n\right)}_{yx}$, that is, any monophonic directed path between x and y and also for all $z\in \wp \left(K_n\right)$, ${\mathbb{D}}_z^{-}={\mathbb{D}}_z^{+}=n$ will be of length one. In this case, we also obtained ${\mathbb{N}}_x^e=\left\{x\right\}$ for all $x\in \wp \left(K_n\right)$, that is, the out mondirected topological space of the complete directed graph $K_n$ is a discrete space.

To obtain the out mondirected topological space in a cycle directed graph $C_n$ with $n>2$, there is no need to determine the monophonic directed paths and their lengths since ${\mathbb{D}}_x^{+}={\mathbb{D}}_x^{-}=1$ for all $x\in \wp \left(C_n\right)$, that is, ${\mathbb{N}}_x^e=\left\{x\right\}$ for all $x\in \wp \left(C_n\right)$, and the out mondirected topological space of the complete directed graph $C_n$ is a discrete space.

The following theorem shows an Alexandroff topological property of the out mondirected topological spaces in locally finite simple directed graphs. By LS-directed graph, we mean a locally finite simple directed graph.

Theorem 1.

The out mondirected topological space in any LS-directed graph is an Alexandroff space.

Proof. 

Let $\aleph =(\wp (\aleph ),\eta (\aleph \left)\right)$ be a LS-directed graph and C be any nonempty subset of $\wp (\aleph )$. Let $\mathcal{C}$ be the collection of all the m-negative closed neighborhoods of the elements of C. We will prove that ${\cap }_{x\in C}{\mathbb{N}}_x^e$ is an open set in $(\wp (\aleph ),T_{\mathcal{NP}(\aleph )})$. Let $y\in {\cap }_{x\in C}{\mathbb{N}}_x^e$, then $y\in {\mathbb{N}}_x^e$ for all $x\in C$. Hence, $x\in {\mathbb{N}}_y^e$ for all $x\in C$, that is, $C\subseteq {\mathbb{N}}_y^e$. Since ℵ is locally finite, then ${\mathbb{N}}_y^e$ is finite and so is C finite. Hence, ${\cap }_{x\in C}{\mathbb{N}}_x^e$ is an open set, that is, the out mondirected topological space $(\wp (\aleph ),T_{\mathcal{NP}(\aleph )})$ is an Alexandroff space. □

In any LS-directed graph $\aleph =(\wp (\aleph ),\eta (\aleph \left)\right)$, through using an Alexandroff topological property of the out mondirected topological spaces $(\wp (\aleph ),T_{\mathcal{NP}(\aleph )})$, the smallest open set including $a\in \wp (\aleph )$ is denoted by ${\mathbb{M}}^{-}\left(a\right)$. As we have mentioned previously, if $a\in \wp (\aleph )$ is an isolated vertex, then ${\mathbb{M}}^{-}\left(a\right)=\left\{a\right\}$, and if ${\aleph }_{ab}\in \eta (\aleph )$ is an isolated directed edge, then ${\mathbb{M}}^{-}\left(a\right)=\left\{a\right\}$ and ${\mathbb{M}}^{-}\left(b\right)=\left\{b\right\}$. Also, if we have the isolated path P in ℵ of length two of the form $P=\{{\aleph }_{ab},{\aleph }_{bc}\}$ or $P=\{{\aleph }_{ab},{\aleph }_{cb}\}$, then ${\mathbb{M}}^{-}\left(a\right)=\left\{a\right\}$, ${\mathbb{M}}^{-}\left(b\right)=\left\{b\right\}$ and ${\mathbb{M}}^{-}\left(c\right)=\left\{c\right\}$.

Theorem 2.

Let $\aleph =(\wp (\aleph ),\eta (\aleph \left)\right)$ be any LS-directed graph and $x\in \wp (\aleph ).$ Then, ${\mathbb{M}}^{-}\left(x\right)$ is the intersection of all m-negative closed neighborhoods including x.

Proof. 

From the definition of the sub-basis $\mathcal{NP}(\aleph )$, ${\mathbb{N}}_x^e$ is an open set in the out mondirected topological space $(\wp (\aleph ),T_{\mathcal{NP}(\aleph )})$ for all $x\in \wp (\aleph )$. From an Alexandroff topological property of the out mondirected topological spaces $(\wp (\aleph ),T_{\mathcal{NP}(\aleph )})$ in Theorem 1, ${\cap }_{y\in {\mathbb{N}}_x^e}{\mathbb{N}}_y^e$ is an open set. If $y\in {\mathbb{N}}_x^e$, then we can easily obtain $x\in {\mathbb{N}}_y^e$. Hence, ${\cap }_{y\in {\mathbb{N}}_x^e}{\mathbb{N}}_y^e$ is an open set including x. Since ${\mathbb{M}}^{-}\left(x\right)$ is the smallest open set including x, then ${\mathbb{M}}^{-}\left(x\right)\subseteq {\cap }_{y\in {\mathbb{N}}_x^e}{\mathbb{N}}_y^e.$ On the other hand, since ${\mathbb{M}}^{-}\left(x\right)$ is the intersection of all open sets including x, then let ${\mathbb{M}}^{-}\left(x\right)={\cap }_{y\in F}{\mathbb{N}}_y^e$ for some subsets F of $\wp (\aleph )$. Then, $x\in {\mathbb{N}}_y^e$ for all $y\in F$, and this implies $y\in {\mathbb{N}}_x^e$ for all $y\in F$, that is, $F\subseteq {\mathbb{N}}_x^e$. Hence, ${\cap }_{y\in {\mathbb{N}}_x^e}{\mathbb{N}}_y^e\subseteq {\cap }_{y\in F}{\mathbb{N}}_y^e={\mathbb{M}}^{-}\left(x\right).$ As such, ${\mathbb{M}}^{-}\left(x\right)={\cap }_{y\in {\mathbb{N}}_x^e}{\mathbb{N}}_y^e$, that is, ${\mathbb{M}}^{-}\left(x\right)$ is the intersection of all m-negative closed neighborhoods, including x. □

Theorem 3.

Let $\aleph =(\wp (\aleph ),\eta (\aleph \left)\right)$ be any LS-directed graph and $x,y\in \wp (\aleph )$ be any two vertices. Then, ${\mathbb{N}}_y^e\subseteq {\mathbb{N}}_x^e$ if and only if $x\in {\mathbb{M}}^{-}\left(y\right)$.

Proof. 

Let $x,y\in \wp (\aleph )$ be any two vertices and ${\mathbb{N}}_y^e\subseteq {\mathbb{N}}_x^e$. By the Theorem above, $x\in {\cap }_{z\in {\mathbb{N}}_x^e}{\mathbb{N}}_z^e$. Since ${\mathbb{N}}_y^e\subseteq {\mathbb{N}}_x^e$, then ${\cap }_{z\in {\mathbb{N}}_x^e}{\mathbb{N}}_z^e\subseteq {\cap }_{z\in {\mathbb{N}}_y^e}{\mathbb{N}}_z^e$. Hence, $x\in {\cap }_{z\in {\mathbb{N}}_y^e}{\mathbb{N}}_z^e={\mathbb{M}}^{-}\left(y\right)$. On the other hand, let $x\in {\mathbb{M}}^{-}\left(y\right)$. Through using Theorem above, we can obtain ${\mathbb{N}}_y^e={\cap }_{z\in {\mathbb{N}}_y^e}{\mathbb{N}}_z^e$. Then, $x\in {\cap }_{z\in {\mathbb{N}}_y^e}{\mathbb{N}}_z^e$, that is, $x\in {\mathbb{N}}_z^e$ for all $z\in {\mathbb{N}}_y^e$. This implies $z\in {\mathbb{N}}_x^e$ for all $z\in {\mathbb{N}}_y^e$. Hence, ${\mathbb{N}}_y^e\subseteq {\mathbb{N}}_x^e$. □

Theorem 4.

Let $\aleph =(\wp (\aleph ),\eta (\aleph \left)\right)$ be any LS-directed graph. Then, for all $x,y\in \wp (\aleph )$, ${\mathbb{N}}_y^e⊈{\mathbb{N}}_x^e$ and ${\mathbb{N}}_x^e⊈{\mathbb{N}}_y^e$ if and only if the out mondirected topological space $(\wp (\aleph ),T_{\mathcal{NP}(\aleph )})$ is a discrete.

Proof. 

Let x be any vertex in $\wp (\aleph )$. It is clear that $x\in {\mathbb{N}}_x^e$. Suppose that $y\in \wp (\aleph )$ is any vertex. If $y\in {\mathbb{N}}_x^e$, then, by Theorem 3, ${\mathbb{N}}_x^e\subseteq {\mathbb{N}}_y^e$, and this is a contradiction with the hypothesis. Hence, ${\mathbb{M}}^{-}\left(x\right)=\left\{x\right\}$ for all $x\in \wp (\aleph )$, that is, $(\wp (\aleph ),T_{\mathcal{NP}(\aleph )})$ is a discrete. On the other hand, it is clear that ${\mathbb{N}}_x^e=\left\{x\right\}$ for all $x\in \wp (\aleph )$. □

Let $\aleph =(\wp (\aleph ),\eta (\aleph \left)\right)$ be any LS-directed graph and $H\subseteq \wp (\aleph )$. Recall [19], where the closure set of H was defined as the intersection of all the closed sets including H in the out mondirected topological space $(\wp (\aleph ),T_{\mathcal{NP}(\aleph )})$ and is denoted by $Cl\left(H\right)$. Recall [19], where $x\in Cl\left(H\right)$ if and only if for every open set O including x, $H\cap O\ne \varnothing$.

Proposition 2.

Let $\aleph =(\wp (\aleph ),\eta (\aleph \left)\right)$ be any LS-directed graph and $x\in \wp (\aleph )$. Then, $Cl\left({\mathbb{N}}_x^e\right)\subseteq Cl\left({\mathbb{N}}_y^e\right)$ for all $y\in {\mathbb{N}}_x^e$.

Proof. 

Let $\beta \in Cl\left({\mathbb{N}}_x^e\right)$. Then, for every open set O including $\beta$, $O\cap {\mathbb{N}}_x^e\ne \varnothing$. Since ${\mathbb{N}}_x^e\subseteq {\mathbb{N}}_y^e$ for all $y\in {\mathbb{N}}_x^e$, then $O\cap {\mathbb{N}}_y^e\ne \varnothing$ for all $y\in {\mathbb{N}}_x^e$, that is, $\beta \in Cl\left({\mathbb{N}}_y^e\right)$ for all $y\in {\mathbb{N}}_x^e$. Hence, $Cl\left({\mathbb{N}}_x^e\right)\subseteq Cl\left({\mathbb{N}}_y^e\right)$ for all $y\in {\mathbb{N}}_x^e$. □

It is clear from the proposition above for any LS-directed graph $\aleph =(\wp (\aleph ),\eta (\aleph \left)\right)$ and for any vertex $x\in \wp (\aleph )$, $Cl\left(\left\{x\right\}\right)\subseteq Cl\left({\mathbb{N}}_y^e\right)$ for all $y\in {\mathbb{N}}_x^e$.

Remark 1.

For any simple graph $\aleph =(\wp (\aleph ),\eta (\aleph \left)\right)$ and $x,y\in \wp (\aleph )$, $x\in Cl\left(\right\{y\left\}\right)$ if and only if ${\mathbb{N}}_x^e\subseteq {\mathbb{N}}_y^e$.

3. Graphical Isomorphisms

Let ${\aleph }_1=(\wp \left({\aleph }_1\right),\eta \left({\aleph }_1\right))$ and ${\aleph }_2=(\wp \left({\aleph }_2\right),\eta \left({\aleph }_2\right))$ be the two SL-directed graphs without isolated vertices. If there is a bijective function $\chi :\wp \left({\aleph }_1\right)\to \wp \left({\aleph }_2\right)$ such that ${\left({\aleph }_1\right)}_{xy}\in \eta \left({\aleph }_1\right)$ if and only if ${\left({\aleph }_2\right)}_{\chi \left(x\right)\chi \left(y\right)}\in \eta \left({\aleph }_2\right)$ for all $x,y\in \wp \left({\aleph }_1\right)$, then we say that the two graphs ${\aleph }_1$ and ${\aleph }_2$ are isomorphic and we write ${\aleph }_1\cong {\aleph }_2$. The function $F:(X_1,{\tau }_1)\to (X_2,{\tau }_2)$ of a topological space $(X_1,{\tau }_1)$ into a topological space $(X_2,{\tau }_2)$ is called continuous if $F\left(Cl\right(G\left)\right)\subseteq Cl\left(F\right(G\left)\right)$ for all $G\subseteq X_1$. A function $F:(X_1,{\tau }_1)\to (X_2,{\tau }_2)$ is called a closed function if $F\left(G\right)$ is a closed set in $X_2$ for all closed sets $G\subseteq X_1$. A function $F:(X_1,{\tau }_1)\to (X_2,{\tau }_2)$ is called a homeomorphism if it is bijective, closed function and continuous function [19].

Theorem 5.

Let ${\aleph }_1=(\wp \left({\aleph }_1\right),\eta \left({\aleph }_1\right))$ and ${\aleph }_2=(\wp \left({\aleph }_2\right),\eta \left({\aleph }_2\right))$ be two LS-directed graphs. A function $\chi :\wp \left({\aleph }_1\right)\to \wp \left({\aleph }_2\right)$ is continuous in the out mondirected topological spaces $(\wp \left({\aleph }_1\right),T_{\mathcal{NP}\left({\aleph }_1\right)})$ in $(\wp \left({\aleph }_2\right),T_{\mathcal{NP}\left({\aleph }_2\right)})$ if and only if ${\mathbb{N}}_x^e\subseteq {\mathbb{N}}_y^e$ implies ${\mathbb{N}}_{\chi \left(x\right)}^e\subseteq {\mathbb{N}}_{\chi \left(y\right)}^e$ for all $x,y\in \wp \left({\aleph }_1\right)$.

Proof. 

Suppose that for all $x,y\in \wp \left({\aleph }_1\right)$, ${\mathbb{N}}_x^e\subseteq {\mathbb{N}}_y^e$ implies ${\mathbb{N}}_{\chi \left(x\right)}^e\subseteq {\mathbb{N}}_{\chi \left(y\right)}^e$. Let G be any subset of $\wp \left({\aleph }_1\right)$ and $x\in G$. If $x\in Cl\left(G\right)$, then $x\in Cl\left(\right\{y\left\}\right)$ for some $y\in G$. Hence, ${\mathbb{N}}_x^e\subseteq {\mathbb{N}}_y^e$. By the hypothesis, we obtain ${\mathbb{N}}_{\chi \left(x\right)}^e\subseteq {\mathbb{N}}_{\chi \left(y\right)}^e$. This implies $\chi \left(x\right)\in Cl\left(\right\{\chi \left(y\right)\left\}\right)\subseteq Cl\left(\chi \right(G\left)\right).$ Hence, $\chi$ is continuous. On the other hand, let $\chi$ be continuous and $x,y\in \wp \left({\aleph }_1\right)$ be any two vertices such that ${\mathbb{N}}_x^e\subseteq {\mathbb{N}}_y^e$. By Remark 1, we obtain $x\in Cl\left(\right\{y\left\}\right)$, and, by the continuity of $\chi$, we have

$$\chi \left(x\right)\in \chi \left(Cl\right(\left\{y\right\}\left)\right)\subseteq Cl\left(\right\{\chi \left(y\right)\left\}\right).$$

Again, by Remark 1, we obtain ${\mathbb{N}}_{\chi \left(x\right)}^e\subseteq {\mathbb{N}}_{\chi \left(y\right)}^e$. □

Theorem 6.

Let ${\aleph }_1=(\wp \left({\aleph }_1\right),\eta \left({\aleph }_1\right))$ and ${\aleph }_2=(\wp \left({\aleph }_2\right),\eta \left({\aleph }_2\right))$ be two LS-directed graphs. If a function $\chi :\wp \left({\aleph }_1\right)\to \wp \left({\aleph }_2\right)$ is onto and for all $x,y\in \wp \left({\aleph }_1\right)$, where ${\mathbb{N}}_{\chi \left(x\right)}^e\subseteq {\mathbb{N}}_{\chi \left(y\right)}^e$ implies ${\mathbb{N}}_x^e\subseteq {\mathbb{N}}_y^e$, then the function χ is a closed function.

Proof. 

Let G be any closed set in $\wp \left({\aleph }_1\right)$. Since $\chi$ is onto it, then there is a function $\psi :\wp \left({\aleph }_2\right)\to \wp \left({\aleph }_1\right)$ such that $\chi \circ \psi =i{d}_{\wp \left({\aleph }_2\right)}$. Now, we prove that $\psi$ is continuous. Let $x,y\in \wp \left({\aleph }_2\right)$ be arbitrary vertices such that ${\mathbb{N}}_x^e\subseteq {\mathbb{N}}_y^e$. Hence, ${\mathbb{N}}_{\chi \left(\psi \right(x\left)\right)}^e\subseteq {\mathbb{N}}_{\chi \left(\psi \right(y\left)\right)}^e$. By the hypothesis, we obtain ${\mathbb{N}}_{\psi \left(x\right)}^e\subseteq {\mathbb{N}}_{\psi \left(y\right)}^e$. By Theorem 5, $\psi$ is continuous. Hence, $\chi \left(G\right)={\psi }^{-1}\left(G\right)$ is a closed set and so $\chi$ is a closed function. □

Theorem 7.

Let ${\aleph }_1=(\wp \left({\aleph }_1\right),\eta \left({\aleph }_1\right))$ and ${\aleph }_2=(\wp \left({\aleph }_2\right),\eta \left({\aleph }_2\right))$ be two LS-directed graphs. If a function $\chi :\wp \left({\aleph }_1\right)\to \wp \left({\aleph }_2\right)$ is a closed function and one to one, then for all $x,y\in \wp \left({\aleph }_1\right)$, ${\mathbb{N}}_{\chi \left(x\right)}^e\subseteq {\mathbb{N}}_{\chi \left(y\right)}^e$ implies ${\mathbb{N}}_x^e\subseteq {\mathbb{N}}_y^e$.

Proof. 

Let $x,y\in \wp \left({\aleph }_2\right)$ be any two vertices such that ${\mathbb{N}}_{\chi \left(x\right)}^e\subseteq {\mathbb{N}}_{\chi \left(y\right)}^e$. Since $\chi$ is one to one, then there is a function $\psi :\wp \left({\aleph }_2\right)\to \wp \left({\aleph }_1\right)$ such that $\psi \circ \chi =i{d}_{\wp \left({\aleph }_1\right)}$. Since $\chi$ is one to one and a closed function, then it is clear to see that $\psi$ is continuous. This implies that ${\mathbb{N}}_{\psi \left(\chi \right(x\left)\right)}^e\subseteq {\mathbb{N}}_{\psi \left(\chi \right(y\left)\right)}^e$, that is, ${\mathbb{N}}_x^e\subseteq {\mathbb{N}}_y^e$. □

Remark 2.

It is easy, via the previous theorems, to obtain a bijective function $\chi :\wp \left({\aleph }_1\right)\to \wp \left({\aleph }_2\right)$ of the two LS-directed graphs ${\aleph }_1=(\wp \left({\aleph }_1\right),\eta \left({\aleph }_1\right))$ and ${\aleph }_2=(\wp \left({\aleph }_2\right),\eta \left({\aleph }_2\right))$, which are a homeomorphism if and only if, for all $x,y\in \wp \left({\aleph }_1\right)$, ${\mathbb{N}}_x^e\subseteq {\mathbb{N}}_y^e$ if and only if ${\mathbb{N}}_{\chi \left(x\right)}^e\subseteq {\mathbb{N}}_{\chi \left(y\right)}^e$.

As we mentioned previously, the out mondirected topological spaces $(C_n,T_{\mathcal{NP}\left(C_n\right)})$ and $(K_n,T_{\mathcal{NP}\left(K_n\right)})$ of a cycle directed graph $C_n$ and a complete directed graph $K_n$, respectively, are discrete spaces. Since $|C_n| = |K_n|$, then $(C_n,T_{\mathcal{NP}\left(C_n\right)})$ and $(K_n,T_{\mathcal{NP}\left(K_n\right)})$ are homeomorphic, while the graphs $C_n$ and $K_n$ are not isomorphic. The following theorem shows that the isomorphic relation of LS-directed graphs without isolated vertices gives us the homeomorphic property of their out mondirected topological spaces.

Theorem 8.

Let ${\aleph }_1=(\wp \left({\aleph }_1\right),\eta \left({\aleph }_1\right))$ and ${\aleph }_2=(\wp \left({\aleph }_2\right),\eta \left({\aleph }_2\right))$ be two LS-directed graphs without isolated vertices. If ${\aleph }_1\cong {\aleph }_2$, then there is a homeomorphism between two out mondirected topological spaces $(\wp \left({\aleph }_1\right),T_{\mathcal{NP}\left({\aleph }_1\right)})$ and $(\wp \left({\aleph }_1\right),T_{\mathcal{NP}\left({\aleph }_1\right)})$.

Proof. 

Let $\chi :\wp \left({\aleph }_1\right)\to \wp \left({\aleph }_2\right)$ be a bijective function such that ${\left({\aleph }_1\right)}_{xy}\in \eta \left({\aleph }_1\right)$ if and only if ${\left({\aleph }_2\right)}_{\chi \left(x\right)\chi \left(y\right)}\in \eta \left({\aleph }_2\right)$ for all $x,y\in \wp \left({\aleph }_1\right)$. Let $x,y\in \wp \left({\aleph }_1\right)$ such that y is an m-negative vertex of x. Then, there is an m-negative path

$$P_{{\aleph }_1}:{\left({\aleph }_1\right)}_{x{x}_1}{\left({\aleph }_1\right)}_{x_1{x}_2}{\left({\aleph }_1\right)}_{x_2{x}_3}\cdots {\left({\aleph }_1\right)}_{x_{n-1}{x}_n}{\left({\aleph }_1\right)}_{x_{n}y}$$

with ${\partial }_{{\aleph }_1}{P}_{{\aleph }_1}>1$ and ${\mathbb{D}}_{x_k}^{-}>{\mathbb{D}}_{x_k}^{+}$ for some $x_k\in \wp \left(P_{{\aleph }_1}\right)$. By the isomorphic relation of ${\aleph }_1$ and ${\aleph }_2$, we obtain

$$P_{{\aleph }_2}:{\left({\aleph }_2\right)}_{\chi \left(x\right)\chi \left(x_1\right)}{\left({\aleph }_2\right)}_{\chi \left(x_1\right)\chi \left(x_2\right)}{\left({\aleph }_2\right)}_{\chi \left(x_2\right)\chi \left(x_3\right)}\cdots {\left({\aleph }_2\right)}_{\chi \left(x_{n-1}\right)\chi \left(x_n\right)}{\left({\aleph }_2\right)}_{\chi \left(x_n\right)\chi \left(y\right)}$$

with ${\partial }_{{\aleph }_2}{P}_{{\aleph }_2}>1$ and ${\mathbb{D}}_{\chi \left(x_k\right)}^{-}>{\mathbb{D}}_{\chi \left(x_k\right)}^{+}$ for some $\chi \left(x_k\right)\in \wp \left(P_{{\aleph }_2}\right)$, that is, $P_{{\aleph }_2}$ is an m-negative path from a vertex $\chi \left(x\right)$ into a vertex $\chi \left(y\right)$. Hence, $\chi \left(y\right)$ is an m-negative vertex of $\chi \left(x\right)$. Thus, for all $x,y\in \eta \left({\aleph }_1\right)$, ${\mathbb{N}}_x^e\subseteq {\mathbb{N}}_y^e$ if and only if ${\mathbb{N}}_{\chi \left(x\right)}^e\subseteq {\mathbb{N}}_{\chi \left(y\right)}^e$. Then, by Remark 2, $\chi$ is a homeomorphism of the out mondirected topological spaces $(\wp \left({\aleph }_1\right),T_{\mathcal{NP}\left({\aleph }_1\right)})$ into $(\wp \left({\aleph }_2\right),T_{\mathcal{NP}\left({\aleph }_2\right)})$. □

4. On Some Fundamental Properties

For the compactness property of the out mondirected topological space $(\wp (\aleph ),T_{\mathcal{NP}(\aleph )})$ of any SL-directed graph $\aleph =(\wp (\aleph ),\eta (\aleph \left)\right)$, it is clear that $(\wp (\aleph ),T_{\mathcal{NP}(\aleph )})$ is a compact space if $\wp (\aleph )$ is finite. The converse of this fact need not be true.

Example 2.

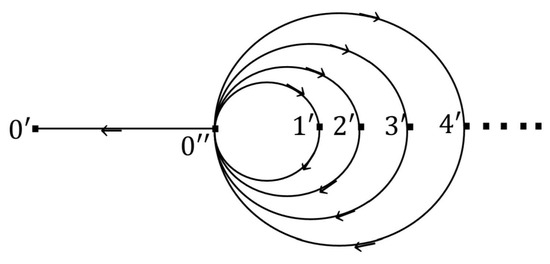
In Figure 2, the SL-directed graph $\aleph =(\wp (\aleph ),\eta (\aleph \left)\right)$ with the infinite vertex set $\wp (\aleph )=\{0^{″},0^{\prime },1^{\prime },2^{\prime },3^{\prime },\cdots \}$ has the sub-basis $\mathcal{NP}(\aleph )$, which is given by $\mathcal{NP}(\aleph )=\{{\mathbb{N}}_k^e:k=0^{″},0^{\prime },1^{\prime },2^{\prime },3^{\prime },\cdots \}$, where ${\mathbb{N}}_{k^{\prime }}^e=\{0^{\prime },1^{\prime },2^{\prime },3^{\prime },\cdots \}$ for all $k=0^{″},0^{\prime },1^{\prime },2^{\prime },3^{\prime },\cdots$ and ${\mathbb{N}}_{0^{″}}^e=\left\{0^{″}\right\}$. The out mondirected topology of a graph ℵ is given by

$$T_{\mathcal{NP}(\aleph )}=\{\varnothing ,\wp (\aleph ),{\mathbb{N}}_{0^{\prime }}^e,{\mathbb{N}}_{0^{″}}^e\}.$$

Figure 2. The compactness property.

The out mondirected topological space $(\wp (\aleph ),T_{\mathcal{NP}(\aleph )})$ is a compact space, while $\wp (\aleph )$ is an infinite set.

The following theorems discuss the connectedness property in the class of the SL-directed graphs and their out mondirected topological spaces.

Theorem 9.

Let $\aleph =(\wp (\aleph ),\eta (\aleph \left)\right)$ be any LS-directed graph. If $(\wp (\aleph ),T_{\mathcal{NP}(\aleph )})$ is a connected space and ℵ does not have isolated vertices, then ℵ is a weakly connected graph.

Proof. 

Let $\aleph =(\wp (\aleph ),\eta (\aleph \left)\right)$ not be a weakly connected LS-directed graph. Then, the corresponding undirected graph $Un(\aleph )$ is disconnected. Consider $\mathcal{H}:=\{{\aleph }_{\theta }:\theta \in \Theta \}$ the family of all components in $Un(\aleph )$, where ${\aleph }_{\theta }=(\wp \left({\aleph }_{\theta }\right),\eta \left({\aleph }_{\theta }\right))$ for all $\theta \in \Theta$. Now, for all $\theta \in \Theta$, $\wp \left({\aleph }_{\theta }\right)={\cup }_{x\in \wp \left({\aleph }_{\theta }\right)}{\mathbb{N}}_x^e$, then $M:=\wp \left({\aleph }_{{\theta }_o}\right)$ is a proper nonempty open subset of $\wp (\aleph )$, where ${\theta }_o\in \Theta$. Then, $G:=M^c={[\wp \left({\aleph }_{\theta }\right)]}^c={\cup }_{\theta \in \Theta \backslash \left\{{\theta }_o\right\}}\wp \left({\aleph }_{\theta }\right)$ is also a proper nonempty open subset of $\wp (\aleph )$, that is, $(\wp (\aleph ),T_{\mathcal{NP}(\aleph )})$ is not a connected space and this contradicts the connectedness of $(\wp (\aleph ),T_{\mathcal{NP}(\aleph )})$. Hence, ℵ is a weakly connected graph. □

The converse of the theorem above need not be true, the out mondirected topological space $(C_n,T_{\mathcal{NP}\left(C_n\right)})$ of a cycle directed graph $C_n$ is a discrete space and so is a disconnected space, while $C_n$ is weakly connected. Also, the cycle directed graph $C_n$ is a connected graph while the out mondirected topological space $(C_n,T_{\mathcal{NP}\left(C_n\right)})$ is disconnected. The complete directed graph $K_n$ is a strongly connected graph while the out mondirected topological space $(K_n,T_{\mathcal{NP}\left(K_n\right)})$ is disconnected.

Let $\aleph =(\wp (\aleph ),\eta (\aleph \left)\right)$ be any LS-directed graph. Define ${\mathbb{D}}_{\pm }(\aleph )$ by the subset of $\wp (\aleph )$, including all vertices x where ${\mathbb{D}}_a^{-}\le {\mathbb{D}}_a^{+}$, that is, ${\mathbb{D}}_{\pm }(\aleph )=\{a\in \wp (\aleph ):{\mathbb{D}}_a^{-}\le {\mathbb{D}}_a^{+}\}$. An LS-directed graph $\aleph =(\wp (\aleph ),\eta (\aleph \left)\right)$ is called a ${\mathbb{D}}_{\pm }$-connected graph if the subgraph ${\aleph }^{{\mathbb{D}}_{\pm }}$ of ℵ, which is induced by ${\mathbb{D}}_{\pm }(\aleph )$, is weakly connected. The out mondirected topological space $(\wp (\aleph ),T_{\mathcal{NP}(\aleph )})$ is called a ${\mathbb{D}}_{\pm }$-discrete if the relative topology $T_{\mathcal{NP}(\aleph )}{|}_{{\mathbb{D}}_{\pm }(\aleph )}$ is a discrete topology on a set ${\mathbb{D}}_{\pm }(\aleph )$. The cycle directed graph $C_n$ with $n>2$ is an ${\mathbb{D}}_{\pm }$-connected graph since ${\mathbb{D}}_{\pm }\left(C_n\right)=\wp \left(C_n\right)$, and the out mondirected topological space $(\wp \left(C_n\right),T_{\mathcal{NP}\left(C_n\right)})$ is ${\mathbb{D}}_{\pm }$-discrete. The complete directed graph $K_n$ with $n>2$ is an ${\mathbb{D}}_{\pm }$-connected graph since ${\mathbb{D}}_{\pm }\left(K_n\right)=\wp \left(K_n\right)$, and the out mondirected topological space $(\wp \left(K_n\right),T_{\mathcal{NP}\left(K_n\right)})$ is ${\mathbb{D}}_{\pm }$-discrete. The complete bipartite directed graph $K_{n\to m}$ with $n,m>2$ is not a ${\mathbb{D}}_{\pm }$-connected graph since ${\mathbb{D}}_{\pm }\left(K_{n\to m}\right)={\wp }_m$, and the subgraph $K_{n\to m}^{{\mathbb{D}}_{\pm }}$ induced by ${\wp }_m$ is not weakly connected, while the out mondirected topological space $(\wp \left(K_{n,m}\right),T_{\mathcal{NP}\left(K_{n,m}\right)})$ is ${\mathbb{D}}_{\pm }$-discrete. The complete bipartite directed graph $K_{n,m}$ with $n,m>2$ is a ${\mathbb{D}}_{\pm }$-connected graph since ${\mathbb{D}}_{\pm }\left(K_{n,m}\right)=\wp \left(K_{n,m}\right)$. Also, the out mondirected topological space $(\wp \left(K_{n,m}\right),T_{\mathcal{NP}\left(K_{n,m}\right)}$ is ${\mathbb{D}}_{\pm }$-discrete. In Figure 2, the set ${\mathbb{D}}_{\pm }(\aleph )$ of the graph $\aleph =(\wp (\aleph ),\eta (\aleph \left)\right)$ is given by ${\mathbb{D}}_{\pm }(\aleph )=\{0^{\prime },1^{\prime },2^{\prime },3^{\prime },\cdots \}$. The subgraph ${\aleph }^{{\mathbb{D}}_{\pm }}$ is not weakly connected while the out mondirected topological space $(\wp (\aleph ),T_{\mathcal{NP}(\aleph )}$ is not ${\mathbb{D}}_{\pm }$-discrete.

Recall [19], where, in a topological space $(X,\tau )$, a subset G is called dense in X if $Cl\left(G\right)=X$, that is, if $X\cap H\ne \varnothing$ for all open sets H. It is clear that Amiri et al. [1] introduced the graphic topological spaces in the undirected graph theory and proved that the graphic topological space $(\wp (\aleph ),T_{\mathcal{A}\wp })$ of any locally finite graph ℵ is an Alexandroff space. As such, here in this paper, for SL-directed graphs $\aleph =(\wp (\aleph ),\eta (\aleph \left)\right)$, we studied the graphic topological space in the following theorems of the corresponding undirected graph $Un(\aleph )$. As such, for any $a\in \wp (\aleph )$, ${\Sigma }_a$ denotes the smallest open set, including a.

Theorem 10.

Let $\aleph =(\wp (\aleph ),\eta (\aleph \left)\right)$ be a ${\mathbb{D}}_{\pm }$-connected graph. Then, the set $\mathbb{Q}$ of all vertices in ${\mathbb{D}}_{\pm }(\aleph )$ with degrees greater than one is dense in $({\mathbb{D}}_{\pm }(\aleph ),T_{\mathcal{A}{\mathbb{D}}_{\pm }(\aleph )})$.

Proof. 

Let $x\in {\mathbb{D}}_{\pm }(\aleph )$. Since ${\Sigma }_x$ is the smallest open set including x, then, to prove that $\mathbb{Q}\cap O\ne \varnothing$ for all open sets O in $({\mathbb{D}}_{\pm }(\aleph ),T_{\mathcal{A}{\mathbb{D}}_{\pm }(\aleph )})$, it will prove that $\mathbb{Q}\cap {\Sigma }_x\ne \varnothing$ for all $x\in {\mathbb{D}}_{\pm }(\aleph )\backslash \mathbb{Q}$. Let $x\in {\mathbb{D}}_{\pm }(\aleph )\backslash \mathbb{Q}$. Since x is not isolated, then there is $y\in {\mathbb{D}}_{\pm }(\aleph )$ such that ${\mathbb{M}}^{-}\left(x\right)=\left\{y\right\}$. Hence, ${\Sigma }_x={\mathbb{M}}^{-}\left(y\right)$. Thus, ${\mathbb{D}}_y>1$, that is, there exists some $z\in \mathbb{Q}$ such that $z\in {\mathbb{M}}^{-}\left(y\right)$. Then, $z\in \mathbb{Q}\cap {\mathbb{M}}^{-}\left(y\right)=\mathbb{Q}\cap {\Sigma }_x$, that is, $\mathbb{Q}\cap {\Sigma }_x\ne \varnothing$ for all $x\in {\mathbb{D}}_{\pm }(\aleph )\backslash \mathbb{Q}$. Hence, $\mathbb{Q}$ is dense in $({\mathbb{D}}_{\pm }(\aleph ),T_{\mathcal{A}{\mathbb{D}}_{\pm }(\aleph )})$. □

Theorem 11.

Let $\aleph =(\wp (\aleph ),\eta (\aleph \left)\right)$ be a ${\mathbb{D}}_{\pm }$-connected graph, γ the family of the smallest open sets of all vertices in ${\mathbb{D}}_{\pm }(\aleph )$ and ${\omega }_{\gamma }$ the family of all minimal sets in γ. If $\mathbb{Q}\subseteq {\mathbb{D}}_{\pm }(\aleph )$ is minimally dense in $({\mathbb{D}}_{\pm }(\aleph ),T_{\mathcal{A}{\mathbb{D}}_{\pm }(\aleph )})$, then there is a function $\psi :{\omega }_{\gamma }\to \mathbb{Q}$ such that $\psi \left({\Sigma }_x\right)\in {\Sigma }_x$ for all ${\Sigma }_x\in {\omega }_{\gamma }$.

Proof. 

By the form of ${\omega }_{\gamma }$, the intersection of every pair of the distinct elements of ${\omega }_{\gamma }$ is an empty set. Since $Cl\left(G\right)={\mathbb{D}}_{\pm }(\aleph )$ in $({\mathbb{D}}_{\pm }(\aleph ),T_{\mathcal{A}\mathcal{A}{\mathbb{D}}_{\pm }(\aleph )})$, then there are some $x\in G\cap \mathbb{Q}$ for all $G\in {\omega }_{\gamma }$. Since $x\in G$ and $G\in {\omega }_{\gamma }$, then $G\subseteq {\Sigma }_x$, and it is clear that ${\Sigma }_x\subseteq G$, that is, ${\Sigma }_x=G$. If $y\in G\cap (\mathbb{Q}\backslash \{x\left\}\right)$, then, similarly, we obtain ${\Sigma }_x={\Sigma }_y=G$. Hence, $Cl\left(\right\{x\left\}\right)=Cl\left(\right\{y\left\}\right)$. Then, $Cl(\mathbb{Q}\backslash \left\{y\right\})={\mathbb{D}}_{\pm }(\aleph )$ and this contradiction. As such, $G\cap \mathbb{Q}=\left\{x\right\}$. Hence, we define a function $\psi :{\omega }_{\gamma }\to \mathbb{Q}$ of ${\omega }_{\gamma }$ into $\mathbb{Q}$ by sending $G\in {\omega }_{\gamma }$ into the single element of $G\cap (\mathbb{Q}\backslash \{x\left\}\right)$. Now, we will prove that $\psi$ is on. If we let $g\in \mathbb{Q}$, then we prove that ${\Sigma }_g\in {\omega }_{\gamma }$ such that $\psi \left({\Sigma }_g\right)=g$. If ${\Sigma }_g\notin {\omega }_{\gamma }$, then there is $x\in {\mathbb{D}}_{\pm }(\aleph )$ such that ${\Sigma }_x\subset {\Sigma }_g$ is a proper subset of ${\Sigma }_g$. Then, $Cl\left({\Sigma }_g\right)=Cl\left({\Sigma }_x\right)$. As such, we obtain $Cl(\mathbb{Q}\backslash \left\{g\right\})={\mathbb{D}}_{\pm }(\aleph )$ and this contradiction. Hence, ${\Sigma }_g\in {\omega }_{\gamma }$ such that $\psi \left({\Sigma }_g\right)=g$. □

Theorem 12.

Let $\aleph =(\wp (\aleph ),\eta (\aleph \left)\right)$ be a ${\mathbb{D}}_{\pm }$-connected graph, γ the collection of the smallest open sets of all the vertices in ${\mathbb{D}}_{\pm }(\aleph )$ and ${\omega }_{\gamma }$ the collection of all the minimal sets in γ. If $\psi :{\omega }_{\gamma }\to \wp (\aleph )$ is a function such that $\psi \left({\Sigma }_x\right)\in {\Sigma }_x$ for all ${\Sigma }_x\in {\omega }_{\gamma }$, then $\psi \left({\omega }_{\gamma }\right)$ is a minimal dense in $({\mathbb{D}}_{\pm }(\aleph ),T_{\mathcal{A}{\mathbb{D}}_{\pm }(\aleph )})$.

Proof. 

Note that for all $x\in {\mathbb{D}}_{\pm }(\aleph )$ there is $y\in {\mathbb{D}}_{\pm }(\aleph )$ such that ${\Sigma }_y\in {\omega }_{\gamma }$ and ${\Sigma }_y\subseteq {\Sigma }_x$. Hence, we obtain $\psi \left({\Sigma }_y\right)\in {\Sigma }_x\cap \psi \left({\omega }_{\gamma }\right)$, that is, $\psi \left({\omega }_{\gamma }\right)$ is dense in $({\mathbb{D}}_{\pm }(\aleph ),T_{\mathcal{A}{\mathbb{D}}_{\pm }(\aleph )})$. To prove that $\psi \left({\omega }_{\gamma }\right)$ is minimally dense in $({\mathbb{D}}_{\pm }(\aleph ),T_{\mathcal{A}{\mathbb{D}}_{\pm }(\aleph )})$, let $Cl\left(\mathbb{Q}\right)={\mathbb{D}}_{\pm }(\aleph )$ and $\mathbb{Q}\subseteq \psi \left({\omega }_{\gamma }\right)$. Suppose that ${\Sigma }_x\in {\omega }_{\gamma }$ such that $\psi \left({\Sigma }_x\right)\notin \mathbb{Q}$. Then, there is $y\in {\mathbb{D}}_{\pm }(\aleph )$ such that ${\Sigma }_y\in {\omega }_{\gamma }$ and $\psi \left({\Sigma }_y\right)\in {\Sigma }_x\cap \mathbb{Q}$. Since $\psi \left({\Sigma }_y\right)\in {\Sigma }_x\cap {\Sigma }_y$ and $\psi \left({\Sigma }_x\right)\notin \mathbb{Q}$, that is, $\psi \left({\Sigma }_x\right)\in {\Sigma }_x\backslash \mathbb{Q}$. Then, we have ${\Sigma }_x={\Sigma }_y$ and so $\psi \left({\Sigma }_x\right)=\psi \left({\Sigma }_y\right)\in \mathbb{Q}$, and this is a contradiction, that is, $\mathbb{Q}=\psi \left({\omega }_{\gamma }\right)$. □

Theorem 13.

${\mathbb{D}}_{\pm }$-connectedness is an isomorphic property in the class of LS-directed graphs without isolated vertices.

Proof. 

Let ${\aleph }_1=(\wp \left({\aleph }_1\right),\eta \left({\aleph }_1\right))$ and ${\aleph }_2=(\wp \left({\aleph }_2\right),\eta \left({\aleph }_2\right))$ be two LS-directed graphs without isolated vertices. Let ${\aleph }_1$ be ${\mathbb{D}}_{\pm }$-connected, and let ${\aleph }_1\cong {\aleph }_2$. We will prove that ${\aleph }_2$ is ${\mathbb{D}}_{\pm }$-connected. Since ${\aleph }_1\cong {\aleph }_2$, then there is a bijective function $\chi :\wp \left({\aleph }_1\right)\to \wp \left({\aleph }_2\right)$ such that ${\left({\aleph }_1\right)}_{ab}\in \eta \left({\aleph }_1\right)$ if and only if ${\left({\aleph }_2\right)}_{\chi \left(a\right)\chi \left(b\right)}\in \eta \left({\aleph }_2\right)$ for all $a,b\in \wp \left({\aleph }_1\right)$. Let $a,b\in \wp \left({\aleph }_1\right)$ such that b is an m-negative vertex of a. Then, by the proof of Theorem 8, $\chi \left(b\right)$ is an m-negative vertex of $\chi \left(a\right)$. Hence, ${\mathbb{D}}_a^{-}\le {\mathbb{D}}_a^{+}$ if and only if ${\mathbb{D}}_{\chi \left(a\right)}^{-}\le {\mathbb{D}}_{\chi \left(a\right)}^{+}$ for all $a\in \wp \left({\aleph }_1\right)$. Now, suppose that ${\aleph }_2$ is not ${\mathbb{D}}_{\pm }$-connected. Then, there are at least two vertices $a^{\prime },b^{\prime }\in {\mathbb{D}}_{\pm }\left({\aleph }_2\right)$ such that there is no path between them in $Un\left({\aleph }_2\right)$. Since $\chi$ is bijective, then there are $a,b\in \wp \left({\aleph }_1\right)$ such that $a^{\prime }=\chi \left(a\right)$ and $b^{\prime }=\chi \left(b\right)$. Since $a^{\prime },b^{\prime }\in {\mathbb{D}}_{\pm }\left({\aleph }_2\right)$, then $a,b\in {\mathbb{D}}_{\pm }\left({\aleph }_1\right)$. Since $a^{\prime }$ and $b^{\prime }$ are not joining by the path in $Un\left({\aleph }_2\right)$, then a and b are also not joining by the path in $Un\left({\aleph }_1\right)$. Hence, ${\left({\aleph }_1\right)}^{\pm }$ is not weakly connected, that is, ${\aleph }_1$ is not ${\mathbb{D}}_{\pm }$-connected and is a contradiction. Therefore, ${\aleph }_1$ is ${\mathbb{D}}_{\pm }$-connected. □

Theorem 14.

${\mathbb{D}}_{\pm }$-discrete is a topological property in class of the LS-directed graphs without isolated vertices.

Proof. 

Let ${\aleph }_1=(\wp \left({\aleph }_1\right),\eta \left({\aleph }_1\right))$ and ${\aleph }_2=(\wp \left({\aleph }_2\right),\eta \left({\aleph }_2\right))$ be two LS-directed graphs without isolated vertices. Let $(\wp \left({\aleph }_1\right),T_{\mathcal{NP}\left({\aleph }_1\right)})$ be ${\mathbb{D}}_{\pm }$-discrete, and let there be a homeomorphism $\gamma :\wp \left({\aleph }_1\right)\to \wp \left({\aleph }_2\right)$. We will prove that $(\wp \left({\aleph }_2\right),T_{\mathcal{NP}\left({\aleph }_2\right)})$ is ${\mathbb{D}}_{\pm }$-discrete. Let $a^{\prime }\in {\mathbb{D}}_{\pm }\left({\aleph }_2\right)$ be arbitrary. Since $\gamma$ is bijective, then there is $a\in {\mathbb{D}}_{\pm }\left({\aleph }_1\right)$ such that $a^{\prime }=\gamma \left(a\right)$. Since $(\wp \left({\aleph }_1\right),T_{\mathcal{NP}\left({\aleph }_1\right)})$ is ${\mathbb{D}}_{\pm }$-discrete, then $\left\{a\right\}$ is an open set in a relative topological space $({\mathbb{D}}_{\pm }\left({\aleph }_1\right),T_{\mathcal{NP}\left({\aleph }_1\right)}{|}_{{\mathbb{D}}_{\pm }\left({\aleph }_1\right)})$. Since $\gamma$ is an open function and bijective, then $\gamma \left(\left\{a\right\}\right)=\left\{\gamma \left(a\right)\right\}=\left\{a^{\prime }\right\}$ is an open set in a relative topological space $({\mathbb{D}}_{\pm }\left({\aleph }_2\right),T_{\mathcal{NP}\left({\aleph }_2\right)}{|}_{{\mathbb{D}}_{\pm }\left({\aleph }_2\right)})$, that is $(\wp \left({\aleph }_2\right),T_{\mathcal{NP}\left({\aleph }_2\right)})$ is ${\mathbb{D}}_{\pm }$-discrete. □

5. On the Nervous System of the Human Body

Recall [18], where it was shown that the nervous system involves a complex network of nerves, the spinal cord and the brain. This system plays important role in sending messages back and forth between the body and the brain. We know that all the body’s functions are controlled by the brain. From the brain down through the back runs the spinal cord, which includes threadlike nerves that branch out to every body part. This network of nerves sends messages back and forth from the brain to different body parts (see Figure 3). In this section, we show the ${\mathbb{D}}_{\pm }$-connectedness and ${\mathbb{D}}_{\pm }$-discrete properties of the corresponding graphs for the diagrams of networks in the nervous system of the human body, such as diagrams of the sensory neuron cells [17] and models of two distinct nicotinic receptor types based on the second messenger signal [18].

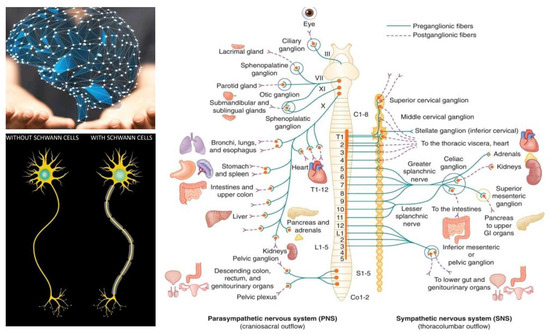
Figure 3. Diagram of the nervous system and nero cells.

Firstly, we studied the above diagram, which presents the vestibular sensory and somatosensory pathways with their integration into the brain and spinal cord, as shown in Figure 4a [17]. Note that the graph $\aleph =(\wp (\aleph ),\eta (\aleph \left)\right)$ in Figure 4b is an LS-directed graph and approximates the vestibular sensory and somatosensory pathways with their integration into the brain and spinal cord, which has the vertices set

$$\wp (\aleph )=\{b,v_{12345},s_{123},t_{123},m_{12345},c_{12}\}$$

which has 19 vertices. The graph ℵ is connected but not a ${\mathbb{D}}_{\pm }$-connected graph since the subgraph ${\aleph }^{{\mathbb{D}}_{\pm }}$ is not weakly connected with the vertex set $\wp \left({\aleph }^{{\mathbb{D}}_{\pm }}\right)=\wp (\aleph )\backslash \{v_{1345},t_2\}$. The out mondirected topological space $(\wp (\aleph ),T_{\mathcal{NP}(\aleph )})$ of ℵ has the sub-basis $\mathcal{NP}(\aleph )$ with the m-negative open neighborhoods

$${\mathbb{N}}^e\left(b\right)=\{t_2,v_{345},m_{1234},c_{12}\},{\mathbb{N}}^e\left(v_1\right)=\{t_{23},s_{23},m_5\},$$

$${\mathbb{N}}^e\left(c_1\right)={\mathbb{N}}^e\left(c_2\right)=\{b,t_{23},s_{23},m_5\},{\mathbb{N}}^e\left(s_1\right)={\mathbb{N}}^e\left(t_1\right)=\{t_2,v_{345},m_{1234}\},$$

$${\mathbb{N}}^e\left(s_2\right)=\{t_2,v_{1345},m_{1234},c_{12}\},{\mathbb{N}}^e\left(s_3\right)={\mathbb{N}}^e\left(t_3\right)={\mathbb{N}}^e\left(m_5\right)=\{c_{12},v_{1345},m_{1234}\},$$

$${\mathbb{N}}^e\left(t_2\right)=\{b,t_1,s_1,c_{12},v_{1345},m_{1234}\},{\mathbb{N}}^e\left(v_2\right)=\{v_{45},m_{1234}\},{\mathbb{N}}^e\left(v_3\right)=\{t_2,m_{1234}\},$$

$${\mathbb{N}}^e\left(v_4\right)={\mathbb{N}}^e\left(v_5\right)=\{b,t_{123},s_{123},v_2,m_5\},{\mathbb{N}}^e\left(m_k\right)=\{b,t_{123},s_{123},v_{23},m_5\}$$

for all $k=1,2,3,4.$ The smallest openings of all the vertices were singles except ${\mathbb{M}}^{-}\left(b\right)=\{b,t_2\}$, ${\mathbb{M}}^{-}\left(s_2\right)=\{s_2,t_2\}$ and ${\mathbb{M}}^{-}\left(t_1\right)=\{t_1,t_2\}$. As such, the out mondirected topological space $(\wp (\aleph ),T_{\mathcal{NP}(\aleph )})$ of ℵ was not discrete nor ${\mathbb{D}}_{\pm }$-discrete, and it was disconnected by two disjoint open sets $\{b,s_2,t_1,t_2\}$ and $\wp (\aleph )\backslash \{b,s_2,t_1,t_2\}$.

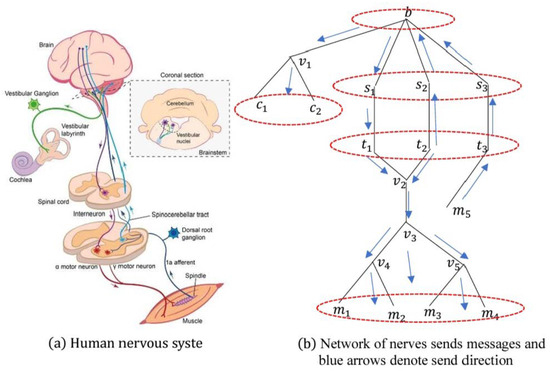
Figure 4. The somatosensory and vestibular sensory pathways.

For a more special study, we will show the previous properties of the corresponding graph of the diagram that presents the sensory neurons in the nervous system of a human body. Recall [17], where it was shown that neurons are the cells that make up the nervous system and the brain. They are the main units that send and receive signals, which allow us to feel the external world, move our muscles, form memories, think, and much more. The sensory neuron is a nerve cell that is activated by sensory input from the environment and has four forms, which are multipolar, pseudounipolar, bipolar, and unipolar, as presented in Figure 5a. For the multipolar sensory neuron cell, the graph ${\aleph }_1=(\wp \left({\aleph }_1\right),\eta \left({\aleph }_1\right))$ in Figure 5b is a LS-directed graph and presents the multipolar sensory neuron cell with the vertex set

$$\wp \left({\aleph }_1\right)=\{d_{12\cdots 10},n_{12345},n,s,s_{12},a_{1234}\}$$

which has 23 vertices. The graph ${\aleph }_1$ is a connected and not ${\mathbb{D}}_{\pm }$-connected graph since the subgraph ${\aleph }_1^{{\mathbb{D}}_{\pm }}$ is not weakly connected with the vertex set $\wp \left({\aleph }_1^{{\mathbb{D}}_{\pm }}\right)=\wp \left({\aleph }_1\right)\backslash \{s,s_{12}\}$. The out mondirected topological space $(\wp \left({\aleph }_1\right),T_{\mathcal{NP}\left({\aleph }_1\right)})$ of ${\aleph }_1$ has the sub-basis $\mathcal{NP}\left({\aleph }_1\right)$ with the m-negative open neighborhoods

$${\mathbb{N}}^e\left(n\right)={\mathbb{N}}^e\left(n_k\right)={\mathbb{N}}^e\left(d_j\right)=\{s,s_{12},a_{1234}\},{\mathbb{N}}^e\left(s\right)=\left\{a_{1234}\right\},$$

$${\mathbb{N}}^e\left(s_1\right)={\mathbb{N}}^e\left(s_2\right)=\wp (\aleph )\backslash \{s,s_{12},a_{1234}\},{\mathbb{N}}^e\left(a_r\right)=\wp (\aleph )\backslash \{s_{12},a_{1234}\}$$

for all $k=1,2,3,4,5$, $r=1,2,3,4$ and $j=1,2,\cdots 10.$ The smallest openings of all the vertices were singles except ${\mathbb{M}}^{-}\left(a_r\right)=\{s,a_r\}$ for all $r=1,2,3,4$. As such, the out mondirected topological space $(\wp \left({\aleph }_1\right),T_{\mathcal{NP}\left({\aleph }_1\right)})$ of ${\aleph }_1$ is not discrete nor ${\mathbb{D}}_{\pm }$-discrete, and it is disconnected by two disjoint open sets, such as, for example, $\left\{s_1\right\}$ and $\wp \left({\aleph }_1\right)\backslash \left\{s_1\right\}$. The study of the pseudounipolar sensory neuron cell was conducted in a similar fashion to the study of the multipolar sensory neuron cell. For the bipolar sensory neuron cell, the graph ${\aleph }_2=(\wp \left({\aleph }_2\right),\eta \left({\aleph }_2\right))$ shown in Figure 6a, which is an LS-directed graph, was constructed, and it presents the multipolar sensory neuron cell with the vertex set $\wp \left({\aleph }_2\right)=\{s,v,n_{12},d_{123456}\}$, which has 10 vertices. The graph ${\aleph }_2$ is a connected and ${\mathbb{D}}_{\pm }$-connected graph since the subgraph ${\aleph }_2^{{\mathbb{D}}_{\pm }}$ is weakly connected with the vertex set $\wp \left({\aleph }_2^{{\mathbb{D}}_{\pm }}\right)=\wp \left({\aleph }_2\right)$. The out mondirected topological space $(\wp \left({\aleph }_2\right),T_{\mathcal{NP}\left({\aleph }_2\right)})$ of ${\aleph }_2$ has the sub-basis $\mathcal{NP}\left({\aleph }_2\right)$ with the single m-negative open neighborhoods of all the vertices; as such, the smallest opening of all the vertices were singles. The out mondirected topological space $(\wp \left({\aleph }_2\right),T_{\mathcal{NP}\left({\aleph }_2\right)})$ of ${\aleph }_2$ is discrete and ${\mathbb{D}}_{\pm }$-discrete, and so it is disconnected space. For the unipolar sensory neuron cell, the graph ${\aleph }_3=(\wp \left({\aleph }_3\right),\eta \left({\aleph }_3\right))$ shown in Figure 6b, which is an LS-directed graph, was constructed, and it presents the unipolar sensory neuron cell with the vertex set $\wp \left({\aleph }_3\right)=\{c,v,n_{12},d_{123456}\}$, which has 10 vertices. The graph ${\aleph }_3$ is a connected but not ${\mathbb{D}}_{\pm }$-connected graph since the subgraph ${\aleph }_3^{{\mathbb{D}}_{\pm }}$ is not weakly connected with the vertex set $\wp \left({\aleph }_3^{{\mathbb{D}}_{\pm }}\right)=\wp \left({\aleph }_3\right)\backslash \{v,n_{12}\}$. The out mondirected topological space $(\wp \left({\aleph }_3\right),T_{\mathcal{NP}\left({\aleph }_3\right)})$ of ${\aleph }_3$ has the sub-basis $\mathcal{NP}\left({\aleph }_3\right)$ with the m-negative open neighborhoods

$${\mathbb{N}}^e\left(c\right)=\{n_{12},d_{123456}\},{\mathbb{N}}^e\left(v\right)=\left\{d_{123456}\right\},{\mathbb{N}}^e\left(n_1\right)={\mathbb{N}}^e\left(n_2\right)=\left\{c\right\}$$

and ${\mathbb{N}}^e\left(d_k\right)=\{c,v\}$ for all $k=1,2,3,4,5,6$. The smallest openings of all the vertices were singles except ${\mathbb{M}}^{-}\left(n_1\right)=\{c,n_1\}$ and ${\mathbb{M}}^{-}\left(n_2\right)=\{c,n_2\}$. As such, the out mondirected topological space $(\wp \left({\aleph }_3\right),T_{\mathcal{NP}\left({\aleph }_3\right)})$ of ${\aleph }_3$ is not discrete nor ${\mathbb{D}}_{\pm }$-discrete, and it is disconnected by two disjoint open sets, such as, for example, $\{n_{12},c\}$ and $\wp \left({\aleph }_3\right)\backslash \{n_{12},c\}$.

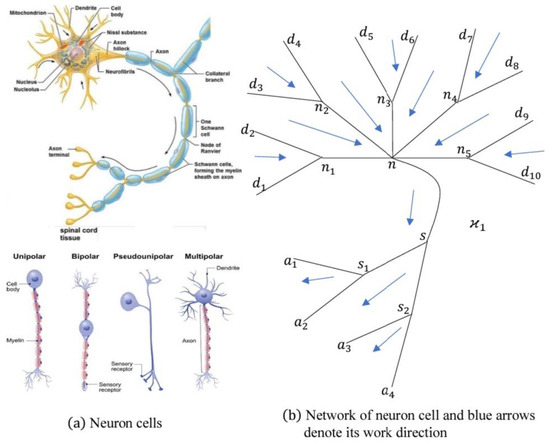
Figure 5. The sensory neuron cells: multipolar and pseudounipolar.

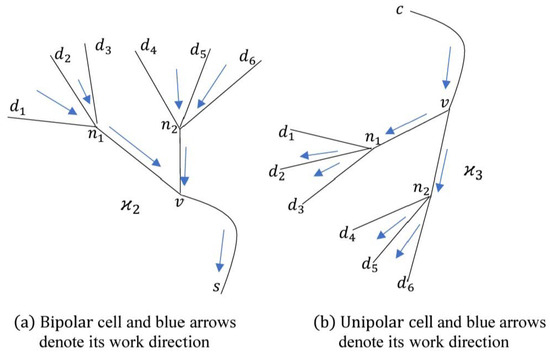
Figure 6. The sensory neuron cells: bipolar and unipolar.

Finally, we showed the connectedness, ${\mathbb{D}}_{\pm }$-connectedness and ${\mathbb{D}}_{\pm }$-discrete properties of the corresponding graphs for the diagrams of two models of two distinct nicotinic receptor types based on the second messenger signal, classification of cholinergic receptors and the classification of adrenergic receptors, which are introduced by [18]. For the model of the classification of cholinergic receptors, as shown in Figure 7a, the corresponding graph ${\aleph }_c=(\wp \left({\aleph }_c\right),\eta \left({\aleph }_c\right))$ is connected with the vertex set

$$\wp \left({\aleph }_c\right)=\{c,n,m,n_{123},m_{12345},o,g,g^{\prime },p,a\}$$

which has 16 vertices and is shown in Figure 7b. Additionally, it is not a ${\mathbb{D}}_{\pm }$-connected graph since the subgraph ${\aleph }_c^{{\mathbb{D}}_{\pm }}$ is not weakly connected with the vertex set $\wp \left({\aleph }_c^{{\mathbb{D}}_{\pm }}\right)=\wp \left({\aleph }_c\right)\backslash \{n,m,c\}$. The out mondirected topological space $(\wp \left({\aleph }_c\right),T_{\mathcal{NP}\left({\aleph }_c\right)})$ of ${\aleph }_c$ has the sub-basis $\mathcal{NP}\left({\aleph }_c\right)$ with the m-negative open neighborhoods

$${\mathbb{N}}^e\left(c\right)=\{o,g,g^{\prime },a,p,n_{123},m_{12345}\},{\mathbb{N}}^e\left(n\right)=\left\{o\right\},{\mathbb{N}}^e\left(n_k\right)=\left\{c\right\},$$

$${\mathbb{N}}^e\left(m\right)=\{g,g^{\prime },a,p\},{\mathbb{N}}^e\left(m_j\right)=\left\{c\right\},{\mathbb{N}}^e\left(o\right)=\{n,c\},{\mathbb{N}}^e\left(g\right)={\mathbb{N}}^e\left(g^{\prime }\right)=\{m,c\}$$

and ${\mathbb{N}}^e\left(p\right)={\mathbb{N}}^e\left(a\right)=\{m,c\}$ for all $k=1,2,3$, $j=1,2,3,4,5.$ The smallest openings of all the vertices are singles except ${\mathbb{M}}^{-}\left(n\right)=\{o,n\}$ and ${\mathbb{M}}^{-}\left(m\right)=\{m,c\}$. As such, the out mondirected topological space $(\wp \left({\aleph }_c\right),T_{\mathcal{NP}\left({\aleph }_c\right)})$ of ${\aleph }_c$ is not discrete nor ${\mathbb{D}}_{\pm }$-discrete, and it is disconnected by two disjoint open sets $\{o,n\}$ and $\wp \left({\aleph }_c\right)\backslash \{o,n\}$. For the model of the classification of adrenergic receptors shown in Figure 8a, a corresponding graph ${\aleph }_a=(\wp \left({\aleph }_a\right),\eta \left({\aleph }_a\right))$ was connected, as shown in Figure 8b, with the vertex set

$$\wp \left({\aleph }_a\right)=\{o,a,b,a_{12},b_{123},a_1^{\prime },a_1^{″},a_1^{‴},a_2^{\prime },a_2^{″},a_2^{‴},b_1^{\prime },b_2^{\prime },g_{123}\}$$

which has 19 vertices and is not a ${\mathbb{D}}_{\pm }$-connected graph since the subgraph ${\aleph }_a^{{\mathbb{D}}_{\pm }}$ is not weakly connected with the vertex set $\wp \left({\aleph }_a^{{\mathbb{D}}_{\pm }}\right)=\wp \left({\aleph }_a\right)\backslash \{v_{1345},t_2\}$. The smallest openings of all the vertices are singles except ${\mathbb{M}}^{-}\left(a_1\right)=\{a_1,a,g_1\}$, ${\mathbb{M}}^{-}\left(a_2\right)=\{a_2,a,g_2\}$, ${\mathbb{M}}^{-}\left(b_1\right)=\{b_1,a\}$, ${\mathbb{M}}^{-}\left(b_2\right)=\{b_2,a\}$ and ${\mathbb{M}}^{-}\left(b_3\right)=\{b_3,a\}$. As such, the out mondirected topological space $(\wp \left({\aleph }_a\right),T_{\mathcal{NP}\left({\aleph }_a\right)})$ of ${\aleph }_a$ is not discrete nor ${\mathbb{D}}_{\pm }$-discrete, and it is disconnected by two disjoint open sets $\{a_{12},g_{12},b_{123},a\}$ and $\wp \left({\aleph }_a\right)\backslash \{a_{12},g_{12},b_{123},a\}$.

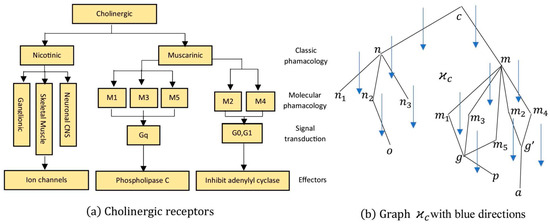
Figure 7. The classification of cholinergic receptors with their networks.

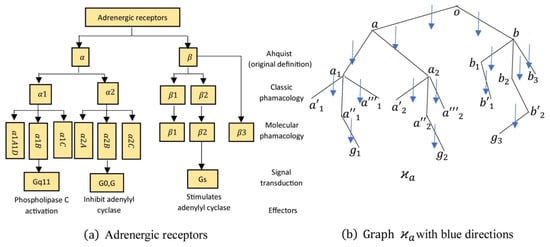
Figure 8. The classification of adrenergic receptors with their networks.

6. Conclusions

As we know that monophonic paths are special cases when it comes to paths, this special case was used to define the notion of the m-negative paths, which we were able to, in this work, construct, i.e., the notion of out mondirected topological space in the theory of directed graphs. We showed the relationship between the graphic isomorphic relation for the directed simple graphs and the homeomorphic property of the out mondirected topologies. Next, we used this relationship together with the connectedness and discrete properties to introduce the notions of ${\mathbb{D}}_{\pm }$-connectedness and ${\mathbb{D}}_{\pm }$-discrete. In using the last properties, we showed the connectedness and discreteness in the representation theory of the diagrams, such as diagrams of sensory neuron cells, of the networks introduced in [17] for the nervous system of the human body. Furthermore, the connectedness and discrete properties of the models of the two distinct nicotinic receptor types based on the second messenger signal [18], the classification of cholinergic receptors and classification of adrenergic receptors were studied. For future research, we suggest constructing a neighborhood system using monophonic eccentric vertices to study the connectedness and discrete properties in the representation theory of diagrams of the sensory neuron cells in the human body.