Monotone Positive Solutions for Nonlinear Fractional Differential Equations with a Disturbance Parameter on the Infinite Interval

Abstract

This paper is concerned with the existence and multiplicity of monotone positive solutions for a class of nonlinear fractional differential equation with a disturbance parameter in the integral boundary conditions on the infinite interval. By using Guo–Krasnosel’skii fixed-point theorem and the analytic technique, we divide the range of parameter for the existence of at least two, one and no positive solutions for the problem. In the end, an example is given to illustrate our main results.

1. Introduction and Preliminaries

In recent ten years, fractional differential equations have been extensively studied, and significant achievements have been made in both theory and application; see [1,2,3,4,5,6,7,8,9,10,11,12] and the references therein.

Boundary value problems on the infinite interval arise naturally in the study of radially symmetric solutions of nonlinear elliptic equations and various physical phenomena, see [13]. So, the study of fractional boundary value problems on the infinite interval has been paid much attention, there appear some excellent results; see, for instance [14,15,16,17,18,19,20,21,22,23,24,25,26] and the references therein. On the other hand, when we apply the methods of the differential equations to solve actual problems, the disturbance is always inevitable and has great influence on the existence of solutions. So, more and more emphases have been put on the research of fractional boundary value problems with disturbance parameters; see [27,28,29,30,31,32,33] and the references therein. Many of these works focused on fractional boundary value problems on the finite interval $[0,1]$ with parameters [27,28,29,30,31], for example, authors of [29] investigated the impact of the disturbance parameters on the existence of positive solutions for the following fractional boundary value problem

$$\left\{\begin{array}{c}{D}_{0^{+}}^{\alpha }x\left(t\right)+f(t,x\left(t\right))=0,a.e.t\in (0,1),\hfill \\ \underset{t\to 0^{+}}{lim}{t}^{2-\alpha }x\left(t\right)=a,x\left(1\right)=b,\hfill \end{array}\right.$$

where $D_{0^{+}}^{\alpha }$ is the Riemann–Liouville fractional derivative, $1<\alpha <2$, disturbance parameters $a\ge 0,b\ge 0$, $f:R^{+}\times R^{+}\to R^{+}$ is an $L^1$-Carathéodory function, and monotone increasing with respect to x. The main tools used in the paper are the method of upper and lower solutions and the Schauder fixed-point theorem.

However, there are a few papers to study the impact of disturbance parameters on the existence of positive solutions for the fractional boundary value problems on the infinite interval [32,33]. In [32], authors considered the following eigenvalue problem with a disturbance parameter on the half-line

$$\left\{\begin{array}{c}{D}_{0^{+}}^{\alpha }x\left(t\right)+\mu f(t,x\left(t\right))=0,t\in (0,+\infty ),\hfill \\ x\left(0\right)=0,x^{\prime }\left(0\right)=0,\hfill \\ D_{0^{+}}^{\alpha -1}x(+\infty )=\beta {\int }_0^{\eta }x\left(s\right)ds+\lambda ,\hfill \end{array}\right.$$

where $D_{0^{+}}^{\alpha }$ is the Riemann–Liouville fractional derivative of order $\alpha$, $2<\alpha <3$, $\beta ,\eta >0$ and $\mathrm{\Gamma }(\alpha +1)>\beta {\eta }^{\alpha }$; $\mu ,\lambda \ge 0$ are two parameters; $f(t,x)=f_1(t,x)+q\left(t\right)f_2\left(x\right)$, $f_1:R^{+}\times R^{+}\to R^{+}$ is monotone in x, $f_2:R^{+}\to R^{+}$ is monotone in x. They discussed the existence and the dependence properties on these two parameters of the unique positive solution by means of the monotone operator theory and analytical technique.

Li et al. [33] considered the following fractional differential equations on the infinite interval

$$\left\{\begin{array}{c}{D}_{0^{+}}^{\alpha }x\left(t\right)+q\left(t\right)f(t,x\left(t\right))=0,t\in (0,+\infty ),\hfill \\ x\left(0\right)=D_{0^{+}}^{\alpha -1}x(+\infty )=0,\hfill \\ D_{0^{+}}^{\alpha -2}x\left(0\right)={\displaystyle \sum _{i=1}^{+\infty }}g\left({\xi }_i\right)D_{0^{+}}^{\alpha -1}x\left({\xi }_i\right)+\lambda ,\hfill \end{array}\right.$$

where $D_{0^{+}}^{\alpha }$ is the Riemann–Liouville fractional derivative, $2<\alpha <3$, $0<{\xi }_1<{\xi }_2<\cdots <{\xi }_i<\cdots <+\infty ,$$g\left({\xi }_i\right)\ge 0$ and ${\displaystyle \sum _{i=1}^{+\infty }}g\left({\xi }_i\right)$ is convergent. $f:R^{+}\times R^{+}\to R^{+}$ is an $L^1$-Carathéodory function, the disturbance parameter $\lambda \in R^{+}$ and $R^{+}=[0,+\infty )$. When $f(t,x)$ is increasing in x, authors investigated the existence, multiplicity and nonexistence of positive solutions and the impact of the disturbance parameters on the existence of positive solutions for the problem by using the method of upper and lower solutions, fixed-point index theory and Schauder’s fixed-point theorems.

We note that the nonlinearity $f(t,x)$ in fractional differential equations in [29,32,33] were required to be monotone in x. However, as we know, nonlinearities in many nonlinear problems do not have monotonicity. Therefore, we would like to know how disturbance parameters in the boundary conditions affect the number of solutions for a boundary value problem, especially one on the infinite interval, if its nonlinearity $f(t,x)$ is not monotone in x, for example,

$$f(t,x)=\frac{4(1+\frac{1}{4}sinx)x^{\tau }}{3{(1+t^{\alpha -1})}^{\tau }},t,x\in [0,+\infty ),\tau >0,$$

see BVP (18) in Section 4. Since $sinx$ is not monotone in $x,$ it is clear that $f(t,x)$ is not monotone in x.

Motivated by this, this paper will study the following fractional integral boundary value problem (BVP) with a disturbance parameter on the infinite interval

$$\left\{\begin{array}{c}{D}_{0^{+}}^{\alpha }x\left(t\right)+q\left(t\right)f(t,x\left(t\right))=0,t\in (0,+\infty ),\hfill \\ x\left(0\right)=0,x^{\prime }\left(0\right)=0,\hfill \\ D_{0^{+}}^{\alpha -1}x(+\infty )=\beta {\int }_0^{\eta }x\left(s\right)ds+\lambda ,\hfill \end{array}\right.$$

(1)

where $D_{0^{+}}^{\alpha }$ is the Riemann–Liouville fractional derivative of order $\alpha$, $2<\alpha <3$, $\beta ,\eta >0$ and $\lambda \ge 0$.

Here, the nonlinearity $f(t,x)$ in our BVP (1) is not monotone in x. The purpose of this paper is to investigate the impact of the disturbance parameter $\lambda$ on the existence and number of positive solutions for BVP (1) without monotonicity for the nonlinearity. Our research is based on the Guo–Krasnosel’skii fixed-point theorem, properties of the Green function and determination of cones.

Throughout this paper, the following conditions always are assumed:

(L1)

$\mathrm{\Gamma }(\alpha +1)>\beta {\eta }^{\alpha }$;

(L2)

$q\in L[0,+\infty )$ is a nonnegative function;

(L3)

$f\in C\left([0,+\infty )\times [0,+\infty ),[0,+\infty )\right)$ and for every $r>0$ there exists ${\phi }_r\left(t\right)\ge 0$ with $q{\phi }_r\in L[0,+\infty )$ such that

$$f(t,(1+t^{\alpha -1})x)\le {\phi }_r\left(t\right),x\in [0,r],t\in [0,+\infty ).$$

Remark 1.

The condition (L1) means that $\mathrm{\Gamma }(\alpha +1)-\beta {\eta }^{\alpha }>0$, which leads to $\rho =\mathrm{\Gamma }\left(\alpha \right)(\mathrm{\Gamma }(\alpha +1)-\beta {\eta }^{\alpha })>0$. It is important for obtaining equivalent integral equations and discussing the properties of Green’s function. The conditions (L1) and (L3) guarantee that $q\left(t\right)f(t,x(t\left)\right)$ is non-negative and integrable on $[0,+\infty )$ for each non-negative function $x\in C[0,+\infty )$ with $\underset{t\in [0,+\infty )}{sup}\frac{\left|x\right(t\left)\right|}{1+t^{\alpha -1}}<+\infty .$

The positive solution $x\left(t\right)$ of BVP (1) means that the solution $x\left(t\right)$ satisfies $x\left(t\right)\ge 0$ for $x\in [0,+\infty )$ and $x\left(t\right)>0$ for $t\in (0,+\infty )$.

For convenience of readers, we first present some basic notations and results. We suggest that one refers to [1,2] for details.

Definition 1.

Let $x:(0,+\infty )\to R$ be a function and $p>0$. The Riemann–Liouville fractional integral of order p of x is defined by

$$I_{0^{+}}^{p}x\left(t\right)=\frac{1}{\mathrm{\Gamma }\left(p\right)}{\int }_0^t{(t-s)}^{p-1}x\left(s\right)ds,t\in (0,+\infty ),$$

provided the integral in the right side exists for each $t\in (0,+\infty )$. The Riemann–Liouville fractional derivative of order p for a continuous function $x:(0,+\infty )\to R$ is defined by

$$D_{0^{+}}^{p}x\left(t\right)=\frac{1}{\mathrm{\Gamma }(n-p)}{\left(\frac{d}{dt}\right)}^n{\int }_0^t{(t-s)}^{n-p-1}x\left(s\right)ds,t\in (0,+\infty ),$$

provided the right side is pointwise defined on $(0,+\infty )$, where n is the smallest integer greater than or equal to p, and $\mathrm{\Gamma }\left(p\right)$ is the gamma function.

Lemma 1

([34] Guo–Krasnosel’skii fixed-point theorem). Let E be a real Banach space, and P be a cone in E. Let ${\mathrm{\Omega }}_1$, ${\mathrm{\Omega }}_2$ be bounded open balls in E with $\theta \in {\mathrm{\Omega }}_1,{\overline{\mathrm{\Omega }}}_1\subset {\mathrm{\Omega }}_2$. Assume that $T:P\cap ({\overline{\mathrm{\Omega }}}_2\setminus {\mathrm{\Omega }}_1)\to P$ is a completely continuous operator such that

(i)

$\parallel Tx\parallel \le \parallel x\parallel$ for $x\in P\cap \partial {\mathrm{\Omega }}_1,$ and $\parallel Tx\parallel \ge \parallel x\parallel$ for $x\in P\cap \partial {\mathrm{\Omega }}_2,$

or

(ii)

$\parallel Tx\parallel \ge \parallel x\parallel$ for $x\in P\cap \partial {\mathrm{\Omega }}_1,$ and $\parallel Tx\parallel \le \parallel x\parallel$ for $x\in P\cap \partial {\mathrm{\Omega }}_2.$

Then T has a fixed point in $P\cap ({\overline{\mathrm{\Omega }}}_2\setminus {\mathrm{\Omega }}_1)$.

Remark 2.

The Guo–Krasnosel’skii fixed-point theorem exhibits a cone expansion and compression of norm type for completely continuous operators on a real Banach space. It has been extensively applied to investigate the existence and multiplicity of positive solutions for nonlinear boundary value problems, see [9,15,19,25,28].

2. Properties of Green’s Function and Equivalent Operator Equation

In this section, we will present the Green’s function and its properties for the associated linear fractional boundary value problem, moreover present the operator equation which is equivalent to BVP (1). This is important for our research.

For $y\in C[0,+\infty )\cap L[0,+\infty )$, consider the linear fractional boundary value problem

$$\left\{\begin{array}{c}{D}_{0^{+}}^{\alpha }x\left(t\right)+y\left(t\right)=0,0<t<+\infty ,\hfill \\ x\left(0\right)=0,x^{\prime }\left(0\right)=0,\hfill \\ D_{0^{+}}^{\alpha -1}x(+\infty )=\beta {\int }_0^{\eta }x\left(s\right)ds+\lambda ,\hfill \end{array}\right.$$

(2)

where $2<\alpha <3$, $\beta ,\eta >0$ and $\lambda \ge 0$.

Lemma 2.

Suppose that $y\in C[0,+\infty )\cap L[0,+\infty )$ and (L1) holds. Then BVP (2) has a unique solution

$$x\left(t\right)={\int }_0^{+\infty }G(t,s)y\left(s\right)ds+\frac{\mathrm{\Gamma }(\alpha +1)\lambda }{\rho }{t}^{\alpha -1},t\in [0,+\infty ),$$

(3)

where

$$G(t,s)=\frac{1}{\rho }\left\{\begin{array}{c}\left(\mathrm{\Gamma }(\alpha +1)-\beta {(\eta -s)}^{\alpha }\right)t^{\alpha -1}-\left(\mathrm{\Gamma }(\alpha +1)-\beta {\eta }^{\alpha }\right){(t-s)}^{\alpha -1},s\le t,s\le \eta ,\hfill \\ \left(\mathrm{\Gamma }(\alpha +1)-\beta {(\eta -s)}^{\alpha }\right)t^{\alpha -1},t\le s\le \eta ,\hfill \\ \mathrm{\Gamma }(\alpha +1)t^{\alpha -1}-\left(\mathrm{\Gamma }(\alpha +1)-\beta {\eta }^{\alpha }\right){(t-s)}^{\alpha -1},\eta \le s\le t,\hfill \\ \mathrm{\Gamma }(\alpha +1)t^{\alpha -1},\eta \le s,t\le s,\hfill \end{array}\right.$$

(4)

where $\rho =\mathrm{\Gamma }\left(\alpha \right)\left(\mathrm{\Gamma }(\alpha +1)-\beta {\eta }^{\alpha }\right).$

Proof. 

It is evident that the equation $D_{0^{+}}^{\alpha }x\left(t\right)+y\left(t\right)=0$ is equivalent to the integral equation

$$\begin{array}{c}\hfill x\left(t\right)=-\frac{1}{\mathrm{\Gamma }\left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}y\left(s\right)ds+c_1{t}^{\alpha -1}+c_2{t}^{\alpha -2}+c_3{t}^{\alpha -3},\end{array}$$

where $c_1,c_2,c_3\in R$ are some constants. Boundary conditions $x\left(0\right)=0$ and $x^{\prime }\left(0\right)=0$ imply that $c_3=c_2=0$. Thus,

$$\begin{array}{ccc}& & x\left(t\right)=-\frac{1}{\mathrm{\Gamma }\left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}y\left(s\right)ds+c_1{t}^{\alpha -1},t\in [0,+\infty ),\hfill \\ & & D_{0^{+}}^{\alpha -1}x\left(t\right)=-{\int }_0^{t}y\left(s\right)ds+c_1\mathrm{\Gamma }\left(\alpha \right),t\in [0,+\infty ).\hfill \end{array}$$

These, together with the boundary condition $D_{0^{+}}^{\alpha -1}x(+\infty )=\beta {\int }_0^{\eta }x\left(s\right)ds+\lambda$ and Remark 1, give

$$\begin{array}{c}\hfill c_1=\frac{1}{\mathrm{\Gamma }(\alpha +1)-\beta {\eta }^{\alpha }}(\alpha {\int }_0^{+\infty }y\left(s\right)ds-\frac{\beta }{\mathrm{\Gamma }\left(\alpha \right)}{\int }_0^{\eta }{(\eta -s)}^{\alpha }y\left(s\right)ds+\alpha \lambda ).\end{array}$$

This means that

$$x\left(t\right)={\int }_0^{+\infty }G(t,s)y\left(s\right)ds+\frac{\mathrm{\Gamma }(\alpha +1)\lambda }{\rho }{t}^{\alpha -1},t\in [0,+\infty ).$$

The proof is complete. □

Lemma 3.

If (L1) holds, then the function $G(t,s)$ defined by (4) satisfies

(i)

$G(t,s)$ is continuous on $[0,+\infty )\times [0,+\infty )$;

(ii)

for any given $s\in [0,+\infty )$, $G(t,s)$ is increasing with respect to t for $[0,+\infty )$;

(iii)

$0\le G(t,s)\le \frac{\mathrm{\Gamma }(\alpha +1)}{\rho }{t}^{\alpha -1},t,s\in [0,+\infty )$;

(iv)

$\frac{\beta {\eta }^{\alpha -1}}{\rho }{t}^{\alpha -1}s\le G(t,s)\le \frac{\alpha \mathrm{\Gamma }(\alpha +1)}{\rho \eta }\left\{\begin{array}{c}{\eta }^{\alpha -1}s,s\le t\le \eta ort\le s\le \eta ,\hfill \\ t^{\alpha -1}s,s\le \eta \le t.\hfill \end{array}\right.$

$\frac{\beta {\eta }^{\alpha }}{\rho }{t}^{\alpha -1}\le G(t,s)\le \frac{\mathrm{\Gamma }(\alpha +1)}{\rho }{t}^{\alpha -1},\eta \le s\le tors\ge max\{\eta ,t\}.$

Proof. 

From (L1) and the expression (4) of $G(t,s)$, it is easy to verify conclusions (i), (ii) and (iii). Next to show the conclusion (iv). There are four cases to be discussed.

Case 1. $s\le t$ and $s\le \eta$. By (4) we have

$$\begin{array}{ccc}\hfill \rho G(t,s)& \le & (\alpha -1)(\mathrm{\Gamma }(\alpha +1)-\beta {\eta }^{\alpha })t^{\alpha -2}s+\alpha \beta {\eta }^{\alpha -1}{t}^{\alpha -1}s.\hfill \end{array}$$

In particular, when $s\le t\le \eta$,

$$\begin{array}{ccc}\hfill \rho G(t,s)& \le & (\alpha -1)(\mathrm{\Gamma }(\alpha +1)-\beta {\eta }^{\alpha }){\eta }^{\alpha -2}s+\alpha \beta {\eta }^{2\alpha -2}s\hfill \\ & \le & (\alpha -1)\mathrm{\Gamma }(\alpha +1){\eta }^{\alpha -2}s+\mathrm{\Gamma }(\alpha +1){\eta }^{\alpha -2}s\hfill \\ & =& \alpha \mathrm{\Gamma }(\alpha +1){\eta }^{\alpha -2}s;\hfill \end{array}$$

and when $s\le \eta \le t$,

$$\begin{array}{ccc}\hfill \rho G(t,s)& \le & \left[(\alpha -1)(\mathrm{\Gamma }(\alpha +1)-\beta {\eta }^{\alpha })\frac{1}{\eta }+\alpha \beta {\eta }^{\alpha -1}\right]t^{\alpha -1}s\hfill \\ & \le & \frac{\alpha \mathrm{\Gamma }(\alpha +1)}{\eta }{t}^{\alpha -1}s.\hfill \end{array}$$

On the other hand,

$$\begin{array}{ccc}\hfill \rho G(t,s)& \ge & \left[\mathrm{\Gamma }(\alpha +1)-(\mathrm{\Gamma }(\alpha +1)-\beta {\eta }^{\alpha })-\beta {\eta }^{\alpha }(1-\frac{s}{\eta })\right]t^{\alpha -1}\hfill \\ & =& \beta {\eta }^{\alpha -1}{t}^{\alpha -1}s.\hfill \end{array}$$

Case 2. $t\le s\le \eta$. In this case, we have

$$\begin{array}{ccc}\hfill \rho G(t,s)& \le & (\mathrm{\Gamma }(\alpha +1)-\beta {\eta }^{\alpha })t^{\alpha -2}s+\alpha \beta {\eta }^{\alpha -1}{t}^{\alpha -1}s\hfill \\ & \le & (\mathrm{\Gamma }(\alpha +1)-\beta {\eta }^{\alpha }){\eta }^{\alpha -2}s+\alpha \beta {\eta }^{\alpha -1}{\eta }^{\alpha -1}s\hfill \\ & \le & \alpha \mathrm{\Gamma }(\alpha +1){\eta }^{\alpha -2}s.\hfill \end{array}$$

On the other hand,

$$\begin{array}{ccc}\hfill \rho G(t,s)& \ge & [\mathrm{\Gamma }(\alpha +1)-\beta {\eta }^{\alpha }(1-\frac{s}{\eta })]t^{\alpha -1}\hfill \\ & \ge & \beta {\eta }^{\alpha -1}{t}^{\alpha -1}s.\hfill \end{array}$$

Case 3. $\eta \le s\le t$. It is clear that $\rho G(t,s)\le \mathrm{\Gamma }(\alpha +1)t^{\alpha -1}$ and

$$\begin{array}{ccc}\hfill \rho G(t,s)& \ge & [\mathrm{\Gamma }(\alpha +1)-(\mathrm{\Gamma }(\alpha +1)-\beta {\eta }^{\alpha })]t^{\alpha -1}\hfill \\ & =& \beta {\eta }^{\alpha }{t}^{\alpha -1}.\hfill \end{array}$$

Case 4. $\eta \le s,t\le s$. It is clear that $\beta {\eta }^{\alpha }{t}^{\alpha -1}\le \rho G(t,s)=\mathrm{\Gamma }(\alpha +1)t^{\alpha -1}.$

This ends the proof. □

Set

$$X=\{x\in C[0,+\infty )|\underset{t\in [0,+\infty )}{sup}\frac{\left|x\right(t\left)\right|}{1+t^{\alpha -1}}<+\infty \},$$

then X is a Banach space with the norm ${\parallel x\parallel }_{\infty }=\underset{t\in [0,+\infty )}{sup}\frac{\left|x\right(t\left)\right|}{1+t^{\alpha -1}}$.

Let

$$K=\{x\in X\mid x\left(t\right)\mathrm{is}\mathrm{increasing}\mathrm{in}t\mathrm{and}x\left(t\right)\ge \gamma t^{\alpha -1}\parallel x{\parallel }_{\infty }\mathrm{for}t\in [0,+\infty )\},$$

where

$$\gamma =\frac{\beta {\eta }^{\alpha }min\left\{\eta ,1\right\}}{\mathrm{\Gamma }(\alpha +1)max\left\{\alpha ,\eta \right\}}.$$

Then K is a cone in X.

Lemma 4.

Suppose that $y\in C[0,+\infty )\cap L[0,+\infty )$ and (L1) holds. If $y\left(t\right)\ge 0$ for $t\in [0,+\infty )$, then the unique solution x of BVP (2) belongs to K.

Proof. 

Since $y\left(t\right)\ge 0$ for $t\in [0,+\infty )$, it is obvious by Lemma 3 that the unique solution $x\left(t\right)$ is non-negative continuous and monotone increasing on $[0,+\infty )$. In addition,

$$\begin{array}{ccc}\hfill \underset{t\in [0,+\infty )}{sup}\frac{\left|x\right(t\left)\right|}{1+t^{\alpha -1}}& \le & \frac{\mathrm{\Gamma }(\alpha +1)}{\rho }\left({\int }_0^{+\infty }y\left(s\right)ds+\lambda \right).\hfill \end{array}$$

In order to prove that

$$x\left(t\right)\ge \gamma t^{\alpha -1}{\parallel x\parallel }_{\infty },t\in [0,+\infty ),$$

we consider two cases.

Case 1. $t\le \eta$. By Lemmas 2 and 3, we have

$$\begin{array}{ccc}& & x\left(t\right)={\int }_0^{t}G(t,s)y\left(s\right)ds+{\int }_t^{\eta }G(t,s)y\left(s\right)ds+{\int }_{\eta }^{+\infty }G(t,s)y\left(s\right)ds+\frac{\mathrm{\Gamma }(\alpha +1)\lambda }{\rho }{t}^{\alpha -1}\hfill \\ & & \le \frac{\mathrm{\Gamma }(\alpha +1)}{\rho }\left(\alpha {\eta }^{\alpha -2}{\int }_0^{t}sy\left(s\right)ds+\alpha {\eta }^{\alpha -2}{\int }_t^{\eta }sy\left(s\right)ds+t^{\alpha -1}{\int }_{\eta }^{+\infty }y\left(s\right)ds+\lambda t^{\alpha -1}\right)\hfill \\ & & \le \frac{\mathrm{\Gamma }(\alpha +1)}{\rho \eta }\left(\alpha {\eta }^{\alpha -1}{\int }_0^{\eta }sy\left(s\right)ds+\eta t^{\alpha -1}{\int }_{\eta }^{+\infty }y\left(s\right)ds+\eta \lambda t^{\alpha -1}\right),\hfill \end{array}$$

and

$$\begin{array}{ccc}& & x\left(t\right)\ge \frac{1}{\rho }{t}^{\alpha -1}(\beta {\eta }^{\alpha -1}{\int }_0^{t}sy\left(s\right)ds+\beta {\eta }^{\alpha -1}{\int }_t^{\eta }sy\left(s\right)ds+\beta {\eta }^{\alpha }{\int }_{\eta }^{+\infty }y\left(s\right)ds+\lambda \mathrm{\Gamma }(\alpha +1))\hfill \\ & & \ge \frac{\beta {\eta }^{\alpha -1}}{\rho }{t}^{\alpha -1}({\int }_0^{\eta }sy\left(s\right)ds+\eta {\int }_{\eta }^{+\infty }y\left(s\right)ds+\eta \lambda ).\hfill \end{array}$$

Case 2. $\eta \le t$. Arguing similarly to Case 1, we can obtain that

$$\begin{array}{ccc}& & x\left(t\right)={\int }_0^{\eta }G(t,s)y\left(s\right)ds+{\int }_{\eta }^{t}G(t,s)y\left(s\right)ds+{\int }_t^{+\infty }G(t,s)y\left(s\right)ds+\frac{\mathrm{\Gamma }(\alpha +1)\lambda }{\rho }{t}^{\alpha -1}\hfill \\ & & \le \frac{\mathrm{\Gamma }(\alpha +1)}{\rho \eta }{t}^{\alpha -1}\left(\alpha {\int }_0^{\eta }sy\left(s\right)ds+\eta {\int }_{\eta }^{+\infty }y\left(s\right)ds+\eta \lambda \right),\hfill \end{array}$$

and

$$\begin{array}{ccc}& & x\left(t\right)\ge \frac{1}{\rho }{t}^{\alpha -1}\left(\beta {\eta }^{\alpha -1}{\int }_0^{\eta }sy\left(s\right)ds+\beta {\eta }^{\alpha }{\int }_{\eta }^{t}y\left(s\right)ds+\beta {\eta }^{\alpha }{\int }_t^{+\infty }y\left(s\right)ds+\mathrm{\Gamma }(\alpha +1)\lambda \right)\hfill \\ & & \ge \frac{\beta {\eta }^{\alpha -1}}{\rho }{t}^{\alpha -1}\left({\int }_0^{\eta }sy\left(s\right)ds+\eta {\int }_{\eta }^{+\infty }y\left(s\right)ds+\eta \lambda \right).\hfill \end{array}$$

Therefore,

$$\begin{array}{ccc}& & \underset{t\in [0,\eta ]}{sup}\frac{\left|x\right(t\left)\right|}{1+t^{\alpha -1}}\le \frac{\mathrm{\Gamma }(\alpha +1)}{\rho \eta }\left(\frac{\alpha {\eta }^{\alpha -1}}{1+{\eta }^{\alpha -1}}{\int }_0^{\eta }sy\left(s\right)ds+\frac{{\eta }^{\alpha -1}\eta }{1+{\eta }^{\alpha -1}}{\int }_{\eta }^{+\infty }y\left(s\right)ds+\frac{{\eta }^{\alpha -1}\eta }{1+{\eta }^{\alpha -1}}\lambda \right)\hfill \\ & & \le \frac{\mathrm{\Gamma }(\alpha +1)}{\rho \eta }\max \{\alpha ,\eta \}\left({\int }_0^{\eta }sy\left(s\right)ds+{\int }_{\eta }^{+\infty }y\left(s\right)ds+\lambda \right),\hfill \\ & & \underset{t\in [\eta ,+\infty )}{sup}\frac{\left|x\right(t\left)\right|}{1+t^{\alpha -1}}\le \frac{\mathrm{\Gamma }(\alpha +1)}{\rho \eta }\max \{\alpha ,\eta \}\left({\int }_0^{\eta }sy\left(s\right)ds+{\int }_{\eta }^{+\infty }y\left(s\right)ds+\lambda \right).\hfill \end{array}$$

Moreover,

$$\begin{array}{ccc}& & \underset{t\in [0,+\infty )}{sup}\frac{\left|x\right(t\left)\right|}{1+t^{\alpha -1}}\le \frac{\mathrm{\Gamma }(\alpha +1)}{\rho \eta }\max \{\alpha ,\eta \}\left({\int }_0^{\eta }sy\left(s\right)ds+{\int }_{\eta }^{+\infty }y\left(s\right)ds+\lambda \right).\hfill \end{array}$$

In addition, we have

$$\begin{array}{c}\hfill x\left(t\right)\ge \frac{\beta {\eta }^{\alpha -1}}{\rho }\min \{\eta ,1\}{t}^{\alpha -1}\left({\int }_0^{\eta }sy\left(s\right)ds+{\int }_{\eta }^{+\infty }y\left(s\right)ds+\lambda \right),t\in [0,+\infty ).\end{array}$$

Consequently, we obtain

$$\begin{array}{c}\hfill x\left(t\right)\ge \gamma t^{\alpha -1}\underset{t\in [0,+\infty )}{sup}\frac{\left|x\right(t\left)\right|}{1+t^{\alpha -1}},t\in [0,+\infty ).\end{array}$$

This ends the proof. □

When (L1), (L2) and (L3) hold, in virtue of Lemma 2, BVP (1) is equivalent to the following integral equation

$$x\left(t\right)={\int }_0^{+\infty }G(t,s)q\left(s\right)f(s,x\left(s\right))ds+\frac{\mathrm{\Gamma }(\alpha +1)\lambda }{\rho }{t}^{\alpha -1}.$$

(5)

For every given $\lambda \ge 0$, define operator $T_{\lambda }$ by

$$\begin{array}{c}\hfill \left(T_{\lambda }x\right)\left(t\right)={\int }_0^{+\infty }G(t,s)q\left(s\right)f(s,x\left(s\right))ds+\frac{\mathrm{\Gamma }(\alpha +1)\lambda }{\rho }{t}^{\alpha -1},x\in K.\end{array}$$

Noticing that $x\in K$ implies $x\left(t\right)\ge 0$ for $t\in [0,+\infty )$, it follows from Lemmas 1 and 4 that $T_{\lambda }:K\to K$. Hence, x is a monotone positive solution of BVP (1) if and only if x is a non-zero solution of $T_{\lambda }x=x$ in K. This leads to the following result.

Lemma 5.

Suppose that (L1), (L2) and (L3) hold. If x is a nonnegative solution of BVP (1), then $x\left(t\right)$ is a monotone increasing positive solution of BVP (1). Moreover, $x\in K\setminus \left\{\theta \right\}$.

Lemma 6.

Suppose that (L1), (L2) and (L3) hold. Then $T_{\lambda }:P\to K$ is a completely continuous operator.

The proof is similar to Lemma 5 in [33]. So, it is omitted.

3. Existence, Multiplicity and Nonexistence

In this section, we will apply Lemma 1 to give the range of the parameter $\lambda$ for the existence of at least one, two, no positive solutions for BVP (1). The following conditions will be used:

(H1)

$\underset{r\in (0,+\infty )}{sup}\left[(\mathrm{\Gamma }(\alpha +1)-\beta {\eta }^{\alpha })r-\alpha {\int }_0^{+\infty }q\left(s\right){\phi }_r\left(s\right)ds\right]>0.$

(H2)

$f_{\infty }:=\underset{x\to +\infty }{lim\; inf}\underset{t\in [\eta ,+\infty )}{inf}\frac{f(t,(1+t^{\alpha -1})x)}{x}>\frac{(1+{\eta }^{\alpha -1})\rho }{\beta {\eta }^{2\alpha -1}\gamma {\int }_{\eta }^{+\infty }q\left(s\right)ds}$.

Theorem 1.

Suppose that (L1), (L2), (L3) and (H1) hold. Then there exists ${\lambda }^{*}>0$ such that for any $0<\lambda <{\lambda }^{*}$, BVP (1) has at least one positive solution $x_{\lambda }\left(t\right)$ satisfying

$$x_{\lambda }\left(t\right)\ge \frac{\mathrm{\Gamma }(\alpha +1)\lambda }{\rho }{t}^{\alpha -1},t\in [0,+\infty ).$$

(6)

Proof. 

For any given $\lambda >0,$ it follows from Lemma 6 that $T_{\lambda }:P\to K$ is a completely continuous operator. Set

$${\mathrm{\Omega }}_1{=\{x\in K\mid \parallel x\parallel }_{\infty }<\frac{\mathrm{\Gamma }(\alpha +1)\lambda }{\rho }\},$$

(7)

then for any $x\in \partial {\mathrm{\Omega }}_1$, it is clear that

$$\begin{array}{c}\hfill \frac{\left(T_{\lambda }x\right)\left(t\right)}{1+t^{\alpha -1}}\ge \frac{\mathrm{\Gamma }(\alpha +1)\lambda }{\rho }\frac{t^{\alpha -1}}{1+t^{\alpha -1}},t\in [0,+\infty ),\end{array}$$

that is,

$$\parallel T_{\lambda }{x\parallel }_{\infty }\ge \frac{\mathrm{\Gamma }(\alpha +1)\lambda }{\rho }={\parallel x\parallel }_{\infty }.$$

(8)

Set

$$\psi \left(r\right)=\frac{1}{\alpha }(\mathrm{\Gamma }(\alpha +1)-\beta {\eta }^{\alpha })r-{\int }_0^{+\infty }q\left(s\right){\phi }_r\left(s\right)ds,r>0,$$

and

$${\lambda }^{*}=\underset{r>0}{sup}\psi \left(r\right)=\underset{r>0}{sup}\left(\frac{1}{\alpha }\left(\mathrm{\Gamma }(\alpha +1)-\beta {\eta }^{\alpha }\right)r-{\int }_0^{+\infty }q\left(s\right){\phi }_r\left(s\right)ds\right),$$

(9)

then the condition (H1) implies that $0<{\lambda }^{*}\le +\infty$. In order to show that for any given $\lambda \in [0,{\lambda }^{*})$, there exists $r_{\lambda }>\frac{\mathrm{\Gamma }(\alpha +1)\lambda }{\rho }$ such that $\lambda <\psi \left(r_{\lambda }\right)\le {\lambda }^{*}$, that is,

$$\lambda <\frac{\rho }{\mathrm{\Gamma }(\alpha +1)}{r}_{\lambda }-{\int }_0^{+\infty }q\left(s\right){\phi }_{r_{\lambda }}\left(s\right)ds\le {\lambda }^{*},$$

(10)

there are two cases to be considered.

Case 1. $\psi \left(r\right)<{\lambda }^{*}$ for all $r\in (0,+\infty )$. It follows from (9) that

$${\lambda }^{*}=\underset{r\to +\infty }{lim\; sup}\left(\frac{1}{\alpha }\left(\mathrm{\Gamma }(\alpha +1)-\beta {\eta }^{\alpha }\right)r-{\int }_0^{+\infty }q\left(s\right){\phi }_r\left(s\right)ds\right).$$

So, we can choose a sufficiently large number $r_{\lambda }>\frac{\mathrm{\Gamma }(\alpha +1)\lambda }{\rho }$ satisfying $\lambda <\psi \left(r_{\lambda }\right)<{\lambda }^{*}$, and this $r_{\lambda }$ meets our requirements.

Case 2. There exists $r_0\in (0,+\infty )$ such that ${\lambda }^{*}=\psi \left(r_0\right)$. In this case, $\lambda \in [0,{\lambda }^{*})$ implies that

$$\lambda <{\lambda }^{*}=\frac{\rho }{\mathrm{\Gamma }(\alpha +1)}{r}_0-{\int }_0^{+\infty }q\left(s\right){\phi }_{r_0}\left(s\right)ds\le \frac{\rho }{\mathrm{\Gamma }(\alpha +1)}{r}_0.$$

Moreover,

$$\frac{\mathrm{\Gamma }(\alpha +1)\lambda }{\rho }<\frac{\mathrm{\Gamma }(\alpha +1){\lambda }^{*}}{\rho }\le \frac{\mathrm{\Gamma }(\alpha +1)}{\rho }\frac{\rho }{\mathrm{\Gamma }(\alpha +1)}{r}_0=r_0.$$

It is easy to see that $r_{\lambda }:=r_0$ meets our requirements.

Set

$${\mathrm{\Omega }}_2{=\{x\in K\mid \parallel x\parallel }_{\infty }<r_{\lambda }\},$$

(11)

then ${\overline{\mathrm{\Omega }}}_1\subset {\mathrm{\Omega }}_2$. For any $x\in \partial {\mathrm{\Omega }}_2$,

$$\begin{array}{c}\hfill \frac{\left(T_{\lambda }x\right)\left(t\right)}{1+t^{\alpha -1}}\le \frac{\mathrm{\Gamma }(\alpha +1)}{\rho }\left({\int }_0^{+\infty }q\left(s\right){\phi }_{r_{\lambda }}\left(s\right)ds+\lambda \right)\frac{t^{\alpha -1}}{1+t^{\alpha -1}},t\in [0,+\infty ).\end{array}$$

In addition, noticing that $\lambda <\psi \left(r_{\lambda }\right)\le {\lambda }^{*}$, we have

$$\begin{array}{c}\hfill {\int }_0^{+\infty }q\left(s\right){\phi }_{r_{\lambda }}\left(s\right)ds+\lambda <{\int }_0^{+\infty }q\left(s\right){\phi }_{r_{\lambda }}\left(s\right)ds+\psi \left(r_{\lambda }\right)=\frac{\rho }{\mathrm{\Gamma }(\alpha +1)}{r}_{\lambda },x\in \partial {\mathrm{\Omega }}_2.\end{array}$$

Hence, for any $\lambda \in [0,{\lambda }^{*})$ we obtain that

$$\parallel T_{\lambda }{x\parallel }_{\infty }\le \frac{\mathrm{\Gamma }(\alpha +1)}{\rho }\left({\int }_0^{+\infty }q\left(s\right){\phi }_{r_{\lambda }}\left(s\right)ds+\lambda \right)<r_{\lambda }={\parallel x\parallel }_{\infty },x\in \partial {\mathrm{\Omega }}_2.$$

(12)

Combining (8), (12), and applying Lemma 1, we conclude that BVP (1) has at least one positive solution $x_{\lambda }\in {\overline{\mathrm{\Omega }}}_2\setminus {\mathrm{\Omega }}_1$ satisfying (6) for any $\lambda \in (0,{\lambda }^{*})$.

This completes the proof. □

Remark 3.

From the proof of Theorem 1, it is easy to see that if ${\lambda }^{*}=+\infty$, then for any $\lambda >0$, BVP (1) has at least one positive solution $x_{\lambda }\left(t\right)$ satisfying (6); and if there exists $r_0>0$ such that ${\lambda }^{*}=\psi \left(r_0\right)$, then for any $0<\lambda \le {\lambda }^{*}$, BVP (1) has at least one positive solution $x_{\lambda }\left(t\right)$ satisfying (6).

Corollary 1.

Suppose that (L1), (L2) and (L3) hold. If ${\phi }^{\infty }:=\underset{r\to +\infty }{lim\; sup}\frac{{\int }_0^{+\infty }q\left(s\right){\phi }_r\left(s\right)ds}{r}<\frac{\mathrm{\Gamma }(\alpha +1)-\beta {\eta }^{\alpha }}{\alpha }$, then for any $\lambda >0$, BVP (1) has at least one positive solution $x_{\lambda }\left(t\right)$ satisfying (6).

Proof. 

Choose $\delta >0$ satisfying ${\phi }^{\infty }<\frac{\mathrm{\Gamma }(\alpha +1)-\beta {\eta }^{\alpha }}{\alpha }-\delta$, then there exists $R>0$ such that

$${\int }_0^{+\infty }q\left(s\right){\phi }_r\left(s\right)ds\le \left({\phi }^{\infty }+\frac{1}{2}\delta \right)r,r\ge R.$$

Moreover,

$${\int }_0^{+\infty }q\left(s\right){\phi }_r\left(s\right)ds<\left(\frac{\mathrm{\Gamma }(\alpha +1)-\beta {\eta }^{\alpha }}{\alpha }-\frac{1}{2}\delta \right)r,r\ge R,$$

which means that

$$\frac{1}{\alpha }(\mathrm{\Gamma }(\alpha +1)-\beta {\eta }^{\alpha })r-{\int }_0^{+\infty }q\left(s\right){\phi }_r\left(s\right)ds>\frac{1}{2}\delta r,r\ge R,$$

that is, $\psi \left(r\right)>\frac{1}{2}\delta r$ for $r\ge R$. So, (H1) is satisfied and ${\lambda }^{*}={sup}_{r>0}\psi \left(r\right)=+\infty$. Therefore, the conclusion follows from Remark 3.

The proof is complete. □

From Remark 3 and Corollary 1, the following Corollary 2 can be obtained.

Corollary 2.

Suppose that (L1), (L2) and (L3) hold. If there exist $\tau \in (0,+\infty )$ and $a\in L[0,+\infty )$ with ${\int }_0^{+\infty }a\left(s\right)ds>0$ such that $q\left(t\right){\phi }_r\left(t\right)=a\left(t\right)r^{\tau }$ for $r>0$.

(i)

If $0<\tau <1$, then for any $\lambda >0$, BVP (1) has at least one positive solution $x_{\lambda }\left(t\right)$ satisfying (6).

(ii)

If $\tau =1$ and ${\int }_0^{+\infty }a\left(s\right)ds<\frac{\mathrm{\Gamma }(\alpha +1)-\beta {\eta }^{\alpha }}{\alpha }$, then for any $\lambda >0$, BVP (1) has at least one positive solution $x_{\lambda }\left(t\right)$ satisfying (6).

(iii)

If $\tau >1$, then there exists ${\lambda }^{*}>0$ such that for any $0<\lambda \le {\lambda }^{*}$, BVP (1) has at least one positive solution $x_{\lambda }\left(t\right)$ satisfying (6).

Set

$$S=\{x\in K\mid \exists \lambda \ge 0s.t.T_{\lambda }x=x\},$$

(13)

$$\mathrm{\Lambda }=\{\lambda \ge 0\mid \exists x_{\lambda }\in Ks.t.T_{\lambda }{x}_{\lambda }=x_{\lambda }\}.$$

(14)

Lemma 7.

Suppose that S is a bounded subset in X. Then

(i)

Λ is bounded above;

(ii)

S is a relatively compact set in X.

Proof. 

Since S is bounded, then there exists $M>0$ such that

$${\parallel x\parallel }_{\infty }=\underset{t\in [0,+\infty )}{sup}\frac{x\left(t\right)}{1+t^{\alpha -1}}\le M,x\in S.$$

(15)

(i) Suppose to the contrary that there exists a sequence ${\left\{{\lambda }_n\right\}}_1^{+\infty }\subset \Lambda$ such that $\underset{n\to +\infty }{lim}{\lambda }_n=+\infty .$ From the definition of $\Lambda$ there exists a sequence ${\left\{x_n\right\}}_1^{+\infty }\subset K$ such that $T_{{\lambda }_n}{x}_n=x_n$. It is clear that ${\left\{x_n\right\}}_1^{+\infty }\subset S$, and

$$\begin{array}{c}\hfill \frac{x_n\left(t\right)}{1+t^{\alpha -1}}=\frac{\left(T_{{\lambda }_n}{x}_n\right)\left(t\right)}{1+t^{\alpha -1}}\ge \frac{\mathrm{\Gamma }(\alpha +1){\lambda }_n}{\rho }\frac{t^{\alpha -1}}{1+t^{\alpha -1}}t\in [0,+\infty ),n=1,2,\cdots .\end{array}$$

This, together with (15), implies that

$$\begin{array}{c}\hfill \frac{\mathrm{\Gamma }(\alpha +1){\lambda }_n}{\rho }\le {\parallel x_n\parallel }_{\infty }\le M,n=1,2,\cdots ,\end{array}$$

which contradicts that $\underset{n\to +\infty }{lim}{\lambda }_n=+\infty .$ So, $\Lambda$ is bounded above.

(ii) Since $\mathrm{\Lambda }$ is bounded above, then there exists $\overline{M}>0$ such that $0\le \lambda <\overline{M}$ for all $\lambda \in \mathrm{\Lambda }$. In addition, $x\in S$ means that there exists $\lambda \in [0,+\infty )$ such that $T_{\lambda }x=x$ and $\lambda \in \mathrm{\Lambda }$. Arguing similarly to the proof of Lemma 5 in [33], we can obtain that S is a relatively compact set in X.

This completes the proof. □

Lemma 8.

Suppose that (L1), (L2), (L3), and (H2) hold. Then S is a bounded subset in X.

Proof. 

From (H2), for $ϵ>0$ with $f_{\infty }-ϵ>\frac{\rho (1+{\eta }^{\alpha -1})}{\beta \gamma {\eta }^{2\alpha -1}{\int }_{\eta }^{+\infty }q\left(s\right)ds}>0$, there exists a constant $R>0$ such that

$$f(t,(1+t^{\alpha -1})x)\ge (f_{\infty }-ϵ)x,t\in [\eta ,+\infty ),x\ge R.$$

(16)

If S is unbounded, there exists $x_0\in S$ with $\parallel x_0{\parallel }_{\infty }>\frac{1+{\eta }^{\alpha -1}}{\gamma {\eta }^{\alpha -1}}R$, that is, there exists ${\lambda }_0\in [0,+\infty )$ such that $T_{{\lambda }_0}{x}_0=x_0$. By the definition of K, we have

$$\underset{t\in [\eta ,+\infty )}{min}\frac{x_0\left(t\right)}{1+t^{\alpha -1}}\ge \frac{\gamma {\eta }^{\alpha -1}}{1+{\eta }^{\alpha -1}}{\parallel x_0\parallel }_{\infty }>R.$$

This, together with (16), gives

$$\begin{array}{ccc}& & \frac{x_0\left(t\right)}{1+t^{\alpha -1}}=\frac{\left(T_{{\lambda }_0}{x}_0\right)\left(t\right)}{1+t^{\alpha -1}}\ge {\int }_{\eta }^{+\infty }\frac{G(t,s)}{1+t^{\alpha -1}}q\left(s\right)f(s,(1+s^{\alpha -1})\frac{x_0\left(s\right)}{1+s^{\alpha -1}})ds\hfill \\ & & \ge (f_{\infty }-ϵ){\int }_{\eta }^{+\infty }\frac{G(t,s)q\left(s\right)}{1+t^{\alpha -1}}\frac{x_0\left(s\right)}{1+s^{\alpha -1}}ds\hfill \\ & & \ge \frac{\gamma \beta {\eta }^{2\alpha -1}(f_{\infty }-ϵ){\parallel x_0\parallel }_{\infty }}{(1+{\eta }^{\alpha -1})\rho }\frac{t^{\alpha -1}}{1+t^{\alpha -1}}{\int }_{\eta }^{+\infty }q\left(s\right)ds,t\in [0,+\infty ),\hfill \end{array}$$

which means that

$$\begin{array}{c}\hfill \parallel x_0{\parallel }_{\infty }\ge \frac{\gamma {\eta }^{2\alpha -1}\beta (f_{\infty }-ϵ){\parallel x_0\parallel }_{\infty }}{(1+{\eta }^{\alpha -1})\rho }{\int }_{\eta }^{+\infty }q\left(s\right)ds>{\parallel x_0\parallel }_{\infty }.\end{array}$$

This is a contradiction. Therefore, S is bounded subset in X.

This completes the proof. □

Theorem 2.

Suppose that (L1), (L2), (L3), (H1) and (H2) hold. Then there exist $0<{\lambda }^{*}\le {\lambda }^{**}<+\infty$ such that

(i)

BVP (1) has at least one positive solution satisfying (6) for $\lambda =0$;

(ii)

BVP (1) has at least two positive solutions satisfying (6) for $0<\lambda <{\lambda }^{*}$;

(iii)

BVP (1) has no positive solutions for $\lambda \ge {\lambda }^{**}$.

Proof. 

Define ${\lambda }^{*}$ as (9). According to the proof of Theorem 1, we obtain that

$$\parallel T_{\lambda }{x\parallel }_{\infty }\ge \frac{\mathrm{\Gamma }(\alpha +1)\lambda }{\rho }={\parallel x\parallel }_{\infty },x\in \partial {\mathrm{\Omega }}_1,\lambda \in (0,{\lambda }^{*}),$$

and

$$\parallel T_{\lambda }{x\parallel }_{\infty }\le \frac{\mathrm{\Gamma }(\alpha +1)}{\rho }\left({\int }_0^{+\infty }q\left(s\right){\phi }_{r_{\lambda }}\left(s\right)ds+\lambda \right)<r_{\lambda }={\parallel x\parallel }_{\infty },x\in \partial {\mathrm{\Omega }}_2,\lambda \in [0,{\lambda }^{*}),$$

where ${\mathrm{\Omega }}_1$ and ${\mathrm{\Omega }}_2$ are defined as (7) and (11), respectively.

In addition, it follows from (H2) that there exists a constant $R_0>0$ such that

$$f(t,(1+t^{\alpha -1})x)\ge \frac{(1+{\eta }^{\alpha +1})\rho }{\beta {\eta }^{2\alpha -1}\gamma {\int }_{\eta }^{+\infty }q\left(s\right)ds}x,t\in [\eta ,+\infty ),x\ge R_0.$$

For any given $\lambda \in [0,{\lambda }^{*})$, let

$$R_{\lambda }>max\{\frac{1+{\eta }^{\alpha -1}}{\gamma {\eta }^{\alpha -1}}{R}_0,r_{\lambda }\},$$

and define

$${\mathrm{\Omega }}_3{=\{x\in K\mid \parallel x\parallel }_{\infty }<R_{\lambda }\}.$$

(17)

For any $x\in \partial {\mathrm{\Omega }}_3$, it is easy to see from the definition of the cone K that

$$\underset{t\in [\eta ,+\infty )}{min}\frac{x\left(t\right)}{1+t^{\alpha -1}}\ge \frac{\gamma {\eta }^{\alpha -1}}{1+{\eta }^{\alpha -1}}{R}_{\lambda }>R_0.$$

In view of Lemmas 1 and 4 we have

$$\begin{array}{ccc}\hfill \frac{\left(T_{\lambda }x\right)\left(t\right)}{1+t^{\alpha -1}}& \ge & \frac{\beta {\eta }^{\alpha }}{\rho }\frac{t^{\alpha -1}}{1+t^{\alpha -1}}{\int }_{\eta }^{+\infty }q\left(s\right)f(s,(1+s^{\alpha -1})\frac{x\left(s\right)}{1+s^{\alpha -1}})ds\hfill \\ & \ge & \frac{t^{\alpha -1}}{1+t^{\alpha -1}}\frac{1+{\eta }^{\alpha +1}}{\gamma {\eta }^{\alpha -1}{\int }_{\eta }^{+\infty }q\left(s\right)ds}{\int }_{\eta }^{+\infty }\frac{q\left(s\right)x\left(s\right)}{1+s^{\alpha -1}}ds\hfill \\ & \ge & \frac{{\parallel x\parallel }_{\infty }{t}^{\alpha -1}}{1+t^{\alpha -1}},t\in [0,+\infty ),\hfill \end{array}$$

which means that

$$\begin{array}{c}\hfill \parallel T_{\lambda }{x\parallel }_{\infty }\ge {\parallel x\parallel }_{\infty },x\in \partial {\mathrm{\Omega }}_3.\end{array}$$

Thus, applying Lemma 1 we conclude that BVP (1) has at least one positive solution $x_{\lambda }\in {\overline{\mathrm{\Omega }}}_3\setminus {\mathrm{\Omega }}_2$ and two positive solutions $x_{\lambda ,1}\in {\overline{\mathrm{\Omega }}}_2\setminus {\mathrm{\Omega }}_1$ and $x_{\lambda ,2}\in {\overline{\mathrm{\Omega }}}_3\setminus {\overline{\mathrm{\Omega }}}_2$ for $\lambda =0$ and $0<\lambda <{\lambda }^{*}$, respectively. It is obvious that these solutions satisfy (6). In addition, it follows from Lemmas 5 and 6 that $0<{\lambda }^{*}<+\infty$.

Now, we take

$${\lambda }^{**}\ge \frac{\rho (1+{\eta }^{\alpha -1})R_0}{{\eta }^{\alpha -1}\mathrm{\Gamma }(\alpha +1)}.$$

When $\lambda \ge {\lambda }^{**}$, if BVP (1) has one positive solution $y_{\lambda }$, it follows from Lemma 5 that $y_{\lambda }\in K.$ Noting that

$$\underset{t\in [\eta ,+\infty )}{min}\frac{y_{\lambda }\left(t\right)}{1+t^{\alpha -1}}=\underset{t\in [\eta ,+\infty )}{min}\frac{T_{\lambda }{y}_{\lambda }\left(t\right)}{1+t^{\alpha -1}}\ge \frac{{\eta }^{\alpha -1}\mathrm{\Gamma }(\alpha +1)}{(1+{\eta }^{\alpha -1})\rho }{\lambda }^{**}\ge R_0,$$

we can obtain that

$$\begin{array}{ccc}\hfill \frac{y_{\lambda }\left(t\right)}{1+t^{\alpha -1}}& =& \frac{\left(T_{\lambda }{y}_{\lambda }\right)\left(t\right)}{1+t^{\alpha -1}}\ge {\int }_{\eta }^{+\infty }\frac{G(t,s)}{1+t^{\alpha -1}}q\left(s\right)f(s,y_{\lambda }\left(s\right))ds+\frac{\mathrm{\Gamma }(\alpha +1){\lambda }^{**}}{\rho }\frac{t^{\alpha -1}}{1+t^{\alpha -1}}\hfill \\ & \ge & \left(\parallel y_{\lambda }{\parallel }_{\infty }+\frac{1+{\eta }^{\alpha -1}}{{\eta }^{\alpha -1}}{R}_0\right)\frac{t^{\alpha -1}}{1+t^{\alpha -1}},t\in [0,+\infty ),\hfill \end{array}$$

which means that

$$\begin{array}{c}\hfill \parallel y_{\lambda }{\parallel }_{\infty }\ge {\parallel y_{\lambda }\parallel }_{\infty }+\frac{1+{\eta }^{\alpha -1}}{{\eta }^{\alpha -1}}{R}_0,\end{array}$$

this is a contradiction. Therefore, BVP (1) has no positive solutions for $\lambda \ge {\lambda }^{**}$. It is obvious that ${\lambda }^{**}\ge {\lambda }^{*}$.

The proof is complete. □

Remark 4.

Theorem 2 presents as much as possible that the impact of the disturbance parameter λ on the number of the positive solutions for BVP (1), that is, BVP (1) has at least one, two, and no positive solutions for $\lambda =0,\lambda \in (0,{\lambda }^{*})$ and $\lambda \in [{\lambda }^{**},+\infty )$, respectively. But unfortunately, we have not yet determined whether the solution exists for $\lambda \in [{\lambda }^{*},{\lambda }^{**})$ when the nonlinearity $f(t,x)$ is not monotonic in x. When $f(t,x)$ satisfies conditions in Corollary 2, for instance, the example in Section 4, we can find an interesting change for this interval $[{\lambda }^{*},{\lambda }^{**})$.

4. Example

In this section, we present an example to illustrate our main results.

Consider the fractional integral boundary value problem on the infinite interval

$$\left\{\begin{array}{c}{D}_{0^{+}}^{\frac{8}{3}}x\left(t\right)+\frac{1}{2}{e}^{-t}\frac{4(1+\frac{1}{4}sinx\left(t\right))x^{\tau }\left(t\right)}{3{(1+t^{\alpha -1})}^{\tau }}=0,t\in [0,+\infty ),\hfill \\ x\left(0\right)=0,x^{\prime }\left(0\right)=0,\hfill \\ D_{0^{+}}^{\frac{5}{3}}x(+\infty )=\frac{1}{10}{\int }_0^{1}x\left(s\right)ds+\lambda ,\hfill \end{array}\right.$$

(18)

where $\tau >0$. Then

(a)

for any $\tau \in (0,1]$, BVP (18) has at least one positive solution $x_{\lambda }$ satisfying (6) for $\lambda >0$.

(b)

for any $\tau >1$, there exist $0<{\lambda }^{*}<{\lambda }^{**}$ such that

(i)

BVP (18) has at least one positive solution $x_{\lambda }$ satisfying (6) for $\lambda =0$;

(ii)

BVP (18) has at least two positive solutions $x_{\lambda ,1}$ and $x_{\lambda ,2}$ satisfying (6) for $0<\lambda <{\lambda }^{*}$;

(iii)

BVP (18) has no positive solutions for $\lambda \ge {\lambda }^{**}$.

Indeed, BVP (18) means that in BVP (1), $\alpha =\frac{8}{3},\beta =1,\eta =1$, $q\left(t\right)=\frac{1}{2}{e}^{-t}$ and $f(t,x)=\frac{4}{3}\frac{(1+\frac{1}{4}sinx)x^{\tau }}{{(1+t^{\alpha -1})}^{\tau }}$.

Since $\mathrm{\Gamma }(\alpha +1)=\frac{80}{27}\mathrm{\Gamma }\left(\frac{2}{3}\right)\approx 4.0122$, then $\mathrm{\Gamma }(\alpha +1)-\beta {\eta }^{\alpha }\approx 3.0122$ and $\frac{\mathrm{\Gamma }(\alpha +1)-\beta {\eta }^{\alpha }}{\alpha }\doteq 1.1296$.

Let ${\phi }_r\left(t\right)=\frac{5}{3}{r}^{\tau }$ for $r\ge 0$, then ${\int }_0^{+\infty }q\left(t\right){\phi }_r\left(t\right)dt=\frac{5}{3}{r}^{\tau }{\int }_0^{+\infty }\frac{1}{2}{e}^{-t}dt=\frac{5}{6}{r}^{\tau }$, and

$$f(t,(1+t^{\alpha -1})x)=\frac{4}{3}(1+\frac{1}{4}sin(1+t^{\alpha -1})x)x^{\tau }\le {\phi }_r\left(t\right),t\in [0,+\infty ),0\le x\le r.$$

Hence, (L1), (L2) and (L3) are satisfied.

In addition,

$$\psi \left(r\right)=\frac{1}{\alpha }(\mathrm{\Gamma }(\alpha +1)-\beta {\eta }^{\alpha })r-{\int }_0^{+\infty }q\left(s\right){\phi }_r\left(s\right)ds=1.1296r-\frac{5}{6}{r}^{\tau }.$$

(19)

Let $a\left(t\right)=\frac{5}{6}{e}^{-t}$, then $q\left(t\right){\phi }_r\left(t\right)=a\left(t\right)r^{\tau }$, and

$${\int }_0^{+\infty }a\left(s\right)ds=\frac{5}{6}\doteq 0.8333<\frac{\mathrm{\Gamma }(\alpha +1)-\beta {\eta }^{\alpha }}{\alpha }.$$

Thus, applying Corollary 2 we can obtain the conclusion (a).

Next to show the conclusion (b). For given $\tau >1$, by simple calculation, we obtain that

$$r_0={\left(\frac{\mathrm{\Gamma }(\alpha +1)-\beta {\eta }^{\alpha }}{\alpha \tau {\int }_0^{+\infty }a\left(s\right)ds}\right)}^{\frac{1}{\tau -1}}={\left(\frac{6(\mathrm{\Gamma }(\alpha +1)-\beta {\eta }^{\alpha })}{5\alpha \tau }\right)}^{\frac{1}{\tau -1}}\doteq {\left(\frac{1.3555}{\tau }\right)}^{\frac{1}{\tau -1}}$$

and it follows from (19) that

$${\lambda }^{*}=\psi \left(r_0\right)=\frac{\mathrm{\Gamma }(\alpha +1)-\beta {\eta }^{\alpha }}{\alpha }{r}_0-\frac{5}{6}{r}_0^{\tau }\doteq 1.1296\left(1-\frac{1}{\tau }\right){\left(\frac{1.3555}{\tau }\right)}^{\frac{1}{\tau -1}},$$

which implies that the condition (H1) holds.

In addition, since

$$\underset{t\in [\eta ,+\infty )}{inf}\frac{f(t,(1+t^{\alpha -1})x)}{x}=\underset{t\in [\eta ,+\infty )}{inf}\frac{4}{3}(1+\frac{1}{4}sin(1+t^{\alpha -1})x)x^{\tau -1}\ge x^{\tau -1},x>0,$$

then

$$f_{\infty }=\underset{x\to +\infty }{lim\; inf}\underset{t\in [\eta ,+\infty )}{inf}\frac{f(t,(1+t^{\alpha -1})x)}{x}=+\infty ,$$

which implies that the condition (H2) holds.

By the proof of Theorem 2, we can take $R_0={\left(\frac{4e\rho }{\alpha \mathrm{\Gamma }(\alpha +1)}\right)}^{\frac{1}{\tau -1}}={\left(\frac{4\left(\mathrm{\Gamma }\right(\alpha +1)-1)e}{{\alpha }^2}\right)}^{\frac{1}{\tau -1}}\doteq {\left(4.6058\right)}^{\frac{1}{\tau -1}}$, Moreover, we can take

$${\lambda }^{**}=\frac{2\rho }{\mathrm{\Gamma }(\alpha +1)}{R}_0\doteq 2.2592{\left(4.6058\right)}^{\frac{1}{\tau -1}}.$$

Thus, the conclusion (b) follows from Theorem 2.

In particular, for every given $\tau >1$ we can calculate the values of ${\lambda }^{*}\left(\tau \right)$ and ${\lambda }^{**}\left(\tau \right)$ in conclusion (b) by the above proof. For example,

• if $\tau =\frac{3}{2}$ then ${\lambda }^{*}\doteq 0.3075$ and ${\lambda }^{**}\doteq 47.9253;$
• if $\tau =2$ then ${\lambda }^{*}\doteq 0.3828$ and ${\lambda }^{**}\doteq 10.4054;$
• if $\tau =10$ then ${\lambda }^{*}\doteq 0.8142$ and ${\lambda }^{**}\doteq 2.6770;$
• if $\tau =100$ then ${\lambda }^{*}\doteq 1.0708$ and ${\lambda }^{**}\doteq 2.2943;$
• if $\tau =1000$ then ${\lambda }^{*}\doteq 1.1210$ and ${\lambda }^{**}\doteq 2.2627.$

The influence of the disturbance parameters on the existence and the number of the positive solutions is shown in the following Figure 1.

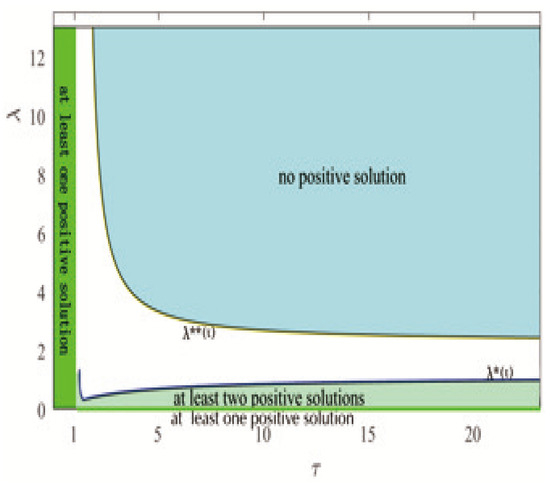
Figure 1. Influence of the disturbance parameters on the existence and the number of the positive solutions.

Remark 5.

As we can see from the example, if ${\phi }_r\left(t\right)$ satisfies $q\left(t\right){\phi }_r\left(t\right)=a\left(t\right)r^{\tau },$ ${\lambda }^{*}$ is closing to ${\lambda }^{**}$ with τ is increasing. This may be helpful for us to further study more accurate parameter interval for the existence of positive solutions.