Categories of Open Sets in Generalized Primal Topological Spaces

Abstract

In this research article, we define some categories of open sets over a generalized topological space given together with a primal collection. In addition, we clarify some of its characteristics and investigate the relationships between these concepts in the space under consideration. The topic of continuity occupies a large space in topological theory and is one of the most important topics therein. Researchers have examined it in light of many variables. We followed the same approach by studying the concept of continuity between two generalized topological spaces in light of the primal collection under the name $(\mathfrak{g},\mathcal{P})$-continuity. We also made a decomposition of this type of function in light of these weak categories of open sets.

1. Introduction

In the field of topology, accurate solutions to many issues cannot be found. For example, proximity space, compactifications, and closure space problems. This has led topologists to provide some tools such as nets, ideals, filters, and grills.

Recently, primal set theory has attracted significant attention from researchers. One of the most important properties under study is the qualitative behavior of the operators that are defined via the primal set.

The above-mentioned tools were employed very well in this regard. Topologists provided associated topological spaces, which were considered triple variables with different behaviors. The primal generalized topological space was studied based on these ideas and methodologies.

In another investigation, topologists introduced different forms of open sets with slightly different features. This kind of work has been on the rise among scientific production in the field of topology. The corresponding concepts of topological theory are affected by this methodology of research. The matter of continuity receives a lot of attention within this approach. This idea has given rise to several decompositions of continuous functions.

Our article contains five sections. This section contains two subsections: first, we provide a literature review connected to this study; second is a brief introduction to the basic definitions, characteristics, and theorems. Section 2 describes the methods that were used in this study. Section 3 contains the main results that appear during the two parts. We provide the definitions of some classes of open sets over a generalized primal topological space. In addition, we present a deep discussion of their properties. We provide a detailed answer to the question: “Are the properties of these classes that are applied in a topological space applicable in a generalized primal topological space too?” In addition, we will present new results and study the relationship among them.

In Section 4, we introduce a new kind of continuity within this new structure, which is named $(\mathfrak{g},\mathcal{P})$-continuity, then use the new categories that are given in Section 3 to find some kind of $(\mathfrak{g},\mathcal{P})$-continuity function. Later, we study the relationship among these categories and establish a decomposition of this type of continuity. Section 5 is a brief discussion of the important findings that came out during the study.

1.1. Literature Review

From the previous literature, we realized that the idea of “semi-open sets” appeared around 1963, when Levine [1] introduced this notion over a topological space $\mathbb{X}$ as follows: $E\subseteq \mathbb{X}$ is deemed semi-open when $E\subseteq cl\left(int\right(E\left)\right),$ where $int\left(E\right)$ indicates the interior of $E,$ while $cl\left(E\right)$ indicates the closure of $E.$ Note that $(\mathbb{X}\backslash E)$ is semi-open; hence, E is named semi-closed. This concept has garnered significant attention from researchers because of its important applications in topology theory (see [2,3,4]).

Moreover, other structures have been defined. For example, $E\subseteq \mathbb{X}$ is named pre-open [5] (respectively, regular open [5], $\beta$-open [6], $\alpha$-open [7], b-open [8]) when $E\subseteq int\left(cl\right(E\left)\right)$ (respectively, $E=int\left(cl\right(E\left)\right),E\subseteq cl\left(int\right(cl\left(E\right)\left)\right),E\subseteq int\left(cl\right(int\left(E\right)\left)\right),E\subseteq int\left(cl\right(E\left)\right)\cup cl\left(int\right(E\left)\right).$

Császár [9] established the concept of “generalized” in 1997, defining it as a collection that satisfied the following two requirements: (i) $\varphi \in \mathfrak{g}$; and (ii) for all $E_{\gamma }\in \mathfrak{g}:\gamma \in \Gamma ,$ we have ${\bigcup }_{\gamma \in \Gamma }{E}_{\gamma }\in \mathfrak{g},$ where $\mathbb{X}\ne \varphi ,$ and $\mathfrak{g}$ is a family of the power set $2^{\mathbb{X}}$. The collection $(\mathbb{X},\mathfrak{g})$ is considered a generalized topological space. Some research has studied the previous types of weak open sets in a generalized topology (see [10,11]).

According to [12], each member belonging to this space is named a $\mathfrak{g}$-open set, as well as $\mathfrak{g}$-closed, which symbolizes its complements. In addition, $C_{\mathfrak{g}}\left(\mathbb{X}\right)$ symbolizes the entire set of $\mathfrak{g}$-closed sets, while $c_{\mathfrak{g}}\left(E\right)$ and $i_{\mathfrak{g}}\left(E\right)$ symbolize the closure and interior of E, respectively, which are described as in the general situation.

Moreover, as per the results of [13], we have $c_{\mathfrak{g}}\left(c_{\mathfrak{g}}\left(E\right)\right)=c_{\mathfrak{g}}\left(E\right),$$i_{\mathfrak{g}}\left(i_{\mathfrak{g}}\left(E\right)\right)=i_{\mathfrak{g}}\left(E\right)$, and $i_{\mathfrak{g}}\left(E\right)\subseteq E\subseteq c_{\mathfrak{g}}\left(E\right)$. In addition, if $E=i_{\mathfrak{g}}\left(E\right),$ thus E is considered as $\mathfrak{g}$-open, and if $E=c_{\mathfrak{g}}\left(E\right),$ then E is considered as $\mathfrak{g}$-closed and $c_{\mathfrak{g}}\left(E\right)=\mathbb{X}\backslash \left(i_{\mathfrak{g}}(\mathbb{X}\backslash E)\right).$ This space required a lot of intention, study, and research (see [14,15,16,17,18]).

On the other hand, some classical structures appeared. “Filter” [19], “ideal” [20], and the well-known structure “grill” [21] were introduced as useful tools for learning topological concepts with numerous significant uses in general topology. The associated topology of a grill has been described and examined in [22]. This space has received significant attention from researchers. Some operators with good properties were defined and investigated (see [23,24,25]).

In 2022, Acharjee [26] proposed the dual structure of a grill; it was given the name “primal.” A collection $\mathcal{P}$ of $2^{\mathbb{X}}$ is known as primal on $\mathbb{X}$ whenever the following conditions are true $\forall E,F\subseteq \mathbb{X}:$ (i) $\mathbb{X}\notin \mathcal{P}$; and (ii) if $E\in \mathcal{P},$ with $F\subseteq E,$ then $F\in \mathcal{P},$ (iii) If $E\cap F\in \mathcal{P},$ then $E\in \mathcal{P}$ or $F\in \mathcal{P}.$ A topological space $(\mathbb{X},\tau )$ with a primal collection given on $\mathbb{X}$ is named a primal topological space and denoted by $(\mathbb{X},\tau ,\mathcal{P}).$ The primal topology has been rigorously studied, and its properties have been investigated (see [26,27,28]).

In 2023, a new category of generalized topology was presented via the concept of the primal by Al-Saadi and Al-Malki [29], whose structure was named a generalized primal topological space. Moreover, some properties were studied, and some theories and results were mentioned.

1.2. $\mathbf{GPT}$ Space

Throughout this section, we will recall the fundamental definitions and results about $\mathbf{GPT}$ spaces, which are presented in [29].

Definition 1. 

The symbol $(\mathbb{X},\mathfrak{g},\mathcal{P})$ references a generalized primal topological space ($\mathbf{GPT}$ space), which is a generalized topological space $(\mathbb{X},\mathfrak{g})$ together with a primal set $\mathcal{P}$ over $\mathbb{X}.$

Remark 1. 

$(\mathfrak{g},\mathcal{P})$-open sets is the symbol for the element of this space, and $(\mathfrak{g},\mathcal{P})$-closed sets denotes their complement.

The entire set of $(\mathfrak{g},\mathcal{P})$-closed symbols is referred to as $C_{(\mathfrak{g},\mathcal{P})}\left(\mathbb{X}\right).$ In addition, $c{l}_{(\mathfrak{g},\mathcal{P})}\left(E\right)$ denotes the closure of $E\subseteq \mathbb{X}.$

Definition 2. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space. Define an operator $\psi :\mathbb{X}\to 2^{2^{\mathbb{X}}}:$$\forall \mathtt{P}\in \psi \left(x\right),$ and we have $x\in \mathtt{P}.$

Remark 2. 

ψ is named as a generalized primal neighbourhood system over a space $\mathbb{X}.$ The entire set of a generalized primal neighbourhood system over $\mathbb{X}$ is symbolized via $\Psi \left(\mathbb{X}\right).$

Definition 3. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space. Let $E\subseteq \mathbb{X}.$ Define an operator ${(.)}^{\diamond }:2^{\mathbb{X}}\to 2^{\mathbb{X}}.$ Hence, an element $x\in \mathbb{X}$ belongs to $E^{\diamond }(\mathbb{X},\mathfrak{g},\mathcal{P})$ iff $E^c\cup {\mathtt{P}}^c\in \mathcal{P},$ for all $\mathtt{P}\in \psi \left(x\right).$

Theorem 1. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space. Let $E\subseteq \mathbb{X}.$ Thus, $E^{\diamond }\subseteq E,$ when $E^c$ is $(\mathfrak{g},\mathcal{P})$-open.

Theorem 2. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space. Let $E,F\subseteq \mathbb{X}.$ Hence, the following is always true:

(i) 

${\varphi }^{\diamond }=\varphi ,$

(ii) 

$E^{\diamond }$ is $(\mathfrak{g},\mathcal{P})$-closed,

(iii) 

${\left(E^{\diamond }\right)}^{\diamond }\subseteq E^{\diamond },$

(iv) 

$E^{\diamond }\subseteq F^{\diamond },$ whenever $E\subseteq F,$

(v) 

${}^{\diamond }E\cup F^{\diamond }={(E\cup F)}^{\diamond },$

(vi) 

${(E\cap F)}^{\diamond }\subseteq E^{\diamond }\cap F^{\diamond }.$

Theorem 3. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space. Let $E\subseteq \mathbb{X}$, and $C_{(\mathfrak{g},\mathcal{P})}\left(\mathbb{X}\right)\backslash \left\{\mathbb{X}\right\}$ is a primal over $\mathbb{X}.$ Hence, for every $(\mathfrak{g},\mathcal{P})$-open set $E,$ we have $E\subseteq E^{\diamond }.$

Lemma 1. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space. Let $E\subseteq \mathbb{X}.$ Thus, $E^{\diamond }=\varphi ,$ when $E^c\subseteq \mathbb{X}$ is not a primal.

Theorem 4. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space. Let $E,F\subseteq \mathbb{X}.$ Hence,

$$E^{\diamond }\backslash F^{\diamond }={(E\backslash F)}^{\diamond }\backslash F^{\diamond }.$$

Corollary 1. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space. Let $E,F\subseteq \mathbb{X}$, and $F^c$ is not a primal. Hence,

$${(E\cup F)}^{\diamond }=E^{\diamond }={(E\backslash F)}^{\diamond }.$$

Definition 4. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space. Let $E\subseteq \mathbb{X}.$ Define an operator $c{l}^{\diamond }:2^{\mathbb{X}}\to 2^{\mathbb{X}}$ given by $c{l}^{\diamond }\left(E\right)=E\cup E^{\diamond }.$

Remark 3. 

The next result states that the operator $c{l}^{\diamond }$ is formalized as a Kuratowski’s closure operator.

Theorem 5. 

Suppose $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space. The following holds for $E,F\subseteq \mathbb{X}$:

(i) 

$c{l}^{\diamond }\left(\varphi \right)=\varphi ,$

(ii) 

$E\subseteq c{l}^{\diamond }\left(E\right),$

(iii) 

$c{l}^{\diamond }\left(c{l}^{\diamond }\left(E\right)\right)=c{l}^{\diamond }\left(E\right),$

(iv) 

$c{l}^{\diamond }\left(E\right)\subseteq c{l}^{\diamond }\left(F\right),$ whenever $E\subseteq F,$

(v) 

$c{l}^{\diamond }\left(E\right)\cup c{l}^{\diamond }\left(F\right)=c{l}^{\diamond }(E\cup F).$

Theorem 6. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space. Let $E,F\subseteq \mathbb{X}.$ Thus, $E\cap F^{\diamond }\subseteq {(E\cap F)}^{\diamond },$ whenever E is $(\mathfrak{g},\mathcal{P})$-open.

2. Methodology

In this part, we introduce the methodologies used. To investigate our aims, we followed the traditional strategies in math. This study is based on projecting one of the important tools in topology, which is called a “primal collection”, into the field of “generalized topology.” This methodology led to the definition of a more general space with different characteristics. Then, we explored all the facts and features to satisfy our aims. We begin with the basic definitions, properties, and theorems of both fields. The operator $c{l}^{\diamond }$ can be considered a pivotal tool in the study, which led to many different results. Therefore, we used it to define some kinds of weak open sets. Consequentially, we proceed to the proper application of these new general weak open sets. The relationships among all concepts are drawn in two simple graphs for the reader.

3. Main Results

This part of the article provides the primary findings, given in two subsections. The first one presents some classes of $(\mathfrak{g},\mathcal{P})$-open sets and examines their fundamental characteristics and relationships. The second subsection is more in-depth and complicated because it presents more classes of $(\mathfrak{g},\mathcal{P})$-open sets depending on the first four concepts. Therefore, a lot of complex results that are connected to the notions appear together.

3.1. Some Classes of $(\mathfrak{g},\mathcal{P})$-Open Sets

This part of the section is focused on four types of weak $(\mathfrak{g},\mathcal{P})$-open sets, given the definitions of them in light of a new operator $c{l}^{\diamond }.$ Moreover, we study the relationships between them by giving proofs or inducing counterexamples. Finally, we present a diagram of these results.

Definition 5. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space. Take $E\subseteq \mathbb{X}.$ Thus,

(i) 

When $E\subseteq c{l}^{\diamond }\left(i_{\mathfrak{g}}E\right),$ E is named a $(\mathfrak{g},\mathcal{P})$-semi-open set.

(ii) 

When $E\subseteq i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(E\right)\right),$ E is named a $(\mathfrak{g},\mathcal{P})$-pre-open set.

(iii) 

When $E=i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(E\right)\right),$ E is named a $(\mathfrak{g},\mathcal{P})$-regular open set.

(iv) 

When $E\subseteq c_{\mathfrak{g}}\left(i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(E\right)\right)\right),$ E is named a $(\mathfrak{g},\mathcal{P})$-β-open set.

(v) 

When $E\subseteq i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(E\right)\right)\right),$ E is named a $(\mathfrak{g},\mathcal{P})$-α-open set.

The whole set of $(\mathfrak{g},\mathcal{P})$-semi-open sets is symbolized by $\sigma ,$ while the whole set of $(\mathfrak{g},\mathcal{P})$-pre-open sets is symbolized by $\pi .$ Moreover, the whole set of $(\mathfrak{g},\mathcal{P})$-$\alpha$-open sets is symbolized by $\alpha ,$ while $\beta$ is the symbolization of all $(\mathfrak{g},\mathcal{P})$-$\beta$-open sets.

Example 1. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space, where $\mathbb{X}=\{x_1,x_2,x_3,x_4\},$$\mathfrak{g}=\{\varphi ,\{x_1,x_2\},$$\{x_2,x_3\},\{x_1,x_2,x_3\},\mathbb{X}\}$, and $\mathcal{P}=\{\varphi ,\left\{x_3\right\},\left\{x_4\right\}\}$. Consider $E=\{x_1,x_2,x_4\}.$ Thus, E is $(\mathfrak{g},\mathcal{P})$-β-open.

Example 2. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space, where $\mathbb{X}=\{x_1,x_2,x_3,x_4\},$$\mathfrak{g}=\{\varphi ,\left\{x_1\right\},$$\left\{x_2\right\},\left\{x_3\right\},\{x_1,x_2\},\{x_2,x_3\},\{x_1,x_3\},\{x_1,x_2,x_3\},\mathbb{X}\}$, and $\mathcal{P}=\{\varphi ,\left\{x_2\right\},\left\{x_4\right\},\{x_2,x_4\}\}$. Consider $E=\{x_1,x_3,x_4\}.$ Thus, E is $(\mathfrak{g},\mathcal{P})$-semi-open.

Example 3. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space, where $\mathbb{X}=\{x_1,x_2,x_3,x_4\},$ $\mathfrak{g}=\{\varphi ,\{x_1,x_2,x_3\}\}$, and $\mathcal{P}=\{\varphi ,\left\{x_3\right\},\left\{x_4\right\},\{x_3,x_4\}\}$. Consider $E=\{x_1,x_2\}.$ Thus, E is $(\mathfrak{g},\mathcal{P})$-pre-open.

Definition 6. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space. Take $E\subseteq \mathbb{X}.$ When $(\mathbb{X}\backslash E)$ is a $(\mathfrak{g},\mathcal{P})$-semi-open (respectively, $(\mathfrak{g},\mathcal{P})$-pre-open, $(\mathfrak{g},\mathcal{P})$- regular open, $(\mathfrak{g},\mathcal{P})$-α-open, $(\mathfrak{g},\mathcal{P})$-β-open), thus E is named a $(\mathfrak{g},\mathcal{P})$-semi-closed (respectively, $(\mathfrak{g},\mathcal{P})$-pre-closed, $(\mathfrak{g},\mathcal{P})$- regular closed, $(\mathfrak{g},\mathcal{P})$-α-closed, $(\mathfrak{g},\mathcal{P})$-β-closed).

Theorem 7. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space. Then, the following holds:

(i) 

Each $(\mathfrak{g},\mathcal{P})$-semi-open set is $\mathfrak{g}$-semi-open.

(ii) 

Each $(\mathfrak{g},\mathcal{P})$-α-open set is $\mathfrak{g}$-α-open.

(iii) 

Each $(\mathfrak{g},\mathcal{P})$-β-open set is $\mathfrak{g}$-β-open.

(iv) 

Each $(\mathfrak{g},\mathcal{P})$-pre-open set is $\mathfrak{g}$-pre-open.

Proof. 

(i) Consider E as $(\mathfrak{g},\mathcal{P})$-semi-open. Thus,

$$E\subseteq c{l}^{\diamond }\left(i_{\mathfrak{g}}E\right)\subseteq \left(i_{\mathfrak{g}}E\right)\cup {\left(i_{\mathfrak{g}}E\right)}^{\diamond }\subseteq \left(i_{\mathfrak{g}}E\right)\cup c{l}_{(\mathfrak{g},\mathcal{P})}\left(i_{\mathfrak{g}}E\right),$$

from Theorem 2 (ii). Hence, $E\subseteq c{l}_{(\mathfrak{g},\mathcal{P})}\left(i_{\mathfrak{g}}E\right)$ implies $E\subseteq c_{\mathfrak{g}}\left(i_{\mathfrak{g}}E\right).$ Therefore, E is $\mathfrak{g}$-semi-open.

In a similar manner, we can also prove the rest of the statements. □

Theorem 8. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space with $E\subseteq \mathbb{X}.$ Thus, the following holds:

(i) 

E forms a $(\mathfrak{g},\mathcal{P})$-α-open set iff E is $(\mathfrak{g},\mathcal{P})$-semi-open as well as $(\mathfrak{g},\mathcal{P})$-pre-open.

(ii) 

Considering E as $(\mathfrak{g},\mathcal{P})$-semi-open, E is $(\mathfrak{g},\mathcal{P})$-β-open.

(iii) 

Considering E as $(\mathfrak{g},\mathcal{P})$-pre-open, E is $(\mathfrak{g},\mathcal{P})$-β-open.

Proof. 

(i) Consider E as $(\mathfrak{g},\mathcal{P})$-$\alpha$-open. Therefore, E is contained in $i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(E\right)\right)\right).$ Since $i_{\mathfrak{g}}\left(E\right)\subseteq E,$$c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(E\right)\right)$ is contained in $c{l}^{\diamond }\left(E\right).$ This implies,

$$E\subseteq i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(E\right)\right)\right),$$

which is contained in $i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(E\right)\right).$ Therefore, E is $(\mathfrak{g},\mathcal{P})$-pre-open. In addition,

$$i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(E\right)\right)\right)\subseteq c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(E\right)\right).$$

This means that E is contained in $c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(E\right)\right).$

Conversely, whenever E is $(\mathfrak{g},\mathcal{P})$-semi-open and $(\mathfrak{g},\mathcal{P})$-pre-open, $E\subseteq i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(E\right)\right)$, which is contained in

$$i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(E\right)\right)\right)\right)=i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(E\right)\right)\right).$$

Therefore, $E\subseteq i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(E\right)\right)\right).$

(ii) Consider E as $(\mathfrak{g},\mathcal{P})$-semi-open. Thus, $E\subseteq c_{\mathfrak{g}}\left(i_{\mathfrak{g}}\left(E\right)\right)$ from Theorem 7 (i). However, $E\subseteq c{l}^{\diamond }\left(E\right)$; thus, $E\subseteq c_{\mathfrak{g}}\left(i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(E\right)\right)\right).$ Therefore, we are done.

(iii) Consider E as $(\mathfrak{g},\mathcal{P})$-pre-open. Thus,

$$E\subseteq i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(E\right)\right)\subseteq c_{\mathfrak{g}}\left(i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(E\right)\right)\right),$$

which proves the claim. □

Corollary 2. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space. Thus, the following holds:

(i) 

$\pi \cap \sigma =\alpha .$

(ii) 

$\mathfrak{g}-\mathit{open}\subset \alpha \subset \sigma \subset \beta .$

(iii) 

$\alpha \subset \pi \subset \beta .$

Proposition 1. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space. Hence, for all $E\subseteq \mathbb{X}$, the following statements are equivalent:

(i) 

E is $(\mathfrak{g},\mathcal{P})$-regular open;

(ii) 

E is $(\mathfrak{g},\mathcal{P})$-semi-closed as well as $(\mathfrak{g},\mathcal{P})$-open;

(iii) 

E is $(\mathfrak{g},\mathcal{P})$-pre-open as well as $(\mathfrak{g},\mathcal{P})$-semi-closed;

(iv) 

E is $(\mathfrak{g},\mathcal{P})$-α-open as well as $(\mathfrak{g},\mathcal{P})$-β-closed;

(v) 

E is $(\mathfrak{g},\mathcal{P})$-α-open as well as $(\mathfrak{g},\mathcal{P})$-semi-closed;

(vi) 

E is $(\mathfrak{g},\mathcal{P})$-open as well as $(\mathfrak{g},\mathcal{P})$-β-closed.

Proof. 

From this, the proof comes automatically. □

Remark 4. 

Based on the previous results, a conclusion is drawn as follows:

Remark 5. 

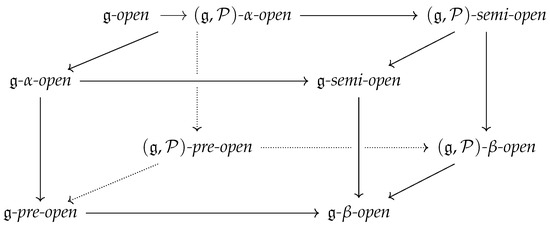
The next examples illustrate that the opposite direction of the relationship in Figure 1 is not always satisfied.

Figure 1. Relationships between the $\mathfrak{g}$-open set and other types of open sets in $\mathbf{GPT}$ space.

Example 4. 

In Example 1, we note that:

(i) 

E is $\mathfrak{g}$-semi-open, where $c_{\mathfrak{g}}\left(i_{\mathfrak{g}}\right)=\mathbb{X}.$ However, E is not $(\mathfrak{g},\mathcal{P})$-semi-open, where $c{l}^{\diamond }\left(i_{\mathfrak{g}}\right)=\{x_1,x_2\}.$

(ii) 

E is $(\mathfrak{g},\mathcal{P})$-β-open, where $c_{\mathfrak{g}}\left(i_{\mathfrak{g}}\left(c_{\mathfrak{g}}\left(E\right)\right)\right)=\mathbb{X}.$ However, E is not $(\mathfrak{g},\mathcal{P})$-semi-open.

(iii) 

E is $(\mathfrak{g},\mathcal{P})$-β-open. However, E is not $(\mathfrak{g},\mathcal{P})$-pre-open, where $i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(E\right)\right)=\{x_1,x_2\}$.

Example 5. 

In Example 2, E is $(\mathfrak{g},\mathcal{P})$-semi-open, where $c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(E\right)\right)=\{x_1,x_3,x_4\}.$ However, E is not $(\mathfrak{g},\mathcal{P})$-α-open.

Example 6. 

In Example 3, E is $(\mathfrak{g},\mathcal{P})$-pre-open, where $i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(E\right)\right)=\{x_1,x_2\}.$ However, E is not $(\mathfrak{g},\mathcal{P})$-α-open.

Proposition 2. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space. Thus, the following holds:

(i) 

The countable union of $(\mathfrak{g},\mathcal{P})$-semi-open sets is $(\mathfrak{g},\mathcal{P})$-semi-open.

(ii) 

The countable union of $(\mathfrak{g},\mathcal{P})$-pre-open sets is $(\mathfrak{g},\mathcal{P})$-pre-open.

(iii) 

The countable union of $(\mathfrak{g},\mathcal{P})$-α-open sets is $(\mathfrak{g},\mathcal{P})$-α-open.

(iv) 

The countable union of $(\mathfrak{g},\mathcal{P})$-β-open sets is $(\mathfrak{g},\mathcal{P})$-β-open.

Proof. 

(i) Consider $\{E_{\gamma }:\gamma \in \Gamma \}$ as a collection of $(\mathfrak{g},\mathcal{P})$-semi-open sets. Thus, $E_{\gamma }\subseteq c{l}^{\diamond }\left(i_{\mathfrak{g}}{E}_{\gamma }\right),$$\forall \gamma \in \Gamma .$ Hence,

$$\bigcup _{\gamma \in \Gamma }{E}_{\gamma }\subseteq \bigcup _{\gamma \in \Gamma }c{l}^{\diamond }\left(i_{\mathfrak{g}}{E}_{\gamma }\right)\subseteq c{l}^{\diamond }(i_{\mathfrak{g}}(\bigcup _{\gamma \in \Gamma }{E}_{\gamma })).$$

Therefore, ${\bigcup }_{\gamma \in \Gamma }\{E_{\gamma }:\gamma \in \Gamma \}$ is $(\mathfrak{g},\mathcal{P})$-semi-open.

In the same way, we can prove (ii), (iii), and (iv). □

Corollary 3. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space. All of the collections $\sigma ,$$\pi ,$$\alpha ,$ and β form generalized primal topological spaces with a primal set $\mathcal{P}$ over $\mathbb{X}.$

3.2. Regular $(\mathfrak{g},\mathcal{P})$-Semi-Open and $(\mathfrak{g},\mathcal{P})$-Dense

Throughout this section, we will give definitions of other types of weak $(\mathfrak{g},\mathcal{P})$-open sets and explain some of the properties and relationships of the previous notions. In addition, we give a comparison between the properties that satisfy in topological spaces but not in the case of $\mathbf{GPT}$ spaces.

Definition 7. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space, with $E\subseteq X.$ If there is $(\mathfrak{g},\mathcal{P})$-regular open set F satisfying $F\subseteq E\subseteq c{l}^{\diamond }\left(E\right),$ then E is called regular $(\mathfrak{g},\mathcal{P})$-semi-open.

Proposition 3. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space, with $E\subseteq \mathbb{X}.$ Thus, the following are equivalent:

(i) 

E is regular $(\mathfrak{g},\mathcal{P})$-semi-open;

(ii) 

E is $(\mathfrak{g},\mathcal{P})$-semi-open as well as $(\mathfrak{g},\mathcal{P})$-semi-closed;

(iii) 

E is $(\mathfrak{g},\mathcal{P})$-β-open as well as $(\mathfrak{g},\mathcal{P})$-semi-closed;

(iv) 

E is $(\mathfrak{g},\mathcal{P})$-semi-open as well as $(\mathfrak{g},\mathcal{P})$-β-closed.

Proof. 

The claim was proven directly from Proposition 1. □

Remark 6. 

By using Proposition 3, we can note that whenever E is regular $(\mathfrak{g},\mathcal{P})$-semi-open, $(\mathbb{X}\backslash E)$ is regular $(\mathfrak{g},\mathcal{P})$-semi-open as well.

Definition 8. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space. Let $E\subseteq \mathbb{X}.$ If $c{l}^{\diamond }\left(E\right)=\mathbb{X}$. Thus, E is named a $(\mathfrak{g},\mathcal{P})$-dense set.

Moreover, E is named $(\mathfrak{g},\mathcal{P})$-dense whenever $(\mathbb{X}\backslash E)$ is $(\mathfrak{g},\mathcal{P})$-dense or $i_{\mathfrak{g}}\left(E\right)=\varphi .$

Remark 7. 

In a $\mathbf{GPT}$ space, the $(\mathfrak{g},\mathcal{P})$-dense sets need not be $(\mathfrak{g},\mathcal{P})$-pre-open sets, unlike in topological spaces. The next example shows that.

Example 7. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space, where $\mathbb{X}=\{x_1,x_2,x_3,x_4\},$$E=\{x_2,x_3,x_4\},$$\mathfrak{g}=\{\varphi ,\{x_1,x_2\},\{x_2,x_3\},\{x_1,x_2,x_3\}\}$, and $\mathcal{P}=\{\varphi ,\left\{x_1\right\},\left\{x_3\right\},\left\{x_4\right\},\{x_1,x_3\},\{x_1,x_4\},$$\{x_3,x_4\}\}.$

Hence, we have $c{l}^{\diamond }\left(E\right)=\mathbb{X}$ and $i_{\mathfrak{g}}\left(\mathbb{X}\right)=\{x_1,x_2,x_3\}.$

Therefore, E is $(\mathfrak{g},\mathcal{P})$-dense, which means it is not a $(\mathfrak{g},\mathcal{P})$-pre-open set.

Lemma 2. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space. Take $E\subseteq \mathbb{X}.$ When F is $(\mathfrak{g},\mathcal{P})$-open, $F\cap c{l}^{\diamond }\left(E\right)\subseteq c{l}^{\diamond }(F\cap E).$

Proof. 

Consider F as $(\mathfrak{g},\mathcal{P})$-open. Thus,

$$F\cap c{l}^{\diamond }\left(E\right)=F\cap (E^{\diamond }\cup E).$$

This implies

$$F\cap c{l}^{\diamond }\left(E\right)=(F\cap E^{\diamond })\cup (F\cap E).$$

Via Theorem 6, we get

$$F\cap c{l}^{\diamond }\left(E\right)\subseteq {(F\cap E)}^{\diamond }\cup (F\cap E)=c{l}^{\diamond }(F\cap E).$$

Therefore, $F\cap c{l}^{\diamond }\left(E\right)\subseteq c{l}^{\diamond }(F\cap E).$ □

Theorem 9. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space. For $E,G\subseteq \mathbb{X},$ the following holds.

(i) 

$c{l}^{\diamond }\left(E\right)=c{l}^{\diamond }\left(i_{\mathfrak{g}}E\right)⟺$ E is $(\mathfrak{g},\mathcal{P})$-semi-open.

(ii) 

E is $(\mathfrak{g},\mathcal{P})$-semi-open ⟺ ∃ a $(\mathfrak{g},\mathcal{P})$-open set F satisfying $F\subseteq E\subseteq c{l}^{\diamond }\left(F\right).$

(iii) 

For $E\subseteq G,$$G\subseteq c{l}^{\diamond }\left(E\right).$ Hence, G is $(\mathfrak{g},\mathcal{P})$-semi-open whenever E is $(\mathfrak{g},\mathcal{P})$-semi-open.

(iv) 

Whenever E is $(\mathfrak{g},\mathcal{P})$-semi-open and F is $(\mathfrak{g},\mathcal{P})$-open, $E\cap F$ is $(\mathfrak{g},\mathcal{P})$-semi-open.

Proof. 

(i) Suppose that E is $(\mathfrak{g},\mathcal{P})$-semi-open. Thus, $E\subseteq c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(E\right)\right).$ Hence, $c{l}^{\diamond }\left(E\right)\subseteq c{l}^{\diamond }\left(c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(E\right)\right)\right).$ From Theorem 5 (iii), we get $c{l}^{\diamond }\left(E\right)\subseteq c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(E\right)\right).$ In addition, $c{l}^{\diamond }$ is monotonic. Then, $i_{\mathfrak{g}}\left(E\right)$ contained in E, which implies $c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(E\right)\right)$ is contained in $c{l}^{\diamond }\left(E\right).$

Conversely, let $c{l}^{\diamond }\left(E\right)=c{l}^{\diamond }\left(i_{\mathfrak{g}}E\right).$ Then, $c{l}^{\diamond }\left(E\right)$ is contained in $c{l}^{\diamond }\left(i_{\mathfrak{g}}E\right).$ However, $E\subseteq c{l}^{\diamond }\left(E\right)$; hence, $E\subseteq c{l}^{\diamond }\left(i_{\mathfrak{g}}E\right).$

(ii) Suppose that E is $(\mathfrak{g},\mathcal{P})$-semi-open. Hence, $E\subseteq c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(E\right)\right).$ Consider $i_{\mathfrak{g}}\left(E\right)=F.$ Thus, F is a subset of $E,$ which is contained in $c{l}^{\diamond }\left(F\right)$, and F is $(\mathfrak{g},\mathcal{P})$-open.

Conversely, suppose that $F\subseteq E\subseteq c{l}^{\diamond }\left(F\right)$ for $(\mathfrak{g},\mathcal{P})$-open set F. Thus, $F\subseteq i_{\mathfrak{g}}\left(E\right).$ Thus, $c{l}^{\diamond }\left(F\right)\subseteq c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(E\right)\right)$ implies $E\subseteq c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(E\right)\right).$ Therefore, E is $(\mathfrak{g},\mathcal{P})$-semi-open.

(iii) Consider E as $(\mathfrak{g},\mathcal{P})$-semi-open. By (ii), ∃$(\mathfrak{g},\mathcal{P})$-open set F satisfying $F\subseteq E\subseteq c{l}^{\diamond }\left(F\right).$ Therefore,

$$c{l}^{\diamond }\left(F\right)\subseteq c{l}^{\diamond }\left(E\right)\subseteq c{l}^{\diamond }\left(c{l}^{\diamond }\left(F\right)\right)=c{l}^{\diamond }\left(F\right).$$

This implies

$$F\subseteq E\subseteq G\subseteq c{l}^{\diamond }\left(E\right)\subseteq c{l}^{\diamond }\left(F\right).$$

Therefore, G is $(\mathfrak{g},\mathcal{P})$-semi-open.

(iv) Consider E as $(\mathfrak{g},\mathcal{P})$-semi-open and F as $(\mathfrak{g},\mathcal{P})$-open. Then, $E\subseteq c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(E\right)\right).$ Hence, from Lemma 2, we get

$$E\cap F\subseteq c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(E\right)\right)\cap F\subseteq c{l}^{\diamond }\left(i_{\mathfrak{g}}(E\cap F)\right).$$

Hence, we prove the claim. □

Theorem 10. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space. Let $E\subseteq \mathbb{X}.$ When E is $(\mathfrak{g},\mathcal{P})$-semi-closed, $i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(E\right)\right)\subseteq E.$

Proof. 

The complement of E is $(\mathfrak{g},\mathcal{P})$-semi-open, whenever E is $(\mathfrak{g},\mathcal{P})$-semi-closed. Thus, by definition, $(\mathbb{X}\backslash E)\subseteq c{l}^{\diamond }\left(i_{\mathfrak{g}}(\mathbb{X}\backslash E)\right).$ From Theorem 7 (i), we have

$$(\mathbb{X}\backslash E)\subseteq c_{\mathfrak{g}}\left(i_{\mathfrak{g}}(\mathbb{X}\backslash E)\right)=(\mathbb{X}\backslash i_{\mathfrak{g}}\left(c_{\mathfrak{g}}\left(E\right)\right))\subseteq (\mathbb{X}\backslash i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(E\right)\right)).$$

Therefore, $i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(E\right)\right)\subseteq E.$ □

Remark 8. 

(i) It is important to know that the inverse of this theory is not necessarily true; this is explained in detail in the next example.

(ii) With extra conditions, the inverse is always true, as the next result shows.

Example 8. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space, where $\mathbb{X}=\{x_1,x_2,x_3,x_4\},$ $E=\{x_1,x_3\},$ $\mathfrak{g}=\{\varphi ,\{x_2,x_3\},\{x_3,x_4\},\mathbb{X}\}$, and $\mathcal{P}=\{\varphi ,\left\{x_2\right\},\left\{x_4\right\},\{x_2,x_4\}\}$. Thus, we have $c{l}^{\diamond }\left(E\right)=\{x_1,x_3\}.$ Hence, $i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(E\right)\right)=\varphi$ implies $i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(E\right)\right)\subseteq E.$ However, $(\mathbb{X}\backslash E)=\{x_2,x_4\}$ and $i_{\mathfrak{g}}\left(\{x_2,x_4\}\right)=\varphi .$ Thus, $c{l}^{\diamond }\left(i_{\mathfrak{g}}(\mathbb{X}\backslash E)\right)=\varphi .$ Hence, $(\mathbb{X}\backslash E)=\{x_2,x_4\}⊈c{l}^{\diamond }\left(i_{\mathfrak{g}}(\mathbb{X}\backslash E)\right)=\varphi .$ Therefore, $(\mathbb{X}\backslash E)$ is not $(\mathfrak{g},\mathcal{P})$-semi-open, and E is not $(\mathfrak{g},\mathcal{P})$-semi-closed.

Theorem 11. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space and $(\mathbb{X}\backslash i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(E\right)\right))=c{l}^{\diamond }\left(i_{\mathfrak{g}}(\mathbb{X}\backslash E)\right),$ for $E\subseteq \mathbb{X}.$ Hence, $i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(E\right)\right)\subseteq E$ iff E is $(\mathfrak{g},\mathcal{P})$-semi closed.

Proof. 

Consider $i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(E\right)\right)\subseteq E.$ By this hypothesis, we obtain

$$(\mathbb{X}\backslash E)\subseteq (\mathbb{X}\backslash i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(E\right)\right))=c{l}^{\diamond }\left(i_{\mathfrak{g}}(\mathbb{X}\backslash E)\right).$$

Hence, $(\mathbb{X}\backslash E)$ is $(\mathfrak{g},\mathcal{P})$-semi-open. The other direction is directly from Theorem 10. □

Theorem 12. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space. The following holds for $E\subseteq \mathbb{X}.$

(i) 

Whenever E is a $(\mathfrak{g},\mathcal{P})$-pre-closed set, $c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(E\right)\right)\subseteq E.$

(ii) 

Whenever E is a $(\mathfrak{g},\mathcal{P})$-α-closed set, $c_{\mathfrak{g}}\left(i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(E\right)\right)\right)\subseteq E.$

(iii) 

Whenever E is a $(\mathfrak{g},\mathcal{P})$-β-closed set, $i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(E\right)\right)\right)\subseteq E.$

Proof. 

(i) Since E is $(\mathfrak{g},\mathcal{P})$-pre-closed, its complement is $(\mathfrak{g},\mathcal{P})$-pre-open. Hence, by definition, $(\mathbb{X}\backslash E)\subseteq i_{\mathfrak{g}}\left(c{l}^{\diamond }(\mathbb{X}\backslash E)\right).$ By Theorem 7 (iv), we obtain

$$(\mathbb{X}\backslash E)\subseteq i_{\mathfrak{g}}\left(c_{\mathfrak{g}}(\mathbb{X}\backslash E)\right)=(\mathbb{X}\backslash c_{\mathfrak{g}}\left(i_{\mathfrak{g}}\left(E\right)\right))\subseteq (\mathbb{X}\backslash c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(E\right)\right)).$$

Hence, $c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(E\right)\right)\subseteq E.$

The proofs of (ii) and (iii) come in the same way. □

Theorem 13. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space. When E is $(\mathfrak{g},\mathcal{P})$-pre-open, thus E can be written as the intersection of $(\mathfrak{g},\mathcal{P})$-dense set and $(\mathfrak{g},\mathcal{P})$-regular open set.

Proof. 

Consider E as $(\mathfrak{g},\mathcal{P})$-pre-open. Then, $E\subseteq i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(E\right)\right).$ Then, E can be represented as

$$E=i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(E\right)\right)\cap (E\cup (\mathbb{X}\backslash c{l}^{\diamond }\left(E\right))).$$

Now, let $F=i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(E\right)\right).$ Let $G=(E\cup (\mathbb{X}\backslash c{l}^{\diamond }\left(E\right))).$ Thus, F is $(\mathfrak{g},\mathcal{P})$-regular open. In addition, since $E\subseteq G,$$c{l}^{\diamond }\left(E\right)\subseteq c{l}^{\diamond }\left(G\right).$ Hence,

$$(\mathbb{X}\backslash c{l}^{\diamond }\left(E\right))\subseteq G\subseteq c{l}^{\diamond }\left(G\right).$$

Thus, $c{l}^{\diamond }\left(G\right)=\mathbb{X}$, which means that G is $(\mathfrak{g},\mathcal{P})$-dense set. Hence, we are done. □

Corollary 4. 

For a $\mathbf{GPT}$ space, whenever E is $(\mathfrak{g},\mathcal{P})$-pre-closed, E is the union of $F,$ which is a $(\mathfrak{g},\mathcal{P})$-regular closed set, and $G,$ for which $i_{\mathfrak{g}}=\varphi .$

Theorem 14. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space. When E is $(\mathfrak{g},\mathcal{P})$-semi-open, E can be written as the intersection of a set $F,$ where $i_{\mathfrak{g}}\left(F\right)$ is $(\mathfrak{g},\mathcal{P})$-dense and $(\mathfrak{g},\mathcal{P})$-regular closed set $G.$

Proof. 

Consider E as $(\mathfrak{g},\mathcal{P})$-semi open. Thus, $E\subseteq c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(E\right)\right).$ Then, E can be represented as

$$E=c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(E\right)\right)\cap (E\cup (\mathbb{X}\backslash c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(E\right)\right))).$$

Now, let $F=E\cup (\mathbb{X}\backslash c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(E\right)\right))$ and $G=c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(E\right)\right)$. Thus, G is $(\mathfrak{g},\mathcal{P})$-regular closed. In addition, since $E\subseteq F,$ $c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(E\right)\right)\subseteq c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(F\right)\right).$ However, $(\mathbb{X}\backslash c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(E\right)\right))\subseteq F$, and $(\mathbb{X}\backslash c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(E\right)\right))$ is $(\mathfrak{g},\mathcal{P})$-open. This implies

$$(\mathbb{X}\backslash c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(E\right)\right))\subseteq i_{\mathfrak{g}}\left(F\right)\subseteq c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(F\right)\right).$$

Thus, $c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(F\right)\right)=\mathbb{X}.$ □

Corollary 5. 

In a $\mathbf{GPT}$ space, whenever E is $(\mathfrak{g},\mathcal{P})$-semi-closed, E is the union of $F,$ which is a $(\mathfrak{g},\mathcal{P})$-regular open set, and $G,$ whose closure is $i_{\mathfrak{g}}=\varphi$ in a $\mathbf{GPT}$ space $\mathbb{X}.$

Proposition 4. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space. For $E,F\subseteq \mathbb{X}$, the following holds:

(i) 

Whenever $E\in \sigma$ and $F\in \alpha ,$$E\cap F\in \sigma .$

(ii) 

Whenever $E\in \pi$ and $F\in \alpha ,$$E\cap F\in \pi .$

(iii) 

Whenever $E,F\in \alpha ,$ $E\cap F\in \alpha .$

Proof. 

By using Theorem 8 and Corollary 2, the proof comes directly. □

4. Decomposition of $(\mathfrak{g},\mathcal{P})$-Continuity

This part of the article provides an important application of the findings in the preceding section. We will give the concept of $(\mathfrak{g},\mathcal{P})$-continuity, which is based on the $(\mathfrak{g},\mathcal{P})$-open set. Then, we present some kinds of continuity that are based on the weak $(\mathfrak{g},\mathcal{P})$-open sets. The relationship between these concepts will be studied and drawn in a simple graph. The study of this combination led to the decomposition of this kind of $(\mathfrak{g},\mathcal{P})$-continuity.

Definition 9. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ and $({\mathbb{X}}^{‵},{\mathfrak{g}}^{‵},{\mathcal{P}}^{‵})$ are $\mathbf{GPT}$ spaces. Suppose that $\mathtt{E}$ is $({\mathfrak{g}}^{‵},{\mathcal{P}}^{‵})$-open. Define a function $\mathcal{U}:\mathbb{X}\to {\mathbb{X}}^{‵}.$ Hence, $\mathcal{U}$ is named $(\mathfrak{g},\mathcal{P})$-continuous iff ${\mathcal{U}}^{-1}\left(\mathtt{E}\right)$ is $(\mathfrak{g},\mathcal{P})$-open.

Definition 10. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space and $({\mathbb{X}}^{‵},{\mathfrak{g}}^{‵})$ is a $\mathbf{GT}$ space. Hence, $\mathcal{U}:\mathbb{X}\to {\mathbb{X}}^{‵}$ is named $(\mathfrak{g},\mathcal{P})$-semi-continuous (respectively, $(\mathfrak{g},\mathcal{P})$-pre-continuous, $(\mathfrak{g},\mathcal{P})$-α-continuous, $(\mathfrak{g},\mathcal{P})$-β-continuous) if every ${\mathcal{U}}^{-1}\left(\mathtt{E}\right),$ where $\mathtt{E}$ is $\mathfrak{g}$-open is $(\mathfrak{g},\mathcal{P})$- semi-open (respectively, $(\mathfrak{g},\mathcal{P})$-pre-open, $(\mathfrak{g},\mathcal{P})$-α-open, $(\mathfrak{g},\mathcal{P})$-β-open).

Theorem 15. 

Consider $\mathcal{U}:(\mathbb{X},\mathfrak{g},\mathcal{P})\to ({\mathbb{X}}^{‵},{\mathfrak{g}}^{‵}).$ Thus, the following are equivalent:

(i) 

$\mathcal{U}$ is $(\mathfrak{g},\mathcal{P})$-α-continuous;

(ii) 

$\forall x\in \mathbb{X}$ and ${\mathtt{E}}^{‵}\in {\mathfrak{g}}^{‵}$ satisfy $\mathcal{U}\left(x\right)\in {\mathtt{E}}^{‵},$ and there exists $\mathtt{E}\in \alpha$ satisfying $x\in \mathtt{E}$ and $\mathcal{U}\left(\mathtt{E}\right)\subset {\mathtt{E}}^{‵};$

(iii) 

${\mathcal{U}}^{-1}\left({\mathtt{F}}^{‵}\right):{\mathtt{F}}^{‵}$ is $\mathfrak{g}$-closed and $(\mathfrak{g},\mathcal{P})$-closed.

Proof. 

$\left(i\right)\Rightarrow \left(ii\right)$ For every $x\in \mathbb{X}$, suppose that ${\mathtt{E}}^{‵}\in {\mathfrak{g}}^{‵}$ with $\mathcal{U}\left(x\right)\in {\mathtt{E}}^{‵}$. Since $\mathcal{U}$ is $(\mathfrak{g},\mathcal{P})$-$\alpha$-continuous, ${\mathcal{U}}^{-1}\left({\mathtt{E}}^{‵}\right)$ is $(\mathfrak{g},\mathcal{P})$-$\alpha$-open with $x\in {\mathcal{U}}^{-1}\left({\mathtt{E}}^{‵}\right).$ Let ${\mathcal{U}}^{-1}\left({\mathtt{E}}^{‵}\right)=\mathtt{E}.$ Hence, $x\in \mathtt{E}$ and $\mathcal{U}\left(\mathtt{E}\right)\subset {\mathtt{E}}^{‵}.$

$\left(ii\right)\Rightarrow \left(i\right)$ Suppose that ${\mathtt{E}}^{‵}\subseteq {\mathbb{X}}^{‵},$ where $x\in {\mathcal{U}}^{-1}\left({\mathtt{E}}^{‵}\right).$ Hence, $\mathcal{U}\left(x\right)\in {\mathtt{E}}^{‵}\in {\mathfrak{g}}^{‵}.$ Thus, by (ii), there exists a $(\mathfrak{g},\mathcal{P})$-$\alpha$-open set $\mathtt{E}$ such that $x\in \mathtt{E}$ and $\mathcal{U}\left(\mathtt{E}\right)\subset {\mathtt{E}}^{‵}.$ Hence,

$$x\in \mathtt{E}\subseteq i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(\mathtt{E}\right)\right)\right)\subseteq i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(i_{\mathfrak{g}}\left({\mathcal{U}}^{-1}\left({\mathtt{E}}^{‵}\right)\right)\right)\right).$$

Thus, ${\mathcal{U}}^{-1}\left({\mathtt{E}}^{‵}\right)\subseteq i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(i_{\mathfrak{g}}\left({\mathcal{U}}^{-1}\left({\mathtt{E}}^{‵}\right)\right)\right)\right).$ Therefore, $\mathcal{U}$ is $(\mathfrak{g},\mathcal{P})$-$\alpha$-continuous.

The proof of the rest of the equivalents is obvious. □

Theorem 16. 

Consider $\mathcal{U}:(\mathbb{X},\mathfrak{g},\mathcal{P})\to ({\mathbb{X}}^{‵},{\mathfrak{g}}^{‵}).$ Thus, we have:

(i) 

$\mathcal{U}$ is $(\mathfrak{g},\mathcal{P})$-α-continuous iff $\mathcal{U}$ is $(\mathfrak{g},\mathcal{P})$-semi continuous as well as $(\mathfrak{g},\mathcal{P})$-pre continuous.

(ii) 

Each $(\mathfrak{g},\mathcal{P})$-semi-continuous as well as each $(\mathfrak{g},\mathcal{P})$-pre-continuous set is $(\mathfrak{g},\mathcal{P})$-β-continuous.

Proof. 

It comes automatically from Theorem 8. □

The next theorem is based on the fact, shown in [7], that follows: If $(\mathbb{X},\tau )$ is a topological space, then the collection of all $\alpha$-open sets on $\mathbb{X}$ forms a topology finer than $\tau$.

Theorem 17. 

A function $\mathcal{U}:(\mathbb{X},\mathfrak{g},\mathcal{P})\to ({\mathbb{X}}^{‵},{\mathfrak{g}}^{‵})$ is $(\mathfrak{g},\mathcal{P})$-α-continuous iff $\mathcal{U}:(\mathbb{X},\alpha )\to ({\mathbb{X}}^{‵},{\mathfrak{g}}^{‵})$ is $\mathfrak{g}$-continuous.

Proof. 

Suppose that $\mathcal{U}:(\mathbb{X},\mathfrak{g},\mathcal{P})\to ({\mathbb{X}}^{‵},{\mathfrak{g}}^{‵})$ is $(\mathfrak{g},\mathcal{P})$-$\alpha$-continuous. By Corollary 3, the collection $\alpha$ forms a $\mathbf{GPT}$ space finer than $(\mathbb{X},\mathfrak{g},\mathcal{P}).$ Hence, $\mathcal{U}:(\mathbb{X},\alpha )\to ({\mathbb{X}}^{‵},{\mathfrak{g}}^{‵})$ is $\mathfrak{g}$-continuous.

Conversely, suppose that $\mathcal{U}:(\mathbb{X},\alpha )\to ({\mathbb{X}}^{‵},{\mathfrak{g}}^{‵})$ is $\mathfrak{g}$-continuous. By Corollary 2 (ii), every $\mathfrak{g}$-open set is $(\mathfrak{g},\mathcal{P})$-$\alpha$-open. Hence, $\mathcal{U}:(\mathbb{X},\mathfrak{g},\mathcal{P})\to ({\mathbb{X}}^{‵},{\mathfrak{g}}^{‵})$ is $(\mathfrak{g},\mathcal{P})$-$\alpha$-continuous. □

Theorem 18. 

Consider $\mathcal{U}:(\mathbb{X},\mathfrak{g},\mathcal{P})\to ({\mathbb{X}}^{‵},{\mathfrak{g}}^{‵}).$ Hence, $\mathcal{U}$ is a $(\mathfrak{g},\mathcal{P})$-α-continuous iff the graph function $\mathcal{H}:\mathbb{X}\to \mathbb{X}\times {\mathbb{X}}^{‵},$ given by $\mathcal{H}\left(x\right)=(x,\mathcal{U}(x\left)\right)$, is $(\mathfrak{g},\mathcal{P})$-α-continuous.

Proof. 

Let $\mathcal{U}$ be $(\mathfrak{g},\mathcal{P})$-$\alpha$-continuous. Consider $x\in \mathbb{X}$ and $\mathtt{F}$ as open sets in $\mathbb{X}\times {\mathbb{X}}^{‵}$ with $\mathcal{H}\left(x\right)\in \mathtt{F}.$ Thus, there exist $\mathtt{E}\in \mathfrak{g}$ and ${\mathtt{E}}^{‵}\in {\mathfrak{g}}^{‵}$ satisfying

$$\mathcal{H}\left(x\right)=(x,\mathcal{U}\left(x\right))\subseteq \mathtt{E}\times {\mathtt{E}}^{‵}\subseteq \mathtt{F}.$$

However, $\mathcal{U}$ is a $(\mathfrak{g},\mathcal{P})$-$\alpha$-continuous; thus, there exists a $(\mathfrak{g},\mathcal{P})$-$\alpha$-open set $\mathtt{G}:x\in \mathtt{G}$, and $\mathcal{U}\left(\mathtt{G}\right)\subseteq {\mathtt{E}}^{‵}.$ From Proposition 4, we determine that $\mathtt{G}\cap \mathtt{E}$ is $(\mathfrak{g},\mathcal{P})$-$\alpha$-open. Hence,

$$\mathcal{H}(\mathtt{G}\cap \mathtt{E})\subseteq \mathtt{E}\times {\mathtt{E}}^{‵}\subseteq \mathtt{F}.$$

Therefore, $\mathcal{H}$ is $(\mathfrak{g},\mathcal{P})$-$\alpha$-continuous.

Conversely, let $\mathcal{H}$ be $(\mathfrak{g},\mathcal{P})$-$\alpha$-continuous. Let $x\in \mathbb{X}$ and ${\mathtt{E}}^{‵}$ be an open set in ${\mathbb{X}}^{‵}$ with $\mathcal{U}\left(x\right)\in {\mathtt{E}}^{‵}.$ Thus, $\mathbb{X}\times {\mathtt{E}}^{‵}$ is open in $\mathbb{X}\times {\mathbb{X}}^{‵}.$ However, $\mathcal{H}$ is $(\mathfrak{g},\mathcal{P})$-$\alpha$-continuous, thus there exists a $(\mathfrak{g},\mathcal{P})$-$\alpha$-open set $\mathtt{E}$ satisfying $x\in \mathtt{E}$ and $\mathcal{H}\left(\mathtt{E}\right)\subseteq \mathbb{X}\times {\mathtt{E}}^{‵}.$ Thus, $\mathcal{U}\left(\mathtt{E}\right)\subseteq {\mathtt{E}}^{‵}.$ Therefore, $\mathcal{U}$ is $(\mathfrak{g},\mathcal{P})$-$\alpha$-continuous. □

Definition 11. 

Consider $\mathcal{U}:(\mathbb{X},\mathfrak{g},\mathcal{P})\to ({\mathbb{X}}^{‵},{\mathfrak{g}}^{‵},{\mathcal{P}}^{‵}).$ Thus, $\mathcal{U}$ is named $(\mathfrak{g},\mathcal{P})$-irresolute if for all $(\mathfrak{g},\mathcal{P})$-semi open ${\mathtt{E}}^{‵}$ in $({\mathbb{X}}^{‵},{\mathfrak{g}}^{‵},{\mathcal{P}}^{‵}),$ we have ${\mathcal{U}}^{-1}\left({\mathtt{E}}^{‵}\right)$ that is also $(\mathfrak{g},\mathcal{P})$-semi open in $(X,\mathfrak{g},\mathcal{P}).$

Remark 9. 

By Theorem 7 and Corollary 2, we obtain:

$$\mathfrak{g}-\mathit{Continuity}⟶(\mathfrak{g},\mathcal{P})-\mathit{Semi}-\mathit{Continuity}⟶\mathfrak{g}-\mathit{Semi}-\mathit{Continuity}.$$

The conclusion in Remark 9 does not always hold; the next examples show that.

Example 9. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space, where $\mathbb{X}=\{x_1,x_2,x_3,x_4\},$$\mathcal{P}=2^{\mathbb{X}}\backslash \mathbb{X},$ and $\mathfrak{g}=\{\varphi ,\left\{x_1\right\},\left\{x_2\right\},\{x_1,x_2\},\mathbb{X}\}.$

Suppose that $({\mathbb{X}}^{‵},{\mathfrak{g}}^{‵})$ is a $\mathbf{GT}$ space, where ${\mathbb{X}}^{‵}=\{a,b\}$ and ${\mathfrak{g}}^{‵}=\{\varphi ,\left\{a\right\}\}.$

Consider $\mathcal{U}:(\mathbb{X},\mathfrak{g},\mathcal{P})\to ({\mathbb{X}}^{‵},{\mathfrak{g}}^{‵})$ given by

$$\mathcal{U}\left(x_1\right)=\mathcal{U}\left(x_3\right)=a,\mathit{and}\mathcal{U}\left(x_2\right)=\mathcal{U}\left(x_4\right)=b.$$

Hence, $\mathcal{U}$ is $(\mathfrak{g},\mathcal{P})$-semi-continuous.

However, it is not $\mathfrak{g}$-continuous, since ${\mathcal{U}}^{-1}\left(\left\{a\right\}\right)=\{x_1,x_3\},$ which is not $\mathfrak{g}$-open.

Example 10. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space, where $\mathbb{X}=\{x_1,x_2,x_3,x_4\},$$\mathcal{P}=\{\varphi ,\left\{x_2\right\}\}$ and $\mathfrak{g}=\{\varphi ,\left\{x_1\right\},\{x_1,x_2\},\mathbb{X}\}.$

Suppose that $({\mathbb{X}}^{‵},{\mathfrak{g}}^{‵})$ is a $\mathbf{GT}$ space, where ${\mathbb{X}}^{‵}=\{a,b\}$ and ${\mathfrak{g}}^{‵}=\{\varphi ,\left\{b\right\}\}.$

Consider $\mathcal{U}:(\mathbb{X},\mathfrak{g},\mathcal{P})\to ({\mathbb{X}}^{‵},{\mathfrak{g}}^{‵})$ given by

$$\mathcal{U}\left(x_2\right)=\mathcal{U}\left(x_3\right)=a,\mathit{and}\mathcal{U}\left(x_1\right)=\mathcal{U}\left(x_4\right)=b.$$

Hence, $\mathcal{U}$ is $\mathfrak{g}$-semi-continuous.

However, it is not $(\mathfrak{g},\mathcal{P})$-continuous, since ${\mathcal{U}}^{-1}\left(\left\{b\right\}\right)=\{x_1,x_4\},$ which is not $(\mathfrak{g},\mathcal{P})$-semi-open.

Definition 12. 

Consider $\mathcal{U}:(\mathbb{X},\mathfrak{g})\to ({\mathbb{X}}^{‵},{\mathfrak{g}}^{‵},{\mathcal{P}}^{‵}).$ Hence, $\mathcal{U}$ is named $(\mathfrak{g},\mathcal{P})$-semi-open (respectively, $(\mathfrak{g},\mathcal{P})$-semi-closed) if for any $\mathfrak{g}$-open set $\mathtt{E}$ (respectively, $\mathfrak{g}$-closed set $\mathtt{F}$) in $(\mathbb{X},\mathfrak{g}),$$\mathcal{U}\left(\mathtt{E}\right)$ is $(\mathfrak{g},\mathcal{P})$-semi-open (resp. $\mathcal{U}\left(\mathtt{F}\right)$ is $(\mathfrak{g},\mathcal{P})$-semi-closed) in $({\mathbb{X}}^{‵},{\mathfrak{g}}^{‵},{\mathcal{P}}^{‵}).$

Remark 10. 

From the above definitions, we conclude that:

(i) 

Each $\mathfrak{g}$-open function is $(\mathfrak{g},\mathcal{P})$-semi-open.

(ii) 

Each $(\mathfrak{g},\mathcal{P})$-semi-open (respectively, $(\mathfrak{g},\mathcal{P})$-semi-closed) function is $\mathfrak{g}$-semi-open (respectively, $\mathfrak{g}$-semi-closed).

The converse of Remark 10 is not always true; the next examples show that.

Example 11. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space, where $\mathbb{X}=\{x_1,x_2,x_3\},$$\mathcal{P}=2^{\mathbb{X}}\backslash \mathbb{X},$ and $\mathfrak{g}=\{\varphi ,\{x_1,x_2\}\}.$

Suppose that $(\mathbb{X},{\mathfrak{g}}^{‵})$ is a $\mathbf{GT}$ space, where ${\mathfrak{g}}^{‵}=\{\varphi ,\left\{x_1\right\},\left\{x_3\right\},\{x_1,x_3\}\}.$

Consider $\mathcal{U}:(\mathbb{X},{\mathfrak{g}}^{‵})\to (\mathbb{X},\mathfrak{g},\mathcal{P}).$ Hence, the identity function is $(\mathfrak{g},\mathcal{P})$-semi-open.

However, it is not $\mathfrak{g}$-open.

Example 12. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space, where $\mathbb{X}=\{x_1,x_2,x_3,x_4\},$ $\mathfrak{g}=\{\varphi ,\{x_1,x_2\},$$\{x_2,x_3\},\{x_1,x_2,x_3\},\mathbb{X}\}$, and $\mathcal{P}=\{\varphi ,\{x_2,x_4\}\}.$ Suppose that $(\mathbb{X},{\mathfrak{g}}^{‵})$ is a $\mathbf{GT}$ space, where ${\mathfrak{g}}^{‵}=\{\varphi ,\{x_1,x_2,x_3\}\}.$ Consider $\mathcal{U}:(\mathbb{X},{\mathfrak{g}}^{‵})\to (\mathbb{X},\mathfrak{g},\mathcal{P}).$ Hence, the identity function is $\mathfrak{g}$-semi-open. However, it is not $(\mathfrak{g},\mathcal{P})$-semi-open, where $c{l}^{\diamond }\left(i_{\mathfrak{g}}\left(\{x_1,x_2,x_3\}\right)\right)=\{x_1,x_2\}.$

Theorem 19. 

Consider $\mathcal{U}:(\mathbb{X},\mathfrak{g})\to ({\mathbb{X}}^{‵},{\mathfrak{g}}^{‵},{\mathcal{P}}^{‵})$ to be $(\mathfrak{g},\mathcal{P})$-semi-open function iff $\forall x\in \mathbb{X}$ and for any generalized neighbourhood $\mathtt{E}$ of $x,$ there exists a $(\mathfrak{g},\mathcal{P})$-semi-open ${\mathtt{E}}^{‵}$ in ${\mathbb{X}}^{‵}$ satisfying $\mathcal{U}\left(x\right)\in {\mathtt{E}}^{‵}\subseteq \mathcal{U}\left(\mathtt{E}\right).$

Proof. 

Consider $\mathcal{U}$ as a $(\mathfrak{g},\mathcal{P})$-semi-open function. Suppose that $x\in \mathbb{X}$, and $\mathtt{E}$ is any generalized neighbourhood of $x.$ Hence, $\exists \mathtt{F}\in \mathfrak{g}$ satisfies $x\in \mathtt{F}\subseteq \mathtt{E}.$ However, $\mathcal{U}$ is $(\mathfrak{g},\mathcal{P})$-semi-open, thus $\mathcal{U}\left(\mathtt{F}\right)={\mathtt{E}}^{‵}$ (say) is a $(\mathfrak{g},\mathcal{P})$-semi-open set such that $\mathcal{U}\left(x\right)\in {\mathtt{E}}^{‵}\subseteq \mathcal{U}\left(\mathtt{E}\right).$

Conversely, let $\mathtt{E}\in \mathfrak{g}.$ Thus, for any $x\in \mathtt{E},$ there exists $(\mathfrak{g},\mathcal{P})$-semi-open set ${\mathtt{E}}_x^{‵}$ satisfying $\mathcal{U}\left(x\right)\in {\mathtt{E}}_x^{‵}\subseteq \mathcal{U}\left(\mathtt{E}\right).$ Hence, $\mathcal{U}\left(\mathtt{E}\right)=\cup \{{\mathtt{E}}_x^{‵}:x\in \mathtt{E}\}.$ By Proposition 2, $\mathcal{U}\left(\mathtt{E}\right)$ is a $(\mathfrak{g},\mathcal{P})$-semi-open set. Therefore, $\mathcal{U}$ is a $(\mathfrak{g},\mathcal{P})$-semi-open function. □

Theorem 20. 

Consider $\mathcal{U}:(\mathbb{X},\mathfrak{g})\to ({\mathbb{X}}^{‵},{\mathfrak{g}}^{‵},{\mathcal{P}}^{‵})$ as a $(\mathfrak{g},\mathcal{P})$-semi-open function. Whenever ${\mathtt{E}}^{‵}\subseteq {\mathbb{X}}^{‵}$ and $\mathtt{F}\subseteq \mathbb{X}$ is a closed set satisfying ${\mathcal{U}}^{-1}\left({\mathtt{E}}^{‵}\right)\subseteq \mathtt{F},$ there exists a $(\mathfrak{g},\mathcal{P})$-semi-open $\mathtt{G}$ in $({\mathbb{X}}^{‵},{\mathfrak{g}}^{‵},{\mathcal{P}}^{‵})$ satisfying ${\mathtt{E}}^{‵}\subseteq \mathtt{G}$ and ${\mathcal{U}}^{-1}\left(\mathtt{G}\right)\subseteq \mathtt{F}.$

Proof. 

Consider $\mathcal{U}$ as a $(\mathfrak{g},\mathcal{P})$-semi-open function. Let ${\mathtt{E}}^{‵}\subseteq {\mathbb{X}}^{‵}$ and $\mathtt{F}\subseteq \mathbb{X}$ be a closed set satisfying ${\mathcal{U}}^{-1}\left({\mathtt{E}}^{‵}\right)\subseteq \mathtt{F}.$ Hence, $(\mathbb{X}\backslash \mathtt{F})$ is $\mathfrak{g}$-open. Thus, $\mathcal{U}(\mathbb{X}\backslash \mathtt{F})$ is $(\mathfrak{g},\mathcal{P})$-semi-open. Thus, $\mathtt{G}={\mathbb{X}}^{‵}\backslash \mathcal{U}(\mathbb{X}\backslash \mathtt{F})$ is $(\mathfrak{g},\mathcal{P})$-semi-closed. Hence, ${\mathcal{U}}^{-1}\left({\mathtt{E}}^{‵}\right)\subseteq \mathtt{F}$ implies ${\mathtt{E}}^{‵}\subset \mathtt{G}.$ Therefore, ${\mathcal{U}}^{-1}\left(\mathtt{G}\right)\subseteq \mathtt{F}.$ □

Corollary 6. 

Consider $\mathcal{U}:\mathbb{X}\to {\mathbb{X}}^{‵}$ as a $\mathfrak{g}$-semi-open function. Whenever ${\mathtt{E}}^{‵}\subseteq {\mathbb{X}}^{‵}$ and $\mathtt{F}\subseteq \mathbb{X}$ is a closed set satisfying ${\mathcal{U}}^{-1}\left({\mathtt{E}}^{‵}\right)\subseteq \mathtt{F},$ there exists a $\mathfrak{g}$-semi-closed ${\mathtt{G}}^{‵}\subseteq {\mathbb{X}}^{‵}$ satisfying ${\mathtt{E}}^{‵}\subseteq {\mathtt{G}}^{‵}$ and ${\mathcal{U}}^{-1}\left({\mathtt{G}}^{‵}\right)\subseteq \mathtt{F}.$

Based on the last few results, we can present the following theorem:

Theorem 21. 

Consider $\mathcal{U}:(\mathbb{X},\mathfrak{g})\to ({\mathbb{X}}^{‵},{\mathfrak{g}}^{‵},{\mathcal{P}}^{‵})$ as a bijection. Hence, the following are equivalent:

(i) 

${\mathcal{U}}^{-1}$ is $(\mathfrak{g},\mathcal{P})$-semi-continuous;

(ii) 

$\mathcal{U}$ is $(\mathfrak{g},\mathcal{P})$-semi-open;

(iii) 

$\mathcal{U}$ is $(\mathfrak{g},\mathcal{P})$-semi-closed.

Proof. 

It is proven consequentially from these definitions, Theorem 19, and Corollary 6. □

Remark 11. 

Based on Theorem 16, we obtain:

The following examples illustrate that the opposite direction of the relationship in Figure 2 is not always satisfied.

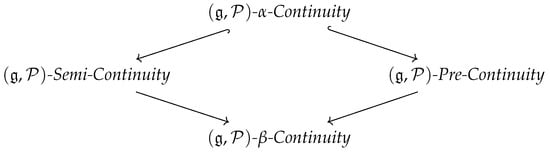
Figure 2. The relationship between the previous kinds of $(\mathfrak{g},\mathcal{P})$-continuity.

Example 13. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space, where $\mathbb{X}=\{x_1,x_2,x_3,x_4\},$$\mathfrak{g}=\{\varphi ,\{x_1,x_2\},$$\{x_2,x_3\},\{x_1,x_2,x_3\},\mathbb{X}\}$, and $\mathcal{P}=\{\varphi ,\{x_2,x_4\}\}.$ Suppose that $(\mathbb{X},{\mathfrak{g}}^{‵})$ is a $\mathbf{GT}$ space, where ${\mathfrak{g}}^{‵}=\{\varphi ,\{x_1,x_2,x_3\}\}.$ Consider $\mathcal{U}:(\mathbb{X},\mathfrak{g},\mathcal{P})\to (\mathbb{X},{\mathfrak{g}}^{‵}).$ Hence, the identity function is $(\mathfrak{g},\mathcal{P})$-β-continuous. However, it is not $(\mathfrak{g},\mathcal{P})$-semi-continuous, since ${\mathcal{U}}^{-1}\left(\{x_1,x_2,x_3\}\right)$ is not $(\mathfrak{g},\mathcal{P})$-semi-open. In addition, it is not $(\mathfrak{g},\mathcal{P})$-pre-continuous, since ${\mathcal{U}}^{-1}\left(\{x_1,x_2,x_3\}\right)$ is not $(\mathfrak{g},\mathcal{P})$-pre-open.

Example 14. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space, where $\mathbb{X}=\{x_1,x_2,x_3,x_4\},$ $\mathfrak{g}=\{\varphi ,\{x_1,x_2,$$x_3\left\}\right\}$, and $\mathcal{P}=\{\varphi ,\left\{x_3\right\},\left\{x_4\right\},\{x_3,x_4\}\}$. Suppose that $({\mathbb{X}}^{‵},{\mathfrak{g}}^{‵})$ is a $\mathbf{GT}$ space, where ${\mathbb{X}}^{‵}=\{a,b,c\}$ and ${\mathfrak{g}}^{‵}=\{\varphi ,\left\{a\right\}\}.$ Consider $\mathcal{U}:(\mathbb{X},\mathfrak{g},\mathcal{P})\to (\mathbb{X},{\mathfrak{g}}^{‵})$, as given by

$$\mathcal{U}\left(x_1\right)=\mathcal{U}\left(x_2\right)=a,\mathcal{U}\left(x_3\right)=b\mathit{and}\mathcal{U}\left(x_4\right)=c.$$

Hence, ${\mathcal{U}}^{-1}\left(\left\{a\right\}\right)=\{x_1,x_2\}.$ Thus, $\mathcal{U}$ is $(\mathfrak{g},\mathcal{P})$-pre-continuous, where $i_{\mathfrak{g}}\left(c{l}^{\diamond }\left(E\right)\right)=\{x_1,x_2\}.$ However, E is not $(\mathfrak{g},\mathcal{P})$-α-continuous.

Definition 13. 

Suppose that $(\mathbb{X},\mathfrak{g},\mathcal{P})$ is a $\mathbf{GPT}$ space and $({\mathbb{X}}^{‵},{\mathfrak{g}}^{‵})$ is a $\mathbf{GT}$ space. A function $\mathcal{U}:\mathbb{X}\to {\mathbb{X}}^{‵}$ is named $(\mathfrak{g},\mathcal{P})$-regular continuous (respectively, regular $(\mathfrak{g},\mathcal{P})$-semi-continuous) if every ${\mathcal{U}}^{-1}\left(\mathtt{E}\right),$ where $\mathtt{E}$ is $\mathfrak{g}$-open; is $(\mathfrak{g},\mathcal{P})$-regular open (respectively, regular $(\mathfrak{g},\mathcal{P})$-semi-open).

Theorem 22. 

$\mathcal{U}:(\mathbb{X},\mathfrak{g},\mathcal{P})\to ({\mathbb{X}}^{‵},{\mathfrak{g}}^{‵}).$ Thus, the following are equivalent:

(i) 

$\mathcal{U}$ is $(\mathfrak{g},\mathcal{P})$-regular continuous;

(ii) 

$\mathcal{U}$ is $(\mathfrak{g},\mathcal{P})$-pre-continuous as well as $(\mathfrak{g},\mathcal{P})$-semi-closed;

(iii) 

$\mathcal{U}$ is $(\mathfrak{g},\mathcal{P})$-α-continuous as well as $(\mathfrak{g},\mathcal{P})$-semi-closed.

Proof. 

It is proven consequentially from Proposition 1. □

Corollary 7. 

$\mathcal{U}:(\mathbb{X},\mathfrak{g},\mathcal{P})\to ({\mathbb{X}}^{‵},{\mathfrak{g}}^{‵}).$ Thus, the following are equivalent:

(i) 

$\mathcal{U}$ is regular $(\mathfrak{g},\mathcal{P})$-semi-continuous;

(ii) 

$\mathcal{U}$ is $(\mathfrak{g},\mathcal{P})$-semi-continuous as well as $(\mathfrak{g},\mathcal{P})$-semi-closed;

(iii) 

$\mathcal{U}$ is $(\mathfrak{g},\mathcal{P})$-β-continuous as well as $(\mathfrak{g},\mathcal{P})$-semi-closed.

Proof. 

It is proven consequentially from Proposition 3. □

5. Discussion

Al-Saadi and Al-Malki [25] introduced a new space with special characteristics in 2023. Their structure was named a generalized primal topological space.

In this paper, we covered some categories of weak $(\mathfrak{g},\mathcal{P})$-open sets. First, in Section 3, we gave their definitions via a specific kind of operator. Later, we investigated the relationship among them by giving proofs or counterexamples, then showed the conclusion in a simple diagram. In addition, we discussed their properties and theories.

Moreover, via a study of the relationship between the notion of $(\mathfrak{g},\mathcal{P})$-dense sets and the notion of $(\mathfrak{g},\mathcal{P})$-pre-open sets, we provided an answer to the question: “Are the properties of these classes that are applied in a topological space applicable in a generalized primal topological space too?” The results appeared in Remarks 7 and 8 in detail.

In Section 4, the concept of “continuity” was given attention when we presented the definition of $(\mathfrak{g},\mathcal{P})$-continuity between two $\mathbf{GPT}$ spaces. We presented $(\mathfrak{g},\mathcal{P})$-continuity via the weak $(\mathfrak{g},\mathcal{P})$-open sets that were introduced in Section 3. Lately, we have performed a decomposition of this type of $(\mathfrak{g},\mathcal{P})$ continuity.

This paper opens the way for many research projects by defining more classes of open sets and finding more relationships between them, as well as studying more topological properties of them, such as continuity, separation axioms, and other topological properties.