Secure Active Intelligent Reflecting Surface Communication against Colluding Eavesdroppers

Abstract

An active intelligent reflecting surface (IRS)-assisted, secure, multiple-input–single-output communication method is proposed in this paper. In this proposed scheme, a practical and unfavorable propagation environment is considered by assuming that multiple colluding eavesdroppers (Eves) coexist. In this case, we jointly optimize the beamformers of the base station (BS) and the active IRS for the formulated sum secrecy rate (SSR) maximization problem. Because the formulated problem is not convex, we apply the alternating optimization method to optimize the beamformers for maximizing the SSR. Specifically, we use the semi-definite relaxation method to solve the sub-problem of the beamforming vector of the BS, and we use the successive convex approximation method to solve the sub-problem of the power amplification matrix of the active IRS. Based on the solutions obtained using these stated methods, numerical results show that deploying an active IRS is superior compared to the cases of a passive IRS and a non-IRS for improving the physical layer security of wireless communication with multiple colluding Eves under different settings, such as the numbers of users, Eves, reflecting elements, and BS antennas as well as the maximum transmit power budget at the BS.

1. Introduction

The use of an intelligent reflecting surface (IRS) is a highly promising technique with significant potential for future communications. It enables the reconfiguration of a wireless propagation environment by controlling a smart controller connected to the IRS which adjusts the phase shifter of each element [1]. However, in traditional passive architectures, the IRS is only capable of adjusting the phase shift of the incident signal, thus limiting the achievable rate at the receiver. A new IRS architecture referred to as an active IRS can provide an additional power ability to the IRS. This means that the active IRS has the capability to amplify the incident signal in addition to adjusting the phase shift matrix of the incident signal compared with a passive IRS.

Security in the physical layer has emerged as a significant concern for the future of wireless communication [2]. Because wireless communications have a broadcasting nature, there is a possibility of eavesdroppers (Eves) wiretapping the signal transmitted by a BS. In other words, the beamformer at the BS may designed to not only maximize the signal-to-noise ratio (SNR) for users but also for Eves. This is discussed in references [3,4,5,6]. To prevent legitimate information from being leaked to an eavesdropper, the authors of [7] proposed a secure SSK communication scheme for the classical eavesdropping scenario by introducing artificial noise (AN) according to the channel state information (CSI) of the user and the eavesdropper. Subsequently, the authors of [8] considered a more practical scenario by assuming that all CSI in their proposed scheme was imperfect. It is difficult to increase the sum secrecy rate (SSR) due to limited spatial degrees of freedom (DoFs) at the transceivers. Additionally, it is known that an IRS can be used to safeguard communication when there are wiretap channels caused by Eves because it can provide more controllable links to improve the SSR by increasing the achievable rate of legitimate users and preventing information from being leaked to the Eves. Recently, several works have introduced IRSs to secure wireless communication between a transmitter and legitimate receivers [9,10,11]. The authors of [9] formulated a maximization problem for maximizing the secrecy rate for -aided wireless communication involving one user and one Eve. In [10], Ye et al. introduced a jamming UAV to interfere with an Eve to safeguard communication between the user and the information UAV aided by an IRS. The maximum secrecy rate problem in the case of multiple ground nodes, including users and colluding Eves, in an IRS-assisted wireless environment was investigated in [11].

1.1. Related Work

Some previous works [12,13] stated that complicity among Eves can pose a serious threat to the physical layer security of wireless communications. From a security point of view, the case of complicit Eves could be treat as a worst-case scenario, and it is more worthy of research. In this case, in order to better protect communication between a transmitter and a legitimate receiver, one can introduce an IRS and adjust its phase shift matrix to provide multiple coherent links so that the SNR at the users is improved or to provide multiple incoherent links for suppressing the SNR at the Eves; thus, the SSR will be improved. In another research work on resource allocation, Qiao et al. proposed an energy-harvesting jammer and an IRS-aided security enhancement scheme to better combat eavesdroppers [14]. In addition, the authors of [15,16] proposed resource allocation methods for passive-IRS- and -IRS-aided wireless networks, respectively. Specifically, the authors of [15] introduced successive convex approximation (SCA), semi-definite relaxation (SDR), and manifold optimization to deal with the SSR maximization problem for a multiple-input–single-output (MISO) wireless network with one Eve and multiple users aided by passive IRS. The authors of [16] designed an algorithm that minimizes the transmit power of the base station (BS) while considering the constraints of quality-of-service (QoS) requirements for each user and the maximum amplification power of the active IRS for an active-IRS-aided communication system with multiple users. To investigate the impact of AN on passive-IRS-assisted secure communications, the authors of [17] considered a challenging scenario in which multiple Eves are in an IRS-aided communication system with one legitimate user. References [18,19] also considered a challenging scenario in which there are multiple users and Eves in a wireless communication system and a passive IRS is introduced to combat wiretapping from the multiple Eves by jointly optimizing beamformers at the BS and the passive IRS. In [20], Zhang et al. proposed a joint precoding algorithm that maximizes the sum rate of active-IRS-assisted multi-user MISO communication in which the numerical results verify that the active IRS has the ability to handle the multiplicative fading effect (MFE). To achieve better performance for secure, symbiotic radio multicast communication and a secure, wireless energy harvesting network, References [21,22] introduced an active IRS to combat multiple eavesdroppers. Moreover, a comparison of related works with our work is listed in Table 1.

Table 1. A comparison of previous studies in the literature with our work.

Reference	Number of Users	Number of Eves	Direct Link	Scenario	Type of IRS
[12]	multiple	multiple	✓	secure resource allocation	/
[13]	multiple	multiple	✓	secure resource allocation	passive IRS
[14]	single	single	✓	resource allocation with the help of an energy-harvesting jammer	passive IRS
[15]	multiple	single	×	secure resource allocation	passive IRS
[16]	multiple	/	✓	resource allocation	active IRS
[17]	single	multiple	✓	IRS-AN-aided secure communication	passive IRS
[18]	multiple	multiple	✓	secure resource allocation	passive IRS
[19]	multiple	multiple	✓	secure resource allocation	passive IRS
[20]	multiple	/	✓	comparison of active IRS and passive IRS	active IRS
[21]	multiple	multiple	✓	symbiotic radio multicast of secure communication	active IRS
[22]	multiple	multiple	✓	secure, wireless energy harvesting network	active IRS
our work	multiple	multiple	✓	secure resource allocation	active IRS

1.2. Motivations and Contributions

These studies show that the active IRS is superior to the passive IRS because the active IRS brings more DoFs to each element than the passive IRS does. Based on the aforementioned discussions, it can be found that the active IRS can be used to handle the MFE and a worsened communication environment caused by colluding Eves. Specifically, we propose the use of an active IRS in the MISO wireless communication system to further suppress information leakage caused by multiple colluding Eves in which multiple users and multiple Eves are all assumed to be equipped with single antennas and the Eves cooperate with each other. To the best of our knowledge, this is the first scheme involving active-IRS-aided downlink MISO communication in which multiple users and multiple colluding Eves exist with direct and cascaded channels between the BS and all ground nodes. The contributions of the scheme proposed this paper are as follows:

• This work proposes a joint optimization framework for optimizing the beamformers of the BS and the active IRS to maximize the system SSR in a secure multi-user MISO wireless network with multiple colluding Eves. Specifically, by considering direct and cascaded links, we can introduce an active IRS to prevent more information from being leaked to the multiple colluding Eves, and it can further improve the SSR of the proposed scheme, as compared with the case with passive IRS.
• The problem of maximizing the SSR involves optimizing the beamforming vectors/ matrices of the BS and the active IRS, while taking into account the constraints of the BS’s maximum transmit power and the active IRS’s maximum amplification power. Given that the original problem is non-convex, we employ the alternating optimization (AO) approach to split it into two sub-problems. This allows us to separate the optimization variables. We then utilize the efficient SDR method to address the sub-problem of optimizing the beamformer vector of the BS. Furthermore, we employ SCA method to address the non-convex constraint in the sub-problem of optimizing the beamforming matrix of the active IRS.
• The proposed scheme is shown to be superior through numerical and simulation results. In other words, the proposed scheme offers a significant improvement in the SSR compared to other baselines, such as the case without an IRS and the case with a passive IRS. This demonstrates that an active IRS is highly effective when dealing with unfavorable wireless communication environments involving multiple colluding Eves.

1.3. Notations

The primary symbols iused n this study are enumerated in Table 2. Specifically, the boldface, uppercase letters denote matrixes, and the italic, boldface lowercase letters denote vectors. $\mathrm{diag}\left(·\right)$ indicates the diagonalization of a vector. Complex and real spaces are denoted by $\mathbb{C}$ and $\mathbb{R}$, respectively. $\mathrm{Tr}\left(·\right)$, $\mathrm{rank}\left(·\right)$, $∥·∥$, ${\left(·\right)}^H$, and ${\left(·\right)}^T$ represent the trace of a matrix, the rank of the matrix, the $L^2$ norm of the vector, a conjugate transpose operation, and a transpose operation, respectively. $\max \left(a_1,\dots ,a_z\right)$ returns the largest value in the set of $\left(a_1,\dots ,a_z\right)$. ${\mathbf{0}}_{M\times N}$ and ${\mathbf{I}}_N$ denote an all-zero matrix with a size of $M\times N$ and a unit matrix with a size of $N\times N$, respectively. ${\mathbf{H}}_{(a,b)}$ denotes an element of a matrix $\mathbf{H}$ at the a-th row and b-th column. Finally, $\mathcal{O}\left(·\right)$ is a big O notation for computational complexity.

Table 2. Definitions of the main symbols used in the proposed scheme.

Symbol	Definition	Symbol	Definition
$\mathbf{G}$	channel between BS and active IRS	$\mathit{v}$	$\mathit{v}={[{\mathbf{\Phi }}_{(1,1)},{\mathbf{\Phi }}_{(2,2)},\dots ,{\mathbf{\Phi }}_{(N,N)}]}^T$
${\mathit{h}}_{ab,k}$	direct channel between BS and k-th user	${\sigma }_b^2$	noise power at each user
${\mathit{h}}_{ae,l}$	direct channel between BS and l-th Eve	${\sigma }_e^2$	noise power at each Eve
${\mathit{h}}_{ib,k}$	channel between active IRS and k-th user	L	number of Eves
${\mathit{h}}_{ie,l}$	channel between active IRS and l-th Eve	K	number of users
${\mathit{\omega }}_k$	BS beamformer tended for k-th user	M	number of antennas at BS
$\mathbf{P}$	amplification factor matrix for active IRS	N	number of reflecting elements at active IRS
$\mathbf{\Theta }$	phase shift matrix for active IRS	$P_{\mathrm{BS}}^{\max }$	maximum power budget at BS
$\mathbf{\Phi }$	beamformer matrix of active IRS, $\mathbf{\Phi }=\mathbf{P}\mathbf{\Theta }$	$P_{\mathrm{A}}^{\max }$	maximum power budget at active IRS

2. System Model

This section presents a scenario of secure communication facilitated by an active IRS with multiple colluding Eves. The scenario is illustrated in Figure 1 and includes a BS with M antennas, an IRS with N elements, K users, and L Eves. Both the users and Eves are each equipped with a single antenna. Define $\mathcal{K}$ as the set of users in which $\mathcal{K}\triangleq \left\{1,\dots ,K\right\}$. Similarly, define $\mathcal{L}$ as the set of Eves in which $\mathcal{L}\triangleq \left\{1,\dots ,L\right\}$. The confidential information tended to the users is wiretapped by multiple colluding Eves. The perfect CSI of all communication channel in Figure 1 is assumed to be accurately obtained because of the following reasons. In practice, cascaded and direct channels can be accurately estimated using the least-squares method and by optimizing training reflection patterns [23]. In addition, multiple colluding Eves can be treated as untrusted users and may be periodically active in the wireless communications. Hence, the CSI of multiple colluding Eves can be accurately obtained via the central control of the active IRS. Moreover, in order to further explore the capabilities of active IRS-assisted wireless communication when faced with multiple colluding Eves, we make the assumption that the perfect CSI is available for the proposed scheme, the SSR value of which serves as an upper bound for the scenario in which imperfect CSI is assumed. Furthermore, the channel estimation of the proposed scheme is beyond the scope of this work. Based on this assumption, the signal transmitted by the BS is given by

$$\mathit{s}=\sum _{k=1}^K{\mathit{\omega }}_k{z}_k,$$

(1)

where ${\mathit{\omega }}_k\in {\mathbb{C}}^{M\times 1}$ represents the beamforming vector tended for the k-th user, and $z_k$ denotes the corresponding signal. Without a loss of generality, we assume that $\mathbb{E}\left\{z_k\right\}=0$, $\mathbb{E}\left\{{\left|z_k\right|}^2\right\}=1$, and $\mathbb{E}\left\{z_k{z}_j\right\}=0$, $\forall k,j\in \mathcal{K},k\ne j$. We denote the channel from the BS to the active IRS, the channel from the BS to the k-th user, the channel from the BS to the l-th Eve, the channel from the active IRS to the k-th user, and the channel from the active IRS to the l-th Eve as $\mathbf{G}\in {\mathbb{C}}^{N\times M}$, ${\mathit{h}}_{ab,k}\in {\mathbb{C}}^{M\times 1}$, ${\mathit{h}}_{ae,l}\in {\mathbb{C}}^{M\times 1}$, ${\mathit{h}}_{ib,k}\in {\mathbb{C}}^{N\times 1}$, and ${\mathit{h}}_{ie,l}\in {\mathbb{C}}^{N\times 1}$, respectively. Then, because of the controller attached to the active IRS and the independent amplifiers connected to each element at the active IRS, the reflected signal adjusted for the phase shifts and amplified for the power can be expressed as

$$\mathit{y}=\mathbf{P}\mathbf{\Theta }\mathit{s}+\mathbf{P}\mathbf{\Theta }\mathit{v},$$

(2)

where the matrix $\mathbf{P}=\mathrm{diag}\left(p_1,\dots ,p_N\right)\in {\mathbb{R}}_{+}^{N\times N}$ depicts the amplification coefficients of the active IRS. It is a diagonal matrix with non-negative elements denoted as $p_1,\dots ,p_N$. The matrix $\mathbf{P}$ belongs to the set of non-negative real numbers denoted as ${\mathbb{R}}_{+}^{N\times N}$. The phase shift matrix $\mathbf{\Theta }$ at the active IRS is represented by $\mathbf{\Theta }=\mathrm{diag}\left(e^{j{\theta }_1},\dots ,e^{j{\theta }_N}\right)$, where ${\theta }_n$ denotes the phase shift of the n-th reflecting element at the active IRS. Since each element of the active IRS is connected to the amplification component, additional amplification power will be consumed, which accounts for amplifying the reflected signal; thus, non-negligible thermal noise will also be amplified, as shown as $\mathit{v}$ in (2). Specifically, $\mathit{v}$ represents the thermal noise and the inherent device noise of the active IRS elements. The thermal noise introduced by the active IRS elements cannot be neglected because of the amplifier, which is connected to the active IRS and amplifies thermal noise. We assume that the thermal noise vector $\mathit{v}$ satisfies the distribution as $\mathit{v}\sim \mathcal{CN}\left({\mathbf{0}}_{N\times 1},{\sigma }_v^2{\mathbf{I}}_N\right)$. Based on the above, the received signals $y_{b,k}$ at the k-th user and $y_{e,l}$ at the l-th Eve can be expressed as

$$y_{b,k}=\left({\mathit{h}}_{ab,k}^H+{\mathit{h}}_{ib,k}^H\mathbf{P}\mathbf{\Theta }\mathbf{G}\right)\sum _{k=1}^K{\mathit{\omega }}_k{z}_k+{\mathit{h}}_{ib,k}^H\mathbf{P}\mathbf{\Theta }\mathit{v}+n_{b,k},$$

(3)

$$y_{e,l}=\left({\mathit{h}}_{ae,l}^H+{\mathit{h}}_{ie,l}^H\mathbf{P}\mathbf{\Theta }\mathbf{G}\right)\sum _{k=1}^K{\mathit{\omega }}_k{z}_k+{\mathit{h}}_{ie,l}^H\mathbf{P}\mathbf{\Theta }\mathit{v}+n_{e,l},$$

(4)

respectively, where the variables $n_{b,k}\sim \mathcal{CN}\left(0,{\sigma }_b^2\right)$ and $n_{e,l}\sim \mathcal{CN}\left(0,{\sigma }_e^2\right)$ stand for the additive white Gaussian noise at the k-th user and the l-th Eve followed by the circularly symmetric complex Gaussian distribution with a mean of 0 and variance of ${\sigma }_b^2$ and a mean of 0 and a variance of ${\sigma }_e^2$, respectively. Let ${\mathit{h}}_{b,k}$ and ${\mathit{h}}_{e,l}$ be the equivalent channels from the BS to the k-th user and the l-th Eve, respectively, including both the direct link and the reflected link, shown as follows:

$$\begin{array}{c}{\mathit{h}}_{b,k}^H={\mathit{h}}_{ib,k}^H\mathbf{P}\mathbf{\Theta }\mathbf{G}+{\mathit{h}}_{ab,k}^H\in {\mathbb{C}}^{1\times M},\forall k\in \mathcal{K},\end{array}$$

(5)

$$\begin{array}{c}{\mathit{h}}_{e,l}^H={\mathit{h}}_{ie,l}^H\mathbf{P}\mathbf{\Theta }\mathbf{G}+{\mathit{h}}_{ae,l}^H\in {\mathbb{C}}^{1\times M},\forall l\in \mathcal{L}.\end{array}$$

(6)

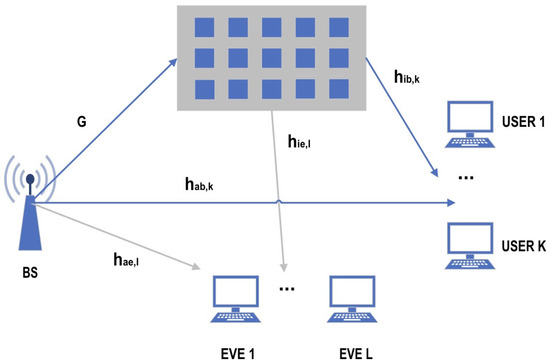
Figure 1. An active-IRS-aided secure communication system with multiple colluding Eves.

The achievable rate of the k-th user is given as ${log}_2\left(1+{\gamma }_k\right)$, where ${\gamma }_k$ is the signal-to-interference-plus-noise ratio (SINR) of the k-th user, which is given in [20]

$${\gamma }_k=\frac{{\left|{\mathit{h}}_{b,k}^H{\mathit{\omega }}_k\right|}^2}{{\sum }_{i\ne k}^K{\left|{\mathit{h}}_{b,k}^H{\mathit{\omega }}_i\right|}^2+{\sigma }_v^2{∥{\mathit{h}}_{ib,k}^H\mathbf{P}\mathbf{\Theta }∥}^2+{\sigma }_b^2},\forall k.$$

(7)

When L colluding Eves work together to wiretap the k-th user, they can be regarded as an Eve with L antennas. Then, the achievable rate of the l-th Eve is represented by $R_k^e={log}_2\left(1+{\sum }_{l=1}^L{\gamma }_{k,l}\right)$, where ${\gamma }_{k,j}$ represents the SINR of the l-th Eve given by

$${\gamma }_{k,l}=\frac{{\left|{\mathit{h}}_{e,l}^H{\mathit{\omega }}_k\right|}^2}{{\sum }_{i\ne k}^K{\left|{\mathit{h}}_{e,l}^H{\mathit{\omega }}_i\right|}^2+{\sigma }_v^2{∥{\mathit{h}}_{ie,l}^H\mathbf{P}\mathbf{\Theta }∥}^2+{\sigma }_e^2},\forall k,l.$$

(8)

By applying Jensen’s inequality, we have the lower bound of $R_k^e$ as follows:

$${\overline{R}}_k^e=\frac{1}{L}\sum _{l=1}^L{log}_2(1+L{\gamma }_{k,l}),\forall k.$$

(9)

With ${\overline{R}}_k^e$ in (9), we have the following tractable upper bound of the SSR of the proposed scheme [12]:

$$R_{\mathrm{sum}}=\sum _{k=1}^K{\left[R_k-{\overline{R}}_k^e\right]}^{+},$$

(10)

where ${\left[a\right]}^{+}=\max (a,0)$. The transmit power of the BS and the amplification power coefficient of the active IRS, namely, $P_{\mathrm{BS}}$ and $P_{\mathrm{A}}$, can, respectively, be written as

$$\begin{array}{c}{P}_{\mathrm{BS}}=\sum _{k=1}^K{∥{\mathit{\omega }}_k∥}^2,\end{array}$$

(11)

$$\begin{array}{c}{P}_{\mathrm{A}}=\sum _{k=1}^K{∥\mathbf{P}\mathbf{\Theta }\mathbf{G}{\mathit{\omega }}_k∥}^2+{\sigma }_v^2{\parallel \mathbf{P}\mathbf{\Theta }\parallel }^2.\end{array}$$

(12)

Note that the proposed scheme always involves the presence of $\mathbf{P}$ and $\mathbf{\Theta }$ in a multiplied form. Thus, $\mathbf{P}$ and $\mathbf{\Theta }$ can be combined into a single matrix $\mathbf{\Phi }$, with $\mathbf{\Phi }=\mathrm{diag}(p_1{e}^{j{\theta }_1},\dots ,$$p_N{e}^{j{\theta }_N})$. The objective is to maximize the SSR by optimizing the beamformers, ${\mathit{\omega }}_k$ and $\mathbf{\Phi }$, with two considered constraints, shown as follows:

$$\begin{array}{cc}\hfill \underset{{\mathit{\omega }}_k,\mathbf{\Phi }}{max}& \sum _{k=1}^K\left(R_k-{\overline{R}}_k^e\right),\hfill \end{array}$$

(13a)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& P_{\mathrm{BS}}\le P_{\mathrm{BS}}^{\max },\hfill \end{array}$$

(13b)

$$\begin{array}{cc}\hfill & \sum _{k=1}^K{∥\mathbf{\Phi }\mathbf{G}{\mathit{\omega }}_k∥}^2+{\sigma }_v^2{∥\mathbf{\Phi }∥}^2\le P_{\mathrm{A}}^{\max }.\hfill \end{array}$$

(13c)

Because the objective value of (13a) is always non-negative due to the DoF of the power control or resource allocation [9], we omit the operation ${[·]}^{+}$ for the objective function in (13a); thus, its smoothness is attained. In other words, if $R_k-{\overline{R}}_k^e<0$, we can allocate power to other users or let ${\mathit{w}}_k=\mathbf{0},\forall k$ so that the objective value is 0. Compared with a passive IRS, the active IRS introduces an additional amplification factor in addition to the phase shifts at the IRS, thus avoiding the unit-modulus constraint and adding a power budget constraint (13c), accounting for the active IRS. However, it is worth investigating whether the newly introduced non-negligible thermal noise at the active IRS will cause a performance loss in the proposed scheme.

3. Proposed Methods

In this section, we employ the AO approach to optimize the beamformers of the BS and the active IRS because of the coupling between ${\mathit{\omega }}_k$ and $\mathbf{\Phi }$. In other words, we optimize ${\mathit{\omega }}_k$ and $\mathbf{\Phi }$ alternately while keeping the other variable fixed. The flow chart of the proposed algorithm is shown in Figure 2. Specifically, for sub-problem 1, to circumvent non-convexity, we begin by introducing Lemma 1, as shown in Section 3.1, to convert the objective function into a more manageable form. Next, we employ the AO approach to decouple ${\mathit{\omega }}_k,\forall k$ and the newly introduced slack variables. Finally, we apply a Gaussian randomization-based SDR method to obtain a rank-one solution, ${\mathit{\omega }}_k,\forall k$. For sub-problem 2, the SCA method is used to approximate non-convex terms in the objective functions.

Figure 2. A flow chart of the proposed algorithm.

3.1. Optimize ${\mathit{\omega }}_k$ with Given $\mathbf{\Phi }$

To tackle the difficulty arising because the fraction in the logarithm function is complex, we let ${\lambda }_{b,k}=\frac{1}{{\sigma }_b^2}$ and then rewrite $R_k$ as follows:

$$\begin{array}{cc}\hfill R_k& ={log}_2\left(\frac{{\sum }_{i=1}^K{\left|{\mathit{h}}_{b,k}^H{\mathit{\omega }}_i\right|}^2+{\sigma }_v^2{∥{\mathit{h}}_{ib,k}^H\mathbf{\Phi }∥}^2+{\sigma }_b^2}{{\sum }_{i\ne k}^K{\left|{\mathit{h}}_{b,k}^H{\mathit{\omega }}_i\right|}^2+{\sigma }_v^2{∥{\mathit{h}}_{ib,k}^H\mathbf{\Phi }∥}^2+{\sigma }_b^2}\right)\hfill \\ \hfill & ={log}_2\left(\frac{{\lambda }_{b,k}\left({\sum }_{i=1}^K{\left|{\mathit{h}}_{b,k}^H{\mathit{\omega }}_i\right|}^2+{\sigma }_v^2{∥{\mathit{h}}_{ib,k}^H\mathbf{\Phi }∥}^2\right)+1}{{\lambda }_{b,k}({\sum }_{i\ne k}^K{\left|{\mathit{h}}_{b,k}^H{\mathit{\omega }}_i\right|}^2+{\sigma }_v^2{∥{\mathit{h}}_{ib,k}^H\mathbf{\Phi }∥}^2)+1}\right).\hfill \end{array}$$

(14)

Noting that (14) is not convex, we resort to using the SDR method to transform the numerator and denominator of the logarithmic function into a linear form. To proceed, we first define ${\mathbf{H}}_{b,k}={\mathit{h}}_{b,k}{\mathit{h}}_{b,k}^H$, and ${\mathbf{W}}_k={\mathit{\omega }}_k{\mathit{\omega }}_k^H$; then, the linear form of ${\left|{\mathit{h}}_{b,k}^H{\mathit{\omega }}_i\right|}^2$ is given by

$$\begin{array}{cc}\hfill {\left|{\mathit{h}}_{b,k}^H{\mathit{\omega }}_i\right|}^2& =\mathrm{Tr}\left({\mathbf{H}}_{b,k}{\mathbf{W}}_k\right).\hfill \end{array}$$

(15)

Let $R_{k,A}={\sum }_{i=1}^K\mathrm{Tr}\left({\mathbf{H}}_{b,k}{\mathbf{W}}_i\right)+{\sigma }_v^2{∥{\mathit{h}}_{ib,k}^H\mathbf{\Phi }∥}^2$, $R_{k,B}={\sum }_{j\ne k}^K\mathrm{Tr}\left({\mathbf{H}}_{b,k}{\mathbf{W}}_j\right)+{\sigma }_v^2{∥{\mathit{h}}_{ib,k}^H\mathbf{\Phi }∥}^2$; we rewrite $R_k$ in (14) as

$$R_{k}ln2=ln({\lambda }_{b,k}{R}_{k,A}+1)-ln({\lambda }_{b,k}{R}_{k,B}+1).$$

(16)

Lemma 1.

Considering the function $f\left(u\right)=-ux+lnu+1$, the maximum value of $f\left(u\right)$ is ${max}_{u>0}f\left(u\right)=-lnx$, where $u=\frac{1}{x}$.

Proof. 

Please refer to Lemma 1, [17].    □

To tackle the non-convex terms in (13a), we need to convert the convex part of (16) into the form shown in Lemma 1. By defining the set $\mathbf{W}\triangleq \left\{{\mathbf{W}}_1,\dots {\mathbf{W}}_K\right\}$, we have

$$\underset{t_{b,k}>0}{max}{f}_b(\mathbf{W},t_{b,k})=R_{k}ln2,$$

(17)

where $f_b(\mathbf{W},t_{b,k})=ln\left({\lambda }_{b,k}{R}_{k,A}+1\right)-t_{b,k}\left({\lambda }_{b,k}{R}_{k,B}+1\right)+ln{t}_{b,k}+1$. By using the SDR method, the original convex function can be transformed into a more tractable concave function. We can use the same method to handle part of the achievable rate of the Eves in (13a). Let ${\lambda }_e=\frac{1}{{\sigma }_e^2}$, $E_l={\sum }_{i\ne l}^K\mathrm{Tr}\left({\mathbf{H}}_{e,l}{\mathbf{W}}_i\right)+{\sigma }_v^2{∥{\mathit{h}}_{e,l}^H\mathbf{\Phi }∥}^2$, and ${\mathbf{H}}_{e,l}={\mathit{h}}_{e,l}{\mathit{h}}_{e,l}^H$. ${\overline{R}}_k^e$ can be written as follows:

$$\begin{array}{cc}\hfill {\overline{R}}_k^e& =\frac{1}{L}\sum _{l=1}^L{log}_2\left(1+\frac{L{\left|{\mathit{h}}_{e,l}^H{\mathit{w}}_k\right|}^2}{E_l+{\sigma }_e^2}\right)\hfill \\ \hfill & =\frac{1}{L}\sum _{l=1}^L{log}_2\left(\frac{{\lambda }_e\left(L\mathrm{Tr}\left({\mathbf{H}}_{e,l}{\mathbf{W}}_k\right)+E_l\right)+1}{{\lambda }_e{E}_l+1}\right).\hfill \end{array}$$

(18)

By defining $R_{e,k,l}=L\mathrm{Tr}\left({\mathbf{H}}_{e,l}{\mathbf{W}}_k\right)+E_l$, (18) can be rewritten as

$${\overline{R}}_k^{e}ln2=\frac{1}{L}\sum _{l=1}^L\left(ln({\lambda }_e{R}_{e,k,l}+1)-ln({\lambda }_e{E}_l+1)\right).$$

(19)

Similarly, by applying Lemma 1, we can obtain the minimum of (19) as follows:

$$\frac{1}{L}\sum _{l=1}^L\underset{t_{e,l}>0}{min}{f}_e({\mathbf{W}}_k,t_{e,k,l})={\overline{R}}_k^{e}ln2,$$

(20)

where $f_e({\mathbf{W}}_k,t_{e,k,l})=t_{e,k,l}({\lambda }_e{R}_{e,k,l}+1)-ln{t}_{e,k,l}-1-ln({\lambda }_e{E}_l+1)$. To obtain the solution, ${\mathbf{W}}_k$, the AO method can be used to tackle the coupling between ${\mathbf{W}}_k$ and $t_{e,k,l}$ or $t_{b,k}$. The detailed steps of using the AO-based method to optimize ${\mathbf{W}}_k$ are described in Algorithm 1. By utilizing the SDR method and removing the rank-1 constraint for convexity, problem (13) with respect to optimizing ${\mathit{\omega }}_k$ is given by

$$\begin{array}{cc}\hfill \underset{\mathbf{W},t_{b,k},t_{e,k,l}}{max}& \sum _{k=1}^K\left\{f_b(\mathbf{W},t_{b,k})-\frac{1}{L}\sum _{l=1}^L{f}_e({\mathbf{W}}_k,t_{e,k,l})\right\},\hfill \end{array}$$

(21a)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& \sum _{k=1}^K\mathrm{Tr}\left({\mathbf{W}}_k\right)\le P_{\mathrm{BS}}^{\max },\hfill \end{array}$$

(21b)

$$\begin{array}{cc}\hfill & \sum _{k=1}^K\mathrm{Tr}\left(\mathbf{C}{\mathbf{W}}_k\right)+{\sigma }_v^2{∥\mathbf{\Phi }∥}^2\le P_{\mathrm{A}}^{\max },\hfill \end{array}$$

(21c)

$$\begin{array}{cc}\hfill & {\mathbf{W}}_k⪰0,\forall k\in \mathcal{K},\hfill \end{array}$$

(21d)

$$\begin{array}{cc}\hfill & t_{e,k,l}\ge 0,\forall k\in \mathcal{K},\forall l\in \mathcal{L},\hfill \end{array}$$

(21e)

$$\begin{array}{cc}\hfill & t_{b,k}\ge 0,\forall k\in \mathcal{K},\hfill \end{array}$$

(21f)

where $\mathbf{C}={\mathbf{G}}^H{\mathbf{\Phi }}^H\mathbf{\Phi }\mathbf{G}$. Note that “$ln2$” is neglected in the objective function without compromising its optimality. Since we omit the rank-1 constraint for tractability, if the rank of the solution of problem (21) satisfies $\mathrm{rank}\left({\mathbf{W}}_k\right)=1$, we can recover the solution for the beamformer at the BS ${\mathit{\omega }}_k$ using eigenvalue decomposition. Otherwise, if the rank of the solution to the problem (21) is larger than 1, i.e., $\mathrm{rank}\left({\mathbf{W}}_k\right)>1$, the Gaussian randomization method can be employed to construct a suboptimal solution with a rank of one [24]. In addition, the convex problem (21) can be effectively solved using the CVX solver [25].

Algorithm 1 Optimize ${\mathit{\omega }}_k$ with given $\mathbf{\Phi }$.

1: Initialization: Iteration index $i=1$, ${\mathbf{W}}_k^1$, $t_{b,k}^1$, and $t_{e,k,l}^1$ 2: repeat 3:    Solve problem (21) for given $t_{b,k}^i$ and $t_{e,k,l}^i$, and denote the solution as ${\mathbf{W}}_k^{i+1}$ 4:    Update $t_{b,k}^{i+1}={({\lambda }_{b,k}{R}_{k,B}+1)}^{-1}$ for given $t_{e,k,l}^i$ and ${\mathbf{W}}_k^{i+1}$ 5:    Update $t_{e,k,l}^{i+1}={({\lambda }_{e,l}{R}_{e,k,l}+1)}^{-1}$ for given $t_{b,k}^{i+1}$ and ${\mathbf{W}}_k^{i+1}$ 6:    Set $i=i+1$ 7: until convergence 8: for $k=1,\dots ,K$ do 9:    if $\mathrm{rank}\left({\mathbf{W}}_k^{i+1}\right)>1$ then 10:      Applying Gaussian randomization method to construct a suboptimal rank-1 solution ${\mathit{\omega }}_k^{\mathrm{op}}$ 11:    else 12:      Using eigenvalue decomposition to obtain the rank-1 solution ${\mathit{\omega }}_k^{\mathrm{op}}$ 13:    end if 14: end for 15: Output: ${\mathit{\omega }}_k^{\mathrm{op}}$

3.2. Optimize $\mathbf{\Phi }$ with Given ${\mathit{\omega }}_k$

For any given ${\mathit{\omega }}_k$, $\forall k$, we first define $\mathit{v}={\left[p_1{e}^{j{\theta }_1},\dots ,p_N{e}^{j{\theta }_N}\right]}^T$ for tractability in the sequel. To obtain the form of a quadratically constrained quadratic problem (QCQP), the terms in the numerator and denominator of (14) can be re-expressed as

$$\begin{array}{cc}\hfill G_{b,k}& =\sum _{i=1}^K{\left|{\mathit{h}}_{b,k}^H{\mathit{\omega }}_i\right|}^2+{\sigma }_v^2{∥{\mathit{h}}_{ib,k}^H\mathbf{\Phi }∥}^2={\mathit{v}}^H{\mathbf{T}}_{b,k}\mathit{v}+2\mathrm{Re}\left\{{\mathit{t}}_{b,k}^H\mathit{v}\right\}+d_{b,k},\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill {\overline{G}}_{b,k}& =\sum _{\begin{array}{c}j=1,\\ j\ne k\end{array}}^K{\left|{\mathit{h}}_{b,k}^H{\mathit{\omega }}_j\right|}^2+{\sigma }_v^2{∥{\mathit{h}}_{ib,k}^H\mathbf{\Phi }∥}^2={\mathit{v}}^H{\overline{\mathbf{T}}}_{b,k}\mathit{v}+2\mathrm{Re}\left\{{\overline{\mathit{t}}}_{b,k}^H\mathit{v}\right\}+{\overline{d}}_{b,k},\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill {∥{\mathit{h}}_{ib,k}^H\mathbf{\Phi }∥}^2& ={\mathit{v}}^H\underset{{\mathbf{N}}_{b,k}}{\underbrace{\mathrm{diag}\left({\mathit{h}}_{ib,k}\right)\mathrm{diag}\left({\mathit{h}}_{ib,k}^H\right)}}\mathit{v},\hfill \end{array}$$

(24)

where

$$\begin{array}{cc}\hfill {\mathbf{T}}_{b,k}& =\sum _{j=1}^K\mathrm{diag}\left({\mathit{\omega }}_j^H{\mathbf{G}}^H\right){\mathit{h}}_{ib,k}{\mathit{h}}_{ib,k}^H\mathrm{diag}\left(\mathbf{G}{\mathit{\omega }}_j\right)+{\sigma }_v^2{\mathbf{N}}_{b,k},\hfill \\ \hfill {\mathit{t}}_{b,k}& =\sum _{j=1}^K\mathrm{diag}\left({\mathit{\omega }}_j^H{\mathbf{G}}^H\right){\mathit{h}}_{ib,k}{\mathit{h}}_{ab,k}^H{\mathit{\omega }}_j,\hfill \end{array}$$

$$\begin{array}{cc}\hfill d_{b,k}& =\sum _{j=1}^K{\mathit{h}}_{ab,k}^H{\mathit{\omega }}_j{\mathit{\omega }}_j^H{\mathit{h}}_{ab,k},\hfill \\ \hfill {\overline{\mathbf{T}}}_{b,k}& =\sum _{\begin{array}{c}j=1,\\ j\ne k\end{array}}^K\mathrm{diag}\left({\mathit{\omega }}_j^H{\mathbf{G}}^H\right){\mathit{h}}_{ib,k}{\mathit{h}}_{ib,k}^H\mathrm{diag}\left(\mathbf{G}{\mathit{\omega }}_j\right)+{\sigma }_v^2{\mathbf{N}}_{b,k},\hfill \\ \hfill {\overline{\mathit{t}}}_{b,k}& =\sum _{\begin{array}{c}j=1,\\ j\ne k\end{array}}^K\mathrm{diag}\left({\mathit{\omega }}_j^H{\mathbf{G}}^H\right){\mathit{h}}_{ib,k}{\mathit{h}}_{ab,k}^H{\mathit{\omega }}_j,\hfill \\ \hfill {\overline{d}}_{b,k}& =\sum _{\begin{array}{c}j=1,\\ j\ne k\end{array}}^K{\mathit{h}}_{ab,k}^H{\mathit{\omega }}_j{\mathit{\omega }}_j^H{\mathit{h}}_{ab,k}.\hfill \end{array}$$

Additionally, constraint (13c), which is related to the active IRS, can be rewritten as

$$\begin{array}{c}\hfill \sum _{k=1}^K{\mathit{v}}^H\left(\mathbf{D}+{\sigma }_v^2{\mathbf{I}}_N\right)\mathit{v}\le P_{\mathrm{A}}^{\max },\end{array}$$

(25)

in which $\mathbf{D}=\mathrm{diag}\left({\mathit{\omega }}_k^H{\mathbf{G}}^H\right)\mathrm{diag}\left(\mathbf{G}{\mathit{\omega }}_k\right)$. Accordingly, the SINR of l-th Eve for wiretapping the k-th user in (8) can be re-expressed as

$$\begin{array}{cc}\hfill G_{e,k,l}& =L{\left|{\mathit{h}}_{e,l}^H{\mathit{\omega }}_k\right|}^2+\sum _{\begin{array}{c}j=1,\\ j\ne k\end{array}}^K{\left|{\mathit{h}}_{e,l}^H{\mathit{\omega }}_j\right|}^2+{\sigma }_v^2{∥{\mathit{h}}_{ie,l}^H\mathbf{\Phi }∥}^2={\mathit{v}}^H{\mathbf{T}}_{e,k,l}\mathit{v}+2\mathrm{Re}\left\{{\mathit{t}}_{e,k,l}^H\mathit{v}\right\}+d_{e,k,l},\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill {\overline{G}}_{e,k,l}& =\sum _{\begin{array}{c}j=1,\\ j\ne k\end{array}}^K{\left|{\mathit{h}}_{e,l}^H{\mathit{\omega }}_j\right|}^2+{\sigma }_v^2{∥{\mathit{h}}_{ie,l}^H\mathbf{\Phi }∥}^2={\mathit{v}}^H{\overline{\mathbf{T}}}_{e,k,l}\mathit{v}+2\mathrm{Re}\left\{{\overline{\mathit{t}}}_{e,k,l}^H\mathit{v}\right\}+{\overline{d}}_{e,k,l},\hfill \end{array}$$

(27)

where

$$\begin{array}{cc}\hfill {\mathbf{T}}_{e,k,l}& =L\mathrm{diag}\left({\mathit{\omega }}_k^H{\mathbf{G}}^H\right){\mathit{h}}_{ie,l}{\mathit{h}}_{ie,l}^H\mathrm{diag}\left(\mathbf{G}{\mathit{\omega }}_k\right)+{\overline{\mathbf{T}}}_{e,k,l},\hfill \\ \hfill {\mathit{t}}_{e,k,l}& =L\mathrm{diag}\left({\mathit{\omega }}_k^H{\mathbf{G}}^H\right){\mathit{h}}_{ie,l}{\mathit{h}}_{ae,l}^H{\mathit{\omega }}_k+{\overline{\mathit{t}}}_{e,k,l},\hfill \\ \hfill d_{e,k,l}& =L{\mathit{h}}_{ae,l}^H{\mathit{\omega }}_k{\mathit{\omega }}_k^H{\mathit{h}}_{ae,l}+{\overline{d}}_{e,k,l},\hfill \end{array}$$

in which

$$\begin{array}{cc}\hfill {\overline{\mathbf{T}}}_{e,k,l}& =\sum _{\begin{array}{c}j=1,\\ j\ne k\end{array}}^K\mathrm{diag}\left({\mathit{\omega }}_j^H{\mathbf{G}}^H\right){\mathit{h}}_{ie,l}{\mathit{h}}_{ie,l}^H\mathrm{diag}\left(\mathbf{G}{\mathit{\omega }}_j\right)+{\sigma }_v^2\underset{{\mathbf{N}}_{e,l}}{\underbrace{\mathrm{diag}\left({\mathit{h}}_{ie,l}\right)\mathrm{diag}\left({\mathit{h}}_{ie,l}^H\right)}},\hfill \\ \hfill {\overline{\mathit{t}}}_{e,k,l}& =\sum _{\begin{array}{c}j=1,\\ j\ne k\end{array}}^K\mathrm{diag}\left({\mathit{\omega }}_j^H{\mathbf{G}}^H\right){\mathit{h}}_{ie,l}{\mathit{h}}_{ae,l}^H{\mathit{\omega }}_j,\hfill \\ \hfill {\overline{d}}_{e,k,l}& =\sum _{\begin{array}{c}j=1,\\ j\ne k\end{array}}^K{\mathit{h}}_{ae,l}^H{\mathit{\omega }}_j{\mathit{\omega }}_j^H{\mathit{h}}_{ae,l}.\hfill \end{array}$$

Based on (14), (22)–(24), (26), and (27), we rewrite $R_k$ and ${\overline{R}}_k^e$ as $R_k={log}_2\left(\frac{{\lambda }_{b,k}{G}_{b,k}+1}{{\lambda }_{b,k}{\overline{G}}_{b,k}+1}\right)$ and ${\overline{R}}_k^e=\frac{1}{L}{\sum }_{l=1}^L{log}_2\left(\frac{{\lambda }_e{G}_{e,k,l}+1}{{\lambda }_e{\overline{G}}_{e,k,l}+1}\right)$, respectively.

To tackle the non-convexity of $R_k$ and ${\overline{R}}_k^e$, we first introduce some slack variables as follows:

$$\begin{array}{cc}\hfill & {log}_2{b}_{1,k}\ge c_{1,k},\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill & {\lambda }_{b,k}{G}_{b,k}+1\ge b_{1,k},\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill & {log}_2{b}_{2,k}\le c_{2,k},\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill & {\lambda }_{b,k}{\overline{G}}_{b,k}+1\le b_{1,k},\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill & {log}_2{b}_{3,k,l}\le c_{3,k,l},\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill & {\lambda }_e{G}_{e,k,l}+1\le b_{3,k,l},\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill & {log}_2{b}_{4,k,l}\ge c_{4,k,l},\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill & {\lambda }_e{\overline{G}}_{e,k,l}+1\ge b_{4,k,l}.\hfill \end{array}$$

(35)

We observe that (29), (30), (32), and (35) are not convex. To tackle this issue, we can utilize the SCA technique to approximate these constraints in a convex form. In particular, by employing the first-order Taylor expansion for these constraints, we have [26]

$$\begin{array}{cc}\hfill & b_{1,k}-{\lambda }_{b,k}\left(2\mathrm{Re}\left\{\left({\tilde{\mathit{v}}}^H{\mathbf{T}}_{b,k}-{\mathit{t}}_{b,k}^H\right)\mathit{v}\right\}-{\tilde{\mathit{v}}}^H{\mathbf{T}}_{b,k}\tilde{\mathit{v}}-d_{b,k}\right)-1\le 0,\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill & {log}_2{\tilde{b}}_{2,k}+\frac{b_{2,k}-{\tilde{b}}_{2,k}}{{\tilde{b}}_{2,k}ln2}-a_{2,k}\le 0,\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill & {log}_2{\overline{b}}_{3,k,l}+\frac{b_{3,k,l}-{\overline{b}}_{3,k,l}}{{\overline{b}}_{3,k,l}ln2}-a_{3,k,l}\le 0,\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill & b_{4,k,l}-{\lambda }_e\left(2\mathrm{Re}\left\{\left({\tilde{\mathit{v}}}^H{\overline{\mathbf{T}}}_{e,k,l}-{\overline{\mathit{t}}}_{e,k,l}^H\right)\mathit{v}\right\}-{\tilde{\mathit{v}}}^H{\overline{\mathbf{T}}}_{e,k,l}\tilde{\mathit{v}}-{\overline{d}}_{e,k,l}\right)-1\le 0,\hfill \end{array}$$

(39)

where $\tilde{\mathit{v}}$ denotes the temporary variable, which is obtained in the last iteration. Then, by defining $c_k=[c_{1,k},c_{2,k},c_{3,k,l},c_{4,k,l}]$ and $b_k=[b_{1,k},b_{2,k},b_{3,k,l},b_{4,k,l}]$, problem (13), with respect to optimizing $\mathit{v}$, can be approximated as

$$\begin{array}{cc}\hfill \underset{\mathit{v},c_k,c_k}{max}& \sum _{k=1}^K\left\{c_{1,k}-c_{2,k}-\frac{1}{L}\sum _{l=1}^L\left(c_{3,k,l}-c_{4,k,l}\right)\right\},\hfill \end{array}$$

(40a)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& \left(25\right),\left(28\right),\left(31\right),\left(33\right),\left(34\right),\left(36\right)\text{–}\left(39\right).\hfill \end{array}$$

(40b)

We approximate all non-convex terms in problem (13) to convex terms in problem (40) for optimizing $\mathbf{\Phi }$ with the given ${\mathit{\omega }}_k$. The convex problem (40) can be solved by a CVX solver. Moreover, in order to obtain the solution to problem (40) based on the SCA method, we iteratively optimize $\mathit{v}$. Detailed steps are described in Algorithm 2.

Algorithm 2 Optimize $\mathbf{\Phi }$ with given ${\mathit{\omega }}_k$.

1: Initialization: Iteration index $i=1$, ${\mathit{\omega }}_k^1$, $c_k^1$, and $b_k^1$ 2: repeat 3:    Solve problem (40) for given ${\mathit{v}}^i$, $a_k^i$, and $b_k^i$, and put the solution into the next iteration as ${\mathit{v}}^{i+1}$, $c_k^{i+1}$, and $b_k^{i+1}$, respectively 4:    Set $i=i+1$ 5: until convergence 6: Output: ${\mathbf{\Phi }}^{\mathrm{op}}=\mathrm{diag}\left({\mathit{v}}^{i+1}\right)$

3.3. Overall Algorithm

3.3.1. Convergence Analysis

The overall algorithm is an iterative optimization algorithm, as shown in Algorithm 3, which alternately optimizes ${\mathit{\omega }}_k$ and $\mathbf{\Phi }$ using iterative updates in each iteration. It can be easily seen that the AO-based algorithm generates a non-decreasing sequence of objective values in each iteration. In particular, by denoting the objective value of the original problem (13) as $R\left(·\right)$, it follows that

$$R\left({\mathit{\omega }}_k^{r+1},{\mathbf{\Phi }}^{r+1}\right)\stackrel{\left(a\right)}{\ge }R\left({\mathit{\omega }}_k^{r+1},{\mathbf{\Phi }}^r\right)\stackrel{\left(b\right)}{\ge }R\left({\mathit{\omega }}_k^r,{\mathbf{\Phi }}^r\right),$$

(41)

where (b) holds because the maximum of the objective value of the original problem (13) is achieved when optimizing ${\mathit{\omega }}_k$ for any given $\mathbf{\Phi }$. Similarly, (a) holds following the same reason as stated before. Therefore, the monotonically non-decreasing sequence for the objective value of the original problem (13) can be obtained. Moreover, because of limited resources, i.e., the bounded maximum transmit power budget of the BS and the maximum amplification power budget of the active IRS, $R\left({\mathit{\omega }}_k,\mathbf{\Phi }\right)$ has a finite upper bound; thus, it can converge to a stationary point.

Algorithm 3 AO algorithm for the proposed scheme.

1: Initialization: Iteration index $r=1$, set ${\mathit{\omega }}_k^1={\mathit{\omega }}_k^{\mathrm{op}}$ obtained from Algorithm 1 and ${\mathbf{\Phi }}^1={\mathbf{\Phi }}^{\mathrm{op}}$ obtained from Algorithm 2 2: repeat 3:    Solve problem (21) by Algorithm 1, and denote the solution as ${\mathit{\omega }}_k^{r+1}$ 4:    Solve problem (40) by Algorithm 2, and denote the solution as ${\mathbf{\Phi }}^{r+1}$ 5:    Set $r=r+1$ 6: until convergence 7: Output: ${\mathit{\omega }}^{\mathrm{op}}={\mathit{\omega }}^{r+1}$ and ${\mathbf{\Phi }}^{\mathrm{op}}={\mathbf{\Phi }}^{r+1}$

3.3.2. Complexity Analysis

The computational complexity of solving the SDR for the problem (21) is $\mathcal{O}\left(\sqrt{M}log\frac{1}{{ϵ}_w}\right.$$\left.\left(2M^3+4M^2+8\right)\right)=\mathcal{O}\left(2M^{3.5}log\frac{1}{{ϵ}_w}\right)$ [27], where ${ϵ}_w$ is the convergence accuracy for problem (21), and the computational complexity of solving problem (40) is $\mathcal{O}\left({\left(4K+4KL+N\right)}^{3.5}\right.$$\left.log\frac{1}{{ϵ}_v}\right)$, where ${ϵ}_v$ denotes the convergence accuracy for problem (40). Therefore, the complexity of the overall AO algorithm is

$$\begin{array}{c}\hfill {\mathcal{O}}_{\mathrm{Total}}=\mathcal{O}\left(2M^{3.5}log\frac{1}{{ϵ}_w}\right)+\mathcal{O}\left({\left(4K+4KL+N\right)}^{3.5}log\frac{1}{{ϵ}_v}\right).\end{array}$$

(42)

4. Numerical and Simulation Results

In this section, we present simulation and numerical results from evaluating the performance of the proposed scheme in an active-IRS-aided secure communication system with multiple colluding Eves. Unless specified otherwise, the simulation parameters of the proposed scheme are listed in Table 3. The locations of the k-th user and l-th Eve are randomly generated within 3 m of the center locations of (20,5) and (20,−5), respectively. All channels in the proposed scheme are assumed to follow Rician channels, and we take the channel $\mathbf{G}$ as an example; it is shown below:

$$\begin{array}{c}\hfill \mathbf{G}=\sqrt{\rho d_i^{-\alpha }}\left(\sqrt{\frac{\beta }{1+\beta }}{\mathbf{G}}_{\mathrm{LoS}}+\sqrt{\frac{1}{1+\beta }}{\mathbf{G}}_{\mathrm{NLoS}}\right),\end{array}$$

(43)

where $\rho =-30-10\alpha {log}_{10}\left(d\right)$ dB is the large-scale path loss; $\alpha$ is the path loss exponent; d is the distance in meters between the BS and the active IRS; $\beta$ is the Rician factor; ${\mathbf{G}}_{\mathrm{LoS}}$ is the line-of-sight link between the BS and the active IRS; and the non-line-of-sight (NLoS) link between the BS and the active IRS is denoted as ${\mathbf{G}}_{\mathrm{NLoS}}$ in (43), where each entry follows the distribution $\mathcal{CN}\left(0,{\sigma }_G^2\right)$. Moreover, for small-scale fading, the Rician factor of the active-IRS-related channels is 10, and that of the direct channels is 0 due to the unfavourable communication conditions in an urban environment. For large-scale fading, i.e., the LoS components, it is determined by multiplying the steering vectors of the transmitter with that of the receiver [27]. Other parameters are described in the specific simulation experiments. The benchmark schemes for comparison are as follows:

Table 3. Values of simulation parameters [20,28].

Symbol/Parameter	Value	Symbol/Parameter	Value
number of users, K	2	path loss of channel ${\mathit{h}}_{ae,l}$	$3.6$
number of Eves, L	2	path loss of channel ${\mathit{h}}_{ib,k}$	3
number of antennas, M	3	path loss of channel ${\mathit{h}}_{ab,k}$	$3.6$
number of elements, N	6	maximum power budget at BS, $P_{\mathrm{BS}}^{\max }$	30 dBm
location of active IRS	[5,5]	maximum power budget at active IRS, $P_{\mathrm{A}}^{\max }$	24 dBm
location of the BS	[0,0]	noise power at each user	$-60$ dBm
Rician factor for Rician channels, $\beta$	10 dB	noise power at each Eve	$-60$ dBm
path loss of channel $\mathbf{G}$	$2.6$	noise power at active IRS	$-50$ dBm
path loss of channel ${\mathit{h}}_{ie,l}$	3	convergence threshold	${10}^{-4}$

• w/o an IRS [12]: We assume that no IRS is deployed, as compared with the proposed scheme. Then, we optimize the beamforming vector ${\mathit{\omega }}_k$, $\forall k$ of the BS to maximize the SSR. We set $\mathbf{\Theta }={\mathbf{0}}_{N\times N}$ and ${\sigma }_v=0$ to obtain simulation diagrams of this case.
• With a passive IRS [13]: We replace active IRS with passive IRS for the proposed scheme. Then, we optimize the beamforming vector ${\mathit{\omega }}_k,\forall k$ of the BS and the phase shift matrix $\mathbf{\Theta }$ of the passive IRS to maximize the SSR. We set $\mathbf{P}={\mathbf{I}}_N$ and ${\sigma }_v=0$ to obtain simulation diagrams of this case.
• With an active IRS: the proposed scheme.

We first show the convergence behaviour of the proposed algorithm in Figure 3 by running the proposed algorithm once. Specifically, all curves are obtained by changing related parameters in the proposed algorithm. We can see in Figure 3 that our proposed algorithm demonstrates a favourable convergence behaviour, which verifies the validation of the proposed algorithm.

Figure 3. Convergence behaviour of proposed algorithm.

Figure 4 shows the influence of the number of legitimate users on security performance. It can be seen that when the number of Eves remains constant and the number of users increases, the interference ability of the multiple colluding Eves will decrease compared to the cases of a passive IRS and w/o an IRS. In addition, Figure 4 shows that when the number of users k increases while the number of Eves remains constant, the SSR of the proposed scheme shows an increasing trend, and the proposed scheme is superior to other two baseline schemes. Specifically, when the number of users is 4, the SSR value of the proposed scheme is about $11.3\%$ and $25.4\%$ higher than in the cases with a passive IRS and without an IRS, respectively, which indicates that deploying an IRS in a wireless communication network can improve the SSR, especially when the power amplification of each element of the IRS is applied.

Figure 4. The SSR values versus the number of users, k.

Figure 5 shows that when the number of Eves, l, increases, the SSR value of each scheme monotonically decreases. This is because when the number of users remains constant and the number of Eves increases, more colluding Eves can jointly eavesdrop on users and decode confidential information transmitted by the BS, which significantly degrades the system’s security performance. Although the SSR values of all schemes decrease, the proposed scheme is superior to the other baselines. Specifically, when the number of Eves is 4, the SSR value of the proposed scheme is about $11.3\%$ and $31.7\%$ higher than in the schemes with and without a passive IRS, respectively. Among the three schemes, our proposed active IRS method consistently outperforms the other two baseline schemes.

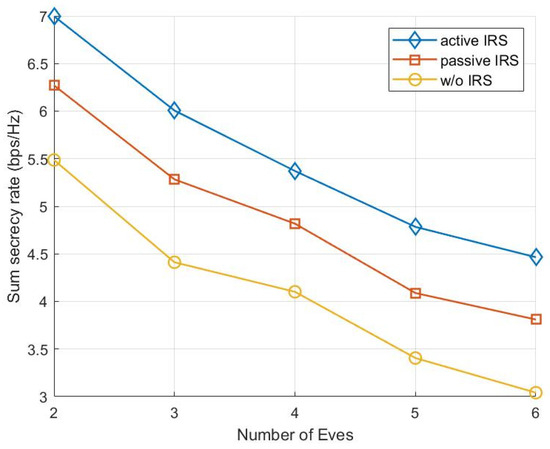
Figure 5. The SSR values versus the number of Eves.

Figure 6 and Figure 7 depict SSR values versus the number of passive/active IRS elements and the number of antennas, respectively. From Figure 6, it can be seen that the SSR values of all IRS-aided schemes increase as the reflecting elements N increase. In particular, our proposed scheme outperforms other schemes, and we can see that when the numbers of elements are 8 and 40, the SSR values of the proposed scheme are about $7\%/16.8\%$ and $7.5\%/29\%$ higher than in the cases with a passive IRS and without a passive IRS, respectively. This result also indicates that increasing the number of reflecting elements can provide more adjustable links to enhance the SSR. From Figure 7, it can be seen that the SSRs of all schemes increase as the number of BS antennas M increases. In particular, we can see that when the number of antennas is 4, the SSR value of the proposed scheme is about $5\%$ and $16.7\%$ higher than in the cases with a passive IRS and without an IRS, respectively. This indicates that increasing the number of transmit antennas can significantly improve the SSR for all schemes because more transmit antennas can provide more spatial DoFs to realize strong beam-focusing for the specific user, thereby enhancing the SSR values.

Figure 6. The SSR values versus the number of reflecting elements.

Figure 7. The SSR values versus the number of antennas.

Figure 8 shows the SSR values versus the maximum power budget of the BS. We can notice that as the maximum transmit power increases, the SSR values of all schemes tend to increase. This is because a larger maximum transmit power budget at the BS leads to more DoFs for the optimization problem; thus, a higher SSR is achieved. Our proposed scheme is always superior to other benchmark schemes. In particular, when the maximum transmit power at the BS is 28 dBm, the SSR value of the proposed scheme is about $13\%$ and $32.6\%$ higher than in the schemes with and without a passive IRS, respectively. Compared with a passive IRS, an active IRS can overcome the fundamental limitation of the MFE. In other words, we can further optimize the power amplification of each element in an active IRS compared to a passive IRS. Simulation results show that the proposed scheme can enhance the values of the SSR in different scenarios with the assistance of the active IRS. These discussions demonstrate the effectiveness of the proposed scheme.

Figure 8. The SSR values versus the maximum transmit power at the BS.

Although perfect CSI is assumed in the proposed scheme, we present Figure 9 to show the impact of imperfect CSI on the security performance of the proposed scheme. Specifically, we let all channels in the proposed scheme be $\mathit{h}=\widehat{\mathit{h}}+\Delta \mathit{h}$, where the real channel $\mathit{h}$ can be replaced by $\mathbf{G}$, ${\mathit{h}}_{ab,k}$, ${\mathit{h}}_{ib,k}$, ${\mathit{h}}_{ae,k}$, and ${\mathit{h}}_{ie,k}$, used for denoting channels in our work, and $\widehat{\mathit{h}}$ and $∥\Delta \mathit{h}∥\le ϵ$ represents the estimated channel and the corresponding channel uncertainty error caused by inaccurate channel estimation, with $ϵ$ being the bound of the channel uncertainty error, respectively. The bound $ϵ$ can be set to $ϵ=\delta ∥\widehat{\mathit{h}}∥$, where $\delta$ denotes the CSI uncertainty level [29]. We can observe that the SSR values of all schemes decrease with an increasing CSI uncertainty level since the inaccurate channel estimation leads to difficulty in designing favourable beamformers for the BS and the active IRS. Although the SSR values of all schemes decrease, the proposed scheme is superior to other schemes. In addition, the performance saturation of the active IRS is achieved when the CSI uncertainty $\delta$ increases as compared with other schemes with a passive IRS and without an IRS, indicating that the introduction of an active IRS in the proposed scheme results in greater robustness compared with other schemes.

Figure 9. The SSR values versus the channel uncertainty level, $\delta$.

5. Conclusions

In this paper, we introduced an active IRS for secure wireless communications with multiple users and Eves and focused on investigating the potential of such a scenario with the help of the active IRS. For the non-convex problem formulated based on the AO algorithm, we first used the SDR method to deal with non-convex terms in an objective function for optimizing the beamforming vectors of the BS with any given beamforming matrix of the active IRS and then used the SCA method to transform the non-convex terms in the objective function into the convex terms for optimizing the beamforming matrix of the active IRS with any given beamforming vectors of the active IRS by applying a first-order Taylor expansion. Furthermore, numerical and simulation results verified that the active IRS in the proposed scheme can enhance SSR values in different settings when compared with other benchmark schemes, which shows that by deploying an active IRS in a scenario of secure resource allocation with multiple users and Eves, the security performance shows the most significant improvement when compared with schemes with and without a conventional passive IRS and different settings, such as numbers of users, Eves, reflecting elements, and BS antennas as well as the maximum transmit power budget of the BS.