Advanced Optimization Methods and Applications

1. Introduction

Optimization methods are finding more applications in all domains, as they play an essential role when dealing with real-life problems. Algorithms for such problems are being continuously developed and improved in order to obtain higher-quality solutions within a reasonable time frame. Metaheuristic methods inspired by the behavior of populations of different groups of people or by the behavior of swarms of animals or insects are currently used to solve optimization problems where optimal solutions cannot be obtained using exact methods in a reasonable amount of time. These metaheuristic algorithms can be classified into four groups: mathematics algorithms, physics algorithms, sociology algorithms, and biology algorithms [1]; or, another classification is evolutionary algorithms, physics-based algorithms, human-based algorithms, and swarm-based algorithms [2]. Metaheuristic algorithms deal with both discrete optimization (e.g., the traveling salesman problem [3]) and continuous optimization problems (e.g., the calculation of parameters of photovoltaic cells and panels [4]). In this Special Issue, different optimization problems are addressed using different methods, where many of the approaches consist of metaheuristic algorithms. The topic of this Special Issue (optimization methods and their applications) attracted many researchers from different countries and different domains (computer science, mathematics, electronics, engineering, economics, statistics, etc.). In Section 2, some statistics are presented about the papers and the authors of the Special Issue. In Section 3, the authors are presented together with their affiliations and contributions to this Special Issue.

2. Statistics of the Special Issue

In total, there were 50 papers submitted to this Special Issue. Out of these papers, 20 papers were published (40%), 39 papers were rejected (58%), and 1 paper (2%) was withdrawn (see Figure 1).

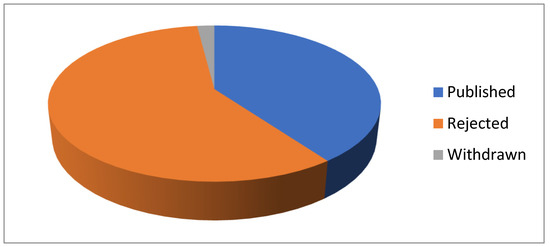
Figure 1. Papers submitted for publication in thi Special Issue.

There were 70 authors that contributed to the papers that were published in the Special Issue. Most of them (64 authors) contributed to only one paper, while the other 6 authors contributed to two papers. Table 1 and Figure 2 present the geographic distribution of the authors. The authors are from 17 different countries.

Table 1. Geographic distribution of authors by country.

No.	Country	No. of Authors
1	China	14
2	Egypt	9
3	India	7
4	Saudi Arabia	6
5	Romania	5
6	Chile	4
7	Japan	4
8	Greece	3
9	Lithuania	3
10	Morocco	3
11	Spain	3
12	Thailand	3
13	Ghana	2
14	Bangladesh	1
15	Colombia	1
16	Iran	1
17	UK	1

Figure 2. Geographic distribution of authors by country.

3. Authors of the Special Issue

The authors of this Special Issue and their main affiliations are shown in Table 2. The average number of authors per manuscript is 3.5.

Table 2. Authors and their affiliations.

No.	Author’s Name	Affiliation(s)	Country	Papers
1	Rana Muhammad Adnan	School of Economics and Statistics, Guangzhou University, Guangzhou	China	[5]
2	Sarita Gajbhiye Meshram	Water Resources and Applied Mathematics Research Lab, Nagpur	India	[5]
3	Reham R. Mostafa	Information Systems Department, Faculty of Computers and Information Sciences, Mansoura University	Egypt	[5]
4	Abu Reza Md. Towfiqul Islam	Department of Disaster Management, Begum Rokeya University, Rangpur	Bangladesh	[5]
5	S. I. Abba	Interdisciplinary Research Center for Membranes and Water Security, King Fahd University of Petroleum & Minerals, Dhahran	Saudi Arabia	[5]
6	Francis Andorful	Department of Geography and Resource Development, University of Ghana, Accra	Ghana	[5]
7	Zhihuan Chen	Engineering Research Center for Metallurgical Automation and Measurement Technology of Ministry of Education, Wuhan University of Science and Technology, Wuhan	Ghana	[5]
8	Lili Zhang	School of Maritime Economics and Management, Dalian Maritime University, Dalian	China	[6]
9	Zhengrui Chen	School of Business, Dalian University of Technology, Panjin	China	[6]
10	Dan Shi	School of Business, Dalian University of Technology, Panjin	China	[6]
11	Yanan Zhao	School of Economics and Management, Liaoning Petrochemical University, Fushun	China	[6]
12	Ke Wang	Department of Mathematics, Shanghai University, Shanghai	China	[7]
13	Zhuo Chen	Department of Mathematics, Shanghai University, Shanghai	China	[7]
14	Shihui Ying	Department of Mathematics, Shanghai University, Shanghai	China	[7]
15	Xinjian Xu	Qianweichang College, Shanghai University, Shanghai	China	[7]
16	Shuen Guo	School of Mathematics and Statistics, Zhengzhou University, Zhengzhou	China	[8]
17	Hao Lang	Department of Logistics and Maritime Studies, The Hong Kong Polytechnic University, Hong Kong SAR	China	[8]
18	Hanxiang Zhang	Department of Logistics and Maritime Studies, The Hong Kong Polytechnic University, Hong Kong SAR	China	[8]
19	Manoharan Madhiarasan	Department of Electronics and Computers, Faculty of Electrical Engineering and Computer Science, Transilvania University of Brașov	Romania	[9]
20	Daniel T. Cotfas	Department of Electronics and Computers, Faculty of Electrical Engineering and Computer Science, Transilvania University of Brașov	Romania	[9]
21	Petru A. Cotfas	Department of Electronics and Computers, Faculty of Electrical Engineering and Computer Science, Transilvania University of Brașov	Romania	[9]
22	Mohamed Abd El-Hady Kassem	Department of Mathematics, Faculty of Science, Tanta University	Egypt	[10]
23	Huda M. Alshanbar	Department of Mathematical Science, College of Science, Princess Nourah bint Abdulrahman University, Riyadh	Saudi Arabia	[10]
24	Diego Noceda-Davila	MODES Research Group, Department of Mathematics, Faculty of Computer Science and CITIC Research Centre, University of A Coruña	Spain	[11]
25	Silvia Lorenzo-Freire	MODES Research Group, Department of Mathematics, Faculty of Computer Science and CITIC Research Centre, University of A Coruña	Spain	[11]
26	Luisa Carpente	MODES Research Group, Department of Mathematics, Faculty of Computer Science and CITIC Research Centre, University of A Coruña	Spain	[11]
27	Mohsine Jennane	LASMA, FSDM, Department of Mathematics Sidi Mohamed Ben Abdellah University, Fez	Morocco	[12]
28	El Mostafa Kalmoun	School of Science and Engineering, Al Akhawayn University in Ifrane, Ifrane	Morocco	[12]
29	Lahoussine Lafhim	LASMA, FSDM, Department of Mathematics, Sidi Mohamed Ben Abdellah University, Fez	Morocco	[12]
30	Anouar Houmia	Department of Mathematics, College of Science, King Khalid University, Abha	Saudi Arabia	[12]
31	Guillermo Cabrera-Guerrero	Escuela de Ingeniería Informática, Pontificia Universidad Católica de Valparaíso,	Chile	[13]
32	Aníbal Álvarez	Escuela de Ingeniería Informática, Pontificia Universidad Católica de Valparaíso,	Chile	[13]
33	Joaquín Vásquez	Escuela de Ingeniería Informática, Pontificia Universidad Católica de Valparaíso,	Chile	[13]
34	Pablo A. Maya Duque	Research Group of Analytics for Decision Making (ALIADO), Industrial Engineering Department, Universidad de Antioquia,	Colombia	[13]
35	Lucas Villavicencio	Escuela de Ingeniería Informática, Pontificia Universidad Católica de Valparaíso,	Chile	[13]
36	Jayashree Piri	Department of CSE, GITAM Institute of Technology (Deemed to be University), Visakhapatnam	India	[14]
37	Puspanjali Mohapatra	Department of CSE, International Institute of Information Technology, Bhubaneswar	India	[14]
38	Biswaranjan Acharya	Department of Computer Engineering-AI, Marwadi University, Rajkot	India	[14]
39	Farhad Soleimanian Gharehchopogh	Department of Computer Engineering, Urmia Branch, Islamic Azad University, Urmia	Iran	[14]
40	Vassilis C. Gerogiannis	Department of Digital Systems, University of Thessaly, Geopolis Campus, Larissa	Greece	[14]
41	Andreas Kanavos	Department of Digital Media and Communication, Ionian University, Kefalonia	Greece	[14]
42	Stella Manika	Department of Planning and Regional Development, University of Thessaly, Volos	Greece	[14]
43	Jiawei Li	School of Computer Science, University of Nottingham Ningbo China, Ningbo	China	[15]
44	Tianxiang Cui	School of Computer Science, University of Nottingham Ningbo China, Ningbo	China	[15]
45	Graham Kendall	School of Computer Science, University of Nottingham UK, Nottingham	UK	[15]
46	Mona A. S. Ali	-Computer Science Department, College of Computer Science and Information Technology, King Faisal University, Al Ahsa -Computer Science, Faculty of Computers and Artificial Intelligence, Benha University, Benha	Saudi Arabia	[16,17]
47	Fathimathul Rajeena P. P.	Computer Science, Faculty of Computers and Artificial Intelligence, Benha University, Benha	Egypt	[16,17]
48	Diaa Salama Abd Elminaam	-Faculty of Computers and Information, Misr International University, Cairo -Computer Science Department, Faculty of Computer Science, Misr International University, Cairo	Egypt	[16,17]
49	Gintaras Palubeckis	Faculty of Informatics, Kaunas University of Technology, Kaunas	Lithuania	[18]
50	Armantas Ostreika	Faculty of Informatics, Kaunas University of Technology, Kaunas	Lithuania	[18]
51	Jurate Platužiene	Faculty of Informatics, Kaunas University of Technology, Kaunas	Lithuania	[18]
52	Mohamed Khamies	Department of Electrical Engineering, Faculty of Engineering, Aswan University, Aswan	Egypt	[19]
53	Salah Kamel	Department of Electrical Engineering, Faculty of Engineering, Aswan University, Aswan	Egypt	[19,20]
54	Mohamed H. Hassan	Department of Electrical Engineering, Faculty of Engineering, Aswan University, Aswan	Egypt	[19,20]
55	Mohamed F. Elnaggar	-Department of Electrical Engineering, College of Engineering, Prince Sattam Bin Abdulaziz University, Al-Kharj -Department of Electrical Power and Machines Engineering, Faculty of Engineering, Helwan University	Saudi Arabia	[19]
63	Ahmed M. Abd-El Wahab	Department of Electrical Engineering, Faculty of Engineering, Aswan University, Aswan	Egypt	[20]
64	Mohamed I. Mosaad	Electrical & Electronics Engineering Technology Department, Royal Commission Yanbu Colleges & Institutes	Saudi Arabia	[20]
65	Tarek A. AbdulFattah	Department of Engineering Physics and Mathematics, Faculty of Engineering, Zagazig University	Egypt	[20]
56	Yaxiong Liu	-Department of Informatics, Kyushu University, Fukuoka -AIP RIKEN, Tokyo	Japan	[21]
57	Ken-ichiro Moridomi	SMN Corporation, Tokyo	Japan	[21]
58	Kohei Hatano	-Department of Informatics, Kyushu University, Fukuoka -AIP RIKEN, Tokyo	Japan	[21]
59	Eiji Takimoto	Department of Informatics, Kyushu University, Fukuoka	Japan	[21]
60	Adisak Hanjing	Department of Science and Mathematics, Rajamangala University of Technology Isan Surin Campus	Thailand	[22]
61	Limpapat Bussaban	Faculty of Science, Chiang Mai University, Chiang Mai	Thailand	[22]
62	Suthep Suantai	-Data Science Research Center, Department of Mathematics, Faculty of Science, Chiang Mai University -Research Group in Mathematics and Applied Mathematics, Department of Mathematics, Faculty of Science, Chiang Mai University	Thailand	[22]
66	Ganesh Bhagwat	Mercedes-Benz Research and Development India, Whitefield, Bangalore	India	[23]
67	Shristi Kumari	Robert Bosch Engineering & Business Solutions Pvt. Ltd., Adugodi, Bangalore	India	[23]
68	Vaishnavi Patekar	KPIT Technologies Pvt. Ltd., Bellandur, Bangalore	India	[23]
69	Adrian Marius Deaconu	Department of Mathematics and Computer Science, Faculty of Mathematics and Computer Science, Transilvania University of Brașov	Romania	[23,24]
70	Luciana Majercsik	Department of Mathematics and Computer Science, Faculty of Mathematics and Computer Science, Transilvania University of Brașov	Romania	[24]