Abstract
For the design of computer experiments, column orthogonality and space-filling are two desirable properties. In this paper, we develop methods for constructing a new class of column-orthogonal designs (ODs) with two-dimensional stratifications on finer grids, including orthogonal Latin hypercube designs (OLHDs) as special cases. In addition to being column-orthogonal, these designs have good space-filling properties in two dimensions. The resulting designs achieve stratifications on or grids, and most column pairs satisfy stratifications on grids. Moreover, many column pairs can achieve stratifications on and grids. Furthermore, the obtained space-filling ODs can have levels, levels, and mixed levels, as required for different needs.
MSC:
62K05; 62K99
1. Introduction
Computer experiments have been widely used recently to explore complex systems in many fields; space-filling and column orthogonality are desirable properties in the design of computer experiments [1]. The space-filling property, which measures the uniformity of the design points in the experimental region, is a fundamental criterion for evaluating designs for computer experiments. Latin hypercube designs (LHDs), proposed by [2], are widely used space-filling designs for computer experiments. An LHD with n runs and m factors, denoted as LHD, is an matrix with each column a permutation of n equally spaced levels. Such a design achieves the maximum stratification in each dimension. Based on the effect sparsity principle [3], for a high-dimensional design region, only a handful of the factors are expected to be active. In [4], the author proposed orthogonal array (OA)-based LHDs which improve the low-dimensional projection properties of random LHDs. In [5,6], the authors discussed space-filling designs with good projection properties in low dimensions. Recently, ref. [7] introduced strong orthogonal arrays, and [8] proposed mappable nearly orthogonal arrays. Both of these two kinds of arrays have better space-filling properties than ordinary orthogonal arrays.
Column orthogonality is a desirable property for LHDs; when a linear model is fitted, this property ensures that the estimates of the main effects are uncorrelated. In addition, orthogonality can be viewed as a stepping stone to space-filling designs when Gaussian process models are considered [9]. There are many ways to construct orthogonal LHDs (OLHDs); see, e.g., [10,11,12,13,14,15] and the references therein. Among them, the method of rotation has attracted widespread attention. In the extant literature, few works have simultaneously considered both the space-filling property and column orthogonality. In [16], the authors constructed OLHDs which achieved stratifications on or grids, with most column pairs achieving stratifications on grids. In [17], the authors provided column-orthogonal designs (ODs) with two-dimensional stratifications. In [18], the authors studied ODs with two-dimensional and three-dimensional stratifications, while [15] proposed ODs with multi-dimensional stratifications.
The goal of the present paper is to construct ODs with stratifications on finer grids, i.e., , , and . We first introduce a new class of OLHDs with runs by rotating s-level OAs, where can be any positive even integer not smaller than 4 and . We additionally introduce a new class of ODs with flexible run sizes. All these designs guarantee desirable two-dimensional space-filling properties. Most column pairs of the resulting designs can achieve stratifications on grids. Moreover, many column pairs can satisfy stratifications on and grids. Furthermore, the resulting ODs can have or levels and mixed levels.
The rest of this paper is organized as follows: Section 2 introduces preliminaries used in this paper; Section 3 proposes the general construction method for OLHDs and extends it to accommodate more factors; Section 4 concentrates on the construction of ODs with levels, levels, and mixed levels; finally, concluding remarks are provided in Section 5. All proofs are deferred to Appendix A.
2. Definitions and Notation
We use to denote a balanced design of n runs and m factors, with each of the levels from . When all the instances of are equal to s, the design is a symmetric balanced design . Further, if , it is an LHD, denoted as LHD.
A mixed-level orthogonal array (OA) with strength t and levels , denoted as OA, satisfies the requirement that all possible level combinations for any columns t occur with the same frequency. When all are equal to s, the array is symmetric and denoted as OA. For an OA, it must have for some integer , which is the index of the OA.
For an array with n runs and m factors, we say it achieves a stratification on an grid for some if the corresponding p columns of it can be collapsed into an OA .
The correlation between two vectors and is defined as
where and . The average correlation of a design is defined as
Two vectors are said to be column-orthogonal if the correlation between them is 0. A design is said to be column-orthogonal, denoted as OD, if any two of its columns are column-orthogonal. Obviously, any OA with is an OD. Similarly, we have OLHD .
To facilitate the study of orthogonality, we sometimes center the levels of an OD into
Let be a Galois field of order and let be a Galois field of order s. We denote an matrix with entries from as , which is called a difference scheme if it satisfies the requirement that, for any i and j with , the vector difference of the ith and jth columns contains every element of equally often.
For two matrices and with entries from , we define
where + is the addition defined on .
For any design A with entries from , let ; we define
for , and define
where , denotes the largest integer less than or equal to h and denotes the lth column in the difference scheme for .
Let
Then, we define
For a prime power , let be an OA with entries from and let D be a difference scheme . We now create
for and define
For a prime s and integer d with and , we denote the d columns of an -run full factorial design as . Any generated column including each column of can be denoted as for some , and corresponds to a nonzero element in . Here, let .
As discussed in [11], the corresponding columns of the first non-zero elements of , modulo form a regular design D, where is a primitive polynomial of order d. Any d consecutive columns of D form a full factorial design, denoted as and mod , . Let , defining for , . Then, we have
and
Without particular explanation, in this paper, s is a prime, , d is an integer with , , and . We provide an illustrative example in the following.
Example 1.

For and , we denote the full factorial design as . Here, , with the primitive polynomial . Then, , , , modulo are 1, x, , , which correspond to columns , , , . Similarly, we have the elements of modulo . For example, is obtained by modulo . The obtained full factorial designs are shown in Table 1, where is the jth column in for and .

Table 1.
The obtained full factorial designs.
3. Construction of Orthogonal LHDs
This section first introduces a rotation method in Algorithm 1 to construct OLHDs with attractive stratification properties, then generalizes the method to enlarge the columns of these LHDs.
To make it easier for readers to understand the algorithm, we provide the flowchart in Figure 1 to explain the algorithm.
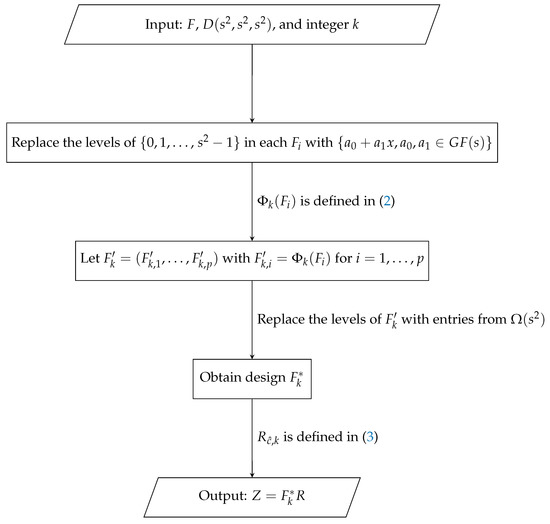
Figure 1.
Flowchart of Algorithm 1.
To measure the stratification properties of a design with m columns, we define the following two proportions:
where is the number of column pairs that achieve stratifications on grids and is the number of column pairs that achieve stratifications on and grids. The properties of the designs in Algorithm 1 are summarized in Theorem 1.
| Algorithm 1 Construction of OLHDs |
|
Theorem 1.
Design Z in Algorithm 1 is an OLHD where and , and has the following properties:
- (1)
- Any two columns achieve a stratification on an or grid;
- (2)
- The proportion of column pairs achieving stratifications on grids satisfies ;
- (3)
- The proportion of column pairs achieving stratifications on and grids satisfies .
For this, we use the following illustrative example.
Example 2.


For and , we denote the four independent columns as , , , , while the generated columns of these four columns are denoted as , , , , , , , , , , . We have with and the primitive polynomial . It is easy to obtain three full factorial designs , , and . Then, we have , , and . Thus, , which is displayed in Table 2.

Table 2.
F in Example 2.
In this way, we obtain a difference scheme , denoted as
with , where for . We can obtain by replacing the levels of with entries from . Then, we rotate by to generate an OLHD, where
The resulting OLHD is displayed in Table A1 of Appendix B. From Table 3, it is apparent that 260 out of all 276 (i.e., ) column pairs achieve stratifications on grids, more than of column pairs achieve stratifications on or grids, and of column pairs achieve stratifications on or grids.

Table 3.
The stratification properties of the resulting design in Example 2.
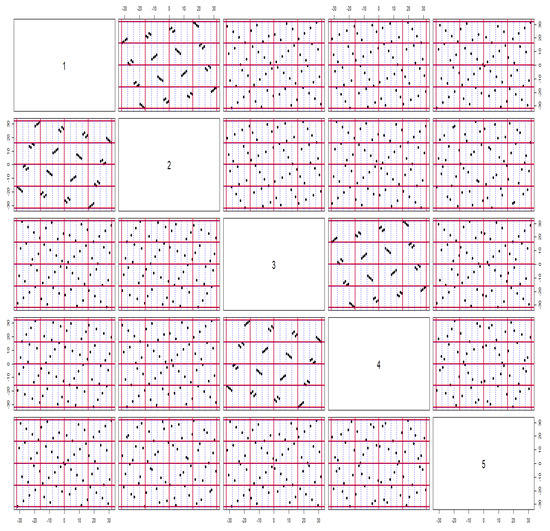
To illustrate the projection property of the resulting OLHD, we display the pairwise scatter plots of the (1–5)th columns of the design in Figure 2.

Figure 2.
The pairwise scatter plots of the (1–5)th columns of OLHD in Example 2.
From Figure 2, it can be seen that all the column pairs of the first five columns achieve stratifications on grids, and most of the same column pairs achieve stratifications on and grids. Other column pairs perform similarly.
Example OLHDs constructed by Algorithm 1 are listed in Table 4. Without loss of generality, we only show the lower bounds of and in Table 4, which are denoted as and , respectively.

Table 4.
Example OLHDs constructed by Algorithm 1.
As shown in Table 4, the lower bounds of are very close to 1, while that of is close to 1 when the run size is large, which means that nearly all the column pairs achieve stratifications on grids and that most column pairs achieve stratifications on and grids.
A comparison between the OLHDs obtained using Algorithm 1 and the OLHDs in [14,15,16] is presented in Table 5. Compared with this class of designs, the resulting OLHDs satisfy two-dimensional space-filling properties on finer grids, i.e., , , and . The OLHDs in [14] satisfy stratifications on and grids, while the designs in [16] satisfy stratifications on grids. Thus, the OLHDs based on Algorithm 1 satisfy better two-dimensional space-filling properties. Moreover, these OLHDs are able to accommodate more factors than OLHDs in [15], and can fill the gap between the run sizes of the available OLHDs in [16]. For example, we can construct OLHDs of 64 and 1024 runs, while such designs are not available in [16].

Table 5.
Comparison with related designs.
Furthermore, we can construct OLHDs with more columns through Algorithm 2. The flowchart of Algorithm 2 is shown in Appendix B.
| Algorithm 2 Enlarging the columns of OLHDs |
|
Corollary 1.
Design M obtained by Algorithm 2 is an OLHD where and . Each sub-design achieves the same stratifications with Z in Algorithm olhds1 for . At least column pairs of M achieve stratifications on grids in all the two dimensions.
In Step 1, we can choose OLHDs obtained by [15,19] when 5, 7, 11, and 17, respectively. According to Algorithm 2, we can obtain OLHDs with t sub-designs, with each satisfying the same stratification properties in Theorem 1. Moreover, when , per Algorithm 2 we can obtain an OLHD that can accommodate more columns than OLHD in [14] and has more attractive space-filling properties.
4. Construction of Orthogonal Designs
This section introduces three rotation methods for constructing ODs. The first two methods can construct ODs with and levels, respectively, while the third can obtain mixed-level ODs. We first present the construction of ODs with levels and investigate their properties. The construction method is provided in Algorithm 3, and the flowchart is shown in Appendix B.
| Algorithm 3 Construction of -level ODs |
|
Based on the form of the rotation matrix, it is easy to see that any column x in obtained in (9) has the following form:
where e and are the two columns in some with for some l; here, is a column which is not in . We call e the leading column of x to facilitate later study. Now, we can consider the mapping
with collapsing the levels in into levels in . For example, when , the 64 levels are collapsed into 4 levels by the mapping, as follows:
Then, we consider the mapping
with collapsing the levels in into levels in . For example, when , the 64 levels are collapsed into 16 levels by the mapping, as follows:
The resulting design is orthogonal and achieves stratifications on or grids; most column pairs can achieve stratifications on grids. Moreover, column pairs can achieve stratifications on and grids as well. We can summarize the properties of in the following theorem.
Theorem 2.
Design in (9) is an OD, where and ; can be partitioned into disjoint groups of columns, each with the following properties:
- (1)
- Any two distinct columns achieve a stratification on an or grid;
- (2)
- Most column pairs achieve stratifications on grids, and the proportion is not less than ;
- (3)
- The proportion of column pairs achieving stratifications on and grids satisfies .
From Theorem 2, it can be understood that the obtained ODs have appealing stratification properties. For example, for and at least of all column pairs of can achieve stratifications on grids. Furthermore, many column pairs of achieve stratifications on finer and grids (). The lower bound of this proportion is relatively loose. Below, we provide an illustrative example.
Example 3.

Consider the same conditions in Example 2 with , , and ; we can obtain and the difference scheme . From Step 1, we have , where
Then, we divide into two groups, as follows: for , where each has two columns, and order the as follows:
We replace the levels of each with entries from and denote the resulting design as . Taking two successive instances of at a time in the order given in (13), we obtain sets of four columns, denoted as . Then, we can obtain an OLHD through
which is displayed in Table A2 of Appendix B. The stratification properties of are summarized in Table 6. It can be seen that this design has the same number of column pairs achieving stratification on a grid as the one in Example 2, and has more column pairs achieving stratifications on or grids than the one in Example 2 with . Furthermore, by calculation, we can say that the obtained OLHD achieves stratifications on a grid in 140 out of all 276 (i.e., ) and on a grid in100 out of all 276 (i.e., ).

Table 6.
The stratification properties of the resulting OLHD in Example 3.
The OAs and difference schemes used in the construction are available in [20] and the library of OAs (http://neilsloane.com/oadir/index.html, accessed on 16 March 2023). It is easy to show that is an OLHD when . Table 7 summarizes example ODs constructed by Algorithm 3. Their space-filling properties are characterized by and . Similar to Section 3, we only list the lower bounds of and in Table 7, denoted as and , respectively. As shown in Table 7, the lower bounds of are very close to 1 and those of are quite large in most cases, which means that nearly all the column pairs of these ODs achieve stratifications on grids, and that most column pairs achieve stratifications on finer and grids as well.

Table 7.
Example ODs constructed by Algorithm 3.
Next, we introduce the construction of ODs with levels with the same space-filling properties as the designs obtained in Algorithm 3. The construction method is provided in Algorithm 4.
| Algorithm 4 Construction of -level ODs |
|
For the resulting design, it is easy to obtain the following theorem.
Theorem 3.
Design Y in (14) is an OD with , that can be partitioned into disjoint groups of columns with the same stratification properties as in Theorem 2.
Compared with the ODs constructed in Algorithm 3, design Y has lower levels and can accommodate more columns than design in Algorithm 3 when d is an odd number. Now, we turn to an illustrative example.
Example 4.
Considering the same conditions in Example 3, we first obtain the Ei,js. For , we define and . We can construct an OD by
which is displayed in Table A3 of Appendix B. It can be seen that the design points are well-scattered in the two-dimensional projections of the resulting OD, and it has the same space-filling properties as the OD constructed in Example 3.
Table 8 lists example ODs obtained by Algorithm 4. Compared with the ODs constructed using Algorithm 3, the obtained designs have lower levels and more columns when d is odd. The resulting designs have the same stratification properties as the ODs constructed by Algorithm 3. These ODs have more flexible run sizes than the OLHDs obtained by Algorithm 1.

Table 8.
Example ODs constructed by Algorithm 4.
Now, we consider the construction of mixed-level ODs, which are very useful when the factors cannot have the same number of levels. The construction method is provided in Algorithm 5.
| Algorithm 5 Construction of mixed-level ODs |
For the resulting design H, the following theorem holds.
Theorem 4.
Design H in (15) is an OD with that can be partitioned into disjoint groups of columns with the same stratification properties as design in Algorithm 3.
Table 9 summarizes example ODs constructed by Algorithms 3–5 for practical needs.

Table 9.
Example ODs constructed by Algorithms 3–5.
5. Conclusions, Limitations, and Future Research
In this paper, we have proposed a new rotation method to generate OLHDs that can achieve stratifications on or grids; moreover, most column pairs can achieve stratifications on grids, and a large portion of column pairs can achieve stratifications on and grids. Furthermore, we introduce a new class of space-filling ODs with levels, levels, and mixed levels, which can guarantee desirable stratifications in two dimensions.
It is worth noting that the resulting OLHDs and ODs enjoy stratifications on finer grids that cannot be satisfied by the existing space-filling designs. To the best of our knowledge, this is a new development in the literature. The theoretical constructions are well established. All these properties make the resulting designs competitive for computer experiments. The proposed designs are constructed systematically, without relying on any optimization algorithm, and the methods are efficient from a time perspective.
Next, we provide a simple simulation example to illustrate the performance of the resulting OLHDs from the model perspective. First, we use the following three methods to screen the active effects: the least absolute shrinkage and selection operator (LASSO) in the ‘glmnet’ R package, the smoothly clipped absolute deviation (SCAD) in the ‘ncvreg’ R package, and the stepwise linear model regression following the AIC criterion; the first two methods were recently used in [21], and further details can be found there. Suppose the true model is
where , , and the random error . We use the first twelve columns of the designed OLHD in Example 2 to generate the responses. All screening results are provided in Table 10, where the truly active factors are marked with the superscript ‘‘a’’ and identified ‘‘active factors’’ are indicated with ‘‘•’’.

Table 10.
Screening result.
From Table 10, it can be seen that each method identifies eleven active effects, and the three methods all obtain the same ten truly active effects. Next, we entered all of these thirteen active effects into the model in order to test the significance of the coefficients. Table 11 shows the estimates and significance test results.

Table 11.
Estimates and significance test results.
From Table 11, the true active effects can be correctly identified as . Then, we fitted the model in (17), with the of the model being 0.9378.
This result is very close to the real model.
The computation was implemented on a personal computer with an Intel i5-4210H CPU and 2.90 GHz, which needed 0.384 seconds to generate the design, screen the active effects, and fit the model.
Due to the utilization of the rotation method, the run sizes of the obtained designs are restricted to prime powers, and certain two-dimensional stratification properties are not satisfied by all the column pairs, only a large proportion of them. Due to time restrictions, we do not provide an empirical example here. These issues are, however, deserving of future work. In this paper, we consider the space-filling properties measured by the two-dimensional stratifications; however, other criteria, for example, the maximin distance criterion, can be suitable choices as well. Constructions of column-orthogonal designs using the maximin distance and flexible run sizes are interesting topics for future research.
Author Contributions
S.-N.L.: conceptualization, methodology, formal analysis, writing—original draft preparation; J.-Y.Y.: methodology, formal analysis, writing—review and editing, supervision; M.-Q.L.: methodology, supervision, writing—review and editing, funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (Grant Nos. 12131001 and 12226343) and the National Ten Thousand Talents Program of China.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
First, we introduce a lemma from [14] that is crucial for the construction in this paper.
Lemma A1
([14]). Let A be an -full factorial and define a difference scheme . For , let . Then, for any column b in , must be an -full factorial for any .
Proof of Theorem 1.
We first show that Z is an LHD. Because each is an full factorial design with elements from , it is the case that has levels and is an full factorial design for any . Due to Lemma A1, is a full factorial design where b is one column in , , and . For each , we can create with and such that by applying Lemma A1 twice; this results in certain sub-arrays of columns being full factorials. In general, for any integer k, with and has the property that certain sub-arrays of columns are full factorials. Thus, all possible -tuples with elements from appear equally often in , for . Due to the property of , it can be verified that the ith column of Z is a permutation of , which implies that Z is an LHD.
Next, we prove the orthogonality of Z. As R is column-orthogonal, we only need to prove the orthogonality of . For any column , has two columns. We denote the first column of as and the second column of as . For any two columns and in with and , we have and . Then,
where and . It follows that is an . Then, we can find that when , the columns in and are column-orthogonal. When and , we can find that and are column-orthogonal based on the properties of the difference scheme. Thus, Z is an OLHD.
Next, we prove the stratification properties of (1) and (2). It can be seen that after collapsing the levels of Z to the level, we obtain . Thus, we only need to prove the stratification property of . For any and , it is easy to find that any two columns from can achieve a stratification on an grid, as is a full factorial design. From the properties of the difference scheme, we can find that if , any two columns from and can achieve a stratification on an grid. Now, we consider two columns from and for . According to proof of Theorem 1 in [16], the column pairs in can only have the following structures:
- (a). or ,
- (b). or ,
- where , , and X, Y, L, M, N are independent columns of F. Here, denotes any interaction of X and Y with and L, M, N denote the factors that are not the interactions of X and Y. If two columns have structure (a) and , they can only achieve a stratification on an or grid. It is easy to check that there are less than such pairs in . The other column pairs having structure (b) or (a) with can achieve stratifications on grids. When the other column pairs have structure (b), then and is orthogonal. Thus, they can achieve stratifications on grids. If the other column pairs have structure (a) with , they can achieve stratifications on grids based on the properties of difference scheme.
Now, we prove property (3). For any two columns and of Z, we collapse the levels of into levels in using mapping and collapse the levels of into levels in using mapping . Then, we have and , where , , and are from F, and . As the column pairs in can only have structure (a) or (b) and if , have structure (b), , from an OA. Thus, they can achieve stratifications on grids. In a similar way, it is clear that they can achieve stratifications on grids as well. It easy to see that only column pairs have structure (b) in F. Thus, we have at least column pairs achieving stratifications on and grids. The proof is completed. □
Proof of Corollary 1.
We only need to prove the stratification property of M which follows from the property of , where . When collapsed into s levels, becomes and becomes , where and are the hth column of and the gth column of , respectively, and and are the (2h − 1)th column of and the (2g − 1)th column of , respectively.
- Case 1:
If and , the two columns are in the same and achieve the same stratification as in Theorem 1.
- Case 2:
If and , and are orthogonal. Based on the properties of difference scheme, is an OA for . Thus, the hth column of and the gth column of can achieve a stratification on an grid. Then, if , may not be an OA and fails to guarantee stratification on an grid. Thus, similar to the proof of Theorem 1, we can find that at least column pairs in M can achieve stratifications on grids. The proof is completed. □
Proof of Theorem 2.
First, we need to prove the orthogonality; as is column-orthogonal, we only need to prove the orthogonality of . It is easy to find that and . Due to the property of ,
where and . Then, we can find that when , and are column-orthogonal. When and , we can find that and are column-orthogonal based on the properties of the difference scheme. Thus, is an OD.
Next, we prove the stratification properties of . Note that
where , , and . The elements of e, , and are in ; thus, all the elements of fall into , . This indicates that the elements of must be less than . Therefore, we have . Similar to the proof of Theorem 1, according to proof of Theorem 1 in [16], the column pairs in have only the following two structures:
(a). or ,
(b). or ,
Here, X, Y, L, M, N are independent columns of F, denotes any interaction of X and Y with , and L, M, N denote the factors that are not interactions of X and Y, where . If two columns have structure (a) and , they can only achieve stratifications on an or grid. It is easy to check that there are less than column pairs in when is even and column pairs in when is odd. The other column pairs with structure (b) or (a) for can achieve stratifications on grids. This completes the proof of properties (1) and (2).
Any two columns and of can be expressed as
Based on the previous discussion, it is easy to see that and are from the same , and as such are and . Now, we collapse the levels in of into levels in using mapping in (11) and collapse the levels in of into levels in using mapping as
Then, we have and , where , , , and , , are independent columns of F. If and have structure (b) and , then the two pairs and have structure (b) and as well. Only if and are not interactions of and , can there be an OA. Similar to the proof of Theorem 1, at least column pairs achieve stratifications on and grids. This completes the proof of property (3). The proof is completed. □
Appendix B
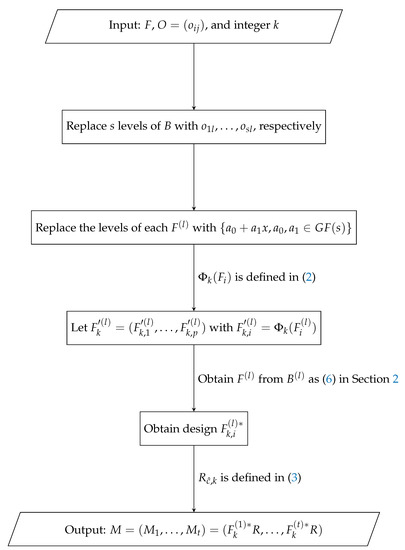
Figure A1.
Flowchart of Algorithm 2.
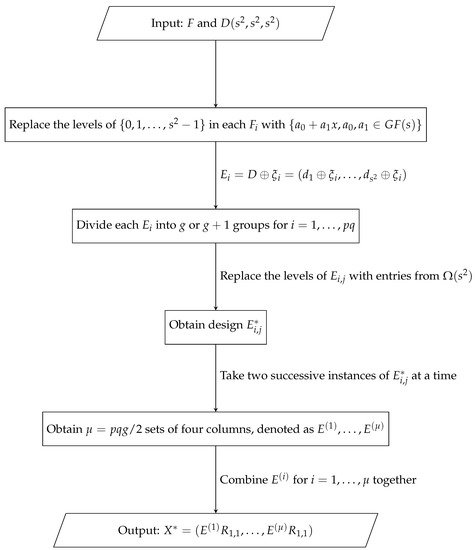
Figure A2.
Flowchart of Algorithm 3.

Table A1.
The OLHD used in Example 2.
Table A1.
The OLHD used in Example 2.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | −31.5 | −16.5 | −28.5 | −19.5 | −31.5 | −16.5 | −28.5 | −19.5 | −31.5 | −16.5 | −28.5 | −19.5 | −31.5 | −16.5 | −28.5 | −19.5 | −31.5 | −16.5 | −28.5 | −19.5 | −31.5 | −16.5 | −28.5 | −19.5 |
| 2 | −27.5 | −1.5 | −24.5 | −2.5 | −27.5 | −1.5 | −24.5 | −2.5 | −19.5 | 28.5 | −16.5 | 31.5 | −19.5 | 28.5 | −16.5 | 31.5 | −10.5 | −5.5 | −9.5 | −6.5 | −10.5 | −5.5 | −9.5 | −6.5 |
| 3 | −23.5 | 13.5 | −20.5 | 14.5 | −23.5 | 13.5 | −20.5 | 14.5 | −6.5 | 9.5 | −5.5 | 10.5 | −6.5 | 9.5 | −5.5 | 10.5 | 14.5 | 20.5 | 13.5 | 23.5 | 14.5 | 20.5 | 13.5 | 23.5 |
| 4 | −19.5 | 28.5 | −16.5 | 31.5 | −19.5 | 28.5 | −16.5 | 31.5 | −10.5 | −5.5 | −9.5 | −6.5 | −10.5 | −5.5 | −9.5 | −6.5 | 27.5 | 1.5 | 24.5 | 2.5 | 27.5 | 1.5 | 24.5 | 2.5 |
| 5 | −14.5 | −20.5 | −13.5 | −23.5 | −14.5 | −20.5 | −13.5 | −23.5 | 23.5 | −13.5 | 20.5 | −14.5 | 23.5 | −13.5 | 20.5 | −14.5 | −2.5 | 24.5 | −1.5 | 27.5 | −2.5 | 24.5 | −1.5 | 27.5 |
| 6 | −10.5 | −5.5 | −9.5 | −6.5 | −10.5 | −5.5 | −9.5 | −6.5 | 27.5 | 1.5 | 24.5 | 2.5 | 27.5 | 1.5 | 24.5 | 2.5 | −23.5 | 13.5 | −20.5 | 14.5 | −23.5 | 13.5 | −20.5 | 14.5 |
| 7 | −6.5 | 9.5 | −5.5 | 10.5 | −6.5 | 9.5 | −5.5 | 10.5 | 14.5 | 20.5 | 13.5 | 23.5 | 14.5 | 20.5 | 13.5 | 23.5 | 19.5 | −28.5 | 16.5 | −31.5 | 19.5 | −28.5 | 16.5 | −31.5 |
| 8 | −2.5 | 24.5 | −1.5 | 27.5 | −2.5 | 24.5 | −1.5 | 27.5 | 2.5 | −24.5 | 1.5 | −27.5 | 2.5 | −24.5 | 1.5 | −27.5 | 6.5 | −9.5 | 5.5 | −10.5 | 6.5 | −9.5 | 5.5 | −10.5 |
| 9 | 2.5 | −24.5 | 1.5 | −27.5 | 2.5 | −24.5 | 1.5 | −27.5 | 6.5 | −9.5 | 5.5 | −10.5 | 6.5 | −9.5 | 5.5 | −10.5 | 10.5 | 5.5 | 9.5 | 6.5 | 10.5 | 5.5 | 9.5 | 6.5 |
| 10 | 6.5 | −9.5 | 5.5 | −10.5 | 6.5 | −9.5 | 5.5 | −10.5 | 10.5 | 5.5 | 9.5 | 6.5 | 10.5 | 5.5 | 9.5 | 6.5 | 31.5 | 16.5 | 28.5 | 19.5 | 31.5 | 16.5 | 28.5 | 19.5 |
| 11 | 10.5 | 5.5 | 9.5 | 6.5 | 10.5 | 5.5 | 9.5 | 6.5 | 31.5 | 16.5 | 28.5 | 19.5 | 31.5 | 16.5 | 28.5 | 19.5 | −27.5 | −1.5 | −24.5 | −2.5 | −27.5 | −1.5 | −24.5 | −2.5 |
| 12 | 14.5 | 20.5 | 13.5 | 23.5 | 14.5 | 20.5 | 13.5 | 23.5 | 19.5 | −28.5 | 16.5 | −31.5 | 19.5 | −28.5 | 16.5 | −31.5 | −14.5 | −20.5 | −13.5 | −23.5 | −14.5 | −20.5 | −13.5 | −23.5 |
| 13 | 19.5 | −28.5 | 16.5 | −31.5 | 19.5 | −28.5 | 16.5 | −31.5 | −14.5 | −20.5 | −13.5 | −23.5 | −14.5 | −20.5 | −13.5 | −23.5 | 23.5 | −13.5 | 20.5 | −14.5 | 23.5 | −13.5 | 20.5 | −14.5 |
| 14 | 23.5 | −13.5 | 20.5 | −14.5 | 23.5 | −13.5 | 20.5 | −14.5 | −2.5 | 24.5 | −1.5 | 27.5 | −2.5 | 24.5 | −1.5 | 27.5 | 2.5 | −24.5 | 1.5 | −27.5 | 2.5 | −24.5 | 1.5 | −27.5 |
| 15 | 27.5 | 1.5 | 24.5 | 2.5 | 27.5 | 1.5 | 24.5 | 2.5 | −23.5 | 13.5 | −20.5 | 14.5 | −23.5 | 13.5 | −20.5 | 14.5 | −6.5 | 9.5 | −5.5 | 10.5 | −6.5 | 9.5 | −5.5 | 10.5 |
| 16 | 31.5 | 16.5 | 28.5 | 19.5 | 31.5 | 16.5 | 28.5 | 19.5 | −27.5 | −1.5 | −24.5 | −2.5 | −27.5 | −1.5 | −24.5 | −2.5 | −19.5 | 28.5 | −16.5 | 31.5 | −19.5 | 28.5 | −16.5 | 31.5 |
| 17 | −30.5 | −17.5 | −8.5 | −7.5 | 11.5 | 4.5 | 29.5 | 18.5 | −30.5 | −17.5 | −8.5 | −7.5 | 11.5 | 4.5 | 29.5 | 18.5 | −30.5 | −17.5 | −8.5 | −7.5 | 11.5 | 4.5 | 29.5 | 18.5 |
| 18 | −26.5 | −0.5 | −12.5 | −22.5 | 15.5 | 21.5 | 25.5 | 3.5 | −18.5 | 29.5 | −4.5 | 11.5 | 7.5 | −8.5 | 17.5 | −30.5 | −11.5 | −4.5 | −29.5 | −18.5 | 30.5 | 17.5 | 8.5 | 7.5 |
| 19 | −22.5 | 12.5 | −0.5 | 26.5 | 3.5 | −25.5 | 21.5 | −15.5 | −7.5 | 8.5 | −17.5 | 30.5 | 18.5 | −29.5 | 4.5 | −11.5 | 15.5 | 21.5 | 25.5 | 3.5 | −26.5 | −0.5 | −12.5 | −22.5 |
| 20 | −18.5 | 29.5 | −4.5 | 11.5 | 7.5 | −8.5 | 17.5 | −30.5 | −11.5 | −4.5 | −29.5 | −18.5 | 30.5 | 17.5 | 8.5 | 7.5 | 26.5 | 0.5 | 12.5 | 22.5 | −15.5 | −21.5 | −25.5 | −3.5 |
| 21 | −15.5 | −21.5 | −25.5 | −3.5 | 26.5 | 0.5 | 12.5 | 22.5 | 22.5 | −12.5 | 0.5 | −26.5 | −3.5 | 25.5 | −21.5 | 15.5 | −3.5 | 25.5 | −21.5 | 15.5 | 22.5 | −12.5 | 0.5 | −26.5 |
| 22 | −11.5 | −4.5 | −29.5 | −18.5 | 30.5 | 17.5 | 8.5 | 7.5 | 26.5 | 0.5 | 12.5 | 22.5 | −15.5 | −21.5 | −25.5 | −3.5 | −22.5 | 12.5 | −0.5 | 26.5 | 3.5 | −25.5 | 21.5 | −15.5 |
| 23 | −7.5 | 8.5 | −17.5 | 30.5 | 18.5 | −29.5 | 4.5 | −11.5 | 15.5 | 21.5 | 25.5 | 3.5 | −26.5 | −0.5 | −12.5 | −22.5 | 18.5 | −29.5 | 4.5 | −11.5 | −7.5 | 8.5 | −17.5 | 30.5 |
| 24 | −3.5 | 25.5 | −21.5 | 15.5 | 22.5 | −12.5 | 0.5 | −26.5 | 3.5 | −25.5 | 21.5 | −15.5 | −22.5 | 12.5 | −0.5 | 26.5 | 7.5 | −8.5 | 17.5 | −30.5 | −18.5 | 29.5 | −4.5 | 11.5 |
| 25 | 3.5 | −25.5 | 21.5 | −15.5 | −22.5 | 12.5 | −0.5 | 26.5 | 7.5 | −8.5 | 17.5 | −30.5 | −18.5 | 29.5 | −4.5 | 11.5 | 11.5 | 4.5 | 29.5 | 18.5 | −30.5 | −17.5 | −8.5 | −7.5 |
| 26 | 7.5 | −8.5 | 17.5 | −30.5 | −18.5 | 29.5 | −4.5 | 11.5 | 11.5 | 4.5 | 29.5 | 18.5 | −30.5 | −17.5 | −8.5 | −7.5 | 30.5 | 17.5 | 8.5 | 7.5 | −11.5 | −4.5 | −29.5 | −18.5 |
| 27 | 11.5 | 4.5 | 29.5 | 18.5 | −30.5 | −17.5 | −8.5 | −7.5 | 30.5 | 17.5 | 8.5 | 7.5 | −11.5 | −4.5 | −29.5 | −18.5 | −26.5 | −0.5 | −12.5 | −22.5 | 15.5 | 21.5 | 25.5 | 3.5 |
| 28 | 15.5 | 21.5 | 25.5 | 3.5 | −26.5 | −0.5 | −12.5 | −22.5 | 18.5 | −29.5 | 4.5 | −11.5 | −7.5 | 8.5 | −17.5 | 30.5 | −15.5 | −21.5 | −25.5 | −3.5 | 26.5 | 0.5 | 12.5 | 22.5 |
| 29 | 18.5 | −29.5 | 4.5 | −11.5 | −7.5 | 8.5 | −17.5 | 30.5 | −15.5 | −21.5 | −25.5 | −3.5 | 26.5 | 0.5 | 12.5 | 22.5 | 22.5 | −12.5 | 0.5 | −26.5 | −3.5 | 25.5 | −21.5 | 15.5 |
| 30 | 22.5 | −12.5 | 0.5 | −26.5 | −3.5 | 25.5 | −21.5 | 15.5 | −3.5 | 25.5 | −21.5 | 15.5 | 22.5 | −12.5 | 0.5 | −26.5 | 3.5 | −25.5 | 21.5 | −15.5 | −22.5 | 12.5 | −0.5 | 26.5 |
| 31 | 26.5 | 0.5 | 12.5 | 22.5 | −15.5 | −21.5 | −25.5 | −3.5 | −22.5 | 12.5 | −0.5 | 26.5 | 3.5 | −25.5 | 21.5 | −15.5 | −7.5 | 8.5 | −17.5 | 30.5 | 18.5 | −29.5 | 4.5 | −11.5 |
| 32 | 30.5 | 17.5 | 8.5 | 7.5 | −11.5 | −4.5 | −29.5 | −18.5 | −26.5 | −0.5 | −12.5 | −22.5 | 15.5 | 21.5 | 25.5 | 3.5 | −18.5 | 29.5 | −4.5 | 11.5 | 7.5 | −8.5 | 17.5 | −30.5 |
| 33 | −29.5 | −18.5 | 11.5 | 4.5 | 29.5 | 18.5 | −11.5 | −4.5 | −29.5 | −18.5 | 11.5 | 4.5 | 29.5 | 18.5 | −11.5 | −4.5 | −29.5 | −18.5 | 11.5 | 4.5 | 29.5 | 18.5 | −11.5 | −4.5 |
| 34 | −25.5 | −3.5 | 15.5 | 21.5 | 25.5 | 3.5 | −15.5 | −21.5 | −17.5 | 30.5 | 7.5 | −8.5 | 17.5 | −30.5 | −7.5 | 8.5 | −8.5 | −7.5 | 30.5 | 17.5 | 8.5 | 7.5 | −30.5 | −17.5 |
| 35 | −21.5 | 15.5 | 3.5 | −25.5 | 21.5 | −15.5 | −3.5 | 25.5 | −4.5 | 11.5 | 18.5 | −29.5 | 4.5 | −11.5 | −18.5 | 29.5 | 12.5 | 22.5 | −26.5 | −0.5 | −12.5 | −22.5 | 26.5 | 0.5 |
| 36 | −17.5 | 30.5 | 7.5 | −8.5 | 17.5 | −30.5 | −7.5 | 8.5 | −8.5 | −7.5 | 30.5 | 17.5 | 8.5 | 7.5 | −30.5 | −17.5 | 25.5 | 3.5 | −15.5 | −21.5 | −25.5 | −3.5 | 15.5 | 21.5 |
| 37 | −12.5 | −22.5 | 26.5 | 0.5 | 12.5 | 22.5 | −26.5 | −0.5 | 21.5 | −15.5 | −3.5 | 25.5 | −21.5 | 15.5 | 3.5 | −25.5 | −0.5 | 26.5 | 22.5 | −12.5 | 0.5 | −26.5 | −22.5 | 12.5 |
| 38 | −8.5 | −7.5 | 30.5 | 17.5 | 8.5 | 7.5 | −30.5 | −17.5 | 25.5 | 3.5 | −15.5 | −21.5 | −25.5 | −3.5 | 15.5 | 21.5 | −21.5 | 15.5 | 3.5 | −25.5 | 21.5 | −15.5 | −3.5 | 25.5 |
| 39 | −4.5 | 11.5 | 18.5 | −29.5 | 4.5 | −11.5 | −18.5 | 29.5 | 12.5 | 22.5 | −26.5 | −0.5 | −12.5 | −22.5 | 26.5 | 0.5 | 17.5 | −30.5 | −7.5 | 8.5 | −17.5 | 30.5 | 7.5 | −8.5 |
| 40 | −0.5 | 26.5 | 22.5 | −12.5 | 0.5 | −26.5 | −22.5 | 12.5 | 0.5 | −26.5 | −22.5 | 12.5 | −0.5 | 26.5 | 22.5 | −12.5 | 4.5 | −11.5 | −18.5 | 29.5 | −4.5 | 11.5 | 18.5 | −29.5 |
| 41 | 0.5 | −26.5 | −22.5 | 12.5 | −0.5 | 26.5 | 22.5 | −12.5 | 4.5 | −11.5 | −18.5 | 29.5 | −4.5 | 11.5 | 18.5 | −29.5 | 8.5 | 7.5 | −30.5 | −17.5 | −8.5 | −7.5 | 30.5 | 17.5 |
| 42 | 4.5 | −11.5 | −18.5 | 29.5 | −4.5 | 11.5 | 18.5 | −29.5 | 8.5 | 7.5 | −30.5 | −17.5 | −8.5 | −7.5 | 30.5 | 17.5 | 29.5 | 18.5 | −11.5 | −4.5 | −29.5 | −18.5 | 11.5 | 4.5 |
| 43 | 8.5 | 7.5 | −30.5 | −17.5 | −8.5 | −7.5 | 30.5 | 17.5 | 29.5 | 18.5 | −11.5 | −4.5 | −29.5 | −18.5 | 11.5 | 4.5 | −25.5 | −3.5 | 15.5 | 21.5 | 25.5 | 3.5 | −15.5 | −21.5 |
| 44 | 12.5 | 22.5 | −26.5 | −0.5 | −12.5 | −22.5 | 26.5 | 0.5 | 17.5 | −30.5 | −7.5 | 8.5 | −17.5 | 30.5 | 7.5 | −8.5 | −12.5 | −22.5 | 26.5 | 0.5 | 12.5 | 22.5 | −26.5 | −0.5 |
| 45 | 17.5 | −30.5 | −7.5 | 8.5 | −17.5 | 30.5 | 7.5 | −8.5 | −12.5 | −22.5 | 26.5 | 0.5 | 12.5 | 22.5 | −26.5 | −0.5 | 21.5 | −15.5 | −3.5 | 25.5 | −21.5 | 15.5 | 3.5 | −25.5 |
| 46 | 21.5 | −15.5 | −3.5 | 25.5 | −21.5 | 15.5 | 3.5 | −25.5 | −0.5 | 26.5 | 22.5 | −12.5 | 0.5 | −26.5 | −22.5 | 12.5 | 0.5 | −26.5 | −22.5 | 12.5 | −0.5 | 26.5 | 22.5 | −12.5 |
| 47 | 25.5 | 3.5 | −15.5 | −21.5 | −25.5 | −3.5 | 15.5 | 21.5 | −21.5 | 15.5 | 3.5 | −25.5 | 21.5 | −15.5 | −3.5 | 25.5 | −4.5 | 11.5 | 18.5 | −29.5 | 4.5 | −11.5 | −18.5 | 29.5 |
| 48 | 29.5 | 18.5 | −11.5 | −4.5 | −29.5 | −18.5 | 11.5 | 4.5 | −25.5 | −3.5 | 15.5 | 21.5 | 25.5 | 3.5 | −15.5 | −21.5 | −17.5 | 30.5 | 7.5 | −8.5 | 17.5 | −30.5 | −7.5 | 8.5 |
| 49 | −28.5 | −19.5 | 31.5 | 16.5 | −9.5 | −6.5 | 10.5 | 5.5 | −28.5 | −19.5 | 31.5 | 16.5 | −9.5 | −6.5 | 10.5 | 5.5 | −28.5 | −19.5 | 31.5 | 16.5 | −9.5 | −6.5 | 10.5 | 5.5 |
| 50 | −24.5 | −2.5 | 27.5 | 1.5 | −13.5 | −23.5 | 14.5 | 20.5 | −16.5 | 31.5 | 19.5 | −28.5 | −5.5 | 10.5 | 6.5 | −9.5 | −9.5 | −6.5 | 10.5 | 5.5 | −28.5 | −19.5 | 31.5 | 16.5 |
| 51 | −20.5 | 14.5 | 23.5 | −13.5 | −1.5 | 27.5 | 2.5 | −24.5 | −5.5 | 10.5 | 6.5 | −9.5 | −16.5 | 31.5 | 19.5 | −28.5 | 13.5 | 23.5 | −14.5 | −20.5 | 24.5 | 2.5 | −27.5 | −1.5 |
| 52 | −16.5 | 31.5 | 19.5 | −28.5 | −5.5 | 10.5 | 6.5 | −9.5 | −9.5 | −6.5 | 10.5 | 5.5 | −28.5 | −19.5 | 31.5 | 16.5 | 24.5 | 2.5 | −27.5 | −1.5 | 13.5 | 23.5 | −14.5 | −20.5 |
| 53 | −13.5 | −23.5 | 14.5 | 20.5 | −24.5 | −2.5 | 27.5 | 1.5 | 20.5 | −14.5 | −23.5 | 13.5 | 1.5 | −27.5 | −2.5 | 24.5 | −1.5 | 27.5 | 2.5 | −24.5 | −20.5 | 14.5 | 23.5 | −13.5 |
| 54 | −9.5 | −6.5 | 10.5 | 5.5 | −28.5 | −19.5 | 31.5 | 16.5 | 24.5 | 2.5 | −27.5 | −1.5 | 13.5 | 23.5 | −14.5 | −20.5 | −20.5 | 14.5 | 23.5 | −13.5 | −1.5 | 27.5 | 2.5 | −24.5 |
| 55 | −5.5 | 10.5 | 6.5 | −9.5 | −16.5 | 31.5 | 19.5 | −28.5 | 13.5 | 23.5 | −14.5 | −20.5 | 24.5 | 2.5 | −27.5 | −1.5 | 16.5 | −31.5 | −19.5 | 28.5 | 5.5 | −10.5 | −6.5 | 9.5 |
| 56 | −1.5 | 27.5 | 2.5 | −24.5 | −20.5 | 14.5 | 23.5 | −13.5 | 1.5 | −27.5 | −2.5 | 24.5 | 20.5 | −14.5 | −23.5 | 13.5 | 5.5 | −10.5 | −6.5 | 9.5 | 16.5 | −31.5 | −19.5 | 28.5 |
| 57 | 1.5 | −27.5 | −2.5 | 24.5 | 20.5 | −14.5 | −23.5 | 13.5 | 5.5 | −10.5 | −6.5 | 9.5 | 16.5 | −31.5 | −19.5 | 28.5 | 9.5 | 6.5 | −10.5 | −5.5 | 28.5 | 19.5 | −31.5 | −16.5 |
| 58 | 5.5 | −10.5 | −6.5 | 9.5 | 16.5 | −31.5 | −19.5 | 28.5 | 9.5 | 6.5 | −10.5 | −5.5 | 28.5 | 19.5 | −31.5 | −16.5 | 28.5 | 19.5 | −31.5 | −16.5 | 9.5 | 6.5 | −10.5 | −5.5 |
| 59 | 9.5 | 6.5 | −10.5 | −5.5 | 28.5 | 19.5 | −31.5 | −16.5 | 28.5 | 19.5 | −31.5 | −16.5 | 9.5 | 6.5 | −10.5 | −5.5 | −24.5 | −2.5 | 27.5 | 1.5 | −13.5 | −23.5 | 14.5 | 20.5 |
| 60 | 13.5 | 23.5 | −14.5 | −20.5 | 24.5 | 2.5 | −27.5 | −1.5 | 16.5 | −31.5 | −19.5 | 28.5 | 5.5 | −10.5 | −6.5 | 9.5 | −13.5 | −23.5 | 14.5 | 20.5 | −24.5 | −2.5 | 27.5 | 1.5 |
| 61 | 16.5 | −31.5 | −19.5 | 28.5 | 5.5 | −10.5 | −6.5 | 9.5 | −13.5 | −23.5 | 14.5 | 20.5 | −24.5 | −2.5 | 27.5 | 1.5 | 20.5 | −14.5 | −23.5 | 13.5 | 1.5 | −27.5 | −2.5 | 24.5 |
| 62 | 20.5 | −14.5 | −23.5 | 13.5 | 1.5 | −27.5 | −2.5 | 24.5 | −1.5 | 27.5 | 2.5 | −24.5 | −20.5 | 14.5 | 23.5 | −13.5 | 1.5 | −27.5 | −2.5 | 24.5 | 20.5 | −14.5 | −23.5 | 13.5 |
| 63 | 24.5 | 2.5 | −27.5 | −1.5 | 13.5 | 23.5 | −14.5 | −20.5 | −20.5 | 14.5 | 23.5 | −13.5 | −1.5 | 27.5 | 2.5 | −24.5 | −5.5 | 10.5 | 6.5 | −9.5 | −16.5 | 31.5 | 19.5 | −28.5 |
| 64 | 28.5 | 19.5 | −31.5 | −16.5 | 9.5 | 6.5 | −10.5 | −5.5 | −24.5 | −2.5 | 27.5 | 1.5 | −13.5 | −23.5 | 14.5 | 20.5 | −16.5 | 31.5 | 19.5 | −28.5 | −5.5 | 10.5 | 6.5 | −9.5 |

Table A2.
The OLHD used in Example 3.
Table A2.
The OLHD used in Example 3.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | −31.5 | −16.5 | −28.5 | −19.5 | −31.5 | −16.5 | −28.5 | −19.5 | −31.5 | −16.5 | −28.5 | −19.5 | −31.5 | −16.5 | −28.5 | −19.5 | −31.5 | −16.5 | −28.5 | −19.5 | −31.5 | −16.5 | −28.5 | −19.5 |
| 2 | −30.5 | −17.5 | −8.5 | −7.5 | −28.5 | −19.5 | 31.5 | 16.5 | −10.5 | −5.5 | −9.5 | −6.5 | −30.5 | −17.5 | −8.5 | −7.5 | −28.5 | −19.5 | 31.5 | 16.5 | −10.5 | −5.5 | −9.5 | −6.5 |
| 3 | −29.5 | −18.5 | 11.5 | 4.5 | −9.5 | −6.5 | 10.5 | 5.5 | 11.5 | 4.5 | 29.5 | 18.5 | −29.5 | −18.5 | 11.5 | 4.5 | −9.5 | −6.5 | 10.5 | 5.5 | 11.5 | 4.5 | 29.5 | 18.5 |
| 4 | −28.5 | −19.5 | 31.5 | 16.5 | −10.5 | −5.5 | −9.5 | −6.5 | 30.5 | 17.5 | 8.5 | 7.5 | −28.5 | −19.5 | 31.5 | 16.5 | −10.5 | −5.5 | −9.5 | −6.5 | 30.5 | 17.5 | 8.5 | 7.5 |
| 5 | −11.5 | −4.5 | −29.5 | −18.5 | 29.5 | 18.5 | −11.5 | −4.5 | −8.5 | −7.5 | 30.5 | 17.5 | −11.5 | −4.5 | −29.5 | −18.5 | 29.5 | 18.5 | −11.5 | −4.5 | −8.5 | −7.5 | 30.5 | 17.5 |
| 6 | −10.5 | −5.5 | −9.5 | −6.5 | 30.5 | 17.5 | 8.5 | 7.5 | −29.5 | −18.5 | 11.5 | 4.5 | −10.5 | −5.5 | −9.5 | −6.5 | 30.5 | 17.5 | 8.5 | 7.5 | −29.5 | −18.5 | 11.5 | 4.5 |
| 7 | −9.5 | −6.5 | 10.5 | 5.5 | 11.5 | 4.5 | 29.5 | 18.5 | 28.5 | 19.5 | −31.5 | −16.5 | −9.5 | −6.5 | 10.5 | 5.5 | 11.5 | 4.5 | 29.5 | 18.5 | 28.5 | 19.5 | −31.5 | −16.5 |
| 8 | −8.5 | −7.5 | 30.5 | 17.5 | 8.5 | 7.5 | −30.5 | −17.5 | 9.5 | 6.5 | −10.5 | −5.5 | −8.5 | −7.5 | 30.5 | 17.5 | 8.5 | 7.5 | −30.5 | −17.5 | 9.5 | 6.5 | −10.5 | −5.5 |
| 9 | 8.5 | 7.5 | −30.5 | −17.5 | 9.5 | 6.5 | −10.5 | −5.5 | 10.5 | 5.5 | 9.5 | 6.5 | 8.5 | 7.5 | −30.5 | −17.5 | 9.5 | 6.5 | −10.5 | −5.5 | 10.5 | 5.5 | 9.5 | 6.5 |
| 10 | 9.5 | 6.5 | −10.5 | −5.5 | 10.5 | 5.5 | 9.5 | 6.5 | 31.5 | 16.5 | 28.5 | 19.5 | 9.5 | 6.5 | −10.5 | −5.5 | 10.5 | 5.5 | 9.5 | 6.5 | 31.5 | 16.5 | 28.5 | 19.5 |
| 11 | 10.5 | 5.5 | 9.5 | 6.5 | 31.5 | 16.5 | 28.5 | 19.5 | −30.5 | −17.5 | −8.5 | −7.5 | 10.5 | 5.5 | 9.5 | 6.5 | 31.5 | 16.5 | 28.5 | 19.5 | −30.5 | −17.5 | −8.5 | −7.5 |
| 12 | 11.5 | 4.5 | 29.5 | 18.5 | 28.5 | 19.5 | −31.5 | −16.5 | −11.5 | −4.5 | −29.5 | −18.5 | 11.5 | 4.5 | 29.5 | 18.5 | 28.5 | 19.5 | −31.5 | −16.5 | −11.5 | −4.5 | −29.5 | −18.5 |
| 13 | 28.5 | 19.5 | −31.5 | −16.5 | −11.5 | −4.5 | −29.5 | −18.5 | 29.5 | 18.5 | −11.5 | −4.5 | 28.5 | 19.5 | −31.5 | −16.5 | −11.5 | −4.5 | −29.5 | −18.5 | 29.5 | 18.5 | −11.5 | −4.5 |
| 14 | 29.5 | 18.5 | −11.5 | −4.5 | −8.5 | −7.5 | 30.5 | 17.5 | 8.5 | 7.5 | −30.5 | −17.5 | 29.5 | 18.5 | −11.5 | −4.5 | −8.5 | −7.5 | 30.5 | 17.5 | 8.5 | 7.5 | −30.5 | −17.5 |
| 15 | 30.5 | 17.5 | 8.5 | 7.5 | −29.5 | −18.5 | 11.5 | 4.5 | −9.5 | −6.5 | 10.5 | 5.5 | 30.5 | 17.5 | 8.5 | 7.5 | −29.5 | −18.5 | 11.5 | 4.5 | −9.5 | −6.5 | 10.5 | 5.5 |
| 16 | 31.5 | 16.5 | 28.5 | 19.5 | −30.5 | −17.5 | −8.5 | −7.5 | −28.5 | −19.5 | 31.5 | 16.5 | 31.5 | 16.5 | 28.5 | 19.5 | −30.5 | −17.5 | −8.5 | −7.5 | −28.5 | −19.5 | 31.5 | 16.5 |
| 17 | −27.5 | −1.5 | −24.5 | −2.5 | −27.5 | −1.5 | −24.5 | −2.5 | −27.5 | −1.5 | −24.5 | −2.5 | 14.5 | 20.5 | 13.5 | 23.5 | 14.5 | 20.5 | 13.5 | 23.5 | 14.5 | 20.5 | 13.5 | 23.5 |
| 18 | −26.5 | −0.5 | −12.5 | −22.5 | −24.5 | −2.5 | 27.5 | 1.5 | −14.5 | −20.5 | −13.5 | −23.5 | 15.5 | 21.5 | 25.5 | 3.5 | 13.5 | 23.5 | −14.5 | −20.5 | 27.5 | 1.5 | 24.5 | 2.5 |
| 19 | −25.5 | −3.5 | 15.5 | 21.5 | −13.5 | −23.5 | 14.5 | 20.5 | 15.5 | 21.5 | 25.5 | 3.5 | 12.5 | 22.5 | −26.5 | −0.5 | 24.5 | 2.5 | −27.5 | −1.5 | −26.5 | −0.5 | −12.5 | −22.5 |
| 20 | −24.5 | −2.5 | 27.5 | 1.5 | −14.5 | −20.5 | −13.5 | −23.5 | 26.5 | 0.5 | 12.5 | 22.5 | 13.5 | 23.5 | −14.5 | −20.5 | 27.5 | 1.5 | 24.5 | 2.5 | −15.5 | −21.5 | −25.5 | −3.5 |
| 21 | −15.5 | −21.5 | −25.5 | −3.5 | 25.5 | 3.5 | −15.5 | −21.5 | −12.5 | −22.5 | 26.5 | 0.5 | 26.5 | 0.5 | 12.5 | 22.5 | −12.5 | −22.5 | 26.5 | 0.5 | 25.5 | 3.5 | −15.5 | −21.5 |
| 22 | −14.5 | −20.5 | −13.5 | −23.5 | 26.5 | 0.5 | 12.5 | 22.5 | −25.5 | −3.5 | 15.5 | 21.5 | 27.5 | 1.5 | 24.5 | 2.5 | −15.5 | −21.5 | −25.5 | −3.5 | 12.5 | 22.5 | −26.5 | −0.5 |
| 23 | −13.5 | −23.5 | 14.5 | 20.5 | 15.5 | 21.5 | 25.5 | 3.5 | 24.5 | 2.5 | −27.5 | −1.5 | 24.5 | 2.5 | −27.5 | −1.5 | −26.5 | −0.5 | −12.5 | −22.5 | −13.5 | −23.5 | 14.5 | 20.5 |
| 24 | −12.5 | −22.5 | 26.5 | 0.5 | 12.5 | 22.5 | −26.5 | −0.5 | 13.5 | 23.5 | −14.5 | −20.5 | 25.5 | 3.5 | −15.5 | −21.5 | −25.5 | −3.5 | 15.5 | 21.5 | −24.5 | −2.5 | 27.5 | 1.5 |
| 25 | 12.5 | 22.5 | −26.5 | −0.5 | 13.5 | 23.5 | −14.5 | −20.5 | 14.5 | 20.5 | 13.5 | 23.5 | −25.5 | −3.5 | 15.5 | 21.5 | −24.5 | −2.5 | 27.5 | 1.5 | −27.5 | −1.5 | −24.5 | −2.5 |
| 26 | 13.5 | 23.5 | −14.5 | −20.5 | 14.5 | 20.5 | 13.5 | 23.5 | 27.5 | 1.5 | 24.5 | 2.5 | −24.5 | −2.5 | 27.5 | 1.5 | −27.5 | −1.5 | −24.5 | −2.5 | −14.5 | −20.5 | −13.5 | −23.5 |
| 27 | 14.5 | 20.5 | 13.5 | 23.5 | 27.5 | 1.5 | 24.5 | 2.5 | −26.5 | −0.5 | −12.5 | −22.5 | −27.5 | −1.5 | −24.5 | −2.5 | −14.5 | −20.5 | −13.5 | −23.5 | 15.5 | 21.5 | 25.5 | 3.5 |
| 28 | 15.5 | 21.5 | 25.5 | 3.5 | 24.5 | 2.5 | −27.5 | −1.5 | −15.5 | −21.5 | −25.5 | −3.5 | −26.5 | −0.5 | −12.5 | −22.5 | −13.5 | −23.5 | 14.5 | 20.5 | 26.5 | 0.5 | 12.5 | 22.5 |
| 29 | 24.5 | 2.5 | −27.5 | −1.5 | −15.5 | −21.5 | −25.5 | −3.5 | 25.5 | 3.5 | −15.5 | −21.5 | −13.5 | −23.5 | 14.5 | 20.5 | 26.5 | 0.5 | 12.5 | 22.5 | −12.5 | −22.5 | 26.5 | 0.5 |
| 30 | 25.5 | 3.5 | −15.5 | −21.5 | −12.5 | −22.5 | 26.5 | 0.5 | 12.5 | 22.5 | −26.5 | −0.5 | −12.5 | −22.5 | 26.5 | 0.5 | 25.5 | 3.5 | −15.5 | −21.5 | −25.5 | −3.5 | 15.5 | 21.5 |
| 31 | 26.5 | 0.5 | 12.5 | 22.5 | −25.5 | −3.5 | 15.5 | 21.5 | −13.5 | −23.5 | 14.5 | 20.5 | −15.5 | −21.5 | −25.5 | −3.5 | 12.5 | 22.5 | −26.5 | −0.5 | 24.5 | 2.5 | −27.5 | −1.5 |
| 32 | 27.5 | 1.5 | 24.5 | 2.5 | −26.5 | −0.5 | −12.5 | −22.5 | −24.5 | −2.5 | 27.5 | 1.5 | −14.5 | −20.5 | −13.5 | −23.5 | 15.5 | 21.5 | 25.5 | 3.5 | 13.5 | 23.5 | −14.5 | −20.5 |
| 33 | −23.5 | 13.5 | −20.5 | 14.5 | −23.5 | 13.5 | −20.5 | 14.5 | −23.5 | 13.5 | −20.5 | 14.5 | 23.5 | −13.5 | 20.5 | −14.5 | 23.5 | −13.5 | 20.5 | −14.5 | 23.5 | −13.5 | 20.5 | −14.5 |
| 34 | −22.5 | 12.5 | −0.5 | 26.5 | −20.5 | 14.5 | 23.5 | −13.5 | −2.5 | 24.5 | −1.5 | 27.5 | 22.5 | −12.5 | 0.5 | −26.5 | 20.5 | −14.5 | −23.5 | 13.5 | 2.5 | −24.5 | 1.5 | −27.5 |
| 35 | −21.5 | 15.5 | 3.5 | −25.5 | −1.5 | 27.5 | 2.5 | −24.5 | 3.5 | −25.5 | 21.5 | −15.5 | 21.5 | −15.5 | −3.5 | 25.5 | 1.5 | −27.5 | −2.5 | 24.5 | −3.5 | 25.5 | −21.5 | 15.5 |
| 36 | −20.5 | 14.5 | 23.5 | −13.5 | −2.5 | 24.5 | −1.5 | 27.5 | 22.5 | −12.5 | 0.5 | −26.5 | 20.5 | −14.5 | −23.5 | 13.5 | 2.5 | −24.5 | 1.5 | −27.5 | −22.5 | 12.5 | −0.5 | 26.5 |
| 37 | −3.5 | 25.5 | −21.5 | 15.5 | 21.5 | −15.5 | −3.5 | 25.5 | −0.5 | 26.5 | 22.5 | −12.5 | 3.5 | −25.5 | 21.5 | −15.5 | −21.5 | 15.5 | 3.5 | −25.5 | 0.5 | −26.5 | −22.5 | 12.5 |
| 38 | −2.5 | 24.5 | −1.5 | 27.5 | 22.5 | −12.5 | 0.5 | −26.5 | −21.5 | 15.5 | 3.5 | −25.5 | 2.5 | −24.5 | 1.5 | −27.5 | −22.5 | 12.5 | −0.5 | 26.5 | 21.5 | −15.5 | −3.5 | 25.5 |
| 39 | −1.5 | 27.5 | 2.5 | −24.5 | 3.5 | −25.5 | 21.5 | −15.5 | 20.5 | −14.5 | −23.5 | 13.5 | 1.5 | −27.5 | −2.5 | 24.5 | −3.5 | 25.5 | −21.5 | 15.5 | −20.5 | 14.5 | 23.5 | −13.5 |
| 40 | −0.5 | 26.5 | 22.5 | −12.5 | 0.5 | −26.5 | −22.5 | 12.5 | 1.5 | −27.5 | −2.5 | 24.5 | 0.5 | −26.5 | −22.5 | 12.5 | −0.5 | 26.5 | 22.5 | −12.5 | −1.5 | 27.5 | 2.5 | −24.5 |
| 41 | 0.5 | −26.5 | −22.5 | 12.5 | 1.5 | −27.5 | −2.5 | 24.5 | 2.5 | −24.5 | 1.5 | −27.5 | −0.5 | 26.5 | 22.5 | −12.5 | −1.5 | 27.5 | 2.5 | −24.5 | −2.5 | 24.5 | −1.5 | 27.5 |
| 42 | 1.5 | −27.5 | −2.5 | 24.5 | 2.5 | −24.5 | 1.5 | −27.5 | 23.5 | −13.5 | 20.5 | −14.5 | −1.5 | 27.5 | 2.5 | −24.5 | −2.5 | 24.5 | −1.5 | 27.5 | −23.5 | 13.5 | −20.5 | 14.5 |
| 43 | 2.5 | −24.5 | 1.5 | −27.5 | 23.5 | −13.5 | 20.5 | −14.5 | −22.5 | 12.5 | −0.5 | 26.5 | −2.5 | 24.5 | −1.5 | 27.5 | −23.5 | 13.5 | −20.5 | 14.5 | 22.5 | −12.5 | 0.5 | −26.5 |
| 44 | 3.5 | −25.5 | 21.5 | −15.5 | 20.5 | −14.5 | −23.5 | 13.5 | −3.5 | 25.5 | −21.5 | 15.5 | −3.5 | 25.5 | −21.5 | 15.5 | −20.5 | 14.5 | 23.5 | −13.5 | 3.5 | −25.5 | 21.5 | −15.5 |
| 45 | 20.5 | −14.5 | −23.5 | 13.5 | −3.5 | 25.5 | −21.5 | 15.5 | 21.5 | −15.5 | −3.5 | 25.5 | −20.5 | 14.5 | 23.5 | −13.5 | 3.5 | −25.5 | 21.5 | −15.5 | −21.5 | 15.5 | 3.5 | −25.5 |
| 46 | 21.5 | −15.5 | −3.5 | 25.5 | −0.5 | 26.5 | 22.5 | −12.5 | 0.5 | −26.5 | −22.5 | 12.5 | −21.5 | 15.5 | 3.5 | −25.5 | 0.5 | −26.5 | −22.5 | 12.5 | −0.5 | 26.5 | 22.5 | −12.5 |
| 47 | 22.5 | −12.5 | 0.5 | −26.5 | −21.5 | 15.5 | 3.5 | −25.5 | −1.5 | 27.5 | 2.5 | −24.5 | −22.5 | 12.5 | −0.5 | 26.5 | 21.5 | −15.5 | −3.5 | 25.5 | 1.5 | −27.5 | −2.5 | 24.5 |
| 48 | 23.5 | −13.5 | 20.5 | −14.5 | −22.5 | 12.5 | −0.5 | 26.5 | −20.5 | 14.5 | 23.5 | −13.5 | −23.5 | 13.5 | −20.5 | 14.5 | 22.5 | −12.5 | 0.5 | −26.5 | 20.5 | −14.5 | −23.5 | 13.5 |
| 49 | −19.5 | 28.5 | −16.5 | 31.5 | −19.5 | 28.5 | −16.5 | 31.5 | −19.5 | 28.5 | −16.5 | 31.5 | −6.5 | 9.5 | −5.5 | 10.5 | −6.5 | 9.5 | −5.5 | 10.5 | −6.5 | 9.5 | −5.5 | 10.5 |
| 50 | −18.5 | 29.5 | −4.5 | 11.5 | −16.5 | 31.5 | 19.5 | −28.5 | −6.5 | 9.5 | −5.5 | 10.5 | −7.5 | 8.5 | −17.5 | 30.5 | −5.5 | 10.5 | 6.5 | −9.5 | −19.5 | 28.5 | −16.5 | 31.5 |
| 51 | −17.5 | 30.5 | 7.5 | −8.5 | −5.5 | 10.5 | 6.5 | −9.5 | 7.5 | −8.5 | 17.5 | −30.5 | −4.5 | 11.5 | 18.5 | −29.5 | −16.5 | 31.5 | 19.5 | −28.5 | 18.5 | −29.5 | 4.5 | −11.5 |
| 52 | −16.5 | 31.5 | 19.5 | −28.5 | −6.5 | 9.5 | −5.5 | 10.5 | 18.5 | −29.5 | 4.5 | −11.5 | −5.5 | 10.5 | 6.5 | −9.5 | −19.5 | 28.5 | −16.5 | 31.5 | 7.5 | −8.5 | 17.5 | −30.5 |
| 53 | −7.5 | 8.5 | −17.5 | 30.5 | 17.5 | −30.5 | −7.5 | 8.5 | −4.5 | 11.5 | 18.5 | −29.5 | −18.5 | 29.5 | −4.5 | 11.5 | 4.5 | −11.5 | −18.5 | 29.5 | −17.5 | 30.5 | 7.5 | −8.5 |
| 54 | −6.5 | 9.5 | −5.5 | 10.5 | 18.5 | −29.5 | 4.5 | −11.5 | −17.5 | 30.5 | 7.5 | −8.5 | −19.5 | 28.5 | −16.5 | 31.5 | 7.5 | −8.5 | 17.5 | −30.5 | −4.5 | 11.5 | 18.5 | −29.5 |
| 55 | −5.5 | 10.5 | 6.5 | −9.5 | 7.5 | −8.5 | 17.5 | −30.5 | 16.5 | −31.5 | −19.5 | 28.5 | −16.5 | 31.5 | 19.5 | −28.5 | 18.5 | −29.5 | 4.5 | −11.5 | 5.5 | −10.5 | −6.5 | 9.5 |
| 56 | −4.5 | 11.5 | 18.5 | −29.5 | 4.5 | −11.5 | −18.5 | 29.5 | 5.5 | −10.5 | −6.5 | 9.5 | −17.5 | 30.5 | 7.5 | −8.5 | 17.5 | −30.5 | −7.5 | 8.5 | 16.5 | −31.5 | −19.5 | 28.5 |
| 57 | 4.5 | −11.5 | −18.5 | 29.5 | 5.5 | −10.5 | −6.5 | 9.5 | 6.5 | −9.5 | 5.5 | −10.5 | 17.5 | −30.5 | −7.5 | 8.5 | 16.5 | −31.5 | −19.5 | 28.5 | 19.5 | −28.5 | 16.5 | −31.5 |
| 58 | 5.5 | −10.5 | −6.5 | 9.5 | 6.5 | −9.5 | 5.5 | −10.5 | 19.5 | −28.5 | 16.5 | −31.5 | 16.5 | −31.5 | −19.5 | 28.5 | 19.5 | −28.5 | 16.5 | −31.5 | 6.5 | −9.5 | 5.5 | −10.5 |
| 59 | 6.5 | −9.5 | 5.5 | −10.5 | 19.5 | −28.5 | 16.5 | −31.5 | −18.5 | 29.5 | −4.5 | 11.5 | 19.5 | −28.5 | 16.5 | −31.5 | 6.5 | −9.5 | 5.5 | −10.5 | −7.5 | 8.5 | −17.5 | 30.5 |
| 60 | 7.5 | −8.5 | 17.5 | −30.5 | 16.5 | −31.5 | −19.5 | 28.5 | −7.5 | 8.5 | −17.5 | 30.5 | 18.5 | −29.5 | 4.5 | −11.5 | 5.5 | −10.5 | −6.5 | 9.5 | −18.5 | 29.5 | −4.5 | 11.5 |
| 61 | 16.5 | −31.5 | −19.5 | 28.5 | −7.5 | 8.5 | −17.5 | 30.5 | 17.5 | −30.5 | −7.5 | 8.5 | 5.5 | −10.5 | −6.5 | 9.5 | −18.5 | 29.5 | −4.5 | 11.5 | 4.5 | −11.5 | −18.5 | 29.5 |
| 62 | 17.5 | −30.5 | −7.5 | 8.5 | −4.5 | 11.5 | 18.5 | −29.5 | 4.5 | −11.5 | −18.5 | 29.5 | 4.5 | −11.5 | −18.5 | 29.5 | −17.5 | 30.5 | 7.5 | −8.5 | 17.5 | −30.5 | −7.5 | 8.5 |
| 63 | 18.5 | −29.5 | 4.5 | −11.5 | −17.5 | 30.5 | 7.5 | −8.5 | −5.5 | 10.5 | 6.5 | −9.5 | 7.5 | −8.5 | 17.5 | −30.5 | −4.5 | 11.5 | 18.5 | −29.5 | −16.5 | 31.5 | 19.5 | −28.5 |
| 64 | 19.5 | −28.5 | 16.5 | −31.5 | −18.5 | 29.5 | −4.5 | 11.5 | −16.5 | 31.5 | 19.5 | −28.5 | 6.5 | −9.5 | 5.5 | −10.5 | −7.5 | 8.5 | −17.5 | 30.5 | −5.5 | 10.5 | 6.5 | −9.5 |

Table A3.
The OD used in Example 4.
Table A3.
The OD used in Example 4.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | −7.5 | −4.5 | −7.5 | −4.5 | −7.5 | −4.5 | −7.5 | −4.5 | −7.5 | −4.5 | −7.5 | −4.5 | −7.5 | −4.5 | −7.5 | −4.5 | −7.5 | −4.5 | −7.5 | −4.5 | −7.5 | −4.5 | −7.5 | −4.5 |
| 2 | −7.5 | −4.5 | −2.5 | −1.5 | −7.5 | −4.5 | 7.5 | 4.5 | −2.5 | −1.5 | −2.5 | −1.5 | −7.5 | −4.5 | −2.5 | −1.5 | −7.5 | −4.5 | 7.5 | 4.5 | −2.5 | −1.5 | −2.5 | −1.5 |
| 3 | −7.5 | −4.5 | 2.5 | 1.5 | −2.5 | −1.5 | 2.5 | 1.5 | 2.5 | 1.5 | 7.5 | 4.5 | −7.5 | −4.5 | 2.5 | 1.5 | −2.5 | −1.5 | 2.5 | 1.5 | 2.5 | 1.5 | 7.5 | 4.5 |
| 4 | −7.5 | −4.5 | 7.5 | 4.5 | −2.5 | −1.5 | −2.5 | −1.5 | 7.5 | 4.5 | 2.5 | 1.5 | −7.5 | −4.5 | 7.5 | 4.5 | −2.5 | −1.5 | −2.5 | −1.5 | 7.5 | 4.5 | 2.5 | 1.5 |
| 5 | −2.5 | −1.5 | −7.5 | −4.5 | 7.5 | 4.5 | −2.5 | −1.5 | −2.5 | −1.5 | 7.5 | 4.5 | −2.5 | −1.5 | −7.5 | −4.5 | 7.5 | 4.5 | −2.5 | −1.5 | −2.5 | −1.5 | 7.5 | 4.5 |
| 6 | −2.5 | −1.5 | −2.5 | −1.5 | 7.5 | 4.5 | 2.5 | 1.5 | −7.5 | −4.5 | 2.5 | 1.5 | −2.5 | −1.5 | −2.5 | −1.5 | 7.5 | 4.5 | 2.5 | 1.5 | −7.5 | −4.5 | 2.5 | 1.5 |
| 7 | −2.5 | −1.5 | 2.5 | 1.5 | 2.5 | 1.5 | 7.5 | 4.5 | 7.5 | 4.5 | −7.5 | −4.5 | −2.5 | −1.5 | 2.5 | 1.5 | 2.5 | 1.5 | 7.5 | 4.5 | 7.5 | 4.5 | −7.5 | −4.5 |
| 8 | −2.5 | −1.5 | 7.5 | 4.5 | 2.5 | 1.5 | −7.5 | −4.5 | 2.5 | 1.5 | −2.5 | −1.5 | −2.5 | −1.5 | 7.5 | 4.5 | 2.5 | 1.5 | −7.5 | −4.5 | 2.5 | 1.5 | −2.5 | −1.5 |
| 9 | 2.5 | 1.5 | −7.5 | −4.5 | 2.5 | 1.5 | −2.5 | −1.5 | 2.5 | 1.5 | 2.5 | 1.5 | 2.5 | 1.5 | −7.5 | −4.5 | 2.5 | 1.5 | −2.5 | −1.5 | 2.5 | 1.5 | 2.5 | 1.5 |
| 10 | 2.5 | 1.5 | −2.5 | −1.5 | 2.5 | 1.5 | 2.5 | 1.5 | 7.5 | 4.5 | 7.5 | 4.5 | 2.5 | 1.5 | −2.5 | −1.5 | 2.5 | 1.5 | 2.5 | 1.5 | 7.5 | 4.5 | 7.5 | 4.5 |
| 11 | 2.5 | 1.5 | 2.5 | 1.5 | 7.5 | 4.5 | 7.5 | 4.5 | −7.5 | −4.5 | −2.5 | −1.5 | 2.5 | 1.5 | 2.5 | 1.5 | 7.5 | 4.5 | 7.5 | 4.5 | −7.5 | −4.5 | −2.5 | −1.5 |
| 12 | 2.5 | 1.5 | 7.5 | 4.5 | 7.5 | 4.5 | −7.5 | −4.5 | −2.5 | −1.5 | −7.5 | −4.5 | 2.5 | 1.5 | 7.5 | 4.5 | 7.5 | 4.5 | −7.5 | −4.5 | −2.5 | −1.5 | −7.5 | −4.5 |
| 13 | 7.5 | 4.5 | −7.5 | −4.5 | −2.5 | −1.5 | −7.5 | −4.5 | 7.5 | 4.5 | −2.5 | −1.5 | 7.5 | 4.5 | −7.5 | −4.5 | −2.5 | −1.5 | −7.5 | −4.5 | 7.5 | 4.5 | −2.5 | −1.5 |
| 14 | 7.5 | 4.5 | −2.5 | −1.5 | −2.5 | −1.5 | 7.5 | 4.5 | 2.5 | 1.5 | −7.5 | −4.5 | 7.5 | 4.5 | −2.5 | −1.5 | −2.5 | −1.5 | 7.5 | 4.5 | 2.5 | 1.5 | −7.5 | −4.5 |
| 15 | 7.5 | 4.5 | 2.5 | 1.5 | −7.5 | −4.5 | 2.5 | 1.5 | −2.5 | −1.5 | 2.5 | 1.5 | 7.5 | 4.5 | 2.5 | 1.5 | −7.5 | −4.5 | 2.5 | 1.5 | −2.5 | −1.5 | 2.5 | 1.5 |
| 16 | 7.5 | 4.5 | 7.5 | 4.5 | −7.5 | −4.5 | −2.5 | −1.5 | −7.5 | −4.5 | 7.5 | 4.5 | 7.5 | 4.5 | 7.5 | 4.5 | −7.5 | −4.5 | −2.5 | −1.5 | −7.5 | −4.5 | 7.5 | 4.5 |
| 17 | −6.5 | −0.5 | −6.5 | −0.5 | −6.5 | −0.5 | −6.5 | −0.5 | −6.5 | −0.5 | −6.5 | −0.5 | 3.5 | 5.5 | 3.5 | 5.5 | 3.5 | 5.5 | 3.5 | 5.5 | 3.5 | 5.5 | 3.5 | 5.5 |
| 18 | −6.5 | −0.5 | −3.5 | −5.5 | −6.5 | −0.5 | 6.5 | 0.5 | −3.5 | −5.5 | −3.5 | −5.5 | 3.5 | 5.5 | 6.5 | 0.5 | 3.5 | 5.5 | −3.5 | −5.5 | 6.5 | 0.5 | 6.5 | 0.5 |
| 19 | −6.5 | −0.5 | 3.5 | 5.5 | −3.5 | −5.5 | 3.5 | 5.5 | 3.5 | 5.5 | 6.5 | 0.5 | 3.5 | 5.5 | −6.5 | −0.5 | 6.5 | 0.5 | −6.5 | −0.5 | −6.5 | −0.5 | −3.5 | −5.5 |
| 20 | −6.5 | −0.5 | 6.5 | 0.5 | −3.5 | −5.5 | −3.5 | −5.5 | 6.5 | 0.5 | 3.5 | 5.5 | 3.5 | 5.5 | −3.5 | −5.5 | 6.5 | 0.5 | 6.5 | 0.5 | −3.5 | −5.5 | −6.5 | −0.5 |
| 21 | −3.5 | −5.5 | −6.5 | −0.5 | 6.5 | 0.5 | −3.5 | −5.5 | −3.5 | −5.5 | 6.5 | 0.5 | 6.5 | 0.5 | 3.5 | 5.5 | −3.5 | −5.5 | 6.5 | 0.5 | 6.5 | 0.5 | −3.5 | −5.5 |
| 22 | −3.5 | −5.5 | −3.5 | −5.5 | 6.5 | 0.5 | 3.5 | 5.5 | −6.5 | −0.5 | 3.5 | 5.5 | 6.5 | 0.5 | 6.5 | 0.5 | −3.5 | −5.5 | −6.5 | −0.5 | 3.5 | 5.5 | −6.5 | −0.5 |
| 23 | −3.5 | −5.5 | 3.5 | 5.5 | 3.5 | 5.5 | 6.5 | 0.5 | 6.5 | 0.5 | −6.5 | −0.5 | 6.5 | 0.5 | −6.5 | −0.5 | −6.5 | −0.5 | −3.5 | −5.5 | −3.5 | −5.5 | 3.5 | 5.5 |
| 24 | −3.5 | −5.5 | 6.5 | 0.5 | 3.5 | 5.5 | −6.5 | −0.5 | 3.5 | 5.5 | −3.5 | −5.5 | 6.5 | 0.5 | −3.5 | −5.5 | −6.5 | −0.5 | 3.5 | 5.5 | −6.5 | −0.5 | 6.5 | 0.5 |
| 25 | 3.5 | 5.5 | −6.5 | −0.5 | 3.5 | 5.5 | −3.5 | −5.5 | 3.5 | 5.5 | 3.5 | 5.5 | −6.5 | −0.5 | 3.5 | 5.5 | −6.5 | −0.5 | 6.5 | 0.5 | −6.5 | −0.5 | −6.5 | −0.5 |
| 26 | 3.5 | 5.5 | −3.5 | −5.5 | 3.5 | 5.5 | 3.5 | 5.5 | 6.5 | 0.5 | 6.5 | 0.5 | −6.5 | −0.5 | 6.5 | 0.5 | −6.5 | −0.5 | −6.5 | −0.5 | −3.5 | −5.5 | −3.5 | −5.5 |
| 27 | 3.5 | 5.5 | 3.5 | 5.5 | 6.5 | 0.5 | 6.5 | 0.5 | −6.5 | −0.5 | −3.5 | −5.5 | −6.5 | −0.5 | −6.5 | −0.5 | −3.5 | −5.5 | −3.5 | −5.5 | 3.5 | 5.5 | 6.5 | 0.5 |
| 28 | 3.5 | 5.5 | 6.5 | 0.5 | 6.5 | 0.5 | −6.5 | −0.5 | −3.5 | −5.5 | −6.5 | −0.5 | −6.5 | −0.5 | −3.5 | −5.5 | −3.5 | −5.5 | 3.5 | 5.5 | 6.5 | 0.5 | 3.5 | 5.5 |
| 29 | 6.5 | 0.5 | −6.5 | −0.5 | −3.5 | −5.5 | −6.5 | −0.5 | 6.5 | 0.5 | −3.5 | −5.5 | −3.5 | −5.5 | 3.5 | 5.5 | 6.5 | 0.5 | 3.5 | 5.5 | −3.5 | −5.5 | 6.5 | 0.5 |
| 30 | 6.5 | 0.5 | −3.5 | −5.5 | −3.5 | −5.5 | 6.5 | 0.5 | 3.5 | 5.5 | −6.5 | −0.5 | −3.5 | −5.5 | 6.5 | 0.5 | 6.5 | 0.5 | −3.5 | −5.5 | −6.5 | −0.5 | 3.5 | 5.5 |
| 31 | 6.5 | 0.5 | 3.5 | 5.5 | −6.5 | −0.5 | 3.5 | 5.5 | −3.5 | −5.5 | 3.5 | 5.5 | −3.5 | −5.5 | −6.5 | −0.5 | 3.5 | 5.5 | −6.5 | −0.5 | 6.5 | 0.5 | −6.5 | −0.5 |
| 32 | 6.5 | 0.5 | 6.5 | 0.5 | −6.5 | −0.5 | −3.5 | −5.5 | −6.5 | −0.5 | 6.5 | 0.5 | −3.5 | −5.5 | −3.5 | −5.5 | 3.5 | 5.5 | 6.5 | 0.5 | 3.5 | 5.5 | −3.5 | −5.5 |
| 33 | −5.5 | 3.5 | −5.5 | 3.5 | −5.5 | 3.5 | −5.5 | 3.5 | −5.5 | 3.5 | −5.5 | 3.5 | 5.5 | −3.5 | 5.5 | −3.5 | 5.5 | −3.5 | 5.5 | −3.5 | 5.5 | −3.5 | 5.5 | −3.5 |
| 34 | −5.5 | 3.5 | −0.5 | 6.5 | −5.5 | 3.5 | 5.5 | −3.5 | −0.5 | 6.5 | −0.5 | 6.5 | 5.5 | −3.5 | 0.5 | −6.5 | 5.5 | −3.5 | −5.5 | 3.5 | 0.5 | −6.5 | 0.5 | −6.5 |
| 35 | −5.5 | 3.5 | 0.5 | −6.5 | −0.5 | 6.5 | 0.5 | −6.5 | 0.5 | −6.5 | 5.5 | −3.5 | 5.5 | −3.5 | −0.5 | 6.5 | 0.5 | −6.5 | −0.5 | 6.5 | −0.5 | 6.5 | −5.5 | 3.5 |
| 36 | −5.5 | 3.5 | 5.5 | −3.5 | −0.5 | 6.5 | −0.5 | 6.5 | 5.5 | −3.5 | 0.5 | −6.5 | 5.5 | −3.5 | −5.5 | 3.5 | 0.5 | −6.5 | 0.5 | −6.5 | −5.5 | 3.5 | −0.5 | 6.5 |
| 37 | −0.5 | 6.5 | −5.5 | 3.5 | 5.5 | −3.5 | −0.5 | 6.5 | −0.5 | 6.5 | 5.5 | −3.5 | 0.5 | −6.5 | 5.5 | −3.5 | −5.5 | 3.5 | 0.5 | −6.5 | 0.5 | −6.5 | −5.5 | 3.5 |
| 38 | −0.5 | 6.5 | −0.5 | 6.5 | 5.5 | −3.5 | 0.5 | −6.5 | −5.5 | 3.5 | 0.5 | −6.5 | 0.5 | −6.5 | 0.5 | −6.5 | −5.5 | 3.5 | −0.5 | 6.5 | 5.5 | −3.5 | −0.5 | 6.5 |
| 39 | −0.5 | 6.5 | 0.5 | −6.5 | 0.5 | −6.5 | 5.5 | −3.5 | 5.5 | −3.5 | −5.5 | 3.5 | 0.5 | −6.5 | −0.5 | 6.5 | −0.5 | 6.5 | −5.5 | 3.5 | −5.5 | 3.5 | 5.5 | −3.5 |
| 40 | −0.5 | 6.5 | 5.5 | −3.5 | 0.5 | −6.5 | −5.5 | 3.5 | 0.5 | −6.5 | −0.5 | 6.5 | 0.5 | −6.5 | −5.5 | 3.5 | −0.5 | 6.5 | 5.5 | −3.5 | −0.5 | 6.5 | 0.5 | −6.5 |
| 41 | 0.5 | −6.5 | −5.5 | 3.5 | 0.5 | −6.5 | −0.5 | 6.5 | 0.5 | −6.5 | 0.5 | −6.5 | −0.5 | 6.5 | 5.5 | −3.5 | −0.5 | 6.5 | 0.5 | −6.5 | −0.5 | 6.5 | −0.5 | 6.5 |
| 42 | 0.5 | −6.5 | −0.5 | 6.5 | 0.5 | −6.5 | 0.5 | −6.5 | 5.5 | −3.5 | 5.5 | −3.5 | −0.5 | 6.5 | 0.5 | −6.5 | −0.5 | 6.5 | −0.5 | 6.5 | −5.5 | 3.5 | −5.5 | 3.5 |
| 43 | 0.5 | −6.5 | 0.5 | −6.5 | 5.5 | −3.5 | 5.5 | −3.5 | −5.5 | 3.5 | −0.5 | 6.5 | −0.5 | 6.5 | −0.5 | 6.5 | −5.5 | 3.5 | −5.5 | 3.5 | 5.5 | −3.5 | 0.5 | −6.5 |
| 44 | 0.5 | −6.5 | 5.5 | −3.5 | 5.5 | −3.5 | −5.5 | 3.5 | −0.5 | 6.5 | −5.5 | 3.5 | −0.5 | 6.5 | −5.5 | 3.5 | −5.5 | 3.5 | 5.5 | −3.5 | 0.5 | −6.5 | 5.5 | −3.5 |
| 45 | 5.5 | −3.5 | −5.5 | 3.5 | −0.5 | 6.5 | −5.5 | 3.5 | 5.5 | −3.5 | −0.5 | 6.5 | −5.5 | 3.5 | 5.5 | −3.5 | 0.5 | −6.5 | 5.5 | −3.5 | −5.5 | 3.5 | 0.5 | −6.5 |
| 46 | 5.5 | −3.5 | −0.5 | 6.5 | −0.5 | 6.5 | 5.5 | −3.5 | 0.5 | −6.5 | −5.5 | 3.5 | −5.5 | 3.5 | 0.5 | −6.5 | 0.5 | −6.5 | −5.5 | 3.5 | −0.5 | 6.5 | 5.5 | −3.5 |
| 47 | 5.5 | −3.5 | 0.5 | −6.5 | −5.5 | 3.5 | 0.5 | −6.5 | −0.5 | 6.5 | 0.5 | −6.5 | −5.5 | 3.5 | −0.5 | 6.5 | 5.5 | −3.5 | −0.5 | 6.5 | 0.5 | −6.5 | −0.5 | 6.5 |
| 48 | 5.5 | −3.5 | 5.5 | −3.5 | −5.5 | 3.5 | −0.5 | 6.5 | −5.5 | 3.5 | 5.5 | −3.5 | −5.5 | 3.5 | −5.5 | 3.5 | 5.5 | −3.5 | 0.5 | −6.5 | 5.5 | −3.5 | −5.5 | 3.5 |
| 49 | −4.5 | 7.5 | −4.5 | 7.5 | −4.5 | 7.5 | −4.5 | 7.5 | −4.5 | 7.5 | −4.5 | 7.5 | −1.5 | 2.5 | −1.5 | 2.5 | −1.5 | 2.5 | −1.5 | 2.5 | −1.5 | 2.5 | −1.5 | 2.5 |
| 50 | −4.5 | 7.5 | −1.5 | 2.5 | −4.5 | 7.5 | 4.5 | −7.5 | −1.5 | 2.5 | −1.5 | 2.5 | −1.5 | 2.5 | −4.5 | 7.5 | −1.5 | 2.5 | 1.5 | −2.5 | −4.5 | 7.5 | −4.5 | 7.5 |
| 51 | −4.5 | 7.5 | 1.5 | −2.5 | −1.5 | 2.5 | 1.5 | −2.5 | 1.5 | −2.5 | 4.5 | −7.5 | −1.5 | 2.5 | 4.5 | −7.5 | −4.5 | 7.5 | 4.5 | −7.5 | 4.5 | −7.5 | 1.5 | −2.5 |
| 52 | −4.5 | 7.5 | 4.5 | −7.5 | −1.5 | 2.5 | −1.5 | 2.5 | 4.5 | −7.5 | 1.5 | −2.5 | −1.5 | 2.5 | 1.5 | −2.5 | −4.5 | 7.5 | −4.5 | 7.5 | 1.5 | −2.5 | 4.5 | −7.5 |
| 53 | −1.5 | 2.5 | −4.5 | 7.5 | 4.5 | −7.5 | −1.5 | 2.5 | −1.5 | 2.5 | 4.5 | −7.5 | −4.5 | 7.5 | −1.5 | 2.5 | 1.5 | −2.5 | −4.5 | 7.5 | −4.5 | 7.5 | 1.5 | −2.5 |
| 54 | −1.5 | 2.5 | −1.5 | 2.5 | 4.5 | −7.5 | 1.5 | −2.5 | −4.5 | 7.5 | 1.5 | −2.5 | −4.5 | 7.5 | −4.5 | 7.5 | 1.5 | −2.5 | 4.5 | −7.5 | −1.5 | 2.5 | 4.5 | −7.5 |
| 55 | −1.5 | 2.5 | 1.5 | −2.5 | 1.5 | −2.5 | 4.5 | −7.5 | 4.5 | −7.5 | −4.5 | 7.5 | −4.5 | 7.5 | 4.5 | −7.5 | 4.5 | −7.5 | 1.5 | −2.5 | 1.5 | −2.5 | −1.5 | 2.5 |
| 56 | −1.5 | 2.5 | 4.5 | −7.5 | 1.5 | −2.5 | −4.5 | 7.5 | 1.5 | −2.5 | −1.5 | 2.5 | −4.5 | 7.5 | 1.5 | −2.5 | 4.5 | −7.5 | −1.5 | 2.5 | 4.5 | −7.5 | −4.5 | 7.5 |
| 57 | 1.5 | −2.5 | −4.5 | 7.5 | 1.5 | −2.5 | −1.5 | 2.5 | 1.5 | −2.5 | 1.5 | −2.5 | 4.5 | −7.5 | −1.5 | 2.5 | 4.5 | −7.5 | −4.5 | 7.5 | 4.5 | −7.5 | 4.5 | −7.5 |
| 58 | 1.5 | −2.5 | −1.5 | 2.5 | 1.5 | −2.5 | 1.5 | −2.5 | 4.5 | −7.5 | 4.5 | −7.5 | 4.5 | −7.5 | −4.5 | 7.5 | 4.5 | −7.5 | 4.5 | −7.5 | 1.5 | −2.5 | 1.5 | −2.5 |
| 59 | 1.5 | −2.5 | 1.5 | −2.5 | 4.5 | −7.5 | 4.5 | −7.5 | −4.5 | 7.5 | −1.5 | 2.5 | 4.5 | −7.5 | 4.5 | −7.5 | 1.5 | −2.5 | 1.5 | −2.5 | −1.5 | 2.5 | −4.5 | 7.5 |
| 60 | 1.5 | −2.5 | 4.5 | −7.5 | 4.5 | −7.5 | −4.5 | 7.5 | −1.5 | 2.5 | −4.5 | 7.5 | 4.5 | −7.5 | 1.5 | −2.5 | 1.5 | −2.5 | −1.5 | 2.5 | −4.5 | 7.5 | −1.5 | 2.5 |
| 61 | 4.5 | −7.5 | −4.5 | 7.5 | −1.5 | 2.5 | −4.5 | 7.5 | 4.5 | −7.5 | −1.5 | 2.5 | 1.5 | −2.5 | −1.5 | 2.5 | −4.5 | 7.5 | −1.5 | 2.5 | 1.5 | −2.5 | −4.5 | 7.5 |
| 62 | 4.5 | −7.5 | −1.5 | 2.5 | −1.5 | 2.5 | 4.5 | −7.5 | 1.5 | −2.5 | −4.5 | 7.5 | 1.5 | −2.5 | −4.5 | 7.5 | −4.5 | 7.5 | 1.5 | −2.5 | 4.5 | −7.5 | −1.5 | 2.5 |
| 63 | 4.5 | −7.5 | 1.5 | −2.5 | −4.5 | 7.5 | 1.5 | −2.5 | −1.5 | 2.5 | 1.5 | −2.5 | 1.5 | −2.5 | 4.5 | −7.5 | −1.5 | 2.5 | 4.5 | −7.5 | −4.5 | 7.5 | 4.5 | −7.5 |
| 64 | 4.5 | −7.5 | 4.5 | −7.5 | −4.5 | 7.5 | −1.5 | 2.5 | −4.5 | 7.5 | 4.5 | −7.5 | 1.5 | −2.5 | 1.5 | −2.5 | −1.5 | 2.5 | −4.5 | 7.5 | −1.5 | 2.5 | 1.5 | −2.5 |
References
- Fang, K.T.; Li, R.; Sudjianto, A. Design and Modeling for Computer Experiments; Chapman and Hall/CRC: New York, NY, USA, 2006. [Google Scholar]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 1979, 21, 239–245. [Google Scholar]
- Wu, C.F.J.; Hamada, M.S. Experiments: Planning, Analysis and Optimization, 3rd ed.; John Wiley & Sons: New York, NY, USA, 2021. [Google Scholar]
- Tang, B. Orthogonal arrays based Latin hypercubes. J. Am. Stat. Assoc. 1993, 88, 1392–1397. [Google Scholar] [CrossRef]
- Joseph, V.R.; Gul, E.; Ba, S. Maximum projection designs for computer experiments. Biometrika 2015, 102, 371–380. [Google Scholar] [CrossRef]
- Sun, F.; Wang, Y.; Xu, H. Uniform projection designs. Ann. Stat. 2019, 47, 641–661. [Google Scholar] [CrossRef]
- He, Y.; Tang, B. Strong orthogonal arrays and associated Latin hypercubes for computer experiments. Biometrika 2013, 1, 254–260. [Google Scholar] [CrossRef]
- Mukerjee, R.; Sun, F.; Tang, B. Nearly orthogonal arrays mappable into fully orthogonal arrays. Biometrika 2014, 101, 957–963. [Google Scholar] [CrossRef]
- Bingham, D.; Sitter, R.R.; Tang, B. Orthogonal and nearly orthogonal designs for computer experiments. Biometrika 2009, 96, 51–65. [Google Scholar] [CrossRef]
- Steinberg, D.M.; Lin, D.K.J. A construction method for orthogonal Latin hypercube designs. Biometrika 2006, 93, 279–288. [Google Scholar] [CrossRef]
- Pang, F.; Liu, M.Q.; Lin, D.K.J. A construction method for orthogonal Latin hypercube designs with prime power levels. Stat. Sin. 2009, 19, 1721–1728. [Google Scholar]
- Lin, C.D.; Mukerjee, R.; Tang, B. Construction of orthogonal and nearly orthogonal Latin hypercubes. Biometrika 2009, 96, 243–247. [Google Scholar] [CrossRef]
- Georgiou, S.D.; Efthimiou, I. Some classes of orthogonal latin hypercube designs. Stat. Sin. 2014, 24, 101–120. [Google Scholar]
- Sun, F.; Tang, B. A general rotation method for orthogonal Latin hypercubes. Biometrika 2017, 104, 465–472. [Google Scholar]
- Yang, X.; Yang, J.F.; Liu, M.Q.; Zhou, Q. Column-orthogonal designs with multi-dimensional stratifications. Sci. China Math. 2021, 64, 1291–1304. [Google Scholar] [CrossRef]
- Li, H.; Yang, L.; Liu, M.Q. Construction of space-filling orthogonal Latin hypercube designs. Stat. Probab. Lett. 2022, 180, 109–245. [Google Scholar] [CrossRef]
- Sun, F.; Tang, B. A method of constructing space-filling orthogonal designs. J. Am. Stat. Assoc. 2017, 112, 683–689. [Google Scholar] [CrossRef]
- Wang, C.; Yang, J.; Liu, M.Q. Construction of space-filling orthogonal designs. J. Stat. Plan. Inference 2021, 213, 130–141. [Google Scholar] [CrossRef]
- Sun, F.; Liu, M.Q.; Lin, D.K.J. Construction of orthogonal Latin hypercube designs. Biometrika 2009, 96, 971–974. [Google Scholar] [CrossRef]
- Hedayat, A.S.; Sloane, N.J.A.; Stufken, J. Orthogonal Arrays: Theory and Applications; Springer: New York, NY, USA, 1999. [Google Scholar]
- Zheng, C.W.; Qi, Z.F.; Zhang, Q.Z.; Liu, M.Q. A method for augmenting supersaturated designs with newly added factors. Mathematics 2023, 11, 60. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).