Restricted Distance-Type Gaussian Estimators Based on Density Power Divergence and Their Applications in Hypothesis Testing

Abstract

In this paper, we introduce the restricted minimum density power divergence Gaussian estimator (MDPDGE) and study its main asymptotic properties. In addition, we examine it robustness through its influence function analysis. Restricted estimators are required in many practical situations, such as testing composite null hypotheses, and we provide in this case constrained estimators to inherent restrictions of the underlying distribution. Furthermore, we derive robust Rao-type test statistics based on the MDPDGE for testing a simple null hypothesis, and we deduce explicit expressions for some main important distributions. Finally, we empirically evaluate the efficiency and robustness of the method through a simulation study.

1. Introduction

Let ${\mathit{Y}}_1,\dots ,$ ${\mathit{Y}}_n$ be independent and identically distributed observations from an m-dimensional random vector $\mathit{Y}$ with probability density function $f_{\mathit{\theta }}\left(\mathit{y}\right),$ $\mathit{\theta }\in \Theta \subset {\mathbb{R}}^d,$ where $\mathit{\theta }$ is the vector of unknown parameters, $\Theta$ is the corresponding parameter space and d is the dimension of $\mathit{\theta },d\ge 1.$ We denote,

$$E_{\mathit{\theta }}\left[\mathit{Y}\right]=\mathit{\mu }\left(\mathit{\theta }\right)\mathrm{and}Co{v}_{\mathit{\theta }}\left[\mathit{Y}\right]=\mathsf{\Sigma }\left(\mathit{\theta }\right).$$

(1)

The log-likelihood function of the assumed model is given by

$$l\left(\mathit{\theta }\right)=\sum _{i=1}^{n}log{f}_{\mathit{\theta }}\left({\mathit{y}}_i\right)$$

for ${\mathit{y}}_1,\dots ,$ ${\mathit{y}}_n$ observations of the m-dimensional random vectors ${\mathit{Y}}_1,\dots ,$ ${\mathit{Y}}_n.$ Then, the maximum likelihood estimator (MLE) is computed as

$${\widehat{\mathit{\theta }}}_{\mathrm{MLE}}={max}_{\mathit{\theta }\in \Theta }l\left(\mathit{\theta }\right).$$

(2)

In many real-life situations, the underlying density function, $f_{\theta }(·),$ is unknown or its computation is quite difficult but contrariwise, the mean vector and variance–covariance matrices of the underlying distribution of the data as a function of $\mathit{\theta }$, namely $\mathit{\mu }\left(\mathit{\theta }\right)$ and $\mathsf{\Sigma }\left(\mathit{\theta }\right),$ are known.

In this case, Zhang [1] proposed a general procedure based on the Gaussian distribution for estimating the model parameter vector $\mathit{\theta }.$ In [1], it is assumed that the m-dimensional random vector $\mathit{Y}$ comes from a multidimensional normal distribution with mean vector $\mathit{\mu }\left(\mathit{\theta }\right)$ and variance-covariance matrix $\mathsf{\Sigma }\left(\mathit{\theta }\right).$ From a statistical point of view, this procedure can be justified on the basis of the maximum-entropy principle (see [2]), as the multidimensional normal distribution has maximum uncertainty in terms of Shannon entropy and is as well consistent with the given information, i.e., vector mean and variance–covariance matrix.

Then, an estimator of the model parameter $\mathit{\theta }$ based on the Gaussian distribution can be obtained by maximizing the log-likelihood function as defined in (2) but using as $f_{\mathit{\theta }}(·)$ the probability density function of a normal distribution with known mean vector $\mathit{\mu }\left(\mathit{\theta }\right)$ and variance–covariance matrix $\mathsf{\Sigma }\left(\mathit{\theta }\right),$ corresponding to the true mean vector and variance–covariance matrix of the underlying distribution. That is, the Gaussian-based likelihood function of $\mathit{\theta }$ is given by

$$l_G\left(\mathit{\theta }\right)=-\frac{nm}{2}log2\pi -\frac{n}{2}log\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|-\frac{1}{2}\sum _{i=1}^n{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)$$

(3)

for any ${\mathit{y}}_1,\dots ,{\mathit{y}}_n$ independent observations of the population $\mathit{Y},$ and the Gaussian MLE of $\mathit{\theta }$ is defined by

$${\widehat{\mathit{\theta }}}_G=arg\underset{\mathit{\theta }\in \Theta }{max}{l}_G\left(\mathit{\theta }\right).$$

The Gaussian estimator is an MLE and thus inherits all the good properties of the likelihood estimators. Consequently, it works well in terms of the asymptotic efficiency, but it has important robustness problems. That is, in the absence of contamination in data, the MLE consistently estimates the true value of the model parameter, but it may be quite heavily affected by outlying observations in the data. For this reason, Castilla and Zografos extended in [3] the concept of Gaussian estimator and defined a robust version of the estimator based on the density power divergence (DPD) introduced in Basu et al. in [4]. The DPD robustly quantifies the statistical difference between two distributions, and it has been widely used for developing robust inferential methods in many different statistical models. Given a set of observations, the robust minimum DPD estimator (MDPDE) is computed as the minimizer of the DPD between the assumed model distribution and the empirical distribution of the data. The MDPDE enjoys good asymptotic properties and produces robust estimators under general statistical models, as discussed later. The minimum density power divergence Gaussian estimator (MDPDGE) of the parameter $\mathit{\theta }$ is defined for $\tau \ge 0$ as

$${\widehat{\mathit{\theta }}}_G^{\tau }=arg\underset{\mathit{\theta }\in \Theta \subset {\mathbb{R}}^d}{max}{H}_n^{\tau }\left(\mathit{\theta }\right),$$

(4)

where

$$\begin{array}{cc}\hfill H_n^{\tau }\left(\mathit{\theta }\right)=& \frac{\tau +1}{\tau {\left(2\pi \right)}^{m\tau /2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{\tau /2}}\frac{1}{n}\left[\sum _{i=1}^{n}exp\left\{-\frac{\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\right.\hfill \\ \hfill & \left.-\frac{\tau }{{\left(1+\tau \right)}^{(m/2)+1}}\right]-\frac{1}{\tau }\hfill \\ \hfill =& a{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}\frac{1}{n}\left[\sum _{i=1}^{n}exp\left\{-\frac{\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}-b\right]-\frac{1}{\tau },\hfill \end{array}$$

(5)

and

$$a=\frac{\tau +1}{\tau {\left(2\pi \right)}^{m\tau /2}}\mathrm{and}b=\frac{\tau }{{\left(1+\tau \right)}^{(m/2)+1}}.$$

(6)

The MDPDGE family is indexed by a tuning parameter $\tau$ controlling the trade-off between robustness and efficiency; the greater the value of $\tau$, the more robust the resulting estimator is, but the efficiency decreases. It has been shown in the literature that values of the tuning parameter above 1 do not provide sufficiently efficient estimators, and so, the tuning parameter would be chosen in the $[0,1]$ interval. Furthermore, at $\tau =0$, the MDPDGE reduces to the Gaussian estimator of [1],

$${\widehat{\mathit{\theta }}}_G=arg\underset{\mathit{\theta }\in \Theta \subset {\mathbb{R}}^d}{max}{H}_n^0\left(\mathit{\theta }\right)$$

with

$$H_n^0\left(\mathit{\theta }\right)=\underset{\tau \to 0}{lim}{H}_n^{\tau }\left(\mathit{\theta }\right)=-\frac{n}{2}log\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|-\frac{1}{2}\sum _{i=1}^n{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right).$$

(7)

Note that the above objective function does not perfectly match with the likelihood function of the model stated in (2), as it lacks the first term of the likelihood. However, this term does not depend on the parameter $\mathit{\theta }$, and thus, both loss functions will lead to the same maximizer. Indeed, the loss in Equation (7) corresponds to the Kullback–Leiber divergence between the assumed normal distribution and the empirical distribution of the data, which justifies the MLE from the point of view of information theory (see [5,6,7]).

Furthermore, the MDPDGE is consistent and asymptotically normal, that is, given ${\mathit{Y}}_1,\dots ,$ ${\mathit{Y}}_n$ independent and identically distributed vectors from the m-dimensional random vector $\mathit{Y}$, the MDPDGE, ${\widehat{\mathit{\theta }}}_G^{\tau },$ defined in (4) satisfies

$$\sqrt{n}\left({\widehat{\mathit{\theta }}}_G^{\tau }-\mathit{\theta }\right)\underset{n⟶\infty }{\stackrel{\mathcal{L}}{⟶}}\mathcal{N}({\mathbf{0}}_d,{\mathit{J}}_{\tau }{\left(\mathit{\theta }\right)}^{-1}{\mathit{K}}_{\tau }\left(\mathit{\theta }\right){\mathit{J}}_{\tau }{\left(\mathit{\theta }\right)}^{-1}),$$

(8)

being

$${\mathit{J}}_{\tau }\left(\mathit{\theta }\right)={\left(J_{\tau }^{ij}\left(\mathit{\theta }\right)\right)}_{i,j=1,\dots ,d}\mathrm{and}{\mathit{K}}_{\tau }\left(\mathit{\theta }\right)={\left(K_{\tau }^{ij}\left(\mathit{\theta }\right)\right)}_{i,j=1,\dots ,d}.$$

and the elements $J_{\tau }^{ij}\left(\mathit{\theta }\right)$ and $K_{\tau }^{ij}\left(\mathit{\theta }\right)$ of the matrices $J_{\tau }\left(\mathit{\theta }\right)$ and $K_{\tau }\left(\mathit{\theta }\right)$ are given by

$$\begin{array}{ccc}\hfill J_{\tau }^{ij}\left(\mathit{\theta }\right)& =& {\left(\frac{1}{{\left(2\pi \right)}^{m/2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{1/2}}\right)}^{\tau }\frac{1}{{\left(1+\tau \right)}^{(m/2)+2}}\hfill \\ & & \times \left[\left(\tau +1\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_j}\right)}^T\right)\right.\hfill \\ & & \left.+{\mathrm{\Delta }}_{\tau }^i{\mathrm{\Delta }}_{\tau }^j+\frac{1}{2}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)\right]\hfill \end{array}$$

(9)

and

$$\begin{array}{ccc}\hfill K_{\tau }^{ij}\left(\mathit{\theta }\right)& =& {\left(\frac{1}{{\left(2\pi \right)}^{m/2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{1/2}}\right)}^{2\tau }\frac{1}{{\left(1+2\tau \right)}^{(m/2)+2}}\left[{\mathrm{\Delta }}_{2\tau }^i{\mathrm{\Delta }}_{2\tau }^j\right.\hfill \\ & & +\left(1+2\tau \right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_j}\right)}^T\right)\hfill \\ & & \left.+\frac{1}{2}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)\right]\hfill \\ & & -{\left(\frac{1}{{\left(2\pi \right)}^{m/2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{1/2}}\right)}^{2\tau }\frac{1}{{\left(1+\tau \right)}^{m+2}}{\mathrm{\Delta }}_{\tau }^i{\mathrm{\Delta }}_{\tau }^j,\hfill \end{array}$$

(10)

with ${\mathrm{\Delta }}_{\tau }^i=\frac{\tau }{2}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right).$ By $trace\left(A\right)$, we mean the trace of matrix A.

The above asymptotic distribution follows from Theorem 2 in [8], where matrices ${\mathit{J}}_{\tau }\left(\mathit{\theta }\right)$ and ${\mathit{K}}_{\tau }\left(\mathit{\theta }\right)$ are defined for general statistical models.

The asymptotic distribution of $\widehat{{\mathit{\theta }}_G}$ has been considered in many papers, see e.g., [9,10,11,12,13].

On the other hand, in some situations, we may have additional knowledge about the true parameter space. Then, these constraints should be included in the definition of the parameter space $\Theta$. Here, we will consider restricted parameter spaces of the form

$${\Theta }_0=\left\{\mathit{\theta }\in \Theta /\mathit{g}\left(\mathit{\theta }\right)={\mathbf{0}}_r\right\},$$

(11)

where $\mathit{g}:{\mathbb{R}}^d\to {\mathbb{R}}^r$ is a vector-valued function mapping such that the $d\times r$ matrix

$$\mathit{G}\left(\mathit{\theta }\right)=\frac{\partial {\mathit{g}}^T\left(\mathit{\theta }\right)}{\partial \mathit{\theta }}$$

(12)

exists and is continuous in $\mathit{\theta }$ and rank $\left(\mathit{G}\left(\mathit{\theta }\right)\right)=r$, and ${\mathbf{0}}_r$ denotes the null vector of dimension r. The notation ${\Theta }_0$ clues the use of the present restricted estimator for defining test statistics under composite null hypothesis.

The most popular estimator of $\mathit{\theta }$ satisfying the constraints in (11) is the restricted MLE (RMLE), which is naturally defined as the maximizer of the log-likelihood function of the model but is subject to the parameter space restrictions $\mathit{g}\left(\mathit{\theta }\right)={\mathbf{0}}_r$ (see [14,15,16,17]). Unfortunately, the RMLE has the same robustness problems as the MLE, and so robust alternatives should be adopted in the presence of contamination in data. Several robust restricted estimators have been considered in the statistical literature to overcome the robustness drawback of the RMLE. For example, Pardo et al. introduced in [18] the restricted minimum Phi-divergence estimator and studied its properties. In [8], the restricted minimum density power divergence estimators (RMDPDE) are presented, and some applications on the testing hypothesis are studied. In [19], the theoretical robustness properties of the RMDPDE were studied. In [20,21], the restricted Rényi pseudodistance estimator is considered, and robust Rao-type tests are derived from it and developed. More recently, in [22], the RMDPD under normal distributions is studied, and independence tests under the normal assumption are developed, and in [23] the RMDPDE is applied in the context of independent but not identically distributed variables under heterocedastic linear regression models. Other interesting papers related to multivariate analysis are [24,25,26,27].

In this paper, we introduce and study the restricted minimum density power divergence Gaussian estimator (RMDPDGE). The aim of this study is to introduce an estimator dealing with situations where Gaussian estimators are useful; there are additional constraints on the parameter space, and the estimator should be robust in terms of contamination. To show the robustness, we compute the corresponding influence function (IF), showing that in general, it is bounded. As an application of these restricted estimators, we develop Rao-type test statistics. The idea in this case is to consider the additional constraints as the constraints defining the null hypothesis of the test. Finally, we show the robustness via a simulation study, in which the good behavior of these estimators is shown comparing it with the behavior of classical restricted estimators based on MLE. We compare the loss in efficiency when comparing these estimators with more specific estimators dealing with the real distribution, showing that the loss is affordable.

The rest of the paper is organized as follows: In Section 2, we introduce the RMDPDGE and we obtain its asymptotic distribution. Section 3 presents the influence function of the RMDPDGE and theoretically proves the robustness of the proposed estimators. Some statistical applications for testing are presented in Section 4, and an explicit expression of the Rao-type test statistics based on the RMDPDGE under exponential, Poisson and Lindley models are given. Section 5 empirically demonstrates the robustness of the method through a simulation study, and the advantages and disadvantages of the Gaussian assumption are discussed there. Section 6 presents some conclusions. The proofs of the main results stated in the paper are included in Appendix A.

2. Restricted Minimum Density Power Divergence Gaussian Estimators

In this section, we present the RMDPDGE under general equality non-linear constraints and we study its asymptotic distribution, showing the consistency of the estimator.

Definition 1.

Let ${\mathit{Y}}_1,\dots ,$ ${\mathit{Y}}_n$ be independent and identically distributed observations from an m-dimensional random vector $\mathit{Y}$ with $E_{\mathit{\theta }}\left[\mathit{Y}\right]=\mathit{\mu }\left(\mathit{\theta }\right)$ and $Co{v}_{\mathit{\theta }}\left[\mathit{Y}\right]=\mathsf{\Sigma }\left(\mathit{\theta }\right)$, $\mathit{\theta }\in \Theta \subset {\mathbb{R}}^d$. The RMDPDGE, ${\tilde{\mathit{\theta }}}_G^{\tau },$ is defined by

$${\tilde{\mathit{\theta }}}_G^{\tau }=arg\underset{{\Theta }_0}{max}{H}_n^{\tau }\left(\mathit{\theta }\right),$$

where $H_n^{\tau }\left(\mathit{\theta }\right)$ is as given in Equation (5) and ${\Theta }_0=\{\mathit{\theta }\in \Theta /\mathit{g}\left({\mathit{\theta }}_r\right)={\mathbf{0}}_r\}$ is the restricted parameter space defined in (11).

Before presenting the asymptotic distribution of the MDPDGE, we present some previous results whose proofs are included in Appendix A.

Proposition 1.

Let ${\mathit{Y}}_1,\dots ,$ ${\mathit{Y}}_n$ be independent and identically distributed observations from an m-dimensional random vector $\mathit{Y}$ with $E_{\mathit{\theta }}\left[\mathit{Y}\right]=\mathit{\mu }\left(\mathit{\theta }\right)$ and $Co{v}_{\mathit{\theta }}\left[\mathit{Y}\right]=\mathsf{\Sigma }\left(\mathit{\theta }\right)$, $\mathit{\theta }\in \Theta \subset {\mathbb{R}}^d.$ Then,

$$\sqrt{n}\left(\frac{1}{\tau +1}\frac{\partial H_n^{\tau }\left(\mathit{\theta }\right)}{\partial \mathit{\theta }}\right)\underset{n⟶\infty }{\stackrel{\mathcal{L}}{⟶}}\mathcal{N}({\mathbf{0}}_d,{\mathit{K}}_{\tau }\left(\mathit{\theta }\right)),$$

where ${\mathit{K}}_{\tau }\left(\mathit{\theta }\right)$ was defined in (10).

Proof. 

See Appendix A.2. □

Proposition 2.

Let ${\mathit{Y}}_1,\dots ,$ ${\mathit{Y}}_n$ be independent and identically distributed observations from an m-dimensional random vector $\mathit{Y}$ with $E_{\mathit{\theta }}\left[\mathit{Y}\right]=\mathit{\mu }\left(\mathit{\theta }\right)$ and $Co{v}_{\mathit{\theta }}\left[\mathit{Y}\right]=\mathsf{\Sigma }\left(\mathit{\theta }\right)$, $\mathit{\theta }\in \Theta \subset {\mathbb{R}}^d.$ Then,

$$\frac{{\partial }^2{H}_n^{\tau }\left(\mathit{\theta }\right)}{\partial \mathit{\theta }\partial {\mathit{\theta }}^T}\underset{n⟶\infty }{\stackrel{\mathcal{P}}{⟶}}-\left(\tau +1\right){\mathit{J}}_{\mathit{\tau }}\left(\mathit{\theta }\right),$$

where ${\mathit{J}}_{\mathit{\tau }}\left(\mathit{\theta }\right)$ was defined in (9).

Proof. 

See Appendix A.3. □

Next, we present the asymptotic distribution of ${\tilde{\mathit{\theta }}}_G^{\tau }.$

Theorem 1.

Let ${\mathit{Y}}_1,\dots ,$ ${\mathit{Y}}_n$ be independent and identically distributed observations from an m-dimensional random vector $\mathit{Y}$ with $E_{\mathit{\theta }}\left[\mathit{Y}\right]=\mathit{\mu }\left(\mathit{\theta }\right)$ and $Co{v}_{\mathit{\theta }}\left[\mathit{Y}\right]=\mathsf{\Sigma }\left(\mathit{\theta }\right)$, $\mathit{\theta }\in \Theta \subset {\mathbb{R}}^d.$ Suppose the true distribution of $\mathit{Y}$ belongs to the model, and we consider $\mathit{\theta }\in {\Theta }_0$. Then, the RMDPDGE ${\tilde{\mathit{\theta }}}_G^{\tau }$ of θ obtained under the constraints $\mathit{g}\left(\mathit{\theta }\right)={\mathbf{0}}_r$ satisfies

$$n^{1/2}({\tilde{\mathit{\theta }}}_G^{\tau }-\mathit{\theta })\underset{n⟶\infty }{\stackrel{\mathcal{L}}{⟶}}\mathcal{N}({\mathbf{0}}_d,{\mathit{M}}_{\mathit{\tau }}\left(\mathit{\theta }\right)),$$

(13)

where

$${\mathit{M}}_{\mathit{\tau }}\left(\mathit{\theta }\right)={\mathit{P}}_{\mathit{\tau }}^{*}\left(\mathit{\theta }\right){\mathit{K}}_{\mathit{\tau }}\left(\mathit{\theta }\right){\mathit{P}}_{\mathit{\tau }}^{*}{\left(\mathit{\theta }\right)}^T,$$

$${\mathit{P}}_{\mathit{\tau }}^{*}\left(\mathit{\theta }\right)={\mathit{J}}_{\mathit{\tau }}{\left(\mathit{\theta }\right)}^{-1}-{\mathit{Q}}_{\mathit{\tau }}\left(\mathit{\theta }\right)\mathit{G}{\left(\mathit{\theta }\right)}^T{\mathit{J}}_{\mathit{\tau }}{\left(\mathit{\theta }\right)}^{-1},$$

(14)

$${\mathit{Q}}_{\mathit{\tau }}\left(\mathit{\theta }\right)={\mathit{J}}_{\mathit{\tau }}^{-1}\left(\mathit{\theta }\right)\mathit{G}\left(\mathit{\theta }\right){\left[\mathit{G}{\left(\mathit{\theta }\right)}^T{\mathit{J}}_{\mathit{\tau }}{\left(\mathit{\theta }\right)}^{-1}\mathit{G}\left(\mathit{\theta }\right)\right]}^{-1},$$

(15)

and ${\mathit{J}}_{\mathit{\tau }}\left(\mathit{\theta }\right)$ and ${\mathit{K}}_{\mathit{\tau }}\left(\mathit{\theta }\right)$ were defined in (9) and (10), respectively.

Proof. 

The estimating equations for the RMDPDGE are given by

$$\left\{\begin{array}{c}\hfill \frac{\partial }{\partial \mathit{\theta }}{H}_n^{\tau }\left(\mathit{\theta }\right)+\mathit{G}\left(\mathit{\theta }\right){\mathit{\lambda }}_n={\mathbf{0}}_d,\\ \hfill \mathit{g}\left({\tilde{\mathit{\theta }}}_G^{\tau }\right)={\mathbf{0}}_r,\end{array}\right.$$

(16)

where ${\mathit{\lambda }}_n$ is a vector of Lagrangian multipliers. Now, we consider ${\mathit{\theta }}_n=\mathit{\theta }+\mathit{m}{n}^{-1/2}$, where $\left|\right|\mathit{m}\left|\right|<k$, for $0<k<\infty$. We have,

$$\frac{\partial }{\partial \mathit{\theta }}{\left.H_n^{\tau }\left(\mathit{\theta }\right)\right|}_{\mathit{\theta }={\mathit{\theta }}_n}=\frac{\partial }{\partial \mathit{\theta }}{H}_n^{\tau }\left(\mathit{\theta }\right)+\frac{{\partial }^2}{\partial {\mathit{\theta }}^T\partial \mathit{\theta }}{\left.H_n^{\tau }\left(\mathit{\theta }\right)\right|}_{\mathit{\theta }={\mathit{\theta }}_{*}}({\mathit{\theta }}_n^{*}-\mathit{\theta })$$

and

$$n^{1/2}{\left.\frac{\partial }{\partial \mathit{\theta }}{H}_n^{\tau }\left(\mathit{\theta }\right)\right|}_{\mathit{\theta }={\mathit{\theta }}_n}=n^{1/2}\frac{\partial }{\partial \mathit{\theta }}{H}_n^{\tau }\left(\mathit{\theta }\right)+\frac{{\partial }^2}{\partial {\mathit{\theta }}^T\partial \mathit{\theta }}{\left.H_n^{\tau }\left(\mathit{\theta }\right)\right|}_{\mathit{\theta }={\mathit{\theta }}_{*}}{n}^{1/2}({\mathit{\theta }}_n-\mathit{\theta }),$$

(17)

where ${\mathit{\theta }}^{*}$ belongs to the segment joining $\mathit{\theta }$ and ${\mathit{\theta }}_n.$ Since

$$\underset{n\to \infty }{lim}\frac{{\partial }^2}{\partial {\mathit{\theta }}^T\partial \mathit{\theta }}{H}_n^{\tau }\left(\mathit{\theta }\right)=-\left(\tau +1\right){\mathit{J}}_{\mathit{\tau }}\left(\mathit{\theta }\right),$$

we obtain

$$n^{1/2}{\left.\frac{\partial }{\partial \mathit{\theta }}{H}_n^{\tau }\left(\mathit{\theta }\right)\right|}_{\mathit{\theta }={\mathit{\theta }}_n}=n^{1/2}\frac{\partial }{\partial \mathit{\theta }}{H}_n^{\tau }\left(\mathit{\theta }\right)-\left(\tau +1\right)n^{1/2}{\mathit{J}}_{\mathit{\tau }}\left(\mathit{\theta }\right)({\mathit{\theta }}_n-\mathit{\theta })+o_p\left(1\right).$$

(18)

Taking into account that $\mathit{G}\left(\mathit{\theta }\right)$ is continuous in $\mathit{\theta }$

$$n^{1/2}\mathit{g}\left({\mathit{\theta }}_n\right)=\mathit{G}{\left(\mathit{\theta }\right)}^T{n}^{1/2}({\mathit{\theta }}_n-\mathit{\theta })+o_p\left(1\right).$$

(19)

The RMDPDGE ${\tilde{\mathit{\theta }}}_G^{\tau }$ must satisfy the conditions in (16), and in view of (18), we have

$$n^{1/2}\frac{\partial }{\partial \mathit{\theta }}{H}_n^{\tau }\left(\mathit{\theta }\right)-\left(\tau +1\right){\mathit{J}}_{\mathit{\tau }}\left(\mathit{\theta }\right)n^{1/2}({\tilde{\mathit{\theta }}}_G^{\tau }-\mathit{\theta })+\mathit{G}\left(\mathit{\theta }\right)n^{1/2}{\mathit{\lambda }}_n+o_p\left(1\right)={\mathbf{0}}_p.$$

(20)

From (19), it follows that

$${\mathit{G}}^T\left(\mathit{\theta }\right)n^{1/2}({\tilde{\mathit{\theta }}}_G^{\tau }-\mathit{\theta })+o_p\left(1\right)={\mathbf{0}}_r.$$

(21)

Now, we can express Equations (20) and (21) in matrix form as

$$\left(\begin{array}{cc}\left(\tau +1\right){\mathit{J}}_{\mathit{\tau }}\left(\mathit{\theta }\right)& -\mathit{G}\left(\mathit{\theta }\right)\\ -{\mathit{G}}^T\left(\mathit{\theta }\right)& \mathbf{0}\end{array}\right)\left(\begin{array}{c}{n}^{1/2}({\tilde{\mathit{\theta }}}_G^{\tau }-\mathit{\theta })\\ n^{1/2}{\mathit{\lambda }}_n\end{array}\right)=\left(\begin{array}{c}{n}^{1/2}\frac{\partial }{\partial \mathit{\theta }}{H}_n^{\tau }\left(\mathit{\theta }\right)\\ {\mathbf{0}}_{}\end{array}\right)+o_p\left(1\right).$$

Therefore,

$$\left(\begin{array}{c}{n}^{1/2}({\tilde{\mathit{\theta }}}_G^{\tau }-\mathit{\theta })\\ n^{1/2}{\mathit{\lambda }}_n\end{array}\right)={\left(\begin{array}{cc}\left(\tau +1\right){\mathit{J}}_{\mathit{\tau }}\left(\mathit{\theta }\right)& -\mathit{G}\left(\mathit{\theta }\right)\\ -{\mathit{G}}^T\left(\mathit{\theta }\right)& \mathbf{0}\end{array}\right)}^{-1}\left(\begin{array}{c}{n}^{1/2}\frac{\partial }{\partial \mathit{\theta }}{H}_n^{\tau }\left(\mathit{\theta }\right)\\ {\mathbf{0}}_r\end{array}\right)+o_p\left(1\right).$$

However,

$${\left(\begin{array}{cc}\left(\tau +1\right){\mathit{J}}_{\mathit{\tau }}\left(\mathit{\theta }\right)& -\mathit{G}\left(\mathit{\theta }\right)\\ -{\mathit{G}}^T\left(\mathit{\theta }\right)& \mathbf{0}\end{array}\right)}^{-1}=\left(\begin{array}{cc}{\mathbf{L}}_{\tau }^{*}\left(\mathit{\theta }\right)& {\mathit{Q}}_{\tau }\left(\mathit{\theta }\right)\\ {\mathit{Q}}_{\tau }{\left({\mathit{\theta }}_0\right)}^T& {\mathit{R}}_{\tau }\left(\mathit{\theta }\right)\end{array}\right),$$

where

$$\begin{array}{ccc}\hfill {\mathit{L}}_{\tau }^{*}\left(\mathit{\theta }\right)& =& \frac{1}{\tau +1}\left({\mathit{J}}_{\mathit{\tau }}{\left(\mathit{\theta }\right)}^{-1}-{\mathit{Q}}_{\tau }\left(\mathit{\theta }\right)\mathit{G}{\left(\mathit{\theta }\right)}^T{\mathit{J}}_{\mathit{\tau }}{\left(\mathit{\theta }\right)}^{-1}\right)\hfill \\ & =& \frac{1}{\tau +1}{\mathit{P}}_{\tau }^{*}\left(\mathit{\theta }\right),\hfill \\ \hfill {\mathit{Q}}_{\tau }\left(\mathit{\theta }\right)& =& {\mathit{J}}_{\mathit{\tau }}^{-1}\left(\mathit{\theta }\right)\mathit{G}\left(\mathit{\theta }\right){\left[\mathit{G}{\left(\mathit{\theta }\right)}^T{\mathit{J}}_{\mathit{\tau }}{\left(\mathit{\theta }\right)}^{-1}\mathit{G}\left(\mathit{\theta }\right)\right]}^{-1},\hfill \\ \hfill {\mathit{R}}_{\tau }\left(\mathit{\theta }\right)& =& \mathit{G}{\left(\mathit{\theta }\right)}^T{\mathit{J}}_{\mathit{\tau }}{\left(\mathit{\theta }\right)}^{-1}\mathit{G}\left(\mathit{\theta }\right),\hfill \end{array}$$

and ${\mathit{P}}_{\tau }^{*}\left({\mathit{\theta }}_0\right)$ and ${\mathit{Q}}_{\tau }\left({\mathit{\theta }}_0\right)$ are as given in (14) and (15), respectively. Then,

$$n^{1/2}({\tilde{\mathit{\theta }}}_G^{\tau }-\mathit{\theta })={\left(\tau +1\right)}^{-1}{\mathit{P}}_{\tau }^{*}\left(\mathit{\theta }\right)n^{1/2}\frac{\partial }{\partial \mathit{\theta }}{H}_n^{\tau }\left(\mathit{\theta }\right)+o_p\left(1\right),$$

(22)

and we know by Proposition 1 that

$$n^{1/2}{\left(\tau +1\right)}^{-1}\frac{\partial }{\partial \mathit{\theta }}{H}_n^{\tau }\left(\mathit{\theta }\right)\underset{n⟶\infty }{\stackrel{\mathcal{L}}{⟶}}\mathcal{N}\left(\mathbf{0},{\mathit{K}}_{\mathit{\tau }}\left(\mathit{\theta }\right)\right).$$

(23)

Now, by (22) and (23), we have the desired result. □

Remark 1.

Notice that the result in (8) is a special case of the previous theorem when there are no restrictions on the parameter space, in the sense that $\mathit{G}$ defined in (12) is the null matrix. In this case, matrix ${\mathit{P}}_{\mathit{\tau }}^{*}\left(\mathit{\theta }\right)$ given in (14) becomes ${\mathit{P}}_{\mathit{\tau }}^{*}\left(\mathit{\theta }\right)={\mathit{J}}_{\mathit{\tau }}{\left(\mathit{\theta }\right)}^{-1}.$ Therefore, the asymptotic variance–covariance matrix of the unrestricted estimator, i.e., the MDPDGE, may be reconstructed from the previous theorem.

In order to compute the MDPDGE, we note that it is an optimum of a differentiable function $H_n^{\tau }$, so it must annul its first derivatives. We will use that

$${\displaystyle \frac{\partial {\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\tau /2}}{\partial \mathit{\theta }}}=-\frac{\tau }{2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\tau /2}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial \mathit{\theta }}}\right),$$

and

$$\begin{array}{cc}\hfill \frac{\partial }{\partial \mathit{\theta }}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)=& -2{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial \mathit{\theta }}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)-{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\hfill \\ \hfill & \times \left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial \mathit{\theta }}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right).\hfill \end{array}$$

Now, taking derivatives in (5), for a certain fixed $\tau ,$ we have that

$$\begin{array}{ccc}\hfill \frac{\partial }{\partial \mathit{\theta }}{H}_n^{\tau }\left(\mathit{\theta }\right)& =& \frac{1}{n}\sum _{i=1}^n\left\{-a\frac{\tau }{2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\tau /2}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial \mathit{\theta }}}\right)\right.\hfill \\ & & \times exp\left(-\frac{\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right)+ba\frac{\tau }{2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\tau /2}\hfill \\ & & \times trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial \mathit{\theta }}}\right)+a\frac{\tau }{2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\tau /2}\hfill \\ & & \times exp\left(-\frac{\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right)\hfill \\ & & \times \left[2{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial \mathit{\theta }}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right.\hfill \\ & & \left.\left.+{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial \mathit{\theta }}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right]\right\}\hfill \\ & =& \frac{1}{n}\sum _{i=1}^n{\mathsf{\Psi }}_{\mathit{\tau }}({\mathit{y}}_i;\mathit{\theta }),\hfill \end{array}$$

with

$$\begin{array}{ccc}\hfill {\mathsf{\Psi }}_{\mathit{\tau }}({\mathit{y}}_i;\mathit{\theta })& =& a\frac{\tau }{2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\tau /2}\left\{\left[-trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial \mathit{\theta }}}\right)\right.\right.\hfill \\ & & +\left(2{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial \mathit{\theta }}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right.\hfill \\ & & \left.\left.+{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial \mathit{\theta }}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right)\right]\hfill \\ & & \times exp\left(-\frac{\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right)\hfill \\ & & \left.+btrace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial \mathit{\theta }}}\right)\right\}.\hfill \end{array}$$

(24)

Therefore, the estimating equations of the MDPDGE for a fixed parameter $\tau$ are given by

$$\sum _{i=1}^n{\mathsf{\Psi }}_{\mathit{\tau }}({\mathit{y}}_i;\mathit{\theta })={\mathbf{0}}_d.$$

(25)

The previous estimating equations characterize the MDPDGE as an M-estimator and so its asymptotic distribution could have been also derived from the general theory of M-estimators. In particular, the MDPDGE, ${\widehat{\mathit{\theta }}}_G^{\tau },$ satisfies for any $\tau \ge 0$

$$\sqrt{n}\left({\widehat{\mathit{\theta }}}_G^{\tau }-\mathit{\theta }\right)\underset{n⟶\infty }{\stackrel{\mathcal{L}}{⟶}}\mathcal{N}\left({\mathbf{0}}_d,{\mathit{S}}^{-1}{\mathit{MS}}^{-1}\right),$$

(26)

with

$$\mathit{S}=-E\left[\frac{{\partial }^2{H}_n^{\tau }\left(\mathit{\theta }\right)}{\partial \mathit{\theta }\partial {\mathit{\theta }}^T}\right]\mathrm{and}\mathit{M}=Cov\left[\sqrt{n}\frac{\partial }{\partial \mathit{\theta }}{H}_n^{\tau }\left(\mathit{\theta }\right)\right].$$

(27)

Based on Propositions 1 and 2, we can express the previous matrices as

$$\mathit{S}=\left(\tau +1\right){\mathit{J}}_{\mathit{\tau }}\left(\mathit{\theta }\right)\mathrm{and}\mathit{M}={\left(\tau +1\right)}^2{\mathit{K}}_{\mathit{\tau }}\left(\mathit{\theta }\right),$$

and we obtain the expressions established in (8). The asymptotic convergence in (26) offers an alternative proof of the asymptotic distribution of MDPDGE developed in [3] in terms of the transformed matrices $\mathit{S}$ and $\mathit{M}$ in Equation (27).

3. Influence Function for the RMDPDGE

To analyze the robustness of an estimator, Hampel et al. introduced in [28] the concept of an Influence Function (IF). Since then, the IF has been widely used in the statistical literature to measure robustness in different statistical contexts. Intuitively, the IF describes the effect of an infinitesimal contamination of the model on the estimation. Robust estimators should be less affected by contamination, and thus, IFs associated to locally robust (B-robust) estimators should be bounded.

The IF of an estimator, ${\tilde{\mathit{\theta }}}_G^{\tau },$ is defined in terms of its statistical functional ${\tilde{T}}_{\tau }$ satisfying ${\tilde{T}}_{\tau }\left(g\right)={\tilde{\mathit{\theta }}}_G^{\tau },$ where g is the true density function underlying the data. Given the density function g, we define its contaminated version at the point perturbation ${\mathit{y}}_0$ as,

$$g=(1-\epsilon )g+\epsilon {\mathrm{\Delta }}_{{\mathit{y}}_0},$$

(28)

where $\epsilon$ is fraction of contamination and ${\mathrm{\Delta }}_{{\mathit{y}}_0}$ denotes the indicator function at ${\mathit{y}}_0.$ Then, the IF of ${\tilde{\mathit{\theta }}}_G^{\tau }$ is defined as the derivative of the functional at $\epsilon =0$

$$IF({\mathit{y}}_0,{\tilde{T}}_{\tau })=\frac{\partial {\tilde{T}}_{\tau }\left(g_{\epsilon }\right)}{\epsilon }{|}_{\epsilon =0}.$$

Hence, the above derivative quantifies the rate of change of the sample estimator when contamination occurs.

Let us now obtain the IF of RMDPDE. We consider the contaminated model

$$g_{\epsilon }\left(\mathit{y}\right)=(1-\epsilon )f_{\mathit{\theta }}\left(\mathit{y}\right)+\epsilon {\mathrm{\Delta }}_{{\mathit{y}}_0},$$

where $f_{\mathit{\theta }}$ is the assumed probability density function of a normal population. The MDPDGE for the contaminated model is then given by ${\tilde{\mathit{\theta }}}_{G,\epsilon }^{\tau }={\tilde{T}}_{\tau }\left(g_{\epsilon }\right).$

By definition, ${\tilde{\mathit{\theta }}}_{G,\epsilon }^{\tau }$ is the maximizer of $H_n^{\tau }\left(\mathit{\theta }\right)$ in (5), subject to the constraints $\mathit{g}({\tilde{\mathit{\theta }}}_{G,\epsilon }^{\tau })=\mathbf{0}.$ Using the characterization of the MDPDGE as an M-estimator, we have that the influence function of the MDPDGE is given by

$$IF(\mathit{y},{\tilde{T}}_{\tau },\mathit{\theta })={\mathit{J}}_{\tau }{\left(\mathit{\theta }\right)}^{-1}{\mathsf{\Psi }}_{\tau }(\mathit{y};\mathit{\theta }),$$

(29)

where ${\mathit{J}}_{\tau }\left(\mathit{\theta }\right)$ was defined in (9) and ${\mathsf{\Psi }}_{\tau }(\mathit{y};\mathit{\theta })$ in (24). The influence function of the RMDPDGE will be obtained with the additional condition $\mathit{g}\left({\tilde{\mathit{\theta }}}_{G,\epsilon }^{\tau }\right)=\mathbf{0}.$ Differentiating this last equation gives, at $\epsilon =0,$

$$\mathit{G}{\left(\mathit{\theta }\right)}^{T}IF(\mathit{y},{\tilde{T}}_{\tau },\mathit{\theta })=\mathbf{0}.$$

(30)

Based on (29) and (30), we have

$$\left(\begin{array}{c}{\mathit{J}}_{\tau }\left(\mathit{\theta }\right)\\ \mathit{G}{\left(\mathit{\theta }\right)}^T\end{array}\right)IF(\mathit{y},{\tilde{T}}_{\tau },\mathit{\theta })=\left(\begin{array}{c}{\mathsf{\Psi }}_{\mathit{\tau }}(\mathit{y};\mathit{\theta })\\ \mathbf{0}\end{array}\right).$$

Therefore,

$$\left({\mathit{J}}_{\tau }{\left(\mathit{\theta }\right)}^T,\mathit{G}\left(\mathit{\theta }\right)\right)\left(\begin{array}{c}{\mathit{J}}_{\tau }\left(\mathit{\theta }\right)\\ \mathit{G}{\left(\mathit{\theta }\right)}^T\end{array}\right)IF(\mathit{y},{\tilde{T}}_{\tau },\mathit{\theta })={\mathit{J}}_{\tau }{\left(\mathit{\theta }\right)}^T{\mathsf{\Psi }}_{\mathit{\tau }}(\mathit{y};\mathit{\theta }),$$

and the influence function of the RMDPDGE, ${\tilde{\mathit{\theta }}}_G^{\tau },$ is given by

$${\left({\mathit{J}}_{\tau }{\left(\mathit{\theta }\right)}^T{\mathit{J}}_{\tau }\left(\mathit{\theta }\right))+\mathit{G}\left(\mathit{\theta }\right)\mathit{G}{\left(\mathit{\theta }\right)}^T\right)}^{-1}{\mathit{J}}_{\tau }{\left(\mathit{\theta }\right)}^T{\mathsf{\Psi }}_{\mathit{\tau }}(\mathit{y};\mathit{\theta }).$$

(31)

We can observe that the influence function of ${\tilde{\mathit{\theta }}}_G^{\tau },$ obtained in (31), will be bounded if the influence function of the MDPDGE, ${\widehat{\mathit{\theta }}}_G^{\tau },$ given in (29) is bounded. In general, it is not easy to see if it is bounded or not, but in particular situations, this can be solved. On the other hand, if there are no restrictions, $\mathit{G}\left(\mathit{\theta }\right)=\mathbf{0},$ and therefore, (31) coincides with (29).

In Section 4.1, we shall present the expression of ${\mathit{J}}_{\tau }\left(\mathit{\theta }\right)$ and ${\mathsf{\Psi }}_{\tau }(y,\mathit{\theta })$ for some models. Based on that explicit expressions, Figure 1 presents the influence function of the MDPDGE, ${\widehat{\mathit{\theta }}}_G^{\tau }$, for the exponential model with $\mathit{\theta }=4$ and $\tau =0,$ $0.2$ and $0.8$. At $\tau =0,$ the influence function of ${\widehat{\mathit{\theta }}}_G^{\tau }$ is not bounded, whereas it is bounded at the positive values of the tuning parameter, $\tau =0.2$ and $0.8$. This fact illustrates the robustness of the MDPDGE for $\tau >0$ for the exponential model.

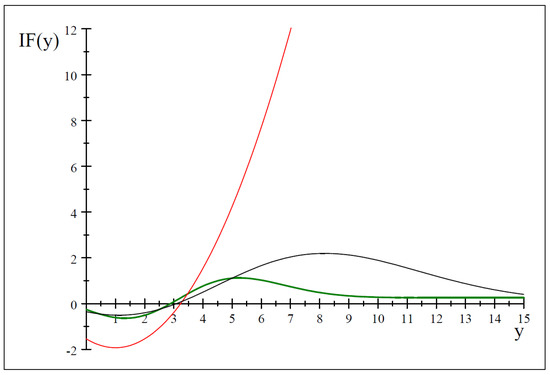
Figure 1. Influence function of the MDPDGE for the exponential model with $\tau =0$ (red), $\tau =0.2$ (black) and $\tau =0.8$ (green).

4. Rao-Type Tests Based on RMDPDGE

Recently, many robust test statistics based on minimum distance estimators have been introduced in the statistical literature for testing under different statistical models. Among them, density power divergence and Rényi’s pseudodistance-based test statistics have shown very competitive performance with respect to classical tests in many different problems. Distance-based test statistics are essentially of two types: Wald-type tests and Rao-type tests. Some applications of these tests can be seen at [8,20,21,22,23,29,30,31,32,33,34,35,36,37] and references therein. In this section, we introduce the Rao-type tests based on RMDPDGE, and we study their asymptotic properties, proving the consistency of the tests.

We analyze here a simple null hypothesis of the form

$$H_0:\mathit{\theta }={\mathit{\theta }}_0\mathrm{vs.}{H}_1:\mathit{\theta }\ne {\mathit{\theta }}_0.$$

(32)

Definition 2.

Let ${\mathit{Y}}_1,\dots ,{\mathit{Y}}_n$ be independent and identically distributed observations from an m-dimensional random vector $\mathit{Y}$ with $E_{\mathit{\theta }}\left[\mathit{Y}\right]=\mathit{\mu }\left(\mathit{\theta }\right)$ and $Co{v}_{\mathit{\theta }}\left[\mathit{Y}\right]=\mathsf{\Sigma }\left(\mathit{\theta }\right)$, $\mathit{\theta }\in \Theta \subset {\mathbb{R}}^d,$ and consider the testing problem defined in (32). The Rao-type test statistic based on RMDPDGE is defined by

$$R_{\mathit{\tau }}\left({\mathit{\theta }}_0\right)=\frac{1}{n}{\mathit{U}}_n^{\mathit{\tau }}{\left({\mathit{\theta }}_0\right)}^T{\mathit{K}}_{\mathit{\tau }}{\left({\mathit{\theta }}_0\right)}^{-1}{\mathit{U}}_n^{\mathit{\tau }}\left({\mathit{\theta }}_0\right),$$

(33)

where

$${\mathit{U}}_n^{\mathit{\tau }}\left(\mathit{\theta }\right)={\left(\frac{1}{\tau +1}\sum _{i=1}^n{\mathsf{\Psi }}_{\mathit{\tau }}^1({\mathit{y}}_i;\mathit{\theta }),\dots ,\frac{1}{\tau +1}{\sum }_{i=1}^n{\mathsf{\Psi }}_{\mathit{\tau }}^d({\mathit{y}}_i;\mathit{\theta })\right)}^T$$

is the score function defining the estimating equations of the MDPDGE and

$${\mathsf{\Psi }}_{\mathit{\tau }}({\mathit{y}}_i;\mathit{\theta })=\left({\mathsf{\Psi }}_{\mathit{\tau }}^1({\mathit{y}}_i;\mathit{\theta }),\dots .,{\mathsf{\Psi }}_{\mathit{\tau }}^d({\mathit{y}}_i;\mathit{\theta })\right).$$

The next result establishes the asymptotic behavior of the proposed Rao-type test statistic.

Theorem 2.

Let ${\mathit{Y}}_1,\dots ,$ ${\mathit{Y}}_n$ be independent and identically distributed observations from an m- dimensional random vector $\mathit{Y}$ with $E_{\mathit{\theta }}\left[\mathit{Y}\right]=\mathit{\mu }\left(\mathit{\theta }\right)$ and $Co{v}_{\mathit{\theta }}\left[\mathit{Y}\right]=\mathsf{\Sigma }\left(\mathit{\theta }\right)$, $\mathit{\theta }\in \Theta \subset {\mathbb{R}}^d.$ Under the null hypothesis given in (32), it holds

$$R_{\mathit{\tau }}\left({\mathit{\theta }}_0\right)\underset{n\to \infty }{\stackrel{L}{\to }}{\chi }_d^2.$$

Proof. 

First, note that we can rewrite

$$\frac{1}{\sqrt{n}}\sum _{i=1}^n\frac{1}{\tau +1}{\mathsf{\Psi }}_{\mathit{\tau }}({\mathit{y}}_i;\mathit{\theta })=\sqrt{n}\frac{1}{\tau +1}\frac{\partial }{\partial \mathit{\theta }}{H}_n^{\tau }\left(\mathit{\theta }\right),$$

and hence, by Proposition 1, we can establish the asymptotic distribution of the $\tau$-score function ${\mathit{U}}_n^{\tau }\left(\mathit{\theta }\right)$

$$\frac{1}{\sqrt{n}}\sum _{i=1}^n\frac{1}{\tau +1}{\mathsf{\Psi }}_{\mathit{\tau }}({\mathit{y}}_i;\mathit{\theta })\underset{n\to \infty }{\stackrel{L}{\to }}\mathcal{N}\left({\mathbf{0}}_p,{\mathit{K}}_{\mathit{\tau }}\left(\mathit{\theta }\right)\right).$$

Hence, as the $\tau$-score function is asymptotically normal,

$$\frac{1}{\sqrt{n}}{\mathit{U}}_n^{\mathit{\tau }}\left(\mathit{\theta }\right)=\frac{1}{\sqrt{n}}\sum _{i=1}^n\frac{1}{\tau +1}{\mathsf{\Psi }}_{\mathit{\tau }}({\mathit{y}}_i;\mathit{\theta })=\sqrt{n}\frac{1}{\tau +1}\frac{\partial }{\partial \mathit{\theta }}{H}_n^{\tau }\left(\mathit{\theta }\right)\underset{n⟶\infty }{\stackrel{\mathcal{L}}{⟶}}\mathcal{N}\left(\mathbf{0},{\mathit{K}}_{\mathit{\tau }}\left(\mathit{\theta }\right)\right).$$

Then, applying a suitable transformation, the result follows. □

Remark 2.

The Rao-type statistic relies on the τ-score function ${\mathit{U}}_n^{\mathit{\tau }}\left(\mathit{\theta }\right)$ defining the estimating equations ${\mathit{U}}_n^{\mathit{\tau }}\left(\mathit{\theta }\right)=0.$ Therefore, if the simple null hypothesis holds, the τ-score function vanishes and conversely, if the true parameter is far from the null hypothesis, large τ-scores will be produced. Based on Theorem 2, for large enough sample sizes, one can use the $100(1-\alpha )$ percentile of the chi-square distribution with d degrees of freedom ${\chi }_{d,\alpha }^2$ satisfying

$$Pr\left({\chi }_d^2>{\chi }_{d,\alpha }^2\right)=\alpha ,$$

to define the reject region of the test with null hypothesis in (32) as

$$RC=\{R_{\mathit{\tau }}\left({\mathit{\theta }}_0\right)>{\chi }_{d,\alpha }^2\}.$$

For illustrative purposes, we present here the application of the proposed method in elliptical distributions.

Example 1. (Elliptical distributions). The m-dimensional random vector $\mathit{Y}$ follows an elliptical distribution if its characteristic function has the form

$${\phi }_{\mathit{Y}}\left(\mathit{t}\right)=exp\left(i{\mathit{t}}^2\mathit{\mu }\right)\psi \left(\frac{1}{2}{\mathit{t}}^2\mathsf{\Sigma }\mathit{t}\right),$$

where μ is an m-dimensional vector, Σ is a positive definite matrix and $\psi \left(t\right)$ denotes the so-called characteristic generator function. The function ψ may depend on the dimension of random vector $\mathit{Y}$. In general, it does not hold that $\mathit{Y}$ has a joint density function, $f_{\mathit{Y}}\left(\mathit{y}\right),$ but if this density exists, it is given by

$$f_{\mathit{Y}}\left(\mathit{y}\right)=c_m{\left|\mathsf{\Sigma }\right|}^{-\frac{1}{2}}{g}_m\left(\frac{1}{2}{\left(\mathit{y}-\mathit{\mu }\right)}^T{\mathsf{\Sigma }}^{-1}\left(\mathit{y}-\mathit{\mu }\right)\right)$$

for some density generator function $g_m$ which could depend on the dimension of the random vector. Moreover, if the density exists, the parameter $c_m$ is given explicitly by

$$c_m={\left(2\pi \right)}^{-\frac{m}{2}}\mathrm{\Gamma }\left(\frac{m}{2}\right){\left(\int x^{\frac{m}{2}-1}{g}_m\left(x\right)dx\right)}^{-1}.$$

The elliptical distribution family is in the following denoted by $E_m\left(\mathit{\mu },\mathsf{\Sigma },g_m\right).$ For more details about the elliptical family $E_m\left(\mathit{\mu },\mathsf{\Sigma },g_m\right),$ see [38,39,40,41,42] and references therein. In [40], for instance, it can be seen that the mean vector and variance–covariance matrix can be obtained as

$$E\left[\mathit{Y}\right]=\mathit{\mu }\mathrm{and}Cov\left[\mathit{Y}\right]=c_{\mathit{Y}}\mathsf{\Sigma },$$

where $c_{\mathit{Y}}=-2{\psi }^{\prime }\left(0\right).$

For the elliptical model, the parameter to be estimated is $\mathit{\theta }=\left({\mathit{\mu }}^T,\mathsf{\Sigma }\right)$ whose dimension is $s=m+\frac{m\left(m+1\right)}{2}.$ In the following, we denote $\mathit{\mu }\left(\mathit{\theta }\right)$ instead of μ and $\mathsf{\Sigma }\left(\mathit{\theta }\right)$ instead of Σ, in order to be consistent with the paper notation.

Let us consider the testing problem

$$H_0:\left(\mathit{\mu }\left(\mathit{\theta }\right),\mathsf{\Sigma }\left(\mathit{\theta }\right)\right)=\left({\mathit{\mu }}_0,{\mathsf{\Sigma }}_0\right)\mathit{vs.}{H}_1:\left(\mathit{\mu }\left(\mathit{\theta }\right),\mathsf{\Sigma }\left(\mathit{\theta }\right)\right)\ne \left({\mathit{\mu }}_0,{\mathsf{\Sigma }}_0\right),$$

(34)

where ${\mathit{\mu }}_0$ and ${\mathsf{\Sigma }}_0$ are known. The Rao-type test statistic based on the MDPDGE for the elliptical model is given as

$$R_{\mathit{\tau }}\left({\mathit{\mu }}_0,{\mathsf{\Sigma }}_0\right)=\frac{1}{n}{\mathit{U}}_n^{\mathit{\tau }}{({\mathit{\mu }}_0,{\mathsf{\Sigma }}_0)}^T{\mathit{K}}_{\mathit{\tau }}{\left({\mathit{\mu }}_0,{\mathsf{\Sigma }}_0\right)}^{-1}{\mathit{U}}_n^{\mathit{\tau }}({\mathit{\mu }}_0,{\mathsf{\Sigma }}_0),$$

where

$${\mathit{U}}_n^{\mathit{\tau }}({\mathit{\mu }}_0,{\mathsf{\Sigma }}_0)=\sum _{i=1}^n\frac{1}{\tau +1}{\mathsf{\Psi }}_{\mathit{\tau }}({\mathit{y}}_i;{\mathit{\mu }}_0,{\mathsf{\Sigma }}_0),$$

with ${\mathsf{\Psi }}_{\mathit{\tau }}({\mathit{y}}_i;{\mathit{\mu }}_0,{\mathsf{\Sigma }}_0)$ and ${\mathit{K}}_{\mathit{\tau }}\left({\mathit{\mu }}_0,{\mathsf{\Sigma }}_0\right)$ as defined in (24) and (10), respectively, but replacing $\mathsf{\Sigma }\left(\mathit{\theta }\right)$ by $c_{\mathit{Y}}\mathsf{\Sigma }$ and $\mathit{\mu }\left(\mathit{\theta }\right)$ by μ. Then, the null hypothesis in (34) should be rejected if

$$R_{\mathit{\tau }}\left({\mathit{\mu }}_0,{\mathsf{\Sigma }}_0\right)>{\chi }_{m+\frac{m(m+1)}{2},\alpha }^2,$$

with ${\chi }_{m+\frac{m(m+1)}{2},\alpha }^2$ the $(1-\alpha )$ upper quantile of a chi-square with $m+\frac{m(m+1)}{2}$ degrees of freedom.

We finally prove the consistency of the Rao-type test based on RMDPDGE. To simplify the statement of the next result, we first define the vector

$$\begin{array}{ccc}\hfill {\mathit{Y}}_{\tau }\left(\mathit{\theta }\right)& =& a\frac{\tau }{2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\tau /2}\left\{-trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial \mathit{\theta }}}\right)\right.\hfill \\ & & exp\left(-\frac{\tau }{2}{\left(\mathit{Y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left(\mathit{Y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right)+btrace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial \mathit{\theta }}}\right)\hfill \\ & & +exp\left(-\frac{\tau }{2}{\left(\mathit{Y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left(\mathit{Y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right)\hfill \\ & & \left[2{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial \mathit{\theta }}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left(\mathit{Y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right.\hfill \\ & & \left.\left.+{\left(\mathit{Y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial \mathit{\theta }}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left(\mathit{Y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right]\right\},\hfill \end{array}$$

(35)

where $a$ and b were defined in (6). We can observe that $\frac{\partial }{\partial \mathit{\theta }}{H}_n\left(\mathit{\theta }\right)$ is the sample mean of a random sample of size n from the m-dimensional population ${\mathit{Y}}_{\tau }\left(\mathit{\theta }\right).$

Theorem 3.

Let ${\mathit{Y}}_1,\dots ,$ ${\mathit{Y}}_n$ be independent and identically distributed observations from an m-dimensional random vector $\mathit{Y}$ with $E_{\mathit{\theta }}\left[\mathit{Y}\right]=\mathit{\mu }\left(\mathit{\theta }\right)$ and $Co{v}_{\mathit{\theta }}\left[\mathit{Y}\right]=\mathsf{\Sigma }\left(\mathit{\theta }\right)$, $\mathit{\theta }\in \Theta \subset {\mathbb{R}}^d.$ Let $\mathit{\theta }\in \Theta$ with $\mathit{\theta }\ne {\mathit{\theta }}_0,$ with ${\mathit{\theta }}_0$ defined in (32), and let us assume that $E_{\mathit{\theta }}\left[{\mathit{Y}}_{\tau }\left({\mathit{\theta }}_0\right)\right]\ne {\mathbf{0}}_d$. Then,

$$\underset{n\to \infty }{lim}{P}_{\mathit{\theta }}\left(R_{\mathit{\tau }}\left({\mathit{\theta }}_0\right)>{\chi }_{d,\alpha }^2\right)=1.$$

Proof. 

From the previous results, it holds that

$$\frac{1}{n}{\mathit{U}}_n^{\mathit{\tau }}\left({\mathit{\theta }}_0\right)=\frac{1}{n}\sum _{i=1}^n\frac{1}{\tau +1}{\mathsf{\Psi }}_{\mathit{\tau }}({\mathit{Y}}_i;{\mathit{\theta }}_0)=\frac{1}{\tau +1}\frac{\partial }{\partial \mathit{\theta }}{H}_n^{\tau }\left({\mathit{\theta }}_0\right)\underset{n\to \infty }{\stackrel{P}{\to }}\frac{1}{\tau +1}{E}_{\mathit{\theta }}\left[{\mathit{Y}}_{\tau }\left({\mathit{\theta }}_0\right)\right],$$

where ${\mathit{Y}}_{\tau }\left({\mathit{\theta }}_0\right)$ is as defined in (35). Therefore,

$$\begin{array}{cc}\hfill P_{\mathit{\theta }}\left(R_{\mathit{\tau }}\left({\mathit{\theta }}_0\right)>{\chi }_{d,\alpha }^2\right)& =P_{\mathit{\theta }}\left(\frac{1}{n}{R}_{\mathit{\tau }}\left({\mathit{\theta }}_0\right)>\frac{1}{n}{\chi }_{d,\alpha }^2\right)\hfill \\ \hfill & \underset{n\to \infty }{⟶}\mathrm{I}\left(\frac{1}{{\left(\tau +1\right)}^2}{E}_{\mathit{\theta }}\left[{\mathit{Y}}_{\tau }\left({\mathit{\theta }}_0\right)\right]{\mathit{K}}_{\tau }^{-1}\left(\mathit{\theta }\right)E_{\mathit{\theta }}^T\left[{\mathit{Y}}_{\tau }\left({\mathit{\theta }}_0\right)\right]>0\right)=1,\hfill \end{array}$$

where $\mathrm{I}(·)$ is the indicator function. □

A natural question that arises here is how the asymptotic power of different test statistics considered for testing the hypothesis in (34) could be compared. Lehmann [43] stated that contiguous alternative hypotheses are of great interest for such purposes, as their associated power functions do not converge to 1. In this regard, we next derive the asymptotic distribution of $R_{\tau }\left({\mathit{\theta }}_0\right)$ under local Pitman-type alternative hypotheses of the form

$$H_{1,n}:\mathit{\theta }={\mathit{\theta }}_n:={\mathit{\theta }}_0+n^{-1/2}\mathit{l},$$

where $\mathit{l}$ is a d-dimensional normal vector. The next result determines the asymptotic power of the Rao-type test based on RMDPDGE under a contiguous alternative hypothesis.

Theorem 4.

Let ${\mathit{Y}}_1,\dots ,{\mathit{Y}}_n$ be independent and identically distributed observations from an m-dimensional random vector $\mathit{Y}$ with $E_{\mathit{\theta }}\left[\mathit{Y}\right]=\mathit{\mu }\left(\mathit{\theta }\right)$ and $Co{v}_{\mathit{\theta }}\left[\mathit{Y}\right]=\mathsf{\Sigma }\left(\mathit{\theta }\right)$, $\mathit{\theta }\in \Theta \subset {\mathbb{R}}^d.$ Under the contiguous alternative hypothesis of the form

$$H_{1,n}:{\mathit{\theta }}_n={\mathit{\theta }}_0+n^{-1/2}\mathit{l},$$

the asymptotic distribution of the Rao-type test based on RMDPDGE, $R_{\tau }\left({\mathit{\theta }}_0\right),$ is a non-central chi-square distribution with d degrees of freedom and non-centrality parameter given by

$${\delta }_{\tau }({\mathit{\theta }}_0,\mathit{l})={\mathit{l}}^T{\mathit{J}}_{\tau }\left({\mathit{\theta }}_0\right){\mathit{K}}_{\tau }^{-1}\left({\mathit{\theta }}_0\right){\mathit{J}}_{\tau }\left({\mathit{\theta }}_0\right)\mathit{l}.$$

Proof. 

Consider the Taylor series expansion

$$\frac{1}{\sqrt{n}}{\mathit{U}}_n^{\mathit{\tau }}\left({\mathit{\theta }}_n\right)=\frac{1}{\sqrt{n}}{\mathit{U}}_n^{\tau }\left({\mathit{\theta }}_0\right)+\frac{1}{n}{\left.\frac{\partial {\mathit{U}}_n^{\tau }\left(\mathit{\theta }\right)}{\partial {\mathit{\theta }}^T}\right|}_{\mathit{\theta }={\mathit{\theta }}_n^{*}}\mathit{l},$$

where ${\mathit{\theta }}_n^{*}$ belongs to the line segment joining ${\mathit{\theta }}_0$ and ${\mathit{\theta }}_0+\frac{1}{\sqrt{n}}\mathit{l}$. Now, by Proposition 2

$$\frac{1}{n}\frac{\partial {\mathit{U}}_n^{\tau }\left(\mathit{\theta }\right)}{\partial {\mathit{\theta }}^T}=\frac{1}{\tau +1}\frac{{\partial }^2{H}_n^{\tau }\left(\mathit{\theta }\right)}{\partial \mathit{\theta }\partial {\mathit{\theta }}^T}\underset{n⟶\infty }{\stackrel{\mathcal{P}}{⟶}}-{\mathit{J}}_{\mathit{\tau }}\left(\mathit{\theta }\right).$$

Therefore,

$${\left.\frac{1}{\sqrt{n}}{\mathit{U}}_n^{\tau }\left(\mathit{\theta }\right)\right|}_{\mathit{\theta }={\mathit{\theta }}_0+n^{-1/2}\mathbf{d}}\underset{n\to \infty }{\stackrel{\mathcal{L}}{⟶}}\mathcal{N}\left(-{\mathit{J}}_{\tau }\left({\mathit{\theta }}_0\right)\mathit{l},{\mathit{K}}_{\tau }\left({\mathit{\theta }}_0\right)\right),$$

and

$$R_{\mathit{\tau }}\left({\mathit{\theta }}_0\right)\underset{n\to \infty }{\stackrel{\mathcal{L}}{⟶}}{\chi }_p^2\left({\delta }_{\tau }({\mathit{\theta }}_0,\mathit{l})\right),$$

with ${\delta }_{\tau }({\mathit{\theta }}_0,\mathbf{d})$ given by

$${\delta }_{\tau }({\mathit{\theta }}_0,\mathit{l})={\mathit{l}}^T{\mathit{J}}_{\tau }\left({\mathit{\theta }}_0\right){\mathit{K}}_{\tau }^{-1}\left({\mathit{\theta }}_0\right){\mathit{J}}_{\tau }\left({\mathit{\theta }}_0\right)\mathit{l}.$$

Hence, the result holds. □

Remark 3.

The previous result can be used for defining an approximation to the power function under any alternative hypothesis, $\mathit{\theta }\in \Theta \backslash {\Theta }_0,$ given as

$$\mathit{\theta }=\mathit{\theta }-{\mathit{\theta }}_0+{\mathit{\theta }}_0=\sqrt{n}\frac{1}{\sqrt{n}}\left(\mathit{\theta }-{\mathit{\theta }}_0\right)+{\mathit{\theta }}_0={\mathit{\theta }}_0+n^{-1/2}\mathit{l},$$

with $\mathit{l}=\sqrt{n}\left(\mathit{\theta }-{\mathit{\theta }}_0\right).$

Remark 4.

In this section, we have dealt with a Rao-type test for a simple null hypothesis. This family can be extended to a composite null hypothesis. If we are interested in testing $H_0:\mathit{\theta }\in {\Theta }_0=\left\{\mathit{\theta }\in \Theta /\mathit{g}\left(\mathit{\theta }\right)={\mathbf{0}}_r\right\},$ we can consider the family of Rao-type tests given by

$$R_{\mathit{\tau }}\left({\tilde{\mathit{\theta }}}_G^{\tau }\right)=\frac{1}{n}{\mathit{U}}_n^{\tau }{\left({\tilde{\mathit{\theta }}}_G^{\tau }\right)}^T{\mathit{Q}}_{\mathit{\tau }}\left({\tilde{\mathit{\theta }}}_G^{\tau }\right){\left[{\mathit{Q}}_{\mathit{\tau }}\left({\tilde{\mathit{\theta }}}_G^{\tau }\right){\mathit{K}}_{\tau }\left({\tilde{\mathit{\theta }}}_G^{\tau }\right){\mathit{Q}}_{\mathit{\tau }}\left({\tilde{\mathit{\theta }}}_G^{\tau }\right)\right]}^{-1}{\mathit{Q}}_{\mathit{\tau }}{\left({\tilde{\mathit{\theta }}}_G^{\tau }\right)}^T{\mathit{U}}_n^{\tau }\left({\tilde{\mathit{\theta }}}_G^{\tau }\right).$$

(36)

However, the extension of the presented results for the family of robust test statistics defined in (36) is not trivial, and it will be established in future research.

In particular, the simple null hypothesis in (32) can be written as a composite null hypothesis with $\mathit{g}\left(\mathit{\theta }\right)=\mathit{\theta }-{\mathit{\theta }}_0.$ In this case, $\mathit{G}\left(\mathit{\theta }\right)$ reduces to the identity matrix of dimension p and the restricted estimator ${\tilde{\mathit{\theta }}}_G^{\tau }$ coincides with ${\mathit{\theta }}_0.$ In this case, the Rao-type test statistic $R_{\mathit{\tau }}\left({\tilde{\mathit{\theta }}}_G^{\tau }\right)$ coincides with the proposed $R_{\mathit{\tau }}\left({\mathit{\theta }}_0\right)$ given in (33). Rao-type test statistics based on RMDPDE have been developed in [22].

4.1. Rao-Type Tests Based on MDPDGE for Univariate Distributions

Let $Y_1,\dots ,Y_n$ be a random sample from the population $Y,$ with

$$E\left[Y\right]=\mu \left(\theta \right)\mathrm{and}Var\left[Y\right]={\sigma }^2\left(\theta \right).$$

Based on (25), the estimating equation is given by

$$\sum _{i=1}^n{\Psi }_{\tau }\left(y_i,\theta \right)=0,$$

with

$$\begin{array}{ccc}\hfill {\Psi }_{\tau }\left(y_i,\theta \right)& =& \frac{\left(\tau +1\right){\left({\sigma }^2\left(\theta \right)\right)}^{-\tau /2}}{2{\left(2\pi \right)}^{\tau /2}}\left\{\left[-\frac{\partial log{\sigma }^2\left(\theta \right)}{\partial \theta }+\frac{\partial log{\sigma }^2\left(\theta \right)}{\partial \theta }\right.\right.\hfill \\ & & \left.{\left(\frac{y_i-\mu \left(\theta \right)}{{\sigma }^2\left(\theta \right)}\right)}^2+2\frac{\partial \mu \left(\theta \right)}{\partial \theta }\left(y_i-\mu \left(\theta \right)\right)\frac{1}{{\sigma }^2\left(\theta \right)}\right]\hfill \\ & & \left.\times exp\left(-\frac{\tau }{2{\sigma }^2\left(\theta \right)}{\left(y_i-\mu \left(\theta \right)\right)}^2\right)+\frac{\tau }{{\left(1+\tau \right)}^{3/2}}\frac{\partial log{\sigma }^2\left(\theta \right)}{\partial \theta }\right\}.\hfill \end{array}$$

(37)

Moreover, the expressions of $J_{\tau }\left(\theta \right)$ and $K_{\tau }\left(\theta \right)$ are, respectively, given by

$$\begin{array}{ccc}\hfill J_{\tau }\left(\theta \right)& =& \frac{1}{{\left(2\pi \sigma {\left(\theta \right)}^2\right)}^{\frac{\tau }{2}}}\frac{1}{{\left(1+\tau \right)}^{5/2}}\left[\left(\tau +1\right){\sigma }^{-2}\left(\theta \right){\left(\frac{\partial \mu \left(\theta \right)}{\partial \theta }\right)}^2+\frac{{\tau }^2}{4}{\left(\frac{\partial log{\sigma }^2\left(\theta \right)}{\partial \theta }\right)}^2\right.\hfill \\ & & \left.+\frac{1}{2}{\left(\frac{\partial log{\sigma }^2\left(\theta \right)}{\partial \theta }\right)}^2\right]\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill K_{\tau }\left(\theta \right)& =& {\left(\frac{1}{{\left(2\pi \right)}^{1/2}\sigma \left(\theta \right)}\right)}^{2\tau }\left\{\frac{1}{{\left(1+2\tau \right)}^{5/2}}\left[{\tau }^2{\left(\frac{\partial log{\sigma }^2\left(\theta \right)}{\partial \theta }\right)}^2\right.\right.\hfill \\ & & \left.+\left(1+2\tau \right){\sigma }^{-2}\left(\theta \right){\left(\frac{\partial \mu \left(\theta \right)}{\partial \theta }\right)}^2+\frac{1}{2}{\left(\frac{\partial log{\sigma }^2\left(\theta \right)}{\partial \theta }\right)}^2\right]\hfill \\ & & \left.-\frac{{\tau }^2}{4{\left(1+\tau \right)}^3}{\left(\frac{\partial log{\sigma }^2\left(\theta \right)}{\partial \theta }\right)}^2\right\}.\hfill \end{array}$$

(38)

Therefore, if we are interesting in testing

$$H_0:\theta ={\theta }_0\mathrm{vs.}{H}_1:\theta \ne {\theta }_0,$$

the Rao-type tests based on RMDPDGE are given by

$$R_{\tau }\left({\theta }_0\right)=\frac{1}{n}{U}_n^{\tau }{\left({\theta }_0\right)}^2{K}_{\tau }{\left({\theta }_0\right)}^{-1},$$

where

$$U_n^{\tau }\left({\theta }_0\right)=\frac{1}{\tau +1}\sum _{i=1}^n{\Psi }_{\tau }\left(y_i,\theta \right)$$

and ${\Psi }_{\tau }\left(y_i,\theta \right)$ and $K_{\tau }\left(\theta \right)$ are given in (37) and (38). The null hypothesis is rejected if

$$R_{\tau }\left({\theta }_0\right)>{\chi }_{1,\alpha }^2,$$

where ${\chi }_{1,\alpha }^2$ is the upper $1-\alpha$ quantile of a chi-square distribution with 1 degree of freedom.

We finally derive explicit expressions of the Rao-type test statistics under Poisson, exponential and Lindley models.

4.1.1. Poisson Model

Let us assume that the random variable Y is Poisson with parameter $\theta .$ In this case, it is well known that $E\left[Y\right]=Var\left[Y\right]=\theta ,$ and so the RMDPDGE, for $\tau >0,$ is given by

$${\widehat{\theta }}_G^{\tau }=arg\underset{\theta }{max}\left\{\frac{\tau +1}{\tau {\left(2\pi \theta \right)}^{\frac{\tau }{2}}}\left(\frac{1}{n}\sum _{i=1}^{n}exp\left(-\frac{\tau }{2\theta }{\left(y_i-\theta \right)}^2\right)-\frac{\tau }{{\left(1+\tau \right)}^{3/2}}\right)-\frac{1}{\tau }\right\}.$$

At $\tau =0,$ the RMDPDGE reduces to the Gaussian MLE,

$${\widehat{\theta }}_G=arg\underset{\theta }{max}\left\{-\frac{1}{2}log2\pi -\frac{1}{2}log\theta -\frac{1}{n}\sum _{i=1}^n\frac{1}{2\theta }{\left(y_i-\theta \right)}^2\right\}.$$

On the other hand, the score function ${\Psi }_{\tau }\left(·\right)$ is given by

$${\Psi }_{\tau }\left(y_i,\theta \right)=\frac{\tau +1}{2{\left(2\pi \theta \right)}^{\frac{\tau }{2}}{\theta }^2}\left\{\left(-{\theta }^2-\theta +y_i^2\right)exp\left(-\frac{\tau }{2\theta }{\left(y_i-\theta \right)}^2\right)+\frac{\tau \theta }{{\left(1+\tau \right)}^{\frac{3}{2}}}\right\},$$

and naturally, at $\tau =0$, we obtain the score function of the Gaussian MLE presented in [1]

$${\Psi }_0\left(y_i,\theta \right)=\frac{1}{2{\theta }^2}\left(-2{\theta }^2+y_i^2\right).$$

On the other hand, the matrix $K_{\tau }\left(\theta \right)$ under the Poisson model has the explicit expression

$$K_{\tau }\left(\theta \right)={\left(\frac{1}{2\pi }\right)}^{\tau }\frac{1}{2{\theta }^{2+\tau }}\left\{\frac{1}{{\left(1+2\tau \right)}^{5/2}}\left(\left(2{\tau }^2+2\theta +4\theta \tau +1\right)-\frac{{\tau }^2}{2{\left(1+\tau \right)}^3}\right)\right\},$$

and hence, the Rao-type tests based on RMDPDGE, $R_{\tau }\left({\theta }_0\right),$ for testing a simple null hypothesis is given, for $\tau >0,$ by

$$\begin{array}{ccc}\hfill R_{\tau }\left({\theta }_0\right)& =& \frac{1}{n}\frac{1}{{\left(2{\left(2\pi \theta \right)}^{\frac{\tau }{2}}{\theta }^2\right)}^2}{\left(\sum _{i=1}^n\left(\left(-2{\theta }_0^2+y_i^2\right)exp\left(-\frac{\tau }{2{\theta }_0}{\left(y_i-{\theta }_0\right)}^2\right)+\frac{\tau \theta }{{\left(1+\tau \right)}^{\frac{3}{2}}}\right)\right)}^2\hfill \\ & & \times {\left(2\pi \right)}^{\tau }\left(2{\theta }^{2+\tau }\right){\left(1+2\tau \right)}^{5/2}{\left\{\left(\left(2{\tau }^2+2\theta +4\theta \tau +1\right)-\frac{{\tau }^2}{2{\left(1+\tau \right)}^3}\right)\right\}}^{-1}.\hfill \end{array}$$

Again, for $\tau =0$, we obtain the expression of the classical Rao test based on the Gaussian MLE,

$$R_0\left({\theta }_0\right)=\frac{1}{4n}{\left(\sum _{i=1}^n\left(\frac{-2{\theta }_0^2+y_i^2}{{\theta }_0^2}\right)\right)}^2\frac{2{\theta }_0^2}{2{\theta }_0+1}.$$

The null hypothesis is rejected if

$$R_{\mathit{\tau }}\left({\theta }_0\right)>{\chi }_{1,\alpha }^2.$$

4.1.2. Exponential Model

Let us assume now that the random variable Y comes from an exponential distribution with probability density function

$$f_{\theta }\left(x\right)=\frac{1}{\theta }exp\left(-\frac{x}{\theta }\right),x>0.$$

(39)

In this case, the true mean and variance are given by $E\left[Y\right]=\theta$ and $Var\left[Y\right]={\theta }^2.$ The RMDPDGE under the exponential model, for $\tau >0,$ is given by

$${\widehat{\theta }}_G^{\tau }=arg\underset{\theta }{max}\left\{\frac{\tau +1}{\tau }{\left(\frac{1}{\theta \sqrt{2\pi }}\right)}^{\tau }\left(\frac{1}{n}\sum _{i=1}^{n}exp\left(-\frac{\tau }{2}{\left(\frac{y_i-\theta }{\theta }\right)}^2\right)-\frac{\tau }{{\left(1+\tau \right)}^{3/2}}\right)-\frac{1}{\tau }\right\},$$

and for $\tau =0,$ we have the Gaussian MLE

$${\widehat{\theta }}_G=arg\underset{\theta }{max}\left\{-\frac{1}{2}log2\pi -log\theta -\frac{1}{n}\sum _{i=1}^n\frac{1}{2}{\left(\frac{y_i-\theta }{\theta }\right)}^2\right\}.$$

On the other hand, the score function is

$${\Psi }_{\tau }\left(y_i,\theta \right)=\frac{\left(\tau +1\right)}{{\theta }^{\tau +3}{\left(\sqrt{2\pi }\right)}^{\tau }}\left\{\left(y_i^2-y_i\theta -{\theta }^2\right)exp\left(-\frac{\tau }{2}{\left(\frac{y_i-\theta }{\theta }\right)}^2\right)+\frac{\tau {\theta }^2}{{\left(1+\tau \right)}^{\frac{3}{2}}}\right\},$$

and for $\tau =0,$ we recover the score function of the Gaussian MLE,

$${\Psi }_0\left(y_i,\theta \right)=\frac{1}{{\theta }^3}\left(y_i^2-y_i\theta +{\theta }^2\right).$$

The value $K_{\tau }\left(\theta \right)$ has the expression

$$K_{\tau }\left(\theta \right)=\frac{1}{{\left(2\pi \right)}^{\tau }{\theta }^{2\left(\tau +1\right)}}\left\{\frac{1}{{\left(1+2\tau \right)}^{5/2}}\left(4{\tau }^2+2\tau +3\right)-\frac{{\tau }^2}{{\left(1+\tau \right)}^3}\right\},$$

and at $\tau =0$

$$K_0\left(\theta \right)=\frac{2}{{\theta }^2}.$$

Correspondingly, the Rao-type tests based on RMDPDGE for testing

$$H_0:\theta ={\theta }_0\mathrm{vs.}{H}_1:\theta \ne {\theta }_0,$$

is given, for $\tau >0,$ by

$$\begin{array}{ccc}\hfill R_{\mathit{\tau }}\left({\theta }_0\right)& =& \frac{1}{n}\frac{1}{{\theta }_0^{2\tau +6}{\left(2\pi \right)}^{\tau }}\left(\sum _{i=1}^n\left\{\left(y_i^2-y_i{\theta }_0-{\theta }_0^2\right)exp\left(-\frac{\tau }{2}{\left(\frac{y_i-{\theta }_0}{{\theta }_0}\right)}^2\right)\right.\right.\hfill \\ & & {\left.\left.+\frac{\tau {\theta }_0^2}{{\left(1+\tau \right)}^{\frac{3}{2}}}\right\}\right)}^2\times {\left(2\pi \right)}^{\tau }{\theta }^{2\left(\tau +1\right)}{\left\{\frac{1}{{\left(1+2\tau \right)}^{5/2}}\left(4{\tau }^2+2\tau +3\right)-\frac{{\tau }^2}{{\left(1+\tau \right)}^3}\right\}}^{-1},\hfill \end{array}$$

(40)

and by

$$R_{\mathbf{0}}\left({\theta }_0\right)=\frac{1}{2n}\sum _{i=1}^n\frac{{\left(y_i^2-y_i{\theta }_0-{\theta }_0^2\right)}^2}{{\theta }_0^4}$$

(41)

for $\tau =0.$

4.1.3. Lindley Model

Let us finally assume that the random variable Y comes from a Lindley distribution [44] with probability density function

$$f_{\theta }\left(x\right)=\frac{{\theta }^2}{\theta +1}(1+x)exp\left(-\theta x\right),x>0,\theta >0.$$

In this case,

$$E\left[Y\right]=\frac{\theta +2}{\theta \left(\theta +1\right)}\mathrm{and}V\left[Y\right]=\frac{{\theta }^2+4\theta +2}{{\theta }^2{\left(\theta +1\right)}^2}.$$

The RMDPGE under the Lindlley model, for $\tau >0,$ is given by

$$\begin{array}{ccc}\hfill {\widehat{\theta }}_G& =& arg\underset{\theta }{max}\left\{\frac{\tau +1}{\tau }{\left(\frac{1}{2\pi }\right)}^{\tau }{\left(\frac{{\theta }^2+4\theta +2}{{\theta }^2{\left(\theta +1\right)}^2}\right)}^{-\frac{\tau }{2}}\right.\hfill \\ & & \left(\frac{1}{n}\sum _{i=1}^{n}exp\left(-\frac{\tau }{2}{\left(y_i-\frac{\theta +2}{\theta \left(\theta +1\right)}\right)}^2{\left(\frac{{\theta }^2+4\theta +2}{{\theta }^2{\left(\theta +1\right)}^2}\right)}^{-1}\right)\right.\left.\left.-\frac{\tau }{{\left(1+\tau \right)}^{\frac{3}{2}}}\right)-\frac{1}{\tau }\right\},\hfill \end{array}$$

and for $\tau =0,$ we have

$${\widehat{\theta }}_G=arg\underset{\theta }{max}\left\{\frac{1}{2}ln\frac{1}{2\pi }-\frac{1}{2}ln\frac{\left({\theta }^2+4\theta +2\right)}{{\theta }^2{\left(\theta +1\right)}^2}-\frac{1}{n}\sum _{i=1}^n\frac{{\left(\theta -y_i\theta -y_i{\theta }^2+2\right)}^2}{2\left({\theta }^2+4\theta +2\right)}\right\}.$$

On the other hand, the score funtion, ${\Psi }_{\tau }(y_i,\theta )$ is given by

$$\begin{array}{ccc}& & \frac{\left(\tau +1\right)}{2{\left(2\pi \right)}^{\frac{\tau }{2}}}{\left(\frac{{\theta }^2+4\theta +2}{{\theta }^2{\left(\theta +1\right)}^2}\right)}^{-\frac{\tau }{2}}\left\{\left[\frac{2{\theta }^3+12{\theta }^2+12\theta +4}{{\theta }^4+5{\theta }^3+6{\theta }^2+2\theta }\right.\right.\hfill \\ & & \left.-\frac{2{\theta }^3+12{\theta }^2+12\theta +4}{{\theta }^4+5{\theta }^3+6{\theta }^2+2\theta }\frac{{\left(\theta -\theta y_i-{\theta }^2{y}_i+2\right)}^2}{{\theta }^2+4\theta +2}-2\left(y_i-\frac{\left(\theta +2\right)}{\theta \left(\theta +1\right)}\right)\right]\hfill \\ & & \left.exp\left(-\frac{\tau }{2}\frac{{\left(\theta -\theta y_i-{\theta }^2{y}_i+2\right)}^2}{{\theta }^2+4\theta +2}\right)-\frac{\tau }{{\left(1+\tau \right)}^{\frac{3}{2}}}\frac{2{\theta }^3+12{\theta }^2+12\theta +4}{{\theta }^4+5{\theta }^3+6{\theta }^2+2\theta }\right\}\hfill \end{array}$$

(42)

and $K_{\tau }\left(\theta \right)$ has the expression

$$\begin{array}{ccc}& & {\left(\frac{{\theta }^2{\left(\theta +1\right)}^2}{2\pi \left({\theta }^2+4\theta +2\right)}\right)}^{\tau }\left\{\frac{1}{{\left(1+2\tau \right)}^{5/2}}\left[{\tau }^2{\left(\frac{2{\theta }^3+12{\theta }^2+12\theta +4}{{\theta }^4+5{\theta }^3+6{\theta }^2+2\theta }\right)}^2\right.\right.\hfill \\ & & \left.+\left(1+2\tau \right)\frac{{\theta }^2+4\theta +2}{{\theta }^2{\left(\theta +1\right)}^2}+\frac{1}{2}{\left(\frac{2{\theta }^3+12{\theta }^2+12\theta +4}{{\theta }^4+5{\theta }^3+6{\theta }^2+2\theta }\right)}^2\right]\hfill \\ & & \left.-\frac{{\tau }^2}{4{\left(1+\tau \right)}^3}{\left(\frac{2{\theta }^3+12{\theta }^2+12\theta +4}{{\theta }^4+5{\theta }^3+6{\theta }^2+2\theta }\right)}^2\right\}\hfill \end{array}$$

(43)

and for $\tau =0,$

$$K_0\left(\theta \right)=\frac{{\left(2{\theta }^3+12{\theta }^2+12\theta +4\right)}^2}{2{\left({\theta }^4+5{\theta }^3+6{\theta }^2+2\theta \right)}^2}+\frac{\left(\theta +2\right)}{\theta \left(\theta +1\right)}.$$

Therefore, the Rao-type test based on RMDPDGE for testing

$$H_0:\theta ={\theta }_0\mathrm{vs.}{H}_1:\theta \ne {\theta }_0$$

is given by

$$R_{\tau }\left({\theta }_0\right)=\frac{1}{n}{U}_n^{\tau }{\left({\theta }_0\right)}^2{K}_{\tau }{\left({\theta }_0\right)}^{-1}>{\chi }_{1,\alpha }^2,$$

where

$$U_n^{\tau }\left({\theta }_0\right)=\frac{1}{\tau +1}\sum _{i=1}^n{\Psi }_{\tau }\left(y_i,\theta \right),$$

with ${\Psi }_{\tau }\left(y_i,\theta \right)$ is defined in (42) and $K_{\tau }\left(\theta \right)$ in (43).

5. Simulation Study

We analyze here the performance of the Rao-type tests based on the MDPDGE, $R_{\tau }\left({\theta }_0\right),$ in terms of robustness and efficiency. We compare the proposed general method assuming Gaussian distribution with Rao-type test statistics based on the true parametric distribution underlying the data.

We consider the exponential model with density function $f_{{\theta }_0}\left(x\right)$ given in (39). For the exponential model, the Rao-type test statistics based on MDPDGE is for $\tau >0$ given in (40) and for $\tau =0$ given in (41). To evaluate the robustness of the tests, we generate samples from an exponential mixture,

$$f_{{\theta }_0}^{\epsilon }\left(x\right)=(1-\epsilon )f_{{\theta }_0}\left(x\right)+\epsilon f_{2{\theta }_0}\left(x\right),$$

where ${\theta }_0$ denotes the parameter of the exponential distribution and $\epsilon$ is the contamination proportion. The uncontaminated model is thus obtained by setting $\epsilon =0.$

For comparison purposes, we have also considered the robust Rao-type tests based on the restricted MDPDE, which was introduced and studied [30]. The efficiency loss caused by the Gaussian assumption should be advertised by the poorer performance of the Rao-type tests based on the restricted MDPDGE with respect to their analogous based on the restricted MDPDE. For the exponential model, the family Rao-type test statistics based on the restricted MDPDE is given, for $\beta >0,$ by

$$S_n^{\beta }\left({\theta }_0\right)={\left(\frac{4{\beta }^2+1}{{(2\beta +1)}^3}-\frac{{\beta }^2}{{(\beta +1)}^4}\right)}^{-1}\frac{1}{n}{\left(\frac{1}{{\theta }_0}\sum _{i=1}^n\left(y_i-{\theta }_0\right)exp\left(-\frac{\beta y_i}{{\theta }_0}\right)+\frac{n\beta }{{(\beta +1)}^2}\right)}^2.$$

For $\beta =0$, the above test reduces to the classical Rao test given by

$$S_n\left({\theta }_0\right)=S_{\beta =0,n}\left({\theta }_0\right)={\left(\sqrt{n}\frac{{\overline{X}}_n-{\theta }_0}{{\theta }_0}\right)}^2.$$

We consider the testing problem

$$H_0:\theta ={\theta }_0\mathrm{vs.}{H}_1:\theta \ne {\theta }_0,$$

and we empirically examine the level and power of both Rao-type test statistics, the usual test based on the parametric model and the Gaussian-based test by setting the true value of the parameter ${\theta }_0=2$ and ${\theta }_0=1,$ respectively. Different sample sizes were considered, namely $n=10,$ $20,$ $30,$ $40,$ $50,$ $60,$ $70,$ $80,$ $90,$ 100 and $200,$ but simulation results were quite similar and so, for brevity, we only report here results for $n=20$ and $n=40.$

The empirical level of the test is computed

$${\widehat{\alpha }}_n\left(\epsilon \right)=\frac{\mathrm{Number}\mathrm{of}\mathrm{times}\left\{R_n^{\tau }\left({\theta }_0\right)(\mathrm{or}{S}_n^{\beta }\left({\theta }_0\right))>{\chi }_{1,0.05}^2=3.84146\right\}}{\mathrm{Number}\mathrm{of}\mathrm{simulated}\mathrm{samples}}.$$

We set $\epsilon =0\%,5\%,$ $10\%$ and $20\%$ of contamination proportions and perform the Monte-Carlo study over R = 10,000 replications. The tuning parameters $\tau$ and $\beta$ are fixed from a grid of values, namely $\{0,0.1,\dots ,0.7\}.$

Simulation results are presented in Table 1 and Table 2 for $n=20$ and $n=40,$ respectively. The empirical powers are denoted by ${\widehat{\pi }}_n\left(\epsilon \right).$ The robustness advantage in terms of level of both Rao-type tests considered, $R_{\mathit{\tau }}\left({\theta }_0\right)$ and $S_n^{\beta }\left({\theta }_0\right)$ with positive values of the turning parameter with respect to the test statistics with $\tau =0$ and $\beta =0$ is clearly shown, as their simulated levels are closer to the nominal value in the presence of contamination.

Table 1. Simulated levels for different contamination proportions and different tuning parameters $\tau ,\beta =0,0.1,0.2,0.3,0.4,0.5,0.6,0.7$ for the Rao-type tests $R_{\tau }\left({\theta }_0\right)$ and $S_n^{\beta }\left({\theta }_0\right)$ for $n=20$.

$\mathit{\tau }$	${\widehat{\mathit{\alpha }}}_{\mathit{n}}\left(0\right)$	${\widehat{\mathit{\alpha }}}_{\mathit{n}}\left(0.05\right)$	${\widehat{\mathit{\alpha }}}_{\mathit{n}}\left(0.10\right)$	${\widehat{\mathit{\alpha }}}_{\mathit{n}}\left(0.20\right)$	${\widehat{\mathit{\pi }}}_{\mathit{n}}\left(0\right)$	${\widehat{\mathit{\pi }}}_{\mathit{n}}\left(0.1\right)$	${\widehat{\mathit{\pi }}}_{\mathit{n}}\left(0.15\right)$	${\widehat{\mathit{\pi }}}_{\mathit{n}}\left(0.20\right)$
0.0	0.2601	0.3093	0.3453	0.4661	0.9278	0.6791	0.6887	0.5088
0.1	0.1895	0.1748	0.1561	0.1989	0.9544	0.7213	0.7301	0.0595
0.2	0.2120	0.1776	0.1417	0.1174	0.9747	0.8398	0.8430	0.6395
0.3	0.2532	0.2113	0.1660	0.1275	0.9826	0.8963	0.8961	0.7301
0.4	0.2963	0.2447	0.1986	0.1471	0.9863	0.9228	0.9257	0.7893
0.5	0.3243	0.2773	0.2307	0.1695	0.9875	0.9363	0.9386	0.8254
0.6	0.3512	0.3055	0.2599	0.1899	0.9885	0.9441	0.9437	0.8434
0.7	0.3751	0.3258	0.2762	0.2060	0.9884	0.9466	0.9469	0.8541
$\beta$
0.0	0.0453	0.0682	0.1048	0.1909	0.7200	0.4365	0.4384	0.2323
0.1	0.0476	0.0602	0.0780	0.1417	0.7799	0.5223	0.5267	0.3029
0.2	0.0498	0.0552	0.0667	0.1103	0.7922	0.5751	0.5780	0.3558
0.3	0.0494	0.0517	0.0584	0.0897	0.7882	0.5997	0.6024	0.3878
0.4	0.0489	0.0505	0.0535	0.0773	0.7779	0.6067	0.6058	0.4106
0.5	0.0494	0.0498	0.0504	0.0692	0.7634	0.6048	0.6037	0.4221
0.6	0.0491	0.0504	0.0497	0.0647	0.7492	0.6008	0.5986	0.4265
0.7	0.0502	0.0495	0.0494	0.0613	0.7348	0.5932	0.5919	0.4259

Table 2. Simulated levels for different contamination proportions and different tuning parameters $\tau ,\beta =0,0.1,0.2,0.3,0.4,0.5,0.6,0.7$ for the Rao-type tests $R_{\tau }\left({\theta }_0\right)$ and $S_n^{\beta }\left({\theta }_0\right)$ for $n=40$.

$\mathit{\tau }$	${\widehat{\mathit{\alpha }}}_{\mathit{n}}\left(0\right)$	${\widehat{\mathit{\alpha }}}_{\mathit{n}}\left(0.05\right)$	${\widehat{\mathit{\alpha }}}_{\mathit{n}}\left(0.10\right)$	${\widehat{\mathit{\alpha }}}_{\mathit{n}}\left(0.20\right)$	${\widehat{\mathit{\pi }}}_{\mathit{n}}\left(0\right)$	${\widehat{\mathit{\pi }}}_{\mathit{n}}\left(0.1\right)$	${\widehat{\mathit{\pi }}}_{\mathit{n}}\left(0.15\right)$	${\widehat{\mathit{\pi }}}_{\mathit{n}}\left(0.20\right)$
0.0	0.3014	0.3588	0.4407	0.5919	0.9948	0.8064	0.7591	0.5957
0.1	0.2393	0.1934	0.1757	0.2032	0.9991	0.9540	0.9229	0.7712
0.2	0.7712	0.2559	0.1970	0.1317	0.9995	0.9916	0.9846	0.9204
0.3	0.4257	0.3485	0.2782	0.1753	0.9997	0.9997	0.9953	0.9694
0.4	0.5021	0.4294	0.3572	0.2388	0.9999	0.9989	0.9978	0.9851
0.5	0.5642	0.4920	0.4253	0.2993	0.9999	0.9992	0.9986	0.9908
0.6	0.6084	0.5415	0.4742	0.3491	1.0000	0.9992	0.9994	0.9935
0.7	0.6416	0.5755	0.5081	0.3831	1.0000	0.9994	0.9994	0.9948
$\beta$
0.0	0.0467	0.0758	0.1309	0.2728	0.9838	0.8093	0.7483	0.4905
0.1	0.0469	0.0623	0.0959	0.1987	0.9870	0.8770	0.8317	0.6072
0.2	0.0464	0.0554	0.0800	0.1526	0.9862	0.9010	0.8687	0.6778
0.3	0.0481	0.0529	0.0704	0.1220	0.9846	0.9084	0.8804	0.7169
0.4	0.0483	0.0518	0.0649	0.1036	0.9808	0.9059	0.8809	0.7316
0.5	0.0500	0.0519	0.0618	0.0929	0.9756	0.9008	0.8742	0.7338
0.6	0.0500	0.0501	0.0577	0.0858	0.9689	0.8914	0.8662	0.7317
0.7	0.0504	0.0519	0.0562	0.0801	0.9634	0.8813	0.8562	0.7258

Regarding the power of the tests for uncontaminated scenarios, there are values at least as good as the corresponding to $\tau =0$ and $\beta =0$, and for contaminated data, the power corresponding to $\tau >0$ and $\beta >0$ is higher.

The loss of efficiency caused by the Guassian assumption can be measured by the discrepancy of the estimated levels and powers between the family of Rao-type tests based on the restricted MDPDGE and the restricted MDPDE. As expected, empirical levels of the test statistics based on the restricted MDPDGE are higher than the corresponding levels of the test based on the restricted MDPDE. However, the test statistic based on the parametric model, $S_n^{\beta }\left({\theta }_0\right),$ is quite conservative and so the corresponding powers are higher than those of the proposed tests, $R_{\mathit{\tau }}\left({\theta }_0\right).$ Based on the presented results, it seems that the proposed Rao-type tests, $R_{\mathit{\tau }}\left({\theta }_0\right),$ performs reasonably well and offers an appealing alternative for situations where the probability density function of the true model is unknown or it is very complicated to work with it.

6. Conclusions

In this paper, we have considered the situation in which the parametric distribution of the variables is unknown and the only available information is given in terms of the mean vector and the variance–covariance matrix. Hence, we only know that the mean vector and variance–covariance matrix depend on the unknown values of a parameter vector $\theta .$ To deal with this problem, Zhang [1] proposed a procedure to estimate $\theta$ assuming that the underlying distribution was Gaussian. This assumption is justified in terms of the maximum entropy of the unknown distribution. However, the estimator developed in [1] is not robust. This procedure was extended using DPD leading to robust estimations of $\theta .$ In this paper, we have dealt with the case in which additional constraints must be imposed to the estimated parameters, thus leading to a new family of estimators that we have named RMDPGE. For these estimators, we have derived their asymptotic distribution and we have studied their robustness properties in terms of the corresponding IF. As an application, we have developed robust Rao-type test statistics under the null hypothesis, where the null hypothesis is indeed the restricted version of the estimator. Finally, we have tested the performance of these test statistics via a simulation study. From the results of this study, we empirically showed that the Rao-type tests considered in this paper seem to have a good performance in terms of efficiency and are more robust than the corresponding approach in [1].

There are several problems to be treated in future research. The most natural seems to develop Rao-type test statistics for composite null hypothesis and study the results obtained in terms of efficiency and robustness.

Appendix A.1. Previous Results

In different parts of Appendix, the following results are applied.

Lemma A1.

The following results can be shown:

• ${\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}=\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|$$trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right).$
• $\frac{\partial trace\left(\mathsf{\Sigma }\left(\mathit{\theta }\right)\right)}{\partial {\theta }_i}=trace\left({\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right).$
• ${{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}}^{-1}=-\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}.$

Lemma A2.

Let $\mathit{Y}$ be a normal population with vector mean μ and variance–covariance $\mathsf{\Sigma }.$ Then, we have

$$E\left[{\left(\mathit{Y}-\mathit{\mu }\right)}^T\mathit{A}\left(\mathit{Y}-\mathit{\mu }\right)\right]=Trace\left(\mathit{A}\mathsf{\Sigma }\right),$$

$$\begin{array}{cc}\hfill E\left[{\left(\mathit{Y}-\mathit{\mu }\right)}^T\mathit{A}\left(\mathit{Y}-\mathit{\mu }\right){\left(\mathit{Y}-\mathit{\mu }\right)}^T\mathit{B}\left(\mathit{Y}-\mathit{\mu }\right)\right]=& Trace\left(\mathit{A}\mathsf{\Sigma }\left(\mathit{B}+{\mathit{B}}^T\right)\mathsf{\Sigma }\right)\hfill \\ \hfill & +Trace\left(\mathit{A}\mathsf{\Sigma }\right)Trace\left(\mathit{B}\mathsf{\Sigma }\right),\hfill \end{array}$$

$$E\left[{\left(\mathit{Y}-\mathit{\mu }\right)}^T\mathit{A}\left(\mathit{Y}-\mathit{\mu }\right)\left(\mathit{Y}-\mathit{\mu }\right)\right]=\mathbf{0}.$$

For more details about these results, see for instance [45].

Appendix A.2

Proof of Proposition 1.

The expression of $H_n^{\tau }\left(\mathit{\theta }\right)$ introduced in (5) is given by

$$H_n^{\tau }\left(\mathit{\theta }\right)=a{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\tau /2}\left(\frac{1}{n}\sum _{i=1}^{n}exp\left\{-\frac{\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}-b\right)-\frac{1}{\tau }.$$

Consider the d-dimensional random vector ${\mathit{Y}}_{\tau }\left(\mathit{\theta }\right)$ defined in (35). Applying the Central Limit Theorem, we have

$$\sqrt{n}\frac{\partial }{\partial \mathit{\theta }}{H}_n^{\tau }\left(\mathit{\theta }\right)=\frac{1}{\sqrt{n}}\sum _{i=1}^n{\mathsf{\Psi }}_{\mathit{\tau }}({\mathit{y}}_i;\mathit{\theta })\underset{n⟶\infty }{\stackrel{\mathcal{L}}{⟶}}\mathcal{N}({\mathbf{0}}_m,{\mathit{S}}_{\mathit{\tau }}\left({\mathit{\theta }}_0\right)),$$

with

$${\mathit{S}}_{\mathit{\tau }}\left({\mathit{\theta }}_0\right)=Cov\left[{\mathit{Y}}_{\tau }\left(\mathit{\theta }\right)\right]=E\left[{\mathit{Y}}_{\tau }{\left(\mathit{\theta }\right)}^T{\mathit{Y}}_{\tau }\left(\mathit{\theta }\right)\right],$$

because

$$E\left[{\mathit{Y}}_{\tau }\left(\mathit{\theta }\right)\right]={\mathbf{0}}_d.$$

To see that $E\left[{\mathit{Y}}_{\tau }\left(\mathit{\theta }\right)\right]={\mathbf{0}}_d,$ consider

$$\begin{array}{ccc}\hfill E\left[{\mathit{Y}}_{\tau }\left(\mathit{\theta }\right)\right]& =& a\frac{\tau }{2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\tau /2}E\left[-trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial \mathit{\theta }}}\right)\right.\hfill \\ & & exp\left\{-\frac{\tau }{2}{\left(\mathit{Y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left(\mathit{Y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}+btrace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial \mathit{\theta }}}\right)\hfill \\ & & +exp\left\{-\frac{\tau }{2}{\left(\mathit{Y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left(\mathit{Y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\hfill \\ & & \left[-2{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial \mathit{\theta }}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left(\mathit{Y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right.\hfill \\ & & \left.\left.+{\left(\mathit{Y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial \mathit{\theta }}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left(\mathit{Y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right]\right]\hfill \\ & =& a\frac{\tau }{2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\tau /2}\left\{-trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial \mathit{\theta }}}\right)\frac{1}{{\left(\tau +1\right)}^{m/2}}\right.\hfill \\ & & +\frac{\tau }{{\left(\tau +1\right)}^{\frac{m}{2}+1}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial \mathit{\theta }}}\right)\hfill \\ & & \left.+\frac{1}{{\left(\tau +1\right)}^{\frac{m}{2}+1}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial \mathit{\theta }}}\right)\right\}\hfill \\ & =& {\mathbf{0}}_d.\hfill \end{array}$$

We can observe that ${\mathit{Y}}_{\tau }\left(\mathit{\theta }\right)$ is a d-dimensional vector whose j-th component is

$$\begin{array}{ccc}\hfill Y_{\tau }^j\left(\mathit{\theta }\right)& =& a\frac{\tau }{2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\tau /2}\left\{-trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\right.\hfill \\ & & exp\left\{-\frac{\tau }{2}{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}+btrace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\hfill \\ & & +exp\left\{-\frac{\tau }{2}{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\hfill \\ & & \left[-2{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_j}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right.\hfill \\ & & \left.\left.+{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right]\right\},j=1,...,d.\hfill \end{array}$$

Therefore, the element $(i,j)$ of the matrix ${\mathit{S}}_{\tau }\left({\mathit{\theta }}_0\right)$ is given by

$$E\left[Y_{\tau }^i\left(\mathit{\theta }\right)Y_{\tau }^j\left(\mathit{\theta }\right)\right].$$

We are going to obtain $Y_{\tau }^i\left(\mathit{\theta }\right)Y_{\tau }^j\left(\mathit{\theta }\right).$ First,

$$\begin{array}{ccc}\hfill Y_{\tau }^i\left(\mathit{\theta }\right)Y_{\tau }^j\left(\mathit{\theta }\right)& =& \left\{a\frac{\tau }{2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\tau /2}\left[-trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)\right.\right.\hfill \\ & & exp\left\{-\frac{\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}+btrace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)\hfill \\ & & +exp\left\{-\frac{\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\hfill \\ & & \left[2{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right.\hfill \\ & & \left.\left.\left.+{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right]\right]\right\}\hfill \\ & & \left\{a\frac{\tau }{2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\tau /2}\left[-trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\right.\right.\hfill \\ & & exp\left\{-\frac{\tau }{2}{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}+btrace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\hfill \\ & & +exp\left\{-\frac{\tau }{2}{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\hfill \\ & & \left[2{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_j}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right.\hfill \\ & & \left.\left.\left.+{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right]\right]\right\}.\hfill \end{array}$$

Therefore, $Y_{\tau }^i\left(\mathit{\theta }\right)Y_{\tau }^j\left(\mathit{\theta }\right)$ is given by

$$\begin{array}{ccc}& & a^2{\left(\frac{\tau }{2}\right)}^2{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\tau }\left\{trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\right.\hfill \\ & & \times exp\left\{-\frac{2\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\hfill \\ & & -trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)b\hfill \\ & & \times exp\left\{-\frac{2\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\hfill \\ & & -trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)exp\left\{-\frac{2\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\hfill \\ & & \times \left[2{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)+{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right]\hfill \\ & & -btrace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)exp\left\{-\frac{\tau }{2}{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\hfill \\ & & +b^{2}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\hfill \\ & & +btrace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)exp\left\{-\frac{\tau }{2}{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\hfill \\ & & \times \left[2{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_j}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)+{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right]\hfill \\ & & -trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)exp\left\{-\frac{2\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\hfill \\ & & \times \left[2{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_j}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)+{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right]\hfill \\ & & +btrace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)exp\left\{-\frac{2\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\hfill \\ & & \times \left[2{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_j}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)+{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right]\hfill \\ & & +exp\left\{-\frac{2\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\hfill \\ & & \times \left[2{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)+{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right]\hfill \\ & & \left.\times \left[2{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_j}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)+{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right]\right\}.\hfill \end{array}$$

Consequently, we can write $Y_{\tau }^i\left(\mathit{\theta }\right)Y_{\tau }^j\left(\mathit{\theta }\right)$ by

$$Y_{\tau }^i\left(\mathit{\theta }\right)Y_{\tau }^j\left(\mathit{\theta }\right)=a^2{\left(\frac{\tau }{2}\right)}^2{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\tau }\left\{C_1+C_2+C_3+C_4+C_5+C_6+C_7+C_8+C_9\right\},$$

and thus,

$$\begin{array}{ccc}\hfill E\left[Y_i\left(\mathit{\theta }\right)Y_j\left(\mathit{\theta }\right)\right]& =& a^2{\left(\frac{\tau }{2}\right)}^2{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\tau }\hfill \\ & & \times E\left[C_1+C_2+C_3+C_4+C_5+C_6+C_7+C_8+C_9\right].\hfill \end{array}$$

(A1)

Now, we are going to calculate the different expectations appearing in Equation A2. We have

$$C_1=trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)exp\left\{-\frac{2\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}.$$

Therefore,

$$\begin{array}{ccc}\hfill E\left[C_1\right]& =& trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\hfill \\ & & \times \int \frac{1}{{\left(2\pi \right)}^{m/2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{1/2}}exp\left\{-\frac{1}{2}{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\hfill \\ & & \times exp\left\{-\frac{1}{2}{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T{\left(\frac{\mathsf{\Sigma }\left(\mathit{\theta }\right)}{2\tau }\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}d\mathit{y}\hfill \\ & =& trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\hfill \\ & \times & {\left(\frac{1}{2\tau +1}\right)}^{\frac{m}{2}}\int \frac{1}{{\left(2\pi \right)}^{m/2}{\left|\frac{\mathsf{\Sigma }\left(\mathit{\theta }\right)}{2\tau +1}\right|}^{1/2}}exp\left\{-\frac{1}{2}{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T{\left(\frac{\mathsf{\Sigma }\left(\mathit{\theta }\right)}{2\tau +1}\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}d\mathit{y}\hfill \\ & =& trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right){\left(\frac{1}{2\tau +1}\right)}^{\frac{m}{2}}.\hfill \end{array}$$

The expression of $C_2$ is given by

$$\begin{array}{ccc}\hfill C_2& =& -trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)b\hfill \\ & & exp\left\{-\frac{2\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\},\hfill \end{array}$$

and thus,

$$\begin{array}{ccc}\hfill E\left[C_2\right]& =& -\frac{\tau }{{\left(1+\tau \right)}^{\frac{m}{2}+1}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\hfill \\ & & \times \int \frac{1}{{\left(2\pi \right)}^{m/2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{1/2}}exp\left\{-\frac{1}{2}{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\hfill \\ & & \times exp\left\{-\frac{1}{2}{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T{\left(\frac{\mathsf{\Sigma }\left(\mathit{\theta }\right)}{\tau }\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}d\mathit{y}\hfill \\ & =& -\frac{\tau }{{\left(1+\tau \right)}^{\frac{m}{2}+1}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\hfill \\ & & \times \frac{1}{{\left(1+\tau \right)}^{\frac{m}{2}}}\int \frac{1}{{\left(2\pi \right)}^{m/2}{\left|\frac{\mathsf{\Sigma }\left(\mathit{\theta }\right)}{\tau +1}\right|}^{1/2}}exp\left\{-\frac{1}{2}{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T{\left(\frac{\mathsf{\Sigma }\left(\mathit{\theta }\right)}{\tau +1}\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}d\mathit{y}\hfill \\ & =& -\frac{\tau }{{\left(1+\tau \right)}^{m+1}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right).\hfill \end{array}$$

The expression of $C_3$ is given by

$$\begin{array}{ccc}\hfill C_3& =& -trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)exp\left\{-\frac{2\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\hfill \\ & & \times \left[2{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)+{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right].\hfill \end{array}$$

Then,

$$\begin{array}{ccc}\hfill E\left[C_3\right]& =& -trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)\frac{1}{{\left(1+2\tau \right)}^{m/2}}\hfill \\ & & \times \int \frac{1}{{\left(2\pi \right)}^{m/2}{\left|\frac{\mathsf{\Sigma }\left(\mathit{\theta }\right)}{2\tau +1}\right|}^{1/2}}exp\left\{-\frac{1}{2}{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\hfill \\ & & \times {\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)d\mathit{y}\hfill \\ & =& -trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\frac{1}{{\left(1+2\tau \right)}^{\frac{m}{2}+1}}.\hfill \end{array}$$

Related to $C_4$, we have

$$C_4=-btrace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)exp\left\{-\frac{\tau }{2}{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\},$$

and

$$\begin{array}{ccc}\hfill E\left[C_4\right]& =& -\frac{\tau }{{\left(1+\tau \right)}^{\frac{m}{2}+1}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\hfill \\ & & \times \int \frac{1}{{\left(2\pi \right)}^{m/2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{1/2}}exp\left\{-\frac{1}{2}{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\hfill \\ & & \times exp\left\{-\frac{\tau }{2}{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T{\left(\mathsf{\Sigma }\left(\mathit{\theta }\right)\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}d\mathit{y}\hfill \\ & =& -\frac{\tau }{{\left(1+\tau \right)}^{\frac{m}{2}+1}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\hfill \\ & & \times \frac{1}{{\left(1+\tau \right)}^{\frac{m}{2}}}\int \frac{1}{{\left(2\pi \right)}^{m/2}{\left|\frac{\mathsf{\Sigma }\left(\mathit{\theta }\right)}{\tau +1}\right|}^{1/2}}exp\left\{-\frac{1}{2}{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T{\left(\frac{\mathsf{\Sigma }\left(\mathit{\theta }\right)}{\tau +1}\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}d\mathit{y}\hfill \\ & =& -\frac{\tau }{{\left(1+\tau \right)}^{m+1}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right).\hfill \end{array}$$

Related to $C_5$, we have

$$C_5=b^{2}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right),$$

and

$$E\left[C_5\right]=\frac{{\tau }^2}{{\left(1+\tau \right)}^{m+2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right).$$

The expression of $C_6$ is given by

$$\begin{array}{ccc}\hfill C_6& =& btrace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)exp\left\{-\frac{\tau }{2}{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\hfill \\ & & \times \left[2{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_j}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)+{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right],\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill E\left[C_6\right]& =& \frac{\tau }{{\left(1+\tau \right)}^{\frac{m}{2}+1}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\frac{1}{{\left(1+\tau \right)}^{\frac{m}{2}+1}}\hfill \\ & =& \frac{\tau }{{\left(1+\tau \right)}^{m+2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right).\hfill \end{array}$$

The expression of $C_7$ is

$$\begin{array}{ccc}\hfill C_7& =& -trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)exp\left\{-\frac{2\tau }{2}{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\hfill \\ & & \times \left[2{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_j}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)+{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right],\hfill \end{array}$$

and

$$E\left[C_7\right]=-\frac{\tau }{{\left(1+2\tau \right)}^{\frac{m}{2}+1}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right).$$

Related to $C_8,$

$$\begin{array}{ccc}\hfill C_8& =& btrace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)exp\left\{-\frac{\tau }{2}{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\hfill \\ & & \times \left[2{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_j}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)+{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right],\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill E\left[C_8\right]& =& \frac{\tau }{{\left(1+\tau \right)}^{\frac{m}{2}+1}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\frac{1}{{\left(1+\tau \right)}^{\frac{m}{2}+1}}\hfill \\ & =& \frac{\tau }{{\left(1+\tau \right)}^{m+2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right).\hfill \end{array}$$

Finally,

$$\begin{array}{ccc}\hfill C_9& =& exp\left\{-\frac{2\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\hfill \\ & & \times \left[2{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)+{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right]\hfill \\ & & \times \left[2{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_j}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)+{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right].\hfill \end{array}$$

Therefore,

$$\begin{array}{ccc}\hfill C_9& =& exp\left\{-\frac{2\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\left\{4{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\right.\hfill \\ & & \times \frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_j}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\hfill \\ & & +2{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right){\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\hfill \\ & & +2{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right){\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_j}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\hfill \\ & & \left.+{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\hfill \\ & =& A_1+A_2+A_3+A_4,\hfill \end{array}$$

and

$$E\left[C_9\right]=E\left[A_1\right]+E\left[A_4\right]$$

because $E\left[A_2\right]=E\left[A_3\right]=0.$ We have

$$\begin{array}{ccc}\hfill E\left[A_1\right]& =& E\left[exp-\frac{2\tau }{2}{\left(\mathit{Y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left(\mathit{Y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)4{\left(\mathit{Y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right.\hfill \\ & & \left.\times {\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_j}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left(\mathit{Y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right]\hfill \\ & =& 4\int \frac{1}{{\left(2\pi \right)}^{m/2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{1/2}}exp\left\{-\frac{1}{2}{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T{\left(\frac{\mathsf{\Sigma }\left(\mathit{\theta }\right)}{2\tau +1}\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\hfill \\ & & \times \mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_j}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)d\mathit{y}\hfill \\ & =& 4\frac{1}{{\left(2\tau +1\right)}^{m/2}}\int \frac{1}{{\left(2\pi \right)}^{m/2}{\left|\frac{\mathsf{\Sigma }\left(\mathit{\theta }\right)}{2\tau +1}\right|}^{1/2}}exp\left\{-\frac{1}{2}{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T{\left(\frac{\mathsf{\Sigma }\left(\mathit{\theta }\right)}{2\tau +1}\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\hfill \\ & & \times {\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_j}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)d\mathit{y}\hfill \\ & =& 4\frac{1}{{\left(2\tau +1\right)}^{m/2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_j}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\frac{\mathsf{\Sigma }\left(\mathit{\theta }\right)}{2\tau +1}\right)\hfill \\ & =& \frac{4}{{\left(2\tau +1\right)}^{m/2+1}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_j}\right).\hfill \end{array}$$

Finally, we are going to obtain $E\left[A_4\right].$

$$\begin{array}{ccc}\hfill E\left[A_4\right]& =& E\left[exp\left\{-\frac{2\tau }{2}{\left(\mathit{Y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left(\mathit{Y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}{\left(\mathit{Y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\right.\hfill \\ & & \left.\times \left(\mathit{Y}-\mathit{\mu }\left(\mathit{\theta }\right)\right){\left(\mathit{Y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left(\mathit{Y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right]\hfill \\ & =& \int \frac{1}{{\left(2\pi \right)}^{m/2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{1/2}}exp\left\{-\frac{1}{2}{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T{\left(\frac{\mathsf{\Sigma }\left(\mathit{\theta }\right)}{2\tau +1}\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\hfill \\ & & \times \left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right){\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\hfill \\ & & \left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)d\mathit{y}\hfill \\ & =& \frac{1}{{\left(2\tau +1\right)}^{m/2}}\left(trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\frac{\mathsf{\Sigma }\left(\mathit{\theta }\right)}{2\tau +1}\right)\right.\hfill \\ & & \left.\times \left[\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}+\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right]\frac{\mathsf{\Sigma }\left(\mathit{\theta }\right)}{2\tau +1}\right)\hfill \\ & & +\frac{1}{{\left(2\tau +1\right)}^{m/2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\frac{\mathsf{\Sigma }\left(\mathit{\theta }\right)}{2\tau +1}\right)\hfill \\ & & \times trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\frac{\mathsf{\Sigma }\left(\mathit{\theta }\right)}{2\tau +1}\right)\hfill \\ & =& \frac{1}{{\left(2\tau +1\right)}^{\frac{m}{2}+2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\hfill \\ & & +\frac{1}{{\left(2\tau +1\right)}^{\frac{m}{2}+2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\left({\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)}^T\right)\hfill \\ & & +\frac{1}{{\left(2\tau +1\right)}^{\frac{m}{2}+2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\hfill \\ & =& 2\frac{1}{{\left(2\tau +1\right)}^{\frac{m}{2}+2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\hfill \\ & & +\frac{1}{{\left(2\tau +1\right)}^{\frac{m}{2}+2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right).\hfill \end{array}$$

Based on the previous results, we have

$$\begin{array}{ccc}\hfill E\left[Y_{\tau }^i\left(\mathit{\theta }\right)Y_{\tau }^j\left(\mathit{\theta }\right)\right]& =& a^2{\left(\frac{\tau }{2}\right)}^2{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\tau }\hfill \\ & & \left\{\frac{1}{{\left(2\tau +1\right)}^{\frac{m}{2}}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\right.\hfill \\ & & -\frac{\tau }{{\left(\tau +1\right)}^{m+1}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\hfill \\ & & -\frac{1}{{\left(2\tau +1\right)}^{\frac{m}{2}+1}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\hfill \\ & & -\frac{\tau }{{\left(\tau +1\right)}^{m+1}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\hfill \\ & & +\frac{{\tau }^2}{{\left(\tau +1\right)}^{m+2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\hfill \\ & & +\frac{\tau }{{\left(\tau +1\right)}^{m+2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\hfill \\ & & -\frac{1}{{\left(2\tau +1\right)}^{\frac{m}{2}+1}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\hfill \\ & & +\frac{\tau }{{\left(\tau +1\right)}^{m+2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\hfill \\ & & +\frac{4}{{\left(2\tau +1\right)}^{\frac{m}{2}+1}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_j}\right)\hfill \\ & & +\frac{2}{{\left(2\tau +1\right)}^{\frac{m}{2}+2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\hfill \\ & & \left.+\frac{1}{{\left(2\tau +1\right)}^{\frac{m}{2}+2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\right\}.\hfill \end{array}$$

The previous expression can be written as

$$\begin{array}{ccc}\hfill E\left[Y_{\tau }^i\left(\mathit{\theta }\right)Y_{\tau }^j\left(\mathit{\theta }\right)\right]& =& a^2{\left(\frac{\tau }{2}\right)}^2\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-\tau }\left\{trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\right.\hfill \\ & & \times \left[\frac{1}{{\left(2\tau +1\right)}^{\frac{m}{2}}}-\frac{1}{{\left(2\tau +1\right)}^{\frac{m}{2}+1}}-\frac{1}{{\left(2\tau +1\right)}^{\frac{m}{2}+1}}+\frac{1}{{\left(2\tau +1\right)}^{\frac{m}{2}+2}}\right]\hfill \\ & & +trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\hfill \\ & & \times \left[-\frac{\tau }{{\left(\tau +1\right)}^{m+1}}-\frac{\tau }{{\left(\tau +1\right)}^{m+1}}+\frac{{\tau }^2}{{\left(\tau +1\right)}^{m+2}}+\frac{\tau }{{\left(\tau +1\right)}^{m+2}}+\frac{\tau }{{\left(\tau +1\right)}^{m+2}}\right]\hfill \\ & & +\frac{4}{{\left(2\tau +1\right)}^{\frac{m}{2}+1}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_j}\right)\hfill \\ & & \left.+\frac{2}{{\left(2\tau +1\right)}^{\frac{m}{2}+2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\right\}.\hfill \end{array}$$

Therefore,

$$\begin{array}{ccc}\hfill E\left[Y_{\tau }^i\left(\mathit{\theta }\right)Y_{\tau }^j\left(\mathit{\theta }\right)\right]& =& {\left(\frac{\tau +1}{\tau {\left(2\pi \right)}^{m\tau /2}}\right)}^2{\left(\frac{\tau }{2}\right)}^2{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\tau }\hfill \\ & & \times \left\{\frac{4{\tau }^2}{{\left(2\tau +1\right)}^{\frac{m}{2}+2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\right.\hfill \\ & & -\frac{{\tau }^2}{{\left(1+\tau \right)}^{m+2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\hfill \\ & & +4\frac{4}{{\left(2\tau +1\right)}^{\frac{m}{2}+1}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_j}\right)\hfill \\ & & \left.+\frac{2}{{\left(2\tau +1\right)}^{\frac{m}{2}+2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\right\}.\hfill \end{array}$$

Finally,

$$\begin{array}{ccc}\hfill E\left[Y_{\tau }^i\left(\mathit{\theta }\right)Y_{\tau }^j\left(\mathit{\theta }\right)\right]& =& {\left(\tau +1\right)}^2\left\{{\left(\frac{1}{{\left(2\pi \right)}^{m\tau /2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{1/2}}\right)}^{2\tau }\frac{1}{{\left(2\tau +1\right)}^{\frac{m}{2}+2}}\right.\hfill \\ & & \times \left({\mathrm{\Delta }}_{2\tau }^i{\mathrm{\Delta }}_{2\tau }^j+\left(2\tau +1\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_j}\right)\right.\hfill \\ & & \left.+\frac{1}{2}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\right)\hfill \\ & & -\left.{\left(\frac{1}{{\left(2\pi \right)}^{m\tau /2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{1/2}}\right)}^{2\tau }\frac{1}{{\left(1+\tau \right)}^{m+2}}{\mathrm{\Delta }}_{\tau }^i{\mathrm{\Delta }}_{\tau }^j\right\}\hfill \\ & =& {\left(\tau +1\right)}^2{K}_{\tau }^{ij}\left(\mathit{\theta }\right),\hfill \end{array}$$

where $K_{\tau }^{ij}\left(\mathit{\theta }\right)$ was defined in (10). Then,

$$\sqrt{n}\frac{\partial }{\partial \mathit{\theta }}{H}_n\left(\mathit{\theta }\right)\underset{n⟶\infty }{\stackrel{\mathcal{L}}{⟶}}\mathcal{N}\left(\mathbf{0},{\left(\tau +1\right)}^2{\mathit{K}}_{\tau }\left(\mathit{\theta }\right)\right),$$

and

$$\sqrt{n}\left(\frac{1}{\tau +1}\frac{\partial }{\partial \mathit{\theta }}{H}_n\left(\mathit{\theta }\right)\right)\underset{n⟶\infty }{\stackrel{\mathcal{L}}{⟶}}\mathcal{N}\left(\mathbf{0},{\mathit{K}}_{\tau }\left(\mathit{\theta }\right)\right).$$

□

Appendix A.3

Proof of Proposition 2.

Note that

$$\begin{array}{ccc}\hfill \frac{\partial }{\partial {\theta }_i}{H}_n^{\tau }\left(\mathit{\theta }\right)& =& -a\frac{\tau }{2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\tau /2}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)\hfill \\ & & \times \left[\frac{1}{n}\sum _{i=1}^{n}exp\left\{-\frac{\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}-b\right]\hfill \\ & & +a{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\tau /2}\left[\frac{1}{n}\sum _{i=1}^{n}exp\left\{-\frac{\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\left(-\frac{\tau }{2}\right)\right.\hfill \\ & & \times \left(2{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right.\hfill \\ & & \left.\left.-{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right)\right]\hfill \\ & =& -a\frac{\tau }{2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\tau /2}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)\hfill \\ & & \times \left[\frac{1}{n}\sum _{i=1}^{n}exp\left\{-\frac{\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}-b\right]\hfill \\ & & +a\frac{\tau }{2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\tau /2}\frac{\tau }{2}\left[\frac{1}{n}\sum _{i=1}^{n}exp\left\{-\frac{\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\right.\hfill \\ & & \times \left(2{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right.\hfill \\ & & \left.\left.\times {\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right)\right].\hfill \end{array}$$

Therefore,

$$\frac{{\partial }^2}{\partial {\theta }_i\partial {\theta }_j}{H}_n^{\tau }\left(\mathit{\theta }\right)=\frac{\partial }{\partial {\theta }_j}{L}_1^{\tau }\left(\mathit{\theta }\right)+\frac{\partial }{\partial {\theta }_j}{L}_2^{\tau }\left(\mathit{\theta }\right),$$

being

$$\begin{array}{ccc}\hfill L_1^{\tau }\left(\mathit{\theta }\right)& =& -a\frac{\tau }{2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\tau /2}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)\hfill \\ & & \times \left[\frac{1}{n}\sum _{i=1}^{n}exp\left\{-\frac{\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}-b\right]\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill L_2^{\tau }\left(\mathit{\theta }\right)& =& a\frac{\tau }{2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\tau /2}\frac{\tau }{2}\left[\frac{1}{n}\sum _{i=1}^{n}exp\left\{-\frac{\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\right.\hfill \\ & & \times \left(2{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right.\hfill \\ & & \left.\left.\times {\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right)\right].\hfill \end{array}$$

We are going to obtain $\frac{\partial }{\partial {\theta }_j}{L}_1^{\tau }\left(\mathit{\theta }\right).$

$$\begin{array}{ccc}\hfill \frac{\partial }{\partial {\theta }_j}{L}_1^{\tau }\left(\mathit{\theta }\right)& =& -a\frac{\tau }{2}\left(-\frac{\tau }{2}\right){\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\tau /2}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)\hfill \\ & & \times \left[\frac{1}{n}\sum _{i=1}^{n}exp\left\{-\frac{\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}-b\right]\hfill \\ & & -a\frac{\tau }{2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\tau /2}trace\left(-\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}+\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{{\partial }^2\mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i\partial {\theta }_j}}\right)\hfill \\ & & \times \left[\frac{1}{n}\sum _{i=1}^{n}exp\left\{-\frac{\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}-b\right]\hfill \\ & & -a\frac{\tau }{2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\tau /2}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)\hfill \\ & & \times \left[\frac{1}{n}\sum _{i=1}^{n}exp\left\{-\frac{\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\left(-\frac{\tau }{2}\right)\right.\hfill \\ & & \times \left(-2{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right.\hfill \\ & & \left.\left.-{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right)\right]\hfill \\ & =& D_1+D_2+D_3,\hfill \end{array}$$

being

$$\begin{array}{ccc}\hfill D_1& =& a{\frac{\tau }{4}}^2{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\tau /2}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\hfill \\ & & \times \left[\frac{1}{n}\sum _{i=1}^{n}exp\left\{-\frac{\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}-b\right],\hfill \end{array}$$

$$\begin{array}{ccc}\hfill D_2& =& -a\frac{\tau }{2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\tau /2}trace\left(-\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right.\hfill \\ & & +\left.\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{{\partial }^2\mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i\partial {\theta }_j}}\right)\hfill \\ & & \times \left[\frac{1}{n}\sum _{i=1}^{n}exp\left\{-\frac{\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}-b\right],\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill D_3& =& a\frac{{\tau }^2}{4}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\tau /2}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)\hfill \\ & & \times \left[\frac{1}{n}\sum _{i=1}^{n}exp\left\{-\frac{\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\right.\hfill \\ & & \times \left(-2{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right.\hfill \\ & & \left.\left.-{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right)\right].\hfill \end{array}$$

Now, we are going to see some result that will be important in order to obtain convergence in probability of $D_1,D_2$ and $D_3.$ □

Lemma A3.

We have

$$l=\frac{1}{n}\sum _{i=1}^{n}exp\left\{-\frac{\tau }{2}{\left({\mathit{Y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{Y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\underset{n⟶\infty }{\stackrel{\mathcal{P}}{⟶}}\frac{1}{{\left(1+\tau \right)}^{m/2}}.$$

Proof. 

It is clear that

$$\begin{array}{ccc}& & l\underset{n⟶\infty }{\stackrel{\mathcal{P}}{⟶}}{E}_{\mathcal{N}\left(\mathit{\mu }\left(\mathit{\theta }\right),\mathsf{\Sigma }\left(\mathit{\theta }\right)\right)}\left[exp\left\{-\frac{\tau }{2}{\left(\mathit{Y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\frac{\mathsf{\Sigma }\left(\mathit{\theta }\right)}{\tau }\right)\left(\mathit{Y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\right]\hfill \\ & =& \int exp\left\{-\frac{\tau }{2}{\left(\mathit{Y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\frac{\mathsf{\Sigma }\left(\mathit{\theta }\right)}{\tau }\right)\left(\mathit{Y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}{f}_{\mathcal{N}\left(\mathit{\mu }\left(\mathit{\theta }\right),\mathsf{\Sigma }\left(\mathit{\theta }\right)\right)}\left(\mathit{y}\right)d\mathit{y}\hfill \\ & =& \frac{1}{{\left(1+\tau \right)}^{m/2}}\int \frac{1}{{\left(2\pi \right)}^{m/2}}\frac{1}{{\left|\frac{\mathsf{\Sigma }\left(\mathit{\theta }\right)}{\tau +1}\right|}^{1/2}}exp\left\{-\frac{\tau +1}{2}{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\frac{\mathsf{\Sigma }\left(\mathit{\theta }\right)}{\tau }\right)\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}d\mathit{y}\hfill \\ & =& \frac{1}{{\left(1+\tau \right)}^{m/2}}.\hfill \end{array}$$

□

Lemma A4.

We have

$$m=\frac{1}{n}\sum _{i=1}^{n}exp\left\{-\frac{\tau }{2}{\left({\mathit{Y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{Y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}-b\underset{n⟶\infty }{\stackrel{\mathcal{P}}{⟶}}\frac{1}{{\left(1+\tau \right)}^{\frac{m}{2}+1}}.$$

Proof. 

Applying the previous Lemma

$$m\underset{n⟶\infty }{\stackrel{\mathcal{P}}{⟶}}\frac{1}{{\left(1+\tau \right)}^{m/2}}-\frac{\tau }{{\left(1+\tau \right)}^{\frac{m}{2}+1}}=\frac{1}{{\left(1+\tau \right)}^{\frac{m}{2}+1}}.$$

□

Lemma A5.

If we denote

$$n=\frac{1}{n}\sum _{i=1}^{n}exp\left\{-\frac{\tau }{2}{\left({\mathit{Y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{Y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}{\left({\mathit{Y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathit{A}\left({\mathit{Y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right),$$

we have

$$n\underset{n⟶\infty }{\stackrel{\mathcal{P}}{⟶}}\frac{trace\left(\mathit{A}\mathsf{\Sigma }\left(\mathit{\theta }\right)\right)}{{\left(1+\tau \right)}^{\frac{m}{2}+1}}.$$

Proof. 

It is clear that

$$\begin{array}{ccc}& & n\underset{n⟶\infty }{\stackrel{\mathcal{P}}{⟶}}{E}_{\mathcal{N}\left(\mathit{\mu }\left(\mathit{\theta }\right),\mathsf{\Sigma }\left(\mathit{\theta }\right)\right)}\left[exp\left\{-\frac{1}{2}{\left(\mathit{Y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T{\left(\frac{\mathsf{\Sigma }\left(\mathit{\theta }\right)}{\tau }\right)}^{-1}\left(\mathit{Y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\right.\hfill \\ & & \left.\times {\left(\mathit{Y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathit{A}\left(\mathit{Y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right]\hfill \\ & =& \frac{1}{{\left(1+\tau \right)}^{m/2}}\int \frac{1}{{\left(2\pi \right)}^{m/2}}\frac{1}{{\left|\frac{\mathsf{\Sigma }\left(\mathit{\theta }\right)}{\tau +1}\right|}^{1/2}}exp\left\{-\frac{1}{2}{\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T{\left(\frac{\mathsf{\Sigma }\left(\mathit{\theta }\right)}{\tau +1}\right)}^{-1}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\hfill \\ & & \times {\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathit{A}\left(\mathit{y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)d\mathit{y}\hfill \\ & =& \frac{1}{{\left(1+\tau \right)}^{m/2}}{E}_{\mathcal{N}\left(\mathit{\mu }\left(\mathit{\theta }\right),\frac{\mathsf{\Sigma }\left(\mathit{\theta }\right)}{1+\tau }\right)}\left[{\left(\mathit{Y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathit{A}\left(\mathit{Y}-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right]\hfill \\ & =& \frac{1}{{\left(1+\tau \right)}^{\frac{m}{2}+1}}trace\left(\mathit{A}\mathsf{\Sigma }\left(\mathit{\theta }\right)\right).\hfill \end{array}$$

□

Based on the previous results we have in relation to $D_{1,}$

$$D_1\underset{n⟶\infty }{\stackrel{\mathcal{P}}{⟶}}\frac{\tau }{4}\frac{{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m\tau /2}{\left(1+\tau \right)}^{m/2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right).$$

With respect to $D_{2,}$

$$\begin{array}{ccc}& & D_2\underset{n⟶\infty }{\stackrel{\mathcal{P}}{⟶}}\frac{1}{{\left(2\pi \right)}^{m/2}}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}\frac{1}{2}\frac{1}{{\left(1+\tau \right)}^{m/2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)\hfill \\ & & -\frac{{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m/2}}\frac{1}{2}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{{\partial }^2\mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j\partial {\theta }_i}}\right).\hfill \end{array}$$

In a similar way, we obtain for $D_3$ that

$$D_3\underset{n⟶\infty }{\stackrel{\mathcal{P}}{⟶}}-\frac{\tau }{4}\frac{{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m\tau /2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)\frac{1}{{\left(1+\tau \right)}^{m/2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right).$$

Therefore, we have

$$\begin{array}{ccc}& & \frac{\partial }{\partial {\theta }_j}{L}_1^{\tau }\left(\mathit{\theta }\right)\underset{n⟶\infty }{\stackrel{\mathcal{P}}{⟶}}\frac{1}{2}\frac{{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m\tau /2}}\frac{1}{{\left(1+\tau \right)}^{m/2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)\hfill \\ & & -\frac{1}{2}\frac{{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m\tau /2}}\frac{1}{{\left(1+\tau \right)}^{m/2}}\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{{\partial }^2\mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j\partial {\theta }_i}}\right).\hfill \end{array}$$

Now, we have

$$\begin{array}{ccc}\hfill \frac{\partial }{\partial {\theta }_j}{L}_2^{\tau }\left(\mathit{\theta }\right)& =& -a\frac{{\tau }^2}{4}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\hfill \\ & & \times \left[\frac{1}{n}\sum _{i=1}^{n}exp\left\{-\frac{\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\left(2{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\right.\right.\hfill \\ & & \left.\left.\times \mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)+{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right)\right]\hfill \\ & & +a\frac{\tau }{2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}\left[\frac{1}{n}\sum _{i=1}^{n}exp\left\{-\frac{\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\right.\hfill \\ & & \times \left(-\frac{\tau }{2}\right)\left(\frac{\partial }{\partial {\theta }_j}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right)\left(2{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right.\hfill \\ & & \left.\left.\times {\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right)\right]\hfill \\ & & +a\frac{\tau }{2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}\left[\frac{1}{n}\sum _{i=1}^{n}exp\left\{-\frac{\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\right.\hfill \\ & & \times \frac{\partial }{\partial {\theta }_j}\left(2{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right)\hfill \\ & & \left.\left.+{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right)\right]\hfill \\ & =& C_1+C_2+C_3.\hfill \end{array}$$

Now,

$$\begin{array}{ccc}\hfill C_1& =& -a\frac{{\tau }^2}{4}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\left[\frac{1}{n}\sum _{i=1}^{n}exp\left\{-\frac{\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\right.\hfill \\ & & \times \left(2{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right.\hfill \\ & & \left.\left.\times {\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right)\right].\hfill \end{array}$$

It is clear that

$$C_1\underset{n⟶\infty }{\stackrel{\mathcal{P}}{⟶}}-\frac{\tau }{4}\frac{1}{{\left(1+\tau \right)}^{m/2}}\frac{{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m\tau /2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right).$$

Next,

$$\begin{array}{ccc}\hfill C_2& =& -a\frac{{\tau }^2}{4}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}\frac{1}{n}\sum _{i=1}^{n}exp\left\{-\frac{\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\left(S_1+S_2+S_3+S_4\right)\hfill \\ & =& L_1^{*}+L_2^{*}+L_3^{*}+L_4^{*}.\hfill \end{array}$$

First,

$$\begin{array}{ccc}\hfill L_1^{*}& =& -a\frac{{\tau }^2}{4}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}\frac{1}{n}\sum _{i=1}^{n}exp\left\{-\frac{\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\hfill \\ & & \times \left(-4{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_j}{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right),\hfill \end{array}$$

and

$$L_1^{*}\underset{n⟶\infty }{\stackrel{\mathcal{P}}{⟶}}\frac{{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m\tau /2}}\frac{\tau }{{\left(1+\tau \right)}^{m/2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_j}{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\right).$$

It is clear that

$$L_2^{*}\underset{n⟶\infty }{\stackrel{\mathcal{P}}{⟶}}\mathbf{0}\mathrm{and}{L}_3^{*}\underset{n⟶\infty }{\stackrel{\mathcal{P}}{⟶}}\mathbf{0}.$$

Finally,

$$\begin{array}{ccc}& & L_4^{*}\underset{n⟶\infty }{\stackrel{\mathcal{P}}{⟶}}\frac{\tau +1}{{\left(2\pi \right)}^{m\tau /2}}\frac{\tau }{4}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}\frac{1}{{\left(1+\tau \right)}^{m/2}}\hfill \\ & & \times \left\{trace\left\{\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)\left[\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}+\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right]\right.\right.\hfill \\ & & \left.\left.\times \frac{\mathsf{\Sigma }\left(\mathit{\theta }\right)}{1+\tau }\right\}+trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\frac{\mathsf{\Sigma }\left(\mathit{\theta }\right)}{1+\tau }\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\frac{\mathsf{\Sigma }\left(\mathit{\theta }\right)}{1+\tau }\right)\right\}\hfill \\ & & =2\frac{\tau }{4}\frac{{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m\tau /2}}\frac{1}{{\left(1+\tau \right)}^{m/2+1}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\mathsf{\Sigma }\left(\mathit{\theta }\right){\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)\hfill \\ & & +\frac{\tau }{4}\frac{{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m\tau /2}}\frac{1}{{\left(1+\tau \right)}^{m/2+1}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right).\hfill \end{array}$$

Therefore,

$$C_2=L_1^{*}+L_2^{*}+L_3^{*}+L_4^{*}\underset{n⟶\infty }{\stackrel{\mathcal{P}}{⟶}}R,$$

where

$$\begin{array}{ccc}\hfill R& =& \frac{\tau {\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m\tau /2}{\left(1+\tau \right)}^{m/2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}{\left({\displaystyle \frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)}^T\right)\hfill \\ & & +\frac{\tau }{2}\frac{{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m\tau /2}{\left(1+\tau \right)}^{m/2+1}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)\hfill \\ & & +\frac{\tau }{4}\frac{{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m\tau /2}{\left(1+\tau \right)}^{m/2+1}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right).\hfill \end{array}$$

Finally,

$$\begin{array}{ccc}\hfill C_3& =& a\frac{\tau }{2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}\frac{1}{n}\sum _{i=1}^{n}exp\left\{-\frac{\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\hfill \\ & & \times \left\{\left(2\frac{\partial }{\partial {\theta }_j}{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right)\right.\hfill \\ & & +2{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T{\displaystyle \frac{\partial \mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}}{\partial {\theta }_i}}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\hfill \\ & & -2{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_j}\right)}^T\hfill \\ & & -2{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right)\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\hfill \\ & & +{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left\{-\right.\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\hfill \\ & & \left.+\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{{\partial }^2\mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}-\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right\}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\hfill \\ & =& A_1^{*}+A_2^{*}+A_3^{*}+A_4^{*}+A_5^{*}.\hfill \end{array}$$

It is clear that

$$A_1^{*}\underset{n⟶\infty }{\stackrel{\mathcal{P}}{⟶}}0A_2^{*}\underset{n⟶\infty }{\stackrel{\mathcal{P}}{⟶}}0\mathrm{and}{A}_4^{*}\underset{n⟶\infty }{\stackrel{\mathcal{P}}{⟶}}0.$$

On the other hand,

$$\begin{array}{ccc}\hfill A_3^{*}& =& -a\frac{\tau }{2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}\frac{1}{n}\sum _{i=1}^{n}exp\left\{-\frac{\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\hfill \\ & & \left(2{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right),\hfill \end{array}$$

and

$$A_3^{*}\underset{n⟶\infty }{\stackrel{\mathcal{P}}{⟶}}-(\tau +1)\frac{{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m\tau /2}{\left(1+\tau \right)}^{m/2}}{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_j}.$$

Related to $A_5^{*}$, we have

$$\begin{array}{ccc}\hfill A_5^{*}& =& a\frac{\tau }{2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}\frac{1}{n}\sum _{i=1}^{n}exp\left\{-\frac{\tau }{2}{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\}\hfill \\ & & \times \left\{{\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)}^T\left[\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right.\right.\hfill \\ & & \left.\left.+\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{{\partial }^2\mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}-\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\right]\left({\mathit{y}}_i-\mathit{\mu }\left(\mathit{\theta }\right)\right)\right\},\hfill \end{array}$$

and

$$\begin{array}{ccc}& & A_5^{*}\underset{n⟶\infty }{\stackrel{\mathcal{P}}{⟶}}-\frac{1}{{\left(2\pi \right)}^{m\tau /2}}\frac{1}{2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}\frac{1}{{\left(1+\tau \right)}^{m/2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)\hfill \\ & & +\frac{1}{{\left(2\pi \right)}^{m\tau /2}}\frac{1}{2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}\frac{1}{{\left(1+\tau \right)}^{m/2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{{\partial }^2\mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i\partial \theta }}\right)\hfill \\ & & -\frac{1}{{\left(2\pi \right)}^{m\tau /2}}\frac{1}{2}{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}\frac{1}{{\left(1+\tau \right)}^{m/2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right).\hfill \end{array}$$

Therefore,

$$\begin{array}{ccc}& & C_3\underset{n⟶\infty }{\stackrel{\mathcal{P}}{⟶}}-\left(\tau +1\right)\frac{{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m\tau /2}}\frac{1}{{\left(1+\tau \right)}^{m/2}}{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_j}\hfill \\ & & -\frac{{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m\tau /2}}\frac{1}{{\left(1+\tau \right)}^{m/2}}\frac{1}{2}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)\hfill \\ & & +\frac{{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m\tau /2}}\frac{1}{{\left(1+\tau \right)}^{m/2}}\frac{1}{2}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{{\partial }^2\mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i\partial {\theta }_j}}\right)\hfill \\ & & -\frac{{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m\tau /2}}\frac{1}{2}\frac{1}{{\left(1+\tau \right)}^{m/2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right).\hfill \end{array}$$

We are going to join all the previous expressions in order to obtain $\frac{\partial }{\partial {\theta }_j}{L}_2^{\tau }\left(\mathit{\theta }\right),$

$$\begin{array}{ccc}\hfill \frac{\partial }{\partial {\theta }_j}{L}_2^{\tau }\left(\mathit{\theta }\right)& =& C_1+C_2+C_3\hfill \\ & =& C_1+L_1^{*}+L_2^{*}+L_3^{*}+L_4^{*}+C_3\hfill \\ & =& C_1+L_1^{*}+L_2^{*}+L_3^{*}+L_4^{*}+A_1^{*}+A_2^{*}+A_3^{*}+A_4^{*}+A_5^{*}.\hfill \end{array}$$

Then,

$$\begin{array}{ccc}& & \frac{\partial }{\partial {\theta }_j}{L}_2^{\tau }\left(\mathit{\theta }\right)\underset{n⟶\infty }{\stackrel{\mathcal{P}}{⟶}}-\frac{\tau }{4}\frac{1}{{\left(1+\tau \right)}^{m/2}}\frac{{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m\tau /2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\hfill \\ & & +\frac{\tau {\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m\tau /2}{\left(1+\tau \right)}^{m/2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)\hfill \\ & & +\frac{\tau }{2}\frac{{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m\tau /2}{\left(1+\tau \right)}^{\frac{m}{2}+1}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)\hfill \\ & & +\frac{\tau }{4}\frac{{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m\tau /2}{\left(1+\tau \right)}^{m/2+1}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)\hfill \\ & & -\left(\tau +1\right)\frac{{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m\tau /2}}\frac{1}{{\left(1+\tau \right)}^{m/2}}{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_j}\hfill \\ & & -\frac{{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m\tau /2}}\frac{1}{{\left(1+\tau \right)}^{m/2}}\frac{1}{2}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)\hfill \\ & & +\frac{{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m\tau /2}}\frac{1}{{\left(1+\tau \right)}^{m/2}}\frac{1}{2}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{{\partial }^2\mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i\partial {\theta }_j}}\right)\hfill \\ & & -\frac{{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m\tau /2}}\frac{1}{2}\frac{1}{{\left(1+\tau \right)}^{m/2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right).\hfill \end{array}$$

Based on the previous results, we have

$$\begin{array}{ccc}\hfill \frac{{\partial }^2}{\partial {\theta }_i\partial {\theta }_j}{H}_n^{\tau }\left(\mathit{\theta }\right)& =& \frac{\partial }{\partial {\theta }_j}{L}_1^{\tau }\left(\mathit{\theta }\right)+\frac{\partial }{\partial {\theta }_j}{L}_2^{\tau }\left(\mathit{\theta }\right)\hfill \\ & =& D_1+D_2+D_3+C_1+C_2+C_3\hfill \\ & =& D_1+D_2+D_3+C_1+L_1^{*}+L_2^{*}+L_3^{*}+L_4^{*}\hfill \\ & & +A_1^{*}+A_2^{*}+A_3^{*}+A_4^{*}+A_5^{*}\hfill \end{array}$$

and

$$\begin{array}{ccc}& & \frac{{\partial }^2}{\partial {\theta }_i\partial {\theta }_j}{H}_n^{\tau }\left(\mathit{\theta }\right)\underset{n⟶\infty }{\stackrel{\mathcal{P}}{⟶}}\frac{1}{2}\frac{{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m\tau /2}}\frac{1}{{\left(1+\tau \right)}^{m/2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)\hfill \\ & & -\frac{1}{2}\frac{{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m\tau /2}}\frac{1}{{\left(1+\tau \right)}^{m/2}}\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{{\partial }^2\mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j\partial {\theta }_i}}\right)\hfill \\ & & -\frac{\tau }{4}\frac{1}{{\left(1+\tau \right)}^{m/2}}\frac{{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m\tau /2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)\hfill \\ & & +\frac{\tau {\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m\tau /2}{\left(1+\tau \right)}^{m/2}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)\hfill \\ & & +\frac{\tau }{2}\frac{{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m\tau /2}{\left(1+\tau \right)}^{m/2+1}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)\hfill \\ & & +\frac{\tau }{4}\frac{{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m\tau /2}{\left(1+\tau \right)}^{m/2+1}}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\right)trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)\hfill \\ & & -\left(\tau +1\right)\frac{{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m\tau /2}}\frac{1}{{\left(1+\tau \right)}^{m/2}}{\left(\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_i}\right)}^T\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}\frac{\partial \mathit{\mu }\left(\mathit{\theta }\right)}{\partial {\theta }_j}\hfill \\ & & -\frac{{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m\tau /2}}\frac{1}{{\left(1+\tau \right)}^{m/2}}\frac{1}{2}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right)\hfill \\ & & +\frac{{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m\tau /2}}\frac{1}{{\left(1+\tau \right)}^{m/2}}\frac{1}{2}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{{\partial }^2\mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i\partial {\theta }_j}}\right)\hfill \\ & & -\frac{{\left|\mathsf{\Sigma }\left(\mathit{\theta }\right)\right|}^{-\frac{\tau }{2}}}{{\left(2\pi \right)}^{m\tau /2}}\frac{1}{{\left(1+\tau \right)}^{m/2}}\frac{1}{2}trace\left(\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_j}}\mathsf{\Sigma }{\left(\mathit{\theta }\right)}^{-1}{\displaystyle \frac{\partial \mathsf{\Sigma }\left(\mathit{\theta }\right)}{\partial {\theta }_i}}\right).\hfill \end{array}$$

After some algebra, we have

$$\frac{{\partial }^2}{\partial {\theta }_i\partial {\theta }_j}{H}_n^{\tau }\left(\mathit{\theta }\right)\underset{n⟶\infty }{\stackrel{\mathcal{P}}{⟶}}-\left(\tau +1\right)J_{\tau }^{ij}\left(\mathit{\theta }\right).$$