Adaptive Output Feedback Control for Constrained Switched Systems with Input Quantization

Abstract

This paper investigates adaptive output feedback control problem for switched uncertain nonlinear systems with input quantization, unmeasured system states and state constraints. Firstly, fuzzy logic systems are introduced to identify system uncertainties, then the fuzzy based observer is constructed to estimate unavailable states. Secondly, combing the backstepping technique and the barrier Lyapunov function method, an adaptive fuzzy output feedback control law is designed, which guarantees that all signals in the closed-loop system are bounded, the system output tracks the reference signal, and system states satisfy their corresponding constraint conditions. Finally, simulation results further show the good performances of the proposed control scheme.

1. Introduction

With the development of social technology and industry, more and more control systems show the complex and multimode characteristics. Switched systems as a kind of hybrid systems have been widely concerned. In recent years, researches on switched systems have made some achievements. For switched linear systems, there are more related results [1,2,3,4]. In [5], an event-triggered based $H_{\infty }$ control issue was investigated for a class of switched linear systems with bounded exogenous disturbances. In [6], the non-fragile finite-time extended dissipative control problem is studied for discrete-time switched linear systems under a switching law with average dwell-time. For switched nonlinear systems, the research results are relatively less [7,8,9]. For example, the multierror constraint control problem was first proposed under different coordinate transformations in [10], and was successfully solved by using dwell time method. In [11], an adaptive output feedback fault tolerant control problem was studied for switched nonstrict-feedback nonlinear systems based on the small-gain technique.

Similar to traditional control systems, it is often difficult to obtain the system states in the control process of switched systems. Then, it is necessary to design a corresponding state observer to eatimate the unmeasurable states [12,13,14,15,16]. However, the switching signal is the unique feature of switched systems compared to other systems. This also makes the design of controller and observer more difficult. As we know, the state observer of a switched system also contains the switching signal. Then, is the switching signal consistent with that of the original control system or not? Moreover, due to the existing of nonlinear structures, these directly affect the design of the controllers. In this paper, an observer design method in which the switching signal is consistent with that of the original control system is considered, which makes it easier to observe the unavailable states. Moreover, the unknown system dynamics are considered in this paper, then an adaptive fuzzy observer is designed. The fuzzy based approach is one of the artificial intelligence techniques widely used in various applications [17,18,19]. In [17], an innovative approach to reducing the mesh-induced error in CFD analysis of an impinging jet using fuzzy logic was proposed.

In addition, both the input quantification problem and the state constraint issue are also considered. These problems are common in the actual production process, so the research of this paper has a certain practical application value. At present, the research on these problems is almost focused on the nonswitched systems [20,21,22,23,24]. For example, in [21] the fault-tolerant attitude control of flexible spacecraft is investigated over digital communication channels, where a uniform quantizer is considered with respect to the sensor signals and controller indexes. An adaptive neural control method was proposed for a class of nonlinear time-varying delayed systems with time-varying full-state constraints in [22]. The related research results of switched systems are few and far between [25,26,27]. This is also one of the motivations of this paper.

Inspired by the above analysis, this paper focuses on switched nonlinear systems with the input quantification problem and the state constraint issue. The fuzzy based observer is constructed to estimate unmeasurable states. The barrier Lyapunov function method is used to ensure the system states satisfy the corresponding constraint conditions. An adaptive output feedback controller is designed that can offset the effect caused by the input quantification by using the backstepping technique. Finally, simulation results further show the good performances of the proposed control scheme.

Compared with the existing results of switched systems, the main contribution of this paper is that the adaptive output feedback control problem for switched systems is studied. As far as we know, this is the first time in this kind of system to ensure that the system states meet the constraint conditions, and to overcome the impact of quantized input at the same time. Combining the barrier Lyapunov function method with backstepping technology, the adaptive controller is designed, and these problems are successfully solved.

This paper is organized as follows. Section 2 shows the system description, the control objective, and the necessary assumption. In Section 3, an fuzzy based observer is designed to estimate the unavailable system states. Section 4 gives the design process of the adaptive controller by using barrier Lyapunov function method. Section 5 expresses the main result and analyzes the stability of the closed-loop system. A simulation example is employed to illustrate the effectiveness of the proposed control approach in Section 6. Finally, Section 7 provides the conclusions.

2. System Description

In this paper, the following switched uncertain nonlinear system is considered

$$\left\{\begin{array}{l}{\dot{x}}_1=x_2+f_{1,\sigma \left(t\right)}\left(x_1\right)+{\rho }_{1,\sigma \left(t\right)}\\ ⋮\\ {\dot{x}}_n=v_{\sigma \left(t\right)}+f_{n,\sigma \left(t\right)}\left(X\right)+{\rho }_{n,\sigma \left(t\right)}\\ y=x_1\end{array}\right.$$

(1)

where ${\overline{x}}_i={\left[x_1,x_2,\cdots ,x_i\right]}^T$, $i=1,\dots ,n-1$ and $X={\left[x_1,x_2,\cdots ,x_n\right]}^T$ are the system state vectors, $y\in R$ represents the system output. The function $\sigma \left(t\right):\left[0,\infty \right)\to \Gamma =\left\{1\right.\left.,2,\cdots ,\pi \right\}$ is the switching signal, which is assumed to be a piecewise continuous (from the right) function of time, and $\pi$ represents the number of subsystems. In addition, $\sigma \left(t\right)=r$ indicates that the $r$th subsystem is in working state. $v_r\in R$ stands for the system control input, which is also the output of the quantizer (the input quantization will be introduced later), $f_{i,r}\left(x\right),i=1,2,\cdots ,n$ is a smooth nonlinear function, which is unknown, ${\rho }_{i,r}\left(t\right)$ is the bounded disturbance, and satisfies $\left|{\rho }_{i,r}\left(t\right)\right|\le {\overline{\rho }}_{i,r}$ with ${\overline{\rho }}_{i,r}$ being a constant. It is worth noting that $x_i$ is unmeasurable, and only $x_1$ is available in this paper.

In addition, the input quantization is considered here, which is expressed as [28]

$$v_r(t)=\left\{\begin{array}{l}\left(1-{\delta }_r\right)q_{1,j}^r, if q_{1,j}^r\le u_r(t)\le q_{1,j+1}^r\\ 0, if 0\le u_r(t)\le q_{1,1}^r\\ -U_r(-u_r(t)), if u_r(t)<0\end{array}\right.$$

(2)

where $u_r(t)$ is the input for quantizer, ${\mathsf{\Xi }}_r=\frac{1-{\varsigma }_r}{1+{\varsigma }_r}$ and $q_{1,j}^r=a{\varsigma }_r^{1-j}>0$ with ${\varsigma }_r$ being the quantitative degree.

To facilitate the analysis, the input quantization (2) is rewritten as

$$v_r(t)=U_r(u_r(t))=q_1^r(t)u_r(t)+q_2^r(t)$$

(3)

where

$$q_1^r(t)=\left\{\begin{array}{l}\frac{U_r(u_r(t))}{u_r(t)}, |u_r(t)|\ge B_r\\ 1, |u_r(t)|<B_r\end{array}\right.$$

(4)

$$q_2^r(t)=\left\{\begin{array}{l}0, |u_r(t)|\ge B_r\\ U_r(u_r(t))-u_r(t), |u_r(t)|<B_r\end{array}\right.$$

(5)

with $B_r>0$ being a constant. Since the sign of the control input is invariant during quantization, it follows from (4) that $q_1^r(t)>0$. To simplify writing, let $\varpi =1/q_1^r(t)$, which is also positive.

Control Objectives: The control objective of this paper is to design an adaptive output feedback controller for the switched system (1) with input quantization (2) and state constraints under the arbitrarily switching law such that (1) all signals in the closed-loop system are bounded, (2) the tracking errors can converge to a small neighborhood of origin, (3) all system states do not violate their corresponding constraint conditions.

Assumption 1 [29].

Assumed that the tracking signal $y_d$ and its time derivatives up to the $n$th order are continuous and bounded.

3. Fuzzy Observer Design

A. Description of Fuzzy Logic Systems

The FLSs consisting of If-Then rules is introduced to solve the unknown function problem in the controlled system:

$R^q$: If $x_1$ is $F_1^q$ $\dots$ and $x_{n-1}$ is $F_{n-1}^q$ and $x_n$ is $F_n^q$, $y$ is $B^q\left(q=1,2\cdots \chi \right)$.

When $x={\left[x_1,\cdots x_n\right]}^T$ is the input and $y$ is the output, $F_i^q$ and $B^q$ are fuzzy sets in $R$, relevant to the fuzzy affiliation functions ${\mu }_{F_i^q}\left(x_i\right)$ and ${\mu }_{B^q}\left(y\right)$. $\chi$ is the fuzzy rule number. Then, the following formula be utilized to describe FLSs

$$y(x(t))=\frac{{\displaystyle {\sum }_{q=1}^{\chi }{\overline{y}}_q{\displaystyle {\prod }_{i=1}^q{\mu }_{F_i^q}(x_i)}}}{{\displaystyle {\sum }_{q=1}^{\chi }({\displaystyle {\prod }_{i=1}^n{\mu }_{F_i^q}(x_i)}})}$$

where ${\overline{y}}_q={\max }_{y\in R}{\mu }_{B^q}\left(y\right)$ refers to the maximum value of ${\mu }_{B^q}\left(y\right)$ on $R$.

Let

$${\phi }_q=\frac{{\displaystyle {\prod }_{i=1}^n{\mu }_{F_i^q}(x_i)}}{{\displaystyle {\sum }_{q=1}^{\chi }({\displaystyle {\prod }_{i=1}^n{\mu }_{F_i^q}(x_i)}})}$$

and denote $w={\left[{\overline{y}}_1,{\overline{y}}_2,\cdots ,{\overline{y}}_{\chi }\right]}^T={\left[w_1,w_2,\cdots ,w_{\chi }\right]}^T$ and ${\phi }^T(x)=[{\phi }_1(x),{\phi }_2(x),\cdots ,{\phi }_{\chi }(x)]$, then FLSs can be expressed as $y(x)=w^T\phi (x)$.

B. Fuzzy Observer Design

To solve the unavailable system state problem, this section introduces a fuzzy state observer. Firstly, rewrite the considered system (1) as follows

$$\dot{X}=AX+\xi y+{\displaystyle \sum _{i=1}^n{B}_i}\left[f_{i,\sigma \left(t\right)}\left(X_i\right)+{\rho }_{i,\sigma \left(t\right)}\left(t\right)\right]+B{v}_{\sigma \left(t\right)}$$

(6)

where $A=\left[\begin{array}{ccc}-{\xi }_1& & \\ ⋮& I_{n-1}& \\ -{\xi }_n& \cdots & 0\end{array}\right], \xi =\left[\begin{array}{c}{\xi }_1\\ ⋮\\ {\xi }_n\end{array}\right], B=\left[\begin{array}{c}0\\ 0\\ ⋮\\ 1\end{array}\right], B_i={\left[\underset{i}{\underbrace{0\cdots 1}}\cdots 0\right]}^T$

Select ${\xi }_i,i=1,\dots ,n$ such that $A^{T}P+PA=-Q$ holds, where $P$ and $Q$ are all positive matrice.

The following adaptive fuzzy observer is designed

$$\left\{\begin{array}{l}\dot{\widehat{X}}=A\widehat{X}+\xi y+{\displaystyle \sum _{i=1}^n{B}_i{\widehat{f}}_{i,\sigma \left(t\right)}}\left({\widehat{X}}_i|{\widehat{w}}_{i,\sigma \left(t\right)}^{}\right)+B{v}_{\sigma \left(t\right)}\\ \widehat{y}=C\widehat{X}\end{array}\right.$$

(7)

where $C=\left[1\cdots 0\cdots 0\right]$, $\widehat{X}={\left[{\widehat{x}}_1, {\widehat{x}}_2, {\widehat{x}}_3, \cdots , {\widehat{x}}_n\right]}^T$ is the estimation of $X$, and ${\widehat{X}}_i=\left[{\widehat{x}}_1\right., {\widehat{x}}_2, {\widehat{x}}_3,\left.\cdots , {\widehat{x}}_i\right]$. ${\widehat{w}}_{i,r}$ is the estimation of $w_{i,r}^{\ast }$ with $w_{i,r}^{\ast }$ being the optimal vector. Let ${\tilde{w}}_{i,r}^{}=w_{i,r}^{\ast }-{\widehat{w}}_{i,r}^{}$ be the estimated error.

Based on the universal approximation of fuzzy logic systems, the uncertain nonlinear system functions are approximated by the following form:

$$\left\{\begin{array}{l}{f}_{i,r}\left(X_i|{\widehat{w}}_{i,r}\right)={\widehat{w}}_{i,r}^T{\phi }_i\left(X_i\right)\\ {\widehat{f}}_{i,r}\left({\widehat{X}}_i|{\widehat{w}}_{i,r}\right)={\widehat{w}}_{i,r}^T{\phi }_i\left({\widehat{X}}_i\right)\end{array}\right.$$

(8)

Define the corresponding error as

$$\left\{\begin{array}{l}{\epsilon }_{i,r}=f_{i,r}\left(X_i\right)-{\widehat{f}}_{i,r}\left({\widehat{X}}_i|w_{i,r}^{\ast }\right)\\ {\delta }_{i,r}=f_{i,r}\left(X_i\right)-{\widehat{f}}_{i,r}\left({\widehat{X}}_i|{\widehat{w}}_{i,r}^{}\right)\end{array}\right.$$

(9)

where ${\delta }_{i,r}$ and ${\epsilon }_{i,r}, i=1,\dots , n$ are corresponding error variables, which are bounded. That is to say, there exist constants ${\overline{\delta }}_{i,r}$ and ${\overline{\epsilon }}_{i,r}$ such that ${\delta }_{i,r}\le {\overline{\delta }}_{i,r}$ and ${\epsilon }_{i,r}\le {\overline{\epsilon }}_{i,r}$.

Define the observation error as $e=X-\widehat{X}={\left[e_1, e_2, \cdots , e_n\right]}^T$.

Based on (1) and (8), the following results can be obtained

$$\begin{array}{l}\dot{e}=Ae+{\displaystyle \sum _{i=1}^n{B}_i}\left[f_{i,r}\left(X_i\right)-{\widehat{f}}_{i,r}\left({\widehat{X}}_i|{\widehat{w}}_{i,r}^{}\right)+{\rho }_{i,r}\right]\\ =Ae+{\delta }_r+D_r\end{array}$$

(10)

where ${\delta }_r={\left[{\delta }_{1,r}, {\delta }_{2,r}, \cdots , {\delta }_{n,r}\right]}^T$, $D_r={\left[{\rho }_{1,r}, {\rho }_{2,r}, \cdots , {\rho }_{n,r}\right]}^T$, and there are two constants ${\overline{\delta }}_r$ and ${\overline{D}}_r$ such that $‖D_r‖\le {\overline{D}}_r$ and $‖{\delta }_r‖\le {\overline{\delta }}_r$ hold.

4. Adaptive Fuzzy Controller

In this section, the backstepping technique and the barrier Lyapunov function method are used to construct the adaptive fuzzy controller. Firstly, the coordinate transformation is defined as

$$\left\{\begin{array}{l}{z}_1=x_1-y_d\\ z_2={\widehat{x}}_2-{\alpha }_1-{\dot{y}}_d\\ ⋮\\ z_n={\widehat{x}}_n-{\alpha }_{n-1}-y_d^{\left(n-1\right)}\end{array}\right.$$

(11)

where $y_d$ is the reference signal, $z_1, \dots , z_n$ denote the transformation errors, ${\alpha }_1, \dots , {\alpha }_{n-1}$ are virtual controllers, which are designed in later steps.

Step 1: According to (1), (8) and (12), the derivative of $z_1$ is

$${\dot{z}}_1=z_2+{\alpha }_1+e_2+w_{1,r}^{\ast T}{\phi }_1\left({\widehat{x}}_1\right)+{\epsilon }_{1,r}+{\rho }_{1,r}$$

(12)

To solve the state constraint problem, the barrier Lyapunov function $V_1$ is selected as follows

$$V_1=e^{T}Pe+\frac{1}{2}\log \frac{k_1^2\left(t\right)}{k_1^2\left(t\right)-z_1^2}+\frac{1}{2}{\zeta }_1^{-1}{\tilde{\mathsf{\Theta }}}_1^2$$

(13)

where $k_m^{}\left(t\right)$ is time-varying function, and $\left|z_m\right|<\left|k_m^{}\left(t\right)\right|, m=1,\cdots ,n$. ${\zeta }_1>0$ is a design parameter. ${\tilde{\mathsf{\Theta }}}_m={\mathsf{\Theta }}_m-{\widehat{\mathsf{\Theta }}}_m,m=1,\dots ,n$ represents the estimation error between ${\mathsf{\Theta }}_m$ and ${\widehat{\mathsf{\Theta }}}_m$, ${\widehat{\mathsf{\Theta }}}_m$ stands for the estimate of ${\mathsf{\Theta }}_m$ with ${\mathsf{\Theta }}_m=\max \left\{{‖w_{m,r}^{\ast }‖}^2\right.,r\left.\in \Gamma \right\}$.

The derivative of $V_1$ is calculated as

$$\begin{array}{l}{\dot{V}}_1={\dot{e}}^{T}Pe+e^{T}P\dot{e}+\frac{z_1}{k_1^2\left(t\right)-z_1^2}\left({\dot{z}}_1-\frac{{\dot{k}}_1\left(t\right)}{k_1\left(t\right)}{z}_1\right)-\frac{1}{{\zeta }_1}{\tilde{\mathsf{\Theta }}}_1{\dot{\widehat{\mathsf{\Theta }}}}_1\\ =-e^{T}Qe+2e^{T}P {\delta }_r+2e^{T}P{D}_r\\ -\frac{1}{{\zeta }_1}{\tilde{\mathsf{\Theta }}}_1{\dot{\widehat{\mathsf{\Theta }}}}_1-\frac{z_1}{k_1^2\left(t\right)-z_1^2}\left(z_2+{\alpha }_1+e_2\right.\\ \left.+w_{1,r}^{\ast T}{\phi }_1\left({\widehat{x}}_1\right)+{\epsilon }_{1,r}+{\rho }_{1,r}-\frac{{\dot{k}}_1\left(t\right)}{k_1\left(t\right)}{z}_1\right)\end{array}$$

(14)

Consider the following facts

$$2e^{T}P{\delta }_r+2e^{T}P{D}_r\le 2{‖e‖}^2+{‖P‖}^2{\overline{\delta }}^2{}_r+{‖P‖}^2{\overline{D}}^2{}_r$$

(15)

$$\frac{z_1}{k_1^2\left(t\right)-z_1^2}\left(e_2\right.+{\epsilon }_{1,r}+\left.{\rho }_{1,r}\right)\le \frac{3}{2}\frac{z_1^2}{{\left(k_1^2\left(t\right)-z_1^2\right)}^2}+\frac{1}{2}\left({\overline{\epsilon }}_{1,r}^2\right.+\left.{\overline{\rho }}_{1,r}^2+{‖e‖}^2\right)$$

(16)

$$\frac{z_1}{k_1^2\left(t\right)-z_1^2}{w}_{1,r}^{\ast T}{\phi }_1\left({\widehat{x}}_1\right)\le \frac{z_1^2{\mathsf{\Theta }}_1}{2a_{1,r}^2{\left(k_1^2\left(t\right)-z_1^2\right)}^2}+\frac{a_{1,r}^2}{2}$$

(17)

where $a_{1,r}>0$ is a design parameter. Then, according to (15)–(18) into (15), one has

$$\begin{array}{l}{\dot{V}}_1\le -e^{T}Qe+\frac{5}{2}{‖e‖}^2+{‖P‖}^2{\overline{\delta }}^2{}_r+{‖P‖}^2{\overline{D}}^2{}_r\\ +\frac{z_1}{k_1^2\left(t\right)-z_1^2}\left(z_2\right.+{\alpha }_1-\frac{{\dot{k}}_1\left(t\right)}{k_1\left(t\right)}{z}_1+\frac{3}{2}\frac{z_1^2}{{\left(k_1^2\left(t\right)-z_1^2\right)}^2}\\ \left.+\frac{z_1{\mathsf{\Theta }}_1}{2a_{1,r}^2\left(k_1^2\left(t\right)-z_1^2\right)}\right)-\frac{1}{{\zeta }_1}{\tilde{\mathsf{\Theta }}}_1{\dot{\widehat{\mathsf{\Theta }}}}_1+\frac{1}{2}\left({\overline{\epsilon }}_{1,r}^2\right.+\left.{\overline{\rho }}_{1,r}^2\right)+\frac{a_{1,r}^2}{2}\end{array}$$

(18)

Design the virtual control law as follows

$${\alpha }_1=-\left(K_1+{\overline{\kappa }}_1\right)z_1-\frac{3}{2}\frac{z_1}{k_1^2\left(t\right)-z_1^2}-\frac{z_1{\widehat{\mathsf{\Theta }}}_1}{2a_{1,\min }^2\left(k_1^2\left(t\right)-z_1^2\right)}$$

(19)

where $K_1>0$ is a design parameter, $a_{1,\min }=\min \left\{a_{1,r}, r\in \Gamma \right\}$, ${\overline{\kappa }}_1=\sqrt{m_1{}^2+p_1}$, $p_1>0$ and $m_1=\frac{{\dot{k}}_1\left(t\right)}{k_1\left(t\right)}$.

Select the following adaptive law

$${\dot{\widehat{\mathsf{\Theta }}}}_1=-{\mathsf{\Psi }}_1{\widehat{\mathsf{\Theta }}}_1+\frac{{\zeta }_1{z}_1^2}{2a_{1,\min }^2{\left(k_1^2\left( t\right)-z_1^2\right)}^2}$$

(20)

where ${\mathsf{\Psi }}_1>0$ is a parameter.

Further, it holds that

$$\frac{{\mathsf{\Psi }}_1}{{\zeta }_1}{\tilde{\mathsf{\Theta }}}_1{\widehat{\mathsf{\Theta }}}_1\le \frac{{\mathsf{\Psi }}_1}{2{\zeta }_1}\left(-{\tilde{\mathsf{\Theta }}}_1^2+{\mathsf{\Theta }}_1^2\right)$$

(21)

Substituting (20)–(22) into (19), one gets

$$\begin{array}{c}{\dot{V}}_1\le -\left[{\lambda }_{\min }\left(Q\right)-\frac{5}{2}\right]{‖e‖}^2+\frac{z_1{z}_2}{k_1^2\left(t\right)-z_1^2}\\ -K_1\frac{z_1^2}{{\left(k_1^2\left(t\right)-z_1^2\right)}^2}-\frac{{\mathsf{\Psi }}_1}{2{\zeta }_1}{\tilde{\mathsf{\Theta }}}_1^2+H_{1,r}\end{array}$$

(22)

where $H_{1,r}={‖P‖}^2{\overline{\delta }}^2{}_r+{‖P‖}^2{\overline{D}}^2{}_r+\frac{1}{2}({\overline{\epsilon }}_{1,r}^2+{\overline{\rho }}_{1,r}^2)+\frac{a_{1,r}^2}{2}+\frac{{\mathsf{\Psi }}_1}{2{\zeta }_1}{\mathsf{\Theta }}_1^2,r\in \Gamma$.

Step $i\left(2\le i\le n-1\right)$: Based on (1) and (12), one obtains

$${\dot{z}}_i=z_{i+1}+{\alpha }_i+{\xi }_i{e}_1+w_{i,r}^{\ast T}{\phi }_i\left({\overline{\widehat{X}}}_i\right)+{\epsilon }_{i,r}-{\delta }_{i,r}-{\dot{\alpha }}_{i-1}$$

(23)

where ${\overline{\widehat{X}}}_i={\left[{\widehat{x}}_1, {\widehat{x}}_2, {\widehat{x}}_3, \cdots , {\widehat{x}}_i\right]}^T$,

$\begin{array}{l}{\dot{\alpha }}_{i-1}={\displaystyle \sum _{m=1}^{i-1}\frac{\partial {\alpha }_{i-1}}{\partial {\widehat{x}}_m}}\left({\widehat{x}}_{m+1}+\right.{\xi }_m{e}_1+w_{m,r}^{\ast T}{\phi }_m\left({\overline{\widehat{X}}}_m\right)+{\epsilon }_{m,r}\\ -\left.{\delta }_{m,r}\right)+{\displaystyle \sum _{m=1}^{i-1}\frac{\partial {\alpha }_{i-1}}{\partial {\widehat{\mathsf{\Theta }}}_m}}{\dot{\widehat{\mathsf{\Theta }}}}_m+{\displaystyle \sum _{m=1}^{i-1}\frac{\partial {\alpha }_{i-1}}{\partial y_d^{\left(m-1\right)}}}{y}_d^{\left(m\right)}\\ +\frac{\partial {\alpha }_{i-1}}{\partial y}\left({\widehat{x}}_2\right.+e_2+w_{1,r}^{\ast T}{\phi }_1\left({\widehat{x}}_1\right)+{\epsilon }_{1,r}\left.+{\rho }_{1,r}\right)\end{array}.$

Select the barrier Lyapunov function $V_i$ as

$$V_i=V_{i-1}+\frac{1}{2}\log \frac{k_i^2\left(t\right)}{k_i^2\left(t\right)-z_i^2}+\frac{1}{2}{\zeta }_i^{-1}{\tilde{\mathsf{\Theta }}}_i^2$$

(24)

where ${\zeta }_i>0$ represents the design parameter.

Taking the time derivative of $V_i$, one has

$$\begin{array}{l}{\dot{V}}_1={\dot{V}}_{i-1}+\frac{z_i}{k_i^2\left(t\right)-z_i^2}\left({\dot{z}}_i-\frac{{\dot{k}}_i\left(t\right)}{k_i\left(t\right)}{z}_i\right)-\frac{1}{{\zeta }_i}{\tilde{\mathsf{\Theta }}}_i{\dot{\widehat{\mathsf{\Theta }}}}_i\\ ={\dot{V}}_{i-1}+\frac{z_i}{k_i^2\left(t\right)-z_i^2}\left(z_{i+1}+{\alpha }_i+{\xi }_i{e}_1+w_{i,r}^{\ast T}{\phi }_i\left({\overline{\widehat{X}}}_i\right)\right.\\ +{\epsilon }_{i,r}-{\delta }_{i,r}-{\dot{\alpha }}_{i-1} \left.-\frac{{\dot{k}}_i\left(t\right)}{k_i\left(t\right)}{z}_i\right)-\frac{1}{{\zeta }_i}{\tilde{\mathsf{\Theta }}}_i{\dot{\widehat{\mathsf{\Theta }}}}_i\\ ={\dot{V}}_{i-1}+\frac{z_i}{k_i^2\left(t\right)-z_i^2}\left(z_{i+1}+{\alpha }_i+{\xi }_i{e}_1+w_{i,r}^{\ast T}{\phi }_i\left({\overline{\widehat{X}}}_i\right)\right.\\ +{\epsilon }_{i,r}-{\delta }_{i,r} -\frac{\partial {\alpha }_{i-1}}{\partial y}\left({\widehat{x}}_2\right.+e_2+w_{1,r}^{\ast T}{\phi }_1\left({\widehat{x}}_1\right)+{\epsilon }_{1,r}\\ \left.+{\rho }_{1,r}\right)-{\displaystyle \sum _{m=1}^{i-1}\frac{\partial {\alpha }_{i-1}}{\partial {\widehat{x}}_m}}\left({\widehat{x}}_{m+1}\right.+{\xi }_m{e}_1+w_{m,r}^{\ast T}{\phi }_m\left({\overline{\widehat{X}}}_m\right)\\ \left.+{\epsilon }_{m,r}-{\delta }_{m,r}\right)-{\displaystyle \sum _{m=1}^{i-1}\frac{\partial {\alpha }_{i-1}}{\partial {\widehat{\mathsf{\Theta }}}_m}}{\dot{\widehat{\mathsf{\Theta }}}}_m-{\displaystyle \sum _{m=1}^{i-1}\frac{\partial {\alpha }_{i-1}}{\partial k_m\left(t\right)}}{\dot{k}}_m\left(t\right)\\ -{\displaystyle \sum _{m=1}^{i-1}\frac{\partial {\alpha }_{i-1}}{\partial y_d^{\left(m-1\right)}}}{y}_d^{\left(m\right)}\left.-\frac{{\dot{k}}_i\left(t\right)}{k_i\left(t\right)}{z}_i\right)-\frac{1}{{\zeta }_i}{\tilde{\mathsf{\Theta }}}_i{\dot{\widehat{\mathsf{\Theta }}}}_i\end{array}$$

(25)

Applying Young’s inequality, it derives that

$$\frac{z_i}{k_i^2\left(t\right)-z_i^2}{w}_{i,r}^{\ast T}{\phi }_i\left({\overline{\widehat{X}}}_i\right)\le \frac{z_i^2{\mathsf{\Theta }}_i}{2a_{i,r}^2{\left(k_i^2\left(t\right)-z_i^2\right)}^2}+\frac{a_{i,r}^2}{2}$$

(26)

where $a_{i,r}^{}>0$ is a design parameter.

$$-\frac{z_i}{k_i^2\left(t\right)-z_i^2}{\displaystyle \sum _{m=1}^{i-1}\frac{\partial {\alpha }_{i-1}}{\partial {\widehat{x}}_m}}{w}_{m,r}^{\ast T}{\phi }_m\left({\overline{\widehat{X}}}_m\right)\le \frac{z_i^2}{2{\left(k_i^2\left(t\right)-z_i^2\right)}^2}{\displaystyle \sum _{m=1}^{i-1}{\left(\frac{\partial {\alpha }_{i-1}}{\partial {\widehat{x}}_m}\right)}^2}+\frac{1}{2}{\displaystyle \sum _{m=1}^{i-1}{\mathsf{\Theta }}_m}$$

(27)

$$-\frac{z_i}{k_i^2\left(t\right)-z_i^2}{\displaystyle \sum _{m=1}^{i-1}\frac{\partial {\alpha }_{i-1}}{\partial {\widehat{x}}_m}}\left({\epsilon }_{m,r}-\left.{\delta }_{m,r}\right)\right.\le \frac{z_i^2}{{\left(k_i^2\left(t\right)-z_i^2\right)}^2}{\displaystyle \sum _{m=1}^{i-1}{\left(\frac{\partial {\alpha }_{i-1}}{\partial {\widehat{x}}_m}\right)}^2}\left.+\frac{1}{2}{\displaystyle \sum _{m=1}^{i-1}\left({\overline{\epsilon }}^2{}_{m,r}\right.}+{\overline{\delta }}^2{}_{m,r}\right)$$

(28)

$$-\frac{z_i}{k_i^2\left(t\right)-z_i^2}\frac{\partial {\alpha }_{i-1}}{\partial y}{w}_{1,r}^{\ast T}{\phi }_1\left({\widehat{x}}_1\right)\le \frac{z_i^2}{2{\left(k_i^2\left(t\right)-z_i^2\right)}^2}{\left(\frac{\partial {\alpha }_{i-1}}{\partial y}\right)}^2+\frac{1}{2}{\mathsf{\Theta }}_1$$

(29)

$$-\frac{z_i}{k_i^2\left(t\right)-z_i^2}\frac{\partial {\alpha }_{i-1}}{\partial y}\left(e_2\right.+{\epsilon }_{1,r}\left.+{\rho }_{1,r}\right)\le \frac{3}{2}\frac{z_i^2}{{\left(k_i^2\left(t\right)-z_i^2\right)}^2}{\left(\frac{\partial {\alpha }_{i-1}}{\partial y}\right)}^2+\frac{1}{2}{\left(‖e‖\right.}^2+{\overline{\epsilon }}^2{}_{1,r}\left.+{\overline{\rho }}^2{}_{1,r}\right)$$

(30)

$$\frac{z_i}{k_i^2\left(t\right)-z_i^2}\left({\epsilon }_{i,r}-{\delta }_{i,r}\right)\le \frac{z_i^2}{{\left(k_i^2\left(t\right)-z_i^2\right)}^2}+\frac{1}{2}\left({\overline{\epsilon }}^2{}_{i,r}\right.\left.+{\overline{\delta }}^2{}_{i,r}\right)$$

(31)

Combing (26)–(32), one gets

$$\begin{array}{l}{\dot{V}}_i={\dot{V}}_{i-1}+\frac{z_i}{k_i^2\left(t\right)-z_i^2}\left(z_{i+1}+{\alpha }_i+{\xi }_i{e}_1-\frac{{\dot{k}}_i\left(t\right)}{k_i\left(t\right)}{z}_i\right.\\ -{\displaystyle \sum _{m=1}^{i-1}\frac{\partial {\alpha }_{i-1}}{\partial {\widehat{\mathsf{\Theta }}}_m}}{\dot{\widehat{\mathsf{\Theta }}}}_m-{\displaystyle \sum _{m=1}^{i-1}\frac{\partial {\alpha }_{i-1}}{\partial {\widehat{x}}_m}}\left({\widehat{x}}_{m+1}+\right.\left.{\xi }_m{e}_1\right)-{\displaystyle \sum _{m=1}^{i-1}\frac{\partial {\alpha }_{i-1}}{\partial y_d^{\left(m-1\right)}}}{y}_d^{\left(m\right)}\\ -{\displaystyle \sum _{m=1}^{i-1}\frac{\partial {\alpha }_{i-1}}{\partial k_m\left(t\right)}}{\dot{k}}_{m-1}\left(t\right)-\frac{\partial {\alpha }_{i-1}}{\partial y}{\widehat{x}}_2+\frac{z_i^{}{\mathsf{\Theta }}_i}{2a_{i,r}^2{\left(k_i^2\left(t\right)-z_i^2\right)}^{}}\\ +\frac{3z_i^{}}{2{\left(k_i^2\left(t\right)-z_i^2\right)}^{}}{\displaystyle \sum _{m=1}^{i-1}{\left(\frac{\partial {\alpha }_{i-1}}{\partial {\widehat{x}}_m}\right)}^2+\frac{z_i}{k_i^2\left(t\right)-z_i^2}}\\ \left.+\frac{2z_i^{}}{{\left(k_i^2\left(t\right)-z_i^2\right)}^{}}{\left(\frac{\partial {\alpha }_{i-1}}{\partial y}\right)}^2\right)+\frac{1}{2}{\left(‖e‖\right.}^2+{\overline{\epsilon }}^2{}_{i,r}\left.+{\overline{\rho }}^2{}_{i,r}\right)\\ +\frac{1}{2}{\displaystyle \sum _{m=1}^{i-1}\left({\overline{\epsilon }}^2{}_{m,r}+{\overline{\delta }}^2{}_{m,r}\right)}+\frac{a_{i,r}^2}{2}+\frac{1}{2}{\mathsf{\Theta }}_1+\frac{1}{2}\left({\overline{\epsilon }}^2{}_{i,r}\right.\left.+{\overline{\delta }}^2{}_{i,r}\right)\\ +\frac{1}{2}{\displaystyle \sum _{m=1}^{i-1}{\mathsf{\Theta }}_m} -\frac{1}{{\zeta }_i}{\tilde{\mathsf{\Theta }}}_i{\dot{\widehat{\mathsf{\Theta }}}}_i\end{array}$$

(32)

For control purposes, the virtual controller is designed as

$$\begin{array}{l}{\alpha }_i=-\left(K_i+{\overline{\kappa }}_i\right)z_i-\frac{z_i}{k_i^2\left(t\right)-z_i^2}-\frac{z_i{\widehat{\mathsf{\Theta }}}_i}{2a_{i,\min }^2\left(k_i^2\left(t\right)-z_i^2\right)}\\ -\frac{k_i^2\left(t\right)-z_i^2}{k_{i-1}^2\left(t\right)-z_{i-1}^2}{z}_{i-1}^{}-R_{i-1}\end{array}$$

(33)

where $K_i>0$ is a design parameter, $a_{i,\min }=\min \left\{a_{i,r}, r\in \Gamma \right\}$, ${\overline{\kappa }}_i=\sqrt{m_i{}^2+p_i}$, $p_i>0$ and $m_i=\frac{{\dot{k}}_i\left(t\right)}{k_i\left(t\right)}$, $R_{i-1}=-{\displaystyle \sum _{m=1}^{i-1}\frac{\partial {\alpha }_{i-1}}{\partial {\widehat{x}}_m}}\left({\widehat{x}}_{m+1}+\right.\left.{\xi }_m{e}_1\right)-{\displaystyle \sum _{m=1}^{i-1}\frac{\partial {\alpha }_{i-1}}{\partial {\widehat{\mathsf{\Theta }}}_m}}{\dot{\widehat{\mathsf{\Theta }}}}_m-\frac{\partial {\alpha }_{i-1}}{\partial y}{\widehat{x}}_2-{\displaystyle \sum _{m=1}^{i-1}\frac{\partial {\alpha }_{i-1}}{\partial y_d^{\left(m-1\right)}}}{y}_d^{\left(m\right)}-{\displaystyle \sum _{m=1}^{i-1}\frac{\partial {\alpha }_{i-1}}{\partial k_m\left(t\right)}}$$\times {\dot{k}}_m{\left(t\right)}^2+2\left(\frac{\partial {\alpha }_{i-1}}{\partial y}\right)\frac{z_i}{k_i^2\left(t\right)-z_i^2}+\frac{3z_i^2}{2{\left(k_i^2\left(t\right)-z_i^2\right)}^2}{\displaystyle \sum _{m=1}^{i-1}{\left(\frac{\partial {\alpha }_{i-1}}{\partial {\widehat{x}}_m}\right)}^2}+{\xi }_i{e}_1$.

And the adaptive law is chosen as

$${\dot{\widehat{\mathsf{\Theta }}}}_i=-{\mathsf{\Psi }}_i{\widehat{\mathsf{\Theta }}}_i+\frac{{\zeta }_i{z}_i^2}{2a_{i,\min }^2{\left(k_i^2\left(t\right)-z_i^2\right)}^2}$$

(34)

where ${\mathsf{\Psi }}_i>0$ is a design parameter.

Consider that

$$\frac{{\mathsf{\Psi }}_i}{{\zeta }_i}{\tilde{\mathsf{\Theta }}}_i{\widehat{\mathsf{\Theta }}}_i\le \frac{{\mathsf{\Psi }}_i}{2{\zeta }_i}\left(-{\tilde{\mathsf{\Theta }}}_i^2+{\mathsf{\Theta }}_i^2\right)$$

(35)

and substituting (34)–(36) into (33), one gets

$$\begin{array}{c}{\dot{V}}_i\le -\left[{\lambda }_{\min }\left(Q\right)-2-\frac{1}{2}i\right]{‖e‖}^2+\frac{z_i{z}_{i+1}}{k_i^2\left(t\right)-z_i^2}\\ -{\displaystyle \sum _{m=1}^i{K}_m\frac{z_m^2}{k_m^2\left(t\right)-z_m^2}}-{\displaystyle \sum _{m=1}^i\frac{{\mathsf{\Psi }}_m}{2{\zeta }_m}{\tilde{\mathsf{\Theta }}}_m^2}+H_{i,r}\end{array}$$

(36)

where $H_{i,r}=H_{i-1,r}+\frac{{\mathsf{\Theta }}_1}{2}+\frac{1}{2}\left({\overline{\epsilon }}_{i,r}^2\right.+\left.{\overline{\rho }}_{i,r}^2+{\displaystyle \sum _{m=1}^i\left({\overline{\epsilon }}^2{}_{m,r}+{\overline{\delta }}^2{}_{m,r}\right)}\right) +a_{i,r}^2+\left.{\displaystyle \sum _{m=1}^{i-1}{\mathsf{\Theta }}_m}\right)+\frac{{\mathsf{\Psi }}_i}{2{\zeta }_i}{\mathsf{\Theta }}_i^2, r\in \Gamma$.

Step $n$: Based on (1), (3) and (8), one gets

$${\dot{z}}_n=q_1^r(t)u_r(t)+q_2^r(t)+{\xi }_n{e}_1+w_{n,r}^{\ast T}{\phi }_n\left({\overline{\widehat{X}}}_n\right)+{\epsilon }_{n,r}-{\delta }_{n,r}-{\dot{\alpha }}_{n-1}$$

(37)

where ${\overline{\widehat{X}}}_n={\left[{\widehat{x}}_1, {\widehat{x}}_2, {\widehat{x}}_3, \cdots , {\widehat{x}}_n\right]}^T$, ${\dot{\alpha }}_{n-1}={\displaystyle \sum _{m=1}^{n-1}\frac{\partial {\alpha }_{n-1}}{\partial {\widehat{x}}_m}}\left({\widehat{x}}_{m+1}+\right.{\xi }_m{e}_1+w_{m,r}^{\ast T}{\phi }_m\left({\overline{\widehat{X}}}_m\right)+{\epsilon }_{m,r}-\left.{\delta }_{m,r}\right)$$+{\displaystyle \sum _{m=1}^{n-1}\frac{\partial {\alpha }_{i-1}}{\partial y_d^{\left(m-1\right)}}}{y}_d^{\left(m\right)}+{\displaystyle \sum _{m=1}^{n-1}\frac{\partial {\alpha }_{i-1}}{\partial {\widehat{\mathsf{\Theta }}}_m}}{\dot{\widehat{\mathsf{\Theta }}}}_m+\frac{\partial {\alpha }_{n-1}}{\partial y}\left({\widehat{x}}_2\right.+e_2+w_{1,r}^{\ast T}{\phi }_1\left({\widehat{x}}_1\right)+{\epsilon }_{1,r}\left.+{\rho }_{1,r}\right)+{\displaystyle \sum _{m=1}^{n-1}\frac{\partial {\alpha }_{n-1}}{\partial k_m\left(t\right)}}{\dot{k}}_m\left(t\right)$.

Choose the following barrier Lyapunov function

$$V_n=V_{n-1}+\frac{1}{2}\log \frac{k_n^2\left(t\right)}{k_n^2\left(t\right)-z_n^2}+\frac{1}{2}{\zeta }_n^{-1}{\tilde{\mathsf{\Theta }}}_n^2$$

(38)

where ${\zeta }_n>0$ indicates a design parameter.

Differentiating $V_n$, one obtains

$$\begin{array}{l}{\dot{V}}_n={\dot{V}}_{n-1}+\frac{z_n}{k_n^2\left(t\right)-z_n^2}\left({\dot{z}}_n-\frac{{\dot{k}}_n\left(t\right)}{k_n\left(t\right)}{z}_n\right)-\frac{1}{{\zeta }_n}{\tilde{\mathsf{\Theta }}}_n{\dot{\widehat{\mathsf{\Theta }}}}_n\\ ={\dot{V}}_{n-1}+\frac{z_n}{k_n^2\left(t\right)-z_n^2}\left(q_1^r(t)u_r(t)+q_2^r(t)+{\xi }_n{e}_1\right.\\ +w_{n,r}^{\ast T}{\phi }_n\left({\overline{\widehat{X}}}_n\right)+{\epsilon }_{n,r}\left.-{\delta }_{n,r}-{\dot{\alpha }}_{n-1}-\frac{{\dot{k}}_n\left(t\right)}{k_n\left(t\right)}{z}_n\right)-\frac{1}{{\zeta }_n}{\tilde{\mathsf{\Theta }}}_n{\dot{\widehat{\mathsf{\Theta }}}}_n\\ ={\dot{V}}_{n-1}+\frac{z_n}{k_n^2\left(t\right)-z_n^2}\left(q_1^r(t)u_r(t)+q_2^r(t)+{\xi }_n{e}_1\right.+w_{n,r}^{\ast T}{\phi }_n\left({\overline{\widehat{X}}}_n\right)\\ +{\epsilon }_{n,r}-{\delta }_{n,r}-{\displaystyle \sum _{m=1}^{n-1}\frac{\partial {\alpha }_{n-1}}{\partial {\widehat{x}}_m}}\left({\widehat{x}}_{m+1}\right.+{\xi }_m{e}_1+w_{m,r}^{\ast T}{\phi }_m\left({\overline{\widehat{X}}}_m\right)+{\epsilon }_{m,r}\\ -\left.{\delta }_{m,r}\right)-{\displaystyle \sum _{m=1}^{n-1}\frac{\partial {\alpha }_{i-1}}{\partial {\widehat{\mathsf{\Theta }}}_m}}{\dot{\widehat{\mathsf{\Theta }}}}_m-\frac{\partial {\alpha }_{n-1}}{\partial y}\left({\widehat{x}}_2\right.+e_2+w_{1,r}^{\ast T}{\phi }_1\left({\widehat{x}}_1\right)+{\epsilon }_{1,r}\\ \left.+{\rho }_{1,r}\right)-{\displaystyle \sum _{m=1}^{n-1}\frac{\partial {\alpha }_{n-1}}{\partial y_d^{\left(m-1\right)}}}{y}_d^{\left(m\right)}\left.-{\displaystyle \sum _{m=1}^{n-1}\frac{\partial {\alpha }_{i-1}}{\partial k_m\left(t\right)}}{\dot{k}}_m\left(t\right)-\frac{{\dot{k}}_n\left(t\right)}{k_n\left(t\right)}{z}_n\right)-\frac{1}{{\zeta }_n}{\tilde{\mathsf{\Theta }}}_n{\dot{\widehat{\mathsf{\Theta }}}}_n\end{array}$$

(39)

Consider the following inequalities

$$\frac{z_n}{k_n^2\left(t\right)-z_n^2}{w}_{n,r}^{\ast T}{\phi }_n\left({\overline{\widehat{X}}}_n\right)\le \frac{z_n^2{\mathsf{\Theta }}_n}{2a_{n,r}^2{\left(k_n^2\left(t\right)-z_n^2\right)}^2}+\frac{a_{n,r}^2}{2}$$

(40)

where $a_{n,r}^{}>0$ is a design parameter.

$$-\frac{z_n}{k_n^2\left(t\right)-z_n^2}{\displaystyle \sum _{m=1}^{n-1}\frac{\partial {\alpha }_{n-1}}{\partial {\widehat{x}}_m}}{w}_{m,r}^{\ast T}{\phi }_m\left({\overline{\widehat{X}}}_m\right)\le \frac{1}{2}{\displaystyle \sum _{m=1}^{n-1}{\mathsf{\Theta }}_m}+\frac{z_n^2}{2{\left(k_n^2\left(t\right)-z_n^2\right)}^2}{\displaystyle \sum _{m=1}^{n-1}{\left(\frac{\partial {\alpha }_{n-1}}{\partial {\widehat{x}}_m}\right)}^2}$$

(41)

$$-\frac{z_n}{k_n^2\left(t\right)-z_n^2}{\displaystyle \sum _{m=1}^{n-1}\frac{\partial {\alpha }_{n-1}}{\partial {\widehat{x}}_m}}\left({\epsilon }_{m,r}\right.-\left.{\delta }_{m,r}\right)\le \frac{z_n^2}{{\left(k_n^2\left(t\right)-z_n^2\right)}^2}{\displaystyle \sum _{m=1}^{n-1}{\left(\frac{\partial {\alpha }_{n-1}}{\partial {\widehat{x}}_m}\right)}^2}+\frac{1}{2}{\displaystyle \sum _{m=1}^{n-1}\left({\overline{\epsilon }}^2{}_{m,r}+{\overline{\delta }}^2{}_{m,r}\right)}$$

(42)

$$-\frac{z_n}{k_n^2\left(t\right)-z_n^2}\frac{\partial {\alpha }_{n-1}}{\partial y}{w}_{1,r}^{\ast T}{\phi }_1\left({\widehat{x}}_1\right)\le \frac{z_n^2}{2{\left(k_n^2\left(t\right)-z_n^2\right)}^2}{\left(\frac{\partial {\alpha }_{n-1}}{\partial y}\right)}^2+\frac{1}{2}{\mathsf{\Theta }}_n$$

(43)

$$-\frac{z_n}{k_n^2\left(t\right)-z_n^2}\frac{\partial {\alpha }_{n-1}}{\partial y}\left(e_2\right.+{\epsilon }_{1,r}\left.+{\rho }_{1,r}\right)\le \frac{3}{2}\frac{z_n^2}{{\left(k_n^2\left(t\right)-z_n^2\right)}^2}{\left(\frac{\partial {\alpha }_{n-1}}{\partial y}\right)}^2+\frac{1}{2}{\left(‖e‖\right.}^2+{\overline{\epsilon }}^2{}_{1,r}\left.+{\overline{\rho }}^2{}_{1,r}\right)$$

(44)

$$\begin{array}{l}\frac{z_n}{k_n^2\left(t\right)-z_n^2}\left({\epsilon }_{n,r}-{\delta }_{n,r}\right)\le \frac{z_n^2}{{\left(k_n^2\left(t\right)-z_n^2\right)}^2}+\frac{1}{2}\left({\overline{\epsilon }}^2{}_{n,r}\right.\left.+{\overline{\delta }}^2{}_{n,r}\right)\\ \end{array}$$

(45)

According (40), (41)–(46), one has

$$\begin{array}{l}{\dot{V}}_n={\dot{V}}_{n-1}+\frac{z_n}{k_n^2\left(t\right)-z_n^2}\left(-{\displaystyle \sum _{m=1}^{n-1}\frac{\partial {\alpha }_{n-1}}{\partial {\widehat{x}}_m}}\left({\widehat{x}}_{m+1}+\right.\left.{\xi }_m{e}_1\right)+q_1^r(t)u_r(t)+q_2^r(t)\right.\\ +{\xi }_n{e}_1-{\displaystyle \sum _{m=1}^{n-1}\frac{\partial {\alpha }_{n-1}}{\partial {\widehat{\mathsf{\Theta }}}_m}}{\dot{\widehat{\mathsf{\Theta }}}}_m-{\displaystyle \sum _{m=1}^{i-1}\frac{\partial {\alpha }_{n-1}}{\partial y_d^{\left(m-1\right)}}}{y}_d^{\left(m\right)}-\frac{\partial {\alpha }_{n-1}}{\partial y}{\widehat{x}}_2+\frac{3z_n^{}}{2{\left(k_n^2\left(t\right)-z_n^2\right)}^{}}\\ \times {\displaystyle \sum _{m=1}^{n-1}{\left(\frac{\partial {\alpha }_{n-1}}{\partial {\widehat{x}}_m}\right)}^2}+\frac{2z_n^{}}{k_n^2\left(t\right)-z_n^2}{\left(\frac{\partial {\alpha }_{n-1}}{\partial y}\right)}^2-{\displaystyle \sum _{m=1}^{n-1}\frac{\partial {\alpha }_{n-1}}{\partial k_m\left(t\right)}}{\dot{k}}_m\left(t\right)-\frac{{\dot{k}}_n\left(t\right)}{k_n\left(t\right)}{z}_n\\ +\frac{z_n{\mathsf{\Theta }}_n}{2a_{n,r}^2\left(k_n^2\left(t\right)-z_n^2\right)}+\left.\frac{z_n}{k_n^2\left(t\right)-z_n^2}\right)+\frac{1}{2}{\left(‖e‖\right.}^2+{\overline{\epsilon }}^2{}_{1,r}\left.+{\overline{\rho }}^2{}_{1,r}\right)+\frac{a_{n,r}^2}{2}\\ +\frac{1}{2}{\mathsf{\Theta }}_1+\frac{1}{2}\left({\overline{\epsilon }}^2{}_{n,r}\right.\left.+{\overline{\delta }}^2{}_{n,r}\right) +\frac{1}{2}{\displaystyle \sum _{m=1}^{n-1}{\mathsf{\Theta }}_m}-\frac{1}{{\zeta }_n}{\tilde{\mathsf{\Theta }}}_n{\dot{\tilde{\mathsf{\Theta }}}}_n+\frac{1}{2}{\displaystyle \sum _{m=1}^{n-1}\left({\overline{\epsilon }}^2{}_{m,r}+{\overline{\delta }}^2{}_{m,r}\right)}\end{array}$$

(46)

Design the adaptive output feedback control law

$$\begin{array}{l}{u}_r=[-\left(K_n+{\overline{\kappa }}_n\right)z_n-R_{n-1}-\frac{z_n{\widehat{\mathsf{\Theta }}}_n}{2a_{n,\min }^2\left(k_n^2\left(t\right)-z_n^2\right)}\\ -\frac{z_n}{k_n^2\left(t\right)-z_n^2}-q_2^r\left(t\right)-\frac{k_n^2\left(t\right)-z_n^2}{k_{n-1}^2\left(t\right)-z_{n-1}^2}{z}_{n-1}^{}]\varpi \end{array}$$

(47)

where $K_n>0$ is design parameter, $a_{n,\min }=\min \left\{a_{n,r}, r\in \Gamma \right\}$, ${\overline{\kappa }}_n=\sqrt{m_n{}^2+p_n}$, $p_n>0$ and $m_n=\frac{{\dot{k}}_n\left(t\right)}{k_n\left(t\right)}$, $R_{n-1}=-{\displaystyle \sum _{m=1}^{n-1}\frac{\partial {\alpha }_{n-1}}{\partial {\widehat{x}}_m}}\left({\widehat{x}}_{m+1}+\right.\left.{\xi }_m{e}_1\right)-{\displaystyle \sum _{m=1}^{n-1}\frac{\partial {\alpha }_{n-1}}{\partial {\widehat{\mathsf{\Theta }}}_m}}{\dot{\widehat{\mathsf{\Theta }}}}_m-\frac{\partial {\alpha }_{n-1}}{\partial y}{\widehat{x}}_2-{\displaystyle \sum _{m=1}^{i-1}\frac{\partial {\alpha }_{i-1}}{\partial y_d^{\left(m-1\right)}}}{y}_d^{\left(m\right)}-{\displaystyle \sum _{m=1}^{n-1}\frac{\partial {\alpha }_{n-1}}{\partial k_m\left(t\right)}}$$\times {\dot{k}}_m\left(t\right)+{\xi }_n{e}_1+\frac{3z_n}{2\left(k_n^2\left(t\right)-z_n^2\right)}{\displaystyle \sum _{m=1}^{n-1}{\left(\frac{\partial {\alpha }_{n-1}}{\partial {\widehat{x}}_m}\right)}^2}+\frac{z_n}{k_n^2\left(t\right)-z_n^2}{\left(\frac{\partial {\alpha }_{n-1}}{\partial {\widehat{x}}_m}\right)}^2+\frac{2z_n}{k_n^2\left(t\right)-z_n^2}{\left(\frac{\partial {\alpha }_{n-1}}{\partial y}\right)}^2$.

Design the adaptive law

$${\dot{\widehat{\mathsf{\Theta }}}}_n=-{\mathsf{\Psi }}_n{\widehat{\mathsf{\Theta }}}_n+\frac{{\zeta }_n{z}_n^2}{2a_{n,\min }^2{\left(k_n^2\left(t\right)-z_n^2\right)}^2}$$

(48)

where ${\mathsf{\Psi }}_n>0$ is a design parameter.

The following inequalities always hold

$$\frac{{\mathsf{\Psi }}_n}{{\zeta }_n}{\tilde{\mathsf{\Theta }}}_n{\widehat{\mathsf{\Theta }}}_n\le \frac{{\mathsf{\Psi }}_n}{2{\zeta }_n}\left(-{\tilde{\mathsf{\Theta }}}_n^2+{\mathsf{\Theta }}_n^2\right)$$

(49)

According to (47)–(50), one obtains

$${\dot{V}}_n\le -\left[{\lambda }_{\min }\left(Q\right)-2-\frac{1}{2}n\right]{‖e‖}^2-{\displaystyle \sum _{m=1}^n\frac{{\mathsf{\Psi }}_m}{2{\zeta }_m}{\tilde{\mathsf{\Theta }}}_m^2}-{\displaystyle \sum _{m=1}^n{K}_m\frac{z_m^2}{k_m^2\left(t\right)-z_m^2}}+H_{n,r}$$

(50)

where $H_{n,r}=H_{n-1,r}+\frac{{\mathsf{\Theta }}_1}{2}+\frac{1}{2}\left({\overline{\epsilon }}_{1,r}^2\right.+\left.{\overline{\rho }}_{1,r}^2+{\displaystyle \sum _{m=1}^n\left({\overline{\epsilon }}^2{}_{m,r}+{\overline{\delta }}^2{}_{m,r}\right)} \right) +a_{n,r}^2+\left.{\displaystyle \sum _{m=1}^{i-1}{\mathsf{\Theta }}_m}\right)+\frac{{\mathsf{\Psi }}_n}{2{\zeta }_n}{\mathsf{\Theta }}_n^2, r\in \Gamma$.

5. Stability Analysis

To facilitate the description, the following notation is defined

$$\mathsf{\Lambda }=\min \left\{\mu , K_m, {\mathsf{\Psi }}_m:m=1, \dots , n\right\}$$

(51)

$$H=\underset{r\in \Gamma }{\max }\left\{H_{n,r}\right\}$$

(52)

where $\mu ={\lambda }_{\min }\left(Q-2-\frac{1}{2}n\right)/{\lambda }_{\min }\left(P\right)$.

Theorem 1.

Consider the switched uncertain nonlinear system (1) with input quantization (2), unmeasurable states and state contraints, under Assumption 1, the adaptive output feedback controller in (48) is constructed by using the barrier Lyapunov function method and the backstepping technique, which can guarantee that all signals in the closed-loop system are bounded, the tracking error converges to a small neighborhood of origin, and none of the states in the system conflict with their corresponding constraints.

Proof. 

Select the barrier Lyapunov function as follows

$$V=V_n=e^{T}Pe+\frac{1}{2}{\displaystyle \sum _{i=1}^n\log \frac{k_i^2\left(t\right)}{k_i^2\left(t\right)-z_i^2}}+\frac{1}{2}{\displaystyle \sum _{i=1}^n{\zeta }_i^{-1}{\tilde{\mathsf{\Theta }}}_i^2}$$

(53)

According to the above analysis and the definitions in (52) and (53), one has

$$\dot{V}\le -\mathsf{\Lambda }V+H$$

(54)

Integrating (55) over the interval $\left[0,t\right]$, one obtains

$$V\left(t\right)\le \left(V\left(0\right)-\frac{H}{\mathsf{\Lambda }}\right)e^{-\mathsf{\Lambda }t}+\frac{H}{\mathsf{\Lambda }}$$

(55)

Based on (54) and (56), one deduces that

$$\left|z_i\right|\le \sqrt{k_i^2\left(t\right)-\frac{k_i^2\left(t\right)}{e^{2\left(V\left(0\right)-\frac{H}{\mathsf{\Lambda }}\right)e^{-\mathsf{\Lambda }t}+\frac{H}{\mathsf{\Lambda }}}}}, i=1, \dots , n$$

(56)

Similarly, it can be derived that

$$‖e‖\le \sqrt{\frac{\left(V\left(0\right)-\frac{H}{\mathsf{\Lambda }}\right)e^{-\mathsf{\Lambda }t}+\frac{H}{\mathsf{\Lambda }}}{{\lambda }_{\min }\left(P\right)}},i=1,\dots ,n$$

(57)

From (54) and (56), one easily knows that transformation errors $z_i$, observer errors $e_i$ and estimation errors ${\tilde{\mathsf{\Theta }}}_i(i=1,\cdots n)$ are all bounded for the bounded initial values. The tracking error $z_1$ is bounded, this implies that the system output tracks the reference signal. Due to the boundedness of ${\mathsf{\Theta }}_i$ and ${\tilde{\mathsf{\Theta }}}_i(i=1,\cdots n)$, then ${\widehat{\mathsf{\Theta }}}_i(i=1,\cdots n)$ is also bounded. According to the definitions of $z_i(i=1,\cdots ,n)$, $e_i(i=1,\cdots ,n)$, ${\alpha }_i(i=1,\cdots ,n-1)$, $u_r$, and Assumption 1, it can be seen that $x_i(i=1,\cdots ,n)$, ${\widehat{x}}_i(i=1,\cdots ,n)$, ${\alpha }_i(i=1,\cdots ,n-1)$, and $u_r$ are all bounded. Thus, all signals in the closed-loop system are all bounded. Moreover, in the proposed control method, the barrier Lyapunov function is employed such that the system states satisfy the corresponding states. □

Remark 1.

It is worth noting that when $\left|u_r\left(t\right)\right|<B_r$ and $q_1^r\left(t\right)=1$ are bounded, $U_r\left(u_r\left(t\right)\right)$ is also bounded. This can be seen from (4). Then, by observing (5), one can easily know that  $q_2^r\left(t\right)$ is bounded, namely $\left|q_2^r\left(t\right)\right|\le Y_r$, where $Y_r$ is a positive constant. Therefore, in the future work, the boundedness case of $q_2^r\left(t\right)$ can be considered.

Remark 2.

In this paper, there are many design parameters in the control, which may affect the system performance. In order to ensure that the system has a good performance, the selection of these design parameters are important. $P$ and $Q$ are positive matrices which should be satisfy the Riccati-like equation. From (58), it is easy to know that the value of the tracking error is associated with $K_m$, ${\mathsf{\Psi }}_m$ and $a_{m,\min }(m=1,2,\cdots n)$. For lager $K_m$, ${\mathsf{\Psi }}_m$ and smaller $a_{m,\min }$, the tracking error are smaller. At the same time the other signals of the system are smaller. For the other parameters, it is enough to choose them satisfy their corresponding conditions, such as positive.

Remark 3.

Compared with the existing results in [30,31,32], in which the mode-dependent Lyapunov function is chosen, a common Lyapunov function which is mode-independent is selected in this paper. This because of that the arbitrary switching law is employed here. Actually, in engineering problems, switching signals are often unknown or unable to be determined in advance, so the stability of switched systems under arbitrary switching signals is of special significance. Thus, in this paper, the arbitrary switching law is selected. If a switched system can be stabilized under the arbitrary signal, then the subsequent research (such as robust control, etc.) does not need to pay attention to the impact of switching signals on the system stability.

6. Simulation Example

In this section, a simulation experiment is used to show the effectiveness of the proposed adaptive fuzzy output feedback control approach. Consider the following uncertain nonlinear switched system

$$\left\{\begin{array}{l}{\dot{x}}_1=x_2+f_{1,\sigma \left(t\right)}+{\rho }_{1,\sigma \left(t\right)}\\ {\dot{x}}_2=v_{\sigma \left(t\right)}+f_{2,\sigma \left(t\right)}+{\rho }_{2,\sigma \left(t\right)}\\ y=x_1\end{array}\right.$$

(58)

where $\sigma \left(t\right)\in \left\{1,2\right\}$ stands for the switching signal. When $\sigma \left(t\right)=1$, the external disturbance are chosen as ${\rho }_{11}=0.02\cos \left(t\right)$, and ${\rho }_{21}=0.015\sin \left(t\right)$, the nonlinear functionss are $f_{11}=0.012x_1{e}^{-0.11x_1}$ and $f_{21}=0.11x_2+x_1^3$. When $\sigma \left(t\right)=2$, the external disturbances are ${\rho }_{12}=0.01\sin \left(t\right)$ and ${\rho }_{22}=0.02\sin \left(0.2t\right)$, and the nonlinear functions are chosen as $f_{12}=0.021x_1{e}^{-x_1^2}$ and $f_{22}=0.016\sin \left(x_2\right)e^{-x_1}$.

Moeover, the input quantization is selected as

$$v_r(t)=\left\{\begin{array}{l}\left(1-{\delta }_r\right)q_{1,j}^r, if q_{1,j}^r\le u_r(t)\le q_{1,j+1}^r\\ 0, if 0\le u_r(t)\le q_{1,1}^r\\ -U_r(-u_r(t)), if u_r(t)<0\end{array}\right.$$

where $r=1,2$. In addition, to solve the problem of unmeasurable states, the following fuzzy-based observer is designed

$$\left\{\begin{array}{l}{\dot{\widehat{x}}}_1={\widehat{x}}_2+{\widehat{w}}_{1,\sigma \left(t\right)}^T{\phi }_1(X_1)+{\xi }_1(x_1-{\widehat{x}}_1)\\ {\dot{\widehat{x}}}_2=v_{\sigma \left(t\right)}+{\widehat{w}}_{2,\sigma \left(t\right)}^T{\phi }_2(X_2)+{\xi }_2(x_1-{\widehat{x}}_1)\\ \widehat{y}={\widehat{x}}_1\end{array}\right.$$

and the adaptive virtual controller and the adaptive quantization controller are chosen as

$${\alpha }_1=-\left(K_1+{\overline{\kappa }}_1\right)z_1-\frac{3}{2}\frac{z_1}{k_1^2\left(t\right)-z_1^2}-\frac{z_1{\widehat{\mathsf{\Theta }}}_1}{2a_{1,\min }^2\left(k_1^2\left(t\right)-z_1^2\right)}$$

$$\begin{array}{l}{u}_r=[-\left(K_2+{\overline{\kappa }}_2\right)z_2-R_1-\frac{z_2{\widehat{\mathsf{\Theta }}}_2}{2a_{2,\min }^2\left(k_2^2\left(t\right)-z_2^2\right)}\\ -\frac{z_2}{k_2^2\left(t\right)-z_2^2}-q_2^r\left(t\right)-\frac{k_2^2\left(t\right)-z_2^2}{k_1^2\left(t\right)-z_1^2}{z}_1^{}]\varpi \end{array}$$

$${\dot{\widehat{\mathsf{\Theta }}}}_1=-{\mathsf{\Psi }}_1{\widehat{\mathsf{\Theta }}}_1+\frac{{\zeta }_1{z}_1^2}{2a_{1,\min }^2{\left(k_1^2\left(t\right)-z_1^2\right)}^2}$$

$${\dot{\widehat{\mathsf{\Theta }}}}_2=-{\mathsf{\Psi }}_2{\widehat{\mathsf{\Theta }}}_2+\frac{{\zeta }_2{z}_2^2}{2a_{2,\min }^2{\left(k_2^2\left(t\right)-z_2^2\right)}^2}$$

In this simulation, the reference signal is selected as $y_d=0.5\sin \left(2t\right)$, the associated initial value is set as $x_1\left(0\right)=0.01$, $x_2\left(0\right)=0.1$, ${\widehat{x}}_1\left(0\right)=0.02$, ${\widehat{x}}_2\left(0\right)=0.2$, ${\widehat{\mathsf{\Theta }}}_1\left(0\right)=0.01$, ${\widehat{\mathsf{\Theta }}}_2\left(0\right)=0.02$, $k_1\left(t\right)=0.8+0.1\sin \left(0.5t\right)$, $k_2\left(t\right)=2+0.1\sin \left(2t\right)$. The relevant design parameters are chosen as $K_1=20,K_2=50,{\xi }_1=15,{\xi }_2=25,{\mathsf{\Psi }}_1=1,{\mathsf{\Psi }}_2=0.5,{\zeta }_1=0.01,{\zeta }_2=0.02$, $a_{1,\min }=0.2,a_{2,\min }=0.5,p_1=10,p_2=20$.

Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 show the simulation results. Figure 1 gives the switching signal. Figure 2 depicts the trajectories of the system output, its constraint bounds and the tracking signal. From which, one sees that the reference signal can be followed well, and the system output successfully satisfies its constraint condition. Figure 3 describes the trajectories of state $x_2$ and its constraint condition. We can find that $x_2$ is limited within prespecified range. Figure 4 expresses the curves of the state $x_1$ and ${\widehat{x}}_1$, and their estimated error $e_1$, respectively. Figure 5 shows the curves of the state $x_2$ and ${\widehat{x}}_2$, and their estimated error $e_2$, respectively. From Figure 4 and Figure 5, we can conclude that the system state $x_1$ and $x_2$ are well observed. Figure 6 gives the curves of the adaptive laws ${\widehat{\mathsf{\Theta }}}_1$, ${\widehat{\mathsf{\Theta }}}_2$, and the input quantization $u$ is presented in Figure 7. Figure 6 and Figure 7 immplies that ${\widehat{\mathsf{\Theta }}}_1$, ${\widehat{\mathsf{\Theta }}}_2$ and $u$ are all bounded. From the simulation results above, it can be concluded that by using the proposed control approach, the control objectives are achieved, thus it is effective.

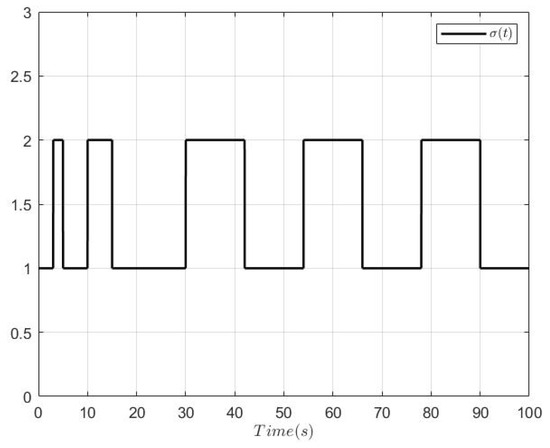
Figure 1. The switching signal.

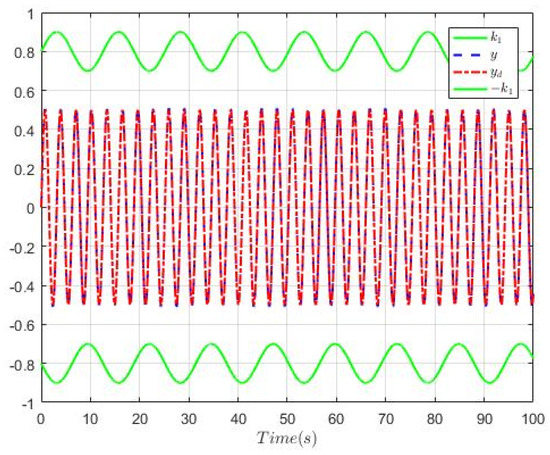
Figure 2. Curves of tracking results.

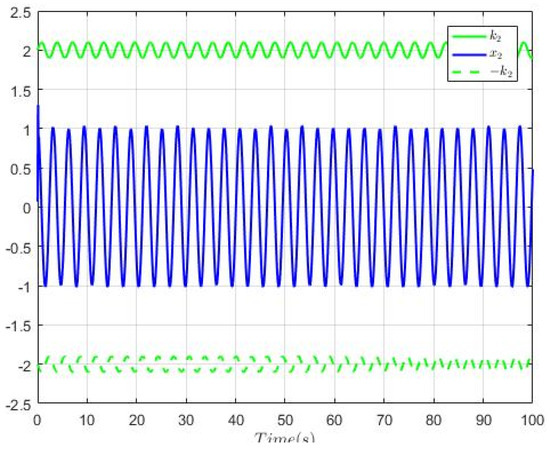
Figure 3. Trajectories of system states $x_2$ and its constraint conditions.

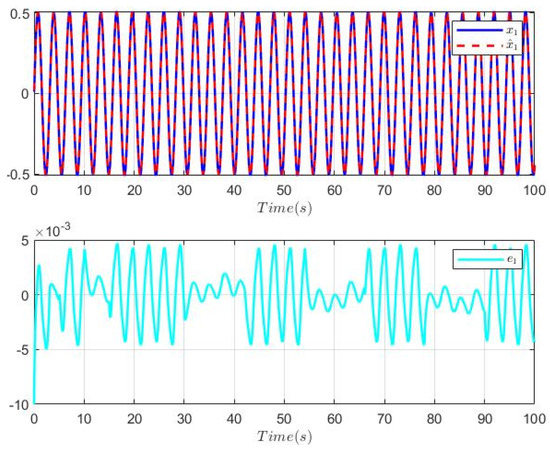
Figure 4. Trajectories of the system state $x_1$, the observer state ${\widehat{x}}_1$, and their estimation error.

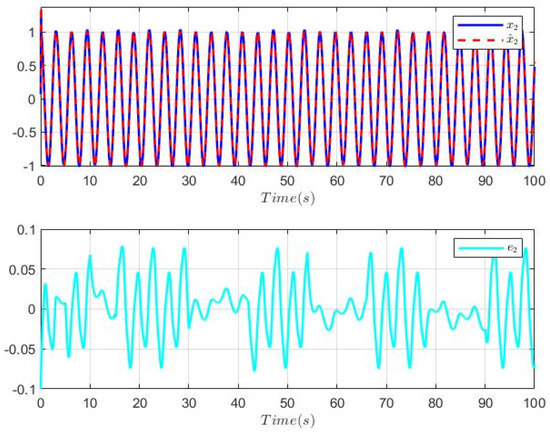
Figure 5. Trajectories of the system state $x_2$, the observer state ${\widehat{x}}_2$, and their estimation error.

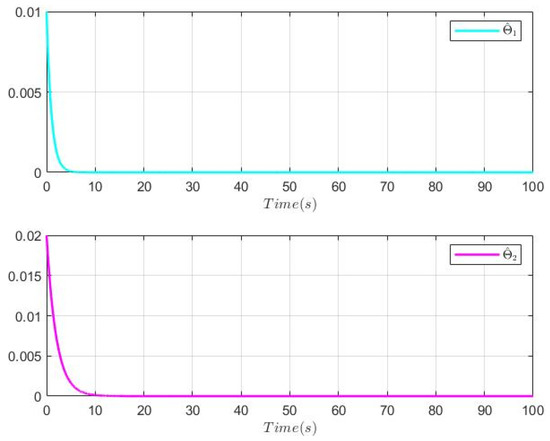
Figure 6. Curves of ${\widehat{\mathsf{\Theta }}}_1$ and ${\widehat{\mathsf{\Theta }}}_2$.

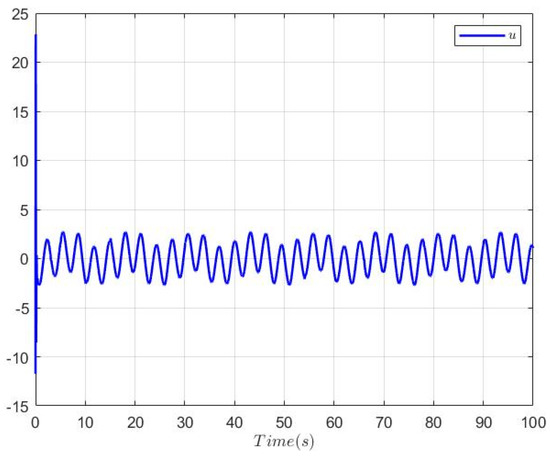
Figure 7. The trajectory of input quantization $u$.

7. Conclusions

This paper focuses on the input quantization, state constraints and unmeasured system states issues for switched nonlinear systems. For the unmeasured states, a fuzzy-based state observer is developed to estimate them. Then, the barrier Lyapunov function approach is employed to guarantee that the system state does not exceed the corresponding constraint bound. Using the backstepping technique, an adaptive control law is designed that can offset the impact of input quantification. However, due to the application of backstepping method, the problem of computation explosion may be caused. Therefore, how to reduce the amount of computation will be studied in future research.