Abstract
In this paper, we find values of depth, Stanley depth, and projective dimension of the quotient rings of the edge ideals associated with r-fold bristled graphs of ladder graphs, circular ladder graphs, some king’s graphs, and circular king’s graphs.
Keywords:
depth; Stanley depth; projective dimension; edge ideal; r-fold bristled graph; ladder graph; circular ladder graph; king’s graph; circular king’s graph MSC:
13C15; 13F20; 05C38; 05E99
1. Introduction
Let be a polynomial ring over a field K with standard grading, that is, , for all i. Let M be a finitely generated graded -module. Suppose that M admits the following minimal free resolution:
The projective dimension of M is defined as . The of M is defined to be the common length of all maximal M-sequences in the unique graded maximal ideal . Let M be a finitely generated -graded -module. For a homogeneous element and a subset , denotes the K-subspace of M generated by all homogeneous elements of the form , where v is a monomial in . The K-subspace, , is called a Stanley space of dimension if it is a free -module, where denotes the number of indeterminates in A. A Stanley decomposition of M is a presentation of the K-vector space M as a finite direct sum of Stanley spaces:
The Stanley depth of decomposition is defined as . The Stanley depth of M is defined as
Stanley conjectured in [1] that ; this conjecture was later disproved by Duval et al. [2] in 2016. However, it is still important to prove Stanley’s inequality for some special classes of ideals. Herzog et al. gave a method in [3] to compute the Stanley depth of modules of the form , where are monomial ideals. But in general, it is still too hard to compute Stanley depth even using their method. For further details, we refer the reader to [4,5,6].
Let be a graph, where is the vertex set and is the edge set of graph G. All graphs considered in this paper are simple and undirected. The edge ideal of the graph G is the ideal generated by all monomials of the form such that . In the last decade, the study of edge ideals has gained considerable attention. Various findings on these ideals have demonstrated how combinatorial and algebraic aspects interact; see, for instance, [7,8]. The algebraic invariant depth, Stanley depth, and projective dimension have significant importance in the field of commutative algebra. Establishing the relationship of these invariants with other invariants of commutative algebra and invariants of graph theory are current trends in research.
In general, the invariant depth, Stanley depth, and projective dimension are hard to compute. There are very few classes of ideals for which the formulae of these invariants are known; see, for instance, [4,9,10]. We prove that when we consider the r-fold graph of a ladder graph, circular ladder graph, some king’s graphs, and some circular king’s graphs, then the value of depth, Stanley depth, and projective dimension of the quotients rings of the edge ideals of these graphs are functions of r. We also prove that Stanley’s inequality also holds for these quotient rings. Furthermore, our results give strong motivation for further studies in this direction. For our main results, see Theorem 3, Corollary 4, Theorem 4, Theorem 6, Corollary 4, and Theorem 7.
2. Preliminaries
In this section, we will recall some definitions and notations from graph theory. For terminology and definitions from graph theory, we refer the reader to [11,12,13,14]. Some known results related to depth and Stanley depth are also given in this section. If I is a monomial ideal then denotes its unique minimal set of monomial generators. If u is a monomial of , then , and for a monomial ideal I, we define . The degree of a vertex denoted by is the number of edges that are incident to . Let , a path of length , denoted by , be a graph with and (if , then ). Let , a cycle of length denoted by , be a graph with and . A graph is said to be a tree if it is acyclic. A vertex is called a pendant vertex if . For , an r-star denoted by is a tree with leaves and a single vertex with degree . A caterpillar is a tree in which the removal of all pendants leaves a path.
Definition 1
([15]). Let G be a graph and be an integer. The graph obtained by attaching r pendant vertices to each vertex of G is called the r-fold bristled graph of G. The r-fold bristled graph of G is denoted by .
Definition 2
([16]). The Cartesian product of graphs and is a graph with vertex set and , whenever
- 1.
- and ;
- 2.
- and .
Definition 3
([16]). The strong product of graphs and is a graph with vertex set and , whenever
- 1.
- and ;
- 2.
- and ;
- 3.
- and .
Here we introduce some notations that will be used throughout the paper. For , let and be graphs. The graph is known as a ladder graph, whereas the graph is called ()-king’s graph. See Figure 1 for examples of and . For , let and ; the graph is called a circular ladder graph. We define the graph as circular ()-king’s graph.
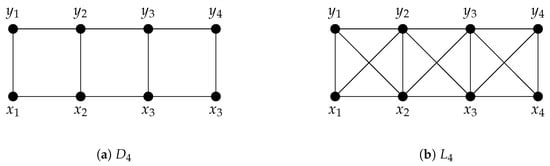
Figure 1.
Ladder graph and king’s graph.
Now we recall some known results that are frequently used in this paper. The following lemma, which is also known as the Depth Lemma, has a crucial role in all proofs of our results concerning depth.
Lemma 1
([17]). If is a short exact sequence of modules over a local ring , or a Noetherian graded ring with local, then
- 1.
- .
- 2.
- .
- 3.
- .
A similar result for Stanley depth as given in the subsequent lemma is proved by Rauf.
Lemma 2
([18]). Let be a short exact sequence of -graded -module. Then
Here is a list of some preliminary lemmas that are referred to many times in the proofs of our results.
Lemma 3
([3]). Let be a monomial ideal. If then and
Lemma 4
([19]). If is an edge ideal of υ-star, then
Lemma 5
([20]). Let , be monomial ideals, where and . Then
Lemma 6
([20]). Let and be monomial ideals, where and . Then
The following results are useful in finding upper bounds for depth and Stanley depth.
Corollary 1
([18]). Let be a monomial ideal. Then for all monomials .
Proposition 1
([21]). Let be a monomial ideal. Then for all monomials ,
Lemma 7
([22]). Let be a squarefree monomial ideal with , let , such that , for all . Then
The following result says that once the value of depth of a module is know then one can find its projective dimension.
Theorem 1
([17]). (Auslander–Buchsbaum formula) If is a commutative Noetherian local ring and M is a non-zero finitely generated -module of finite projective dimension, then
For and , if , then clearly is a caterpillar and we have the following values for depth and Stanley depth.
Theorem 2
([23]). Let and . Then
Throughout this paper, we set , where r and are positive integers. Also,
3. Depth and Stanley Depth of r-Fold Bristled Graph of Ladder Graph and Some King’s Graph
In this section, we determine depth, projective dimension, and Stanley depth of the quotient rings associated with edge ideals of r-fold bristled graphs of graphs and . See Figure 2a and Figure 3 for 2-fold bristled graph of graphs and , respectively. We label the vertices of and , as shown in Figure 2a and Figure 3, respectively. For , let and . If denotes the minimal set of monomial generators of the monomial ideal I, using our labeling, we have
and
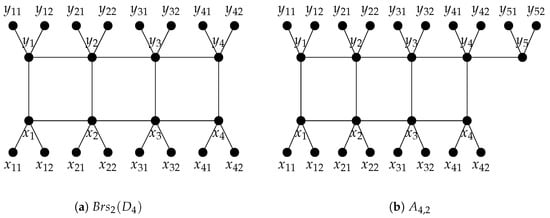
Figure 2.
2-Fold bristled graph of a ladder graph and its modification by adding some vertices and edges.
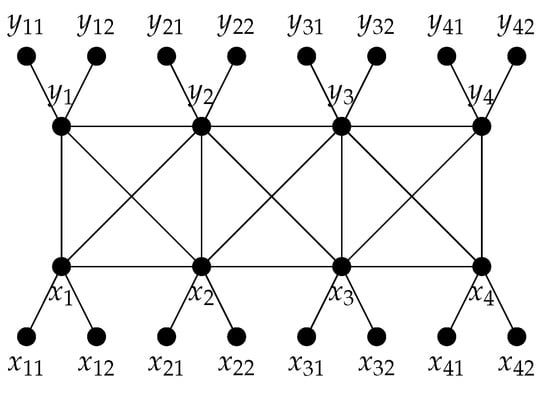
Figure 3.
.
If , then we have
and
Note that and . We also define a modified graph of denoted by with the set of vertices and . See Figure 3b for an example of graph and labeling of vertices of this graph. We set and . Clearly, . Note that , and . To determine depth and Stanley depth of , we shall first determine the depth and Stanley depth of .
Remark 1.
Let I be a squarefree monomial ideal of whose monomial generators have degrees of at most 2. We associate a graph to the ideal I with and . Let be a variable of the polynomial ring such that . Then and are monomial ideals of such that and are subgraphs of . See Figure 4a and Figure 4b for graphs and , respectively.

Figure 4.
Graphs corresponding to ideals and .
Remark 2.
While proving our results by induction on , the special cases, say and , that might appear in the proofs need to be addressed first. We define and . Thus, we have , and by Lemma 4, we have .
Lemma 8.
Let . Then
Proof.
First we will prove the result for depth. We will prove this by induction on . We consider the following short exact sequence:
By the Depth Lemma,
If , then by Theorem 2, , as required. Let . After renumbering the variables, we have
Thus, by induction and Lemma 3,
Also,
By Lemmas 3 and 5,
Using induction and Lemma 4,
By Equation (1), we have Now we prove the other inequality. We have by Lemma 3, By induction, we have
As , so by Corollary 1 This completes the proof for depth.
Now we prove the result for Stanley depth. If , then by Theorem 2, . For , the required result follows by applying Lemma 2 instead of the Depth Lemma, Lemma 6 instead of Lemma 5, and Proposition 1 instead of Corollary 1. □
Corollary 2.
Let . Then
Proof.
The required result follows by using Lemma 8 and Theorem 1. □
Now using the previous lemma, we are able to prove one of the main results of this section.
Theorem 3.
Let . Then
Proof.
First we will prove the result for depth. Consider the following short exact sequence:
When , it is clear from Theorem 2 that . Let . We have By Lemma 3, we have
By Lemma 8, Now clearly and , and using Lemma 3, By Lemma 8,
Applying the Depth Lemma,
Now we prove the result for Stanley depth. If , then by Theorem 2, we have
Let . Applying Lemma 2 on the short exact sequence, we obtain
Proceeding on the same lines as we did for the depth, we obtain and and by Equation (2), we have . For the other inequality, since and , by Lemma 8,
By Proposition 1, we have
This completes the proof for Stanley depth. □
Corollary 3.
Let . Then
Proof.
The required result follows by using Theorem 3 and Theorem 1. □
Now we find the depth and Stanley depth of .
Theorem 4.
Let . Then
Proof.
First we will prove the result for depth. We will prove this by induction on . Consider the following short exact sequence:
By the Depth Lemma,
When , it is clear from Theorem 2 that .
Let , Using Lemma 3 and induction on , clearly
Now let and Consider the following short exact sequence:
Again, using the Depth Lemma, we have
Here Using Lemma 3 and induction on , we have
As and By Lemma 3 and induction on , we obtain
By Equation (4), we have
Now by using Equation (3), we obtain
For upper bound as and . By Corollary 1, This completes the proof for depth. Now we prove the result for Stanley depth. When , it is clear from Theorem 2 that . For , the required result follows by applying Lemma 2 instead of the Depth Lemma and Proposition 1 instead of Corollary 1. □
Corollary 4.
Let . Then
Proof.
The result follows by using Theorem 4 and Theorem 1. □
Example 1.
If and , then by Theorem 4, we have . Also, by Corollary 4, we have
4. Depth and Stanley Depth of r-Fold Bristled Graph of Circular Ladder Graph and Some Circular King’s Graph
In this section, we determine the depth and Stanley depth of the quotient rings associated with the edge ideal of r-fold bristled graph of circular ladder graph and graph. Figure 5a,b are examples of 2-fold bristled graphs of a circular ladder graph and graph, respectively. For positive integers such that and , the minimal set of monomial generators of the edge ideal is given as . For , we also define a new graph with and
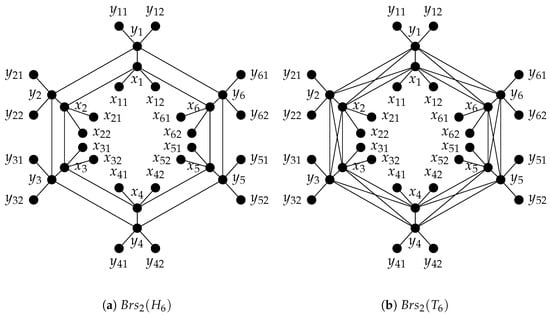
Figure 5.
2-fold bristled graphs of circular ladder and circular king’s graphs.
See Figure 6 for an example of graph. We set and . Let and . Clearly, .
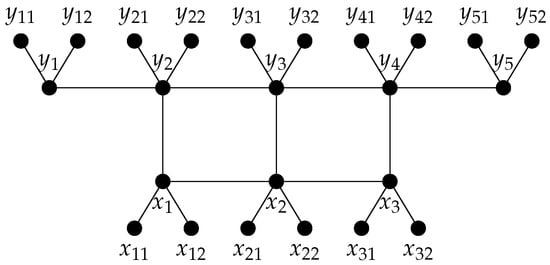
Figure 6.
.
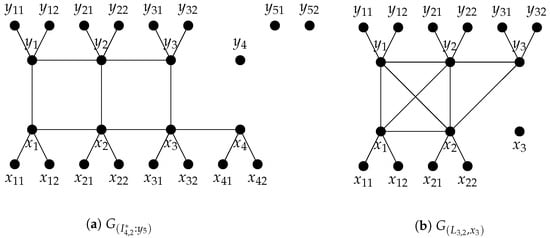
To determine the depth and Stanley depth of the quotient rings associated with the edge ideal of the r-fold bristled graph of the circular ladder graph, we shall first determine the depth and Stanley depth of the quotient ring associated with the edge ideal of graph. In Figure 7 we give examples of graphs associated to squarefree monomial ideals , , and , as discussed in Remark 1. These examples will be helpful in understanding the proofs of our next results.
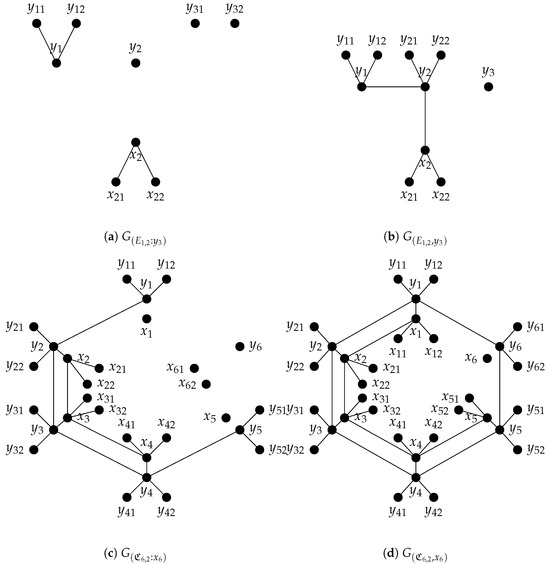
Figure 7.
Graphs corresponding to ideals , , and .
Remark 3.
While proving our results by induction on υ, we have special case , so we define . By using Theorem 2, .
Theorem 5.
Let . Then
Proof.
First we will prove the result for depth by using induction on . Consider the following short exact sequence:
Let . We have , and by Lemmas 3–5, we have
Also, we can see that . By Lemma 3 and Theorem 2, we have
Since , then by then Depth Lemma,
This prove the result for
Let and . Now consider the following short exact sequence:
We have
and
Thus, by using Lemma 3, we obtain and We consider two cases:
Case 1. If is even, then by induction on ,
Similarly, by induction on , we have
Since Applying the Depth Lemma, we obtain
Now By Lemmas 3 and 8, we have . Again, since , then by the Depth Lemma,
Case 2. If is odd, then by induction on ,
Also, by induction on , we have
By the Depth Lemma, It is easy to see that By Lemma 3, we have . Using the Depth Lemma, . For upper bound as , and
Thus, by Lemmas 3 and 4 and induction on ,
Using Corollary 1, This completes the proof for depth.
For Stanley depth, when , by applying Lemma 2 instead of the Depth Lemma and Lemma 6 instead of Lemma 5 on the short exact sequence, we obtain For upper bound, consider ; clearly , for all . Therefore, by Lemma 7, . For , the required result follows by applying Lemma 2 instead of the Depth Lemma, Lemma 6 instead of Lemma 5, and Proposition 1 instead of Corollary 1. If is even, then we obtain . For upper bound, consider
Clearly , for all ; therefore, by Lemma 7, . Hence, If is odd, then we obtain . For upper bound, consider
Clearly , for all ; therefore, by Lemma 7, . This completes the proof for Stanley depth. □
Corollary 5.
Let and . Then
Proof.
The required result can be obtained by using Theorem 5 and Theorem 1. □
Now we find depth, Stanley depth, and projective dimension of the edge ideals of the r-fold bristled graph of the circular ladder graph.
Theorem 6.
Let and . Then
Proof.
First we will prove the result for depth. Consider the following short exact sequence:
After a suitable renumbering of variables, we have
By Lemma 3,
Let and Consider the following short exact sequence:
After renumbering of variables, we have
and
Case 1. When is even, using Lemma 3, . As is even, so will be an odd number. So by Theorem 5, we have
Similarly, by Lemma 3 and Theorem 3,
By the Depth Lemma, Now by Theorem 5,
Applying the Depth Lemma on short exact sequence 5, we obtain This completes the proof when is even.
Case 2. If is odd, using Lemma 3, . As is odd, so will be an even number. So by Theorem 5, we have
Now by Lemma 3 and Theorem 3,
By the Depth Lemma, By Theorem 5,
Applying the Depth Lemma on short exact sequence 5, we obtain This completes the proof for depth.
For Stanley depth, the required result follows by applying Lemma 2 instead of the Depth Lemma and Lemma 6 instead of Lemma 5. When is even, we have . For upper bound as and , by Theorem 5 and Proposition 1 Similarly, when is odd, we obtain For upper bound as and , by Theorem 5 and Proposition 1, . Hence,
□
Corollary 6.
Let and . Then
Proof.
The required result can be obtain by using Theorem 6 and Theorem 1. □
We also have formulae for values of depth, Stanley depth, and projective dimension of the quotient rings of the edge ideals of the graph, as given in the next theorem and corollary.
Theorem 7.
Let and . Then
Proof.
First we will prove the result for depth. We will prove this for . Consider the following short exact sequence:
After renumbering the variables, we have
Using Lemma 3 and Theorem 4,
Let , where Consider the following short exact sequence:
After renumbering the variables, we have
By Lemma 3 and Theorem 4,
Now and Using Lemma 3 and Theorem 4, we have By the Depth Lemma,
Applying the Depth Lemma on short exact sequence 6, This completes the proof for depth.
For Stanley depth, the required result follows by applying Lemma 2 instead of the Depth Lemma. We obtain For upper bound as we have
by Theorem 4 and Proposition 1,
This completes the proof. □
Corollary 7.
Let and . Then
Proof.
The required result can be obtain by using Theorem 7 and Theorem 1. □
Example 2.
If and , then by Theorem 7, we have . Also, by Corollary 4 we have pdim
Author Contributions
Conceptualization, Y.W., S.S., M.I., F.T., F.M.T. and A.A.; methodology, Y.W., M.I., F.T., F.M.T. and A.A.; validation, Y.W., S.S., M.I., F.T., F.M.T. and A.A.; formal analysis, S.S.; investigation, Y.W.; writing—original draft preparation, S.S.; writing—review and editing, M.I. and A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research work is supported by Researchers Supporting Project number (RSP2023R440), King Saud University, Riyadh, Saudi Arabia.
Data Availability Statement
No data is required to support the study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Stanley, R.P. Linear Diophantine equations and local cohomology. Invent. Math. 1982, 68, 175–193. [Google Scholar] [CrossRef]
- Duval, A.M.; Goeckneker, B.; Klivans, C.J.; Martine, J.L. A non-partitionable Cohen-Macaulay simplicial complex. Adv. Math. 2016, 299, 381–395. [Google Scholar] [CrossRef]
- Herzog, J.; Vladoiu, M.; Zheng, X. How to compute the Stanley depth of a monomial ideal. J. Algebra 2009, 322, 3151–3169. [Google Scholar] [CrossRef]
- Herzog, J. A survey on Stanley depth. In Monomial Ideals, Computations and Applications; Springer: Berlin/Heidelberg, Germany, 2013; pp. 3–45. [Google Scholar]
- Popescu, D. An inequality between depth and Stanley depth. Bull. MathéMatique SociéTé Des Sci. MathéMatiques Roum. 2009, 52, 377–382. [Google Scholar]
- Pournaki, M.R.; Fakhari, S.A.; Tousi, M.; Yassemi, S. What is Stanley Depth? Not. AMS 2009, 56, 1106–1108. [Google Scholar]
- Banerjee, A.; Das, P.; Selvaraja, S. Bounds for the regularity of product of edge ideals. Algebr. Comb. 2022, 5, 1015–1032. [Google Scholar] [CrossRef]
- Van Tuyl, A. A Beginners Guide to Edge and Cover Ideals. In Monomial Ideals, Computations and Applications; Bigatti, A., Gimenez, P., Saenz-de-Cabezon, E., Eds.; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 2013; Volume 2083. [Google Scholar]
- Morey, S. Depths of powers of the edge ideal of a tree. Commun. Algebra 2010, 38, 4042–4055. [Google Scholar] [CrossRef]
- Pournaki, M.R.; Seyed Fakhari, S.A.; Yassemi, S. Stanley depth of powers of the edge ideals of a forest. Proc. Am. Math. Soc. 2013, 141, 3327–3336. [Google Scholar] [CrossRef]
- Chartrand, G. Introduction to Graph Theory; Tata Mcgraw-Hill Education: New York, NY, USA, 2006. [Google Scholar]
- Harary, F. Graph Theory; Addison-Wesley: Boston, MA, USA, 1969. [Google Scholar]
- Lei, S.; Guan, H.; Jiang, J.; Zou, Y.; Rao, Y. A Machine Proof System of Point Geometry Based on Coq. Mathematics 2023, 11, 2757. [Google Scholar] [CrossRef]
- Rao, Y.; Zhou, Q.; Akhoundi, M.; Talebi, A.A.; Amiri, S.O.; GMuhiuddin, G. Novel Concepts in Rough Cayley Fuzzy Graphs with Applications. J. Math. 2023, 2023, 2244801. [Google Scholar] [CrossRef]
- Saha, S.; Mandal, A.; Narasimhamurthy, A.; Sangam, S. Handbook of Research on Applied Cybernetics and Systems Science; IGI Global: Hershey, PA, USA, 2017. [Google Scholar]
- Hammack, R.H.; Imrich, W.; Klavžar, S.; Imrich, W.; Klavžar, S. Handbook of Product Graphs; CRC Press: Boca Raton, FL, USA, 2011; Volume 2. [Google Scholar]
- Bruns, W.; Herzog, J. Cohen-Macaulay Rings; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Rauf, A. Depth and Stanley depth of multigraded modules. Commun. Algebra 2010, 38, 773–784. [Google Scholar] [CrossRef]
- Alipour, A.; Tehranian, A. Depth and Stanley depth of edge ideals of star graphs. Int. J. Appl. Math. Stat. 2017, 56, 63–69. [Google Scholar]
- Din, N.U.; Ishaq, M.; Sajid, Z. Values and bounds for depth and Stanley depth of some classes of edge ideals. AIMS Math. 2021, 6, 8544–8566. [Google Scholar] [CrossRef]
- Cimpoeas, M. Several inequalities regarding Stanley depth. Rom. J. Math. Comput. Sci. 2012, 2, 28–40. [Google Scholar]
- Iqbal, Z.; Ishaq, M.; Aamir, M. Depth and Stanley depth of the edge ideals of square paths and square cycles. Commun. Algebra 2018, 46, 1188–1198. [Google Scholar] [CrossRef]
- Shaukat, B.; Ishaq, M.; Haq, A.U.; Iqbal, Z. Algebraic properties of edge ideals of corona product of certain graphs. arXiv 2022. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).