Abstract
Let be a finite and simple graph of order n and size m. The complement of G, denoted by , is the graph obtained by removing the lines of G and adding the lines that are not in G. A graph is self-complementary if and only if it is isomorphic to its complement. In this paper, we define -complement and -complement of a graph as follows. For any two points u and v of G with remove the lines between u and v in G and add the lines between u and v which are not in G. The graph thus obtained is called -complement of G. For any two points u and v of G with remove the lines between u and v in G and add the lines between u and v that are not in G. The graph thus obtained is called -complement of G. The graph G is -self-complementary if . The graph G is -co-self-complementary if . This paper presents different properties of and -complement of a given graph.
MSC:
05C07; 05C40; 05C45
1. Introduction
Let G be a simple, finite and undirected graph. The number of lines in G is the size of G, denoted by m. The number of lines incident on a point v is the degree of v denoted by . An open neighborhood of a point v, denoted by is the set of all points that are adjacent to v. A graph G is Eulerian if it contains a closed trail that covers all the lines of G. A graph G is Hamiltonian if it contains a cycle that visits all the points exactly once. The complement of G is the graph obtained from G by removing all the lines of G and adding the lines between the points that are not in G. The graph G is said to be self-complementary if and only if G is isomorphic to . For more information on self-complementary graphs, one can refer [1,2,3]. For all notations and terminologies we refer to [4,5].
2. Motivation
1. The concept of -complement of a graph can be used in a scenario where the user changes the adjacency of points based on his requirements in order to optimize his end goal. For example, employees working in a company have various skills, qualifications, and strengths.
In comparison to the graph, let graph G specify a task. Each point in G represents an employee of the company. A line connecting two points symbolizes a shared competence between two employees. We explore the following two scenarios.
An employee intends to work with other workers having similar skills, with whom he has not previously worked but does not wish to work with the same skilled employees with whom he has previously worked. This situation is very well described by the -complement of a graph.
Suppose an employee wants to work with workers of different skills with whom he has not previously worked and wishes to discontinue his work with employees of different skills with whom he has previously worked. This situation is definitely achieved via -complement of a graph.
2. Let be the labeling of the points of a graph, where j represents the degree of a point. Suppose that each degree signifies a certain activity. The number of points with the label represent the number of persons carrying out the kth activity. The line connecting two points indicates that the information, resources, or time required for the execution of the activity has already been shared. Since each member is equally capable, -complement can be used to determine the output when non-adjacent or non-linked members of the same(different) activity are made to share information, resources, or time.
For example, The graph G in Figure 1 consists of five people and who are assigned to accomplish three activities, namely, 1, 2, and 3. The person is in charge of activity 1, the persons and are in charge of activity 2 and the person is in charge of activity 3. It is observed that and of activity 2 have already shared information among themselves. Hence, and share the information and continue to execute the activity 2 in .
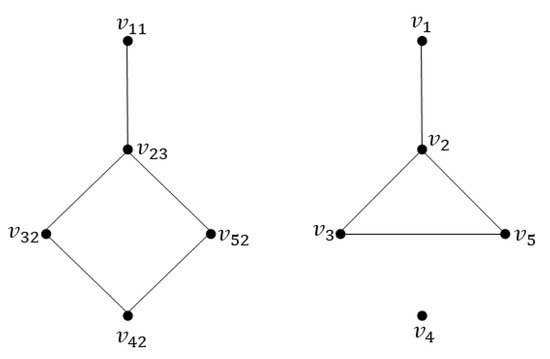
Figure 1.
The graphs G and .
3. Results
-Complement of a Graph
In this section, we define a new graph complement based on the degree sequence. We begin by defining the -complement of a graph.
Definition 1.
Letbe any graph of order n and size m. For any two points u and v in V withremove the lines between u and v in G and add the lines ofbetween u and v. The graph thus obtained is called δ-complement of G and is denoted by .
Definition 2.
A graph G is δ-self-complementary (δ-s.c.) ifand G is δ-co-self-complementary - if, whereis the complement of G.
Definition 3.
Let be any graph of order n and size m. For any two points u and v in V with remove the lines between u and v in G and add the lines of between u and v. The graph thus obtained is called -complement of G and is denoted by
Definition 4.
A graph G is -self-complementary (-s.c.) if and G is -co-self-complementary (-co.s.c.) if , where is the complement of G.
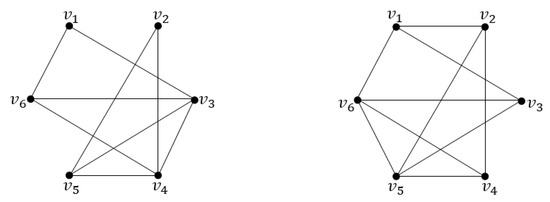
Figure 2 gives self-complementary and co-self-complementary graphs and Figure 3 gives co-self-complementary and self-complementary graphs
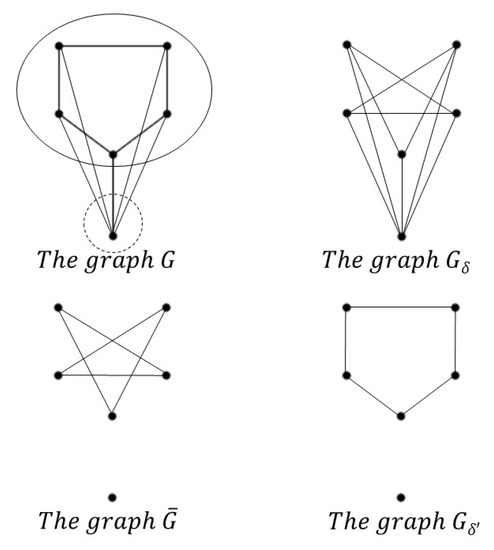
Figure 2.
and .
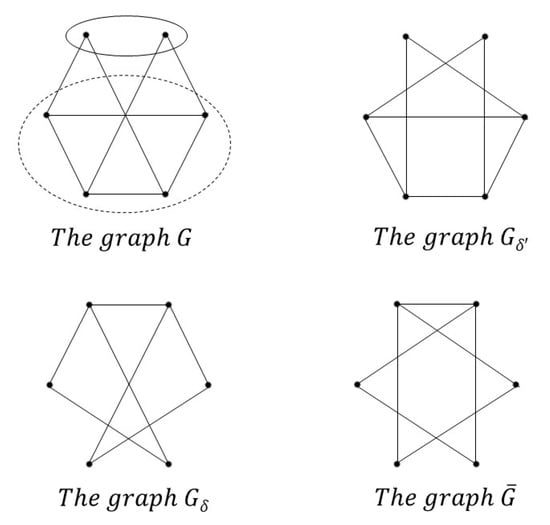
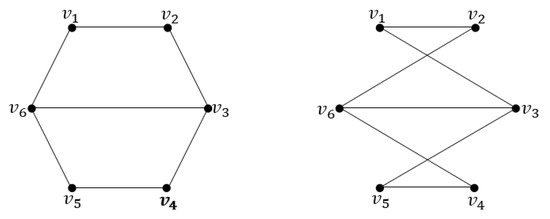
Figure 3.
and .
The Table 1 displays the degree sequence and number of lines in -complement of various graphs.

Table 1.
The degree sequence and number of lines in -complement of various graphs.
The degree sequence and number of lines of -complement for different graphs are summarized in Table 2.

Table 2.
The degree sequence and number of lines of -complement for different graphs.
Proposition 1.
For any graph G,
- 1.
- and
- 2.
- .
Proof.
- Let .Then u is adjacent to v in⇔ either and u is not adjacent to v in G or and u is adjacent to v in G⇔ u is adjacent to v in ;
- Let .Then u is adjacent to v in⇔ either and u is not adjacent to v in G or and u is adjacent to v in G⇔ u is adjacent to v in .
□
Corollary 1.
For any graph G,
- 1.
- if and only if;
- 2.
- if and only if.
Proof.
- ⇔ ⇔ from Proposition 1;
- ⇔ ⇔ from Proposition 1.
□
Corollary 2.
For any graph G,
- 1.
- if and only if;
- 2.
- if and only if.
Proof.
□
We now characterize -self-complement of a graph based on its degree sequence.
Proposition 2.
The graphs G andare degree preserving if and only ifcan be partitioned assuch thatisregular graph of order.
Proof.
Suppose is a partition of the point set of G such that has points with regularity . First, note that every point of each partite is adjacent to all the points of the remaining partites. Otherwise, G cannot be partitioned into l partites such that each consisting of points with regularity Let and let The lines between different partites are unaltered in . Also with regularity of each point in is in Thus the graphs G and are degree preserving.
Suppose that the graph G cannot be partitioned into l partites such that each consists of points with regularity Then the adjacency between the points of different degree is the same in both G and However, the adjacency between the points of the same degree varies in . Thus, the degree sequence does not remain the same in both G and . Hence, G and are not degree preserving. □
Remark 1.
A graph G is δ-self-complementary if and only if can be partitioned as such that each is a self-complementary graph.
Proposition 3.
A graph G is co-self-complementary if and only if each point of a given degree is adjacent to exactly half of the number of points of different degrees.
Proof.
Suppose each point of a given degree, say is adjacent to exactly half of the number of points of different degrees, then in both and a point of degree is adjacent to exactly half of the number of points of different degrees. The adjacency of points of degree remains the same in both and by definition of . Since each point of a given degree is adjacent to exactly half of the number of points of different degrees, the structure of both and remains the same. Hence .
Suppose each point of a given degree is not adjacent to exactly half of the number of points of different degrees, then in a point v of degree is adjacent to either less or more than the number of points of different degrees as in G. Also in , point v is adjacent to the same number of points of different degrees as in G. Thus in ≠ in and hence . □
Proposition 4.
A graph G is -self-complementary if and only if each point of a given degree is adjacent to exactly half of the number of points of different degrees.
Proof.
If each point v of a given degree in G is adjacent to exactly half of the number of points of different degrees, then v is adjacent to half of the remaining points of different degrees in and to the same points of given degree as in G. Since every point v of a given degree is adjacent to exactly half of the number of points of different degrees, the adjacency between every pair of points is preserved in . Hence .
Suppose each point of a given degree is not adjacent to exactly half of the number of points of different degrees in G. Then a point of a given degree is adjacent to either less or more than the number of points of different degrees and to equal number of points of the same degree as in G. Thus . □
Proposition 5.
The graphs and are degree preserving if and only if can be partitioned as such that is regular graph of order .
Proof.
Suppose is a partition of the point set of G such that has points with regularity . Every point of each partite is adjacent to all the points of the remaining partites. Otherwise, G cannot be partitioned into l partites such that each consisting of points with regularity Let order of . There are lines between the points of different partites. Then both the graphs and consist of l connected components where each connected component is a regular graph. Therefore, the graphs and are degree preserving.
Suppose the graph G cannot be partitioned into l partites such that each consists of points with regularity Then the adjacency between the points of different degree is the same in both and The adjacency between the points of equal degree remains the same in as in G but it varies in . Thus, the degree sequence does not remain the same in both and . Hence, and are not degree preserving. ߓ□
Remark 2.
A graph G is -co-self-complementary if and only if can be partitioned as such that each is a self-complementary graph.
Proposition 6.
and of a graph G are degree preserving if and only if G is -regular graph.
Proof.
Suppose G is regular graph, then both and are regular graph and hence both and are degree preserving graphs. Conversely, from Proposition 2, G and are degree preserving if and only if G contains points of the same degree and all the points of a given degree are adjacent to exactly points of the same degree. Also from Proposition 4, if and only if each point of a given degree is adjacent to exactly half of the number of points of different degrees. Thus Proposition 3 and 5 together imply that G is regular graph of order n. □
4. Some Properties of -Complement of a Graph
Theorem 1.
A graph is a complete graph if and only if G is a complete multipartite graph with the partition of the point set with for all .
Proof.
Since the lines between and of G remain in and each is isomorphic to complete subgraph, the resultant is a complete graph.
Conversely, suppose that G is not a complete multipartite graph, then G may have a line between the points of the same degree or there may exist two non-adjacent points of different degrees in If G has a line between the points u and v of same degree, then in there is no line between u and v and hence is not complete. If G has two non-adjacent points of different degrees, then those two points are non-adjacent in also. Hence is not a complete graph. □
Remark 3.
The δ-complement of the star graph of order n is isomorphic to complete graph .
Theorem 2.
If G is a disconnected graph of order n with each connected component of G is regular, then is a connected regular graph.
Proof.
Let be connected regular components of G. Then the degree of each point of is , which is . □
Theorem 3.
Let G be a connected graph. The graphis disconnected if
- 1.
- G is a complete graph;
- 2.
- G is a connected regular graph of order n;
- 3.
- G has a point v of degree k which is only adjacent to every point of degree k.
Proof.
Let G be a connected graph.
- If G is a complete graph then is completely disconnected by the definition of ;
- Suppose G is a connected regular graph of order n. Then n must be even and is isomorphic to ;
- Suppose G has a point v of degree k that is only adjacent to every point of degree k. Then v is not adjacent to any of the points in . Thus, is disconnected.
□
Remark 4.
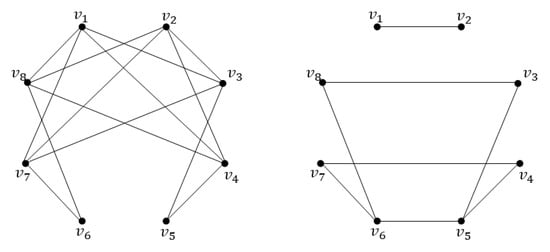
The converse of Theorem 3 need not be true.
For example, consider a regular graph C in Figure 4. C is a connected 3-regular graph of order where However, the graph is a disconnected 2-regular graph.

Figure 4.
The graph C and its -complement .
Consider a non-regular graph of order 8 in Figure 5. Here, no point is adjacent to all the points of the same degree. However, is disconnected.

Figure 5.
The graph D and its -complement .
Theorem 4.
Let G be an Eulerian graph of order n. Then is Eulerian if G has odd number of points of the same degree and every point of a given degree is adjacent to at most half of the points of same degree and at least half of the points of each different degrees.
Proof.
Let G be an Eulerian graph of order n. G has an odd number of points of the same degree. Consider point of degree m. Either v is adjacent to points of degree m or points of degree other than m.
Suppose v is adjacent to an even number of points of degree m and an even number of points of degree other than m. As G has an odd number of points of the same degree and by definition of , even number of lines incident on v are removed and an even number of lines that were non-incident on v in G are added. Hence, the degree of v is even in .
Suppose v is adjacent to an odd number of points of degree m and an odd number of points of degree other than m. In v is adjacent to an odd number of points of degree m since G has an odd number of points of the same degree and to an odd number of points of a different degree. Therefore, v is of even degree in
In addition, it is given that every point of a given degree is adjacent to at most half of the points of the same degree and at least half of the points of each different degrees. In every point is adjacent to at least half of the points of same degree and at most half of the points of each different degrees. Therefore, the degree of each vertex of is at least and hence it is connected. Therefore, the graph is Eulerian. □
Theorem 5.
Let G be a Hamiltonian graph. Thenis Hamiltonian if
- 1.
- G is an regular graph with , ;
- 2.
- G is a non-regular graph with no point v adjacent to any point with a degree, as that of v.
Proof.
Let G be a Hamiltonian graph.
- If G is an regular graph with , , then is regular graph with . From this, it follows that is Hamiltonian;
- Suppose G is a non-regular graph with no point v adjacent to any point with degree as that of v. As every adjacent points of Hamiltonian cycle have different degrees in G, we see that the Hamiltonian cycle of G remains in
□
Remark 5.
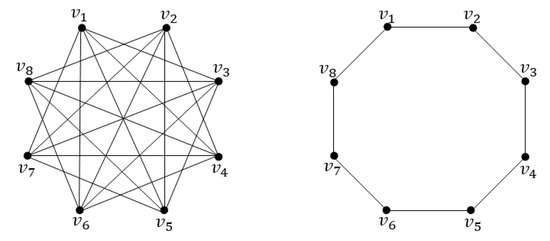
The converse of Theorem 5 need not be true.
For example, consider the graph in Figure 6. The graph is a 5-regular graph and It is a Hamiltonian graph with Hamiltonian cycle The δ-complement of the graph is , which is also a Hamiltonian graph.

Figure 6.
The graph and its -complement .
Consider a non-regular graph H in Figure 7. The graph H is a Hamiltonian graph with Hamiltonian cycle The point is of degree 4 and it is adjacent to the point of degree 4. However, the graph is also Hamiltonian with a Hamiltonian cycle

Figure 7.
The graph H and its -complement .
Theorem 6.
For any point in in G if and only if G has an m odd number of points of equal degree and u is adjacent to exactly points of equal degree.
Proof.
Suppose that G has an m odd number of points of equal degree and the point u is adjacent to exactly points of equal degree, then in in in G.
Conversely, suppose that u is adjacent to less than points of the equal degree, then in the point u will be adjacent to more than points of the equal degree and the same number of points of unequal degree and hence the degree of u in will be more than the degree of u in G. A similar argument holds if u is adjacent to more than points of the same degree. Thus in in G. □
Theorem 7.
ininfor allif
- 1.
- G is regular or;
- 2.
- G is an even order bi-regular graph of degree r and s such that every point of a particular degree is adjacent to half of the points of different degree.
Proof.
Suppose that G is regular. Then is a regular graph. Thus in in for all .
Suppose G is a bi-regular graph of degree r and s such that every point of degree r is adjacent to half of the points of degree s. Let and be the number of points of degree r and s respectively. Consider a point v of degree r. Suppose v is adjacent to points of degree s and x points of degree r. In the point v is adjacent to points of degree s and points of degree r. Thus, in in . □
5. Some Properties of -Complement of a Graph
Proposition 7.
Let be the only point of maximum degree . If G is -self-complementary, then G has a point of degree .
Proof.
Let be the only point of maximum degree . Then in . Since G is s.c., G must have a point of degree . □
Proposition 8.
Let be the only one point of minimum degree . If G is self-complementary, then G has a point of degree .
Proof.
Let be the only point of degree . Then, in . Since G is -s.c., G must have a point of degree . □
Theorem 8.
Let G be a graph with n points. Then is disconnected if
- 1.
- There exists such that ;
- 2.
- Every point of equal degree is adjacent to all the points of different degree;
- 3.
- G is a disconnected regular graph.
Proof.
- Suppose there exists a point such that. Then v is an isolated point in
- Suppose every point of degree m is adjacent to all the points of degree other than In all the points of degree m will not be adjacent to any point of degree other than m, which makes it disconnected;
- if G is a regular graph and is hence disconnected.
□
Theorem 9.
Let G be an Eulerian graph of order n. Thenis Eulerian if
- 1.
- G is regular;
- 2.
- G is a non-regular graph such that the number of points of equal degree are even and every point of a given degree is adjacent to at least half of the points of the same degree and at most half of the points of each different degree.
Proof.
- Let G be an Eulerian graph of order n. Then, all the points of G are of even degree. If G is regular, then is a regular graph with and hence is Eulerian;
- Suppose that G is non-regular Eulerian graph and the number of points of same degree are even in G. Let v be a point of degree m that is adjacent to an even number of points of degree m and an even number of points of degree other than Then, in , the point v is adjacent to the same number of points of degree m and an even number of points of degree other than m, since there are an even number of points of equal degree. If a point v of degree m is adjacent to an odd number of points of degree m and an odd number of points of degree other than m, then in , the point v is adjacent to the same number of points of degree m and an odd number of points of degree other than m, since there is an even number of points of equal degree. Thus in all the cases, the degree of every point of is even. In addition, it is given that every point of a given degree is adjacent to at least half of the points of the same degree and at most half of the points of each different degrees. Therefore, in every point of a given degree is adjacent to at least half of the points of same degree and at least half of the points of distinct degrees. Then, the degree of each point is at least in Hence is a connected graph with all even degree points. Therefore, is Eulerian.
□
Remark 6.
Let G be a Hamiltonian graph. The graph is Hamiltonian if G is a r-regular graph.
Proof.
Let G be a Hamiltonian graph. From Table 2, it is clear that if G is regular. Hence, is Hamiltonian. □
Remark 7.
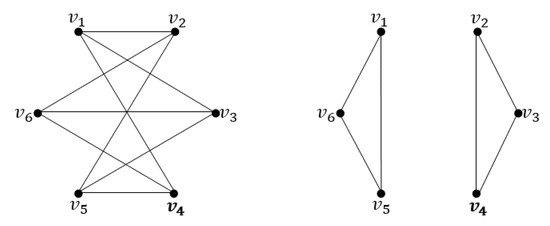
The converse of Remark 6 need not be true. For example, consider a non-regular graph J in Figure 8. Both the graphs J and are Hamiltonian with Hamiltonian cycles and respectively.

Figure 8.
The graph J and its -complement .
6. Conclusions
In this paper, the authors defined the and -complement of a graph and explored properties such as degree preserving, -self-complementary, -co-self-complementary, and connectedness. As these complements are based on like/unlike characters, they can be easily applied in social network problems and optimization problems. There is a huge scope to study these complements in comparison with existing self-complementary graphs.
Author Contributions
Writing—original draft, A.P. and H.A.R.; writing—review and editing, S.D., P.G.B. and S.U. These authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Richard, A. Gibbs, Self-complementary graphs. J. Comb. Theory 1974, 16, 106–123. [Google Scholar]
- Nair, P.S. Construction of self-complementary graphs. Discret. Math. 1997, 175, 283–287. [Google Scholar] [CrossRef][Green Version]
- Nayak, S.; Dsouza, S.; Gowtham, H.J.; Bhat, P.G. Energy of Partial Complements of a Graph. Proc. Jangjeon Math. Soc. 2020, 22, 369–379. [Google Scholar]
- Harary, F. Graph Theory; Addison-Wesley: New York, NY, USA, 1971. [Google Scholar]
- West, D.B. Introduction to Graph Theory; Prentice Hall: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).