$\mathbf{(}{\mathit{\alpha }}^{\mathit{F}}\mathbf{,}{\mathit{\alpha }}^{\overline{\mathit{F}}}\mathbf{)}$-Information Fusion Generated by Information Segmentation and Its Intelligent Retrieval

Abstract

Making use of the mathematical model with dynamic features and attribute disjunctive characteristics, the new concepts of ${\alpha }^F$-information segmentation, ${\alpha }^{\overline{F}}$-information segmentation, $({\alpha }^F,{\alpha }^{\overline{F}})$-information segmentation and their attribute characteristics are given, and the intelligent acquisition of matrix reasoning and information segmentation is given, as well as the information segmentation theorem. Moreover, the equivalence between information segmentation and information fusion is discussed, and the information fusion intelligent acquisition intelligent retrieval algorithm is given. Based on these theoretical results, the intelligent information fusion retrieval algorithm and its simple application in health big data are presented. In conclusion, the results presented in this paper are entirely based on new ideas.

1. Introduction

Facts I~III encountered in the application research of information fusion and information retrieval are as follows: $(x)=\{x_1,x_2,\cdots ,x_k\}$ is information, $x_i\in (x)$ is an information element; $\alpha =\{{\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_k\}$ is the attribute set of $(x)$ ($\alpha$ is the characteristic set of $(x)$); and attribute ${\alpha }_i\in \alpha$ of information element $x_i\in (x)$ satisfies the “disjunctive normal form”. Information $(x)$ has dynamic characteristics:

• Some information elements $x_i$ outside $(x)$ are added to $(x)$, $(x)$ generates ${(\overline{x})}^F$,$(x)\subseteq {(\overline{x})}^F$;
• Some information elements $x_j$ in $(x)$ are deleted from $(x)$, $(x)$ generates ${(\overline{x})}^{\overline{F}}$, and ${(\overline{x})}^{\overline{F}}\subseteq (x)$;
• Under the condition that I and II exist at the same time, $(x)$ generates ${(\overline{x})}^F$ and ${(\overline{x})}^{\overline{F}}$ at the same time, and ${(\overline{x})}^{\overline{F}}\subseteq (x)\subseteq {(x)}^F$.

Facts I~III have not attracted people’s attention in the application research of information fusion and information retrieval. I is internal information fusion (the information element $x_i$ outside $(x)$ is fused into $(x)$, and $(x)$ generates ${(\overline{x})}^F$); II is the external information fusion (the information element $x_j$ in $(x)$ is fused outside $(x)$, and $(x)$ generates ${(\overline{x})}^{\overline{F}}$); III is internal and external information fusion. I and II are two forms of information fusion. Many authors have studied the theory and applications of information fusion (see [1,2,3,4,5,6,7]). The following new concepts are obtained by re-understanding and re-studying I~III:

• ${\mathrm{I}}^{*}$. I is ${\alpha }^F$-information segmentation;
• ${\mathrm{II}}^{*}$. II is ${\alpha }^{\overline{F}}$-information segmentation;
• ${\mathrm{III}}^{*}$. III is $({\alpha }^F,{\alpha }^{\overline{F}})$-information segmentation; “Information segmentation” has become a new concept in the application of information fusion.

A number of authors are focusing to find a mathematical model and method with dynamic characteristics to study I~III; in article [8], the authors propose an inverse packet sets (p-sets) model is given and it also gives the structure of the model; several applications of inverse p-sets are given in [8,9,10,11,12]. The inverse p-sets is obtained by introducing the dynamic characteristics into the finite ordinary element set $X$ and improving the finite ordinary element set $X$. The characteristics of inverse p-sets are exactly the same as facts I~III. Therefore, inverse p-sets is a new mathematical method to study information fusion, information dynamic retrieval and application. Refs. [13,14,15,16,17,18,19] presented p-sets that are are dual forms of inverse p-sets, and [20,21,22] presented function inverse p-sets as the functional form of inverse p-sets. Function p-sets are the functional forms of p-sets as given in [23,24], and they are widely used in dynamic information systems.

The main results of this paper are as follows:

• The structure and characteristics of inverse packet sets are introduced, and the fact of the existence of inverse p-sets and its logical characteristics are given, which are important and indispensable.
• The concept of information segmentation is given, and their attribute characteristics are discussed.
• The intelligent acquisition theorem of information segmentation is given by using inverse p-augmented matrix reasoning;
• The equivalence concept and theorem of information segmentation and information fusion are given;
• The information fusion intelligent acquisition–retrieval algorithm and its application are presented. Application examples come from the disease diagnostic–treatment block of “Health Big Data”. The conceptual and theoretical results presented in this paper are new.

2. Inverse P-Sets Mathematical Model and Its Dynamic Structure

Given finite ordinary element set $X=\{x_1,x_2,\cdots ,x_q\}\subset U$,$\alpha =\{{\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_q\}\subset V$ is the attribute set of $X$, and ${\overline{X}}^F$ is referred to as the internal inverse p-sets generated by $X$,

$${\overline{X}}^F=X\cup X^{+}$$

(1)

$X^{+}$ is called the F-element supplementary set,

$$X^{+}=\{u_{\mathrm{i}}|u_{\mathrm{i}}\in U,u_{\mathrm{i}}\notin X,f(u_{\mathrm{i}})={x^{\prime }}_i\in X,f\in F\}$$

(2)

If attribute set ${\alpha }^F$ of ${\overline{X}}^F$ meets

$${\alpha }^F=\alpha \cup \left\{{{\alpha }^{\prime }}_i\right|f({\beta }_i)={{\alpha }^{\prime }}_i\in \alpha ,f\in F\}$$

(3)

here, in (3), ${\beta }_i\in V,{\beta }_i\notin \alpha ,$ and $f\in F$ changes ${\beta }_i$ into $f({\beta }_i)={{\alpha }^{\prime }}_i\in \alpha$; in (1), ${\overline{X}}^F=\left\{x_1,x_2,\cdots ,x_r\right\},q<r,q,r\in N^{+}$.

Call ${\overline{X}}^{\overline{F}}$ the outer inverse p-sets of $X$,

$${\overline{X}}^{\overline{F}}=X-X^{-}$$

(4)

$X^{-}$ is called the $\overline{F}$-element deletion set of $X$,

$$X^{-}=\left\{x_i\right|x_i\in X,\overline{f}(x_i)=u_i\notin X,\overline{f}\in \overline{F}\}$$

(5)

If attribute set ${\alpha }^{\overline{F}}$ of ${\overline{X}}^{\overline{F}}$ meets

$${\alpha }^{\overline{F}}=\alpha -\left\{{\beta }_i\right|\overline{f}({\alpha }_i)={\beta }_i\notin \alpha ,\overline{f}\in \overline{F}\}$$

(6)

here, in (6), ${\alpha }_i\in \alpha ,$ and $\overline{f}\in \overline{F}$ changes ${\alpha }_i$ into $\overline{f}({\alpha }_i)={\beta }_i\notin \alpha$; and ${\alpha }^{\overline{F}}\ne \varnothing$; in (4), ${\overline{X}}^{\overline{F}}=\{x_1,x_2,\cdots ,x_p\},p<q,p,q\in N^{+}$.

The element set pairs constituted by internal inverse p-sets ${\overline{X}}^{\overline{F}}$ and outer inverse p-sets ${\overline{X}}^{\overline{F}}$ are called the inverse p-sets generated by $X$, inverse p-sets for short, and recorded as

$$({\overline{X}}^F,{\overline{X}}^{\overline{F}})$$

(7)

Cantor set $X$ is referred to as the ground set of inverse packet sets.

From (1)–(3), we have that if ${\alpha }_1^F\subseteq {\alpha }_2^F\subseteq \cdots \subseteq {\alpha }_{n-1}^F\subseteq {\alpha }_n^F$, then

$${\overline{X}}_1^F\subseteq {\overline{X}}_2^F\subseteq \cdots \subseteq {\overline{X}}_{n-1}^F\subseteq {\overline{X}}_n^F$$

(8)

From (4)–(6), we also have that if ${\alpha }_n^{\overline{F}}\subseteq {\alpha }_{n-1}^{\overline{F}}\subseteq \cdots \subseteq {\alpha }_2^{\overline{F}}\subseteq {\alpha }_1^{\overline{F}}$, then

$${\overline{X}}_n^{\overline{F}}\subseteq {\overline{X}}_{n-1}^{\overline{F}}\subseteq \cdots \subseteq {\overline{X}}_2^{\overline{F}}\subseteq {\overline{X}}_1^{\overline{F}}$$

(9)

From (7)–(9), we obtain

$$({\overline{X}}_1^F,{\overline{X}}_n^{\overline{F}})\subseteq ({\overline{X}}_2^F,{\overline{X}}_{n-1}^{\overline{F}})\subseteq \cdots \subseteq ({\overline{X}}_{n-1}^F,{\overline{X}}_2^{\overline{F}})\subseteq ({\overline{X}}_n^F,{\overline{X}}_1^{\overline{F}})$$

(10)

From (8) and (9), we obtain

$$\left\{\right({\overline{X}}_i{}^F,{\overline{X}}_j{}^{\overline{F}}\left)\right|i\in I,j\in J\}$$

(11)

(11) is referred to as the family of inverse p-sets generated by $X$, and (11) is the general expression of inverse packet sets.

From (1)–(11), we obtain the following theorem.

Theorem 1.

In the case of$F=\overline{F}=\varnothing$, the inverse p-sets$({\overline{X}}^F,{\overline{X}}^{\overline{F}})$and finite common element set$X$meet:

$$({\overline{X}}^F,{\overline{X}}^{\overline{F}}{)}_{F=\overline{F}=\varnothing }=X$$

(12)

Proof. 

1. If $F=\varnothing$, then we have

in (3), ${\alpha }^F=\alpha \cup \varnothing =\alpha ,\left\{{{\alpha }^{\prime }}_i\right|f({\beta }_i)={{\alpha }^{\prime }}_i\in \alpha ,f\in F\}=\varnothing$,

in (2), $X^{+}=\{u_{\mathrm{i}}|u_{\mathrm{i}}\in U,u_{\mathrm{i}}\notin X,f(u_{\mathrm{i}})={x^{\prime }}_i\in X,f\in F\}=\varnothing$,

in (1), ${\overline{X}}^F=X\cup X^{+}=X\cup \varnothing =X$.

2. if $\overline{F}=\varnothing$, then in (6), ${\alpha }^{\overline{F}}=$$\alpha -\left\{{\beta }_i\right|\overline{f}({\beta }_i)={\alpha }_i\notin \alpha ,\overline{f}\in \overline{F}\}=\alpha -\varnothing =\alpha ,$$\left\{{\beta }_i\right|\overline{f}({\beta }_i)={\alpha }_i\notin \alpha ,\overline{f}\in \overline{F}\}=\varnothing$, in (5), $X^{-}=$$\left\{x_i\right|x_i\in X,\overline{f}(x_i)=u_i\notin X,\overline{f}\in \overline{F}\}$, in (4), ${\overline{X}}^{\overline{F}}=X-X^{-}=X-\varnothing =X$.

From 1 and 2, we can complete this theorem. □

Theorem 2.

In the case of$F=\overline{F}=\varnothing$, the inverse p-sets family

$$\left\{\right({\overline{X}}_i{}^F,{\overline{X}}_j{}^{\overline{F}}\left)\right|i\in I,j\in J\}$$

and finite common element set$X$meet:

$$\left\{\right({\overline{X}}_i{}^F,{\overline{X}}_j{}^{\overline{F}}\left)\right|i\in I,j\in J{\}}_{F=\overline{F}=\varnothing }=X$$

The proof is similar to Theorem 1, and it is omitted.

Proposition 1.

Under static dynamic conditions, finite ordinary element set$X$is a special case of inverse p-sets$({\overline{X}}^F,{\overline{X}}^{\overline{F}})$, and inverse p-sets$({\overline{X}}^F,{\overline{X}}^{\overline{F}})$is the general form of finite ordinary element set$X$.

Proposition 2.

The dynamic characteristics of the inverse p-sets$({\overline{X}}^F,{\overline{X}}^{\overline{F}})$come from the attribute supplement and attribute deletion in the attribute set$\alpha$of$X$, the opposite is true.

Remark 1.

(1)$U$is a finite element domain and$V$is a finite attribute domain;

(2)$F=\{f_1,f_2,\cdots ,f_n\}$and$\overline{F}=\{{\overline{f}}_1,{\overline{f}}_2,\cdots ,{\overline{f}}_n\}$are the family of element (attribute) transfer; $f\in F,\overline{f}\in \overline{F}$are element (attribute) transfer, element (attribute) migration is the concept of transformation or function;

(3) The characteristics of$f\in F$are that for element$u_i\in U,$$u_i\notin X,f\in F$changes$u_i$into$f(u_i)={x^{\prime }}_i\in X$; for attribute${\beta }_i\in V,{\beta }_i\notin \alpha ,f\in F$changes${\beta }_i$into$f({\beta }_i)={\alpha }_i^{’}\in \alpha$;

(4) The characteristics of$\overline{f}\in \overline{F}$are that for element$x_i\in X,\overline{f}\in \overline{F}$changes$x_i$into$\overline{f}(x_i)=u_i\notin X$; for attribute${\alpha }_i\in \alpha ,\overline{f}\in \overline{F}$changes${\alpha }_i$into$\overline{f}({\alpha }_i)={\beta }_i\notin \alpha$;

(5) The dynamic characteristics of (1) are the same as the dynamic characteristics of accumulator$T=T+1$;

(6) The dynamic characteristics of (4) are the same as the dynamic characteristic of down-counter$T=T-1$. For example, in (1)${\overline{X}}_1^F=X\cup X_1^{+}$, let${\overline{X}}_1^F=X$,${\overline{X}}_2^F$$={\overline{X}}_1^F\cup X_2^{+}=(X\cup X_1^{+})\cup X_2^{+},\cdots ,$and so forth.

The fact of the existence of inverse p-sets and its logical characteristics.

$\overline{X}=\{x_1,x_2,x_3,x_4,x_5\}$ is a finite set of common elements composed of five children’s toys, $\alpha =\{{\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4,{\alpha }_5\}$ is the attribute set of $X$ (the color set of the children’s toys), where ${\alpha }_1$ denotes red color, ${\alpha }_2$ denotes yellow color, ${\alpha }_3$ denotes blue color, ${\alpha }_4$ denotes blue color, and ${\alpha }_5$ denotes orange color. The attribute ${\alpha }_i$ of $\forall x_i\in X$ satisfies the “disjunctive” feature in mathematical logic, or the attribute ${\alpha }_i$ of $\forall x_i\in X$ satisfies ${\alpha }_i={\alpha }_1\vee {\alpha }_2\vee {\alpha }_3\vee {\alpha }_4\vee {\alpha }_5;i=1,2,\cdots ,5$; and ”$\vee$“ is a “disjunctive” operation.

1. If the attributes ${\alpha }_6$ and ${\alpha }_7$ are supplemented in $\alpha$, among them, ${\alpha }_6$ denotes black color, ${\alpha }_7$ denotes purple color, $\alpha$ generates

$${\alpha }^F=\alpha \cup \{{\alpha }_6,{\alpha }_7\}=\{{\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4,{\alpha }_5,{\alpha }_6,{\alpha }_7\}$$

then $X$ is supplemented with $x_6$ and $x_7$,

$X$ generates ${\overline{X}}^F=X\cup \{x_6,x_7\}=\{x_1,x_2,x_3,x_4,x_5,x_6,x_7\}$, the attribute of $x_i$ is

$${\alpha }_i=({\alpha }_1\vee {\alpha }_2\vee {\alpha }_3\vee {\alpha }_4\vee {\alpha }_5)\vee {\alpha }_6\vee {\alpha }_7={\alpha }_1\vee {\alpha }_2\vee {\alpha }_3\vee {\alpha }_4\vee {\alpha }_5\vee {\alpha }_6\vee {\alpha }_7$$

2. If the attributes ${\alpha }_4$ and ${\alpha }_5$ are deleted in $\alpha$, $\alpha$ generates ${\alpha }^{\overline{F}}=\alpha -\{{\alpha }_4,{\alpha }_5\}$$=\{{\alpha }_1,{\alpha }_2,{\alpha }_3\}$, then $x_4$ and $x_5$ are deleted in $X$, $X$ generates ${\overline{X}}^{\overline{F}}=X-X^{-}=$$\{x_1,x_2,x_3,x_4,x_5\}-\{x_4,x_5\}=\{x_1,x_2,x_3\}$, and the attribute of $\forall x_i\in {\overline{X}}^{\overline{F}}$ is

$${\alpha }_i=({\alpha }_1\vee {\alpha }_2\vee {\alpha }_3\vee {\alpha }_4\vee {\alpha }_5)-\vee {\alpha }_4\vee {\alpha }_5={\alpha }_1\vee {\alpha }_2\vee {\alpha }_3$$

3. If the supplementary attribute and deletion attribute are carried out simultaneously in $\alpha$, $\alpha$ generates ${\alpha }^F$ and ${\alpha }^{\overline{F}}$ at the same time, $X$ generates ${\overline{X}}^F$ and ${\overline{X}}^{\overline{F}}$, or $X$ generates $({\overline{X}}^F,{\overline{X}}^{\overline{F}})$; the attribute ${\alpha }_i$ of $\forall x_i\in {\overline{X}}^F$ and the attribute ${\alpha }_j$ of $\forall x_j\in {\overline{X}}^{\overline{F}}$ satisfy $(({\vee }_{k=1}^5{\alpha }_k){\vee }_{k=6}^7{\alpha }_k,({\vee }_{k=1}^5{\alpha }_k)-{\vee }_{k=4}^5{\alpha }_k)$. This is a simple fact which can be accepted by ordinary people.

The concepts and models given in Section 2 are the preparation of the research theories, and the related methods are given in Section 3, Section 4, Section 5 and Section 6; it is important to read and accept the research results of Section 3, Section 4, Section 5 and Section 6.

Agreement: $(x)=X,{(\overline{x})}^F={\overline{X}}^F,$${(\overline{x})}^{\overline{F}}={\overline{X}}^{\overline{F}},({(\overline{x})}^F,{(\overline{x})}^{\overline{F}})=({\overline{X}}^F,{\overline{X}}^{\overline{F}})$ in Section 2. These marks are used in Section 3, Section 4, Section 5 and Section 6 without special explanation.

3. Information Segmentation and Its Attribute Characteristics

If there exists $\mathsf{\Delta }x\ne \varnothing ,\mathsf{\Delta }x\cap (x)=\varnothing$ meet

$${(\overline{x})}^F=(x)\cup \mathsf{\Delta }x$$

(13)

then ${(\overline{x})}^F$ is the ${\alpha }^F$-information segmentation of information $(x)$.

If there are $\nabla x\ne \varnothing ,\nabla x\cap (x)=\varnothing$ meet

$${(\overline{x})}^{\overline{F}}=(x)-\nabla x$$

(14)

then ${(\overline{x})}^{\overline{F}}$ is the ${\alpha }^{\overline{F}}$-information segmentation of information $(x)$.

The information segmentation pair composed of ${(\overline{x})}^F$ and ${(\overline{x})}^{\overline{F}}$ is called $({\alpha }^F,{\alpha }^{\overline{F}})$-information segmentation of information $(x)$, recorded as

$$({(\overline{x})}^F,{(\overline{x})}^{\overline{F}})$$

(15)

called

$$\{({(\overline{x})}_i^F,{(\overline{x})}_j^{\overline{F}})|i\in I,j\in J\}$$

(16)

is the $({\alpha }^F,{\alpha }^{\overline{F}})$-information segmentation family of information $(x)$, and (16) is a general expression of $({\alpha }^F,{\alpha }^{\overline{F}})$-information segmentation.

In (13), $\mathsf{\Delta }x$ is the composition of information element $x_i$ supplemented in information $(x)$;

In (14), $\nabla x$ is the composition of the deleted information element $x_j$ in the information $(x)$.

From (13)–(16), we obtain the following.

Theorem 3.

(${\alpha }^F$-information segmentation attribute theorem) If${(\overline{x})}_k^F$is the${\alpha }^F$-information partition of information$(x)$,${\alpha }_k^F$and$\alpha$are the attribute set of${(\overline{x})}_k^F$and$(x)$, respectively, then

$${\alpha }_k^F-(\alpha \cup \mathsf{\Delta }\alpha )=\varnothing$$

(17)

In (17),$\mathsf{\Delta }\alpha \ne \varnothing ,\alpha \cap \mathsf{\Delta }\alpha =\varnothing ,$$\mathsf{\Delta }\alpha$consists of the attribute${\alpha }_i$added to$\alpha$.

Proof. 

From (1)–(3) and (13) in Section 2, $\alpha \subseteq {\alpha }_k^F,$$\mathsf{\Delta }\alpha$ is the supplementary attribute set in $\alpha$, or ${\alpha }_k^F=\alpha \cup \mathsf{\Delta }\alpha$, we can directly obtained (17). □

Theorem 4.

(${\alpha }^{\overline{F}}$-information segmentation attribute theorem) If${(\overline{x})}_k^{\overline{F}}$is the${\alpha }^{\overline{F}}$-information partition of information$(x)$,${\alpha }_k^{\overline{F}}$and$\alpha$are the attribute set of${(\overline{x})}_k^{\overline{F}}$and$(x)$, respectively, then

$${\alpha }_k^{\overline{F}}-(\alpha -\nabla \alpha )=\varnothing$$

(18)

In (18), $\nabla \alpha \ne \varnothing ,\alpha \cap \nabla \alpha =\varnothing ,$ $\nabla \alpha$ is the composition of attribute ${\alpha }_j$ in $\alpha$.

The proof is similar to Theorem 3, and it is omitted.

From Theorems 3 and 4, we can obtain directly the following.

Inference 1.

If$({(\overline{x})}_k^F,{(\overline{x})}_k^{\overline{F}})$is the$({\alpha }^F,{\alpha }^{\overline{F}})$-information segmentation of$(x)$, the attribute set$({\alpha }_k^F,{\alpha }_k^{\overline{F}})$of$({(\overline{x})}_k^F,{(\overline{x})}_k^{\overline{F}})$and the attribute set$\alpha$of$(x)$meet

$$({\alpha }_k^F,{\alpha }_k^{\overline{F}})-(\alpha \cup \mathsf{\Delta }\alpha ,\alpha -\nabla \alpha )=\varnothing$$

(19)

In (19), $({\alpha }_k^F,{\alpha }_k^{\overline{F}})-(\alpha \cup \mathsf{\Delta }\alpha ,\alpha -\nabla \alpha )=\varnothing$ represents ${\alpha }_k^F-(\alpha \cup \mathsf{\Delta }\alpha )=\varnothing$,${\alpha }_k^{\overline{F}}-(\alpha -\nabla \alpha )=\varnothing$.

Theorem 5.

(Attribute disjunctive extension theorem of${\alpha }^F$-information segmentation) If${(\overline{x})}_k^F$is the${\alpha }^F$-information partition of information$(x)$, then the attribute${\alpha }_i$of information element$x_i\in {(\overline{x})}_k^F$meets

$${\alpha }_i=({\vee }_{\lambda =1}^q{\alpha }_{\lambda }){\vee }_{\lambda =q+1}^r{\alpha }_{\lambda }$$

(20)

In (20), $\alpha =\{{\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_q\}$ is the attribute set of information $\left(x)=\right\{x_1,x_2,\cdots ,x_q\}$, and ${\alpha }_k^F=\{{\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_q,{\alpha }_{q+1},\cdots ,{\alpha }_r\}$ is the attribute set of ${(\overline{x})}_k^F$.

Theorem 6.

(Attribute disjunctive contraction theorem of${\alpha }^{\overline{F}}$-information segmentation) If${(\overline{x})}_k^{\overline{F}}$is the${\alpha }^{\overline{F}}$-information partition of information$(x)$, then the attribute${\alpha }_j$of information element$x_j\in {(\overline{x})}_k^{\overline{F}}$meets

$${\alpha }_j=({\vee }_{\lambda =1}^q{\alpha }_{\lambda })-{\vee }_{\lambda =p+1}^q{\alpha }_{\lambda }$$

(21)

In (21), $\alpha =\{{\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_p,{\alpha }_{p+1},\cdots ,{\alpha }_q\}$ is the attribute set of information $\left(x)=\right\{x_1,x_2,\cdots ,x_p,x_{p+1},\cdots ,x_q\}$, and ${\alpha }_k^{\overline{F}}=\{{\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_p\}$ is the attribute set of ${(\overline{x})}_k^{\overline{F}}=\{x_1,x_2,\cdots ,x_p\}$.

Through the fact and logical characteristics of the existence of inverse p-sets in Section 2. It is easy to prove theorems 5 and 6, and the proof is omitted.

Inference 2.

If$({\alpha }_k^F,{\alpha }_k^{\overline{F}})$is the attribute set of$({\alpha }^F,{\alpha }^{\overline{F}})$-information segmentation$({(\overline{x})}_k^F,{(\overline{x})}_k^{\overline{F}})$, then$({\alpha }_i,{\alpha }_j)$composed of attribute${\alpha }_i$of information element$x_i\in {(\overline{x})}_k^F$and attribute${\alpha }_j$of$x_j\in {(\overline{x})}_k^{\overline{F}}$meets

$$({\alpha }_i,{\alpha }_j)=(({\vee }_{\lambda =1}^q{\alpha }_{\lambda }){\vee }_{\lambda =q+1}^r{\alpha }_{\lambda },({\vee }_{\lambda =1}^q{\alpha }_{\lambda })-{\vee }_{\lambda =p+1}^q{\alpha }_{\lambda })$$

(22)

here, (22) represents${\alpha }_i=({\vee }_{\lambda =1}^q{\alpha }_{\lambda }){\vee }_{\lambda =q+1}^r{\alpha }_{\lambda },{\alpha }_j=({\vee }_{\lambda =1}^q{\alpha }_{\lambda })-{\vee }_{\lambda =p+1}^q{\alpha }_{\lambda }$; in (20)–(22),$p<q<r;p,q,r\in N^{+}$.

By utilizing the concepts and results in Section 3 and Ref. [25], we will give Section 4.

4. Inverse P-Matrix Reasoning and Intelligent Acquisition of $\mathbf{\left(}{\mathit{\alpha }}^{\mathit{F}}\mathbf{,}{\mathit{\alpha }}^{\overline{\mathit{F}}}\right)$-Information Segmentation

If ${\overline{A}}_k^F,{\overline{A}}_{k+1}^F$ and ${(\overline{x})}_k^F,{(\overline{x})}_{k+1}^F$ meet

$$if\hspace{1em}{\overline{A}}_k^F\Rightarrow {\overline{A}}_{k+1}^F,\hspace{1em}then\hspace{1em}{(\overline{x})}_k^F\Rightarrow {(\overline{x})}_{k+1}^F$$

(23)

(23) is referred to as internal inverse packet matrix reasoning generated by an internal inverse packet matrix; ${\overline{A}}_k^F\Rightarrow {\overline{A}}_{k+1}^F$ is referred to as the condition of the internal inverse packet matrix reasoning, and ${(\overline{x})}_k^F\Rightarrow {(\overline{x})}_{k+1}^F$ is referred to as the conclusion of the internal inverse packet matrix reasoning.

If ${\overline{A}}_{k+1}^{\overline{F}},{\overline{A}}_k^{\overline{F}}$ and ${(\overline{x})}_{k+1}^{\overline{F}},{(\overline{x})}_k^{\overline{F}}$ meet

$$if\hspace{1em}{\overline{A}}_{k+1}^{\overline{F}}\Rightarrow {\overline{A}}_k^{\overline{F}},then\hspace{1em}{(\overline{x})}_{k+1}^{\overline{F}}\Rightarrow {(\overline{x})}_k^{\overline{F}}$$

(24)

(24) is referred to as the outer inverse packet matrix reasoning generated by an outer inverse packet matrix; ${\overline{A}}_{k+1}^{\overline{F}}\Rightarrow {\overline{A}}_k^{\overline{F}}$ is referred to as the condition of outer inverse packet matrix reasoning, and ${(\overline{x})}_{k+1}^{\overline{F}}\Rightarrow {(\overline{x})}_k^{\overline{F}}$ is referred to as the conclusion of the outer inverse packet matrix reasoning.

Here, in (23) and (24), “$\Rightarrow$” is equivalent to “$\subseteq$”.

If $({\overline{A}}_k^F,{\overline{A}}_{k+1}^{\overline{F}}),({\overline{A}}_{k+1}^F,{\overline{A}}_k^{\overline{F}})$ and $({(\overline{x})}_k^F,{(\overline{x})}_{k+1}^{\overline{F}}),({(\overline{x})}_{k+1}^F{(\overline{x})}_k^{\overline{F}})$ meet

$$if\hspace{1em}({\overline{A}}_k^F,{\overline{A}}_{k+1}^{\overline{F}})\Rightarrow ({\overline{A}}_{k+1}^F,{\overline{A}}_k^{\overline{F}}),then\hspace{1em}({(\overline{x})}_k^F,{(\overline{x})}_{k+1}^{\overline{F}})\Rightarrow ({(\overline{x})}_{k+1}^F{(\overline{x})}_k^{\overline{F}})$$

(25)

(25) is referred to as the inverse packet matrix reasoning generated by the inverse packet matrix; $({\overline{A}}_k^F,{\overline{A}}_{k+1}^{\overline{F}})\Rightarrow ({\overline{A}}_{k+1}^F,{\overline{A}}_k^{\overline{F}})$ is referred to as the condition of inverse packet matrix reasoning, and $({(\overline{x})}_k^F,{(\overline{x})}_{k+1}^{\overline{F}})\Rightarrow ({(\overline{x})}_{k+1}^F{(\overline{x})}_k^{\overline{F}})$ is referred to as the conclusion of the inverse packet matrix reasoning.

From (23)–(25), we obtain the following.

Theorem 7.

(${\alpha }^F$-information segmentation intelligent acquisition theorem)

If${\overline{A}}_k^F,{\overline{A}}_{k+1}^F$and${(\overline{x})}_k^F,{(\overline{x})}_{k+1}^F$meet (23), then we have the following:

1.${(\overline{x})}_{k+1}^F$is segmented outside${(x)}_k^F$for intelligent acquisition and meets

$$card({(\overline{x})}_{k+1}^F)-card({(\overline{x})}_k^F)>0$$

(26)

2. The attribute set${\alpha }_{k+1}^F$of${(\overline{x})}_{k+1}^F$and the attribute set${\alpha }_k^F$of${(\overline{x})}_k^F$meet

$${\alpha }_{k+1}^F\cap {\alpha }_k^F\ne \varnothing$$

(27)

Proof. 

1. If ${\overline{A}}_k^F,{\overline{A}}_{k+1}^F$ and ${(\overline{x})}_k^F,{(\overline{x})}_{k+1}^F$ meet $if\hspace{1em}{\overline{A}}_k^F\Rightarrow {\overline{A}}_{k+1}^F,\hspace{1em}then\hspace{1em}{(\overline{x})}_k^F\Rightarrow {(\overline{x})}_{k+1}^F$. From (1)–(3) in Section 2 and (13), supplement the information element $x_j$ in ${(\overline{x})}_k^F$ to generate ${(\overline{x})}_{k+1}^F$, or ${(\overline{x})}_k^F\subseteq {(\overline{x})}_{k+1}^F$, under the condition of ${\overline{A}}_k^F\Rightarrow {\overline{A}}_{k+1}^F$, ${(\overline{x})}_{k+1}^F$ is segmented and intelligently acquired outside ${(\overline{x})}_k^F$ or $card({(\overline{x})}_{k+1}^F)-$$card({(\overline{x})}_k^F)>0$, we get (26).

2. With the help of ${(\overline{x})}_k^F\subseteq {(\overline{x})}_{k+1}^F$, and the attribute set ${\alpha }_k^F$ of ${(\overline{x})}_k^F$ and the attribute set ${\alpha }_{k+1}^F$ of ${(\overline{x})}_{k+1}^F$ meet ${\alpha }_k^F\subseteq {\alpha }_{k+1}^F$, or ${\alpha }_{k+1}^F\cap {\alpha }_k^F\ne \varnothing$, we get (27). □

Theorem 8.

(${\alpha }^{\overline{F}}$-information segmentation intelligent acquisition theorem)

If${\overline{A}}_{k+1}^{\overline{F}},{\overline{A}}_k^{\overline{F}}$and${(\overline{x})}_{k+1}^{\overline{F}},{(\overline{x})}_k^{\overline{F}}$meet (24), then we have the following:

1.${(\overline{x})}_{k+1}^{\overline{F}}$is segmented and intelligently acquired in${(\overline{x})}_k^{\overline{F}}$and meets

$$card({(x)}_{k+1}^{\overline{F}})-card({(x)}_k^{\overline{F}})<0$$

(28)

2. The attribute set${\alpha }_{k+1}^{\overline{F}}$of${(\overline{x})}_{k+1}^{\overline{F}}$and the attribute set${\alpha }_k^{\overline{F}}$of${(\overline{x})}_k^{\overline{F}}$meet

$${\alpha }_{k+1}^{\overline{F}}\cap {\alpha }_k^{\overline{F}}\ne \varnothing$$

(29)

The proof of Theorem 8 is similar to Theorem 7, and the proof is omitted.

Inference 3.

If the reasoning condition$({\overline{A}}_k^F,{\overline{A}}_{k+1}^{\overline{F}})\Rightarrow ({\overline{A}}_{k+1}^F,{\overline{A}}_k^{\overline{F}})$of the inverse P-matrix is met, the information segmentation${(\overline{x})}_{k+1}^F$of${\alpha }^F$and the information segmentation${(\overline{x})}_{k+1}^{\overline{F}}$of${\alpha }^{\overline{F}}$are obtained intelligently at the same time.

Theorem 9.

(${\alpha }^F$-information segmentation relation theorem)

If$\{{(\overline{x})}_i^F|{(\overline{x})}_i^F\subseteq {(\overline{x})}_{i+1}^F,{\alpha }_i^F\subseteq {\alpha }_{i+1}^F,i=1,2,\cdots ,n\}$is the${\alpha }^F$-information partition chain generated by$(x)$, then${(\overline{x})}_k^F$and its attribute set${\alpha }_k^F$meet

$$\underset{i=1}{\overset{k-1}{\cup }}{(\overline{x})}_i^F\subseteq {(\overline{x})}_k^F\subseteq \underset{i=k+1}{\overset{n}{\cap }}{(\overline{x})}_i^F$$

(30)

$$\underset{i=1}{\overset{k-1}{\cup }}{\alpha }_i^F\subseteq {\alpha }_k^F\subseteq \underset{i=k+1}{\overset{n}{\cap }}{\alpha }_i^F$$

(31)

Proof. 

${(\overline{x})}_i$ meets ${(\overline{x})}_1^F\subseteq {(\overline{x})}_2^F\subseteq \cdots \subseteq {(\overline{x})}_{k-1}^F\subseteq {(\overline{x})}_k^F\subseteq {(\overline{x})}_{k+1}^F\subseteq \cdots \subseteq {(\overline{x})}_n^F$, directly obtained (30). The attribute set of ${(\overline{x})}_1^F,{(\overline{x})}_2^F,\cdots ,{(\overline{x})}_{k-1}^F,{(\overline{x})}_k^F,{(\overline{x})}_{k+1}^F,\cdots ,{(\overline{x})}_n^F$ meets ${\alpha }_1^F\subseteq {\alpha }_2^F\subseteq \cdots$$\subseteq {\alpha }_{k-1}^F\subseteq {\alpha }_k^F\subseteq {\alpha }_{k+1}^F\subseteq \cdots \subseteq {\alpha }_n^F$, directly obtained (31). □

Theorem 10.

(${\alpha }^{\overline{F}}$-information segmentation relation theorem)

If$\{{(\overline{x})}_j^{\overline{F}}|{(\overline{x})}_{j+1}^{\overline{F}}\subseteq {(\overline{x})}_j^{\overline{F}},{\alpha }_{j+1}^{\overline{F}}\subseteq {\alpha }_j^{\overline{F}},j=1,2,\cdots ,n\}$is the${\alpha }^{\overline{F}}$-information partition chain generated by$(x)$, then${(\overline{x})}_k^{\overline{F}}$and its attribute set${\alpha }_k^{\overline{F}}$meet

$$\underset{j=1}{\overset{k-1}{\cup }}{(\overline{x})}_j^{\overline{F}}\subseteq {(\overline{x})}_k^{\overline{F}}\subseteq \underset{j=k+1}{\overset{n}{\cap }}{(\overline{x})}_j^{\overline{F}}$$

(32)

$$\underset{j=1}{\overset{k-1}{\cup }}{\alpha }_j^{\overline{F}}\subseteq {\alpha }_k^{\overline{F}}\subseteq \underset{j=k+1}{\overset{n}{\cap }}{\alpha }_j^{\overline{F}}$$

(33)

Theorem 11.

($({\alpha }^F,{\alpha }^{\overline{F}})$-information segmentation relation theorem)

If$\{({(\overline{x})}_i^F,{(\overline{x})}_j^{\overline{F}})|({(\overline{x})}_i^F,{(\overline{x})}_{j+1}^{\overline{F}})\subseteq ({(\overline{x})}_{i+1}^F,{(\overline{x})}_j^{\overline{F}}),({\alpha }_i^F,{\alpha }_{j+1}^{\overline{F}})\subseteq ({\alpha }_{i+1}^F,{\alpha }_j^{\overline{F}}),i,j=1,2,\cdots ,n\}$, is the $({\alpha }^F,{\alpha }^{\overline{F}})$-information partition chain generated by$(x)$, then$({(\overline{x})}_k^F,{(\overline{x})}_k^{\overline{F}})$and its attribute set$({\alpha }_k^F,{\alpha }_k^{\overline{F}})$meet

$$(\underset{i=1}{\overset{k-1}{\cup }}{(\overline{x})}_i^F,\underset{j=1}{\overset{k-1}{\cup }}{(\overline{x})}_j^{\overline{F}})\subseteq ({(\overline{x})}_k^F,{(\overline{x})}_k^{\overline{F}})\subseteq (\underset{i=k+1}{\overset{n}{\cap }}{(\overline{x})}_i^F,\underset{j=k+1}{\overset{n}{\cap }}{(\overline{x})}_j^{\overline{F}})$$

(34)

$$(\underset{i=1}{\overset{k-1}{\cup }}{\alpha }_i^F,\underset{j=1}{\overset{k-1}{\cup }}{\alpha }_j^{\overline{F}})\subseteq ({\alpha }_k^F,{\alpha }_k^{\overline{F}})\subseteq (\underset{i=k+1}{\overset{n}{\cap }}{\alpha }_i^F,\underset{j=k+1}{\overset{n}{\cap }}{\alpha }_j^{\overline{F}})$$

(35)

Inference 4.

The attribute set$\mathsf{\Delta }\alpha$of$\mathsf{\Delta }x$and the attribute set$\alpha$of$(x)$meet$\mathsf{\Delta }\alpha \cap \alpha =\varnothing$.

Inference 5.

The attribute set$\nabla \alpha$of$\nabla x$and the attribute set$\alpha$of$(x)$meet$\nabla \alpha \cap \alpha \ne \varnothing$.

Remark 2.

A$n\times n$matrix$A_{n\times n}$is given, and supplement$t$columns into$n$columns of$A_{n\times n}$, where$A_{n\times n}$becomes$A_{n\times (n+t)}$and$A_{n\times (n+t)}$is an ordinary augmented matrix of$A_{n\times n}$. In the application research of dynamic information system, we often encounter the following:

(1) If deleting$\lambda$columns from$n$columns of$A_{n\times n}$,$\lambda <n$,$A_{n\times n}$becomes$A_{n\times (n-\lambda )}$;

(2) Matrix pair$(A_{n\times (n-\lambda )},A_{n\times (n+t)})$composed of$A_{n\times (n-\lambda )}$and$A_{n\times (n+t)}$. In ordinary mathematics, we cannot find the definition and name of$A_{n\times (n-\lambda )}$and$(A_{n\times (n-\lambda )},A_{n\times (n+t)})$. Using the structure of P-sets, the finite ordinary set$X=\{x_1,x_2,\cdots ,x_q\}$is given, and$\alpha =\{{\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_k\}$is the attribute set of$X$;$X^{\overline{F}}=\{x_1,x_2,\cdots ,x_p\}$is called the internal p-sets generated by$X$,$X^F=\{x_1,x_2,\cdots ,x_r\}$is called the outer p-sets generated by $X$, and$(X^{\overline{F}},X^F)$is called the p-set generated by$X$where$p<q<r,$$p,q,r\in N^{+}$. If $\forall x_i\in X$has$n$element values$y_i$, take$y_j={(y_{1,j},y_{2,j},\cdots ,y_{q,j})}^T$as the column, then$X$generates matrix$A_{n\times q}$. Ref. [25] gives the following: $X^{\overline{F}}$ generates matrix $A_{n\times p}^{\overline{F}}$ , and $X^F$ generates matrix $A_{n\times r}^F$; $A_{n\times p}^{\overline{F}}$ is called the internal p-augmented matrix of $A_{n\times q}$; $A_{n\times r}^F$ is called the outer p-augmented matrix of $A_{n\times q}$; and $(A_{n\times p}^{\overline{F}},A_{n\times r}^F)$ is called the p-augmented matrix of$A_{n\times q}$. $A_{n\times r}^F$ is the same concept as an ordinary augmented matrix, where$A_{n\times p}^{\overline{F}}\subseteq A_{n\times q},A_{n\times q}\subseteq A_{n\times r}^F$. In Ref. [26], an augmented matrix was applied in the information fusion research.

By using the research results of Refs. [25,27] gives ${\overline{A}}_{n\times r}^F$. ${\overline{A}}_{n\times p}^{\overline{F}}$ and $({\overline{A}}_{n\times r}^F,{\overline{A}}_{n\times p}^{\overline{F}})$ are respectively called the internal inverse p-augmented matrix, outer inverse p-augmented matrix and inverse p-augmented matrix of $A_{n\times q}$. Here, $A_{n\times q}\subseteq {\overline{A}}_{n\times r}^F,$${\overline{A}}_{n\times p}^{\overline{F}}\subseteq A_{n\times q}$. The reasoning (23)–(25) in Section 4 can be easily obtained by using the properties of the inverse p-augmented matrix. The properties and applications of the inverse p-augmented matrix are widely discussed in Refs. [28,29,30].

Based on the results in Section 4 and Section 5 is given.

5. Equivalence of Information Segmentation and Information Fusion

If ${\eta }^F$ is the ${\alpha }^F$-fusion coefficient of ${[\overline{x}]}^F$ and ${\eta }^F$ meets

$${\eta }^F-1>0$$

(36)

then ${\alpha }^F$-information segmentation ${(\overline{x})}^F$ is the ${\alpha }^F$-information fusion ${[\overline{x}]}^F$ generated by $[x]$.

If ${\eta }^{\overline{F}}$ is the ${\alpha }^{\overline{F}}$-fusion coefficient of ${[\overline{x}]}^{\overline{F}}$ and ${\eta }^{\overline{F}}$ meets

$${\eta }^{\overline{F}}-1<0$$

(37)

then ${\alpha }^{\overline{F}}$-information segmentation ${(\overline{x})}^{\overline{F}}$ is ${\alpha }^{\overline{F}}$-information fusion ${[\overline{x}]}^{\overline{F}}$ generated by $[x]$.

If ${\eta }^F$ and ${\eta }^{\overline{F}}$ form a discrete interval ${[{\eta }^F,{\eta }^{\overline{F}}]}^{-1}$, then $({\alpha }^F,{\alpha }^{\overline{F}})$-information segmentation $({(\overline{x})}^F,{(\overline{x})}^{\overline{F}})$ is $({\alpha }^F,{\alpha }^{\overline{F}})$-information fusion $({[\overline{x}]}^F,{[\overline{x}]}^{\overline{F}})$ generated by $[x]$.

Here ${(\overline{x})}^F={[\overline{x}]}^F$, ${(\overline{x})}^{\overline{F}}={[\overline{x}]}^{\overline{F}}$, $({(\overline{x})}^F,{(\overline{x})}^{\overline{F}})=({[\overline{x}]}^F,{[\overline{x}]}^{\overline{F}})$,$(x)=[x]$; in (36), ${\eta }^F=card({[\overline{x}]}^F)/card([x])$; in (37), ${\eta }^{\overline{F}}=card({[\overline{x}]}^{\overline{F}})/card([x])$; ${[{\eta }^F,{\eta }^{\overline{F}}]}^{-1}=$$[{\eta }^F,{\eta }^{\overline{F}}]$; $card=cardinal\hspace{0.17em}number$.

Theorem 12.

(Interval outer point theorem of${\eta }^F$-fusion coefficient)

The${\alpha }^F$-fusion coefficient${\eta }^F$of${\alpha }^F$-information fusion${[\overline{x}]}^F$is the outer point of unit discrete interval$[0,1]$, and meets

$${\eta }^F\notin [0,1]$$

(38)

Theorem 13.

(Interval interior point theorem of${\eta }^{\overline{F}}$-fusion coefficient)

The${\alpha }^{\overline{F}}$-fusion coefficient${\eta }^{\overline{F}}$of${\alpha }^{\overline{F}}$-information fusion${[\overline{x}]}^{\overline{F}}$is the interior point of unit discrete interval$[0,1]$, and meets

$${\eta }^{\overline{F}}\in [0,1]$$

(39)

Theorem 14.

(Interval relation theorem of$({\alpha }^F,{\alpha }^{\overline{F}})$-fusion coefficient.) The interval${[{\eta }^F,{\eta }^{\overline{F}}]}^{-1}$formed by the fusion coefficient of$({\alpha }^F,{\alpha }^{\overline{F}})$-information fusion$({[\overline{x}]}^F,{[\overline{x}]}^{\overline{F}})$and the unit discrete interval$[0,1]$meet

$${[{\eta }^F,{\eta }^{\overline{F}}]}^{-1}\cap [0,1]\ne \varnothing$$

(40)

here, in (38)–(40),$[0,1]$is the unit discrete interval of values$0$and$1=\eta =card([x])/card([x])$, and$\eta =1$is the fusion coefficient of$[x]$itself.

Theorem 15.

(Equivalence theorem of${\alpha }^F$-information segmentation and${\alpha }^F$-information fusion)${\alpha }^F$-information segmentation${(\overline{x})}^F$and${\alpha }^F$-information fusion${[\overline{x}]}^F$are equivalent classes about attribute set${\alpha }^F$

$${[{(\overline{x})}^F]}_{{\alpha }^F}={[{[\overline{x}]}^F]}_{{\alpha }^F}$$

(41)

Theorem 16.

(Equivalence theorem of${\alpha }^{\overline{F}}$-information segmentation and${\alpha }^{\overline{F}}$-information fusion)${\alpha }^{\overline{F}}$-information segmentation${(\overline{x})}^{\overline{F}}$and${\alpha }^{\overline{F}}$-information fusion${[\overline{x}]}^{\overline{F}}$are equivalent classes about attribute set${\alpha }^{\overline{F}}$

$${[{(\overline{x})}^{\overline{F}}]}_{{\alpha }^{\overline{F}}}={[{[\overline{x}]}^{\overline{F}}]}_{{\alpha }^{\overline{F}}}$$

(42)

Theorem 17.

(Equivalence theorem of$({\alpha }^F,{\alpha }^{\overline{F}})$-information segmentation and$({\alpha }^F,{\alpha }^{\overline{F}})$-information fusion)$({\alpha }^F,{\alpha }^{\overline{F}})$-information segmentation$({(\overline{x})}^F,{(\overline{x})}^{\overline{F}})$and$({\alpha }^F,{\alpha }^{\overline{F}})$-information fusion$[{(\overline{x})}^F,{(\overline{x})}^{\overline{F}}]$are equivalent classes about attribute set$({\alpha }^F,{\alpha }^{\overline{F}})$

$${({(\overline{x})}^F,{(\overline{x})}^{\overline{F}})}_{({\alpha }^F,{\alpha }^{\overline{F}})}={[{[\overline{x}]}^F,{[\overline{x}]}^{\overline{F}}]}_{({\alpha }^F,{\alpha }^{\overline{F}})}$$

(43)

Remark 3.

The complete concept of “information fusion” is composed of two sub concepts: external information fusion (or${\alpha }^F$information fusion) and internal information fusion (or${\alpha }^{\overline{F}}$information fusion). Information$(x)=\{x_1,x_2,\cdots ,x_q\}$is given, under certain conditions, the information element$x_i$outside$(x)$is migrated into$(x)$,$(x)$generates${(\overline{x})}^F$, and${(\overline{x})}^F$is the external information fusion${[\overline{x}]}^F$generated by$[x]$,$[x]\subseteq {[\overline{x}]}^F$. Under certain conditions, the information element$x_j$in$(x)$is migrated from inside$(x)$to outside x, and$(x)$generates${(\overline{x})}^{\overline{F}}$;${(\overline{x})}^{\overline{F}}$is the internal information fusion${[\overline{x}]}^{\overline{F}}$generated by$[x]$,${[\overline{x}]}^{\overline{F}}\subseteq [x]$. In the application research of information fusion, two basic forms of information fusion: information outer fusion and information internal fusion are often encountered. The inverse p-sets given in Section 2 are a dynamic mathematical model for studying information fusion. The concepts of${\alpha }^F$-information segmentation${(\overline{x})}^F$and${\alpha }^{\overline{F}}$-information segmentation${(\overline{x})}^{\overline{F}}$given in Section 3 are obtained through a new understanding of the concept of information fusion. Obviously,${\alpha }^F$-information segmentation and the external information fusion are two equivalent concepts, and${\alpha }^{\overline{F}}$-information segmentation and internal information fusion are two equivalent concepts,${\alpha }^F$-information segmentation and${\alpha }^{\overline{F}}$-information segmentation are new concepts to study two kinds of information fusion.

Using the concepts and models in Section 2, and the theoretical results in Section 3, Section 4 and Section 5, the applications of these theoretical results are given in Section 6.

6. $\mathbf{(}{\mathit{\alpha }}^{\mathit{F}}\mathbf{,}{\mathit{\alpha }}^{\overline{\mathit{F}}}\mathbf{)}$-Information Fusion Intelligent Acquisition-Intelligent Retrieval Algorithm and Its Application

6.1. $({\alpha }^F,{\alpha }^{\overline{F}})$-Information Fusion Intelligent Acquisition Intelligent Retrieval Algorithm

In this section, only the ${\alpha }^{\overline{F}}$-intelligent fusion intelligent acquisition intelligent retrieval algorithm is given, which is a part of the $({\alpha }^F,{\alpha }^{\overline{F}})$-information fusion intelligent acquisition intelligent retrieval algorithm; the complete $({\alpha }^F,{\alpha }^{\overline{F}})$-information fusion intelligent acquisition intelligent retrieval algorithm is composed of the ${\alpha }^F$-information fusion intelligent acquisition intelligent retrieval algorithm and ${\alpha }^F$-intelligent fusion intelligent acquisition intelligent retrieval algorithm. The ${\alpha }^{\overline{F}}$-information fusion intelligent acquisition intelligent retrieval algorithm is shown in Figure 1.

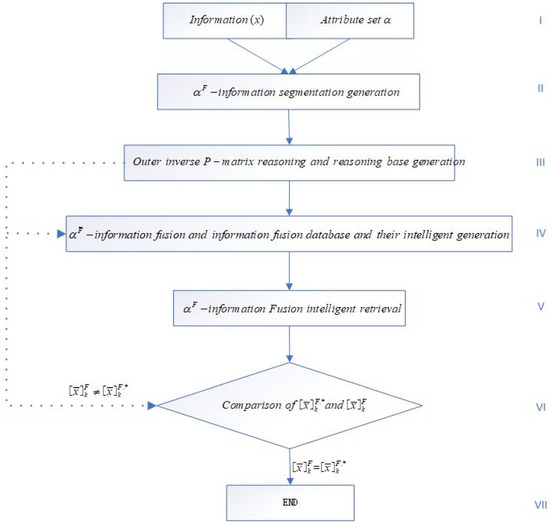
Figure 1. ${\alpha }^{\overline{F}}$-information fusion intelligent acquisition intelligent retrieval algorithm.

The detailed process of the algorithm is as follows:

(1)

Algorithm preparation: information $(x)$ and its attribute set $\alpha$ are given;

(2)

Using information $(x)$, attribute set $\alpha$ generates ${\alpha }^{\overline{F}}$-information segmentation ${(\overline{x})}_k^{\overline{F}},$ $k=1,2,\cdots ,n$;

(3)

The outer inverse P-matrix reasoning is established: $if {\overline{A}}_{k+1}^{\overline{F}}\Rightarrow {\overline{A}}_k^{\overline{F}},$ $then {(\overline{x})}_{k+1}^{\overline{F}}\Rightarrow {(\overline{x})}_k^{\overline{F}}$, and the outer inverse P-matrix inference database is generated;

(4)

${\alpha }^{\overline{F}}$-information fusion ${[\overline{x}]}_k^{\overline{F}}$ and the ${\alpha }^{\overline{F}}$-information fusion database are generated by II and III, $k=1,2,\cdots ,n$;

(5)

The ${\alpha }^{\overline{F}}$-information fusion intelligent retrieval rules are given;

(6)

Given the standard ${\alpha }^{\overline{F}}$-information fusion ${[\overline{x}]}_k^{\overline{F},*}$, if ${[\overline{x}]}_k^{\overline{F}}={[\overline{x}]}_k^{\overline{F},*}$, then the algorithm ends; if ${[\overline{x}]}_k^{\overline{F}}\ne {[\overline{x}]}_k^{\overline{F},*}$, return to (3) and (4); repeat (2)–(6). If ${[\overline{x}]}_k^{\overline{F}}={[\overline{x}]}_k^{\overline{F},*}$ is satisfied, the algorithm ends.

6.2. Application of $({\alpha }^F,{\alpha }^{\overline{F}})$-Information Fusion Intelligent Retrieval

In this section, only a simple application of ${\alpha }^{\overline{F}}$-information fusion intelligent retrieval is given; the application of ${\alpha }^F$-information fusion intelligent retrieval and $({\alpha }^F,{\alpha }^{\overline{F}})$-information fusion intelligent retrieval is omitted; application examples are taken from the “heart disease” block in “health big data”. The concepts and models in Section 2, the theoretical results in Section 3, Section 4 and Section 5, and the algorithms in Section 6.1 are applied in this section.

Given information $(x)$ and its attribute set $\alpha$, $y_j$ is the diagnostic value of $x_j\in (x)$ (examination value of disease, such as blood pressure, heart rate, etc.).

$$(x)=\{x_1,x_2,x_3,x_4,x_5,x_6\}$$

(44)

$$\alpha =\{{\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4,{\alpha }_5,{\alpha }_6\}$$

(45)

$$y_j={(y_{1,j},y_{2,j},y_{3,j},y_{4,j},y_{5,j},y_{6,j})}^T$$

(46)

$j=1,2,3,4,5,6.$

$(x)$ is composed of patients with “heart disease”, and ${\alpha }_i\in \alpha$ is the “symptom” (attribute) of $x_i\in (x)$; $\forall x_i,x_j\in (x)$ meets $i\ne j,{\alpha }_i\ne {\alpha }_j$. In order to protect the privacy of patients, patients and symptoms are represented by information element $x_i$ and attribute ${\alpha }_i$, respectively; $i=1,2,\cdots ,6$. The attribute ${\alpha }_i$ of $\forall x_i\in (x)$ satisfies the attribute disjunctive normal form (22): ${\alpha }_i={\alpha }_1\vee {\alpha }_2\vee {\alpha }_3\vee {\alpha }_4\vee$${\alpha }_5\vee {\alpha }_6={\vee }_{\lambda =1}^6{\alpha }_{\lambda }$.

I. In the treatment of $t_1\sim t_4\in T$, the symptom ${\alpha }_3,{\alpha }_5$ of $x_3,x_5$ disappears and $\alpha$ generates ${\alpha }_1^{\overline{F}}$, where

$${\alpha }_1^{\overline{F}}={\alpha }_1-\{{\alpha }_3,{\alpha }_5\}=\{{\alpha }_1,{\alpha }_2,{\alpha }_4,{\alpha }_6\}$$

(47)

$x_3,x_5\in (x)$ returns to the standard of healthy people, $x_3,x_5$ disappears from $(x)$, and $(x)$ generates ${\alpha }_1^{\overline{F}}$-information segmentation ${(\overline{x})}_1^{\overline{F}}$, where

$${(\overline{x})}_1^{\overline{F}}=x_1-\{x_3,x_5\}=\{x_1,x_2,x_4,x_6\}$$

(48)

$y_j={(y_{1,j},y_{2,j},y_{3,j},y_{4,j},y_{5,j},y_{6,j})}^T$ generates $y_1^{\overline{F}}$ in (46), where

$$y_1^{\overline{F}}={(y_{1,j},y_{2,j},y_{4,j},y_{6,j})}^T$$

(49)

$y_j$ and $y_1^{\overline{F}}$ constitute matrices $A_{6\times 6}$ and ${\overline{A}}_{6\times 4}^{\overline{F}}$ respectively, from the algorithm in Section 6.1: ${\alpha }_1^{\overline{F}}$-information segmentation ${(\overline{x})}_1^{\overline{F}}$ is intelligently retrieved, obtained in $(x)$.

II. In the treatment of $t_1\sim t_8\in T$, the symptom ${\alpha }_1,{\alpha }_6$ of $x_1,x_6$ disappears and ${\alpha }_1^{\overline{F}}$ generates ${\alpha }_2^{\overline{F}}$, where

$${\alpha }_2^{\overline{F}}={\alpha }_1^{\overline{F}}-\{{\alpha }_1,{\alpha }_6\}=\{{\alpha }_2,{\alpha }_4\}$$

(50)

$(x)$ generates ${\alpha }_2^{\overline{F}}$-information segmentation ${(\overline{x})}_2^{\overline{F}}$, where

$${(\overline{x})}_2^{\overline{F}}={(\overline{x})}_1^{\overline{F}}-\{x_1,x_6\}=\left\{x_2,x_4\right\}$$

(51)

${\alpha }_2^{\overline{F}}$-information segmentation ${(\overline{x})}_2^{\overline{F}}$ is intelligently retrieved and acquired in ${(\overline{x})}_1^{\overline{F}}$. $x_2,x_4\in (x)$ entered the ICU ward for treatment.

6.3. Result Authentication in Application Example

The search results (44)–(51) given in the example are accepted and confirmed by medical experts.

7. Discussion

The inverse p-set model with dynamic features and element attributes satisfying attribute extraction feature matches a class of information fusion features. If this kind of information fusion has dynamic characteristics, then the attributes ${\alpha }_i$ of the information element $x_i$ have the characteristics of attribute extraction. This kind of information fusion is commonly encountered in applied research. The inverse p-set model provides the support of mathematical models and methods for the study of this kind of information fusion and application. Information fusion is a dynamic concept with two forms: internal information fusion and external information fusion. In this paper, a new concept of information segmentation is proposed by using the inverse p-set mathematical model to re-recognize and re-study the concept of information fusion. Many new results can be obtained by using the concept of information segmentation to study information fusion and application, among which what is given in 3–6 is only a part of them.

In this paper, the information fusion intelligent retrieval algorithm and simple application are given on the basis of matrix reasoning. If the results in the paper are further improved, new ${\alpha }^F$-information fusion and ${\alpha }^{\overline{F}}$-information fusion are obtained, which are ${\alpha }^F$-information chain fusion and ${\alpha }^{\overline{F}}$-information chain fusion, respectively. These new studies are in progress and are obtained from the inverse p-sets family (11) in Section 2.