Analytic Valuation Formula for American Strangle Option in the Mean-Reversion Environment
Abstract
:1. Introduction
2. Model
3. Analytic Representation for American Strangle Options
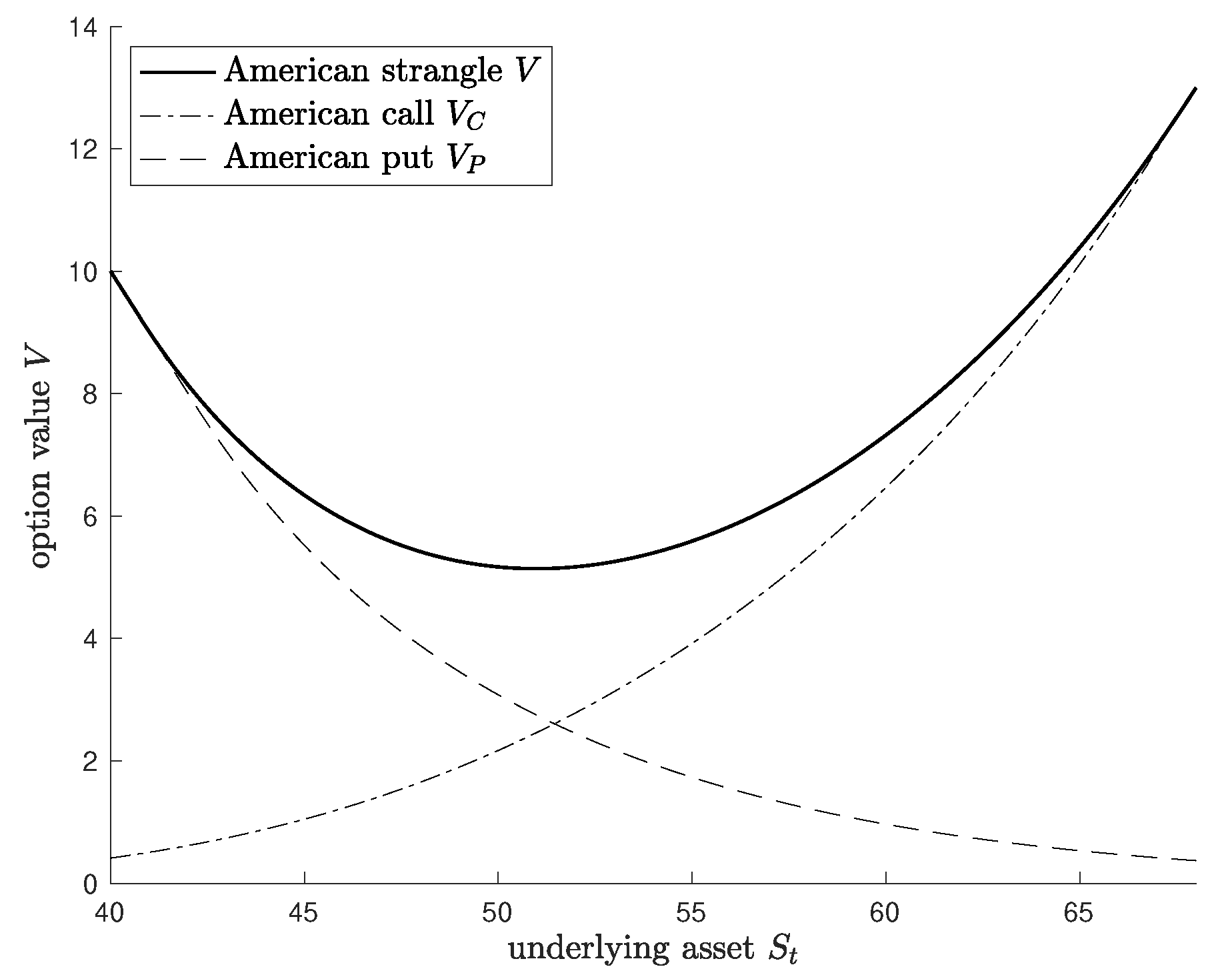
4. Numerical Results
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. The Nonhomogeneous PDE with the Operator L
Appendix B. Integral Equation Representation for American Options
References
- Black, F.; Scholes, M. The pricing of options and corporate liabilities. J. Political Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef] [Green Version]
- Cox, J.C.; Ross, S.A.; Rubinstein, M. Option pricing: A simplified approach. J. Financ. Econ. 1979, 7, 229–263. [Google Scholar] [CrossRef]
- Boyle, P.P. A lattice framework for option pricing with two state variables. J. Financ. Quant. Anal. 1988, 23, 1–12. [Google Scholar] [CrossRef]
- Tian, Y. A modified lattice approach to option pricing. J. Futur. Mark. (1986–1998) 1993, 13, 563. [Google Scholar] [CrossRef]
- Brennan, M.J.; Schwartz, E.S. Finite difference methods and jump processes arising in the pricing of contingent claims: A synthesis. J. Financ. Quant. Anal. 1978, 13, 461–474. [Google Scholar] [CrossRef]
- Courtadon, G. A more accurate finite difference approximation for the valuation of options. J. Financ. Quant. Anal. 1982, 17, 697–703. [Google Scholar] [CrossRef]
- Johnson, H.E. An analytic approximation for the American put price. J. Financ. Quant. Anal. 1983, 18, 141–148. [Google Scholar] [CrossRef]
- Geske, R.; Johnson, H.E. The American put option valued analytically. J. Financ. 1984, 39, 1511–1524. [Google Scholar] [CrossRef]
- Kim, I.J. The analytic valuation of American options. Rev. Financ. Stud. 1990, 3, 547–572. [Google Scholar] [CrossRef]
- Jacka, S.D. Optimal stopping and the American put. Math. Financ. 1991, 1, 1–14. [Google Scholar] [CrossRef]
- Longstaff, F.; Schwartz, E. Valuing American Options by Simulation: A Simple Least-Squares Approach. Rev. Financ. Stud. 2001, 14, 113–147. [Google Scholar] [CrossRef] [Green Version]
- Rogers, L.C. Monte Carlo valuation of American options. Math. Financ. 2002, 12, 271–286. [Google Scholar] [CrossRef]
- Park, K.; Jeon, J. A simple and fast method for valuing American knock-out options with rebates. Chaos Solitons Fractals 2017, 103, 364–370. [Google Scholar] [CrossRef]
- Kang, M.; Jeon, J.; Han, H.; Lee, S. Analytic solution for American strangle options using Laplace–Carson transforms. Commun. Nonlinear Sci. Numer. Simul. 2017, 47, 292–307. [Google Scholar] [CrossRef]
- Zaevski, T.S. A new form of the early exercise premium for American type derivatives. Chaos Solitons Fractals 2019, 123, 338–340. [Google Scholar] [CrossRef]
- Lee, J.K. A simple numerical method for pricing American power put options. Chaos Solitons Fractals 2020, 139, 110254. [Google Scholar] [CrossRef]
- Deng, G. Pricing perpetual American floating strike lookback option under multiscale stochastic volatility model. Chaos Solitons Fractals 2020, 141, 110411. [Google Scholar] [CrossRef]
- Qiu, S. American strangle options. Appl. Math. Financ. 2020, 27, 228–263. [Google Scholar] [CrossRef]
- Zaevski, T.S. A new approach for pricing discounted American options. Commun. Nonlinear Sci. Numer. Simul. 2021, 97, 105752. [Google Scholar] [CrossRef]
- Jeon, J.; Kim, G. An integral equation representation for American better-of option on two underlying assets. Adv. Contin. Discret. Model. 2022, 2022, 39. [Google Scholar] [CrossRef]
- Zaevski, T.S. Pricing discounted American capped options. Chaos Solitons Fractals 2022, 156, 111833. [Google Scholar] [CrossRef]
- Sorensen, C. An equilibrium approach to pricing foreign currency options. Eur. Financ. Manag. 1997, 3, 63–84. [Google Scholar] [CrossRef]
- Hui, C.; Lo, C. Currency barrier option pricing with mean reversion. J. Futur. Mark. 2006, 26, 939–958. [Google Scholar] [CrossRef]
- Wong, H.; Lau, K. Path-dependent currency options with mean reversion. J. Futur. Mark. 2008, 29, 275–293. [Google Scholar] [CrossRef]
- Panini, R. Option Pricing with Mellin Transforms; State University of New York at Stony Brook: Stony Brook, NY, USA, 2004. [Google Scholar]
- Frontczak, R.; Schöbel, R. On modified Mellin transforms, Gauss–Laguerre quadrature, and the valuation of American call options. J. Comput. Appl. Math. 2010, 234, 1559–1571. [Google Scholar] [CrossRef] [Green Version]
- Rodrigo, M.R. Approximate ordinary differential equations for the optimal exercise boundaries of American put and call options. Eur. J. Appl. Math. 2014, 25, 27–43. [Google Scholar] [CrossRef] [Green Version]
- Jeon, J.; Han, H.; Kang, M. Valuing American floating strike lookback option and Neumann problem for inhomogeneous Black–Scholes equation. J. Comput. Appl. Math. 2017, 313, 218–234. [Google Scholar] [CrossRef]
- Huang, J.Y.; Subrahmanyam, M.; Yu, G. Pricing and hedging American options: A recursive integration method. Rev. Financ. Stud. 1996, 9, 277–300. [Google Scholar] [CrossRef]
- Jeon, J.; Kim, G. Pricing European continuous-installment strangle options. N. Am. J. Econ. Financ. 2019, 50, 101049. [Google Scholar] [CrossRef]
- Jeon, J.; Kwak, M. Pricing Variable Annuity with Surrender Guarantee. J. Comput. Appl. Math. 2021, 393, 113508. [Google Scholar] [CrossRef]
- Erdlyi, A.; Magnus, W.; OberhettingerF, F.; Tricomi, F. Tables of Integral Transforms; McGraw-Hill: New York, NY, USA, 1954. [Google Scholar]
- Sneddon, I. The Use of Integral Transforms; McGraw-Hill: New York, NY, USA, 1972. [Google Scholar]
- Bertrand, J.; Bertrand, P.; Ovarlez, J. The Mellin Transform; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
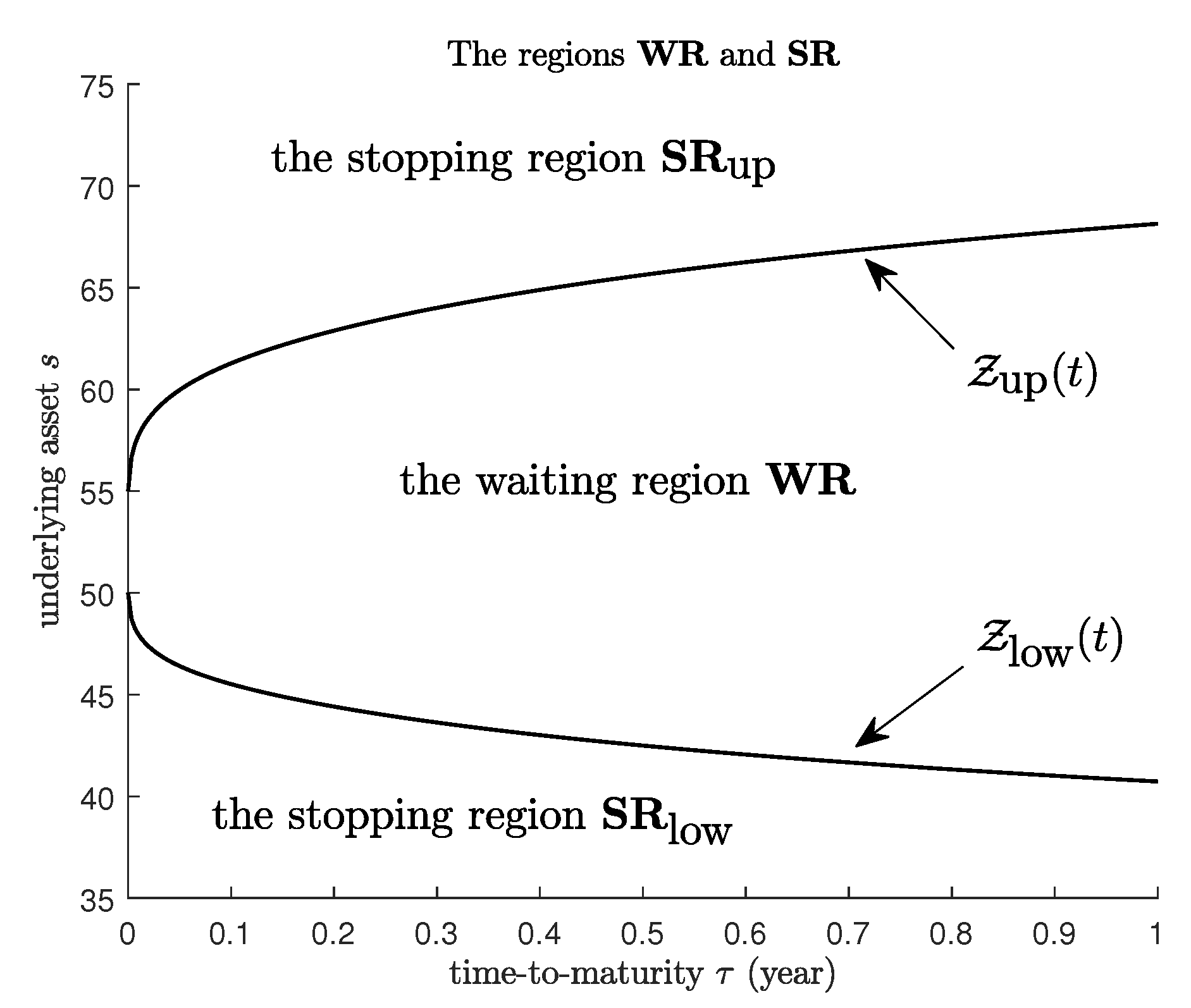
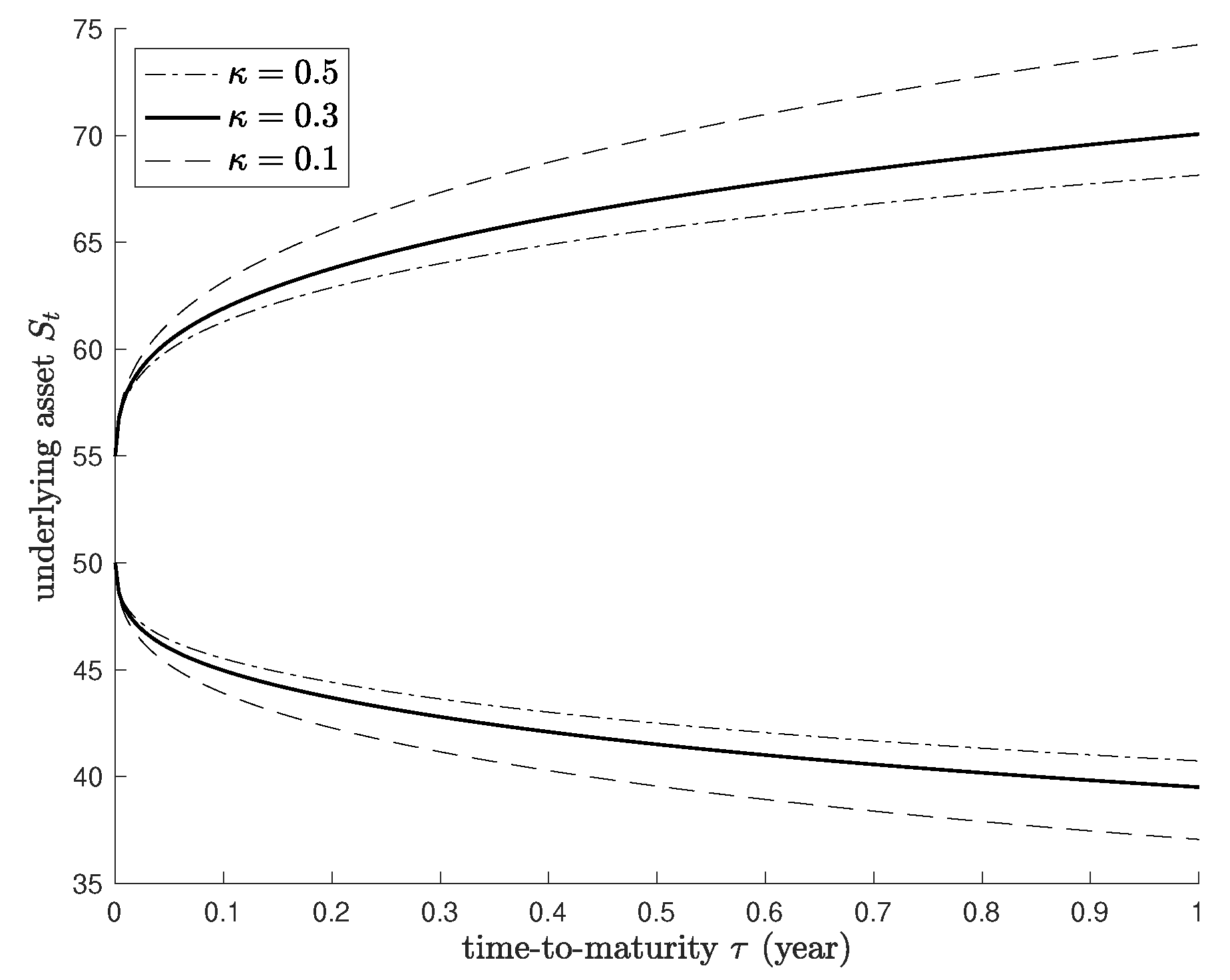


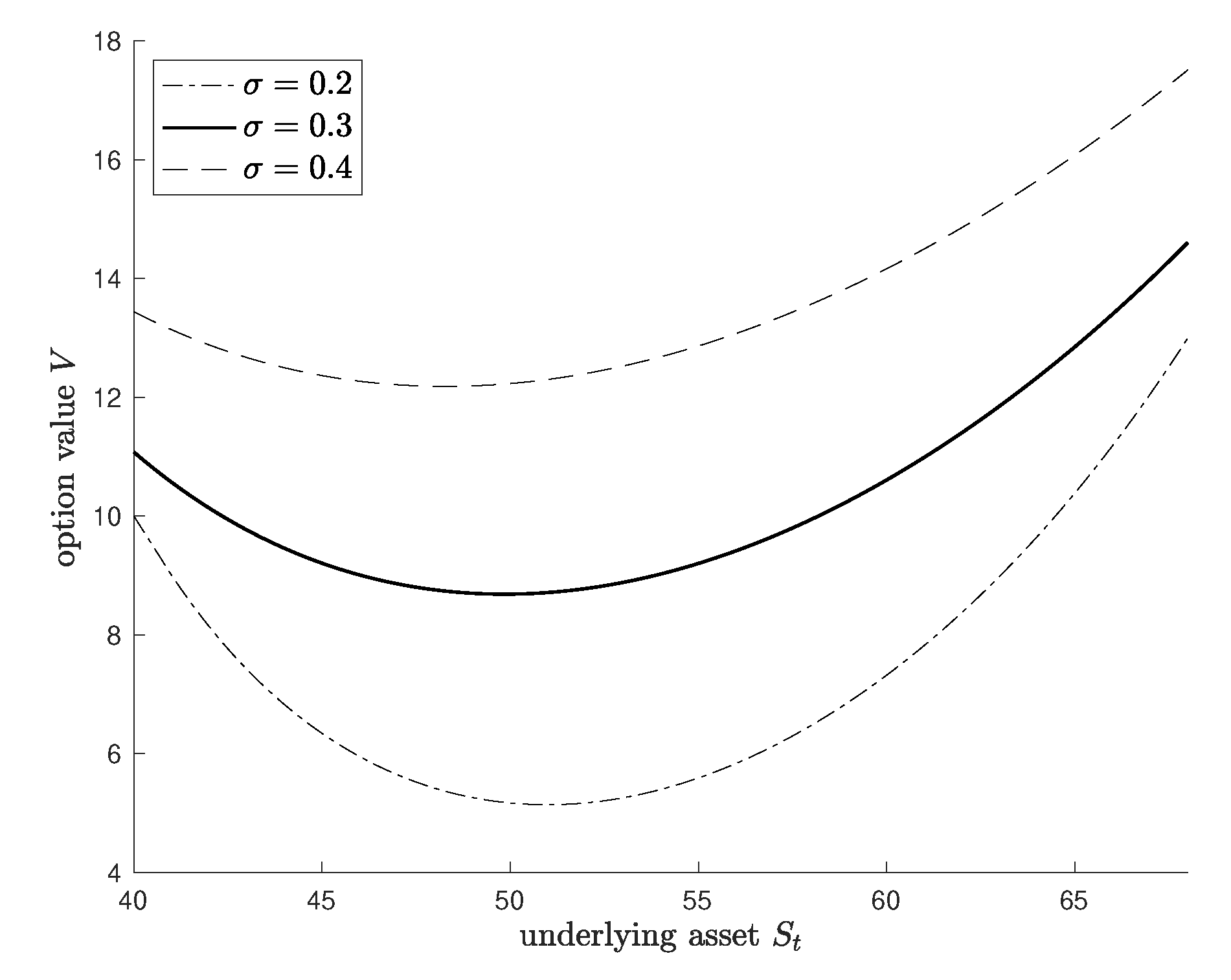
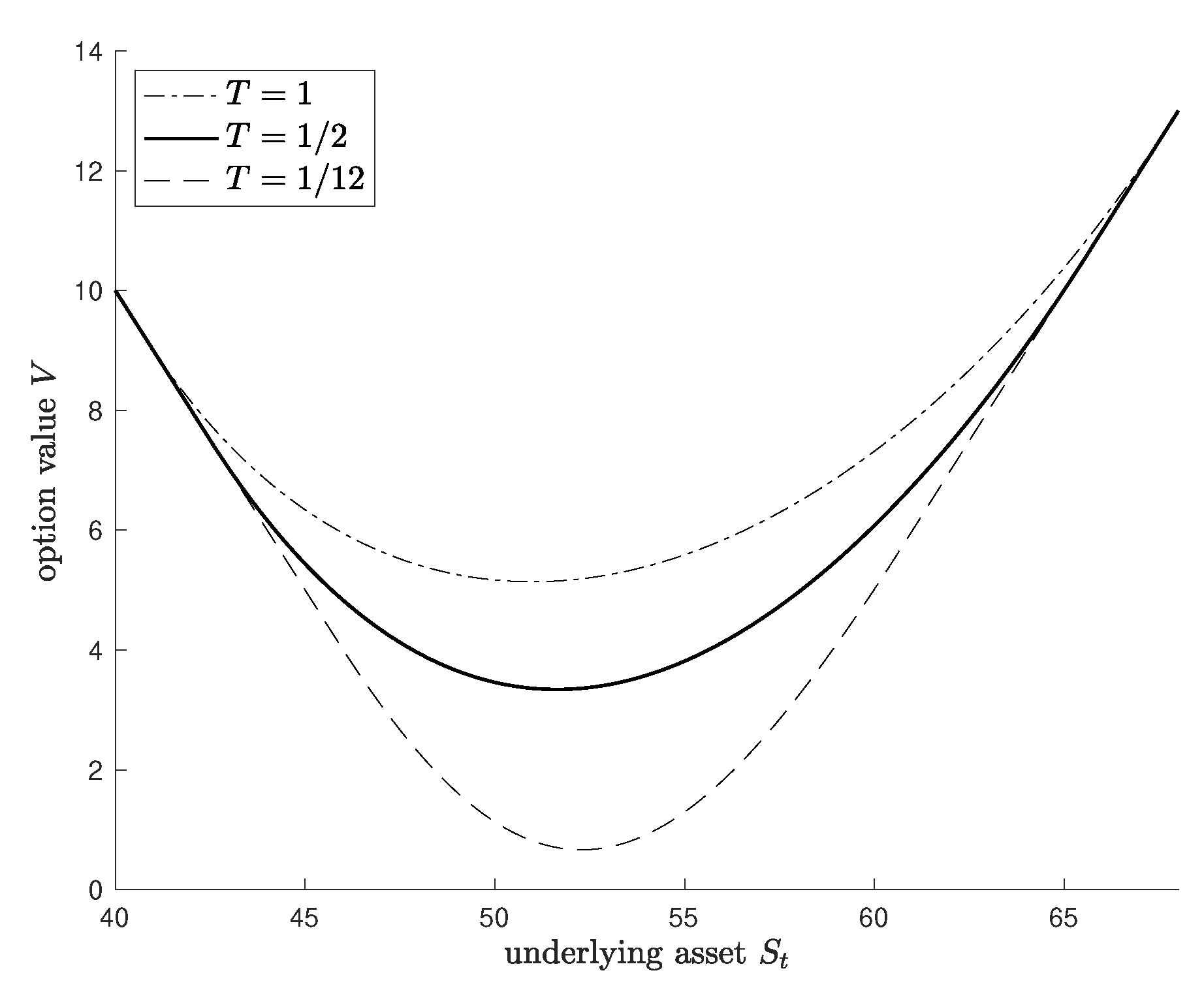

| r | RIM | MC | Relative Error (RE) | RIM | MC | Relative Error (RE) | ||
|---|---|---|---|---|---|---|---|---|
| 50 | 0.01 | 0.3 | 19.418 | 19.369 | 0.25% | 5.474 | 5.434 | 0.74% |
| 0.5 | 26.245 | 26.220 | 0.17% | 5.215 | 5.186 | 0.54% | ||
| 0.7 | 30.665 | 30.677 | 0.04% | 5.029 | 5.002 | 0.53% | ||
| 0.03 | 0.3 | 19.034 | 19.004 | 0.16% | 5.401 | 5.354 | 0.87% | |
| 0.5 | 25.726 | 25.755 | 0.11% | 5.149 | 5.166 | 0.83% | ||
| 0.7 | 30.058 | 30.088 | 0.10% | 4.968 | 4.938 | 0.61% | ||
| 0.05 | 0.3 | 18.657 | 18.688 | 0.17% | 5.329 | 5.279 | 0.94% | |
| 0.5 | 25.216 | 25.234 | 0.07% | 5.084 | 5.044 | 0.81% | ||
| 0.7 | 29.462 | 29.465 | 0.01% | 4.909 | 4.872 | 0.72% | ||
| 55 | 0.01 | 0.3 | 17.247 | 17.183 | 0.37% | 5.876 | 5.821 | 0.95% |
| 0.5 | 24.862 | 24.819 | 0.17% | 5.598 | 5.566 | 0.57% | ||
| 0.7 | 29.752 | 29.728 | 0.08% | 5.382 | 5.771 | 0.21% | ||
| 0.03 | 0.3 | 16.907 | 16.810 | 0.58% | 5.797 | 5.743 | 0.94% | |
| 0.5 | 24.369 | 24.314 | 0.23% | 5.526 | 5.505 | 0.37% | ||
| 0.7 | 29.163 | 29.168 | 0.02% | 5.317 | 5.338 | 0.39% | ||
| 0.05 | 0.3 | 16.573 | 16.502 | 0.43% | 5.719 | 5.680 | 0.69% | |
| 0.5 | 23.887 | 23.847 | 0.17% | 5.455 | 5.438 | 0.31% | ||
| 0.7 | 28.585 | 28.594 | 0.03% | 5.525 | 5.228 | 0.46% | ||
| 60 | 0.01 | 0.3 | 15.262 | 15.128 | 0.89% | 7.639 | 7.604 | 0.46% |
| 0.5 | 23.526 | 23.603 | 0.33% | 7.304 | 7.348 | 0.60% | ||
| 0.7 | 28.879 | 28.865 | 0.05% | 7.063 | 7.055 | 0.10% | ||
| 0.03 | 0.3 | 14.966 | 14.829 | 0.92% | 7.561 | 7.567 | 0.07% | |
| 0.5 | 23.060 | 23.069 | 0.04% | 7.239 | 7.248 | 0.12% | ||
| 0.7 | 28.307 | 28.329 | 0.07% | 7.008 | 7.062 | 0.76% | ||
| 0.05 | 0.3 | 14.676 | 14.534 | 0.98% | 7.486 | 7.505 | 0.26% | |
| 0.5 | 22.603 | 22.632 | 0.12% | 7.177 | 7.216 | 0.53% | ||
| 0.7 | 27.747 | 27.755 | 0.03% | 6.954 | 6.953 | 0.02% | ||
| Av. run time (s) | RIM | 0.016 | MC | 18.672 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeon, J.; Kim, G. Analytic Valuation Formula for American Strangle Option in the Mean-Reversion Environment. Mathematics 2022, 10, 2688. https://doi.org/10.3390/math10152688
Jeon J, Kim G. Analytic Valuation Formula for American Strangle Option in the Mean-Reversion Environment. Mathematics. 2022; 10(15):2688. https://doi.org/10.3390/math10152688
Chicago/Turabian StyleJeon, Junkee, and Geonwoo Kim. 2022. "Analytic Valuation Formula for American Strangle Option in the Mean-Reversion Environment" Mathematics 10, no. 15: 2688. https://doi.org/10.3390/math10152688
APA StyleJeon, J., & Kim, G. (2022). Analytic Valuation Formula for American Strangle Option in the Mean-Reversion Environment. Mathematics, 10(15), 2688. https://doi.org/10.3390/math10152688






