Identifying Hazardous Crash Locations Using Empirical Bayes and Spatial Autocorrelation

Abstract

Identifying and prioritizing hazardous road traffic crash locations is an efficient way to mitigate road traffic crashes, treat point locations, and introduce regulations for area-wide changes. A sound method to identify blackspots (BS) and area-wide hotspots (HS) would help increase the precision of intervention, reduce future crash incidents, and introduce proper measures. In this study, we implemented the operational definitions criterion in the Hungarian design guideline for road planning, reducing the huge number of crashes that occurred over three years for the accuracy and simplicity of the analysis. K-means and hierarchical clustering algorithms were compared for the segmentation process. K-means performed better, and it is selected after comparing the two algorithms with three indexes: Silhouette, Davies–Bouldin, and Calinski–Harabasz. The Empirical Bayes (EB) method was employed for the final process of the BS identification. Three BS were identified in Budapest, based on a three-year crash data set from 2016 to 2018. The optimized hotspot analysis (Getis-Ord Gi*) using the Geographic Information System (GIS) technique was conducted. The spatial autocorrelation analysis separates the hotspots, cold spots, and insignificant areas with 95% and 90% confidence levels.

1. Introduction

The typical process of eliminating or improving hazardous crash locations involves the following main steps; identification of blackspots and hotspots, diagnosis, finding countermeasures, estimating effects, prioritizing, implementation, and follow-up and evaluation. In this process, blackspot (BS) or hotspot (HS) identification comes as the first and most significant step. In this paper, we use the term blackspot to represent hazardous locations that require single site or point action, and hotspot to represent hazardous locations that require zonal or area action. When we refer to both, we use the term hazardous locations (HL). A reasonably significant body of literature is devoted to approaches for identifying blackspots that address a wide range of challenges [1]. There are numerous ways of identifying BS, Yuan et al. [2] summarized, from simple parametric models (based on crash frequency [3], crash rate [4], crash severity index [5], equivalent crash number [6], cumulative frequency [7], and quality control [8]) to complex parametric models (based on the derivation of safety performance functions, e.g., matrix analysis [9], regression analysis [10], fuzzy-based evaluation [11], Bayesian hierarchical [12], and neural network [13]). Many researchers also implemented the Empirical Bayes method as the most effective blackspot identification approach [14].

The Empirical Bayes (EB) method is powerful since it combines the observed and the predicted crashes in one model. In this paper, we implemented the EB method for the identification of BS along with Getis-Ord Gi* optimized hotspot analysis [15]. We analyzed both blackspots and hotspots to find different ways of looking at the hazardous locations so decision-makers may intervene in multiple ways. The benefits of identifying point-based BS are (i) it is easy to understand contributing factors for crashes, (ii) it is easy to introduce corrective measures, and (iii) it is feasible where there is a limited budget. Hotspots on the other hand, since they are area-wide, will offer insights for policy makers who plan to make regulatory and policy measures in the zonal level, which might be budget intensive and complicated compared to BS interventions.

Road safety has been studied for many years as a separate issue rather than as a pillar for sustainable urban transportation. An extensive effort to improve road safety would also have a big impact on improving overall urban mobility. As sustainable mobility became a mainstream agenda recently, area-wide crash hotspot identification has become of paramount importance. This study aims at filling this gap. This study combines the following three approaches: (i) the traditional BS screening approach, which is based on operational definitions and criteria, (ii) cluster analysis based on unsupervised machine learning algorithms such as K-means and hierarchical clustering to segment the preliminary BS locations identified in the first step, (iii) the Empirical Bayes method is implemented after segmentation to finalize the BS identification process, and iv) hotspot analysis based on Getis-Ord Gi* spatial autocorrelation to locate areas that require the highest priorities finally.

The most popular way of managing interventions in recent times to promote road safety and active mobility in many cities worldwide is through restricting the movement of cars in selected sections, or areas, in cities, but there are no clear criteria for identifying these areas. The area-wide or optimized hotspot analysis using the three-year crash dataset in Budapest from 2016 to 2018 would help decision-makers introduce area-wide interventions to significantly reduce or avoid crashes and introduce sustainable mobility options.

The objectives of this study can be summarized as follows: (i) to identify point-based blackspots for single-site action using the EB approach in Budapest city; (ii) to distinguish area-wide classes as hotspots and cold spots based on their spatial contiguity for an efficient area action in Budapest city; and (iii) to provide an overall framework by combining the first and second objectives for identifying hazardous locations (BS and HS).

2. Literature Review

There is no universally agreed and standard definition of a blackspot, but many studies define a blackspot as a place where crashes are historically concentrated. According to the Organization for Economic Cooperation and Development (OECD) report [16] and other latest works, a blackspot can have one of the following three definitions: numerical definitions (accident number, accident rate, and accident number and rate); statistical definitions (critical value of accident number and critical value of accident rate); and model-based definitions (Empirical Bayes and dispersion value). Numerous studies adopted one of these three definitions or a combination of them. Yuan and Shi [2] summarized some of the blackspot identification methods, and we included additional methods below from recent studies, as presented in Table 1.

The study period is another issue that differs across studies in blackspot identification. Many studies consider a period from 1 to 5 years to aggregate the crashes. Additionally, three years is the most commonly used period. In their experimental examination of blackspot identification methods, Cheng and Washington [1] found that the accuracy of blackspot identification obtained by employing a period longer than three years is marginal and drops fast as the duration of the period grows. Sørensen and Elvik [17] provided a summary of blackspot identification methods for selected European countries with six different characteristics including the operational definition of hotspot of the Hungarian design guideline for road planning, which is considered as the first screening method to reduce the number of crashes in a manageable size for the analysis in our paper.

Road safety specialists recognize four main approaches to treating roads with bad crash records: single site or spot action, route action, mass action, and area action. In this paper, we implemented the combination of a single site (blackspot) and area-wide (hotspots) action approaches.

Although there are numerous works on single-site or blackspot identification, only a limited body of work can be found on the area-wide identification of hotspots and cold spots, as far as the researchers’ knowledge goes. The purpose of identifying blackspots is to identify single sites and prioritize resources allocation, while the purpose of identifying hotspots is to bring significant impacts in transport safety or to ensure sustainable mobility through area-wide intervention. Measures such as safety treatment or protecting pedestrians and cyclists, who are regarded as vulnerable road users, by giving less access for motorized vehicles in favor of active mobility modes and mass transits throughout a hotspot area can be taken. Identifying locations with bad crash records and ranking them would help decision-makers allocate resources efficiently and prioritize interventions. Ghadi et al. [18] demonstrated that spatial clustering segmentation approaches performed better compared to other segmentation approaches, such as the constant length, constant traffic, and the standard highway safety manual (HSM) segmentation approaches. They also implemented the K-means clustering algorithm in their EB analysis [19]. Zhou et al. [20] also demonstrated that EB analysis techniques based on clustering are preferred to traditional statistical techniques. Wan et al. [21] also implemented the EB method by combining it with the Grey Verhuls model. This paper combined traditional approaches based on operational definitions, a machine learning clustering algorithm, the EB method, and a GIS-based optimized hotspot analysis for identifying crash blackspots and hotspots.

In their recent study, Ghadi and Török [22] compared the sliding window and spatial autocorrelation methods of blackspot identification for roads that differ in terms of average speed. They concluded that sliding window is favorable for high-speed roads while spatial autocorrelation method works best for low-speed roads. The dataset analyzed in the current study comes from the city of Budapest. Since it is an urban environment, the speed is characterized as low. Therefore, the spatial autocorrelation method is employed for identifying the hotspots.

The gaps in the literature that this paper tries to fill are: (i) many previous studies use only one method of segmentation, mostly K-means, but we implemented two machine learning algorithms, namely, K-means and hierarchical clustering, and we picked the one that performs better after evaluating them with different indexes; (ii) previous studies single handedly analyze blackspots or single site actions, but our work added optimized hotspot analysis or area action based on spatial autocorrelation as a complementary step to the single site action; and (iii) no such previous works were found in the case of Budapest City. Combining the two actionable approaches (single site and area-wide) is powerful because it gives a complete framework for dealing with hazardous locations in urban networks and assists policy makers in their transport safety planning process.

Table 1. Comparison of Blackspot Identification Methods.

Method	Advantage	Disadvantage	Suitable Condition	Related Work
Accident frequency	Considers the length and functionality of a road section.	Does not incorporate the regression effect of crashes.	Applicable to less traffic with a similar condition.	[3]
Matrix analysis	Evaluation of results is flexible and accurate.	Subjective identification criteria.	Applicable to less traffic with a similar condition.	[23]
Accident Severity	Considers types of crashes.	Inadequate representation of factors.	Applicable to a well-defined severity and consistent crash data.	[24]
Accident rate	Considers many crash factors.	Needs a huge crash dataset and ignores the randomness of crash events.	Applicable to rural roads.	[4]
Joint model (crash count and severity)	Considers correlated errors between crash count and severity.	Model complexity (Difficult to interpret and implement).	Applicable to different geographic scales.	[25]
Equivalent accidents number	Considers many crash factors.	Needs a huge crash dataset and difficult to estimate the value of weight.	Applicable to urban roads with a similar condition.	[26]
Quality control	Considers functionality of a road section and evaluation of result is accurate.	Needs huge traffic data and classification task.	Applicable to low traffic road sections.	[27]
Accident spacing distribution	Looks at the distribution of crashes.	It can be affected by the scale of the analysis.	Applicable to areas where crashes are occurring as a result of environmental factors.	[28]
Cumulative frequency	Uses many basic traffic data.	Does not consider the condition of a crash.	Applicable to crashes of varying conditions.	[7]
Regression analysis	Considers different factors for crashes.	Needs huge basic data and many model parameters.	Applicable to the quantification of rural crashes.	[29]
Fuzzy evaluation	Simple and suitable for multi-level problems.	Index of weight is subjective.	Wide applicability.	[30]
Expert experience	Estimate a result easily and quickly.	It is quite subjective.	Applicable to roads that lack basic data.	[31]
BP neural network	Evaluate crashes comprehensively.	An indicator is not directly related to a crash.	Applicable to highways.	[32]

Table 1. Comparison of Blackspot Identification Methods.

Method	Advantage	Disadvantage	Suitable Condition	Related Work
Accident frequency	Considers the length and functionality of a road section.	Does not incorporate the regression effect of crashes.	Applicable to less traffic with a similar condition.	[3]
Matrix analysis	Evaluation of results is flexible and accurate.	Subjective identification criteria.	Applicable to less traffic with a similar condition.	[23]
Accident Severity	Considers types of crashes.	Inadequate representation of factors.	Applicable to a well-defined severity and consistent crash data.	[24]
Accident rate	Considers many crash factors.	Needs a huge crash dataset and ignores the randomness of crash events.	Applicable to rural roads.	[4]
Joint model (crash count and severity)	Considers correlated errors between crash count and severity.	Model complexity (Difficult to interpret and implement).	Applicable to different geographic scales.	[25]
Equivalent accidents number	Considers many crash factors.	Needs a huge crash dataset and difficult to estimate the value of weight.	Applicable to urban roads with a similar condition.	[26]
Quality control	Considers functionality of a road section and evaluation of result is accurate.	Needs huge traffic data and classification task.	Applicable to low traffic road sections.	[27]
Accident spacing distribution	Looks at the distribution of crashes.	It can be affected by the scale of the analysis.	Applicable to areas where crashes are occurring as a result of environmental factors.	[28]
Cumulative frequency	Uses many basic traffic data.	Does not consider the condition of a crash.	Applicable to crashes of varying conditions.	[7]
Regression analysis	Considers different factors for crashes.	Needs huge basic data and many model parameters.	Applicable to the quantification of rural crashes.	[29]
Fuzzy evaluation	Simple and suitable for multi-level problems.	Index of weight is subjective.	Wide applicability.	[30]
Expert experience	Estimate a result easily and quickly.	It is quite subjective.	Applicable to roads that lack basic data.	[31]
BP neural network	Evaluate crashes comprehensively.	An indicator is not directly related to a crash.	Applicable to highways.	[32]

3. Materials and Methods

Researchers should have better knowledge of their data in order to perform appropriate traffic safety studies and practices [33]. A three-year aggregate crash dataset from 2016 to 2018 from the Hungarian capital Budapest was used for the analysis in this study. The crash datasets were initially split as an intersection crash dataset and a road link crash dataset, setting a buffer radius of 50 m from the center of the junction using the ArcGIS application. Information about road elements is normally collected in the form of nodes and links, with nodes as intersections and links as segments [34]. The Budapest road network shape files and crash datasets were imported into ArcMap [35] to prepare the crashes for further analysis and meaningful interpretations. Crashes are not entirely random [36], but they strongly correlate with the geometry and flow of vehicles on the road. Researchers conduct segment-based traffic safety analyses because of this hypothesis. Every junction or node is within the 50 m buffer radius. The midblock section, which is outside the buffer radius, was treated as a road link. After buffering, the intersection point between the buffer and the links was found where splitting was carried out. After splitting the crash data, road links were spatially joined using the ArcGIS Software application to merge the crash-related information and the geometric or spatial features.

3.1. Blackspot (BS) Analysis

3.1.1. Preliminary Screening Based on Operational Definitions

This stage implemented the common approach to blackspot identification based on historical crash datasets and screening of crash BS locations based on a certain definition. It could be based on any parametric or non-parametric model. We chose the “operational definition”-based screening of crash BS to reduce a huge number of crashes based on a reasonable criterion. This stage gives preliminary locations of BS, which will serve as a basis for the next steps.

Two operational definitions of blackspots are provided in Hungary. Outside built-up areas, it is a location where at least four accidents have been recorded in three years on a road segment no longer than 1000 m. Inside built-up areas, it is a location where at least four accidents have been recorded in three years. The sliding window for the search of the blackspot is given to be between 100 m and 1000 m. The operational definition does not refer to a specific type of road segment. In this study, we separate crashes at the junction from those on road sections. We treated each segment as a single separate window, and segments with more than four crash events in the three years period are treated as preliminary blackspots. Since the grand objective of blackspot identification is to improve road safety, the number of blackspots identified in this stage is still too high and prioritization would still face difficulties. Therefore, based on the preliminary blackspots at this stage, the next stage was clustering them down into manageable sizes before implementing the EB method. Two unsupervised machine learning algorithms are selected based on their popularity and efficiency in the analysis. They are also widely applied across many disciplines.

3.1.2. Final Segmentation Based on Unsupervised Machine Learning

Unsupervised learning occurs when algorithms learn independently without supervision or a target variable. It is a matter of discovering hidden patterns and relationships in the given data [37]. Two unsupervised clustering algorithms, namely K-means and hierarchical, were employed to further analyze the preliminary blackspots identified in the previous step. An elbow method was used to find the optimal number of clusters in the case of K-means, and a dendrogram method in the case of hierarchical.

K-Means Clustering

First introduced by Edward W. Forgy [38], researchers across different fields widely use the K-means clustering algorithm. The minimized objective function is presented as follows in Equation (1) [39]. The objective function’s main purpose is to decrease the intra-cluster distance by minimizing the distance between the points from the centroids for each cluster in each set of points.

$$J={\displaystyle \sum }_{j=1}^k{\displaystyle \sum }_{i=1}^n\Vert X_i^{\left(j\right)}-C_j\Vert {}^2$$

(1)

where $J$: objective function, $k$: number of clusters, $n$: number of cases, and $C_j$: centroid for cluster j.

The number of clusters is determined by the elbow method based on the “within clusters sum of square” (WCSS) method and is calculated by Equation (2) below.

$$WCSS={\displaystyle \sum }_{i=1}^{number of clusters \left(k\right)}{\displaystyle \sum }_{j=1}^{N_i}{d}_j^i$$

(2)

where $WCSS$ is within clusters sum of the square, $N_i$: number of points within cluster “$i$”, and $d_j^i$: squared distance between point “$j$” and the centroid of cluster “$i$”.

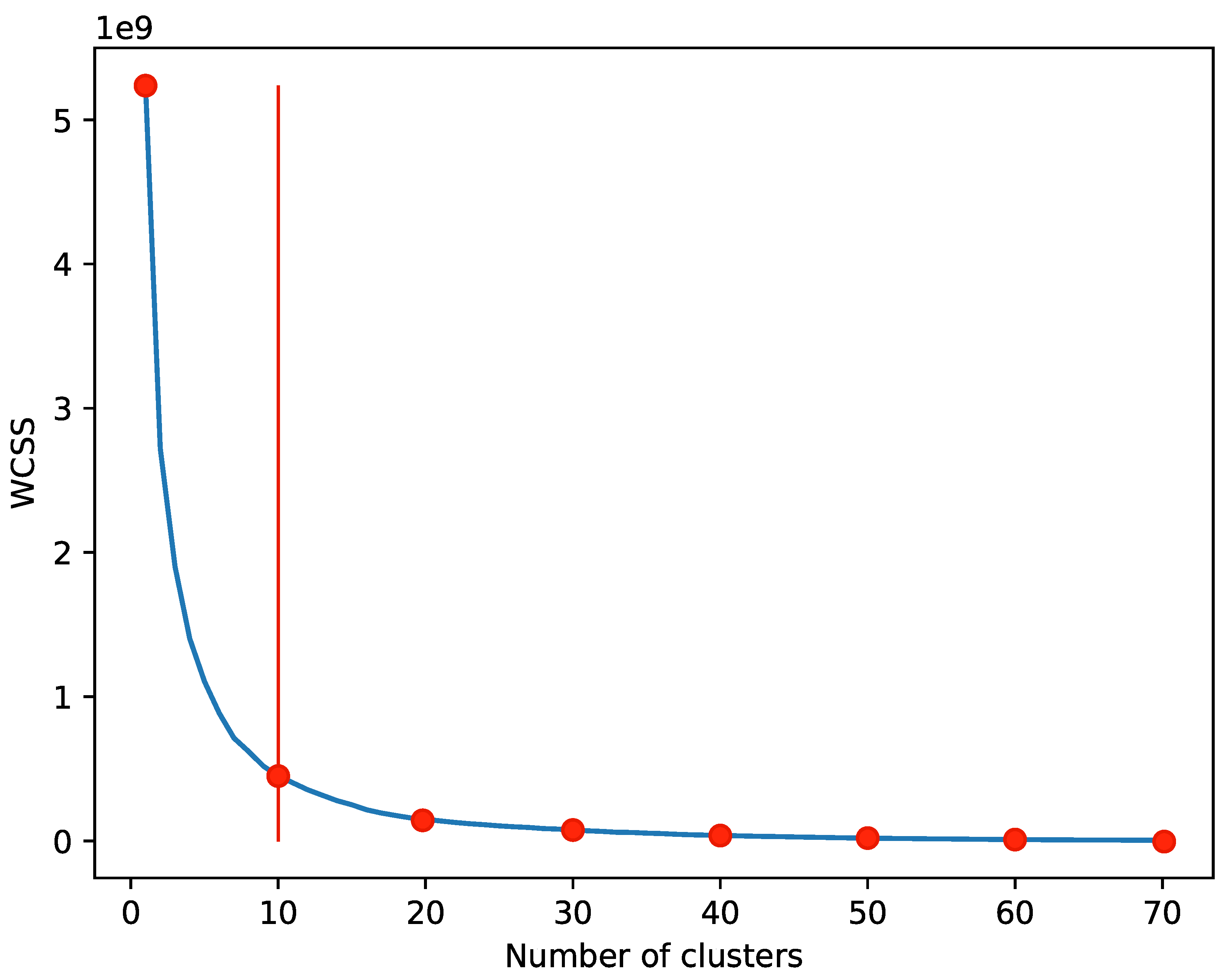
$WCSS$ values were estimated for 70 iterations of different cluster numbers, and the curve presented in Figure 1 below is built. The $WCSS$ value dropped very fast for the iteration at ten clusters.

Hierarchical Clustering

There are two types of hierarchical clustering algorithms. Agglomerative and divisible hierarchical clustering algorithms. Agglomerative hierarchical clustering is the most common method of the iterative hierarchical clustering algorithm. It is built with a bottom-up approach, while divisive is a top-down approach. Initially, every data point is treated as a cluster. At each iterative cycle, comparable clusters merge until a single cluster is formed. Additionally, this process can be visualized with the sequence of merges recorded and the dendrogram plotted as shown in Figure 2 below. In hierarchical clustering, no mathematical objective function can be directly solved. Instead, the proximity matrix is calculated to define inter-cluster similarity. It involves the following four steps.

Step 1: Make each data point a single-point cluster that forms N clusters.

Step 2: Take the two closest data points and make them one cluster that forms N-1 clusters.

Step 3: Take the two closest clusters and make them one cluster that forms N-2 clusters.

Step 4: Repeat step 3 until there is only one cluster.

Finish.

The dendrogram in Figure 2 below shows that the optimal number of clusters is ten, which is a similar result from the elbow method shown in Figure 1 above in the case of the K-means clustering model.

Once the clustering models were built, results were compared with three different metrics: Silhouette score, Davies–Bouldin index, and Calinski–Harabasz score. The indexes were used to compare the performance of the two unsupervised machine learning algorithms.

Silhouette score (s) for a single sample is then given by Equation (3) [40]:

$$s=\frac{a-b}{\max \left(a,b\right)}$$

(3)

where $a$ is the mean distance between a sample and all other points in the same class. $b$ is the mean distance between a sample and all other points in the next nearest cluster.

The higher the Silhouette Coefficient, the better that the model defined the clusters.

Calinski–Harabasz score (s) is defined as the ratio of the between-clusters dispersion mean and the within-cluster dispersion given by Equation (4) [41]:

$$s=\frac{tr\left(B_k\right)}{tr\left(W_k\right)}\times \frac{x{n}_E-k}{k-1}$$

(4)

where $tr\left(B_k\right)$ is the trace of the between group dispersion matrix and $tr\left(W_k\right)$ is the trace of the within-cluster dispersion matrix defined by Equations (5) and (6), respectively:

$$B_k={\displaystyle \sum }_{q=1}^k{n}_q\left(c_q-c_E\right){\left(c_q-c_E\right)}^T$$

(5)

$$W_k={\displaystyle \sum }_{q=1}^k{\displaystyle \sum }_{xЄC_q}\left(x-c_q\right){\left(x-c_q\right)}^T$$

(6)

where $C_q$ is the set of points in cluster $q$, $c_q$ is the center of cluster q, $c_E$ is the center of $E$, and $n_q$ is the number of points in cluster $q$.

Davies–Bouldin index (DB) is defined by Equation (7) [42,43]:

$$DB=\frac{1}{k}{\displaystyle \sum }_{i=1}^k{}_{i\ne j}{}^{max}R{}_{ij}$$

(7)

$$R_{ij}=\frac{S_i+S_j}{d_{ij}}$$

(8)

where $R_{ij}$ is the difference between $C_i$ for $i=1,\dots ,k$ and its most similar one $C_j$, $S_i$ is the average distance between each point of cluster $i$ and the centroid of that cluster, and $d_{ij}$ is the distance between cluster centroids $i$ and $j$.

3.1.3. Empirical Bayes Method

Empirical Bayes (EB) is considered as a sound method in BS identification and has been implemented by numerous researchers, as explained in Section 2 of this paper. It is a method for estimating the parameters of a prior distribution using data. Once we have chosen a prior distribution, we then need to estimate its parameters using the area-wide or urban network crash data. After estimating the prior distribution parameters, we can then use these estimates to make predictions about future crashes in the urban network [44]. The EB approach has a strong theoretical foundation. Both the Interactive Highway Safety Design Model [45] and the Comprehensive Highway Safety Improvement Model [46] now use it.

The typical steps in EB procedure presented in the HSM are the following.

• Determine whether the EB method is applicable,
• Determine whether observed crash frequency data are available,
• Assign crashes to individual roadway segments for use in the EB method,
• Apply the site-specific EB method.

The EB method is powerful because it applies Equation (9) below to incorporate the observed and future crash frequencies for a specific road network in a single statistical model.

$$N_E=w{N}_P+\left(1-w\right)N_0$$

(9)

where $N_E$ is the number of expected crashes; $N_P$ is the number of predicted crashes; and $N_0$ is the number of observed crashes. $w$ is a factor for weight adjustment where 0 ≤ $w$ ≤ 1 and is calculated by Equation (10).

$$w=\frac{1}{1+q\times \{{{\displaystyle \sum }}_{study years}{N}_P\}}$$

(10)

where q is the over-dispersion parameter in the prediction model $N_P$.

The predicted crash frequency $N_P$ is calculated by Equation (11) below [47].

$$N_P=\exp \left(\alpha +\beta \times \ln \left(AADT\right)+\ln \left(L\right)\right)$$

(11)

where $\alpha$ and $\beta$ are the regression parameters; $AADT$ is the average daily traffic; and $L$ is the length of the road segments within a specific cluster.

Once the expected ($N_E$) and predicted ($N_P$) numbers of crashes are estimated, the next and final step is to calculate their difference and determine the blackspots. If the difference is positive, the cluster is labeled as a blackspot. In addition to identifying the BS, we can also use the values to rank the BS in their risk magnitude.

The EB estimating procedure might be either full or abridged. The abridged version uses crash data from the last two to three years as well as the average traffic volume during the same time. This reflects the increasingly widespread notion that crash data older than two to three years may not accurately reflect the situation right now. However, the EB procedure eliminates most objections to using older data. Accordingly, a more extensive crash and traffic flow history is used in the full version of the EB method. However, since we were able to acquire the three-year crash data, we opted for the abridged version of the EB method.

3.2. Optimised Hotspot Analysis (Getis-Ord Gi* Spatial Autocorrelation)

Optimized Hotspot Analysis runs the Hotspot Analysis (Getis-Ord Gi*) tool to utilize parameters determined from the given input data features. Optimized hotspot analysis based on spatial autocorrelation (Getis-Ord Gi*) is conducted using ArcMap.

The resulting z-scores and p-values show where geographic clustering of characteristics with high or low values occurs. This technique operates by examining each feature in light of its surrounding features. Even while a feature with a high value may not be a statistically significant hotspot, it is nonetheless interesting. A feature must have a high value and be surrounded by additional features that have high values in order to be a statistically significant hotspot.

The equation for Getis-Ord Gi* is given by Equation (12) below [48].

$$G{i}^{*}=\frac{{{\displaystyle \sum }}_{j=1}^n{w}_{i,j}{x}_j-\overline{x}{{\displaystyle \sum }}_{j=1}^n{w}_{i,j}}{\sqrt[s]{\frac{n{{\displaystyle \sum }}_{j=1}^n{w}^2{}_{i,j}-{({{\displaystyle \sum }}_{j=1}^n{w}_{i,j})}^2}{n-1}}}$$

(12)

where $x_j$ is the attribute value for feature j, $w_{i,j}$ is the spatial weight between feature I and j, $n$ is the total number of features, and

$$\overline{X}=\frac{{{\displaystyle \sum }}_{j=1}^n{x}_j}{n} \mathrm{and} S=\sqrt{\frac{{{\displaystyle \sum }}_{j=1}^n{x}_j^2}{n}-{\overline{x}}^2}$$

(13)

Gi* statistic is a z-score, and no further calculations are required.

It is a density analysis and tells us where the clusters exist in our dataset, whereas blackspot analysis (micro) considers a feature (crash) in the entire dataset. A feature has a value in case of crash events, features are aggregated, and their count within aggregation represents the value [49].

The dataset analyzed in this study is from the city of Budapest. Since it is an urban environment, the speed is characterized as low. Therefore, the spatial autocorrelation method is employed for the analysis in this study to identify the hotspots.

4. Results and Discussions

First, using the operational definition, 99 locations were identified out of 5645 road segments in the city of Budapest on which 3403 crashes are distributed. Based on the Hungarian operational definition, road segments that registered at least four crashes in the three-year period are identified as preliminary crash blackspots. We gave different weights from the highest value for fatal crashes to the lowest value for property damage only (PDO) crashes, since it is not reasonable to merely aggregate different types of crashes.

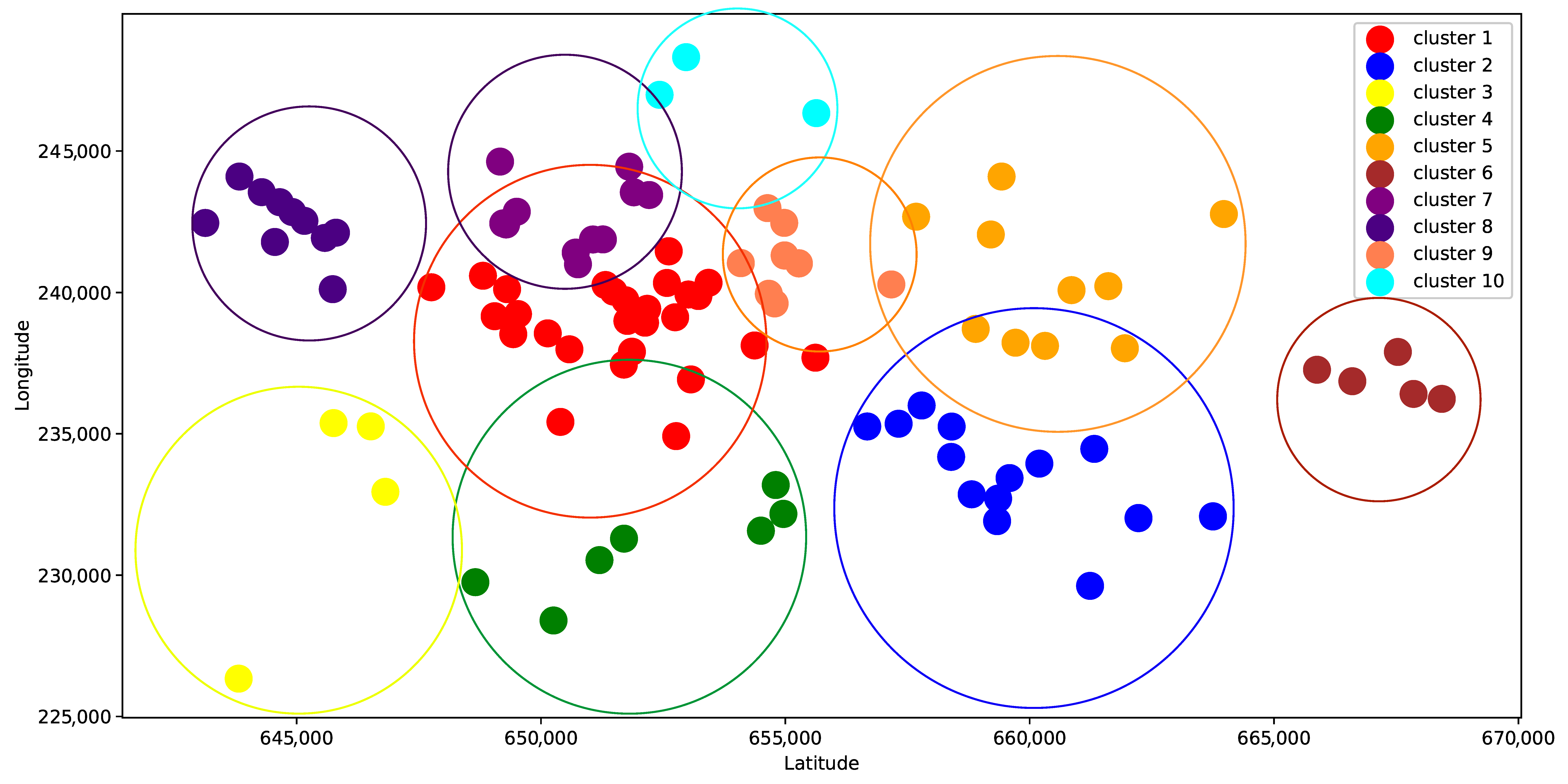
These 99 preliminary BS are clustered down into 10 groups using the hierarchical and K-means clustering models, as shown in Figure 3 and Figure 4 below.

The two clustering models were compared with the three metrics to identify the model with better performance, as presented in

Table 2. Comparing the two machine learning algorithms with three different criteria to find out the best.

Indices	Clustering Models
	K-Means	Hierarchical
Silhoutte score	0.409	0.399
Davies–Bouldin index	0.775	0.724
Calinski–Harabasz score	105.012	93.541

below. Considering Silhouette and Calinski–Harabasz scores, the K-means cluster model performs better since the values are higher than those in the corresponding hierarchical clustering models. However, when we see the Davies–Bouldin index, it seems that the hierarchical clustering model is the better one because it has a lower value. However, our data clusters are mostly convex clusters. The Davies–Bouldin index usually gives higher values in the case of convex clusters, which is one of its drawbacks. Therefore, it cannot be taken as a reliable metric. Therefore, we selected the K-means clustering model as a final model in the segmentation process and in preparing for the BS analysis using EB method.

Silhouette scores range from −1 to 1, with values closer to 1 indicating that the samples in a cluster are more similar to each other than to samples in other clusters, and values closer to −1 indicate the opposite. Adequate values for the Silhouette score are generally considered to be above 0.5. Calinski–Harabasz index values can range from 0 to infinity, with higher values indicating a better separation of clusters. Adequate values for the Calinski–Harabasz index are highly dependent on the specific data set and application. The Davies–Bouldin index ranges from 0 to infinity, with lower values indicating the better separation of clusters. Adequate values for the Davies–Bouldin index are generally considered to be below 1.

As a first step in the EB method, we determined if the method is applicable. According to the HSM, the EB method is not applicable in one of the following two conditions: (i) projects where a new alignment is created for a significant portion of the project’s duration; and (ii) intersections where a project changes the basic number of intersection legs or the kind of traffic control. Neither are the case in our project; therefore, we can apply the EB method. After we determined its applicability, we assigned crashes to each cluster from the K-means clustering model. Only fatal crashes were assigned to the ten clusters. The HSM aggregates fatal and serious injury crashes in the BS analysis, but, in our analysis, we considered fatal crashes only to be more accurate about the BS determination. After assigning the crashes to each cluster, the next step was to prepare the parameters for the EB-based BS analysis. The road links within each cluster were summed up and incorporated as a length (in km) parameter in Equation (11) to calculate the predicted number of crashes ($N_P$). In addition to length, the average daily traffic and the regression parameters were used in predicting the number of crashes for each cluster. The weight adjustment factor was calculated using the summation of the predicted number of crashes for the study years and an over-dispersion parameter. An over-dispersion parameter value of 0.84 was taken according to our dataset’s HSM and road types. The expected number of crashes was calculated for each cluster using the predicted number of crashes of each cluster, the observed number of crashes for each cluster, and the weight adjustment factor. The difference between the expected and predicted number of crashes was calculated. Clusters, which have a positive value of the difference, were labeled as BS and summarized as shown in

Table 3. BS identification using the EB method.

Cluster ID	Length (km)	Average Daily Traffic	NE − NP	Label
1	5.42	13,157	−7.916	-
2	5.21	9069	−1.667	-
3	4.83	8915	1.837	BS
4	3.26	8569	0.744	BS
5	3.23	10,827	−1.727	-
6	2.29	12,595	−1.328	-
7	4.45	10,873	−3.526	-
8	7.52	10,911	−8.065	-
9	4.46	10,404	0.837	BS
10	2.58	15,369	−4.742	-

below. Cluster 3, 4, and 9 were identified to be the BS points.

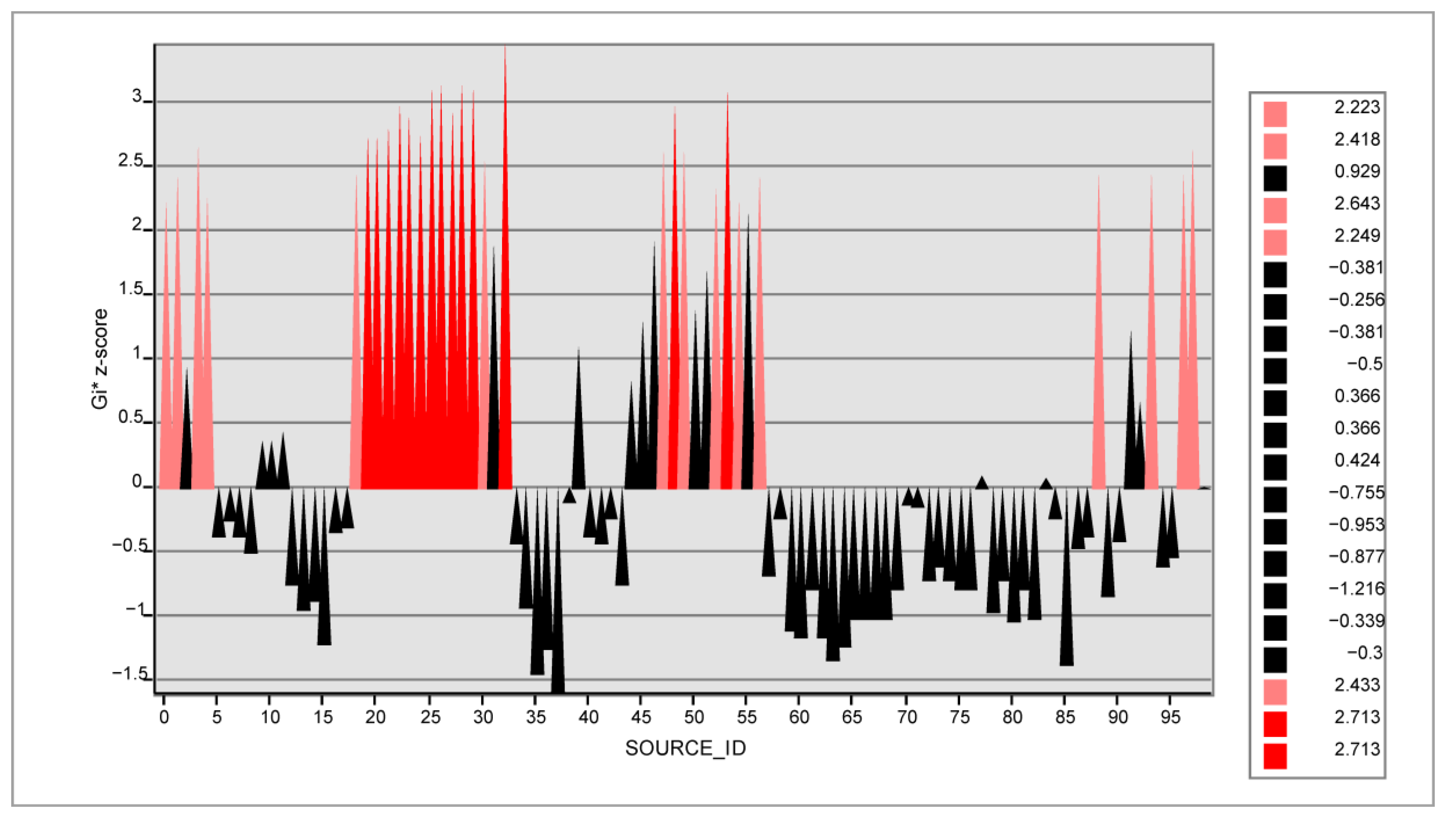
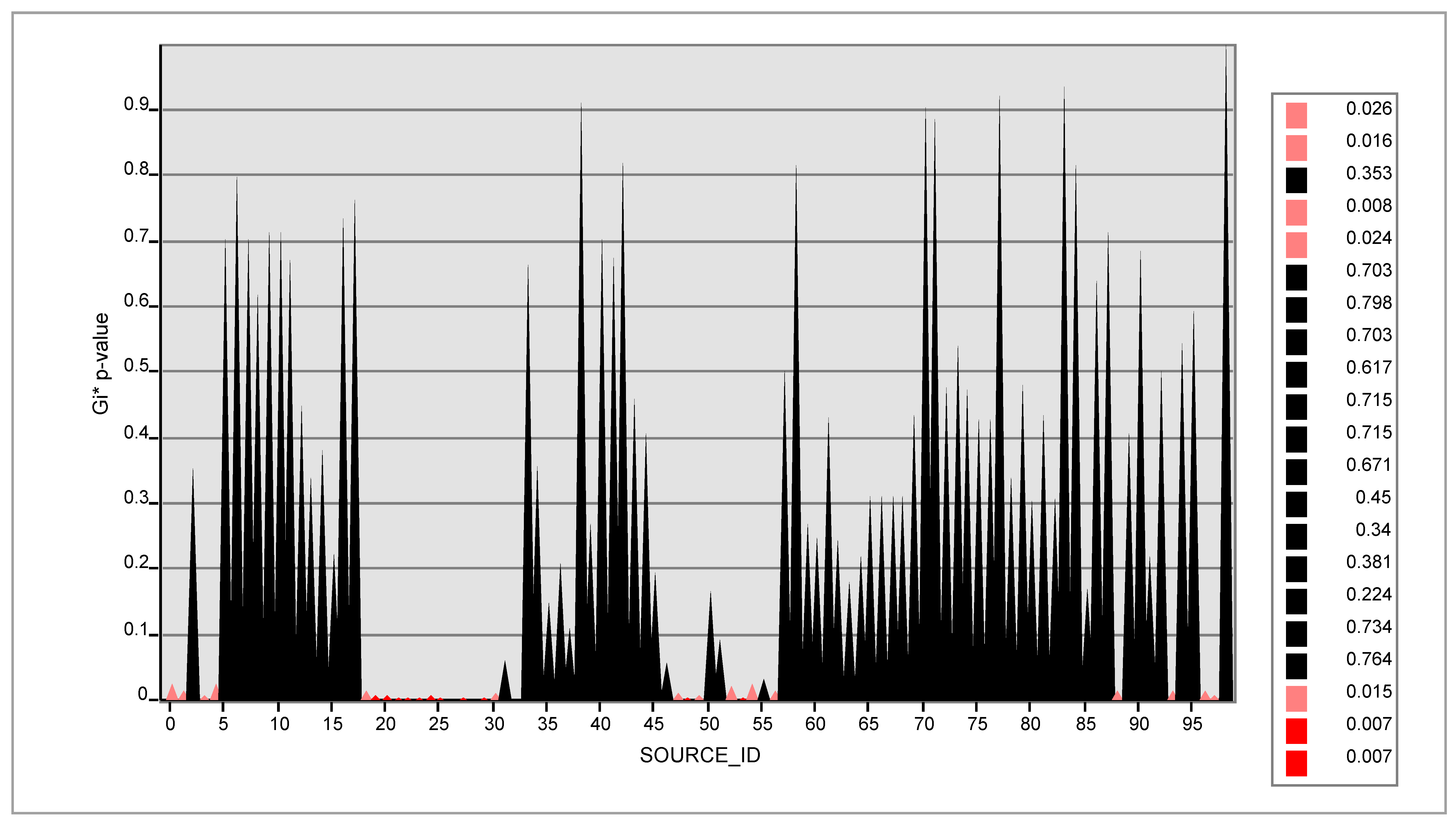
The optimized hotspot analysis tool identifies statistically significant spatial clusters of high values (hotspots) and low values (cold spots). Many tools in the Spatial Statistics toolbox, including ArcGIS, employ distance in their calculations. These tools allow the user to use either Euclidean or Manhattan distance. Euclidean distance is the linear and shortest distance, while Manhattan distance is the distance between two points measured along right-angled axes. In this study, Manhattan distance is employed because streets in cities are built within blocks and the Euclidean distance may not represent the real distance between two crash locations. Because of that, Euclidean distance may overestimate the hotspots compared to the Manhattan distance [2]. Very high (positive) or very low (negative) z-scores are associated with very small p-values, which are very well visualized. The results are presented in Figure 5 and Figure 6 below. The numerical values of z-score and p-values are indicated in the legends. The dark red and light red color codes represent the hotspot class or area, and the black color code represents the non-significant class or area.

Based on our analysis, we identified two clearly separated areas in the crashes distributed on the city road network: the hotspot area and the insignificant area. It was witnessed that there was no cold spot area in our dataset. However, the first class (hotspot) could further be classified as hotspots with a 95% confidence level, which cover an area that contained 13 crash data points, and hotspots with a 90% confidence level, which cover an area that contained 15 crash data points. The remaining area that contained 61 crash data points was regarded as insignificant, meaning it was neither a hotspot nor a cold spot. The confidence level bin (Gi bin) was analyzed as an output feature class for the entirety of the ninety-nine crash data points of the hotspot area of a 95% confidence level with a Gi bin value of two and a hotspot area of a 90% confidence level, with a Gi bin value of one. The area regarded as insignificant with a Gi bin value of one was identified. As shown in Figure 7 below, the hotspot areas with 95% and 90% confidence levels were concentrated approximately at the city’s center. The area was a business district where many activities, from leisure to shopping, were carried out, and there was a considerable movement of motorized cars.

The purpose of conducting a optimized hotspot analysis is to use it as a complementary step for the framework of identifying hazardous locations in addition to the blackspot analysis. While the BS identification aims to find a point location for single site action, distinguishing area-wide hotspots is essential when we need to take an area action. An area action is more complicated and budget intensive; therefore, it should be as narrow as possible. Since spatial autocorrelation-based optimized hotspot analysis works with spatial contiguity, it is a reasonable choice for analysis.

5. Conclusions

The ever-growing fatalities and property damages due to road traffic crashes necessitate an effective methodological framework to deal with the problem. Resources should be allocated efficiently, and identifying the highest priority or most hazardous locations is very important. There are different ways of intervening or prioritizing hazardous areas. The most common one is identifying point locations, which we referred to in this paper as blackspots (BS), where fatal or serious injury crashes are accumulated in a given period. However, as the mobility challenge is also growing in tandem with the road crashes problem, governments are introducing different regulations including limiting access for motorized vehicles in favor of active mobility and mass transits to promote safety and sustainable mobility. The second way of acting or prioritizing hazardous locations in this paper is distinguishing areas where crashes are contiguous to each other, which we referred to in this paper as hotspots (HS).

The paper’s first objective was to identify the point-based BS locations based on the EB method in the City of Budapest. The second objective was to identify areas of distinguished classes as a hotspot or cold spot, based on a Getis-Ord Gi* spatial autocorrelation, using the optimized hotspot analysis tool offered by ArcGIS. The third objective was to set up the framework for future research in this domain.

This work is novel in the following aspects. The raw crash data were initially screened using the operational definition in the Hungarian design guideline for road planning with different weights for different types of crashes. While the K-means clustering method is frequently used in BS studies, we also included the hierarchical clustering algorithm in our study and compared the two approaches using various metrics to determine which clustering model performs better. Other researchers aggregated fatal crashes with serious injury crashes. In this paper, we considered only fatal crashes for the sake of accuracy in identifying the BS, based on the EB approach. The paper combined EB-based BS identification with spatial autocorrelation-based area-wide HS identification as a complete framework.

During the screening process, ninety-nine locations were identified using the modified operational definition. For the final segmentation process, K-means and hierarchical clustering models were built. After comparing them with three performance metrics, the Silhouette, Davies–Bouldin, and Calinski–Harabasz scores, the K-means model was a better model. Both the elbow and dendrogram methods gave ten as an optimal number of clusters after 70 iterations. Having identified the ten clusters, the EB method was applied, and three BS were identified. An optimized hotspot analysis was conducted using ArcGIS, based on Getis-Ord Gi* spatial autocorrelation. With z-scores and p-values, the 95% and 90% confidence level hotspot and cold spot were analyzed. An area of thirteen hotspots with a 95% confidence level and another fifteen with a 90% confidence level were identified while the remaining area of sixty-one crash points were labelled as non-significant.

Blackspot and hotspot studies have several policy implications. They can help identify areas where traffic safety measures are needed, such as improved road design, increased enforcement, and public education campaigns. They can also help prioritize limited resources for traffic safety initiatives. The findings in this study and the methodological framework can assist decision-makers and planners in identifying and ranking crash-prone areas so that they can prioritize interventions. Sustainability-oriented area-wide interventions are of paramount importance today than ever. As a further step, in the case of BS points, it is possible for the decision-makers to analyze crash-causing factors at the identified three locations, suggest and implement treatments, and then evaluate the treatments.

The limitation of this study is that we analyzed only three years of crash data. That is why we implemented the abridged procedure of EB. The estimate generated by the full procedure is more accurate than the estimate generated by the abridged procedure since the full technique employs more crash counts. Therefore, one should try to employ the full EB procedure instead of the abridged one when data are available for longer. However, they can be more computationally intensive.

Future works may consider additional clustering algorithms to determine the one that performs best. They may also implement other BS analysis methods and compare the results for better accuracy.