A Self-Error-Correction-Based Reversible Watermarking Scheme for Vector Maps

Abstract

The existing digital watermarking schemes for vector maps focus mainly on the process of watermark embedding, while few works have been conducted on the topic of the self-optimization of watermark data in the process of watermark detection. There is thus still much room for accuracy improvement in watermark detection. In this paper, a model of mixed watermark data construction is built first. It constructs the error-correction codes and checking code of the original copyright watermark data and combines them to generate the final watermark data. Additionally, a lossless compression algorithm is designed for watermark data to constrain the total watermark length. Based on the constructed model, a self-error-correction-based reversible watermarking scheme is put forward for vector maps. In this scheme, map vertices are divided into non-intersecting groups first according to stability, and mixed watermark data are then embedded with respective vertex groups. Simulation results demonstrate that the watermark capacity of this scheme is 1.0000, the coordinate error caused by the watermark embedding process can be limited to no more than 0.00001 when the strength of watermark embedding is set to five, and several watermark bits can be effectively detected and corrected after watermark extraction. Experimental results and analysis show that it can strike a good balance among reversibility, invisibility, capacity and robustness. It can provide a novel solution to improve the watermark detection accuracy of digital watermarking schemes for vector maps.

1. Introduction

Vector maps, in which geo-spatial elements are represented by points, polylines and polygons, are the basic data of national infrastructure construction and geo-information science research. They are playing a more and more important role in various fields of national economic construction [1,2]. On the one hand, vector map data must make a breakthrough in terms of data opening and sharing, so as to develop their full use value. On the other one, the opening and sharing of vector map data poses a great threat to its security protection. As a kind of digital product, vector maps are easy to copy, tamper and disseminate, making it very convenient for map piracy, infringement and other illegal acts [3,4]. Accordingly, the security protection of vector maps in the environment of data opening and sharing has captured high attention from governments at all levels and scholars at home and abroad [5,6].

As an important branch of information hiding, digital watermarking technology has been applied widely in the integrity authentication and copyright protection of multi-source heterogeneous data, e.g., digital images [7], CAD drawings [8], convolutional neural networks [9], etc. Moreover, it has been considered as a promising solution for the copyright protection of vector maps. Traditional research, however, focuses mainly on the optimization of the methods and positions of watermark embedding, while the watermark detection process is usually the inverse one of watermark embedding. To the best of our knowledge, there are only a few works that have been conducted on the topic of the self-error-correction of watermark data, and there is still plenty of room for improvement in watermarking detection accuracy.

In this paper, we try to propose a self-error-correction-based reversible watermarking scheme for vector maps. A construction model of mixed watermark data is first constructed, which can strength the self-correcting ability of watermark data under the constraint of watermark length. Based on this model, a self-error-correction-based reversible watermarking scheme for vector maps is put forward. The contributions of this paper include the following:

(1)

Analysis of the existing works indicates that they concentrate mainly on methods of watermark embedding, while very few works have been reported about error detection and the control of watermark extraction results. Moreover, there is still plenty of room for accuracy improvement in watermarking detection.

(2)

A construction model of mixed watermark data is proposed. It combines the original copyright watermark data and their corresponding error-correction codes and checking code to generate the final mixed watermark data, which can strengthen the self-correcting ability of watermark data under the constraint of watermark length.

(3)

Based on the above model, a reversible watermarking scheme is proposed for vector maps. Experimental results and analysis demonstrate that it has good performance in terms of reversibility, invisibility, capacity and robustness.

The rest of this paper is organized as follows. The related work is introduced in Section 2. The construction model of mixed watermark data is proposed in Section 3. In Section 4, a reversible watermarking scheme is put forward for vector maps based on the constructed model of mixed watermark data. Experimental results and analysis are provided in Section 5. Finally, some conclusions are given in Section 6.

2. Related Works

As a kind of professional application of digital watermarking technology, digital watermarking technology for vector maps has gradually become a hot topic in recent years. According to the watermark embedding positions, traditional research can be divided into two categories, i.e., space domain schemes and transform domain schemes.

2.1. Spatial Domain Watermarking Schemes for Vector Maps

Spatial domain watermarking schemes for vector maps embed watermark data by directly modifying vertex coordinates. Earlier schemes were generally in the spatial domain because of the simple computation process and the large watermark capacity. The robustness of them, however, is weak under geometric transformation, map simplification and clipping, vertex addition and deletion, etc. Accordingly, it has become a research focus to improve the robustness of these kinds of schemes.

Map content blocking [10], map vertex grouping [3] and element classification [11] have been regarded as effective means for the robustness enhancement of spatial domain schemes. In these schemes, watermark bits are embedded repeatedly group by group, and the robustness of watermarking schemes can be thus enhanced under vertex addition and deletion, map clipping, etc. Establishing a mapping relation among watermark bits and map vertices is also conducive to robustness improvement in watermarking schemes, for the embedded watermark data can be relatively evenly distributed across map content [12]. Moreover, a difference expansion method has been applied widely in watermarking schemes of vector maps [13], embedding watermark bits by expanding distances between adjacent vertices. There are two main shortcomings of these kinds of schemes, i.e., small watermark capacity and poor invisibility. The normalized modulation of vertex coordinates [11] and redundant vertex addition [14] are two useful solutions for the above two problems. While the former can effectively improve watermark capacity, the latter is conducive to the distortion reduction of original map content. Nevertheless, the robustness of the above two categories of schemes under map simplification is quite poor. To improve the immunity of watermarking schemes to data compression, some scholars have proposed optimized schemes based on feature vertex extraction [15,16], embedding watermark data into feature vertices of vector maps.

Geometric transformation is a common category of operations for vector maps, which greatly disturbs the watermarked coordinates of map vertices and thus has a great impact on watermark extraction. The robustness of watermarking schemes against geometric transformation can be enhanced by modifying the ratio of the distances between feature points [17], but the watermark capacity is not satisfying. Taking polar coordinates of map vertices as the carrier of watermark embedding can enhance the robustness of watermarking schemes under translation and rotation, and the watermark embedding capacity is also ideal [3]. However, this scheme is quite fragile to scaling operations. By constructing invariant features of map content under translation, rotation and scaling operations and taking it as the carrier of watermark embedding, the robustness of watermarking schemes against geometric transformation can be significant enhanced [6,18,19].

Compared with geometric transformation, projection transformation has a greater disturbance on the watermarked coordinates of map vertices. Considering that the topological relationship among map vertices is invariant during projection, several watermarking schemes have been designed taking the inclusion relations of vertices and graticules as the carrier of watermark embedding, and they can resist effectively projection transformation [20]. Furthermore, the robustness of watermarking algorithms can also be enhanced under geometric transformation by setting a reference coordinate system and taking it as the basic framework for both watermark embedding and extraction [21].

2.2. Transform Domain Watermarking Schemes for Vector Maps

Different from spatial domain watermarking schemes, transform domain watermarking schemes for vector maps transform original vector data mathematically before watermark embedding, and watermark data are then embedded by modifying the obtained coefficients. The mathematical transformation methods of vector maps can be divided into four categories, i.e., discrete Fourier transform (DFT), discrete cosine transform (DCT), discrete wavelet transform (DWT) and others.

2.2.1. Schemes Based on DFT (Discrete Fourier Transform)

DFT transformation has been applied widely in the digital watermarking schemes of vector maps, due to its invariance property under geometric transformation [22,23]. In these schemes, vertex coordinates are first transformed into complex numbers, which are then transformed by DFT method. After DFT transformation, the value sequences of phase and amplitude can be obtained, which are then modified to embed watermark data. Because of the special characteristic of DFT transformation, these schemes are robust to geometric transformations. However, due to the global-transform characteristics of DFT, small local modifications of map content will lead to obvious changes in DFT coefficients. Accordingly, the ability of these schemes in resisting map modification attack is poor. By adopting an autocorrelation detection method to assist watermark extraction, the robustness of watermarking algorithms to vertex deletion and data format conversion can be improved to a certain extent [24]. However, watermark data are embedded by directly modifying DFT coefficients in this scheme, and the accuracy of the original data is greatly disturbed and the normal use of the watermarked data is affected. The imperceptibility of watermarking schemes can be enhanced by enlarging the DFT coefficients of map content and selecting an optimal quantization step for watermark embedding [25].

2.2.2. Schemes Based on DCT (Discrete Cosine Transform)

DCT transformation, which has a good performance in terms of decorrelation, can concentrate energy in low-frequency regions. Thus, it has been applied in digital watermarking technology for vector maps. DCT transformation was usually performed on coordinates of feature vertices, and watermark data were then embedded by modifying the AC component of the gained coefficients [26]. Eight vertices are necessary for embedding a watermark bit in these kinds of schemes, and thus the watermark capacity of them is generally small. Another improved scheme was proposed to realize watermark capacity enlargement [27]. In this scheme, a feature image of the vector map is first constructed based on feature vertices, and the generated image is then transformed exploiting DCT transformation. Afterwards, the obtained coefficients are modified to embed watermark data. The watermark extraction process in this scheme, however, needs the participation of original vector map data. Consequently, this scheme belongs to a non-blind scheme, and its application is limited to a large extent. Polygonising the original vector map by its minimum closed rectangle, and then embedding watermark data into intermediate-frequency coefficients, can improve the robustness of the watermarking algorithm against some kinds of attacks [28], e.g., noise, vertex deletion, map clipping, etc. However, the ability of this scheme in resisting geometric attacks is not strong, due to the instability of the minimum closed rectangle under geometric transformation. Additionally, the capacity, invisibility and robustness of watermarking schemes can be improved effectively by selecting noise-insensitive regions of the original vector map first and then transforming decimal parts of vertex coordinates within the selected regions by DCT transformation and finally modifying the obtained AC coefficients to complete watermark embedding [29].

2.2.3. Schemes Based on DWT (Discrete Wavelet Transform)

As a common mathematical transformation method, DWT transformation has also been applied in the digital watermarking technology of vector maps. The robustness of watermarking schemes under geometric transformation can be enhanced by representing broken lines by wavelet descriptors and embedding watermark data by modifying the obtained amplitudes [30]. However, the ability of this scheme in resisting non-geometric attacks is not strong. Another scheme was proposed for robustness enhancement under multiple kinds of attacks [31], embedding watermark data into low- and high-frequency coefficients of DWT at the same time. This scheme, however, belongs to a non-blind scheme and the original data are necessary for watermark extraction. Considering that the high-frequency component of DWT transformation is weak under noise attacks, another scheme embeds watermark data repeatedly into the intermediate- and low-frequency components [32]. Both the invisibility and anti-noise ability of this scheme are satisfying, but it cannot resist vertex addition, vertex deletion and map clipping operations. To realize satisfying concealment and robustness of the watermarking scheme, map content can be divided into equal-size grids and each grid can be treated as a “pixel” in the raster image, and watermark data can be finally embedded exploiting classical watermarking algorithms for raster images based on DWT [33].

2.2.4. Other Transform Domain Schemes

In addition to the aforementioned schemes based on DFT, DCT and DWT, many watermarking schemes based on other kinds of transformations have also been researched. A scheme was proposed that constructs Delaunay triangular mesh based on map vertices first then performs “grid spectrum” analysis on the generated mesh and finally embeds watermark data into the obtained spectrum coefficients [34]. The robustness of this scheme can be improved significantly under several kinds of attacks, e.g., data simplification, map overlap, map clipping and random noise. By parameterizing angles of polygons in vector maps and embedding watermark data into the parameterization results, the robustness of watermarking scheme can be enhanced against common attacks, e.g., vertex reordering, map translation, etc. [35]. Moreover, some other improved schemes have also been put forward to enhance the invisibility and robustness of watermarking schemes, based on authentication [36], attribute features of vector maps [23] and spectral domain transformation [29].

In general, digital watermarking technology for vector maps has been highly valued by scholars at home and abroad, and rich research results have been achieved. However, the existing works focus mainly on the process of watermark embedding and improving the comprehensive performances of watermarking schemes by optimizing watermark embedding methods. Conversely, the process of watermark detection is usually the inverse process of watermark embedding, and there is almost no in-depth study on the self-optimization methods of watermark extraction results. There is thus still much room for accuracy improvement in watermark detection.

To make a breakthrough in this field, a model of mixed watermark data construction is first built in this paper based on error detection and control methods of digital signals, and then a novel reversible watermarking scheme for vector maps is proposed. In the field of digital signal processing, error detection and control methods are exploited widely for controlling data quality during the processes of data storage and transmission [37,38]. Moreover, these works have a certain reference significance for the study of self-error-correction-based digital watermarking schemes.

3. Construction Model of Mixed Watermark Data

To equip watermarking schemes with the ability to detect and correct error bits after watermark extraction, the error-correction code (ECC) of the original copyright watermark data, as well as the corresponding checking code (CC), is first constructed. In addition, the above three types of data are then combined to generate the final watermark data to be embedded. The generated final watermark data are called mixed watermark data in this paper. Generally, the introduction of ECC and CC will enlarge the total watermark length, and the robustness of the watermarking scheme will be affected accordingly. To solve this problem, a lossless compression method is designed for watermark data in this paper. The basic framework of mixed watermark data construction is shown in Figure 1.

3.1. Error-Correcting Coding and Checking Coding

Binary images are adopted frequently to represent copyright information in common digital watermarking algorithms. Consequently, a binary watermark image is exploited in this section to explain the method of error-correcting coding and checking coding. Two stages of ECCs are generated first for original copyright watermark data, so as to detect and correct error bits in the watermark detection phase. Afterwards, the checking code of ECCs is generated so that a few error bits of ECCs can be identified in the watermark detection phase. Additionally, Huffman coding is conducted on the copyright watermark data, ECCs and CC to shorten the total watermark length. Given a $l\times m$ (unit: pixel) binary watermark image, assumed $bw$, the process of error-correcting coding and checking coding can be summarized as the following steps:

Step 1. Generate the first stage of the ECC of the $bw$. Create an $l\times m$ (unit: pixel) blank binary image, named $ECC01$, and assign it by parity-checking coding, i.e., the total number of black pixels in $bw\left[i,j\right]$, $bw\left[\left(i+1\right) mod l,j\right]$, $bw\left[i,\left(j+1\right) mod m\right]$ and $ECC01\left[i,j\right]$ is an odd (resp. even) number.

Step 2. Generate the second stage of the ECC of the $bw$, i.e., the ECC of $ECC01$, adopting the same method described in Step 1. Let $ECC02$ be the obtained second stage of ECC. It can be inferred that the size of $ECC02$ is $l\times m$ (unit: pixel).

Step 3. Generate the XOR code of $ECC01$ and $ECC02$ and take the obtained result as the checking code (CC) of the two stages of ECCs. Create an $l\times m$ (unit: pixel) blank binary image to represent the obtained XOR code, assumed $CC01$. Then, assign $CC01$ by Equation (1). Here, ⨂ means an operation between two binary pixels (black or white), i.e., if the two pixels participating in the operation are the same, the operation result is a white pixel or the operation result is a black pixel.

$$CC01\left[i,j\right]=ECC01\left[i,j\right]\otimes ECC02\left[i,j\right]$$

(1)

Step 4. Perform the Hamming coding operation on $CC01$, taking each row as a unit. For each unit, the coding process can be completed by the following sub-steps:

(i)

Calculate the number of redundant bits. The minimum value of $r$ that satisfies the condition described in Equation (2) is taken as the number of redundant bits, where m means the number of original bits in this unit.

$$2^r\ge m+r+1$$

(2)

(ii)

Position the redundant bits. The r redundant bits are placed at bit positions of powers of 2, i.e., 1, 2, 4, 8, etc. They are referred to in the rest of this step as $r_1$ (at position 1), $r_2$ (at position 2), $r_3$ (at position 4), $r_4$ (at position 8) and so on.

(iii)

Calculate the values of each redundant bit. The redundant bits are parity bits. Each redundant bit, $r_i$, is calculated as the parity based upon its bit position. It covers all bit positions whose binary representation includes a “1” in the $i\mathrm{th}$ position except the position of $r_i$. Thus, $r_1$ is the parity bit for all data bits in positions whose binary representation includes a “1” in the least significant position excluding 1 (3, 5, 7, 9, 11 and so on). The other redundant bits, e.g., $r_2$, $r_3$, etc., can be calculated by a similar method.

An example of error-correcting coding of copyright watermark data is shown in Figure 2 (odd-parity checking is adopted). Exploiting the same data, the result of checking coding is shown in Figure 3.

3.2. Mixed Watermark Data Construction Based on Lossless Compression

The introduction of ECCs and CC will inevitably lead to an increase in the total watermark length, a reduction in the average embedding times of watermark bits and a decrease in the watermark robustness. As a result, Huffman coding is adopted in this paper to solve the problem of an increased watermark length. Take the copyright watermark data in Figure 2a as an example, the process of Huffman coding can be summarized as the following steps, and the ECCs and CC can be operated with the same method.

Step 1. Divide the copyright watermark data into several $2\times 2$ blocks, and then replace each block by a single value based on the correspondence shown in

Table 1. Correspondence between 2 × 2 blocks and single values.

Single value	A	B	C	D	E	F	G	H
$2\times 2$ block
Single value	I	J	K	L	M	N	O	P
$2\times 2$ block

. The result is shown in Figure 4.

Step 2. Encode the obtained single values based on Huffman coding by the following sub-steps, i.e., (i) count total numbers of each letter in Figure 3 (the result is shown in

Table 2. Statistical results of letter frequency.

Letter	B	C	J	L	O
Number of times	2	1	2	3	1

), (ii) construct a Huffman tree based on the statistical results (the result is shown in Figure 5) and (iii) generate Huffman code for each letter based on the constructed Huffman tree (the result is shown in

Table 3. Result of Huffman coding for each letter.

Letter	B	C	J	L	O
Huffman code	01	000	10	11	001

).

Step 3. Replace each element in the original letters (i.e., “LBOBLJJLC”) by the corresponding Huffman code, and take the obtained result (i.e., “11010010111101011000”) as the final result of Huffman coding.

4. The Proposed Watermarking Scheme

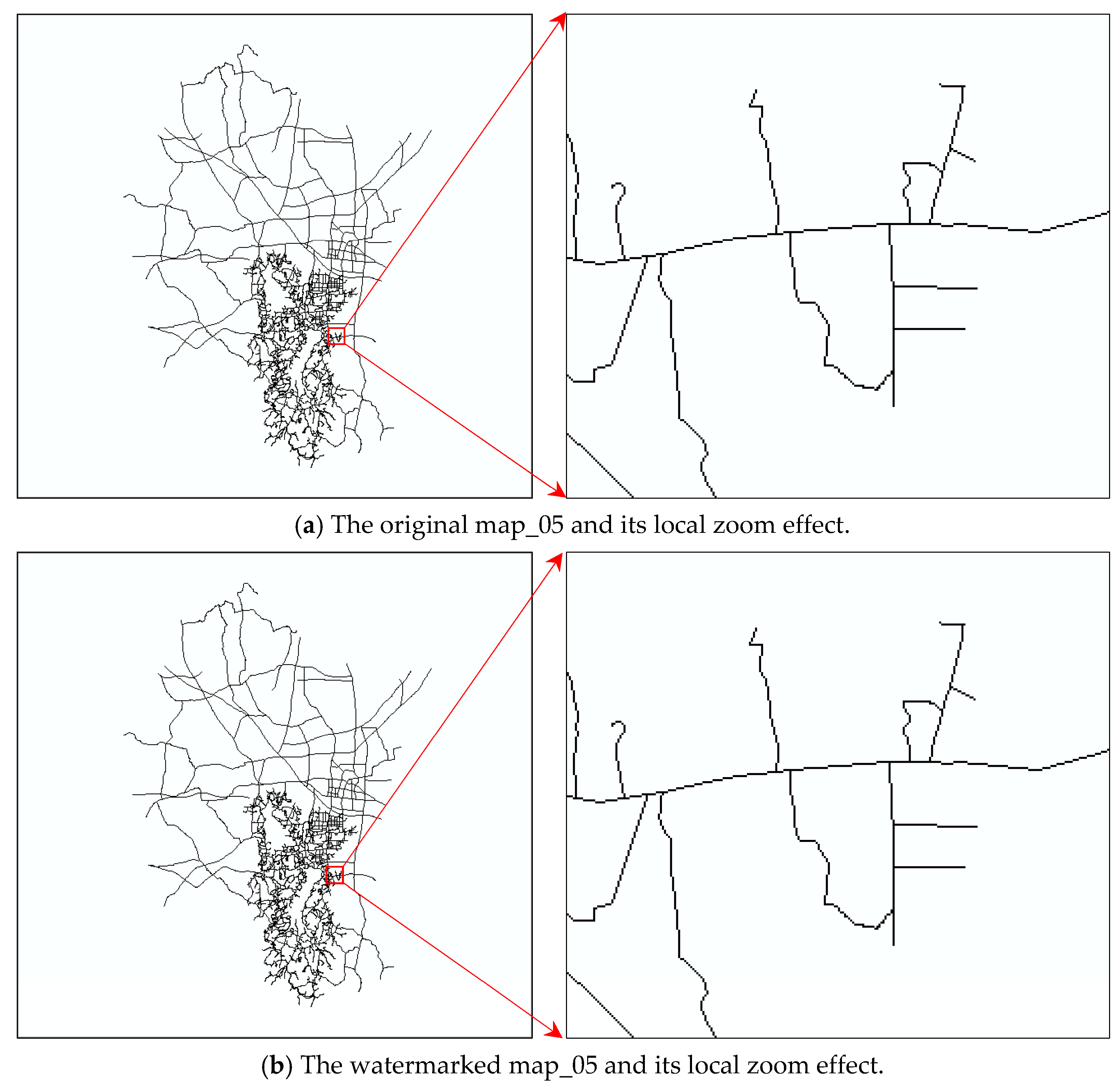
The proposed scheme will be described in three stages in this section. The designed algorithm of vertex grouping and watermark embedding will be introduced first, and the process of watermark extraction and map content recovery will be described in detail afterwards. Finally, the method of self-optimization of watermark data after watermark extraction will be explained minutely.

4.1. Vertex Grouping and Watermark Embedding

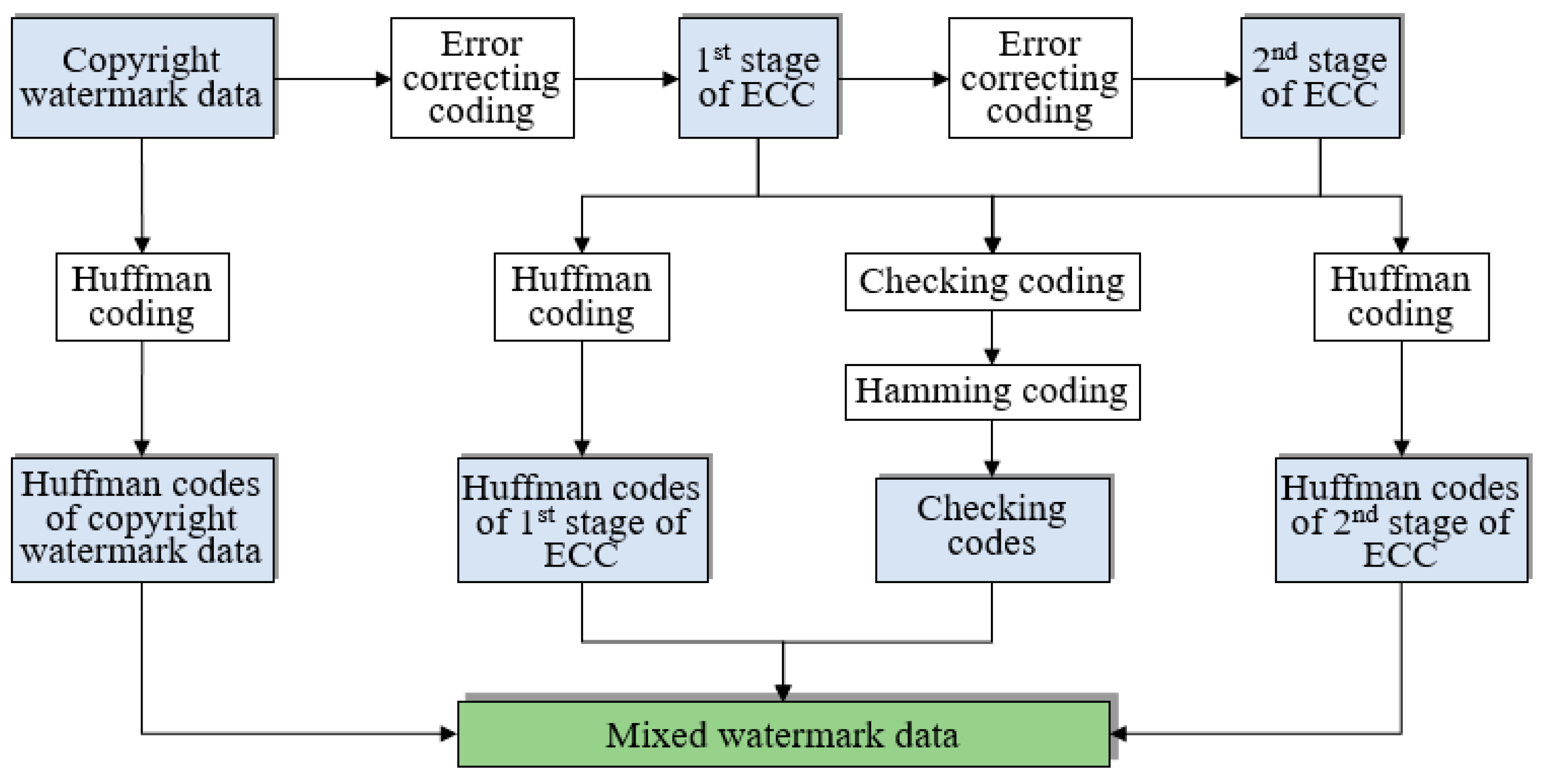
Map vertices are grouped first in this section by feature vertex extraction. Then, the given mixed watermark data will be separated into four individual parts, i.e., copyright watermark data, the first stage of ECC, the second stage of ECC and Hamming codes. Afterwards, the obtained Hamming codes will be embedded into feature vertices, and copyright watermark data and two stages of ECCs will be embedded into non-feature vertices. Finally, the watermarked feature vertices and non-feature vertices will be combined to generated the watermarked vector map.

Given the original vector map and the mixed watermark data, the procedure of vertex grouping and watermark embedding is shown in Figure 6, which can be summarized as the following steps:

Step 1. Extract feature vertices of the original vector map adopting the $Douglas-Peucker$ algorithm [3], and then allocate all map vertices to a feature vertex set $F=\left\{f_i,0\le i\le l_f-1\right\})$ and a non-feature vertex set $N=\left\{n_i,0\le i\le l_n-1\right\})$.

Step 2. Separate the given mixed watermark data into four individual parts, i.e., copyright watermark data $W_C=\left\{W_C\left(i\right),0\le i\le l_{wc}-1\right\}$, the first stage of ECC $E_1=\left\{e_1\left(i\right),0\le i\le l_{e1}-1\right\}$, the second stage of ECC $E_2=\left\{e_2\left(i\right),0\le i\le l_{e2}-1\right\}$ and Hamming codes $H=\left\{h\left(i\right),0\le i\le l_h-1\right\}$.

Step 3. Establish correspondence between elements in $H$ and $F$. The virtual reference vertex of the original vector map, assumed $v_r\left(x_r,y_r\right)$, will be determined first according to Equation (3), where $\left(x_i^{*},y_i^{*}\right)$ is the integer part of the coordinate of $f_i$ and $\lfloor ·\rfloor$ denotes the rounding function. Afterwards, for each $f_t\left(x_t,y_t\right)$, the corresponding Hamming code $h_t$ can be determined according to Equation (4), where $Has{h}_1\left(·\right)$ is an existing function that can transform inputs with arbitrary lengths into outputs with fixed lengths, and $x_t^{*}$ and $y_t^{*}$ are integer parts of $x_t$ and $y_t$, respectively.

$$\left\{\begin{array}{l}{x}_r=⌊\frac{1}{l_f}{\displaystyle \sum _{i=0}^{l_f-1}{x}_i^{*}}⌋\\ y_r=⌊\frac{1}{l_f}{\displaystyle \sum _{i=0}^{l_f-1}{y}_i^{*}}⌋\end{array}\right.$$

(3)

$$h_t=h\left[Has{h}_1\left(\sqrt{{\left(x_t^{*}-x_r\right)}^2+{\left(y_t^{*}-y_r\right)}^2}\right)mod{l}_h\right]$$

(4)

Step 4. Combine elements in $W_C$, $E_1$ and $E_2$ into one large code list, assumed $T=\left\{t\left(i\right),0\le i\le l_{wc}+l_{e1}+l_{e2}-1\right\}$. Establish correspondence between elements in $T$ and $N$. For each $n_s\left(x_s,y_s\right)$, the corresponding watermark bit $T_s$ can be determined according to Equation (5), where $Has{h}_2\left(·\right)$ is an existing function that can transform inputs with arbitrary lengths into outputs with fixed lengths, and $x_s^{*}$ and $y_s^{*}$ are integer parts of $x_s$ and $y_s$, respectively.

$$T_s=t\left[Has{h}_2\left(\sqrt{{\left(x_s^{*}-x_r\right)}^2+{\left(y_s^{*}-y_r\right)}^2}\right)mod\left(l_{wc}+l_{e1}+l_{e2}\right)\right]$$

(5)

Step 5. Embed each bit in $H$ into its corresponding feature vertices in $F$, and a watermarked feature vertex set $F^{\prime }$ can be obtained. Take a feature vertex $f_a\left(x_a,y_a\right)$ and its corresponding Hamming code $h\left(b\right)$ as an example, and the embedding process can be completed by the following sub-steps, i.e., (i) calculate the polar coordinate of $f_a$ by Equation (6) (let $\left({\rho }_a,{\theta }_a\right)$ be the obtained polar coordinate), (ii) embed $h\left(b\right)$ into ${\rho }_a$ by Equation (7) where $k\left(k\ge 1\right)$ denotes the strength of watermark embedding and (iii) convert the watermarked polar coordinates $\left({\rho }_a^{\prime },{\theta }_a\right)$ into rectangular ones $\left(x_a^{\prime },y_a^{\prime }\right)$ by Equation (8).

$$\left\{\begin{array}{l}{\rho }_a=\sqrt{{\left(x_a-x_r\right)}^2+{\left(y_a-y_r\right)}^2}\\ {\theta }_a=\arctan \frac{y_r-y_a}{x_r-x_a}\end{array}\right.$$

(6)

$${\rho }_a{}^{\prime }=\frac{{\left({\rho }_a\times {10}^k\right)}^{+}}{{10}^k}+\frac{h\left(b\right)+\left({\rho }_a\times {10}^k\right)-{\left({\rho }_a\times {10}^k\right)}^{+}}{{10}^{k+1}}$$

(7)

$$\left\{\begin{array}{l}{x}_a{}^{\prime }=x_r+{\rho }_a{}^{\prime }\times \cos \left({\theta }_a\right)\\ y_a{}^{\prime }=y_r+{\rho }_a{}^{\prime }\times \sin \left({\theta }_a\right)\end{array}\right.$$

(8)

For example, if ${\rho }_a=8.912354$, $h\left(b\right)=1$ and $k=4$, then

$$\begin{array}{ll}{\rho }_a{}^{\prime }& =\frac{{\left(8.912354\times {10}^4\right)}^{+}}{{10}^4}+\frac{1+\left(8.912354\times {10}^4\right)-{\left(8.912354\times {10}^4\right)}^{+}}{{10}^5}\\ & =\frac{\mathrm{89,123}}{{10}^4}+\frac{1+\mathrm{89,123.54}-\mathrm{89,123}}{{10}^5}\\ & =8.9123+0.0000154\\ & =8.9123154\end{array}$$

Step 6. Embed all bits in $T$ into non-feature vertices in $N$ by the same method as that described in Step 5, and a watermarked non-feature vertex set $N^{\prime }$ can be obtained. Combine all vertices in $F^{\prime }$ and $N^{\prime }$ to obtain the final watermarked vector map.

4.2. Watermark Extraction and Map Content Recovery

As shown in Figure 7, the process of watermark extraction and map content recovery is the inverse one of watermark embedding, and the details are described as follows:

Step 1. Extract feature vertices of the watermarked vector map and allocate all map vertices into a feature vertex set $F^{″}=\left\{f_i^{″},0\le i\le l_f^{\prime }-1\right\}$ and a non-feature vertex set $N^{″}=\left\{n_i^{″},0\le i\le l_n^{\prime }-1\right\}$, as described in Step 1 of Section 4.1.

Step 2. Determine the virtual reference vertex of the watermarked vector map, assumed $v_r^{\prime }\left(x_r^{\prime },y_r^{\prime }\right)$, by Equation (9), where $x_i^{*}$ and $y_i^{*}$ are integer parts of $x_i$ and $y_i$, respectively.

$$\left\{\begin{array}{l}{x}_r{}^{\prime }=⌊\frac{1}{l_f{}^{\prime }}{\displaystyle \sum _{i=0}^{l_f{}^{\prime }-1}{x}_i^{*}}⌋\\ y_r{}^{\prime }=⌊\frac{1}{l_f{}^{\prime }}{\displaystyle \sum _{i=0}^{l_f{}^{\prime }-1}{y}_i^{*}}⌋\end{array}\right.$$

(9)

Step 3. Extract watermarks from vertices in $F^{″}$ and recovery map content. For each $f_t^{″}\left(x_t^{″},y_t^{″}\right)$, the corresponding watermark bit $h^{\prime }\left(t\right)$ can be extract by the following sub-steps, i.e., (i) calculate the polar coordinate of $f_t^{″}$ by Equation (10), (ii) extract $h^{\prime }\left(t\right)$ from the obtained polar coordinate by Equation (11) where ${\left(·\right)}^{+}$ is a function getting the integer part of a decimal number, (iii) create a list $H^{\prime }$ to store the extracted watermark bits, and the correspondence between watermark bits and elements in $H^{\prime }$ can be constructed by the method mentioned in Step 3 of Section 4.1 (a simple statistical method, i.e., the minority is subordinate to the majority, is adopted here for optimal value selection), (iv) obtain the recovered polar coordinate of $f_t^{″}$, assumed $\left({\rho }_t^{‴},{\theta }_t^{‴}\right)$, by Equation (12) where ${\left(·\right)}^{-}$ is a function getting the fraction part of a decimal number and (v) convert the recovered polar coordinates of $f_t^{″}$ into rectangular ones by Equation (13).

$$\left\{\begin{array}{l}{\rho }_t{}^{″}=\sqrt{{\left(x_t{}^{″}-x_r{}^{\prime }\right)}^2+{\left(y_t{}^{″}-y_r{}^{\prime }\right)}^2}\\ {\theta }_t{}^{″}=\arctan \frac{y_t{}^{″}-y_r{}^{\prime }}{x_t{}^{″}-x_r{}^{\prime }}\end{array}\right.$$

(10)

$$h_t{}^{\prime }={\left\{\left[{\rho }_t{}^{″}\times {10}^k-{\left({\rho }_t{}^{″}\times {10}^k\right)}^{+}\right]\times 10\right\}}^{+}$$

(11)

$$\left\{\begin{array}{l}{\rho }_t{}^{‴}=\frac{{\left({\rho }_t{}^{″}\times {10}^k\right)}^{+}+{\left[{\left({\rho }_t{}^{″}\times {10}^k\right)}^{-}\times 10\right]}^{-}}{{10}^k}\\ {\theta }_t{}^{‴}={\theta }_t{}^{″}\end{array}\right.$$

(12)

$$\left\{\begin{array}{l}{x}_t{}^{‴}=x_r{}^{\prime }+{\rho }_t{}^{‴}\times \cos \left({\theta }_t{}^{‴}\right)\\ y_t{}^{‴}=y_r{}^{\prime }+{\rho }_t{}^{‴}\times \sin \left({\theta }_t{}^{‴}\right)\end{array}\right.$$

(13)

Take the data in Step 5 of Section 4.1 as an example, i.e., ${\rho }_a^{\prime }=8.9123154$ and $k=4$, and the watermark bit can be extracted by

$$\begin{array}{ll}{h}_t{}^{\prime }& ={\left\{\left[8.9123154\times {10}^4-{\left(8.9123154\times {10}^4\right)}^{+}\right]\times 10\right\}}^{+}\\ & ={\left[\left(\mathrm{89,123.154}-\mathrm{89,123}\right)\times 10\right]}^{+}\\ & ={\left(1.54\right)}^{+}\\ & =1\end{array}$$

Then, the map content can be recovered by

$$\begin{array}{ll}{\rho }_t{}^{‴}& =\frac{{\left(8.9123154\times {10}^4\right)}^{+}+{\left[{\left(8.9123154\times {10}^4\right)}^{-}\times 10\right]}^{-}}{{10}^4}\\ & =\frac{\mathrm{89,123}+{\left[0.154\times 10\right]}^{-}}{{10}^4}\\ & =\frac{\mathrm{89,123}+0.54}{{10}^4}\\ & =8.912354\end{array}$$

Step 4. Extract watermarks from vertices in $N^{″}$ by the same method as that described in Step 3. Copyright watermark data and two stages of ECCs can be obtained, and watermarked non-feature vertices can be recovered.

Step 5. Combine the recovered map vertices to generate the recovered vector map. Similarly, combine the obtained Hamming codes, copyright watermark data and two stages of ECCs to generate the extracted mixed watermark data.

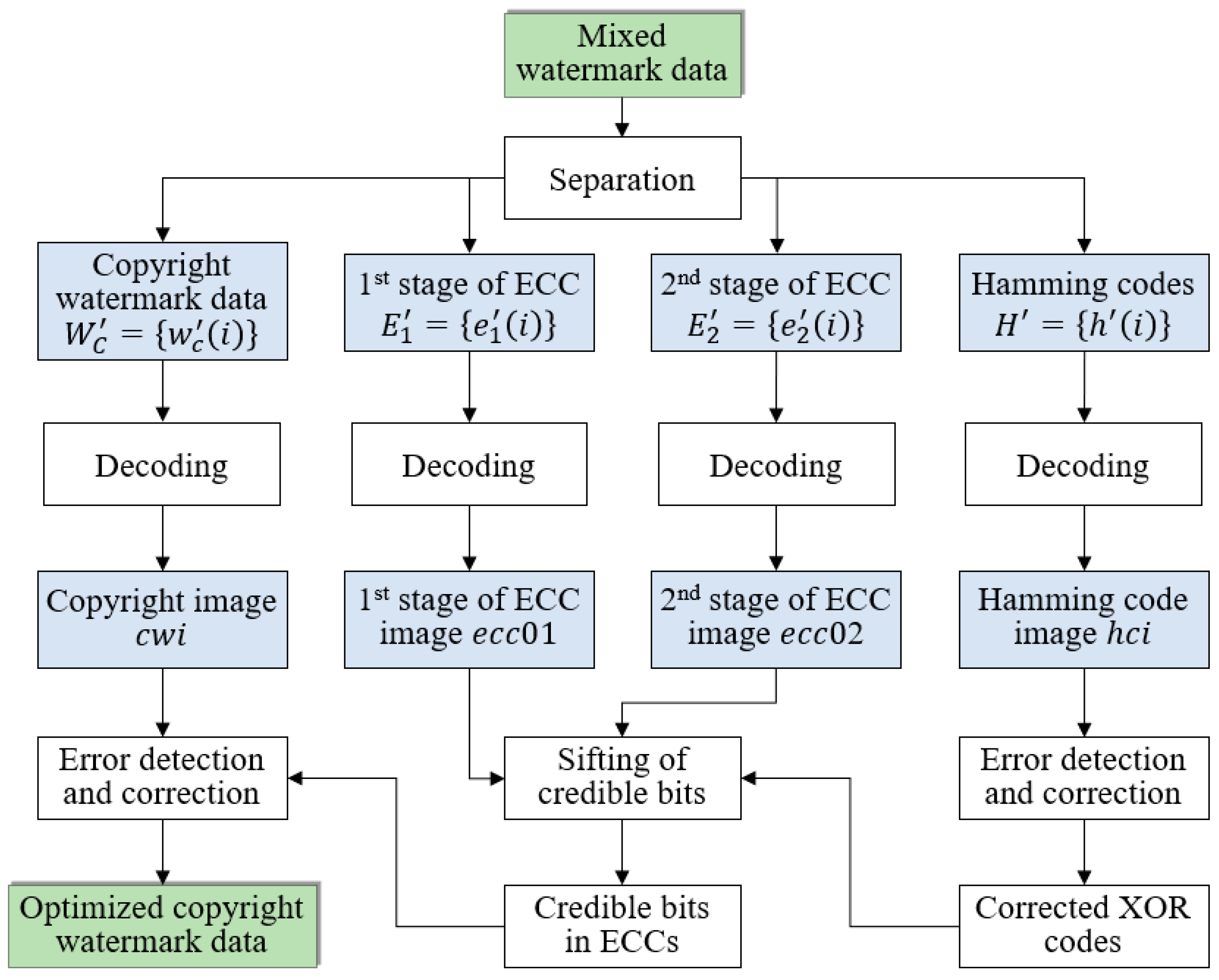
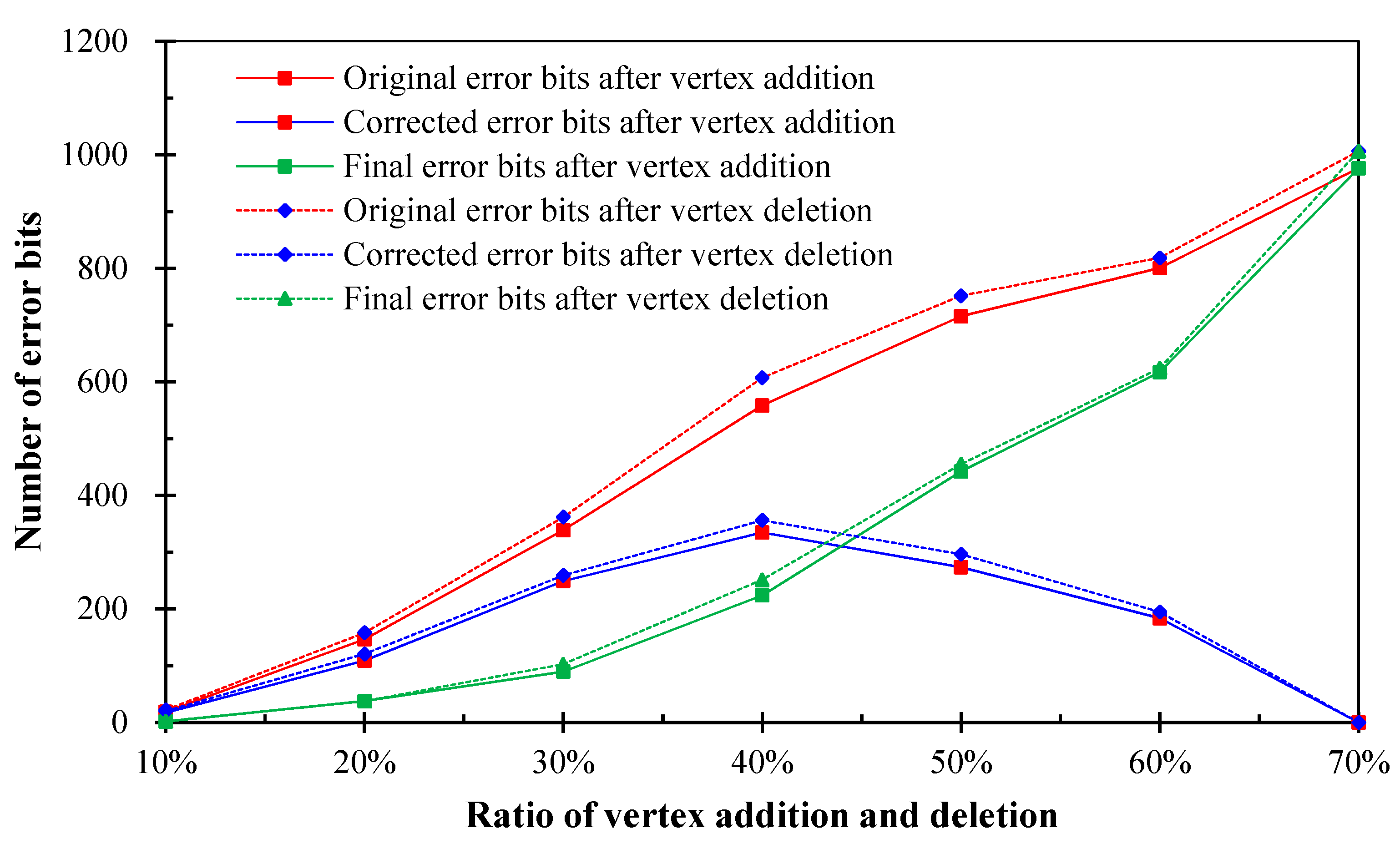
4.3. Self-Optimization of Watermark Extracting Results

After watermark extraction, the accuracy of copyright watermark detection can be further improved in this paper from the perspective of the self-error-correction of mixed watermark data. Given the extracted mixed watermark data, the self-optimization procedure (Figure 8) can be summarized as follows:

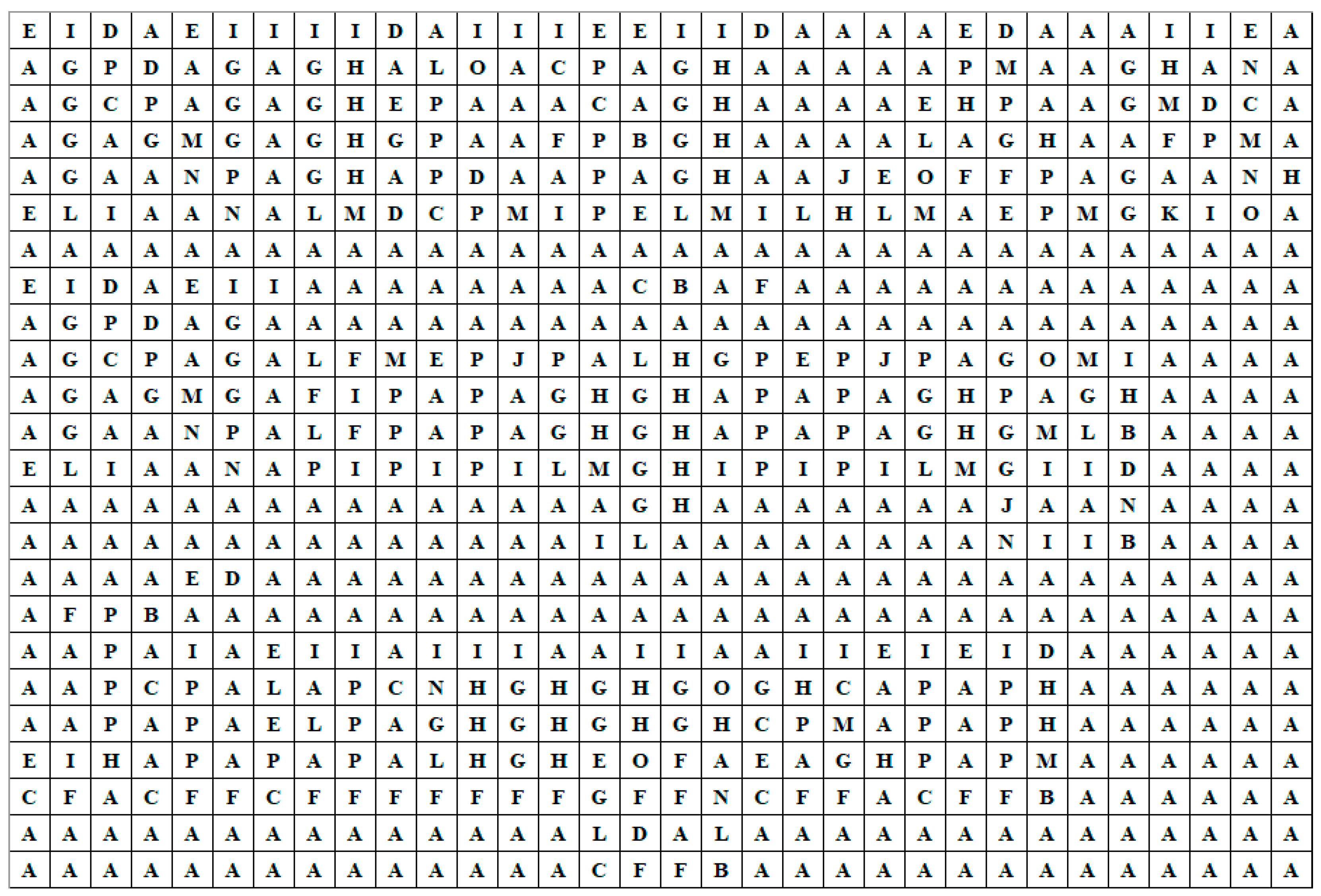
Step 1. Separate the mixed watermark data into four parts, i.e., copyright watermark data, first stage of ECC, second stage of ECC and Hamming codes. Then, decode the four parts, replacing each code by its corresponding $2\times 2$ block (the correspondence is shown in Table 1). Then, four binary images can be obtained, assumed $cwi$ (copyright watermark image), $ecc01$ (first stage of ECC), $ecc02$ (second stage of ECC) and $hci$ (Hamming code image).

Step 2. Detect and correct error elements in $hci$, taking each row as a unit. For each unit, assumed $\left(b_1,b_2,\cdots ,b_{m+r}\right)$, the process of error bit detection and correction can be completed by the following sub-steps:

(i)

Calculate the number of redundant bits and position them using the same formula as in Step 4 of Section 3.1.

(ii)

Parity checking. Calculate parity bits based upon the data bits and the redundant bits using the same rule as in Step 4 of Section 3.1. Thus, let $c_1$ be the first redundant bit and $c_1=parity\left(b_1,b_3,b_5,b_{7}andsoon\right)$. The other redundant bits can be ascertained similarly.

(iii)

Detect and correct error bits. Calculate the decimal equivalent of the parity bits (binary values) first. If it is 0, there is no error. Otherwise, the decimal value gives the bit position that has an error. For example, if $c_1{c}_2{c}_3{c}_4=1001$, it implies that the data bit at position 9, decimal equivalent of 1001, has an error. Then, flip the bit to get the correct bit value.

Step 3. Obtain the corrected XOR code by eliminating redundant bits from the optimized $hci$. All positions of redundant bits are calculated in sub-step (i) of Step 2.

Step 4. Choose credible bits in $ecc01$, $ecc02$ and the obtained XOR codes (assumed $X^{\prime }=\left\{x^{\prime }\left(i,j\right)\right\}$). For each $ecc01\left(i,j\right)$, $ecc02\left(i,j\right)$ and $x^{\prime }\left(i,j\right)$, if $ecc01\left(i,j\right)=ecc02\left(i,j\right)$ and $x^{\prime }\left(i,j\right)$ is a white pixel, they will be considered “credible” or they will be considered “incredible”.

Step 5. Correct incredible bits in $ecc01$. For each incredible $ecc01\left(i,j\right)$, if $ecc02\left(i,j\right)$ and $x^{\prime }\left(i,j\right)$ are all credible, then it can be corrected: if $x^{\prime }\left(i,j\right)$ is a black pixel, let $ecc01\left(i,j\right)=ecc02\left(i,j\right)$ or assign $ecc01\left(i,j\right)$by flipping $ecc02\left(i,j\right)$.

Step 6. Detect and correct error bits in $cwi$ based on the corrected $ecc01$. Firstly, choose credible bits from $cwi$. For each $cwi\left(i,j\right)$, it will be considered credible if the total number of black pixels in $cwi\left(i,j\right)$, $cwi\left(i,j+1\right)$, $cwi\left(i+1,j\right)$ and $ecc01\left(i,j\right)$ is an odd (resp. even) number or it will be considered incredible. Afterwards, correct incredible bits in $cwi$. For each incredible $cwi\left(i,j\right)$, if one of the following conditions is satisfied, i.e., (i) $cwi\left(i,j+1\right)$, $cwi\left(i+1,j\right)$ and $ecc01\left(i,j\right)$ are all credible, (ii) $cwi\left(i,j-1\right)$, $cwi\left(i+1,j-1\right)$ and $ecc01\left(i,j-1\right)$ are all credible and (iii) $cwi\left(i-1,j\right)$, $cwi\left(i-1,j+1\right)$ and $ecc01\left(i-1,j\right)$ are all credible, it can be corrected according to the rule that the total number of black pixels in the aforementioned four pixels is an odd (resp. even) number.

5. Experimental Results and Analysis

Experiments have been conducted using a PC with the following configuration: CPU Inter Core i7-8700 3.20 GHz, RAM 64 GB, OS Windows 10 Education 64-bit, ArcGIS Engine 10.2 and Visual Studio 2010. Fifty vector maps (in .shp format) are used as the experimental data, and eight of them are shown in Figure 9. The properties of the used vector maps are listed in

Table 4. Properties of the fifty adopted experimental vector maps.

Vector Map	Number of Vertices	Coordinate Range (x)	Coordinate Range (y)
Map_01	50,362	525,906.942198596~551,873.293302004	3,510,038.946350692~3,514,418.357030126
Map_02	53,888	548,677.147787786~ 551,873.293316376	3,476,498.368236518~3,479,170.777547691
Map_03	55,248	553,970.275999775~556,450.364688622	3,509,553.780099213~3,514,093.764811436
Map_04	229,515	540,407.308824611~556,136.685007801	3,436,908.383376304~3,438,960.8345924134
Map_05	192,570	40,435,288.344740412~40,439,197.231339764	3,487,778.279717544~3,506,166.176337725
Average of 50 maps	43,126.7	7,642,708.182471635~7,650,228.971872101	4,174,137.323747180~4,376,688.915974203

. The result of mixed watermark data generation is shown in Figure 10. The strength of watermark embedding is set to five.

Based upon the results of error-correcting coding and checking coding, results of single-value replacement and Huffman coding are calculated as described in Section 3.2. Limited by the length of this article, only the results of the original copyright watermark data are shown here (Figure 11 and

Table 5. Results of Huffman coding taking the original copyright watermark data as an example.

Letter	A	B	C	D	E	F	G	H
Number of times	426	7	17	14	25	28	54	37
Huffman code	1	011000	01010	000101	00011	0100	0010	0111
Letter	I	J	K	L	M	N	O	P
Number of times	46	4	1	20	17	10	6	56
Huffman code	0000	00010001	00010000	01101	01011	011001	0001001	0011

).

After Huffman coding, the total length of the original copyright data is 1946. By the same method, Huffman codes of the two stages of ECCs and Hamming codes of XOR code are then calculated. The statistical results of compression coding are listed in

Table 6. Statistical results of compression coding.

Watermark Data	Copyright Watermark Data	The 1st Stage of ECC	The 2nd Stage of ECC	Humming Code of XOR Code
Original length	3072	3072	3072	3456
Coded length	1946	1640	1877	2747
Compression ratio	1.58	1.87	1.64	1.26

, from which it can be seen that various parts of watermark data can be compressed effectively after Huffman coding.

5.1. Experimental Results

First of all, a set of simulation experiments were conducted to test the stability of the result of feature vertex extraction. Feature vertices of the fifty experimental vector maps were first extracted and then mixed watermark data were embedded, as described in Section 4.1. Afterwards, feature vertices were extracted from the fifty watermarked vector maps. Experimental results show that all original extracted feature vertices can be successfully obtained after watermark embedding.

Afterwards, the statistical analysis was conducted during the watermark embedding procedure to evaluate the benefits of the designed watermarking scheme.

Table 7. Statistical results of watermark embedding.

Vector Map	Number of Vertices	Average Embedded Times of Watermark Bits	Count of Unembedded Watermark Bits
Map_01	50,362	6.13	0
Map_02	53,888	6.56	0
Map_03	55,248	6.73	0
Map_04	229,515	27.96	0
Map_05	192,570	23.46	0
Average of 50 maps	43,126.7	5.25	0

shows the results of the statistical analysis, indicating that the embedded times of watermark bits is ideal and the robustness of the designed scheme can be guaranteed in theory.

5.2. Performance Analysis

5.2.1. Analysis about Reversibility

It can be inferred from the procedure of watermark extraction and map content recovery (Section 4.2) that the embedded watermark bits can be eliminated precisely from the cover data. Moreover, the reversibility of this scheme can be guaranteed in theory. To further verify the reversibility of the proposed scheme, a set of experiments were carried out based upon the fifty experimental vector maps. Watermarks were embedded first into the fifty vector maps, and then watermarks were extracted and map content was recovered. Finally, coordinate differences between original map vertices and their watermarked counterparts were calculated. The experimental results indicate that all map vertices can be recovered after watermark extraction, and the reversibility of this scheme is thus validated.

5.2.2. Analysis about Invisibility

It is described in Section 4.1 that only the decimal portion of vertex coordinates are modified to embed watermark data, and the distortion of map coordinates can be controlled by setting a reasonable strength of watermark embedding. In this work, the watermark embedding strength is set to five. Accordingly, the original vector maps will not be affected significantly in visualization in theory. An experimental vector map is shown in Figure 12, as well as its watermarked counterpart. It is quite difficult to distinguish the difference between the two vector maps from the visual aspect, even in the local zoom mode.

To further evaluate the invisibility of this scheme, errors of map coordinates were calculated, and two indicators, i.e., max error ($ME$) and root-mean-square error ($RMSE$), were adopted to express quantificationally the distortion of map vertices caused by watermark embedding. The $ME$ and $RMSE$ of each vector map can be calculated by Equation (14), where $n$ is the total number of vertices, $Max\left\{·\right\}$ is a function that can get the maximal value of a given sequence and $\left(x_i,y_i\right)$ and $\left(x_i^{\prime },y_i^{\prime }\right)$ are the original and the watermarked coordinates of the $i-\mathrm{th}$ map vertex, respectively.

$$\left\{\begin{array}{l}ME=Max\left\{\sqrt{{\left(x_i-x_i{}^{\prime }\right)}^2+{\left(y_i-y_i{}^{\prime }\right)}^2},0\le i\le n-1\right\}\\ RMSE=\sqrt{\frac{1}{n}{\displaystyle \sum _{i=0}^{n-1}\left[{\left(x_i-x_i{}^{\prime }\right)}^2+{\left(y_i-y_i{}^{\prime }\right)}^2\right]}},0\le i\le n-1\end{array}\right.$$

(14)

Additionally, a comparison of the aspect of invisibility has been made among this scheme and three representative schemes in [5,6,13]. The results are shown in

Table 8. The comparison results of invisibility among different watermarking schemes.

Vector Map	Error (Unit: Meter)	Scheme in [5]	Scheme in [6]	Scheme in [13]	This Scheme
Map_01	ME	0.0084032	0.0000033	0.0024207	0.0000076
	RMSE	0.0023402	0.0000012	0.0004830	0.0000042
Map_02	ME	0.0083379	0.0000039	0.0008215	0.0000088
	RMSE	0.0018908	0.0000009	0.0003428	0.0000043
Map_03	ME	0.0124506	0.0000077	0.0041063	0.0000093
	RMSE	0.0079785	0.0000045	0.0001725	0.0000037
Map_04	ME	0.0244354	0.0000044	0.0019035	0.0000054
	RMSE	0.0036835	0.0000018	0.0004156	0.0000034
Map_05	ME	0.0092951	0.0000055	0.0021639	0.0000086
	RMSE	0.0108089	0.0000036	0.0006311	0.0000040
Average of 50 maps	ME	0.0092346	0.0000040	0.0011487	0.0000090
	RMSE	0.0018346	0.0000027	0.0006367	0.0000038

, indicating that both the $ME$ and $RMSE$ of the proposed scheme are acceptable (less than $1\times {10}^{-5}$) and satisfying compared with the three state-of-the-art works.

5.2.3. Analysis about Capacity

In this scheme, each vertex is adopted for embedding a watermark bit, and it can be thus inferred that the total number of embedded watermark bits equals to the number of map vertices. Contrasting experiments were made among the proposed scheme and three representative schemes in [5,6,13] for the aspect of watermark capacity. Experimental results (

Table 9. Comparison results of watermark capacity among different schemes (bit/vertex).

Vector Map	Scheme in [5]	Scheme in [6]	Scheme in [13]	This Scheme
Map_01	0.9311	3.2355	0.2638	1.0000
Map_02	0.9565	3.7679	0.2354	1.0000
Map_03	0.9352	3.9870	0.2087	1.0000
Map_04	0.9427	3.6627	0.2179	1.0000
Map_05	0.9336	3.7426	0.2259	1.0000
Average of 50 maps	0.9511	3.8782	0.2351	1.0000

) indicates that the watermark capacity of this scheme is basically at a normal level.

5.2.4. Analysis about Robustness

(1)

Vertex reordering

Vertex reordering is a common kind of attack that vector maps suffer frequently, which may change the organization structure of the watermarked vector data and cause an impact on the result of watermark extraction. In this paper, the key sub-steps of the watermark embedding procedure, i.e., feature vertex extraction, polar coordinate conversion, etc., are all independent in the order of the map vertices. Consequently, it can be inferred that the proposed scheme will not be disturbed by vertex reordering. Moreover, simulation experiments were also carried out and the results confirmed the strong robustness of this scheme under vertex reordering operations.

(2)

Map translation and rotation

It can be inferred from the watermark embedding procedure mentioned in Section 4.1 that the proposed watermarking scheme is immune to map translation and rotation for the constancy of polar coordinates under geometric transformation. A set of experiments have been conducted to verify the robustness of this scheme under map translation and rotation, and the results show that the proposed scheme is quite robust under various intensities of translations and rotations.

(3)

Vertex addition and deletion

Vertex addition and deletion are two common operations of vector maps. While the former may introduce some interference vertices to the cover data, the latter may eliminate several map vertices, as well as the included watermark bits. Both the introduction of interference vertices and the loss of watermarked vertices have appreciable effects on the accurate extraction of watermark data. In this scheme, each watermark bit is embedded simultaneously into multiple map vertices, and a statistical method is adopted for optimal value selection in the watermark extraction phase. As a result, the ability of this scheme in resisting vertex addition can be enhanced theoretically. More importantly, after watermark extraction, a self-error-correction algorithm is put forward in this paper that is helpful for accuracy in watermark detection in theory.

Simulation attack experiments have been conducted to verify the robustness of this scheme under map translation and rotation. The generated mixed watermark data were first embedded into the fifty experimental vector maps, and then various proportions (from 10% to 70%) of vertices were added into (resp. removed from) the watermarked data. Finally, watermark data were extracted from the attacked cover data and self-optimized adopting the designed method. The results of the watermark extraction were generated by calculating the average value of fifty vector maps. Experimental results (Figure 13) show that (i) the accuracy of watermark detection can be improved effectively by the proposed self-error-correction algorithm; (ii) the smaller the attack intensity, the better the effect of self-error-correction of watermark data, and the relationship between attacking intensity and corrected error bits is not linear; and (iii) the robustness of this scheme under vertex addition is slightly better than under vertex deletion. Here, the bit error rate (BER) is used to express quantificationally the effect of watermark extraction.

(4)

Map simplification and clipping

Map simplification and clipping are two other kinds of attacks that vector maps suffer frequently. The former preserves feature vertices and removes non-feature vertices, and the latter retains vertices in an object region and deletes all the other vertices. Similar to vertex deletion, map simplification and clipping may lead to the loss of some watermarked vertices and thus affect the accuracy of watermark extraction. In this paper, copyright watermark data and ECCs are embedded into non-feature vertices, while Hamming codes are embedded into feature vertices. It can be inferred that the Hamming codes in the cover data are relatively stable, compared with copyright watermark data and ECCs. Therefore, a number of error bits in ECCs and copyright watermark data can be detected and corrected based upon Hamming codes in theory.

Simulation experiments have been carried out in this section to verify the robustness of the proposed scheme under map simplification and clipping. Moreover, comparisons have been made among this scheme and three representative schemes in [5,6,13] to evaluate objectively the performance of this scheme. Experimental results (Figure 14) show that the watermarking scheme proposed in this paper has a better performance in resisting map simplification and clipping attacks, compared with the three representative schemes. Moreover, the proposed scheme is more robust under map simplification than under map clipping.

6. Conclusions

In this paper, a novel self-error-correction-based reversible watermarking scheme is put forward for vector maps, to provide new means to improve the accuracy of watermark detection. To equip the final watermark data with the self-correcting ability, a model of mixed watermark data construction is first built. It combines the copyright watermark data and its corresponding ECCs and CC to generate the final watermark data to be embedded. Moreover, to limit the total watermark length, a lossless compression method is designed for watermark data. After watermark extraction, a portion of error bits in the obtained copyright watermark data can be detected and corrected based upon the obtained ECCs and CC. Experimental results have demonstrated the reversibility, invisibility, capacity and robustness of the proposed scheme. In theory, the method of mixture watermark data construction is also worthy of being referenced in watermarking schemes of other types of geo-spatial data, e.g., remote sensing images, 3D models, etc.

The core innovation of this paper is the method of equipping the watermark data with the self-correcting ability under the constraints of total watermark length, and there are three aspects of work that are valuable for further study. Firstly, although the final watermark length is limited to a considerable extent in this paper by a designed lossless compression algorithm, it is a little bigger than the original length of copyright watermark data. In the near future, more attention should be paid to the development of more efficient lossless compression schemes for watermark data. Moreover, watermark data are embedded into the polar coordinates of map vertices in this paper, and the scheme is thus quite fragile under map scaling attacks. In future work, the construction of geometric invariants of vector maps should be researched, as well as the methods of embedding watermarks into the constructed geometric invariants, so as to improve significantly the robustness of watermarking schemes under geometric transformation. Finally, feature vertex extraction is a key step of the proposed watermarking scheme, and the Douglas–Peucker algorithm is used in this step. Accordingly, this scheme is not suitable for point data. The feature vertex extraction of point data is worthy of being researched in-depth in future work.