Abstract
This paper presents a hexapod-type reconfigurable parallel mechanism that operates from a single actuator. The mechanism design allows reproducing diverse output link trajectories without using additional actuators. The paper provides the kinematic analysis where the analytical relationships between the output link coordinates and actuated movement are determined. These relations are used next to develop an original and computationally effective algorithm for the reconfiguration procedure. The algorithm enables selecting mechanism parameters to realize a specific output link trajectory. Several examples demonstrate the implementation of the proposed techniques. CAD simulations on a mechanism virtual prototype verify the correctness of the suggested algorithm.
1. Introduction
A reconfigurable parallel mechanism (RPM) allows changing its configuration to obtain different output link trajectories or vary the dimensions of its workspaces. This type of mechanisms also has the advantages of a parallel structure: particularly, high positioning accuracy, ability to manipulate heavy loads, and high rigidity [1,2,3]. These characteristics allow the wide use of such mechanisms in technology. For example, they are applied as rehabilitation manipulators [4], grippers [5], robots for additive technologies [6,7], multi-axis machine tools [8,9,10], and force sensors [11].
Based on the structure, there are different types of RPMs. Some RPMs can change their configuration by attaching or detaching independent modules [12,13]. In addition, the configuration of RPMs can be modified by coupling additional kinematic chains, providing the entire system with a hybrid structure [14]. Works [15,16] present RPMs in which it is possible to change the number of degrees-of-freedom (DOFs), while the structure of these mechanisms remains unchanged. Several types of RPMs use metamorphic kinematic chains in the design, i.e., the chains that provide adaptability and reconfigurability by changing their topology [17,18]. The original design concept for RPMs is presented in [19], where types of output link movements vary when mechanisms come through singular positions. The problem of avoiding singularities in RPMs using actuation redundancy is proposed in [20].
Despite the indicated advantages of the RPMs discussed above, they are still designed with multiple actuators, making their structures and control more complex. In this regard, paper [21] proposed a novel RPM with the least possible number of actuators, i.e., one actuator, and without additional kinematic chains or modular elements that are used independently of the primary mechanism to change its configuration. This mechanism can reproduce diverse trajectories of its output link by a simple reconfiguration procedure, including disconnecting several flexible elements (belts) and reorienting some links (cranks). However, the problem of how to reorient the cranks to achieve the required output link motion has not yet been studied completely.
The discussed mechanism belongs to the type of parallel mechanisms with a circular guide that can provide a sufficiently large rotational angle around one of the coordinate axes. References [22,23,24] show known examples of these mechanisms with three, four, and six legs. The analytical review showed that the mechanisms of this type lack reconfigurability (except a 3-DOF spherical mechanism presented in [25] and a 6-DOF cable-driven mechanism shown in [26]). The proposed mechanism fills this gap. In this paper, we consider an algorithm that can be applied to find reconfiguration parameters needed to realize a particular motion type.
The work is arranged as follows. Section 2 briefly describes the architecture of the studied RPM. Section 3 provides kinematic relations that are used next in Section 4, which considers a reconfiguration algorithm in detail. Section 5 demonstrates the application of the proposed techniques in several examples. Section 6 discusses the features of the suggested methods, their limitations, and potential development. Finally, the conclusions (Section 7) recap the results of the whole paper.
2. Mechanism Architecture
Let us consider the design features of the proposed parallel mechanism. Figure 1 shows its virtual prototype, where six kinematic chains are mounted between the fixed link—circular guide 1, driving link—wheel 2, and output link—platform 11. Each kinematic chain includes planar and spatial elements. The planar ones stay within circular guide 1: gear 3 and drive pulley 4, having a common axis, driven pulley 5 and crank 6, also having a common axis, link block 7, swinging arm 8, and carriage 9. The last two links are rigidly connected. The spatial element is rod 10.
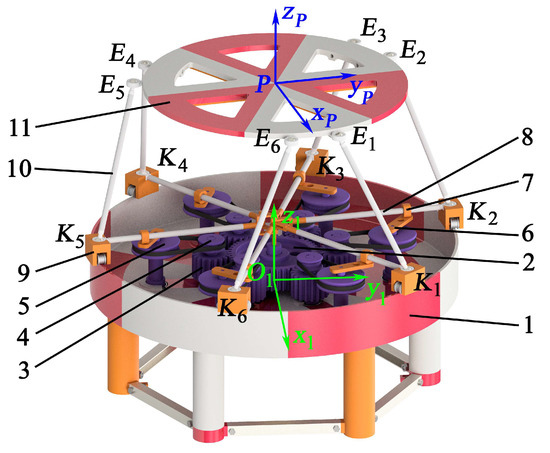
Figure 1.
Virtual prototype of the hexapod-type reconfigurable parallel mechanism with single actuation.
Pulleys 4 and 5 connect between themselves by a belt. Rod 10 forms spherical joints on both sides with carriage 9 and platform 11. Points and with i = 1 ... 6 determine the centers of spherical joints 9–10 and 10–11. Base coordinate system attaches to circular guide 1. Local coordinate system is attached to platform 11 with point P in the center of platform 11.
The mechanism has one DOF, as we have proved using screw calculus in [27]. Moreover, this mechanism has reconfigurable capabilities, which allow changing the output link motion while having a single drive. For this purpose, we can disconnect the belt between pulleys 4 and 5 to reorient crank 6 in each kinematic chain. Thus, the platform can realize a particular trajectory.
In the following sections, we will show how to choose initial orientations of the cranks for a specific output link trajectory. This procedure uses kinematic relations between the coordinates of the mechanism links, and we will consider them first.
3. Kinematic Relations
First, let us consider how to set the position and orientation of the output link. The first one can be described by the Cartesian coordinates of its geometric center, point P, relative to the base coordinate system:
where is the vector, defining the position of point P in base coordinate system ; , , and are the components of vector .
We can determine the orientation of local coordinate system relative to fixed one using rotation matrix . In this study, we will use three Euler angles φ, θ, and ψ to set the platform orientation. Matrix will be a product of three matrices:
where O1′y1′ is the axis of the rotated coordinate system after the platform rotation by angle φ around axis O1z1; O1″x1″ is the axis of the rotated coordinate system after the platform rotation by angle θ around axis O1′y1′. Elementary rotation matrices included in (2) are calculated in the following way:
Coordinates of the output link can be grouped into one vector X:
Suppose the variable q defines the rotational angle of the driving link. This section aims to obtain relations between angle q and coordinates X, i.e., to find vector function f:
f(q, X) = 0.
First, let us consider the planar part of the mechanism. Figure 2 shows a fragment of one of the six kinematic chains.
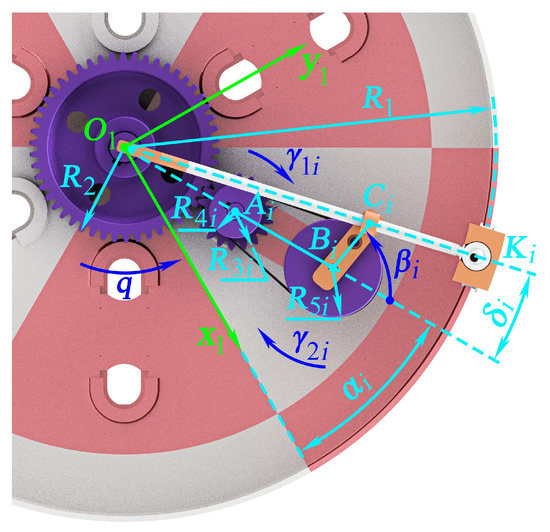
Figure 2.
Planar kinematic chain placed within the circular guide.
We can calculate rotational angle of gear 3 in the following way:
where i = 1…6 is the index number of a kinematic chain; is the radius of driving wheel 2; is the radius of gear 3.
Further, it becomes possible to determine rotational angle of driven pulley 5:
where is the radius of driving pulley 4; is the radius of driven pulley 5.
Center of driving wheel 2, center of driving pulley 4, and center of driven pulley 5 lie on a common straight line (Figure 2). Then, distance between the axes of wheel 2 and pulley 5 can be found:
where is the distance between points and (i.e., between the centers of pulleys 4 and 5).
We can find length from the cosine law for triangle , where point corresponds to the line block (Figure 2):
where is the length of (the length of crank 6); is the rotational angle of crank 6:
where is an initial orientation of crank 6.
Rotational angle between sides and can be determined from the sine law for triangle :
The coordinates of point of carriage 9 relative to base coordinate system will have the following form:
where is the radius of circular guide 1; is the angle between axis and line (Figure 2).
Next, consider the output link. Coordinates of point of joint 10–11 relative to base coordinate system can be derived in the following form:
where are the coordinates of point relative to local coordinate system .
Finally, we can write a relationship connecting the coordinates in expressions (14) and (15) with rod length :
Expressions (16), written for each of the six kinematic chains, form a system of six equations. These equations connect platform coordinates X with coordinates of other links, which depend on angle q. Thus, (16) presents system (7) that we looked for. In the following section, we will show how to handle the obtained relations to choose the initial orientations of the cranks for different output link trajectories.
4. Reconfiguration Algorithm
As mentioned earlier, and as shown in [28], the output link can perform various trajectories by disconnecting the belt between pulleys 4 and 5 and reorienting cranks 6, i.e., by changing the value of angles . Our aim is to select these values for a particular trajectory. To undertake this, we can first rewrite Equation (16) as:
Here we should mention a caveat. Since the mechanism has only one DOF, we cannot independently set all six components of vector X. Only one of the platform coordinates can have an explicit form. Let us specify the prescribed coordinate as , which represents any component of vector X. We can group the five remaining unknown coordinates as vector . System (17) in this case can be written as follows:
We can solve this system numerically for variables , q, and for each value of given coordinate . If coordinate has a form of trajectory , where t is the time, values must remain constant for each value of coordinate over the considered time interval to realize a given motion. From this perspective, the following approach can be applied to find a solution for system (18).
Let us represent trajectory , given on some time interval [0, T], in the form of N discrete values:
where corresponds to the value of coordinate at the moment , j = 1…N, with and .
For given trajectory Xg(t), variables and q, determined in the calculation results, will also be time dependences of (t) and q(t), which we can represent similarly in a discrete form:
Considering the performed discretization, we can write system (18) in the following form:
The equations above represent a system of 6N equations relative to 6 + 6N parameters: 6 unknown variables are ; N unknown variables are q[j]; 5N unknown variables are the components of vectors [j].
The structure of the obtained equation system has some features. To show this, we first group all unknown variables as vector s of dimension 6 + 6N:
where is the vector containing the values of initial crank angles .
We can also group system (22) as vector-function f:
Jacobian matrix for vector-function (24) has a form:
For any pair of integers m and n, m = 1…6, n = 1…N, function depends only on those variables [j] and q[j], which have j = n, and only on that variable , for which i = m, and does not depend on other variables. Consequently, Jacobian matrix (25) will have a sparse structure of the following form:
where
where
Variable in (27) is the k-th component of vector [j], k = 1…5.
All elements in the right side of expression (26) except , , and are zeros; the latter can be found in Appendix A. Thus, the Jacobian matrix for vector-function f is highly sparse. We can estimate the matrix sparsity, sp, as the ratio of its zero elements to the total number of the elements. In the discussed case, there are 6N × (6 + 6N) elements in total, and the number of nonzero elements is 42N. As a result, we obtain the following equation:
The sparsity tends to one, i.e., almost all elements of the matrix are zero at large values of N. The large number of zero elements facilitates and speeds up the numerical solution of system (22). To find a solution, we should set some initial guess, which choice is a key factor. System (22) includes nonlinear equations, and the number of variables is greater than the number of equations. As a result, different initial guesses will lead to various solutions, and the solution may not exist at all for an incorrect initial guess. The problem of choosing this initial guess is still not studied completely. There are possibilities to facilitate this choice, for example, using experimental data or a virtual prototype of the hexapod.
Note that we also find angle q and coordinates during the numerical solution of system (22). Thus, the procedure implicitly includes an algorithm to solve the inverse kinematics.
5. Examples
Let us consider several examples of reconfiguration analysis for various output link trajectories with the mechanism parameters corresponding to the virtual prototype shown in Figure 1 and presented in Table 1.

Table 1.
Geometrical parameters of the hexapod-type reconfigurable parallel mechanism.
In the first case, let us take orientation angle φ of the platform as given coordinate with the following time law:
which corresponds to one complete oscillation around axis with amplitude 10°.
The numerical solution was carried out in MATLAB package using standard function “fsolve” with the tolerance 1 × 10−8 as a stopping criterion. To find a solution, “fsolve” applies a least-squares method for system (24). At this step, we also provided Jacobian matrix (26), the nonzero elements of which were found in an explicit form by differentiating expression (17) with respect to the corresponding variables (see Appendix A). We set N equal to 125, which corresponded to sp = 0.99 according to expression (28). All variables had zero initial guesses, except output link coordinate with the initial guess of 195 mm taken for each value of j.
The numerical solution has been obtained after five iterations. Initial rotational angles of cranks 6 have taken the following values (accurate to a tenth):
Figure 3 presents the calculation results for platform trajectory X(t), where φ(t) corresponds to expression (29). It follows from Figure 3 that four of the six platform coordinates remain unchanged and equal to zero, while coordinate changes in a small range.
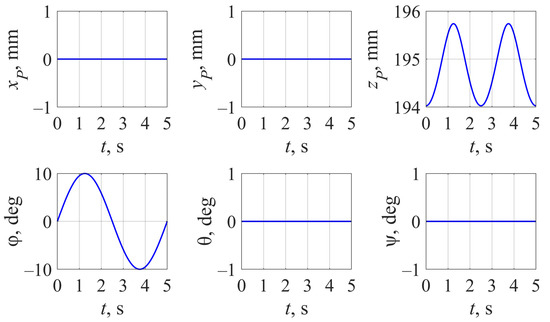
Figure 3.
Output link trajectory with according to (29).
Let us study another example and take output link displacement as given coordinate with the following time law:
which corresponds to one complete oscillation along axis with an amplitude of 10 mm.
The numerical simulation was performed under the same conditions as in the previous example, and we have found the solution after 13 iterations. Initial rotational angles of cranks 6 have taken the following values:
Figure 4 shows the calculation results for output link trajectory X(t), where corresponds to expression (31). It follows from Figure 4 that the changes in Cartesian coordinates and of the platform center and its orientation angles θ and ψ are negligible, and angle φ varies in a small range. The coordinates have the same values at t = 0 s and t = 5 s.
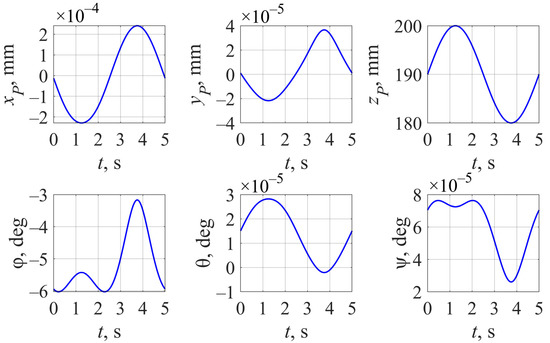
Figure 4.
Output link trajectory with according to (31).
Let us consider one more example and take platform displacement as given coordinate with the following time law:
which corresponds to one complete oscillation along axis with an amplitude of 10 mm.
The conditions of the numerical simulation corresponded to the previous examples, and the solution has been determined after 99 iterations. We have found the following values of initial rotational angles of cranks 6:
Figure 5 demonstrates the calculation results for platform trajectory X(t), where corresponds to expression (33). In this case, all six coordinates of the output link vary and have the same values at t = 0 s and t = 5 s.
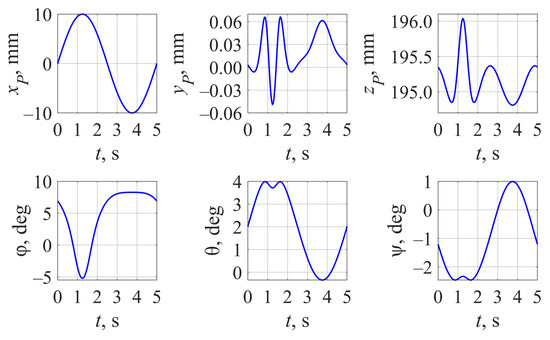
Figure 5.
Output link trajectory with according to (33).
To complete the analysis, Figure 6 presents the calculated time laws q(t) for all the examples. Notice that angle q has the same values at t = 0 s and t = 5 s in each example.
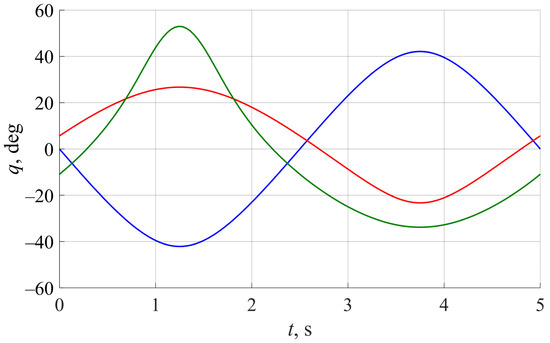
Figure 6.
Angle q calculated for various given output link coordinates : blue line for according to (29); red line for according to (31); green line for according to (33).
As mentioned earlier, solutions obtained by numerical methods can significantly depend on an initial guess. The importance of this fact increases in situations such as ours, where we have a number of variables (6 + 6N) greater than the number of equations (6N). To demonstrate this, let us perform simulations for a different initial guess.
In the previous examples, we set a zero guess for all the variables except for the platform coordinate . Suppose we arbitrarily change the guess for initial crank orientations from zero to the following one:
Using MATLAB, we performed similar simulations for this updated initial guess. In the first case with according to (29), we have found the following values of after six iterations:
The values differ from (30) and have no “symmetry” as before. This leads to displacements in all the platform coordinates, which can be seen from Figure 7 (φ(t) corresponds to expression (29)). The results have a big contrast with the ones in Figure 3, where the output link motion varied only in two coordinates.
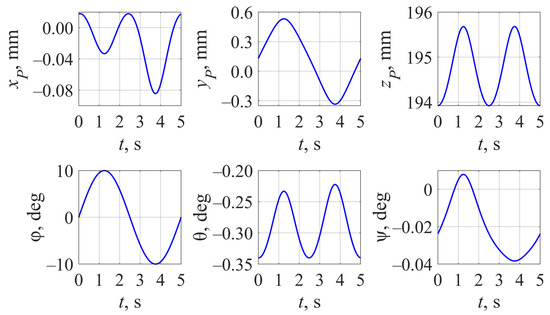
Figure 7.
Output link trajectory with according to (29) and an updated initial guess (35) for .
The next example considers the case with as in Equation (31). Given the updated initial guess for , we have found the following values of the crank initial rotational angles after nine iterations:
The calculation took fewer iterations than before, and the obtained results are close to (32) but differ from them and are slightly “unsymmetrical.” Figure 8 also demonstrates the resulting platform trajectory. Notice that coordinates , , θ, and ψ vary much more than earlier (Figure 4), though the output link continues to track given motion .
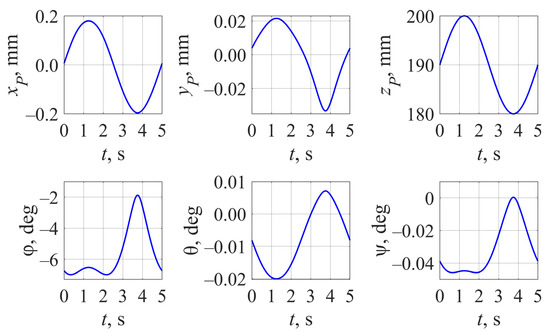
Figure 8.
Output link trajectory with according to (31) and an updated initial guess (35) for β0.
In the final case, according to expression (33). After 24 iterations, we have found the next values of :
The calculation took four times fewer iterations than the previous one with the zero initial guess. Obtained values of and the resulted output link trajectory (Figure 9) differ significantly from (34) and Figure 5. Platform coordinates vary at the same order of magnitude as before but have an alternative form.
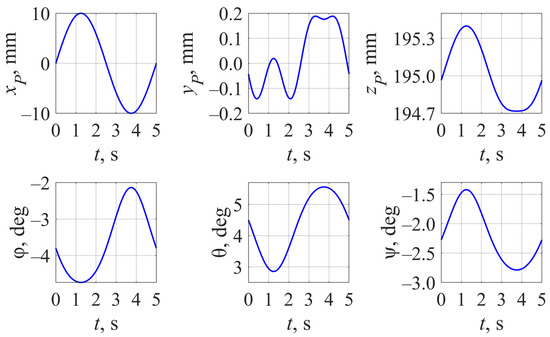
Figure 9.
Output link trajectory with according to (33) and an updated initial guess (35) for .
Figure 10 shows the calculated values of drive rotational angle q for all the examples. Again, for each case, we can see the differences between these results and the ones in Figure 6. The biggest difference exists in the third case when .
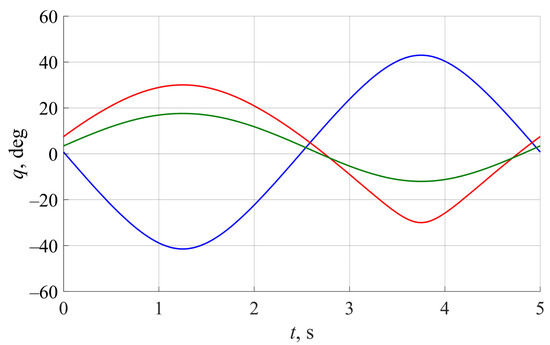
Figure 10.
Angle q calculated for various given output link coordinates and an updated initial guess (35) for : blue line for according to (29); red line for according to (31); green line for according to (33).
6. Discussion
To implement the suggested techniques in practice, one should follow the next simple steps:
- Set desired motion Xg(t) for one output link coordinate and calculate crank initial configuration together with drive control law q(t) using the proposed reconfiguration algorithm;
- On the mechanism, manually disconnect the belts and reorient the cranks according to calculated values . Reconnect the belts;
- Rotate the drive from its initial (zero) position to q(0). At this step, one can use any control law for the drive, e.g., an ordinary rotation with a constant speed;
- Control the drive according to calculated time law q(t).
We applied the steps above on the virtual prototype (Figure 1) and verified all the examples of Section 5 using an Autodesk Inventor Dynamic Simulation module. During the CAD simulations, we first set the initial orientations of the cranks according to obtained values . Next, we controlled the drive rotation using time laws in Figure 6 or Figure 10 and tracked the platform displacements. In all examples, the relative difference between the MATLAB and CAD results was less than 0.1%, caused mainly by numerical inaccuracies. This confirms the correctness of the suggested reconfiguration algorithm.
The examples studied in the previous section show that the given output link trajectory can be realized with different initial rotational angles of the cranks and various drive motions q(t). In some cases, uncontrolled platform coordinates have negligible changes, while in others, they vary considerably. This leaves us an opportunity to form an optimization problem that will seek for parameters and drive motion q(t) minimizing deviations in the uncontrolled coordinates. One should remember that the considered kinematic relations are highly nonlinear: as a result, convergence to a global optimum solution cannot be guaranteed for inappropriate initial conditions. The choice of initial guess remains an open and interesting problem.
We can use the proposed reconfiguration procedure in any other cases when it is necessary to provide a specified output link motion for one of the six coordinates, and the remaining five are arbitrary. The method allows determining the initial orientations of the cranks and the drive control law required to realize such a motion. To get more accurate results, we can either increase the sampling rate, i.e., parameter N, or diminish the tolerance value. However, the calculation time will rise in both cases.
Nevertheless, the suggested algorithm is computationally effective and can be developed for solving a dimensional synthesis problem. We addressed both topics in [29]. The considered techniques can also be extended for other mechanisms.
7. Conclusions
In this study, we have presented a variation of the hexapod-type reconfigurable parallel mechanism equipped with a single drive. The mechanism allows changing trajectories of the output link by disconnecting the belt in each kinematic chain.
During the kinematic analysis, we have formed the explicit relations between the output link coordinates and the rotation angle of the driving link. Based on these relations, we have developed the reconfiguration algorithm. This algorithm allows choosing the values of reconfigurable parameters (initial orientation of the cranks) and the driving link control law to realize a specific output link trajectory along any one of six coordinates. The suggested algorithm contains an implicit solution of the inverse kinematics problem and allows finding five remaining coordinates of the platform. Features of the equation system being solved (high sparsity of its Jacobian matrix) make the numerical solution procedure fast.
Given the geometry of the mechanism virtual prototype, we have considered three examples with different specified output link trajectories and various initial conditions. These examples have confirmed the effectiveness of the proposed algorithm. All calculations have been successively verified by CAD simulations.
The considered mechanism can be used for various technological applications related to vibration testing, mixing materials, and for rehabilitation procedures. The algorithms presented in this study can be extended to solve optimization problems, including optimal design, and adapted for other mechanisms. Developing a subsystem that could automate the reconfiguration procedure (crank reorientation) represents another direction for future research.
Author Contributions
Conceptualization, A.F. and A.A.; methodology, A.F. and A.A.; software, A.F.; validation, A.F. and A.A.; formal analysis, A.F. and A.A.; investigation, A.F. and A.A.; resources, A.F. and A.A.; writing—original draft preparation, A.F. and A.A.; writing—review and editing, A.F. and A.A.; visualization, A.F.; supervision, A.F., A.A. and V.G.; project administration, A.F. and A.A.; funding acquisition, A.F. and A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Russian Science Foundation (RSF) under grant No. 21-79-10409, https://rscf.ru/project/21-79-10409/ (accessed on 15 November 2021).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare that they have no conflict of interest.
Appendix A. Components of Jacobian Matrix
This appendix expands components (27) of Jacobian matrix (25)–(26). For , we present the derivatives with respect to each component of vector X. In the expressions below, we omit discretization index j for clarity:
where
References
- Merlet, J.-P. Parallel Robots, 2nd ed.; Springer: Dordrecht, The Netherlands, 2006. [Google Scholar] [CrossRef]
- Ceccarelli, M. Fundamentals of Mechanics of Robotic Manipulation; Springer: Dordrecht, The Netherlands, 2004. [Google Scholar] [CrossRef]
- Kong, X.; Gosselin, C.M. Type Synthesis of Parallel Mechanisms; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar] [CrossRef]
- Zhang, M.; Cao, J.; Zhu, G.; Miao, Q.; Zeng, X.; Xie, S.Q. Reconfigurable workspace and torque capacity of a compliant ankle rehabilitation robot (CARR). Robot. Auton. Syst. 2017, 98, 213–221. [Google Scholar] [CrossRef] [Green Version]
- Herrero, S.; Mannheim, T.; Prause, I.; Pinto, C.; Corves, B.; Altuzarra, O. Enhancing the useful workspace of a reconfigurable parallel manipulator by grasp point optimization. Robot. Comput. Manuf. 2015, 31, 51–60. [Google Scholar] [CrossRef]
- Tian, C.; Fang, Y.; Guo, S.; Qu, H. A class of reconfigurable parallel mechanisms with five-bar metamorphic linkage. Proc. Inst. Mech. Eng. C J. Mech. 2016, 231, 2089–2099. [Google Scholar] [CrossRef]
- Ye, W.; Fang, Y.; Guo, S. Design and analysis of a reconfigurable parallel mechanism for multidirectional additive manufacturing. Mech. Mach. Theory 2017, 112, 307–326. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Xu, L.; Chen, Q.; Ye, W. New family of RPR-equivalent parallel mechanisms: Design and application. Chin. J. Mech. Eng. 2017, 30, 217–221. [Google Scholar] [CrossRef]
- Carbonari, L.; Callegari, M.; Palmieri, G.; Palpacelli, M.-C. A new class of reconfigurable parallel kinematic machines. Mech. Mach. Theory 2014, 79, 173–183. [Google Scholar] [CrossRef]
- Bi, Z.; Wang, L. Optimal design of reconfigurable parallel machining systems. Robot. Comput. Integr. Manuf. 2009, 25, 951–961. [Google Scholar] [CrossRef]
- Huang, G.; Zhang, D.; Guo, S.; Qu, H. Design and optimization of a novel three-dimensional force sensor with parallel structure. Sensors 2018, 18, 2416. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, T.; Li, Z.; Li, M.; Chetwynd, D.G.; Gosselin, C.M. Conceptual design and dimensional synthesis of a novel 2-DOF translational parallel robot for pick-and-place operations. J. Mech. Des. 2004, 126, 449–455. [Google Scholar] [CrossRef]
- Huang, H.; Deng, Z.; Li, B.; Liu, R. Analysis and synthesis of a kind of mobility reconfigurable robot with multitask capability. J. Adv. Mech. Des. Sys. Manuf. 2011, 5, 87–102. [Google Scholar] [CrossRef] [Green Version]
- Huang, G.; Zhang, D.; Tang, H.; Kong, L.; Song, S. Analysis and control for a new reconfigurable parallel mechanism. Int. J. Adv. Rob. Sys. 2020, 17, 1729881420931322. [Google Scholar] [CrossRef]
- Fanghella, P.; Galletti, C.; Giannotti, E. Parallel robots that change their group of motion. In Advances in Robot Kinematics, Proceedings of the 10th International Symposium on Advances in Robot Kinematics, Ljubljana, Slovenia, 26–29 June 2006; Lenarčič, J., Roth, B., Eds.; Springer: Dordrecht, The Netherlands, 2006; pp. 49–56. [Google Scholar] [CrossRef]
- Ye, W.; Chai, X.; Zhang, K. Kinematic modeling and optimization of a new reconfigurable parallel mechanism. Mech. Mach. Theory 2020, 149, 103850. [Google Scholar] [CrossRef]
- Zhang, K.; Dai, J.S.; Fang, Y. Topology and constraint analysis of phase change in the metamorphic chain and its evolved mechanism. J. Mech. Des. 2010, 132, 121001. [Google Scholar] [CrossRef]
- Gan, D.; Dias, J.; Seneviratne, L. Unified kinematics and optimal design of a 3rRPS metamorphic parallel mechanism with a reconfigurable revolute joint. Mech. Mach. Theory 2016, 96, 239–254. [Google Scholar] [CrossRef]
- Kong, X.; Gosselin, C.M.; Richard, P. Type synthesis of parallel mechanisms with multiple operation modes. J. Mech. Des. 2007, 129, 595–601. [Google Scholar] [CrossRef]
- Karimi, A.; Masouleh, M.-T.; Cardou, P. Avoiding the singularities of 3-RPR parallel mechanisms via dimensional synthesis and self-reconfigurability. Mech. Mach. Theory 2016, 99, 189–206. [Google Scholar] [CrossRef]
- Fomin, A.; Glazunov, V.; Terekhova, A. Development of a novel rotary hexapod with single drive. In ROMANSY 22—Robot Design, Dynamics and Control, Proceedings of the 22nd CISM IFToMM Symposium, Rennes, France, 25–28 June 2018; Arakelian, V., Wenger, F., Eds.; Springer: Cham, Switzerland, 2018; pp. 141–146. [Google Scholar] [CrossRef]
- Shin, H.; Kim, S.; Jeong, J.; Kim, J. Stiffness enhancement of a redundantly actuated parallel machine tool by dual support rims. Int. J. Precis. Eng. Manuf. 2012, 13, 1539–1547. [Google Scholar] [CrossRef]
- Glazunov, V.A.; Lastochkin, A.B.; Rashoyan, G.V.; Skvortsov, S.A.; Shevchenko, E.F. Spatial mechanism with six degrees of freedom. Patent RU 160612, 27 March 2016. [Google Scholar]
- Coulombe, J.; Bonev, I.A. A new rotary hexapod for micropositioning. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 877–880. [Google Scholar] [CrossRef]
- Wu, G.; Dong, H.; Wang, D.; Bai, S. A 3-RRR spherical parallel manipulator reconfigured with four-bar linkages. In Proceedings of the 2018 International Conference on Reconfigurable Mechanisms and Robots (ReMAR), Delft, The Netherlands, 20–22 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Chen, T.; Qian, S.; Li, Y.; Yi, Z. Mechanism design and analysis for an automatical reconfiguration cable-driven parallel robot. In Proceedings of the 2017 2nd International Conference on Cybernetics, Robotics and Control, Chengdu, China, 21–23 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 45–50. [Google Scholar] [CrossRef]
- Fomin, A.; Petelin, D.; Antonov, A.; Glazunov, V.; Ceccarelli, M. Virtual and physical prototyping of reconfigurable parallel mechanisms with single actuation. Appl. Sci. 2021, 11, 7158. [Google Scholar] [CrossRef]
- Fomin, A.; Antonov, A.; Glazunov, V. Forward kinematic analysis of a rotary hexapod. In ROMANSY 23—Robot Design, Dynamics and Control, Proceedings of the 23rd CISM IFToMM Symposium, Sapporo, Japan, 20–24 September 2020; Venture, G., Solis, J., Takeda, Y., Konno, A., Eds.; Springer: Cham, Switzerland, 2021; pp. 486–494. [Google Scholar] [CrossRef]
- Fomin, A.; Antonov, A.; Glazunov, V.; Carbone, G. Dimensional (parametric) synthesis of the hexapod-type parallel mechanism with reconfigurable design. Machines 2021, 9, 117. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).