Abstract
Scale-invariance has rapidly established itself as one of the most used concepts in space plasmas to uncover underlying physical mechanisms via the scaling-law behavior of the statistical properties of field fluctuations. In this work, we characterize the scaling properties of the magnetic field fluctuations in a sub-alfvénic region in contrast with those of the nearby super-alfvénic zone during the ninth Parker Solar Probe perihelion. With our observations, (i) evidence of an extended self-similarity (ESS) for both the inertial and the sub-ion/kinetic regimes during both solar wind intervals is provided, (ii) a multifractal nature of field fluctuations is observed across inertial scales for both solar wind intervals, and (iii) a mono-fractal structure of the small-scale dynamics is reported. The main novelty is that a universal character is found at the sub-ion/kinetic scale, where a unique rescaling exponent describes the high-order statistics of fluctuations during both wind intervals. Conversely, a multitude of scaling symmetries is observed at the inertial scale with a similar fractal topology and geometrical structures between the magnetic field components in the ecliptic plane and perpendicular to it, in contrast with a different level of intermittency, more pronounced during the super-alfvénic interval rather than the sub-alfvénic one, along the perpendicular direction to the ecliptic plane. The above features are interpreted in terms of the possible underlying heating and/or acceleration mechanisms in the solar corona resulting from turbulence and current sheet formation.
1. Introduction
Since the early 1980s, increased attention has been paid to investigating scaling properties in physical systems, due to the seminal work by Mandelbrot introducing the concept of fractals [1]. Nowadays, fractals, i.e., geometrical objects undergoing self-affine and self-similar rules over a wide range of scales [2], widely populate different works in the literature, including space plasmas [3] and geosciences [4]. One of the most peculiar aspects of fractals is their scale-invariant nature, i.e., statistical properties are preserved over a wide range of scales and can be described via simple mathematical rules [1]. A scale-invariant object obeys a rescaling transformation
i.e., it is a homogeneous function of degree h. Thus, how the statistical properties change with the scale only depend on a single exponent h, usually named rescaling exponent or Hölder exponent [5]. Sometimes, a single exponent h is not enough to describe the dynamics of fractals, requiring a continuous spectrum of exponents to fulfill its statistical properties. These systems are usually termed multifractals [6]. In a multifractal system, a generalization of the scale invariance (Equation (1)) needs to be introduced as
Multifractals are common in nature: from the length of coastlines [7] to fully developed turbulence [8], passing through human brain activity [9] and finance [10].
Solar wind is one of the natural examples where fractal concepts and properties can be touched by the hand. Solar wind observables, such as the magnetic field, the velocity field, and plasma thermal parameters, usually display a scale-invariant nature over different range of scales, typically related to different approximations in describing physical processes and regimes [3,11]. Solar wind, indeed, exhibits a multitude of physical phenomena, ranging from microscopic (dominated by individual charged particle dynamics in electromagnetic fields) to macroscopic (described as a turbulent fluid) scales [3]. These features are evidenced by a very broadband power spectral density (PSD) that, at 1 astronomical unit (AU), is mainly characterized by three different regimes: a large-scale forcing, related to the variability of the source of the solar wind, an inertial range, where the classic fluid-like or magnetohydrodynamic (MHD) approximation is valid and related to the energy cascade from large to small scales, and a sub-ion range, sometimes known as the dissipative or kinetic regime, where kinetic physics begins [12]. In terms of fractal properties, the MHD and the sub-ion/kinetic regimes are characterized by different high-order statistical properties: while the former presents a multifractal nature, the latter is characterized by a mono-fractal topology [13,14,15,16,17]. The source of multifractal features at the MHD scale is usually related to the intermittent nature of the energy cascade mechanism, producing a heterogeneous distribution of energy at different scales that cannot be described as a global scale-invariant system (i.e., with only one rescaling exponent) [3,6,13]. Conversely, the mono-fractal nature of the sub-ion/kinetic regimes can be associated with the fine structure of the dissipation field, mainly consisting of thin flux tubes or current sheets [16,17,18,19]. These features have been observed at different heliocentric locations, both close to the Sun [17], at 1 AU [3], and far-away in the outer heliosphere [20,21,22]. All these studies provide a universal picture of the scaling properties of the super-alfvénic solar wind, i.e., the solar wind plasma whose speed is larger than the Alfvén speed. This corresponds to a fluid-dominated description of the solar wind, usually observed with different space missions. The recently launched Parker Solar Probe (PSP) mission [23], reaching the closest distance to the Sun than any of other spacecraft before, sampled the sub-alfvénic coronal region [24], where a magnetically dominated solar wind is observed. This allows us to characterize the nature of the solar wind plasma below the Alfvén critical point, where the wind speed equals the Alfvén speed, providing deeper information on the physics of lower coronal altitudes than explored before, both in terms of fluctuations, waves, and structures [24,25,26]. Nevertheless, none of these studies focused on the high-order statistics of field fluctuations, mainly describing their spectral features (e.g., [24,27], in terms of Fourier PSD), their anisotropy and/or the occurrence rate of switchbacks [26].
In this work, we study the scaling properties of the magnetic field fluctuations in a sub-alfvénic region in contrast with those of the nearby super-alfvénic zone during the ninth PSP perihelion. With our observations, (i) evidence of an extended self-similarity (ESS) for both the MHD/inertial and the sub-ion/kinetic regimes during both solar wind intervals is provided, (ii) a multifractal nature of field fluctuations is observed across inertial scales for both solar wind intervals, and (iii) a mono-fractal structure of the small-scale dynamics is reported. The ESS property allows us to connect in a simple way the generalized scaling properties across scales as a function of the smallest scales, which is in agreement with the generalized Markovian property observed for the magnetic field fluctuations [28]. Although the difference in terms of the fractal nature of field fluctuations across both regimes is not a novel result, since it was previously reported [15,16,17,29], the main novelty is that a universal character is found at small scales which shows scale-invariance with the same rescaling exponent during both wind intervals, also similar with near-Earth and near-Sun solar wind [17,18,19,29]. Furthermore, although MHD scales show a multifractal nature during both intervals, the most intriguing aspect is the similar fractal topology and geometrical structures between magnetic field components in the ecliptic plane and perpendicular to it, in contrast with a different level of intermittency, more pronounced during the super-alfvénic interval rather than the sub-alfvénic one, along the perpendicular direction to the ecliptic plane. The above features are interpreted in terms of possible underlying heating and/or acceleration mechanisms in solar coronal heating processes, resulting from turbulence and current sheet formation.
2. Data
Our study focuses on the scaling properties of magnetic field observations coming from the SCaM data product of the FIELDS instrument suite [30] merging measurements from the flux-gate magnetometer (FGM) and the search-coil (SCM) [31] with a sampling rate of 293 samples/s. Specifically, we consider two intervals in the near-Sun solar wind lasting two hours each where PSP sampled a super-alfvénic and a sub-alfvénic solar wind stream. Both intervals were sampled on 9 August 2021 during the ninth PSP perihelion: the super-alfvénic interval is from 17:00 UT to 19:00 UT, while the sub-alfvénic interval is from 22:00 UT to 00:00 UT. These intervals were previously investigated by Bandyopadhyay et al. [26] and were identified by means of the evaluation of the local Alfvén Mach number : specifically, the super-alfvénic interval corresponds to , while the sub-alfvénic one corresponds to , respectively. Furthermore, to avoid effects due to the crossing of the Alfvén critical surface/point, we considered a reduced time interval with respect to Bandyopadhyay et al. [26] for investigating scaling properties of the sub-alfvénic solar wind (the full period is between 21:24 UT and 00:20 UT). Figure 1 reports the three magnetic field components in the radial–tangential–normal (RTN)1 reference system for the two intervals considered in this study.
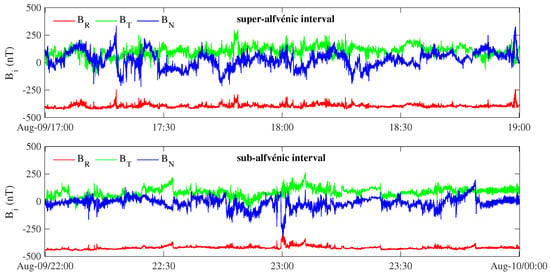
Figure 1.
The three magnetic field components in the radial–tangential–normal (RTN) reference system for the two intervals considered in this study: (upper panel) the super-alfvénic, and (lower panel) the sub-alfvénic solar wind, respectively.
3. Methods
Scaling properties are usually investigated by means of the high-order statistics of fluctuations represented via field increments and generalized structure functions [32]. Given a magnetic field component with , the field increment (or fluctuation) at the scale is defined as
These increments are thought to be representative of the fluctuations at different timescales (or equivalently, at spatial scales if the Taylor’s hypothesis is employed, , where V is the plasma bulk speed) and have been widely used in searching for scale-invariant features, especially in the field of turbulence [3,4,5,6,8,13]. Indeed, the incompressible MHD equations
written in terms of the Elssaser fields [33], where p is the plasma kinetic pressure and is the sum or the difference between the kinematic viscosity and magnetic diffusivity [34], possess a scale-invariant nature. This means that they are formally invariant with respect to scaling transformations (also in the limit of finite )
for any constant and, in principle, for any [35]. Assuming that the small-scale turbulence, described in terms of field increments , is statistically invariant under scaling transformations, we can select the scaling exponent h by considering that nonlinear interactions across the inertial range must preserve the energy transfer rate [35,36]. Under this assumption, two scenarios emerge according to the characteristic time that is responsible for the cascade mechanism: (i) a fluid-like scenario, e.g., [8,36], and (ii) an Alfvénic scenario, e.g., [35,37,38]. In the fluid-like case, the characteristic time in which the cascade is realized is the eddy turnover time [8]
while in the Alfvénic case [35], the characteristic time is the Alfvén time that reduces the time to develop the cascade to
Since the energy transfer rate is defined as , by using Equations (10) and (11), we can write it in a compact form as
such that the scale invariance implies
With the Kolmogorov assumption of preserving the energy transfer rate across the cascade, it immediately follows that
Assuming the so-called self-similarity hypothesis, e.g., [36] the high-order statistics of the field increment, usually termed order structure function , must satisfy a generalized scale-invariance law as
Both the Kolmogorov and the Iroshnikov–Kraichnan theories describe a turbulent fluid/plasma as a mono-fractal system, possessing a global scale-invariance with a well-defined rescaling exponent h. Since the first laboratory experiments on fluids, and later on with the first in situ measurements of the solar wind parameters, a failure of this mono-fractal picture of turbulence was pointed out [35,39]. The main source of the anomalous scaling of exponents, i.e., on the existence of more than a single h, is the intermittent character of the cascade mechanism [6,35], forming topological structures of different size and with different geometries [5]. This traduces in observing a wide spectrum of rescaling exponents h at different scales, moving from a global to a local concept of scale invariance [39], due to the fact that the energy transfer rate is not preserved along scales but it fluctuates both in space and time [1,8]. This means that instead of having a specific rescaling exponent with probability equal to 1, we have now a probability of observing a rescaling exponent h for the turbulent fluctuation at the scale ℓ. Thus, the order structure function must be written as
with being a nonlinear convex function of q [6,8], with taken into account for intermittency correction of the energy transfer rate at different scales [35,39]. Similar considerations can be drawn in terms of time scales instead of spatial scales ℓ, thus allowing us a direct comparison with measurements coming from space mission, typically released as time series [3,5,8].
In the following, we evaluate the magnetic field increments at different scales , and we evaluate the high-order statistics via the structure function approach. Our two intervals consists of a number of points 1,054,800, thus, since the accuracy of high-order statistics is affected by finite sample effects, we can explore a range of statistical moments up to [40]. Furthermore, since the length of our time intervals is 2 h each, we evaluate increments over a range of scales, in terms of power of 2, from up to . This choice allows us to explore both the inertial and the sub-ion/kinetic regimes. In the following, we evaluate the high-order statistics in terms of the order structure functions for each magnetic field component, i.e., , as well as their respective scaling exponents , with .
4. Results
We begin our analysis by comparing the second-order structure function for both time intervals since it allows us to have a first indication on the existence of scale invariance over specific range of scales (similarly to the Fourier PSD). Figure 2 reports the behavior of the trace of the 2nd-order structure function, Tr for the super-alfvénic (black circles) and the sub-alfvénic (blue circles) intervals, respectively.
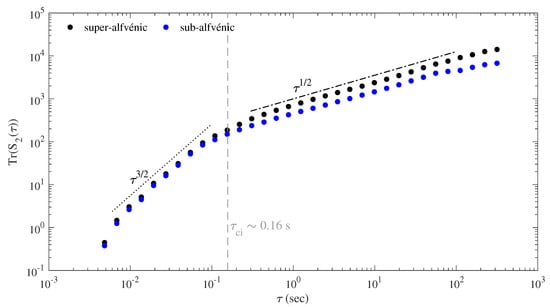
Figure 2.
The trace of the 2nd-order structure function, Tr, for the super-alfvénic (black circles) and the sub-alfvénic (blue circles) intervals, respectively. The two scale-invariant curves, (dashed-dotted black) and (dotted black), are drawn as reference for the scalings. The vertical gray dashed line marks the proton cyclotron scale.
At least two different scale-invariant regimes can be identified, covering the short-scale ( s) and the mid-scale ( s) ranges, respectively. The former can be related to sub-ion/kinetic dynamical processes, occurring below the proton cyclotron scale (: proton rest mass, e: proton charge, B: magnetic field intensity), while the latter can be associated with the dynamics of the MHD range, mainly related to nonlinear energy transfer mechanisms across the inertial cascade [36,37,38]. The scale break between the two different regimes is located around the proton cyclotron scale, although a smooth transition is observed for the super-alfvénic interval, while a sharper transition characterized the sub-alfvénic interval. The observation of a transition region between scaling regimes is usually observed in the “standard” (super-alfvénic) solar wind, both at 1 AU, e.g., [41] and close to the Sun [17]. The lack of a transition region between MHD and sub-ion scales for the sub-alfvénic interval was also recently reported by Kasper et al. [24] for a different sub-alfvénic interval during the eighth PSP perihelion, who found a steep drop of the spectrum at proton cyclotron scales. However, both intervals are characterized by the same level of fluctuations at sub-ion/kinetic scales, mostly decaying with a similar scaling exponent close to 3/2. This estimation is consistent with the typical spectral exponents observed at sub-ion scales (we remark that the spectral exponent ), although the value of this exponent can vary as a function of plasma conditions (e.g., temperature, density, ratio between kinetic and magnetic pressure) and anisotropy of field fluctuations [12].
At larger scales ( s), a less steep scaling regime is observed, whose scaling exponent is close to the Iroshnikov–Kraichnan prediction for the MHD inertial range [37,38]. This scaling characterizes both the sub- and the super-alfvénic intervals, although the level of fluctuations is larger during the super-alfvénic one. These observations are consistent with recent studies based on Elsasser variables [27] and magnetic/kinetic energy spectral densities [24]. Thus, since in the super-alfvénic region closely resembles those in the sub-alfvénic one in terms of the scaling exponent, similar basic turbulence physics holds in both regions. However, the lack of a transition region, counter-parting an extension at smaller scales of an inertial range scale-invariant behavior for the sub-alfvénic interval, could suggest that alfvénic interactions between outward and inward propagating modes dominate the nonlinear interactions near the proton cyclotron scale or as a signature of parametric decaying instability indicating heating and/or dissipation physics [24].
Furthermore, since the sub-alfvénic interval is characterized by the presence of a shock wave that could affect the scaling properties, we also repeated our evaluation of increments and structure functions on a shorter interval, i.e., from 22:00 UT to 22:45 UT, that still allows us to cover both the sub-ion range and the MHD/inertial scales. Apart from some differences in the amplitude of the fluctuations (increments), the scale-invariant properties across the two range of scales that we are interested in are not affected, thus supporting the significance of our results and suggesting that they are not affected by the presence of the shock wave.
As a further step, we need to evaluate the scaling exponents that characterize the high-order statistical properties of the magnetic field fluctuations represented by the increments. Usually, in fully developed turbulence, according to the Kolmogorov theory [36], inertial range scaling exponents are evaluated over the range of scales, where a linear relation holds between and , which is independent of the viscosity. For plasmas, this linear relation is verified, according to the Iroshnikov–Kraichnan theory [37,38], when looking at vs. . However, both predictions fail for moderate to low Reynolds numbers, consequently affecting the accuracy of the scaling exponents. Furthermore, the self-similar scaling with the scale has been shown to be accurate only when we can access to both the integral scale and the dissipation/Kolmogorov scale, thus requiring knowledge on different physical properties, such as the injection scale and/or the viscosity/diffusivity parameters. Finally, the extension of the inertial range depends on the Reynolds number and on the rescaling exponent h, thus making a proper identification of boundaries for scale invariance difficult. In 1993, Benzi et al. [42] proposed a novel form of self-similarity, usually known as extended self-similarity (ESS), allowing good estimates for scaling exponents. The main idea is to search for a scale-invariance between two structure functions, i.e.,
such that for fluid turbulence and for MHD turbulence . The ESS is a powerful technique for investigating scale invariance, widely used in many different systems [14,43,44], with several advantages with respect to the “usual” scaling against :
- 1.
- It provides an accurate determination of scaling exponents;
- 2.
- It holds down to the dissipative regime;
- 3.
- It holds for both high and mid-to-low Reynolds numbers.
The main novelty is that the concept of scale invariance and self-similarity can be extended widely below the “naive” inertial range definition via the scaling of the 2nd-order structure function vs. the scale, allowing us a proper estimation of scaling exponent for both the inertial and the sub-ion regimes. Figure 3 reports the ESS analysis for both time intervals by comparing the the trace of the 2nd-order structure function, Tr, vs. the trace of the 4th-order structure function, Tr.
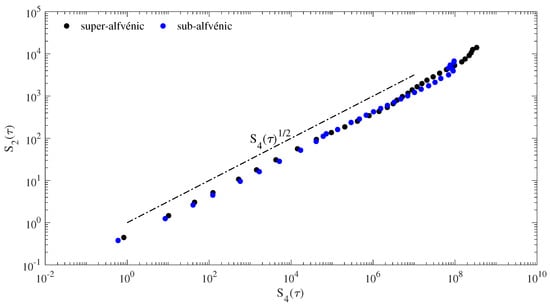
Figure 3.
The ESS analysis: the trace of the 2nd-order structure function, Tr, vs. the trace of the 4th-order structure function, Tr, for the super-alfvénic (black circles) and the sub-alfvénic (blue circles) intervals, respectively.
As expected for plasmas, the ESS holds for both the MHD/inertial and the sub-ion/kinetic regimes with an extended scaling exponent matching the scaling exponent . The derived scaling exponents via ESS analysis across both regimes and for each magnetic field component are reported in Figure 4 during both the super-alfvénic and the sub-alfvénic intervals, respectively.
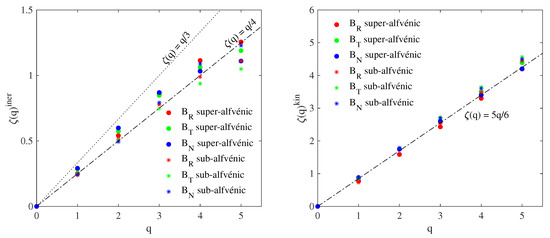
Figure 4.
The scaling exponents derived via ESS analysis for each magnetic field component (: red symbols, : green symbols, : blue symbols) during both the super-alfvénic (circles) and the sub-alfvénic (asterisks) intervals: inertial range (left panel) and sub-ion/kinetic range (right panel). The dashed-dotted and the dotted lines in the left panel refer to the Iroshnikov-Kraichnan and the Kolmogorov predictions. The dashed–dotted line in the right panel is used as a reference for linear scaling.
A rough look seems to highlight that there are no differences in the scaling properties of the super-alfvénic interval with respect to the sub-alfvénic one. This is true both for the inertial range (Figure 4, left panel) and for the kinetic regime (Figure 4, right panel). Indeed, scaling exponents across the inertial range show deviations from both the Kolmogorov and the Iroshnikov–Kraichnan linear predictions, being characterized by a nonlinear convex behavior with q, more pronounced for , for both solar wind intervals. This means that anomalous scaling features are observed, as expected for intermittent turbulence, supporting the multifractal nature of the inertial range both in the sub-alfvénic and in the super-alfvénic regions close to the Sun. Furthermore, different scaling exponents are obtained for the different magnetic field components as well as for the two intervals, thus indicating a possible source of anisotropy of scaling features reflecting the anisotropic nature of the field fluctuations [26]. At sub-ion/kinetic scales (Figure 4, right panel) a linear scaling is observed, with a Hurst exponent close to 5/6, quite similar for all magnetic field components and for both intervals. This observation suggests the absence of intermittency at kinetic scales, with a mono-fractal nature of field fluctuations, consistent with near-Earth [15,16] and near-Sun [17] solar wind. Thus, our results suggest that there are no differences in terms of scaling features and self-similar nature between the sub-alfvénic and the super-alfvénic near-Sun solar wind, although some differences emerge across the inertial range.
As a final step and to further highlight possible differences between the two intervals, we report in Figure 5 a scatter-plot of the scaling exponents for both regimes of the sub-alfvénic vs. the super-alfvénic interval.
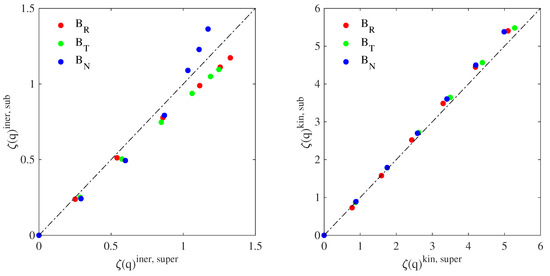
Figure 5.
The scaling exponents of the sub-alfvénic solar wind vs. those of the super-alfvénic interval for each magnetic field component (: red symbols, : green symbols, : blue symbols): inertial range (left panel) and sub-ion/kinetic range (right panel). The dashed–dotted lines mark the bisector of the plane where the equality holds.
We need to remark the following relations:
- If , then the two intervals are characterized by the same fractal topology, i.e., they share the same geometrical structures and the same symmetries;
- If , then the two intervals are characterized by a fractal topology belonging to the same class, i.e., they share the same geometrical structures but with different symmetries;
- If , then the two intervals are characterized by a different fractal topology, i.e., they do not share neither the same geometrical structures nor the same symmetries.
It is evident that at the sub-ion/kinetic scale, a linear identity relation holds between the scaling exponents of the sub-alfvénic and those of the super-alfvénic intervals, thus suggesting that the two intervals share the same fractal topology with the same distribution of fractal dimensions, symmetries, and geometrical structures. Conversely, by looking at MHD/inertial scale, a linear relation holds for the radial and the tangential components, while a nonlinear relation seems to be observed for the normal one. The former suggests that along the radial and the tangential components of the magnetic field, a similar fractal topology, in terms of geometrical structures of field fluctuations, is observed, although with different symmetry properties. On the other hand, the nonlinear relation along the normal component N indicates a different fractal topology, both in terms of geometrical features and symmetries, with a different level of intermittency, more pronounced during the super-alfvénic interval rather than during the sub-alfvénic one. The increased level of intermittency during the super-alfvénic interval is consistent with recent studies [26], although here, we point out where the source of increased intermittency is located in terms of scales.
5. Discussions and Conclusions
In this study, we provided a side-by-side comparison of the scaling properties of the magnetic field fluctuations in a sub-alfvénic region and in the nearby super-alfvénic zone during the ninth PSP perihelion. To our knowledge, this is the first study contrasting the high-order statistics of magnetic field fluctuations during two nearby solar wind streams with different alfvénic conditions. Our main findings can be summarized as follows:
- 1.
- An extended self-similarity is observed for both the MHD/inertial and the sub-ion/kinetic regimes during both intervals;
- 2.
- A multifractal nature of field fluctuations is reported across inertial scales for both solar wind intervals;
- 3.
- A mono-fractal character is observed for field fluctuations at small scales during both solar wind intervals.
5.1. Extended Self-Similarity
Magnetic field fluctuations during the super-alfvénic and the sub-alfvénic intervals display an extended range of self-similarity, covering almost all range of scales accessible due to the time resolution and length of measurements. Furthermore, both intervals present a universal behavior, being characterized by similar scaling exponents . Let us now discuss the consequences of our observation of an ESS. If Equation (17) holds, following Benzi et al. [45] see also, [46] and Carbone et al. [43], the high-order statistics can be written in terms of a function depending on the dissipation scale
where is a dimensionless constant and is the magnetic field intensity at the largest (integral) scale T such that . This means that the statistical properties of magnetic field fluctuations can be related to those at the smallest scale via the function that describes the relation between the statistics of field fluctuations when moving from the dissipation scale to the integral scale. One of the most interesting aspects of Equation (18) is the close connection between the order statistical properties of field fluctuations and two fundamental scales in turbulence, i.e., the integral scale T and the dissipation scale . Another intriguing aspect could be the possible connection between the Markovian property of field fluctuations recently observed by Benella et al. [28] with the functional form of that could open a novel framework for describing the statistical properties across the sub-ion and the inertial range of scales.
5.2. Multifractality of Inertial Range
The observed multifractal nature of field fluctuations across the inertial range for both time intervals clearly support previous findings in the literature evidencing the role of intermittent processes in redistributing energy across MHD scales via the nonlinear cascade mechanisms, e.g., [3,8]. One of the most intriguing aspects is the observed similar nature, in terms of fractal topology and geometrical structures, between the radial and the tangential components of both intervals, in contrast with a different level of intermittency, more pronounced during the super-alfvénic interval rather than the sub-alfvénic one, along the normal component. A possible physical explanation of the observed difference could be related to the nature of alfvénic fluctuations observed below and above the Alfvén critical point at which the alfvénic Mach number . As recently pointed out by Bandyopadhyay et al. [26], the sub-alfvénic wind presents a higher anisotropy and lower amplitude fluctuations with respect to the super-alfvénic one, likely related to coronal heating processes resulting from turbulence and current sheet formation, e.g., [47]. Another source of difference can be related to the coupling between inward and outward alfvénic fluctuations, mostly producing circularly polarized waves [48], usually interpreted as a signature of heating and acceleration mechanisms via linear resonance and instabilities, e.g., [49,50]. Both these sources are thought to be responsible for launching transverse (with respect to the main field) fluctuations due to photospheric deflection of field lines [47,51]. Thus, the observed stretching of the geometrical features along the normal component could reflect some underlying heating and/or acceleration mechanisms in solar corona.
To further highlight the geometrical properties of intermittent structures, we employed two different multifractal models widely used in turbulence, allowing us to retrieve a quantitative measure of the geometry of intermittent structures. The two models are the p-model [35,52] and the She–Leveque (SL) model [53,54,55]. The p-model describes the cascade mechanism as a two-scale Cantor set, i.e., an eddy at the scale ℓ with measure breaks into two eddies with measures and , respectively. Thus, the parameter p is a measure of the distribution of energy across scales and can vary in the range 0.5–1 [35]. The scaling exponents of the p-model satisfy the following relation
with for fluid turbulence and for MHD. The She–Leveque model assumes instead an infinite hierarchical structure for the high-order moments of the energy transfer rate as , with divergent singularities as . In this case, the scaling exponents read as
with and C being the co-dimension of the intermittent structures. The two models reconcile at large q provided that [43]. Table 1 reports the best fit, obtained using a nonlinear least-square fitting procedure via the Levenberg–Marquardt algorithm, for the free parameters m, p, and C, of the two models (the SL model is solved by fixing [54]).

Table 1.
The best-fit values of the parameters m, p, and C based on fitting the inertial range scaling exponents for each magnetic field component. The 95% significance range is shown as subscript and superscript.
First of all, since , both the sub-alfvénic and the super-alfvénic wind are characterized by a MHD scenario à la Iroshnikov–Kraichnan. This also allows us to justify the use of both models to describe the deviation from the linear scaling, i.e., the effects of intermittency across the cascade, of the scaling exponents. Indeed, these models were developed for the velocity field e.g., [35,52,53] assuming that a similar scaling is observed for magnetic field fluctuations (we remark that MHD scale-invariant features are drawn in terms of Elsasser variables). The observation is that assures this condition is valid for , thus allowing us to use these intermittency models to describe the behavior of scaling exponents. By looking at the values of the p parameter, we note, as expected, that both intervals show signatures of multifractality, being . The super-alfvénic wind is characterized by , in agreement with previous findings on non-alfvénic solar wind, e.g., [3,43]. The super-alfvénic wind is instead characterized by an increased level of intermittency along the normal component (), while being almost unchanged with the sub-alfvénic wind along the radial and the tangential directions (p = 0.74–0.78). This observation provides a quantitative measure of the observed increased level of intermittency along N. Furthermore, by looking at the co-dimension C derived via the SL model, we clearly observe larger C in the sub-alfvénic wind than the nearby super-alfvénic zone. Since the co-dimension C gives us information on the geometry of the most intermittent structures of the dissipation field, our findings suggest that, for the sub-alfvénic case, most of the dissipation occurs via two-dimensional structures, such as planar current sheets and/or reconnection sites; conversely, the super-alfvénic wind is characterized by a fractal dimension of the dissipation field larger than 2, suggesting that dissipation occurs via deformed planar sheets and/or flux tubes. The source of this geometrical variation has not yet been established or evidenced, thus requiring a deeper investigation with further PSP orbits closer to the Sun and/or transiting within the Alfvén critical surface to assess if the observed difference may be due to the comparative analysis of these two specific intervals or if the difference of the values of C is due to the sub- or super-alfvénic nature of the solar wind. Plausible sources could be MHD/plasma instabilities and/or acceleration/heating mechanisms [26,47].
5.3. Mono-Fractality at Sub-Ion/Kinetic Scales
Magnetic field fluctuations at small scales, below the proton cyclotron scale , display a universal mono-fractal behavior, both in the sub-alfvénic and the super-alfvénic winds. Our results indicate a linear relation for the scaling of the high-order moments of the probability distribution function of increments/fluctuations with an exponent, i.e., the Hurst exponent, close to 5/6 (). Our findings are consistent with both near-Earth observations [15,16,29] and near-Sun ones [17,18,19,28], indicating the absence of intermittency at kinetic scales with a clear deviation from both the Kolmogorov and the Iroshnikov–Kraichnan scalings ( should 1/3 and 1/4, respectively). The observation of a global (along the full sub-ion range) scale invariance, implying mono-scaling of structure functions distinct from the multi-scaling observed across the MHD scales, suggests that the small-scale dynamics between the proton and the electron scales mainly corresponds to a fragmented sheet-like configuration, likely representative of the first structure of the dissipation field, although dissipation should occur at lower scales below the electron gyroscale. One of interpretations is that the observed mono-scaling could result from the breakdown of the fluid-like description, usually employed when investigating scaling regimes. Indeed, the scale invariance is a property of MHD equations, which is a field description, in terms of the velocity and the magnetic fields, of plasmas. At smaller scales, wave–particle/particle–particle interactions and small-scale (dissipative) structures (such as current sheets) become the most prominent features, thus requiring a field theory, based on electric currents and electric fields, to properly overcome some assumptions of MHD theory (neglecting displacement currents), and/or using a kinetic description [34]. This would accomplish investigating how a highly dynamic sub-ion-scale population of current sheets [18,19,56] and/or an effect of (in)coherent waves [17] could be at basis of the observed mono-fractality, together with dispersive phenomena due to velocity–space effects, electron dynamics, scattering and damping processes [11,57]. Nevertheless, deeper investigations on the source of mono-fractality as well as its observation on different sub-/super-alfvénic intervals need further research.
Author Contributions
Conceptualization, T.A. and V.C.; methodology, T.A. and S.B.; formal analysis, T.A. and M.S.; investigation, T.A. and G.C.; data curation, V.Q.; writing—original draft preparation, T.A. and S.B.; writing—review and editing, V.C., G.C., V.Q. and M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data used in this study are available at the NASA Space Physics Data Facility (SPDF), https://spdf.gsfc.nasa.gov/index.html (accessed on 10 May 2022).
Acknowledgments
We are deeply indebted to everyone that helped make the Parker Solar Probe (PSP) mission possible. S.B., V.C. and G.C. acknowledge the financial support by Italian MIUR-PRIN grant 2017APKP7T on Circumterrestrial Environment: Impact of Sun-Earth Interaction. M.S. acknowledges the National Institute for Astrophysics, the University of Rome “Tor Vergata” and the University of Rome “La Sapienza” for the joint Ph.D. program “Astronomy, Astrophysics and Space Science”.The authors deeply acknowledge fruitful comments and suggestions by two anonymous reviewers.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AU | Astronomical Unit |
| ESS | Extended Self-Similarity |
| FGM | Flux-Gate Magnetometer |
| MHD | Magnetohydrodynamic |
| PSD | Power Spectral Density |
| PSP | Parker Solar Probe |
| RTN | Radial–Tangential–Normal |
| SCM | Search Coil Magnetometer |
| SL | She–Leveque |
| UT | Universal Time |
Note
| 1 | The RTN is a spacecraft-centered reference system in which the radial (R) direction is identified as the spacecraft-Sun line, the tangential (T) direction is identified as the tangent to the orbit of the spacecraft, and the N direction is obtained as the curl product of R and T, completing a right-handed triad. |
References
- Mandelbrot, B.B. The Fractal Geometry of Nature; WH Freeman: New York, NY, USA, 1982. [Google Scholar]
- Mandelbrot, B.B.; Wheeler, J.A. The Fractal Geometry of Nature. Am. J. Phys. 1983, 51, 286–287. [Google Scholar] [CrossRef]
- Bruno, R.; Carbone, V. Turbulence in the Solar Wind; Springer: Berlin/Heidelberg, Germany, 2016; Volume 928. [Google Scholar] [CrossRef]
- Lovejoy, S.; Schertzer, D. The Weather and Climate: Emergent Laws and Multifractal Cascades; Cambridge Press Univeristy: Cambridge, UK, 2013; p. 512. [Google Scholar]
- Dubrulle, B. Beyond Kolmogorov cascades. J. Fluid Mech. 2019, 867, P1. [Google Scholar] [CrossRef] [Green Version]
- Benzi, R.; Paladin, G.; Vulpiani, A.; Parisi, G. On the multifractal nature of fully developed turbulence and chaotic systems. J. Phys. Math. Gen. 1984, 17, 3521–3531. [Google Scholar] [CrossRef]
- Mandelbrot, B. How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Frisch, U. Turbulence. The Legacy of A.N. Kolmogorov; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Hofman, M.A. The Fractal Geometry of the Human Brain: An Evolutionary Perspective. In The Fractal Geometry of the Brain; Di Ieva, A., Ed.; Springer: New York, NY, USA, 2016; pp. 169–186. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Fractals and Scaling in Finance: Discontinuity, Concentration, Risk, 1st ed.; Springer Publishing Company, Incorporated: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Narita, Y. Space-time structure and wavevector anisotropy in space plasma turbulence. Living Rev. Sol. Phys. 2018, 15, 2. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kiyani, K.H.; Osman, K.T.; Chapman, S.C. Dissipation and heating in solar wind turbulence: From the macro to the micro and back again. Philos. Trans. R. Soc. Lond. Ser. A 2015, 373, 20140155. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carbone, V.; Bruno, R.; Veltri, P. Scaling Laws in the Solar Wind Turbulence. In Small-Scale Structures in Three-Dimensional Hydrodynamic and Magnetohydrodynamic Turbulence; Meneguzzi, M., Pouquet, A., Sulem, P.L., Eds.; Springer: Berlin/Heidelberg, Germany, 1995; Volume 462, p. 153. [Google Scholar] [CrossRef] [Green Version]
- Chapman, S.C.; Nicol, R.M.; Leonardis, E.; Kiyani, K.; Carbone, V. Observation of Universality in the Generalized Similarity of Evolving Solar Wind Turbulence as Seen by Ulysses. Astrophys. J. Lett. 2009, 695, L185–L188. [Google Scholar] [CrossRef]
- Consolini, G.; Alberti, T.; Yordanova, E.; Marcucci, M.F.; Echim, M. A Hilbert-Huang transform approach to space plasma turbulence at kinetic scales. Proc. J. Phys. Conf. Ser. 2017, 900, 012003. [Google Scholar] [CrossRef] [Green Version]
- Alberti, T.; Consolini, G.; Carbone, V.; Yordanova, E.; Marcucci, M.; De Michelis, P. Multifractal and Chaotic Properties of Solar Wind at MHD and Kinetic Domains: An Empirical Mode Decomposition Approach. Entropy 2019, 21, 320. [Google Scholar] [CrossRef] [Green Version]
- Chhiber, R.; Matthaeus, W.H.; Bowen, T.A.; Bale, S.D. Subproton-scale Intermittency in Near-Sun Solar Wind Turbulence Observed by the Parker Solar Probe. Astrophys. J. Lett. 2021, 911, L7. [Google Scholar] [CrossRef]
- Vasko, I.Y.; Alimov, K.; Phan, T.; Bale, S.D.; Mozer, F.S.; Artemyev, A.V. Kinetic-scale Current Sheets in the Solar Wind at 1 au: Scale-dependent Properties and Critical Current Density. Astrophys. J. Lett. 2022, 926, L19. [Google Scholar] [CrossRef]
- Lotekar, A.B.; Vasko, I.Y.; Phan, T.; Bale, S.D.; Bowen, T.A.; Halekas, J.; Artemyev, A.V.; Khotyaintsev, Y.V.; Mozer, F.S. Kinetic-scale Current Sheets in Near-Sun Solar Wind: Properties, Scale-dependent Features and Reconnection Onset. Astrophys. J. 2022, 929, 58. [Google Scholar] [CrossRef]
- Macek, W.M.; Wawrzaszek, A.; Carbone, V. Observation of the multifractal spectrum at the termination shock by Voyager 1. Geophys. Res. Lett. 2011, 38, L19103. [Google Scholar] [CrossRef] [Green Version]
- Macek, W.M.; Wawrzaszek, A.; Carbone, V. Observation of the multifractal spectrum in the heliosphere and the heliosheath by Voyager 1 and 2. J. Geophys. Res. (Space Phys.) 2012, 117, A12101. [Google Scholar] [CrossRef] [Green Version]
- Wawrzaszek, A.; Echim, M. On the variation of intermittency of fast and slow solar wind with radial Distance, heliospheric Latitude, and Solar Cycle. Front. Astron. Space Sci. 2021, 7, 99. [Google Scholar] [CrossRef]
- Fox, N.J.; McComas, D.J. Editorial: Topical Volume on Developing the Solar Probe Plus Mission. Space Sci. Rev. 2016, 204, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Kasper, J.C.; Klein, K.G.; Lichko, E.; Huang, J.; Chen, C.H.K.; Badman, S.T.; Bonnell, J.; Whittlesey, P.L.; Livi, R.; Larson, D.; et al. Parker Solar Probe Enters the Magnetically Dominated Solar Corona. Phys. Rev. Lett. 2021, 127, 255101. [Google Scholar] [CrossRef]
- Chhiber, R.; Usmanov, A.V.; Matthaeus, W.H.; Goldstein, M.L. Contextual Predictions for the Parker Solar Probe. I. Critical Surfaces and Regions. Astrophys. J. Suppl. Ser. 2019, 241, 11. [Google Scholar] [CrossRef] [Green Version]
- Bandyopadhyay, R.; Matthaeus, W.H.; McComas, D.J.; Chhiber, R.; Usmanov, A.V.; Huang, J.; Livi, R.; Larson, D.E.; Kasper, J.C.; Case, A.W.; et al. Sub-Alfvénic Solar Wind Observed by the Parker Solar Probe: Characterization of Turbulence, Anisotropy, Intermittency, and Switchback. Astrophys. J. Lett. 2022, 926, L1. [Google Scholar] [CrossRef]
- Zank, G.P.; Zhao, L.L.; Adhikari, L.; Telloni, D.; Kasper, J.C.; Stevens, M.; Rahmati, A.; Bale, S.D. Turbulence in the Sub-Alfvénic Solar Wind. Astrophys. J. Lett. 2022, 926, L16. [Google Scholar] [CrossRef]
- Benella, S.; Stumpo, M.; Consolini, G.; Alberti, T.; Carbone, V.; Laurenza, M. Markovian Features of the Solar Wind at Subproton Scales. Astrophys. J. Lett. 2022, 928, L21. [Google Scholar] [CrossRef]
- Kiyani, K.H.; Chapman, S.C.; Khotyaintsev, Y.V.; Dunlop, M.W.; Sahraoui, F. Global Scale-Invariant Dissipation in Collisionless Plasma Turbulence. Phys. Rev. Lett. 2009, 103, 075006. [Google Scholar] [CrossRef] [PubMed]
- Bale, S.D.; Goetz, K.; Harvey, P.R.; Turin, P.; Bonnell, J.W.; Dudok de Wit, T.; Ergun, R.E.; MacDowall, R.J.; Pulupa, M.; Andre, M.; et al. The FIELDS Instrument Suite for Solar Probe Plus. Measuring the Coronal Plasma and Magnetic Field, Plasma Waves and Turbulence, and Radio Signatures of Solar Transients. Space Sci. Rev. 2016, 204, 49–82. [Google Scholar] [CrossRef]
- Bowen, T.A.; Bale, S.D.; Bonnell, J.W.; Dudok de Wit, T.; Goetz, K.; Goodrich, K.; Gruesbeck, J.; Harvey, P.R.; Jannet, G.; Koval, A.; et al. A Merged Search-Coil and Fluxgate Magnetometer Data Product for Parker Solar Probe FIELDS. J. Geophys. Res. (Space Phys.) 2020, 125, e27813. [Google Scholar] [CrossRef]
- Lovejoy, S.; Schertzer, D. Haar wavelets, fluctuations and structure functions: Convenient choices for geophysics. Nonlinear Process. Geophys. 2012, 19, 513–527. [Google Scholar] [CrossRef] [Green Version]
- Elsasser, W.M. The Hydromagnetic Equations. Phys. Rev. 1950, 79, 183. [Google Scholar] [CrossRef]
- Biskamp, D. Magnetohydrodynamic Turbulence; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Carbone, V. Cascade model for intermittency in fully developed magnetohydrodynamic turbulence. Phys. Rev. Lett. 1993, 71, 1546–1548. [Google Scholar] [CrossRef]
- Kolmogorov, A. The Local Structure of Turbulence in Incompressible Viscous Fluid for Very Large Reynolds’ Numbers. Akad. Nauk SSSR Dokl. 1941, 30, 301–305. [Google Scholar]
- Iroshnikov, P.S. Turbulence of a Conducting Fluid in a Strong Magnetic Field. Sov. Ast. 1964, 7, 566. [Google Scholar]
- Kraichnan, R.H. Inertial-Range Spectrum of Hydromagnetic Turbulence. Phys. Fluids 1965, 8, 1385–1387. [Google Scholar] [CrossRef] [Green Version]
- Frisch, U. From global scaling, a la Kolmogorov, to local multifractal scaling in fully developed turbulence. Proc. R. Soc. Lond. Ser. A 1991, 434, 89–99. [Google Scholar] [CrossRef]
- Dudok de Wit, T. Can high-order moments be meaningfully estimated from experimental turbulence measurements? Phys. Rev. E 2004, 70, 055302. [Google Scholar] [CrossRef] [PubMed]
- Alexandrova, O.; Saur, J.; Lacombe, C.; Mangeney, A.; Mitchell, J.; Schwartz, S.J.; Robert, P. Universality of Solar-Wind Turbulent Spectrum from MHD to Electron Scales. Phys. Rev. Lett. 2009, 103, 165003. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Benzi, R.; Ciliberto, S.; Tripiccione, R.; Baudet, C.; Massaioli, F.; Succi, S. Extended self-similarity in turbulent flows. Phys. Rev. E 1993, 48, R29–R32. [Google Scholar] [CrossRef]
- Carbone, V.; Bruno, R.; Veltri, P. Evidences for extended self-similarity in hydromagnetic turbulence. Geophys. Res. Lett. 1996, 23, 121–124. [Google Scholar] [CrossRef]
- Benzi, R.; Marrocu, M.; Mazzino, A.; Trovatore, E. Characterization of the Long-Time and Short-Time Predictability of Low-Order Models of the Atmosphere. J. Atmos. Sci. 1999, 56, 3495–3507. [Google Scholar] [CrossRef]
- Benzi, R.; Biferale, L.; Ciliberto, S.; Struglia, M.V.; Tripiccione, R. Generalized scaling in fully developed turbulence. Phys. D Nonlinear Phenom. 1996, 96, 162–181. [Google Scholar] [CrossRef] [Green Version]
- Benzi, R.; Ciliberto, S.; Baudet, C.; Chavarria, G.R. On the scaling of three-dimensional homogeneous and isotropic turbulence. Phys. D Nonlinear Phenom. 1995, 80, 385–398. [Google Scholar] [CrossRef]
- Einaudi, G.; Velli, M.; Politano, H.; Pouquet, A. Energy Release in a Turbulent Corona. Astrophys. J. Lett. 1996, 457, L113. [Google Scholar] [CrossRef]
- Leamon, R.J.; Smith, C.W.; Ness, N.F.; Matthaeus, W.H.; Wong, H.K. Observational constraints on the dynamics of the interplanetary magnetic field dissipation range. J. Geophys. Res. 1998, 103, 4775–4788. [Google Scholar] [CrossRef]
- Gary, S.P.; Borovsky, J.E. Alfvén-cyclotron fluctuations: Linear Vlasov theory. J. Geophys. Res. (Space Phys.) 2004, 109, A06105. [Google Scholar] [CrossRef]
- Narita, Y.; Roberts, O.W.; Vörös, Z.; Hoshino, M. Transport ratios of the kinetic Alfvén mode in space plasmas. Front. Phys. 2020, 8, 166. [Google Scholar] [CrossRef]
- Cranmer, S.R. Some Turbulent Predictions for Parker Solar Probe. Res. Notes AAS 2018, 2, 158. [Google Scholar] [CrossRef]
- Meneveau, C.; Sreenivasan, K.R. Simple multifractal cascade model for fully developed turbulence. Phys. Rev. Lett. 1987, 59, 1424–1427. [Google Scholar] [CrossRef]
- She, Z.S.; Leveque, E. Universal scaling laws in fully developed turbulence. Phys. Rev. Lett. 1994, 72, 336–339. [Google Scholar] [CrossRef]
- Grauer, R.; Krug, J.; Marliani, C. Scaling of high-order structure functions in magnetohydrodynamic turbulence. Phys. Lett. A 1994, 195, 335–338. [Google Scholar] [CrossRef]
- Politano, H.; Pouquet, A. Model of intermittency in magnetohydrodynamic turbulence. Phys. Rev. E 1995, 52, 636–641. [Google Scholar] [CrossRef]
- Retinò, A.; Sundkvist, D.; Vaivads, A.; Mozer, F.; André, M.; Owen, C.J. In situ evidence of magnetic reconnection in turbulent plasma. Nat. Phys. 2007, 3, 236–238. [Google Scholar] [CrossRef] [Green Version]
- Alexandrova, O.; Lacombe, C.; Mangeney, A.; Grappin, R.; Maksimovic, M. Solar Wind Turbulent Spectrum at Plasma Kinetic Scales. Astrophys. J. 2012, 760, 121. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).