Abstract
We show that the r-modes of slowly rotating nonbarotropic neutron stars are described by nonanalytic functions of stellar angular velocity, which makes the perturbation techniques, used so far in the r-mode theoretical studies, inapplicable. In contrast to those studies and in accordance with numerical calculations beyond the slow rotation approximation, the obtained r-mode spectrum is discrete, which resolves the continuous spectrum problem, lasting since 1997. Our findings imply that the relativistic r-modes in slowly rotating neutron stars dramatically differ from their Newtonian cousins, which may have important implications for the detectability of r-mode signatures in observations, in particular for the r-mode excitation efficiency during the neutron star inspirals.
1. Introduction
The r-modes are the oscillations of rotating stars, restored by the Coriolis force. In the absence of dissipation, they are unstable with respect to the emission of gravitational radiation at any rotation rate [1,2] (CFS mechanism), which makes them one of the most promising sources of gravitational waves in future [3,4] and current [5,6,7,8,9] observations (see also [10,11,12,13,14,15,16,17,18] and [19,20] for a review of the r-mode physics).
A standard approach in theoretical studies of r-modes in slowly rotating stars (i.e., stars with angular velocity, , significantly lower than the Keplerian velocity, ) is to assume that the r-mode eigenfunctions and eigenfrequencies can be Taylor-expanded in small parameter and the r-mode equations can be obtained following the perturbation theory with respect to this parameter. While this traditional approach turns out to be very fruitful in the Newtonian theory (see [19,20] and the references therein), in relativistic theory, it leads to a set of contradictory results, known as “the problem of the continuous r-mode spectrum”. In General Relativity (GR), the frame-dragging effect at position r leads to the entrainment of local inertial reference frames with angular velocity , as measured by the distant observer. As a result, in barotropic stars (where the pressure is a function of one thermodynamic variable), r-modes cease to exist [21], while in nonbarotropic stars (the pressure depends on several variables), the traditional approach predicts the r-mode frequencies, , to fill the continuous band [21,22,23,24,25,26,27]:
where l and m are the r-mode quantum numbers and R is the stellar radius. The continuous spectrum is not affected by accounting for the gravitational radiation in the problem [28,29]; the discrete r-modes [21,30] with frequencies beyond the band (1) very likely do not exist in typical neutron stars [30], and the isolated r-modes [27] with hidden discrete frequencies within the band (1) have divergent velocity perturbations (see also a discussion of different spectrum regularization methods in [31,32,33]). Numerical calculations [34,35] beyond the slow rotation approximation, in turn, predict a discrete r-mode spectrum, as in the Newtonian theory, thus indicating the failure of the traditional approach in application to relativistic r-modes. In this letter, we develop a new original approach to the r-mode problem, which reveals the reason for that failure and uncovers quite unexpected properties of relativistic r-modes.
2. General Oscillation Equations
We considered a neutron star as a non-magnetized quasineutral mixture of normal (i.e., nonsuperfluid and nonsuperconducting) degenerate particle species (further labeled by Latin indices ). Thermodynamic functions in this case—pressure p, energy density , enthalpy density , and chemical potentials —depend only on the set of number densities of different particle species. For simplicity, we ignore perturbations of the gravitational field (Cowling approximation), which leads to a relative error in the r-mode oscillation frequency of only a few percent [36]. Then, gravity plays the role of the stationary background, described in the -coordinates (c is the speed of light) by Hartle’s metric tensor of a slowly rotating massive body [37]:
Under these assumptions, small stellar oscillations are governed by the linearized Euler equation, linearized continuity equations for different particle species, thermodynamic relations in degenerate matter, and the equation of state (EOS), assumed in this study to be nonbarotropic (summation over all repeated indices is implied):
Here, is the four-velocity of the macroscopic material flows inside the star ( in equilibrium), and covariant derivative is associated with the interval (2). Due to the axial symmetry of a rotating star, the periodic Eulerian perturbation of any quantity f can be sought in the form .
Below, we express through the Lagrangian displacement , showing the variation of the world lines of fluid elements in the star due to an oscillation (see, e.g., [38]):
The gauge freedom in the definition (4), where f is some arbitrary function, allows us to impose the additional algebraic condition .
3. Deriving r-Mode Equations
Based on the results of the Newtonian theory, one expects relativistic r-modes to be oscillations with frequency and quasi-toroidal displacement (by definition, ):
where we introduced the toroidal function T to be found below. Although for , only even powers of enter the equations (3) and it seems natural to assume that (for brevity, below, we omit the factor in ), such an approach leads to the continuous spectrum problem. Here, to facilitate the analysis of the equations, we assumed that the frame-dragging effect, which is the cause of the continuous spectrum, is weak, , where . We also ignored the oblateness of the star ( terms in Equation (2)), which leaves the mathematical structure of the problem unaffected. Then, we look for the solution of the oscillation Equation (3) in the form (5), assuming that the terms correspond to the limit and (i.e., we account for the frame-dragging effect for arbitrarily slow rotation rates), while the terms , whose dependence on and is not postulated, should be small due to small , a weak frame-dragging effect, or both.
To derive general r-mode equations, we followed three subsequent steps [33]. First, we excluded scalar perturbations , , and from the system (3). Second, we used decompositions (5) in the thus-reduced system and in the and limit found:
where is the associated Legendre polynomial. Third, we simplified the reduced system using (7) and discarded small terms, according to the following selection rule: if there is a term f in a chosen equation, then the terms and in this equation are ignored. An analysis of the thus-obtained equations reveals that the r-mode radial displacement has the form
and that the problem reduces to the solution of the closed system of equations for and , which for the case (most CFS unstable mode) can be written as
The explicit form [33] of the coefficients and is not important for further discussion. Near the stellar center, the solution should smoothly match its asymptote [33]. At the stellar surface, the total pressure should vanish, which in our case is equivalent to [33]
where the prime denotes . Those values of , for which these boundary conditions can be simultaneously met, form the relativistic r-mode spectrum. In the Newtonian limit, Equation (9) and boundary conditions correctly reduce to those of traditional Newtonian theory.
4. R-Modes in the Limit
It is easy to see that, if , as in the traditional ordering, then the first equation of the system (9) leads to a continuous spectrum in the limit. At the same time, by numerically solving the system, we obtain regular r-mode eigenfunctions and discrete eigenfrequencies with no signatures of the continuous spectrum (see below). To find the ordering, corresponding to this solution, we note that for extremely slow rotation rates, the leading contribution to is defined by the weak frame-dragging effect (rotational corrections become negligible). Since and enter the system (9) only in combination , this implies that in this limit, is a quantity of order . Then, we assume that, in the limit, the leading contributions to the r-mode frequency correction and eigenfunctions behave as
where . The latter condition in (11) means that the operator , when acting on the eigenfunctions, should be considered as a “quantity” of order . The inequalities or indicate that the functions under consideration are nonanalytic in or (see below for a further explanation).
Under these assumptions, some terms in the system (9) can be small compared to others. Since this system should allow finding the eigenfrequency correction, the terms with and should be of the same order as at least one of the other terms in the first equation, while the remaining terms are allowed to be comparatively small. In the second equation, at least two terms should be of the same order and not smaller than the remaining term; otherwise, the solution is trivial. The analysis shows that these conditions are met only for and ; therefore,
In the vicinity of the stellar center, , some of the discarded terms are not small, and, therefore the solution to Equation (13) does not satisfy (9) (the value of can be estimated from (9) and tends to zero for small ). Further, from (9) and the asymptote of the toroidal function, it follows that, near the center, . The leading contribution to the radial displacement cannot satisfy this condition and, therefore, should vanish when approaching . Similarly, it should also vanish at the stellar surface. As a result, the boundary conditions for the leading contribution to the radial displacement are . In order to satisfy the “correct” boundary conditions, discussed after (9), one should account for the higher-order rotational corrections to the radial displacement.
For a simple toy model with , we obtain for and for . These nonanalytic functions of produce, under the action of the operator , the factor, which reveals the idea behind the notation in (12). In reality, however, the function is not constant and can have turning points, where it changes sign. Since the explicit form of the coefficients and implies that [33] and is a positive monotonically decreasing function [37], we can have only one turning point , related (if exists) to the eigenfrequency as
Based on the toy model, we expect the toroidal function will behave exponentially at and oscillate at . The r-mode eigenfunctions can then be classified by the number of nodes (zeros) n of the toroidal function. For any n, the distance between the nodes tends to zero as ; therefore, the turning point and eigenfrequencies .
To find the approximate solution of (13) in the limit, we used the WKB method. Far from the turning point, where noticeably differs from zero (region I with and region III with ), we looked for the solution in the form , where is some analytic function of . In the vicinity of the turning point (region II), we used the Taylor expansion , introduced a new variable , and reduced the second-order Equation (13) to the Airy equation. In the regions, where noticeably differs from zero, but its Taylor expansion is still accurate, the solutions in regions I and III should, with high accuracy, coincide with that found in the region II. This condition and the equality allow us to find the r-mode eigenfunctions:
The remaining boundary condition at the surface then leads to the quantization rule:
which, being combined with (15), defines the discrete r-mode spectrum in the limit. For those , for which the turning point is so close to the stellar surface that the Taylor expansion of can be applied up to , one can obtain the following explicit expressions for the turning point and for the r-mode spectrum:
5. Gravitational Radiation Timescale
The instability with respect to the emission of gravitational waves causes the r-mode energy E to slowly increase with average rate , leading to the mode growth on a typical timescale . A reasonable and commonly used way to estimate the efficiency of this process is to adopt the general post-Newtonian expressions for E and [10,39]. In our case, is mainly defined by the current multipole moment and equals
where is some (weakly depending on ) combination of the fundamental constants G and c, stellar mass M and radius R, the mode order l, and the total frequency . Since nonanalytically enters the toroidal function, the dependence becomes highly non-trivial and significantly differs from the traditional . In particular, for those rotation rates, for which the Taylor expansion is valid up to , one can replace the toroidal function T with (see Equation (16)) and expand in Taylor series other, slowly changing subintegral functions near the stellar surface. Then, one can show that, in this limit, .
6. Numerical Results
To verify the predictions of the theory in the limit, we calculated the r-mode spectrum and eigenfunctions from (9) for different . We employed the BSK24 equation of state [40] and considered a neutron star model with mass ( is the solar mass).
According to our calculations, for , relativistic toroidal eigenfunctions weakly depend on and resemble their -independent Newtonian counterparts, while for , as decreases, they start to be localized near the stellar surface. Figure 1, in which we plot the relativistic (GR, blue line) and Newtonian (Newt, red dashes) toroidal functions with four nodes, shows the example of such behavior at . In accordance with (16), the eigenfunction is exponentially suppressed at and oscillates at .
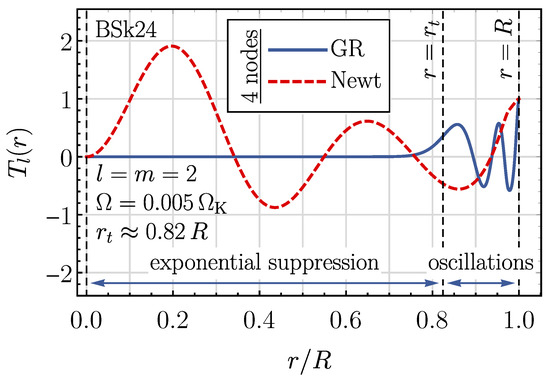
Figure 1.
Relativistic (GR, blue line) and Newtonian (Newt, red dashes) toroidal r-mode eigenfunctions with 4 nodes at .
In our calculations, performed for , we found no signatures of the continuous part in the r-mode oscillation spectrum. The spectrum is discrete and, as one can see from Figure 2, coincides for extremely slow rotation rates with that predicted by the theory in the limit. Here, the eigenfrequencies, obtained numerically via solving Equation (9), are shown by filled circles, while curves show the spectrum, obtained from the quantization rule (17). Different colors correspond to different numbers of nodes n of the toroidal function.
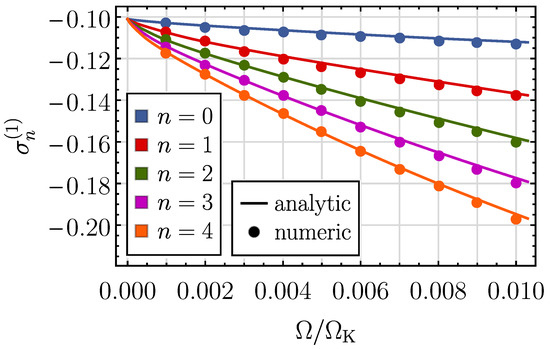
Figure 2.
The numerically obtained (numeric) and predicted by the quantization rule (analytic) r-mode spectrum. The number of nodes n of the toroidal function ranges from 0 to 4.
7. Conclusions
Summarizing, we applied a new original approach to study relativistic r-modes of slowly rotating nonbarotropic neutron stars. Unlike the traditional one, it does not require any Taylor expansions in of the r-mode eigenfunctions and oscillation spectrum, and the only essential assumptions made are the stellar rotation being slow and the frame-dragging effect being weak. Within this approach, we explicitly showed that the relativistic generalization of the Newtonian r-modes in nonbarotropic stars is described by nonanalytic functions of the stellar angular velocity. Because of this nonanalyticity, these functions are undetermined at (see Equation (16)), and relativistic r-modes cannot be considered as small rotational corrections to the zero-frequency modes of the non-rotating star. They cannot be Taylor-expanded in small parameter and, therefore, cannot be studied within the traditional approach used so far.
Nonanalyticity affects the r-mode ordering: instead of the “classical” and , we have , , and moreover, the operator , when acting on the relativistic eigenfunctions. These results may affect the interpretation of the observed periodic oscillations in electromagnetic radiation of rotating NSs [41,42]. Further, analysis of the general oscillation equations (Equation (3)) shows [33] that, while the pressure perturbation retains its usual order, other scalar perturbations instead of being of order , as in the Newtonian case. Such nonanalyticity and peculiar ordering should significantly influence the typical mode dissipation timescales due to shear viscosity , bulk viscosity , and diffusion [43,44]. We expect the effect to be especially pronounced for and , defined by non-toroidal components of the motion. Moreover, we expect that such ordering of scalar functions should modify the mode coupling to the tidal potential and affect the r-mode excitation during NS inspiral, which may imprint in the gravitational wave signal (e.g., [45]). Finally, according to our post-Newtonian estimate, because of the nonanalyticity, the mode growth timescale due to the CFS mechanism has non-standard dependence , reducing for extremely slow rotation rates to instead of the traditional .
The performed numerical calculations show that the nonanalytic r-mode spectrum is discrete and, for extremely slow rotation rates, is accurately described by the quantization rule (17) (which, notably, has no counterparts in the Newtonian theory). Relativistic r-mode eigenfunctions in this limit drastically differ from the Newtonian ones: they are exponentially suppressed everywhere in the star except for the narrow region in the vicinity of the stellar surface, where they oscillate. Such behavior makes the employed Cowling approximation even more justified: the r-mode dynamics can be significantly influenced only by the gravitational field perturbations of the internal stellar layers, where the modes are suppressed. Such behavior also justifies the assumption of the weak frame-dragging effect: near the surface, where the r-modes are localized, we have , and it is, indeed, weak. We note that, according to our preliminary results, the r-mode nonanalyticity takes place beyond the weak framedrag approximation. However, the r-mode equations are more complicated in this case and deserve separate consideration. Finally, accounting for the oblateness of the rotating star produces additional terms depending on in the general system (9). Generally, these terms should be accounted for, but at , they become small and do not affect the results, obtained in this limit.
Although we have managed to obtain discrete relativistic r-modes, our study, strictly speaking, did not completely exclude the existence of the r-modes with the continuous oscillation spectrum discussed in the literature [21,22,23,24,25,26,27,28,29]. We believe, however, that, since the continuous spectrum does not manifest itself in our numerical calculations, as well as in the numerical calculations of [34,35], such r-modes possibly do not exist as a result of some internal inconsistency of the theory, based on the traditional approach.
The mathematical structure of the equations, describing relativistic r-modes, resembles that of the Newtonian r-mode equations in differentially rotating stars. The ideas, developed in this letter, can be applied to study these equations and may lead to the discovery of a new class of nonanalytic solutions, similar to the nonanalytic relativistic r-modes. In particular, this may affect the modeling of the recently observed solar Rossby waves [46]. Keeping in mind that solar rotation is strongly differential, while is extremely small, one could expect the peculiar behavior of solar Rossby waves analogous to those discussed in this letter.
Author Contributions
K.Y.K. contributed to the formulation of the problem, performed the analytic and numerical calculations, and took part in the discussion of the obtained results and in writing the paper. M.E.G. formulated the problem, performed the analytic calculations, and contributed to the discussion of the obtained results and writing the paper. E.M.K. contributed to the formulation of the problem, the discussion of the obtained results, and writing the paper. Conceptualization, K.Y.K., M.E.G. and E.M.K.; formal analysis, K.Y.K., M.E.G. and E.M.K.; investigation, K.Y.K., M.E.G. and E.M.K.; methodology, K.Y.K. and M.E.G.; validation, E.M.K.; visualization, K.Y.K.; writing—original draft, K.Y.K.; writing—review and editing, M.E.G. and E.M.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Russian Science Foundation (Grant No. 22-12-00048).
Data Availability Statement
The data presented in this study are available in the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Andersson, N. A New Class of Unstable Modes of Rotating Relativistic Stars. Astrophys. J. 1998, 502, 708–713. [Google Scholar] [CrossRef]
- Friedman, J.L.; Morsink, S.M. Axial Instability of Rotating Relativistic Stars. Astrophys. J. 1998, 502, 714–720. [Google Scholar] [CrossRef]
- Maggiore, M.; Van Den Broeck, C.; Bartolo, N.; Belgacem, E.; Bertacca, D.; Bizouard, M.A.; Branchesi, M.; Clesse, S.; Foffa, S.; García-Bellido, J.; et al. Science case for the Einstein telescope. JCAP 2020, 2020, 050. [Google Scholar] [CrossRef]
- Sieniawska, M.; Bejger, M. Continuous Gravitational Waves from Neutron Stars: Current Status and Prospects. Universe 2019, 5, 217. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; the Virgo Collaboration. Searches for Continuous Gravitational Waves from 15 Supernova Remnants and Fomalhaut b with Advanced LIGO. Astrophys. J. 2019, 875, 122. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; the Virgo Collaboration. All-sky search in early O3 LIGO data for continuous gravitational-wave signals from unknown neutron stars in binary systems. Phys. Rev. D 2021, 103, 064017. [Google Scholar] [CrossRef]
- The LIGO Scientific Collaboration; the Virgo Collaboration; the KAGRA Collaboration. Searches for continuous gravitational waves from young supernova remnants in the early third observing run of Advanced LIGO and Virgo. arXiv 2021, arXiv:2105.11641. [Google Scholar]
- The LIGO Scientific Collaboration; the Virgo Collaboration; the KAGRA Collaboration. Search for continuous gravitational waves from 20 accreting millisecond X-ray pulsars in O3 LIGO data. arXiv 2021, arXiv:2109.09255. [Google Scholar]
- The LIGO Scientific Collaboration; the Virgo Collaboration; the KAGRA Collaboration. All-sky search for continuous gravitational waves from isolated neutron stars in the early O3 LIGO data. Phys. Rev. D 2021, 104, 082004. [Google Scholar] [CrossRef]
- Lindblom, L.; Owen, B.J.; Morsink, S.M. Gravitational Radiation Instability in Hot Young Neutron Stars. Phys. Rev. Lett. 1998, 80, 4843–4846. [Google Scholar] [CrossRef]
- Lindblom, L.; Tohline, J.E.; Vallisneri, M. Nonlinear Evolution of the r-Modes in Neutron Stars. Phys. Rev. Lett. 2001, 86, 1152–1155. [Google Scholar] [CrossRef]
- Reisenegger, A.; Bonačić, A. Millisecond Pulsars with r-Modes as Steady Gravitational Radiators. Phys. Rev. Lett. 2003, 91, 201103. [Google Scholar] [CrossRef]
- Mannarelli, M.; Manuel, C.; Sa’D, B.A. Mutual Friction in a Cold Color-Flavor-Locked Superfluid and r-Mode Instabilities in Compact Stars. Phys. Rev. Lett. 2008, 101, 241101. [Google Scholar] [CrossRef]
- Ho, W.C.G.; Andersson, N.; Haskell, B. Revealing the Physics of r Modes in Low-Mass X-ray Binaries. Phys. Rev. Lett. 2011, 107, 101101. [Google Scholar] [CrossRef]
- Alford, M.G.; Schwenzer, K. What the Timing of Millisecond Pulsars Can Teach us about Their Interior. Phys. Rev. Lett. 2014, 113, 251102. [Google Scholar] [CrossRef] [PubMed]
- Gusakov, M.E.; Chugunov, A.I.; Kantor, E.M. Instability Windows and Evolution of Rapidly Rotating Neutron Stars. Phys. Rev. Lett. 2014, 112, 151101. [Google Scholar] [CrossRef] [PubMed]
- Haskell, B.; Patruno, A. Are Gravitational Waves Spinning Down PSR J 1023 +0038 ? Phys. Rev. Lett. 2017, 119, 161103. [Google Scholar] [CrossRef] [PubMed]
- Kantor, E.M.; Gusakov, M.E.; Dommes, V.A. Constraining Neutron Superfluidity with R-Mode Physics. Phys. Rev. Lett. 2020, 125, 151101. [Google Scholar] [CrossRef]
- Andersson, N.; Kokkotas, K.D. The R-Mode Instability in Rotating Neutron Stars. Int. J. Mod. Phys. D 2001, 10, 381–441. [Google Scholar] [CrossRef]
- Haskell, B. R-modes in neutron stars: Theory and observations. Int. J. Mod. Phys. E 2015, 24, 1541007. [Google Scholar] [CrossRef]
- Lockitch, K.H.; Andersson, N.; Friedman, J.L. Rotational modes of relativistic stars: Analytic results. Phys. Rev. D 2001, 63, 024019. [Google Scholar] [CrossRef]
- Kojima, Y. Chapter 4. The Rotational Effects of General Relativity on the Stellar Pulsations. Prog. Theor. Phys. Suppl. 1997, 128, 251–293. [Google Scholar] [CrossRef]
- Kojima, Y. Quasi-toroidal oscillations in rotating relativistic stars. Mon. Not. R. Astron. Soc. 1998, 293, 49–52. [Google Scholar] [CrossRef]
- Beyer, H.R.; Kokkotas, K.D. On the r-mode spectrum of relativistic stars. Mon. Not. R. Astron. Soc. 1999, 308, 745–750. [Google Scholar] [CrossRef]
- Kojima, Y.; Hosonuma, M. The r-Mode Oscillations in Relativistic Rotating Stars. Astrophys. J. 1999, 520, 788–796. [Google Scholar] [CrossRef]
- Kojima, Y.; Hosonuma, M. Approximate equation relevant to axial oscillations on slowly rotating relativistic stars. Phys. Rev. D 2000, 62, 044006. [Google Scholar] [CrossRef]
- Ruoff, J.; Kokkotas, K.D. On the r-mode spectrum of relativistic stars in the low-frequency approximation. Mon. Not. R. Astron. Soc. 2001, 328, 678–688. [Google Scholar] [CrossRef][Green Version]
- Yoshida, S.; Futamase, T. R-mode instability of slowly rotating nonisentropic relativistic stars. Phys. Rev. D 2001, 64, 123001. [Google Scholar] [CrossRef]
- Ruoff, J.; Kokkotas, K.D. On the r-mode spectrum of relativistic stars: The inclusion of the radiation reaction. Mon. Not. R. Astron. Soc. 2002, 330, 1027–1033. [Google Scholar] [CrossRef][Green Version]
- Yoshida, S. r-Modes of Slowly Rotating Nonisentropic Relativistic Stars. Astrophys. J. 2001, 558, 263–269. [Google Scholar] [CrossRef][Green Version]
- Lockitch, K.H.; Andersson, N.; Watts, A.L. Regularizing the r-mode problem for nonbarotropic relativistic stars. Class. Quantum Gravity 2004, 21, 4661–4675. [Google Scholar] [CrossRef]
- Pons, J.A.; Gualtieri, L.; Miralles, J.A.; Ferrari, V. Relativistic r modes and shear viscosity: Regularizing the continuous spectrum. Mon. Not. R. Astron. Soc. 2005, 363, 121–130. [Google Scholar] [CrossRef]
- Kraav, K.Y.; Gusakov, M.E.; Kantor, E.M. Nonanalytic behavior of the relativistic r-modes in slowly rotating neutron stars. arXiv 2021, arXiv:2112.01171. [Google Scholar]
- Yoshida, S.; Lee, U. Relativistic r-Modes in Slowly Rotating Neutron Stars: Numerical Analysis in the Cowling Approximation. Astrophys. J. 2002, 567, 1112–1120. [Google Scholar] [CrossRef]
- Villain, L.; Bonazzola, S.; Haensel, P. Inertial modes in stratified rotating neutron stars: An evolutionary description. Phys. Rev. D 2005, 71, 083001. [Google Scholar] [CrossRef]
- Jasiulek, M.; Chirenti, C. R-mode frequencies of rapidly and differentially rotating relativistic neutron stars. Phys. Rev. D 2017, 95, 064060. [Google Scholar] [CrossRef]
- Hartle, J.B. Slowly Rotating Relativistic Stars. I. Equations of Structure. Astrophys. J. 1967, 150, 1005. [Google Scholar] [CrossRef]
- Friedman, J.L. Generic instability of rotating relativistic stars. Commun. Math. Phys. 1978, 62, 247–278. [Google Scholar] [CrossRef]
- Thorne, K.S. Multipole expansions of gravitational radiation. Rev. Mod. Phys. 1980, 52, 299–340. [Google Scholar] [CrossRef]
- Goriely, S.; Chamel, N.; Pearson, J.M. Further explorations of Skyrme-Hartree-Fock-Bogoliubov mass formulas. XIII. The 2012 atomic mass evaluation and the symmetry coefficient. Phys. Rev. C 2013, 88, 024308. [Google Scholar] [CrossRef]
- Strohmayer, T.; Mahmoodifar, S. Discovery of a Neutron Star Oscillation Mode During a Superburst. Astrophys. J. Lett. 2014, 793, L38. [Google Scholar] [CrossRef]
- Strohmayer, T.; Mahmoodifar, S. A Non-radial Oscillation Mode in an Accreting Millisecond Pulsar? Astrophys. J. 2014, 784, 72. [Google Scholar] [CrossRef]
- Kraav, K.Y.; Gusakov, M.E.; Kantor, E.M. Diffusion as a leading dissipative mechanism in superconducting neutron stars. Mon. Not. R. Astron. Soc. 2021, 506, L74–L78. [Google Scholar] [CrossRef]
- Dommes, V.A.; Gusakov, M.E.; Shternin, P.S. Dissipative relativistic magnetohydrodynamics of a multicomponent mixture and its application to neutron stars. Phys. Rev. D 2020, 101, 103020. [Google Scholar] [CrossRef]
- Xu, W.; Lai, D. Resonant tidal excitation of oscillation modes in merging binary neutron stars: Inertial-gravity modes. Phys. Rev. D 2017, 96, 083005. [Google Scholar] [CrossRef]
- Löptien, B.; Gizon, L.; Birch, A.C.; Schou, J.; Proxauf, B.; Duvall, T.L.; Bogart, R.S.; Christensen, U.R. Global-scale equatorial Rossby waves as an essential component of solar internal dynamics. Nat. Astron. 2018, 2, 568–573. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).