Intensity and Polarization of Radiation Emerging from Rotating Accretion Disc with Increasing Height

Abstract

We consider the radiation emission in continuum and spectral lines from rotating accretion disc with the progressive increasing height. It is known that for the plane accretion disc with homogeneous atmosphere the wave electric field $\mathbf{E}$ is perpendicular to the plane between line of sight $\mathbf{n}$ and the normal to the disc $\mathbf{N}$. For the expanding accretion disc the wave electric field from every inclined cone-like part with given azimuthal angle $\phi$ has direction perpendicular to the plane between $\mathbf{n}$ and local normal ${\mathbf{N}}^{\prime }$ to the inclined surface. This behaviour is the consequence of homogeneity of inclined atmosphere and has purely geometrical origin. The geometrical consideration shows that the position angles of polarized radiation in the right and left parts relative to plane (nN) of the inclined accretion disc have opposite values. Therefore, for inclined accretion disc the integral continuum radiation has the usual polarization angle perpendicular to the plane $\left(\mathbf{nN}\right)$, but smaller degree of polarization and less alongated along the normal $\mathbf{N}$ than that for the plane accretion disc. For spectral line, due to the Doppler effect, the polarization (position) angles have opposite signs for the red and blue wings. Such behaviour is frequently observed in H$\alpha$-radiation.

1. Introduction

The plane accretion discs are most considered in theoretical papers. These discs are simpler for study of various effects. Sometimes the authors mention that in general case the accretion discs can have the progressively expanding height (see e.g., Shakura & Sunyaev [1], Abramowicz & Fragile [2]).

Our aim is to show the change of the intensity $I\left(\mathbf{n}\right)$ and polarization Stokes parameters $Q\left(\mathbf{n}\right)$ and $U(\mathbf{n}$) for radiation emerging from cone-like inclined rotating accretion discs both in continuum and resonance lines.

We suppose that the inclined atmosphere is similar to usual atmosphere in the plane accretion disc, i.e., we study what arises if this atmosphere is cone-like inclined.

It will be demonstrated that the cone-like atmosphere considerably changes both the polarization degree and angular distribution of emerging radiation. So, it is important to know if the accretion disc is plane or not. It appears, the best technique for this is to consider the polarization angle $\chi$ in resonance line radiation.

The wave electric field oscillations $\mathbf{E}$ of the emerging radiation are parallel to the surface of a plane disc, namely $\mathbf{E}\Vert \left[\mathbf{n}\mathbf{N}\right]$. Here $\mathbf{n}$ if line of sight and $\mathbf{N}$ is the normal to the disc. Due to symmetry of atmosphere relative to plane (nN) the possible direction of $\mathbf{E}$ is to be $\mathbf{E}\Vert \left[\mathbf{n}\mathbf{N}\right]$. Such situation corresponds to homogeneous atmosphere and the absence of the regular magnetic field. This occurs, for example, in the Milne problem (see Chandrasekhar [3]).

Strictly speaking, the another possible polarization for homogeneous atmosphere corresponds to $\mathbf{E}$ lying in the plane $\left(\mathbf{nN}\right)$, but this case practically is not observed (see Dolginov et al. [4]). Polarization of emerged radiation appears as a result of the last scatterings before escaping the homogeneous atmosphere. Inside the atmosphere the radiation can be nonpolarized.

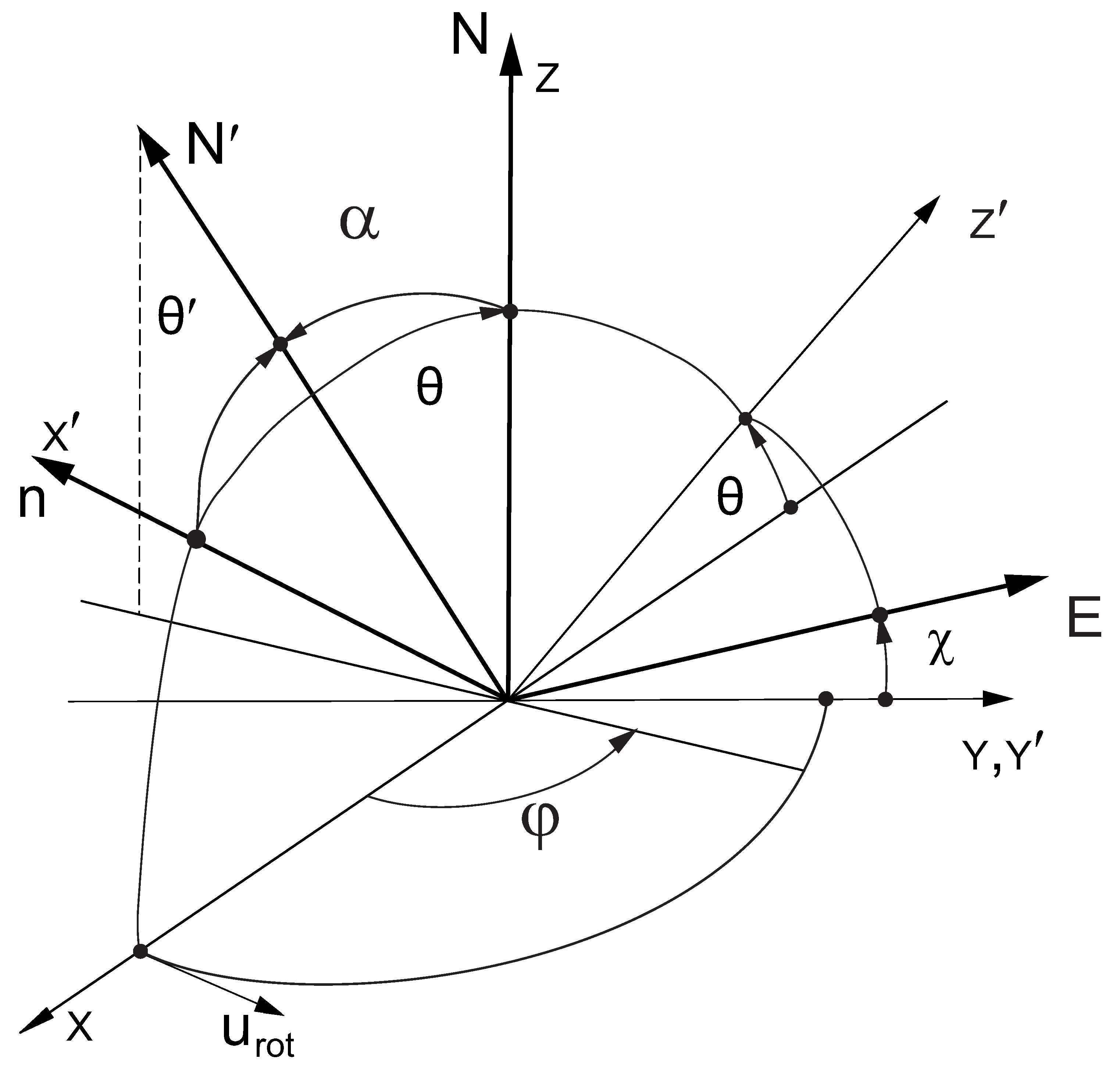
Now we consider the rotating accretion disc with the progressive increasing (cone-like) height. We assume that small local surface $\Delta S$ is characterized by azimuthal angle $\phi$ and the normal ${\mathbf{N}}^{\prime }$ to the cone-like radiating atmosphere having the inclination angle $\alpha$ (see Figure 1). The every $\Delta S$ surface of cone-like atmosphere possesses the right-left symmetry and, as a consequence, the wave electric field is $\mathbf{E}\Vert (\pm \left[\mathbf{n}{\mathbf{N}}^{\prime }\right])$ (remember that oscillatting $\mathbf{E}$ corresponds to ($\pm \mathbf{E}$)). This occurs both for optically thick and optically thin atmospheres with right-left symmetry relative to the plane $\left({\mathbf{nN}}^{\prime }\right)$.

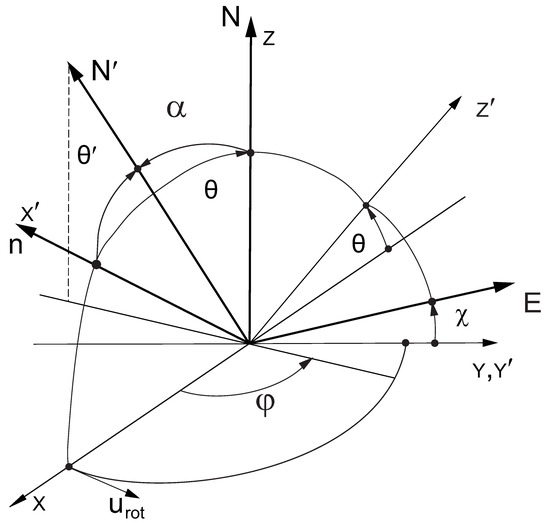
Figure 1. Basic notions.

In rotating accretion disc the Doppler effect gives rise to the following change of wavelength $\lambda$:

$$\lambda \to {\lambda }_{rest}+\frac{u_{rot}}{c}{\lambda }_0\sin \theta \sin \phi .$$

(1)

Here ${\lambda }_0$ is the central wavelength, ${\lambda }_{rest}$ is the wavelength in nonrotating atmosphere, $u_{rot}$ is the the rotation velocity in the orbital plane (for $u_{rot}=n·1000\mathrm{km}{\mathrm{s}}^{-1}$ the parameter $u_{rot}/c=n/300$, i.e., is small for n = 1, 2, 3, 4…). The angle $\theta$ is the inclination angle of the mean plane of accretion disc relative to the line of sight $\mathbf{n}$, $\phi$ is the azimuthal angle of the radiating surface $\Delta S$. Here we take the right-hand rotation with the azimuthal rotation velocity $u_{rot}$. In this case the right part of rotating disc corresponds to larger wavelength and the left part corresponds to the less wavelength. The centre of a line ${\lambda }_0$ corresponds to $\phi =0$.

Note that for continuum radiation is not important whether inclined disc is rotating or not.

The observations of polarized spectral line H$\alpha$-radiation and nearby continuum radiation are given in a number of papers (see, e.g., Smith et al. [5], Afanasiev et al. [6]). In these papers the Seyfert-1 AGNs are considered. The observations show that for the most sources the polarization (position) angle $\chi$ is not constant over the spectral line wavelength $\lambda$.

Below we show that in accretion disc with progressively increasing height the resonance line acquires polarization angle $\chi$ depending on the wavelength $\lambda$.

Our consideration is valid both for continuum radiation and the resonance line one. Note, that the cone inclination angle $\alpha$ can be estimated from observed angle $\chi$ of a line. Our main assumption is that electric field oscillations are perpendicular to the plane $\left({\mathbf{nN}}^{\prime }\right)$. This is quite analogy to the plane accretion disc, where $\mathbf{E}\perp \left(\mathbf{nN}\right)$. Remember that the line of sight (the direction to a telescope) is characterized by the unite vector $\mathbf{n}$.

Due to symmetry of the atmospheres relative to the plane $\left({\mathbf{nN}}^{\prime }\right)$, the determination of polarization angle $\chi$ is pure geometrical problem. Let us give the solution of this problem.

2. Geometric Derivation of Polarization Angle $\mathit{\chi }$

Let us denote ${\mathbf{N}}^{\prime }\left(\phi \right)$ as the normal to small local surface element $\Delta S$ on the inclined ring. This surface element is characterized by the azimuthal angle $\phi$. The angle between the normal ${\mathbf{N}}^{\prime }$ and the normal to the central plane of accretion disc $\mathbf{N}$ is the ring’s inclination angle $\alpha$: ${\mathbf{N}}^{\prime }·\mathbf{N}=\cos \alpha$. The normal ${\mathbf{N}}^{\prime }$ depends on the angles $\alpha$ and $\phi$:

$${\mathbf{N}}^{\prime }={\mathbf{e}}_z\cos \alpha -{\mathbf{e}}_x\sin \alpha \cos \phi -{\mathbf{e}}_y\sin \alpha \sin \phi .$$

(2)

Here ${\mathbf{e}}_z=\mathbf{N},{\mathbf{e}}_x$ and ${\mathbf{e}}_y$ are the unit vectors of the common coordinate system $(X,Y,Z)$ (see Figure 1). The line of sight $\mathbf{n}$ is taken in the plane $\left({\mathbf{e}}_x\mathbf{N}\right)$:

$$\mathbf{n}={\mathbf{e}}_z\cos \theta +{\mathbf{e}}_x\sin \theta .$$

(3)

The angle $\theta$ is the angle between vectors $\mathbf{n}$ and $\mathbf{N}$. Frequently one denotes $\theta \equiv i$. The wave electric field oscillations $\mathbf{E}$ of the emerging radiation from the element $\Delta S$ of inclined atmosphere is parallel to the vector product $\left[\mathbf{n}{\mathbf{N}}^{\prime }\right]$ direction (remember that $\left[{\mathbf{e}}_{\mathbf{x}}{\mathbf{e}}_{\mathbf{y}}\right]={\mathbf{e}}_{\mathbf{z}}$, $\left[{\mathbf{e}}_{\mathbf{x}}{\mathbf{e}}_{\mathbf{z}}\right]=-{\mathbf{e}}_{\mathbf{y}}$, $\left[{\mathbf{e}}_{\mathbf{y}}{\mathbf{e}}_{\mathbf{z}}\right]={\mathbf{e}}_{\mathbf{x}}$):

$$\begin{array}{c}\left[\mathbf{n}{\mathbf{N}}^{\prime }\right]={\mathbf{e}}_x\cos \theta \sin \alpha \sin \phi -{\mathbf{e}}_y(\sin \theta \cos \alpha +\\ \cos \theta \sin \alpha \cos \phi )-{\mathbf{e}}_z\sin \theta \sin \alpha \sin \phi .\end{array}$$

(4)

Note that vector $\left[\mathbf{n}{\mathbf{N}}^{\prime }\right]$ is perpendicular to the plane $\left({\mathbf{nN}}^{\prime }\right)$. The sources in the inclined ring are assumed homogeneous. The right-left symmetry of such distribution gives rise to the wave electric oscillations perpendicular to the plane $\left({\mathbf{nN}}^{\prime }\right)$, i.e., $\mathbf{E}\left|\right|\left[\mathbf{n}{\mathbf{N}}^{\prime }\right]$. It is convenient to choose $\mathbf{E}=-\left[\mathbf{n}{\mathbf{N}}^{\prime }\right]$ and consider the positive axis Y as the basic one. The $\mathbf{E}$ directed along positive Y is taken having polarization angle $\chi =0$. It is convenient to use the vector algebra, but taking into mind that $\mathbf{E}$ and $-\mathbf{E}$ describe the same wave electric oscillations.

The direction of $\mathbf{E}$-oscillations from all places of the plane accretion disc ($\alpha =0)$ holds along the vector $-\left[\mathbf{n}\mathbf{N}\right]=\sin \theta {\mathbf{e}}_y$, i.e., is parallel to the Y-axis (in this case we take the polarization angle $\chi \left(0^{\circ }\right)=0$).

Note that at $\phi =0^{\circ }$ and $\phi ={180}^{\circ }$ the direction of $\left[\mathbf{n}{\mathbf{N}}^{\prime }\right]\sim {\mathbf{e}}_y$, i.e., electric wave oscillations hold along ${\mathbf{e}}_y$. Futher we take $\mathbf{E}\sim (-\left[\mathbf{n}{\mathbf{N}}^{\prime }\right]$), where $\mathbf{E}$ looks like in Figure 1.

The wave electric vector $\mathbf{E}$ is perpendicular to the line of sight $\mathbf{n}$. It holds in the plane $\left({\mathbf{e}}_{z^{\prime }}{\mathbf{e}}_y\right)$, where the unit vector ${\mathbf{e}}_{z^{\prime }}$ lies in the plane $\left(\mathbf{n}\mathbf{N}\right)$ (see Figure 1):

$${\mathbf{e}}_{z^{\prime }}={\mathbf{e}}_z\sin \theta -{\mathbf{e}}_x\cos \theta .$$

(5)

Equation (4) transforms to:

$$\begin{array}{c}\mathbf{E}=-\left[\mathbf{n}{\mathbf{N}}^{\prime }\right]={\mathbf{e}}_z^{\prime }\sin \alpha \sin \phi +{\mathbf{e}}_y(\sin \theta \cos \alpha +\\ \cos \theta \sin alpha\cos \phi ).\end{array}$$

(6)

We take reference frame $(X^{\prime },Y^{\prime },Z^{\prime })$ as corresponding to the telescope coordinate system. If the radiating surface element $\Delta S\left(\phi \right)$ lies on the conical surface, then the $\mathbf{E}$-vector oscillates along the direction, characterized by the angle $\chi$ (see Figure 1). Formula for $\chi$ is:

$$\tan \chi =\frac{E_{z^{\prime }}}{E_y}=\frac{\sin \alpha \sin \phi }{\sin \theta \cos \alpha +\cos \theta \sin \alpha \cos \phi }.$$

(7)

The angles $\phi =0^{\circ }$ and $\phi ={180}^{\circ }$ describe the electric oscillations along the Y-axis. Note that the vectors $\mathbf{E}$ and $-\mathbf{E}$, i.e., the angles $\chi$ and $\chi \pm {180}^{\circ }$ describe the same radiative oscillations. The vector $-\mathbf{E}$ corresponds to negative signs of $E_{z^{\prime }}$ and $E_{y^{\prime }}$. The values $\sin \alpha ,\cos \alpha ,\sin \theta ,\cos \theta$ are positive. The Equation (7) can be written in the form:

$$\tan \chi =\frac{\sin \phi }{\cos \theta (\tan \theta /\tan \alpha +\cos \phi )}.$$

(8)

For $\phi >{90}^{\circ }$ the value $\cos \phi <0$. It is seen that the denominator of Equation (8) diminishes with $\phi \to {180}^{\circ }$. This means that the polarization angle $\chi \left(\phi \right)$ acquires the maximum in the range of $\phi >{90}^{\circ }$.

Note, that for $\theta >\alpha$ we have $E_y>0$ and the the expression (8) is positive for all values $\phi$ from $\phi =0$ up to $\phi ={180}^{\circ }$. This corresponds to the polarization angle $\chi$ lying in the first quadrant of $(z^{\prime },y^{\prime })$ coordinates.

For $\theta =0$ we observe the all inclined atmosphere perpendicular to the central plane of accretion disc. In this case $\tan \chi =\tan \phi$. This means that $\chi =\phi$. In this case $\chi \left(\phi \right)$ is independent of inclination angle $\alpha$.

Below we consider the case when a telescope observes all surface of inclined atmosphere, i.e., the angle $\theta$ is taken in the interval $(0,{90}^{\circ }-\alpha )$. For cases, when we observe only part of inclined atmosphere, the results depend on the unclear contribution of the lateral part of the atmosphere, which is not considered in our model. It should be noted that this restriction leaves a large field of applications.

In the case $\theta <\alpha$ there is the negative part of $E_y<0$, corresponding to negative $\tan \chi$. In this case

$$\tan {\chi }_1=E_z^{\prime }/\left|E_y\right|,$$

(9)

where ${\chi }_1$ is the angle between $\mathbf{E}$ and the negative part of the Y axis. The additional inclination angle relatively positive Y-axis is equal to

$$\chi {\left(\phi \right)}_{add}={90}^{\circ }-{\chi }_1.$$

(10)

So, the total inclination angle is ${90}^{\circ }+{\chi }_{add}\equiv {180}^{\circ }-{\chi }_1$. Instead of Formula (8) we obtain the relation:

$$\tan \chi ={180}^{\circ }-\frac{\sin \phi }{\cos \theta \left|\right(\tan \theta /\tan \alpha +\cos \phi \left)\right|}.$$

(11)

Thus, for $\theta <\alpha$ the expression for $\chi \left(\phi \right)$ is to be obtained by two stages: for positive ($\tan \theta /\tan \alpha +\cos \phi$) one can use the Formula (8), and for negative ($\tan \theta /\tan \alpha +\cos \phi$) it is necessary to use Formula (11).

As an example, in Table 1 we give the polarization angle $\chi \left(\phi \right)$ for $\alpha ={10}^{\circ }$ and different values of angle $\theta$.

Table 1. The polarization angles $\chi {\left(\phi \right)}^{\circ }$ for inclination angle $\alpha ={10}^{\circ }$.

${\mathit{\phi }}^{\circ }$	$\mathit{\theta }=0^{\circ }$	$5^{\circ }$	${20}^{\circ }$	${45}^{\circ }$	${70}^{\circ }$	${80}^{\circ }$
0	0	0	0	0	0	0
10	10	6.7 1	3.47	2.11	1.75	1.73
20	20	13.45	6.91	4.18	3.46	3.40
30	30	20.23	10.29	6.17	5.08	4.98
40	40	27.08	13.59	8.04	6.56	6.41
50	50	34.02	16.76	9.73	7.86	7.66
60	60	41.11	19.77	11.22	8.95	8.68
70	70	48.38	22.57	12.46	9.79	9.45
80	80	55.88	25.09	13.40	10.36	9.95
90	90	63.70	27.27	14.00	10.63	10.15
100	100	71.93	29.00	14.22	10.58	10.05
110	110	80.72	30.14	14.00	10.22	9.65
120	120	90.25	30.51	13.32	9.53	8.95
130	130	100.79	29.83	12.16	8.53	7.97
140	140	112.70	27.78	10.50	7.23	6.72
150	150	126.39	23.94	8.37	5.67	5.26
160	160	142.26	17.94	5.84	3.91	3.61
170	170	160.73	9.72	3.00	1.99	1.84
175	175	170.27	4.96	1.51	1.00	0.92
178	178	176.02	2.00	0.60	0.40	0.37
0	180	180	0	0	0	0

The Case of Spectral Line

It is interesting to obtain the $\lambda$—dependence of polarization angle $\chi$ in spectral lines, which is frequently presented in atlases.

Equation (1) gives the $\lambda$—dependence of $\sin \phi$:

$$\sin \phi =\frac{\lambda -{\lambda }_{rest}}{{\lambda }_0}{\left(\frac{u_{rot}}{c}\sin \theta \right)}^{-1}.$$

(12)

Substitution of $\sin \phi$ and $\cos \phi$ into Formula (8) gives rise to $\lambda$-dependence of $\tan \chi \left(\lambda \right)$:

$$\begin{array}{c}\tan \chi \left(\lambda \right)=\frac{\lambda -{\lambda }_{rest}}{{\lambda }_0\cos \theta }\left[\frac{u_{rot}\sin \theta }{c}·\frac{\tan \theta }{\tan \alpha }+\right.\\ {\left.{\left({\left(\frac{u_{rot}\sin \theta }{c}\right)}^2-{\left(\frac{\lambda -{\lambda }_{rest}}{{\lambda }_0}\right)}^2\right)}^{1/2}\right]}^{-1}.\end{array}$$

(13)

Note, that the main difficulty is to obtain $(\lambda -{\lambda }_{rest})$ from observed spectral line. The authors are working on this problem.

The polarization angle $\chi$ near the centre of a line depends on ${(\lambda -{\lambda }_{rest})}^m$ with $m>0$. Such dependence of $\chi \left(\lambda \right)$ is frequently seen in atlases Smith et al. [5] and Afanasiev et al. [6].

How to estimate the inclination angle $\alpha$ of conical atmosphere from observed resonance line? The maximum value of ${\chi }_{max}$ in resonance line occurs at azimuthal angle ${\phi }_{max}$. Equation (7) gives for $\cos {\phi }_{max}$ the following formula:

$$\cos {\phi }_{max}=-\frac{\tan \alpha }{\tan \theta }.$$

(14)

Introducing this value into Formula (8) for $\tan {\chi }_{max}$, we obtain the value ${\tan }^2\alpha$:

$${\tan }^2\alpha =\frac{{\tan }^2{\chi }_{max}{\sin }^2\theta }{1+{\tan }^2{\chi }_{max}{\cos }^2\theta }.$$

(15)

The values ${\chi }_{max}$ can be taken from the data of observed resonance line polarization. There are many techniques to estimate the inclination angle $\theta$ of mean plane of accretion disc (see, e.g., Marin [7]). Thus, Formula (15) allows us to estimate the inclination angle $\alpha$ of cone-like atmosphere.

For example, let us consider the source Akn 120, where ${\chi }_{max}={25}^{\circ }$. According to Marin [7] we take $\theta ={42}^{\circ }$. From Formula (15) we obtain $\alpha ={16.4}^{\circ }$. Of course, this result takes place if we assume that the source Akn 120 exists in accretion disc with progressively increasing height.

The inclination angle $\chi \left(\lambda \right)$ is related with rotation velocity $u_{rot}$. This gives an additional technique to estimate the velocity $u_{rot}$.

The polarization angle $\chi$ is asymmetric function of $\phi$. This is why there exist the opposite polarization angles in red and blue wings of a spectral line. Further we consider $\phi$ in the interval $0^{\circ }\le \phi \le {180}^{\circ }$. For $\theta >\alpha$ the angle $\chi$ increases steadily from zero at $\phi =0$ up to ${\chi }_{max}$ and then decreases up to zero at $\phi ={180}^{\circ }$ (see Table 1).

We see that the polarization angle $\chi$ does not depend on the intensity and polarization of the radiation, emerging from the $\phi$-point. The angle $\chi$ depends on the angles $\alpha ,\theta$ and $\phi$, i.e., depends on pure geometrical values.

In particular, angle $\chi$ can take the values greater than ${45}^{\circ }$ for large $\alpha$. This case corresponds to the total observed radiation having the $\mathbf{E}$—ocillations in the plane $\left(\mathbf{nN}\right)$. Such position angle holds in many Seyfert-1 AGNs.

3. Calculation of Observed Angular Distribution and Polarization

It is known that the Stokes parameters depend on $\mu =\cos \theta =\mathbf{n}·\mathbf{N}$ (see Chandrasekhar [3]). The Stokes parameters of radiation, escaping from the inclined ring, depend on ${\mu }^{\prime }=\mathbf{n}·{\mathbf{N}}^{\prime }$:

$${\mu }^{\prime }=\cos \alpha \cos \theta -\sin \alpha \sin \theta \cos \phi .$$

(16)

The obtained formulas for $\chi$ are valid for every radiation—continuum or spectral one. They describe the polarization angle of radiation from inclined surface $\Delta S\left(\phi \right)=\rho d\rho d\phi$, where $\rho$ is the distance from the centre of an accretion disc.

We observe the radiation fluxes $F_I(\theta ,\alpha )$ and $F_{Q,U}(\theta ,\alpha )$ from accretion discs visible as point-like sources:

$$F_I(\theta ,\alpha )=\frac{Const}{R^2}\underset{0}{\overset{2\pi }{\int }}d\phi {\mu }^{\prime }J\left({\mu }^{\prime }\right),$$

$$F_Q(\theta ,\alpha )=\frac{Const}{R^2}\underset{0}{\overset{2\pi }{\int }}d\phi {\mu }^{\prime }J\left({\mu }^{\prime }\right)p\left({\mu }^{\prime }\right)\cos 2\chi (\theta ,\alpha ,\phi ),$$

$$F_U(\theta ,\alpha )=\frac{Const}{R^2}\underset{0}{\overset{2\pi }{\int }}d\phi {\mu }^{\prime }J\left({\mu }^{\prime }\right)p\left({\mu }^{\prime }\right)\sin 2\chi (\theta ,\alpha ,\phi ).$$

(17)

Parameter $F_U$ for continuum radiation, due to symmetry of an accretion disc, is equal to zero. The unknown factors in intensity and the radiating ring area we denoted as Const. The value R is the distance to the accretion disc, $J\left(\mu \right)=I\left(\mu \right)/I\left(0\right)$ is the angular distribution and $p\left(\mu \right)=-Q/I$ is the polarization degree of outgoing radiation from the plane atmospfere ($\alpha =0$). Considering the spectral radiation, we can use the relation (see Equation (1)): $d\lambda =(u_{rot}/c){\lambda }_0\sin \theta \cos \phi d\phi$, i.e., in this case the $\phi$—integration is related with the spectrum of the resonance line.

4. Some Results

The detailed tables of $J\left(\mu \right)$ and $p\left(\mu \right)$ in % (with $\Delta \mu =0.005$) are given in Silant’ev et al. [8]. They describe the Milne problem in optically thick electron atmosphere (see Chandrasekhar [3]). Using these tables, one can calculate the values of $J\left({\mu }^{\prime }\right)$ and $p\left({\mu }^{\prime }\right)$ for different values of parameters $\alpha$ and $\theta$.

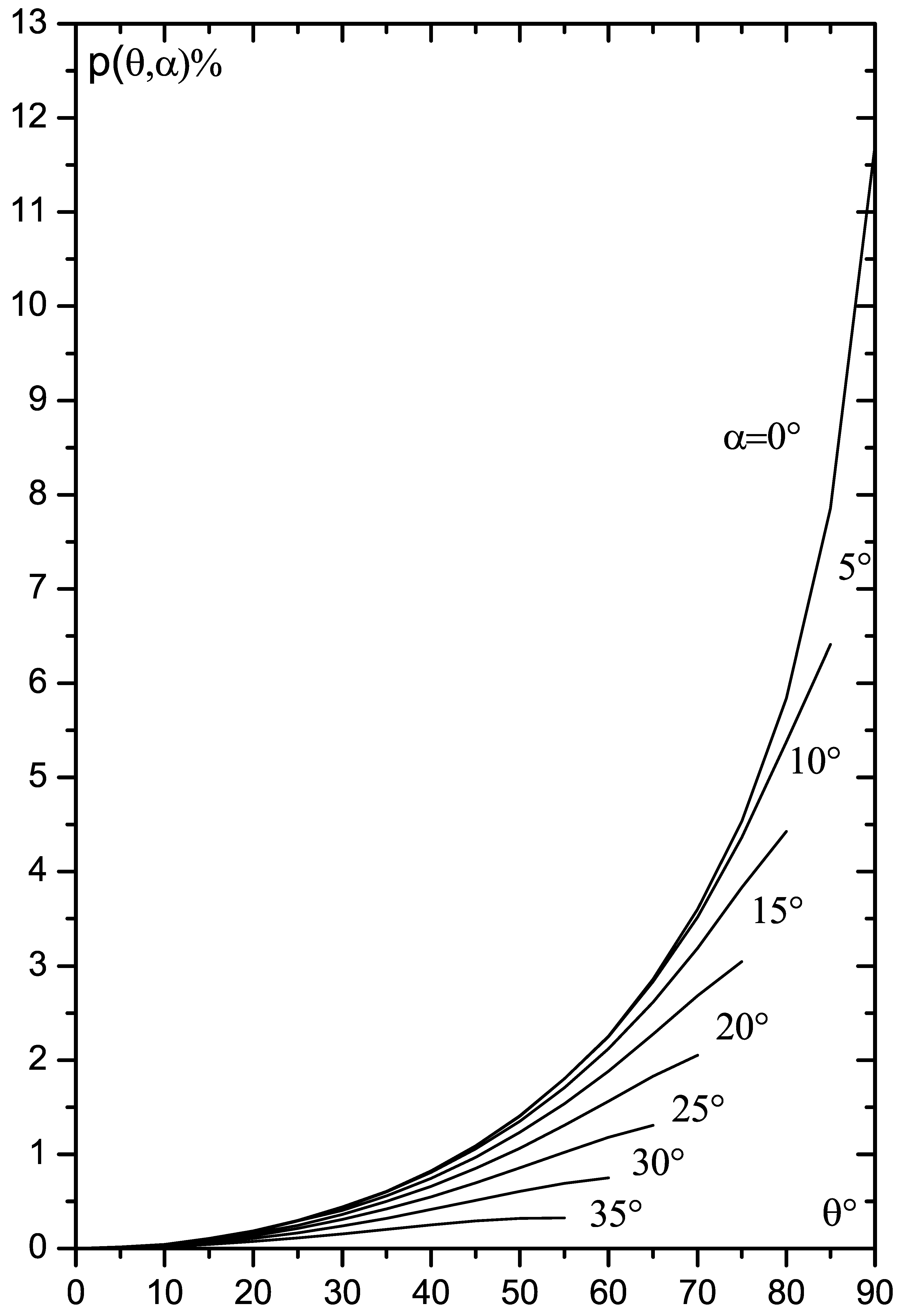
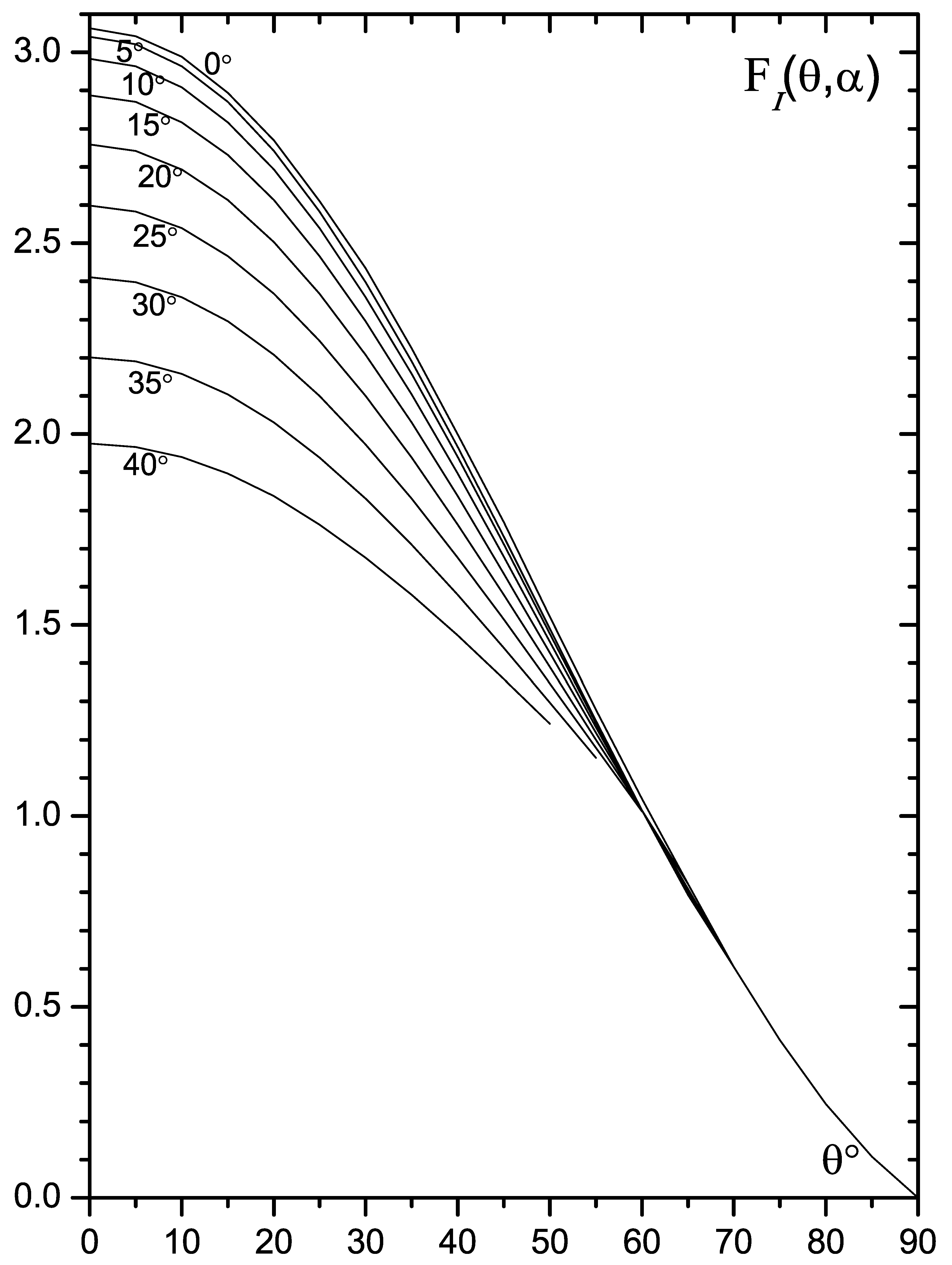
The values $p(\theta ,\alpha )=-F_Q/F_I$ and $F_I(\theta ,\alpha )$ for total observed continuum radiation are given in Figure 2 and Figure 3. In these figures we take $\theta \le ({90}^{\circ }-\alpha )$, i.e., a telescope observes all surface of a radiating ring.

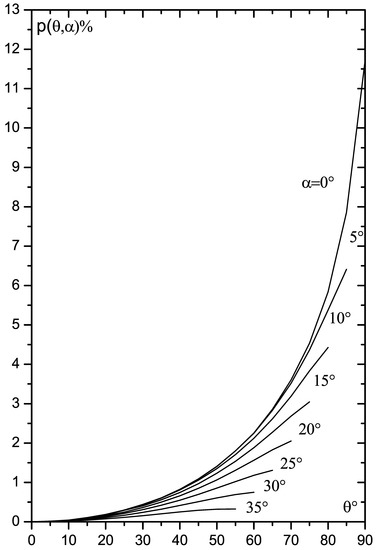
Figure 2. Polarization degree of continuum radiation $p(\theta ,\alpha )=-F_Q(\theta ,\alpha )/F_I(\theta ,\alpha )$ in %. The numbers denote the inclination angle $\alpha$. The Stokes parameter $F_U\equiv 0$.

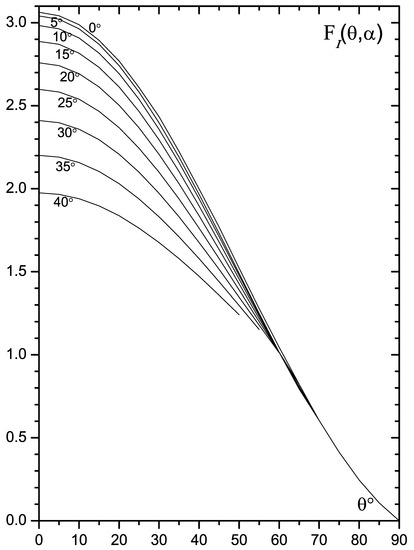
Figure 3. The angular distribution of cotinuum radiation $F_I(\theta ,\alpha )$ (without the factor $Const/R^2$). The numbers denote the inclination angle $\alpha$.

Figure 2 demonstrates that the radiation polarization from the total inclined ring diminishes with the increase of the inclination angle $\alpha$. Figure 3 shows that the flux of radiation sharply decreases with the increase of $\alpha$. Its form becomes more flat as compared to the plane accretion disc ($\alpha =0^{\circ }$).

Note that our negative $p(\theta ,\alpha )$ corresponds to the wave electric field $\mathbf{E}$ oscillations perpendicular to the plane $\left(\mathbf{nN}\right)$. This corresponds to standard polarization angle in the Milne problem. It is very interesting that for $\alpha >{45}^{\circ }$ (positive p) the oscillations hold in the plane $\left(\mathbf{nN}\right)$, as in many Seyfert 1 galaxies.

Clearly, that for large $\alpha$ the plane $\left({\mathbf{nN}}^{\prime }\right)$ takes the position close to be perpendicular to the normal $\mathbf{N}$. In this case the $\mathbf{E}$-oscillations become close to the plane $\left(\mathbf{n}\mathbf{N}\right)$. Note that, if we observe such sidelong part of gas-dusty torus with $\alpha >{45}^{\circ }$, then the $\mathbf{E}$-oscillations will be in the plane ($\mathbf{N})$.

As far as resonance line, it should be noted that the rotation gives rise to an additional broadening of parameters $F_I(\theta ,\alpha ),F_Q(\theta ,\alpha )$ and $F_U(\theta ,\alpha )$ (see e.g., Silant’ev et al. [9]).

Our theory calls in question the known technique of inclination angle $\theta$ estimation from measurement of radiation polarization degree. The latter uses the polarization degree for plane accretion disc. We have shown that the inclined atmosphere gives smaller values of polarization.

5. Conclusions

We considered the influence of the progressively increasing height of accretion disc on the polarization and angular dependence of observed radiation in continuum and spectral lines. The estimation of polarization angle ${\chi }_{max}$ from the observed polarization of spectral line allows us to estimate the inclination angle $\alpha$ of conical atmosphere, if we know the inclination angle of accretion disc $\theta$. The polarization angle $\chi \left(\lambda \right)$ is related to the rotation velocity of the accretion disc. This gives the additional technique to estimate the rotation velocity.