1. Introduction
Hardware-in-the-loop (HIL) simulation is an industrial methodology used in the development of power systems to reduce risks and costs [
1,
2]. In a HIL setup, a real controller is connected to a simulated plant in closed loop. Better performances are achieved when the round trip time of the signals is as fast as possible—ideally, a few
s or less. A HIL simulation is typically performed using PC clusters, in which case the simulator offers flexibility and programmability [
3]. However, when the power system requirements impose a latency limited or close to 1
s, field-programmable gate arrays (FPGAs) are usually the best choice for HIL [
4].
Recent publications address the FPGA-based real-time simulation problem from an application, system or circuit modelling point of view [
5,
6,
7]. Their purpose is either to reduce the simulation time-step, to propose new switch modelling techniques or to augment the parallelism of the simulation. The approach adopted in the paper addresses the subject from a hardware implementation perspective. Our aim is to propose a design methodology that will help reduce development time of an FPGA-based RTS—also designated as a hardware solver (HS) in this paper.
The implementation of a HS is typically described at the register transfer level (RTL) [
8]. The utilization of high-level synthesis (HLS) tools has been considered as an alternative to facilitate hardware development on FPGA [
9,
10,
11], but has been shown to impose certain limitations on performance and resource utilization [
11]. Furthermore, the HLS design approach does not remove the synthesis process stage, which takes from minutes to hours, depending on the complexity of the design.
The main contribution of this paper is to propose a novel design methodology for the development of HS. The methodology uses an overlay architecture (OA) based on a decentralized control scheme using a latency-insensitive design (LID) approach. An OA is a configurable and regular hardware structure composed of functional and interconnection elements. An OA is configurable at two levels: (i) at an architectural level, to modify the number and characteristics of operators and generate a new bitstream; (ii) at a software level, which is done by filling the content of embedded memories. On the other hand, LID facilitates the design integration task by allowing data transfers between units on the datapath to be self-synchronized. In the proposed LID approach, processes are synchronous systems driven by the events at their point-to-point communication channels following a specific protocol. This ensures that the correct functioning of processes independently of the latency on the channels that interconnect them. Modules designed with this method are easily integrated to reach the correctness of the system [
12].
The remainder of this paper is organized as follows:
Section 2 presents the works related to this research—that is, FPGA-based real-time simulation of power converter techniques referenced in the literature. The purpose of
Section 3 is to provide the reader with a review of the background material pertaining to overlay architectures and latency-insensitive design.
Section 4 presents the proposed solution. It reviews the mathematical foundation of our approach and the programming model of the proposed hardware solver as well as its building blocks.
Section 5 presents the simulation and implementation results for the case studies as well as the performance exploration. A discussion is given in
Section 6.
2. Related Work
2.1. Switch Model
The design of a HS must obey tight constraints due to the high switching frequencies of semiconductors, which typically require simulation time-steps below 1
s [
11,
13]. To achieve a low time-step solution, the switching behavior is either emulated using an ideal switch model or a switching function [
14]. The ideal switch model, in turn, resorts to one the two commonly used switch models: the resistive switch model (RSM) or the associated discrete circuit (ADC) switch model.
The RSM replaces the switch by a low and high resistor when on and off, respectively. It is known to be a more accurate approach than ADC but suffers from certain limitations such as heavy memory requirements for storing precomputed network equations, and higher computational cost due to iterations. The Sherman–Morrison–Woodbury formula to compute the updated inverse matrix at each time-step was proposed in [
15], but such an approach neglects the iterations needed to determine the state of diodes. A method to handle diodes has been proposed in [
16], but it introduces unrealistic parasitic elements that alter the behavior of the converter. The use of iterations, the compensation method and circuit partitioning have also been considered [
17,
18], but it results in large time-steps. A predictor–corrector algorithm has been used in [
6] to decouple the switches from the circuit elements and to simulate them simultaneously, but such an approach relies on a forward integration scheme and may become unstable. Finally, a direct map method was proposed in [
7] to simulate a high switching frequency resonant converter, but it is unclear at the moment how the method could apply to more complex topologies. The ADC switch model [
19] replaces the switch by a Norton equivalent with a fixed impedance. It gives a fixed system of equations irrespective of switch statuses, which considerably reduces memory requirements. Because it does not require an iterative solution, the ADC model is less computationally hungry than RSM, and has been widely used for HS implementations on FPGA [
13,
20,
21]. However, ADC is prone to fictitious oscillations that can alter the behavior of the converter’s model. Various techniques have been proposed for minimizing the effect of these undesired oscillations [
22,
23,
24]. These techniques often require a special routing mechanism in the HS to handle the various conditions the modified algorithm has to account for.
The switching function is a simple model which replaces the converter by a circuit only consisting of controlled voltage and current sources. Hence, the switching function describes the behavior of the converter through its interfaces. However, by doing so, it fails to accurately emulate transients or certain operational modes of the converter (the rectification for an inverter for instance). The switching function was utilized in such works as [
5,
25,
26], where transients were not the primary focus of the investigation.
2.2. Hardware Description Languages
The implementation of a HS is mainly obtained using hardware description languages such as Verilog or VHDL at the RTL. Describing a digital design in RTL abstraction is known to be a difficult and error-prone task. Increasing the level of abstraction for hardware design is supposed to reduce the development time and increase productivity [
27], which is why the utilization of high-level synthesis (HLS) tools has been considered as an alternative to facilitate hardware development on FPGA [
9,
10,
11].
HLS becomes a popular trend for the implementation of hardware accelerators in areas such as image processing, economics, robotics, etc. [
28,
29,
30]. More recently, HLS has also been used for custom implementations of HS for HIL [
26,
31] and for its testbenches. The use of HLS for HIL has been shown to impose limitations on hardware performance and resource utilization when intended to be used in HS for HIL [
11]. Furthermore, once an HLS code is finished, the development cycle is not completed: the RTL code needs to be generated, and the code needs to be synthesized and implemented, then tested on the FPGA for timing, accuracy, etc. All these tasks can take from hours to days, depending on the complexity of the design.
2.3. Number Format
An FPGA implements real arithmetic computations using either fixed-point or floating-point (FP) format. The fixed-point number is basically an integer scaled by an implicit factor. The fixed-point format is known to uses less hardware resources, which yields a low latency datapath. However, the fixed-point format suffers from a restricted dynamic range that can restrict its utilization for HIL applications. These limitations have been addressed by means of appropriate optimizations such as scaling the operands to the dimensions of the hardened blocks of the FPGA, or by normalizing all the physical quantities to a per unit scale [
7,
16,
32].
On the other hand, the FP number format allows for a larger dynamic range, but its operators are costly in terms of hardware and require deeper pipelines. This is even more true when double precision is considered. Hence, most HSs reported in the literature make use of single precision FP to save hardware and to reduce latency [
18]. The utilization of a non-standard FP is often privileged in the FPGA context—that is, a FP which does not adhere to IEEE-754 standard to provide better resource consumption. For instance, in [
33], the authors proposed a low-cost FP with soft normalization and showed the benefits to HIL applications.
The solution considered in this paper is based on a non-standard FP format with intermediate precision which balances hardware consumption, computing power and computational accuracy. The arithmetic operators are built using a fused datapath approach [
34], which consists of removing all intermediate packing and unpacking stages from a complex FP datapath and performing all the computations jointly. All internal additions are performed using the self-alignment format (SAF) [
35]. Such an approach was previously adopted in [
17,
21,
36].
3. Background
Improving the computing performance to reach lower time-steps while keeping a reasonable FPGA resource consumption increases the difficulty associated with the development of a HS. Most of the research devoted to the development of HSs is performed at an application level, where the main energy is invested on the elaboration of new modelling techniques, circuit partitioning schemes and parallelizing calculations.
Generally, the implementation of a HS follows a centralized design approach. It consists of a datapath, comprised of memory elements and functional units (FU), under the command of a control unit that sequences all data transfers. The sequence of execution determines the timing of data transfers and needs to be designed by taking into account the sequence of reads and writes and the latency of each processing unit.
In this work, we propose a parametrizable and reconfigurable architecture inspired from OAs that uses a modularized LID approach. All data transfers are handled by an efficient simple interconnection scheme that facilitates programmability and system expansion. This section presents an overview of OA and LID to clarify these concepts.
3.1. Overlay Architectures
Custom design using RTL is a good way to achieve high performance due to the fine granularity of the hardware description and the direct access to FPGA resources it allows. However, the difficulty behind such a low-level design is the long time associated with FPGA development cycles. Overlay architectures have been introduced by such initiatives as ZUMA [
37], Quku [
38] and DeCO [
39] with the aim to increase the abstraction level, improve the productivity, ease the programmability and reduce the time of design [
40].
An OA is a reconfigurable implementation over a FPGA. An OA is formed by two main parts: an implementation (hardware architecture) and a mapping tool.
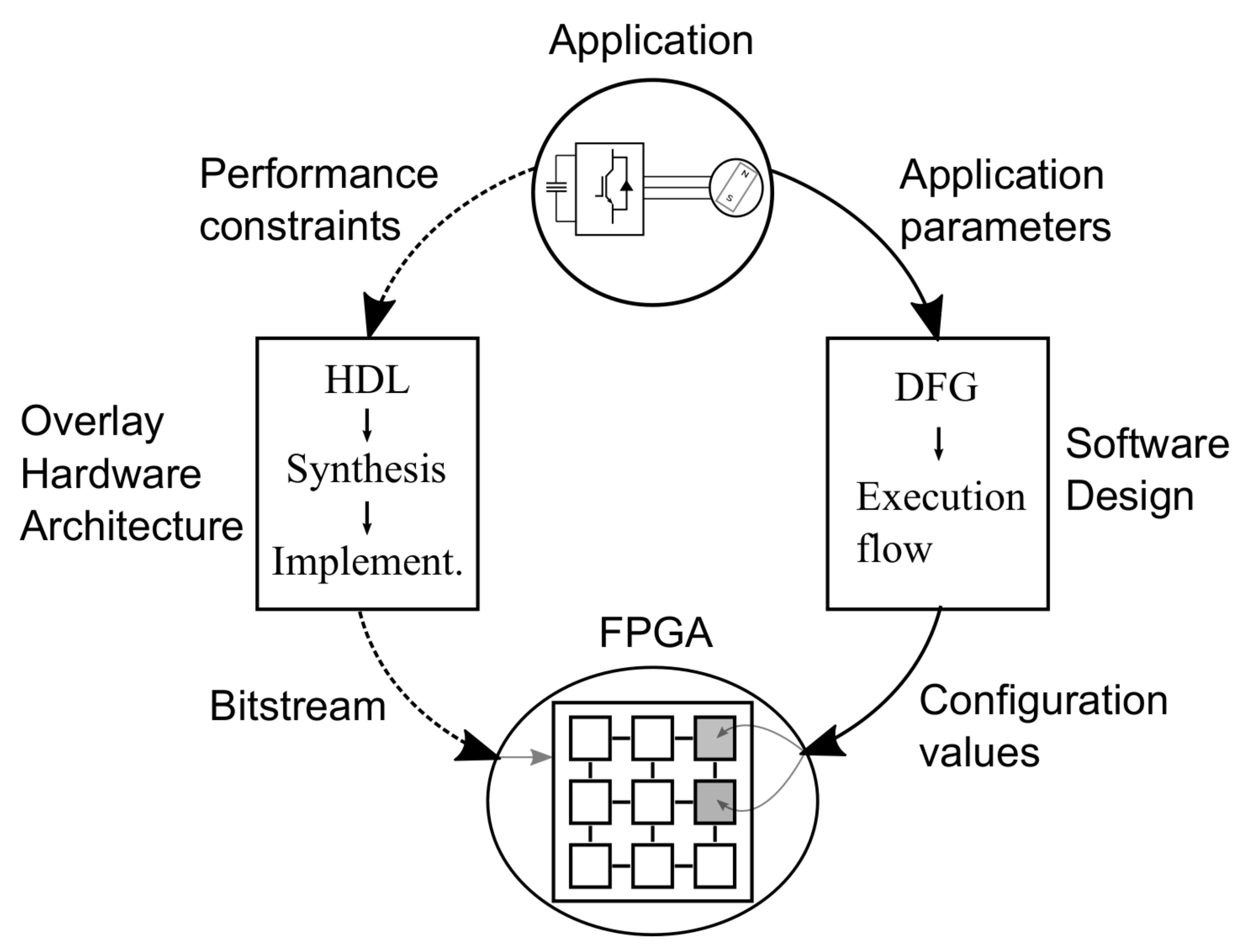
Figure 1 shows a condensed workflow for OA-based design. For the implementation part (left of
Figure 1), the type of applications determines the OA topology. Performance requirements are then taken into account to define a set of parameters to generate an instance of the OA and to generate the FPGA programming bitstream using the traditional FPGA workflow. Once the hardware is generated, a mapping tool (right of
Figure 1) is used to interpret the application code and to extract its data flow graph (DFG). This way, the application is rapidly mapped on the hardware without passing trough the synthesis process again.
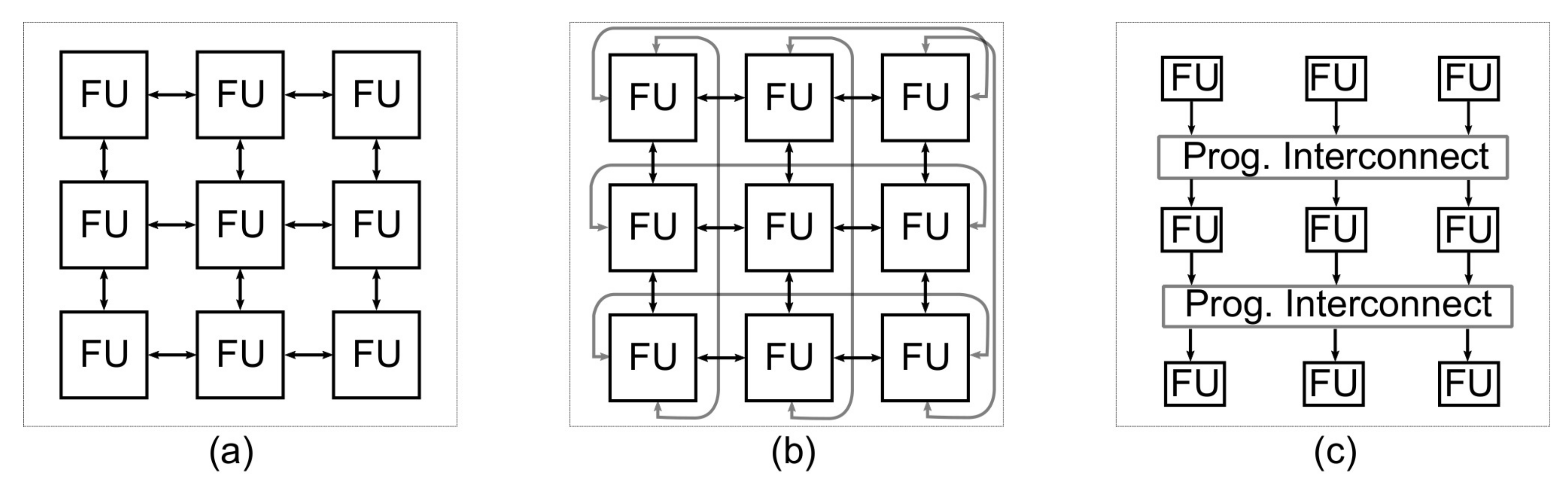
The performance delivered by an OA depends on the selected topology. In the two-dimensional array topologies shown in
Figure 2a,b (nearest neighbor and torus, respectively), each tile is connected to four surrounding tiles (top, bottom, right and left) in a bidirectional way. This results in a high connectivity among units and offers wide configuration possibilities. However, this also implies that data have multiples paths to reach a desired destination, putting extra effort on the control and its synchronization, while also increasing the design complexity and cost due to the overhead related to the interconnection. In the linear topology shown in
Figure 2c, the tiles are arranged in stages, and data can only by transmitted from one stage to the following one in a unidirectional way. This topology presents a reduced connectivity which leads to a potentially reduced capability of reconfiguration and reduce the variety of applications but gains in simplicity and in performance.
3.2. Latency-Insensitive Design
Timing performance of a large digital design is determined by the delay of its longest combinational path. This is often curated using pipelining techniques, which is done by inserting register stages within the datapath. However, the pipeline depth must be matched on all paths and effects of the control sequence. The purpose of an LID approach is to solve this issue by making functional modules independent of the arrival time of their inputs [
43]. In LID, the interconnection elements are separate from the functional elements, and correct operation of the system is warranted by construction [
12]. Such an approach has the merit to ease the design process by allowing the hardware designer to invest more efforts on the design of small processing blocks while their interaction is taken into account at a later stage through interface communication protocols.
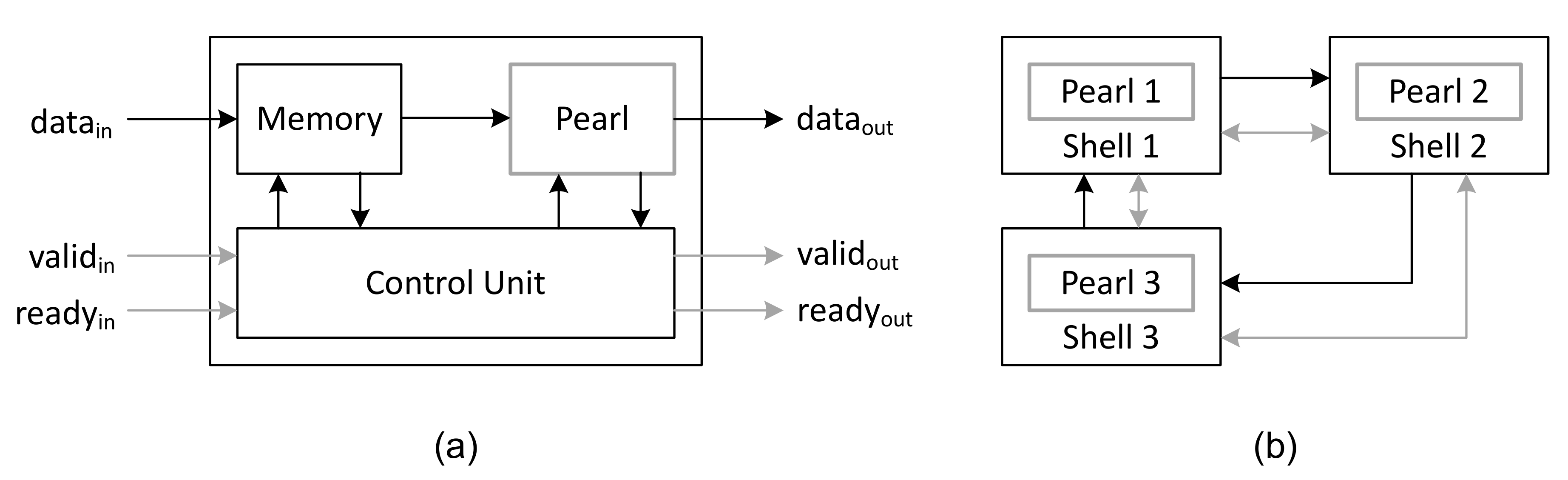
A basic functional module is termed a pearl in the literature. The pearl is stallable, and is encapsulated in a so-called shell. As shown in
Figure 3a, the shell is comprised of memory elements and a control logic. The memory elements are connected to the input channels and help to sustain data contention. The control logic serves the purpose of managing the channel’s protocol and serving the module’s functionality [
44]. All data transfers are then performed only when the pearl is available to process them. All data signals are accompanied by control signals for handshake purposes. Two control signals in opposite direction are typically used: a
valid forward signal to indicate that the source has valid data to send, and a
ready backward signal to indicate that the target is ready to accept the incoming data.
Figure 3b illustrates an LID-based system with multiple shells interconnected.
4. Proposed Solution
This section presents the proposed solution in a detailed fashion. We start with the mathematical formulation of the power converter model—the ADC switch for modelling the power converter. We then discuss the latency-insensitive design of an HS. The LID HS is an OA, in the sense that it respects the principle of having a fixed yet parametrized architecture over which an application is deployed. Interconnection between functional units is implemented using a crossbar that connects all FUs together. The crossbar is implemented using an LID. The arithmetic operators use a custom floating point number representation to achieve high performance.
4.1. Mathematical Formulation
Using the associate discrete circuit modelling approach, all components are replaced by Norton equivalents resulting from a fixed time-step backward Euler integration rule. The network equations can then be assembled to yield:
where subscript
n denotes present time point,
is the nodal matrix obtained from modified augmented nodal analysis (MANA) [
45],
is a composite vector of unknowns node voltages and voltage source currents and
is a vector of known input sources (
) and history terms. We distinguish between switch history terms (
) and L/C component history terms (
).
being simply a linear combinations of those terms, it can be expressed as:
Using the ADC switch model, the matrix
is fixed, irrespective of switch statuses, and its inverse can be precomputed. Moreover, to improve the computational efficiency, rewriting the network equations in a state-space-like form was found to be convenient [
7,
11,
21,
46], which yields:
where
is a fixed matrix obtained from algebraic manipulations of
, and
. The terms with subscript
are history terms computed for the next time-point of the simulation, and
are outputs of interest.
It is worth mentioning that
comprises the switch history terms for switches in ON and OFF states (both are computed), whereas
includes only one of the two terms for each switch, with respect to actual switch status (
is hence twice as large as
). This matter has been thoroughly discussed in [
11,
21,
46]. It is also worth mentioning that history terms are referred to as state variables in the remainder of this text.
4.2. Hardware Solver Architecture
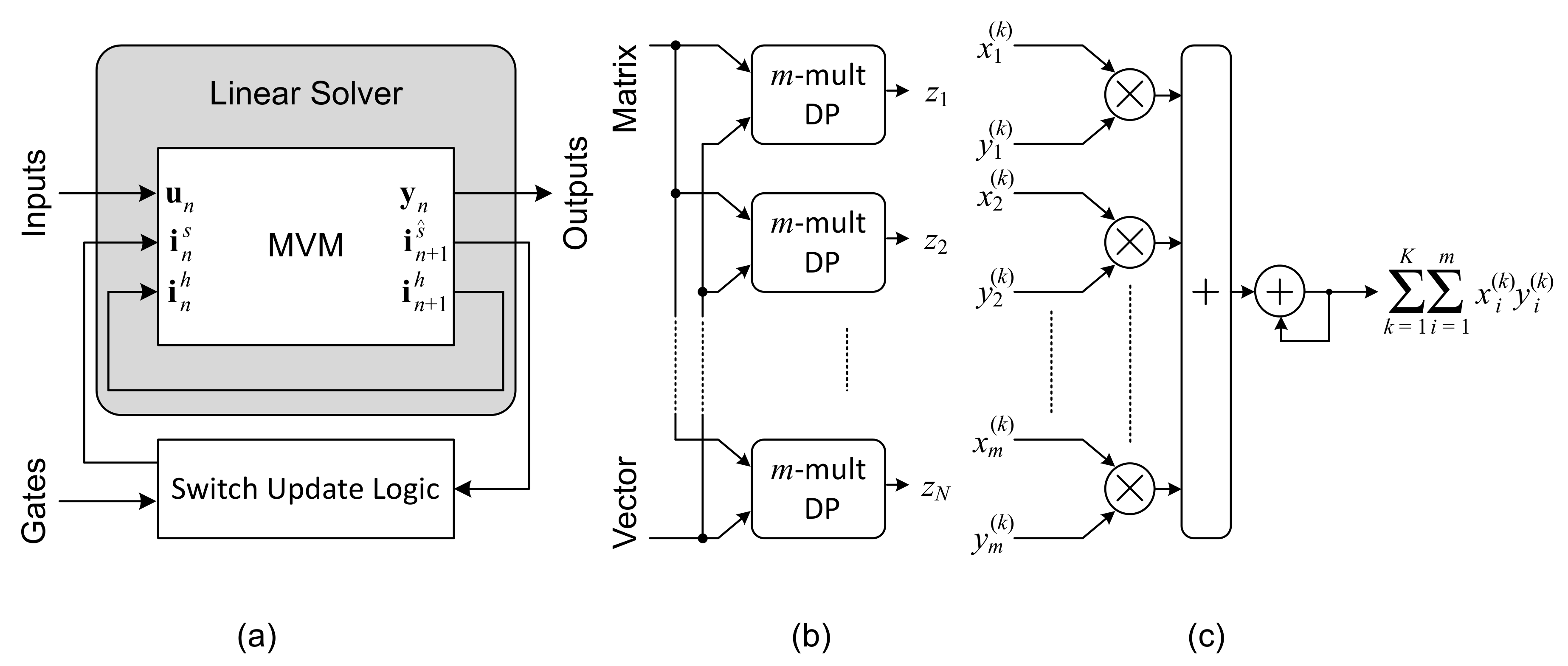
Figure 4a presents a general structure of a HS architecture. It consists of a linear solver connected in a closed loop to a switch update module. The linear solver feeds vectors
,
,
to an MVM module, which, in turn, produces vectors
,
,
. The linear solver sends those results to appropriate locations. The switch update module receives
and extracts the switch history terms
, according to the input gates and switch logic [
11,
21,
46].
Figure 4b illustrates how the MVM unit is built. It consists of
N dot product (DP) units with each DP unit consisting of
m parallel multipliers (termed DP-type
m) feeding an addition tree, and terminated by an accumulation function, as shown in
Figure 4c. The DP operator is designed to process
pairs of operands
,
,
in
K successive clock cycles, and produces:
4.3. Programming Model
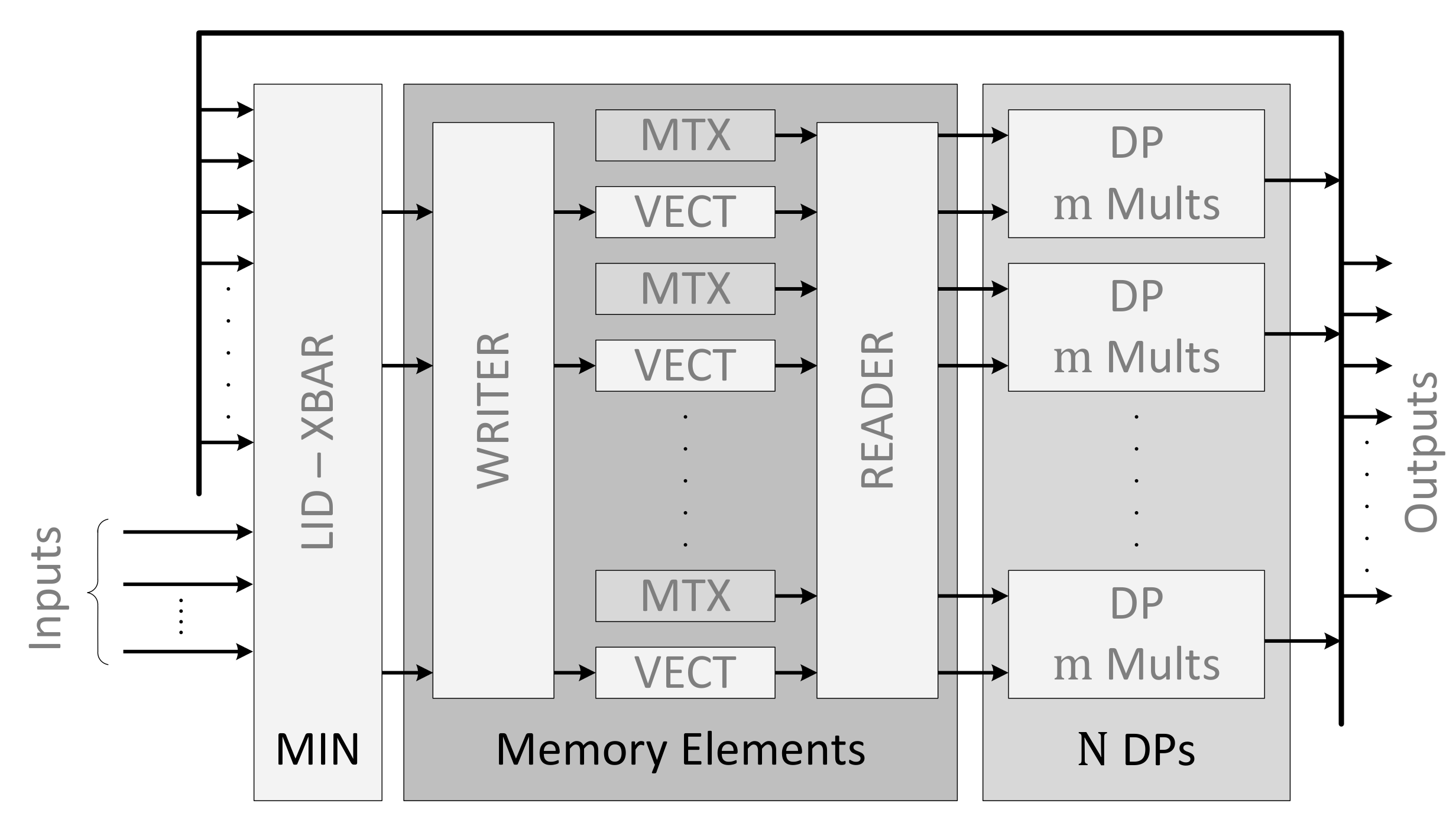
Figure 5 presents a more detailed view of the architecture of the linear solver. It is composed of three stages: (i) a crossbar (XBAR), (ii) memory elements and (iii)
N DPs. It is worth mentioning that, compared to similar works from the literature, this HS does not contain a global control unit, and all operations are self-synchronized thanks to the adopted LID approach. The XBAR is in charge of routing data to appropriate locations. The memory elements are simply embedded RAM blocks (MTX and VECT in
Figure 5) with read and write logic. The DPs form the functional part of the linear solver. The XBAR is presented in
Section 4.4, the memory elements in
Section 4.5 and the DP operators in
Section 4.6.
The computing power of the linear solver is determined by the number of DP (
N) and the number of multipliers each DP has (
m), also referred to as DP-type in this paper. Hence, the OA is determined by parameters
N and
m. Once the overlay is generated, the application can be reprogrammed on top of it. This is simply done by mapping Equation (
3) over the OA, which is solely determined by the number of independent sources, the number of states variables, the number of switches and the number of outputs. These parameters are used to generate the programming bits of code used to configure the XBAR, the writer and reader and to fill the contents of the VECT and MTX memories.
4.4. Interconnection Network
The role of the interconnection network is to move data to the appropriate VECT memory locations from either the inputs of the linear solver or the outputs of the DPs, as shown in
Figure 5. The data should be able to move freely from any input to any ouput of the interconnection network, which motivates the use of a crossbar. However, an
N-node crossbar requires
connections, and each node has a fan-out of
N [
47]. Multistage interconnection networks (MINs) solve this problem by splitting the crossbar into a succession of intermediate crossbars of smaller size [
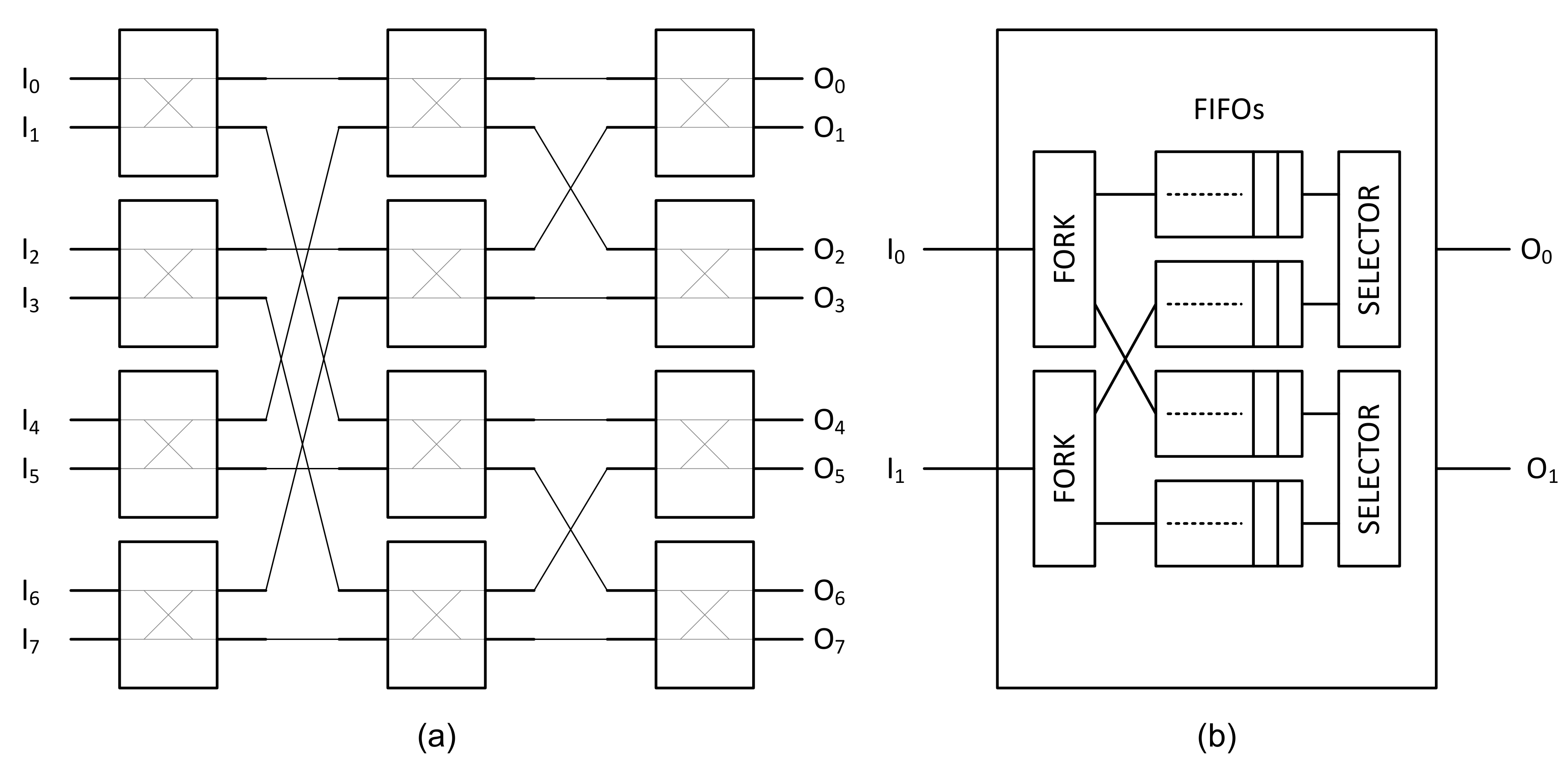
48]. The MIN considered in this paper is formed by
cells arranged in a butterfly topology [
49], as shown in
Figure 6a. Each cell has two input and two output channels that are used to connect to neighbouring stages. The number of cells in the butterfly MIN amounts to
.
For this work, we have adopted the MIN implementation presented in [
50], which offers a straightforward routing scheme and such capabilities as multi-casting, broadcasting and data contention handling.
Figure 6b illustrates the associated
cell, which is designed using a LID approach. The cell is composed of two fork units, four FIFOs and two output selectors. The fork units receive incoming data from the previous stage and route them to one or both output channels on the following stage. In a butterfly MIN, there exists a unique path for each pair of input and output channels, which may result in blocking situations [
51]. The FIFOs in
Figure 6b are used to handle contention and avoid blocking. The output selectors are connected to two FIFOs each and are responsible for sending the data to the next stage. If at least one of the two FIFOs connected to a given selector is not empty and the cell from the next stage is ready to receive data, the data is read and passed forward. When the two FIFOs have data, the selector will read from one of the two FIFOs using a simple round robin scheduling, switching the priority of the FIFOs for the next time the situation occurs.
4.5. Memory Elements
The main tasks of the memory elements unit of
Figure 5 are: (i) store circuit network equations entries (MTX), as well as inputs and state variables (VECT), and (ii) sequence read and write operations.
The data in MTX are fixed during simulation time while the data in VECT are updated at each time step. The MTX and VECT are implemented using m parallel RAM blocks each, to allow simultaneous access to multiple elements at a time. Moreover, the VECT memories use a double buffering technique to avoid read/write overlaps. While one segment of the memory is used for reads, the other is dedicated to writes. Read and write segments are swapped at the following simulation time-point of the simulation.
The round robin rule implemented by the MIN cell of
Figure 6b provides it with the capability of not prioritizing one incoming channel over the other. However, it makes the output order of the MIN harder to predict. A simple way to manage the problem is by adding a tag at the input of the MIN. For each time-step, and each input channel, a tag formed by the input port ID and the arrival order is concatenated with the data token. Hence, the variables are easily identifiable at the output of the MIN, even if they arrive out of order.
The role of the reader block of
Figure 5 is to read data from the memory locations when all state variables are available, with respect to the double buffering scheme. Its role is also to make the read order deterministic so that state variables are produced in a specific order, and feed to the input channels of the MIN in a predefined sequence. On the other hand, the role of the writer block of
Figure 5 is to identify the incoming variables from their tag and write them to correct memory locations, with respect to the double buffering scheme.
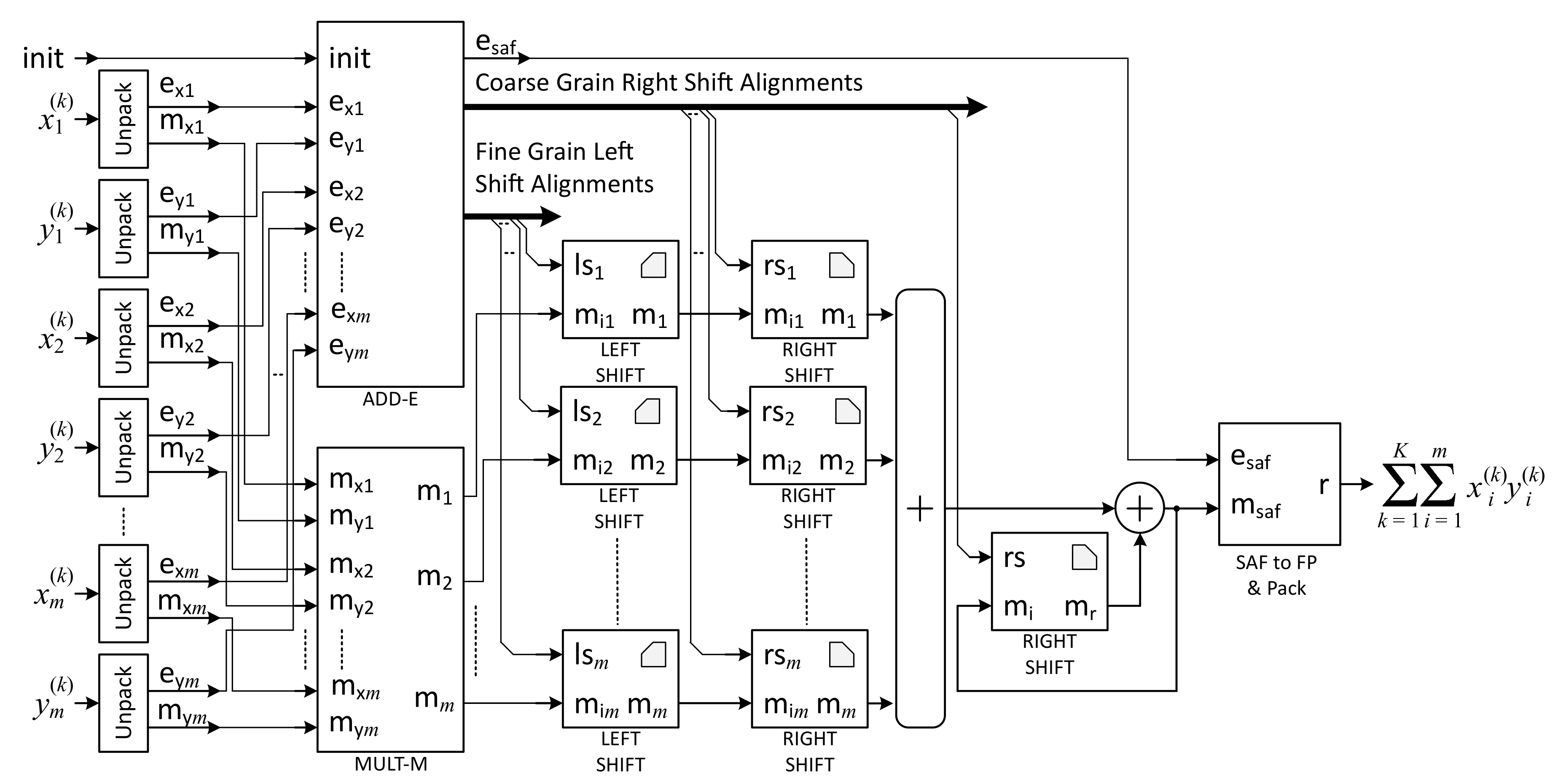
4.6. Dot Product Operator
As discussed previously, a DP operator is an arithmetic unit consisting of
m parallel multipliers feeding an addition tree and terminated by an accumulation function, as shown in
Figure 4c. The DP considered in the paper is based on an approach that combines the fused datapath [
34] and self-alignment format (SAF) [
35], and is shown in
Figure 7.
The fused datapath (FDP) is a paradigm that consists of building a complex FP datapath by removing all intermediate packing and unpacking stages and performing all the computations jointly. This is explicit from
Figure 7, where unpacking blocks are found at the inputs and the output of the DP. SAF, on the other hand, is a format made to process FP additions efficiently and to reduce the latency of the arithmetic operator: all mantissas are aligned with respect to the last bits of the number’s exponent (fine grain left shifts), whereas all additions can be performed at a higher clock frequency and in a single clock cycle, since only coarse grain right shift alignments are needed [
35].
The FDP/SAF approach was previously adopted in [
17,
21,
36] to generate dot product operators for the real-time simulation of power converters, and was shown to be computationally efficient, capable of sustaining higher clock frequencies while offering significant hardware resource savings.
5. Results
This section presents synthesis results, time-step evaluation and simulation assessments for a selection of overlays, along with a discussion. We discuss resource consumption and timing performance for each synthesized architecture, and determine the minimum achievable time-step for each overlay for a variety of circuit sizes. Simulation results for an AC–DC–AC converter test case are presented and used to discuss the computational accuracy of the HS.
5.1. Synthesis Results
The hardware overlay was implemented using a vendor-agnostic VHDL, following a generic coding style, free from any directive or primitive specific to a particular technology. The overlay is generated from a set of parameters—that is, the number of DPs and their type. The architecture also supports changing the data size and memory depth, but these two parameters were considered with default values, which are sufficient for all the test cases considered for this evaluation. Namely, we have used a non-standard IEEE format with 8-bit exponents and 34-bit mantissa, which is consistent with previously published works such as [
46]. The memory depth was fixed to
entries, simply to match the size of hardened RAM blocks. The Virtex 7 (7vx485tffg1157-1), was considered for this evaluation. Without being the latest technology, this device offers the resources and timing capabilities to implement the HS of appreciable sizes. Synthesis results were obtained using Vivado 2015.3.
Three OAs have been considered for this study, namely:
Architecture 1: 4 DPs, of DP-type 8: ;
Architecture 2: 8 DPs, of DP-type 16: ;
Architecture 3: 16 DPs, of DP-type 32: .
Table 1 outlines the synthesis results for these overlays. It clearly shows that Architecture 3 is indeed the largest overlay than can be implemented on the selected FPGA, given the scarcity of reconfigurable resources (LUTs). It is interesting to discuss the results of
Table 1 in light of the reported computing power (CP) of each overlay, expressed in giga floating-point operations per second (GFLOPS). CP is given at peak performance, and is computed using the formula
, where
is the maximum sustainable clock frequency, and
is the number of simultaneous FP operations by an
overlay. It appears that CP is four folds higher from one set of parameters to the next, which is consistent with the fact that parameter
m and
N are multiplied by 2 each time we move from Architecture 1 to Architecture 2, and from Architecture 2 to Architecture 3. We see that DSP block utilization is increased by a factor of 4 each time, whereas registers increase by factors
and
respectively; LUTs by
and
respectively, block RAMs by
and
respectively. This shows that the area occupation scales linearly with the CP (a slightly sub-linear scale, one could say). This is very advantageous and can be attributed to the use of the proposed MIN, which scales as
with the number of ports
n.
Table 2 outlines a set of comparable works from the literature. For each reference, the details of the architecture are not necessarily known, and so CP was approximated by associating each DSP block with a FP operation, as that is the case for the proposed overlays.
Table 2 shows that the proposed overlay is one of the must powerful; as none of the reported architectures has even exceeded 50 GFLOPS equivalent, Architectures 2 and 3 do so here. Finally, it is worth mentioning that the largest overlay, namely Architecture 3, offers close to
as much CP as the most powerful architectures reported in
Table 2. This is very promising as more recent FPGAs are more roomier, and should help to reach 1 TFLOP of computing power in the near future.
5.2. Time-Step Exploration
The overlays have been tested for different power converter sizes, by varying the number of states from 5 to 340, or until the time-step exceeded 1
s. The number of inputs and outputs was fixed to 16, which is reasonable for a wide range of applications. A similar approach was adopted in [
11].
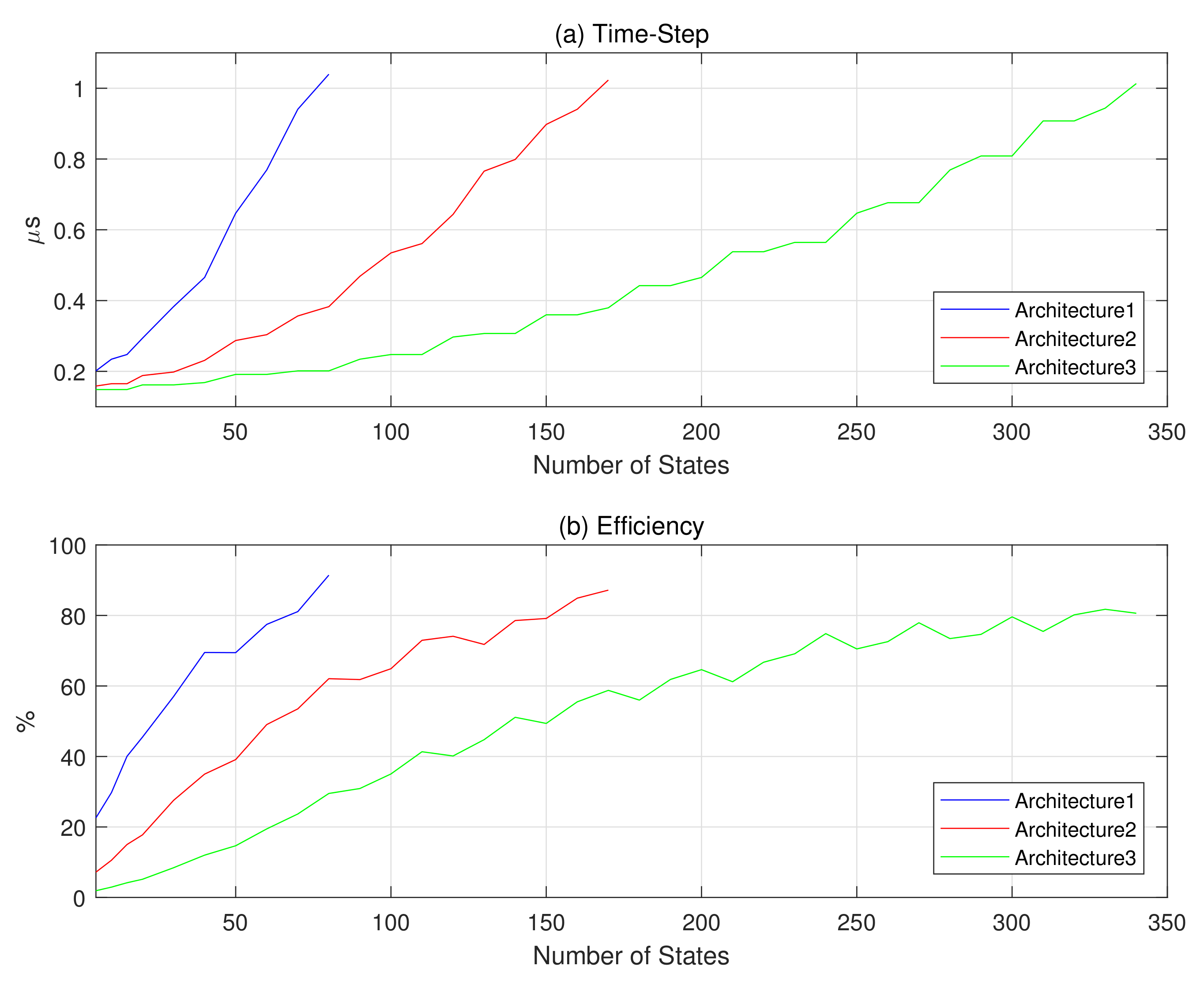
Figure 8a gives for each overlay the simulation time-step as a function of the number of states. The
s limit was chosen as a rule of thumb to accommodate for the high switching frequencies (≥10 kHz) of modern power electronics. It is also a time-step that can not be sustained by CPU-based approaches [
4], and justifies the use of an FPGA.
It is interesting to see that for a given simulation time-step, the number of states that the solver can handle doubles as we move from Architecture 1 to 2, or from Architecture 2 to 3, whereas the cost in hardware is multiplied by 4. This indicates that it is worth tearing the network up whenever it is possible. For example, if a circuit has 240 states, the time-step is 600 ns using Architecture 3. However, if one can manage a decoupling that breaks the network in two sub-circuits of equal size (120 states), them 2 HS of Architecture 2 could be used instead, for half the cost.
Another way to look at this is from an efficiency point of view.
Figure 8b shows the efficiency for each overlay and for the various power converter sizes discussed earlier. The efficiency is defined as the ratio of the computing power deployed to solve a given problem in the time-step reported in
Figure 8a over the peak performance given in
Table 1. In general, the efficiency of an overlay increases with the size of the power converter, although the curve is not monotonic, and slight periodic decreases can be observed. These periodic declines are a side effect of a DP-based overlay, which treats inputs in batches of
m pairs of values. This phenomena is more observable with Architectures 2 and 3 as
m increases. We also see that all the architectures are not very efficient when the circuit is small, although the simulation time-step is very low in those case (≤200 ns). This means that when the power converter is small, the data spends most of the time in the pipeline or the interconnection network. This last observation is a motivation for low latency arithmetic operators. However, as the network equations get bigger, the latency has limited or no effect.
5.3. Open-Loop Test Case 1
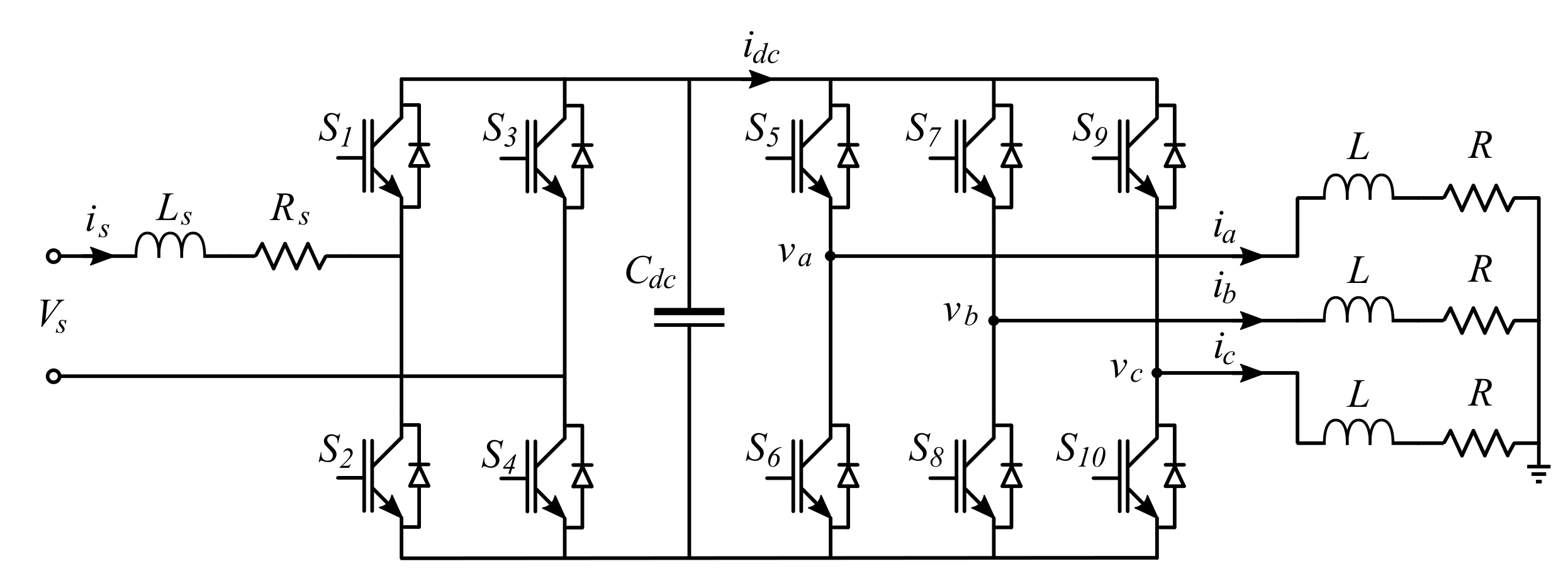
We will be considering two open loop test cases and a closed loop test case. For all these tests, we have chosen the AC–DC–AC power converter depicted in
Figure 9 as a target circuit. The same circuit was considered in [
6]. The circuit parameters are listed in
Table 3. Contrarily to [
6], we consider here a higher switching frequency, namely 10 kHz instead of 2 kHz.
The circuit has been modelled using the ADC model. As previously discussed, the ADC is known to introduced fictitious oscillations and the conductance needs to be tuned [
31]. The tuning was performed using the 2-norm relative error of the load currents [
53]:
where
is the current obtained from the FPGA model, whereas
is the reference obtained using the SimPowerSystem (SPS) Matlab toolbox. We have found that the accuracy of the simulation is less sensitive to the conductances associated with the switches at the rectification than the inversion stage. The values of 0.7 ℧ for the rectifier, and 0.02 ℧ for the inverter side were found to give satisfactory results. Our investigation also showed that the model behaves better when the simulation time-step is small, as evidenced by
Table 4, which gives the 2-norm relative error for a wide range of time-steps. Typically, for real-time simulation purposes, an error below
is required. Hence, a time-step of 300 ns or less is targeted for this test case.
Here are the simulation time-steps for the AC-DC-AC for the various AOs:
Architecture 1: 55 clock cycles, i.e., 200 ns @275 MHz;
Architecture 2: 44 clock cycles, i.e., 160 ns @275 MHz;
Architecture 3: 41 clock cycles, i.e., 149 ns @275 MHz.
From the results above, it appears that Architecture 1 is sufficiently performing to simulate the AC-DC-AC converter.
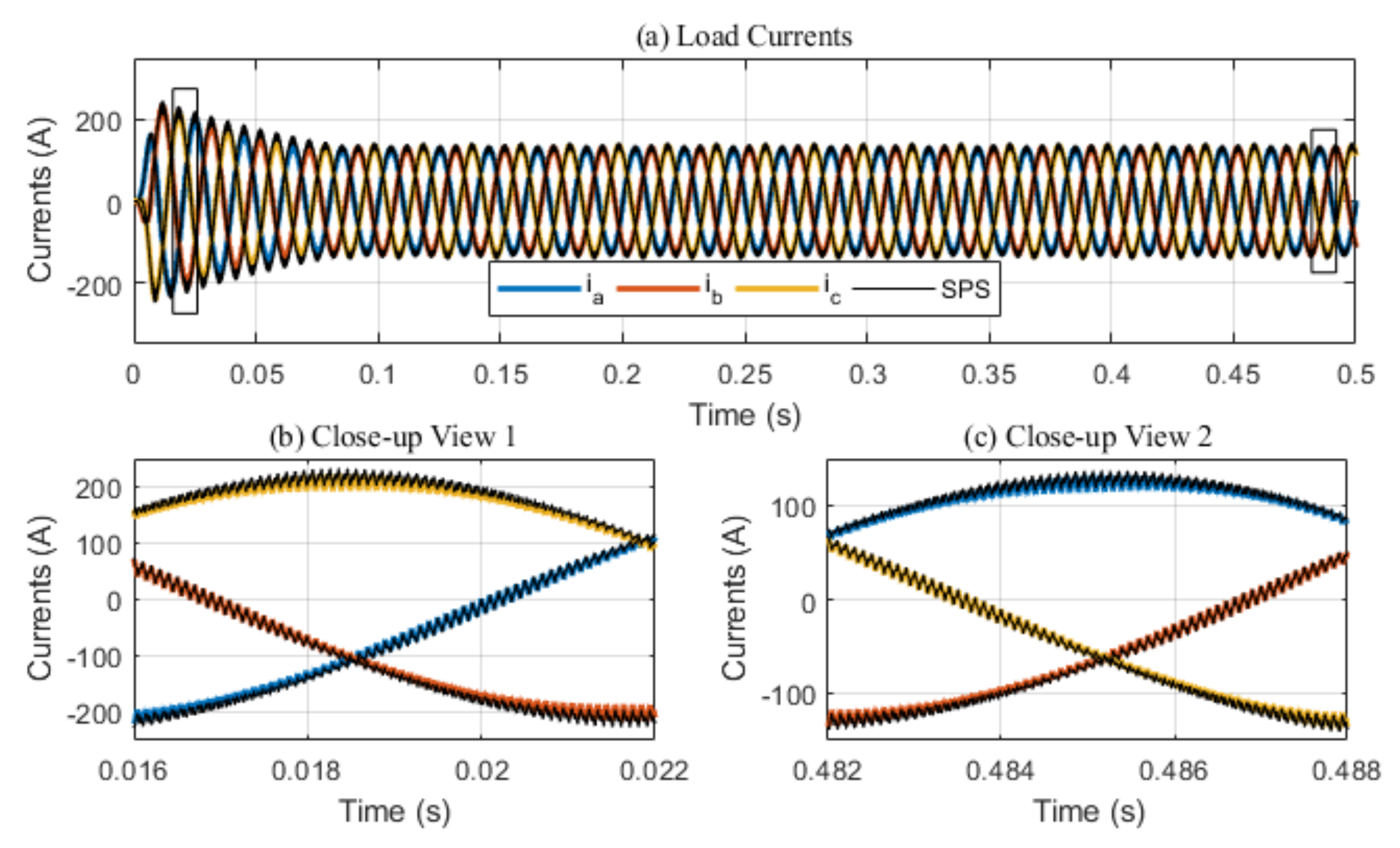
Figure 10a presents the load currents obtained with a time-step of 200 ns using Architecture 1 and over a time span of 0.5 s. Two close-up views illustrated as rectangles in
Figure 10a—that is, a short time following start-up (0.016 s) and during steady state (0.482 s)—are shown in
Figure 10b,c.
Figure 10 shows the good agreement of the FPGA simulation with the SPS reference.
Table 5 compares the total harmonic distortion (THD) of the FPGA results generated a time-step of 200 ns with the THD from the SPS model. Such an evaluation can be useful to determine if the FPGA-based simulation is wrongly introducing new harmonics to the generated signals; or to the contrary, if it reducing its harmonic content. As shown in
Table 5, the SPS reference and the HS show similar THD, are in the same range with a relative error below 3%.
We have also assessed the computational accuracy of the hardware DP operators by comparing the FPGA results to MATLAB code implementing the ADC switch model. The resulting relative errors are calculated for each time-point of the simulation using the Equation (
6):
where
is the matlab results used as a reference. We have found that relative error varies between
and
, as shown in
Figure 10b.
Figure 11b also shows that the relative increases at certain moments during the simulation, over the
threshold. However, by correlating these moments with the current signals from
Figure 10a, it appears that these spikes occur only during zero crossing of the currents, and as such can be neglected.
5.4. Open-Loop Test Case 2
For the second open-loop test case, the test sequence starts with the amplitude of the ac voltage input set to 1800 V. At s, the amplitude is set to 3600 V and maintained at that level for the rest of the remainder of the test. A third test sequence starts at s, when a change in load resistor is applied, moving from to .
Figure 12 presents the load currents for this second test.
Figure 12a identifies the position of the close-up views shown in
Figure 12b–d, each from one test sequence. The results shows the very good agreement between the simulation and the SPS reference under changing working conditions.
5.5. Closed-Loop Test Case
In this section, we assess the performance of the HS in a closed-loop configuration. The digital proportional resonant (PR) controller of
Figure 13 was connected to the system. The controller is formed by a proportional gain
added to a resonant path formed by a gain
and a resonant filter. The filter equation is given by:
The parameters of the controller (filter coefficients and gains) are listed in
Table 6, and were calculated using the process described in [
54]. For this test, the load currents are sampled at 100 ksps, which is typical of low-cost A/D, and accounts for the worst case scenarios.
Figure 14 shows the load currents obtained in close-loop over a time span of 0.5 s. The test is comprised of two test sequences: From
s to
s, the load resistor is
; After
s the load resistor changes to
.
Figure 14a identifies the position of the close-up views shown in
Figure 14b–d, one from each test sequence (resp.
Figure 14b,d) and the load transition instant (
Figure 14c).
The close-up views show that the controller compensates for the change in load and presents very fast response time at transition (so that is not even visible on the figure). Most notably, we see a very good agreement between the model and the SPS reference in all the conditions.
6. Discussion
The methodology presented in this paper is an alternative design approach based on an overlay architecture, and aims at reducing the gap between RTL and HLS. New overlays can be generated by simply changing design parameters at the top level. It is difficult to establish a fair comparison among results in the literature and our approach due to the differences on technologies, type of circuit simulated, numerical representation, etc. However, we used the computing power as metric to assess the capability of a given design and were able to show that the proposed overlays are among the most capable in the literature.
All generated architectures (Architectures 1, 2 and 3) are sub-microsecond capable as shown in
Figure 8. Typically, for a given circuit size, larger overlays result in smaller time-steps, but offer less efficiency. For example, a circuit with 50 states will be simulated at 660 ns (70% efficiency) on Architecture 1, 300 ns (40% efficiency) on Architecture 2, and 200 ns (18% efficiency) on Architecture 3. This is explained in part by the fact that DP inputs are treated in batches, and zero padding is required when the vector size is not an integer multiple of the DP type.
That being said, the main concern of a real-time simulator designer is achieving a small simulation time-step, which is clearly a target met for this work. For example, for the circuit discussed in [
13], a time-step of 300 ns can be reached by Architecture 1, instead of the 500 ns reported in the paper. Also, for the circuit discussed in [
18], Architectures 2 can reach a time-step of 200 ns, instead of the 800 ns reported in the paper.
At the present time, the synthesis of the overlay architecture is done manually, and it is still the work of the developer to determine the set of parameters (DP number and type) to choose from to find the architecture that best suits the circuits size vs. simulation times-step required. That could be improved by a automating the analysis from the circuit specifications (size and target time-step).
The main limitation of this methodology is that the minimum time-step for a given circuit can no be foretold due non-deterministic behavior of the MIN (round robin). Hence, a simulation must be executed to determine the time-step. A fast simulation tool could improve this drawback, for instance by having cycle-accurate models of the overlay.
7. Conclusions
This paper presented a new methodology for the design of programmable HS for the FPGA-based real-time simulation of power converters. The programmability of the HS results from the use of an overlay architecture that separates the execution of an application from the hardware development. The overlay on the other hand is implemented using a latency insensitive design approach that makes all modules auto-synchronized, allows modularity and eases integration. The overlay was implemented using a vendor-agnostic VHDL code, that uses generic parameters to easily scale the hardware solver to the desired performance. To achieve high performance and reach small time-steps, low latency custom floating-point operators that combine a fused datapath approach and a self-alignment format, were used. Three different overlays were generated and implemented on a Xilinx Virtex 7 FPGA, and were shown to achieve high performance while being cost effective. An in-depth analysis of the performances of the overlays has shown that the area occupation scales linearly with the computing power; that the decoupling can achieve higher efficiency at a lower hardware cost; and that the low latency of the arithmetic operators matters only for small circuit sizes. A test AC–DC–AC test case was also considered. A time-step of 200 ns was achieved on the smallest overlay without any decoupling. The test case showed the good agreement of FPGA-based results with a Simulink/Matlab reference and confirmed the computational accuracy achieved by the proposed arithmetic units.
Author Contributions
Conceptualization, F.M. and T.O.-B.; methodology, T.O.-B.; software, F.M.; validation, F.M.; formal analysis, F.M. and T.O.-B.; investigation, F.M. and T.O.-B.; data curation, F.M.; writing—original draft preparation, F.M. and T.O.-B.; writing—review and editing, T.O.-B. and J.P.D.; visualization, F.M. and T.O.-B.; supervision, T.O.-B. and J.P.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations and acronyms are used in this manuscript:
| ADC | Associated Discete Circuit |
| CP | Computing Power |
| DP | Dot Product |
| DSP | Digital Signal Processor |
| FDP | Fused Datapath |
| FLOPS | FLoating-point OPerations per Second |
| FPGA | Field Programmable Gate Array |
| HIL | Hardware-In-the-Loop |
| HLS | High-Level Synthesis |
| HS | Hardware Solver |
| LID | Latency-Insensitive Design |
| LUT | Look-Up Table |
| MANA | Modified-Augmented Nodal Analysis |
| MIN | Multi-stage Interconnection Network |
| MVM | Matrix-Vector Multiplication |
| NTT | Network Tearing Technique |
| OA | Overlay Architecture |
| PEC | Power Electronic Circuit |
| RAM | Random Access Memory |
| RSM | Resistive Switch Model |
| RTL | Register-Transfer Level |
| RTS | Real-Time Simulator |
| SAF | Self-Alignment Format |
| SPS | SimPowerSystem |
| THD | Total Harmonic Distortion |
| VHDL | Very high speed integrated circuit Hardware Description Language |
| XBAR | Crossbar |
References
- Vijay, A.S.; Doolla, S.; Chandorkar, M.C. Real-Time Testing Approaches for Microgrids. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 1356–1376. [Google Scholar] [CrossRef]
- Hollman, J.; Marti, J. Real time network simulation with PC-cluster. IEEE Trans. Power Syst. 2003, 18, 563–569. [Google Scholar] [CrossRef]
- Larose, C.; Guerette, S.; Guay, F.; Nolet, A.; Yamamoto, T.; Enomoto, H.; Kono, Y.; Hasegawa, Y.; Taoka, H. A fully digital real-time power system simulator based on PC-cluster. Math. Comput. Simul. 2003, 63, 151–159. [Google Scholar] [CrossRef]
- Lauss, G.; Faruque, M.O.; Schoder, K.; Dufour, C.; Viehweider, A.; Langston, J. Characteristics and design of power hardware-in-the-loop simulations for electrical power systems. IEEE Trans. Ind. Electron. 2016, 63, 406–417. [Google Scholar] [CrossRef]
- Milton, M.; Benigni, A.; Monti, A. Real-time multi-FPGA simulation of energy conversion systems. IEEE Trans. Energy Convers. 2019, 34, 2198–2208. [Google Scholar] [CrossRef]
- Liu, C.; Bai, H.; Zhuo, S.; Zhang, X.; Ma, R.; Gao, F. Real-time simulation of power electronic systems based on predictive behavior. IEEE Trans. Ind. Electron. 2020, 67, 8044–8053. [Google Scholar] [CrossRef]
- Chalangar, H.; Ould-Bachir, T.; Sheshyekani, K.; Mahseredjian, J. A direct mapped method for accurate modeling and real-time simulation of high switching frequency resonant converters. arXiv 2020, arXiv:2006.04155. [Google Scholar] [CrossRef]
- Vahid, F. Digital Design with RTL Design, Verilog and VHDL; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Navarro, D.; Lucia, O.; Barragan, L.A.; Urriza, I.; Jimenez, O. High-level synthesis for accelerating the FPGA implementation of computationally demanding control algorithms for power converters. IEEE Trans. Ind. Inform. 2013, 9, 1371–1379. [Google Scholar] [CrossRef]
- Jiménez, O.; Lucía, O.; Urriza, I.; Barragan, L.A.; Navarro, D.; Dinavahi, V. Implementation of an FPGA-based online hardware-in-the-loop emulator using high-level synthesis tools for resonant power converters applied to induction heating appliances. IEEE Trans. Ind. Electron. 2015, 62, 2206–2214. [Google Scholar] [CrossRef]
- Montano, F.; Ould-Bachir, T.; David, J.P. An evaluation of a high-level synthesis approach to the FPGA-based submicrosecond real-time simulation of power converters. IEEE Trans. Ind. Electron. 2018, 65, 636–644. [Google Scholar] [CrossRef]
- Carloni, L.P.; McMillan, K.L.; Saldanha, A.; Sangiovanni-Vincentelli, A.L. A methodology for correct-by-construction latency insensitive design. In Proceedings of the 1999 IEEE/ACM International Conference on Computer-Aided Design (ICCAD ’99), San Jose, CA, USA, 7–11 November 1999. [Google Scholar]
- Dagbagi, M.; Hemdani, A.; Idkhajine, L.; Naouar, M.W.; Monmasson, E.; Slama-Belkhodja, I. ADC-based embedded real-time simulator of a power converter implemented in a low-cost FPGA: Application to a fault-tolerant control of a grid-connected voltage-source rectifier. IEEE Trans. Ind. Electron. 2016, 63, 1179–1190. [Google Scholar] [CrossRef]
- Jin, H. Behavior-mode simulation of power electronic circuits. IEEE Trans. Power Electron. 1997, 12, 443–452. [Google Scholar] [CrossRef]
- Hadizadeh, A.; Hashemi, M.; Labbaf, M.; Parniani, M. A matrix-inversion technique for FPGA-based real-time EMT simulation of power converters. IEEE Trans. Ind. Electron. 2019, 66, 1224–1234. [Google Scholar] [CrossRef]
- Blanchette, H.F.; Ould-Bachir, T.; David, J.P. A state-space modeling approach for the FPGA-based real-time simulation of high switching frequency power converters. IEEE Trans. Ind. Electron. 2012, 59, 4555–4567. [Google Scholar] [CrossRef]
- Ould-Bachir, T.; Blanchette, H.F.; Al-Haddad, K. A network tearing technique for FPGA-based real-time simulation of power converters. IEEE Trans. Ind. Electron. 2015, 62, 3409–3418. [Google Scholar]
- Mirzahosseini, R.; Iravani, R. Small time-step FPGA-based real-time simulation of power systems including multiple converters. IEEE Trans. Power Deliv. 2019, 34, 2089–2099. [Google Scholar] [CrossRef]
- Pejovic, P.; Maksimovic, D. A method for fast time-domain simulation of networks with switches. IEEE Trans. Power Electron. 1994, 9, 449–456. [Google Scholar] [CrossRef]
- Matar, M.; Iravani, R. FPGA implementation of the power electronic converter model for real-time simulation of electromagnetic transients. IEEE Trans. Power Deliv. 2010, 25, 852–860. [Google Scholar] [CrossRef]
- Ould-Bachir, T.; Dufour, C.; Bélanger, J.; Mahseredjian, J.; David, J.P. A fully automated reconfigurable calculation engine dedicated to the real-time simulation of high switching frequency power electronic circuits. Math. Comput. Simul. 2013, 91, 167–177. [Google Scholar] [CrossRef]
- Mu, Q.; Liang, J.; Zhou, X.; Li, Y.; Zhang, X. Improved ADC model of voltage-source converters in DC grids. IEEE Trans. Power Electron. 2014, 29, 5738–5748. [Google Scholar] [CrossRef]
- Dufour, C. Method and System for Reducing Power Losses and State-Overshoots in Simulators for Switched Power Electronic Circuit. U.S. Patent 9,665,672, 30 May 2017. [Google Scholar]
- Wang, K.; Xu, J.; Li, G.; Tai, N.; Tong, A.; Hou, J. A generalized associated discrete circuit model of power converters in real-time simulation. IEEE Trans. Power Electron. 2019, 34, 2220–2233. [Google Scholar] [CrossRef]
- Milton, M.; Benigni, A.; Vygoder, M.; Gudex, J.; Cuzner, R. Power electronic system real-time simulation on national instruments FPGA platforms. In Proceedings of the 2019 IEEE Electric Ship Technologies Symposium (ESTS), Washington, DC, USA, 14–16 August 2019; pp. 32–38. [Google Scholar] [CrossRef]
- Milton, M.; Benigni, A. Software and synthesis development libraries for power electronic system real-time simulation. In Proceedings of the IEEE Electric Ship Technologies Symposium (ESTS), Washington, DC, USA, 14–16 August 2019; pp. 368–376. [Google Scholar]
- Cong, J.; Liu, B.; Neuendorffer, S.; Noguera, J.; Vissers, K.; Zhang, Z. High-level synthesis for FPGAs: From prototyping to deployment. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2011, 30, 473–491. [Google Scholar] [CrossRef]
- Reiche, O.; Häublein, K.; Reichenbach, M.; Schmid, M.; Hannig, F.; Teich, J.; Fey, D. Synthesis and optimization of image processing accelerators using domain knowledge. J. Syst. Archit. 2015. [Google Scholar] [CrossRef]
- Inggs, G.; Fleming, S.; Thomas, D.; Luk, W. Is high level synthesis ready for business? A computational finance case study. In Proceedings of the 2014 International Conference on Field-Programmable Technology (FPT), Shanghai, China, 10–12 December 2014; pp. 12–19. [Google Scholar] [CrossRef]
- Mahmood, S.; Shydlouski, P.; Hubner, M. An application specific framework for HLS-based FPGA design of articulated robot inverse kinematics. In Proceedings of the 2018 International Conference on ReConFigurable Computing and FPGAs (ReConFig), Cancun, Mexico, 3–5 December 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Guo, X.; Yuan, J.; Tang, Y.; You, X. Hardware in the loop real-time simulation for the associated discrete circuit modeling optimization method of power converters. Energies 2018, 11, 3237. [Google Scholar] [CrossRef]
- Zamiri, E.; Sanchez, A.; de Castro, A.; Martínez-García, M.S. Comparison of power converter models with losses for hardware-in-the-loop using different numerical formats. Electronics 2019, 8, 1255. [Google Scholar] [CrossRef]
- Sanchez, A.; de Castro, A.; Martínez-García, M.S.; Garrido, J. LOCOFloat: A low-cost floating-point format for FPGAs: Application to HIL simulators. Electronics 2020, 9, 81. [Google Scholar] [CrossRef]
- Langhammer, M. High performance matrix multiply using fused datapath operators. In Proceedings of the 2008 42nd Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 26–29 October 2008; pp. 153–159. [Google Scholar] [CrossRef]
- Ould-Bachir, T.; David, J.P. Self-alignment schemes for the implemention of addition-related floating-point operators. ACM Trans. Reconfigurable Technol. Syst. 2013, 6, 1–21. [Google Scholar] [CrossRef]
- Ould-Bachir, T.; Saad, H.; Dennetière, S.; Mahseredjian, J. CPU/FPGA-based real-time simulation of a two-terminal MMC-HVDC system. IEEE Trans. Power Del. 2017, 32, 647–655. [Google Scholar] [CrossRef]
- Brant, A.; Lemieux, G.G.F. ZUMA: An open FPGA overlay architecture. In Proceedings of the 2012 IEEE 20th International Symposium on Field-Programmable Custom Computing Machines, Toronto, ON, Canada, 29 April–1 May 2012; pp. 93–96. [Google Scholar]
- Shukla, S.; Bergmann, N.W.; Becker, J. QUKU: A two-level reconfigurable architecture. In Proceedings of the IEEE Computer Society Annual Symposium on Emerging VLSI Technologies and Architectures (ISVLSI), Karlsruhe, Germany, 2–3 March 2006; pp. 1–6. [Google Scholar]
- Jain, A.K.; Li, X.; Singhai, P.; Maskell, D.L.; Fahmy, S.A. DeCO: A DSP block based FPGA accelerator overlay with low overhead interconnect. In Proceedings of the 2016 IEEE 24th Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM), Washington, DC, USA, 1–3 May 2016; pp. 1–8. [Google Scholar]
- Ijaz, Q.; Bourennane, E.B.; Bashir, A.K.; Asghar, H. Revisiting the high-performance reconfigurable computing for future datacenters. Future Internet 2020, 12, 64. [Google Scholar] [CrossRef]
- Liu, C.; Ng, H.; So, H.K. QuickDough: A rapid FPGA loop accelerator design framework using soft CGRA overlay. In Proceedings of the 2015 International Conference on Field Programmable Technology (FPT), Queenstown, New Zealand, 7–9 December 2015; pp. 56–63. [Google Scholar]
- Kapre, N.; Gray, J. Hoplite: Building austere overlay NoCs for FPGAs. In Proceedings of the International Conference on Field Programmable Logic and Applications (FPL), London, UK, 2–4 September 2015; pp. 1–8. [Google Scholar]
- Carloni, L.P.; McMillan, K.L.; Sangiovanni-Vincentelli, A.L. Theory of latency-insensitive design. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2001, 20, 1059–1076. [Google Scholar] [CrossRef]
- Abbas, M.; Betz, V. Latency insensitive design styles for FPGAs. In Proceedings of the 2018 28th International Conference on Field Programmable Logic and Applications (FPL), Dublin, Ireland, 27–31 August 2018; pp. 360–3607. [Google Scholar] [CrossRef]
- Mahseredjian, J.; Dennetière, S.; Dubé, L.; Khodabakhchian, B.; Gérin-Lajoie, L. On a new approach for the simulation of transients in power systems. Electr. Power Syst. Res. 2007, 77, 1514–1520. [Google Scholar] [CrossRef]
- Ould-Bachir, T.; Dufour, C.; Bélanger, J.; Mahseredjian, J.; David, J.P. Effective floating-point calculation engines intended for the FPGA-based HIL simulation. In Proceedings of the International Symposium on Industrial Electronics (ISIE), Hangzhou, China, 28–31 May 2012; pp. 1363–1368. [Google Scholar] [CrossRef]
- Cakir, C.; Ho, R.; Lexau, J.; Mai, K. Modeling and design of high-radix on-chip crossbar switches. In Proceedings of the 9th International Symposium on Networks-on-Chip, New York, NY, USA, 1 September 2015; pp. 1–8. [Google Scholar] [CrossRef]
- Goke, L.R.; Lipovski, G.J. Banyan networks for partitioning multiprocessor systems. SIGARCH Comput. Archit. News 1973, 2, 21–28. [Google Scholar] [CrossRef]
- Wu, C.L.; Feng, T.Y. On a class of multistage interconnection networks. IEEE Trans. Comput. 1980, C-29, 694–702. [Google Scholar]
- Montano, F.; Ould-Bachir, T.; Mahseredjian, J.; David, J.P. A low-latency reconfigurable multistage interconnection network. In Proceedings of the IEEE Canadian Conference of Electrical and Computer Engineering (CCECE), Edmonton, AB, Canada, 5–8 May 2019; pp. 1–4. [Google Scholar]
- Agrawal, D.P. Graph theoretical analysis and design of multistage interconnection networks. IEEE Trans. Comput. 1983, C-32, 637–648. [Google Scholar] [CrossRef]
- Milton, M.; Benigni, A.; Bakos, J. System-Level, FPGA-Based, Real-Time Simulation of Ship Power Systems. IEEE Trans. Energy Convers. 2017, 32, 737–747. [Google Scholar] [CrossRef]
- Gautschi, W. Numerical Analysis: An Introduction; Birkhauser: Boston, MA, USA, 1997. [Google Scholar]
- Busarello, T.D.C.; Pomilio, J.A.; Simoes, M.G. Design Procedure for a Digital Proportional-Resonant Current Controller in a Grid Connected Inverter. In Proceedings of the 2018 IEEE 4th Southern Power Electronics Conference (SPEC), Singapore, 10–13 December 2018; pp. 1–8. [Google Scholar] [CrossRef]
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).