Design of a Ka-Band U-Shaped Bandpass Filter with 20-GHz Bandwidth in 0.13-μm BiCMOS Technology
Abstract
1. Introduction
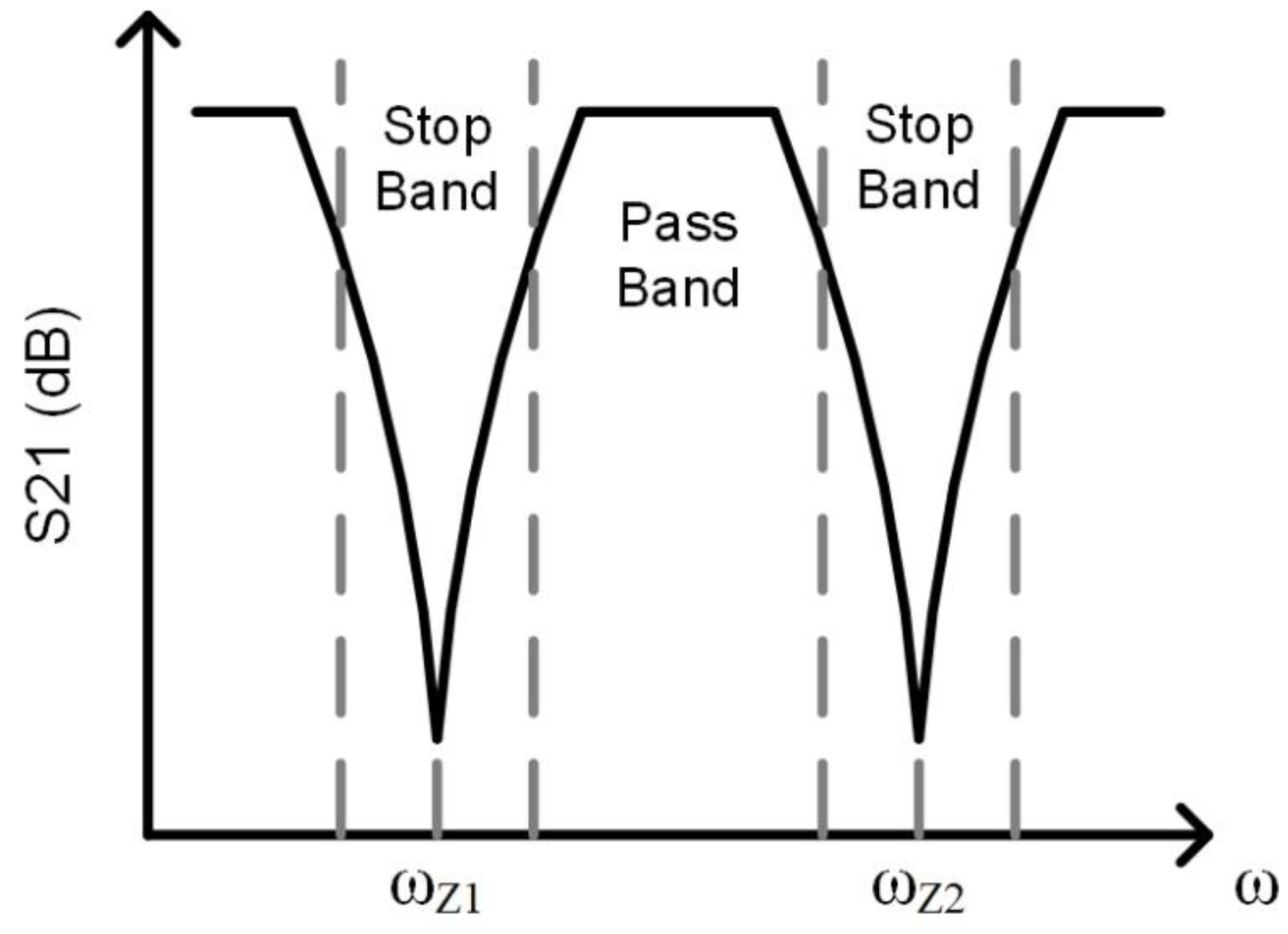
2. Circuit Analysis
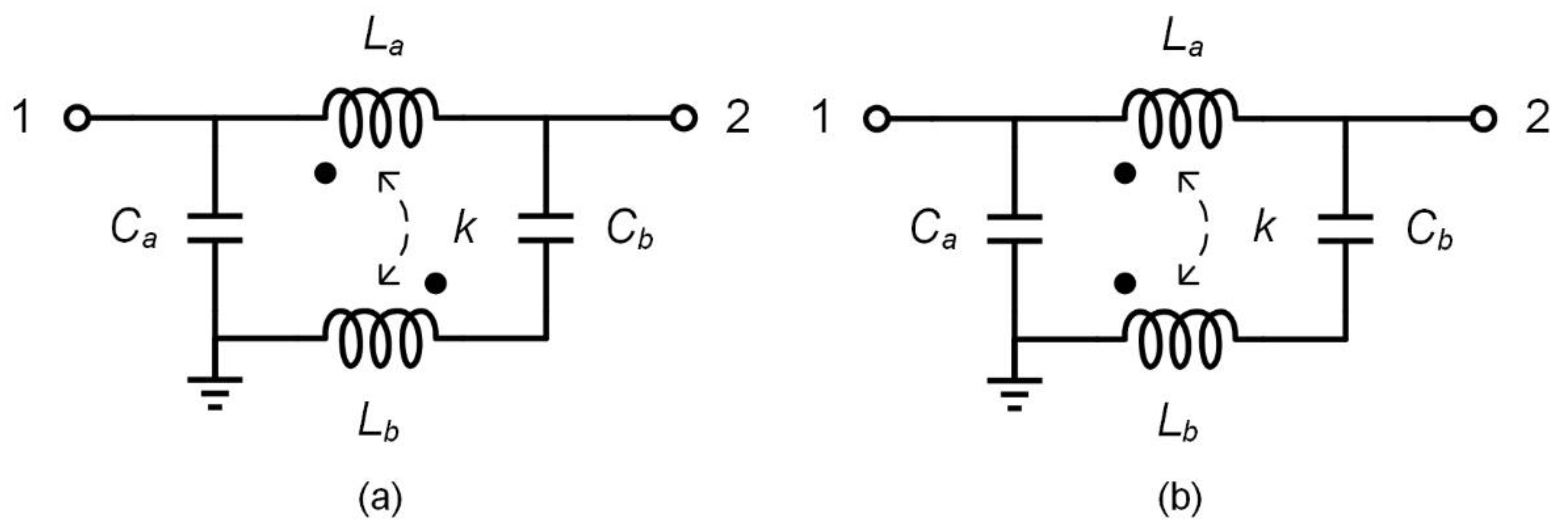
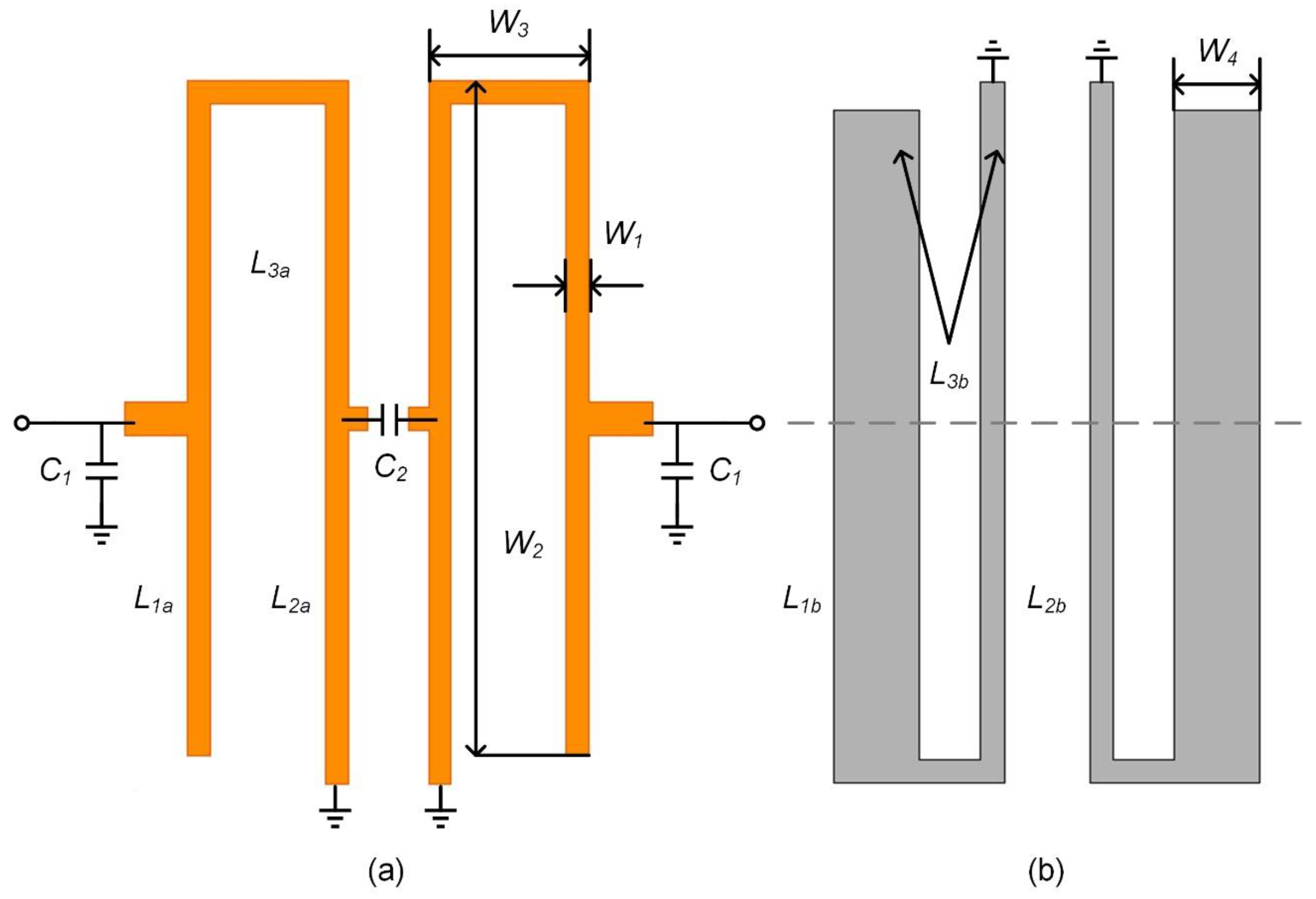
2.1. Analysis of Coupled Transmission Lines Based Resonators
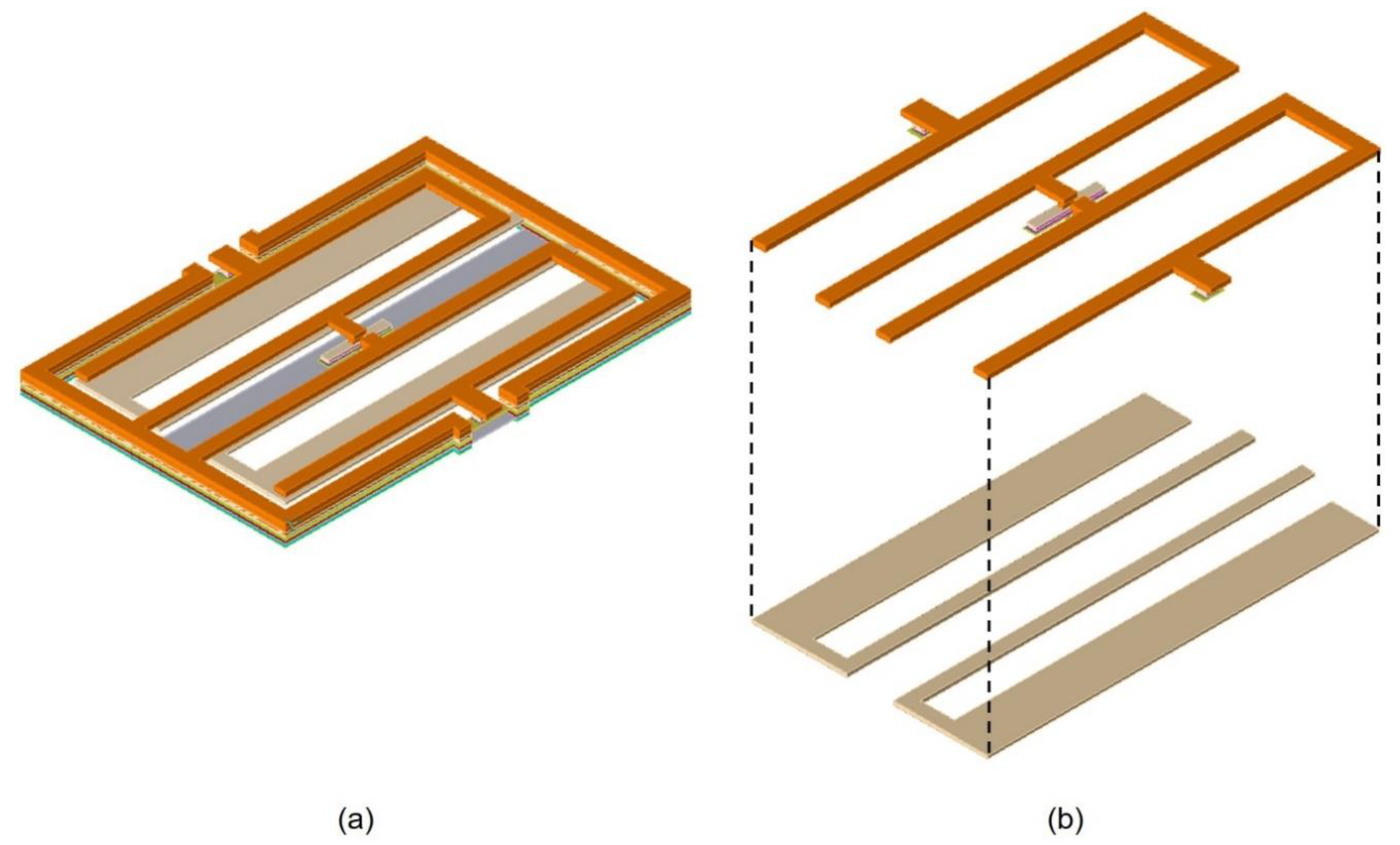
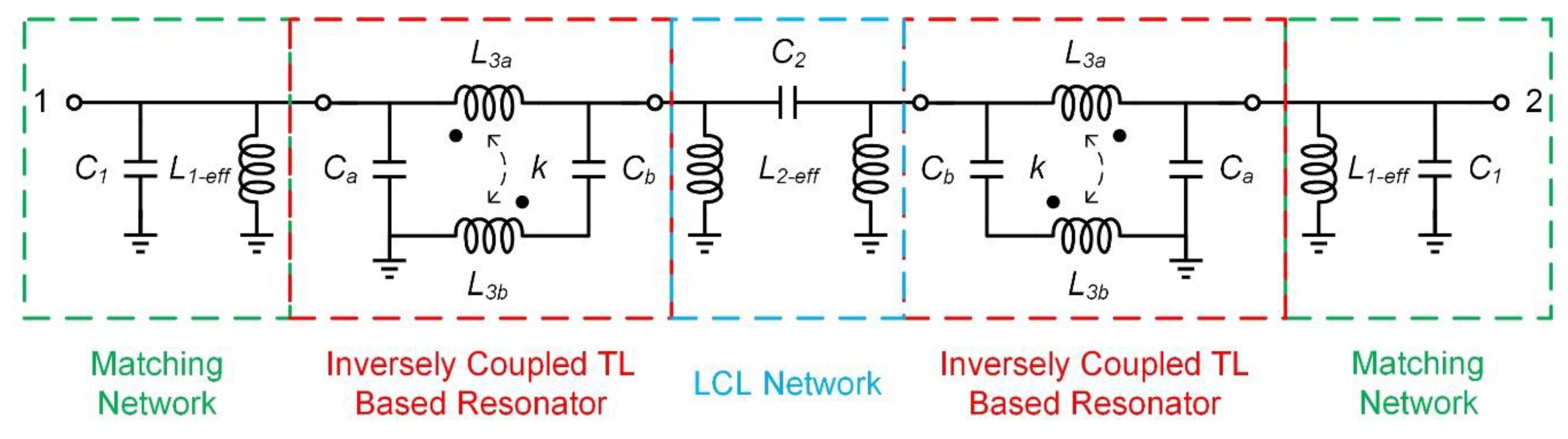
2.2. Proposed Bandpass Filter
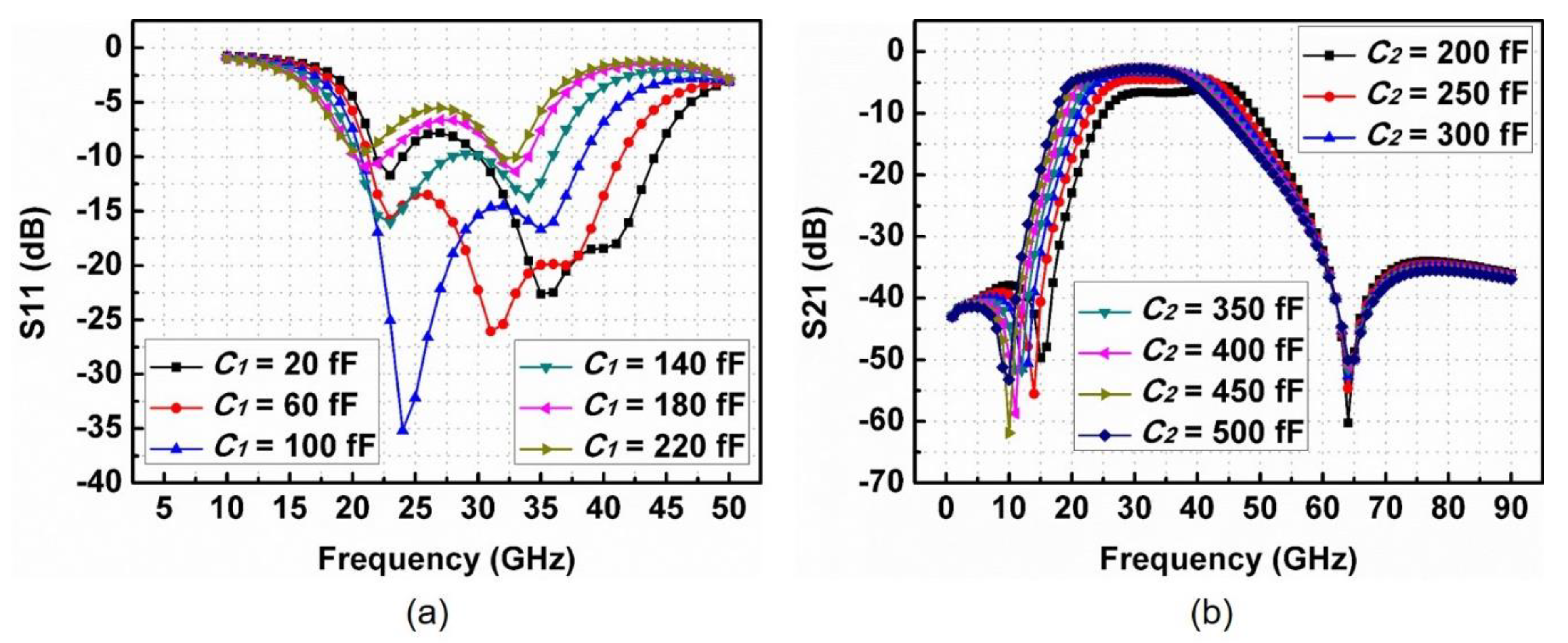
2.3. Case Studies of the Designed BPF
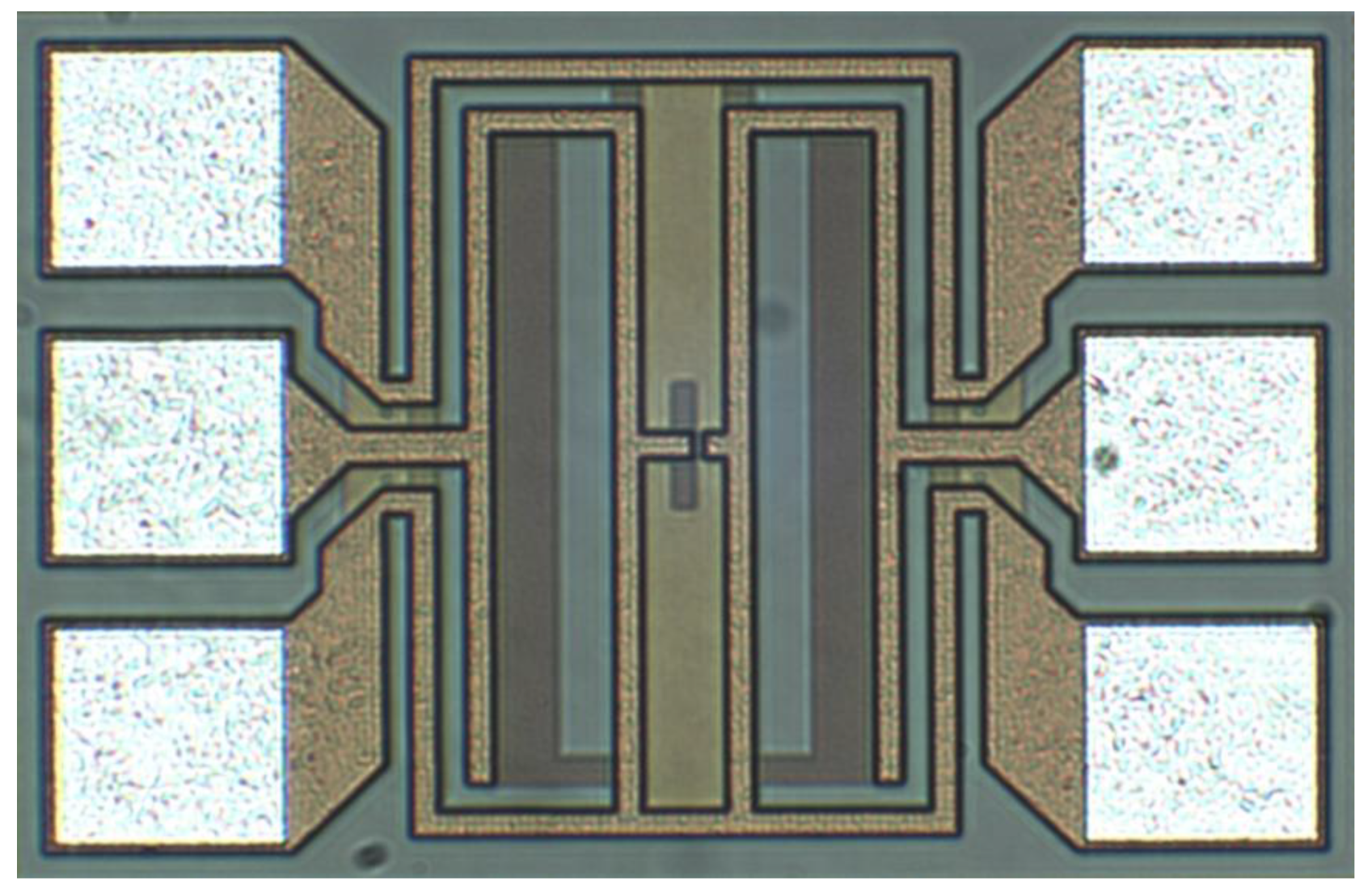
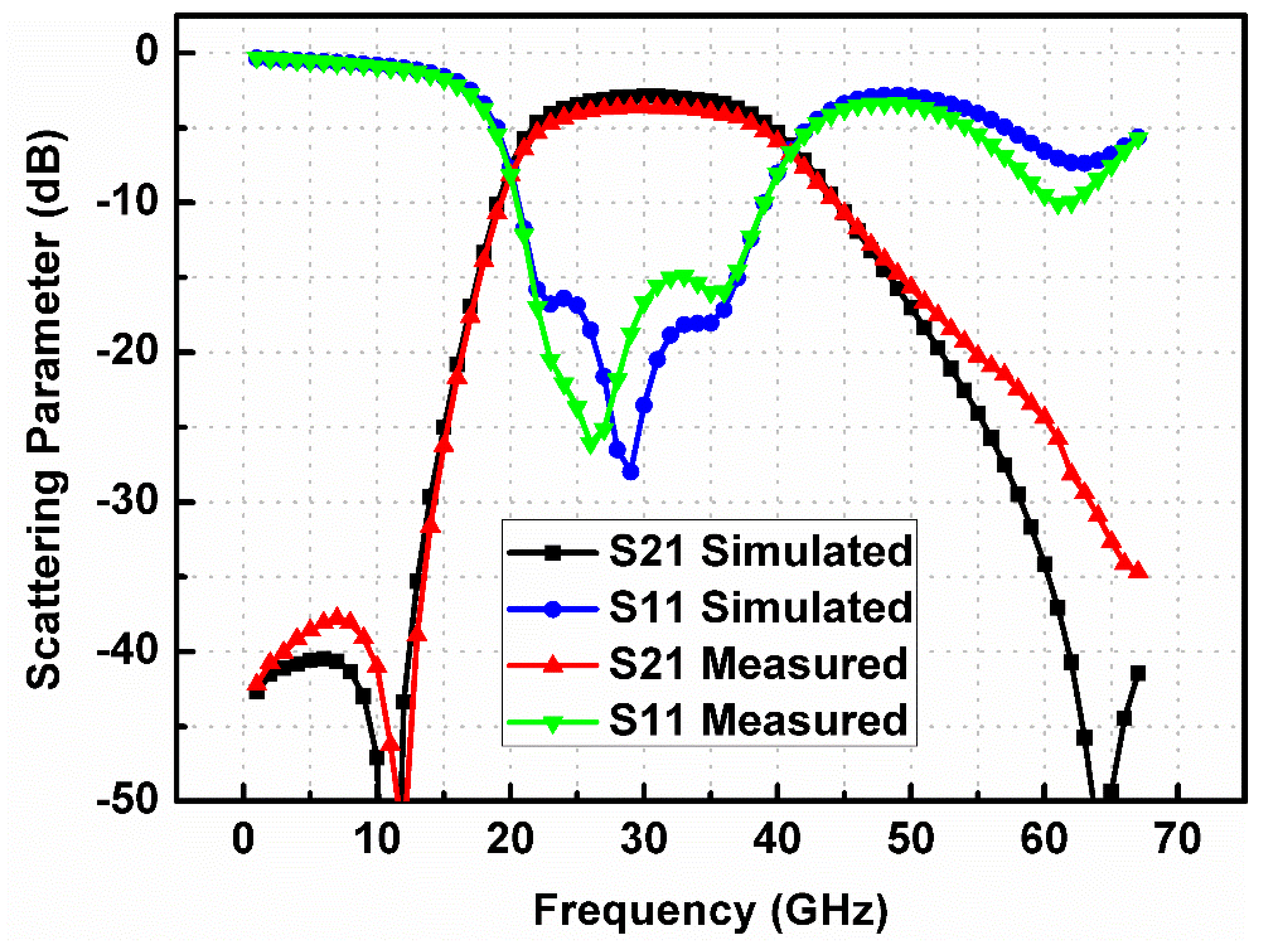
3. Experimental Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, W.; Yao, Z.; Zhang, J.; Kim, E.-S.; Kim, N.-Y. A Compact Dual-Mode Bandpass Filter with High Out-of-Band Suppression Using a Stub-Loaded Resonator Based on the GaAs IPD Process. Electronics 2020, 9, 712. [Google Scholar] [CrossRef]
- Zhang, P.; Liu, L.; Chen, D.; Weng, M.-H.; Yang, R.-Y. Application of a Stub-Loaded Square Ring Resonator for Wideband Bandpass Filter Design. Electronics 2020, 9, 176. [Google Scholar] [CrossRef]
- Weng, M.-H.; Zheng, F.-Z.; Lai, H.-Z.; Liu, S.-K. Compact Ultra-Wideband Bandpass Filters Achieved by Using a Stub-Loaded Stepped Impedance Resonator. Electronics 2020, 9, 209. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, P.; Weng, M.-H.; Tsai, C.-Y.; Yang, R.-Y. A Miniaturized Wideband Bandpass Filter Using Quarter-Wavelength Stepped-Impedance Resonators. Electronics 2019, 8, 1540. [Google Scholar] [CrossRef]
- Hou, Z.; Liu, C.; Zhang, B.; Song, R.; Wu, Z.; Zhang, J.; He, D. Dual-/Tri-Wideband Bandpass Filter with High Selectivity and Adjustable Passband for 5G Mid-Band Mobile Communications. Electronics 2020, 9, 205. [Google Scholar] [CrossRef]
- Chen, W.-Z.; Chen, W.-H.; Hsu, K.-C. Three-Dimensional Fully Symmetric Inductors, Transformer, and Balun in CMOS Technology. IEEE Trans. Circuits Syst. I Regul. Pap. 2007, 54, 1413–1423. [Google Scholar] [CrossRef]
- Chirala, M.; Guan, X.; Nguyen, C. Integrated Multilayered On-Chip Inductors for Compact CMOS RFICs and Their Use in a Miniature Distributed Low-Noise-Amplifier Design for Ultra-Wideband Applications. IEEE Trans. Microw. Theory Tech. 2008, 56, 1783–1789. [Google Scholar] [CrossRef]
- Chang, S.-C.; Chen, Y.; Chang, S.-F.; Jeng, Y.-H.; Wei, C.-L.; Huang, C.-H.; Jeng, C.-P. Compact Millimeter-Wave CMOS Bandpass Filters Using Grounded Pedestal Stepped-Impedance Technique. IEEE Trans. Microw. Theory Tech. 2010, 58, 3850–3858. [Google Scholar] [CrossRef]
- Lin, Y.-S.; Nguyen, V.K. 94-GHz CMOS Power Amplifiers Using Miniature Dual Y-Shaped Combiner With RL Load. IEEE Trans. Circuits Syst. I Regul. Pap. 2017, 64, 1–14. [Google Scholar] [CrossRef]
- Lai, I.C.H.; Kambayashi, Y.; Fujishima, M. 60-GHz CMOS Down-Conversion Mixer with Slow-Wave Matching Transmission Lines. In Proceedings of the 2006 IEEE Asian Solid-State Circuits Conference; Institute of Electrical and Electronics Engineers, China, Hangzhou, 13–15 November 2006. [Google Scholar]
- Franc, A.-L.; Pistono, E.; Meunier, G.; Gloria, D.; Ferrari, P. A Lossy Circuit Model Based on Physical Interpretation for Integrated Shielded Slow-Wave CMOS Coplanar Waveguide Structures. IEEE Trans. Microw. Theory Tech. 2012, 61, 754–763. [Google Scholar] [CrossRef]
- Mahmoud, N.; Barakat, A.; Abdel-Rahman, A.B.; Allam, A.; Pokharel, R.K. Compact Size On-Chip 60 GHz H-Shaped Resonator BPF. IEEE Microw. Wirel. Components Lett. 2016, 26, 681–683. [Google Scholar] [CrossRef]
- El-Hameed, A.S.A.; Barakat, A.; Abdel-Rahman, A.B.; Allam, A.; Pokharel, R.K. Ultracompact 60-GHz CMOS BPF Employing Broadside-Coupled Open-Loop Resonators. IEEE Microw. Wirel. Components Lett. 2017, 27, 818–820. [Google Scholar] [CrossRef]
- Yang, Y.; Zhu, X.; Xue, Q. Design of an Ultracompact On-Chip Bandpass Filter Using Mutual Coupling Technique. IEEE Trans. Electron. Devices 2018, 65, 1087–1093. [Google Scholar] [CrossRef]
- Yang, Y.; Zhu, H.; Zhu, X.; Xue, Q. A Low-Loss Bandpass Filter using Edge-Coupled Resonator With Capacitive Feeding in (Bi)-CMOS Technology. IEEE Electron. Device Lett. 2018, 39, 787–790. [Google Scholar] [CrossRef]
- Zhu, H.; Yang, Y.; Zhu, X.; Sun, Y.; Wong, S.-W. Miniaturized Resonator and Bandpass Filter for Silicon-Based Monolithic Microwave and Millimeter-Wave Integrated Circuits. IEEE Trans. Circuits Syst. I: Regul. Pap. 2018, 65, 4062–4071. [Google Scholar] [CrossRef]
- Hou, Z.J.; Yang, Y.; Zhu, X.; Li, Y.C.; Dutkiewicz, E.; Xue, Q. A Compact and Low-Loss Bandpass Filter Using Self-Coupled Folded-Line Resonator With Capacitive Feeding Technique. IEEE Electron. Device Lett. 2018, 39, 1. [Google Scholar] [CrossRef]
- Zhu, H.; Zhu, X.; Yang, Y.; Xue, Q. Design of Wideband Third-Order Bandpass Filters Using Broadside-Coupled Resonators in 0.13-μm (Bi)-CMOS Technology. IEEE Trans. Microw. Theory Tech. 2018, 66, 5593–5604. [Google Scholar] [CrossRef]
- Li, M.; Yang, Y.; Xu, K.; Zhu, X.; Wong, S.-W. Microwave On-Chip Bandpass Filter Based on Hybrid Coupling Technique. IEEE Trans. Electron. Devices 2018, 65, 5453–5459. [Google Scholar] [CrossRef]
- Bautista, M.G.; Zhu, H.; Zhu, X.; Yang, Y.; Sun, Y.; Dutkiewicz, E. Compact Millimeter-Wave Bandpass Filters Using Quasi-Lumped Elements in 0.13-μm (Bi)-CMOS Technology for 5G Wireless Systems. IEEE Trans. Microw. Theory Tech. 2019, 67, 3064–3073. [Google Scholar] [CrossRef]
- Sun, F.; Zhu, H.; Zhu, X.; Yang, Y.; Sun, Y.; Zhang, X. Design of Millimeter-Wave Bandpass Filters With Broad Bandwidth in Si-Based Technology. IEEE Trans. Electron. Devices 2019, 66, 1174–1181. [Google Scholar] [CrossRef]
- Zhu, H.; Zhu, X.; Yang, Y.; Sun, Y. Design of Miniaturized On-Chip Bandpass Filters Using Inverting-Coupled Inductors in (Bi)-CMOS Technology. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 67, 647–657. [Google Scholar] [CrossRef]
- Sun, F.; Zhu, H.; Zhu, X.; Yang, Y.; Gomez-Garcia, R. Design of On-Chip Millimeter-Wave Bandpass Filters Using Multilayer Patterned-Ground Element in 0.13-μm (Bi)-CMOS Technology. IEEE Trans. Microw. Theory Tech. 2019, 67, 5159–5170. [Google Scholar] [CrossRef]
- Chakraborty, S.; Yang, Y.; Zhu, X.; Sevimli, O.; Xue, Q.; Esselle, K.P.; Heimlich, M. A Broadside-Coupled Meander-Line Resonator in 0.13-μm SiGe Technology for Millimeter-Wave Application. IEEE Electron. Device Lett. 2016, 37, 329–332. [Google Scholar] [CrossRef]
- Zhong, Y.; Yang, Y.; Zhu, X.; Dutkiewicz, E.; Shum, K.M.; Yang, Y. An On-Chip Bandpass Filter Using a Broadside-Coupled Meander Line Resonator with a Defected-Ground Structure. IEEE Electron. Device Lett. 2017, 38, 626–629. [Google Scholar] [CrossRef]
- Weng, M.-H.; Hsu, C.-W.; Lan, S.-W.; Yang, R.-Y. An Ultra-Wideband Bandpass Filter with a Notch Band and Wide Upper Bandstop Performances. Electronics 2019, 8, 1316. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, H.; Hou, Z.J.; Zhu, X.; Dutkiewicz, E.; Yang, Y. Compact On-Chip Bandpass Filter With Improved In-Band Flatness and Stopband Attenuation in 0.13-μm (Bi)-CMOS Technology. IEEE Electron. Device Lett. 2017, 38, 1359–1362. [Google Scholar] [CrossRef]



| Ref. | Center Frequency (GHz) | Insertion Loss (dB) | Fractional Bandwidth (%) | Suppression at Lower Stopband (dB) | Suppression at Upper Stopband (dB) | Area (mm2) |
|---|---|---|---|---|---|---|
| [15] | 35 | 1.7 | 21.9 | N.A. | 20 | 0.039 |
| [17] | 30 | 1.66 | 23.4 | N.A. | 25.4 | 0.009 |
| [18] | 31 | 3.9 | 51 | N.A. | 45 | 0.075 |
| [19] | 26.5 | 3.8 | 50.9 | N.A. | 36 | 0.176 |
| [20] | 29 | 3.5 | 26.7 | 47 | 24 | 0.028 |
| [21] | 26.6 | 2.6 | 70 | 45 | 32 | 0.066 |
| [23] | 31 | 3.2 | 11.4 | >25 | >25 | 0.024 |
| [23] | 31 | 2.7 | 17.5 | >25 | >25 | 0.044 |
| [24] | 31 | 2.4 | 23 | N.A. | 20 | 0.024 |
| [25] | 33 | 2.6 | 18 | N.A. | 44 | 0.038 |
| This Work | 30.8 | 3.6 | 65.6 | 54 | 34.6 | 0.047 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Men, K.; Liu, H.; Yeo, K.S. Design of a Ka-Band U-Shaped Bandpass Filter with 20-GHz Bandwidth in 0.13-μm BiCMOS Technology. Electronics 2020, 9, 1608. https://doi.org/10.3390/electronics9101608
Men K, Liu H, Yeo KS. Design of a Ka-Band U-Shaped Bandpass Filter with 20-GHz Bandwidth in 0.13-μm BiCMOS Technology. Electronics. 2020; 9(10):1608. https://doi.org/10.3390/electronics9101608
Chicago/Turabian StyleMen, Kai, Hang Liu, and Kiat Seng Yeo. 2020. "Design of a Ka-Band U-Shaped Bandpass Filter with 20-GHz Bandwidth in 0.13-μm BiCMOS Technology" Electronics 9, no. 10: 1608. https://doi.org/10.3390/electronics9101608
APA StyleMen, K., Liu, H., & Yeo, K. S. (2020). Design of a Ka-Band U-Shaped Bandpass Filter with 20-GHz Bandwidth in 0.13-μm BiCMOS Technology. Electronics, 9(10), 1608. https://doi.org/10.3390/electronics9101608






