Multistable Memristor Synapse-Based Coupled Bi-Hopfield Neuron Model: Dynamic Analysis, Microcontroller Implementation and Image Encryption

Abstract

The memristor, a revolutionary electronic component, mimics both neural synapses and electromagnetic induction phenomena. Recent study challenges are the development of effective neural models and discovering their dynamics. In this study, we propose a novel Hopfield neural network model leveraging multistable memristors, showcasing its efficacy in encoding biomedical images. We investigate the equilibrium states and dynamic behaviors of our designed model through comprehensive numerical simulations, revealing a rich array of phenomena including periodic orbits, chaotic dynamics, and homogeneous coexisting attractors. The practical realization of our model is achieved using a microcontroller, with experimental results demonstrating strong agreement with theoretical analyses. Furthermore, harnessing the chaos inherent in the neural network, we develop a robust biomedical image encryption technique, validated through rigorous computational performance tests.

1. Introduction

Hopfield networks have emerged as pivotal models in the field of neuroscience owing to their dynamic behavior and efficient structure [1]. These networks provide a valuable framework for exploring human memory mechanisms, with both continuous and discrete models being extensively studied [2,3,4]. Their practicality lies in their ability to capture associative memory processes, making them indispensable tools for investigating cognition and learning [5,6,7,8].

Recent research has exposed an overabundance of intriguing dynamics within memristor-based Hopfield networks. Notably, Sun et al. introduced the concept of boosting dynamics, amplifying the network’s computational capabilities [9]. Investigations into multistability have shed light on the diverse states these networks can exhibit, offering potential avenues for information storage and retrieval [8,10]. Furthermore, the exploration of chaos and multiple scrolls in memristor-cascaded Hopfield networks underscores their rich dynamical repertoire [11,12,13]. Symmetric behaviors observed in bi-neuron Hopfield networks hint at their robustness and potential for pattern recognition tasks [14]. Synapse-coupled architectures have revealed intriguing phenomena such as initial sensitivity, further enhancing our understanding of network dynamics [15]. Additionally, the incorporation of hidden neurons has bolstered the recognition abilities of Hopfield models, paving the way for more sophisticated cognitive architectures capable of long-term memory storage [16,17,18,19].

The attraction of Hopfield networks lies not only in their theoretical elegance but also in their myriad practical applications. Image encryption utilizing Hopfield networks has garnered considerable attention due to its promise of robust security and efficient encoding schemes [20,21,22,23]. Beyond encryption, these networks have found utility in various artificial intelligence applications, harnessing their associative memory properties for tasks such as pattern recognition and optimization [24]. Implementation-wise, the realization of both continuous and discrete Hopfield networks has been achieved using diverse hardware platforms, ranging from STM32 microcontrollers to DSPs and analog circuits [25,26]. In other papers, authors focus on optimizing the realization of Hopfield networks through both analog and digital circuit implementations, aiming to harness the full potential of these networks in practical applications [27,28,29,30].

This paper introduces a novel approach to a coupled bi-Hopfield network, unraveling its dynamics and laying the groundwork for its practical deployment. By delving into the intricacies of network realization and dynamics, we aim to facilitate its application. A comparison of this work related to published ones is made in Table 1.

Table 1. A comparison of this work related to published ones.

References	Number of Neurons	Coexisting Attractors	Implementation	Applications
[8]	3	Yes	Pspice and DSP board	NA
[9]	4	Yes	NA	Image encryption
[10]	3	Yes	Hardware breadboard	NA
[12]	3	Yes	PSIM simulation	NA
[14]	2	Yes	PSIM circuit simulation	NA
This work	2	Yes	Microcontroller	Biomedical image encryption

2. System Description and Mathematical Model

In this work, we consider a multi-state flux-controlled memristor described as

$$\left\{\begin{array}{l}{i}_M=W\left(z\right)V_M=\cos \left(z\right)V_M\\ \dot{z}=\sin \left(z\right)-V_M\end{array}\right.$$

(1)

where $W(z)$ is the memductance.

In order to characterize the elaborated memristor described above, we apply an external force $v_M=A\sin \left(2\pi ft\right)$ into the memristor. The I-V characteristics of the considered memristor are presented in Figure 1. All system parameter values are given in the figure caption. From Figure 1c, we can remark that the hysteresis loop areas retain the same shapes and the characteristic has different states depending on the initial conditions. Thus, the considered memristor is multistable.

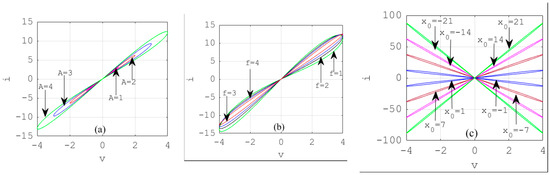
Figure 1. I-V characteristics of the considered memristor. (a) A = 1 V, 2 V, 3 V, 4 V and f = 1 Hz; (b) f = 1 Hz, 2 Hz, 3 Hz, 4 Hz and A = 4 V. The initial state $x_0=0$; (c) initial states: x₀ = ±1, ±7, ±14, ±21, A = 4 V and f = 1 Hz.

We use the multi-state flux-controlled memristor described above to couple two neurons, as shown in Figure 2.

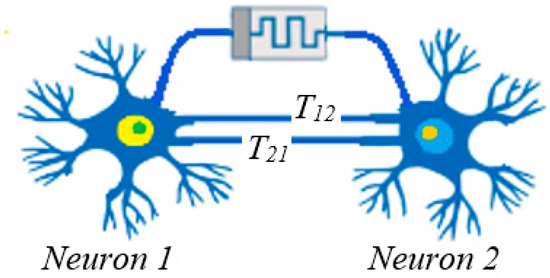
Figure 2. The designed multistable memristor synapse-based coupled bi-Hopfield neuron model.

In Figure 2, an electromagnetic induction current, created by the difference in membrane potential between the two neurons, flows between the two neurons. This electromagnetic induction current influences the two neurons, and the state equations can be expressed as follows

$$\left\{\begin{array}{l}\dot{x}=-x+T_{11}f\left(x\right)+T_{12}f(y)+kW(\phi )V_M\\ \dot{y}=-y-T_{21}f\left(x\right)+T_{22}f(y)-kW(\phi )V_M\\ \dot{z}=V_M-\phi \end{array}\right.$$

(2)

The parameters $T_{11}$, $T_{12}$, $T_{21}$, and $T_{22}$ represent the synaptic connection weights considering constant. $\rho$ represents the memristor coupling strength parameter, $f\left(x\right)$ and $f\left(y\right)$ are applied to activate the neurons and expressed as

$$f\left(u\right)=\tanh \left(2u-3\right)+\tanh \left(2u+3\right)-2\tanh \left(2u\right)$$

(3)

By taking a synaptic weight matrix as follows

$$T=\left(\begin{array}{cc}{T}_{11}& T_{12}\\ T_{21}& T_{22}\end{array}\right)=\left(\begin{array}{cc}0& \gamma \\ -1& 0\end{array}\right)$$

(4)

We obtain the multistable memristor synapse-based coupled bi-Hopfield neuron model as

$$\left\{\begin{array}{l}\dot{x}=-x+\gamma f\left(y\right)+\rho \cos \left(z\right)\left(y-x\right)\\ \dot{y}=-y-f\left(x\right)-\rho \cos \left(z\right)\left(y-x\right)\\ \dot{z}=\sin \left(z\right)-\left(y-x\right)\end{array}\right.$$

(5)

In system (5), the auto-connection weights for the two Hopfield neurons are set to zero in order to simplify the final model.

3. Equilibrium Analysis

The equilibrium can be expressed as

$$P=\left(x_0, y_0, z_0\right)$$

(6)

in which $z_0={\sin }^{-1}\left(y_0-x_0\right)$, $x_0$ and $y_0$ are solved using the following equations

$$\left\{\begin{array}{l}{H}_1\left(x_0, y_0\right)=-x_0+\gamma f\left(y_0\right)+\rho \left(y_0-x_0\right)\sqrt{1-{\left(y_0-x_0\right)}^2}\\ H_2\left(x_0, y_0\right)=-y_0-f\left(x_0\right)-\rho \left(y_0-x_0\right)\sqrt{1-{\left(y_0-x_0\right)}^2}\end{array}\right.$$

(7)

where $f\left(x_0\right)$ and $f\left(y_0\right)$ are the functions used to activate the neurons.

The Jacobin matrix can be calculated at $P$ as

$$J_P=\left[\begin{array}{ccc}-1-\rho \cos \left(z_0\right)& \gamma f^{\prime }\left(y_0\right)+\rho \cos \left(z_0\right)& -\rho \sin \left(z_0\right)\left(y_0-x_0\right)\\ \rho \cos \left(z_0\right)-f^{\prime }\left(x_0\right)& -1-\rho \cos \left(z_0\right)& \rho \sin \left(z_0\right)\left(y_0-x_0\right)\\ 1& -1& \cos \left(z_0\right)\end{array}\right]$$

(8)

in which $f^{\prime }\left(u\right)=2\left({\mathrm{sech}}^2\left(2u-3\right)+{\mathrm{sech}}^2\left(2u+3\right)-2{\mathrm{sech}}^2\left(2u\right)\right)$.

According to Equation (7), the features of the equilibrium states $P$ are studied based on the system parameters $\gamma$ and $\rho$. The two functions $H_1\left(x_0, y_0\right)$ and $H_2\left(x_0, y_0\right)$ given in Equation (7) with the parameters $\left(\gamma , \rho \right)=\left(0.7, 1\right)$ are plotted in Figure 3. The values of $x_0$ and $y_0$ are determined at the intersections of the two function curves.

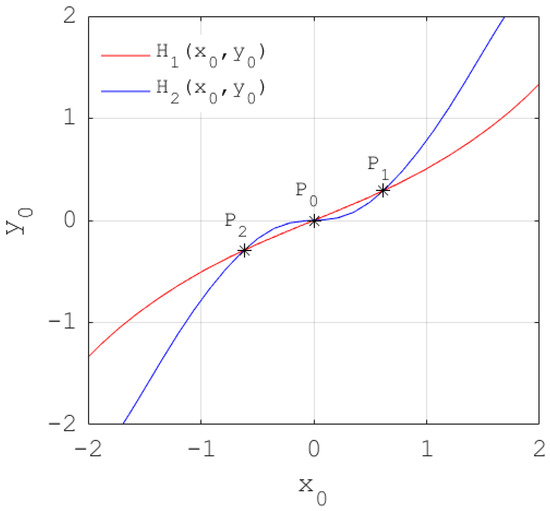
Figure 3. Determination of the equilibrium states $x_0$ and $y_0$, which are indicated by the intersections of two function curves.

From Figure 3, system (5) has three equilibrium states for $\left(\gamma , \rho \right)=\left(0.7, 1\right)$. The analysis of these equilibrium states is presented in Table 2.

Table 2. Equilibria and their stability.

ρ	γ	Equilibria	Eigenvalues	Stability
1	0.7	$P_0=\left(0, 0, 0\right)$	$1, -1.1\pm j3.2941$	Unstable saddle point (USP)
		$P_{1, 2}=\left(\pm 0.62, \pm 0.29, \mp 0.3363\right)$	$-1.0927\pm j2.3594, 0.9406$	Unstable saddle point (USP)

From the results in Table 2, we can conclude that the equilibrium points are unstable saddle points for the considered values of the system parameters $\gamma$ and $\rho$.

4. Numerical Study

Bifurcation diagrams associated with corresponding Lyapunov exponents as a function of system parameters, as well as initial states, phase portraits, and basin of attraction, are computed to illustrate the complicated behaviors of the model under consideration.

Figure 4 shows the bifurcation diagram and Lyapunov exponents versus $\rho$ computed from 1 to 2, for $\gamma =0.7$ and $\left(x(0), y(0), z(0)\right)=\left(0, {10}^{-9}, 0\right)$.

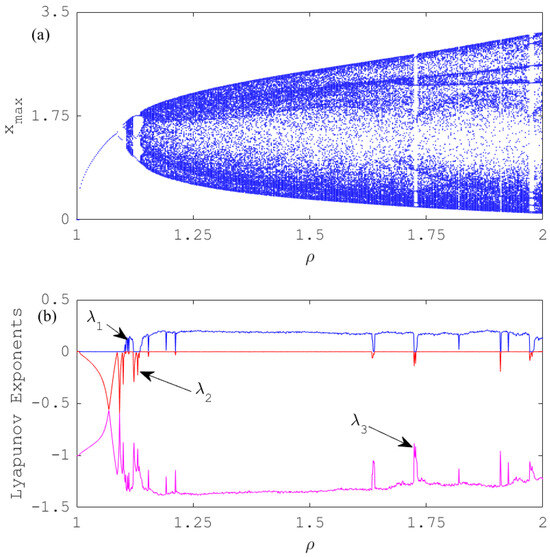
Figure 4. Influence of $\rho$ on the behaviors of the model: (a) bifurcation diagram (b) Lyapunov exponents for $\gamma =0.7$ and $\left(x(0), y(0), z(0)\right)=\left(0, {10}^{-9}, 0\right)$.

Figure 4 reveals that chaos occurs in the considered model through period-doubling bifurcation. We can identify some windows indicating periodic oscillations intercalated by chaos. The route to chaos is confirmed by plotting phase spaces presented in Figure 5, for $\gamma =0.7$ and diverse selected values of $\rho$.

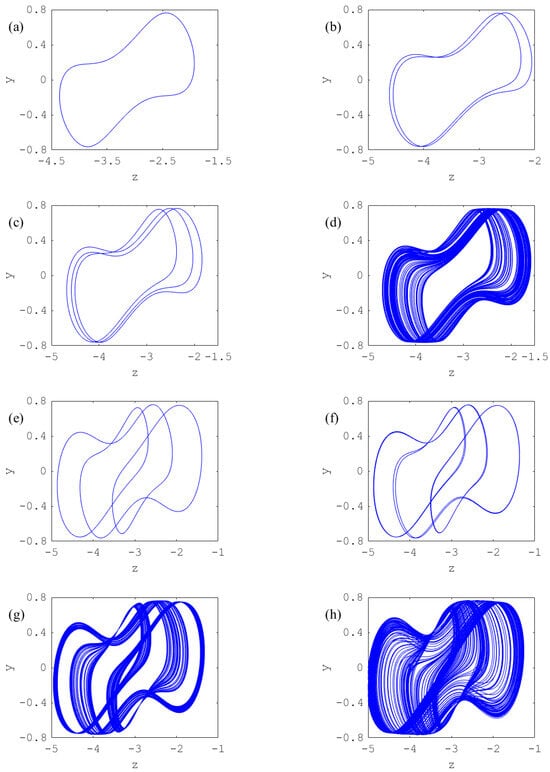
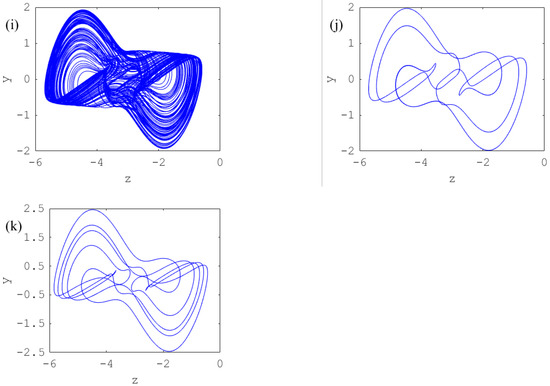
Figure 5. Phase spaces confirming the occurrence of chaos in the system for $\gamma =0.7$, $\left(x(0), y(0), z(0)\right)=\left(0, {10}^{-9}, 0\right)$ and diverse selected values of $\rho$: (a) period-1 for $\rho =1.087$, (b) period-2 for $\rho =1.1$, (c) period-3 for $\rho =1.105$, (d) chaos for $\rho =1.107$, (e) period-3 for $\rho =1.13$, (f) period-6 for $\rho =1.134$, (g) chaos for $\rho =1.14$, (h) chaos for $\rho =1.15$, (i) chaos for $\rho =1.4$, (j) period-3 for $\rho =1.728$, (k) period-6 for $\rho =1.972$.

It is very clear from Figure 5 that the system in the study displays complex and abundant patterns.

The impact of the initial state $z\left(0\right)$ associated with the memristor on the comportments of the model is shown in Figure 6, for $\gamma =0.7$ and $\rho =1.97$.

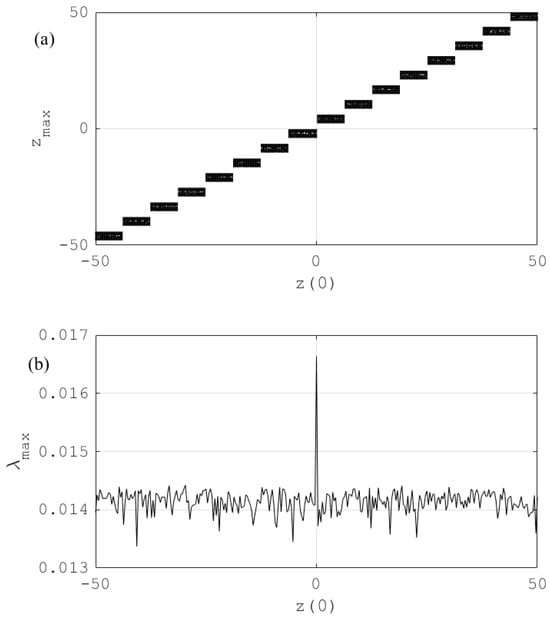
Figure 6. Impact of the initial state $z\left(0\right)$ on the comportment of the model: (a) bifurcation diagram and (b) maximum Lyapunov exponent, for $\gamma =0.7$, $\rho =1.97$, and $\left(x(0), y(0), z(0)\right)=\left(0, {10}^{-9}, z(0)\right)$.

The initial state $z\left(0\right)$ considerably impacts the dynamic behavior of the considered model (see Figure 6).

Phase portraits and basin of attraction are shown in Figure 7 and Figure 8 in order to support the result carried out in Figure 6, for $\gamma =0.7$ and $\rho =1.97$.

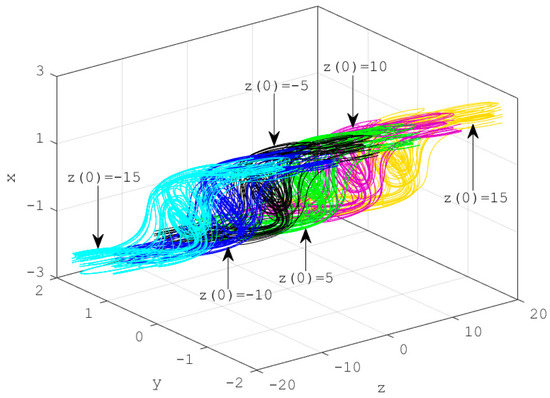
Figure 7. Several coexisting chaotic attractors at diverse positions for several value initial states $z\left(0\right)$ with $\gamma =0.7$, $\rho =1.97$, and $\left(x(0), y(0)\right)=\left(0, {10}^{-9}\right)$.

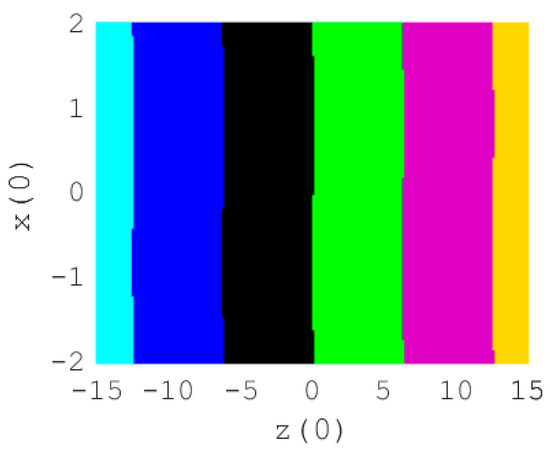
Figure 8. Cross section of the basin of attraction for $\gamma =0.7$, $\rho =1.97$, and $\left(x(0), y(0)\right)=\left(0, {10}^{-9}\right)$. Each domain of initial states leads to a color representing a particular phase space.

5. Experimental Study

We carried out here a microcontroller implementation of the system. Implementing chaotic systems using microcontrollers has many advantages over using electronic components. These advantages include high computing performances, excellent precision, flexibility and stability, and the facility to manage the system parameters conveniently [25,26,27,28,29]. In this work, we use an Arduino Due microcontroller card, which is constructed with an Atmel SAM3X8E ARM Cortex-M3 processor having a clock frequency of 84 MHz. Compared with other boards, this card has the advantage of incorporating two digital-to-analog converters, which makes it easy to implement chaotic systems. The main steps, which describe the implementation procedure of the elaborated multistable memristor synapse-based coupled bi-Hopfield neuron model, are shown in Figure 9.

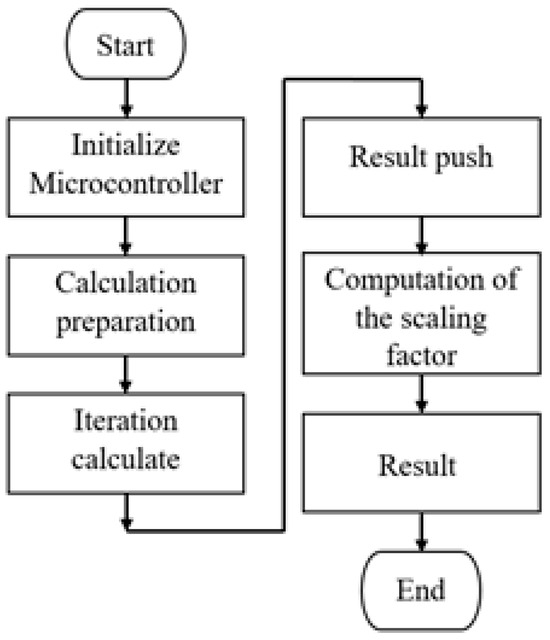
Figure 9. Implementation procedure of the elaborated multistable memristor synapse-based coupled bi-Hopfield neuron model.

The microcontroller implements the discrete form of system (5) using the Runge–Kutta algorithm with a fixed iteration step size of 0.01. The model parameters and initial conditions are chosen as they have identical values to those used in the numerical simulations. The hardware implementation devices are shown in Figure 10.

Figure 10. Hardware implementation devices. The dual-channel digital oscilloscope displays a chaotic attractor in the plane ($V_z-V_y$) for $\gamma =0.7$, $\rho =1.15$, and $\left(x\left(0\right), y\left(0\right), z\left(0\right)\right)=\left(0, {10}^{-9}, 0\right)$.

Figure 11 shows the route to chaos for a fixed value of $\gamma$ and specific values of the coupling strength $\rho$.

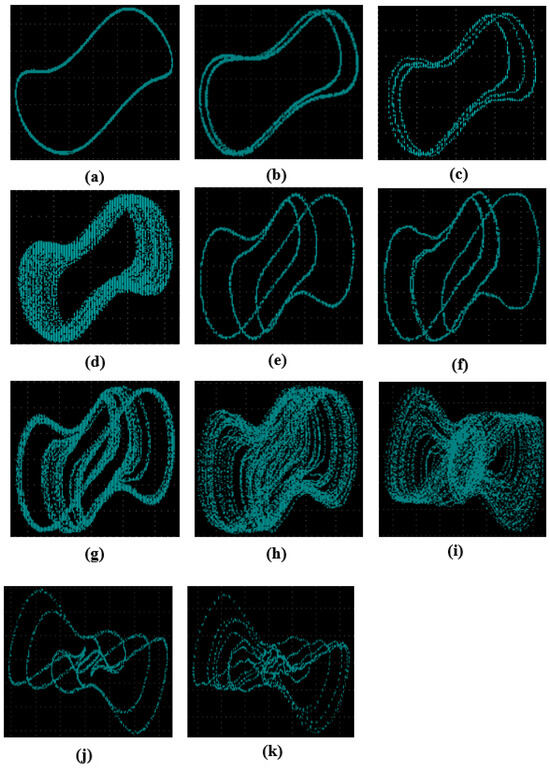
Figure 11. Phase portraits for $\gamma =0.7$ and specific values of the coupling strength $\rho$: (a) period-1 for $\rho =1.087$, (b) period-2 for $\rho =1.1$, (c) period-3 for $\rho =1.105$, (d) chaos for $\rho =1.107$, (e) period-3 for $\rho =1.13$, (f) period-6 for $\rho =1.134$, (g) chaos for $\rho =1.14$, (h) chaos for $\rho =1.15$, (i) chaos for $\rho =1.4$, (j) period-3 for $\rho =1.728$, (k) period-6 for $\rho =1.972$, and $\left(x\left(0\right), y\left(0\right), z\left(0\right)\right)=\left(0, {10}^{-9}, 0\right)$.

The results carried out from the microcontroller implementation (see Figure 11) are very similar to those obtained from numerical simulations (see Figure 5). This confirms that the Arduino Due microcontroller card is able to investigate the complete dynamics of the designed multistable memristor synapse-based coupled bi-Hopfield neuron model.

6. Application of the Designed Model for Biomedical Encryption Image

We exploit here the abundant dynamics of the elaborated model for image encryption.

6.1. Designing of Encryption Algorithm

Figure 12 presents the encryption algorithm.

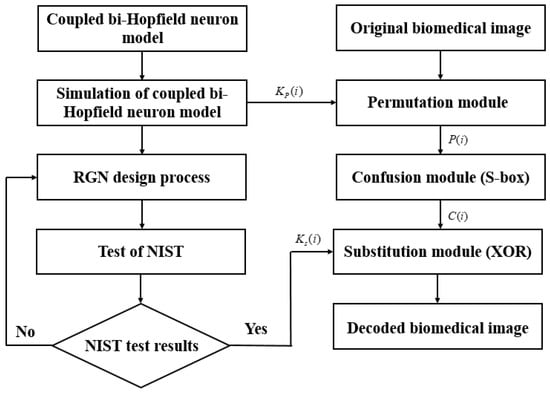
Figure 12. Complete diagram of the encryption algorithm.

There are five steps in the algorithm:

(1)

Integrate the chaotic system and carry out the public key $K_P(i)$;

(2)

Generate and test the random bits to construct the key $K_S(i)$;

(3)

In the layer of permutation, build the permuted image $P(i)$ with the initial image and the public key $K_P(i)$;

(4)

Introduce the permuted image into the layer of confusion, which works with the S-box function to construct the confused image $C(i)$;

(5)

Using a substitution operation (XOR), combine the image resulting from the confusion layer $C(i)$ with the key $K_S(i)$ to obtain the masked image.

For the decryption process, we apply the reverse of all operations realized during the encryption procedure.

The NIST test results are shown in Table 3.

Table 3. NIST test results.

Name of the Considered Test	p-Value			Test Results
	x	y	z
Frequency	0.17360	0.50790	0.49918	Validated
Block-frequency	0.18189	0.14409	0.18861	Validated
Runs	0.96599	0.15381	0.21472	Validated
Longest runs of ones	0.63350	0.65267	0.74264	Validated
Rank	0.49885	0.49928	0.44669	Validated
DFT	0.79219	0.30442	0.25890	Validated
No overlapping templates	0.59850	0.07790	0.04530	Validated
Overlapping templates	0.28548	0.37728	0.79657	Validated
Universal	0.76180	0.99902	0.35890	Validated
Linear complexity	0.79980	0.22241	0.94489	Validated
Serial test 1	0.81870	0.68489	0.22395	Validated
Serial test 2	0.34090	0.70814	0.11562	Validated
Approximate entropy	0.43162	0.72734	0.61123	Validated
Cumulative sums (forward)	0.26100	0.82875	0.45276	Validated
Random excursions x = 1	0.51045	0.57860	0.35246	Validated
Random excursions variant x = 1	0.96169	0.59897	0.84990	Validated

As all p-values in Table 3 are greater than the standard value 0.001, all NIST tests are validated.

6.2. Numerical Results

The numerical results are carried out in MATLAB16b environment. We use biomedical images of size 256 × 256 for cerebrovascular accident, pulmonary fibrosis, and lung cancer. Applying the encryption and decryption algorithm described below, the results for encrypted and decrypted biomedical images are shown in Figure 13.

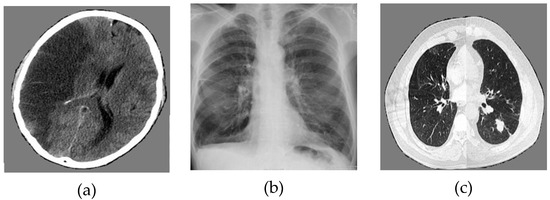
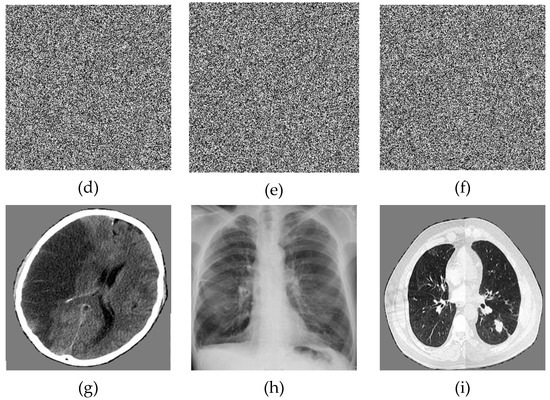
Figure 13. Numerical results: (a) initial image of cerebrovascular accident, (b) initial image of pulmonary fibrosis, (c) initial image of lung cancer, (d) encrypted image of cerebrovascular accident, (e) encrypted image of pulmonary fibrosis, (f) encrypted image of lung cancer, (g) decrypted image of cerebrovascular accident, (h) decrypted image of pulmonary fibrosis, (i) decrypted image of lung cancer.

We can see that the unencrypted biomedical images (see Figure 13a–c) are very different from those obtained after the decryption process (see Figure 13d–f). Thus, the algorithm is efficient.

6.3. Analysis of Performances of the Elaborated Biomedical Image Encryption Method

6.3.1. Analysis of Key Space and Key Sensibility

To withstand exhaustive attacks, the key space of the cryptosystem must exceed $2^{100}$ [31]. Our elaborated multistable memristor synapse-based coupled bi-Hopfield neuron model involves two constant system parameters and three initial states. For a precision of ${10}^{17}$, the key space is ${10}^{17\times 3}={10}^{85}$, which exceeds the required value. This confirms that the developed algorithm will be able to withstand exhaustive attacks.

The key sensitivity is analyzed by introducing a small perturbation of ${10}^{17}$ to all parameters of the system before the decryption of the sending image (cerebrovascular accident), as reported in Figure 14.

Figure 14. Results of slight key modification: (a) correct keys, (b) $\gamma +{10}^{-17}$, (c) $\rho +{10}^{-17}$, (d) $x(0)+{10}^{-17}$, (e) $y(0)+{10}^{-17}$, and (f) $z(0)+{10}^{-17}$.

Looking at Figure 14, the key changes ${10}^{17}$, generating a high impact on the decrypted image. The initial image can no longer be received after a small key modification. We can conclude that this algorithm is very sensitive to secret keys.

6.3.2. Information Entropy

The entropy is examined using its expression [32]

$$H\left(m\right)=-{\displaystyle \sum _{i=0}^{N}P(m_i){\log }_2}P(m_i)$$

(9)

in which $N$ and $P(m_i)$ refer to the total number and frequency of occurrences of symbol $m_i$, respectively.

The entropy is reported in Table 4, and its value for encrypted images approaches the standard value 8, which means that the encrypted image is more random. This confirms the good performance of the scheme.

Table 4. Information entropies of initial images and their corresponding encrypted versions.

Entropy	Gray-Scale Images
	Cerebrovascular Accident	Pulmonary Fibrosis	Lung Cancer
Initial image	5.9029	7.3089	6.0119
Encrypted version	7.9972	7.9974	7.9973

6.3.3. Correlation Analysis

The correlation coefficient (CC) is calculated using its expression [33]

$$\left\{\begin{array}{l}E\left(x\right)=\frac{1}{N}{\displaystyle \sum _{i=1}^N{x}_i}\\ D\left(x\right)=\frac{1}{N}{\displaystyle \sum _{i=1}^N{\left(x_i-E\left(x\right)\right)}^2}\\ \mathrm{cov}\left(x,y\right)=\frac{1}{N}{\displaystyle \sum _{i=1}^N\left(x_i-E\left(x\right)\right)\left(y_i-E\left(y\right)\right)}\\ r_{xy}=\frac{\mathrm{cov}\left(x,y\right)}{\sqrt{D\left(x\right)}\sqrt{D\left(y\right)}}\end{array}\right.$$

(10)

in which x and y are the pixel values. The CC is reported in Table 5.

Table 5. Computed correlation coefficients.

Direction	Gray-Scale Images
	Initial Image			Encrypted Version
	Cerebrovascular Accident	Pulmonary Fibrosis	Lung Cancer	Cerebrovascular Accident	Pulmonary Fibrosis	Lung Cancer
Horizontal	0.9440	0.9923	0.9434	0.0048	−0.0019	−0.0024
Vertical	0.9487	0.9927	0.9668	0.0022	−0.0020	−0.0034
Diagonal	0.9004	0.9868	0.9255	0.0064	−0.0026	−0.0025
Average	0.9310	0.9906	0.9452	0.0045	−0.0022	−0.0027

Looking at the values in Table 5, we can remark that the values of correlation coefficient in horizontal, vertical, and diagonal directions of the image approach the standard values (i.e., CC is 1 for initial biomedical images and 0 for their encrypted versions). This means that the correlation coefficients of the initial image are highly correlated and those for the encrypted image are uncorrelated. In conclusion, the designed encryption algorithm will resist statistical aggressions.

6.3.4. Histogram Study

The histogram should dispose uniformly for an encrypted image and randomly for an unencrypted one. Figure 15 illustrates the distribution of the pixels of biomedical images.

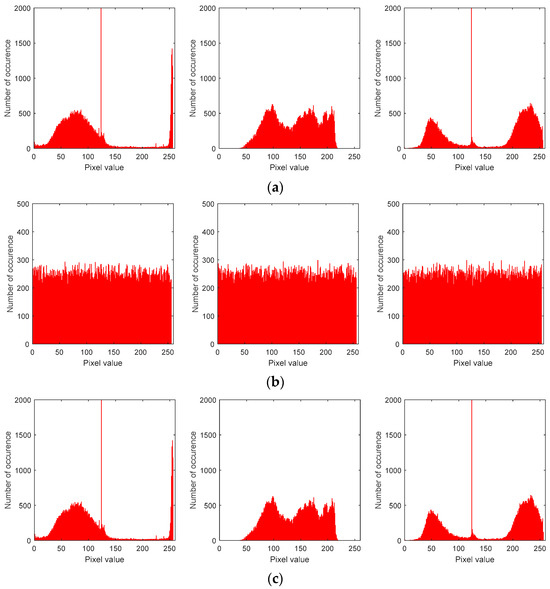
Figure 15. The distribution of the pixels of the unencrypted images (a), encrypted images (b), and decrypted images (c).

From Figure 15, we can see that the histograms of the unencrypted images and those of the encrypted ones are completely different. The distribution of the pixels of the initial image is random and the one of the encrypted image is uniform, respecting the above characteristics. Thus, the biomedical image encryption system can resist differential attacks.

6.3.5. Impacts of External Perturbations and Information Loss on the Performances of the Scheme

Every encryption system is subjected to external perturbations and information loss. Therefore, it is necessary to study their impacts on the performance of the encryption system. Two different external perturbations, namely, Gaussian and Salt and Pepper noise, are subjected to the initial images before using them in the encryption system. The results for decrypted images are shown in Figure 16(a2(i)–a2(iii)) for Gaussian noise and Figure 16(b2(i)–b2(iii)) for Salt and Pepper noise. The intensity of each noise is indicated in the figure caption. Similarly, a part of the unencrypted image (see Figure 16(c1(i)–c1(iii)) is canceled before encryption. Figure 16(c2(i)–c2(iii)) present decrypted images. The percentage of the canceled data is indicated in the figure caption.

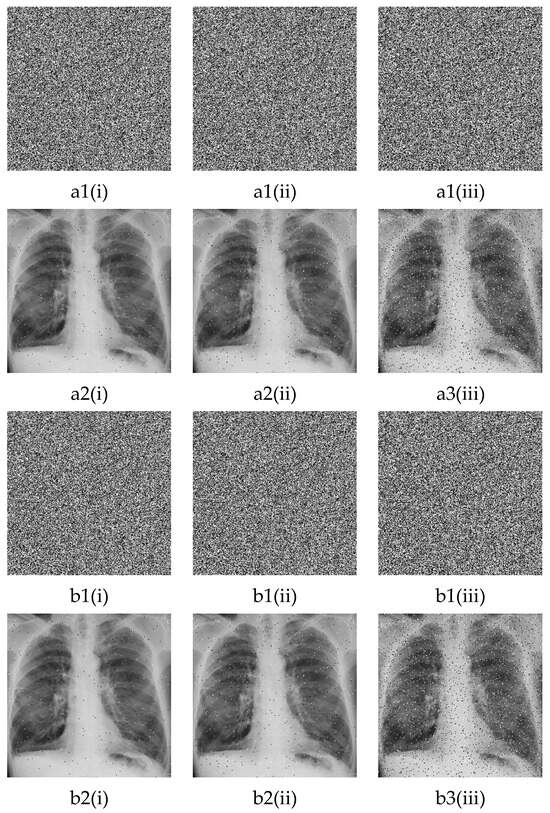
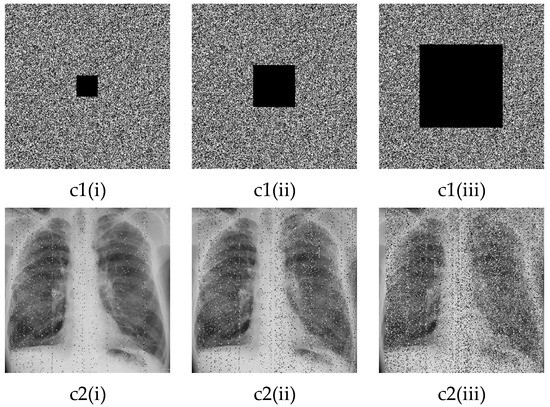
Figure 16. Impacts of external perturbations and information loss on the performances of the algorithm: (a1(i)–a1(iii)) encrypted images with $0.001$, $0.005$, and $0.01$ Gaussian noise, respectively. (a2(i)–a2(iii)) corresponding decrypted images. (b1(i)–b1(iii)) encrypted images with $0.001$, $0.005$, and $0.01$ salt and pepper noise, respectively. b2(i)–b2(iii) corresponding decrypted images. (c1(i)–c1(iii)) encrypted image with $1/32$, $1/16$, and $1/4$ information loss, respectively. (c2(i)–c2(iii)) corresponding decrypted images.

From Figure 16, we observe that, although a part of the initial image has been canceled and the noise has been subjected to the encryption system, the decrypted images remain exploitable. These results mean that the designed encryption algorithm has the ability to prevent noise and occlusion attacks.

6.3.6. NPCR and UACI Analysis

The performance of an encryption system is influenced by differential attacks. Common methods called NPCR and UACI are used to study their effects on the encryption system. They are expressed as [34]:

$$NPCR=\frac{{\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^{n}d\left(i,j\right)}}}{m\times n}\times 100$$

(11)

in which $d\left(i,j\right)$ is defined by: $d\left(i,j\right)=\left\{\begin{array}{l}1, if p\left(i,j\right)\ne p^{\prime }\left(i,j\right),\\ 0, else.\end{array}\right.$

$$UACI=\frac{100}{m\times n}{\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^n\frac{\left|p\left(i,j\right)-p^{\prime }\left(i,j\right)\right|}{2^l-1}}}$$

(12)

NPCR and UACI are computed and their values are recorded in Table 6.

Table 6. NPCR and UACI test results.

	Plaintext Sensitivity
Images	NPCR (%)	UACI (%)
Cerebrovascular accident	99.6201	30.5290
Pulmonary fibrosis	99.6094	28.3197
Lung cancer	99.5773	33.3278

From the data in Table 6, we can conclude that the encryption system is impacted by small modifications of the image’s pixels. This means that the studied image encryption algorithm has a strong capacity to resist differential attacks.

6.3.7. Comparison of this Scheme with Certain Recent Encryption Methods

The performance of the image encryption scheme is compared with that of certain recent studies and the comparisons are recorded in Table 7.

Table 7. Comparison of this image encryption scheme with certain recent encryption methods.

Algorithm	Entropy	Correlation Coefficients of Adjacent Pixels			NPCR (%)	UACI (%)
		H	V	D
Our algorithm	7.9971	−0.0048	0.0034	−0.0013	99.5651	30.6253
Ref. [35]	7.8152	0.0692	0.0544	0.0396	96.42	27.35
Ref. [36]	7.9964	−0.0057	−0.0034	0.0073	99.6185	33.6245
Ref. [37]	7.9972	−0.0245	−0.0193	−0.0226	99.60	28.62
Ref. [38]	7.9969	0.0059	0.0016	0.0029	99.2172	33.4639

The results of Table 7 confirm that the developed image encryption algorithm is more robust than some of the ones studied in recent works.

7. Conclusions

We designed a Hopfield neural network with a multistable memristor and its use for encoding biomedical image encryption. The equilibrium states, their stability, and the dynamics of the model were studied. Numerical simulations revealed that the model exhibits abundant and complicated comportments such as periodic orbits, chaos, and homogenous coexisting chaotic attractors. The model was realized using a microcontroller board. Numerical results and those obtained from the microcontroller looked very similar. The attractive behaviors of the Hopfield neural network were used to construct a scheme to mask images of cerebrovascular accidents, pulmonary fibrosis, and lung cancer. The performance of the scheme was verified by computing different statistical and security tests.

In future work, to construct a high-order neural network model that is closer to the biological one, we will use a non-polynomial memristor to couple two sub-neural networks. The two sub-neural networks will represent two different encephalic regions in the brain.