Transfer-Learning-Enhanced Regression Generative Adversarial Networks for Optimal eVTOL Takeoff Trajectory Prediction

Abstract

Electric vertical takeoff and landing (eVTOL) aircraft represent a crucial aviation technology to transform future transportation systems. The unique characteristics of eVTOL aircraft include reduced noise, low pollutant emission, efficient operating cost, and flexible maneuverability, which in the meantime pose critical challenges to advanced power retention techniques. Thus, optimal takeoff trajectory design is essential due to immense power demands during eVTOL takeoffs. Conventional design optimizations, however, adopt high-fidelity simulation models in an iterative manner resulting in a computationally intensive mechanism. In this work, we implement a surrogate-enabled inverse mapping optimization architecture, i.e., directly predicting optimal designs from design requirements (including flight conditions and design constraints). A trained inverse mapping surrogate performs real-time optimal eVTOL takeoff trajectory predictions with no need for running optimizations; however, one training sample requires one design optimization in this inverse mapping setup. The excessive training cost of inverse mapping and the characteristics of optimal eVTOL takeoff trajectories necessitate the development of the regression generative adversarial network (regGAN) surrogate. We propose to further enhance regGAN predictive performance through the transfer learning (TL) technique, creating a scheme termed regGAN-TL. In particular, the proposed regGAN-TL scheme leverages the generative adversarial network (GAN) architecture consisting of a generator network and a discriminator network, with a combined loss of the mean squared error (MSE) and binary cross-entropy (BC) losses, for regression tasks. In this work, the generator employs design requirements as input and produces optimal takeoff trajectory profiles, while the discriminator differentiates the generated profiles and real optimal profiles in the training set. The combined loss facilitates the generator training in the dual aspects: the MSE loss targets minimum differences between generated profiles and training counterparts, while the BC loss drives the generated profiles to share analogous patterns with the training set. We demonstrated the utility of regGAN-TL on optimal takeoff trajectory designs for the Airbus $A^3$ Vahana and compared its performance against representative surrogates, including the multi-output Gaussian process, the conditional GAN, and the vanilla regGAN. Results showed that regGAN-TL reached the 99.5% generalization accuracy threshold with only 200 training samples while the best reference surrogate required 400 samples. The 50% reduction in training expense and reduced standard deviations of generalization accuracy achieved by regGAN-TL confirmed its outstanding predictive performance and broad engineering application potential.

1. Introduction

Electric vertical takeoff and landing (eVTOL) aircraft represent a disruptive technology in the field of aviation. The implementation of electric propulsion systems and vertical takeoff and landing (VTOL) makes eVTOL aircraft an essential component in future transportation. Compared with traditional propulsion systems, electric propulsion not only reduces carbon emission and operation noise during flight tasks but also alleviates expenses due to less maintenance and no jet fuel consumption.These characteristics make eVTOL aircraft more environment-friendly and cost-effective. Furthermore, the VTOL capability reduces the need for traditional infrastructures, such as long runways, which lowers construction expenses and potentially prevents the over-exploitation of natural resources. In addition, paired with the aforementioned features, the flexible maneuverability and advanced flight control system position eVTOL aircraft as ideal candidates for package delivery, passenger-carrying air taxis, etc. However, one of the bottlenecks prohibiting eVTOL aircraft from broad applications and long-distance tasks is the considerable electrical energy consumption.

Increasingly mature technologies in the autonomous control, battery, and material fields have triggered numerous eVTOL studies [1,2], especially in their implementation as urban transportation. Several emerging concepts have given rise to distinct eVTOL aircraft classifications, including lift+cruise (e.g., Airbus CityAirbus NextGen [3] and Aurora Flight Sciences eVTOL [4]), multicopter (e.g., EHang 216 [5]), tilt-wing (e.g., Airbus ${\mathrm{A}}^3$ Vahana [6,7] and Dufour Aerospace VTOL Technology Demonstrator [8]), and tilt-rotor (e.g., Joby S4 [9]). Tilt-wing eVTOL aircraft typically possess rotational wings with propellers built on leading edges that as a whole, rotate upwards for VTOL and forwards for conventional cruising flights. This unique feature integrates the advantages of the agility of helicopters during takeoff and landing and the aerodynamic efficiency of traditional fixed-wing airplanes during cruising. Thus, the tilt-wing eVTOL tends to have better overall energy efficiency, which could expand flight ranges. In the meantime, investigating alternative energy-efficient avenues besides hardware configurations is greatly needed.

The transition phase attracts considerable attention by virtue of the high energy cost in this phase [10]. Consequently, optimizing the transition phase plays a crucial role in power retention for tilt-wing eVTOL aircraft. Kubo and Suzuki [11] proposed an innovative design for a tail-sitter VTOL-based unmanned aerial vehicle (UAV) configuration. By adding slats and flaps to the UAV, they achieved an optimal transition from hover to forward flight without obvious altitude change, which saved the energy consumption to reach the required altitudes. Li et al. [12] emphasized the optimal transition trajectory with a minimal energy cost, which allowed the tail-sitter UAV to complete both forward and backward transitions with less altitude change and operational time than using traditional linear transition methods. From the perspective of the critical constraint on the operational time limited by batteries, Pradeep and Wei [13] proposed a formulation of an optimal control problem taking energy consumption as a performance index for multi-rotor eVTOL aircraft. This formulation with numerical simulations enabled eVTOL vehicles to obtain the most energy-efficient trajectory while fulfilling the required arrival time. These results demonstrated the possibility of efficient energy consumption and maintaining safe operations for future eVTOL aircraft. However, there are still relatively few works in the literature concentrating on the takeoff trajectory optimization for tilt-wing eVTOL aircraft considering real-world situations. Specifically, an optimal eVTOL takeoff trajectory must take into consideration the aircraft performance, the payload, and passenger comfort, together with energy consumption.

Among the few studies on optimal takeoff trajectory for eVTOL aircraft, we can identify Chauhan and Martins [14], who optimized takeoff-to-cruise trajectories for the Airbus ${\mathrm{A}}^3$ Vahana [6] model with the energy consumption as the objective function. They considered passenger comfort via a maximum acceleration constraint and flight performance via a stall constraint on the wing angle of attack. They concluded that optimal takeoff trajectories typically occurred under conditions of wing stall or operations close to the stall angle of attack. Panish and Bacic [15] highlighted the significance of active flow control (AFC) in optimizing the transition trajectory for tilt-wing configurations. Their approach achieved minimum energy consumption at zero altitude variation and the leading-edge AFC effectively prevented wing aerodynamic stall by introducing a constant-altitude constraint during the cruise-to-hover maneuver and improved performance during hover-to-cruise transitions. Conventional design optimizations (including optimal takeoff trajectory designs), however, adopt physics-based simulation models, which prohibits real-time decision making [11,12].

Surrogate models represent a viable avenue for rapid decision making, in lieu of computationally intensive simulation models [16,17,18]. In contrast with conventional simulation-based optimizations, surrogate-based designs demonstrate various advantages, including computational efficiency [19,20], sensitivity analysis [21], uncertainty analysis [22,23], and reduced-space exploitation of high-dimensional design spaces [24]. The Gaussian process (GP) [25] is one of the most commonly used traditional surrogate models due to its capability and flexibility for modeling and predicting unknown functions based on observed data [26]. The concept of multi-output GP (MOGP) has emerged to handle problems with multiple outputs [27,28] by extending the concept of GP. In particular, by jointly modeling the outputs through estimating the covariance matrix (also known as correlation function), MOGP leverages the shared information among the outputs which reduces the overall modeling complexity. For more mathematical and surrogate modeling details, please refer to Section 2.3.

Deep neural networks (DNNs), as the core of deep learning, have substantially advanced state-of-the-art research in the surrogate modeling and design optimization communities. Thelen et al. [29] were able to address the high-dimensional aerodynamic and aeroelastic design cases with design space dimensions ranging from 17 to 321 through two-fold configurations. They first enabled accurate and efficient gradient-based optimization methods using analytically computed design variable derivatives and then further alleviated the computational burden by a multi-fidelity modeling algorithm. Tao and Sun [30] developed a multi-fidelity surrogate-based optimization framework using deep belief networks. Their results showed that the multi-fidelity surrogate achieved remarkable optimization efficiency and effectiveness according to airfoil and wing design under uncertainty results. Renganathan et al. [31] incorporated the predictive power of DNNs and confidence interval of GP for surrogate modeling in surrogate-based aerodynamic design optimization. The proposed surrogate enabled relatively high-dimensional Bayesian optimization on aerodynamic design and outperformed adjoint-based optimization in terms of efficiency.

An alternative branch for addressing the “curse of dimensionality”, which prohibits large-scale practical applications, is dimensionality reduction. O’Leary-Roseberry et al. [32] developed adaptive residual networks on reduced-dimensional space, exploiting principal component analysis to predict optimal designs directly based on design requirements. This work successfully demonstrated the outstanding performance of reduced-space surrogates over full-space surrogates on aerodynamic wing design cases. Goodfellow et al. [33] developed a state-of-the-art generative model, generative adversarial networks (GANs). GANs consist of a generator network and a discriminator network, which compete with each other. Specifically, the generator aims to generate similar shapes to existing training data patterns while the discriminator aims to differentiate between generated and existing shapes. Therefore, by automatically filtering out unrealistic shapes and generating only realistic designs, the use of GANs enabled implicit dimensionality reduction when fed with realistic airfoil or wing design shapes [34]. Du et al. [35] developed a B-spline-based generative adversarial network (BSplineGAN) for airfoil intelligent parameterization with the UIUC airfoil database as training data. The design space can be reduced automatically by BSplineGAN while sustaining sufficient shape variations, which was verified by fitting optimizations towards arbitrary UIUC airfoils. They constructed DNN surrogates on the reduced space exploiting BSplineGAN and realized rapid aerodynamic designs.

In addition to implicit dimensionality reduction, GAN variants also handle regression tasks. Du and Martins [36] developed a new multi-fidelity surrogate modeling architecture using a super-resolution GAN (SRGAN) for predicting airfoil pressure distributions based on low-fidelity counterparts. Specifically, high-fidelity pressure distributions were predicted by the SRGAN generator while the discriminator sought to distinguish between predicted and high-fidelity pressure distributions. Thus, training the generator minimized the difference between the super-resolution predictions and corresponding high-fidelity data and maximized the similarity between the predictions and the high-fidelity training set. Their results showed that SRGAN outperformed low-fidelity simulations and a direct DNN by accurately capturing the locations and magnitudes of strong shocks. Mirza and Osindero [37] incorporated conditioning information together with random inputs into the generative process for regression tasks, creating the conditional GAN (cGAN). cGAN aimed to generate shapes that are not only similar to existing data but also adhered to the specified conditions, which served as labels in regression tasks. Aggarwal et al. [38] successfully demonstrated the capability of a cGAN model for regression problems by conducting experiments on an F-16 ailerons dataset. cGAN was able to predict the aileron control input, which was described by 40 continuous inputs, including climb rates, pitches, and curvatures of the flight trajectory. However, although SRGAN and cGAN demonstrated the potential for regression tasks, neither model directly realized the mapping from original input space (such as design requirements) to output space (such as optimal designs).

In addition, it is important to implement multi-disciplinary design optimization (MDO) and leverage uncertainties and errors in the design process and operation for eVTOL aircraft. For system-level eVTOL designs, Ha et al. [39] assembled a large-scale MDO to minimize the required power. By merging thrust margin as a model uncertainty, significant improvements in robustness were made with a relatively minimal cost in efficiency. Chinthoju et al. [40] implemented a distributed MDO method, Analytical Target Cascading (ATC), which was capable of considering complex interactions between different disciplines and subsystems effectively. This feature further improved the design of the eVTOL aircraft. ATC showed the potential of utilizing customized optimization algorithms for different subproblems, instead of using a general optimization solver. Rostami et al. [41] presented an implementation of a robust and efficient possibility-based design optimization method for the MDO of an eVTOL tilt-wing aircraft in the design phase. To achieve an optimal design, the uncertainties raised from early design phases due to low-fidelity calculation were evaluated and utilized to adjust the final design.

Moreover, as claimed in a document published by the Federal Aviation Administration [42], eVTOL is one of the major aircraft innovations capable of facilitating more frequent travel between desired locations, such as metropolitan areas. Urban air mobility (UAM) corridors are necessary for cooperatively managed operations. However, due to continuous growth, UAM corridors may result in exceeding initial design capacities. Moreover, when also including environmental factors, for instance, weather, obstacles, and other constraint information, UAM operators must have the ability to respond instantaneously to manage real-time operations. Therefore, on-board optimal trajectory prediction becomes crucial for eVTOL aircraft, as it provides the aircraft with efficient operations and real-time decision-making.

In this work, we propose a transfer learning (TL)-enhanced regression GAN (regGAN), termed regGAN-TL, surrogate. In particular, we implement a regGAN surrogate [43] to predict optimal takeoff trajectory designs directly from design requirements [44]. On the one hand, the regGAN surrogate adopts the GAN architecture except that the generator reads design requirements as input and predicts optimal takeoff trajectory designs. Training the generator involves a combined loss function on a contextual loss to minimize the difference between surrogate predictions and corresponding training observations and an adversarial loss for matching the predicted optimal trajectory shapes toward training data patterns. Specifically, the mean squared error (MSE) represents the contextual loss while the binary cross-entropy (BC) constitutes the adversarial loss. On the other hand, TL is a machine learning technique leveraging pre-trained models on different but related tasks [45]. Representative TL works include the multi-fidelity convolutional neural network surrogate model with TL that mapped the relation between shape parameters and aerodynamic performance [46]. Results showed that the TL-based surrogate noticeably reduced computational costs with satisfactory predictive performance compared with corresponding reference surrogate models. In this work, we first train a regGAN with zero weight on the adversarial loss, which is in effect a direct DNN, then implement TL on the trained regGAN while keeping the weight on the contextual loss as one and increasing the weight on the adversarial loss. Please refer to Section 3 for more details. We summarize the contribution of this paper as follows: (1) We implement the new inverse mapping concept for predicting optimal eVTOL takeoff trajectory designs; (2) We propose and develop the novel regGAN-TL surrogate; (3) We realize real-time surrogate-based optimal takeoff trajectory designs for eVTOL aircraft to enrich research studies in this field.

To more effectively introduce our work, Figure 1 demonstrates the prediction of optimal eVTOL takeoff trajectory profiles for design variables. The predictions of the regGAN-TL surrogate model target the match with the reference profile generated by simulation-based optimal designs. An illustration of an Airbus $A^3$ Vahana is also provided to assist in understanding the system.

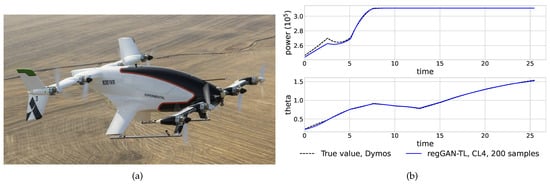
Figure 1. The test case considered in this work: (a) Airbus $A^3$ Vahana drone (https://www.airbus.com/, accessed on 10 April 2024); (b) optimal takeoff trajectory profile of design variables: electrical power ($\mathbf{P}$) and wing angle to vertical ($\mathit{\theta }$), comparing regGAN-TL predictions with simulation-based optimal design.

The rest of the paper is organized as follows. We elaborate on the MOGP and GAN variant setups for surrogate modeling in Section 2, which also includes the optimization framework, simulation models, and verification metrics. In Section 3, we demonstrate the use of the proposed regGAN-TL on eVTOL optimal takeoff trajectory predictions and compare results with reference surrogates. Section 4 ends this paper with conclusions and future work.

2. Methodology

This section introduces an open-source optimization toolbox, Dymos [47] within the OpenMDAO framework (https://github.com/OpenMDAO/OpenMDAO, accessed on 1 August 2022) [48], optimal control problems, and simulation models. Furthermore, the MOGP, DNN and GAN series models within TensorFlow [49] version 2 for surrogate modeling as well as surrogate verification metrics are detailed.

2.1. Dymos and Optimal Control

An open-source framework for multidisciplinary design, analysis, and optimization (MDAO), OpenMDAO [48], enables researchers to efficiently analyze and optimize complex engineering systems. This framework is fundamentally designed for gradient-based optimization, which is based on efficient coupled derivative computation and problem sparsity exploitation [48]. The characteristic of component-based architecture enables the ease of multidisciplinary model integration, facilitating seamless collaboration and reusability. OpenMDAO transcends in managing data flow, coupling interdisciplinary subsystems, solving equation systems, as well as providing efficient automatic differentiation for gradient-based optimization and sensitivity analysis. Built upon the OpenMDAO framework, Dymos [47] is an advanced software toolkit for optimizing complex aerospace systems. Dymos offers additional specialized tools and algorithms for dynamic system analysis and optimization and excels in solving problems that involve the evolution of systems over time. This feature is beneficial for trajectory optimization, where several objectives and constraints need to be taken into account. In addition, Dymos possesses an intuitive interface and visualization tools for basic problem formulation and manipulation while supporting integration with external models and software. Thus, Dymos represents one of the state-of-the-art MDAO toolkits, allowing for efficient optimal control of complicated aerospace systems.

Optimal control aims to discover a control of a dynamic system such that an objective function is optimized with constraints satisfied. The evolution of a system state is typically governed by an ordinary differential Equation (ODE) or a differential algebraic equation. Dymos characterize all dynamics as ODEs and formulates a general optimal control problem as follows [47].

$$\begin{array}{cc}\hfill \mathrm{Minimize}& J=f_{\mathrm{obj}}(\mathbf{x},t,\mathbf{u},\mathbf{d})\hfill \\ \hfill \mathrm{subject}\mathrm{to}& \dot{\mathbf{x}}={\mathbf{f}}_{\mathrm{ode}}(\mathbf{x},t,\mathbf{u},\mathbf{d}),\hfill \\ \hfill & t_{lb}\le t\le t_{ub},\hfill \\ \hfill & {\mathbf{x}}_{lb}\le \mathbf{x}\le {\mathbf{x}}_{ub},\hfill \\ \hfill & {\mathbf{u}}_{lb}\le \mathbf{u}\le {\mathbf{u}}_{ub},\hfill \\ \hfill & {\mathbf{d}}_{lb}\le \mathbf{d}\le {\mathbf{d}}_{ub},\hfill \\ \hfill & {\mathbf{g}}_{0,lb}\le {\mathbf{g}}_0({\mathbf{x}}_0,t_0,{\mathbf{u}}_0,{\mathbf{d}}_0)\le {\mathbf{g}}_{0,ub},\hfill \\ \hfill & {\mathbf{g}}_{f,lb}\le {\mathbf{g}}_f({\mathbf{x}}_f,t_f,{\mathbf{u}}_f,{\mathbf{d}}_f)\le {\mathbf{g}}_{f,ub},\hfill \\ \hfill & {\mathbf{p}}_{lb}\le \mathbf{p}(\mathbf{x},t,\mathbf{u},\mathbf{d})\le {\mathbf{p}}_{ub},\hfill \end{array}$$

(1)

where J is a scalar objective function computed by $f_{\mathrm{obj}}$, $\mathbf{x}$ is a state variable vector, t is a time variable, $\mathbf{u}$ is a dynamic control vector, $\mathbf{d}$ is a fixed design parameter vector, $\dot{\mathbf{x}}$ is a temporal derivative vector of state variables governed by the ODE ${\mathbf{f}}_{\mathrm{ode}}$, ${\mathbf{g}}_0$ is an initial condition (at $t_0$) constraint vector, ${\mathbf{g}}_f$ is a final condition (at $t_f$) constraint vector, $\mathbf{p}$ is a path constraint vector, subscript $lb$ represents lower bounds, and subscript $ub$ represents upper bounds.

Solving optimal control problems involves a transcription process, i.e., discretizing the continuous problem into a form that a nonlinear optimizer can handle. Dymos supports two types of transcriptions, explicit shooting and implicit collocation. Explicit shooting (such as the Euler method) is a numerical integration technique propagating a current state (${\mathbf{x}}_i$) to the next state (${\mathbf{x}}_{i+1}$) subject to given controls [50,51].

$${\mathbf{x}}_{i+1}={\mathbf{x}}_i+(t_{i+1}-t_i)·{\mathbf{f}}_{\mathrm{ode}}({\mathbf{x}}_i,t_i,{\mathbf{u}}_i,\mathbf{d}),$$

(2)

which is also known as the rectangular rule. Shooting methods are explicit since ${\mathbf{x}}_{t+1}$ is not used for computing a discrete value of ${\mathbf{f}}_{\mathrm{ode}}$. In contrast, implicit collocation methods separate control and state trajectories into one or multiple segments over the time range and solve the whole trajectories together. Collocation methods assume that the states ($\mathbf{x}$), controls ($\mathbf{u}$), and state rates ($\dot{\mathbf{x}}$) are continuous within each segment [47]. This feature guarantees no instantaneous changes in $\mathbf{x}$, $\mathbf{u}$, and $\dot{\mathbf{x}}$ and enables polynomial curve representations within each segment. Collocation methods propose state and control discrete points in time within each segment and adopt high-order Gauss–Lobatto rules [52] to reconstruct polynomial curves. The polynomial curves approximate the entire state ($\tilde{\mathbf{x}}$) and control ($\tilde{\mathbf{u}}$) trajectories via interpolation and estimate state rates ($\widetilde{\dot{\mathbf{x}}}$) via first-order derivatives of the curves. In the meantime, Dymos computes $\dot{\mathbf{x}}$ using $\tilde{\mathbf{x}}$ and $\tilde{\mathbf{u}}$ via ${\mathbf{f}}_{\mathrm{ode}}$ and calculates the difference with $\widetilde{\dot{\mathbf{x}}}$ at collocation locations (center points of each time segment in this work). In addition, a nonlinear solver or optimizer is in charge of minimizing the differences. We use the Gauss–Lobatto collocation method in this work due to its higher computational efficiency compared to explicit shooting [47].

Gauss–Lobatto rules generalize the trapezoidal rule and Simpson’s rule to higher orders [52]. Specifically, the trapezoidal rule adopts a linear function to approximate ${\mathbf{f}}_{\mathrm{ode}}$ and Simpson’s rule adopts a quadratic function, while Gauss–Lobatto enables higher-order approximation functions. Note that $\mathbf{u}$ is of the same polynomial order as ${\mathbf{f}}_{\mathrm{ode}}$ while $\mathbf{x}$ is one order higher due to the integral operation. As suggested by Dymos, we use the quadratic Gauss–Lobatto rule, which is essentially the Simpson’s integration rule, within each segment to represent $\mathbf{u}$ and thus, Hermite cubic polynomials for $\mathbf{x}$ and compute ${\mathbf{x}}_c$ at $t_c=(t_i+t_{i+1})/2$ by interpolating the Hermite polynomials

$$\begin{array}{c}\hfill {\mathbf{x}}_c=\frac{1}{2}({\tilde{\mathbf{x}}}_i+{\tilde{\mathbf{x}}}_{i+1})+\frac{(t_{t+1}-t_i)}{8}\left[{\mathbf{f}}_{\mathrm{ode}}\left({\tilde{\mathbf{x}}}_i,t_i,{\tilde{\mathbf{u}}}_i,\mathbf{d}\right)-{\mathbf{f}}_{\mathrm{ode}}\left({\tilde{\mathbf{x}}}_{i+1},t_{i+1},{\tilde{\mathbf{u}}}_{i+1},\mathbf{d}\right)\right].\end{array}$$

(3)

Then we can compute discrete values of the governing ODEs at $t_c$ by plugging in ${\tilde{\mathbf{x}}}_c$ and ${\tilde{\mathbf{u}}}_c$. We approximate ${\widetilde{\dot{\mathbf{x}}}}_c$ by taking the first-order temporal derivatives of the Hermite cubic polynomials and equate ${\widetilde{\dot{\mathbf{x}}}}_c$ with ${\mathbf{f}}_{\mathrm{ode}}$ at $t_c$ to achieve

$${\mathbf{g}}_{HS}={\tilde{\mathbf{x}}}_i-{\tilde{\mathbf{x}}}_{i+1}+\frac{t_{i+1}-t_i}{6}\left({\mathbf{f}}_{\mathrm{ode}}({\tilde{\mathbf{x}}}_i,t_i,{\tilde{\mathbf{u}}}_i,\mathbf{d})+4·{\mathbf{f}}_{\mathrm{ode}}\left({\tilde{\mathbf{x}}}_c,t_c,{\tilde{\mathbf{u}}}_c,\mathbf{d}\right)+{\mathbf{f}}_{\mathrm{ode}}\left({\tilde{\mathbf{x}}}_{i+1},t_{i+1},{\tilde{\mathbf{u}}}_{i+1},\mathbf{d}\right)\right)=\mathbf{0},$$

(4)

which are also termed Hermite–Simpson system constraints [52]. Dymos adds the Hermite–Simpson constraints to Equation (1) and we use the IPOPT (Interior Point OPTimizer) [53] within the pyoptsparse [54] to solve the optimal control problem in this work. In this work, we leverage 10 segments within the whole time duration, which results in 21 design variables (quadratic polynomial points) for parameterizing each control input in this work. We force the continuity of $\mathbf{x}$ and $\mathbf{u}$ within Dymos by setting the corresponding values shared at segment boundaries.

2.2. Simulation Models

In this work, the simulation models include aerodynamics, propulsion, propeller–wing interaction, and dynamics to govern eVTOL aircraft attitudes.

2.2.1. Aerodynamics

The aerodynamics models assume that there is no flow interaction between wings. The forward and rear wings have the same reference area and the rotations of both wings are set to be the same, which leads to the same angle of attack, lift, and drag by the two wings. Separated-flow conditions are considered during the vertical to horizontal transition phase. Tangler and Ostowari [55] developed a model for wing aerodynamics to predict the lift and drag beyond the linear-lift region. The post-stall lift coefficient is expressed as

$$C_L=A_1\sin 2\alpha +A_2\frac{{\cos }^2\alpha }{\sin \alpha },$$

(5)

where

$$A_1=\frac{C_1}{2},$$

(6)

$$A_2=(C_{L_s}-C_1\sin {\alpha }_s\cos {\alpha }_s)\frac{\sin {\alpha }_s}{{\cos }^2{\alpha }_s},$$

(7)

and

$$C_1=1.1+0.018AR,$$

(8)

where $\alpha$ is the wing angle of attack, ${\alpha }_s$ is the angle of attack at stall, $C_{L_s}$ is the lift coefficient at stall, and $AR$ is the wing aspect ratio.

At a wing angle of attack of between 27.5 and 90 degrees, the drag coefficient is given by

$$C_D=B_1\sin \alpha +B_2\cos \alpha ,$$

(9)

where

$$B_1=C_{D_{\max }},$$

(10)

$$B_2=\frac{C_{D_s}-C_{D_{\max }}\sin {\alpha }_s}{\cos {\alpha }_s},$$

(11)

and

$$C_{D_{\max }}=\frac{1.0+0.065AR}{0.9+t/c},$$

(12)

where $C_{D_s}$ is the drag coefficient at stall, and $t/c$ is the airfoil thickness-to-chord ratio. For the post-stall drag coefficient at a wing angle of attack below 27.5 degrees, the equation is

$$C_D=0.008+1.107{\alpha }^2+1.792{\alpha }^4,$$

(13)

where $\alpha$ is in radians.

The NACA 0012 symmetric airfoil is used as the cross-section due to the configuration of interest. Additionally, the well-known finite wing corrections from lifting-line theory for unswept wings in incompressible flow are utilized to correct the lift-curve slope prior to stalling [14] as

$${\alpha }_{\mathrm{wing}}=\frac{{\alpha }_{\mathrm{airfoil}}}{1+\left({\alpha }_{\mathrm{airfoil}}/\left(\pi ·AR·e\right)\right)},$$

(14)

where ${\alpha }_{\mathrm{wing}}$ is the finite-wing lift-curve slope, ${\alpha }_{\mathrm{airfoil}}$ is the airfoil lift-curve slope, and e is the span efficiency factor. The pre-stall lift curve is assumed to be linear and the wing stall angle of attack is 15 degrees.

For pre-stall parasite drag coefficients, induced drag has been added with a formula based on lifting-line theory to obtain the total drag of the wing before stall,

$$C_{D_i}=\frac{C_L^2}{\pi ·AR·e},$$

(15)

where $C_{D_i}$ is the induced drag coefficient, $C_L$ is the wing’s lift coefficient, and $AR=8$ for each wing of the configuration.

For the fixed landing gear and the fuselage, additional drag on an assumed drag area is assumed to be independent of the free-stream angle of attack. The induced drag for the configuration is given by

$$D_{\mathrm{induced}}=2\left(1.4\frac{L_{\mathrm{wing}}^2}{\pi q{b}^2·0.95}\right)=2\left(\frac{L_{\mathrm{wing}}^2}{\pi q{b}^2·0.68}\right),$$

(16)

where $L_{\mathrm{wing}}$ is lift per wing, q is the free-stream dynamic pressure, and b is the wing span.

The fuselage is assumed not to contribute any additional lift and the wings are located forward and aft of the center of gravity, so that, without any extra tuning, the moments of wings are automatically balanced. Please refer to Chauhan and Martins [14] for more details.

2.2.2. Propulsion

The Momentum theory [56] calculates the thrust from propellers as a function of power,

$$P_{\mathrm{disk}}=T{V}_{\infty \perp }+\kappa T\left(-\frac{V_{\infty \perp }}{2}+\sqrt{\frac{V_{\infty \perp }^2}{4}+\frac{T}{2\rho A_{\mathrm{disk}}}}\right),$$

(17)

where $P_{\mathrm{disk}}$ is the power supplied to the propeller disk excluding profile power, T is the thrust, $V_{\infty \perp }$ is the free-stream velocity component normal to the propeller disk, $\rho$ is the air density, $A_{\mathrm{disk}}$ is the disk area of the propeller, and $\kappa$ is the correction factor utilized to incorporate induced power losses associated with non-uniform flow, tip effects, and other simplifications made in momentum theory ($\kappa =1$ for ideal power). Power is chosen as a design variable in the optimization problems. Moreover, the Newton–Raphson method [57] is used to solve the nonlinear equation for thrust with power as an input.

McCormick [58] and Leishman [59] both applied blade-element theory to a rotor operating in nonaxial forward flight and estimated the profile power coefficient as

$$C_{P_p}=\frac{\sigma C_{d_{0p}}}{8}(1+4.6{\mu }^2),$$

(18)

where $C_{P_p}$ is defined as $P_p/\rho A_{\mathrm{disk}}{R}^3{\Omega }^3$, $P_p$ is the profile power, R is the radius of the propeller, $\Omega$ is the angular speed, $\sigma$ is the solidity, $C_{d_{0p}}$ is a representative constant profile drag coefficient, and $\mu$ is defined as

$$\mu =\frac{V_{\infty \Vert }}{\Omega R},$$

(19)

where $V_{\infty \Vert }$ is the free-stream velocity component parallel to the disk. For our cases, we assume that $\Omega =181$ rad/s for $R=0.75$ m, $\sigma =0.13$, and $C_{d_{0p}}=0.012$.

With electric powers as input, a factor $k_{\mathrm{elec}}$ is used to account for mechanical and electrical loss related to electric systems, batteries, and motors. Then, $P_{\mathrm{disk}}$ is given by

$$P_{\mathrm{disk}}=k_{\mathrm{elec}}{P}_{\mathrm{elec}}-P_p,$$

(20)

where $P_{\mathrm{elec}}$ is the power from the batteries. The limit of maximum available electrical power is set to 311 kW. We take the loss factor $k_{\mathrm{elec}}$, ranging from 0.7 to 0.9, as one of our design requirement inputs for surrogate modeling.

Furthermore, when the free-stream flow is not normal to the propeller disks, the normal force N is estimated as

$$N=\frac{4.25{\sigma }_{e}sin(\beta +8^{\circ })f{q}_{\perp }{A}_{\mathrm{disk}}}{1+2{\sigma }_e}tan{\alpha }_{in},$$

(21)

where $q_{\perp }$ is the dynamic pressure based on the free-stream velocity component normal to the propeller disk, $\beta$ is the blade pitch angle at $0.75R$ and is assumed to change linearly from 10 degrees at a flight speed of 0 m/s to 35 degrees at the cruise speed of 67 m/s, $A_{\mathrm{disk}}$ is the propeller area, and ${\alpha }_{in}$ is the incidence angle. The remaining terms are given in the following manner. ${\sigma }_e$ is the effective solidity and given by,

$${\sigma }_e=\frac{2B{c}_{\mathrm{b}}}{3\pi R},$$

(22)

where B is the number of blades per propeller, $c_{\mathrm{b}}$ is the average chord length of the blades, and R is the propeller radius. We compute the thrust factor as

$$f=1+\frac{\sqrt{1+T_c}-1}{2}+\frac{T_c}{4(2+T_c)},$$

(23)

where $T_c$ is a thrust coefficient defined as

$$T_c=\frac{T}{q_{\perp }{A}_{\mathrm{disk}}},$$

(24)

and T is the thrust.

2.2.3. Propeller–Wing Interaction

In order to model the interaction between a wing and the flow induced by propellers, momentum theory is implemented. The induced speed at the disk $v_i$ is calculated as    

$$v_i=\left(-\frac{V_{\infty \perp }}{2}+\sqrt{\frac{V_{\infty \perp }^2}{4}+\frac{T}{2\rho A_{\mathrm{disk}}}}\right).$$

(25)

According to momentum theory, the increase in the chord-wise component of the free-stream velocity due to the propeller–wing interaction is quantified by an empirical induced factor $k_{\mathrm{in}}$. The effective $k_{\mathrm{in}}$ for the wing is anticipated to be close to but slightly less than 1, especially at low-speed conditions for the aircraft. Moreover, if $k_{\mathrm{in}}$ is too low the propeller–wing interaction would not match realistic scenarios, hence, we vary $k_{\mathrm{in}}\in [0.3,1.0]$ in this paper.

2.2.4. Dynamics

The aircraft trajectory simulation uses a two-degrees-of-freedom (DOF) representation [60]. Figure 2 displays the forces and the angles on the aircraft. The horizontal and vertical components of the aircraft velocity are solved as functions of time, considering the control variables, namely, the electrical power and wing-tilt angle. The horizontal and vertical components of velocity rate (i.e., acceleration) at each time step are given as

$${\dot{v}}_x=\frac{Tsin\theta -D_{\mathrm{fuse}}sin(\theta +{\alpha }_{\infty })-D_{\mathrm{wings}}sin(\theta +{\alpha }_{\mathrm{EFS}})-L_{\mathrm{wings}}cos(\theta +{\alpha }_{\mathrm{EFS}})-Ncos\theta }{m},$$

(26)

and

$${\dot{v}}_y=\frac{Tcos\theta -D_{\mathrm{fuse}}cos(\theta +{\alpha }_{\infty })-D_{\mathrm{wings}}cos(\theta +{\alpha }_{\mathrm{EFS}})+L_{\mathrm{wings}}sin(\theta +{\alpha }_{\mathrm{EFS}})+Nsin\theta -mg}{m},$$

(27)

where $\theta$ is a wing angle relative to the vertical, ${\alpha }_{\infty }$ is a free-stream angle of attack, and ${\alpha }_{\mathrm{EFS}}$ is the effective free-stream angle of attack experienced by the wings due to propeller influence, m is the mass of the aircraft, T is the total thrust, $D_{\mathrm{fuse}}$ is the drag of the fuselage, $D_{\mathrm{wings}}$ is the total drag of the two wings, $L_{\mathrm{wings}}$ is the total lift of the two wings, N is the total normal force generated by the propellers, and g is the gravitational acceleration. We use implicit collocation methods to solve for states as described in Section 2.1.

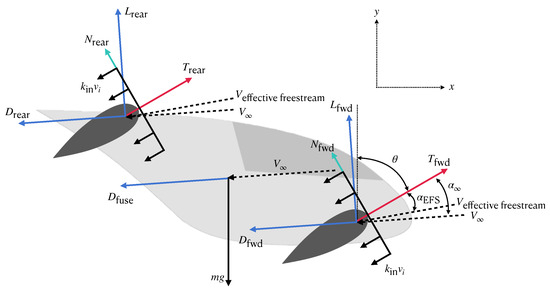
Figure 2. Definition of angles and forces on the aircraft.

2.3. Multi-Output Gaussian Processes

GP assumes a model response is a realization of a Gaussian process indexed by input parameters ($\mathbf{x}$) [61]

$$y^{GP}\left(x\right)={\mathit{\beta }}^{⊺}\mathbf{f}\left(\mathbf{x}\right)+{\sigma }^2\mathcal{GP},$$

(28)

where $\mathit{\beta }$ is an unknown coefficient vector to be determined, $\mathbf{f}$ is a user-selected basis function (typically a polynomial function), ${\sigma }^2$ is the variance of the GP, and $\mathcal{GP}$ is a zero-mean, unit-variance, stationary GP represented by a correlation function. Specifically, when applied for predictions, GP assumes that the quantity to be predicted ($\widehat{y}$) at a query point (${\mathbf{x}}^{\prime }$) and training observations ($\mathbf{y}$) follow a multi-variate normal (MVN) distribution defined by [62]

$$\left\{\begin{array}{c}\widehat{y}\left({\mathbf{x}}^{\prime }\right)\hfill \\ \mathbf{y}\hfill \end{array}\right\}\sim \mathcal{MVN}\left(\left\{\begin{array}{c}{\mathbf{f}}^{⊺}\left({\mathbf{x}}^{\prime }\right)·\mathit{\beta }\hfill \\ \mathbf{F}·\mathit{\beta }\hfill \end{array}\right\},{\sigma }^2\left\{\begin{array}{c}1{\mathbf{r}}^{⊺}\left({\mathbf{x}}^{\prime }\right)\hfill \\ \mathbf{r}\left({\mathbf{x}}^{\prime }\right)\mathbf{R}\hfill \end{array}\right\}\right),$$

(29)

where $\mathbf{F}$ is a basis function matrix with $F_{ij}=f_j\left({\mathbf{x}}_i\right)$, $i=1,\dots ,N;j=0,\dots ,P$, N is number of training samples, P is the number of polynomial terms in $\mathbf{f}$, and $\mathbf{r}\left({\mathbf{x}}^{\prime }\right)$ is a cross-correlation vector between ${\mathbf{x}}^{\prime }$ and each of the input vectors in training data with $r_i=\mathcal{C}\left({\mathbf{x}}^{\prime },{\mathbf{x}}_i;\theta \right),i=1,\dots ,N$, $\mathbf{R}$ is a correlation matrix between the training inputs with $R_{i,j}=\mathcal{C}\left({\mathbf{x}}_i,{\mathbf{x}}_j;\theta \right),i,j=1,\dots ,N$, and $\mathcal{C}$ is a user-selected correlation function.

The training GP is estimating unknown parameters $\mathit{\theta }$ using optimization algorithms, such as the maximum-likelihood estimation (MLE) in this work. MLE determines $\mathit{\theta }$ by maximizing the likelihood of the observations $\mathbf{y}$ since each observation is a GP realization

$$\mathcal{L}(\mathit{\theta };\mathbf{y})=\frac{{\left(\mathrm{Det}\left(\mathbf{R}\right)\right)}^{-1/2}}{{\left(2\pi {\sigma }^2\right)}^{N/2}}\exp \left[\frac{-1}{2{\sigma }^2}{(\mathbf{y}-\mathbf{F}\mathit{\beta })}^{⊺}{\mathbf{R}}^{-1}(\mathbf{y}-\mathbf{F}\mathit{\beta })\right],$$

(30)

where $\mathrm{Det}\left(·\right)$ is determinant of a matrix, exp is the exponential operation, and $\mathit{\beta }$ and ${\sigma }^2$ are functions of $\mathit{\theta }$ and can be approximated as

$$\widehat{\mathit{\beta }}={\left({\mathbf{F}}^{⊺}{\mathbf{R}}^{-1}\mathbf{F}\right)}^{-1}{\mathbf{F}}^{⊺}{\mathbf{R}}^{-1}\mathbf{y},$$

(31)

$${\widehat{\sigma }}^2=\frac{1}{N}{(\mathbf{y}-\mathbf{F}\mathit{\beta })}^{⊺}{\mathbf{R}}^{-1}(\mathbf{y}-\mathbf{F}\mathit{\beta }).$$

(32)

Thus, determining $\theta$ results in the following form

$$\begin{array}{cc}\hfill \widehat{\mathit{\theta }}& =\arg \underset{\mathit{\theta }}{\min }[-\log \mathcal{L}(\mathit{\theta };\mathbf{y})]\hfill \\ \hfill & =\arg \underset{\mathit{\theta }}{\min }\frac{1}{2}\left[\log \left(\mathrm{Det}\left(\mathbf{R}\right)\right)+N·\log \left(2\pi {\sigma }^2\right)+N\right].\hfill \end{array}$$

(33)

In the prediction phase, GP provides at a query point not only the prediction but also a variance, which enables confidence intervals [62]

$$\widehat{y}\left({\mathbf{x}}^{\prime }\right)={\mathbf{f}}^{⊺}\widehat{\mathit{\beta }}+\mathbf{r}{\left({\mathbf{x}}^{\prime }\right)}^{⊺}{\mathbf{R}}^{-1}\left(\mathbf{y}-\mathbf{F}\widehat{\mathit{\beta }}\right),$$

(34)

$${\sigma }_{\widehat{y}}^2\left({\mathbf{x}}^{\prime }\right)={\sigma }^2\left(1-{\mathbf{r}}^{\prime }\left({\mathbf{x}}^{\prime }\right){\mathbf{R}}^{-1}\mathbf{r}\left({\mathbf{x}}^{\prime }\right)+{\mathbf{u}}^{⊺}\left({\mathbf{x}}^{\prime }\right){\left({\mathbf{F}}^{⊺}{\mathbf{R}}^{-1}\mathbf{F}\right)}^{-1}\mathbf{u}\left({\mathbf{x}}^{\prime }\right)\right),$$

(35)

where

$$\mathbf{u}\left({\mathbf{x}}^{\prime }\right)={\mathbf{F}}^{⊺}{\mathbf{R}}^{-1}\mathbf{r}\left({\mathbf{x}}^{\prime }\right)-\mathbf{f}\left({\mathbf{x}}^{\prime }\right).$$

(36)

In this work, we apply a constant basis function $\mathbf{f}\left(\mathbf{x}\right)=\mathbf{0}$ and a linear basis function $\mathbf{f}\left(\mathbf{x}\right)=\mathbf{x}$. The correlation function $\mathcal{C}\left(\mathbf{x},{\mathbf{x}}^{\prime }\right)$ captures the relationship between the function values at different input points $\mathbf{x}$ and ${\mathbf{x}}^{\prime }$. We implement the Matérn 3/2 kernel and the square exponential (SE) kernel. The Matérn covariance between two points ($\mathbf{x}$ and ${\mathbf{x}}^{\prime }$) is

$${\mathcal{C}}_{\nu }\left(\tau \right)=\frac{2^{1-\nu }}{\Gamma \left(\nu \right)}\left(\sqrt{2\nu }\frac{\tau }{\theta }\right)K_{\nu }\left(\sqrt{2\nu }\frac{\tau }{\theta }\right),$$

(37)

where $\Gamma$ is the gamma function, $K_{\nu }$ is the modified Bessel function of the second kind, and $\theta$ is the unknown kernel length scale, $\nu$ is a smoothness parameter ($\nu =3/2$ representing a once differentiable function in this work), and $\tau =|\mathbf{x}-{\mathbf{x}}^{\prime }|$ is the Euclidean distance. The Matérn kernel is stationary since the covariance only depends on distances between points. We also test the SE kernel, which is an example of a radial basis function

$${\mathcal{C}}_{SE}=exp\left(-\frac{1}{2}\left(\frac{|\mathbf{x}-{\mathbf{x}}^{\prime }|}{\theta }\right)\right).$$

(38)

MOGP extends GP to handle multiple outputs simultaneously, especially when dealing with correlated outputs which enables dependent modeling. MOGP introduces additional complexity due to modeling correlations between multiple outputs, but MOGP remains efficient and more capable than training individual GPs for each output. Thus, a key feature of MOGP is to harness applicable information across outputs to provide more accurate predictions than separately modeling correlated outputs [28]. Mathematically, MOGP extends Equation (29) to a multi-output prediction ($\widehat{\mathbf{y}}\in {\mathbb{R}}^{T\times 1}$) at a query point (${\mathbf{x}}^{\prime }$)

$$\left\{\begin{array}{c}\widehat{\mathbf{y}}\left({\mathbf{x}}^{\prime }\right)\hfill \\ {\mathbf{y}}_M\hfill \end{array}\right\}\sim \mathcal{MVN}\left(\left\{\begin{array}{c}{\mathbf{F}}_{\widehat{\mathbf{y}}}^{⊺}·\mathit{\beta }\hfill \\ {\mathbf{F}}_M·\mathit{\beta }\hfill \end{array}\right\},{\sigma }_M^2\left\{\begin{array}{c}{\mathbf{R}}_{\ast \ast }{\mathbf{R}}_{M\ast }^{⊺}\hfill \\ {\mathbf{R}}_{M\ast }{\mathbf{R}}_{MM}\hfill \end{array}\right\}\right),$$

(39)

where ${\mathbf{y}}_M\in {\mathbb{R}}^{NT\times 1}$ is a training response vector containing multiple outputs, N is the number of training samples, and T is the dimension of multiple outputs at one query point; ${\mathbf{F}}_{\widehat{\mathbf{y}}}\in {\mathbb{R}}^{P\times T}$ has T columns of $\mathbf{f}$ basis functions as defined above, ${\mathbf{F}}_M\in {\mathbb{R}}^{NT\times P}$ has blocks of $\left[{\mathbf{F}}_{\widehat{\mathbf{y}},i}^{⊺}\right]$ for $i=1,\dots ,N$, and P is the number of polynomial terms, which also denotes the number of components in $\mathit{\beta }$; ${\mathbf{R}}_{\ast \ast }\in {\mathbb{R}}^{T\times T}$ is a correlation matrix between two arbitrary model response at ${\mathbf{x}}^{\prime }$

$${\mathbf{R}}_{\ast \ast }=\left[\begin{array}{c}{r}_{11}({\mathbf{x}}^{\prime },{\mathbf{x}}^{\prime })\dots r_{1T}({\mathbf{x}}^{\prime },{\mathbf{x}}^{\prime })\hfill \\ \dots \dots \dots \hfill \\ r_{T1}({\mathbf{x}}^{\prime },{\mathbf{x}}^{\prime })\dots r_{TT}({\mathbf{x}}^{\prime },{\mathbf{x}}^{\prime })\hfill \end{array}\right],$$

(40)

$r_{t_1,t_2}$ corresponds to the correlation between output $y_{t_1}\left({\mathbf{x}}^{\prime }\right)$ and $y_{t_2}\left({\mathbf{x}}^{\prime }\right)$; ${\mathbf{R}}_{M\ast }\in {\mathbb{R}}^{NT\times T}$ has blocks of ${\mathbf{R}}_{t_1,t_2}(\mathbf{X},{\mathbf{x}}^{\prime })=\left[r_{t_1,t_2}({\mathbf{x}}_i,{\mathbf{x}}^{\prime })\right]$ for $i=1,\dots ,N$, and $t_1,t_2=1,\dots ,T$; and similarly, ${\mathbf{R}}_{MM}\in {\mathbb{R}}^{NT\times NT}$ has blocks of ${\mathbf{R}}_{t_1,t_2}(\mathbf{X},\mathbf{X})=\left[r_{t_1,t_2}({\mathbf{x}}_i,{\mathbf{x}}_j)\right]$ for $i,j=1,\dots ,N$, and $t_1,t_2=1,\dots ,T$. MOGP makes predictions following the same principle as a single-output GP (Equations (31)–(36)) but using the generalized multi-output variables [28].

We use the MOGPTK [27] MOGP toolkit to establish the MOGP models. MOGPTK is an open-source Python package that provides a natural way to train and use MOGP. MOGPTK is built upon GPflow [63], an extensive GP framework with a wide variety of implemented kernels, likelihoods, and training strategies. The main components of MOGPTK include MOGP modeling, data handling, parameter initialization, and parameter interpretation (please refer to de Wolff et al. [27] for more details).

2.4. Deep Neural Networks

2.4.1. DNN Model Setup

DNNs [64] are composed of multiple layers of interconnected nodes, also known as neurons, to read input data and make predictions. In each layer, a DNN transforms the data from its previous layer utilizing a combination of linear operations and activation functions. Neurons in the same layer share a weight matrix ($\mathbf{W}$) and a bias vector ($\mathbf{b}$) to be tuned. The operation within each layer follows $\mathbf{o}=\sigma (\mathbf{W}\mathbf{x}+\mathbf{b})$, where $\mathbf{x}$ is a data vector from the previous layer, $\sigma \left(·\right)$ represents an activation function used for injecting nonlinearity, and $\mathbf{o}$ is an output vector. During model training, $\mathbf{W}$ and $\mathbf{b}$ are tuned to optimize DNN performance. In this work, we use two activation functions, (1) the rectified linear unit (relu) [65] activation function, ${\sigma }_{\mathtt{relu}}\left(x\right)=\max (0,x)$, which replaces all negative input values with zeros while passing positive input values unchanged, and (2) the sigmoid [66] activation function, ${\sigma }_{\mathtt{sigmoid}}\left(x\right)=1/\left(1+e^{-x}\right)$, which maps input values to a range between zeros and ones, making it suitable for problems where the output is normalized within this range.

To complete model training, a loss function is used to measure the difference being minimized between predictions and training observations. We implement two commonly used loss functions in this work: (1) Mean square error (MSE) [67] loss, which measures the average squared difference.

$${\mathcal{L}}_{\mathrm{MSE}}=\frac{1}{N}\sum _{i=1}^N{\left|{\mathbf{y}}_i-{\widehat{\mathbf{y}}}_i\right|}_2^2,$$

(41)

where N is the number of training samples, ${\mathbf{y}}_i$ and ${\widehat{\mathbf{y}}}_i$ are true values and predictions of the ith training sample, respectively, and ${\left|·\right|}_2$ is the $L_2$ norm operation. (2) Binary cross-entropy (BC) [68], which measures the dissimilarity between predictions and actual binary labels.

$${\mathcal{L}}_{\mathrm{BC}}=-\frac{1}{N}\sum _{i=1}^N\left(y_i·\log {\widehat{y}}_i+\left(1-y_i\right)·\log \left(1-{\widehat{y}}_i\right)\right),$$

(42)

where $y_i$ is the true binary label (0 or 1) for the data point, and ${\widehat{y}}_i$ is the predicted probability (between 0 and 1) generated by the model. Thus, unknown parameters in the DNN are tuned through the gradient-based Adam optimizer (see the following section) enabled by backpropagation within Tensorflow [49].

2.4.2. Adam Optimizer

As an efficient stochastic optimization algorithm, the Adam optimizer operates with moderate memory usage and first-order gradients [69]. Adam has proved to be powerful and effective by combining the principles of gradient descent with the momentum [70] and root-mean-square propagation (RMSP) [71] algorithms.

The gradient descent algorithm has been enhanced by the momentum algorithm [70] by incorporating the weighted average of the gradients. The update is expressed as

$$w_{i+1}=w_i-\alpha m_i,$$

(43)

where

$$m_i=\beta m_{i-1}+(1-\beta )\left[\frac{\mathsf{\partial }L}{\mathsf{\partial }{w}_i}\right],$$

(44)

where the subscripts $i-1$, i, and $i+1$ are the indices of previous, current, and next optimization steps, respectively, initially $m_0=0$, w is an unknown to be determined, $\alpha$ is a user-defined learning rate, $\frac{\mathsf{\partial }L}{\mathsf{\partial }{w}_i}$ is the derivative of the loss function with respect to the unknown at the current optimization step, and $\beta$ is a constant moving average parameter.

By employing the exponential moving average, RMSP [71] is an adaptive learning algorithm and is expressed as

$$w_{i+1}=w_i-\frac{\alpha }{{(v_i+ϵ)}^{1/2}}{\left[\frac{\mathsf{\partial }L}{\mathsf{\partial }{w}_i}\right]}^2,$$

(45)

where

$$v_i=\beta v_{i-1}+(1-\beta )\left[\frac{\mathsf{\partial }L}{\mathsf{\partial }{w}_i}\right].$$

(46)

A small positive constant ($ϵ={10}^{-7}$) is utilized. The remaining variables remain the same as in Equation (44).

The Adam optimizer integrates the momentum and RMSP algorithms in the following formulation:

$$w_{i+1}=w_i-{\widehat{m}}_i\left(\frac{\alpha }{\sqrt{{\widehat{v}}_i}+ϵ}\right),$$

(47)

where

$${\widehat{m}}_i=\frac{m_i}{1-{\beta }_1},{\widehat{v}}_i=\frac{v_i}{1-{\beta }_2},$$

(48)

where $m_t$ and $v_t$ follow the updating process as described above. We utilize the Adam optimizer within Tensorflow and set ${\beta }_1=0.9,{\beta }_2=0.999$ for all neural network training in this study.

2.5. Generative Adversarial Network Models

GANs are a state-of-the-art generative modeling strategy with an innovative DNN architecture. In this section, we introduce GANs along with their variations, namely, cGAN and the regGAN-TL.

2.5.1. Generative Adversarial Networks

As a type of generative model, GANs consist of two neural networks, a generator and a discriminator (Figure 3) [33]. Initially, the generator produces random outputs according to random input variables, however, as it receives feedback from the discriminator, it learns to generate more realistic samples over training. Conversely, the discriminator is trained on generated samples by the generator and an existing training dataset. The discriminator distinguishes between existing and generated shapes and provides feedback to the generator by assigning probabilities to each sample, indicating how likely the shape is from the existing data. During the training process, the generator and the discriminator compete with each other in an adversarial manner, which encourages the improvement of both models. Once trained, the generator generates samples so similar to the existing data that the discriminator cannot differentiate between them.

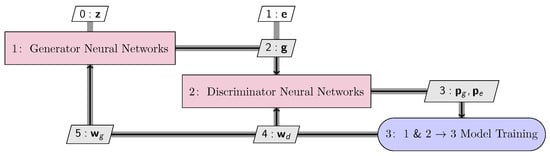
Figure 3. GANs contain a discriminator to compete with the generator. The generator generates shapes ($\mathbf{g}$) based on random variables ($\mathbf{z}$), typically following user-defined distributions (uniform distributions in this work). The discriminator distinguishes between the existing data ($\mathbf{e}$) and the generated data ($\mathbf{g}$) by predicting probabilities. During training, the discriminator adjusts its weights (${\mathbf{w}}_d$) to make the probability ${\mathbf{p}}_g$ (i.e., $\mathbf{g}$ being existing data) approach zero, while increasing the probability ${\mathbf{p}}_e$ (i.e., $\mathbf{e}$ being existing data) towards one. In contrast, the generator adjusts its weights (${\mathbf{w}}_g$) to increase the probability of ${\mathbf{p}}_g$ towards one. The generator after training generates shapes similar to the existing data.

Training a GAN model mathematically follows a minimax setup [33]

$$\underset{G}{\min }\underset{D}{\max }{\mathcal{L}}_{\mathrm{GAN}}(D,G)={\mathbb{E}}_{\mathbf{x}\sim P_{\mathrm{data}}}\left[\log D\left(\mathbf{x}\right)\right]+{\mathbb{E}}_{\mathbf{z}\sim P_{\mathbf{z}}}\left[\log \left(1-D\left(G\left(\mathbf{z}\right)\right)\right)\right],$$

(49)

where $\mathbf{x}$ is sampled from the existing data distribution $P_{\mathrm{data}}$, $\mathbf{z}$ is sampled from random variable distributions $P_{\mathbf{z}}$, and G and D are the generator and discriminator, respectively. Hence, a trained GAN model is able to generate realistic designs with ample shape variability within prior noise variable distributions.

2.5.2. Conditional Generative Adversarial Networks

As an extension to the vanilla GAN, cGAN [37] integrates additional conditioning information into the generative process (Figure 4). In cGAN, both the generator and the discriminator receive random noise samples as input as well as additional conditioning information $\mathbf{d}$. The $\mathbf{d}$ condition provides guidance to the generator to produce samples that correspond with the specified conditions. The $\mathbf{d}$ condition can be represented in various forms—for example, class labels and text descriptions—that depend on the implementation. The generator combines the prior input $\mathbf{z}$ and $\mathbf{d}$ in a joint hidden representation that takes advantage of the adversarial training framework’s flexibility in composing. In addition, the discriminator takes $\mathbf{d}$ and $\mathbf{y}$ pairs as well as generated shapes by the generator to accomplish the adversarial competition with the generator. Similar to the GAN loss function (Equation (49)), the cGAN loss function is given by a minimax problem involving the $\mathbf{d}$ condition,

$$\underset{G}{\min }\underset{D}{\max }{\mathcal{L}}_{\mathrm{cGAN}}(D,G)={\mathbb{E}}_{\mathbf{y}\sim P_{\mathrm{data}}\left(\mathbf{y}\right)}\left[\log D\left(\mathbf{y}\right|\mathbf{d})\right]+{\mathbb{E}}_{\mathbf{z}\sim P_{\mathbf{z}}\left(\mathbf{z}\right)}\left[\log (1-D(G\left(\mathbf{z}\right|\mathbf{d}\left)\right))\right].$$

(50)

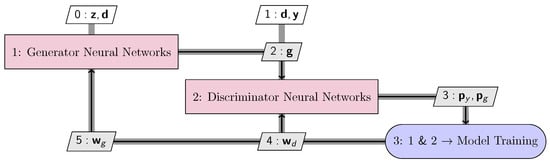
Figure 4. cGAN has similar structures to the vanilla GAN (Figure 3). cGAN take design requirements ($\mathbf{d}$) and random variables ($\mathbf{z}$) as input for the generator network. The true optimal takeoff trajectories ($\mathbf{y}$), corresponding $\mathbf{d}$, and generated data ($\mathbf{g}$) are considered as inputs for the discriminator. The discriminator outputs the probabilities of $\mathbf{y}$ and $\mathbf{g}$ being existing data.

Furthermore, cGAN is capable of dealing with regression tasks encoding the regression labels (i.e., model observations) as additional conditioning information (Figure 4). Similar to the original GAN, the cGAN generator takes random variables combined with arbitrary model observations as an additional group of inputs. The purpose is to create data associated with model observations. Attempting to distinguish between generated and real data, the discriminator takes both generated samples $\mathbf{g}$ and real data pairs ($\mathbf{d}$ and $\mathbf{y}$) as inputs. The cGAN generator learns to map the random noise variables and model observations to corresponding data samples through training, assisting in regression tasks by generating samples consistent with the given aim values. This technique provides a means to handle problems with complex mappings and incorporate the adversarial feature of GAN into the regression process. In our work, $\mathbf{y}$ are the predicted eVTOL optimal takeoff trajectory control points, $\mathbf{d}$ includes design requirements, and we set $\mathbf{z}$ with only one element and assign the Uniform(0, 1) distribution to $\mathbf{z}$. For regression tasks, an average of the predictions over a fixed set of $\mathbf{d}$ and 100 randomly sampled $\mathbf{z}$ is considered as the predicted model response [37], which is the optimal takeoff trajectory in this work. The network architecture settings for the generator and the discriminator within cGAN will be discussed in Section 2.5.3.

2.5.3. Regression Generative Adversarial Networks with Transfer Learning

The regGAN model has a similar structure to cGAN (Figure 4) but only takes design requirements ($\mathbf{d}$) as the input to the generator (Figure 5). Moreover, regGAN incorporates a combined loss function of a contextual loss via ${\mathcal{L}}_{\mathrm{MSE}}$ (Equation (41)) and an adversarial loss via ${\mathcal{L}}_{\mathrm{BC}}$ (Equation (42)) for model training. Thus, regGAN couples the predictive feature of surrogate models and the generative feature of GAN models. The combined loss function is as follows.

$$\begin{array}{cc}\hfill \underset{G}{\min }\underset{D}{\max }{\mathcal{L}}_{\mathrm{regGAN}}(D,G)& =w_{\mathrm{MSE}}·\left(\underset{G}{\min }{\mathcal{L}}_{\mathrm{MSE}}\left(G\right)\right)+w_{\mathrm{BC}}·\left(\underset{G}{\min }\underset{D}{\max }{\mathcal{L}}_{\mathrm{BC}}(D,G)\right)\hfill \end{array}$$

(51)

$$\begin{array}{cc}\hfill & =w_{\mathrm{MSE}}·\underset{G}{\min }\frac{1}{N}\sum _{i=1}^N{\left({\left|{\mathbf{y}}_i-G\left({\mathbf{d}}_i\right)\right|}_2\right)}^2\hfill \end{array}$$

(52)

$$\begin{array}{cc}\hfill & +w_{\mathrm{BC}}·\underset{G}{\min }\underset{D}{\max }\left({\mathbb{E}}_{\mathbf{y}\sim P_{\mathrm{data}}}\left[\log D\left(\mathbf{y}\right)\right]+{\mathbb{E}}_{\mathbf{d}\sim P_{\mathbf{d}}}\left[\log (1-D(G\left(\mathbf{d}\right)\left)\right)\right]\right),\hfill \end{array}$$

(53)

where $w_{\mathrm{MSE}}$ and $w_{\mathrm{BC}}$ are constant weights on ${\mathcal{L}}_{\mathrm{MSE}}$ and ${\mathcal{L}}_{\mathrm{BC}}$, respectively.

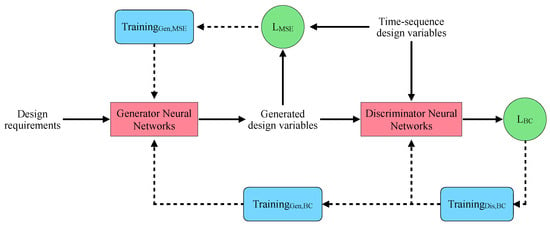
Figure 5. regGAN includes a generator and a discriminator in common with the vanilla GAN and cGAN. The generator generates time-sequence design variables on corresponding design requirements through a DNN. The discriminator takes generated optimal designs and true time-sequence optimal trajectories in order to distinguish the differences. This results in an adversarial competition, which causes an adversarial loss function via ${\mathcal{L}}_{\mathrm{BC}}$ to train the generator and the discriminator. Additionally, we minimize the contextual loss via ${\mathcal{L}}_{\mathrm{MSE}}$ between generated and true design variables to explicitly train the generator for regression tasks.

Similar to conventional surrogates, the ${\mathcal{L}}_{\mathrm{MSE}}$ navigates the predictions of regGAN to match ground truth observations. Meanwhile, ${\mathcal{L}}_{\mathrm{BC}}$ arrives at similar patterns between observations and predicted results because of competitive training through the GAN architecture. In this work, the regGAN generator reads design requirements ($\mathbf{d}$) and predicts corresponding optimal takeoff trajectories ($\mathbf{y}$). The characteristics of the eVTOL takeoff trajectory prediction make it necessary to develop and introduce the regGAN surrogate. First, regGAN adopts the predictive ability of DNNs through the generator. Second, the optimal takeoff trajectory profiles typically follow realistic patterns, such as ascending optimal power and wing-to-vertical angles in general. In this manner, the adversarial loss based on the GAN architecture facilitates the training by automatically filtering out unrealistic trajectory profiles.

The regGAN-TL method consists of two key steps for implementation. First, we train regGAN models with only the ${\mathcal{L}}_{\mathrm{MSE}}$ by setting $w_{\mathrm{MSE}}=1$ and $w_{\mathrm{BC}}=0$ that are in effect direct DNN surrogates. We save the best model with the highest validation accuracy on 200 validation samples during the training. We then integrate the ${\mathcal{L}}_{\mathrm{BC}}$ into ${\mathcal{L}}_{\mathrm{regGAN}}$ by setting $w_{\mathrm{BC}}=0.01,0.001,\mathrm{and}0.0001$, respectively. regGAN-TL models are then trained starting with the pre-trained best regGAN model for an enhanced predictive performance. The core ingredient of regGAN-TL is to harness the predictive power of DNNs and fine-tune the trained model by matching the predicted shapes further with training data patterns. The observations in training datasets by the generator are scaled within the range of [0, 1] via MinMaxScaler within Scikit-learn.

To summarize, the key difference between regGAN-TL and conventional surrogates (such as MOGP) lies in the introduction of a discriminator to facilitate the model training. Within the GAN-series variants, regGAN-TL directly captures the mapping between input and output spaces rather than relying on the conditioning information of cGAN and enhances vanilla regGAN performance via the TL strategy. For fair comparisons, we implement the same architectures and setups (Table 1) to train cGAN, regGAN, and regGAN-TL surrogates and predict the power profile, wing angle profile, and total takeoff time, separately. Please refer to Section 3 for a detailed comparison between the proposed regGAN-TL and the reference surrogates.

Table 1. Neural architectures and training setups of the generator and the discriminator within regGAN.

	Generator	Discriminator
Input layer	5 neurons, no activation	21 neurons, no activation
Hidden layer 1	100 neurons, relu activation	100 neurons, relu activation
Hidden layer 2	100 neurons, relu activation	100 neurons, relu activation
Output layer	21 neurons/1 neuron, sigmoid activation	1 neurons, sigmoid activation
Training algorithm	Adam optimizer	Adam optimizer
Training parameters	${\beta }_1=0.9$, ${\beta }_2=0.999$	${\beta }_1=0.9$, ${\beta }_2=0.999$
Learning rate	0.001	0.001
Batch size	20	20
Epochs	1000	1000

2.6. Verification Metrics

Mean $L_1$ relative error (${\overline{ϵ}}_{L_1}$) is commonly used to evaluate surrogate predictive performance. The $L_1$ relative error, also known as the mean absolute percentage error, is a metric used to measure the relative $L_1$ norm difference between predictions compared with actual values.

$${\overline{ϵ}}_{L_1}=\frac{1}{N_{\mathrm{test}}}\sum _{i=1}^{N_{\mathrm{test}}}\frac{\left|{\mathbf{y}}_{\mathrm{pred},i}-{\mathbf{y}}_{\mathrm{true},i}\right|}{\left|{\mathbf{y}}_{\mathrm{true},i}\right|}\times 100\%,$$

(54)

where $N_{\mathrm{test}}$ is the number of testing samples, ${\mathbf{y}}_{\mathrm{true},i}$ and ${\mathbf{y}}_{\mathrm{pred},i}$ are the true observations and predicted values of the ith set of design requirements, and $\left|·\right|$ is the $L_1$ norm operation. The relative accuracy is calculated as

$$AC{C}_{L_1}=1-{\overline{ϵ}}_{L_1}.$$

(55)

The $L_1$ relative accuracy measures the average relative match between predicted values and true observations, expressed as a percentage. It gives an indication of the degree to which surrogate predictions agree with true observations, relative to true observations, providing deeper insights through the errors relative to model response magnitudes. In this work, we compute relative accuracy for each testing sample and quantify the predictive performance using the mean and standard deviation of the computed accuracy.

3. Results and Discussion

In this section, we demonstrate the performance of regGAN-TL on the optimal takeoff trajectory predictions and compare its performance against MOGP, cGAN, and vanilla regGAN surrogates. MOGP represents a promising traditional surrogate method while cGAN and vanilla regGAN both adopt GAN architectures. We elaborate on the problem formulation and result discussion as follows.

3.1. Problem Formulation

Table 2 presents the formulation of the takeoff trajectory optimization problem. We aim to minimize the electrical energy consumed to reach a minimum vertical displacement of 305 m and a minimum horizontal speed of 67 m/s. The design requirements (i.e., design constraints and flight conditions) consist of angle of attack range constraints ${\alpha }_{lim}\in [10,15]$ deg, the maximum acceleration magnitude constraint $a_{\max }\in [0.2g,0.4g]$ (g is the gravitational acceleration), the propeller-induced velocity factor $k_{\mathrm{in}}\in [0.3,1.0]$, the electrical and mechanical loss factor $k_{\mathrm{elec}}\in [0.7,0.9]$, and the wing size factor $S_{\mathrm{ref}}\in [0.9,1.0]$. Note that the $a_{\max }$ constraint addresses passenger comfort for future air transportation systems, although eVTOL vehicles currently have not been widely utilized for these applications. The design variables are the time-sequence electrical power ($\mathbf{P}$) and wing angle to vertical ($\mathit{\theta }$), each of which is parameterized using 21 quadratic curve control points, and the total takeoff time ($t_{\mathrm{flight}}$). As mentioned in Section 2, we solve this takeoff trajectory design problem using the open-source Dymos package within OpenMDAO.

Table 2. Takeoff trajectory optimization problem formulation.

	Function or Variable	Description	Quantity
minimize	E	Electrical energy consumed
w.r.t.
	$\mathbf{P}$	Electrical power using 21 quadratic curve control points	21
	$\mathit{\theta }$	Wing angle to vertical using 21 quadratic curve control points	21
	$t_{\mathrm{flight}}$	Takeoff time	1
		Total design variables	43
subject
	$y_{\mathrm{final}}\ge 305$ m	Final vertical displacement constraint	1
to
	$x_{\mathrm{final}}\le 1400$ m	Final horizontal displacement constraint	1
	$v_x=67$ m/s	Final horizontal speed constraint	1
	$y\ge 0$ m	Vertical displacement constraint	1
	$a\le a_{\max }$	Acceleration constraint	1
	$\alpha \le {\alpha }_{lim}$	Positive stall-angle constraint	1
	$\alpha \ge -{\alpha }_{lim}$	Negative stall-angle constraint	1
		Total constraints	7
Conditions
	$k_{\mathrm{in}}$	Propeller-induced velocity factor
	${\alpha }_{lim}$	Angle of attack constraint value
	$a_{\max }$	Maximum acceleration magnitude
	$k_{\mathrm{elec}}$	Electrical and mechanical loses factor
	$S_{\mathrm{ref}}$	Wing size factor

3.2. Surrogate-Base Inverse Mapping

We use 1000 random Latin hypercube sampling (LHS) points [72] as training data for the MOGP and cGAN surrogates and 300 LHS testing samples to verify predictive performance. Additionally, we use 200 LHS validation samples to evaluate the predictive performance and save the model with the lowest validation error during the training. We integrate MOGP with Matérn 3/2 and SE correlation functions paired with constant and linear basis functions (Section 2.3). Results show that the SE correlation function provides higher testing accuracy (${\mu }_{\mathrm{test}}$) than the Matérn 3/2 function, while the basis function exerts only minor effects (Table 3). As the Matérn parameter $\nu$ approaches zero, the Matérn function converges to the SE function, which is infinitely differentiable. Thus, a smooth mapping via MOGP fits well with the eVTOL takeoff trajectory predictions. In addition, the MOGP M2 surrogate (SE correlation and linear basis function) in Table 3 significantly reduces the standard deviations (${\sigma }_{\mathrm{test}}$) in testing accuracy compared with the Matérn-based MOGP surrogates. A lower ${\sigma }_{\mathrm{test}}$ represents consistent predictive accuracy over the testing dataset, which further confirms the better performance of the SE-based MOGP. Moreover, we train the cGAN models through MSE loss or BC loss, both of which improve the ${\mu }_{\mathrm{test}}$ to above 98%, while the best MOGP ${\mu }_{\mathrm{test}}$ on $\mathbf{P}$ and $\mathit{\theta }$ are 92.5% and 94.7%, respectively, (Table 4). The cGAN surrogates are able to further reduce the ${\sigma }_{\mathrm{test}}$ for more robust predictive performance.

Table 3. MOGP model configurations and mean ± standard deviation of testing accuracy on the testing data set. SE stands for SE kernel function.

Model	Correlation Function	Basis Function	${\mathbf{ACC}}_{{\mathit{L}}_1}$, ${\mathit{t}}_{\mathbf{flight}}$ (%)	${\mathbf{ACC}}_{{\mathit{L}}_1}$, P (%)	${\mathbf{ACC}}_{{\mathit{L}}_1}$, $\mathit{\theta }$ (%)
M1	SE	constant	99.6 ± 0.313	92.5 ± 2.93	94.7 ± 2.30
M2	SE	linear	99.5 ± 0.372	92.5 ± 2.89	94.7 ± 2.32
M3	Matérn	constant	96.7 ± 2.65	88.7 ± 4.85	94.6 ± 2.20
M4	Matérn	linear	96.7 ± 2.61	91.4 ± 2.73	94.6 ± 2.20

Table 4. cGAN models exhibit better predictive performance than MOGP (Table 3) in terms of mean and standard deviation of testing accuracy.

Model	Loss Function	${\mathbf{ACC}}_{{\mathit{L}}_1}$, ${\mathit{t}}_{\mathbf{flight}}$ (%)	${\mathbf{ACC}}_{{\mathit{L}}_1}$, P (%)	${\mathbf{ACC}}_{{\mathit{L}}_1}$, $\mathit{\theta }$ (%)
cGANBC	${\mathcal{L}}_{\mathrm{BC}}$	98.4 ± 0.858	99.0 ± 0.653	98.6 ± 0.424
cGANMSE	${\mathcal{L}}_{\mathrm{MSE}}$	98.3 ± 0.843	98.8 ± 0.745	98.7 ± 0.426

For a clearer and more convincing comparison, we select an arbitrary case from the testing data for visualization (Table 5). The predictive performances of MOGP M2 and cGAN surrogates (Table 6) agree well with testing accuracy counterparts. Under the design requirement setup in Table 5, we complete simulation-based design as a reference (Figure 6). The simulation-based optimal design shows that the $\mathbf{P}$ and $\mathit{\theta }$ profiles follow ascending trends in general. The eVTOL aircraft tends to start with lower powers at low wing angles (close to vertical displacement direction). Especially in the first 7.5 s, the optimal trajectory design gradually increases power to the maximum and almost linearly turns the wings towards the forward direction, which maintains the acceleration at the upper bound constraint. From 7.5 s to 12.5 s, the aircraft maintains the maximum power and minor changes of wing angle and achieves a decreasing acceleration until the latter is close to zero. The vertical displacement plot shows that the aircraft completes most of the vertical displacement in the first half of the trajectory, i.e., 0∼12.5 s. In the second half of the trajectory, i.e., 12.5∼25 s, the power remains at the maximum level while the wings almost linearly turn forward until reaching the horizontal direction. The increasing acceleration and minor change in vertical displacement reveal that the second phase is mainly concerned with reaching the required horizontal speed constraint. The surrogate predictions show that the best MOGP model has obvious differences with the reference optimal while the cGAN surrogates could match the optimal $\mathbf{P}$ and $\mathit{\theta }$ profiles well. These results confirm that cGAN outperforms MOGP, meaning that the GAN-architecture-enabled surrogates are capable of regression tasks. However, the computed quantities, such as acceleration, exhibit unreasonable wiggles and even violate the acceleration constraint during the flight task, which would lead to poor passenger comfort experience. Therefore, we must seek novel strategies that more effectively leverage the GAN architecture for predictions.

Table 5. Design requirements for visualization case 1.

Design Requirements	Values
Propeller-induced velocity factor, $k_{\mathrm{in}}$	87.75 (%)
Angle of attack constraint, ${\alpha }_{\lim }$	±12.25833333 (deg)
Acceleration, $a_{\max }$	0.38766667 (g)
Electrical and mechanical loses factor, $k_{\mathrm{elec}}$	0.761
Wing size, $S_{\mathrm{ref}}$	0.9285

Table 6. Predictive accuracy of visualization case 1 using MOGP M2 and a cGAN surrogate with ${\mathcal{L}}_{\mathrm{BC}}$ and ${\mathcal{L}}_{\mathrm{MSE}}$ agree well with the mean testing accuracy.

Model	${\mathbf{ACC}}_{{\mathit{L}}_1}$, ${\mathit{t}}_{\mathbf{flight}}$ (%)	${\mathbf{ACC}}_{{\mathit{L}}_1}$, P (%)	${\mathbf{ACC}}_{{\mathit{L}}_1}$, $\mathit{\theta }$ (%)
MOGP M2	99.8	94.7	91.0
cGANBC	98.8	99.8	98.7
cGANMSE	98.9	99.7	98.7

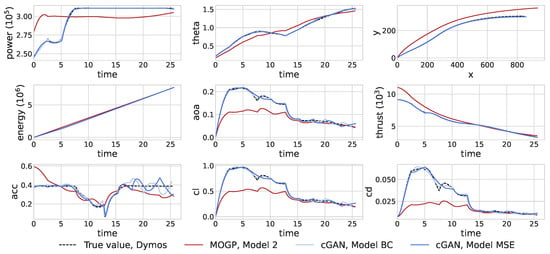
Figure 6. Optimal takeoff trajectory profile verification against simulation-based ground truth shows that cGAN surrogates capture the general trends well and outperform MOGP. However, cGAN predictions still miss minor features and exhibit unreasonable shapes on computed quantities such as acceleration.

To further improve the predictive performance, we implement the proposed regGAN-TL (Section 2.5.3). Table 7 indicates that the vanilla regGAN with $w_{\mathrm{MSE}}=1$ and $w_{\mathrm{BC}}=0$, which is in effect a feed-forward neural network, achieves over 99% accuracy using only 200 training samples and 99.5% accuracy using 400 samples. As introduced in Section 2.5.3, we aim to integrate the predictive power of deep neural networks and the pattern-matching feature of GAN architectures. The regGAN-TL surrogates enhance the predictive performance of the CL1 model (regGAN with $w_{\mathrm{BC}}=0$ and CL means combined loss) to achieve over 99.5% accuracy on $\mathbf{P}$ and $\mathit{\theta }$ predictions (CL4 TL in Table 7) using only 200 training samples. In view of the outstanding predictive capability of the model, we completed a parametric study with respect to fewer training samples while using the same validation and testing datasets. The results show that CL4 TL extensively and consistently improves the predictive performance. Specifically, CL4 TL reaches over 95% accuracy using only 10 samples, 98% using 50 samples, and 99% using 100 training samples. Since the cGAN prediction results reveal that over 98% accuracy is not sufficient to satisfy constraints, we set the accuracy threshold to 99% or 99.5%. The regGAN-TL CL4 surrogate reduces the training cost by half to achieve either accuracy threshold, 99% or 99.5%, compared with regGAN CL1. In addition, regGAN-TL CL4 consistently and extensively lowers the ${\sigma }_{\mathrm{test}}$ at different numbers of training samples compared with the regGAN CL1 counterparts. We also conducted a parametric study by setting the weighting factor $w_{\mathrm{BC}}$ to be 0.01, 0.001, or 0.0001 (Table 7). The results show that the regGAN-TL surrogates possess increasing accuracy with decreasing $w_{\mathrm{BC}}$. This is due to the fact that the GAN architecture tends to match data patterns rather than predict observations such that a relatively low $w_{\mathrm{BC}}$ better respects the prediction feature of feed-forward neural networks.

Table 7. Parametric study for regGAN-TL models further confirms the outstanding performance of regGAN-TL in terms of the mean and standard deviation of testing accuracy with respect to the number of training samples for each design variable group. Note that we only vary $w_{\mathrm{BC}}$ while keeping $w_{\mathrm{MSE}}$ as 1. CL represents a combined loss for model training.

Model	${\mathit{w}}_{\mathbf{BC}}$	Samples	${\mathbf{ACC}}_{{\mathit{L}}_1}$, ${\mathit{t}}_{\mathbf{flight}}$ (%)	${\mathbf{ACC}}_{{\mathit{L}}_1}$, P (%)	${\mathbf{ACC}}_{{\mathit{L}}_1}$, $\mathit{\theta }$ (%)
CL1	0	10	94.4 ± 3.96	92.1 ± 5.15	96.9 ± 1.13
		20	93.6 ± 3.80	96.2 ± 1.91	97.3 ± 1.19
		50	96.3 ± 2.33	97.7 ± 1.20	98.0 ± 0.771
		100	98.4 ± 0.748	98.8 ± 0.785	99.1 ± 0.377
		200	99.2 ± 0.468	99.3 ± 0.434	99.5 ± 0.226
		400	99.5 ± 0.314	99.5 ± 0.389	99.6 ± 0.167
CL2 TL	0.01	10	93.7 ± 3.62	93.7 ± 2.52	96.6 ± 1.21
		20	93.4 ± 3.57	96.0 ± 2.24	96.8 ± 1.34
		50	95.3 ± 0.993	97.4 ± 1.37	97.3 ± 0.835
		100	98.4 ± 0.528	98.2 ± 1.21	98.2 ± 0.323
		200	99.0 ± 0.326	98.2 ± 0.712	98.6 ± 0.301
CL3 TL	0.001	10	94.3 ± 3.13	95.4 ± 3.12	97.5 ± 1.16
		20	95.7 ± 1.99	97.8 ± 1.27	98.1 ± 0.908
		50	97.3 ± 0.871	98.4 ± 1.21	98.6 ± 0.476
		100	99.0 ± 0.471	98.7 ± 0.830	99.3 ± 0.274
		200	99.1 ± 0.347	99.0 ± 0.447	99.3 ± 0.213
CL4 TL	0.0001	10	95.1 ± 3.36	95.4 ± 3.01	97.5 ± 1.20
		20	96.8 ± 1.95	97.8 ± 1.27	98.1 ± 0.950
		50	98.1 ± 1.05	98.5 ± 1.06	98.7 ± 0.526
		100	99.2 ± 0.530	99.1 ± 0.828	99.4 ± 0.267
		200	99.3 ± 0.364	99.5 ± 0.296	99.6 ± 0.179

To achieve a more thorough comparison, we completed another parametric study on the vanilla regGAN surrogates by varying $w_{\mathrm{BC}}$ from 0.01, 0.001, to 0.0001 (Table 8). The results indicate that regGAN with $w_{\mathrm{BC}}=0.001$ achieves over 99% accuracy using 200 training samples while only regGAN with $w_{\mathrm{BC}}=0.01$ can achieve 99.5% accuracy on $\mathbf{P}$ and $\mathit{\theta }$ using 400 samples. This further confirms the outstanding predictive performance of regGAN-TL and a 50% computational cost reduction on reaching either the 99% or 99.5% accuracy thresholds. Note that the accuracy comparison is mainly on $\mathbf{P}$ and $\mathit{\theta }$ since $t_{\mathrm{flight}}$ exerts lower effects and regGAN-TL handles the model response with data patterns, such as ascending trends of trajectory profiles.

Table 8. A parametric study on $w_{\mathrm{BC}}$ of the vanilla regGAN in terms of testing accuracy mean ± standard deviation confirms that regGAN-TL (Table 7) possess better performance when provided with the same training data. We keep $w_{\mathrm{MSE}}$ as 1.

Model	${\mathit{w}}_{\mathbf{BC}}$	Samples	${\mathbf{ACC}}_{{\mathit{L}}_1}$, ${\mathit{t}}_{\mathbf{flight}}$ (%)	${\mathbf{ACC}}_{{\mathit{L}}_1}$, P (%)	${\mathbf{ACC}}_{{\mathit{L}}_1}$, $\mathit{\theta }$ (%)
CL2	0.01	200	99.3 ± 0.443	97.8 ± 0.980	98.9 ± 0.427
		400	99.6 ± 0.251	99.6 ± 0.257	99.6 ± 0.145
CL3	0.001	200	99.3 ± 0.380	99.0 ± 0.557	99.1 ± 0.308
		400	99.6 ± 0.343	99.4 ± 0.378	99.4 ± 0.230
CL4	0.0001	200	99.2 ± 0.384	98.8 ± 0.706	98.9 ± 0.494
		400	99.4 ± 0.346	99.4 ± 0.358	99.3 ± 0.249

Similar to the comparison between the MOGP and cGAN surrogates, we select an arbitrary case in the testing dataset for visualization (Table 9). Visualization case 2 has a lower $a_{\max }$ of ∼0.29 m²/s and a higher $k_{\mathrm{elec}}$ of 0.819 while visualization case 1 has $a_{\max }=\sim$0.388 m²/s and $k_{\mathrm{elec}}=0.761$. A lower $a_{\max }$ demands a more smooth and gradual transition and a higher $k_{\mathrm{elec}}$ allows higher power efficiency, which saves energy. The simulation-based optimal design shows that the eVTOL aircraft starts with a lower power than visualization case 1, which is due to the lower $a_{\max }$ constraint and higher $k_{\mathrm{elec}}$ (Figure 7). We note a smoother $\mathit{\theta }$ transition from the vertical to the horizontal direction, with the immediate acceleration staying as $a_{\max }$ for the whole takeoff process. Visualization case 1 exhibits two “separate” phases, with the first phase focused on vertical displacement and the second on horizontal speed. In contrast, visualization case 2 presents no obvious separation, rather, the optimal takeoff designs exhibit a smooth transition, especially on $\mathit{\theta }$. In both visualization cases, we note that the optimal takeoff designs tend to proceed at $a_{\max }$, which makes $a_{\max }$ essential for considering passenger comfort.

Table 9. Design requirements for visualized case 2.

Design Requirements	Values
Propeller-induced velocity factor, $k_{\mathrm{in}}$	82.38333333 (%)
Angle of attack constraint, ${\alpha }_{\lim }$	±12.85833333 (deg)
Acceleration, $a_{\max }$	0.29166667 (g)
Electrical and mechanical loses factor, $k_{\mathrm{elec}}$	0.819
Wing size, $S_{\mathrm{ref}}$	0.92916667

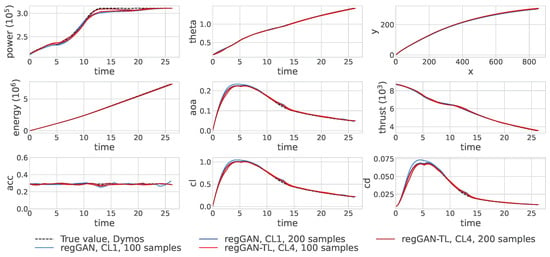
Figure 7. Optimal takeoff trajectory profiles predicted by regGAN-TL CL4 using 200 training samples reach almost no visualizable differences with simulation-based ground truth and outperform the other surrogates. In addition, the regGAN-TL CL4 surrogate has over 99.5% accuracy and is able to match the computed quantities to guarantee constraint satisfaction.

Table 10 shows that regGAN-TL CL4 is able to achieve 99.5% on $\mathbf{P}$ and $\mathit{\theta }$, which agree with the mean testing accuracy (Table 7). Figure 7 shows that all predicted trajectories by the regGAN-TL CL4 surrogates match the simulation-based reference optimal design with almost no noticeable difference. Even for the reconstructed acceleration profile, which cGAN struggles to deal with, regGAN-TL CL4 matches very well with this almost straight-line profile. In contrast, the vanilla regGAN surrogates using 200 samples cannot perform as well as regGAN-TL CL4 with 200 training samples. We thus conclude that the proposed regGAN-TL method does exhibit outstanding predictive potential.

Table 10. Testing accuracy for visualization case 2 of regGAN model CL1 and CL4 TL.

Model	${\mathit{w}}_{\mathbf{BC}}$	Samples	${\mathbf{ACC}}_{{\mathit{L}}_1}$, ${\mathit{t}}_{\mathbf{flight}}$ (%)	${\mathbf{ACC}}_{{\mathit{L}}_1}$, P (%)	${\mathbf{ACC}}_{{\mathit{L}}_1}$, $\mathit{\theta }$ (%)
CL1	0	100	98.4	98.7	99.2
CL1	0	200	99.3	99.1	99.7
CL4 TL	0.0001	100	98.4	98.8	99.6
CL4 TL	0.0001	200	99.4	99.5	99.7

4. Conclusions

In this paper, we investigated surrogate-based optimal takeoff trajectory predictions with minimum energy consumption for electric vertical takeoff and landing (eVTOL) aircraft. We proposed and demonstrated the regGAN-TL surrogate, i.e., regression generative adversarial network (regGAN) enhanced by transfer learning (TL). The proposed regGAN-TL outperformed reference surrogates to achieve over 99.5% accuracy with a lower training cost. The main contribution of this work can be summarized as follows.

Firstly, we introduced the surrogate-based inverse mapping optimization architecture into eVTOL optimal trajectory design. In particular, we leverage surrogate models to predict optimal takeoff trajectories directly from design requirements, including flight conditions and design requirements. Well-trained surrogates enabled real-time eVTOL takeoff trajectory designs with no need to execute any optimization. However, each training sample requires a simulation-based trajectory design optimization, which necessitates developing novel surrogate modeling strategies.

Secondly, we proposed the regGAN-TL surrogate to further enhance regGAN predictive performance. Results showed that regGAN-TL achieved a 99.5% accuracy in predicting optimal design variables using only 200 training samples. In addition, visualization cases verified that the regGAN-TL trajectory exhibited no noticeable differences with simulation-based optimal designs. Moreover, regGAN-TL extensively outperformed representative reference surrogate models, including the multi-output Gaussian process, conditional generative adversarial networks, and a vanilla regGAN. The best reference surrogate required at least 400 samples to achieve a 99.5% accuracy, denoting a 50% computational cost reduction by the use of regGAN-TL.

Thirdly, the successful implementation of regGAN-TL in eVTOL aircraft optimal takeoff trajectory design enriches the literature in this field. We introduced various surrogate modeling strategies into eVTOL takeoff trajectory design, with the proposed regGAN-TL exhibiting the best predictive performance. The energy efficiency achieved in this work pushes eVTOL aircraft another step forward toward broad, real-world applications. The inverse mapping architecture and the regGAN-TL method are also extendable toward other relevant engineering optimizations.

At the same time, it is acknowledged that, despite the promising performance by regGAN-TL, the simulation models used in this work are not high-fidelity but simply effective for describing the physics. We will increase the fidelity of the simulation models in future work, which may lead to a more challenging mapping and higher training cost for surrogate modeling, especially when strong nonlinear characteristics (such as strong shocks in high-speed flow mechanics) exist. In addition, the inverse mapping optimization architecture requires each training sample to be an optimal design through design optimization, which may make the data acquisition process computationally more intensive. So, we plan to investigate and develop other advanced deep learning architectures within the structure of regGAN-TL. Finally, we would also like to compare our method with more reference approaches and validate its performance via flight tests with real drones.