Graph Convolution Point Cloud Super-Resolution Network Based on Mixed Attention Mechanism

Abstract

In recent years, point cloud super-resolution technology has emerged as a solution to generate a denser set of points from sparse and low-quality point clouds. Traditional point cloud super-resolution methods are often optimized based on constraints such as local surface smoothing; thus, these methods are difficult to be used for complex structures. To address this problem, we proposed a novel graph convolutional point cloud super-resolution network based on a mixed attention mechanism (GCN-MA). This network consisted of two main parts, i.e., feature extraction and point upsampling. For feature extraction, we designed an improved dense connection module that integrated an attention mechanism and graph convolution, enabling the network to make good use of both global and local features of the point cloud for the super-resolution task. For point upsampling, we adopted channel attention to suppress low-frequency information that had little impact on the up-sampling results. The experimental results demonstrated that the proposed method significantly improved the point cloud super-resolution performance of the network compared to other corresponding methods.

1. Introduction

The point cloud, a collection of sampling points with spatial coordinates obtained by 3D scanning, finds extensive use in various fields, including autonomous driving and robotics. However, its unstructured and irregular characteristics also pose significant challenges. For instance, the point cloud data collected using acquisition equipment is often locally sparse and non-uniform due to terrain conditions and weather factors. The original point cloud’s characteristics make subsequent processing and applications extremely challenging. As a solution to this problem, the technology of point cloud super-resolution (SR) has drawn broad attention from industry and academia. This technology generates dense, complete, and uniform outputs, thereby resolving the limitations of the original point cloud data set.

Most traditional point cloud SR methods [1,2,3,4] are optimized based on constraints such as local surface smoothness and other shape priors. While these methods are effective for simple models, they fall short when it comes to complex and specialized structures. They require significant computation and perform poorly in practical applications. Hence, there is a pressing need for further improvement in both computation and performance to make them more suitable for real-world scenarios.

Deep learning has achieved significant success in the field of image SR, resulting in the emergence of various excellent image SR networks such as SRCNN [5], MDSR [6], VDSR [7], and ESPCN [8], which have further promoted the development of point cloud SR technology. Currently, researchers use either multi-branch MLPs (Multilayer Perceptron) [9] or methods based on duplicated upsampling operations [10,11]. Multi-branch MLPs are widely used as a general feature extraction method to extract features from point cloud data in deep learning. However, they may overlook critical information from neighboring nodes in 3D point cloud data while performing feature extraction. Moreover, methods based on duplicated upsampling operations not only lead to the loss of local information in the generated high-resolution point clouds, but they also increase the model’s computational parameters, reducing its training efficiency and consuming significant computational resources.

In this paper, we propose a graph convolution point cloud super-resolution network based on a mixed attention mechanism (GCN-MA) to address the challenges faced by traditional point cloud SR methods. GCN-MA consists of two primary parts. The first part is designed for feature extraction, where an improved dense connected network (DCN) comprising multiple feature extraction modules (FEM) is employed to generate high-quality feature maps. Each FEM consists of a dilated graph convolution block (DGCB) and mixed attention mechanism. The mixed attention mechanism involves channel attention within a DGCB to filter information on the channel dimension and multi-head attention between a DGCB to make the network focus on the most valuable information from the convolution layer of different depths. Therefore, the mixed attention mechanism can extract useful high-frequency information for point cloud detail recovery. Finally, the different feature information of each FEM is assigned adaptive weights to enhance the network’s learning ability for better results. The second part of the GCN-MA is the point upsampling module followed by a standard coordinate reconstructor. The output features from the DCN are first extended through the point upsampling module. Then, the channel attention is adopted to suppress low-frequency information that has little impact on the upsampling results. Finally, the feature vectors are rearranged to generate high-quality point cloud data using a standard coordinate reconstructor.

In summary, the main contributions of this paper are summarized as follows:

(1)

We propose the Graph Convolution Point Cloud Super-Resolution Network based on a Mixed Attention Mechanism (GCN-MA), which is designed to fully exploit the global and local features of point cloud through the attention mechanism and improve the network’s learning ability. The GCN-MA pipeline comprises two major parts: feature extraction and point upsampling.

(2)

For feature extraction, we employ an improved dense connected network (DCN) consisting of multiple feature extraction modules (FEM) to generate high-quality feature maps. Each FEM includes a dilated graph convolution block (DGCB) and a mixed attention mechanism. Moreover, adaptive weight allocation between FEMs enhances the learning ability for better point cloud detail recovery.

(3)

The mixed attention mechanism is designed to integrate channel attention within DGCB and multi-head attention between DGCB to make the network focus on the most valuable information from the convolution layer of different depths, making good use of global and local features of point cloud.

(4)

In the point upsampling module, we also adopt channel attention to suppress low-frequency information with little impact on the upsampling results. Following the point upsampling module, feature vectors are rearranged to generate high-quality point cloud data through a standard coordinate reconstructor.

The remainder of the paper is structured as follows. Section 2 presents a review of related work, while Section 3 outlines the details of our proposed point cloud super-resolution method. In Section 4, we conduct an ablation study and provide experimental comparisons with other relevant point cloud super-resolution methods. Finally, in Section 5, we offer our conclusions and discuss potential future research directions.

2. Related Works

In this section, we mainly introduce two important categories of point cloud SR methods, i.e., traditional point cloud SR and deep-learning-based point cloud SR. For each category of the point cloud SR method, we discuss the main challenges they face, respectively.

2.1. Traditional Point Cloud SR

Point Cloud Super-Resolution (SR), also known as Point Cloud Sampling, aims to generate a uniform and dense point set from a given sparse, uneven, and noisy low-resolution input. The main objective of Point Cloud SR is not only to produce a dense output from sparse input but also to fit the geometric surface represented by the input point set as accurately as possible. Due to the influence of point cloud acquisition equipment, the obtained input point cloud is typically very sparse, noisy, and contains small, unclosed holes. This makes it challenging to express the fine structure of geometric objects.

The traditional Point Cloud Super-Resolution (SR) algorithm is based on optimizing existing point cloud data. Alexa et al. proposed a method based on interpolation that continuously interpolated the vertices of the Voronoi graph in the local tangent space of the point cloud to make the sparse point cloud dense [1]. Although this method could achieve good performance, it could only increase points one by one, making it unsuitable for point clouds with large magnifications. Later, Lipman et al. resampled the surface by introducing the Local Optimal Projection (LOP) operator and reconstructed the surface based on the L1 norm [2]. The algorithm also performed well on noisy data, but it struggled to deal with point clouds that had an uneven initial distribution. Huang et al. improved the LOP method by introducing weights and iterative normal estimation [3]. Later, Huang et al. proposed a progressive method for edge resampling of points, but this method heavily relied on the accuracy of the initial normal direction and required strong prior knowledge to manually adjust the parameters [4]. Heimann V. et al. proposed frequency-selective geometry upsampling for point cloud upsampling, which used DCT basis functions to locally estimate a continuous representation of the point cloud’s surface [12]. In general, most of the traditional methods rely heavily on artificial prior knowledge, such as surface smoothing assumptions, normal direction estimation, etc., and lack the ability to obtain a priori independently from data.

2.2. Deep Learning Based Point Cloud SR

Due to their data-driven nature and learning abilities, deep learning methods have achieved promising success in image super-resolution [5,6,7,8]. Recently, several image SR methods [13,14,15,16,17] incorporate an attention mechanism into networks to emphasize the important components in deep features for more discriminative learning. Liang G. et al. proposed a remote sensing image SR method, which was composed of a graph convolution neural network and multi-scale hybrid attention module [16]. The hybrid attention mechanism they designed aimed to learn the spatial dependence on each channel of the feature graph and focus on the extraction of spatial features. Zhang Q. et al. presented a single-image super-resolution method based on a hybrid domain attention network [17]. Here, two parallel self-attention modules, namely, the spatial self-attention module and the channel self-attention module, were designed in the feature extraction process, which enabled the network to focus on more useful information for image SR reconstruction.

With the success of deep learning in the field of image super-resolution, there have also been significant developments in point cloud super-resolution reconstruction based on deep learning. Some methods incorporate underlying geometric structures from given sparse point clouds into deep learning, making them fundamentally different from the existing image super-resolution techniques. Qian Y. presented a way to upsample point clouds by learning two basic forms of local geometric structures, which required additional supervision in the form of normals, reducing the versatility of the network to a certain extent [18].

Recently, hierarchical feature learning has been commonly used for super-resolution reconstruction of point cloud images. Yu L. et al. proposed the Point Cloud Upsampling Network (PU-Net), which used a multi-branching Multilayer Perceptron (MLP) for feature extraction of point cloud information [9]. The core idea of PU-Net was to learn the multi-scale feature information of each point and expand it at the channel level in the feature space using the MLP. The expanded feature information could be decomposed and reconstructed into a high-resolution point cloud. Wang Y. et al. proposed a block-based upsampling method called 3PU [10]. This progressive upsampling method was conducive to preserving local information, but it was less efficient. Bai Y. et al. constructed BIMS-PU, which integrated the feature pyramid architecture with a bi-directional up and down path [19]. In a parallel manner, the multi-scale features could be produced and aggregated to capture the fine-grained geometric details. PU-Dense was designed to employ a 3D multiscale architecture using sparse convolutional networks, which could hierarchically reconstruct an upsampled point cloud geometry via progressive rescaling and multiscale feature extraction [20].

Furthermore, generative adversarial networks (GANs) have also been widely adopted to achieve better super-resolution reconstruction quality of point clouds. Li R. et al. proposed the PU-GAN method, which incorporated two innovative modules: the up–down–up sampling-based feature expansion and the self-attention module [21]. The use of these modules effectively avoided the complexity of the network structure in the MPU. A frequency-aware GAN for 3D point cloud upsampling was proposed, which could extract high frequency (HF) points and reconstruct a uniform upsampled point cloud with clear HF regions [22]. Liu H. et al. designed a GAN with geometry refiner for point cloud upsampling (PU-Refiner), which could restore the dense point cloud in a coarse-to-fine fashion based on a coarse upsampled point cloud [23]. A multi-modal GAN was developed for LiDAR point cloud sampling, which combined the rich contextual information of images and geometric information of point clouds [24].

In addition, graph convolution has been employed for point cloud super-resolution. Wu H. et al. proposed AR-GCN based on graph networks and adversarial losses to exploit the local similarity of point cloud and the analogy between LR input and HR output [25]. Han B. et al. proposed a graph attention convolution network for point cloud upsampling, which aimed to capture the global and local structured features of point clouds, but the reconstructed performance could be improved [26]. Qian G. et al. proposed PU-GCN, which combined both Inception DenseGCN and NodeShuffle (NS) upsampling modules [27]. In PU-GCN, Inception DenseGCN, as a feature extraction block, could effectively encode multi-scale information, while the NodeShuffle module, similar to PixelShuffle [8], could be seamlessly integrated into current point upsampling pipelines and consistently improved performance. The experiments showed that the combination of the two modules could indeed achieve good upsampling performance, but the focus of each branch was not fully considered, and the feature fusion effect needs to be further improved.

3. Proposed Method

In this section, we will present the design methodology of our proposed GCN-MA for point cloud SR. We will begin by introducing the overall architecture of our network, followed by a detailed explanation of each individual module.

3.1. Overview

The proposed GCN-MA architecture consists of two main parts: an improved dense connected network (DCN) and a point upsampling module, which is depicted in Figure 1. Initially, the GCN-MA network takes the point cloud’s 3D coordinates as input and encodes the coordinate information through KNN and single-layer graph convolution. Then, DCN extracts deep features using multiple feature extraction modules with a mixed attention mechanism. Each feature extraction module adaptively assigns different weights to enhance the learning ability, producing the final output features. In the point upsampling module, the output features are first channel expanded through a bottleneck layer comprising single-layer graph convolution. To suppress low-frequency information that has little impact on upsampling results, a channel attention mechanism is employed on the expanded feature map. Finally, the feature maps after the output of the channel attention mechanism are coordinate reconstructed to output a super-resolution reconstructed point cloud of shape $\mathrm{N}\times 3$.

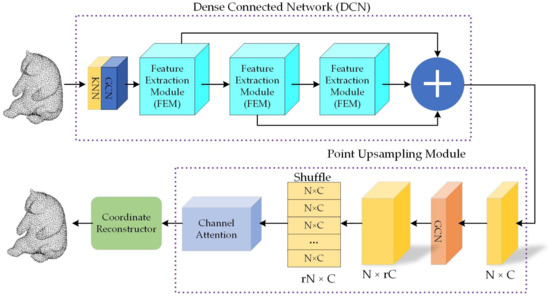
Figure 1. The whole architecture of the proposed GCN-MA. The GCN-MA pipeline comprises two major parts: feature extraction and point upsampling.

3.2. Improved Dense Connected Network (DCN)

Figure 2 shows the detailed structure of the improved DCN used in the proposed GCN-MA, which is designed to generate high-quality feature maps. The improved DCN consists of multiple feature extraction modules (FEMs), each composed of a dilated graph convolution block (DGCB) with channel and multi-head attention mechanisms. The mixed attention mechanism in FEM combines channel attention and multi-head attention to make optimal use of the global and local features of the point cloud. The channel attention within DGCB filters information on the channel dimension, while multi-head attention between DGCB enables the network to focus on the most valuable information from the convolution layer of different depths. Furthermore, adaptive weights can be assigned to different extracted features from each FEM, allowing the high-frequency feature information that is useful for the upsampling performance to be utilized, resulting in higher-precision point cloud super-resolution results. More details of the improved DCN will be presented in the following sub-sections.

Figure 2. The structure of improved DCN in the proposed GCN-MA. DCN consists of multiple feature extraction modules (FEM) to generate high-quality feature maps. Each FEM includes a dilated graph convolution block (DGCB) and mixed attention mechanism.

3.2.1. DGCB with Channel Attention

Multi-branch feature fusion is an effective approach to learning features from different branches, where each branch’s feature extraction module can achieve distinct feature extraction results by adaptively learning different parameters. Therefore, in the improved DCN, we employ a multi-branch structure to extract richer features. Additionally, on each branch, dilated graph convolution is utilized to increase the receptive field of the network.

Figure 3 shows the structure of the dilated graph convolution block (DGCB) in the feature extraction module. The DGCB consists of two dilated graph convolution layers, a global maximum pooling layer, and a channel attention mechanism module. To reduce computation, the input features first pass through a bottleneck layer with a 1 × 1 convolution kernel, which reduces the dimension to 64. The feature information computed in the bottleneck layer is then fed into the two dilated graph convolution layers and the global maximum pooling layer. The two dilated graph convolution layers have different dilation rates to capture different receptive fields. The feature information from the dilated graph convolution layer and the global pooling layer are fused at the channel level using the concatenate operation. Due to the disordered nature of point clouds, only the channel attention mechanism is used to filter information on the channel dimension. The final output features are obtained by summing the jump connections from the initial input features. By introducing the channel attention mechanism to the DGCB, the model can refine high-frequency information for point cloud detail recovery and improve the model’s training capability.

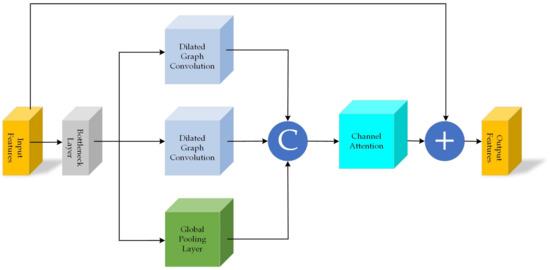
Figure 3. DGCB with Channel Attention. The DGCB consists of two dilated graph convolution layers, a global maximum pooling layer, and a channel attention mechanism module.

3.2.2. Multi-Head Attention Mechanism

To enable the network to learn the influence of different point features on point cloud SR, the improved DCN integrates Multi-head Attention with channel attention as a mixed attention mechanism. The channel attention within DGCB filters information on the channel dimension, while the multi-head attention between DGCB helps the network focus on more valuable information from the convolution layer of different depths. By using the multi-head attention mechanism, the network can screen out important information in the feature and ignore most of the unimportant information. The attention is reflected in the weight coefficients, where larger weight coefficients signify more important information.

Figure 4 shows the multi-head attention mechanism used in this paper. In traditional multi-head attention, each single head calculates global information, which often includes a significant amount of irrelevant data that can adversely affect point cloud super-resolution results. To address this issue, we introduce a mask matrix $M$ that suppresses nodes beyond the adjacent points, preventing them from contributing to the weight calculation. The mask matrix is a symmetric matrix centered on the main diagonal, where the number of sub-diagonals on either side represents the number of selected adjacent points. Specifically, the values of the selected primary and secondary diagonals are set to 1, while the others are set to 0. When combined with the weight matrix through a Hadamard product, the positions set to 0 effectively exclude information from points far from the center point. As a result, the mask matrix can significantly reduce computation while improving the point cloud recovery performance.

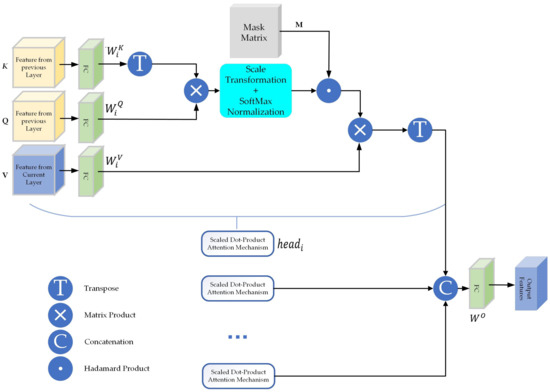
Figure 4. Multi-head Attention Mechanism. Compared with the traditional multi-head attention mechanism, we introduce a mask matrix M that suppresses nodes beyond the adjacent points, preventing them from contributing to the weight calculation.

Inspired by [28], the attention function of each head can be represented as follows

$$hea{d}_i=Attention\left(Q_i,K_i,V_i,M_i\right)=\mathrm{softmax}\left(\frac{Q_i{K}_i^T}{\sqrt{d_k}}\right)·M_i\times V_i$$

(1)

where $Q,K,V,$ and $d_k$ have the same meaning with the traditional attention function in [28]. Furthermore, in Figure 4, $Q_i=Q{W}_i^Q$; $K_i=K{W}_i^K$; and $V_i=V{W}_i^V$. $M_i$ denotes the proposed mask matrix of $hea{d}_i$. As a result, the final multihead attention function can be indicated as

$$MultiHead\left(Q,K,V,M\right)=Concat\left(hea{d}_1,\dots ,hea{d}_h\right)W^O$$

(2)

where $W^O$ means the projection parameter matrices for the output features.

3.2.3. Adaptive Weights Allocation between FEMs

Residual connection and dense connection are two commonly used network structures for feature extraction in deep learning tasks. While the traditional dense connection method allows each layer in the network to fully utilize the features of its previous layer, it can lead to increased problems as the network deepens. With more layers, the dense connection requires more parameters, leading to a significant increase in computational complexity, training time, and even overfitting.

To overcome these challenges, we propose an approach to adaptively allocate weights between FEMs, which reduces the redundancy of feature information across layers. By preserving the network’s ability to learn effectively, we further reduce computational complexity through the use of fewer parameters. Specifically, we introduce a multilayer perceptron to control the final output features through adaptive learning weight parameters. This enables us to assign the proportion of output features from each layer to achieve more efficient feature learning.

Figure 5 illustrates the process of encoding point cloud features and extracting feature information from each FEM, which is then fused using a dense connection. Unlike traditional dense connections, which usually use channel-level concatenation for feature information, this paper proposes adaptive weight allocation to achieve feature fusion. In this method, feature information generated by each FEM is multiplied by a weight coefficient of adaptive learning, and the final output feature is obtained by summing the multiplication results. The weight coefficient is calculated by MLPs and SoftMax normalization, which are learned using the back-propagation mechanism. Compared to traditional dense connections, the improved dense connection not only learns the weight coefficient adaptively but also focuses on the feature information that is more valuable to the model generation results, which further enhances the model’s learning ability.

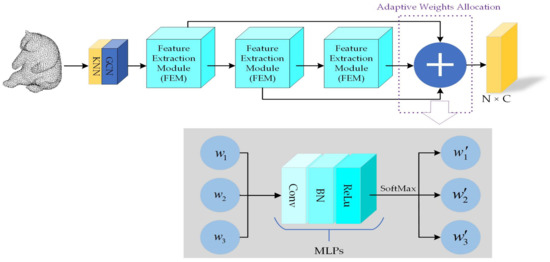
Figure 5. Adaptive Weights Allocation. The weights between FEMs can be adaptively allocated to reduce the redundancy of feature information across layers.

3.3. Point Cloud Upsampling Module

In the field of image super-resolution, rearranging image feature information is a common method for image reconstruction. Drawing inspiration from PixelShuffle [8], which is used for image super-resolution, NodeShuffle [27] has been proposed to effectively upsample point clouds. In this paper, we have combined NodeShuffle with channel attention to design the point cloud upsampling module of GCN-MA, as shown in Figure 6. The node feature $F_l$ with shape $\mathrm{N}\times \mathrm{C}$, after feature extraction, is input to the upsampling module, which first goes through a graph convolution layer to expand the number of channels $\mathrm{C}$ to $\mathrm{rC}$, where r is the upsampling rate, to obtain the feature information with shape $\mathrm{N}\times \mathrm{rC}$. The expanded node features are then rearranged to obtain node features of shape $\mathrm{rN}\times \mathrm{C}$. Next, the channel attention module is applied to extract high-frequency node information that is valid for upsampling in the global and neighborhood through the attention mechanism. Finally, the feature information is input into the coordinate reconstructor to obtain the new point cloud super-resolution image with shape $\mathrm{rN}\times 3$. This approach enables us to obtain better quality point cloud reconstructions.

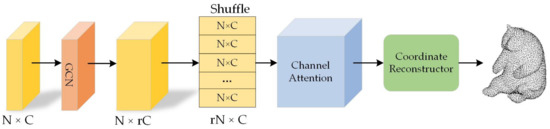
Figure 6. Point Cloud Upsampling Module. In the point upsampling module, we also adopt channel attention to suppress low-frequency information with little impact on the upsampling results.

3.4. Loss Function

The loss function is a crucial component in point cloud SR, as it greatly influences the overall performance of the network. By accurately representing the difference between the high-resolution original point cloud and the SR reconstructed point cloud estimated by the network, a well-designed loss function can significantly improve the quality of the super-resolution results. Ultimately, a smaller difference value between the two point clouds indicates a more robust network.

In point cloud SR reconstruction models, the loss function typically uses the minimized Chamfer distance to calculate the absolute distance between the SR-reconstructed point cloud image and the original high-resolution point cloud image. The Chamfer distance loss function can be calculated as follows.

$$Los{s}_{CD}\left(P,Q\right)=\frac{1}{\left|P\right|}{{\displaystyle \sum }}_{p\in P}\underset{q\in Q}{\mathit{min}}\Vert p-q{\Vert }_2^2+\frac{1}{\left|Q\right|}{{\displaystyle \sum }}_{q\in Q}\underset{p\in P}{\mathit{min}}\Vert p-q{\Vert }_2^2$$

(3)

where $P$ and $Q$ represent the SR point cloud image generated by model prediction and the original high-resolution point cloud image, respectively, while $p$ and $q$ represent any points in $P$ and $Q$, respectively. ${\Vert ·\Vert }_2^2$ denotes the squared Euclidean norm. The aim of this loss function is to calculate the point-to-point absolute distance between two point cloud images and minimize this loss value. By training the network model through the back-propagation algorithm, the generated SR point cloud image becomes more approximate to the original high-resolution point cloud image.

In the field of point cloud SR reconstruction, the most frequently used objective evaluation metric for the quality of the SR reconstructed point cloud image is the Chamfer distance. As mentioned above, the Chamfer distance as the evaluation metric is also calculated as the absolute distance between two point cloud images. The smaller the value of the Chamfer distance metric, the closer the generated SR point cloud image is to the original high-resolution point cloud image, representing better model training performance.

4. Experiments

This section presents the datasets used to train and test our models, followed by the implementation details of our proposed framework. Next, we analyze the different modules in our proposed network and compare our results with several corresponding methods, in terms of both quantitative evaluations and visual quality.

4.1. Datasets

In this paper, we utilized the training set from the PU1K [27] and PUGAN [1] datasets to train our proposed network model and evaluate its performance on the corresponding test sets also provided in the datasets. The PU1K dataset comprised 1147 3D models, with 1020 samples in the training set and 127 samples in the test set. The dataset included models with both simple and complex shapes, allowing us to assess the model’s generalization ability. The PUGAN dataset comprised 147 3D models, with 120 samples in the training set and 27 samples in the test set.

In this paper, we used Chamfer distance (CD) and Hausdorff distance (HD) as evaluation metrics to compare our point cloud SR method with others in a quantitative analysis. CD has been previously introduced in Section 3.4, while HD can be calculated as follows:

$$Distanc{e}_{HD}\left(S_1,S_2\right)=\max \left(h\left(S_1,S_2\right),h\left(S_2,S_1\right)\right)$$

(4)

$$\left\{\begin{array}{c}h\left(S_1,S_2\right)=\underset{x\in S_1}{\mathit{max}} \underset{y\in S_2}{\mathit{min}}\Vert x-y\Vert \\ h\left(S_2,S_1\right)=\underset{y\in S_2}{\mathit{max}} \underset{x\in S_1}{\mathit{min}}\Vert y-x\Vert \end{array}\right.$$

(5)

where $Distanc{e}_{HD}\left(S_1,S_2\right)$ is the bi-directional Hausdorff distance, and $h\left(S_1,S_2\right)$ is the one directional Hausdorff distance. Similar to the Chamfer distance metric, a smaller HD value indicates better reconstruction quality, while a larger HD value indicates more severe distortion in the reconstructed point cloud.

4.2. Implementation Details

In this paper, we have implemented our proposed model using the deep learning framework of TensorFlow. The difference in model parameters could greatly impact experimental results, thus we adjusted the parameters through several experiments combined with experience to achieve an acceptable effect. The network parameters were set as follows: the learning rate was 0.0001, and the batch size was 64. We optimized the models using the Adam optimizer and trained for 200 epochs to obtain our experimental results. Specifically, batchsize denoted the size of the batch, and epoch denoted the number of trainings.

4.3. Ablation Study

In this subsection, we began by examining the fundamental network parameters of the proposed GCN-MA, specifically, the number of FEMs. We then explored the mask matrix settings in the multi-head attention and analyzed the positions of the channel attention. Finally, we conducted a detailed analysis of the proposed components.

4.3.1. Number of FEMs

Each FEM in our proposed GCN-MA network consisted of a dilated graph convolution block (DGCB) with channel and multi-head attention mechanisms. To investigate the impact of the number of FEMs on point cloud super-resolution, we conducted comparison experiments with the same hyperparameters and experimental settings, except for varying the number of FEMs. Table 1 presents the results of the experiments, indicating that the number of FEMs had a significant effect on the performance of the network. We found that the performance improvement of the point cloud super-resolution was the greatest when the number of FEMs was three. Our results demonstrated that increasing the number of FEMs led to a deeper network and helped improve network performance.

Table 1. Performance test of different FEMs on point cloud super-resolution.

Number of FEM	CD	HD
1	0.655	8.643
2	0.593	7.632
3	0.475	5.503

4.3.2. Mask Matrix Settings in the Multi-Head Attention

In this paper, we employed the multi-head attention mechanism with a mask matrix, and different mask matrix settings could have varying effects on experimental results. The mask matrix could suppress nodes beyond neighboring points, making full use of local structural features for SR reconstruction tasks.

In this subsection, we further investigated the influence of different numbers of nearest neighbor points on SR performance of the network model. The comparison experiments used the same hyperparameters and experimental settings, except for the number of nearest neighbor points selected by the mask matrix. Table 2 presents the SR performance test with different mask matrix settings, where the last row corresponded to the method without a mask matrix. From Table 2, we can see that the selection of the number of nearest neighbor points had an impact on the SR performance of the model. The SR performance of the compared methods was similar when a small number of nearest neighbor points were selected by the mask matrix, as shown in the first five rows of the table. However, the network SR performance decreased when a large number of points were selected, as in the last two rows of the table.

Table 2. SR performance comparisons with different mask matrix settings.

Number of Nearest Neighbor Points	CD	HD
16	0.489	5.513
32	0.484	5.519
64	0.475	5.503
128	0.476	5.493
256	0.476	5.560
512	0.492	5.792
1024	0.509	5.970
the method without a mask matrix	0.547	6.136

4.3.3. Positions of the Channel Attention

The proposed GCN-MA incorporated a channel attention mechanism in both the FEM and point cloud upsampling module, which improved the model’s ability to learn feature information in the channel dimension. Table 3 presents the impact of the channel attention mechanism at different positions in the network. The first row of Table 3 shows the performance of the channel attention mechanism only in the FEM, the second row shows its performance only in the upsampling module, and the third row shows its performance in both FEM and the upsampling module. The last row corresponds to the model’s performance without the channel attention mechanism. The experimental results demonstrate that the channel attention mechanism, used at different locations in the network, had different effects on the SR performance and incorporating the channel attention mechanism in both FEM and the upsampling module achieved the best performance compared to the other methods.

Table 3. SR performance comparisons with different positions of the channel attention mechanism.

Position	CD	HD
FEM	0.575	7.248
Upsampling module	0.523	6.537
FEM+ Upsampling module	0.475	5.503
Without channel attention	0.580	7.645

4.3.4. Study of the Proposed Components

In this subsection, we verified the performance of the proposed components, namely, the attention mechanism and mask matrix. Note that the following experiments were based on the parameter settings described above. Table 4 shows the ablation experiments involving different components. The first row represents adding only the channel attention mechanism, the second row represents adding only the multi-head attention mechanism, the third row represents using the mask matrix in adding the multi-head attention mechanism, and the last row represents adding both the channel attention mechanism module and the multi-head attention mechanism module with the mask matrix. The experiments demonstrated that the different components had varying effects on the network performance, and the proposed method in this paper outperformed the other methods.

Table 4. Ablation experiments involving different components.

Channel Attention	Multi-Head Attention	Mask Matrix	CD	HD
√	✕	✕	0.562	6.374
✕	√	✕	0.503	5.890
✕	√	√	0.483	5.732
√	√	√	0.475	5.503
√	✕	✕	0.562	6.374

4.4. Comparisons with Corresponding Methods

In order to evaluate the effectiveness of the proposed GCN-MA network, we compared the experimental results with several corresponding point cloud SR algorithms, including PU-Net, 3PU, PU-GACNet, AR-GCN, PU-GAN, and PU-GCN.

Firstly, Table 5 presents a comparison of objective evaluation metrics on the PU1K dataset, with Chamfer distance (CD) and Hausdorff distance (HD) being used as evaluation standards. As shown in the table, the proposed model in this paper, which utilized dilated graph convolution and mixed attention mechanisms, achieved lower Chamfer and Hausdorff distances. Table 6 presents a comparison of objective evaluation metrics on PUGAN dataset with CD and HD metrics, which shows that the proposed GCN-MA had better reconstruction performance.

Table 5. Objective quality evaluation results of different algorithms on PU1K dataset.

Method	CD	HD
PU-Net	1.155	15.170
3PU	0.935	13.327
PU-GACNet	0.665	9.053
AR-GCN	0.642	6.559
PU-GCN	0.585	7.577
GCN-MA	0.475	5.503

Table 6. Objective quality evaluation results of different algorithms on PUGAN dataset.

Method	CD	HD
PU-Net	0.556	4.750
3PU	0.298	4.700
PU-GAN	0.280	4.640
PU-GCN	0.258	1.885
GCN-MA	0.214	1.126

Moreover, we conducted a subjective evaluation of the reconstruction quality by comparing it with other advanced methods. As depicted in Figure 7, while the point cloud SR images generated by the other compared algorithms exhibited some SR effect when compared to the point cloud low-resolution images, the subjective quality could still be further improved. In contrast, the proposed GCN-MA produced smoother edge features and enhanced the overall SR effect, as shown in Figure 7. For instance, in the reconstruction of the seat backrest corners, our method provided clearer details and less noise. Similarly, in the reconstruction of the camel’s ears and feet, as well as the bird’s beak and feet, our proposed method was more effective than the other algorithms.

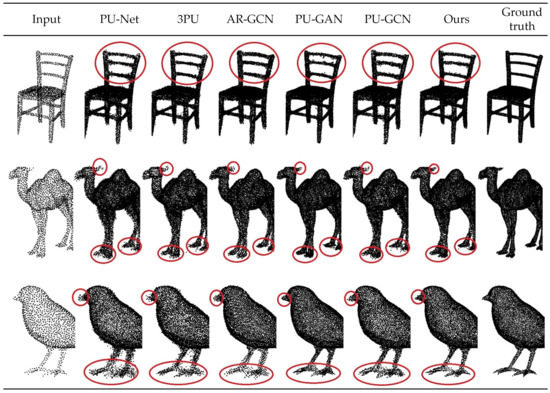
Figure 7. Subjective reconstruction quality comparison of various methods.

5. Conclusions

In this paper, we proposed a point cloud SR network that combined graph convolution with attention mechanisms. Graph convolution effectively extracted neighborhood information, and a well-designed attention mechanism filtered meaningful information to improve the feature extraction ability of the network. Specifically, we incorporated two different attention mechanisms: the multi-head attention mechanism with mask matrix, which utilized global and neighborhood information and prevented overfitting, and the channel attention mechanism, which improved the learning efficiency and perceptual ability of the model from the channel dimension. Compared with other methods, our proposed GCN-MA achieved better SR reconstruction results in both subjective quality and objective evaluation metrics.