Impacts of Work Function Variation and Line-Edge Roughness on TFET and FinFET Devices and 32-Bit CLA Circuits †
Abstract
:1. Introduction
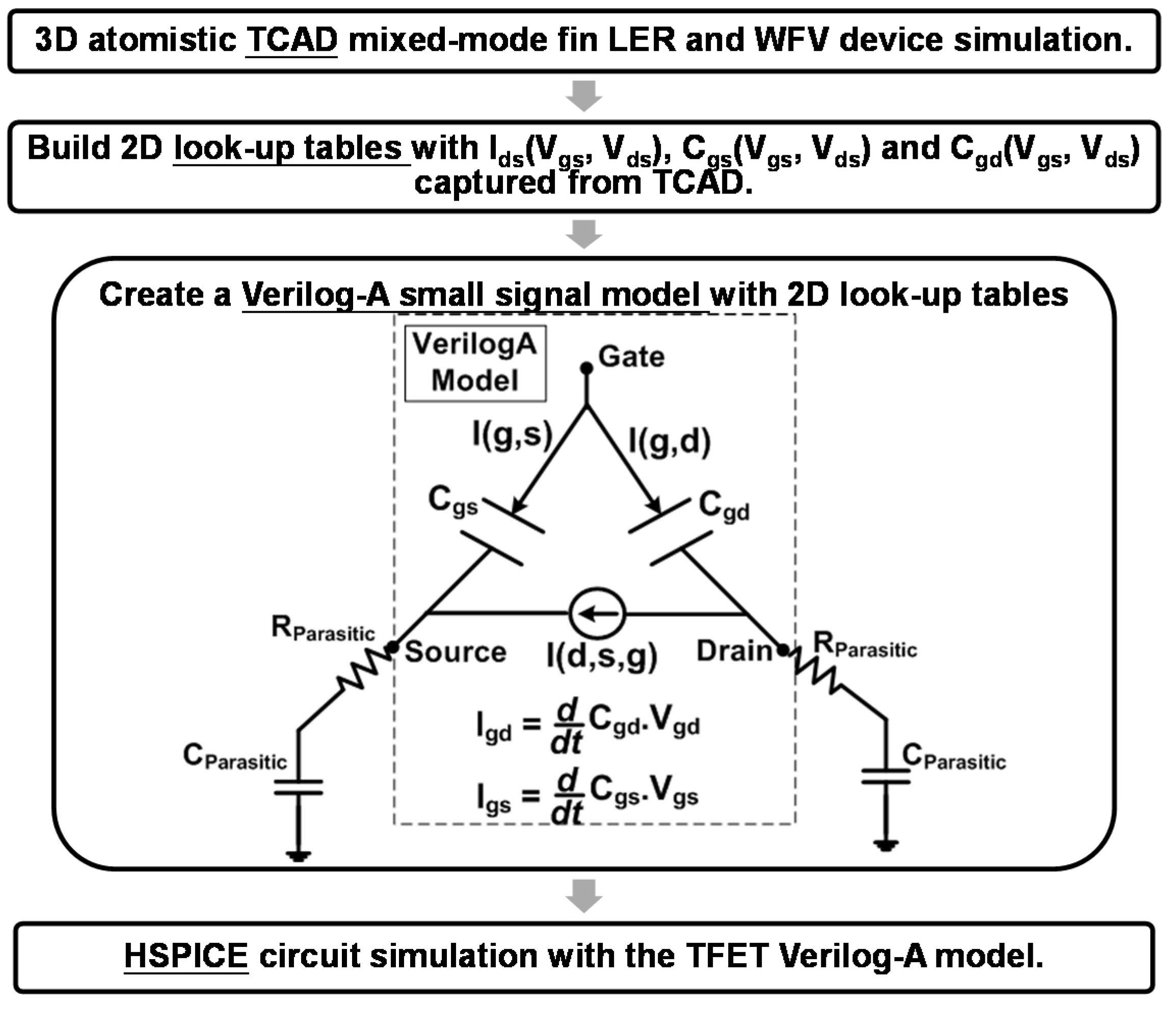
2. Device Structures, Characteristics and Simulation Methodology
2.1. Device Structures and Characteristics
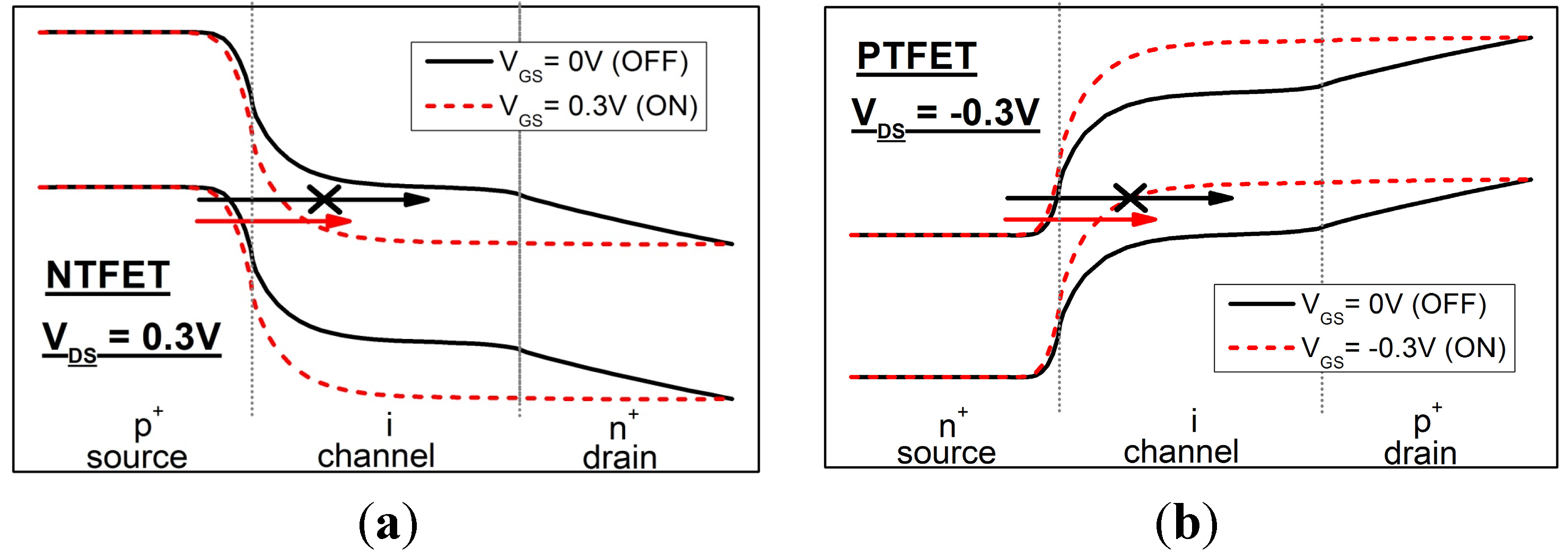

| Devices | TFET | FinFET | |
|---|---|---|---|
| Leff = 25 nm | Wfin = 7 nm | Hfin = 20 nm | EOT = 0.65 nm |
| nTFET | pTFET | FinFET | |
| Material | In0.53Ga0.47As | Ge0.925Sn0.075 | In0.53Ga0.47As |
| Nch (cm−3) | undoped | undoped | 1 × 1017 |
| Ns (cm−3) | 4.5 × 1019 (p-type) | 2 × 1019 (n-type) | 1 × 1020 |
| Nd (cm−3) | 2 × 1017 (n-type) | 2 × 1017 (p-type) | 1 × 1020 |
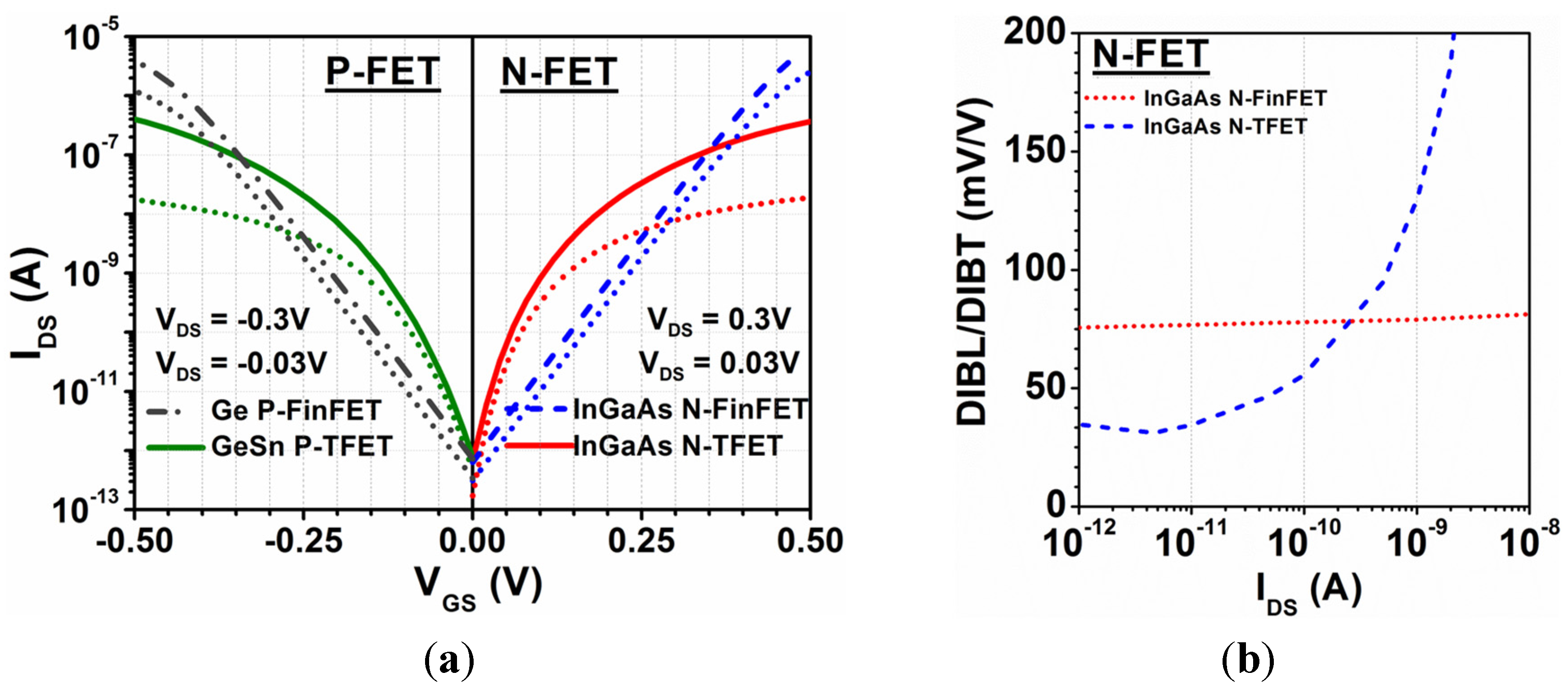
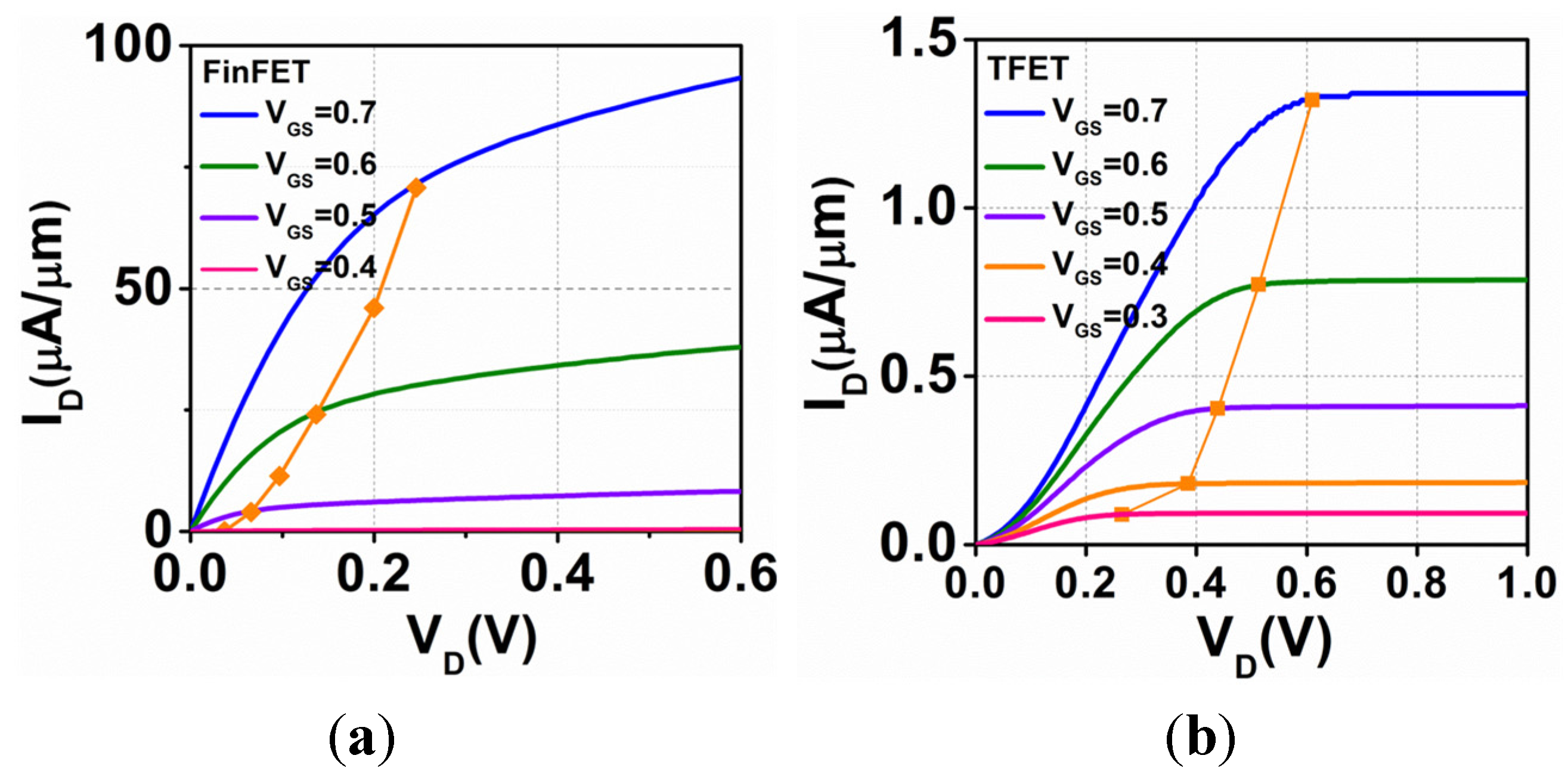
2.2. Simulation Methodology

| Gate Material = TiN | Grain Size = 5 nm | ||
|---|---|---|---|
| Work function (eV) | Nominal | <200> (60%) | <111> (40%) |
| InGaAs N-TFET | 4.53 | 4.61 | 4.41 |
| GeSn P-TFET | 4.82 | 4.9 | 4.7 |
| InGaAs N-FinFET | 4.88 | 4.96 | 4.76 |
| Ge P-FinFET | 4.27 | 4.35 | 4.15 |
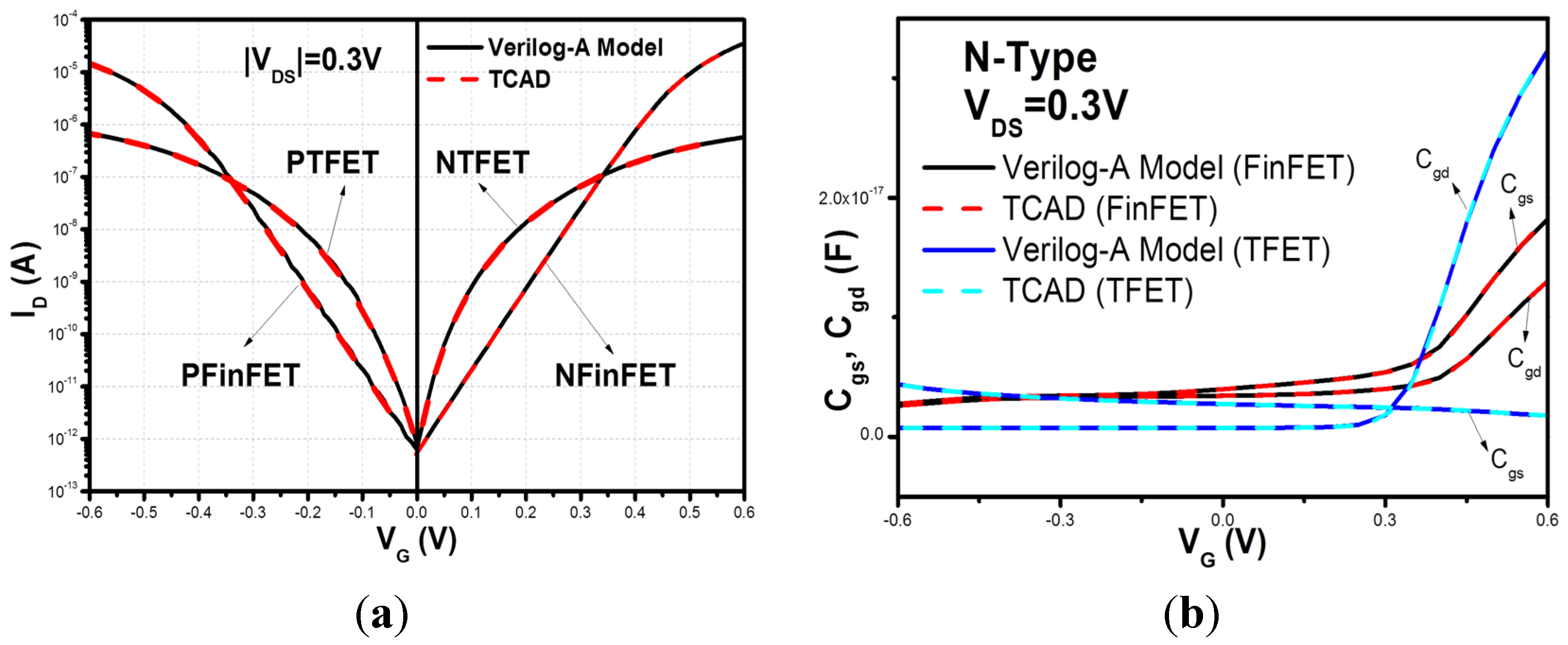
3. Device Variability Due to WFV and Fin LER
3.1. Ioff and Ion Variability
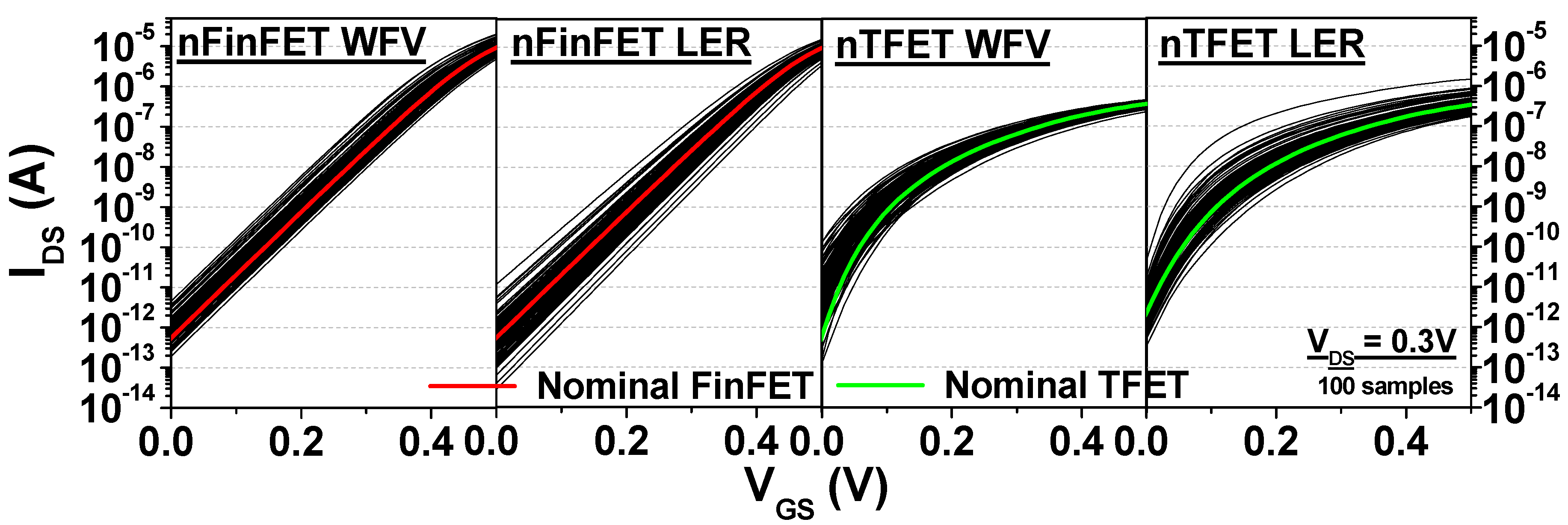
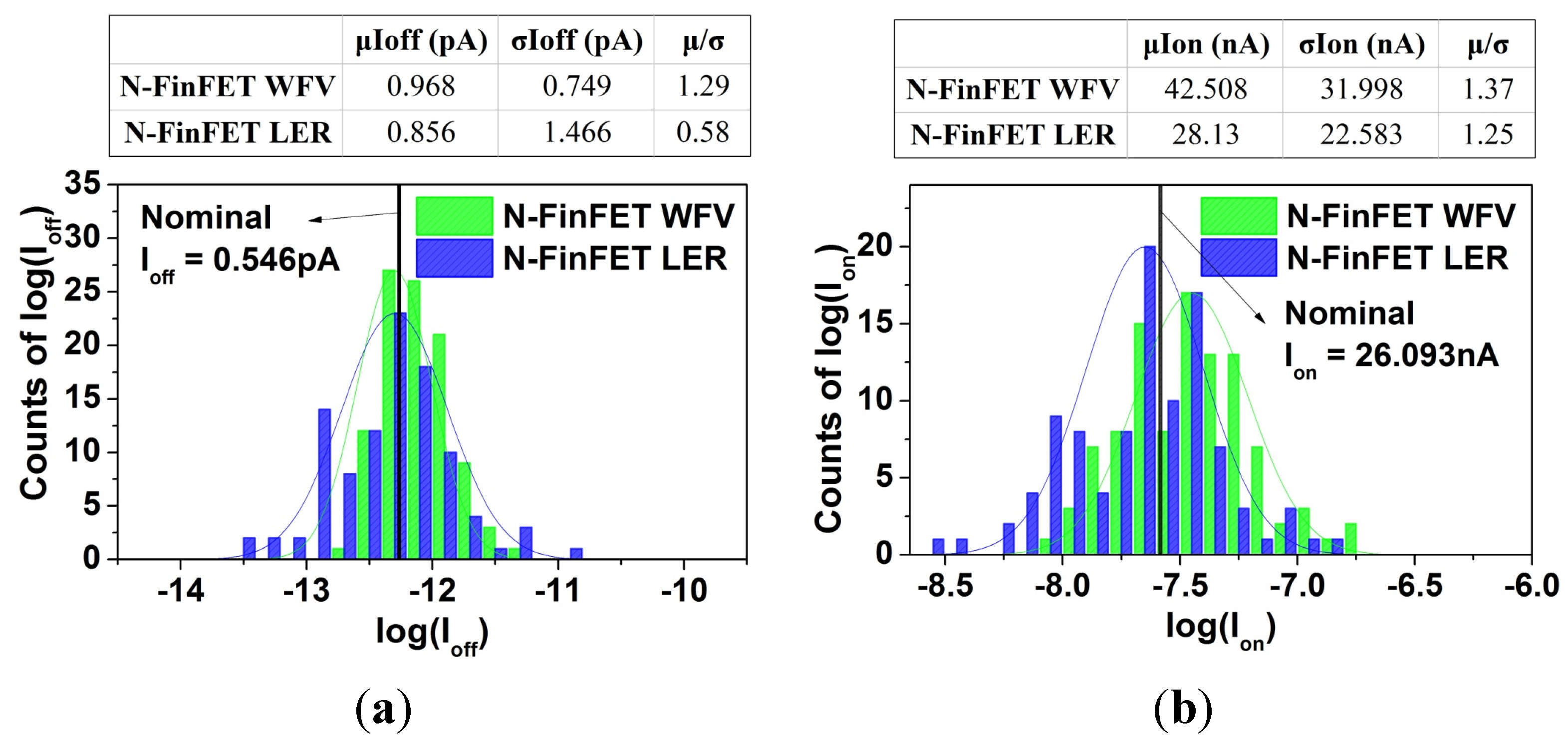
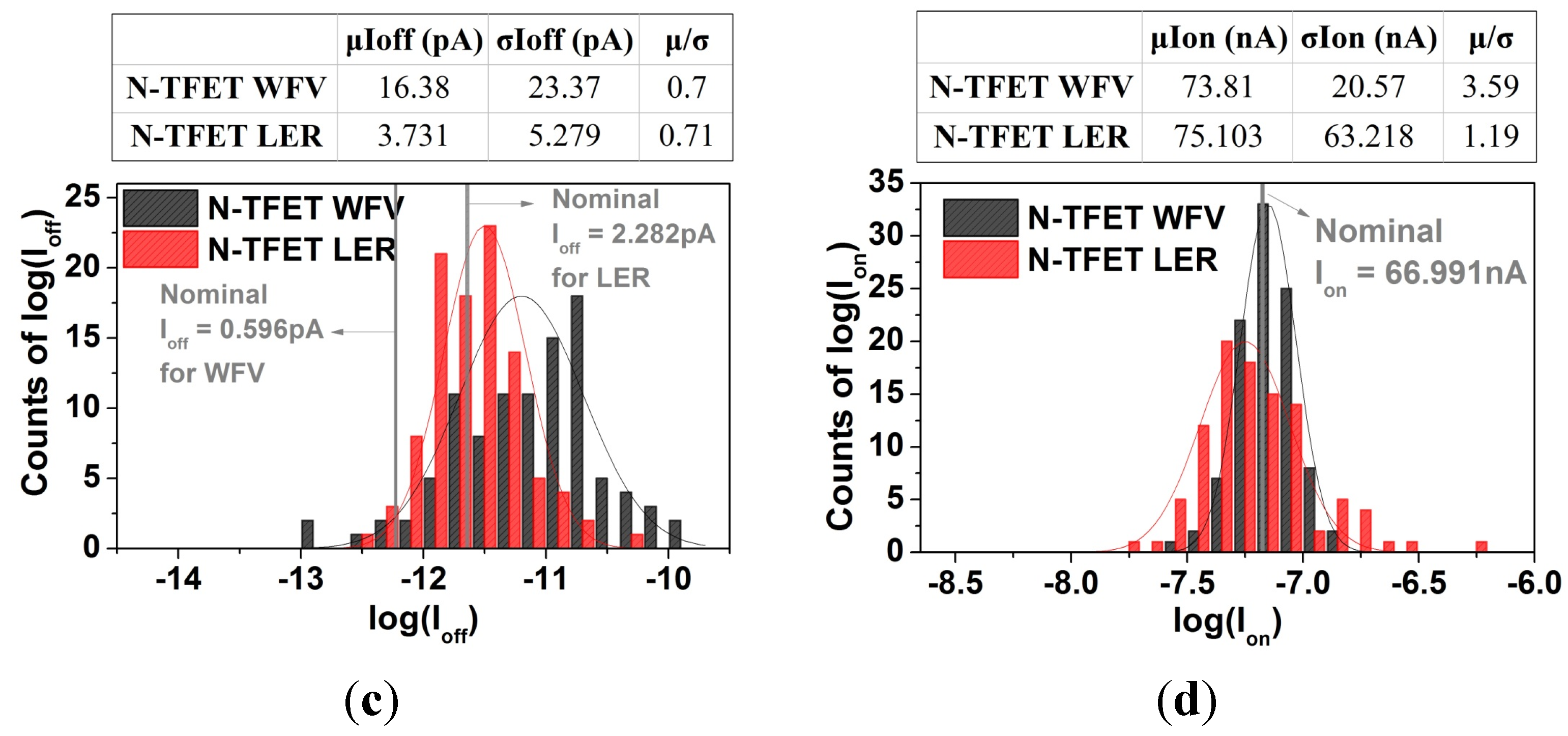
3.2. Cg Variability
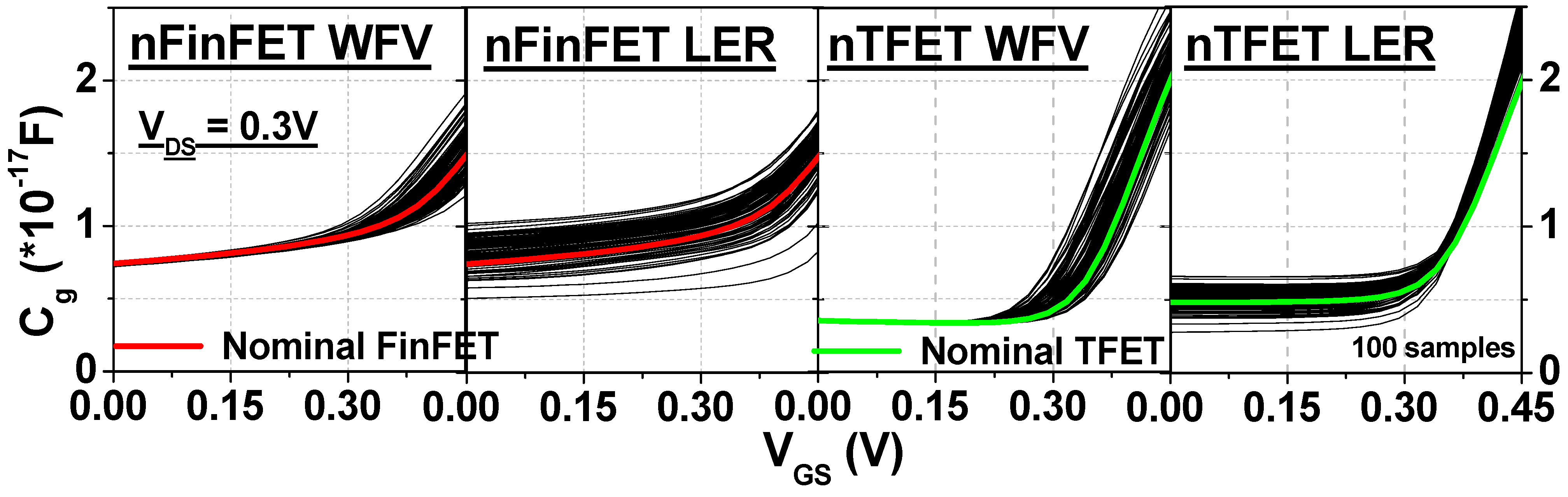
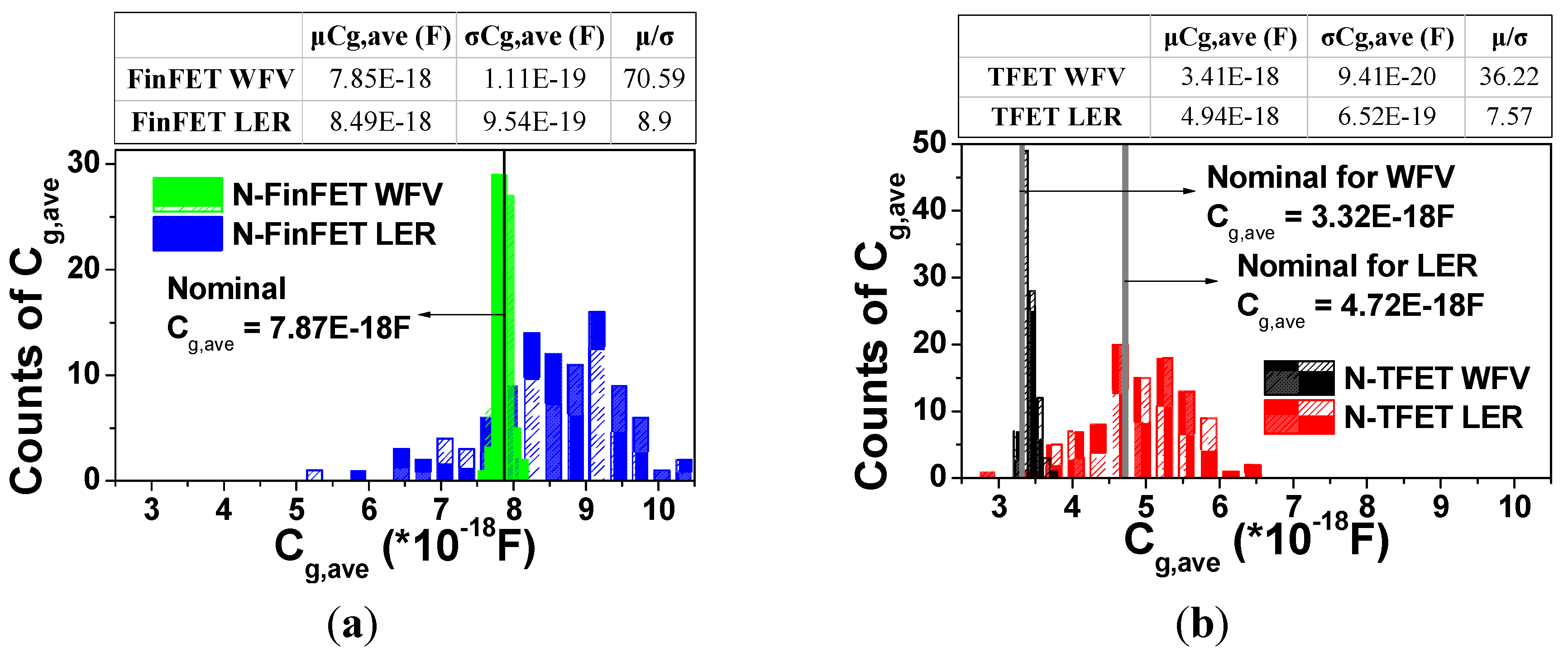
4. Impacts of WFV and Fin LER on CLA Circuits
4.1. Delay Variability
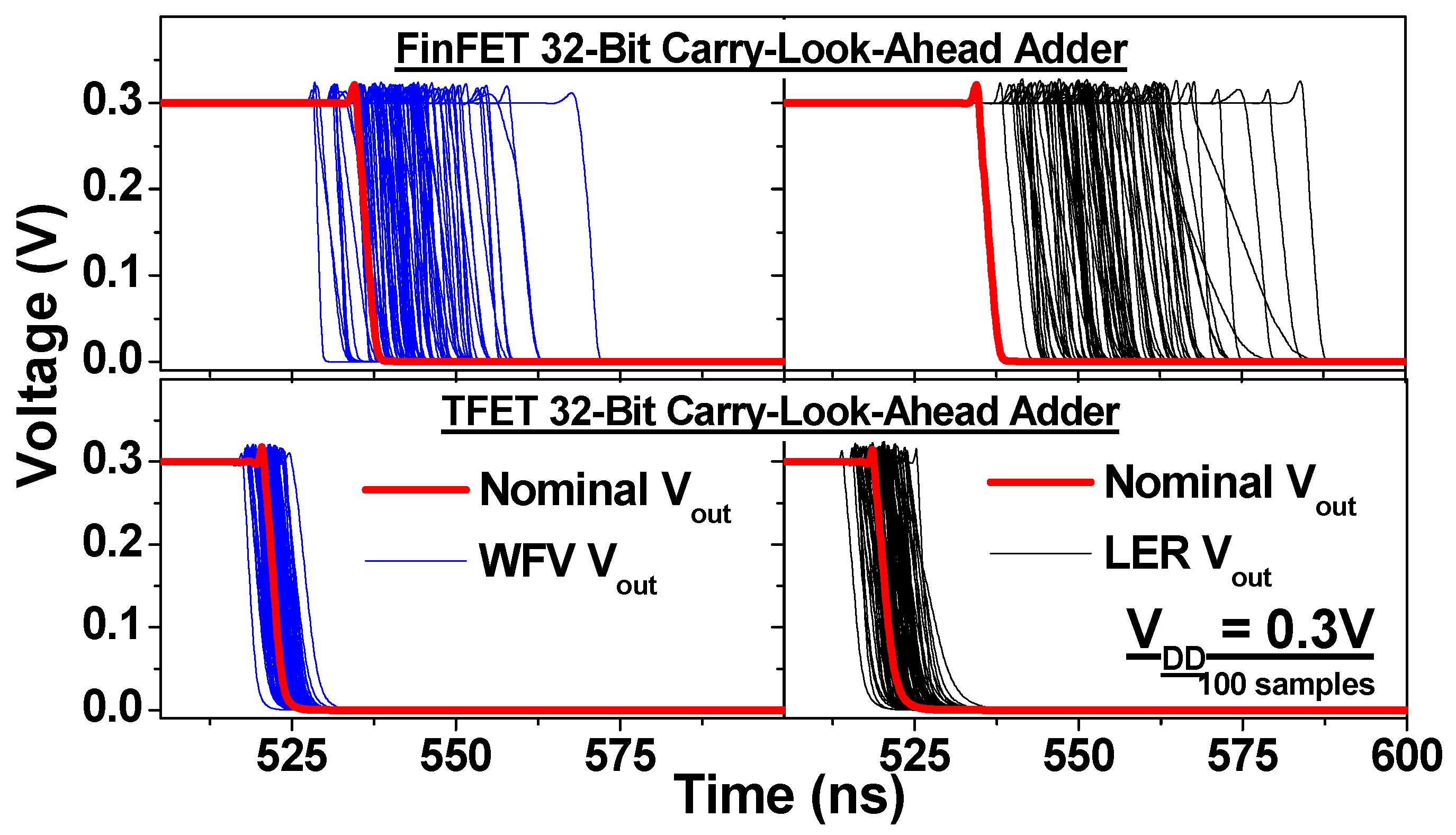
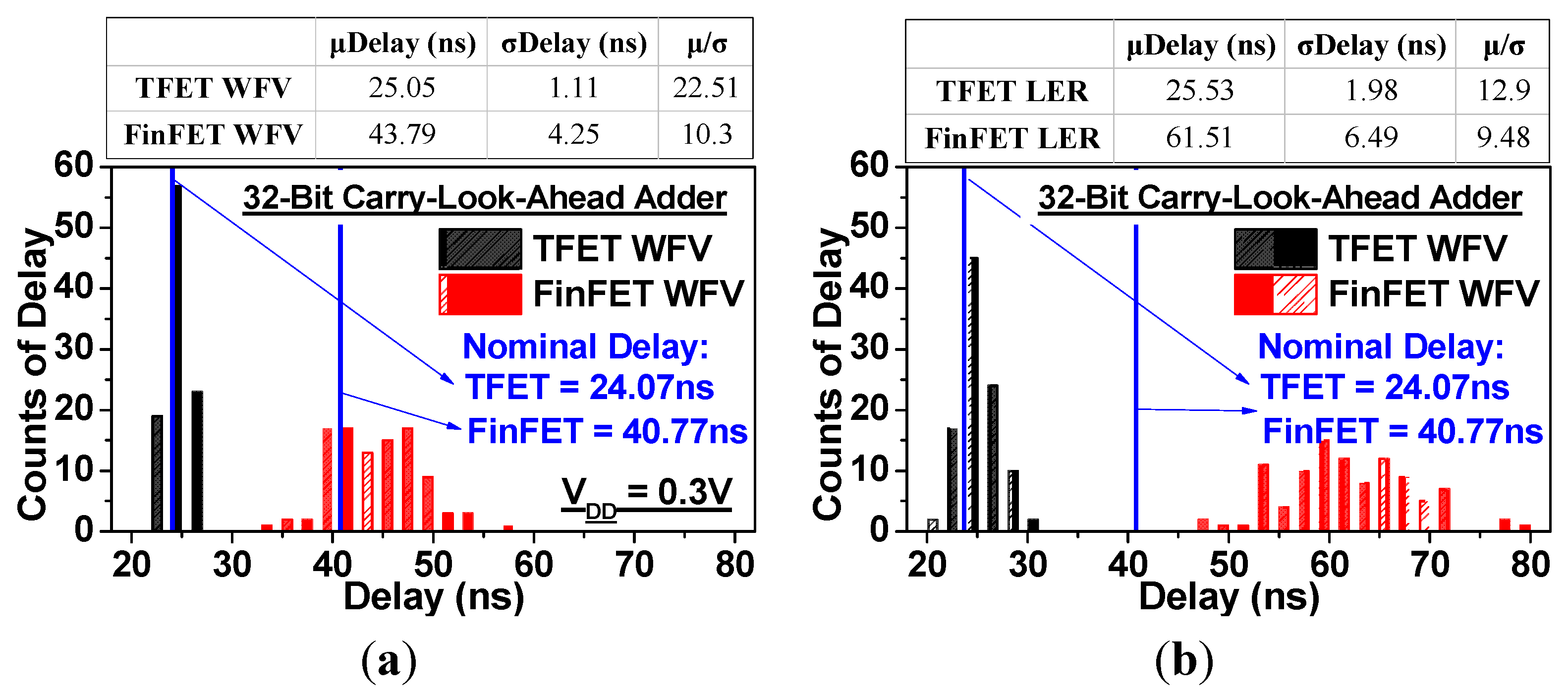
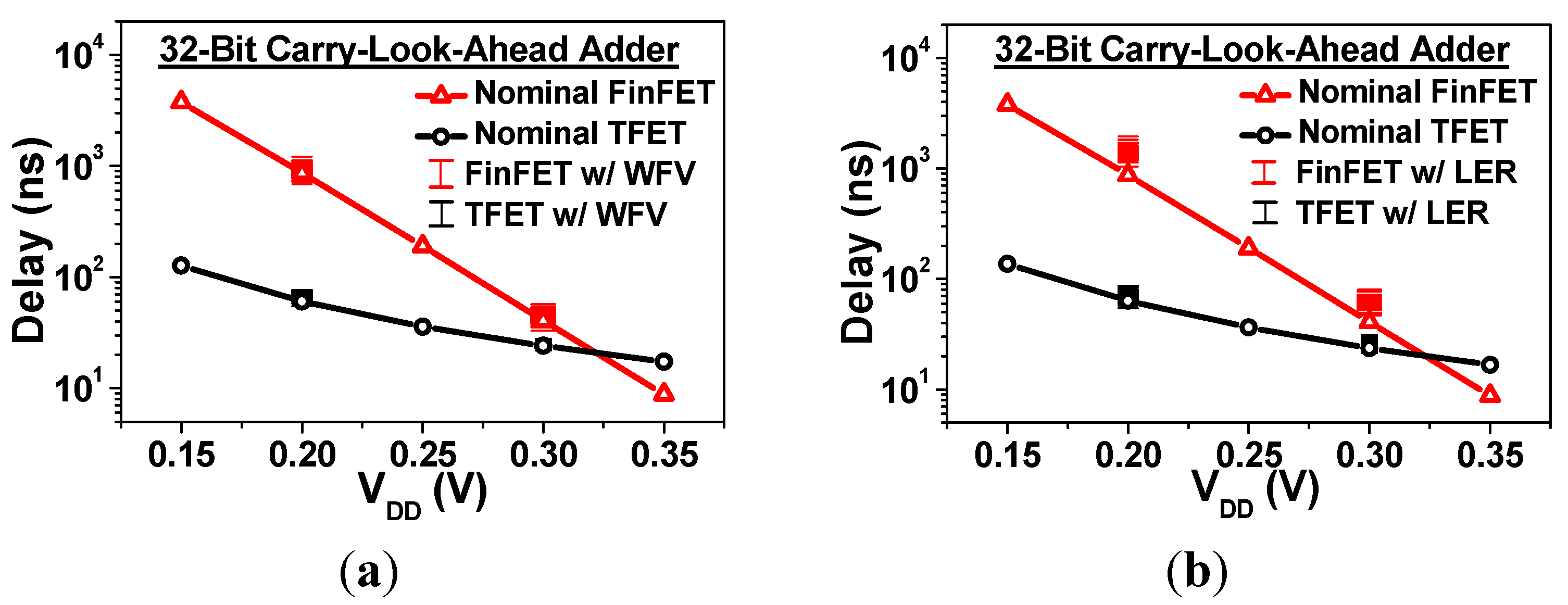
4.2. PDP Variability
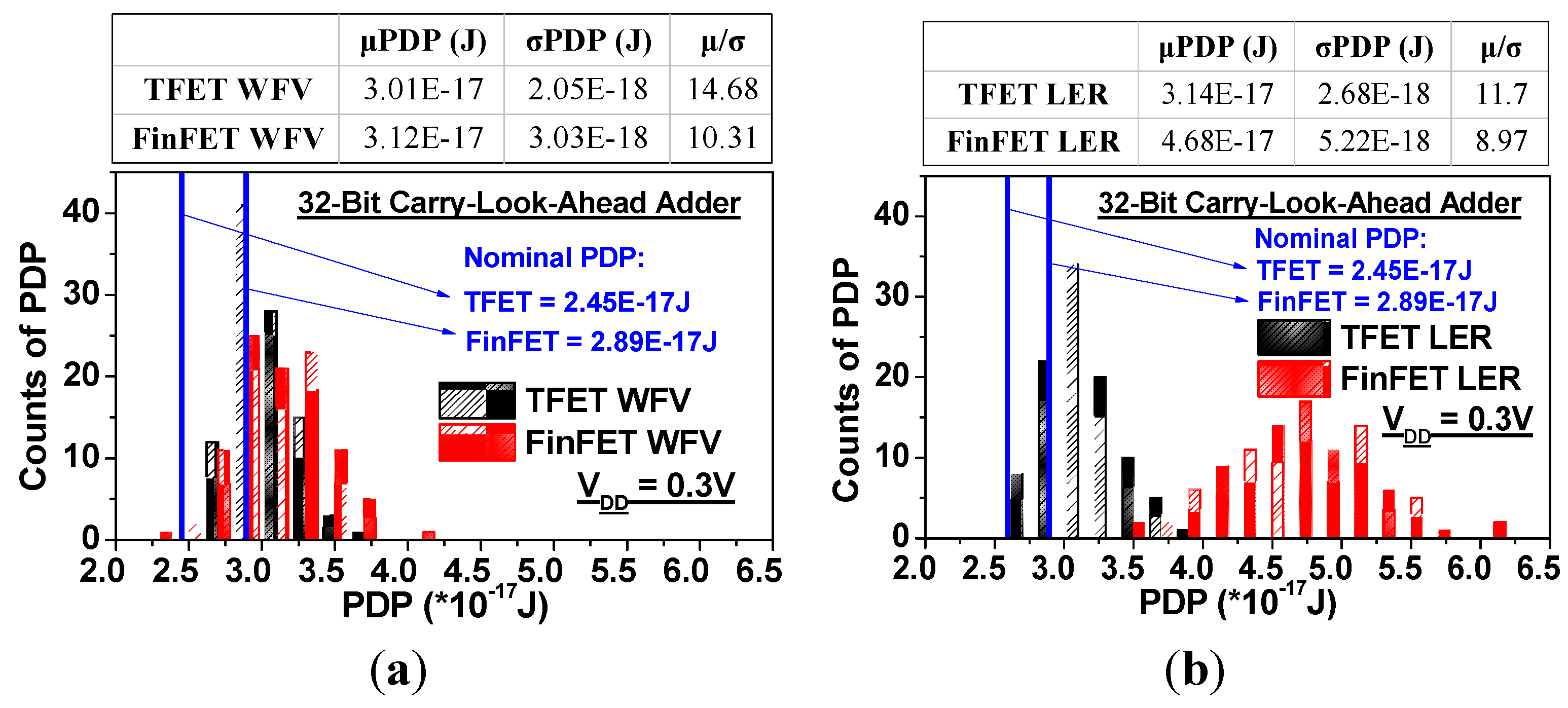
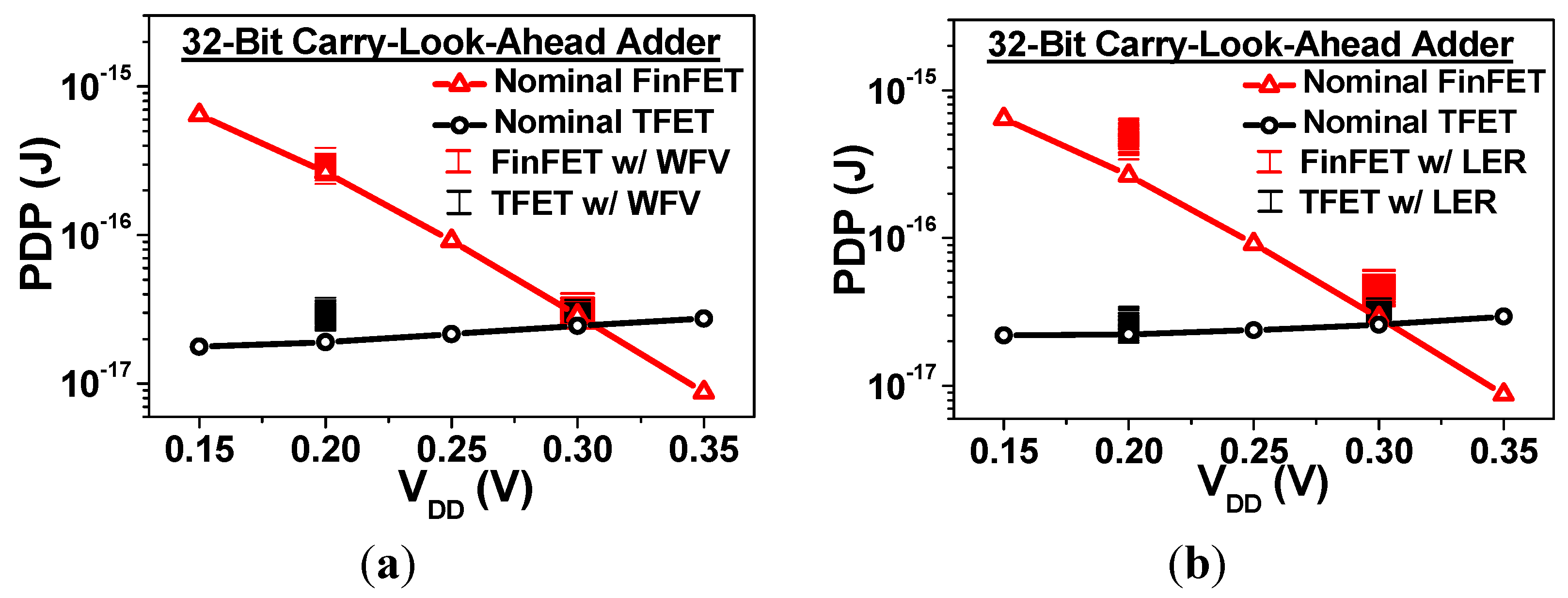
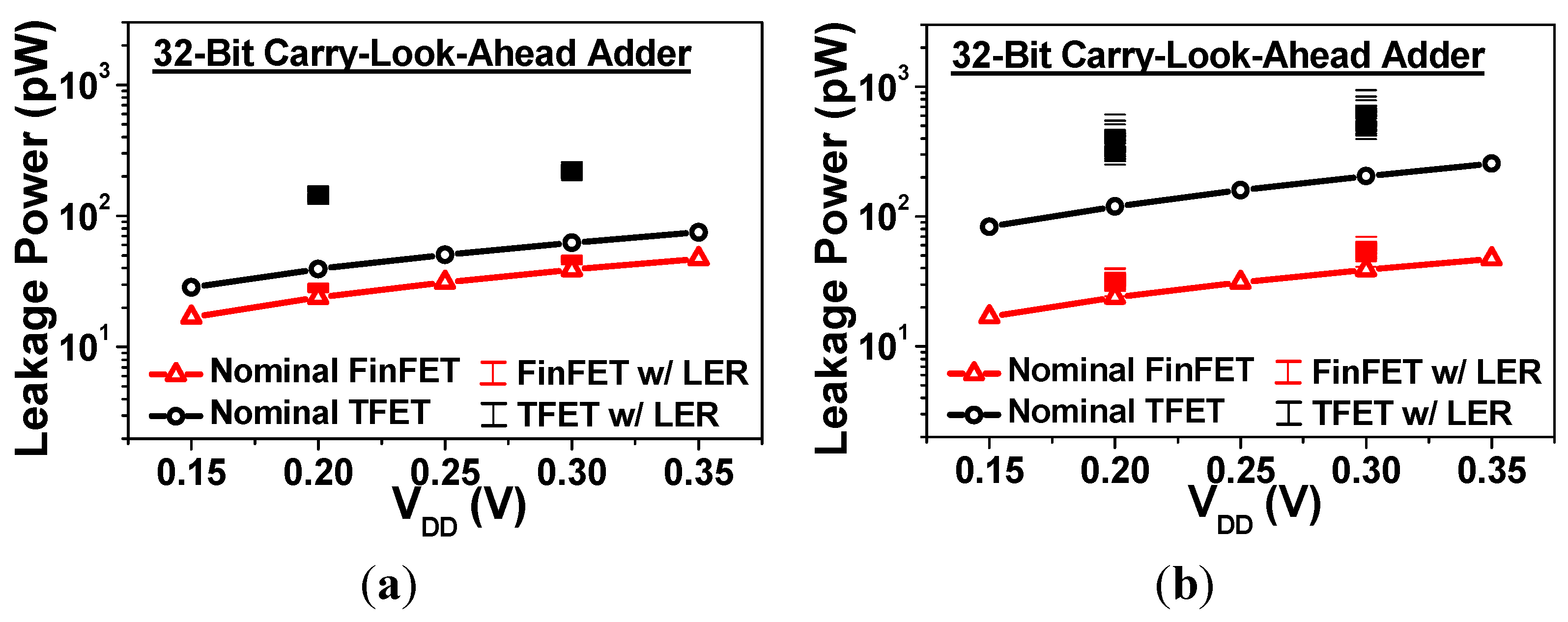
4.3. Leakage Power Variability
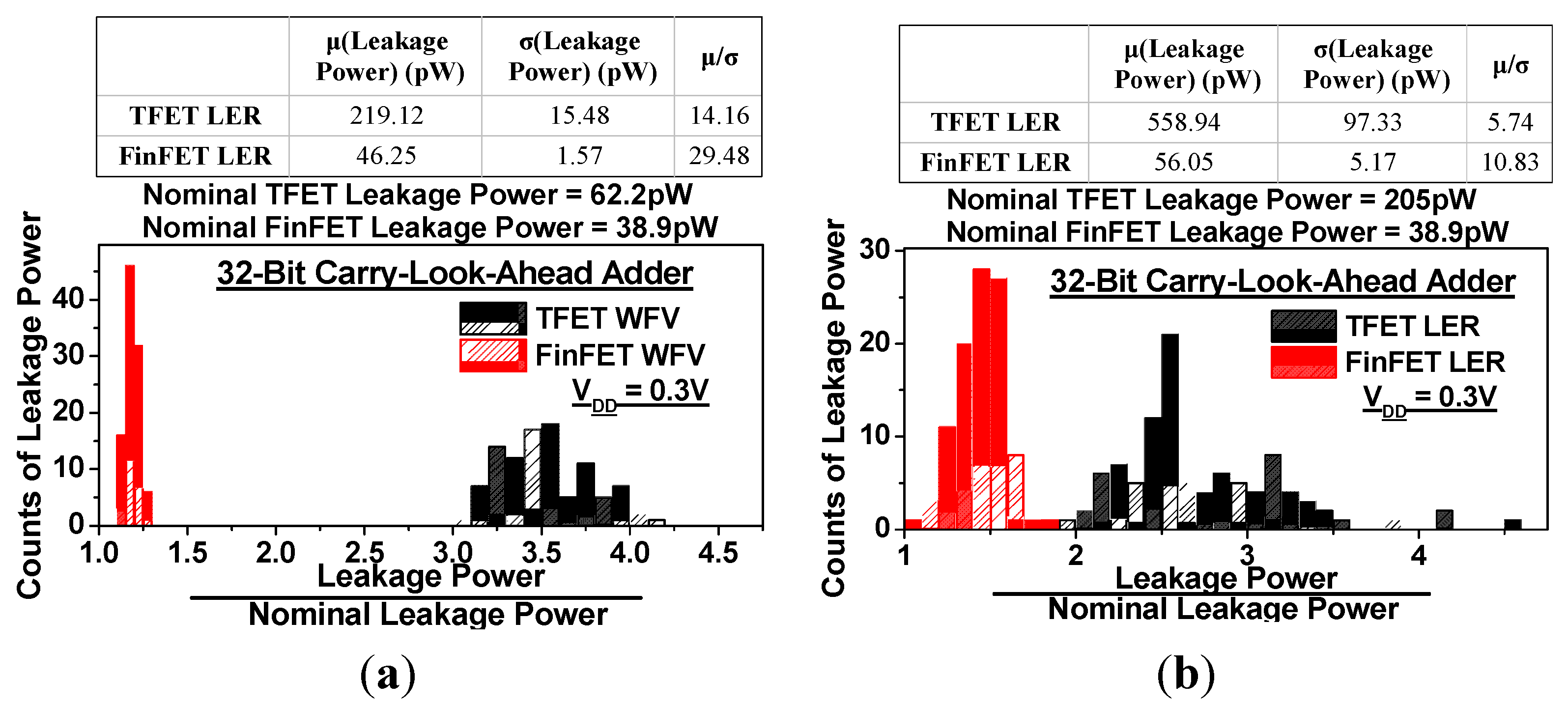
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ionescu, A.M.; Riel, H. Tunnel field-effect transistors as enrgy-efficient electronics switches. Nature 2011, 479, 329–337. [Google Scholar] [CrossRef] [PubMed]
- Saripalli, V.; Datta, S.; Narayanan, V.; Kulkarni, J.P. Variation-tolerant ultra low-power heterojunction tunnel FET SRAM design. In Proceedings of the 2011 IEEE/ACM International Symposium on Nanoscale Architectures (NANOARCH), San Diego, CA, USA, 8–9 June 2011; pp. 45–52.
- Cotter, M.; Liu, H.C.; Datta, S.; Narayanan, V. Evaluation of tunnel FET-based flip-flop designs for low power, high performance applications. In Proceedings of the 2013 14th International Symposium on Quality Electronic Design (ISQED), Santa Clara, CA, USA, 4–6 March 2013; pp. 430–437.
- Datta, S.; Bijesh, R.; Liu, H.; Mohata, D.; Narayanan, V. Tunnel transistors for energy efficient computing. In Proceedings of the 2013 IEEE International Reliability Physics Symposium (IRPS), Anaheim, CA, USA, 14–18 April 2013; pp. 6A.3.1–6A.3.7.
- Leung, G.; Chui, C.O. Stochastic Variability in Silicon Double-Gate Lateral Tunnel Field-Effect Transistors. IEEE Trans. Electron Devices 2012, 60, 84–91. [Google Scholar] [CrossRef]
- Fan, M.L.; Hu, V.P.H.; Chen, Y.N.; Su, P.; Chuang, C.T. Analysis of Single-Trap-Induced Random Telegraph Noise and its Interaction With Work Function Variation for Tunnel FET. IEEE Trans. Electron Devices 2013, 60, 2038–2044. [Google Scholar] [CrossRef]
- Choi, K.M.; Choi, W.Y. Work-function variation effects of tunneling field-effect transistors (TFETs). IEEE Trans. Electron Device Lett. 2013, 34, 942–944. [Google Scholar] [CrossRef]
- Damrongplasi, N.; Kim, N.S.; Shin, H.C.; Liu, T.J.K. Impact of Gate Line-Edge Roughness (LER) vs. Random Dopant Fluctuations (RDF) on Germanium-Source Tunnel FET Performance. IEEE Trans. Nanotechnol. 2013, 12, 1061–1067. [Google Scholar] [CrossRef]
- Avci, U.E.; Rios, R.; Kuhn, K.J.; Young, I.A. Comparison of performance, switching energy and process variations for the TFET and MOSFET in logic. In Proceedings of the 2011 Symposium on VLSI Technology (VLSIT), Honolulu, HI, USA, 14–16 June 2011; pp. 124–125.
- Saripalli, V.; Mishra, A.; Datta, S.; Narayanan, V. An energy-efficient heterogeneous CMP based on hybrid TFET-CMOS cores. In Proceedings of the 48th ACM/EDAC/IEEE on Design Automation Conference (DAC), New York, NY, USA, 5–9 June 2011; pp. 729–734.
- Sentaurus TCAD Manual; Sentaurus Device: Mountain View, CA, USA, 2011.
- Liu, L.; Mohata, D.K.; Datta, S. Scaling Length Theory of Double-Gate Interband Tunnel Field-Effect Transistors. IEEE Trans. Electron Devices 2012, 59, 902–908. [Google Scholar] [CrossRef]
- Kotlyar, R.; Avci, U.E.; Cea, S.; Rios, R.; Linton, T.D.; Kuhn, K.J.; Young, I.A. Bandgap engineering of group IV materials for complementary n and p tunneling field effect transistors. Appl. Phys. Lett. 2013, 102, 106–113. [Google Scholar] [CrossRef]
- Pal, A.; Sachid, A.B.; Gossner, H.; Rao, V.R. Insights into design and optimization of TFET devices and circuits. IEEE Trans. Electron Devices 2011, 58, 1045–1053. [Google Scholar] [CrossRef]
- Chou, S.H.; Fan, M.L.; Su, P. Investigation and Comparison of Work Function Variation for FinFET and UTB SOI Devices Using a Voronoi Approach. IEEE Trans. Electron Devices 2013, 60, 1485–1489. [Google Scholar] [CrossRef]
- Asenov, A.; Kaya, S.; Brown, A.R. Intrinsic parameter fluctuations in decananometer MOSFETs introduced by gate line edge roughness. IEEE Trans. Electron Devices 2003, 50, 1254–1260. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.-N.; Chen, C.-J.; Fan, M.-L.; Hu, V.P.-H.; Su, P.; Chuang, C.-T. Impacts of Work Function Variation and Line-Edge Roughness on TFET and FinFET Devices and 32-Bit CLA Circuits. J. Low Power Electron. Appl. 2015, 5, 101-115. https://doi.org/10.3390/jlpea5020101
Chen Y-N, Chen C-J, Fan M-L, Hu VP-H, Su P, Chuang C-T. Impacts of Work Function Variation and Line-Edge Roughness on TFET and FinFET Devices and 32-Bit CLA Circuits. Journal of Low Power Electronics and Applications. 2015; 5(2):101-115. https://doi.org/10.3390/jlpea5020101
Chicago/Turabian StyleChen, Yin-Nien, Chien-Ju Chen, Ming-Long Fan, Vita Pi-Ho Hu, Pin Su, and Ching-Te Chuang. 2015. "Impacts of Work Function Variation and Line-Edge Roughness on TFET and FinFET Devices and 32-Bit CLA Circuits" Journal of Low Power Electronics and Applications 5, no. 2: 101-115. https://doi.org/10.3390/jlpea5020101
APA StyleChen, Y.-N., Chen, C.-J., Fan, M.-L., Hu, V. P.-H., Su, P., & Chuang, C.-T. (2015). Impacts of Work Function Variation and Line-Edge Roughness on TFET and FinFET Devices and 32-Bit CLA Circuits. Journal of Low Power Electronics and Applications, 5(2), 101-115. https://doi.org/10.3390/jlpea5020101





