Photothermal Effects and Heat Conduction in Nanogranular Silicon Films
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample Preparation
2.2. Micro-Raman Spectroscopy
2.3. Local Temperature Measurements
2.4. FDTD Electromagnetic and FEM Heat Modeling
3. Results and Discussion
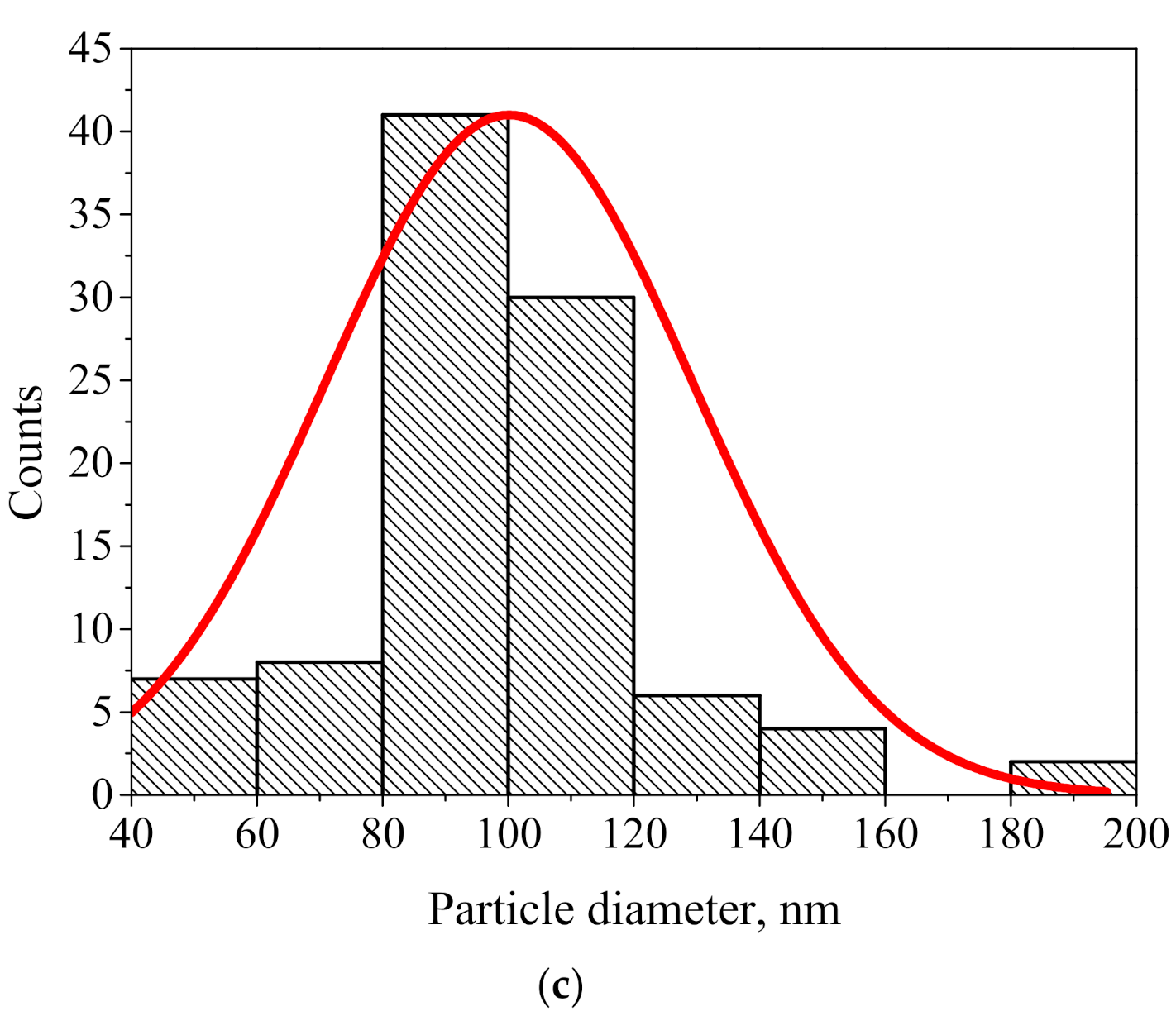
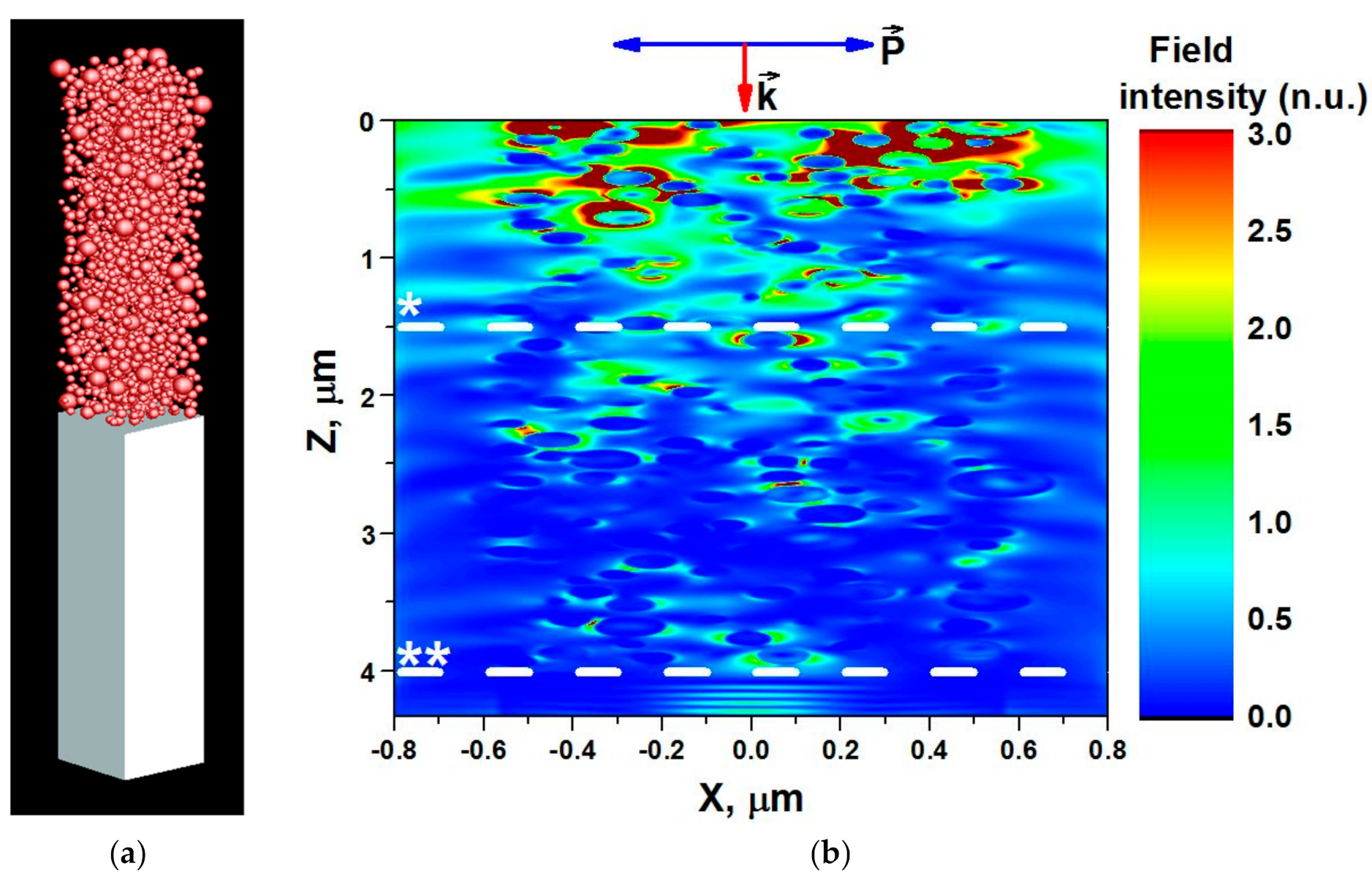
3.1. FDTD Modeling of Light Penetration
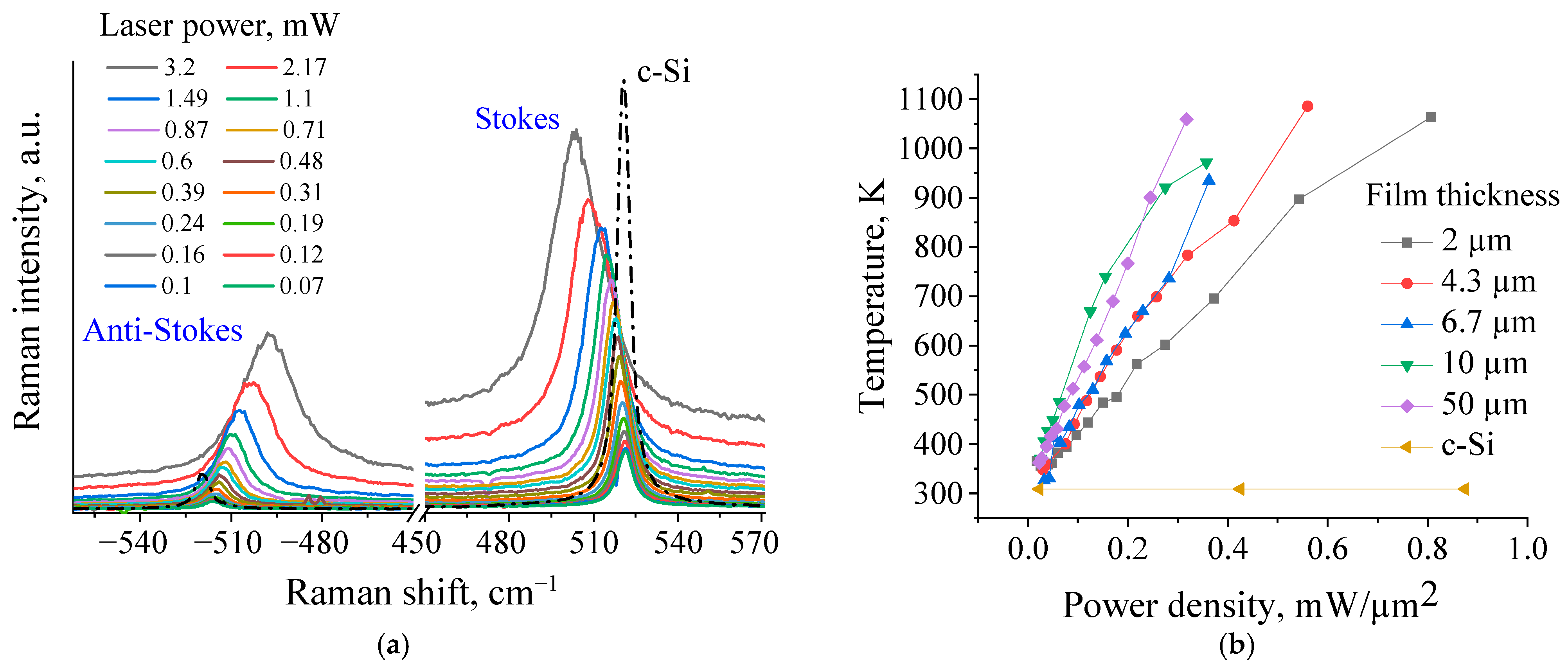
3.2. Laser-Induced Phase Transition in Si Nanogranular Films
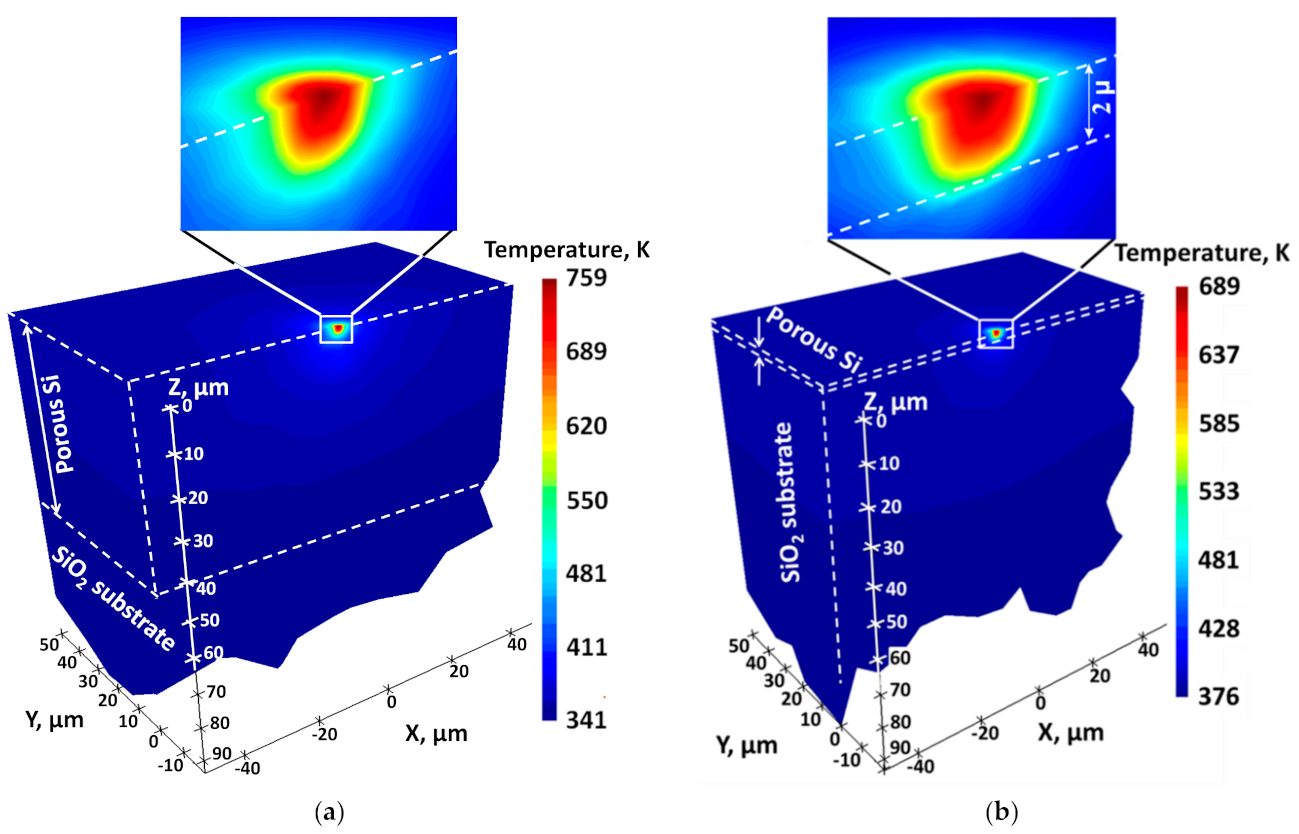
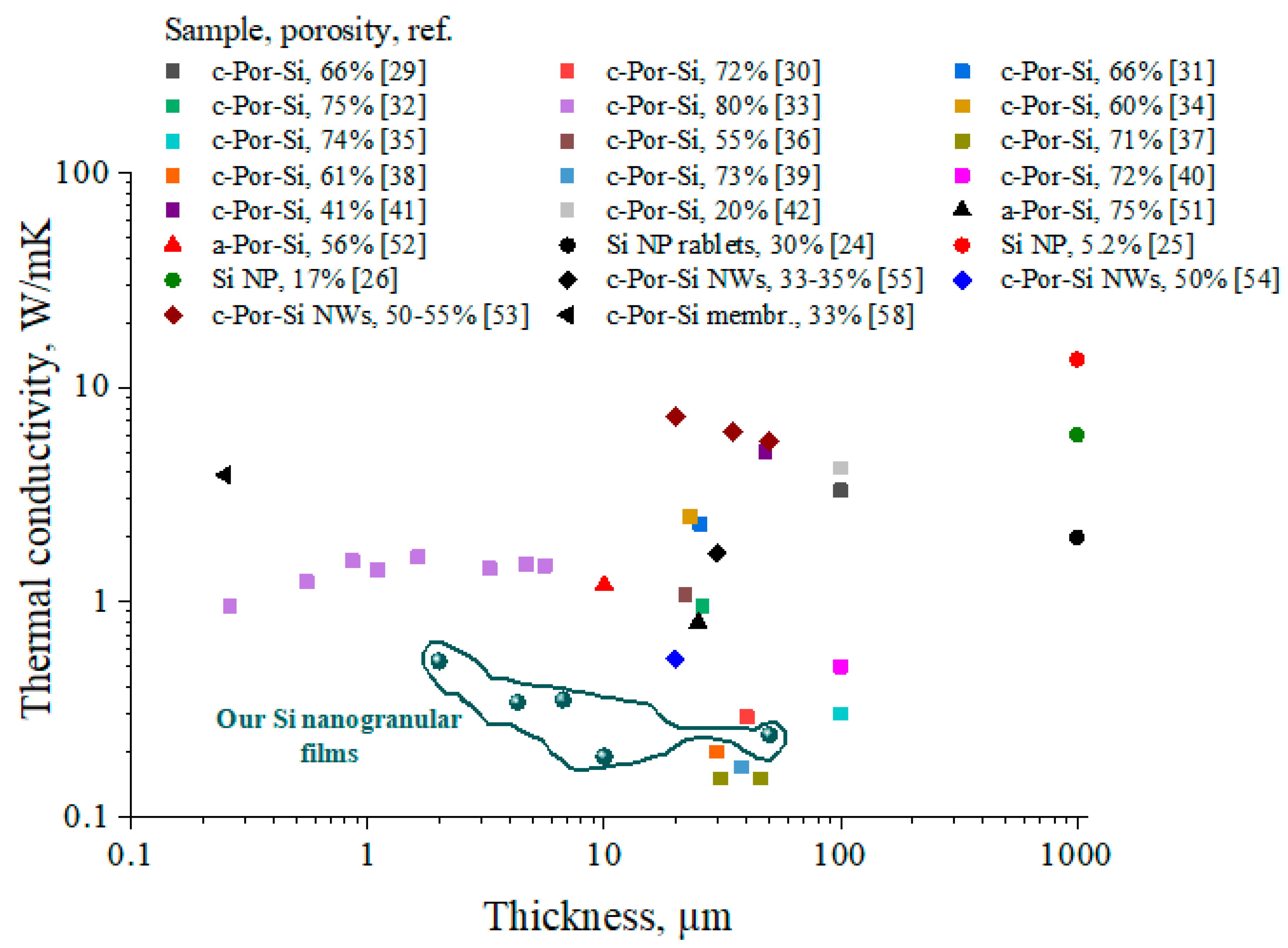
3.3. Laser Induced Heating and Thermal Conductivity of Si Nanogranular Films
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schierning, G. Silicon nanostructures for thermoelectric devices: A review of the current state of the art. Phys. Status Solidi A 2014, 211, 1235–1249. [Google Scholar] [CrossRef]
- Elsahati, M.; Clarke, K.; Richards, R. Thermal conductivity of copper and silica nanoparticle packed beds. Int. Commun. Heat Mass Transf. 2016, 71, 96–100. [Google Scholar] [CrossRef]
- Hong, Y.; Kim, H.; Lee, G.; Kim, W.; Park, J.; Cheon, J.; Koo, J. Controlled two-dimensional distribution of nanoparticles by spin-coating method. Appl. Phys. Lett. 2002, 80, 844–846. [Google Scholar] [CrossRef]
- Fernández-Arias, M.; Zimbone, M.; Boutinguiza, M.; del Val, J.; Riveiro, A.; Privitera, V.; Grimaldi, M.G.; Pou, J. Synthesis and deposition of Ag nanoparticles by combining laser ablation and electrophoretic deposition techniques. Coatings 2019, 9, 571. [Google Scholar] [CrossRef] [Green Version]
- Markelonis, A.R.; Wang, J.S.; Ullrich, B.; Wai, C.M.; Brown, G.J. Nanoparticle film deposition using a simple and fast centrifuge sedimentation method. Appl. Nanosci. 2015, 5, 457–468. [Google Scholar] [CrossRef] [Green Version]
- Yabuki, H.; Yonezawa, S.; Eguchi, R.; Takashir, M. Flexible thermoelectric films formed using integrated nano-composites with single wall carbon nanotubes and Bi2Te3 nanoplates via solvothermal synthesis. Sci. Rep. 2020, 10, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Toshima, N.; Oshima, K.; Anno, H.; Nishinaka, T.; Ichikawa, S.; Iwata, A.; Shiraishi, Y. Novel hybrid organic thermoelectric materials: Three-component hybrid films consisting of a nanoparticle polymer complex, carbon nanotubes, and vinyl polymer. Adv. Mater. 2015, 27, 2246–2251. [Google Scholar] [CrossRef] [PubMed]
- Ishii, S.; Higashino, M.; Goya, S.; Shkondin, E.; Tanaka, K.; Nagao, T.; Takayama, O.; Murai, S. Extreme thermal anisotropy in high-aspect-ratio titanium nitride nanostructures for efficient photothermal heating. Nanophotonics 2021, 10, 1487–1494. [Google Scholar] [CrossRef]
- Abdullaev, A.; Chauhan, V.S.; Muminov, B.; O’Connell, J.; Skuratov, V.A.; Khafizov, M.; Utegulov, Z.N. Thermal transport across nanoscale damage profile in sapphire irradiated by swift heavy ions. J. Appl. Phys. 2020, 127, 035108. [Google Scholar] [CrossRef]
- Salazar, A.; Fuente, R.; Apinaniz, E.; Mendioroz, A.; Celorrio, R. Simultaneous measurement of thermal diffusivity and optical absorption coefficient using photothermal radiometry. II Multilayered solids. J. Appl. Phys. 2011, 110, 033516. [Google Scholar] [CrossRef] [Green Version]
- Cheng, P.; Wang, H.; Wang, H.; Aken, P.A.V.; Wang, D.; Schaaf, P. High-efficiency photothermal water evaporation using broadband solar energy harvesting by ultrablack silicon structures. Adv. Energy Sustain. Res. 2021, 2, 2000083. [Google Scholar] [CrossRef]
- Cheng, P.; Wang, H.; Müller, B.; Müller, J.; Wang, D.; Schaaf, P. Photo-thermoelectric conversion using black silicon with enhanced light trapping performance far beyond the band edge absorption. ACS Appl. Mater. Interfaces 2021, 13, 1818–1826. [Google Scholar] [CrossRef]
- Kaur, P.; Aliru, M.; Chadha, A.; Asea, A.; Krishnan, S. Hyperthermia using nanoparticles—Promises and pitfalls. Int. J. Hyperth. 2016, 32, 76–88. [Google Scholar] [CrossRef]
- Xu, W.; Tamarov, K.; Fan, L.; Granroth, S.; Rantanen, J.; Nissinen, T.; Peräniemi, S.; Uski, O.; Hirvonen, M.-R.; Lehto, V.-P. Scalable synthesis of biodegradable black mesoporous silicon nanoparticles for highly efficient photothermal therapy. ACS Appl. Mater. Interfaces 2018, 10, 23529–23538. [Google Scholar] [CrossRef]
- Li, Q.-Y.; Xia, K.; Zhang, J.; Zhang, Y.; Li, Q.; Takahashi, K.; Zhang, X. Measurement of specific heat and thermal conductivity of supported and suspended graphene by a comprehensive Raman optothermal method. Nanoscale 2017, 9, 10784–10793. [Google Scholar] [CrossRef] [PubMed]
- Poborchii, V.; Uchida, N.; Miyazaki, Y.; Tada, T.; Geshev, P. A simple efficient method of nanofilm-on-bulk-substrate thermal conductivity measurement using Raman thermometry. Int. J. Heat Mass Transf. 2017, 123, 137–142. [Google Scholar] [CrossRef]
- Périchon, S.; Lysenko, V.; Remaki, B.; Barbier, D.; Champagnon, B. Measurement of porous silicon thermal conductivity by micro-Raman scattering. J. Appl. Phys. 1999, 86, 4700–4702. [Google Scholar] [CrossRef]
- Chávez-Ángel, E.; Reparaz, J.S.; Gomis-Bresco, J.; Wagner, M.R.; Cuffe, J.; Graczykowski, B.; Shchepetov, A.; Jiang, H.; Prunnila, M.; Ahopelto, J.; et al. Reduction of the thermal conductivity in free-standing silicon nano-membranes investigated by non-invasive Raman thermometry. APL Mater. 2014, 2, 012113. [Google Scholar] [CrossRef]
- Doerk, G.S.; Carraro, C.; Maboudian, R. Single nanowire thermal conductivity measurements by Raman thermography. ACS Nano 2010, 4, 4908–4914. [Google Scholar] [CrossRef]
- Mishra, P.; Jain, K.P. Temperature-dependent Raman scattering studies in nanocrystalline silicon and finite-size effects. Phys. Rev. B 2000, 62, 14790–14795. [Google Scholar] [CrossRef]
- Balkanski, M.; Wallis, R.F.; Haro, E. Anharmonic effects in light scattering due to optical phonons in silicon. Phys. Rev. B 1983, 28, 1928–1934. [Google Scholar] [CrossRef]
- Rodichkina, S.; Lysenko, V.; Belarouci, A.; Bezverkhyy, I.; Chassagnon, R.; Isaiev, M.; Nychyporuk, T.; Timoshenko, V.Y. Photo-induced cubic-to-hexagonal polytype transition in silicon nanowires. Cryst. Eng. Comm. 2019, 21, 4747–4752. [Google Scholar] [CrossRef]
- Popović, Z.V.; Dohčević-Mitrović, Z.; Konstantinović, M.J.; Šćepanović, M. Raman scattering characterization of nanopowders and nanowires (rods). J. Raman Spectrosc. 2007, 38, 750–755. [Google Scholar] [CrossRef]
- Ashby, S.P.; Bian, T.; Ning, H.; Reece, M.J.; Chao, Y. Thermal diffusivity of SPS pressed silicon powders and the potential for using bottom-up silicon quantum dots as a starting material. J. Electron. Mater. 2015, 44, 1931–1935. [Google Scholar] [CrossRef]
- Suzuki, T.; Ohishi, Y.; Kurosaki, K.; Muta, H.; Yamanaka, S. Thermal conductivity of size-controlled bulk silicon nanocrystals using self-limiting oxidation and HF etching. Appl. Phys. Express 2012, 5, 081302. [Google Scholar] [CrossRef]
- Wang, Z.; Alaniz, J.E.; Jang, W.; Garay, J.E.; Dames, C. Thermal conductivity of nanocrystalline silicon: Importance of grain size and frequency-dependent mean free paths. Nano Lett. 2011, 11, 2206–2213. [Google Scholar] [CrossRef]
- Zhu, G.H.; Lee, H.; Lan, Y.C.; Wang, X.W.; Joshi, G.; Wang, D.Z.; Yang, J.; Vashaee, D.; Guilbert, H.; Pillitteri, A.; et al. Increased phonon scattering by nanograins and point defects in nanostructured silicon with a low concentration of germanium. Phys. Rev. Lett. 2009, 102, 196803. [Google Scholar] [CrossRef]
- Bux, S.K.; Blair, R.; Gogna, P.K.; Lee, H.; Chen, G.; Dresselhaus, M.S.; Kaner, R.B.; Fleurial, J.-P. Nanostructured bulk silicon as an effective thermoelectric material. Adv. Funct. Mater. 2009, 19, 2445–2452. [Google Scholar] [CrossRef]
- Boor, J.D.; Kim, D.S.; Ao, X.; Hagen, D.; Cojocaru, A.; Foll, H.; Schmidt, V. Temperature and structure size dependence of the thermal conductivity of porous silicon. EPL 2011, 96, 16001. [Google Scholar] [CrossRef]
- Lettieri, S.; Bernini, U.; Massera, E.; Maddalena, P.M. Optical investigations on thermal conductivity in n- and p-type porous silicon. Phys. Status Solidi C 2005, 2, 3414–3418. [Google Scholar] [CrossRef]
- Wolf, A.; Brendel, R. Thermal conductivity of sintered porous silicon films. Thin Solid Films 2006, 513, 385–390. [Google Scholar] [CrossRef]
- Amato, G.; Angelucci, R.; Benedetto, G.; Boarino, L.; Dori, L.; Maccagnani, P.; Rossi, A.; Spagnolo, R. Thermal Characterisation of Porous Silicon Membranes. J. Porous Mater. 2000, 7, 183–186. [Google Scholar] [CrossRef]
- Gomes, S.; David, L.; Lysenko, V.; Descamps, A.; Nychyporuk, T.; Raynaud, M. Application of scanning thermal microscopy for thermal conductivity measurements on meso-porous silicon thin films. J. Phys. D Appl. Phys. 2007, 40, 6677–6683. [Google Scholar] [CrossRef]
- Benedetto, G.; Boarino, L.; Spagnolo, R. Evaluation of thermal conductivity of porous silicon layers by a photoacoustic method. Appl. Phys. A 1997, 6, 155–159. [Google Scholar] [CrossRef]
- Lysenko, V.; Périchon, S.; Remaki, B.; Barbier, D.; Champagnon, B. Thermal conductivity of thick meso-porous silicon layers by micro-Raman scattering. J. Appl. Phys. 1999, 86, 6841–6846. [Google Scholar] [CrossRef]
- Kihara, Y.; Harada, T.; Koshida, N. Precise thermal characterization of confined nanocrystalline silicon by a 3ω method. Jpn. J. Appl. Phys. 2005, 44, 4084–4087. [Google Scholar] [CrossRef]
- Gesele, G.; Linsmeier, J.; Drach, V.; Fricke, J.; Arens-Fischer, R. Temperature-dependent thermal conductivity of porous silicon. J. Phys. D Appl. Phys. 1997, 30, 2911–2916. [Google Scholar] [CrossRef]
- Shen, Q.; Toyoda, T. Dependence of thermal conductivity of porous silicon on porosity characterized by photo-acoustic technique. Rev. Sci. Instrum. 2003, 74, 601. [Google Scholar] [CrossRef]
- Bernini, U.; Lettieri, S.; Maddalena, P.M.; Vitiello, R.; di Francia, G. Evaluation of the thermal conductivity of porous silicon layers by an optical pump-probe method. J. Physics Condens. Matter 2001, 13, 1141–1150. [Google Scholar] [CrossRef]
- Valalaki, K.; Nassiopoulou, A.G. Improved approach for determining thin layer thermal conductivity using the 3ω method. Application to porous Si thermal conductivity in the temperature range 77–300 K. J. Phys. D Appl. Phys. 2017, 50, 195302. [Google Scholar] [CrossRef]
- Melhem, A.; Meneses, D.D.S.; Andreazza-Vignolles, C.; Defforge, T.; Gautier, G.; Semmar, N.; Andreazza-Vignolle, C. Structural, optical, and thermal analysis of n-type mesoporous silicon prepared by electrochemical etching. J. Phys. Chem. C 2015, 119, 21443–21451. [Google Scholar] [CrossRef]
- Siegert, L.; Capelle, M.; Roqueta, F.; Lysenko, V.; Gautier, G. Evaluation of mesoporous silicon thermal conductivity by electrothermal finite element simulation. Nanoscale Res. Lett. 2012, 7, 1–7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dubyk, K.; Nychyporuk, T.; Lysenko, V.; Termentzidis, K.; Castanet, G.; Lemoine, F.; Lacroix, D.; Isaiev, M. Thermal properties study of silicon nanostructures by photoacoustic techniques. J. Appl. Phys. 2020, 127, 225101. [Google Scholar] [CrossRef]
- Alvarez, F.X.; Jou, D.; Sellito, A. Pore-size dependence of thermal conductivity of porous silicon: A phonon hydrodynamic approach. Appl. Phys. Lett. 2010, 97, 033103. [Google Scholar] [CrossRef] [Green Version]
- Radrianalisoa, J.; Baillis, D. Monte Carlo simulation of cross-plane thermal conductivity of nanostructured porous silicon films. J. Appl. Phys. 2008, 103, 053502. [Google Scholar] [CrossRef]
- Song, D.; Chen, G. Thermal conductivity of periodic microporous silicon films. Appl. Phys. Lett. 2004, 84, 687–689. [Google Scholar] [CrossRef]
- Sellitto, A.; Jou, D.; Cimmelli, V.A. A phenomenological study of pore-size dependent thermal conductivity of porous silicon. Acta Appl. Math. 2012, 122, 435–445. [Google Scholar] [CrossRef]
- Fang, J.; Pilon, L. Tuning thermal conductivity of nanoporous crystalline silicon by surface passivation: A molecular dynamics study. Appl. Phys. Lett. 2012, 101, 011909. [Google Scholar] [CrossRef] [Green Version]
- Newby, P.; Canut, B.; Bluet, J.-M.; Gomès, S.; Isaiev, M.; Burbelo, R.; Termentzidis, K.; Chantrenne, P.; Fréchette, L.G.; Lysenko, V. Amorphization and reduction of thermal conductivity in porous silicon by irradiation with swift heavy ions. J. Appl. Phys. 2013, 114, 014903. [Google Scholar] [CrossRef]
- Isaiev, M.; Newby, P.; Canut, B.; Tytarenko, A.; Lishchuk, P.; Andrusenko, D.; Gomès, S.; Bluet, J.-M.; Fréchette, L.G.; Lysenko, V.; et al. Thermal conductivity of partially amorphous porous silicon by photoacoustic technique. Mater. Lett. 2014, 128, 71–74. [Google Scholar] [CrossRef]
- Gomès, S.; Newby, P.; Canut, B.; Termentzidis, K.; Marty, O.; Fréchette, L.G.; Chantrenne, P.; Aimez, V.; Bluet, J.-M.; Lysenko, V. Characterization of the thermal conductivity of insulating thin films by scanning thermal microscopy. Microelectron. J. 2013, 44, 1029–1034. [Google Scholar] [CrossRef]
- Massoud, A.M.; Chapuis, P.-O.; Canut, B.; Bluet, J.-M. Thermal conductivity of irradiated porous silicon down to the oxide limit investigated by Raman thermometry and scanning thermal microscopy. J. Appl. Phys. 2020, 128, 175109. [Google Scholar] [CrossRef]
- Dubyk, K.; Pastushenko, A.; Nychyporuk, T.; Burbelo, R.; Isaiev, M.; Lysenko, V. Thermal conductivity of silicon nanomaterials measured using the photoacoustic technique in a piezoelectric configuration. J. Phys. Chem. Solids 2019, 126, 267–273. [Google Scholar] [CrossRef]
- Isaiev, M.; Didukh, O.; Nychyporuk, T.; Timoshenko, V.; Lysenko, V. Anisotropic heat conduction in silicon nanowire network revealed by Raman scattering. Appl. Phys. Lett. 2017, 110, 11908. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T.; Wu, S.; Xu, J.; Zheng, R.; Cheng, G. High thermoelectric figure-of-merits from large-area porous silicon nanowire arrays. Nano Energy 2015, 13, 433–441. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, L.; Kong, L.; Nai, M.H.; Liu, D.; Wu, J.; Liu, Y.; Chiam, S.Y.; Chim, W.K.; Lim, C.T.; et al. Ultralow thermal conductivity of single-crystalline porous silicon nanowires. Adv. Funct. Mater. 2017, 27, 1702824. [Google Scholar] [CrossRef] [Green Version]
- Dettori, R.; Melis, C.; Cartoixà, X.; Rurali, R.; Colombo, L. Model for thermal conductivity in nanoporous silicon from atomistic simulations. Phys. Rev. B 2015, 91, 054305. [Google Scholar] [CrossRef]
- Graczykowski, B.; Sachat, A.E.; Reparaz, J.S.; Sledzinska, M.; Wagner, M.R.; Chavez-Angel, E.; Wu, Y.; Volz, S.; Wu, Y.; Alzina, F.; et al. Thermal conductivity and air-mediated losses in periodic porous silicon membranes at high temperatures. Nat. Commun. 2017, 8, 415. [Google Scholar] [CrossRef] [Green Version]
- Jaque, D.; Maestro, M.L.; Rosal, B.D.; Haro-Gonzalez, P.; Benayas, A.; Plaza, J.L.; Rodrıguez, E.M.; Sole, J.G. Nanoparticles for photothermal therapies. Nanoscale 2014, 6, 9494–9530. [Google Scholar] [CrossRef] [PubMed]
- Ziegler, M.; Dathe, A.; Pollok, K.; Langenhorst, F.; Hübner, U.; Wang, D.; Schaaf, P. Metastable atomic layer deposition: 3D self-assembly toward ultradark materials. ACS Nano 2020, 14, 15023–15031. [Google Scholar] [CrossRef] [PubMed]
- Yukhymchuk, V.O.; Dzhagan, V.M.; Valakh, M.Y.; Klad’ko, V.P.; Gudymenko, O.J.; Yefanov, V.S.; Zahn, D.R.T. In situ photoluminescence/Raman study of reversible photo-induced structural transformation of nc-Si. Mater. Res. Express 2014, 1, 045905. [Google Scholar] [CrossRef]
- Iqbal, Z.; Veprek, S. Raman scattering from hydrogenated microcrystalline and amorphous silicon. J. Phys. C Solid State Phys. 1982, 15, 377–392. [Google Scholar] [CrossRef]
- Pazionis, G.; Tang, H.; Herman, I. Raman microprobe analysis of temperature profiles in CW laser heated silicon microstructures. IEEE J. Quantum Electron. 1989, 25, 976–988. [Google Scholar] [CrossRef]
- Han, L.; Zeman, M.; Smets, A.H.M. Raman study of laser-induced heating effects in free-standing silicon nanocrystals. Nanoscale 2015, 7, 8389–8397. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, G. Phonon heat conduction in nanostructures. Int. J. Therm. Sci. 2000, 39, 471–480. [Google Scholar] [CrossRef]
- Chantrenne, P.; Lysenko, V. Thermal conductivity of interconnected silicon nanoparticles: Application to porous silicon nanostructures. Phys. Rev. B 2005, 72, 035318. [Google Scholar] [CrossRef]
- Wu, D.; Huanga, C. Thermal conductivity study of SiC nanoparticle beds for thermal insulation applications. Phys. E Low-Dimens. Syst. Nanostruct. 2020, 118, 113970. [Google Scholar] [CrossRef]
- Poborchii, V.; Tada, T.; Kanayama, T. Giant heating of Si nanoparticles by weak laser light: Optical microspectroscopic study and application to particle modification. J. Appl. Phys. 2005, 97, 104323. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kurbanova, B.A.; Mussabek, G.K.; Timoshenko, V.Y.; Lysenko, V.; Utegulov, Z.N. Photothermal Effects and Heat Conduction in Nanogranular Silicon Films. Nanomaterials 2021, 11, 2379. https://doi.org/10.3390/nano11092379
Kurbanova BA, Mussabek GK, Timoshenko VY, Lysenko V, Utegulov ZN. Photothermal Effects and Heat Conduction in Nanogranular Silicon Films. Nanomaterials. 2021; 11(9):2379. https://doi.org/10.3390/nano11092379
Chicago/Turabian StyleKurbanova, Bayan A., Gauhar K. Mussabek, Viktor Y. Timoshenko, Vladimir Lysenko, and Zhandos N. Utegulov. 2021. "Photothermal Effects and Heat Conduction in Nanogranular Silicon Films" Nanomaterials 11, no. 9: 2379. https://doi.org/10.3390/nano11092379
APA StyleKurbanova, B. A., Mussabek, G. K., Timoshenko, V. Y., Lysenko, V., & Utegulov, Z. N. (2021). Photothermal Effects and Heat Conduction in Nanogranular Silicon Films. Nanomaterials, 11(9), 2379. https://doi.org/10.3390/nano11092379






