Approximating Fixed Points of Nonexpansive Type Mappings via General Picard–Mann Algorithm

Abstract

The aim of this paper is to approximate fixed points of nonexpansive type mappings in Banach spaces when the set of fixed points is nonempty. We study the general Picard–Mann (GPM) algorithm, obtaining the weak and strong convergence theorems. We provide an example to illustrate the convergence behaviour of the GPM algorithm. We compare the GPM algorithm with other existing (well known) algorithms numerically (under different parameters and initial guesses).

1. Introduction and Preliminaries

Let $(\mathcal{Z},\parallel .\parallel )$ be a Banach space. The mapping $\mathsf{\Phi }:\mathcal{Z}\to \mathcal{Z}$ is nonexpansive if

$$\parallel \mathsf{\Phi }\left(\vartheta \right)-\mathsf{\Phi }\left(\nu \right)\parallel \le \parallel \vartheta -\nu \parallel \forall \vartheta ,\nu \in \mathcal{Z}.$$

(1)

A point $\vartheta \in \mathcal{Z}$ is a fixed point of $\mathsf{\Phi }$ if $\mathsf{\Phi }\left(\vartheta \right)=\vartheta .$ Let $F\left(\mathsf{\Phi }\right)$ denote the set of fixed points of $\mathsf{\Phi }$. Finding a fixed point of nonlinear mappings is an important problem and various algorithms have been used by many researchers. The Picard algorithm [1] is mostly used (simplest and popular) to find the fixed points of contractive mappings. However, for nonexpansive mappings, the Picard algorithm need not converge to a fixed point. Krasnosel’skiĭ [2], Schaefer [3] and Mann [4] proposed more general algorithms to find fixed points of nonexpansive mappings.

Many mathematicians extended and generalized the class of nonexpansive mappings in different directions, see [5]. In 2011, García-Falset et al. [6] considered the following class of mappings:

Definition 1

([6]). Let $\mathcal{Y}$ be a subset of a Banach space $\mathcal{Z}$ such that $\mathcal{Y}\ne \varnothing .$ A mapping $\mathsf{\Phi }:\mathcal{Y}\to \mathcal{Y}$ is said to satisfy condition $\left(E_{\mu }\right)$ on $\mathcal{Y}$ if there exists $\mu \ge 1$ such that

$$\parallel \vartheta -\mathsf{\Phi }\left(\nu \right)\parallel \le \mu \parallel \vartheta -\mathsf{\Phi }\left(\vartheta \right)\parallel +\parallel \vartheta -\nu \parallel ,\forall \vartheta ,\nu \in \mathcal{Y}.$$

A mapping $\mathsf{\Phi }$ satisfies condition (E) on $\mathcal{Y}$ whenever $\mathsf{\Phi }$ satisfies $\left(E_{\mu }\right)$ for some $\mu \ge 1.$

A number of papers have been appeared in literature dealing with condition (E), see [5,7,8,9] and references therein. In the last two decades, a number of algorithms (from one step to four steps) were studied by mathematicians to improve the fastness of the algorithm, see [4,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34].

Motivated by the above results, we approximate fixed points of the class of mappings satisfying condition (E). We employ general Picard–Mann (in short GPM) and obtain a number of weak and strong convergence results. We supply a numerical example and compare the GPM algorithm with various algorithms presented in Section 2.

We denote → for strong convergence, ⇀ for weak convergence, and ${\omega }_w\left({\vartheta }_n\right)$ denotes a cluster points ($\omega$-limit) set of a sequence $\left\{{\vartheta }_n\right\},$ that is, ${\omega }_w\left({\vartheta }_n\right):=\{\vartheta :\exists {\vartheta }_{n_k}\rightharpoonup \vartheta \}.$

Lemma 1

([35] p. 484). Let $\mathcal{Z}$ be a uniformly convex Banach space and $0<a\le p_n\le b<1$ for all $n\in \mathbb{N}.$ Let $\left\{{\vartheta }_n\right\}$ and $\left\{{\nu }_n\right\}$ be two sequences such that $\underset{n\to \infty }{lim\; sup}\parallel {\vartheta }_n\parallel \le r,$$\underset{n\to \infty }{lim\; sup}\parallel {\nu }_n\parallel \le r$ and $\underset{n\to \infty }{lim}\parallel p_n{\vartheta }_n+(1-p_n){\nu }_n\parallel =r$ hold for some $r\ge 0.$ Then, $\underset{n\to \infty }{lim}\parallel {\vartheta }_n-{\nu }_n\parallel =0.$

Lemma 2

((Demiclosedness principle). [6]). Let $\mathcal{Y}$ be a nonempty subset of a Banach space $\mathcal{Z}$ which has the Opial property. Let $\mathsf{\Phi }:\mathcal{Y}\to \mathcal{Y}$ be a mapping satisfying condition (E). Suppose $\left\{{\vartheta }_n\right\}$ is a sequence in $\mathcal{Y}$ such that $\left\{{\vartheta }_n\right\}$ converges weakly to ϑ and $\underset{n\to \infty }{lim}\parallel {\vartheta }_n-\mathsf{\Phi }\left({\vartheta }_n\right)\parallel =0.$ Then, $\mathsf{\Phi }\left(\vartheta \right)=\vartheta .$ That is, $I-\mathsf{\Phi }$ is demiclosed at zero.

Lemma 3

([6]). Let $\mathcal{Y}$ be a nonempty subset of a Banach space $\mathcal{Z}$ and $\mathsf{\Phi }:\mathcal{Y}\to \mathcal{Y}$ satisfies condition (E) with $F\left(\mathsf{\Phi }\right)\ne \varnothing$. Then, $\mathsf{\Phi }$ is quasi-nonexpansive.

2. Various Iterative Methods (or Algorithms)

In this section, we present a number of iterative methods considered in the literature: for a given ${\vartheta }_1\in \mathcal{Y}$ and $\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\},\left\{{\gamma }_n\right\}\subseteq [0,1].$

• Mann [4]

  $$\begin{array}{c}\hfill {\vartheta }_{n+1}=(1-{\alpha }_n){\vartheta }_n+{\alpha }_n\mathsf{\Phi }\left({\vartheta }_n\right).\end{array}$$

  (2)
• Ishikawa [10]

  $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\nu }_n=(1-{\beta }_n){\vartheta }_n+{\beta }_n\mathsf{\Phi }\left({\vartheta }_n\right)\hfill \\ {\vartheta }_{n+1}=(1-{\alpha }_n){\vartheta }_n+{\alpha }_n\mathsf{\Phi }\left({\nu }_n\right).\hfill \end{array}\right.\end{array}$$

  (3)
• Noor [11]

  $$\begin{array}{c}\hfill \left\{\begin{array}{c}{z}_n=(1-{\gamma }_n){\vartheta }_n+{\gamma }_n\mathsf{\Phi }\left({\vartheta }_n\right)\hfill \\ {\nu }_n=(1-{\beta }_n){\vartheta }_n+{\beta }_n\mathsf{\Phi }\left(z_n\right)\hfill \\ {\vartheta }_{n+1}=(1-{\alpha }_n){\vartheta }_n+{\alpha }_n\mathsf{\Phi }\left({\nu }_n\right).\hfill \end{array}\right.\end{array}$$

  (4)
• Agarwal et al. [12]

  $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\nu }_n=(1-{\beta }_n){\vartheta }_n+{\beta }_n\mathsf{\Phi }\left({\vartheta }_n\right)\hfill \\ {\vartheta }_{n+1}=(1-{\alpha }_n)\mathsf{\Phi }\left({\vartheta }_n\right)+{\alpha }_n\mathsf{\Phi }\left({\nu }_n\right).\hfill \end{array}\right.\end{array}$$

  (5)
• Phuengrattana and Suantai [13]

  $$\begin{array}{c}\hfill \left\{\begin{array}{c}{z}_n=(1-{\gamma }_n){\vartheta }_n+{\gamma }_n\mathsf{\Phi }\left({\vartheta }_n\right)\hfill \\ {\nu }_n=(1-{\beta }_n)z_n+{\beta }_n\mathsf{\Phi }\left(z_n\right)\hfill \\ {\vartheta }_{n+1}=(1-{\alpha }_n){\nu }_n+{\alpha }_n\mathsf{\Phi }\left({\nu }_n\right).\hfill \end{array}\right.\end{array}$$

  (6)
• Sahu [14]

  $$\begin{array}{c}\hfill {\vartheta }_{n+1}=\mathsf{\Phi }\{(1-{\alpha }_n){\vartheta }_n+{\alpha }_n\mathsf{\Phi }\left({\vartheta }_n\right)\}.\end{array}$$

  (7)

  Remark1.

  In 2013, S. H. Khan [36] introduced the same iterative method like (7) and called it the Picard–Mann hybrid iterative method.
• Chugh et al. [15]

  $$\begin{array}{c}\hfill \left\{\begin{array}{c}{z}_n=(1-{\gamma }_n){\vartheta }_n+{\gamma }_n\mathsf{\Phi }\left({\vartheta }_n\right)\hfill \\ {\nu }_n=(1-{\beta }_n)\mathsf{\Phi }\left({\vartheta }_n\right)+{\beta }_n\mathsf{\Phi }\left(z_n\right)\hfill \\ {\vartheta }_{n+1}=(1-{\alpha }_n){\nu }_n+{\alpha }_n\mathsf{\Phi }\left({\nu }_n\right).\hfill \end{array}\right.\end{array}$$

  (8)
• Karaca and Yildirim [16]

  $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\nu }_n=(1-{\beta }_n){\vartheta }_n+{\beta }_n\mathsf{\Phi }\left({\vartheta }_n\right)\hfill \\ {\vartheta }_{n+1}=\mathsf{\Phi }\{(1-{\alpha }_n)\mathsf{\Phi }\left({\vartheta }_n\right)+{\alpha }_n\mathsf{\Phi }\left({\nu }_n\right)\}.\hfill \end{array}\right.\end{array}$$

  (9)
• Abbas and Nazir [17]

  $$\begin{array}{c}\hfill \left\{\begin{array}{c}{z}_n=(1-{\gamma }_n){\vartheta }_n+{\gamma }_n\mathsf{\Phi }\left({\vartheta }_n\right)\hfill \\ {\nu }_n=(1-{\beta }_n)\mathsf{\Phi }\left({\vartheta }_n\right)+{\beta }_n\mathsf{\Phi }\left(z_n\right)\hfill \\ {\vartheta }_{n+1}=(1-{\alpha }_n)\mathsf{\Phi }\left({\nu }_n\right)+{\alpha }_n\mathsf{\Phi }\left(z_n\right).\hfill \end{array}\right.\end{array}$$

  (10)
• Thakur et al. [18]

  $$\begin{array}{c}\hfill \left\{\begin{array}{c}{z}_n=(1-{\gamma }_n){\vartheta }_n+{\gamma }_n\mathsf{\Phi }\left({\vartheta }_n\right)\hfill \\ {\nu }_n=(1-{\beta }_n)z_n+{\beta }_n\mathsf{\Phi }\left(z_n\right)\hfill \\ {\vartheta }_{n+1}=(1-{\alpha }_n)\mathsf{\Phi }\left({\vartheta }_n\right)+{\alpha }_n\mathsf{\Phi }\left({\nu }_n\right).\hfill \end{array}\right.\end{array}$$

  (11)
• Sintunavarat and Pitea [19]

  $$\begin{array}{c}\hfill \left\{\begin{array}{c}{z}_n=(1-{\gamma }_n){\vartheta }_n+{\gamma }_n\mathsf{\Phi }\left({\vartheta }_n\right)\hfill \\ {\nu }_n=(1-{\beta }_n){\vartheta }_n+{\beta }_n{z}_n\hfill \\ {\vartheta }_{n+1}=(1-{\alpha }_n)\mathsf{\Phi }\left({\nu }_n\right)+{\alpha }_n\mathsf{\Phi }\left(z_n\right).\hfill \end{array}\right.\end{array}$$

  (12)
• Thakur et al. [20]

  $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\nu }_n=(1-{\beta }_n){\vartheta }_n+{\beta }_n\mathsf{\Phi }\left({\vartheta }_n\right)\hfill \\ {\vartheta }_{n+1}=\mathsf{\Phi }\{(1-{\alpha }_n)\mathsf{\Phi }\left({\vartheta }_n\right)+{\alpha }_n{\nu }_n\}.\hfill \end{array}\right.\end{array}$$

  (13)
• Ullah and Arshad et al. [22]

  $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\nu }_n=(1-{\beta }_n){\vartheta }_n+{\beta }_n\mathsf{\Phi }\left({\vartheta }_n\right)\hfill \\ {\vartheta }_{n+1}={\mathsf{\Phi }}^2\{(1-{\alpha }_n){\vartheta }_n+{\alpha }_n\mathsf{\Phi }\left({\nu }_n\right)\}.\hfill \end{array}\right.\end{array}$$

  (14)
• Ullah and Arshad [23]

  $$\begin{array}{c}\hfill {\vartheta }_{n+1}={\mathsf{\Phi }}^2\{(1-{\alpha }_n){\vartheta }_n+{\alpha }_n\mathsf{\Phi }\left({\vartheta }_n\right)\}.\end{array}$$

  (15)

  Remark2.

  In 2020, F. Ali and J. Ali [37] introduced the same iterative method like (15) and called it the $F^{*}$ iterative method.
• Hussain et al. [24]

  $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\nu }_n=(1-{\beta }_n){\vartheta }_n+{\beta }_n\mathsf{\Phi }\left({\vartheta }_n\right)\hfill \\ {\vartheta }_{n+1}={\mathsf{\Phi }}^2\{(1-{\alpha }_n)\mathsf{\Phi }\left({\vartheta }_n\right)+{\alpha }_n\mathsf{\Phi }\left({\nu }_n\right)\}.\hfill \end{array}\right.\end{array}$$

  (16)
• Ullah and Arshad [25]

  $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\nu }_n=(1-{\beta }_n){\vartheta }_n+{\beta }_n\mathsf{\Phi }\left({\vartheta }_n\right)\hfill \\ {\vartheta }_{n+1}={\mathsf{\Phi }}^2\{(1-{\alpha }_n){\nu }_n+{\alpha }_n\mathsf{\Phi }\left({\nu }_n\right)\}.\hfill \end{array}\right.\end{array}$$

  (17)
• Piri et al. [26]

  $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\nu }_n=\mathsf{\Phi }\{(1-{\beta }_n){\vartheta }_n+{\beta }_n\mathsf{\Phi }\left({\vartheta }_n\right)\}\hfill \\ {\vartheta }_{n+1}=(1-{\alpha }_n)\mathsf{\Phi }\left({\nu }_n\right)+{\alpha }_n{\mathsf{\Phi }}^2\left({\nu }_n\right).\hfill \end{array}\right.\end{array}$$

  (18)
• Bhutia and Tiwary [27]

  $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\nu }_n=\mathsf{\Phi }\{(1-{\beta }_n){\vartheta }_n+{\beta }_n\mathsf{\Phi }\left({\vartheta }_n\right)\}\hfill \\ {\vartheta }_{n+1}={\mathsf{\Phi }}^2\{(1-{\alpha }_n){\nu }_n+{\alpha }_n\mathsf{\Phi }\left({\nu }_n\right)\}.\hfill \end{array}\right.\end{array}$$

  (19)
• Garodia and Uddin [28]

  $$\begin{array}{c}\hfill {\vartheta }_{n+1}={\mathsf{\Phi }}^2\{(1-{\alpha }_n)\mathsf{\Phi }\left({\vartheta }_n\right)+{\alpha }_n{\mathsf{\Phi }}^2\left({\vartheta }_n\right)\}.\end{array}$$

  (20)
• Garodia and Uddin [29], and Hussain et al. [38] (D-iterative algorithm, see also [39])

  $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\nu }_n=\mathsf{\Phi }\{(1-{\beta }_n){\vartheta }_n+{\beta }_n\mathsf{\Phi }\left({\vartheta }_n\right)\}\hfill \\ {\vartheta }_{n+1}={\mathsf{\Phi }}^2\{(1-{\alpha }_n)\mathsf{\Phi }\left({\vartheta }_n\right)+{\alpha }_n\mathsf{\Phi }\left({\nu }_n\right)\}.\hfill \end{array}\right.\end{array}$$

  (21)

  Remark3.

  If we look at the submission dates, it can be noticed that the paper by Hussain et al. [38] has been received on 3 May 2020, while Garodia and Uddin’s paper [29] has no submission information. Thus, we cannot say which iterative method appeared first.
• Ali et al. [30]

  $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\nu }_n=\mathsf{\Phi }\{(1-{\beta }_n){\vartheta }_n+{\beta }_n\mathsf{\Phi }\left({\vartheta }_n\right)\}\hfill \\ {\vartheta }_{n+1}=\mathsf{\Phi }\{(1-{\alpha }_n)\mathsf{\Phi }\left({\nu }_n\right)+{\alpha }_n{\mathsf{\Phi }}^2\left({\nu }_n\right)\}.\hfill \end{array}\right.\end{array}$$

  (22)
• Ali and Ali [31]

  $$\begin{array}{c}\hfill {\vartheta }_{n+1}={\mathsf{\Phi }}^3\{(1-{\alpha }_n){\vartheta }_n+{\alpha }_n\mathsf{\Phi }\left({\vartheta }_n\right)\}.\end{array}$$

  (23)
• Hassan et al. [32]

  $$\begin{array}{c}\hfill \left\{\begin{array}{c}{w}_n=\mathsf{\Phi }\{(1-{\delta }_n){\vartheta }_n+{\delta }_n\mathsf{\Phi }\left({\vartheta }_n\right)\}\hfill \\ z_n=\mathsf{\Phi }\{(1-{\gamma }_n)w_n+{\gamma }_n\mathsf{\Phi }\left(w_n\right)\}\hfill \\ {\nu }_n=\mathsf{\Phi }\{(1-{\beta }_n)z_n+{\beta }_n\mathsf{\Phi }\left(z_n\right)\}\hfill \\ {\vartheta }_{n+1}=\mathsf{\Phi }\{(1-{\alpha }_n){\nu }_n+{\alpha }_n\mathsf{\Phi }\left({\nu }_n\right)\}.\hfill \end{array}\right.\end{array}$$

  (24)
• Rani and Arti [33]

  $$\begin{array}{c}\hfill \left\{\begin{array}{c}{z}_n=(1-{\gamma }_n){\vartheta }_n+{\gamma }_n\mathsf{\Phi }\left({\vartheta }_n\right)\}\hfill \\ {\nu }_n=\mathsf{\Phi }\{(1-{\beta }_n)\mathsf{\Phi }\left({\vartheta }_n\right)+{\beta }_n\mathsf{\Phi }\left(z_n\right)\}\hfill \\ {\vartheta }_{n+1}=\mathsf{\Phi }\{(1-{\alpha }_n){\nu }_n+{\alpha }_n\mathsf{\Phi }\left({\nu }_n\right)\}.\hfill \end{array}\right.\end{array}$$

  (25)
• Ahmad et al. [34]

  $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\nu }_n=(1-{\beta }_n){\vartheta }_n+{\beta }_n\mathsf{\Phi }\left({\vartheta }_n\right)\hfill \\ {\vartheta }_{n+1}=\mathsf{\Phi }\{(1-{\alpha }_n)\mathsf{\Phi }\left({\nu }_n\right)+{\alpha }_n{\mathsf{\Phi }}^2\left({\nu }_n\right)\}.\hfill \end{array}\right.\end{array}$$

  (26)

3. A General Picard–Mann Iterative Method

In [40], Shukla et al. proposed the following algorithm (known as GPM):

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\vartheta }_1=\vartheta \in \mathcal{Y}\hfill \\ {\vartheta }_{n+1}={\mathsf{\Phi }}^k\{(1-{\alpha }_n){\vartheta }_n+{\alpha }_n\mathsf{\Phi }\left({\vartheta }_n\right)\},n\in \mathbb{N},\hfill \end{array}\right.\end{array}$$

(27)

where $\left\{{\alpha }_n\right\}$ is a sequence in $[0,1]$, and k is a fixed natural number.

Remark 4.

It is easy to see that none of the iterative methods (from (2) to (26)) reduces to iterative method (27).

4. Convergence Theorems

In this section, we present some convergence results for the sequence generated by iterative method (27).

Lemma 4.

Let $\mathcal{Y}$ be a nonempty closed convex subset of a Banach space $\mathcal{Z}$ and $\mathsf{\Phi }:\mathcal{Y}\to \mathcal{Y}$ a mapping satisfying condition (E) with $F\left(\mathsf{\Phi }\right)\ne \varnothing .$ Let $\left\{{\vartheta }_n\right\}$ be a sequence defined by (27). Then, the following assertions hold:

(1)

If $p^{†}\in F\left(\mathsf{\Phi }\right)$, then $\underset{n\to \infty }{lim}\parallel {\vartheta }_n-p^{†}\parallel$ exists;

(2)

$\underset{n\to \infty }{lim}d({\vartheta }_n,F\left(\mathsf{\Phi }\right))$ exists, where $d(\vartheta ,F(\mathsf{\Phi }\left)\right)$ denotes the distance from ϑto $F\left(\mathsf{\Phi }\right).$

Proof. 

Let $p^{†}\in F\left(\mathsf{\Phi }\right)$. From (27), we have

$$\begin{array}{ccc}\hfill \parallel {\vartheta }_{n+1}-p^{†}\parallel & =& \parallel {\mathsf{\Phi }}^k\{(1-{\alpha }_n){\vartheta }_n+{\alpha }_n\mathsf{\Phi }\left({\vartheta }_n\right)\}-p^{†}\parallel \hfill \\ & \le & \parallel (1-{\alpha }_n){\vartheta }_n+{\alpha }_n\mathsf{\Phi }\left({\vartheta }_n\right)-p^{†}\parallel \hfill \\ & \le & (1-{\alpha }_n)\parallel {\vartheta }_n-p^{†}\parallel +{\alpha }_n\parallel \mathsf{\Phi }\left({\vartheta }_n\right)-p^{†}\parallel \hfill \\ & \le & \parallel {\vartheta }_n-p^{†}\parallel .\hfill \end{array}$$

(28)

Therefore, the sequence $\{\parallel {\vartheta }_n-p^{†}\parallel \}$ is nonincreasing and bounded. Hence, $\underset{n\to \infty }{lim}\parallel {\vartheta }_n-p^{†}\parallel$ exists for each $p^{†}\in F\left(\mathsf{\Phi }\right)$. Therefore, $\underset{n\to \infty }{lim}d({\vartheta }_n,F\left(\mathsf{\Phi }\right))$ exists. □

Lemma 5.

Let $\mathcal{Z}$ be a uniformly convex Banach space, $\mathcal{Y}$ and $\mathsf{\Phi }$ be the same as in Lemma 4 with $F\left(\mathsf{\Phi }\right)\ne \varnothing .$ Let $\left\{{\vartheta }_n\right\}$ be a sequence defined by (27) with ${\alpha }_n\in (a,b)\subset (0,1),$ for all $n\in \mathbb{N}$, where $a,b\in (0,1).$ Then, $\underset{n\to \infty }{lim}\parallel {\vartheta }_n-\mathsf{\Phi }\left({\vartheta }_n\right)\parallel =0.$

Proof. 

By Lemma 4, the sequence $\left\{{\vartheta }_n\right\}$ is bounded and $\underset{n\to \infty }{lim}\parallel {\vartheta }_n-p^{†}\parallel$ exists. Call it r. That is,

$$\underset{n\to \infty }{lim}\parallel {\vartheta }_n-p^{†}\parallel =r.$$

(29)

Using the condition on mapping $\mathsf{\Phi }$, we have

$$\parallel p^{†}-\mathsf{\Phi }\left({\vartheta }_n\right)\parallel \le \parallel p^{†}-\mathsf{\Phi }\left(p^{†}\right)\parallel +\parallel {\vartheta }_n-p^{†}\parallel$$

and using (29)

$$\underset{n\to \infty }{lim\; sup}\parallel \mathsf{\Phi }\left({\vartheta }_n\right)-p^{†}\parallel \le r.$$

(30)

Now, by (27) and (29), we have

$$\begin{array}{ccc}\hfill r=\underset{n\to \infty }{lim}\parallel {\vartheta }_{n+1}-p^{†}\parallel & =& \underset{n\to \infty }{lim\; sup}\parallel {\mathsf{\Phi }}^k\{(1-{\alpha }_n){\vartheta }_n+{\alpha }_n\mathsf{\Phi }\left({\vartheta }_n\right)\}-p^{†}\parallel \hfill \\ & \le & \underset{n\to \infty }{lim\; sup}\parallel (1-{\alpha }_n){\vartheta }_n+{\alpha }_n\mathsf{\Phi }\left({\vartheta }_n\right)-p^{†}\parallel \hfill \\ & \le & \underset{n\to \infty }{lim}\parallel {\vartheta }_n-p^{†}\parallel =r.\hfill \end{array}$$

Thus,

$$\underset{n\to \infty }{lim}\parallel (1-{\alpha }_n)({\vartheta }_n-p^{†})+{\alpha }_n(\mathsf{\Phi }\left({\vartheta }_n\right)-p^{†})\parallel =r.$$

(31)

From (29)–(31) and Lemma 1, it follows that

$$\underset{n\to \infty }{lim}\parallel {\vartheta }_n-\mathsf{\Phi }\left({\vartheta }_n\right)\parallel =0.$$

□

Theorem 1.

Let $\mathcal{Z}$ be a uniformly convex Banach space, $\mathcal{Y}$ and $\mathsf{\Phi }$ be the same as in Lemma 4 with $F\left(\mathsf{\Phi }\right)\ne \varnothing$. Let $\left\{{\vartheta }_n\right\}$ be a sequence defined by (27) with ${\alpha }_n\in (a,b)\subset (0,1),$ for all $n\in \mathbb{N}$, where $a,b\in (0,1).$ If $\mathcal{Z}$ satisfies the Opial property, then $\left\{{\vartheta }_n\right\}$ weakly converges to a point in $F\left(\mathsf{\Phi }\right).$

Proof. 

By Lemma 4, the sequence $\left\{{\vartheta }_n\right\}$ is bounded and by Lemma 5, $\underset{n\to \infty }{lim}\parallel {\vartheta }_n-\mathsf{\Phi }\left({\vartheta }_n\right)\parallel =0.$ Since $\mathcal{Z}$ is uniformly convex, there exists a subsequence $\left\{{\vartheta }_{n_j}\right\}$ of $\left\{{\vartheta }_n\right\}$ that weakly converges to a point $p\in \mathcal{Y}.$ From the demiclosedness principle of $I-\mathsf{\Phi }$ (Proposition (2)), $p\in {\omega }_w\left({\vartheta }_n\right)\subset F\left(\mathsf{\Phi }\right).$ Now, we claim that ${\omega }_w\left({\vartheta }_n\right)$ is a singleton, and there is a unique weak limit for each subsequence of $\left\{{\vartheta }_n\right\}$. This implies that $\left\{{\vartheta }_n\right\}$ weakly converges to a fixed point of $\mathsf{\Phi }$. In view of the Opial property, it can be seen that ${\omega }_w\left({\vartheta }_n\right)$ is a singleton. This completes the proof. □

Theorem 2.

Let $\mathcal{Y}$, $\mathsf{\Phi }$ and $\left\{{\vartheta }_n\right\}$ be the same as in Theorem 1 with $F\left(\mathsf{\Phi }\right)\ne \varnothing$ and $\mathcal{Z}$ a uniformly convex Banach space. If the range of $\mathcal{Y}$ under $\mathsf{\Phi }$ is contained in a compact subset of $\mathcal{Z}$, then $\left\{{\vartheta }_n\right\}$ strongly converges to a fixed point of $\mathsf{\Phi }$.

Proof. 

Since the range of $\mathcal{Y}$ under $\mathsf{\Phi }$ is contained in a compact set, there exists a subsequence $\left\{\mathsf{\Phi }\left({\vartheta }_{n_j}\right)\right\}$ of $\left\{\mathsf{\Phi }\left({\vartheta }_n\right)\right\}$ that strongly converges to $p^{†}\in \mathcal{Y}.$ By the triangle inequality, we obtain

$$\parallel {\vartheta }_{n_j}-p^{†}\parallel \le \parallel {\vartheta }_{n_j}-\mathsf{\Phi }\left({\vartheta }_{n_j}\right)\parallel +\parallel \mathsf{\Phi }\left({\vartheta }_{n_j}\right)-p^{†}\parallel$$

and, by Lemma 5, the subsequence $\left\{{\vartheta }_{n_j}\right\}$ strongly converges to ${\vartheta }^{†}.$ By the condition on mapping $\mathsf{\Phi }$,

$$\parallel {\vartheta }_{n_j}-\mathsf{\Phi }\left(p^{†}\right)\parallel \le \mu \parallel {\vartheta }_{n_j}-\mathsf{\Phi }\left({\vartheta }_{n_j}\right)\parallel +\parallel {\vartheta }_{n_j}-p^{†}\parallel .$$

Taking $j\to \infty$ implies

$$\underset{j\to \infty }{lim\; sup}\parallel {\vartheta }_{n_j}-\mathsf{\Phi }\left(p^{†}\right)\parallel \le \mu \underset{j\to \infty }{lim}\parallel {\vartheta }_{n_j}-\mathsf{\Phi }\left({\vartheta }_{n_j}\right)\parallel +\underset{j\to \infty }{lim\; sup}\parallel {\vartheta }_{n_j}-p^{†}\parallel ,$$

and we have $\mathsf{\Phi }\left(p^{†}\right)=p^{†}.$ In view of Lemma 4, it follows that $\underset{n\to \infty }{lim}\parallel {\vartheta }_n-p^{†}\parallel$ exists. Therefore, $\left\{{\vartheta }_n\right\}$ strongly converges to $p^{†}$. □

Theorem 3.

Let$\mathcal{Y}$, $\mathsf{\Phi }$and$\left\{{\vartheta }_n\right\}$be the same as in Theorem 1 with$F\left(\mathsf{\Phi }\right)\ne \varnothing$and$\mathcal{Z}$a uniformly convex Banach space with$F\left(\mathsf{\Phi }\right)\ne \varnothing .$Then, the sequence$\left\{{\vartheta }_n\right\}$strongly converges to a fixed point of$\mathsf{\Phi }$if$\underset{n\to \infty }{lim\; inf}d({\vartheta }_n,F\left(\mathsf{\Phi }\right))=0$.

Proof. 

This can be completed following Theorem 4.12 [7]. □

Theorem 4.

Let $\mathcal{Y}$, $\mathcal{Z}$, $\mathsf{\Phi }$ and $\left\{{\vartheta }_n\right\}$ be the same as in Theorem 3 with $F\left(\mathsf{\Phi }\right)\ne \varnothing .$ If $\mathsf{\Phi }$ satisfies condition $\left(I\right)$, then $\left\{{\vartheta }_n\right\}$ strongly converges to a point in $F\left(\mathsf{\Phi }\right).$

Proof. 

This can be completed following Theorem 4.13 [7]. □

5. Numerical Results

In this section, we present an example and employ it to compare various iterative methods for different initial guess and parameters.

Example 1.

Let ${\mathbb{R}}^2$ be a Banach space equipped with the norm

$$\parallel ({\vartheta }^{\left(1\right)},{\vartheta }^{\left(2\right)})\parallel =|{\vartheta }^{\left(1\right)}|+|{\vartheta }^{\left(2\right)}|$$

and $\mathcal{Y}=[0,1]\times [0,1]$ a subset of ${\mathbb{R}}^2$. Let $\mathsf{\Phi }:\mathcal{Y}\to \mathcal{Y}$ be a mapping defined by

$$\mathsf{\Phi }({\vartheta }^{\left(1\right)},{\vartheta }^{\left(2\right)})=\left\{\begin{array}{c}\left(\frac{1}{3}{({\vartheta }^{\left(1\right)}+\frac{1}{4})}^2,1-\frac{3}{4}{\vartheta }^{\left(2\right)}\right),if{\vartheta }^{\left(1\right)}\in [0,\frac{3}{4}),\hfill \\ \left(\frac{{\vartheta }^{\left(1\right)}}{7}+\frac{1}{3},1-\frac{3}{4}{\vartheta }^{\left(2\right)}\right),if{\vartheta }^{\left(1\right)}\in [\frac{3}{4},1].\hfill \end{array}\right.$$

Now, we show that $\mathsf{\Phi }$ satisfies the condition (E) for $\mu =6$, and, for this, we consider the following cases:

Case (i)

Let ${\vartheta }^{\left(1\right)}\in \left[0,\frac{3}{4}\right).$ If ${\nu }^{\left(1\right)}\in \left[0,\frac{3}{4}\right);$ then,

$$\begin{array}{ccc}\hfill \parallel \mathsf{\Phi }\left(\vartheta \right)-\mathsf{\Phi }\left(\nu \right)\parallel & =& \frac{1}{3}\left|{\left({\vartheta }^{\left(1\right)}+\frac{1}{4}\right)}^2-{\left({\nu }^{\left(1\right)}+\frac{1}{4}\right)}^2\right|+\frac{3}{4}|{\vartheta }^{\left(2\right)}-{\nu }^{\left(2\right)}|\hfill \\ & \le & \frac{1}{3}|({\vartheta }^{\left(1\right)}+{\nu }^{\left(1\right)})({\vartheta }^{\left(1\right)}-{\nu }^{\left(1\right)})|+\frac{1}{6}|{\vartheta }^{\left(1\right)}-{\nu }^{\left(1\right)}|+\frac{3}{4}|{\vartheta }^{\left(2\right)}-{\nu }^{\left(2\right)}|\hfill \\ & \le & \frac{2}{3}|{\vartheta }^{\left(1\right)}-{\nu }^{\left(1\right)}|+\frac{3}{4}|{\vartheta }^{\left(2\right)}-{\nu }^{\left(2\right)}|\le \parallel \vartheta -\nu \parallel .\hfill \end{array}$$

Let ${\nu }^{\left(1\right)}\in \left[\frac{3}{4},1\right].$ Now, we show that

$$\begin{array}{ccc}\hfill \left|\frac{1}{3}{\left({\vartheta }^{\left(1\right)}+\frac{1}{4}\right)}^2-\frac{{\nu }^{\left(1\right)}}{7}-\frac{1}{3}\right|+\frac{3}{4}\left|{\vartheta }^{\left(2\right)}-{\nu }^{\left(2\right)}\right|& \le & 5\left\{\left|{\vartheta }^{\left(1\right)}-\frac{1}{3}{\left({\vartheta }^{\left(1\right)}+\frac{1}{4}\right)}^2\right|+\left|{\vartheta }^{\left(2\right)}-1+\frac{3}{4}{\vartheta }^{\left(2\right)}\right|\right\}\hfill \\ & & +|{\vartheta }^{\left(1\right)}-{\nu }^{\left(1\right)}|+|{\vartheta }^{\left(2\right)}-{\nu }^{\left(2\right)}|.\hfill \end{array}$$

(32)

Now, we can break the above inequality into two parts. First, we show the following inequality:

$$\left|\frac{1}{3}{\left({\vartheta }^{\left(1\right)}+\frac{1}{4}\right)}^2-\frac{{\nu }^{\left(1\right)}}{7}-\frac{1}{3}\right|\le 5\left|{\vartheta }^{\left(1\right)}-\frac{1}{3}{\left({\vartheta }^{\left(1\right)}+\frac{1}{4}\right)}^2\right|+|{\vartheta }^{\left(1\right)}-{\nu }^{\left(1\right)}|.$$

(33)

From the triangle inequality, we have

$$\begin{array}{c}\hfill \left|\frac{1}{3}{\left({\vartheta }^{\left(1\right)}+\frac{1}{4}\right)}^2-\frac{{\nu }^{\left(1\right)}}{7}-\frac{1}{3}\right|\le \left|\frac{1}{3}{\left({\vartheta }^{\left(1\right)}+\frac{1}{4}\right)}^2-{\vartheta }^{\left(1\right)}\right|+\left|{\vartheta }^{\left(1\right)}-\frac{{\nu }^{\left(1\right)}}{7}-\frac{1}{3}\right|.\end{array}$$

(34)

From the considered range of ${\vartheta }^{\left(1\right)}$ and ${\nu }^{\left(1\right)}$, we estimate that

$$\left|{\vartheta }^{\left(1\right)}-\frac{{\nu }^{\left(1\right)}}{7}-\frac{1}{3}\right|\le \frac{10}{21}.$$

For ${\vartheta }^{\left(1\right)}\in \left[0,\frac{167}{756}\right),$ it can be seen that $|{\nu }^{\left(1\right)}-{\vartheta }^{\left(1\right)}|\ge \frac{10}{21}$. In view of (34), we can see that (33) is true for this case. Again, for ${\vartheta }^{\left(1\right)}\in \left[\frac{167}{756},\frac{3}{4}\right),$ the function ${\vartheta }^{\left(1\right)}-\frac{1}{3}{\left({\vartheta }^{\left(1\right)}+\frac{1}{4}\right)}^2$ is increasing and $\left|{\vartheta }^{\left(1\right)}-\frac{1}{3}{\left({\vartheta }^{\left(1\right)}+\frac{1}{4}\right)}^2\right|\ge \frac{63005}{428652}.$ Thus,

$$4\left|{\vartheta }^{\left(1\right)}-\frac{1}{3}{\left({\vartheta }^{\left(1\right)}+\frac{1}{4}\right)}^2\right|\ge \frac{10}{21}.$$

In light of (34), it follows that (33) is true for this case too. However,

$$\begin{array}{c}\hfill \frac{3}{4}\left|{\vartheta }^{\left(2\right)}-{\nu }^{\left(2\right)}\right|\le |{\vartheta }^{\left(2\right)}-{\nu }^{\left(2\right)}|.\end{array}$$

(35)

Combining (33) and (35), we can see that (32) is true. By the triangle inequality,

$$\begin{array}{c}\hfill \parallel \vartheta -\mathsf{\Phi }\left(\nu \right)\parallel \le \parallel \mathsf{\Phi }\left(\vartheta \right)-\mathsf{\Phi }\left(\nu \right)\parallel +\parallel \vartheta -\mathsf{\Phi }\left(\vartheta \right)\parallel \end{array}$$

(36)

mapping $\mathsf{\Phi }$ satisfies condition (E).

Case (ii)

Let ${\vartheta }^{\left(1\right)}\in \left[\frac{3}{4},1\right].$ If ${\nu }^{\left(1\right)}\in \left[\frac{3}{4},1\right]$, then $\mathsf{\Phi }$ is a contractive mapping and satisfies condition (E). Let ${\nu }^{\left(1\right)}\in \left[0,\frac{3}{4}\right).$ We prove the following conditions:

$$\begin{array}{ccc}\hfill \left|\frac{{\vartheta }^{\left(1\right)}}{7}+\frac{1}{3}-\frac{1}{3}{\left({\nu }^{\left(1\right)}+\frac{1}{4}\right)}^2\right|+\frac{3}{4}\left|{\vartheta }^{\left(2\right)}-{\nu }^{\left(2\right)}\right|& \le & 5\left\{\left|\frac{6}{7}{\vartheta }^{\left(1\right)}-\frac{1}{3}\right|+\left|\frac{7}{4}{\vartheta }^{\left(2\right)}-1\right|\right\}\hfill \\ & +& |{\vartheta }^{\left(1\right)}-{\nu }^{\left(1\right)}|+|{\vartheta }^{\left(2\right)}-{\nu }^{\left(2\right)}|.\hfill \end{array}$$

(37)

We shall break the above inequality into two parts. First, we shall prove the following inequality:

$$\left|\frac{{\vartheta }^{\left(1\right)}}{7}+\frac{1}{3}-\frac{1}{3}{\left({\nu }^{\left(1\right)}+\frac{1}{4}\right)}^2\right|\le 5\left|\frac{6}{7}{\vartheta }^{\left(1\right)}-\frac{1}{3}\right|+|{\vartheta }^{\left(1\right)}-{\nu }^{\left(1\right)}|.$$

(38)

By the triangle inequality, we have

$$\left|\frac{{\vartheta }^{\left(1\right)}}{7}+\frac{1}{3}-\frac{1}{3}{\left({\nu }^{\left(1\right)}+\frac{1}{4}\right)}^2\right|\le \left|\frac{6}{7}{\vartheta }^{\left(1\right)}-\frac{1}{3}\right|+\left|{\vartheta }^{\left(1\right)}-\frac{1}{3}{\left({\nu }^{\left(1\right)}+\frac{1}{4}\right)}^2\right|.$$

(39)

From the considered range of ${\vartheta }^{\left(1\right)}$ and ${\nu }^{\left(1\right)}$, we can estimate

$$\left|{\vartheta }^{\left(1\right)}-\frac{1}{3}{\left({\nu }^{\left(1\right)}+\frac{1}{4}\right)}^2\right|\le \frac{47}{48}$$

and $\left|\frac{6}{7}{\vartheta }^{\left(1\right)}-\frac{1}{3}\right|\ge \frac{13}{42}.$ Therefore, $4\left|\frac{6}{7}{\vartheta }^{\left(1\right)}-\frac{1}{3}\right|\ge \frac{47}{48}.$ From the above estimate and (39), it implies that (38) is true. However,

$$\frac{3}{4}\left|{\vartheta }^{\left(2\right)}-{\nu }^{\left(2\right)}\right|\le |{\vartheta }^{\left(2\right)}-{\nu }^{\left(2\right)}|.$$

(40)

Combining (38) and (40), it can be seen that (37) is true. In view of (36) and (37), mapping $\mathsf{\Phi }$ satisfies condition (E). Since $\mathsf{\Phi }$ is not continuous, $\mathsf{\Phi }$ is not nonexpansive. It can be seen that $\left(\frac{5-2\sqrt{6}}{4},\frac{4}{7}\right)$ is a fixed point of $\mathsf{\Phi }.$

Now, we compare convergence behavior of various algorithms in view of Example (32). We make different choices of initial guesses and parameters $({\alpha }_n,{\beta }_n,{\gamma }_n)$ and set $\parallel {\vartheta }_n-p\parallel <{10}^{-15}$ as our stopping criterion (p is a fixed point of $\mathsf{\Phi }$).

Observations: In view of Table 1 and Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6, we note that, for different choices of initial guesses and parameters, the general Picard–Mann algorithm (GPM) (27) (with $k=4$) converges faster to a fixed point of mapping satisfying condition (E) than other algorithms considered in Section 2. We also conclude that (GPM) algorithm is consistent.

Table 1. Influence of initial guesses and parameters: comparison of various iterative methods.

Iterations	Initial Points
	(0.3, 0.3)	(0.6, 0.6)	(0.9, 0.9)
Case (i): ${\alpha }_n={\displaystyle \frac{1}{(3n+1)}}$, ${\beta }_n={\displaystyle \frac{1}{{(n+2)}^2}}$, ${\gamma }_n={\displaystyle \frac{n}{(n^3+10)}}$
GPM with $k=4$ (27)	26	25	27
Bhutia and Tiwary (19)	38	35	38
Garodia and Uddin (20)	35	33	36
Garodia and Uddin, and Hussain et al. (D-iterative method) (21)	35	33	36
Hussain et al. (16)	38	36	38
Ullah and Arshad (17)	53	49	53
Piri et al. (18)	52	49	53
Ali et al. (23)	35	33	36
Rani and Arti (25)	35	33	36
Ahmad et al. (26)	53	49	53
Case (ii): ${\alpha }_n={\displaystyle \frac{1}{{(10n+100)}^{1/2}}}$, ${\beta }_n={\displaystyle \frac{1}{{(n+5)}^3}}$, ${\gamma }_n={\displaystyle \frac{1}{{(9n+10)}^2}}$
GPM with $k=4$ (27)	25	24	26
Bhutia and Tiwary (19)	38	33	38
Garodia and Uddin (20)	33	31	34
Garodia and Uddin, and Hussain et al. (D-iterative method) (21)	33	31	34
Hussain et al. (16)	38	36	38
Ullah and Arshad (17)	48	45	48
Piri et al. (18)	48	45	49
Ali et al. (23)	33	31	34
Rani and Arti (25)	33	31	34
Ahmad et al. (26)	48	45	49

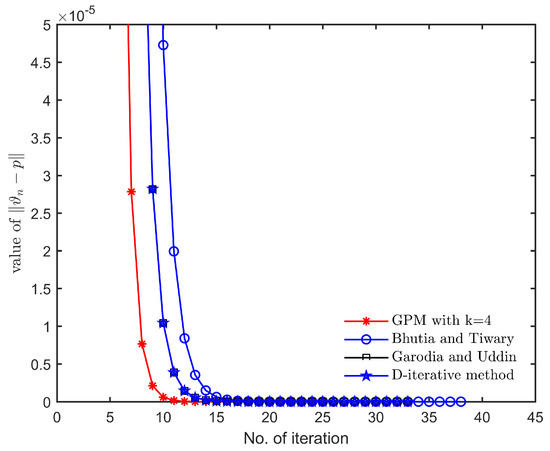
Figure 1. Convergence behavior with parameters $\left({\alpha }_n={\displaystyle \frac{1}{{(10n+100)}^{1/2}}},{\beta }_n={\displaystyle \frac{1}{{(n+5)}^3}}\right.$, $\left.{\gamma }_n={\displaystyle \frac{1}{{(9n+10)}^2}}\right)$ and initial guess $(0.3,0.3)$.

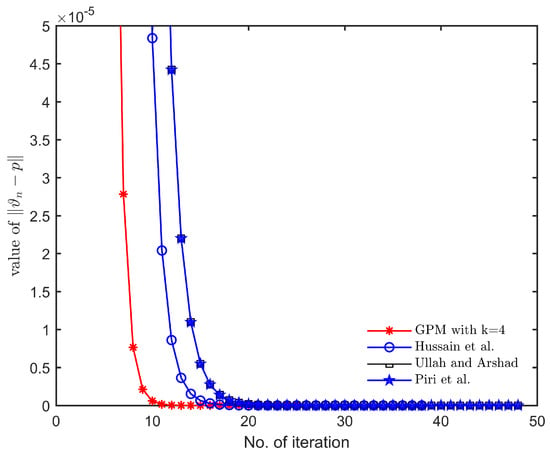
Figure 2. Convergence behavior with parameters $\left({\alpha }_n={\displaystyle \frac{1}{{(10n+100)}^{1/2}}},{\beta }_n={\displaystyle \frac{1}{{(n+5)}^3}}\right.$, $\left.{\gamma }_n={\displaystyle \frac{1}{{(9n+10)}^2}}\right)$ and initial guess $(0.3,0.3)$.

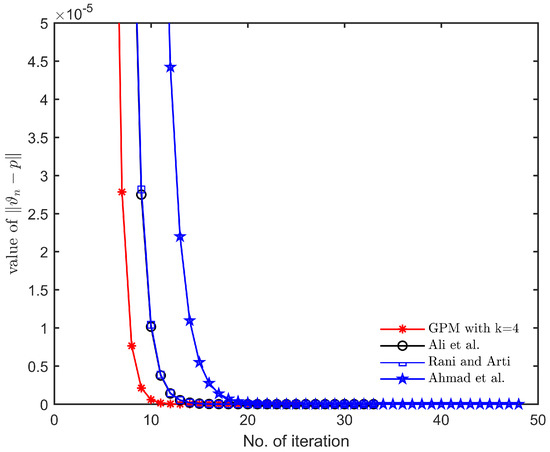
Figure 3. Convergence behavior with parameters $\left({\alpha }_n={\displaystyle \frac{1}{{(10n+100)}^{1/2}}},{\beta }_n={\displaystyle \frac{1}{{(n+5)}^3}}\right.$, $\left.{\gamma }_n={\displaystyle \frac{1}{{(9n+10)}^2}}\right)$ and initial guess $(0.3,0.3)$.

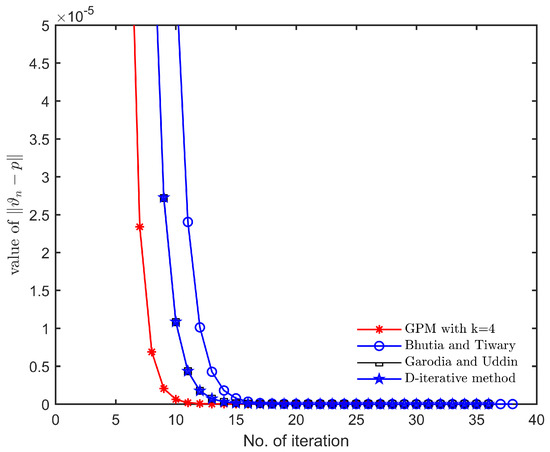
Figure 4. Convergence behavior with parameters $\left({\alpha }_n={\displaystyle \frac{1}{(3n+1)}},{\beta }_n={\displaystyle \frac{1}{{(n+2)}^2}}\right.$, $\left.{\gamma }_n={\displaystyle \frac{n}{(n^3+10)}}\right)$ and initial guess $(0.9,0.9)$.

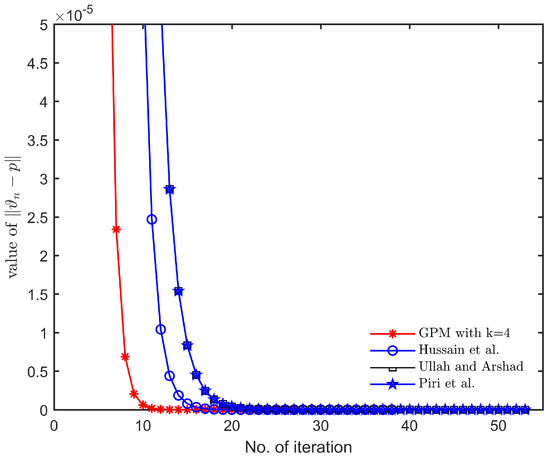
Figure 5. Convergence behavior with parameters $\left({\alpha }_n={\displaystyle \frac{1}{(3n+1)}},{\beta }_n={\displaystyle \frac{1}{{(n+2)}^2}}\right.$, $\left.{\gamma }_n={\displaystyle \frac{n}{(n^3+10)}}\right)$ and initial guess $(0.9,0.9)$.

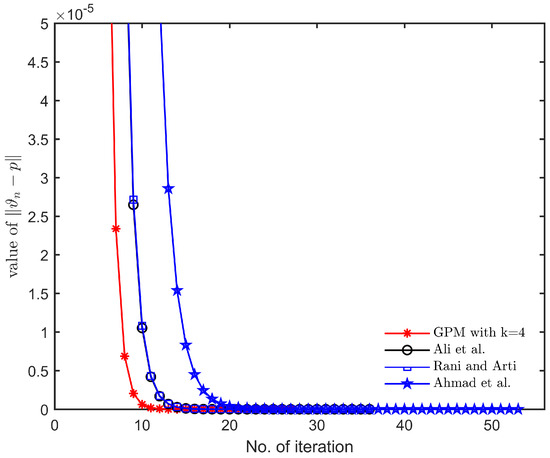
Figure 6. Convergence behavior with parameters $\left({\alpha }_n={\displaystyle \frac{1}{(3n+1)}},{\beta }_n={\displaystyle \frac{1}{{(n+2)}^2}}\right.$, $\left.{\gamma }_n={\displaystyle \frac{n}{(n^3+10)}}\right)$ and initial guess $(0.9,0.9)$.