Smart Contract Security in Decentralized Finance: Enhancing Vulnerability Detection with Reinforcement Learning

Abstract

The growing interest in decentralized finance (DeFi), driven by advancements in blockchain technologies such as Ethereum, highlights the crucial role of smart contracts. However, the inherent openness of blockchains creates an extensive attack surface, exposing participants’ funds to undetected security flaws. In this work we investigated the use of deep reinforcement learning techniques, specifically Deep Q-Network (DQN) and Proximal Policy Optimization (PPO), for detecting and classifying vulnerabilities in smart contracts. This approach utilizes control flow graphs (CFGs) generated through EtherSolve to capture the semantic features of contract bytecode, enabling the reinforcement learning models to recognize patterns and make more accurate predictions. Experimental results from extensive public datasets of smart contracts revealed that the PPO model performs better than DQN and demonstrates effectiveness in identifying unchecked-call vulnerability. The PPO model exhibits more stable and consistent learning patterns and achieves higher overall rewards. This research introduces a machine learning method for enhancing smart contract security, reducing financial risks for users, and contributing to future developments in reinforcement learning applications.

1. Introduction

The rapid expansion of decentralized finance (DeFi) applications, especially on public blockchain platforms such as Ethereum, has significantly transformed the financial landscape [1]. Unlike conventional banking systems, DeFi utilizes the transparency and openness of decentralized networks, particularly blockchain technologies, to provide diverse financial services. In this context, a smart contract is a self-executing program deployed on the blockchain that governs the terms and logic of financial transactions without requiring intermediaries. These contracts underpin core functionalities such as token swaps, lending protocols, automated market making, and yield aggregation. Economically, smart contracts reduce reliance on centralized entities, lower transaction costs, and enable programmable financial instruments with deterministic execution. Yet, this automation and immutability also mean that any vulnerability embedded in the code can lead to irreversible losses once deployed. Moreover, the inherent openness of DeFi makes it highly susceptible to external attacks, posing serious risks to the security of participants’ funds. According to Kirişçi’s [2] study employing the Fermatean fuzzy AHP approach to rank various risks in DeFi, technical risks are paramount, whereas financial risks are the most significant sub-risk, followed by transaction risks. Solidity, the primary language for developing smart contracts, has certain design flaws that necessitate a strong focus on code security by developers. In addition, the immutable nature of blockchain technology means that deploying a vulnerable contract can result in irreversible financial losses.

Potential dangers arising from security vulnerabilities in DeFi can be enormous, as the ramifications extend beyond financial losses, encompassing broader systemic threats including diminished user trust [3]. A notable example is the 2016 DAO attack [4], where hackers exploited a vulnerability in a smart contract, stealing approximately $60 million from Ether, leading to a 40% drop in its market value. Another significant incident occurred in 2017 when Parity [5], an Ethereum wallet provider, lost around $270 million due to a vulnerability that destroyed a multi-signature wallet contract. More recently, in October 2022, a hacker exploited a cross-chain bridge vulnerability on the BNB Chain, resulting in the theft of 2 million BNB tokens, valued at approximately $566 million [6]. As of 2024, SlowMist [7] reports that cumulative losses from blockchain hacks have surpassed $3.5 billion. These recurring security breaches have severely impeded the development of the DeFi ecosystem and adversely affected stakeholders’ interests. Therefore, conducting thorough and precise security analyses of smart contracts prior to their deployment on Ethereum is crucial to minimize vulnerabilities, mitigate further security incidents, and safeguard users’ assets and their trust in the DeFi ecosystem.

Recent advancements in predictive modeling have shown the importance of integrating both spatial and temporal information to detect complex vulnerabilities in distributed systems. A notable example is the work by Wang et al. [8], which presents a detection model for false data injection attacks in smart grids based on graph spatial features and Temporal Convolutional Networks (TCNs). By encoding the system structure as a graph and using TCNs to capture sequential patterns in the control data, their model effectively identifies sophisticated attack behaviors that evolve over time. Such spatio-temporal approaches have demonstrated strong performance in cyber-physical systems, and their underlying principles, modeling structured data over time, can be extended to smart contract analysis. While powerful, these models typically require labeled data and fixed architectures, which may limit adaptability in fast-evolving DeFi environments. In contrast, reinforcement learning provides an alternative strategy where agents can learn optimal detection policies through interactions, even in the absence of exhaustive labels or prior definitions of vulnerability patterns.

Beyond smart grids, spatio-temporal prediction networks have been applied in various security-critical domains. Al-Harbi [9] proposed a spatio-temporal graph neural network (STGNN) for fraud detection in blockchain, combining graph convolution for transaction structure and gated recurrent units to model temporal behavior. Similarly, Thiruloga et al. [10] introduced TENET, a lightweight Temporal CNN with attention, for detecting cyber intrusions in automotive systems, demonstrating high efficiency and accuracy under resource constraints. In the industrial context, Wang et al. [11] utilized a multi-scale dynamic graph neural network to detect anomalies in multivariate sensor data, capturing both its hierarchical structure and temporal evolution. These approaches underscore the value of modeling both execution flow and time-series dynamics to identify malicious behaviors. Inspired by these works, our study applied similar principles to the smart contract setting, while shifting from supervised learning to reinforcement learning, allowing agents to adaptively explore and identify vulnerabilities without requiring static labels or exhaustive expert knowledge.

Machine learning techniques have proven to be an effective approach for detecting security vulnerabilities in smart contracts. While traditional methods like static analysis and symbolic execution are used to identify issues such as reentrancy, integer overflows, and timestamp dependencies, these automated techniques are limited to detecting known vulnerabilities, are often time-intensive, and depend heavily on predefined rules from experts. As a result, machine learning and deep learning approaches have been developed to minimize the need for heavy feature engineering. Despite the growing success of supervised learning-based detection methods, the exploration of reinforcement learning in smart contract vulnerability detection remains relatively underdeveloped in the existing literature.

To address this gap, this paper applied reinforcement learning techniques to the process of smart contract vulnerability detection and conducting an empirical analysis with a substantial dataset.

The main contributions of this paper are as follows:

• We designed and implemented a reinforcement learning architecture for detecting and classifying smart contract vulnerabilities and showed its viability through a comparison analysis.
• Based on the characteristics of smart contract bytecode, we proposed CFGs, a graph-base method for input representations to capture richer semantic information within the bytecode.
• We proposed a machine learning approach for improving blockchain security and future reinforcement learning applications.

The rest of the paper is organized as follows. Section 2 provides a comprehensive review of the research work related to this paper. In Section 3, we elaborate the data work in the analysis and the methodology for building feature representations and model architectures. Section 4 examines and discusses the experimental results, and Section 5 summarizes and highlights possible future research work. The code for the paper is presented in the Supplementary Materials section.

2. Related Works

Extensive research on formal methods has been conducted on the detection of vulnerabilities in smart contracts in earlier times. Traditional methods, distinguished by the software testing techniques utilized, can be classified into four categories: symbolic execution, formal verification, fuzz testing and static analysis [12]. Symbolic execution was first used in automated analysis tool such as Oyente [13] and Mythril [14] for Ethereum smart contracts, where it simulates all possible execution paths on contract codes for detecting potential vulnerabilities but may face difficulty when analyzing complex contracts. The formal verification tool Securify [15] and static analysis tools such as SmartCheck [16] and Slither [17] improve the efficacy of addressing complex issues by adopting a specialized domain-specific representation to describe compliance and violation patterns, thereby facilitating the identification of potential security flaws. However, it may overlook new vulnerabilities that do not conform to known patterns. Numerous dynamic analysis tools, including ReDefender [18] and ConFuzzius [19], have gained popularity as the fuzz testing technique develops. These tools generate fuzzing inputs and verify vulnerabilities through dynamic data dependency analysis, but their detection scope is restricted to a narrow window of vulnerability types.

Traditional tools predominantly depend on predefined hard logic rules established by experts for detecting vulnerabilities. However, as smart contract technology advances, these tools are becoming insufficient to meet contemporary requirements due to the following limitations [20].

• The complexity of smart contract structures and functionalities is increasing. As the variety of vulnerabilities in smart contracts continues to grow, expert-defined rules based on existing vulnerability definitions struggle to keep pace with these updates.
• Smart contracts may demonstrate varied behaviors at runtime depending on different conditions, complicating the process of vulnerability verification and rendering the analysis highly resource- and time-consuming due to their dynamic and conditional nature.

In recent years, machine learning-based approaches for detecting vulnerabilities in smart contracts have garnered extensive attention and research, as more accurate and efficient results are achieved during smart contract security analysis. Within this field, supervised learning techniques have in particular made significant progress and are widely applied in real-world scenarios, including the web service tool SmartEmbed [21] for detecting repetitive code and clone-related bugs and the support vector machine embedded scanning system SCScan [22], a tree-based approach using an improved CatBoost algorithm for early detection of Ponzi Smart Contracts on Ethereum [23]. More deep learning approaches have emerged since 2020. The bidirectional Long Short-Term Memory networks enhance detection accuracy for reentrancy vulnerabilities and reduce the occurrence of false positives by incorporating contract snippet representations and attention mechanisms [24,25]. And convolutional neural network and graph neural network architectures are used to detect vulnerabilities in smart contracts and achieve over 80% accuracy by maintaining the semantic and contextual information under abstract syntax tree representations [26,27]. There also emerges specialized bidirectional encoder representations from transformer models for smart contract vulnerability detection to mitigate the challenge of insufficient labeled data [28,29].

While supervised learning techniques have yielded notable successes in the detection of smart contract vulnerabilities, reinforcement learning approaches have received relatively less attention and exploration in this field. Andrijasa et al.’s [30] review paper proposed a deep reinforcement learning with multi-agent fuzzing for exploit generation on cross-contract, and Su et al. [31] introduced a novel reinforcement learning fuzzer (RLF) a year later, which utilized reinforcement learning to guide fuzzing for generating vulnerable transaction sequences in smart contracts and effectively detecting sophisticated vulnerabilities requiring specific transaction sequences. However, RLF merely investigated the efficiency of detecting Ether-Leaking and Suicidal vulnerabilities, and the dataset used for training RLF consists of just 1291 entries, which may restrict the generalizability and reliability of reinforcement learning methods.

This paper seeks to address the aforementioned challenges and other undisclosed gaps by applying deep reinforcement learning algorithms to the vulnerability detection task and utilizing a more comprehensive dataset for model training.

3. Materials and Methods

3.1. Data

The dataset adopted in this study was obtained from the public dataset released by Rossini et al. [32] on HuggingFace [33]. Combined with other open-source datasets sorted in earlier research, this dataset is extensive, high-quality, and includes over 100,000 entries from active contracts on the Ethereum main net, where the source code of every contract was obtained via Etherscan API [34] and bytecode was retrieved using the ‘web3’ Python package (version 7.10.0).

Entries in this dataset are labeled as each contract’s code is verified by the Slither static analyzer to detect its vulnerability type. It has been mapped to the following five categories.

• Access control: This vulnerability occurs when smart contracts inadequately enforce permission controls, enabling attackers to perform unauthorized actions. It contains several subclasses. (1) Suicidal: This refers to contracts that include functions capable of terminating the contract and transferring its funds; (2) Arbitrary send: Code loophole leading to Ether loss when the contract sends Ether to arbitrary addresses; (3) tx.origin: Relying on ‘tx.origin’ for authentication can be risky as it may enable attacks where a malicious contract can impersonate the original sender; (4) Controlled delegatecall: Security issues may arise when a contract improperly uses the delegatecall() function.
• Arithmetic: This class is related to integer underflow and overflow errors as well as divide-before-multiply errors where division is performed before multiplication.
• Reentrancy: A security issue occurs when a contract allows an external call to another contract before it resolves the initial call, potentially allowing an attacker to drain funds or exploit the contract’s state. This type of vulnerability can be further subclassified as Reentrancy-no-eth where attacks do not involve Ether and Reenthrancy-eth where attacks involve Ether transfers.
• Unchecked calls: This class refers to a security issue that arises when a contract makes an external call to another contract or address without properly checking the success of that call. It includes three main types, which are Unused-return, Unchecked-low level and Unchecked-transfer calls.
• Other vulnerabilities: (1) Uninitialized storage: Storage pointers that are not initialized can redirect data to unexpected storage slots; (2) Mapping deletion: The belief that deleting a mapping deletes its contents; (3) Time dependency: a smart contract depends on the block timestamp or block number where time-related values can be influenced or predicted to some extent by miners, leading to potential manipulation; (4) Constant function state: Functions marked as constant/view that can modify state lead to unexpected behaviors; (5) Array-by-reference: Passing arrays by reference can lead to unexpected side effects if they are modified.

Following initial data cleaning, list-type labels were expanded so that each row corresponds to a single vulnerability type, reflecting that a smart contract can have multiple vulnerabilities.

Table 1. Number of elements per class in the training set.

Vulnerability	Contracts
unchecked calls	36,770
safe	26,280
reentrancy	24,120
other	20,650
arithmetic	14,140
access control	11,820

illustrates the distribution of contracts across each vulnerability class in our training set. A notable observation is the significant class imbalance, with the unchecked calls, safe, and reentrancy classes being the most prevalent, whereas the access-control vulnerability class is underrepresented and contains only about 11,820 smart contracts, making it the minority class.

The dataset was split into training, validation, and testing sets while preserving the class distribution. The final splits consist of approximately 134k entries for training, 18k for validation, and 27k for testing. As shown in Figure 1, although the vulnerability classes are imbalanced, their distribution remains proportionally consistent across all subsets, as expected.

Lastly, we eliminated duplicate rows and dropped elements for which the bytecode was not available before forming a reinforcement learning environment.

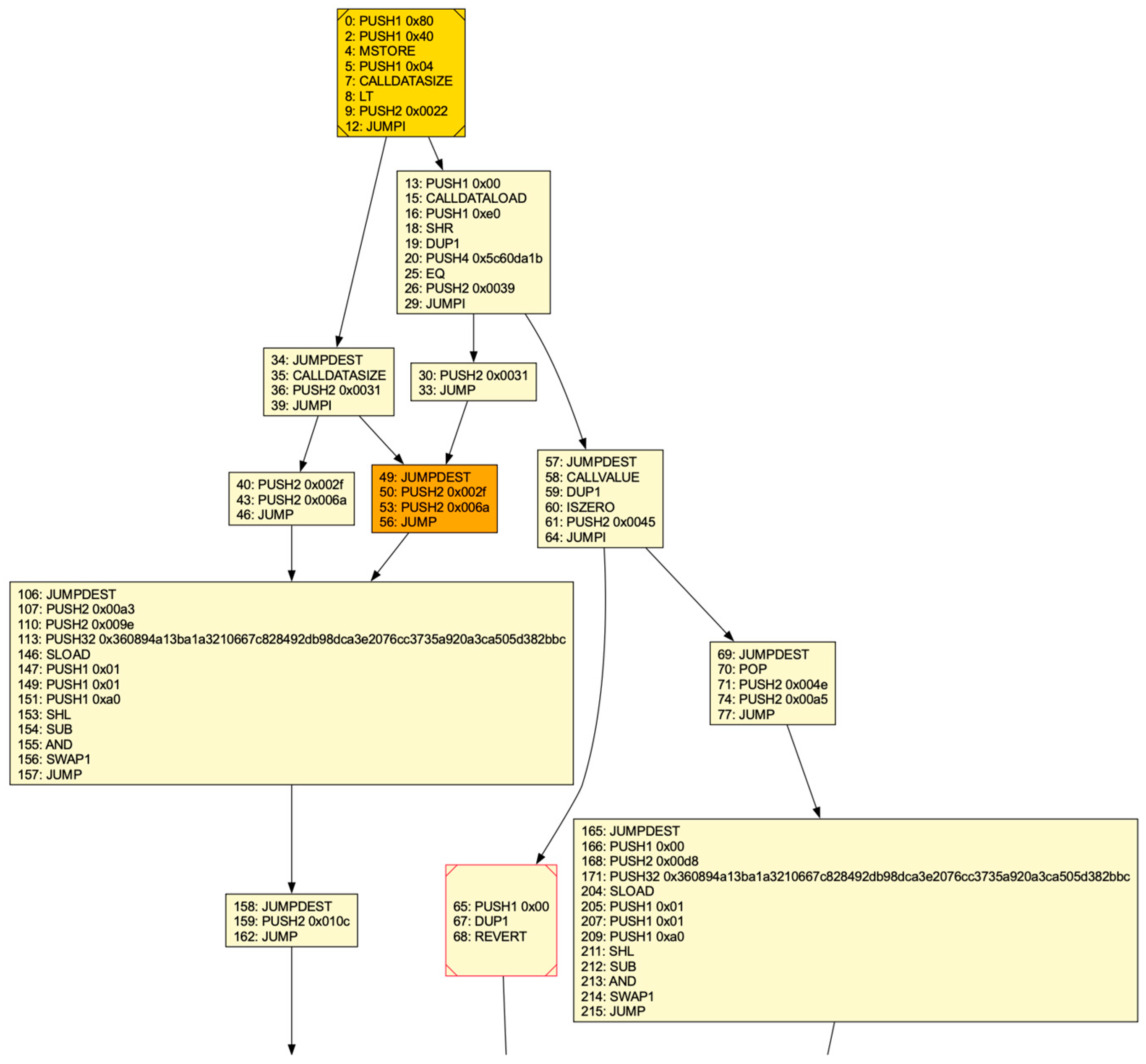
3.2. Control Flow Graphs

The key concept in the feature engineering process is the generation of control flow graphs. Rather than utilizing decompiled raw opcode at a sequence level to retain semantic information of how the contract operates within Ethereum Virtual Machine, this paper leveraged a graph representation approach for bytecode parsing. CFGs are often preferred over the raw opcode of bytecode as input representations for reinforcement learning (RL) methods because CFGs provide a structured and high-level abstraction of the program’s execution flow. A CFG captures the possible paths that might be traversed through a program during its execution, which allows for a more comprehensive understanding of the logical flow and control dependencies within the code. This is particularly important in detecting vulnerabilities in smart contracts, where understanding the control flow can reveal critical insights into how different parts of the contract interact and where potential security flaws might be located. Also, RL algorithms like PPO rely on the environment’s state representation to learn optimal policies. When the state space is well-structured, as with CFGs, the learning process becomes more efficient and effective.

However, the inherent complexity of Ethereum bytecode, particularly in jump resolution, presents substantial challenges for static analysis and reduces the accuracy of extraction of CFGs by existing automated tools. EtherSolve, introduced by Contro et al. [35], provided a novel static analysis tool leveraging symbolic execution of the Ethereum operand stack. This approach enables the resolution of jumps within the Ethereum bytecode, facilitating the construction of accurate CFGs for compiled smart contracts. The CFG is a directed graph that illustrates the execution flow within a program, where nodes represent the program’s basic blocks—sequences of opcodes that lack jumps except in the final opcode—while edges connect potential successive basic blocks. The process of generating a CFG is detailed through the series of steps given below.

• Bytecode parsing. It begins by identifying and removing the metadata section of the raw bytecode, followed by parsing the remaining bytes into opcodes.
• Basic block identification. A basic block is a sequence of opcodes executed consecutively without any other instructions altering the flow of control. Specific opcodes JUMP (unconditional jumps), JUMPI (conditional jumps), STOP, REVERT, RETURN, INVALID and SELFDESTRUCT, mark the end of a basic block, while JUMPDEST marks the start.
• Symbolic stack execution. This step is used to resolve the destinations of orphan jumps during CFG construction. Orphan jumps are common in smart contracts, especially when a function call returns, and their destinations need to be determined. The approach involves symbolically executing the stack by focusing only on opcodes that interact with jump addresses (PUSH, DUP, SWAP, AND and POP), while treating other opcodes as unknown.
• Static data separation. It involves removing static data from the CFG by identifying and excluding sections of the code that are not executable. This is achieved by detecting the 0xFE opcode, which marks the transition from executable code to static data with a representation for invalid instructions, and subsequently removes any unconnected basic blocks from the graph.
• CFG decoration. It involves adding additional information to the control flow graph to make it more useful for analysts and subsequent static analysis tasks (e.g., for vulnerability detection). Specifically, EtherSolve highlights important components of the CFG, such as the dispatcher, fallback function, and final basic block.

This paper utilized EtherSolve.jar, sourced from Github [36], to generate control flow graphs from the bytecode of smart contracts. The generated CFGs were stored in .dot format for features extraction and were subsequently used to feed reinforcement learning agents. Figure 2 shows a partial CFG for one contract from the training set, illustrating the basic block structure and control flow edges extracted by EtherSolve.

To make the control flow graphs compatible with reinforcement learning agents, each .dot file generated by EtherSolve was parsed using the NetworkX interface and converted into a compact numerical feature vector. Specifically, we extracted two structural properties from each CFG: the number of nodes (representing basic blocks of opcodes) and the number of directed edges (representing control flow transitions). These values were combined into a fixed-dimensional vector [num_nodes, num_edges], which serves as the environment’s observation for each contract. This minimalist representation ensures computational efficiency while preserving fundamental structural characteristics of the contract’s execution logic. The extract_features_from_cfg() function performs this transformation for every contract sample and is called within the environment’s _get_observation() method. This design enables reinforcement learning agents—DQN and PPO in our case—to interpret the execution structure of smart contracts as compact state vectors, facilitating effective policy learning without the need for explicit opcode-level parsing.

3.3. Model Architectures

Reinforcement learning centers on the decision-making process, where agents interact with their environment to maximize the rewards they receive. This paper implemented two model-free reinforcement learning algorithms, Deep Q-Network (DQN) and PPO, where “model-free” indicates the agent has no access to a model of the environment.

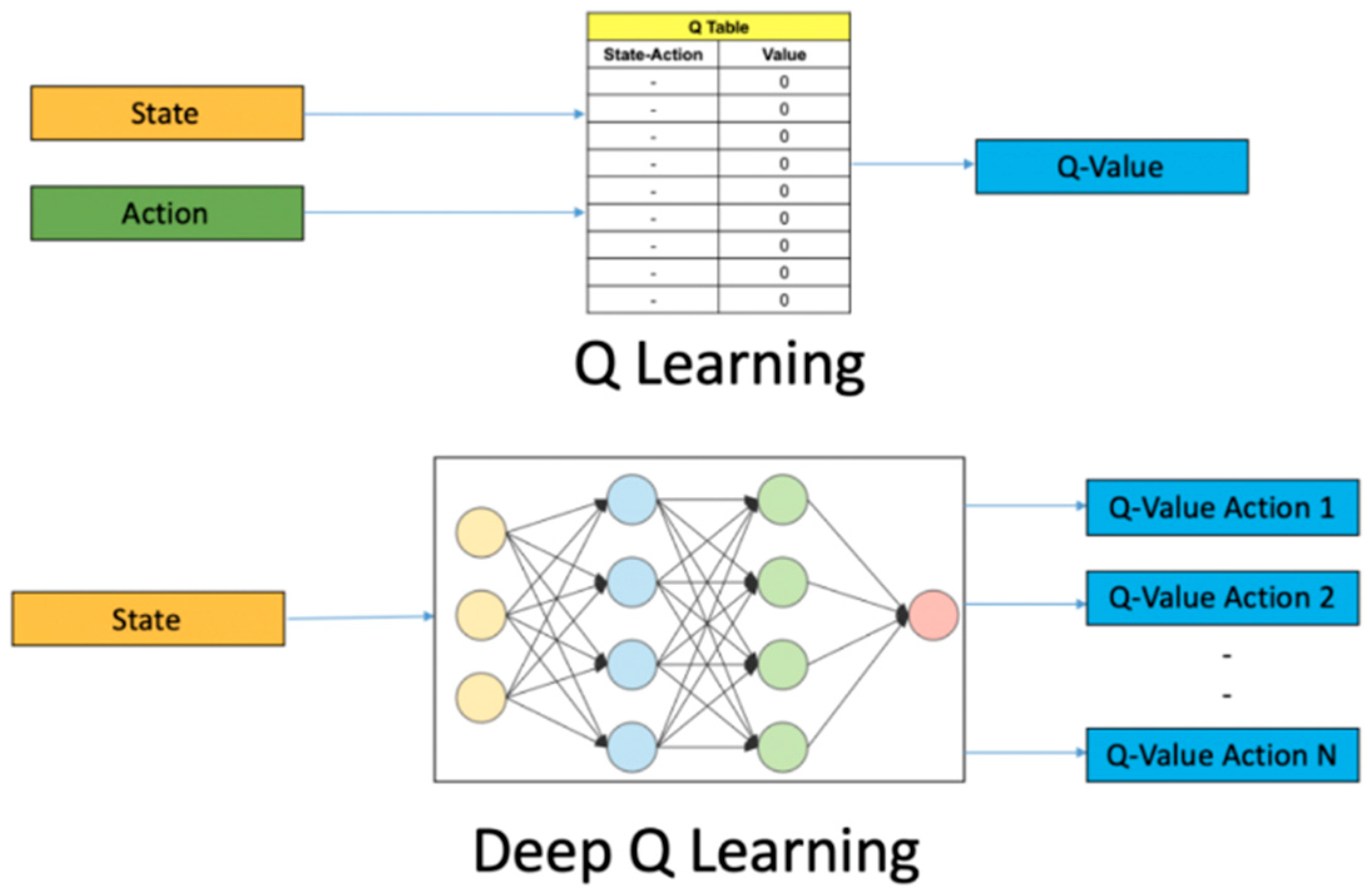
3.3.1. Deep Q-Network

DQN is an off-policy reinforcement learning algorithm that combines Q-learning with deep neural networks. According to Mnih et al. [37], DQN agents can often be simulated through the probability distribution function derived from the state-value function in the action space or the scoring rules of the action-value function in the action space. This study used agents that rely on action-value functions to define the vulnerability detection logic. Here, the agent can be mathematically modeled by $Q\left(s_t,a_t\right)$, where $a_t$ represents the action at time $t$ and $s_t$ denotes the state at time $t$. The $Q$ agent acts like a prophet to evaluate each action in the action space based on the current state, thereby making optimal decisions at each moment to maximize the reward $r_t$ during the progress. In the Q-learning algorithm, the agent is formed using a Q-table to store all actions across various states. However, in a real-world problem such as vulnerability detection in smart contracts, the vast number of states poses a challenge for Q-tables to manage effectively. To address this, the improved DQN utilizes deep neural networks to approximate Q-tables for constructing agents by taking a state as input and outputting Q-values for all possible actions (Figure 3) [38]. This allows the algorithm to handle high-dimensional state spaces, such as images or graphs.

The training process for agent $Q\left(s_t,a_t\right)$ in Q-learning relies on the algorithm of temporal difference (TD) in Equation (1), where $\alpha$ is the learning rate, $\gamma$ represents the discount factor, and $a\left(s_{t+1}\right)=arg\underset{a}{\max }Q\left(s_{t+1},a_{t+1}\right)$ indicates the action taken by the Q-learning agent.

$$Q\left(s_t,a_t\right)\leftarrow Q\left(s_t,a_t\right)+\alpha \left[r_{t+1}+\gamma \underset{a}{\max }Q\left(s_{t+1},a_{t+1}\right)-Q\left(s_t,a_t\right)\right]$$

(1)

In the DQN framework, the TD equation is employed to update the parameters of the neural network. Instead of learning from consecutive samples, DQN uses a replay buffer to store the agent’s experiences. Specifically, the replay buffer records state transitions, selected actions, and the corresponding immediate rewards from each agent–environment interaction, forming a tuple $\langle s_t,a_t,r_t,s_{t+1}\rangle$. During training, mini-batches of experiences are randomly sampled from the buffer to update the Q-network. This technique helps to break the correlation between consecutive samples and leads to more stable training. This approach leads to the definition of the DQN objective function as in Equation (2), where $\theta$ is the vector of parameters of agent $Q$.

$$J\left(\theta \right)=E\left[{(r_{t+1}+\gamma ma{x}_{a}Q\left(s_{t+1},a_{t+1};\theta \right)-Q\left(s_t,a_t;\theta \right))}^2\right]$$

(2)

In this paper, the procedure for employing DQN agents in vulnerability detection is outlined as follows: begin at time $t=0$, the pair set of CFG’s node and edge is initialized and fills in the data inputs. An action $a_0$ is randomly selected to establish the initial state $s_0$. Subsequently, for $t$ in $\left[1,T\right]$, the agent chooses the action $a_t$ that yields the highest score based on the function $Q\left(s_t,a_t;\theta \right)$ and executes this action within the environment. Following this, the agent receives the immediate reward $r_t$ from the environment and observes the subsequent state $t+1$, updating the agent’s parameter vector $\theta$ accordingly, leading to the formation of the next state $s_{t+1}$. This procedure is repeated until the environment reaches the terminal state $T$. The primary objective of the agent is to maximise the cumulative return of $r_t$. The specific algorithm for using a neural network to train the agent can be found in Algorithm 1.

Algorithm 1. DQN with Replay Buffer

Initialize experience replay buffer $\mathit{D}$ to capacity $\mathit{N}$

$\text{Initialize Q-network }\mathit{Q}\left({\mathit{s}}_{\mathit{t}},{\mathit{a}}_{\mathit{t}};\mathit{\theta }\right)$ with random weights $\mathit{\theta }$ $\mathrm{Initialize}\mathrm{a}\mathrm{target}\mathrm{network}\widehat{\mathit{Q}}\left({\mathit{s}}_{\mathit{t}},{\mathit{a}}_{\mathit{t}};\widehat{\mathit{\theta }}\right)$$\mathrm{where}\widehat{\mathit{\theta }}=\mathit{\theta }$ $\mathrm{Set}\mathrm{action}\mathrm{space}\mathit{a}$ = [0, 1, 2, 3, 4, 5] for six possible class labels For episode = 1, $M$ do:     $\mathrm{Initialize}\mathrm{state}{\mathit{s}}_{\mathbf{1}}$ from first observation of CFG features     $\mathrm{For}\mathrm{step}\mathit{t}=\mathbf{1}$ to $\mathit{T}$ do:       With probability $\mathit{\epsilon }$$\mathrm{select}\mathrm{a}\mathrm{random}\mathrm{action}{\mathit{a}}_{\mathit{t}}$        $\mathrm{or}\mathrm{select}\mathrm{action}{\mathit{a}}_{\mathit{t}}=\mathit{arg}{\mathit{max}}_{\mathit{a}}\mathit{Q}\left({\mathit{s}}_{\mathit{t}},{\mathit{a}}_{\mathit{t}};\mathit{\theta }\right)$      $\mathrm{Execute}\mathrm{action}{\mathit{a}}_{\mathit{t}}$ on the environment (i.e., predict vulnerability type)      $\mathrm{Observe}\mathrm{reward}{\mathit{r}}_{\mathit{t}}$$\mathrm{and}\mathrm{next}\mathrm{state}{\mathit{s}}_{\mathit{t}+\mathbf{1}}$      $\mathrm{Store}\mathrm{state}\mathrm{transition}\langle {\mathit{s}}_{\mathit{t}},{\mathit{a}}_{\mathit{t}},{\mathit{r}}_{\mathit{t}},{\mathit{s}}_{\mathit{t}+\mathbf{1}}\rangle$ in replay buffer $\mathit{D}$      $\mathrm{Randomly}\mathrm{sample}\mathrm{minibatch}\mathrm{of}\mathrm{transition}\mathrm{tuple}\langle {\mathit{s}}_{\mathit{i}},{\mathit{a}}_{\mathit{i}},{\mathit{r}}_{\mathit{i}},{\mathit{s}}_{\mathit{i}+\mathbf{1}}\rangle$ from $D$      $\mathrm{Set}{\mathit{y}}_{\mathit{i}}={\mathit{r}}_{\mathit{i}}+\mathit{\gamma }\underset{{\mathit{a}}^{\prime }}{\mathbf{max}}\widehat{\mathit{Q}}\left({\mathit{s}}_{\mathit{i}+\mathbf{1}},{\mathit{a}}^{\prime };\widehat{\mathit{\theta }}\right)$        $\mathrm{or}{\mathit{y}}_{\mathit{i}}={\mathit{r}}_{\mathit{i}}$$\mathrm{if}\mathrm{episode}\mathrm{ends}\mathrm{at}\mathrm{step}\mathit{i}+\mathbf{1}$      $\mathrm{Perform}\mathrm{a}\mathrm{gradient}\mathrm{descent}\mathrm{step}\mathrm{on}\mathrm{loss}{\left({\mathit{y}}_{\mathit{i}}-\mathit{Q}\left({\mathit{s}}_{\mathit{i}},{\mathit{a}}_{\mathit{i}};\mathit{\theta }\right)\right)}^2$ for $\mathit{\theta }$      $\mathrm{Set}\widehat{\mathit{\theta }}=$$\mathit{\theta }$ for every C step     end for end for

3.3.2. Proximal Policy Optimization

Unlike the off-policy DQN, PPO is an on-policy reinforcement learning algorithm that relies heavily on policy gradients where the key idea is to push up the probabilities of actions that lead to a higher return, and in the meantime, push down the probabilities of actions that lead to lower return, until it arrives at the optimal policy. Under a normal policy gradient, it keeps new and old policies close in parameter space. However, since even minor variations in parameter space can result in significant performance differences, a single bad step can collapse the policy performance. This risk makes large step sizes particularly dangerous when applying vanilla policy gradients, thereby hurting the sample efficiency. To address this challenge, an improved PPO algorithm, firstly introduced by Schulman et al. [39] from OpenAI [40], refines policies by taking the largest step possible to enhance performance while adhering to a constraint that ensures the new policy remains sufficiently similar to the previous one. This paper implemented the clip version of PPO, which uses specialized clipping (positive or negative advantage) instead of KL-divergence in the objective function to remove incentives for the new policy to get far from the old policy.

Let ${\pi }_{\theta }$ denote a policy with parameter $\theta$, and $J({\pi }_{\theta })$ denotes the expected finite-horizon undiscounted return of the policy. The gradient of $J({\pi }_{\theta })$ can be defined as:

$${\nabla }_{\theta }J({\pi }_{\theta })=\underset{\tau ~{\pi }_{\theta }}{\underbrace{E}}\left[{\displaystyle \sum }_{t=0}^T{\nabla }_{\theta }log{\pi }_{\theta }(a_t|s_t)A^{{\pi }_{\theta }}\left(s_t,a_t\right)\right],$$

(3)

where $\tau$ is a trajectory and $A^{{\pi }_{\theta }}$ is the advantage function for the current policy.

PPO-clip updates policies via:

$${\theta }_{k+1}=arg\underset{\theta }{\max }\underset{s,a~{\pi }_{{\theta }_k}}{\underbrace{E}}\left[L\left(s,a,{\theta }_k,\theta \right)\right],$$

(4)

which takes multiple steps of minibatch size to maximize the objective. Here $L$ is given by:

$$L\left(s,a,{\theta }_k,\theta \right)=\min \left({\displaystyle \frac{{\pi }_{\theta }\left(a|s\right)}{{\pi }_{{\theta }_k}\left(a|s\right)}}{A}^{{\pi }_{{\theta }_k}}\left(s,a\right),g\left(ϵ,A^{{\pi }_{{\theta }_k}}\left(s,a\right)\right)\right),$$

(5)

where

$$g\left(ϵ,A\right)=\{\begin{array}{c}\left(1+ϵ\right)A, A\ge 0\\ \left(1-ϵ\right)A, A<0\end{array}$$

(6)

in which $ϵ$ represents a (small) hyperparameter that dictates the permissible deviation of the new policy from the old.

To derive meaningful insights from this clipping setup, let us focus on a specific state-action pair $\left(s,a\right)$ and think of cases.

• Advantage is positive: Suppose the advantage for that state-action pair is positive; its contribution to the objective function diminishes to:

  $$L\left(s,a,{\theta }_k,\theta \right)=\min \left({\displaystyle \frac{{\pi }_{\theta }\left(a|s\right)}{{\pi }_{{\theta }_k}\left(a|s\right)}},\left(1+ϵ\right)\right)A^{{\pi }_{{\theta }_k}}\left(s,a\right).$$

  (7)

  Since the advantage is positive, the objective will increase if the action becomes more likely, i.e., if ${\pi }_{\theta }\left(a|s\right)$ increases. However, the $\min$ function in this expression imposes a cap on how much the objective can rise. Once ${\pi }_{\theta }\left(a|s\right)$ exceeds $\left(1+ϵ\right){\pi }_{{\theta }_k}\left(a|s\right)$, the minimum constraint activates, causing the term to reach a ceiling of $\left(1+ϵ\right){\pi }_{{\theta }_k}\left(a|s\right)$. Consequently, the new policy does not gain further benefit by diverging significantly from the previous policy.
• Advantage is negative: Suppose the advantage for that state-action pair is negative; its contribution to the objective function diminishes to:

  $$L\left(s,a,{\theta }_k,\theta \right)=\max \left({\displaystyle \frac{{\pi }_{\theta }\left(a|s\right)}{{\pi }_{{\theta }_k}\left(a|s\right)}},\left(1-ϵ\right)\right)A^{{\pi }_{{\theta }_k}}\left(s,a\right).$$

  (8)

Since the advantage is negative, the objective will increase if the action becomes less likely, i.e., if ${\pi }_{\theta }\left(a|s\right)$ decreases. However, the $\max$ function in this expression imposes a cap on how much the objective can rise. Once ${\pi }_{\theta }\left(a|s\right)$ falls below $\left(1-ϵ\right){\pi }_{{\theta }_k}\left(a|s\right)$, the maximum constraint activates, causing the term to reach a ceiling of $\left(1-ϵ\right){\pi }_{{\theta }_k}\left(a|s\right)$. Consequently, again, the new policy does not gain further benefit by diverging significantly from the previous policy.

In this study, the PPO-clip algorithm was utilized to train a stochastic policy using an on-policy approach, where it explores by sampling actions based on the most recent iteration of its stochastic policy. The degree of randomness in action selection (the vulnerability type) is influenced by initial conditions and the training process. As training progresses, the policy tends to become less random since the update mechanism encourages the exploitation of rewards that have already been found. However, one drawback of PPO is that this process may cause the policy to get trapped in local optima.

In the context of smart contract vulnerability detection, the clipping mechanism in PPO plays a vital role in maintaining policy stability during training. Due to the imbalanced nature of the dataset and the sparse reward structure (where correct classification often yields a binary reward), policy gradients can become highly volatile, especially when the agent overreacts to rare classes or noise in the data. The clip range in PPO ensures that updates to the policy remain conservative, preventing drastic shifts that could otherwise lead the model to prematurely overfit to dominant classes or fall into local optima. By bounding the policy change during optimization, the agent incrementally improves its decision making over time, maintaining robustness across classes and achieving more consistent learning across episodes. This is particularly valuable in environments like ours, where sequential decisions are driven by subtle graph structures rather than dense or uniform feedback. The full details can be found in Algorithm 2 below.

Algorithm 2. PPO-Clip

$\mathrm{Initialize}\mathrm{policy}\mathrm{parameter}{\mathit{\theta }}_{\mathbf{0}}$

$\mathrm{Initialize}\mathrm{value}\mathrm{function}\mathrm{parameters}{\mathit{\varphi }}_{\mathbf{0}}$ $\mathrm{For}\mathit{k}=\mathbf{0},\mathbf{1},\mathbf{2},\dots$ do:    $\mathrm{Collect}\mathrm{set}\mathrm{of}\mathrm{trajectories}{\mathcal{D}}_{\mathit{k}}=\left\{{\mathit{\tau }}_{\mathit{i}}\right\}$$\mathrm{by}\mathrm{running}\mathrm{policy}{\mathit{\pi }}_{\mathit{k}}=\mathit{\pi }\left({\mathit{\theta }}_{\mathit{k}}\right)$ in the environment    $\mathrm{Compute\; rewards-to-go}\widehat{{\mathit{R}}_{\mathit{t}}}$    $\mathrm{Compute}\mathrm{advantage}\mathrm{estimates}\widehat{{\mathit{A}}_{\mathit{t}}}$$\mathrm{based}\mathrm{on}\mathrm{current}\mathrm{value}\mathrm{function}{\mathit{V}}_{{\mathit{\varphi }}_{\mathit{k}}}$     Update the policy by maximizing the PPO-Clip objective:    ${\mathit{\theta }}_{\mathit{k}+\mathbf{1}}=\mathit{a}\mathit{r}\mathit{g}\underset{\mathit{\theta }}{\mathbf{max}}{\displaystyle \frac{\mathbf{1}}{\left|{\mathcal{D}}_{\mathit{k}}\right|\mathit{T}}}{\displaystyle {\displaystyle \sum }_{\mathit{\tau }\in {\mathcal{D}}_{\mathit{k}}}}{\displaystyle {\displaystyle \sum }_{\mathit{t}=\mathbf{0}}^{\mathit{T}}}\mathbf{min}\left({\displaystyle \frac{{\mathit{\pi }}_{\mathit{\theta }}\left(\mathit{a}|\mathit{s}\right)}{{\mathit{\pi }}_{{\mathit{\theta }}_{\mathit{k}}}\left(\mathit{a}|\mathit{s}\right)}}{\mathit{A}}^{{\mathit{\pi }}_{{\mathit{\theta }}_{\mathit{k}}}}\left({\mathit{s}}_{\mathit{t}},{\mathit{a}}_{\mathit{t}}\right),\mathit{g}\left(\mathit{ϵ},{\mathit{A}}^{{\mathit{\pi }}_{{\mathit{\theta }}_{\mathit{k}}}}\left({\mathit{s}}_{\mathit{t}},{\mathit{a}}_{\mathit{t}}\right)\right)\right),$     typically via stochastic gradient ascent with Adam    $\mathrm{Fit}\mathrm{value}\mathrm{function}\mathrm{by}\mathrm{regression}\mathrm{on}\mathrm{mean}\text{-}\mathrm{squared}\mathrm{error}\text{:}$           ${\mathit{\varphi }}_{\mathit{k}+\mathbf{1}}=\mathit{a}\mathit{r}\mathit{g}\underset{\mathit{\varphi }}{\mathbf{max}}{\displaystyle \frac{\mathbf{1}}{\left|{\mathcal{D}}_{\mathit{k}}\right|\mathit{T}}}{\displaystyle {\displaystyle \sum }_{\mathit{\tau }\in {\mathcal{D}}_{\mathit{k}}}}{\displaystyle {\displaystyle \sum }_{\mathit{t}=\mathbf{0}}^{\mathit{T}}}{\left({\mathit{V}}_{\mathit{\varphi }}\left({\mathit{s}}_{\mathit{t}}\right)-\widehat{{\mathit{R}}_{\mathit{t}}}\right)}^{\mathbf{2}},$     typically via some gradient decent algorithm end for

3.4. Model Configurations

3.4.1. Agent Environment

To ensure the reinforcement learning agent performs well, it is necessary to set up a custom environment tailored to the classification task as formed in this paper. It involves constructing the action and observation spaces, implementing functions to retrieve the current observation and transition between states, and incorporating a function to compute the immediate reward. After setup, it is necessary to apply the training, validation and testing sets to the environment. The complete framework for environment setup is detailed in Algorithm 3.

Algorithm 3. Agent Environment Setup

class SmartContractEnv()

function extract_features_from_cfg()        Extract graph features from .dot file of CFGs     function __init__()        Initialize current step as 0        Initialize action space as spaces. Discrete(6) to capture six classes        Initialize observation space as feature shape of extract_features_from_cfg()     function _get_observation()        Extract the CFG features for the current contract     function step()        Set current step forward        while episode not done, do:           Set next state by _get_observation()           Calculate reward by _calculate_reward()        end while     function _calculate_reward()        Define the reward calculation rules as: when action matches true labels, get a reward 1 Initialize environments to training, validation and test sets by SmartContractEnv()

3.4.2. Hyperparameter Tuning

Hyperparameter tuning is a critical aspect of optimizing reinforcement learning algorithms like DQN and PPO because it directly influences the model’s performance and convergence. In reinforcement learning, hyperparameters control various aspects of the learning process, such as how quickly the model adapts to changes (learning rate), the size and management of experience replay buffers (buffer size, etc.), how actions are selected (gamma), and the frequency and the way updates are made (batch size, steps, epochs). In this paper, the following hyperparameters were considered for tuning:

• Learning rate: This parameter controls how much the model updates its knowledge after each step. A too-high learning rate might cause the model to overlook optimal solutions, while a too-low rate may result in slow learning and the model getting stuck in local optima.
• Batch size: Size of the minibatch for training. Larger batch sizes generally lead to more stable updates but require more computational resources.
• Gamma: The discount factor belonging to (0, 1) that represents the importance of future rewards. A gamma close to 1.0 makes the model value long-term rewards, while a smaller gamma makes it prioritize immediate rewards.
• Steps before learning (DQN specific): This defines how many steps of the model to collect transitions for before learning starts. Delaying learning can help the model accumulate a diverse set of experiences, improving the stability and performance of the learning process.
• Buffer size (DQN specific): Size of the replay buffer that stores past experiences for the model to learn. A larger buffer allows the model to learn from a broader range of experiences but may increase memory usage and slow down training.
• Number of steps (PPO specific): The number of steps to run for each environment per update. More steps can stabilize the model by providing more data for each update but may also slow down the learning process.
• Number of epochs (PPO specific): This parameter specifies how many times the model iterates over collected experience data to optimize the policy during each update. In the context of smart contract vulnerability detection, more epochs can help the model better generalize patterns associated with vulnerabilities by revisiting observed contract behaviors more thoroughly. However, excessive epochs can lead the model to overfit to specific contract structures or vulnerability patterns in the training data, reducing its ability to detect novel or rare vulnerabilities in real-world DeFi contracts. Therefore, a careful balance is necessary to ensure robustness without compromising generalization.
• Entropy coefficient (PPO specific): Entropy coefficient for the loss calculation. A higher coefficient can promote exploration and help in avoiding local minima.
• Clip range (PPO specific): Clipping parameter. It can be a function of the current progress remaining (from 1 to 0). In PPO, the clip range limits how much the policy can change during training, which helps maintain the balance between exploring new policies and retaining what has already been learned.

The results of hyperparameter tuning for DQN and PPO algorithms are presented in

Table 2. Hyperparameter tuning for DQN.

Parameters	Tuning Range	Optimal Results
Learning rate	[1 × 10−5, 1 × 10−3]	0.00015
Batch size	<32, 64, 128>	64
Gamma	[0.9, 0.9999]	0.9400
Steps before learning	[1000, 10,000]	3738
Buffer size	[50,000, 1,000,000]	86245
Max rewards achieved		551.0

and

Table 3. Hyperparameter tuning for PPO.

Parameters	Tuning Range	Optimal Results
Learning rate	[1 × 10−5, 1 × 10−3]	0.0002
Batch size	<32, 64, 128>	32
Gamma	[0.9, 0.9999]	0.9543
Number of steps	<64, 128, 256, 512>	256
Number of epochs	[1, 10] (int)	9
Entropy coefficient	[1 × 10−8, 1 × 10−2]	1.3426
Clip range	[0.1, 0.4]	0.2195
Max rewards achieved		584.0

, where the max rewards achieved by both models are 551.0 and 584.0, respectively.

3.5. Evaluation Metrics

Considering that the objective of this study is formulated as a multi-label classification task with an imbalanced dataset, we adopted three primary metrics to evaluate our models, which are Accuracy, Micro-Recall and Micro-F1. The ROC curve and Precision–Recall (PR) curve were also implemented to evaluate the model performance across classes using One-Vs.-All methodology.

• Label Accuracy: this measures the proportion of correct predictions for each label across all instances. Formally, denote $y_{ij}$ as the true label value (either 0 or 1) of the $j$th label for the $i$th sample, and ${\widehat{y}}_{ij}$ as its predicted label value. Label accuracy can be defined as:

  $$LabelAccuracy={\displaystyle \frac{{{\displaystyle \sum }}_{i=1}^N{{\displaystyle \sum }}_{j=1}^Q\delta \left(y_{ij},{\widehat{y}}_{ij}\right)}{N\times Q}},$$

  (9)

  where $N$ represents the total number of samples, $Q$ is the total number of labels, $\delta$ is the indicator function that equals 1 when $y_{ij}={\widehat{y}}_{ij}$ and 0 otherwise.
• Subset Accuracy: a stricter accuracy score that measures the proportion of instances where all labels are correctly predicted. The mathematical formulation is:

  $$SubsetAccuracy={\displaystyle \frac{1}{N}}{{\displaystyle \sum }}_{i=1}^N\delta \left(y_{ij},{\widehat{y}}_{ij}\right).$$

  (10)
• Micro-Recall: Recall measures the proportion of correctly identified out of all actual positives. For micro-level evaluation, labels from all samples are merged into a single comprehensive set. The recall is then calculated based on this aggregated set with the following formula:

  $$MicroRecall={\displaystyle \frac{{{\displaystyle \sum }}_{i=1}^N{{\displaystyle \sum }}_{j=1}^Q\left(y_{ij}\times {\widehat{y}}_{ij}\right)}{{{\displaystyle \sum }}_{i=1}^N{{\displaystyle \sum }}_{j=1}^Q{y}_{ij}}}.$$

  (11)
• Micro-F1: The F1 score is the harmonic mean between precision and recall, bounded between 0 and 1. At the micro-level, the F1 score can be calculated as:

  $$MicroF1={\displaystyle \frac{2\times MicroPrecision\times MicroRecall}{MicroPrecision\times MicroRecall}},$$

  (12)

  where

  $$MicroPrecision={\displaystyle \frac{{{\displaystyle \sum }}_{i=1}^N{{\displaystyle \sum }}_{j=1}^Q\left(y_{ij}\times {\widehat{y}}_{ij}\right)}{{{\displaystyle \sum }}_{i=1}^N{{\displaystyle \sum }}_{j=1}^Q{\widehat{y}}_{ij}}}$$

  (13)
• Learning curve: The learning curve plots the model’s performance (in our case the reward) against the number of training iterations or episodes. It helps to visualize the learning process, showing how quickly the model learns and how well it generalizes to new data.
• Receiver operating characteristic (ROC) curve: The ROC curve is a visual tool used to assess a classification model’s effectiveness by illustrating the relationship between the true positive rate (TPR) and the false positive rate (FPR). TPR reflects the percentage of actual positives that the model correctly identifies, while FPR represents the percentage of negatives mistakenly classified as positives. An ideal ROC curve would rise along the y-axis toward the upper left corner, indicating high TPR and low FPR. The area under the ROC curve (AUC) provides an overall performance metric for the model. AUC values range from 0 to 1, with values near 1 indicating superior model performance and those around 0.5 suggesting performance comparable to random guessing. In a multi-label classification task, One-Vs.-All methodology is adopted to plot the ROC curve.
• Precision–Recall (PR) curve: The PR curve is particularly insightful when dealing with imbalanced datasets, where the positive class is rare. It focuses on the precision (positive predictive value) and recall (sensitivity) of the model, providing a clear view of the trade-off between these two metrics. By adjusting this threshold, different combinations of precision and recall can be achieved, which are then visualized on the PR curve. Lowering the threshold typically increases the likelihood of predicting positive instances, which may result in more false positives, thus reducing precision but raising recall. Conversely, raising the threshold makes the model more selective, leading to fewer false positives and higher precision, but potentially at the cost of reduced recall. Ideally, a model would achieve both high precision and recall, with the PR curve nearing the top-right corner of the graph. The area under the PR curve (AUC-PR) serves as a single summary metric, with higher values indicating better performance.

4. Experiment and Analysis

In this study, our experiments were conducted on GPU nodes from a high-performance computing facility. Each node was equipped with two NVIDIA Tesla V100 GPUs (16 GB HBM2 memory each), 64 GB of DDR4 RAM, and an eight-core Intel Xeon E5-2698 v4 CPU.

Experiments in this section began by evaluating the performance of reinforcement learning models using three metrics during the validation phase, accompanied by an analysis of their learning curves. Following the evaluation, the optimal one was selected and deployed to the test set for effectiveness examination. The section concludes by discussing the experimental results.

4.1. Evaluation of RL Model Performance

Table 4. Comparison of DQN, PPO and baseline ML methods performance.

Model	DQN	PPO	SVM	Random Forest	MLP
Accuracy	0.1869	0.2947	0.2532	0.2487	0.2214
Recall	0.1768	0.1930	0.1750	0.1634	0.1535
F1 score	0.1452	0.1463	0.1376	0.1308	0.1250

Abbreviations: DQN, Deep Q-Network; PPO, Proximal Policy Optimization; SVM, Support Vector Machine; MLP, Multi-Layer Perceptron. The best results are bolded.

presents the validation metrics for DQN and PPO performances. Both models underperformed in this multi-label classification task, achieving only 18.69% and 29.47% accuracy, respectively. While limited data per class is a probable factor contributing to these suboptimal outcomes—our training set comprises just 13,400 contracts across six labels—additional aspects could contribute to these suboptimal outcomes. One of them could be our state encoding since compressing each CFG to only its node- and edge-count may be too simplistic to capture the fine-grained semantic patterns necessary for distinguishing vulnerability types. What is more, our binary reward scheme (correct vs. incorrect) yields very sparse feedback, which slows convergence and can lead to high variance in value estimates. Despite these challenges, PPO still outperformed DQN across the accuracy, recall, and F₁ metrics, suggesting that on-policy updates better accommodate the combined difficulties of sparse rewards and imbalanced classes.

To place our RL approaches in context, we trained three off-the-shelf classifiers: support vector machine (SVM), random forest, and a simple multi-layer perceptron (MLP), using two scalar CFG features (number of nodes and edges). We extracted these features automatically by parsing each .dot file in our dataset and counting nodes and edges. Hyperparameters (e.g., SVM’s C and kernel, number/depth of trees, MLP’s layer sizes and learning rates) were chosen via five-fold cross-validation on the training split. As shown in the following table, while these models reach moderate performance, PPO still leads overall, confirming the benefit of sequential policy learning on graph structures.

4.2. Evaluation of RL Model Effectiveness

Based on the validation performance, the PPO model was selected as the optimal model and subsequently deployed on the test set, with the classification report summarized in

Table 5. Classification report of PPO model on the test set.

	Precision	Recall	F1 Score	Support
access control	0.03	0.01	0.01	193
arithmetic	0.11	0.02	0.04	249
other	0.15	0.03	0.05	410
reentrancy	0.25	0.03	0.05	441
safe	0.21	0.17	0.19	565
unchecked calls	0.28	0.81	0.46	693
accuracy			0.30	2534
micro avg	0.19	0.19	0.17	2534
macro avg	0.20	0.18	0.14	2534
weighted avg	0.21	0.28	0.20	2534

. The accuracy stands at 30%, which is consistent with the accuracy observed on the validation set, indicating the stability of the PPO model. However, the predictive performance varies significantly across different classes. The recall for unchecked calls is notably high at 0.81, with an F1 score of 0.46, the highest among all classes. We attribute PPO’s particularly strong recall on unchecked calls to the ample representation of that category in the training set. Safe class follows, achieving an F1 score of 0.19. The remaining four classes exhibit suboptimal prediction performance. This outcome is consistent with the dataset’s characteristics identified during data preparation, where a pronounced class imbalance was observed, with the ratio of unchecked calls to access control classes being approximately three to one. Given that nearly half of the contracts fall within the unchecked calls and safe classes, these categories have a substantial amount of data available for training the reinforcement model, leading to better predictive performance for these classes.

To illustrate PPO’s typical behaviour, we manually inspected two test-set contracts. In one (0x1a2b3c4d5e6f7a8b9c0d1e2f3a4b5c6d7e8f9a0), the CFG is just a single external-call block, so PPO easily learns the clear control-flow pattern and correctly flags it as an unchecked call vulnerability.

In another (0x3b7a1c2e4d5f6a8b9c0d1e2f3a4b5c6d7e8f9012), the underflow happens inside a loop whose repeated arithmetic operations span multiple basic blocks—our crude node-and-edge summary collapses that structure, PPO never “sees” the data flow dependency, and it misses the vulnerability.

A close inspection of Table 5 shows that PPO’s weakest classes, access control (F1 = 0.01), arithmetic (F1 = 0.04) and reentrancy (F1 = 0.05), all hinge on semantic patterns lost in our simple node-and-edge-count summary. Permission checks for access control typically span multiple disjoint basic blocks (e.g., owner-only branches), arithmetic underflows often occur inside loops or data-dependent branches, and reentrancy involves interleaved function entry/exit blocks. Collapsing these structures into flat counts removes the exact control and data flow cues PPO needs. Safe (F1 = 0.19) and unchecked calls (F1 = 0.46) produce more uniform graphs (single-block safety idioms or lone external calls) that PPO can readily learn.

To visualize the model effectiveness among various vulnerability categories, both the ROC curve and the precision–recall (PR) curve were plotted for analysis (Figure 4). The ROC curve reveals similar suboptimal model performance across six classes, with the area under the curve (AUC) values hovering around 0.55. However, in the case of imbalanced datasets where positive class is infrequent, the ROC curve can be misleading, as it might indicate high performance even if the model performs poorly on the positive class. Thus, the PR curve offers a more insightful evaluation for our task, as it focuses on the positive class (i.e., the vulnerability class) and aims to mitigate the significant costs associated with false positives (i.e., falsely detecting vulnerabilities). The results align with the classification report, as the area under the PR curve for unchecked calls stands at 0.78, indicating that the model demonstrates moderate effectiveness when predicting the majority class.

4.3. Discussion

Despite the creative effort in applying reinforcement learning algorithms to vulnerability detection, there are still some limitations faced by this study and directions for future research. One significant limitation lies in the use of a limited dataset for training the reinforcement learning models. This limitation hinders the models’ ability to adequately learn patterns across individual classes. This research primarily relies on CFGs to extract high-level semantics from contract bytecode. However, other graph representations, such as abstract syntax tree and program dependency graph, may offer richer syntactic and semantic insights.

Another important direction for future work involves the integration of this approach into practical smart contract auditing tools. By embedding the reinforcement learning model into platforms such as Slither, MythX, or even custom development environments, the vulnerability detection process could be made more dynamic and adaptive. Unlike traditional static analyzers that rely on predefined heuristics, a reinforcement learning-based tool could learn from emerging patterns and improve over time. This would significantly enhance its utility in real-world development settings, offering developers real-time guidance and automated vulnerability detection throughout the contract development lifecycle.

5. Conclusions

This paper shows that reinforcement learning techniques could be a viable tool for detecting and classifying smart contract vulnerabilities. Utilizing a publicly sourced dataset, two distinct model architectures were trained and evaluated. Treating vulnerability detection as a multi-label classification problem, graph representations were generated to capture relevant semantic features from the contract bytecode. The results indicate that, given the configurations in terms of custom environment setup and hyperparameter tuning, the PPO model exhibits more stable and consistent learning patterns and achieves higher overall rewards. When applied to the test set, the PPO model displays effectiveness, particularly for the majority class of vulnerabilities, as evidenced by metrics such as Micro Recall, Micro F1, and the PR curve. The findings of this study offer valuable insights that may encourage scholars and developers to explore the potential of reinforcement learning techniques for improving smart contract security and mitigating financial risks for DeFi stakeholders.