Adaptive Scale and Correlative Attention PointPillars: An Efficient Real-Time 3D Point Cloud Object Detection Algorithm

Abstract

Recognizing 3D objects from point clouds is a crucial technology for autonomous vehicles. Nevertheless, LiDAR (Light Detection and Ranging) point clouds are generally sparse, and they provide limited contextual information, resulting in unsatisfactory recognition performance for distant or small objects. Consequently, this article proposes an object recognition algorithm named Adaptive Scale and Correlative Attention PointPillars (ASCA-PointPillars) to address this problem. Firstly, an innovative adaptive scale pillars (ASP) encoding method is proposed, which encodes point clouds using pillars of varying sizes. Secondly, ASCA-PointPillars introduces a feature enhancement mechanism called correlative point attention (CPA) to enhance the feature associations within each pillar. Additionally, a data augmentation algorithm called random sampling data augmentation (RS-Aug) is proposed to solve the class imbalance problem. The experimental results on the KITTI 3D object dataset demonstrate that the proposed ASCA-PointPillars algorithm significantly boosts the recognition performance and RS-Aug effectively enhances the training effects on an imbalanced dataset.

1. Introduction

LiDAR (Light Detection and Ranging) has gained widespread acceptance owing to its capability to capture three-dimensional information on objects regardless of lighting conditions. Consequently, recognizing 3D objects from LiDAR point clouds has attracted significant attention in the field of autonomous driving. Nevertheless, LiDAR point clouds possess unique challenges such as sparsity, disorderliness, and unstructured data, with the sparsity issue posing an even greater hurdle for distant and small objects. This has resulted in the recognition of distant and small objects becoming a noteworthy challenge. Currently, point-based methods [1,2,3,4,5,6,7] and grid-based methods [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22] are two popular categories of recognition algorithms for point clouds.

Point-based methods generally take original point clouds as an input and directly recognize objects from the point cloud. This category maximizes the retention of the original information from the point clouds. However, when dealing with large-scale point cloud data, such methods can potentially consume significant computational resources. The voxelization of point clouds serves as an effective solution to address this challenge.

Grid-based methods typically encode point clouds into voxels or pillars and then process them separately using different approaches. Voxel-based methods [8,9,10,11,12,13,14] usually convert the input point cloud data into a voxel space and then use 3D convolution or sparse convolution [9] to extract features from voxels and complete the recognition task. Pillars are a specialized type of voxel that do not take height information into account. Pillar-based methods [15,16,17,18,19,20,21,22] usually encode point clouds into 2D pillars before projecting the point clouds as a 2D pseudo image. Then, a 2D CNN can be employed to recognize it. However, encoding point clouds into voxels/pillars inevitably results in spatial information loss. Moreover, as point clouds’ locations become more distant and objects get smaller, the number of points within an individual voxel decreases, leading to even more severe information loss and recognition accuracy being affected as a consequence.

Currently, the prevalent methods typically adopt a single-scale voxel/pillar to encode point clouds, rendering them powerless in addressing the exacerbated issue of spatial information loss at long distances. But using multiple multi-scale pillars can help solve this difficulty. Consequently, this article introduces Adaptive Scale and Correlative Attention PointPillars (ASCA-PointPillars). The cornerstone of ASCA-PointPillars lies in the adaptive scale pillars (ASP) module and the correlative point attention (CPA) module. The ASP module employs various sizes of pillar to encode the point clouds based on the sparsity of the point clouds. The smaller the size of the pillar, the stronger the feature representation ability of each point, resulting in less spatial loss. Sparser point clouds in the distance are then encoded using smaller pillars to mitigate the spatial information loss of distant objects and enable the network to capture richer feature information for these objects. After encoding the point clouds into multi-scale pillars, the CPA module is utilized to enhance the feature association within the pillars, providing richer contextual features. The CPA module incorporates a self-attention mechanism that effectively establishes connections between pieces of contextual information [23]. Consequently, the CPA module not only strengthens the feature association within small pillars representing distant objects, but also enhances the feature correlation among point clouds representing small objects, ultimately improving the recognition performance for both distant and small objects.

Moreover, imbalanced amounts of training samples belonging to different categories generally lead to imbalanced recognition performance, and categories with significantly fewer training samples tend to have lower recognition accuracy. Data augmentation, which can overcome this imbalance problem, is therefore critical for the training process. In most algorithms [1,2,3,4,5,6,7,10,11,12,13,14,15,16,18,19,20,21,22], ground truths (bounding boxes and the points inside them) may randomly be inserted into existing samples to augment the training dataset [9]. However, this method may insert ground truths into inappropriate areas. This may create incorrect contextual information for the training of the model [24]. But semantic information of the current scene could help to resolve this problem. So, a random sampling data augmentation algorithm (RS-Aug), based on scene semantic information, is proposed.

RS-Aug can identify reasonable areas for placing ground truths. It initially acquires semantic information regarding obstacles and road surface areas in point cloud scenes. Based on this semantic information, it then removes the areas on the road surface occupied by obstacles. The remaining road surface areas are therefore suitable spaces for placement. By identifying these reasonable areas, RS-Aug can strategically position the ground truths of less frequently occurring categories in appropriate areas, such as the road surface, effectively balancing the number of categories within the dataset.

The contributions of this paper are summarized as follows:

• This study proposes an object recognition algorithm called ASCA-PointPillars. In the algorithm, we design an ASP module that innovatively utilizes multi-scale pillars to encode point clouds, effectively reducing the loss of spatial information. Subsequently, a CPA module is employed to establish contextual associations within a pillar’s point cloud, thereby enhancing the point cloud’s features.
• A data augmentation algorithm called RS-Aug is proposed, leveraging semantic information to identify reasonable areas for placing ground truths, addressing the issue of imbalanced categories in datasets.

The first section of this paper is an introduction, indicating the contributions of this article. The second section presents a literature review of related works. The third section is the methodology, which introduces the algorithm of this paper in detail. The fourth section presents the experiment, evaluating the algorithm of this paper and analyzing the experimental results. The fifth section is the conclusion, summarizing the method of this paper and looking forward to the future.

2. Related Works

This section will introduce related works on three aspects: point cloud object recognition, point cloud object recognition for distant or small objects, and data augmentation for point cloud object recognition.

Point cloud object recognition.

Point cloud object recognition encompasses both point-based and grid-based methods. Point-based methods [1,2,3,4,5,6,7] process points directly to recognize objects. Among these, PointNet [1] represents a pioneering work that laid the foundation for subsequent research. It was the first to employ neural networks to directly handle point clouds and extract features from them. PointNet++ [2] further improved upon PointNet by enabling the network to extract not only local but also global features. Subsequent studies often utilized these works [1,2] as the backbone for feature extraction from point clouds. This paper also employs a simplified version of PointNet for feature extraction from point clouds. Works [3,4,5] focused on feature extraction and object proposal generation during the first stage, followed by proposal refinement for classification and bounding box regression in the second stage. PointRCNN [3] segments the point clouds into foreground and background in the first stage, generating a small number of 3D proposals. Subsequently, in the second stage, it extracts local features and integrates them with the global semantic features obtained in the first stage, enabling the accurate prediction of bounding boxes. VoteNet [4] leverages PointNet++ [2] for feature extraction from point clouds, then uses a voting module to generate votes based on the features of seed points and aggregates these vote features to form object proposals. STD [5] also uses PointNet++ [2] for feature extraction in the first stage, but it voxelizes the proposals in the second stage before classification, combining the advantages of both point-based and voxel-based methods, thereby enhancing the recognition speed. Moreover, 3DSSD [6] eliminates the refinement modules and feature propagation layers used in previous works, proposing a distance-based feature sampling method (F-FPS) to preserve object points and remove background points, and introduces an anchor-free regression head, significantly increasing the speed of the method beyond previous point-based approaches. Point-GNN [7] innovatively applies a graph neural network to 3D recognition, encoding the point clouds into a graph representation and utilizing the designed graph neural network for object identification, demonstrating the potential of using graph neural networks for object recognition. While point-based methods have garnered considerable research attention, their high computational resource requirements have led to increased interest in grid-based methods.

Grid-based methods have received extensive research attention and are categorized into two primary approaches: voxel-based and pillar-based methods. The voxel-based approach [8,9,10,11,12,13,14] typically encodes point clouds into voxels and employs 3D backbones to extract features, followed by 2D convolution (e.g., RPN [25]) for classification and regression tasks. VoxelNet [8] represents a seminal work in this domain, utilizing Voxel Feature Encoding (VFE) to transform point clouds into voxels and leveraging 3D convolution to extract features. However, 3D convolution is computationally expensive. Thus, Second: Sparsely Embedded Convolutional Detection [9] adopts 3D sparse convolution (SpConv) for feature extraction, thereby enhancing computational efficiency. Voxel R-CNN [10] further introduces Voxel RoI pooling to directly extract RoI features from voxel features, aiming to reduce the computational cost. PDV [11] proposes a Density-Aware RoI Grid Pooling method that captures the density information of local point clouds for better refinement in the second stage. TED [12] initially employs SpConv to extract transformation-equivariant voxel features and then aligns and aggregates these features into a lightweight representation, thereby reducing computational costs. Traditional methods often apply VFE to single-frame point clouds, while DynStaF [13] incorporates a branch of multi-frame VFE, capitalizing on the rich semantic information of multi-frame data and the precise positional information of single-frame data to enhance the localization accuracy of bounding boxes. DSVT [14] innovates the backbone network, employing a transformer-based backbone with Dynamic Sparse Window Attention to process sparse voxels in parallel, and proposing a learnable 3D pooling operation to effectively encode spatial information, effectively improving detection performance. Voxel-based methods can achieve high detection accuracy, but the existence of a large number of empty voxels necessitates the consumption of significant memory space. Conversely, pillar-based methods significantly reduce the number of empty voxels, resulting in higher inference speeds.

The pillar-based approach [15,16,17,18,19,20] generally encodes point clouds into 2D pillars, which are then further processed by 2D backbones to extract features and recognize objects. PointPillars [15] and PillarNeXt [16] initially transform point clouds into pillars and subsequently convert these pillars into pseudo images. After this conversion, PointPillars utilizes RPN [25] and PillarNeXt employs a ResNet-based [26] backbone to extract 2D features. The detection paradigm proposed by PointPillars significantly accelerates the speed of point cloud object recognition, marking a milestone in the field. The creators of PillarNet [17] designed a simple encoder based on 2D detection prior to the Detection Neck, enabling the extraction of sparse pillar features and achieving high precision and efficiency in recognition tasks. Pillar R-CNN [18] translates the pillar representation into a Bird’s Eye View (BEV) representation and employs RPN [25] to generate object proposals, followed by refinement to identify objects.

In summary, grid-based methods for point cloud processing have evolved significantly, with voxel-based approaches offering higher accuracy at the cost of increased computational resources, and with pillar-based methods providing a faster alternative with slightly lower precision. The continuous advancements in these techniques contribute to the growing capabilities in the field of point cloud object recognition.

Point cloud recognition for distant and small objects.

Due to the sparsity of point clouds, it is challenging to accurately recognize distant and small objects. Many scholars have conducted research to address this issue. TimePillars [19] introduces a memory unit between the 2D CNN and the Detection Head. This memory unit is composed of convolutional Gated Recurrent Units (GRUs), which enhances the recognition accuracy of distant objects. FastPillars [20] utilizes a Maximum-Attention Pillar Encoding (MAPE) approach. MAPE first encodes points, then utilizes max-pooling encoding to aggregate features within pillars, then employs attention-pooling encoding to capture fine-grained features, and finally merges the two. This method effectively improves recognition capability for small objects. Ref. [21] introduces a Fully Sparse Object Detector (FSD), proposing Sparse Instance Recognition (SIR) to address the issue of vanishing central features in sparse feature maps. Additionally, an enhanced version of FSD called FSD++ is proposed which utilizes temporal information to eliminate data redundancy and combines information from multiple frames to form a Super-Sparse Input. Experiments demonstrate that both FSD and FSD++ possess strong distant recognition capabilities. Since the instances in the FSD method require clustering, which involves manually setting thresholds and is prone to inductive bias, the improved FSD v2 [22] employs virtual voxels to replace these instances, then utilizes a Sparse Virtual Voxel Mixer (VVM) to aggregate the features of virtual voxels belonging to the same object, further enhancing the recognition ability for distant objects.

Data augmentation for point cloud object recognition.

Data augmentation can effectively enhance the generalization ability of networks, thus playing a crucial role in point cloud object recognition. Commonly used point cloud data augmentation techniques include random rotations around coordinate axes, random global scaling, the application of random rotations and translations to each ground truth and its corresponding point clouds, etc. These methods are ubiquitous in point cloud object detectors. Ref. [9] introduced an efficient data augmentation technique known as Sample Ground Truths from the Database (GT-Aug). This approach initially creates a database encompassing all ground truths from the training dataset and subsequently selects several ground truths randomly to place in current training samples during training. GT-Aug significantly increases the number of ground truths in the training samples, greatly aiding network training and boosting generalization ability. GT-Aug has been extensively applied in subsequent studies, such as [5,6,7,10,11,12,13,14,15,16,18,19,20,21,22]. Some of these methods [14,18,21,22] discontinued the use of GT-Aug in the final epochs to facilitate training convergence. However, GT-Aug may occasionally introduce ground truths into unreasonable areas, leading the network to learn erroneous contextual information and preventing further performance enhancements. Addressing this issue, Ref. [24] proposed Context-Aware augmentation (CA-aug), which initially segments training samples into ground points and obstacle points. These are then projected onto a range view (RV) to identify a “ValidSpace” (an area suitable for placement). Subsequently, ground truths are randomly selected from the database and inserted into the training samples after rotating them around the Z-axis to find an appropriate position. Ref. [12] introduced Distance-Aware Data Augmentation (DA-aug), which initially applies random offsets to the bounding boxes of ground truths and their internal points. These points are then voxelized using spherical voxels, and sampling is conducted based on the distance from the voxel centers, resulting in a series of sampled points. These sampled points exhibit a similar distribution pattern to LiDAR scanning points, thus better simulating realistic point clouds.

While these methods have produced positive effects on training, the assistance of semantic information from the scene in finding suitable placement areas has been overlooked. Therefore, this paper proposes a point cloud data augmentation method that considers scene semantic information.

3. Method

3.1. Overall Architecture of ASCA-PointPillars

Fixed-size pillars are adopted in most pillar-based methods [15,16,17,18,19,20]. However, fixed-size pillar sampling inevitably results in spatial information loss, which is exacerbated for distant objects. Therefore, this section proposes ASCA-PointPillars.

The overall architecture of ASCA-PointPillars is shown in Figure 1, and consists of three blocks called Feature Encoding Network (FEN), Detection Neck, and Detection Head. ASCA-PointPillars uses RPN [25] as its Detection Neck, as in PointPillars [15], and uses SSD [27] as its Detection Head.

Figure 1. The architecture of ASCA-PointPillars. Within this framework, FEN serves to generate a pseudo image from point clouds, while the Detection Neck is responsible for extracting and fusing the features of the pseudo image. Finally, the Detection Head produces classification results and regresses the bounding boxes, enabling accurate object detection.

3.2. Feature Encoding Network

The role of the FEN is to first encode the point clouds into multi-scale pillars and then convert them into pseudo images so that they can be extracted by the 2D CNN backbone of the Detection Neck for feature extraction. Our work is mainly focused on ASP and CPA in the FEN, as shown in Figure 2.

Figure 2. Feature Encoding Network of ASCA-PointPillars. This section begins with the utilization of ASP to encode point clouds into multi-scale pillars, generating tensor data. Subsequently, a simplified version of PointNet is employed to extract high-dimensional features. Then, CPA is applied to enhance these features. Finally, the enhanced features are projected as a pseudo image, facilitating accurate object detection.

The closer an object is, the larger the point cluster it will form. Consequently, the closer the object is, the larger the pillar used to abstract larger-scale features. Conversely, a smaller pillar is used for distant objects to provide a more focused abstract to reduce the spatial information loss caused by distant objects. Below are the details of the ASP module.

• ASP module

In this module, the input point clouds are first divided into pillars, whose sizes are $V_x\times V_y$ on the X-Y plane (the Z-axis is ignored). Here, $V_x$ and $V_y$ are the sizes of the pillars along the X and Y-axis, respectively, and the value of $V_y$ is 0.16 m. The $V_x$ value for the pillars nearest to the LiDAR along the X-axis is 0.32 m, which is the biggest among all pillars, and $V_x$ is adaptively decreased with the increasing size of X. Therefore, the ASP module forms bigger pillars near the LiDAR and smaller pillars in distant areas. Figure 3 shows the schematic diagram of the ASP module.

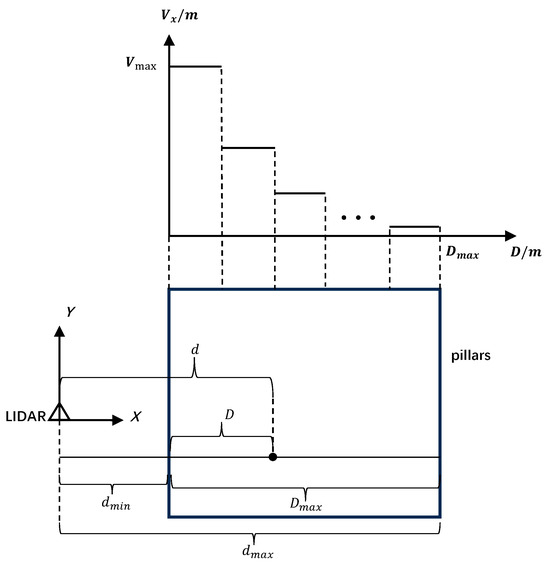
Figure 3. Schematic diagram of ASP module. The horizontal axis D represents the distance from a specific row of pillars to the first row of pillars, which is the row closest to the LiDAR, and the vertical axis $V_x$ represents the size of the pillars along the X-axis. It indicates that the size of the pillars along the X-axis, denoted as $V_x$, decreases as the distance D increases.

In Figure 3, $d_{min}$ is defined as the shortest distance along the X-axis between the pillars and the LiDAR, while $d_{max}$ is the longest. $D_{max}$ stands for the greatest distance between any two pillars along the X-axis, as determined by Equation (4). d refers to the distance from a specific row of pillars to the LiDAR, and D denotes the distance from a specific row of pillars to the first row of pillars, which is the row closest to the LiDAR. The relationship between d and D is depicted in Equation (3).

In the coordinate system, $V_x$ decreases as D increases. $V_{max}$ is the value of $V_x$ for the first row of pillars. The value $V_x$ for the nth size of the pillar can be derived from Equation (1). Equation (2) provides the value of n, which is associated with the distance ratio a. Equation (5) reveals that a is the ratio of D to $D_{max}$. According to Equation (2), there can be at most K different sizes of pillars.

$$V_x=\frac{1}{2^{\left(n-1\right)}}{V}_{max}$$

(1)

$$n=\left\{\begin{array}{c}1,a\in \left[0,\frac{1}{K}\right)\\ \begin{array}{l}2,a\in [\frac{1}{K},\frac{2}{K})\\ \cdots \end{array}\\ K,a\in \left[\frac{K-1}{K},1\right]\end{array},K\in N^{+}\right.$$

(2)

$$D=d-d_{min}$$

(3)

$$D_{max}=d_{max}-d_{min}$$

(4)

$$a=\frac{D}{D_{max}}$$

(5)

Upon encoding the point clouds into pillars, the data are converted into tensors of size (B, P, N). Here, B signifies the data dimension of each point and is set to 9, including coordinates x, y, z, reflectivity r, distance to the arithmetic mean of all points inside the pillar $x_r,x_r,x_r$, and the offset to the center of the pillar’s X-Y plane $x_p,y_p$. P denotes the count of non-empty pillars in each sample, and N represents the number of points within each pillar. Subsequently, a simplified version of PointNet (a linear layer with 64 output channels followed by BatchNorm [28] and ReLU [29]) is employed to generate a high-dimension feature metric (C, P, N), followed by a max pooling in the N dimension, generating a tensor of size (C, P) [15]. This tensor, referred to as the feature matrix F, will be input into the CPA module subsequently.

2.

CPA module

After converting the point clouds into tensors, the CPA module is employed to enhance the feature association among points within the pillar. Since the self-attention mechanism [23] can effectively establish contextual information association, it is introduced here. Ultimately, the features of points within the pillar are strengthened. Figure 4 illustrates the principle of the CPA module.

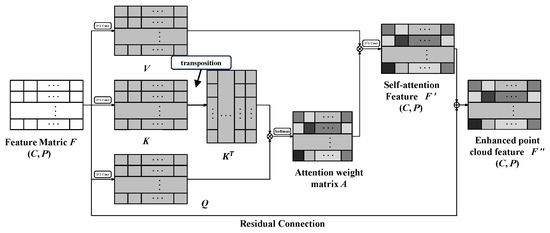
Figure 4. Schematic diagram of CPA module. It consists of a self-attention module and residual connection, which are used to establish feature associations among points within a pillar.

As shown in Figure 4, the input for the CPA module is feature metric F. According to [15], F is sent into a Multilayer Perceptron (MLP) layer to obtain matrices Q (query), K (Key), and V (value), as shown in Equations (6)–(8). Then, Q, K, and V are input into Equation (9) to obtain attention weight matrix A. $d_q$, $d_k$, and $d_v$ in the following equation represent the dimensions of Q, K, and V, respectively.

$$\mathit{Q}={\mathrm{M}\mathrm{L}\mathrm{P}}_{\mathrm{Q}}\left(\mathit{F}\right),\mathit{Q}\in {\mathbb{R}}^{C\times d_q}$$

(6)

$$\mathit{K}={\mathrm{M}\mathrm{L}\mathrm{P}}_{\mathrm{K}}\left(\mathit{F}\right),\mathit{K}\in {\mathbb{R}}^{C\times d_k}$$

(7)

$$\mathit{V}={\mathrm{M}\mathrm{L}\mathrm{P}}_{\mathrm{V}}\left(\mathit{F}\right),\mathit{V}\in {\mathbb{R}}^{C\times d_v}$$

(8)

$$\mathit{A}=softmax\left(\frac{\mathit{Q}{\mathit{K}}^{\mathit{T}}}{\sqrt{d_k}}\right)\mathit{V},\mathit{A}\in {\mathbb{R}}^{C\times C}$$

(9)

Then, MLP is used to restore A to the original dimension P and obtain the self-attention feature F′, as shown in Equation (10).

$${\mathit{F}}^{\prime }=\mathrm{M}\mathrm{L}\mathrm{P}\left(\mathit{A}\right),{\mathit{F}}^{\prime }\in {\mathbb{R}}^{C\times P}$$

(10)

Because the self-attention might increase the complexity of the model, it might not outperform Convolutional Neural Networks (CNNs) on small-scale datasets. To circumvent this issue, residual connection is employed. This connection adds the original feature F to the self-attention feature F′, as shown in Equation (11). As a result, the correlation between points within local spaces is enhanced to improve the network’s recognition capability.

$${\mathit{F}}^{″}={\mathit{F}}^{\prime }+\mathit{F},{\mathit{F}}^{″}\in {\mathbb{R}}^{C\times P}$$

(11)

Because the improved self-attention can enhance the feature correlation within each pillar, it can thus enhance robustness against sparse points.

As shown in Figure 2, the enhanced features obtained from the CPA module are redistributed to their original positions based on the pillar index, resulting in a 2D pseudo image [15]. As shown in Figure 1, the pseudo image is then input into the Detection Neck to further extract features, after which the Detection Head obtains the detection result.

3.3. Detection Neck

The Detection Neck adopts the classic RPN [25] structure. As shown in Figure 5, it includes three consecutive convolutional blocks (Block1, Block2, and Block3) to obtain feature maps with three different resolutions. Then, these three feature maps are up-sampled using three transposed convolutional blocks (DeBlock1, DeBlock2, and DeBlock3) to obtain three feature maps with the same resolution, and finally, these three feature maps are concatenated together to obtain the final feature map. The details of the blocks and deblocks are shown in Table 1. In Table 1, Conv2d represents a 2D convolutional layer, while DeConv2d represents a 2D transposed convolutional layer. The numbers enclosed in parentheses indicate the number of input channels, the number of output channels, and the size of the convolution kernels, stride, and padding, respectively. Furthermore, the output of the Detection Neck is fed into the Detection Head to produce the final recognition results.

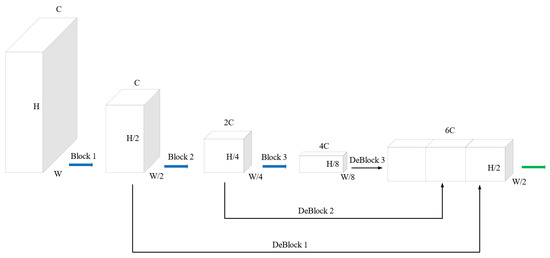
Figure 5. Structure of RPN. Three consecutive convolutional blocks are employed to obtain feature maps of three different resolutions. Subsequently, these feature maps are up-sampled to match a common resolution, and then concatenated to obtain the final feature output.

Table 1. Details of blocks and deblocks.

Module	Details	Module	Details
Block1	Conv2d (64, 64, 3, 2, 0) × 1 Conv2d (64, 64, 3, 1, 1) × 3	DeBlock1	DeConv2d (64, 128, 1, 1, 0) × 1
Block2	Conv2d (64, 128, 3, 2, 0) × 1 Conv2d (128, 128, 3, 1, 1) × 3	DeBlock2	DeConv2d (128, 128, 2, 2, 0) × 1
Block3	Conv2d (128, 256, 3, 2, 1) × 1 Conv2d (256, 256, 3, 1, 1) × 3	DeBlock3	DeConv2d (256, 128, 4, 4, 0) × 1

3.4. Loss Function

In this paper, the same loss function as [15] is adopted. Ground truth bounding boxes (GT boxes) and anchor boxes are represented as (x, y, z, w, l, h, $\theta$), where x, y, and z represent the coordinates, w, l, and h represent the width, height, and length, respectively, and $\theta$ indicates the angle offset. Therefore, the offsets of each parameter between the GT boxes and anchor boxes are calculated accordingly:

$$∆x=\frac{x^{gt}-x^a}{d^a},∆y=\frac{y^{gt}-y^a}{d^a},∆z=\frac{x^{gt}-x^a}{d^a}$$

$$∆w=\log \frac{w^{gt}-w^a}{d^a},∆l=\log \frac{l^{gt}-l^a}{d^a},∆h=\log \frac{h^{gt}-h^a}{d^a}$$

(12)

$$∆\theta =\sin \left({\theta }^{gt}-{\theta }^a\right)$$

In Equation (12), the superscripts “gt” and “a” indicate the GT boxes and anchor boxes, respectively, and $d^a=\sqrt{{{(w}^a)}^2+{{(l}^a)}^2}$. Consequently, the localization loss is

$$L_{loc}=\sum _{b\in \left(x,y,z,w,l,h,\theta \right)}SmoothL1\left(∆b\right)$$

(13)

The classification loss adopts focal loss [30]. The classification loss is calculated as below, where $p^a$ represents the predicted class score for an anchor box. According to [30], ${\alpha }_a=0.25$ and $\gamma =2$.

$$L_{cls}=-{\alpha }_a{\left(1-p^a\right)}^{\gamma }\log p^a$$

(14)

Based on [9], a SoftMax function is utilized as the angle classification loss ($L_{cls}$) to enable the learning of object orientations. Consequently, the overall loss is shown in Equation (15):

$$Loss=\frac{1}{N_{pos}}\left({\beta }_1{L}_{loc}+{\beta }_2{L}_{cls}+{\beta }_3{L}_{dir}\right)$$

(15)

In the equation above, $N_{pos}$ represents the number of positive anchor boxes. ${\beta }_1$, ${\beta }_2$, and ${\beta }_3$ are the weights for the three types of losses, where ${\beta }_1=2$, ${\beta }_2=1$, and ${\beta }_3=0.2$ [9].

3.5. RS-Aug Algorithm

The widely used GT-Aug [9] overlooks the semantic information of the scene during random sampling and augmentation. Consequently, it might introduce ground truths into unreasonable areas, resulting in unreasonable scenes [24]. These unreasonable augmentations could mislead networks to learn incorrect information.

Here, we propose RS-Aug, which considers the semantic information of the scene in augmenting the samples, as depicted in Figure 6a.

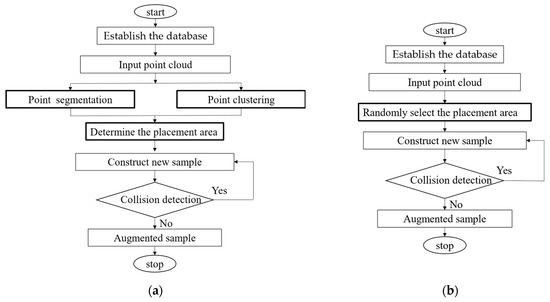
Figure 6. Flow charts of RS-Aug (a) and GT-Aug (b). The bold boxes indicate the differences between the two algorithms, including “Points segmentation”, “Points clustering”, and “Determine the placement area” versus “Randomly select the placement area”.

As shown in Figure 6a, RS-Aug includes 6 steps.

• Establish the database. Establish a database that includes all the ground truths (bounding boxes and the points inside them). For instance, in our following experiment, three categories of ground truths are included. They are vehicles, cyclists, and pedestrians.
• Segment the ground and non-ground points. Input a training sample, then apply the RANSAC algorithm to segment the non-ground points and ground points and obtain ground fitting parameters.
• Points clustering. Utilize the DBSCAN algorithm to cluster non-ground points, thereby obtaining clusters of non-ground points.
• Determine the placement area. Obtain the semantic information of the current scene through Steps 2 and 3, classifying the point cloud into ground and non-ground points. Subsequently, apply the Minimum Bounding Rectangle algorithm to fit the bounding boxes of the non-ground point clusters, acquiring the position and size of the bounding boxes. Using the size and position information, exclude the regions occupied by the bounding boxes from the ground area identified in Step 2, leaving the remaining space as the designated area for placement.
• Construct a new sample. Randomly select the ground truths from the database based on the proportions of different categories appearing in the training dataset. Then, randomly insert ground truths into the designated placement area.
• Collision checking. Check whether the newly placed point cluster collides with the existing point clusters. If a collision is detected, repeat step (5) and then perform the collision check again. If no collision is detected, the enhanced data will be fed into the network for training, and this process ends.

By following the steps above, in a road environment, RS-Aug places ground truths on paved surfaces while avoiding existing objects. Conversely, in non-road environments, ground truths are placed on flat terrain while avoiding the occlusion of existing objects. Benefiting from these measures, RS-Aug ensures that the augmented samples are reasonable.

There are differences between RS-Aug and GT-Aug. As shown in Figure 6a,b, GT-Aug lacks the operations of “Points segmentation”, “Points clustering”, and “Determine the placement area”, which correspond to Steps 2, 3, and 4 mentioned previously. Therefore, RS-Aug can selectively place ground truths into a scene based on the semantic information of the point cloud scene, whereas GT-Aug can only randomly place ground truths into a scene without being able to judge the reasonableness of the placement.

To demonstrate the effects of RS-Aug and the shortcomings of GT-Aug, a comparison is presented based on PointPillars. This comparison is conducted on a single sample from the KITTI 3D object dataset [31]. In this instance, six cyclists and pedestrians are added to the current scene. Figure 7a,b show the image and point cloud of the original scene, respectively. Figure 7c,d illustrate the augmented results. It can be seen that some pedestrians and cyclists (green and blue boxes) have been inserted into the scene. However, as shown in Figure 7c, GT-Aug places some pedestrians and cyclists outside the road (highlighted with black boxes), failing to accurately reflect actual driving scenarios. Consequently, this could lead to incorrect information being utilized during the training. In contrast, RS-Aug can strategically place ground truths onto the drivable road area of the scene while avoiding occlusion among objects. Thus, a reasonable augmentation to the training dataset is achieved.

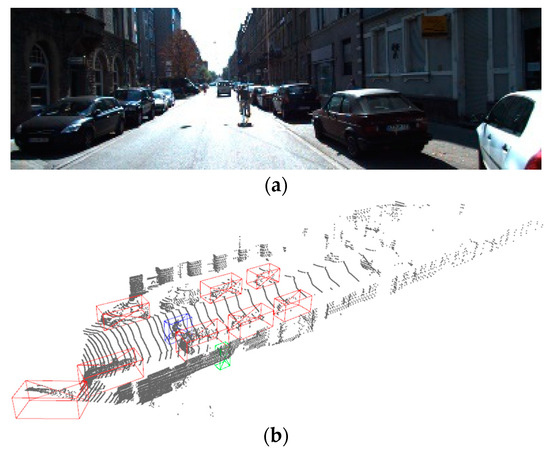
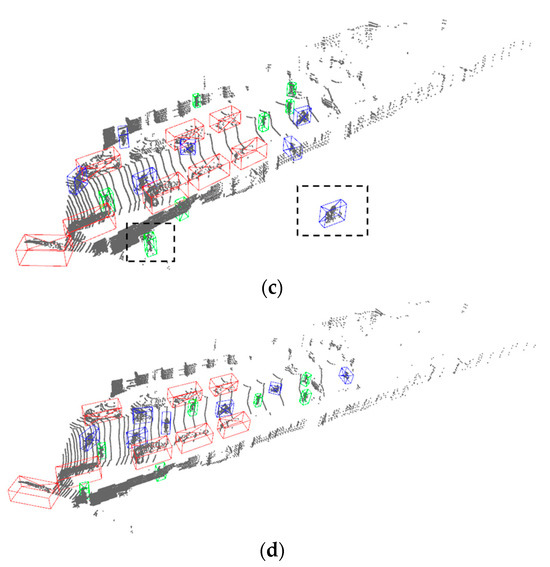
Figure 7. Comparison of visualization results of GT-Aug and RS-Aug: (a) point cloud collection scenarios; (b) ground truth; (c) visualization result of GT-Aug; (d) visualization result of RS-Aug. Cars are represented by red bounding boxes, cyclists by blue bounding boxes, and pedestrians by green bounding boxes.

4. Experiment and Result Analysis

4.1. Experimental Setup

The experiment was initially conducted on the KITTI 3D object dataset: 7481 training samples were divided into a training set containing 3712 samples and a validation set containing 3769 samples. A deep learning server was set up for the experiment, the configuration of which is shown in Table 2.

Table 2. Deep learning server.

Category	Model
CPU	Inter i9 11,900 k
Memory	32 G
Hard disk	512 G + 1 T
GPU	NVIDIA GeForce RTX 3080Ti 12 GB
OS	Ubuntu 18.04 LTS 64 bit
Programming language	Python
Dependency library	CUDA 11.1, CUDNN8.0.5, PyTorch 1.8.1, Open3d 0.13.0, etc.

The training epoch was set to 160 with a batch size of 6. The deep learning optimizer utilizes Adam (Adaptive Moment Estimation) with an initial learning rate of 2 × 10⁻⁴. The learning rate decays by 0.8 times every 15 epochs. Pass-through filtering is used to intercept regions of interest, with a specific range as shown in Equation (12).

$$\begin{array}{c}0\le x\le 69.12\\ -39.68\le y\le 39.68\\ -3\le z\le 1\end{array}$$

(16)

In this approach, the maximum number of pillars (denoted as P) in each sample is set to 12,000, with each pillar containing a maximum of 64 points. If the number of pillars in each sample and the number of points in each pillar exceed the preset threshold, random sampling will be adopted. Conversely, if the number is too small to form a tensor, zero padding will be utilized instead. When calculating the 2D Intersection over Union (IoU) metric, positive matches usually choose the highest values or those marked values that surpass the positive match threshold. Conversely, negative matches consider marked values below the negative threshold. Redundant anchor points are excluded during loss calculation. Following the methodology of VoxelNet [8], our study defines overlap thresholds for the car category at 0.7 IoU across easy, moderate, and hard recognition scenarios. For cyclists and pedestrians, the overlap thresholds are uniformly set at 0.5 IoU across easy, moderate, and hard recognition scenarios.

4.2. Experimental Results

Average Precision (AP) was adopted as the evaluation metric for this study. As demonstrated in Table 3, ASCA-PointPillars outperforms other algorithms in terms of pedestrian recognition accuracy. This highlights the effectiveness of the ASP module and RS-Aug in improving the recognition performance of small objects. Although the recognition accuracy for cars and cyclists may not exceed that of other algorithms, ASCA-PointPillars achieves a higher Frames Per Second (FPS) than all other algorithms (except PointPillars), ensuring real-time recognition. Moreover, ASCA-PointPillars exhibits superior recognition accuracy across all three categories compared to PointPillars, demonstrating its ability to maintain high accuracy in real-time scenarios.

Table 3. Results on the KITTI 3D object dataset (%). NaN indicates that there are no relevant data in the KITTI test benchmark.

Method	FPS	Car			Pedestrian			Cyclist
		Easy	Mod.	Hard	Easy	Mod.	Hard	Easy	Mod.	Hard
ASCA-PointPilars	31	86.51	75.77	69.24	55.24	46.04	43.58	75.63	59.91	55.34
PointPillars	62.5	82.58	74.31	68.99	51.45	41.92	38.89	77.10	58.65	51.92
3DSSD	25	88.36	79.57	74.55	54.64	44.27	40.23	82.48	64.10	56.90
Point-GNN	1.7	88.33	79.47	72.29	51.92	43.77	40.14	78.60	63.48	57.08
Voxel R-CNN	25	90.90	81.62	77.06	NaN	NaN	NaN	NaN	NaN	NaN
PV-RCNN	12.5	90.25	81.43	76.82	52.17	43.29	40.29	78.60	63.71	57.65
PDV	10	90.43	81.86	77.36	47.80	40.56	38.46	83.04	67.81	60.46

ASCA-PointPillars was also implemented on NVIDIA Xavier AGX, an edge computing device, and achieved a frame rate of 21.82 FPS. This demonstrates that the proposed algorithm can provide real-time recognition capabilities in vehicle terminals.

Table 4 shows the recognition results of PointPillars and the proposed ASCA-PointPillars on objects at two distance ranges in the KITTI dataset, using mean Average Precision (mAP) as the evaluation metric. As can be seen from the table, the recognition accuracy of both algorithms inevitably decreases as the distance increases. However, compared to PointPillars, the proposed ASCA-PointPillars exhibits a higher recognition accuracy for objects at longer distances. Specifically, it achieves accuracy improvements of 2.94% and 3.02% in the ranges of 0–40 m and 40–80 m, respectively. This demonstrates that the proposed ASP module can effectively enhance the recognition accuracy of objects at long distances.

Table 4. Distance-wise recognition results on the KITTI 3D object validation dataset (%).

Method	0–40 m	40–80 m
PointPillars	71.48	51.33
ASCA-PointPillars	74.42	54.35

Figure 8 offers a qualitative analysis of the recognition results, with cars represented by red bounding boxes, cyclists by blue bounding boxes, and pedestrians by green bounding boxes. As shown in Figure 8c,d, the recognition results clearly show that while PointPillars may fail to detect distant objects, ASCA-PointPillars can accurately recognize certain severely occluded or sparse objects at a distance. Only a few distant objects and those with excessively sparse point clouds remain undetected.

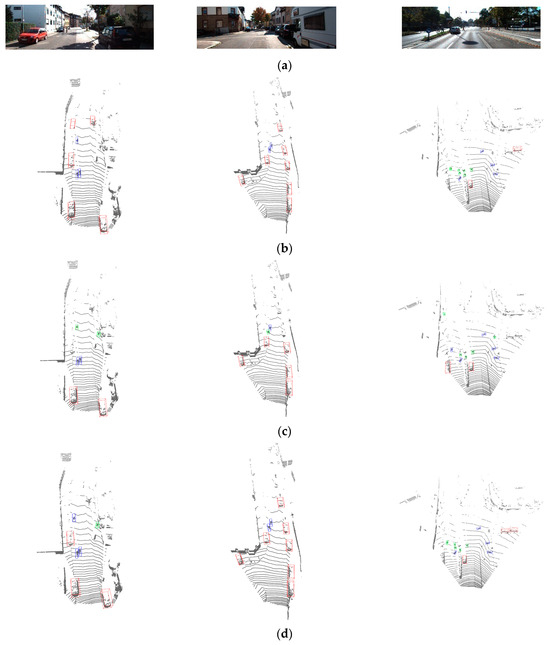
Figure 8. Visualization of recognition results for PointPillars and ASCA-PointPillars: (a) scene; (b) ground truth; (c) prediction of PointPillars; (d) prediction of ASCA-Pointpillars. Cars are represented by red bounding boxes, cyclists by blue bounding boxes, and pedestrians by green bounding boxes.

As shown in Figure 9, in order to demonstrate the effectiveness of RS-Aug, this article compares the PointPillars of GT-Aug and RS-Aug, respectively. Red bounding boxes represent cars, blue bounding boxes represent cyclists, and green bounding boxes represent pedestrians. From Figure 9c, it is evident that the PointPillars using GT-Aug exhibit some misdetections (in the red boxes) and missed detections in certain scenarios. Conversely, as shown in Figure 9d, the PointPillars based on RS-Aug demonstrate superior performance in detecting pedestrians and cyclists with sparse and fewer surface point clouds, effectively reducing the instances of missed detections.

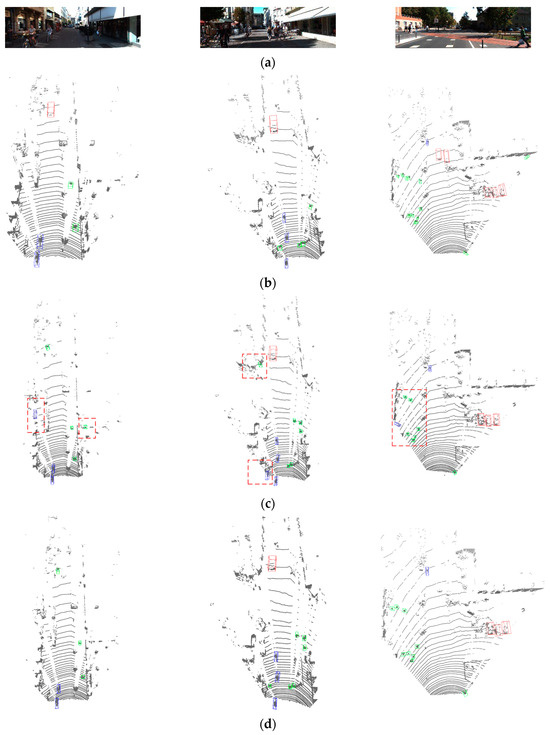
Figure 9. Recognition results of PointPillars using different data augmentation algorithms: (a) scene; (b) ground truth; (c) prediction of GT-Aug-PointPillars; (d) prediction of RS-Aug-PointPillars. Cars are represented by red bounding boxes, cyclists by blue bounding boxes, and pedestrians by green bounding boxes.

4.3. Ablation Experiment

This section analyzes the impact of each component on recognition accuracy in the KITTI 3D object validation dataset. The replication results of PointPillars on the validation dataset are taken as the baseline. As shown in Table 5, the average recognition accuracy under three levels of difficulty for cars, pedestrians, and cyclists improved by 1.14%, 0.96%, and 1.2%, respectively, after implementing the ASP module. This suggests that multi-scale pillar sampling is effective for recognizing small and distant objects. After implementing the CPA module, the average recognition accuracy for the three categories increased by 3.03%, 2.09%, and 2.74%, respectively. This indicates that the CPA module can effectively strengthen the feature correlation of point clouds in each pillar, enabling the network to learn richer contextual features, and thereby improving recognition accuracy. When combining these two modules, ASCA-PointPillars achieved an average improvement of 4.23%, 3.1%, and 3.58% in the three categories, respectively, achieving the highest average recognition accuracy for the car category. This demonstrates the effectiveness of the ASP and CPA modules. Using the RS-Aug algorithm alone increased the average recognition accuracy of the three categories by 2.59%, 2.49%, and 2.96%. When ASCA-PointPillars was combined with RS-Aug, it achieved the highest average recognition accuracy for pedestrians and cyclists, with improvements of 4.09%, 5.08%, and 5.07% in the three categories, respectively. This shows that RS-Aug can effectively improve the recognition performance of categories that have fewer instances in a dataset.

Table 5. The effect of each component on accuracy (%). “√” indicates that the component is used.

ASP	CPA	RS-Aug	GT-Aug	Car			Pedestrian			Cyclist
				Easy	Mod.	Hard	Easy	Mod.	Hard	Easy	Mod.	Hard
				81.85	72.28	67.27	50.82	41.48	38.47	76.33	56.23	50.97
			√	83.17	73.59	69.12	51.79	42.13	39.24	77.28	58.43	52.07
		√		83.83	74.3	69.65	53.57	43.64	40.12	79.07	58.43	53.5
√				83.32	73.33	68.18	52.14	42.35	39.17	77.84	57.86	51.43
	√			85.67	75.58	69.24	53.22	43.55	40.26	79.66	58.87	53.22
√	√			86.85	76.89	70.34	54.07	44.61	41.38	80.45	60.02	53.79
√	√	√		86.46	76.63	70.58	56.76	46.56	42.69	82.21	61.28	55.25

5. Conclusions

This study introduces ASCA-PointPillars, a novel object recognition algorithm. The algorithm leverages an ASP module sampling point clouds with multi-scale pillars to mitigate the spatial information loss typically associated with single-scale pillar sampling. Furthermore, a CPA module is proposed to establish interconnections among points within the same pillars. To address the issue of the imbalanced distribution of various categories in a dataset, an RS-Aug algorithm is also proposed. The experimental results show that the proposed ASCA-PointPillars can effectively improve the recognition performance of distant and smaller objects, and the proposed RS-Aug algorithm can effectively improve the recognition performance of categories that have fewer instances in a dataset. The recognition accuracy of ASCA-PointPillars for pedestrians exceeds that of other comparison algorithms, demonstrating its advantage in identifying small objects. However, the recognition accuracy of the algorithm for cars and cyclists does not reach the highest level. This may be because encoding point clouds of larger objects such as cars and cyclists into pillars leads to greater information loss. Therefore, future efforts will continue to focus on implementing measures to reduce information loss during the encoding process for large objects.